MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
Trabajamos con matrices y vectores en MQL5

Trabajamos con matrices y vectores en MQL5

MetaTrader 5 — Ejemplos | 3 octubre 2022, 09:52
765 1
MetaQuotes
MetaQuotes

Para resolver una amplia clase de problemas matemáticos, el lenguaje MQL5 dispone ahora de tipos especiales de datos: matrices y vectores. Los nuevos tipos tienen métodos incorporados para escribir un código conciso y fácilmente comprensible que se acerque a una notación matemática. En este artículo, haremos una breve descripción de los métodos incorporados de la sección de ayuda "Métodos de matrices y vectores".


Contenido


En todos los lenguajes de programación existen tipos de datos como los arrays, que permiten almacenar conjuntos de tipos numéricos: int, double, etcétera. El acceso a los elementos de los arrays se realiza por índices, lo cual permite realizar operaciones en los arrays usando ciclos. Los arrays unidimensionales y bidimensionales son los más utilizados:

int    a[50];       // Array unidimensional de 50 números enteros
double m[7][50];    // Array bidimensional de 7 subarrays, cada uno de los cuales consta de 50 números
MyTime t[100];      // Array que contiene elementos del tipo MyTime

Para tareas de almacenamiento y procesamiento de datos relativamente sencillas, los arrays suelen ser suficientes, pero cuando se trata de problemas matemáticos complejos, el gran número de ciclos anidados hace que tratar con arrays sea un reto, tanto en términos de programación como de lectura de código. Incluso las operaciones de álgebra lineal más simples exigen mucho código y una buena comprensión de las matemáticas.

Las tecnologías de datos modernas, como el aprendizaje automático, las redes neuronales y los gráficos en 3D, usan ampliamente las soluciones a los problemas del álgebra lineal que aplican los conceptos de vectores y matrices. Por eso se han añadido a MQL5 nuevos tipos de datos, las matrices y vectores, para trabajar de forma nativa con dichos objetos. Esto nos ahorrará mucha programación rutinaria y mejorará la calidad del código.


Tipos de matrices y vectores

En resumen, un vector es un array unidimensional de tipo double, y una matriz es un array bidimensional de tipo double. Los vectores pueden ser verticales y horizontales, pero en MQL5 no están separados.

Las matrices pueden representarse como un array de vectores horizontales, donde el primer índice de la matriz indica el número de fila, mientras que el segundo índice indica el número de columna.


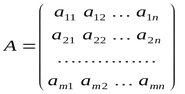
Lo único es que la numeración de las filas y las columnas, a diferencia del álgebra lineal, comienza desde cero, como en los arrays.

Además de los tipos matrix y vector, que contienen el tipo de datos double, existen otros 4 tipos para trabajar con los tipos de datos correspondientes:

  • matrixf — es una matriz que contiene elementos de tipo float
  • matrixc — es una matriz que contiene elementos de tipo complex
  • vectorf — es un vector que contiene elementos de tipo float
  • vectorc — es un vector que contiene elementos de tipo complex

Al momento de escribir este artículo, los tipos matrixc y vectorc están todavía en desarrollo y no pueden usarse aún en los métodos incorporados.

Para su uso en las funciones de plantilla, podemos utilizar la notación matrix<double>, matrix<float>, matrix<complex>, vector<double>, vector<float>, vector<complex> en lugar de los tipos correspondientes.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */


Creación e inicialización

Los métodos de matrices y vectores se dividen en nueve categorías según su finalidad. Existen varias formas de declarar e inicializar matrices y vectores.

El método de creación más sencillo es declarar sin especificar un tamaño, es decir, sin asignar memoria a los datos. Simplemente deberemos escribir el tipo de datos y el nombre de la variable:

  matrix         matrix_a;   // matriz del tipo double
  matrix<double> matrix_a1;  // otra forma de declarar una matriz double adecuada para usar en plantillas
  matrix<float>  matrix_a3;  // matriz de tipo float
  vector         vector_a;   // vector del tipo double
  vector<double> vector_a1;  // otra entrada para crear un vector del tipo double 
  vector<float>  vector_a3;  // vector del tipo float

A continuación, podremos cambiar el tamaño de los objetos creados y rellenarlos con los valores deseados. También podremos utilizarlos en los métodos matriciales incorporados para obtener los resultados de los cálculos.

Es posible declarar una matriz o vector indicando además el tamaño, es decir, asignando la memoria para los datos, pero sin ninguna inicialización. Para ello, especificaremos el tamaño(s) entre paréntesis después del nombre de la variable:

  matrix         matrix_a(128,128);           // en calidad de parámetros, podemos usar tanto constantes,
  matrix<double> matrix_a1(InpRows,InpCols);  // como variables
  matrix<float>  matrix_a3(InpRows,1);        // análogo del vector vertical
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float>  vector_a3(InpSize+16);       // como parámetro, podemos utilizar una expresión

La tercera forma de crear objetos es usando una declaración con inicialización. En este caso, las dimensiones de las matrices y vectores vendrán determinadas por la secuencia de inicialización indicada entre corchetes:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // deben ser matrices del mismo tipo
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                     // deben ser vectores del mismo tipo


También existen métodos estáticos para crear matrices y vectores de un tamaño determinado y con una inicialización determinada:  

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Además, existen métodos no estáticos para inicializar una matriz/vector con los valores Init y Fill establecidos:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

En este ejemplo, hemos utilizado el método Init para cambiar el tamaño de una matriz ya inicializada, lo cual hace que los nuevos elementos se rellenen con valores aleatorios.

Una ventaja importante del método Init es la posibilidad de especificar una función de inicialización en los parámetros para rellenar los elementos de la matriz/vector de acuerdo con una ley determinada. Por ejemplo:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Resultado de la ejecución
  init = 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Rellena la matriz con grados de un número                        |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 }


Copiando matrices y matrices

El método Copy se usa para copiar matrices y vectores, pero hay una forma más sencilla y familiar de copiar, con la ayuda del operador de asignación "=". También existe el método Assign.

//--- copiado de matrices
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

La diferencia entre el método Assign y el método Copy es que este último permite copiar arrays además de matrices. El siguiente ejemplo muestra cómo se copia un array de tipo entero int_arr en una matriz de tipo double. La matriz resultante se ajusta automáticamente al tamaño del array copiado. 

//--- copiado de un array en una matriz
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

Así, el método Assign permite una transición fluida en el código de arrays a matrices con conversiones automáticas de tamaño y tipo.


Copiando series temporales a una matriz o vector

El análisis de los gráficos de precios requiere la obtención y el procesamiento de los arrays de las estructuras MqlRates correspondientes, pero ahora hay otra forma de trabajar con ellos.

El método CopyRates copia las series históricas de la estructura MqlRates directamente en una matriz o vector. No tendremos que recuperar las series temporales necesarias usando las funciones de "Acceso a las series temporales e indicadores" en las matrices correspondientes. Además, ahora no será necesario trasponerlas a una matriz o vector. Las cotizaciones se pueden obtener en una matriz o vector en una sola llamada. Vamos a mostrar con un ejemplo cómo calcular la matriz de correlación para una lista de símbolos; para ello, calcularemos estos valores de dos maneras y compararemos los resultados.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- lista de símbolos para el cálculo
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- matrices y vectores para obtener los precios Close
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- obtenemos los precios Close en el vector
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- pegamos un vector en la matriz de series temporales
      rates.Col(close, i);
      PrintFormat("%d. %s: %d precios Close añadidos a la matriz", i+1, symbols[i], close.Size());
      //--- mostramos para la depuración los 20 primeros valores del vector
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 precios Close añadidos a la matriz
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 precios Close añadidos a la matriz
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 precios Close añadidos a la matriz
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 precios Close añadidos a la matriz
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 precios Close añadidos a la matriz
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- preparamos una matriz de correlaciones entre los símbolos
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Calculamos los coeficientes de correlación por pares");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Matriz de correlaciones en los vectores: \n", corr_from_vector);
  /*
  Calculamos los coeficientes de correlación por pares
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0.397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0.744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Matriz de correlaciones en los vectores
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- ahora mostramos cómo calcular una matriz de correlaciones en una misma línea
  matrix corr_from_matrix=rates.CorrCoef(false);   // false indica que los vectores se encuentran en las columnas de la matriz
  Print("Matriz de correlaciones rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- comparamos si las matrices obtenidas divergen
  Print("¿Cuántos errores de divergencia hay entre las matrices de resultados?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Matriz de correlaciones rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  ¿Cuántos errores de divergencia hay entre las matrices de resultados?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- mostramos la matriz de correlaciones de una forma bonita
  Print("Mostramos la matriz de correlaciones con encabezados");
  string header="        ";  // encabezado
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- ahora, las líneas
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Mostramos la matriz de correlaciones con encabezados
            EURUSD  GBPUSD  USDJPY  USDCAD  USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Retorna una línea con los valores del vector                     |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- componemos la línea
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- añadimos una cola si la longitud del vector supera el tamaño establecido
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//|  Retorna una línea con el número indicado de espacios            |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

El ejemplo muestra cómo podemos:

    • Obtener los precios de cierre utilizando CopyRates
    • insertar un vector en la matriz usando el método Col
    • calcular el coeficiente de correlación entre los dos vectores usando CorrCoef
    • utilizar CorrCoef para calcular una matriz de correlación sobre una matriz con vectores de valores
    • convertir una matriz a una forma triangular superior usando el método TriU
    • comparar 2 matrices sobre su divergencia usando Compare


      Operaciones con matrices y vectores

      Las operaciones matemáticas -suma, resta, multiplicación y división- pueden realizarse sobre matrices y vectores, elemento a elemento. Para ello, ambos objetos deberán ser del mismo tipo y tener el mismo tamaño. Cada miembro de la matriz/vector opera con el elemento correspondiente de una segunda matriz/vector.

      Como segundo término (multiplicador, sustraendo o divisor) también podemos utilizar un escalar del tipo correspondiente (double, float o complex). En este caso, cada elemento de la matriz o vector operará con el escalar indicado.

        matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // producto de Hadamard (Hadamard product) 
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- las operaciones en el lugar son posibles
  matrix_a+=matrix_b;
  matrix_a/=2;

      Además, las matrices y los vectores pueden transmitirse como parámetros a la mayoría de las funciones matemáticas, incluyendo MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. En este caso, la matriz o el vector se procesarán por elementos. Ejemplo

      //---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

      En el caso de MathMod y MathPow, el segundo parámetro podrá ser tanto un escalar, como una matriz o vector del tamaño correspondiente. 

         matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }


      Manipulaciones

      Al trabajar con matrices y vectores, podemos realizar una manipulación básica sin necesidad de hacer ningún cálculo:

      • transposición
      • extracción de filas, columnas y diagonales
      • cambiar el tamaño y la forma de la matriz
      • reordenar las filas y columnas indicadas
      • copiar en un nuevo objeto
      • comparación de dos objetos
      • dividir una matriz en varias submatrices
      • clasificación
      Ejemplo de transposición con el método Transpose:
        matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

      Algunos ejemplos sobre cómo establecer y extraer diagonales con el método Diag:

         vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

      Cambio del tamaño de una matriz utilizando el método Reshape:

         matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

      Ejemplos de partición vertical de una matriz usando el método Vsplit:

         matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

      Los métodos Col y Row no solo permiten obtener los elementos correspondientes de la matriz, sino también insertar elementos en matrices no asignadas, es decir, matrices sin tamaños definidos. Veámoslo en un ejemplo:

         vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("col 1 - ",m2.Col(1));
  /*
   col 1 - [8,8,8,8]
  */

   Print("col 2 - ",m2.Col(2));
  /*
   col 1 - [8,8,8,8]  col 2 - [1,2,3,8]
  */


      Productos

      La multiplicación de matrices es uno de los algoritmos básicos que se usan ampliamente en diversos métodos numéricos. Muchas implementaciones de la propagación de señales hacia adelante y hacia atrás en las capas de las redes neuronales convolucionales se basan en esta operación. A menudo, hasta el 90-95% del tiempo total dedicado al aprendizaje automático se emplea en esta operación. Todos los métodos de productos se pueden encontrar en la sección de la ayuda "Productos de matrices y vectores".

      Aquí tenemos un ejemplo del producto matricial de dos matrices usando el método MatMul:

         matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

      Este sería un ejemplo del producto de Kronecker para dos matrices, así como una matriz y un vector con el método Kron:

         matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

      Más ejemplos del artículo "Matrices y vectores en MQL5":

      //--- inicializamos las matrices
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Producto del vector horizontal v[3] por la matriz m[3,5]");
   vector v3 = {1,2,3};
   Print("A la izquierda v3 = ",v3);
   Print("A la derecha m35 = \n",m35);
   Print("v3.MatMul(m35) = vector horizontal v[5] \n",v3.MatMul(m35));
   /*
   1. Producto del vector horizontal v[3] por la matriz m[3,5]
   A la izquierda v3 = [1,2,3]
   A la derecha m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = vector horizontal v[5]
   [40,46,52,58,64]
   */

//--- mostramos que este es realmente un vector horizontal
   Print("\n2. Producto de la matriz m[1,3] por la matriz m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("A la izquierda m13 = \n",m13);
   Print("A la derecha m35 = \n",m35);
   Print("m13.MatMul(m35) = matriz m[1,5] \n",m13.MatMul(m35));
   /*
   2. Producto de la matriz m[1,3] por la matriz m[3,5]
   A la izquierda m13 =
   [[1,2,3]]
   A la derecha m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = matriz m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Producto de la matriz m[3,5] por el vector vertical v[5]");
   vector v5 = {1,2,3,4,5};
   Print("A la izquierda m35 = \n",m35);
   Print("A la derecha v5 = ",v5);
   Print("m35.MatMul(v5) = vector vertical v[3] \n",m35.MatMul(v5));
   /*
   3. Producto de la matriz m[3,5] por el vector vertical v[5]
   A la izquierda m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   A la derecha v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vector vertical v[3]
   [40,115,190]
   */

//--- mostramos que este es realmente un vector vertical
   Print("\n4. Producto de la matriz m[3,5] por la matriz m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("A la izquierda m35 = \n",m35);
   Print("A la derecha m51 = \n",m51);
   Print("m35.MatMul(m51) = matriz v[3] \n",m35.MatMul(m51));
   /*
   4. Producto de la matriz m[3,5] por la matriz m[5,1]
   A la izquierda m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   A la derecha m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = matriz v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Producto de la matriz m[3,5] por la matriz m[5,2]");
   Print("A la izquierda m35 = \n",m35);
   Print("A la derecha m52 = \n",m52);
   Print("m35.MatMul(m52) = matriz m[3,2] \n",m35.MatMul(m52));
   /*
   5. Producto de la matriz m[3,5] por la matriz m[5,2]
   A la izquierda m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   A la derecha m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = matriz m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Producto del vector horizontal v[5] por la matriz m[5,2]");
   Print("A la izquierda v5 = \n",v5);
   Print("A la derecha m52 = \n",m52);
   Print("v5.MatMul(m52) = vector horizontal v[2] \n",v5.MatMul(m52));
   /*
   6. Producto del vector horizontal v[5] por la matriz m[5,2]
   A la izquierda v5 =
   [1,2,3,4,5]
   A la derecha m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = vector horizontal v[2]
   [80,95]
   */

   Print("\n7. Producto de Outer() del vector horizontal v[5] por el vector vertical v[3]");
   Print("A la izquierda v5 = \n",v5);
   Print("A la derecha v3 = \n",v3);
   Print("v5.Outer(v3) = matriz m[5,3] \n",v5.Outer(v3));
   /*
   7. Producto de Outer() del vector horizontal v[5] por el vector vertical v[3]
   A la izquierda v5 =
   [1,2,3,4,5]
   A la derecha v3 =
   [1,2,3]
   v5.Outer(v3) = matriz m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */


      Transformaciones

      Las transformaciones de matrices son las operaciones más populares al trabajar con datos. Dicho esto, muchas operaciones matriciales complejas no pueden resolverse de forma eficiente o con estabilidad usando la limitada precisión de las computadoras.

      Las transformaciones de matrices (o descomposiciones, en otras palabras) son métodos que reducen una matriz a sus partes componentes, lo cual facilita el cálculo de operaciones matriciales más complejas. Los métodos de descomposición de matrices, también llamados métodos de factorización de matrices, son la base del álgebra lineal en las computadoras, incluso para operaciones básicas como la resolución de sistemas de ecuaciones lineales, el cálculo de la inversa y el cálculo del determinante de una matriz.

      En el aprendizaje automático, la descomposición de valores singulares (Singular Values Decomposition, SVD) se utiliza ampliamente para representar una matriz fuente como el producto de otras tres matrices. La descomposición SVD se usa en aplicaciones que van desde la aproximación por mínimos cuadrados hasta la compresión y el reconocimiento de imágenes.

      Veamos un ejemplo de descomposición singular con el método SVD:

        matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- hacemos la descomposición SVD
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// bloque de verificación
//--- U * singular diagonal * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- una verificación más
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

      Otra transformación comúnmente usada es la descomposición de Cholesky, que puede aplicarse para resolver un sistema de ecuaciones lineales Ax=b si la matriz A es simétrica y está definida positivamente.

      En MQL5, la descomposición de Cholesky se realiza con el método Cholesky: 

        matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

      La lista de métodos disponibles se muestra en la tabla a continuación:

      Función

      Acción

      Cholesky

      Calcula la descomposición de Cholecki

      Eig

      Calcula los valores propios y los vectores propios derechos de una matriz cuadrada

      EigVals

      Calcula los valores propios de una matriz general

      LU

      Realiza una factorización LU de una matriz como el producto de una matriz triangular inferior y una matriz triangular superior

      LUP

      Realiza una factorización LUP con rotación parcial, que es una factorización LU con permutaciones solo de cadenas: PA=LU

      QR

      Calcula la factorización qr de la matriz

      SVD

      Calcula la descomposición del valor singular

      Obtención de estadísticas

        Para obtener estadísticas descriptivas de las matrices y vectores, se han previsto los métodos de la sección "Estadísticas". Estos hacen posible obtener:
        • los valores máximos y mínimos y sus índices en la matriz/vector
        • la suma y el producto de los elementos, así como la suma y el producto acumulados
        • la mediana, la media, la media aritmética y la media aritmética ponderada de los valores de la matriz/vector
        • la desviación típica y la varianza de los elementos
        • los percentiles y los cuantiles
        • la métrica de regresión como el error de desviación de la línea de regresión construida en la matriz de datos especificada

          Ejemplo de cálculo de la desviación estándar con el método Std:

             matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

          Ejemplo de cálculo de cuantiles mediante el método Quantile:

             matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */


          Características de las matrices

          Los métodos del apartado "Características" permiten obtener los siguientes valores:

          • el número de filas y columnas de la matriz
          • la norma y el número de la condicionalidad
          • el determinante, el rango, la traza y el espectro de la matriz

          Ejemplo de cálculo del rango de una matriz usando el método Rank:

            matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // déficit de la matriz
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 dimensionalidad - rango 1, a no ser que todos sean "0"
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

          Ejemplo de cálculo de la norma de una matriz usando el método Norm:

            matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */


          Resolviendo ecuaciones

          En los problemas de aprendizaje automático y optimización, con frecuencia resulta necesario encontrar una solución a un sistema de ecuaciones lineales. El apartado "Soluciones" contiene 4 métodos que nos permiten resolver dichas ecuaciones según el tipo de matriz. 

          Función

          Acción

          Solve

          Resuelve una ecuación matricial lineal o un sistema de ecuaciones algebraicas lineales

          LstSq

          Resuelve un sistema de ecuaciones algebraicas lineales de forma aproximada (para matrices no cuadradas o degeneradas)

          Inv

          Calcula una matriz multiplicativa inversa con respecto a una matriz cuadrada no degenerada mediante el método de Jordan-Gauss

          PInv

          Calcula la matriz pseudoinversa usando el método de Moore-Penrose

          Vamos a analizar un ejemplo de resolución de la ecuación A*x=b.  


          Debemos encontrar un vector de soluciones x. La matriz A no es cuadrada y, por tanto, el método Solve no resulta adecuado en este caso. 

          Aquí usaremos el método LstSq, que está diseñado para la resolución aproximada de matrices no cuadradas o degeneradas. 

             matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- solucionamos el sistema A*x = b
   vector x=a.LstSq(b);
//--- comprobamos la solución, x debe ser igual a [5, -4]
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- comprobamos A*x = b1, el vector obtenido debe ser igual a [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

          La comprobación muestra que el vector x encontrado es la solución de este sistema de ecuaciones.


          Métodos de aprendizaje automático

          Para las matrices y vectores, se ofrecen 3 métodos de uso en el aprendizaje automático.

          Función

          Acción

          Activation

          Calcula los valores de la función de activación y los escribe en el vector/matriz transmitido

          Derivative

          Calcula los valores de la derivada de la función de activación y los escribe en el vector/matriz transmitido

          Loss

          Calcula los valores de la función de pérdida y los escribe en el vector/matriz transmitido

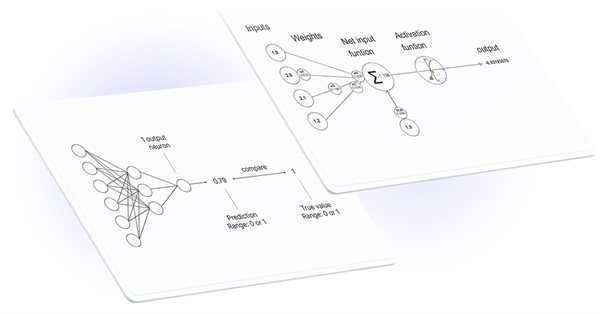
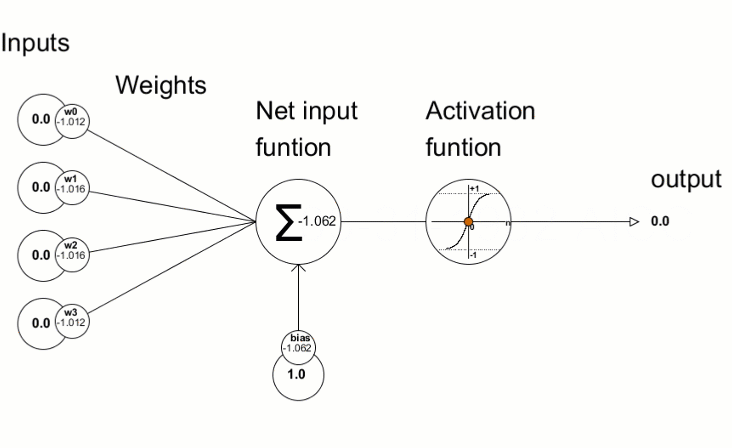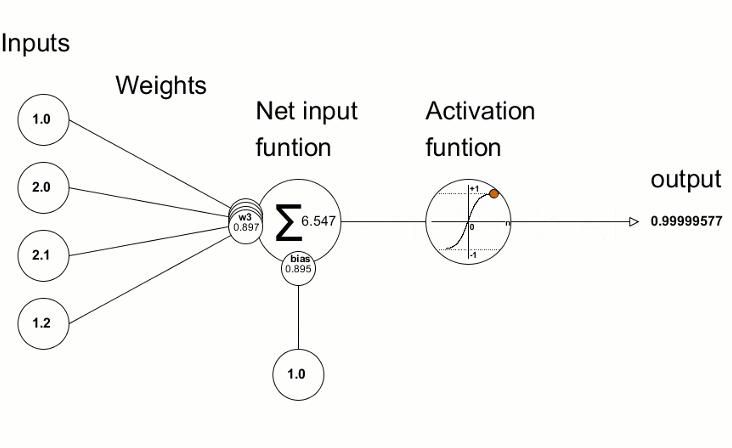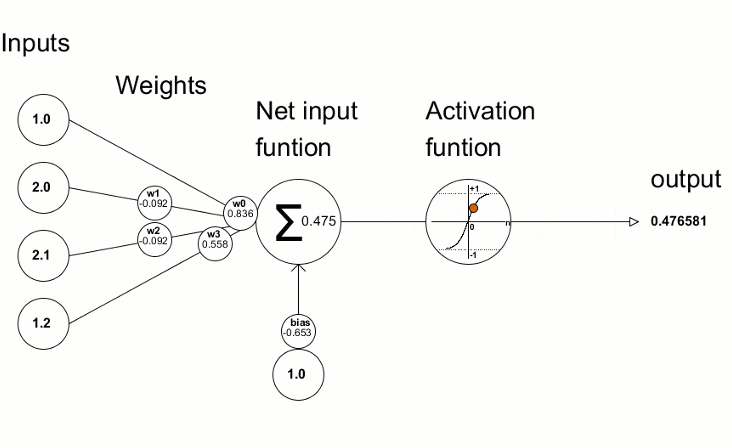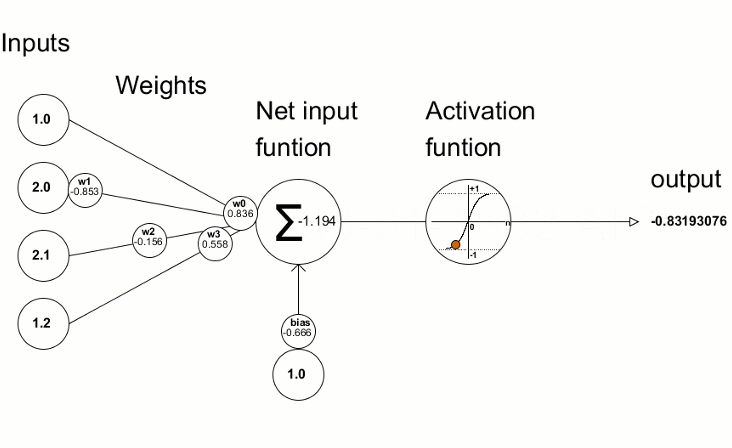
          Las funciones de activación se usan en las redes neuronales para producir un valor de salida según el resultado de la suma ponderada de las entradas. La elección de la función de activación tiene un gran impacto en las capacidades y el rendimiento de la red neuronal.


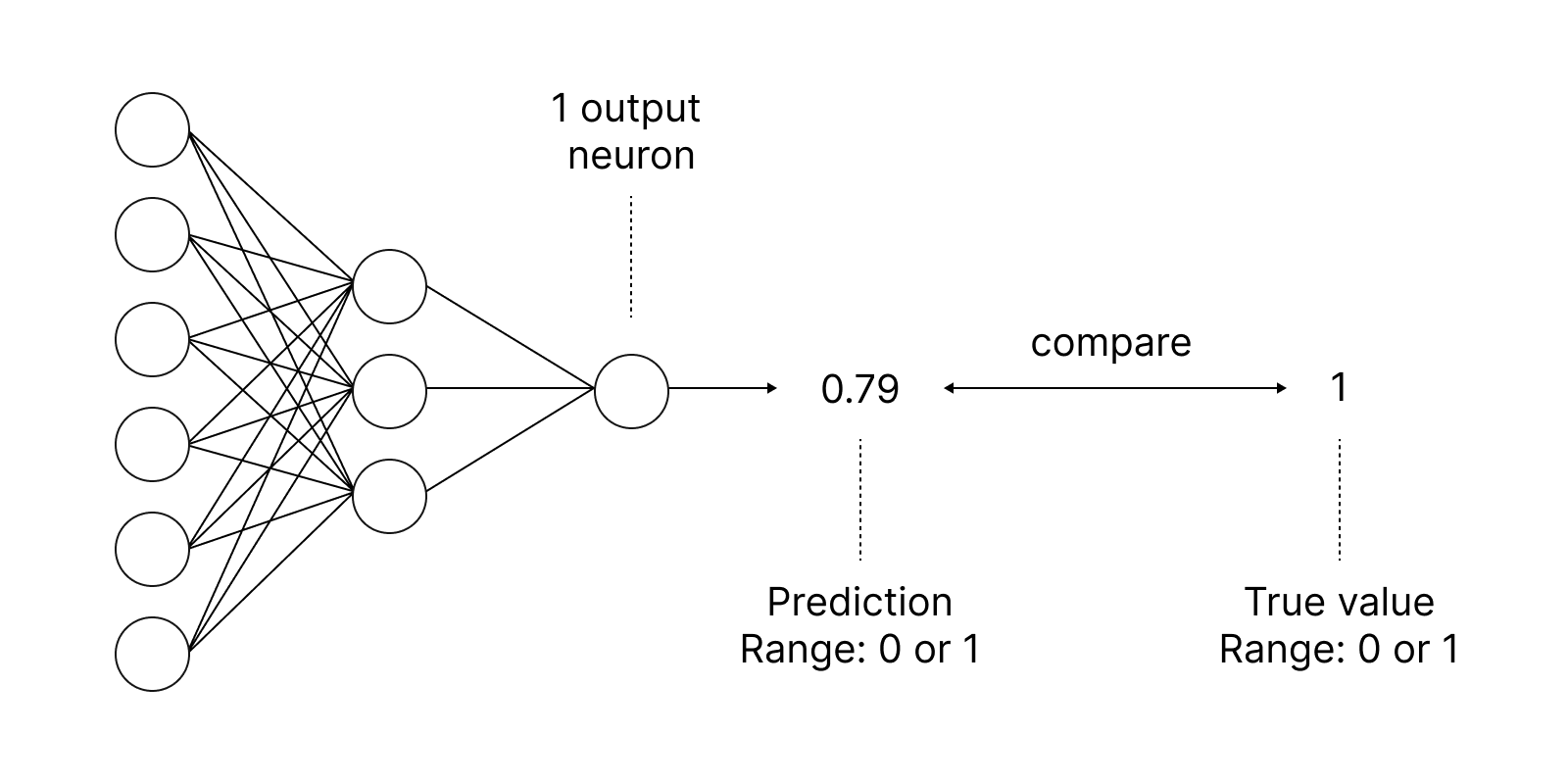
          La función de activación más célebre es la sigmoidea.



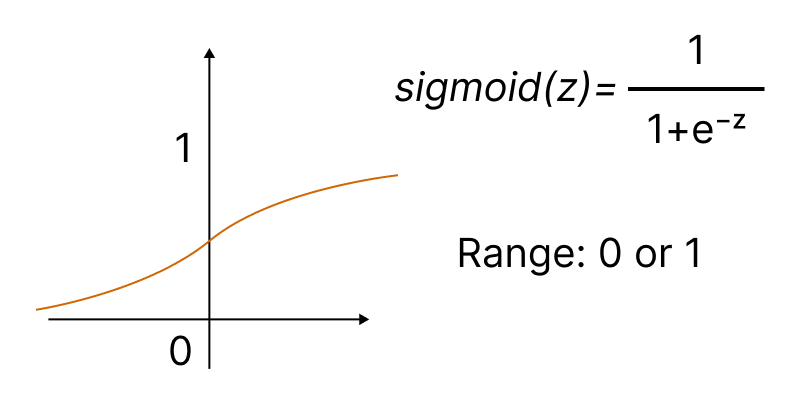
          El método incorporado Activation, con la ayuda de la enumeración ENUM_ACTIVATION_FUNCTION, permite establecer una de las quince funciones de activación.

          Identificador

          Descripción

          AF_ELU                      

          Unidad lineal exponencial

          AF_EXP                      

          Exponencial

          AF_GELU                      

          Unidad lineal de error de Gauss

          AF_HARD_SIGMOID              

          Sigmoide duro

          AF_LINEAR                    

          Lineal

          AF_LRELU                    

          Rectificador lineal con «fugas» (Leaky ReLU)

          AF_RELU                      

          Transformación Lineal Rectificada ReLU

          AF_SELU                      

          Función lineal exponencial escalada (ELU escalada)

          AF_SIGMOID                  

          Sigmoide

          AF_SOFTMAX                  

          Softmax

          AF_SOFTPLUS                  

          Softplus

          AF_SOFTSIGN                  

          Softsign

          AF_SWISH                    

          Función Swish

          AF_TANH                      

          Tangente hiperbólica

          AF_TRELU                    

          Rectificador lineal con umbral


          El entrenamiento de una red neuronal consiste en encontrar un algoritmo que minimice el error en la muestra de entrenamiento, usando la función de pérdida. Para calcular la desviación, se usa el método Loss, que permite especificar uno de los tipos de enumeración ENUM_LOSS_FUNCTION.

          Los valores de desviación resultantes se usan para perfeccionar los parámetros de la red neuronal: esto se logra con la ayuda del método Derivative, que calcula los valores derivados de la función de activación y los escribe en el vector/matriz transmitido. Podemos visualizar el proceso de aprendizaje de la red con la animación del artículo "Programamos una red neuronal profunda desde cero usando el lenguaje MQL".



          Mejoras en OpenCL

          También hemos añadido soporte para matrices y vectores a las funciones CLBufferWrite y CLBufferRead. Para estas funciones han aparecido las sobrecargas correspondientes, por ejemplo, para la matriz:

          Escribe los valores de la matriz en el buffer y retorna true si tiene éxito.

          uint  CLBufferWrite(
   int           buffer,                    // manejador en el búfer OpenCL
   uint          buffer_offset,             // desplazamiento en el búfer OpenCL en bytes
   matrix<T>     &mat                       // matriz de valores para escribir en el búfer
   );

          Lee el buffer OpenCL en la matriz y retorna true si tiene éxito.

          uint  CLBufferRead(
   int           buffer,                    // manejador en el búfer OpenCL
   uint          buffer_offset,             // desplazamiento en el búfer OpenCL en bytes
   const matrix& mat,                       // matriz para obtener los valores  del búfer
   ulong         rows=-1,                   // número de líneas en la matriz
   ulong         cols=-1                    // número de columnas en la matriz
   );

          Vamos a mostrar el uso de las nuevas sobrecargas usando el ejemplo del producto matricial de dos matrices. Realizaremos los cálculos utilizando tres métodos:

            • un método ingenuo que ilustra el propio algoritmo de multiplicación de matrices
            • el método integrado MatMul
            • la computación paralela en OpenCL

              Las matrices resultantes se comprueban mediante el método Compare, que compara los elementos de las dos matrices con una precisión determinada.

              #define M       3000      // número de líneas en la primera matriz
#define K       2000      // el número de columnas en la primera matriz es igual al número de líneas en la segunda
#define N       3000      // número de columnas en la segunda matriz
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- inicializamos el generador de números aleatorios
  MathSrand((int)TimeCurrent());
//--- rellenamos la matriz del tamaño indicado con valores aleatorios
  matrixf mat1(M, K, MatrixRandom) ;    // primera matriz
  matrixf mat2(K, N, MatrixRandom);     // segunda matriz
 
//--- calculamos el producto de las matrices de forma ingenua
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// aquí escribimos el resultado de la multiplicación de las dos matrices
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- calculamos el producto de las matrices usando MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- calculamos el producto de las matrices en OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // manejador de contexto
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL no se ha encontrado, salimos");
    return;
   }
  int cl_prg;             // manejador del programa 
  int cl_krn;             // manejador del kernel
  int cl_mem_in1;         // manejador del primer búfer (de entrada)
  int cl_mem_in2;         // manejador del segundo búfer (de entrada)
  int cl_mem_out;         // manejador del tercer búfer (de salida)
//--- creamos el programa y el kernel
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- creamos los tres búferes para las tres matrices
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- la tercera matriz es de salida
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- establecemos los argumentos del kernel
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- escribimos las matrices en los búferes del dispositivo
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- iniciando el tiempo de ejecución del código de OpenCL
  start=GetTickCount();
//--- establecemos los parámetros del espacio de trabajo de la tarea y ejecutamos el programa de OpenCL
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- calculamos el resultado en la matriz
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Se ha leído la matriz [%d x %d] ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Comparamos el tiempo de cálculo con cada método");
  PrintFormat("Naive product time = %d ms",time_naive);
  PrintFormat("MatMul product time = %d ms",time_matmul);
  PrintFormat("OpenCl product time = %d ms",time_opencl);  
//--- liberamos todos los contextos de OpenCL
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- comparamos entre sí todas las matrices de resultados obtenidas 
  Print("¿Cuántos errores de divergencia hay entre las matrices de resultados?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Resultado: 
   
   Leída la matriz [3000 x 3000] 
   Comparamos el tiempo de cálculo con cada método
   Naive product time = 54750 ms
   MatMul product time = 4578 ms
   OpenCl product time = 922 ms
   ¿Cuántos errores de divergencia hay entre las matrices de resultados?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Rellenamos la matriz con valores aleatorios                      |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//| Liberamos todos los contextos OpenCL                             |
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- eliminamos en una secuencia inversa todos los contextos de OpenCL creados
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

              Para leer una explicación detallada del código OpenCL en este ejemplo, le recomendamos "OpenCL: De una programación simple a una más intuitiva".


              Unas pocas mejoras más

              En el build 3390, también hemos eliminado dos restricciones para trabajar con OpenCL que podrían dificultar el uso de la GPU.

                El número máximo de objetos OpenCL puede llegar ahora a 65536, antes, el límite era de 256. Los manejadores de los objetos OpenCL en el programa MQL5 se crean usando las funciones CLContextCreate, CLBufferCreate y CLProgramCreate. La anterior limitación de 256 manejadores no permitía usar métodos eficientes de aprendizaje automático.

                Además, ahora se permite OpenCL en tarjetas sin soporte double. Antes, los programas MQL5 solo usaban GPUs con soporte double, aunque muchas tareas permiten y están diseñadas para cálculos utilizando float. El tipo float se considera originalmente nativo de la computación paralela porque ocupa menos espacio. Este requisito ha sido eliminado.

                Si la tarea requiere usar solo GPUs con soporte double, esto podrá indicarse explícitamente al llamar a CLContextCreate utilizando el nuevo valor CL_USE_GPU_DOUBLE_ONLY (solo pueden utilizarse dispositivos que soporten el cálculo de tipo double).
                   int cl_ctx;
//--- inicializamos el contexto OpenCL
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL not found");
      return;
     }

                Aunque estos cambios en OpenCL no están directamente relacionados con las matrices y los vectores, también son el resultado de nuestros esfuerzos por desarrollar el lenguaje MQL5 según las necesidades del aprendizaje automático.


                El futuro de MQL5 en el aprendizaje automático

                En los últimos años, hemos hecho mucho por incorporar tecnología avanzada al lenguaje MQL5:

                • Hemos implementado la migración de la biblioteca de métodos numéricos ALGLIB a MQL5
                • Hemos añadido una biblioteca matemática con funciones de lógica difusa y estadística
                • Hemos implementado una librería gráfica como análogo de la función plot
                • Hemos realizado la integración con Python, ahora es posible ejecutar scripts de Python directamente en el terminal
                • Hemos añadido funciones de DirectX para crear gráficos en 3D
                • Hemos introducido la compatibilidad nativa con SQLite para trabajar con bases de datos
                • Hemos añadido nuevos tipos de datos -matrices y vectores- con la implementación de todos los métodos necesarios

                  El lenguaje MQL5 seguirá evolucionando y el aprendizaje automático supone una prioridad. Tenemos grandes planes, y no nos conformaremos con las metas alcanzadas. Quédese con nosotros, apóyenos y aprenda cosas nuevas con nosotros.

                  Traducción del ruso hecha por MetaQuotes Ltd.
                  Artículo original: https://www.mql5.com/ru/articles/10922

                  Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

                  Otros artículos del autor

                  Últimos comentarios | Pasar a la discusión en el foro de los operadores (1)
                  Enrique Enguix
                  Enrique Enguix | 3 oct. 2022 en 11:21
                  Fantástica explicación. Muy útil.
                  Desarrollo de un EA comercial desde cero (Parte 24): Dotando de robustez al sistema (I) Desarrollo de un EA comercial desde cero (Parte 24): Dotando de robustez al sistema (I)
                  En este artículo haremos que el sistema sea más robusto, para que sea más estable y seguro de usar. Una forma de conseguir robustez es intentar reutilizar el código lo máximo posible, de esta forma él mismo será probado todo el tiempo y en diversas ocasiones. Pero esta es solo una de las formas, otra forma es el uso de la programación OOP.
                  DoEasy. Elementos de control (Parte 10): Objetos WinForms: dando vida a la interfaz DoEasy. Elementos de control (Parte 10): Objetos WinForms: dando vida a la interfaz
                  Ha llegado el momento de revitalizar la interfaz gráfica de usuario, haciendo que los objetos interactúen con el usuario y otros objetos. Y para que los objetos más complejos funcionen correctamente, necesitaremos una funcionalidad que permita a los objetos interactuar entre sí y con el usuario.
                  Desarrollo de un EA comercial desde cero (Parte 25): Dotando de robustez al sistema (II) Desarrollo de un EA comercial desde cero (Parte 25): Dotando de robustez al sistema (II)
                  Aquí terminaremos de dar un empujón en el rendimiento del EA... así que prepárense para una larga lectura. Lo primero que haremos para que nuestro EA sea robusto es eliminar del código todo y absolutamente todo lo que no forme parte del sistema comercial.
                  Desarrollo de un EA comercial desde cero (Parte 23): Un nuevo sistema de órdenes (VI) Desarrollo de un EA comercial desde cero (Parte 23): Un nuevo sistema de órdenes (VI)
                  Haremos más fluido el sistema de ordenes. Aquí les mostraré cómo y dónde hacer cambios en el código para tener algo más fluido que nos permita modificar los límites de posición mucho más rápido.