Factorización de matriсes: un modelado más práctico

Introducción

Hola a todos y bienvenidos a otro de mis artículos, enfocado en ofrecer un contenido didáctico.

En el artículo anterior Factorización de matrices: lo básico, hablé un poco sobre cómo tú, mi querido y entusiasta lector, puedes utilizar matrices en tu forma general de efectuar cálculos. Sin embargo, en esa ocasión queríamos que entendieras cómo se realizaban los cálculos, por lo que no nos preocupamos demasiado en crear un modelado adecuado de las matrices.

Es muy probable que no te hayas dado cuenta de que el modelado de las matrices era un tanto extraño, ya que no se indicaban filas y columnas, solo columnas. Esto resulta muy raro al leer un código que realiza factorizaciones de matrices. Si esperabas ver las filas y columnas indicadas, podrías haberte sentido bastante confundido al intentar implementar la factorización.

Además, esa forma de modelar las matrices no es, ni de cerca, la mejor manera. Esto se debe a que, cuando modelamos matrices de esa forma, nos enfrentamos a ciertas limitaciones que nos obligan a usar otras técnicas o funciones que no serían necesarias si el modelado se realiza de manera más adecuada.

Dado que el procedimiento, aunque no es complicado, necesita ser bien comprendido para poder ser utilizado adecuadamente, preferí no entrar en detalles en el artículo anterior. En este artículo, podré explicar todo con más calma, sin apresuramientos ni el riesgo de transmitir una idea equivocada sobre cómo deberías pensar al modelar tus matrices para que sean adecuadamente factorizadas.

Las matrices son, de hecho, la mejor manera de realizar ciertos tipos de cálculos, ya que requieren pocas implementaciones adicionales. Sin embargo, precisamente por esta razón, es necesario tener mayor cuidado al implementar cualquier cosa en matrices. A diferencia de un modelado convencional, si modelas algo incorrectamente en matrices, obtendrás resultados bastante extraños o, en el mejor de los casos, tendrás grandes dificultades para mantener el código desarrollado.

Cuidados en el modelado de una matriz

Tal vez te estés preguntando: ¿Por qué este sujeto dijo que el modelado en el artículo anterior era extraño? ¡Yo lo entendí! No logro comprender por qué decir que era raro. Bien, querido lector, veamos el fragmento del código del artículo anterior donde se modelaban las matrices. Tal vez así quede un poco más claro lo que quiero mostrarte. El fragmento puede verse a continuación.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2] = {
24.                            cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                           -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                         },
27.            M_2[][2]  =  {
28.                            0.0,  0.0,
29.                            1.5, -.75,
30.                            1.0,  0.0,
31.                            1.5,  .75
32.                         },
33.            M_3[M_2.Size() / 2][2];

A pesar de funcionar, como se muestra en el fragmento, la cuestión está bastante enredada. Es difícil de entender. Observa lo siguiente: cuando escribimos en el código un array multidimensional, usamos la siguiente configuración:

Etiqueta[Dimensión_01][Dimensión_02]....[Dimensión_N];

Aunque parezca sencillo de entender en un código general, este tipo de notación es difícil de comprender cuando la aplicamos al campo de la factorización de matrices. Esto se debe a que, al trabajar con matrices, esta forma de expresar un array multidimensional hace que todo se vuelva confuso. Pronto entenderás por qué. Para simplificar, reduciremos el concepto a un sistema bidimensional, es decir, solo filas y columnas. Sin embargo, las matrices pueden tener cualquier número de dimensiones. Simplificando a una matriz bidimensional, la notación quedaría como se muestra a continuación.

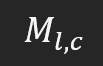
¿Y qué significa esto? Bien, la "M" representa el nombre de la matriz, mientras que "l" indica el número de filas y "c" el número de columnas. En términos generales, al acceder a un elemento de la matriz, usarás la misma notación, lo que lo haría lucir como se muestra a continuación.

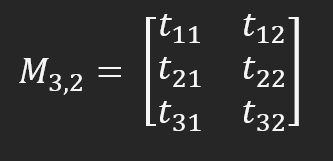
Observa que ahora la matriz M está formada por seis elementos, que pueden ser accedidos utilizando el sistema de filas y columnas. Pero mira atentamente la imagen de arriba. ¿A qué se parece? Dependiendo de tu experiencia, puede parecerse a muchas cosas. Sin embargo, en términos de computación, ¿qué sería? Bien, esto es un array de dos dimensiones. Pero pensar en ello de esta forma hace que la matriz se vea estática. Y una matriz es una entidad dinámica; puede ser leída de muchas formas diferentes según lo que estés calculando. Hay casos en los que debe leerse en diagonal, otros en los que debe leerse columna por columna, y algunos en los que debe leerse fila por fila. Entonces, pensar en una matriz como un array multidimensional transforma algo dinámico en algo estático. Esto complica la implementación de ciertos cálculos con matrices.

Sin embargo, no estoy aquí para enseñarle a un cura a rezar el padrenuestro. Estoy aquí para mostrarte, mi querido lector y entusiasta, cómo puedes visualizar cualquier matriz de una manera mejor, permitiendo que siga siendo una entidad dinámica, como debe ser.

De esta forma, la idea de pensar en una matriz como un array no es incorrecta. El problema surge al considerarla un array multidimensional. Lo ideal es pensar en la matriz como un array unidimensional, pero sin un número fijo de dimensiones. Suena extraño lo que acabo de escribir, pero el problema está en el lenguaje. Actualmente, no existen términos o expresiones adecuados para describir ciertos conceptos.

Piensa en la dificultad que debió enfrentar Isaac Newton al elaborar las primeras explicaciones sobre el Cálculo. Debió ser bastante complicado debido a la falta de términos adecuados para algunos conceptos. Pero volvamos a nuestra cuestión.

Ok, ya tenemos una manera de imaginar la matriz en términos de array. Pero ahora surge el primer problema: ¿Cómo ordenar los elementos en el array? Si no entiendes por qué esto es un problema, es porque no comprendes todo lo que implica la factorización de matrices. La forma en que los elementos se ordenen influirá profundamente en cómo se implementará el código de factorización. Aunque los resultados sean los mismos en cualquier caso, podrías necesitar más o menos saltos dentro del array para obtener el resultado correcto. Esto se debe precisamente a que la memoria del ordenador es lineal. Si ordenas los elementos de la siguiente forma: t11, t12, t21, t22, t31 y t32, que es adecuada en muchos casos, necesitarás forzar saltos para acceder a los elementos en un orden diferente, lo que será necesario para realizar algún cálculo específico. Y esto, sin duda, sucederá, hagas lo que hagas.

Normalmente, cuando ordenamos los elementos en un array, lo hacemos leyendo fila por fila. Pero nada impide que lo hagas de otra manera, como leer columna por columna o de cualquier otra forma que imagines. Sé libre de hacerlo como te convenga.

Una vez hecho esto, surge otro pequeño problema, pero no proviene de la programación, sino de cómo se factorizan las matrices. En este caso, no entraré en detalles. La razón es simple: cómo lo manejes dependerá de cómo hayas implementado la matriz o del tipo de matriz que estés usando. Te sugiero que estudies libros o literatura matemática para entender cómo implementar la solución a los problemas que puedan surgir, de modo que puedas realizar las factorizaciones correctamente. Sin embargo, nunca es realmente complicado implementar el código; el código es la parte fácil del trabajo. Lo complicado es entender cómo se ejecutará la factorización. Un ejemplo de esto es calcular el determinante de la matriz mostrada en la figura anterior. Nota que no es una matriz cuadrada, y generar el determinante en este caso es un poco diferente de lo que se haría en una matriz cuadrada. Como se ha mencionado, estudia la parte matemática, ya que cada caso específico puede requerir un enfoque particular.

La confusión está armada

Bien, ahora que ya expliqué y nivelé un poco las cosas, podemos pasar a la fase de codificación. Vamos a continuar con el ejemplo visto en el artículo anterior, ya que es bastante práctico y fácil de entender. Además, es más sencillo mostrar, usando este ejemplo, otra ventaja de usar cálculos matriciales en algunos casos. Entonces, recordemos cómo era el código. Esto se puede hacer observando el código a continuación.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[][], const double &B[][], double &R[][], const int nDim)
13. {
14.     for (int c = 0, size = (int)(B.Size() / nDim); c < size; c++)
15.     {
16.         R[c][0] = (A[0][0] * B[c][0]) + (A[0][1] * B[c][1]);
17.         R[c][1] = (A[1][0] * B[c][0]) + (A[1][1] * B[c][1]);
18.     }
19. }
20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double M_1[2][2]{
24.                         cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                         -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                     },
27.            M_2[][2] {
28.                         0.0,  0.0,
29.                         1.5, -.75,
30.                         1.0,  0.0,
31.                         1.5,  .75
32.                     },
33.            M_3[M_2.Size() / 2][2];
34. 
35.     int dx[M_2.Size() / 2], dy[M_2.Size() / 2];
36.     
37.     MatrixA_x_MatrixB(M_1, M_2, M_3, 2);
38.     ZeroMemory(M_1);
39.     M_1[0][0] = M_1[1][1] = size;
40.     MatrixA_x_MatrixB(M_1, M_3, M_2, 2);
41. 
42.     for (int c = 0; c < (int)M_2.Size() / 2; c++)
43.     {
44.         dx[c] = x + (int) M_2[c][0];
45.         dy[c] = y + (int) M_2[c][1];
46.     }
47. 
48.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
49.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
50. }
51. //+------------------------------------------------------------------+
52. int OnInit()
53. {    
54.     int px, py;
55.     
56.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
60.     canvas.Erase(ColorToARGB(clrWhite, 255));
61.         
62.     Arrow(px / 2, py / 2, 160);
63. 
64.     canvas.Update(true);
65.     
66.     return INIT_SUCCEEDED;
67. }
68. //+------------------------------------------------------------------+
69. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
70. {
71.     return rates_total;
72. }
73. //+------------------------------------------------------------------+
74. void OnDeinit(const int reason)
75. {
76.     canvas.Destroy();
77. }
78. //+------------------------------------------------------------------+

Como este código fue explicado en el artículo anterior, y también está disponible en el anexo de dicho artículo, no vamos a explicarlo de nuevo aquí. Nos enfocaremos solo en el fragmento que realmente necesita ser manipulado, es decir, el procedimiento Arrow y el procedimiento MatrixA_x_MatrixB, que son los que realmente hacen algo en nuestro código de demostración.

Muy bien, para comenzar, vamos a cambiar la forma en que se construyeron los arrays. En realidad, el cambio será más simple y sutil de lo que podría parecer, pero aun así marcará una diferencia en la manera en que deberíamos comenzar a trabajar.

Para que empieces a entender, vamos a tomar el array M_1, que se ve en el código anterior. Obsérvalo para comprender lo que será explicado.

Nota algo interesante aquí, que es precisamente el tema explicado en el apartado anterior. En la línea 23, el array o matriz M_1 se declara con dos filas y dos columnas. En este caso, no hay dudas al respecto. Al igual que el array o matriz M_2, que no tiene una definición de número de filas, pero sí de columnas, que son dos. Hasta este punto, no hay dudas ni problemas; es bastante simple de entender lo que estamos haciendo, ya que cada nueva línea en el código corresponde a una nueva fila en la matriz, y cada nueva columna en esa línea sería una nueva columna en la matriz. Así de simple. Sin embargo, existe un problema, y este está en el código del procedimiento MatrixA_x_MatrixB. ¿Puedes identificar el problema? ¿Sí? ¿No? Tal vez. Quizás lo estés viendo, pero no lo entiendas.

Bien, de hecho, hay un problema en este procedimiento MatrixA_x_MatrixB, que es el encargado de multiplicar las matrices. Sin embargo, dado que lo que estamos haciendo aquí es algo bastante sencillo, esto no compromete la implementación del código. No obstante, no justifica que el problema permanezca ahí, existiendo y ralentizando nuestro progreso. En el momento en que necesitamos implementar una multiplicación más compleja, será un problema, o una verdadera piedra en el zapato.

Si no has detectado el problema, quiero que prestes atención a la variable B. Esta representa una matriz que está multiplicando a otra matriz. Para visualizar mejor el problema, vamos a reducir la matriz B a una única columna, pero con dos filas, ya que la matriz A tiene dos columnas. Para que la multiplicación ocurra, se debe hacer lo que se muestra en la figura a continuación.

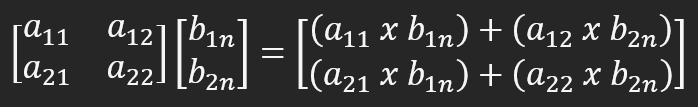
Así obtendremos el resultado adecuado. Esto es lo que sucede en una multiplicación de matrices o una factorización matricial. Para más detalles, te sugiero estudiar sobre el tema. De cualquier manera, la multiplicación se realiza fila por columna, resultando en un valor que quedará en la columna. Esto es porque el segundo factor es una columna. Si la multiplicación se hiciera de forma columna por fila, el valor resultante debería colocarse en forma de líneas.

A pesar de que lo que acabo de decir pueda parecer que solo busca confundirte, en realidad esta es la regla para realizar la multiplicación de matrices. Entonces, cuando otro programador analice el código, no verá que esto se está haciendo correctamente. Y este es precisamente el problema que se puede observar en las líneas 16 y 17, donde debería realizarse el cálculo mostrado en la figura anterior. Sin embargo, observa que en la matriz A estamos usando el cálculo por filas, pero en la matriz B también estamos usando el cálculo por filas. Esto es confuso, aunque en este ejemplo simple proporciona los datos correctos.

Muy bien, puedes pensar: ¿Y qué? Si está funcionando, déjalo como está. Pero esa no es la cuestión. Si en algún momento necesitas mejorar el código, ya sea para trabajar con una matriz más grande o para cubrir un caso ligeramente diferente, bueno pues, terminarás complicándote mucho al intentar hacer que algo relativamente sencillo funcione. Entonces, es necesario que este tipo de cosas se hagan sin tanta confusión. Para resolver esto, necesitamos dejar de usar este modelo y adoptar uno un poco diferente. Aunque al principio pueda parecer confuso, al menos será correcto, siguiendo exactamente lo que se muestra en la figura anterior.

Bien, para separar las cosas, veamos cómo hacerlo en un nuevo tema.

Haciendo las cosas menos complicadas

Aunque lo que vamos a hacer aquí pueda parecer complicado, en realidad no lo es tanto si se hace de la manera correcta y tomando los debidos cuidados. Lograrás hacer algo que, de otra manera, sería mucho más tedioso, pero de una forma bastante simple. Observa la figura a continuación.

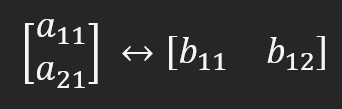
Esta representación muestra que ambas matrices son equivalentes. Esto es porque la matriz con los elementos A, en el lado izquierdo, que es una matriz de filas. Al convertirla en una matriz con los elementos B, en el lado derecho, que en este caso es una matriz de columnas, no necesitaremos hacer muchos cambios, quizás un simple giro o cambiar un índice en algunos casos. De cualquier manera, esto será necesario muchas veces: convertir una matriz de filas en una de columnas y viceversa, para permitir la factorización entre matrices. Pero para que todo sea correcto, a11 deberá ser igual a b11 y a21 deberá ser igual a b12.

Habrá casos en los que notarás que no es necesario hacer grandes cambios, solo cambiar un índice, lo que nos permitirá convertir una estructura de filas en una de las columnas. Pero hacer esto adecuadamente dependerá de cada caso específico. Por eso, es importante que estudies cómo se hace la factorización matricial, leyendo libros de matemáticas para familiarizarte con el tema.

Ahora, volviendo a nuestro código, que vimos en el tema anterior. Comencemos corrigiendo la representación en primer lugar. Para hacerlo, basta con modificar el código, como se muestra en el fragmento a continuación.

20. //+------------------------------------------------------------------+
21. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
22. {
23.     double  M_1[]= {
24.                        cos(_ToRadians(angle)), sin(_ToRadians(angle)),
25.                        -sin(_ToRadians(angle)), cos(_ToRadians(angle))
26.                    },
27.             M_2[]= {
28.                        0.0,  0.0,
29.                        1.5, -.75,
30.                        1.0,  0.0,
31.                        1.5,  .75
32.                    },
33.            M_3[M_2.Size()];

Observa que ahora ya no tenemos índices en los arrays. La estructura de las matrices se está creando como se muestra en el código, es decir, las filas son filas y las columnas son columnas. Sin embargo, presta atención a los arrays o matrices dinámicas, como la M_3. Debemos definir correctamente la longitud a ser asignada, precisamente para evitar errores de RUN-TIME al acceder a los elementos de estas matrices.

Esta es la primera parte. No obstante, al hacer esto, el procedimiento MatrixA_x_MatrixB ya no podrá realizar los cálculos correctamente. Además, el bucle presente en la línea 42 (ver el código en el tema anterior) no podrá decodificar los datos de manera adecuada.

Primero, vamos a corregir el cálculo que se está realizando en el procedimiento MatrixA_x_MatrixB y luego corregiremos la graficación en pantalla. Pero antes de continuar, nota que la matriz M_1 prácticamente no ha cambiado, ya que es simétrica y cuadrada. Este es uno de los casos en los que podemos leerla tanto en filas como en columnas.

Bien, como gran parte del código cambiará, veamos el nuevo fragmento de código a continuación. Creo que será más sencillo explicar cómo todo funcionará.

09. //+------------------------------------------------------------------+
10. #define _ToRadians(A) (A * (M_PI / 180.0))
11. //+------------------------------------------------------------------+
12. void MatrixA_x_MatrixB(const double &A[], const ushort Rows, const double &B[], double &R[])
13. {
14.     uint Lines = (uint)(A.Size() / Rows);
15. 
16.     for (uint cbl = 0; cbl < B.Size(); cbl += Rows)
17.         for (uint car = 0; car < Rows; car++)
18.         {
19.             R[car + cbl] = 0;
20.             for (uint cal = 0; cal < Lines; cal++)
21.                 R[car + cbl] += (A[(cal * Rows) + car] * B[cal + cbl]);
22.         }
23. }
24. //+------------------------------------------------------------------+
25. void Plot(const int x, const int y, const double &A[])
26. {
27.     int dx[], dy[];
28. 
29.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
30.     {
31.         ArrayResize(dx, c0 + 1, A.Size());
32.         ArrayResize(dy, c0 + 1, A.Size());
33.         dx[c0] = x + (int)(A[c1++]);
34.         dy[c0] = y + (int)(A[c1++]);
35.     }
36. 
37.     canvas.FillPolygon(dx, dy, ColorToARGB(clrPurple, 255));
38.     canvas.FillCircle(x, y, 5, ColorToARGB(clrRed, 255));
39. 
40.     ArrayFree(dx);
41.     ArrayFree(dy);
42. }
43. //+------------------------------------------------------------------+
44. void Arrow(const int x, const int y, const ushort angle, const uchar size = 100)
45. {
46.     double  M_1[]={
47.                      cos(_ToRadians(angle)), sin(_ToRadians(angle)),
48.                      -sin(_ToRadians(angle)), cos(_ToRadians(angle))
49.                   },
50.             M_2[]={
51.                      0.0,  0.0,
52.                      1.5, -.75,
53.                      1.0,  0.0,
54.                      1.5,  .75
55.                   },
56.            M_3[M_2.Size()];
57.     
58.     MatrixA_x_MatrixB(M_1, 2, M_2, M_3);
59.     ZeroMemory(M_1);
60.     M_1[0] = M_1[3] = size;
61.     MatrixA_x_MatrixB(M_1, 2, M_3, M_2);
62.     Plot(x, y, M_2);
63. }
64. //+------------------------------------------------------------------+

Uau, ahora parece que todo se ha vuelto mucho más complicado. ¡No entiendo nada de nada! ¿Realmente necesitamos toda esta confusión? Tranquilo, querido lector. Este código no es nada complicado ni confuso. En realidad, lo considero muy simple y bastante directo. Además, es extremadamente flexible, y ahora te explicaré por qué digo esto.

En este fragmento, la multiplicación entre dos matrices ocurre de la forma correcta. En este caso, se implementó el modelo columna por fila, lo que resultó en una nueva fila como producto de la multiplicación. La multiplicación ocurre exactamente en la línea 21. Sé que lo que se está haciendo en el procedimiento de la línea 12 puede parecer extremadamente complicado, pero no lo es. Todas esas variables están ahí justamente para permitirnos acceder correctamente a un índice específico en el array.

Como no hay pruebas que garanticen que el número de filas de una matriz sea igual al número de columnas de la otra, debes tener cuidado al usar este procedimiento para evitar errores de RUN-TIME.

Ahora que la matriz A, que debe organizarse en términos de columnas, está multiplicando a la matriz B, que debe organizarse en términos de filas, y el resultado se coloca en la matriz R, que se construirá en términos de filas, podemos ver cómo se realizan las llamadas. Esto ocurre en las líneas 58 y 61. Primero, observemos la línea 58. Nota que la matriz M_1, organizada en columnas, debe pasarse como la primera matriz. La matriz M_2, que es dinámica y organizada en filas, debe pasarse como la segunda matriz. Si cambias este orden en la línea 58, obtendrás un error en los valores calculados. Sé que parece extraño decir que 2 x 3 es diferente de 3 x 2, pero cuando se trata de matrices, el orden de los factores realmente afecta el producto. De cualquier manera, nota que esto es similar a lo que se estaba haciendo antes. Claro, el segundo argumento de la llamada indica el número de columnas en la primera matriz. Como el propósito aquí es ser didáctico, no me preocupo por verificar si la matriz B (en este caso, M_2) puede o no ser multiplicada por la matriz A (M_1). Supongo que no cambiarás la estructura, quizás solo aumentarás el número de filas en la matriz M_2, lo cual no afectará la factorización en MatrixA_x_MatrixB.

Ok. Las líneas 59 y 60 ya fueron explicadas en el artículo anterior, y lo que ocurre en la línea 61 es equivalente a lo que sucede en la línea 58, por lo que podemos considerarlo explicado. Sin embargo, en la línea 62 tenemos una nueva llamada, que invoca el procedimiento en la línea 25. ¿Por qué? La razón es que puedes usar este procedimiento en la línea 25 para graficar otros objetos o imágenes directamente en la pantalla. Todo lo que necesitas hacer es pasar una matriz del tipo fila a este procedimiento, donde cada fila representa un vértice de la imagen a dibujar. Estos puntos, que deben estar en la matriz, deben seguir el siguiente orden: X en la primera columna y Y en la segunda columna, ya que estamos trazando algo en una pantalla bidimensional. Así, aunque dibujes algo en 3D, deberás realizar los cálculos en la matriz para que un vértice en la dimensión Z sea proyectado en el plano XY. No necesitas preocuparte por separar las cosas o por el tamaño de la matriz. El procedimiento Plot se encargará de eso. Observa que en la línea 27, declaramos dos arrays dinámicos. En la línea 29, creamos un bucle for algo curioso, diferente de cómo muchos están acostumbrados a escribirlo. En este bucle, tenemos dos variables: una controlada por el bucle y otra controlada dentro del código. La variable c0 es la controlada por el bucle, cuyo objetivo es instanciar correctamente el índice para dx y dy, y asignar más memoria cuando sea necesario. Esto se hace en las líneas 31 y 32. Puede parecer ineficiente, pero revisa la documentación de MQL5 y verás que no lo es tanto.

Por otro lado, la variable c1 es controlada dentro del código. Para entenderlo, observa lo que sucede con c1 en las líneas 33 y 34. Con cada iteración, se incrementa en una unidad. Sin embargo, es precisamente c1 la que determina cuándo debe finalizar el bucle for. Si no lo has notado, observa en la línea 29 cuál es la condición para terminar el bucle.

Aquí no estamos verificando si el array o matriz A está correctamente estructurado. Si no tiene dos columnas por fila, en algún momento dentro de este bucle for, se generará un error de RUN-TIME indicando que se ha intentado acceder a una posición fuera del rango. Así que presta atención al crear la matriz A.

Al final de todo esto, usamos la línea 37 para llamar a un procedimiento en la clase CCanvas. Este tiene como objetivo trazar la figura de la matriz en el gráfico. La línea 38 muestra dónde está el punto de origen de la graficación. Si todo sale bien, verás la imagen que aparece justo abajo.

Y como no podía faltar, en las líneas 40 y 41 devolvemos la memoria asignada al sistema operativo, liberando así el recurso que fue asignado.

Consideraciones finales

En estos dos artículos, el anterior y este, intenté presentar algo que muchos consideran complicado o difícil de implementar: la factorización matricial. Sé que el material presentado aquí no cubre todos los aspectos y ventajas de usar matrices en algunos de tus cálculos. Sin embargo, quiero resaltar que entender cómo desarrollar formas de calcular matrices es importante. No es casualidad que programas 3D, ya sean juegos o editores de imágenes vectoriales, utilicen este tipo de factorización. Incluso algunos programas aparentemente simples, como los que manipulan imágenes tipo bitmap, también utilizan cálculos matriciales para optimizar la implementación del sistema.

En estos dos artículos, traté de mostrar esto de la manera más simple posible, ya que veo que muchos que están iniciando en la programación simplemente ignoran la necesidad de realmente aprender a programar ciertas cosas. Muchas veces usan bibliotecas u otros programas de moda sin siquiera darse cuenta de lo que se está haciendo detrás de escena.

Aquí, traté de dejar las cosas de la manera más simple posible. Enfocándome en una única operación: la multiplicación de dos matrices. Y para demostrar lo simple que lo dejé, no llegué a mostrar cómo usar la GPU para realizar el trabajo que se hace en el procedimiento MatrixA_x_MatrixB, que es lo que en realidad ocurre en muchos casos. Aquí, usamos únicamente el poder de la CPU. Pero, en general, las factorizaciones de matrices suelen realizarse no por la CPU, sino por la GPU, utilizando OpenCL para programarla correctamente.

Creo que, de alguna manera, he mostrado que podemos hacer mucho más de lo que algunos consideran posible. Así que estudia el material presentado en estos dos artículos, porque en breve pretendo explicar un tema en el que la factorización mediante matrices es fundamental.

Un último detalle que quiero agregar es que esta multiplicación de dos matrices está enfocada en resolver un problema específico. No es ni de lejos el método que se estudia en los libros o en la escuela. No esperes usar este modelo de factorización de forma genérica, porque no funcionará. Solo es adecuado para el problema propuesto, que era rotar un objeto.