¡Visualice esto! La biblioteca gráfica en MQL5 como un análogo de plot en el lenguaje R
Una gran ventaja de la función plot es que para constuir cualquier gráfico se necesitan solo unas cuantas líneas de código. Basta con transmitir como parámetros una matriz de datos, indicar el tipo de gráfico deseado ¡y ya está listo! Todo el trabajo rutinario de cálculo de la escala, la construcción de los ejes, la elección del color y muchos más será realizado por plot.
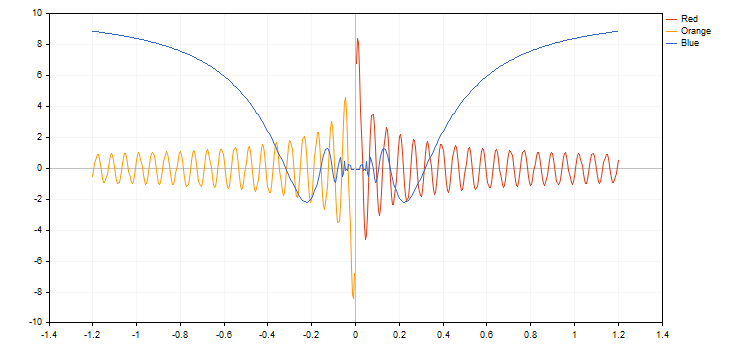
En el lenguaje MQL5 todas las posibilidades de esta función se presentan con los métodos de la biblioteca gráfica de la Biblioteca estándar. Aquí tenemos un ejemplo del código de su ejecución:
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- Functions
double BlueFunction(double x) { return(RESULT_OR_NAN(x,10*x*sin(1/x))); }
double RedFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
double from=-1.2;
double to=1.2;
double step=0.005;
CGraphic graphic;
graphic.Create(0,"G",0,30,30,780,380);
//--- colors
CColorGenerator generator;
uint blue= generator.Next();
uint red = generator.Next();
uint orange=generator.Next();
//--- plot all curves
graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
graphic.CurvePlotAll();
graphic.Update();
}
La clase básica CCanvas y su desarrollo
La Biblioteca estándar contiene la clase básica CCanvas, diseñada para crear imágenes de forma rápida y sencilla directamente en los gráficos de precio. La base del funcionamiento de la clase consiste en la creación de un recurso gráfico y el posterior dibujado en un lienzo de primitivos sencillos: puntos, líneas rectas y quebradas, circunferencias, triángulos y polígonos. En la clase también se han implementado funciones para colorear figuras y mostrar información de texto con la fuente, el color y el tamaño necesarios.
Inicialmente, la clase CCanvas contenía solo dos modos de dibujado de primitivos gráficos — con suavizado (antialiasing, AA) y sin él. Después se añadieron nuevas funciones para crear primitivos basados en el algoritmo de Wu:
- LineWu — línea recta
- PolylineWu — línea quebrada
- PolygonWu — polígono
- TriangleWu — triángulo
- CircleWu — circunferencia
- EllipseWu — elipse
El algoritmo de Wu aúna la corrección de alta calidad del escalonado y una velocidad de funcionamiento cercana a la velocidad del algoritmo de Bresenham sin suavizado. Hay en él una diferencia visual con respecto al algoritmo estándar de suavizado (AA), implementado en CCanvas. Aquí tenemos un ejemplo de una circunferencia usando tres funciones diferentes:
CCanvas canvas;
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
int Width=800;
int Height=600;
//--- create canvas
if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
{
Print("Error creating canvas: ",GetLastError());
}
//--- draw
canvas.Erase(clrWhite);
canvas.Circle(70,70,25,clrBlack);
canvas.CircleAA(120,70,25,clrBlack);
canvas.CircleWu(170,70,25,clrBlack);
//---
canvas.Update();
}
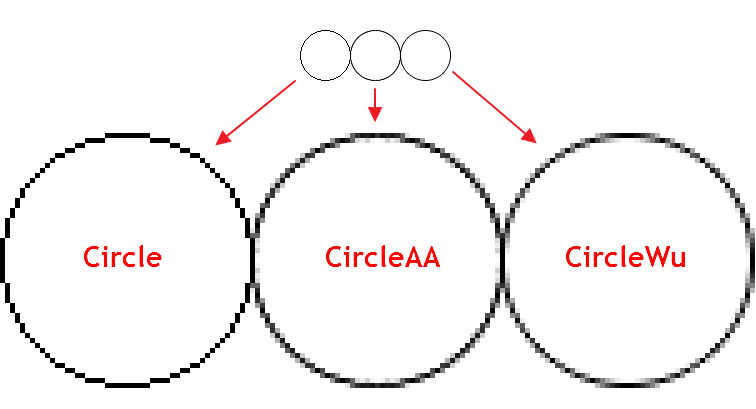
Como se puede ver por la imagen, CircleAA() dibuja con el algoritmo estándar de suavizado una línea más gruesa que la función CircleWu(), según el algoritmo de Wu. Gracias a su menor grosor y al mejor cálculo de los matices de transición, la circunferencia CircleWu tiene un aspecto más pulcro y natural.
También se han hecho otras mejoras en la clase CCanvas:
- Se ha añadido el nuevo primitivo elipse con dos variantes de suavizado EllipseAA() y EllipseWu()
- Añadida la sobrecarga de la función de rellenado con un nuevo parámetro responsable de la "sensibilidad de rellenado" (parámetro threshould).
Algoritmo de trabajo con la biblioteca
1. Después de incluir la biblioteca será necesario crear un objeto de la clase CGraphic. Precisamente en él se añadirán las curvas que se deben dibujar.
A continuación, para el objeto creado hay que llamar el método Create(), en el que se indican los parámetros básicos del gráfico:
- Indicador del gráfico
- Nombre del objeto
- Índice de la ventana
- Punto de anclaje del gráfico
- Altura y anchura del gráfico
Este método creará, basándose en los parámetros introducidos, un objeto en el gráfico o recurso gráfico en el que se construirá el gráfico.
CGraphic graphic;
//--- crear un lienzo
graphic.Create(0,"Graphic",0,30,30,830,430);
En conclusión, disponemos de un lienzo ya preparado para dibujar.
2. Ahora rellenamos nuestro objeto con curvas. La adición se lleva a cabo con el método CurveAdd(), que, a su vez, tiene la posibilidad de crear curvas de cuatro maneras diferentes:
- Basándose en una matriz unidemensional del tipo double. En este caso, los valores de la matriz se representarán en el eje Y, y los índices de la matriz serán las coordenadas de X.
- Basándose en dos matrices x[] e y[] del tipo double.
- Basándose en la matriz CPoint2D.
- Basándose en el puntero a la función CurveFunction() y los tres valores para la construcción de los argumentos de la función: inicial, final e incremento según el argumento.
El método CurveAdd() retorna el puntero a la clase CCurve, de esta forma, tendremos acceso rápido a la curva recién creada y podremos modificar sus propiedades.
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);3. A continuación, cualquiera de las curvas añadidas se puede representar en el gráfico. Esto se puede hacer de tres formas.
- Usando el método CurvePlotAll() que dibuja todas las curvas añadidas al gráfico de forma automática.
graphic.CurvePlotAll();
- Usando el método CurvePlot() que dibuja una curva según el índice establecido.
graphic.CurvePlot(0);
- Usando el método Redraw() y poniendo el valor true a la propiedad Visible de la curva.
curve.Visible(true);
graphic.Redraw();
4. Para dibujar propiamente el diseño en el gráfico, solo quedar llamar el método Update(). Como resultado, obtendremos el código de un script para crear un gráfico sencillísimo:
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
graphic.CurvePlotAll();
graphic.Update();
}
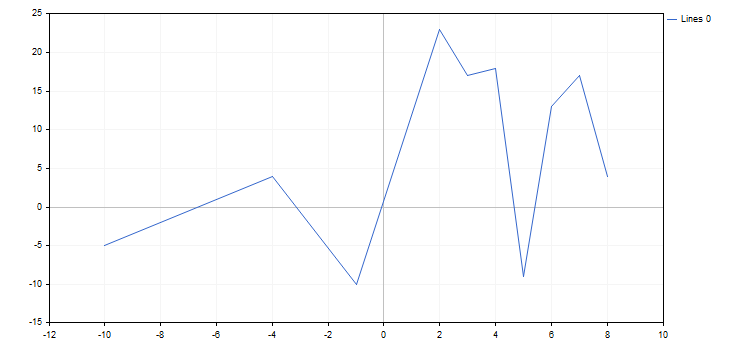
Este es el aspecto que tiene este gráfico:
Es posible modificar el código del propio gráfico y de cada una de sus funciones en cualquier momento. Por ejemplo, podemos añadir rótulos al eje del gráfico, cambiar el nombre de la curva e incluir para ella el modo de curva de aproximación:
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
curve.Name("Example");
curve.LinesIsSmooth(true);
graphic.XAxis().Name("X - axis");
graphic.XAxis().NameSize(12);
graphic.YAxis().Name("Y - axis");
graphic.YAxis().NameSize(12);
graphic.YAxis().ValuesWidth(15);
graphic.CurvePlotAll();
graphic.Update();
DebugBreak();
}
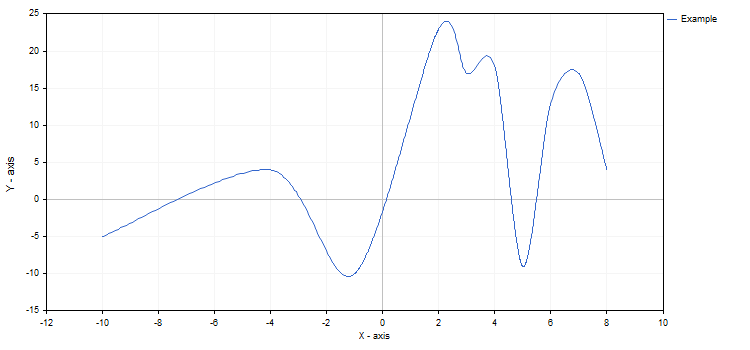
Si los cambios continuasen tras la llamada de CurvePlotAll, deberíamos llamar adicionalmente el método Redraw para verlos.
Como sucede en la mayoría de bibliotecas actuales, Graphics implementa diferentes algoritmos preparados que simplifican notablemente el proceso de construcción de los gráficos:
- La biblioteca es capaz de generar por sí misma colores de contraste para las curvas, si aquellos no se han indicado de forma implícita.
- Los ejes de los gráficos disponen de un modo paramétrico de autoescalado que se puede desactivar si así lo desea.
- Los nombres se generan de forma automática dependiendo de su tipo y orden de adición.
- La zona de trabajo del grafíco es delineada de forma automática, también se destacan la coordenadas reales de los ejes.
- Existe la posibilidad de suavizar las curvas al dibujar las líneas.
Asimismo, entre las posibilidades adicionales de la bilbioteca Graphics hay que destacar los métodos que permiten añadir nuevos elementos al gráfico:
- TextAdd() añade texto en un espacio aleatorio en el gráfico, las coordenadas deben establecerse en la escala real. Para el ajuste de precisión del texto mostrado, use FontSet.
- LineAdd() añade una línea en un espacio aleatorio en el gráfico, las coordenadas deben establecerse en la escala real.
- MarksToAxisAdd() añade nuevas etiquetas en la coordenada indicada del eje.
Es importante destacar que los datos sobre la adición de estos elementos no se guardan en ninguna parte, por consiguiente, después del dibujado de una nueva curva en el gráfico o después de su redibujado, todos los datos serán borrados.
Tipos de gráfico
La biblioteca Graphics da soporte a los tipos básicos de dibujado de curvas, todos ellos se indican en la enumeración ENUM_CURVE_TYPE:
- CURVE_POINTS — dibuja una curva con puntos
- CURVE_LINES — dibuja una curva con líneas
- CURVE_POINTS_AND_LINES — dibuja una curva tanto con puntos, como con líneas
- CURVE_STEPS — dibuja una curva escalonada
- CURVE_HISTOGRAM — dibuja una curva en forma de histograma
- CURVE_NONE — no dibuja una curva
Cada uno de los modos indicados tiene sus propiedades, cuyo cambio influye cualitativamente en la representación de la curva en el gráfico. Disponiendo del puntero CCurve a una curva se pueden cambiar rápidamente estas propiedades. Por eso precisamente se recomienda guardar todos los punteros que retorna el método CurveAdd. El nombre de la propiedad siempre comienza con el nombre del modo de dibujado de la curva en el que se usa.
Vamos a analizar con más detalle las propiedades para cada uno de los tipos.
1 El modo de dibujado con puntos CURVE_POINTS es el más rápido y sencillo, pues dibuja cada coordenada de la curva con un punto con las propiedades establecidas:
- PointsSize — tamaño de los puntos
- PointsFill — bandera que indica la presencia de rellanado
- PointsColor — color del rellenado
- PointsType — tipo de puntos
El color de la propia curva en este caso lo define el color de los puntos.
curve.PointsSize(20);
curve.PointsFill(true);
curve.PointsColor(ColorToARGB(clrRed,255));
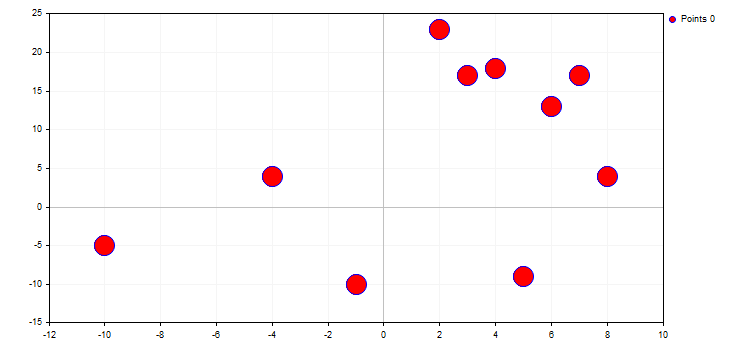
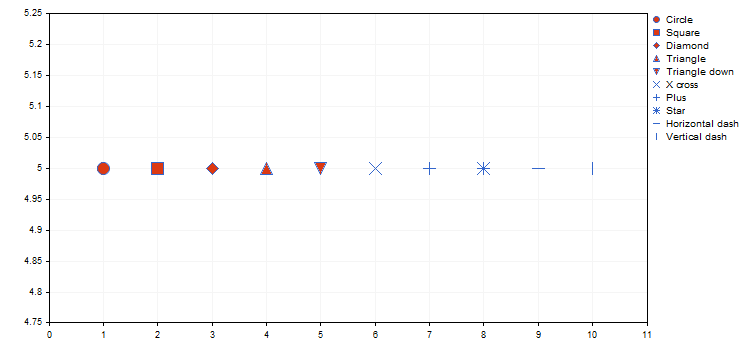
El tipo de los puntos define la figura geométrica concreta de la enumeración ENUM_POINT_TYPE con el que se representarán todos los puntos de la curva. En total, ENUM_POINT_TYPE incluye diez figuras geométricas básicas:
- POINT_CIRCLE — círculo (se usa por defecto)
- POINT_SQUARE — cuadrado
- POINT_DIAMOND — rombo
- POINT_TRIANGLE — triángulo
- POINT_TRIANGLE_DOWN — triángulo invertido
- POINT_X_CROSS — cruz
- POINT_PLUS — símbolo más
- POINT_STAR — asterisco
- POINT_HORIZONTAL_DASH — línea horizontal
- POINT_VERTICAL_DASH — línea vertical
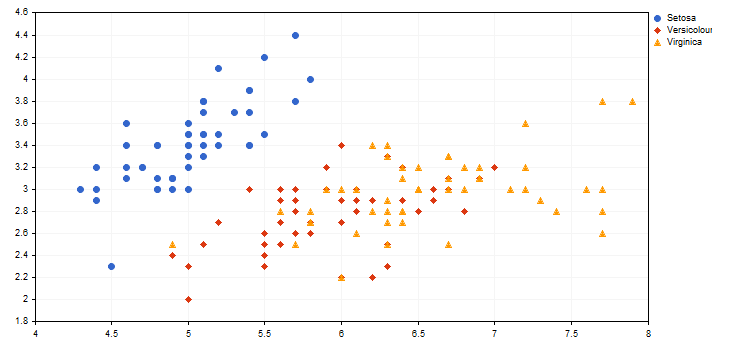
Ejemplo de representación visual de los diferentes tipos de iris (ver el artículo MetaTrader 5 — Asesores Expertos
Utilizar Mapas con Función de Auto-Organización (Mapas Kohonen)) del script adjunto IrisSample.mq5.
2. El modo de dibujado CURVE_LINES es el principal modo de visualización de curvas, en el que cada pareja de puntos se une con una o varias (en el caso del suavizado) rectas. Las propiedades de este modo son las siguientes:
- LinesStyle — estilo de la línea de la enumeración ENUM_LINE_STYLE
- LinesSmooth — bandera que indica si hay que realizar el suavizado
- LinesSmoothTension — nivel de suavizado
- LinesSmoothStep — longitud de las líneas que se aproximan durante el suavizado
En Graphics se ha implementado el algoritmo paramétrico estándar de suavizado de curvas. Este consta de dos etapas:
- Para cada pareja de puntos, basándonos en su derivada, encontramos los dos puntos de control
- Usando como base estos cuatro puntos se construye la curva de Bézier con el sato de aproximación establecido
El parámetro LinesSmoothTension adopta los valores (0.0; 1.0]. Si LinesSmoothTension se ha definido con el valor 0.0, el suavizado no tendrá lugar. Al aumentar el valor de este parámetro obtendremos una curva más y más suavizada.
curve.LinesStyle(STYLE_DOT);
curve.LinesSmooth(true);
curve.LinesSmoothTension(0.8);
curve.LinesSmoothStep(0.2);
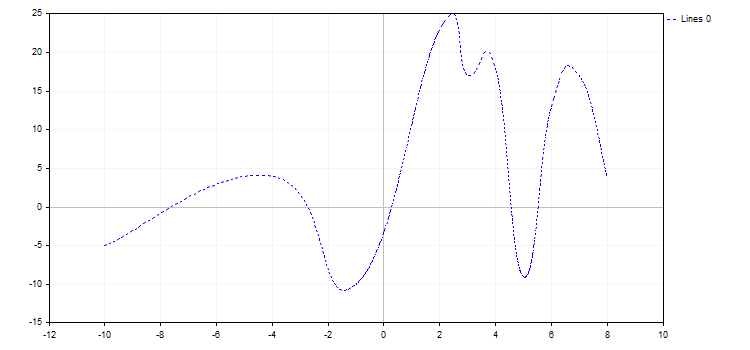
3. El modo de dibujado con puntos y la línea CURVE_POINTS_AND_LINES aúna los dos primeros modos de dibujado y sus propiedades.
4. El modo de dibujado de la curva escalonada CURVE_STEPS es el modo en el que cada pareja de puntos se une con dos líneas en forma de escalón. Este modo tiene dos propiedades:
- LinesStyle — esta propiedad se ha tomado de CURVE_POINTS y caracteriza el estilo de la línea
- StepsDimension — dimensión en la que se hace el salto: 0 — x (primero la línea horizontal, luego la vertical) o 1 — y (primero la línea vertical, luego la horizontal).
curve.LinesStyle(STYLE_DASH);
curve.StepsDimension(1);

5. El modo de dibujado con el histograma CURVE_HISTOGRAM dibuja un histograma estándar en columna. Este modo tiene solo una propiedad:
- HistogramWidth — anchura de cada columna del histograma
Si el valor de anchura es alto, los datos comenzarán a fusionarse, y las columnas con valores altos de Y "absorberán" las columnas colindantes con valores menores.
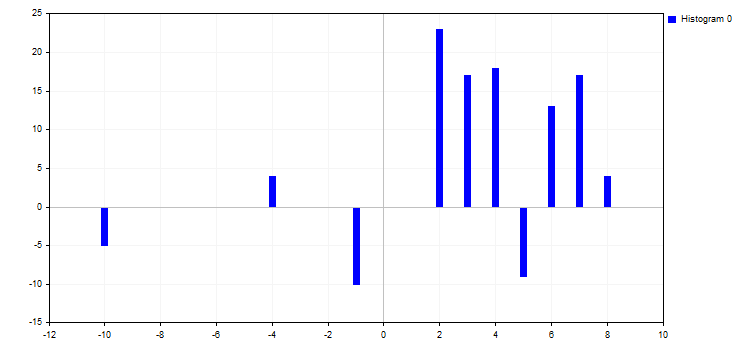
6. El último modo CURVE_NONE no presupone ninguna representación gráfica de la curva, independientemente de su visibilidad.
Conviene destacar que al realizar el escalado automático todas las curvas añadidas al gráfico tienen valor, por consiguiente, incluso si una curva no ha sido dibujada o tiene el modo CURVE_NONE, sus valores se tendrán en cuenta.
Los gráficos en las funciones, generación rápida en varias líneas
Otro aspecto cómodo de la biblioteca es el trabajo con los punteros a la función CurveFunction. Los punteros a la función MQL5 usan solo funciones globales o estáticas, en este caso, la sintaxis de la función debe corresponderse plenamente con la sintaxis del puntero. En nuestro caso, el puntero CurveFunction se configura de acuerdo con las funciones que reciben un parámetro del tipo double, y retorna asimismo double.
Para construir una curva según un puntero a una función también necesitaremos definir con exactitud el valor inicial (from) y el valor final (to) del argumento, así como su salto de crecimiento (step). Por consiguiente, cuanto menor sea el valor de crecimiento, más puntos de la función tendremos para su construcción. Para crear una serie de datos, use CurveAdd(), y para el dibujado, la función CurvePlot() o CurvePlotAll().
Para el ejemplo, crearemos una función de parábola y la dibujaremos con diferentes crecimientos:
//+------------------------------------------------------------------+
//| Parabola |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
double from1=-5;
double to1=0;
double step1=1;
double from2=0;
double to2=5;
double step2=0.2;
CurveFunction function = Parabola;
CGraphic graph;
graph.Create(0,"Graph",0,30,30,780,380);
graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
graph.CurvePlotAll();
graph.Update();
}
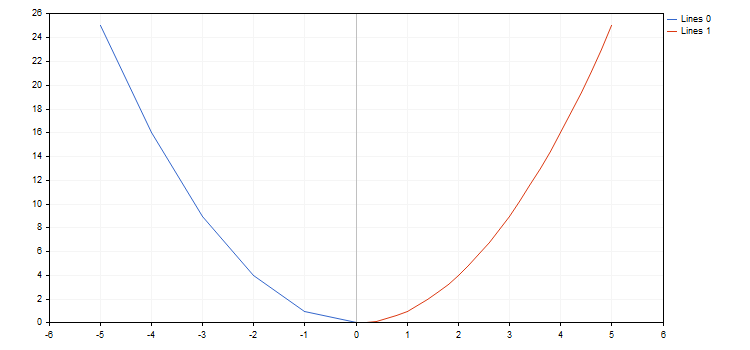
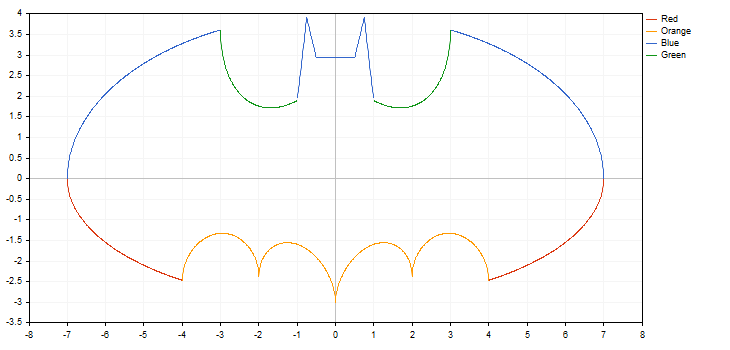
Además, la biblioteca es capaz de trabajar con funciones que tienen punto de interrupción (una de las coordenadas tiene el valor más o menos infinito, o bien no es numérico). Es importante el crecimiento según la función, puesto que en ciertos casos podemos simplemente omitir el punto de interrupción, cuando el gráfico no se corresponda con lo esperado. Por ejemplo, dibujamos dos funciones de hipérbole en el segmento [-5.0; 5.0], la primera, con un salto de 0.7, y la segunda, con un salto de 0.1. Obtenemos el siguiente resultado:
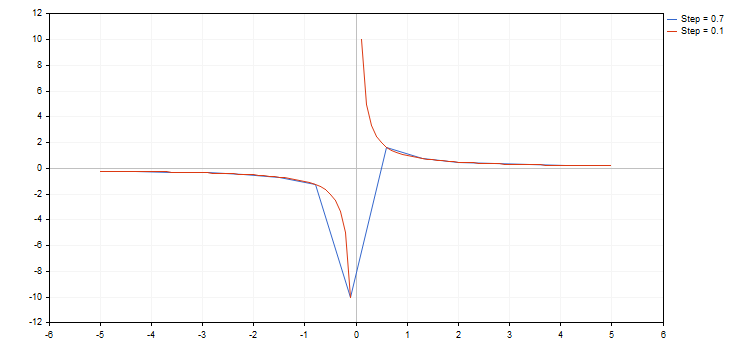
Por el dibujo podemos ver que con el salto 0.7 sencillamente hemos pasado de largo el punto de interrupción, y como conclusión el gráfico de la curva obtenida tiene poco en común con la función real de la hipérbole.
Al usar las funciones, puede aparecer el error "división por cero". Este problema se puede resolver de dos formas:
- desactivar en el archivo metaeditor.ini el control de la división por cero
[Experts]
FpNoZeroCheckOnDivision=1 - o bien analizar la fórmula usada en la función y retornar para estos casos un valor válido. Encontrará un ejemplo de este procesamiento con ayuda de una macro en los archivos adjuntos 3Functions.mq5 y bat.mq5.
Funciones de dibujado rápido
Asimismo, la biblioteca Graphics incluye una serie de funciones globales GraphPlot(), que basadas en los datos ejecutarán por sí mismas todas las etapas de creación del gráfico y como resultado retornarán el nombre del objeto en el gráfico. Estas funciones son semejantes a la función plot de R o Phyton, y permiten visualizar los datos disponibles en diferentes formatos.
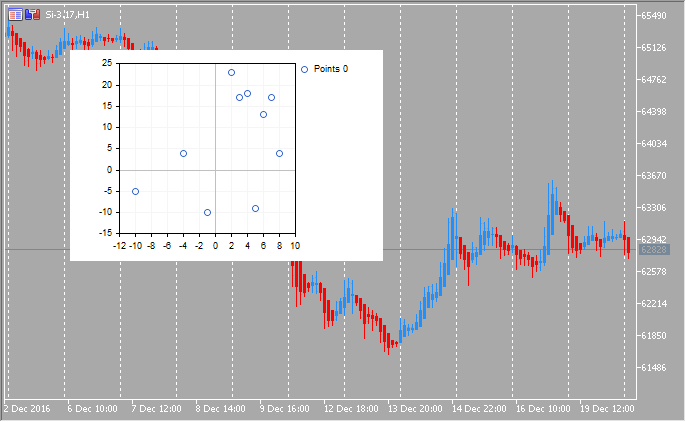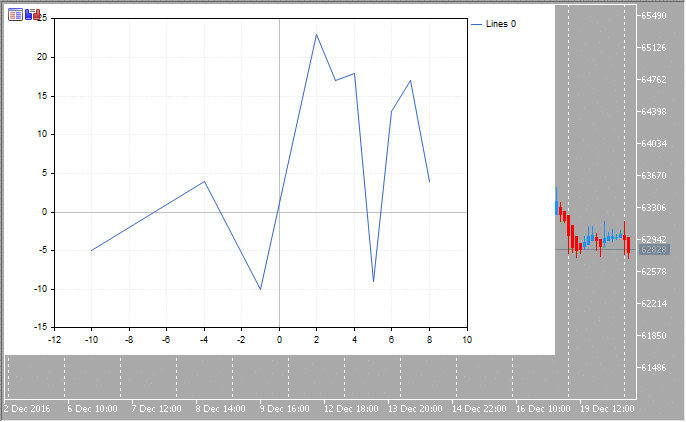
En total, la función GraphPlot tiene 10 sobrecargas diferentes, que permiten dibujar un número distinto de curvas en un gráfico y definirlas de formas diferentes. Lo único que tiene que hacer el usuario es generar los datos para la construcción de la curva con uno de los métodos. Por ejemplo, el código fuente para el dibujado rápido de dos matrices x[] e y[] tendrá el aspecto siguiente:
{
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
GraphPlot(x,y);
}
Esto tendrá un aspecto análogo en R:
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)
Comparación de gráficos según los tres modos principales de representación de dibujado construidos por la función GraphPlot en MQL5 y la función plot en R:
1 Dibujado de curvas mediante puntos
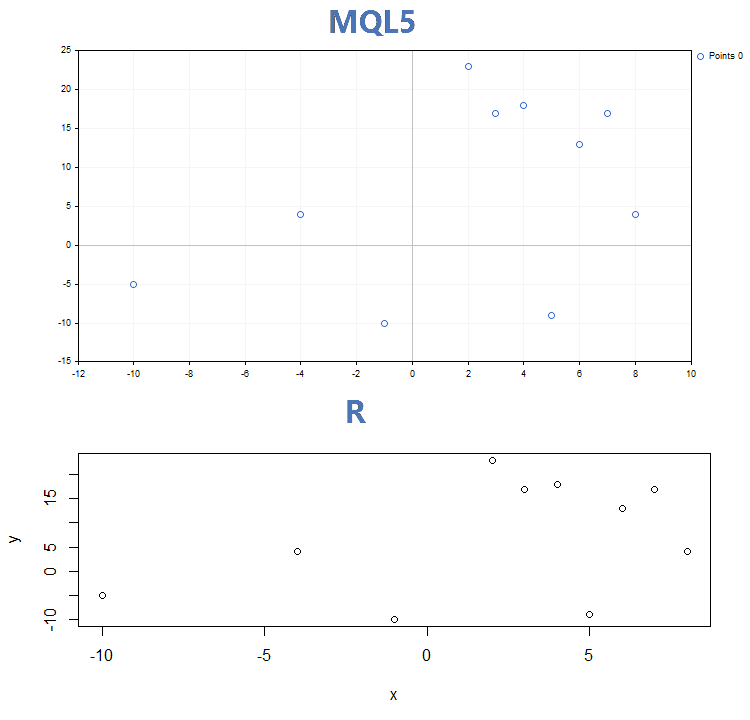
2. Dibujado con líneas
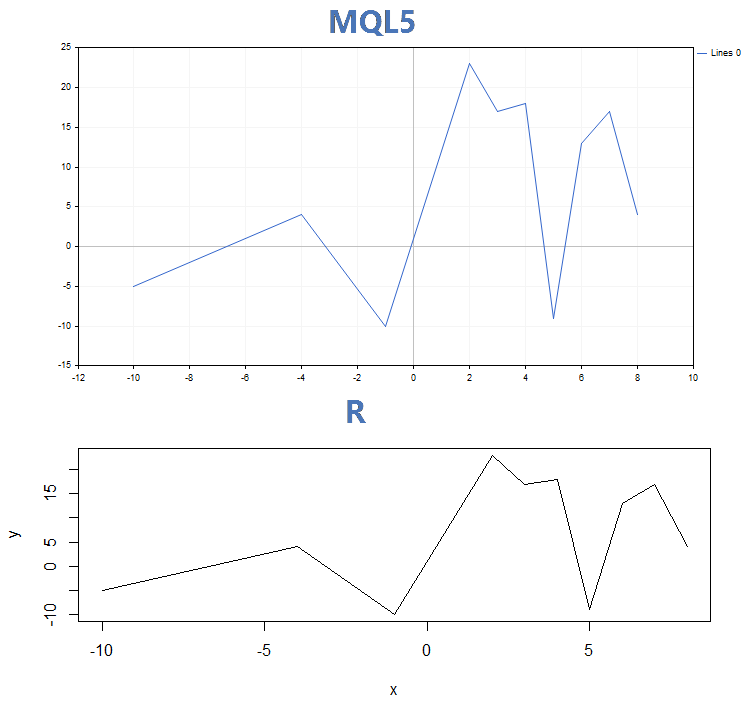
3. Dibujado con histograma
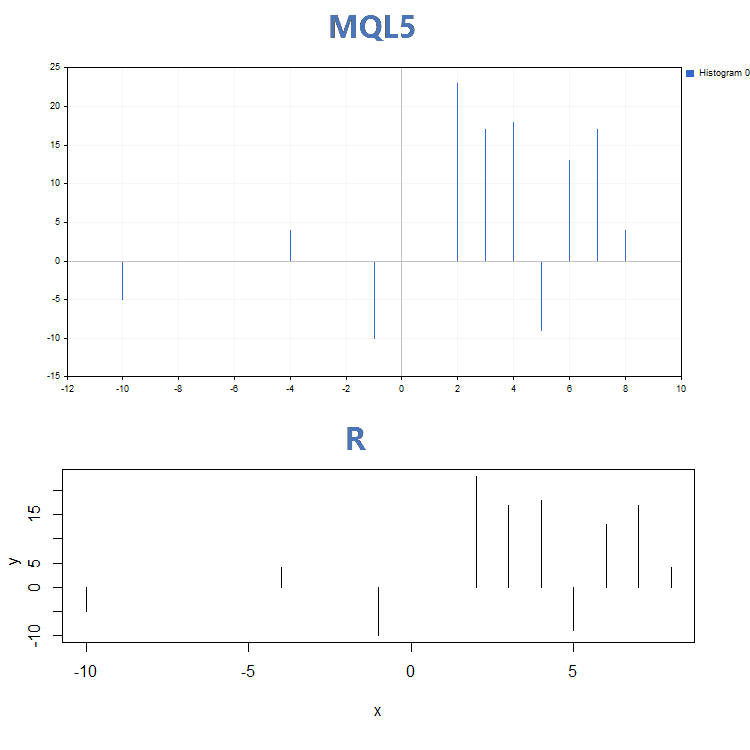
Aparte de las diferencias visuales sustanciales en lo que respecta a los resultados del funcionamiento de la función GraphPlot() en MQL5 y plot() en R, también se distinguen por sus parámetros de entrada. A diferencia de la función plot(), en la que se pueden indicar parámetros concretos de la curva (por ejemplo, lwd, anchura cambiante de la línea), la función GraphPlot() incluye solo los parámetros clave necesarios para construir los datos.
Vamos a enumerarlos:
- Datos de la curva en uno de los cuatro formatos descritos más arriba.
- Tipo de dibujado (por defecto es CURVE_POINTS).
- Nombre del objeto (por defecto, NULL).
Cada gráfico creado por la biblioteca Graphics constituye una pareja: el objeto en el gráfico y el recurso gráfico vinculado al objeto. El nombre del recurso gráfico se crea usando como base el nombre del objeto, añadiendo simplemente "::" antes del nombre. De esta forma, si el nombre del objeto fuera "SomeGraphic", el nombre de su objeto gráfico sería "::SomeGraphic".
La función GraphPlot() tiene un punto de anclaje fijo en el gráfico, x=65 y y=45. La altura y la anchura se calculan usando como base las dimensiones del propio gráfico: la anchura será del 60% de la anchura del gráfico, y la altura, del 65% de su altura. Por consiguiente, si las dimensiones del gráfico actual son inferiores a 65 por 45, la función GraphPlot() no podrá funcionar correctamente en el mismo.
Si intenta crear un gráfico y usa el nombre de un objeto ya creado, la biblioteca Graphics intentará representar el gráfico en este objeto, comprobando previamente su tipo de recurso. Si el tipo de recurso es OBJ_BITMAP_LABEL, el dibujado tendrá lugar en esta misma pareja de objeto-recurso.
Si a la función GraphPlot() se le transmite explícitamente el nombre del objeto, primero se intentará encontrar este objeto y representarlo en el gráfico. Si el objeto no ha sido localizado, se creará de forma automática una nueva pareja de objeto-recurso usando como base el nombre indicado. Al usar la función GraphPlot() sin indicación explícita del nombre del objeto, se usará el nombre estándar "Graphic".
Además, se abre una nueva posibilidad: es posible indicar de forma manual el punto de anclaje del gráfico y su tamaño. Para ello, es necesario crear manualmente una pareja objeto-recurso con los parámetros necesarios y transmitir a la función GraphPlot() el nombre del objeto creado. Resulta obvio que al crear una pareja donde el nombre del objeto sea "Graphic", nosotros, por así decirlo, redefinimos y fijamos el lienzo estándar para la función GraphPlot, evitando la necesidad de transmitir el nombre del objeto con cada llamada.
Para el ejemplo, tomaremos los datos del ejemplo de arriba y definiremos el nuevo tamaño del gráfico 750х350, y el punto de anclaje lo trasladaremos a la esquina superior izquierda:
{
//--- create object on chart and dynamic resource
string name="Graphic";
long x=0;
long y=0;
int width=750;
int height=350;
int data[];
ArrayResize(data,width*height);
ZeroMemory(data);
ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- create x and y array
double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- plot x and y array
GraphPlot(arr_x,arr_y,CURVE_LINES);
}
Ejemplos de gráficos científicos
En la Biblioteca estándar entra el apartado Estadística, en el que se presentan las funciones para trabajar con los conjuntos de las distribuciones estadísticas de la teoría de probabilidad. Para cada distribución se da un ejemplo de gráfico y del código para obtenerlo. Aquí solo vamos a mostrar estos gráficos con una imagen GIF. Los códigos fuente de los ejemplos se adjuntan igualmente en el archivo MQL5.zip, se pueden descomprimir en la carpeta MQL5\Scripts.
En todos estos ejemplos se usa la desactivación de la muestra del gráfico de precio con la ayuda de la propiedad CHART_SHOW:
ChartSetInteger(0,CHART_SHOW,false);
Esto permite, en caso necesario, convertir la ventana del gráfico en un pequeño lienzo y dibujar en el mismo objetos de cualquier complejidad usando recusos gráficos.
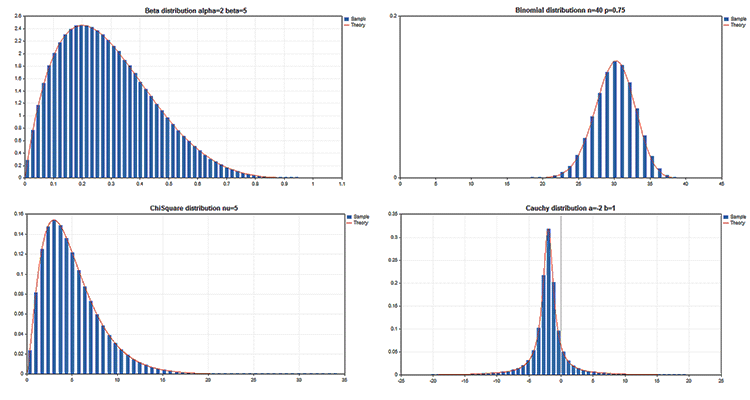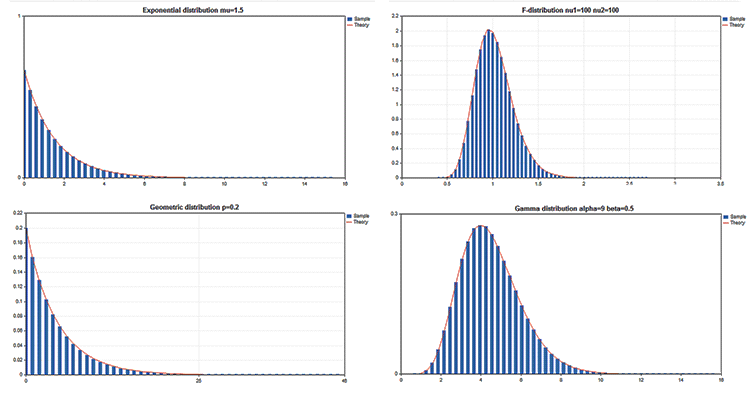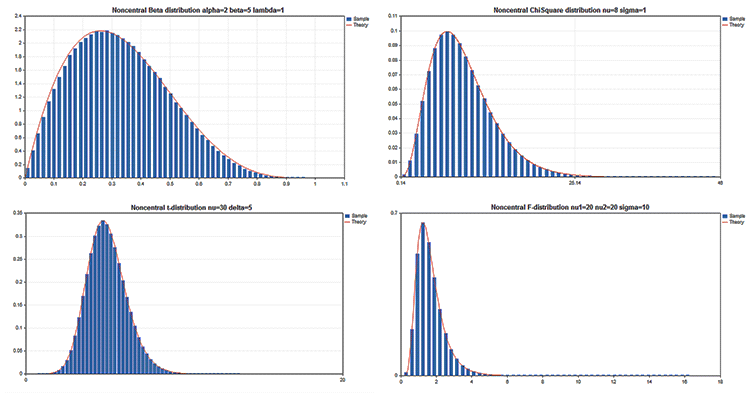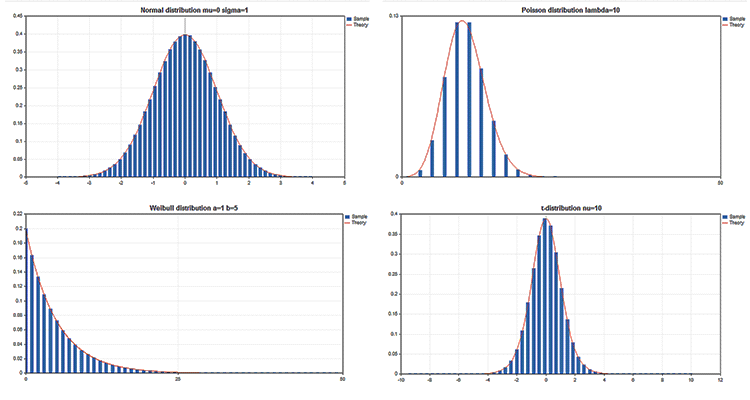
Ventajas clave de la biblioteca gráfica
En el lenguaje MQL5 los desarrolladores pueden no solo crear robots comerciales e indicadores técnicos, sino también analizar cálculos matemáticos complejos con la ayuda de las bibliotecas ALGLIB, Fuzzy y Estadística. Los datos obtenidos se pueden visualizar después con facilidad con la ayuda de la biblioteca gráfica proporcionada. Además, la mayoría de las operaciones están automatizadas: la biblioteca propone una funcionalidad muy amplia:
- 5 tipos de dibujado del gráfico
- 10 tipos de marcadores para el gráfico
- escalado automático de los gráficos en el eje X e Y
- elección automática del color, incluso si en el gráfico se muestran varias construcciones
- suavizado de líneas con ayuda del antialiasing clásico o un algoritmo de Bresenham más complejo
- posibilidad de definir los parámetros de curva-aproximación para mostrar las líneas
- posibilidad de crear el gráfico de una línea de código usando como base las dos matrices x[] e y[]
- posibilidad de crear gráficos con la ayuda de punteros a las funciones
El uso de la biblioteca gráfica no solo facilita la creación de gráficos científicos, sino que también permite elevar el desarrollo de aplicaciones comerciales a un nuevo nivel. La plataforma MetaTrader 5 permite no solo realizar cálculos matemáticos de cualquier complejidad, sino también mostrar los resultados directamente en la ventana del terminal de una forma profesional.
¡Pruebe los códigos anexos al artículo y se convencerá de que los paquetes construidos no le volverán a ser necesarios!
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2866
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Necesitamos una nueva clase con menos funciones que CCanvas. Es mejor hacer esta clase lo más parecida posible a JS canvas, que no tiene muchas funciones en esencia, para facilitar el aprendizaje y la adopción, ya que toda la TI se está moviendo hacia la web.
pero esto es lo ideal.
Probablemente podría escribir algo como esto yo mismo, pero me llevaría al menos medio año a tiempo completo
aunque personalmente no me gusta todo en JS Canvas, pero para la estandarización sería correcto implementar algo similar con pequeños cambios para prescindir del análisis sintáctico de cadenas.
Pero para el trabajo normal que necesitamos para rehacer MT5 modelo de eventos, ya que es simplemente horrible
Está claro que todo está "bajo el cuchillo", pero aún así la pregunta era un poco diferente. Lo que es deseable cambiar / refinar en la clase existente ...
Está claro que todo está "bajo el cuchillo", pero aun así la pregunta era un poco diferente. Qué es deseable cambiar/mejorar en la clase existente...
métodos suaves para darles vida. Ahora creo que incluso hay funciones en CCanvas que no están documentadas.
métodos suavizados para darles vida. Ahora parece que incluso hay funciones en CCanvas que no están documentadas.
¿En serio? No había prestado atención a eso... Tendré que echar un vistazo a mi ocio....
Necesito los gráficos del tipo "cajones con bigote", ¿hay algún plan para añadirlos?
También falta la posibilidad de utilizar subventanas/sótanos, es decir, cuando se quieren utilizar dos escalas diferentes.
Hola.
¿Tiene la clase CGraphic métodos incorporados para dibujar mapas térmicos?