Cómo crear gráficos 3D en DirectX en MetaTrader 5
3 146
1
Los gráficos computerizados en 3D se ocupan de representar los objetos de un espacio tridimensional en la superficie plana de un monitor. En este caso, además, los propios objetos o la posición del observador pueden cambiar en el tiempo, por consiguiente, deberá también cambiar la imagen en dos dimensiones, creando la ilusión de profundidad de la imagen: el giro, la aproximación, el cambio de iluminación, etcétera. MQL5 permite crear y controlar los gráficos computerizados directamente en el terminal MetaTrader 5 con la ayuda de las funciones DirectX. Para trabajar con estas funciones, la tarjeta gráfica del usuario deberá soportar DX 11 y los sombreadores de la versión 5.0.
- Modelo del objeto
- Creación de una figura
- Cálculo y dibujado de una escena
- Rotación de un objeto en el eje Z y ángulo de visión sobre una escena
- Control de la posición de la cámara
- Control del color del objeto
- Rotación y desplazamiento
- Trabajo con la iluminación
- Animación
- Control de la cámara con ayuda del ratón
- Aplicando texturas
- Creación de objetos personalizados
- Superficie 3D basada en datos
Modelo del objeto
Para dibujar un objeto tridimensional en una superficie plana, debemos crear un modelo de este objeto en las coordenadas espaciales X, Y y Z. Es decir, debemos describir cada punto en la superficie de este objeto, indicando sus coordenadas. De forma ideal, necesitaríamos describir un número infinito de puntos en la superficie del objeto, para que, fuera cual fuera el escalado, la calidad de la imagen no disminuyese. En la práctica, para describir un modelo tridimensional, se usa una red primitiva formada por polígonos. Cuanto mayor nivel de detalle tenga la red, más polígonos tendrá, y más real parecerá el modelo. Sin embargo, también será mayor el nivel de recursos de la computadora necesarios para construir un gráfico 3D.
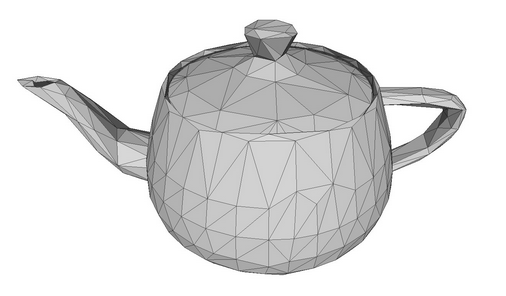
Modelo de una tetera en forma de red de polígonos.
Al principio, cuando las computadoras y las tarjetas gráficas no eran tan potentes como ahora, cada polígono se dividía en triángulos, dado que, con la ayuda de un triángulo, se puede describir de forma unívoca la posición de una pequeña área de la superficie y calcular sobre ella parámetros tan necesarios como la iluminación y el reflejo de la luz incidente. Un conjunto de varios de estos pequeños triángulos permite crear una imagen realista en tres dimensiones de un objeto. Aquí y en lo sucesivo, triángulo y polígono van a actuar como sinónimos, ya que representar un triángulo resulta bastante más sencillo que representar un polígono con N vértices.
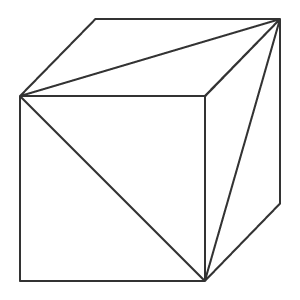
Cubo compuesto por triángulos.
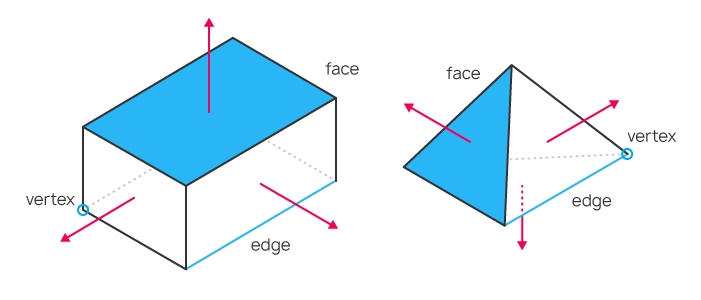
De esta forma, para crear un modelo tridimensional de un objeto, basta con describir las coordenadas de cada vértice del triángulo, para después calcular las coordenadas de cada punto del objeto, incluso si el propio objeto se desplaza en el espacio o cambia la posición del observador. Los picos del triángulo se llaman vértices (vertex), los segmentos que los unen se llaman bordes (edge), y la superficie confinada entre los segmentos se llama cara (face). Conociendo la ubicación de un triángulo en el espacio, podremos construir el vector normal (el vector que parte desde la superficie y es perpendicular a la misma) con respecto al mismo según las leyes del álgebra lineal, y calcular de esta forma cómo la luz que incide en la cara procedente de una fuente coloreará la superficie y se reflejará en ella.
Ejemplos de objetos sencillos con vértices, bordes, caras y vectores normales. El vector normal es la flecha de color rojo.
Hay diferentes métodos para crear el modelo de un objeto, la topología, por ejemplo, describe la forma en que los polígonos forman un modelo 3D (mesh). La topología regular permite usar un número mínimo de polígonos para describir un objeto y, en algunos casos, hace más simple el desplazamiento y el giro del objeto en el espacio.
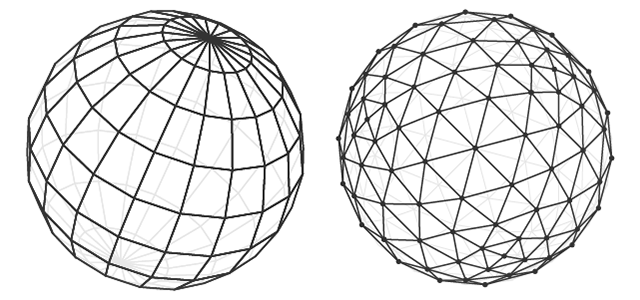
Modelo de esfera en las dos topologías.
Precisamente el juego de luz y sombra sobre los polígonos de un objeto le confiere volumen al mismo, y esta es exactamente la tarea de los gráficos computerizados: calcular para cada punto de un objeto su ubicación en el espacio, así como su color e iluminación, para después proyectar el objeto en la pantalla del monitor.
Creación de una figura
Vamos a escribir un sencillo programa que creará un cubo. Para ello, usaremos la clase CCanvas3D de la biblioteca de gráficos 3D.
La clase CCanvas3DWindow para el dibujado de la ventana 3D tiene un número mínimo de miembros y métodos, fáciles de comprender. A continuación, añadiremos todos los métodos nuevos con aclaraciones del concepto de gráficos 3D implementado en la función de trabajo con DirectX.
//+------------------------------------------------------------------+ //| Application window | //+------------------------------------------------------------------+ class CCanvas3DWindow { protected: CCanvas3D m_canvas; //--- dimensiones del lienzo int m_width; int m_height; //--- objeto Cubo CDXBox m_box; public: CCanvas3DWindow(void) {} ~CCanvas3DWindow(void) {m_box.Shutdown();} //-- creando la escena virtual bool Create(const int width,const int height){} //--- calculando la escena void Redraw(){} //--- procesando los eventos del gráfico void OnChartChange(void) {} };
Al crear una escena, comenzamos por el lienzo. Después, establecemnos para la matriz de proyección:
- Un ángulo de visión de 30 grados (M_PI/6), desde el que miramos a la escena en 3D;
- La relación de aspecto (aspect ratio) del fotograma como la relación de la anchura respecto a la altura;
- Y, finalmente, la distancia hasta las superficies de cruce cercana (0.1f) y lejana (100.f).
Esto significa que en la matriz de proyección se representarán solo los objetos que se encuentren entre estas dos paredes virtuales (0.1f y 100.f); en este caso, además, el objeto también deberá entrar en el ángulo de visión horizontal, igual a 30 grados. En general, en los gráficos computerizados, tanto las distancias como las coordenadas son virtuales, Dado que son importantes, no las magnitudes absolutas, sino la relación entre las distancias y los tamaños.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { //--- guardamos las dimensiones del lienzo m_width=width; m_height=height; //--- creamos el lienzo para dibujar la escena 3D sobre el mismo ResetLastError(); if(!m_canvas.CreateBitmapLabel("3D Sample_1",0,0,m_width,m_height,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return(false); } //--- establecemos los parámetros de la matriz de proyección: el ángulo de visión, la relación de los lados, la distancia hasta las superificies de corte cercana y lejana m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- creamos un cubo que transmitimos al gestor de recursos, los parámetros de la escena y las coordenadas de los dos ángulos opuestos del cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,5.0),DXVector3(1.0,1.0,7.0))) { m_canvas.Destroy(); return(false); } //--- añadimos el cubo a la escena m_canvas.ObjectAdd(&m_box); //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Después de la matriz de proyección, se crea el propio objeto en 3D, en nuestro caso, el cubo basado en la clase CDXBox. Para crear el cubo, será necesario y suficiente indicar dos vectores que muestren los ángulos opuestos del cubo. Si usted monitorea la creación del cubo para su depuración, podrá ver cómo en el método DXComputeBox() se crean todos los vértices del cubo (sus coordenadas se anotan en la matriz vertices), y cómo las caras del cubo se dividen en triángulos que se enumerarn y guardan en la matriz indiсes. En total, el cubo tiene 8 vértices, 6 caras divididas en 12 triángulos, y 36 índices con los vértices enumerados de estos triángulos.
Aunque el cubo solo tiene 8 vértices, para su descripción se crean 24 vectores, ya que para cada una de las 6 caras es necesario indicar su propio conjunto de vértices con su propio vector normal. La dirección del vector normal influirá en lo sucesivo en el cálculo de la iluminación de cada cara. El orden de enumeración de los vértices del triángulo en el índice influye en el lado desde el que el triángulo será visible. El orden de rellenado de los vértices e índices se puede ver en el código DXUtils.mqh:
for(int i=20; i<24; i++) vertices[i].normal=DXVector4(0.0,-1.0,0.0,0.0);
Además, en ese mismo lugar, se describen para cada cara las coordenadas de textura para el mapeado de texturas:
//--- texture coordinates for(int i=0; i<faces; i++) { vertices[i*4+0].tcoord=DXVector2(0.0f,0.0f); vertices[i*4+1].tcoord=DXVector2(1.0f,0.0f); vertices[i*4+2].tcoord=DXVector2(1.0f,1.0f); vertices[i*4+3].tcoord=DXVector2(0.0f,1.0f); }
Cada uno de los 4 vectores de la cara establece uno de los 4 ángulos de despliegue del mapeado de texturas. Esto significa que al realizar la renderización en cada cara del cubo se mapeará una estructura en forma de cuadrado para su dibujado. Si, por supuesto, se indica la textura.
Cálculo y dibujado de una escena
Con cado cambio de la escena 3D, será necesario realizar todos los cálculos de nuevo. Esto significa que deberemos calcular de forma consecutiva:
- La posición del centro del objeto en el espacio en las coordenadas del mundo;
- La posición de cada elemento del objeto, es decir, de cada vértice;
- La profundidad del píxel y su visibilidad para el observador;
- La posición de cada píxel en el polígono establecido por sus vértices;
- El color de cada píxel en el polígono de acuerdo con la textura establecida;
- La dirección del color incidente en el píxel y el reflejo del mismo;
- Aplicar luz difusa a cada píxel;
- La conversión de todas las coordenadas del mundo en coordenadas de la cámara;
- La conversión de las coordenadas de la cámara en coordenadas en la matriz de proyección.
//+------------------------------------------------------------------+ //| actualizamos la escena | //+------------------------------------------------------------------+ void Redraw() { //--- calculando la escena 3D m_canvas.Render(DX_CLEAR_COLOR|DX_CLEAR_DEPTH,ColorToARGB(clrBlack)); //--- actualizando la imagen en el lienzo de acuerdo con la escena actual m_canvas.Update(); }
En nuestro ejemplo, el cubo se crea solo una vez, y en lo sucesivo no sufre ningún cambio. Por eso, solo deberemos actualizar el fotograma en el lienzo en el caso de que haya cambios en el gráfico, como por ejemplo un cambio en sus dimensiones. En este caso, se reajustará el tamaño del lienzo según las dimensiones actuales del gráfico, se restablecerá la matriz de proyección y se actualizará la imagen en el lienzo.
//+------------------------------------------------------------------+ //| Process chart change event | //+------------------------------------------------------------------+ void OnChartChange(void) { //--- obteniendo las dimensiones actuales del gráfico int w=(int)ChartGetInteger(0,CHART_WIDTH_IN_PIXELS); int h=(int)ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS); //--- actualizando las dimensiones del lienzo de acuerdo con las dimensiones del gráfico if(w!=m_width || h!=m_height) { m_width =w; m_height=h; //--- cambiando las dimensiones del lienzo m_canvas.Resize(w,h); DXContextSetSize(m_canvas.DXContext(),w,h); //--- actualizando la matriz de proyección de acuerdo con las dimensiones del lienzo m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- recalculamos la escena 3-D y la dibujamos en el lienzo Redraw(); } }
Iniciamos el asesor "Step1 Create Box.mq5" y vemos un cuadrado blanco sobre un fondo negro. Como desconocemos la iluminación, el color blanco se establece por defecto para los objetos durante la creación.
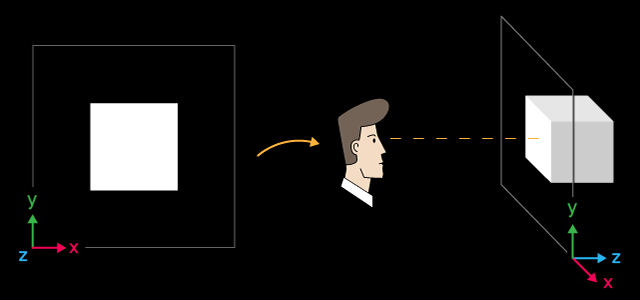
Un cubo blanco y su esquema de ubicación en el espacio
En este caso, además, el eje X está orientado a la derecha, el eje Y, hacia arriba, y el Z, hacia el fondo de la escena 3D respecto a nosotros. Este sistema de coordenadas se conoce como zurdo.
El centro del cubo se encuentra en el punto con las coordenadas X=0, Y=0, Z=6. La posición desde la que observamos el cubo se encuentra en el centro de las coordenadas, este es el valor por defecto. Si queremos cambiar la posición del punto de vista sobre la escena en 3D, deberemos indicar las coordenadas explícitamente con la ayuda de la función ViewPositionSet().
Para finalizar el funcionamiento del programa, deberemos pulsar sobre la tecla "Escape".
Rotación de un objeto en el eje Z y ángulo de visión sobre una escena
Para avivar un poco la escena, transmitiremos al cubo la rotación alrededor del eje Z. Para ello, añadiremos un temporizador cuyos eventos marcarán la rotación del cubo en el sentido opuesto a las agujas del reloj.
Vamos a crear una matriz de giro alrdedor del eje Z en el ángulo establecido, usando para ello la función DXMatrixRotationZ(), y después la transmitiremos como parámetro al método TransformMatrixSet(): esto cmabiará la posición del cubo en el espacio. Para actualizar la imagen en el lienzo, llamaremos de nuevo Redraw().
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variables para calcular el ángulo de giro static ulong last_time=0; static float angle=0; //--- obtenemos la hora actual ulong current_time=GetMicrosecondCount(); //--- calculamos delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumentamos el ángulo de giro del cubo alrededor del eje Z angle+=deltatime; //--- guardamos la hora last_time=current_time; //--- establecemos para el cubo el ángulo de giro alrededor del eje Z DXMatrix rotation; DXMatrixRotationZ(rotation,angle); m_box.TransformMatrixSet(rotation); //--- recalculamos la escena 3-D y la dibujamos en el lienzo Redraw(); }
Iniciamos y obtenemos un cuadrado blanco giratorio.
El cubo rota alrededor del eje Z en el sentido opuesto a las agujas del reloj
El código fuente de este ejemplo se encuentra en el archivo "Step2 Rotation Z.mq5". Debemos tener en cuenta que, para crear una escena, ahora se indica el ángulo M_PI/5, que es superior al ángulo=M_PI/6 del ejemplo anterior.
//--- establecemos los parámetros de la matriz de proyección: el ángulo de visión, la relación de los lados, la distancia hasta las superificies de corte cercana y lejana m_matrix_view_angle=(float)M_PI/5; m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- creamos un cubo que transmitimos al gestor de recursos, los parámetros de la escena y las coordenadas de los dos ángulos opuestos del cubo
Pero, en este caso, las dimensiones del cubo en la pantalla son ahora visualmente menores. Cuanto menor sea el ángulo de visión que indicamos al establecer la matriz de proyección, mayor será la parte del fotograma que ocupa el objeto. El proceso se asemeja al funcionamiento de un telescopio, que muestra los objetos más grandes, aunque el ángulo de visión se reduzca.
Control de la posición de la cámara
La clase CCanvas3D dispone de 3 métodos -relacionados entre sí- para establecer los parámetros importantes de una escena 3D:
- ViewPositionSet — establece la posición del punto de vista de la escena 3D
- ViewTargetSet — establece las coordinadas del punto hacia el que está dirigida la vista
- ViewUpDirectionSet — establece la dirección del borde superior del fotograma en el espacio
Todos estos métodos se usan de forma conjunta: esto significa que si queremos indicar cualquiera de estos parámetros en una escena 3D, deberemos inicializar los dos parámetros restantes, aunque sea en la etapa de generación de la escena. Vamos a mostrar esto en el ejemplo siguiente, donde balancearemos a izquierda y derecha el borde superior del fotograma. Para ello, añadiremos al método Create() 3 líneas:
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { .... //--- añadimos el cubo a la escena m_canvas.ObjectAdd(&m_box); //--- establecemos los parámetros de la escena m_canvas.ViewUpDirectionSet(DXVector3(0,1,0)); // establecemos el vector de dirección hacia arriba a lo largo del eje Y m_canvas.ViewPositionSet(DXVector3(0,0,0)); // dirigimos la mirada desde el centro de las coordenadas m_canvas.ViewTargetSet(DXVector3(0,0,6)); // orientamos la mirada hacia el centro del cubo //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Modificamos el método OnTimer() de forma que balancee el vector del horizonte a izquierda y derecha.
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { //--- variables para calcular el ángulo de giro static ulong last_time=0; static float max_angle=(float)M_PI/30; static float time=0; //--- obtenemos la hora actual ulong current_time=GetMicrosecondCount(); //--- calculamos delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumentamos el ángulo de giro del cubo alrededor del eje Z time+=deltatime; //--- guardamos la hora last_time=current_time; //--- establecemos el ángulo de giro alrededor del eje Z DXVector3 direction=DXVector3(0,1,0); // dirección inicial de la parte superior DXMatrix rotation; // vector de giro //--- calculamos la matriz de giro DXMatrixRotationZ(rotation,float(MathSin(time)*max_angle)); DXVec3TransformCoord(direction,direction,rotation); m_canvas.ViewUpDirectionSet(direction); // establecemos la nueva dirección de la parte superior //--- recalculamos la escena 3-D y la dibujamos en el lienzo Redraw(); }
Guardamos el ejemplo con el nombre "Step3 ViewUpDirectionSet.mq5" e iniciamos. Obtenemos la imagen de un cubo balanceándose, aunque en realidad permanece inmóvil. Este efecto se consigue balanceando a izquierda y derecha la propia cámara en la que se filma el vídeo.
La dirección de la parte superior se balancea a izquierda y derecha
Control del color del objeto
Vamos a modificar ligeramente nuestro código, ubicando el cubo en el centro de las coordenadas y desplazando la cámara.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... //--- creamos un cubo que transmitimos al gestor de recursos, los parámetros de la escena y las coordenadas de los dos ángulos opuestos del cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- establecemos el color m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- añadimos el cubo a la escena m_canvas.ObjectAdd(&m_box); //--- establecemos las posiciones de la cámara, el objetivo y la dirección de la parte superior m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); // establecemos el vector de dirección hacia arriba a lo largo del eje Y m_canvas.ViewPositionSet(DXVector3(3.0,2.0,-5.0)); // establecemos la cámara a la derecha, encima y delante del cubo m_canvas.ViewTargetSet(DXVector3(0,0,0)); // orientamos la mirada hacia el centro del cubo //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Asimismo, coloreamos el cubo de azul celeste: el color se establece en el formato RGB con el canal alfa (el canal alfa se indica en último lugar), pero, en este caso, los valores se normalizan hasta la unidad. De esta manera, el valor 1 indica 255, y el 0.5 indica 127.
Añadimos la rotación alrededor del eje X y guardamos los cambios en "Step4 Box Color.mq5".
Vista sobre el cubo en rotación desde arriba y a la derecha.
Rotación y desplazamiento
Podemos desplazar y rotar objetos en tres direcciones al mismo al mismo tiempo. Todos los cambios de los objetos se realizan con la ayuda de matrices, cada una de las cuales se puede calcular por separado: la rotación, el desplazamiento y la transformación de las dimensiones. Vamos a modificar el ejemplo: ahora, la cámara mira hacia el cubo desde arriba y de frente.
//+------------------------------------------------------------------+ //| Create | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- ubicamos la cámara por encima y delante del centro de las coordenadas m_canvas.ViewPositionSet(DXVector3(0.0,2.0,-5.0)); m_canvas.ViewTargetSet(DXVector3(0.0,0.0,0.0)); m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); //--- creamos un cubo que transmitimos al gestor de recursos, los parámetros de la escena y las coordenadas de los dos ángulos opuestos del cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- establecemos el color del cubo m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- calculamos la posición del cubo y la matriz de traslado DXMatrix rotation,translation; //--- giramos el cubo sucesivamente alrededor de los ejes X, Y y Z DXMatrixRotationYawPitchRoll(rotation,(float)M_PI/4,(float)M_PI/3,(float)M_PI/6); //-- desplazamos el cubo a la derecha-hacia abajo-hacia el fondo DXMatrixTranslation(translation,1.0,-2.0,5.0); //--- obtenemos la matriz de transformación como producto del giro y el traslado DXMatrix transform; DXMatrixMultiply(transform,rotation,translation); //--- establecemos la matriz de transformación m_box.TransformMatrixSet(transform); //--- añadimos el cubo a la escena m_canvas.ObjectAdd(&m_box); //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Creamos secuencialmente las matrices de giro y traslado, aplicamos la matriz de transformación obtenida y dibujamos el cubo. Guardamos los cambios en "Step5 Translation.mq5" e iniciamos.
Rotación y desplazamiento del cubo
Recordemos que la cámara mira inmóvil hacia el centro de las coordenas, un poco desde arriba. El cubo ha sido girado en tres direcciones y desplazado hacia la derecha, hacia abajo y hacia el fondo de la escena.
Trabajo con la iluminación
Para obtener una imagen realista en tres dimensiones, necesitamos calcular la iluminación de cada punto en la superficie del objeto. Para ello, se usa el modelo de Phong, que calcula la intensidad del color de los tres componentes de la iluminación: el del fondo (ambient), el difuso (diffuse) y el especular (specular). En este caso, se utilizan los siguientes parámetros:
- DirectionLight — la dirección de la fuente de iluminación directa se establece en CCanvas3D
- AmbientLight — el color y la intensidad de la iluminación indirecta se establecen en CCanvas3D
- DiffuseColor — el cálculo del componente de luz difusa se establece en CDXMesh y sus clases herederas
- EmissionColor — el componente de iluminación de fondo se establece en CDXMesh y sus clases herederas
- SpecularColor — el compoenente de reflejo especular se establece en CDXMesh y sus clases herederas
Modelo de iluminación de Phong
El modelo de iluminación se ha implementado en sombreadores estándar; los propios parámetros del modelo se indican en CCanvas3D, y los de los objetos, en CDXMesh y sus clases herederas. Vamos a introducir los cambios en nuestro ejemplo:
- Devolvemos el cubo al centro de las coordenadas.
- Le asignamos el color blanco.
- Añadimos una fuente directa de luz amarilla que ilumina la escena de arriba hacia abajo.
- Establecemos el color azul para la iluminación indirecta.
//--- establecemos el color amarillo para la fuente y lo dirigimos de arriba hacia abajo m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- establecemos el color azul para la iluminación ambiental m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); //--- creamos un cubo que transmitimos al gestor de recursos, los parámetros de la escena y las coordenadas de los dos ángulos opuestos del cubo if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- establecemos el color blanco para el cubo m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); // añadimos verde al cubo m_box.EmissionColorSet(DXColor(0.0,1.0,0.0,0.2f));
Notemos que en el modelo Canvas3D no se establece la posición de la fuente directa de iluminación, sino solo la dirección de difusión de la luz. Se supone que la fuente de luz directa se encuentra a una distancia infinita, y que sobre la escena incide un flujo de luz estrictamente paralelo.
m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); En este caso, el vector de difusión de la luz está dirigido a lo largo del eje Y en dirección negativa, es decir, de arriba hacia abajo. Además, si usted establece los parámetros de la fuente de luz directa (LightColorSet y LightDirectionSet), será necesario establecer también el color de la iluminación ambiental difusa (AmbientColorSet), ya que, por defecto, el color de la iluminación ambiental se establece como blanco y a la máxima intensidad, y todas las sombras serán de color blanco. Esto significa que los objetos en la escena estarán saturados con el color blanco de la iluminación indirecta, y el color de la iluminación ambiental será interrumpido por la luz blanca.
//--- establecemos el color amarillo para la fuente y lo dirigimos de arriba hacia abajo m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- establecemos el color azul para la iluminación ambiental m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); // indicar necesariamente
En la figura, se muestra con la ayuda de una animación GIF el cambio secuencial de la imagen al añadir iluminación. El código fuente del ejemplo se encuentra en el archivo "Step6 Add Light.mq5".
Cubo blanco con iluminación verde bajo una fuente de luz amarilla dentro de una iluminación ambiental azul.
Usted podrá desactivar en el código adjunto los métodos de trabajo con el color, para ver cómo funciona esto.
Animación
Una animación consiste en el cambio de los parámetros de una escena y unos objetos durante un determinado tiempo. Se puede cambiar cualquier propiedad, dependiendo del tiempo o el evento. Como evento que controla la actualización de la escena, crearemos un temporizador de 10 milisegundos:
int OnInit() { ... //--- create canvas ExtAppWindow=new CCanvas3DWindow(); if(!ExtAppWindow.Create(width,height)) return(INIT_FAILED); //--- set timer EventSetMillisecondTimer(10); //--- return(INIT_SUCCEEDED); }
Añadimos a la clase CCanvas3DWindow el procesador de este evento, en el que cambiaremos los parámetros del objeto (rotación, desplazamiento y escalado) y la dirección de la iluminación:
//+------------------------------------------------------------------+ //| Timer handler | //+------------------------------------------------------------------+ void OnTimer(void) { static ulong last_time=0; static float time=0; //--- obtenemos la hora actual ulong current_time=GetMicrosecondCount(); //--- calculamos delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumentamos el valor del tiempo transcurrido time+=deltatime; //--- guardamos la hora last_time=current_time; //--- calculamos la posición del cubo y la matriz de giro DXMatrix rotation,translation,scale; DXMatrixRotationYawPitchRoll(rotation,time/11.0f,time/7.0f,time/5.0f); DXMatrixTranslation(translation,(float)sin(time/3),0.0,0.0); //--- calculamos la compresión/expansión del cubo a lo largo del eje DXMatrixScaling(scale,1.0f+0.5f*(float)sin(time/1.3f),1.0f+0.5f*(float)sin(time/1.7f),1.0f+0.5f*(float)sin(time/1.9f)); //--- multiplicamos las matrices para obtener la transformación final DXMatrix transform; DXMatrixMultiply(transform,scale,rotation); DXMatrixMultiply(transform,transform,translation); //--- establecemos la matriz de transformación m_box.TransformMatrixSet(transform); //--- calculamos el giro de la fuente de luz alrededor del eje Z DXMatrixRotationZ(rotation,deltatime); DXVector3 light_direction; //--- obtenemos la dirección actual de la fuente de luz m_canvas.LightDirectionGet(light_direction); //--- calculamos la nueva dirección de la fuente de luz y la establecemos DXVec3TransformCoord(light_direction,light_direction,rotation); m_canvas.LightDirectionSet(light_direction); //--- recalculamos la escena 3D y dibujamos en el lienzo Redraw(); }
Notemos que los cambios del objeto se superponen sobre los valores iniciales, como si tomaramos cada vez un cubo desde el punto en que se creó y realizásemos todas las operaciones de rotación/desplazamiento/expansión desde cero, es decir, no se guarda memoria alguna sobre el estado actual. Al mismo tiempo, cambiamos la dirección de la fuente de luz según los incrementos de deltatime desde el valor actual hacia el nuevo.
Cubo giratorio con cambio dinámico de dirección de la fuente de luz.
Como resultado, hemos obtenido una animación en 3D muy compleja. El código del ejemplo se encuentra en el archivo "Step7 Animation.mq5".
Control de la cámara con ayuda del ratón
No queda el último elemento de animación en el gráfico 3D: la reacción a las acciones del usuario. Vamos a añadir a nuestro ejemplo el control de la cámara con la ayuda del ratón. Para ello, nos suscribimos a los eventos del ratón y creamos los manejadores correspondientes:
int OnInit() { ... //--- establecemos el temporizador EventSetMillisecondTimer(10); //--- activamos la obtención de eventos del ratón: el desplazamiento y la pulsación de botones ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,1); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,1) //--- return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { //--- eliminamos el temporizador EventKillTimer(); //--- desactivamos la obtención de eventos del ratón ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,0); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,0); //--- eliminamos el objeto delete ExtAppWindow; //--- devolvemos el gráfico al modo de muestra habitual de los gráficos de precio ChartSetInteger(0,CHART_SHOW,true); } void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { ... //--- evento de cambio del gráfico if(id==CHARTEVENT_CHART_CHANGE) ExtAppWindow.OnChartChange(); //--- evento de desplazamiento del ratón if(id==CHARTEVENT_MOUSE_MOVE) ExtAppWindow.OnMouseMove((int)lparam,(int)dparam,(uint)sparam); //--- evento de giro de la ruleta del ratón if(id==CHARTEVENT_MOUSE_WHEEL) ExtAppWindow.OnMouseWheel(dparam);
Creamos en CCanvas3DWindow el manejador del movimiento del ratón, que cambia los ángulos de dirección de la cámara al mover el ratón con el botón izquierdo pulsado:
//+------------------------------------------------------------------+ //| Procesando el movimiento del ratón | //+------------------------------------------------------------------+ void OnMouseMove(int x,int y,uint flags) { //--- botón izquierdo del ratón if((flags&1)==1) { //--- no hay información sobre la anterior posición del ratón if(m_mouse_x!=-1) { //--- actualizar el ángulo de la cámara según el cambio de posición m_camera_angles.y+=(x-m_mouse_x)/300.0f; m_camera_angles.x+=(y-m_mouse_y)/300.0f; //--- establecer el ángulo vertical en el intervalo (-Pi/2,Pi2) if(m_camera_angles.x<-DX_PI*0.49f) m_camera_angles.x=-DX_PI*0.49f; if(m_camera_angles.x>DX_PI*0.49f) m_camera_angles.x=DX_PI*0.49f; //--- actualizar la posición de la cámara UpdateCameraPosition(); } //--- guardamos la posición del ratón m_mouse_x=x; m_mouse_y=y; } else { //--- reseteamos la posición guardada si el botón izquierdo del ratón no está pulsado m_mouse_x=-1; m_mouse_y=-1; } }
Y el manejador del giro de la ruleta, que cambia la distancia de la cámara hasta el centro de la escena:
//+------------------------------------------------------------------+ //| Procesamiento de los eventos de la ruleta del ratón | //+------------------------------------------------------------------+ void OnMouseWheel(double delta) { //--- actualizando el distanciamiento de la cámara según el giro de la ruleta del ratón m_camera_distance*=1.0-delta*0.001; //--- estableciendo la distancia en el intervalo [3,50] if(m_camera_distance>50.0) m_camera_distance=50.0; if(m_camera_distance<3.0) m_camera_distance=3.0; //--- actualizar la posición de la cámara UpdateCameraPosition(); }
Los dos manejadores llaman al método UpdateCameraPosition() para actualizar la posición de la cámara de acuerdo con los parámetros modificados:
//+------------------------------------------------------------------+ //| Actualiza la posición de la cámara | //+------------------------------------------------------------------+ void UpdateCameraPosition(void) { //--- posición de la cámara sin giro, teniendo en cuenta la distancia hasta el centro de las coordenadas DXVector4 camera=DXVector4(0.0f,0.0f,-(float)m_camera_distance,1.0f); //--- rotación de la cámara alrededor del eje X DXMatrix rotation; DXMatrixRotationX(rotation,m_camera_angles.x); DXVec4Transform(camera,camera,rotation); //--- rotación de la cámara alrededor del eje Y DXMatrixRotationY(rotation,m_camera_angles.y); DXVec4Transform(camera,camera,rotation); //--- ponemos la cámara en posición m_canvas.ViewPositionSet(DXVector3(camera)); }
El código modificado se encuentra en el archivo "Step8 Mouse Control.mq5".
Control de la cámara con la ayuda del ratón.
Aplicando texturas
Una textura es una imagen de mapa de bits superpuesta sobre la superficie de un polígono para representar colores, patrones o transmitir la sensación de relieve. El uso de texturas permite reproducir en una superficie objetos pequeños cuya representación requeriría muchos recursos si usáramos polígonos. Por ejemplo, un dibujo que imite una piedra, un árbol, una pared o tierra.
La clase CDXMesh y sus clases herederas permiten establecer para un objeto una textura que, en un sombreador de píxeles estándar, se usa de forma conjunta con su color de difusión (DiffuseColor). Vamos a quitar la animación del objeto y a superponer sobre el mismo la textura de una piedra que deberá encontrarse en la carpeta MQL5\Files del directorio de trabajo del terminal:
virtual bool Create(const int width,const int height) { ... //--- establecemos el color blanco para la iluminación indirecta m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- añadimos la textura para dibujar las caras del cubo m_box.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- añadimos el cubo a la escena m_canvas.ObjectAdd(&m_box); //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Cubo con una textura de piedra colocada.
Creación de objetos personalizados
Todos los objetos constan de vértices (DXVector3), y estos vértices se conectan con ayuda de índices en ciertas primitivas. La primitiva más extendida es el triángulo. Para crear un objeto en 3D, debemos crear una lista de vértices que contengan como mínimo sus coordenadas (pero pueden contener multitud de datos adicionales, como el vector normal, el color, etcétera), el tipo de primitivas en las que se unen y una lista con los índices de los vértices, según la cual se unirán en primitivas.
En la Biblioteca Estándar se ha definido el tipo de vértice DXVertex, que contiene su coordenada, el vértice normal para el cálculo, las coordenadas de textura y el color. Con este tipo de vértices trabaja el sombreador de vértices estándar.
struct DXVertex
{
DXVector4 position; // coordenadas de los vértices
DXVector4 normal; // vector normal
DXVector2 tcoord; // coordenadas de la cara para colocar la textura
DXColor vcolor; // color
};
El archivo auxiliar MQL5\Include\Canvas\DXDXUtils.mqh contiene un conjunto de métodos para generar la geometría (vértices e índices) de las primitivas básicas, así como para cargar la geometría 3D desde archivos .OBJ.
Vamos a añadir la creación de la esfera y el toro, superponiendo sobre ellos la misma textura de piedra:
virtual bool Create(const int width,const int height) { ... //--- vértices e índices para los objetos creados manualmente DXVertex vertices[]; uint indices[]; //--- preparamos los vértices e índices para la esfera if(!DXComputeSphere(0.3f,50,vertices,indices)) return(false); //--- establecemos el color blanco para los vértices DXColor white=DXColor(1.0f,1.0f,1.0f,1.0f); for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- creamos el objeto de esfera if(!m_sphere.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- establecemos el color de iluminación dispersa para la esfera m_sphere.DiffuseColorSet(DXColor(0.0,1.0,0.0,1.0)); //--- establecemos el color blanco para el reflejo de la esfera m_sphere.SpecularColorSet(white); m_sphere.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- añadimos la esfera a la escena m_canvas.ObjectAdd(&m_sphere); //--- preparamos los vértices e índices para el toro if(!DXComputeTorus(0.3f,0.1f,50,vertices,indices)) return(false); //--- establecemos el color blanco para los vértices for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- creamos el objeto toro if(!m_torus.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- establecemos el color de iluminación dispersa para el toro m_torus.DiffuseColorSet(DXColor(0.0,0.0,1.0,1.0)); m_torus.SpecularColorSet(white); m_torus.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- añadimos el toro a la escena m_canvas.ObjectAdd(&m_torus); //--- redibujamos la escena Redraw(); //--- succeed return(true); }
Asimismo, añadimos la animación para los nuevos objetos:
void OnTimer(void) { ... m_canvas.LightDirectionSet(light_direction); //--- órbita de la esfera DXMatrix translation; DXMatrixTranslation(translation,1.1f,0,0); DXMatrixRotationY(rotation,time); DXMatrix transform; DXMatrixMultiply(transform,translation,rotation); m_sphere.TransformMatrixSet(transform); //--- órbita del toro con rotación alrededor de su eje DXMatrixRotationX(rotation,time*1.3f); DXMatrixTranslation(translation,-2,0,0); DXMatrixMultiply(transform,rotation,translation); DXMatrixRotationY(rotation,time/1.3f); DXMatrixMultiply(transform,transform,rotation); m_torus.TransformMatrixSet(transform); //--- recalculamos la escena 3D y dibujamos en el lienzo Redraw(); }
Guardamos los cambios en "Three Objects.mq5" e iniciamos.
Figuras rotando en la órbita del cubo.
Superficie 3D basada en datos
Para crear informes y analizar datos, se suelen usar gráficos diversos: gráficos lineales, histogramas, diagramas circulares, etcétera. MQL5 también ofrece para dichos objetivos usar una cómoda biblioteca gráfica, pero esta puede dibujar solo gráficos planos.
La clase CDXSurface permite visualizar en el espacio una superficie basada en los datos de usuario guardados en una matriz bidimensional. Vamos a mostrar cómo se hace esto usando una función matemática
z=sin(2.0*pi*sqrt(x*x+y*y))
Creamos un objeto para dibujar la superficie, y una matriz para guardar los datos:
virtual bool Create(const int width,const int height) { ... //--- preparamos la matriz para el guardado de datos m_data_width=m_data_height=100; ArrayResize(m_data,m_data_width*m_data_height); for(int i=0;i<m_data_width*m_data_height;i++) m_data[i]=0.0; //--- creamos el objeto de superficie if(!m_surface.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { m_canvas.Destroy(); return(false); } //--- establecemos la textura y el reflejo para la superficie m_surface.SpecularColorSet(DXColor(1.0,1.0,1.0,1.0)); m_surface.TextureSet(m_canvas.DXDispatcher(),"checker.bmp"); //--- añadimos la superficie a la escena m_canvas.ObjectAdd(&m_surface); //--- succeed return(true); }
La superficie se dibujará dentro de un paralelepípedo con una base de 4x4 y una altura de 1. El tamaño de la textura será de 0.25x0.25.
- SF_TWO_SIDED indica que la superficie se dibujará tanto por arriba como por abajo, en el caso de que la cámara se mueva por debajo de la superficie.
- SF_USE_NORMALS indica que se usarán los cálculos de los vectores normales para calcular los reflejos sobre la superficie provocados por una fuente de luz directa.
- CS_COLD_TO_HOT establece el mapa de color de la superficie, yendo del color azul al rojo con transiciones de verde y amarillo.
Para animar la superficie, vamos a añadir la hora bajo el signo del seno, actualizándola después según el temporizador.
void OnTimer(void) { static ulong last_time=0; static float time=0; //--- obtenemos la hora actual ulong current_time=GetMicrosecondCount(); //--- calculamos delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- aumentamos el valor del tiempo transcurrido time+=deltatime; //--- guardamos la hora last_time=current_time; //--- calculamos los valores de la superficie teniendo en cuenta los cambios temporales for(int i=0; i<m_data_width; i++) { double x=2.0*i/m_data_width-1; int offset=m_data_height*i; for(int j=0; j<m_data_height; j++) { double y=2.0*j/m_data_height-1; m_data[offset+j]=MathSin(2.0*M_PI*sqrt(x*x+y*y)-2*time); } } //--- actualizamos los datos para el dibujado de la superficie if(m_surface.Update(m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { //--- recalculamos la escena 3D y dibujamos en el lienzo Redraw(); } }El archivo fuente se encuentra en "3D Surface.mq5". En el vídeo se muestra un ejemplo del funcionamiento.
En este artículo, hemos mostrado cómo las funciones DirectX permiten crear figuras geométricas sencillas y gráficos 3D animados para analizar datos visualmente. Podrá encontrar ejemplos más complejos en la carpeta de instalación del terminal MetaTrader 5: los expertos "Correlation Matrix 3D" y "Math 3D Morpher", así como el script "Remnant 3D".
Con la ayuda de MQL5, podemos solucionar varias tareas importantes de trading algorítmico sin recurrir a paquetes externos:
- Optimizar estrategias comerciales complejas que contienen multitud de parámetros de entrada
- Obtener los resultados de la optimización
- Representar de una forma más conveniente en la pantalla los datos obtenidos usando imágenes en tres dimensiones.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/7708
Biblioteca para el desarrollo rápido y sencillo de programas para MetaTrader (Parte XXXIV): Solicitudes comerciales pendientes - Eliminación de órdenes y posiciones según condiciones
Biblioteca para el desarrollo rápido y sencillo de programas para MetaTrader (Parte XXXIII): Solicitudes comerciales pendientes - Cierre de posiciones según condiciones
Trabajando con las funciones de red, o MySQL sin DLL: Parte II - El programa para monitorear los cambios de las propiedades de las señales
Pronosticación de series temporales (Parte 1): el método de descomposición modal empírica (EMD)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso