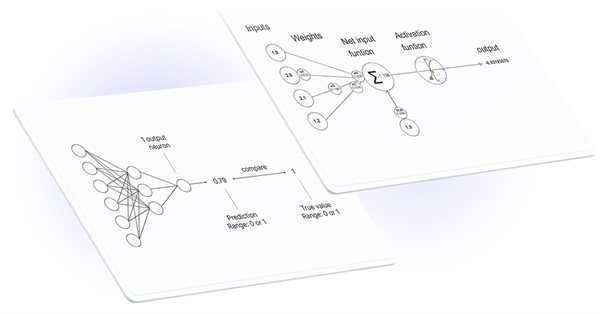
MQL5'te matrisler ve vektörlerle çalışma

Çok çeşitli matematik problemlerinin verimli bir şekilde çözülebilmesi adına MQL5 diline özel veri türleri - matrisler ve vektörler - eklendi. Yeni türler, matematiksel gösterime yakın, öz ve anlaşılır kodlar yazmak için yerleşik metotlar sağlar. Bu makalede, “Matris ve vektör metotları” bölümündeki yerleşik metotların kısa bir açıklamasını sunacağız.

İçindekiler

• Matris ve vektör türleri
• Oluşturma ve başlatma
• Matrisleri ve dizileri kopyalama
• Zaman serilerini matrislere veya vektörlere kopyalama
  
• Matris ve vektör işlemleri
• Manipülasyonlar
  
• Çarpımlar
  
• Dönüşümler
• İstatistikler
  
• Özellikler
• Denklem çözme
  
• Makine öğrenimi metotları
• OpenCL'de iyileştirmeler
• Makine öğreniminde MQL5'in geleceği
  

Her programlama dilinde int, double vb. sayısal değişken kümelerinin depolanmasına olanak sağlayan diziler gibi veri türleri vardır. Dizi elemanlarına erişim indekslerle gerçekleştirilir, bu da döngüler kullanılarak dizi işlemlerinin yapılmasına olanak tanır. En yaygın kullanılan diziler tek boyutlu ve iki boyutlu dizilerdir:

int    a[50];       // One-dimensional array of 50 integers
double m[7][50];    // Two-dimensional array of 7 subarrays, each consisting of 50 integers
MyTime t[100];      // Array containing elements of MyTime type

Dizilerin yetenekleri genellikle veri depolama ve işleme gibi nispeten basit görevler için yeterlidir. Ancak karmaşık matematik problemleri söz konusu olduğunda, çok sayıda iç içe döngü nedeniyle dizilerle çalışmak hem programlama hem de kod okuma açısından zorlaşır. En basit lineer cebir işlemleri bile aşırı derecede kodlama ve iyi bir matematik bilgisi gerektirir.

Makine öğrenimi, sinir ağları ve 3D grafikler gibi modern veri teknolojileri, vektör ve matris kavramlarını kullanan lineer cebir problem çözmeden kapsamlı bir şekilde yararlanmaktadır. Dolayısıyla, bu tür nesnelerle yerel olarak çalışılabilmesi için MQL5’e özel veri türleri eklenmiştir: matrisler ve vektörler. Yeni türler, birçok rutin programlama işlemini ortadan kaldırır ve kod kalitesini artırır.

Matris ve vektör türleri

Kısaca ifade edecek olursak, bir vektör, tek boyutlu bir double türü dizidir ve bir matris ise iki boyutlu bir double türü dizidir. Vektörler dikey ve yatay olabilir, ancak MQL5'te ayrılmazlar.

Bir matris, birinci indeksin satır numarası, ikinci indeksin de sütun numarası olduğu bir yatay vektörler dizisi şeklinde düşünülebilir.

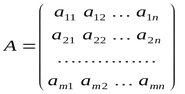
Satırların ve sütunların numaralandırması, dizilere benzer şekilde 0'dan başlar.

double türü veriler içeren matrix ve vector türlerine ek olarak, ilgili veri türleriyle çalışmak için dört tür daha vardır:

• matrixf - float elemanlar içeren matris
  
• matrixc - complex elemanlar içeren matris
  
• vectorf - float elemanlar içeren vektör
• vectorc - complex elemanlar içeren vektör

Bu makalenin yazıldığı sırada, matrixc ve vectorc türleri üzerindeki çalışmalar henüz tamamlanmamıştır ve bu nedenle bu türleri yerleşik metotlarda kullanmak henüz mümkün değildir.

Şablon fonksiyonlarında ilgili dört tür yerine matrix<double>, matrix<float>, vector<double> ve vector<float> kullanılabilir.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */

Oluşturma ve başlatma

Matris ve vektör metotları amaçlarına göre dokuz kategoriye ayrılır. Matrisleri ve vektörleri bildirmenin ve başlatmanın birkaç yolu vardır.

En basit oluşturma yöntemi, boyut belirtmeden, yani veriler için bellek ayırmadan bildirim yapmaktır. Burada sadece veri türünü ve değişken adını yazıyoruz:

  matrix         matrix_a;   // double type matrix
  matrix<double> matrix_a1;  // another way to declare a double matrix, suitable for use in templates
  matrix<float>  matrix_a3;  // float type matrix
  vector         vector_a;   // double type vector
  vector<double> vector_a1;  // another notation to create a double vector
  vector<float>  vector_a3;  // float type vector

Ardından, oluşturulan nesnelerin boyutlarını değiştirebilir ve onları istediğimiz değerlerle doldurabilirsiniz. Hesaplama sonuçlarını elde etmek için yerleşik matris metotlarında da kullanılabilirler.

Ayrıca, matrisler ve vektörler, herhangi bir başlatma yapmadan, boyut belirterek, yani veriler için bellek ayırarak da bildirilebilir. Burada değişken adından sonra parantez içerisinde boyutları belirtiyoruz:

  matrix         matrix_a(128,128);           // the parameters can be either constants
  matrix<double> matrix_a1(InpRows,InpCols);  // or variables
  matrix<float>  matrix_a3(InpRows,1);        // analogue of a vertical vector
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float>  vector_a3(InpSize+16);       // expression can be used as a parameter

Nesne oluşturmanın üçüncü yolu, başlatmayla bildirim yapmaktır. Bu durumda, matrislerin ve vektörlerin boyutları süslü parantezlerin içerisinde belirtilen başlatma sırasına göre belirlenir:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // the matrices must be of the same type
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                     // the vectors must be of the same type 

Belirli bir formda matrisler ve vektörler oluşturmak için statik metotlar da kullanılabilir: 

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Ayrıca, bir matrisi veya vektörü istenen değerlerle başlatmak için statik olmayan metotlar da mevcuttur - Init ve Fill:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

Bu örnekte, halihazırda başlatılmış bir matrisi yeniden boyutlandırmak için Init metodunu kullandık ve bu, yeni elemanların rastgele değerlerle doldurulmasıyla sonuçlandı.

Init metodunun önemli bir avantajı, matris/vektör elemanlarının belirli bir kurala göre doldurulabilmesi için parametrelerde bir başlatma fonksiyonun belirtebilmesi yeteneğidir. Örneğin:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Execution result
  init = 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Fills the matrix with powers of a number                         |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 } 

Matrisleri ve dizileri kopyalama

Matrisler ve vektörler Copy metodu kullanılarak kopyalanabilir. Ancak, bu veri türlerini kopyalamanın daha basit ve daha tanıdık yolu, = atama operatörünü kullanmaktır. Ayrıca, kopyalama için Assign metodu da kullanılabilir.

//--- copying matrices
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

Assign'ın Copy'den farkı, yalnızca matrisler için değil, hem matrisler hem de diziler için kullanılabilmesidir. Aşağıdaki örnekte int_arr int türü dizisinin bir double türü matrise kopyalanması gösterilmektedir. Elde edilen matris, kopyalanan dizinin boyutuna göre otomatik olarak ayarlanır.

//--- copying an array to a matrix
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

Böylece, Assign metodu, otomatik boyut ve tür dönüştürmeyle dizilerden matrislere sorunsuz bir şekilde geçiş yapılmasına olanak sağlar.

Zaman serilerini matrislere veya vektörlere kopyalama

Fiyat grafiklerinin analiz edilebilmesi için MqlRates yapısı dizilerinin alınması ve işlenmesi gereklidir. Ancak artık onlarla çalışmanın başka bir yolu daha vardır.

CopyRates metodu, MqlRates yapısının geçmiş verileri serisini doğrudan bir matrise veya vektöre kopyalar. Böylece, “Zaman Serilerine ve Gösterge Verilerine Erişim” bölümündeki fonksiyonları kullanarak gerekli zaman serilerini ilgili dizilere almanıza gerek kalmaz. Ayrıca bir matrise veya vektöre aktarılmaları da gerek yoktur. CopyRates metoduyla fiyatları tek bir çağrıda bir matrise veya vektöre alabilirsiniz. Bir sembol listesi için korelasyon matrisinin nasıl hesaplanacağına dair bir örnek ele alalım: bu değerleri iki şekilde hesaplayalım ve sonuçları karşılaştıralım.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- list of symbols for calculation
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- matrix and vector to receive Close prices
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- get Close prices to a vector
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- insert the vector to the timeseries matrix
      rates.Col(close, i);
      PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size());
      //--- output the first 20 vector values for debugging
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 Close prices were added to the matrix
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 Close prices were added to the matrix
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 Close prices were added to the matrix
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 Close prices were added to the matrix
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 Close prices were added to the matrix
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- prepare a matrix of correlations between symbols
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Compute pairwise correlation coefficients");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Correlation matrix on vectors: \n", corr_from_vector);
  /*
  Calculate pairwise correlation coefficients
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0.397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0.744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Correlation matrix on vectors:
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- now let's see how a correlation matrix can be calculated in one line
  matrix corr_from_matrix=rates.CorrCoef(false);   // false means that the vectors are in the matrix columns
  Print("Correlation matrix rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- compare the resulting matrices to find discrepancies
  Print("How many discrepancy errors between result matrices?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Correlation matrix rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  How many discrepancy errors between result matrices?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- create a nice output of the correlation matrix
  Print("Output the correlation matrix with headers");
  string header="        ";  // header
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- now rows
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Output the correlation matrix with headers
            EURUSD  GBPUSD  USDJPY  USDCAD  USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Returns a string with vector values                              |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- compose a string
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- add a tail if the vector length exceeds the specified size
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//|  Returns a string with the specified number of spaces            |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

Örnek, şunların nasıl yapılabileceğini göstermektedir:

• CopyRates’i kullanarak kapanış fiyatlarını alma
• Col metodunu kullanarak matrise vektör ekleme
  
• CorrCoef’i kullanarak iki vektör arasındaki korelasyon katsayısını hesaplama
• CorrCoef’i kullanarak değer vektörlerini içeren matris üzerinde korelasyon matrisini hesaplama
• TriU metodunu kullanarak matrisi üst üçgensel matris haline getirme
  
• Compare metodunu kullanarak iki matrisi karşılaştırma ve tutarsızlıkları bulma

Matris ve vektör işlemleri

Matrisler ve vektörler üzerinde, eleman bazlı olarak toplama, çıkarma, çarpma ve bölme gibi matematik işlemleri gerçekleştirilebilir. Bunun yapılabilmesi için her iki nesnenin de aynı türde ve aynı boyutlara sahip olması gerekir. Matrisin veya vektörün her bir elemanı ikinci matrisin veya vektörün karşılık gelen elemanıyla işleme girer.

İkinci terim (çarpan, çıkaran veya bölen) olarak uygun türde (double, float veya complex) bir skaler de kullanılabilir. Bu durumda, matrisin veya vektörün her bir elemanı belirtilen skalerle işleme girecektir.

  matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // Hadamard product
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- operations in place are possible
  matrix_a+=matrix_b;
  matrix_a/=2;

Ayrıca, matrisler ve vektörler çoğu matematiksel fonksiyona parametre olarak da iletilebilir. İlgili fonksiyonlar şunlardır: MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. Burada da matrisler ve vektörler eleman bazında işlenir. Örnek:

//---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

MathMod ve MathPow durumunda, ikinci parametre olarak uygun boyutta bir skaler veya matris/vektör kullanılabilir.

   matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }

Manipülasyonlar

Matrisler ve vektörler üzerinde, herhangi bir hesaplama gerektirmeyen temel manipülasyonlar da gerçekleştirilebilir:

• Transpozisyon
• Satırları, sütunları ve köşegenleri alma
• Matrisleri yeniden boyutlandırma ve yeniden şekillendirme
  
• Satırları ve sütunları değiştirme
  
• Yeni bir nesneye kopyalama
  
• İki nesneyi karşılaştırma
  
• Bir matrisi birden çok alt matrise bölme
• Sıralama
  

Aşağıda, Transpose metoduyla bir matris transpozisyonu örneği gösterilmektedir:

  matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

Aşağıdaki örneklerde Diag metoduyla bir köşegenin nasıl ayarlanacağı ve alınacağı gösterilmektedir:

   vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

Reshape metoduyla matris boyutunu değiştirme:

   matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

Vsplit metoduyla matrisin dikey olarak bölünmesine örnekler:

   matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

Col ve Row metotları, yalnızca bir matrisin ilgili elemanlarını almaya değil, aynı zamanda ayrılmamış (unallocated) matrislere, yani boyuta sahip olmayan matrislere elemanlar eklenmesine de olanak tanır. Bunu bir örnekle gösterelim:

   vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("col 1 - ",m2.Col(1));
  /*
   col 1 - [8,8,8,8]
  */

   Print("col 2 - ",m2.Col(2));
  /*
   col 1 - [8,8,8,8]  col 2 - [1,2,3,8]
  */

Çarpımlar

Matris çarpımı, sayısal metotlarda yaygın olarak kullanılan temel algoritmalardan biridir. Sinir ağı evrişimli katmanlarında ileri ve geri yayılım algoritmalarının birçok uygulaması bu işleme dayanmaktadır. Genellikle, makine öğrenimi için harcanan tüm zamanın %90-95'e varan kısmında bu işlem yer alır. Tüm çarpım metotları, “Matrislerin ve vektörlerin çarpımları” bölümünde yer almaktadır.

Aşağıdaki örnekte MatMul metoduyla iki matrisin çarpımı gösterilmektedir:

   matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

Kron metoduyla iki matrisin veya bir matris ile bir vektörün Kronecker çarpımına bir örnek:

   matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

“MQL5'te matrisler ve vektörler” makalesinden daha fazla örnek:

//--- initialize matrices
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Product of horizontal vector v[3] and matrix m[3,5]");
   vector v3 = {1,2,3};
   Print("On the left v3 = ",v3);
   Print("On the right m35 = \n",m35);
   Print("v3.MatMul(m35) = horizontal vector v[5] \n",v3.MatMul(m35));
   /*
   1. Product of horizontal vector v[3] and matrix m[3,5]
   On the left v3 = [1,2,3]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = horizontal vector v[5]
   [40,46,52,58,64]
   */

//--- show that this is really a horizontal vector
   Print("\n2. Product of matrix m[1,3] and matrix m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("On the left m13 = \n",m13);
   Print("On the right m35 = \n",m35);
   Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35));
   /*
   2. Product of matrix m[1,3] and matrix m[3,5]
   On the left m13 =
   [[1,2,3]]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = matrix m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Product of matrix m[3,5] and vertical vector v[5]");
   vector v5 = {1,2,3,4,5};
   Print("On the left m35 = \n",m35);
   Print("On the right v5 = ",v5);
   Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5));
   /*
   3. Product of matrix m[3,5] and vertical vector v[5]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vertical vector v[3]
   [40,115,190]
   */

//--- show that this is really a vertical vector
   Print("\n4. Product of matrix m[3,5] and matrix m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("On the left m35 = \n",m35);
   Print("On the right m51 = \n",m51);
   Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51));
   /*
   4. Product of matrix m[3,5] and matrix m[5,1]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = matrix v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Product of matrix m[3,5] and matrix m[5,2]");
   Print("On the left m35 = \n",m35);
   Print("On the right m52 = \n",m52);
   Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52));
   /*
   5. Product of matrix m[3,5] and matrix m[5,2]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = matrix m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Product of horizontal vector v[5] and matrix m[5,2]");
   Print("On the left v5 = \n",v5);
   Print("On the right m52 = \n",m52);
   Print("v5.MatMul(m52) = horizontal vector v[2] \n",v5.MatMul(m52));
   /*
   6. The product of horizontal vector v[5] and matrix m[5,2]
   On the left v5 =
   [1,2,3,4,5]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = horizontal vector v[2]
   [80,95]
   */

   Print("\n7. Outer() product of horizontal vector v[5] and vertical vector v[3]");
   Print("On the left v5 = \n",v5);
   Print("On the right v3 = \n",v3);
   Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3));
   /*
   7. Outer() product of horizontal vector v[5] and vertical vector v[3]
   On the left v5 =
   [1,2,3,4,5]
   On the right v3 =
   [1,2,3]
   v5.Outer(v3) = matrix m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */

Dönüşümler

Matris dönüşümleri, verilerle çalışırken en sık kullanılan işlemlerdir. Birçok karmaşık matris işlemi, bilgisayarların sınırlı doğruluğu nedeniyle verimli veya kararlı bir şekilde çözülemez.

Matris dönüşümleri (veya ayrışmaları), matrisi bileşen parçalarına indirgeyen metotlardır, bu da daha karmaşık matris işlemlerinin hesaplanmasını kolaylaştırır. Matrisi çarpanlara ayırma metotları olarak da adlandırılan matris ayrışması metotları, lineer denklem sistemlerinin çözülmesi, matrisin tersinin ve determinantının hesaplanması gibi temel işlemler için bile bilgisayarlarda lineer cebirin bel kemiğidir.

Makine öğrenimi, orijinal matrisin farklı üç matrisin çarpımı olarak temsil edilmesini sağlayan Tekil Değer Ayrışmasını (Singular Value Decomposition, SVD) yaygın olarak kullanır. SVD, en küçük kareler yaklaşımından sıkıştırma ve görüntü tanımaya kadar çeşitli problemleri çözmek için kullanılır.

SVD metoduyla bir tekil değer ayrışması örneği:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- execute SVD decomposition
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// check block
//--- U * singular diagonal * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- another check
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

Yaygın olarak kullanılan bir diğer dönüşüm de, Ax=b lineer denklem sisteminin (A matrisi simetrik ve pozitif tanımlıysa) çözülmesi için kullanılabilen Cholesky ayrışmasıdır.

MQL5'te, Cholesky ayrışması, Cholesky metodu kullanılarak gerçekleştirilir:

  matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

Mevcut metotların listesi aşağıdaki tabloda gösterilmektedir:

Fonksiyon	Eylem
Cholesky	Matrisin Cholesky ayrışmasını hesaplar
Eig	Kare matrisin özdeğerlerini ve sağ özvektörlerini hesaplar
EigVals	Genel matrisin özdeğerlerini hesaplar
LU	Alt üçgensel matris ve üst üçgensel matrisin çarpımı olan matrisin LU ayrışması
LUP	Yalnızca satır permütasyonları ile LU ayrışması olarak, kısmi pivotlu LUP ayrışması: PA=LU PA=LU
QR	Matrisin qr ayrışmasını hesaplar
SVD	Matrisin tekil değer ayrışmasını hesaplar

İstatistikler

“İstatistik metotları” bölümündeki metotlar, matrislerin ve vektörlerin tanımlayıcı istatistiklerinin hesaplanması için kullanılır. Şunların elde edilmesine olanak tanırlar:

• Matrisdeki/vektördeki maksimum ve minimum değer ve indeksleri
• Elemanların toplamı ve çarpımının yanı sıra kümülatif toplamı ve çarpımı
• Matris/vektör değerlerinin medyanı, ortalaması, aritmetik ortalaması ve ağırlıklı aritmetik ortalaması
• Standart sapma ve eleman varyansı
• Yüzdelik dilimler ve dağılım dilimleri
• Belirtilen veri dizisi üzerinde oluşturulan regresyon çizgisinden sapma hatası olarak regresyon metriği

Std metoduyla standart sapmanın hesaplanmasına bir örnek:

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

Quantile metoduyla dağılım dilimlerinin hesaplanması:

   matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */

Özellikler

"Özellik metotları" bölümündeki metotlar aşağıdaki değerlerin elde edilmesine olanak sağlar:

• Matristeki satır ve sütun sayısı
  
• Norm ve koşul numarası
• Matrisin determinantı, rankı, izi ve spektrumu
  

Rank metoduyla bir matrisin rankını hesaplama:

  matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // matrix deficit
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 size - rank 1, unless all 0
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

Norm metoduyla bir matrisin normunu hesaplama:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */

Denklem çözme

Makine öğrenimi metotlarında ve optimizasyon problemlerinde, genellikle bir doğrusal denklem sisteminin çözümünü bulmak gerekir. “Lineer denklem sistemlerini çözmek için matris metotları” bölümü, matris türüne bağlı olarak bu tür denklemlerin çözülmesine olanak sağlayan dört metot içerir. 

Fonksiyon	Eylem
Solve	Lineer matris denklemini veya lineer cebirsel denklem sistemini çözer
LstSq	Lineer cebirsel denklem sisteminin en küçük kareler çözümünü geri döndürür (kare olmayan veya dejenere matrisler için)
Inv	Jordan-Gauss yöntemiyle kare tersinir matrisin çarpımsal tersini hesaplar
PInv	Moore-Penrose yöntemiyle matrisin yalancı tersini hesaplar

A*x=b denklemini çözmek için bir örnek ele alalım:  

Çözüm vektörü x'i bulmamız gerekiyor. A matrisi kare değildir ve bu nedenle burada Solve metodunu kullanamayız. 

Dolayısıyla, kare olmayan veya dejenere matrislerin yaklaşık olarak çözülmesini sağlayan LstSq metodunu kullanacağız.

   matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- solve the system A*x = b
   vector x=a.LstSq(b);
//--- check the solution, x must be equal to [5, -4]
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- check A*x = b1, the resulting vector must be [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

Kontrol, bulunan x vektörünün bu denklem sisteminin çözümü olduğunu gösterdi.

Makine öğrenimi metotları

Makine öğreniminde kullanılabilecek üç matris ve vektör metodu vardır.

Fonksiyon	Eylem
Activation	Aktivasyon fonksiyonunun değerlerini hesaplar ve onları iletilen vektöre/matrise yazar
Derivative	Aktivasyon fonksiyonunun türevinin değerlerini hesaplar ve onları iletilen vektöre/matrise yazar
Loss	Kayıp fonksiyonunun değerlerini hesaplar ve onları iletilen vektöre/matrise yazar

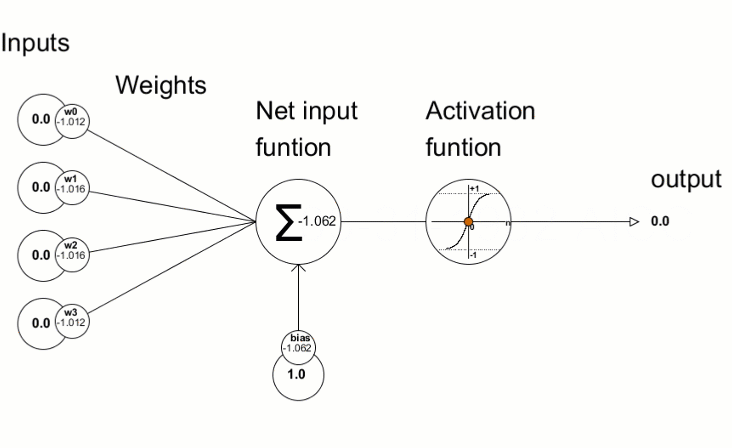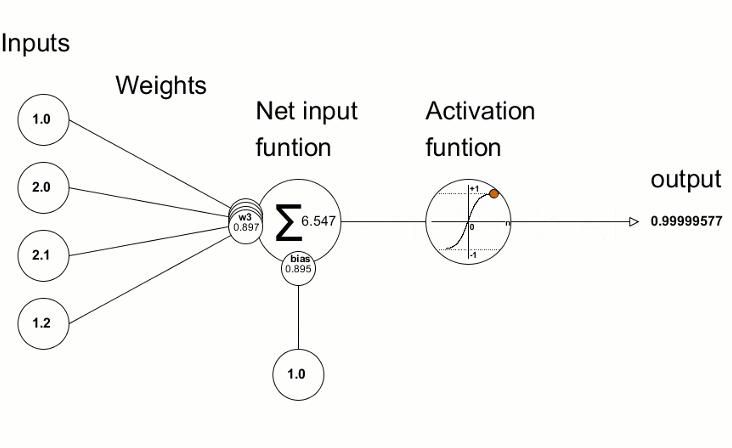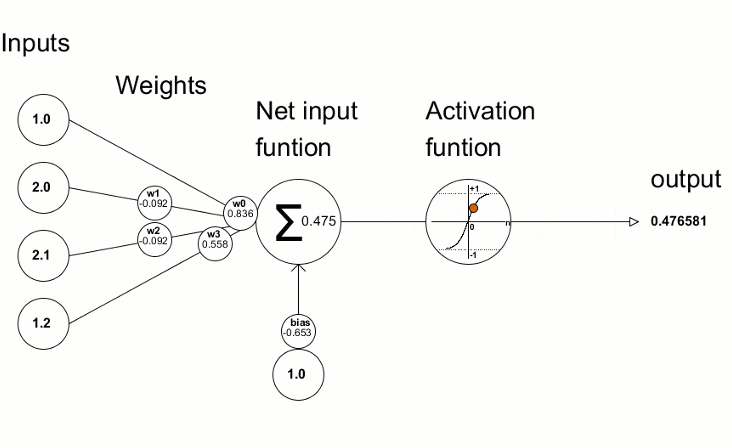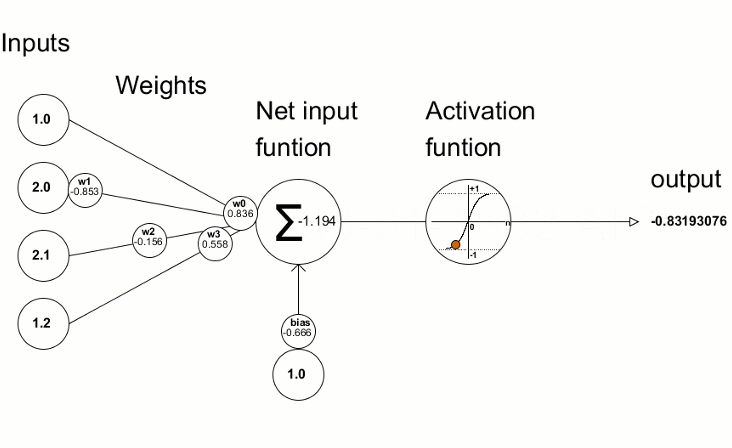
Aktivasyon fonksiyonları, sinir ağlarında girdilerin ağırlıklı toplamına dayalı olarak çıktı değeri elde etmek için kullanılır. Aktivasyon fonksiyonunun seçimi, sinir ağının yetenekleri ve performansı üzerinde büyük bir etkiye sahiptir.

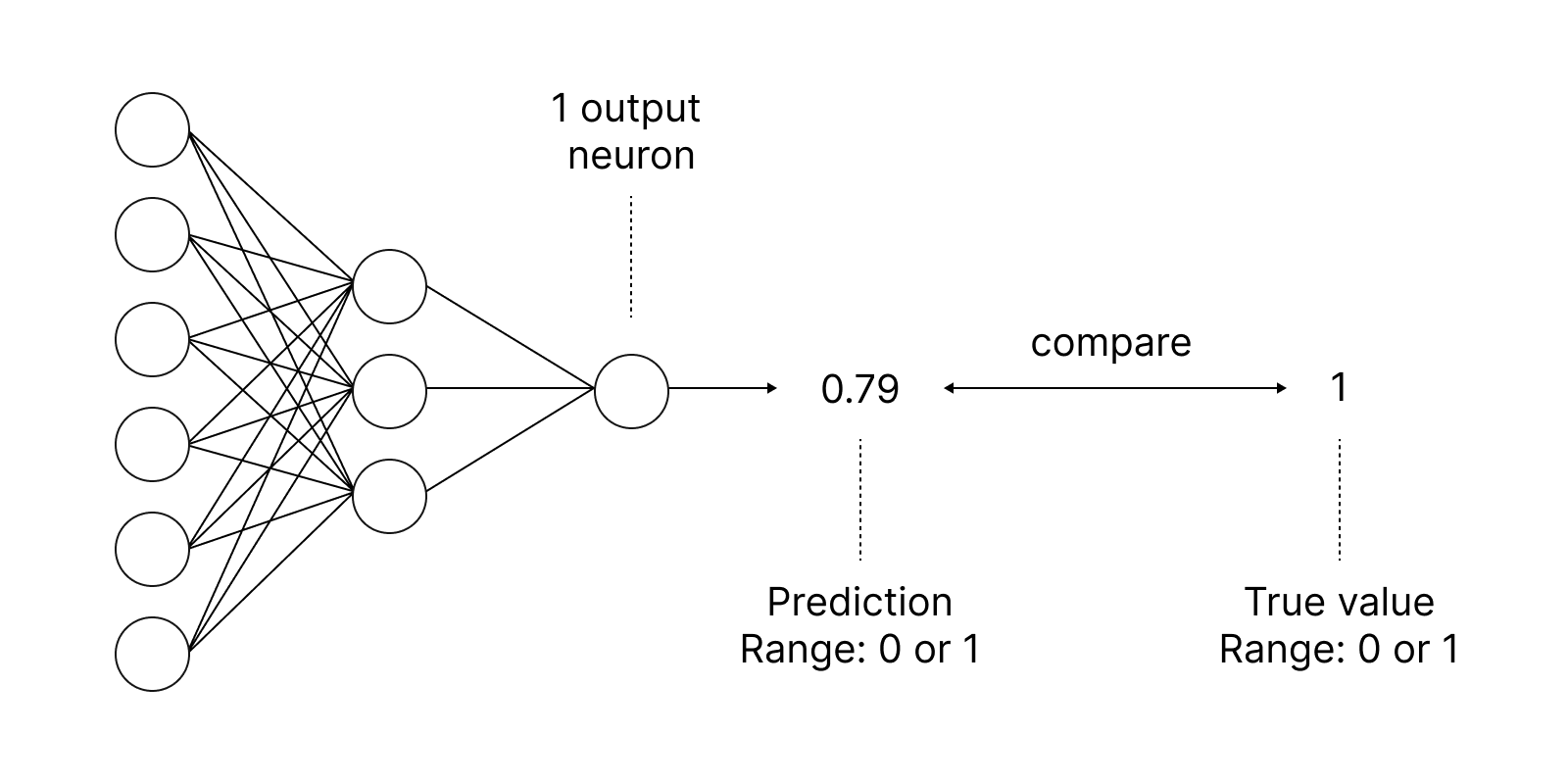
En iyi bilinen aktivasyon fonksiyonlarından biri sigmoiddir.

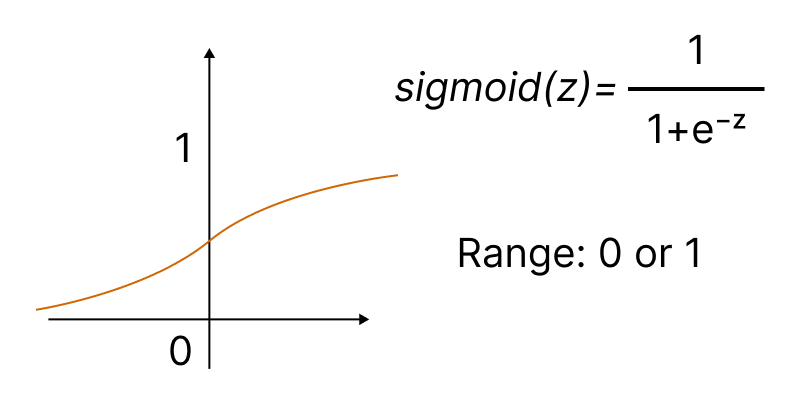
Yerleşik Activation metodu, ENUM_ACTIVATION_FUNCTION numaralandırmasında bulunan on beş tür aktivasyon fonksiyonundan birinin ayarlanmasına olanak tanır:

Tanımlayıcı	Açıklama
AF_ELU	Üstel Lineer Birim (Exponential Linear Unit)
AF_EXP	Üstel (Exponential)
AF_GELU	Gauss Hata Lineer Birimi (Gaussian Error Linear Unit)
AF_HARD_SIGMOID	Sert Sigmoid (Hard Sigmoid)
AF_LINEAR	Lineer (Linear)
AF_LRELU	Sızıntılı Düzeltilmiş Lineer Birim (Leaky REctified Linear Unit)
AF_RELU	Düzeltilmiş Lineer Birim (REctified Linear Unit)
AF_SELU	Ölçekli Üstel Lineer Birim (Scaled Exponential Linear Unit)
AF_SIGMOID	Sigmoid
AF_SOFTMAX	Softmax
AF_SOFTPLUS	Softplus
AF_SOFTSIGN	Softsign
AF_SWISH	Swish
AF_TANH	Hiperbolik tanjant fonksiyonu
AF_TRELU	Eşikli Düzeltilmiş Lineer Birim (Thresholded REctified Linear Unit)

Bir sinir ağını eğitmenin görevi, kayıp fonksiyonunun kullanıldığı eğitim örneklemindeki hatayı en aza indiren bir algoritma bulmaktır. Sapma, ENUM_LOSS_FUNCTION numaralandırmasında bulunan on dört türden birinin ayarlanmasına olanak tanıyan Loss metodu kullanılarak hesaplanır.

Elde edilen sapma değerleri daha sonra sinir ağının parametrelerinin iyileştirilmesi için kullanılır. Bu da aktivasyon fonksiyonunun türevinin değerlerini hesaplayan ve onları iletilen vektöre/matrise yazan Derivative metodu kullanılarak yapılır. Sinir ağı eğitim süreci "MQL dili kullanarak sıfırdan bir Derin Sinir Ağı programlama" makalesindeki animasyonda görsel olarak ifade edilmektedir.

OpenCL'de iyileştirmeler

CLBufferWrite ve CLBufferRead fonksiyonlarına matrisler ve vektörler için destek eklendi. Bu fonksiyonlar için ilgili overloadlar mevcuttur. Matris için bir örnek aşağıda gösterilmektedir.

Matristeki değerleri arabelleğe yazar ve başarı durumunda true geri döndürür.

uint  CLBufferWrite(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   matrix<T>     &mat                       // matrix of values to write to buffer
   );

OpenCL arabelleğini matrise okur ve başarı durumunda true geri döndürür.

uint  CLBufferRead(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   const matrix& mat,                       // matrix to get values from the buffer
   ulong         rows=-1,                   // number of rows in the matrix
   ulong         cols=-1                    // number of columns in the matrix
   );

İki matrisin çarpımı örneğiyle yeni overloadların kullanımını inceleyelim. Hesaplamaları üç şekilde yapalım:

• Matris çarpımı algoritmasını gösteren saf yol
• Yerleşik MatMul metodu
  
• OpenCL'de paralel hesaplama

Elde edilen matrisler, iki matrisin elemanlarını belirli bir hassasiyetle karşılaştıran Compare metodu kullanılarak kontrol edilecektir.

#define M       3000      // number of rows in the first matrix
#define K       2000      // number of columns in the first matrix equal to the number of rows in the second one
#define N       3000      // number of columns in the second matrix
 
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- initialize the random number generator
  MathSrand((int)TimeCurrent());
//--- fill matrices of the given size with random values
  matrixf mat1(M, K, MatrixRandom) ;    // first matrix
  matrixf mat2(K, N, MatrixRandom);     // second matrix
 
//--- calculate the product of matrices using the naive way
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// here we rite the result of multiplying two matrices
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- calculate the product of matrices using MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- calculate the product of matrices in OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // context handle
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL not found, exit");
    return;
   }
  int cl_prg;             // program handle
  int cl_krn;             // kernel handle
  int cl_mem_in1;         // handle of the first buffer (input)
  int cl_mem_in2;         // handle of the second buffer (input)
  int cl_mem_out;         // handle of the third buffer (output)
//--- create the program and the kernel
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- create all three buffers for the three matrices
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- third matrix - output
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- set kernel arguments
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- write matrices to device buffers
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- start the OpenCL code execution time
  start=GetTickCount();
//--- set the task workspace parameters and execute the OpenCL program
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- read the result into the matrix
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Compare computation times of the methods");
  PrintFormat("Naive product time = %d ms",time_naive);
  PrintFormat("MatMul product time = %d ms",time_matmul);
  PrintFormat("OpenCl product time = %d ms",time_opencl);  
//--- release all OpenCL contexts
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- compare all obtained result matrices with each other 
  Print("How many discrepancy errors between result matrices?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Result: 
   
   Matrix [3000 x 3000] read 
   Compare computation times of the methods
   Naive product time = 54750 ms
   MatMul product time = 4578 ms
   OpenCl product time = 922 ms
   How many discrepancy errors between result matrices?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Fills the matrix with random values                              |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//| Release all OpenCL contexts                                      |
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- release all created OpenCL contexts in reverse order
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

Bu örnekteki OpenCL kodunun ayrıntılı açıklaması "OpenCL: Sade Programlamadan Daha Öngörülü Programlamaya Doğru” makalesinde yer almaktadır.

Daha fazla iyileştirme

Ek olarak, yapı 3390’da, OpenCL ile çalışma konusunda GPU kullanımını etkileyen iki kısıtlama kaldırdı.

Artık maksimum OpenCL nesnesi sayısı 65536'ya kadar çıkabilir, öncesinde bu sayı 256’yla sınırlıydı. MQL5 programında OpenCL nesnesi tanıtıcıları, CLContextCreate, CLBufferCreate ve CLProgramCreate fonksiyonları kullanılarak oluşturulur. Önceki 256 tanıtıcı sınırı, makine öğrenimi metotlarının etkili kullanımı için yeterli değildi.

Artık, double desteği olmayan grafik kartlarında da OpenCL kullanımına izin veriliyor. Öncesinde, MQL5 programlarında yalnızca double desteği olan GPU'lara izin veriliyordu. Ancak birçok görev ise float kullanılarak yapılan hesaplamaları mümkün kılmaktadır. float türü, daha az yer kapladığından, paralel hesaplama için yerel olarak kabul edilir. Dolayısıyla, eski gereklilik artık kaldırılmıştır.

Belirli görevler için double desteği olan GPU'ların zorunlu kullanımını ayarlamak için CLContextCreate çağrısında CL_USE_GPU_DOUBLE_ONLY kullanabilirsiniz.

   int cl_ctx;
//--- initialization of OpenCL context
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL not found");
      return;
     }

OpenCL ile çalışma konusundaki bu değişiklikler, doğrudan matrisler ve vektörlerle ilgili olmasa da, makine öğreniminin ihtiyaçları doğrultusundaki MQL5 dilini geliştirme çabalarımızla ilişkilidir.

Makine öğreniminde MQL5'in geleceği

Geçtiğimiz yıllarda, gelişmiş teknolojileri MQL5 diline dahil etmek için çok şey yaptık:

• ALGLIB sayısal metotlar kütüphanesini MQL5'e port ettik
  
• Bulanık mantık ve istatistik metotları içeren matematik kütüphanesini uyguladık
  
• plot fonksiyonunun analoğu olarak grafik kütüphanesini hayata geçirdik
  
• Python komut dosyalarının doğrudan terminalde çalıştırılabilmesi için Python ile entegrasyon gerçekleştirdik
  
• 3D grafikler oluşturulabilmesi için DirectX fonksiyonları ekledik
  
• Veri tabanlarıyla çalışmak için yerel SQLite desteğini tanıttık
• Yeni veri türleri ekledik: gerekli tüm metotlarla birlikte matrisler ve vektörler

MQL5 dili gelişmeye devam ederken, en öncelikli yönlerden biri de makine öğrenimi olacaktır. Daha fazla gelişmek için büyük planlarımız var. Bu yüzden bizimle kalın, bizi destekleyin ve bizimle birlikte öğrenmeye devam edin.