MetaTrader 5 / Beispiele
English Русский 中文 Español 日本語 Português 한국어 Français Italiano Türkçe
preview
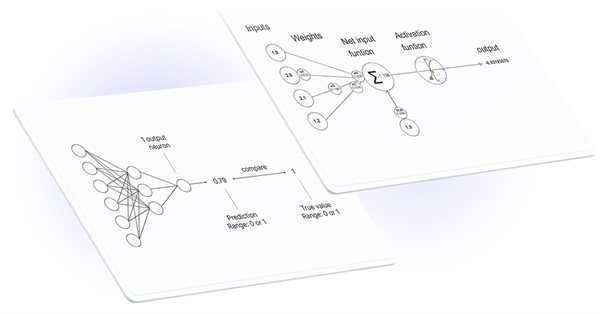
Matrix- und Vektoroperationen in MQL5

Matrix- und Vektoroperationen in MQL5

MetaTrader 5 — Beispiele | 3 Oktober 2022, 14:05
694 0
MetaQuotes
MetaQuotes

Spezielle Datentypen - Matrizen und Vektoren - wurden der Sprache MQL5 hinzugefügt, um eine große Klasse von mathematischen Problemen zu lösen. Die neuen Typen bieten integrierte Methoden zur Erstellung von prägnantem und verständlichem Code, der der mathematischen Notation nahe kommt. In diesem Artikel finden Sie eine kurze Beschreibung der eingebauten Methoden aus dem Hilfeabschnitt Matrix- und Vektormethoden.


Inhalt


Jede Programmiersprache bietet Array-Datentypen, die Gruppen von numerischen Variablen speichern, darunter int, double und andere. Auf Array-Elemente wird über einen Index zugegriffen, was Array-Operationen mit Schleifen ermöglicht. Am häufigsten werden eindimensionale und zweidimensionale Arrays verwendet:

int    a[50];       // Eindimensionales Array mit 50 Ganzzahlen
double m[7][50];    // Zweidimensionales Array mit 7 Unterarrays,  diejeweils aus 50 Ganzzahlen bestehen
MyTime t[100];      // Array mit Elementen vom Typ MyTime

Die Fähigkeiten von Arrays reichen in der Regel für relativ einfache Aufgaben im Zusammenhang mit der Datenspeicherung und -verarbeitung aus. Wenn es jedoch um komplexe mathematische Probleme geht, wird die Arbeit mit Arrays aufgrund der großen Anzahl verschachtelter Schleifen sowohl für die Programmierung als auch für das Lesen des Codes schwierig. Selbst die einfachsten Operationen der linearen Algebra erfordern eine exzessive Kodierung und ein gutes Verständnis der Mathematik.

Moderne Datentechnologien wie maschinelles Lernen, neuronale Netze und 3D-Grafiken nutzen in großem Umfang Lösungen der linearen Algebra, die mit den Konzepten von Vektoren und Matrizen verbunden sind. Um Operationen mit solchen Objekten zu erleichtern, bietet MQL5 spezielle Datentypen: Matrizen und Vektoren. Die neuen Typen eliminieren viele Routineprogrammiervorgänge und verbessern die Codequalität.


Matrix- und Vektortypen

Kurz gesagt, ein Vektor ist ein eindimensionales Array vom Typ double, und eine Matrix ist ein zweidimensionales Array vom Typ double. Vektoren können vertikal und horizontal sein; sie werden jedoch in MQL5 nicht getrennt.

Eine Matrix kann als ein Array von horizontalen Vektoren dargestellt werden, wobei der erste Index die Zeilennummer und der zweite Index die Spaltennummer ist.


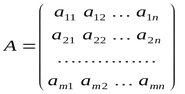
Die Nummerierung der Zeilen und Spalten beginnt bei 0, ähnlich wie bei Arrays.

Neben den Typen „matrix“ und „vector“, die Daten vom Typ double enthalten, gibt es vier weitere Typen für Operationen mit den entsprechenden Datentypen:

  • matrixf — eine Matrix mit float-Elementen.
  • matrixc — eine Matrix mit complex-Elementen
  • vectorf — ein Vektor mit Float-Elementen
  • vectorc — ein Vektor mit komplexen Elementen

Zum Zeitpunkt der Erstellung dieses Artikels ist die Arbeit an den Typen matrixc und vectorc noch nicht abgeschlossen, sodass es noch nicht möglich ist, diese Typen in integrierten Methoden zu verwenden.

Template-Funktionen unterstützen Notationen wie matrix<double>, matrix<float>, vector<double>, vector<float> anstelle der entsprechenden Typen.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */


Erstellung und Initialisierung

Matrix- und Vektormethoden werden je nach ihrem Zweck in neun Kategorien unterteilt. Es gibt mehrere Möglichkeiten, Matrizen und Vektoren zu deklarieren und zu initialisieren.

Die einfachste Erstellungsmethode ist die Deklaration ohne Größenangabe, d.h. ohne Speicherzuweisung für die Daten. Hier schreiben wir nur den Datentyp und den Variablennamen:

  matrix         matrix_a;   // Matrix des Typs double
  matrix<double> matrix_a1;  // eine andere Art, eine Doppelmatrix zu deklarieren, geeignet für die Verwendung in Vorlagen
  matrix<float>  matrix_a3;  // Matrix des Typs float 
  vector         vector_a;   // Vektor des Typs double
  vector<double> vector_a1;  // eine andere Schreibweise zur Erstellung eines Vektors mit dem Typ double
  vector<float>  vector_a3;  // Vektor des Typs float

Anschließend können Sie die Größe der erstellten Objekte ändern und sie mit den gewünschten Werten füllen. Sie können auch in integrierten Matrixmethoden verwendet werden, um Berechnungsergebnisse zu erhalten.

Eine Matrix oder ein Vektor kann mit der angegebenen Größe deklariert werden, wobei Speicher für die Daten zugewiesen, aber nichts initialisiert wird. Hier geben Sie nach dem Variablennamen die Größe(n) in Klammern an:

  matrix matrix_a(128,128);                  // die Parameter können entweder Konstanten sein
  matrix<double> matrix_a1(InpRows,InpCols); // oder Variablen
  matrix<float> matrix_a3(InpRows,1);        // analog zu einem vertikalen Vektor
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float> vector_a3(InpSize+16);       // der Ausdruck kann als Parameter verwendet werden

Die dritte Möglichkeit, Objekte zu erstellen, ist die Deklaration mit Initialisierung. In diesem Fall werden die Matrix- und Vektorgrößen durch die in geschweiften Klammern angegebene Initialisierungssequenz bestimmt:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                       // die Matrizen müssen vom gleichen Typ sein
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                      // die Vektoren müssen vom gleichen Typ sein


Es gibt auch statische Methoden zur Erstellung von Matrizen und Vektoren der angegebenen Größe, die auf eine bestimmte Weise initialisiert werden:  

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Darüber hinaus gibt es nicht-statische Methoden zur Initialisierung einer Matrix oder eines Vektors mit den angegebenen Werten — Init und Fill:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

In diesem Beispiel haben wir die Init-Methode verwendet, um die Größe einer bereits initialisierten Matrix zu ändern, wodurch alle neuen Elemente mit Zufallswerten gefüllt wurden.

Ein wichtiger Vorteil der Init-Methode ist die Möglichkeit, eine Initialisierungsfunktion in Parametern anzugeben, um Matrix-/Vektor-Elemente gemäß dieser Regel zu füllen. Zum Beispiel:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Ausführungsergebnis:
  Init 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Füllt die Matrix mit Potenzen einer Zahl                         |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 }


Kopieren von Matrizen und Feldern

Matrizen und Vektoren können mit der Methode Copy kopiert werden. Eine einfachere und vertrautere Art, diese Datentypen zu kopieren, ist jedoch die Verwendung des Zuweisungsoperators „=“. Sie können auch die Methode „Assign“ zum Kopieren verwenden.

//--- Kopieren von Matrizen
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

Der Unterschied zwischen Assign und Copy besteht darin, dass es sowohl für Matrizen als auch für Arrays verwendet werden kann. Das folgende Beispiel zeigt das Kopieren des Integer-Arrays int_arr in eine double-Matrix. Die resultierende Matrix passt sich automatisch an die Größe des kopierten Arrays an. 

//--- Kopieren eines Arrays in eine Matrix
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

Die Methode Assign ermöglicht einen nahtlosen Übergang von Arrays zu Matrizen mit automatischer Größen- und Typzuweisung.


Kopieren von Zeitreihen in Matrizen oder Vektoren

Die Analyse von Preischarts setzt Operationen mit Strukturarrays MqlRates voraus. MQL5 bietet eine neue Methode für die Arbeit mit solchen Preisdatenstrukturen.

Die Methode CopyRates kopiert historische Datenreihen der Struktur MqlRates direkt in eine Matrix oder einen Vektor. So können Sie vermeiden, dass Sie die benötigten Zeitreihen den entsprechenden Arrays zuweisen müssen, indem Sie Funktionen aus dem Abschnitt Zeitreihen und Indikatorenzugriff verwenden. Es ist auch nicht nötig, sie in eine Matrix oder einen Vektor zu übertragen. Mit der Methode CopyRates können Sie mit nur einem Aufruf Kurse einer Matrix oder einem Vektor zuweisen. Betrachten wir ein Beispiel für die Berechnung einer Korrelationsmatrix für eine Liste von Symbolen: Berechnen wir diese Werte mit zwei verschiedenen Methoden und vergleichen wir die Ergebnisse.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Skript Programm Start Funktion                                   |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- Liste der Symbole für die Berechnung
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- Matrix und Vektor zur Aufnahme der Schlusskurse
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- Schlusskurse in einen Vektor umwandeln
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- Einfügen des Vektors in die Zeitreihenmatrix
      rates.Col(close, i);
      PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size());
      //--- Ausgabe der ersten 20 Vektorwerte zur Fehlersuche
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 Schlusskurse wurden in die Matrix aufgenommen
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 Schlusskurse wurden in die Matrix aufgenommen
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 Schlusskurse wurden in die Matrix aufgenommen
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 Schlusskurse wurden in die Matrix aufgenommen
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 Schlusskurse wurden in die Matrix aufgenommen
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- Erstellung einer Matrix der Korrelationen zwischen den Symbolen
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Compute pairwise correlation coefficients");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Correlation matrix on vectors: \n", corr_from_vector);
  /*
  Berechnung der paarweisen Korrelationskoeffizienten
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0,397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0,744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Korrelationsmatrix für Vektoren:
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- nun wollen wir sehen, wie eine Korrelationsmatrix in einer Zeile berechnet werden kann
  matrix corr_from_matrix=rates.CorrCoef(false); // false bedeutet, dass die Vektoren in den Spalten der Matrix stehen
  Print("Korrelationsmatrix rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- Vergleich der sich ergebenden Matrizen, um Diskrepanzen festzustellen
  Print("Anzahl der Diskrepanzfehler zwischen den Ergebnismatrizen?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Correlation matrix rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  Anzahl der Diskrepanzfehler zwischen den Ergebnismatrizen?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- Erstellen einer gestalteten Ausgabe der Korrelationsmatrix
  Print("Ausgabe der Korrelationsmatrix mit Kopfzeilen");
  string header=""; // Kopfzeile
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- jetzt die Zeilen
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Ausgabe der Korrelationsmatrix mit Kopfzeile
            EURUSD GBPUSD USDJPY USDCAD USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Rückgabe einer Zeichenkette mit Vektorwerten                     |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- eine Zeichenkette zusammenstellen
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- Hinzufügen der Ergänzung, wenn die Vektorlänge die angegebene Größe überschreitet
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//| Rückgabe einer Zeichenkette mit angegebener Leerzeichenzahl      |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

Das Beispiel zeigt, wie verwendet werden kann:

    • Mit CopyRates die Schlusskurse abrufen.
    • Einfügen eines Vektors in eine Matrix mit der Methode Col.
    • Berechnen des Korrelationskoeffizienten zwischen zwei Vektoren mit CorrCoef.
    • Berechnen der Korrelationsmatrix über eine Matrix mit Wertvektoren mit CorrCoef.
    • Rückgabe einer oberen Dreiecksmatrix mit Hilfe der Methode TriU.
    • Vergleichen zweier Matrizen und Auffinden von Diskrepanzen mit Compare.


      Matrix- und Vektoroperationen

      Elementweise mathematische Operationen wie Addition, Subtraktion, Multiplikation und Division können mit Matrizen und Vektoren durchgeführt werden. Beide Objekte in solchen Operationen müssen vom gleichen Typ sein und die gleiche Größe haben. Jedes Element der Matrix oder des Vektors wirkt auf das entsprechende Element der zweiten Matrix oder des Vektors.

      Sie können auch einen Skalar des entsprechenden Typs (double, float oder complex) als zweiten Term (Multiplikator, Subtrahend oder Divisor) verwenden. In diesem Fall wird jedes Element der Matrix oder des Vektors auf den angegebenen Skalarwert wirken.

        matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // Hadamard product
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- Operationen an Ort und Stelle sind möglich
  matrix_a+=matrix_b;
  matrix_a/=2;

      Darüber hinaus können Matrizen und Vektoren als zweiter Parameter den meisten mathematischen Funktionen übergeben werden, darunter MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. Solche Operationen implizieren eine elementweise Behandlung von Matrizen und Vektoren. Beispiel:

      //---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

      Bei MathMod und MathPow kann das zweite Element entweder ein Skalar oder eine Matrix/ein Vektor mit der entsprechenden Größe sein. 

         matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }


      Manipulationen

      MQL5 unterstützt die folgenden grundlegenden Manipulationen von Matrizen und Vektoren, die keine Berechnungen erfordern:

      • Transposition
      • Extraktion von Zeilen, Spalten und Diagonalen
      • Größenänderung und Umformung von Matrizen
      • Vertauschen der angegebenen Zeilen und Spalten
      • Kopieren in ein neues Objekt
      • Vergleich von zwei Objekten
      • Aufteilung einer Matrix in mehrere Submatrizen
      • Sortieren
      Das folgende Beispiel zeigt die Matrixtransposition mit der Methode Transpose:
        matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("Matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

      Die folgenden Beispiele zeigen, wie eine Diagonale mit der Methode Diag festgelegt und extrahiert werden kann:

         vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

      Changing a matrix size using the Reshape method:

         matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

      Beispiele für eine vertikale Aufteilung einer Matrix mit der Methode Vsplit:

         matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

      Die Methoden Col und Row ermöglichen es, die entsprechenden Matrixelemente zu erhalten und Elemente in nicht zugeordnete Matrizen einzufügen, d. h. in Matrizen ohne die angegebene Größe. Hier ist ein Beispiel:

         vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("Spalte 1 - ",m2.Col(1));
  /*
   Spalte 1 - [8,8,8,8]
  */

   Print("Spalte 2 - ",m2.Col(2));
  /*
   Spalte 1 - [8,8,8,8]  Spalte 2 - [1,2,3,8]
  */


      Produkte

      Die Matrixmultiplikation ist einer der grundlegenden Algorithmen, der in numerischen Methoden weit verbreitet ist. Viele Implementierungen von Vorwärts- und Backpropagation-Algorithmen in Convolutionalen Neuronalen Netzwerken basieren auf dieser Operation. Oft entfallen 90-95 % der gesamten für maschinelles Lernen aufgewendeten Zeit auf diesen Vorgang. Alle Produktmethoden sind im Abschnitt Produkte von Matrizen und Vektoren der Sprachreferenz aufgeführt.

      Das folgende Beispiel zeigt die Multiplikation von zwei Matrizen mit der Methode MatMul:

         matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

      Ein Beispiel für das Kronecker-Produkt zweier Matrizen oder einer Matrix und eines Vektors unter Verwendung der Methode Kron.

         matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

      Weitere Beispiele aus dem Artikel Matrizen und Vektoren in MQL5:

      //--- Matrizen initialisieren
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Produkt aus horizontalem Vektor v[3] und Matrix m[3,5]");
   vector v3 = {1,2,3};
   Print("Auf der linken Seite v3 = ",v3);
   Print("Auf der rechten Seite m35 = \n",m35);
   Print("v3.MatMul(m35) = horizontaler Vektor v[5] \n",v3.MatMul(m35));
   /*
   1. Produkt aus horizontalem Vektor v[3] und Matrix m[3,5]
   auf der linken Seite.
   Auf der rechten Seite m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = horizontalem Vektor v[5]
   [40,46,52,58,64]
   */

//--- zeigen, dass es sich wirklich um einen horizontalen Vektor handelt
   Print("\n2. Produkt aus Matrix m[1,3] und Matrix m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("Auf der linken Seite m13 = \n",m13);
   Print("Auf der rechten Seite m35 = \n",m35);
   Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35));
   /*
   2. Produkt aus Matrix m[1,3] und Matrix m[3,5]");
   auf der linken Seite.
   [[1,2,3]]
   Auf der rechten Seite m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = matrix m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Produkt der Matrix m[3,5] und des vertikalen Vektors v[5]");
   vector v5 = {1,2,3,4,5};
   Print("Auf der linken Seite m35 = \n",m35);
   Print("und rechts v5 = ",v5);
   Print("m35.MatMul(v5) = vertikaler Vektor v[3] \n",m35.MatMul(v5));
   /*
   3. Produkt der Matrix m[3,5] und des vertikalen Vektors v[5]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Auf der rechten Seite v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vertical vector v[3]
   [40,115,190]
   */

//--- zeigen, dass es sich wirklich um einen vertikalen Vektor handelt
   Print("\n4. Produkt aus Matrix m[3,5] und Matrix m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("Auf der linken Seite m35 = \n",m35);
   Print("Auf der rechten Seite m51 = \n",m51);
   Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51));
   /*
   4. Produkt aus Matrix m[3,5] und Matrix m[5,1]");
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Auf der rechten Seite m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = matrix v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Produkt aus Matrix m[3,5] und Matrix m[5,2]");
   Print("Auf der linken Seite m35 = \n",m35);
   Print("Auf der rechten Seite m52 = \n",m52);
   Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52));
   /*
   5. Produkt aus Matrix m[3,5] und Matrix m[5,2]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Auf der rechten Seite m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = matrix m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Produkt aus horizontalem Vektor v[5] und Matrix m[5,2]");
   Print("Auf der linken Seite v5 = \n",v5);
   Print("Auf der rechten Seite m52 = \n",m52);
   Print("v5.MatMul(m52) = horizontaler Vector v[2] \n",v5.MatMul(m52));
   /*
   6. Produkt aus horizontalem Vektor v[5] und Matrix m[5,2]
   auf der linken Seite v5 =
   [1,2,3,4,5]
   Auf der rechten Seite m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = horizontaler Vektor v[2]
   [80,95]
   */

   Print("\n7. Outer()-Produkt des horizontalen Vektors v[5] und des vertikalen Vektors v[3]");
   Print("Auf der linken Seite v5 = \n",v5);
   Print("On the right v3 = \n",v3);
   Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3));
   /*
   7. Outer()-Produkt des horizontalen Vektors v[5] und des vertikalen Vektors v[3]
   auf der linken Seite v5 =
   [1,2,3,4,5]
   Auf der rechten Seite v3 =
   [1,2,3]
   v5.Outer(v3) = matrix m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */


      Transformationen

      Matrixtransformationen werden häufig bei Datenoperationen verwendet. Viele komplexe Matrixoperationen können jedoch aufgrund der begrenzten Genauigkeit von Computern nicht effizient oder stabil gelöst werden.

      Matrixtransformationen (oder Zerlegungen) sind Methoden, mit denen eine Matrix in ihre Bestandteile zerlegt werden kann, was die Berechnung komplexerer Matrixoperationen erleichtert. Matrixzerlegungsmethoden, auch Matrixfaktorisierungsmethoden genannt, sind das Rückgrat der linearen Algebra in Computern, selbst für grundlegende Operationen wie das Lösen von linearen Gleichungssystemen, die Berechnung der Inversen und die Berechnung der Determinante einer Matrix.

      Beim maschinellen Lernen wird häufig die Singulärwertzerlegung (Singular Value Decomposition, SVD) verwendet, die es ermöglicht, die ursprüngliche Matrix als Produkt von drei anderen Matrizen darzustellen. SVD wird zur Lösung einer Vielzahl von Problemen eingesetzt, von der Annäherung an die kleinsten Quadrate bis hin zur Komprimierung und Bilderkennung.

      Ein Beispiel für eine Singulärwertzerlegung nach der Methode SVD:

        matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("Matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- SVD-Zerlegung durchführen
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// Prüfblock
//--- U * singuläre Diagonale * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- eine weitere Prüfung
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

      Eine weitere häufig verwendete Transformation ist die Cholesky-Zerlegung, die zur Lösung eines linearen Gleichungssystems Ax=b verwendet werden kann, wenn die Matrix A symmetrisch und positiv definit ist.

      In MQL5 wird die Cholesky-Zerlegung mit der Methode Cholesky durchgeführt: 

        matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

      Die folgende Tabelle zeigt die Liste der verfügbaren Methoden:

      Funktion

      Aktion

      Cholesky

      Berechnet die Cholesky-Zerlegung

      Eig

      Berechnet die Eigenwerte und die rechten Eigenvektoren einer quadratischen Matrix

      EigVals

      Berechnet die Eigenwerte einer allgemeinen Matrix

      LU

      LU-Faktorisierung einer Matrix als Produkt aus einer unteren Dreiecksmatrix und einer oberen Dreiecksmatrix

      LUP

      LUP-Faktorisierung mit partieller Pivotisierung, d.h. LU-Zerlegung nur mit Zeilenpermutationen: PA=LU

      QR

      Berechnen der qr-Faktorisierung einer Matrix

      SVD

      Singulärwertzerlegung

      Einholen von Statistiken

        Methoden aus dem Abschnitt Statistics werden zur Berechnung der deskriptiven Statistik von Matrizen und Vektoren verwendet. Verwenden Sie sie, um Folgendes zu finden:
        • Maximal- und Minimalwerte zusammen mit ihren Indizes in einer Matrix/einem Vektor
        • Die Summe und das Produkt von Elementen sowie die kumulative Summe und das kumulative Produkt
        • Median, Mittelwert, arithmetisches Mittel und gewichtetes arithmetisches Mittel von Matrix-/Vektorwerten
        • Standardabweichung und Elementvarianz
        • Perzentile und Quantile
        • Regressionsmetrik als Abweichungsfehler von der Regressionslinie, die auf der angegebenen Datenreihe konstruiert wurde

          Ein Beispiel für die Berechnung der Standardabweichung mit der Methode Std:

             matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

          Berechnung von Quantilen nach der Methode Quantil:

             matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */


          Eigenschaften der Matrix

          Verwenden Sie Methoden aus dem Abschnitt Eigenschaften, um die folgenden Werte zu erhalten:

          • Die Anzahl der Zeilen und Spalten in einer Matrix.
          • Norm und Konditionsnummer.
          • Determinante, Rang, Spur und Spektrum einer Matrix.

          Berechnung des Rangs einer Matrix mit der Methode Rank:

            matrix a=matrix::Eye(4, 4);;
  Print("Matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.; // Matrixdefizit
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rang()=", b.Rang());;// 1 Größe - Rang 1, außer alles ist 0
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

          Berechnung einer Norm mit der Methode Norm:

            matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("Matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */


          Lösen von Gleichungen

          Bei Methoden des maschinellen Lernens und bei Optimierungsproblemen müssen häufig Lösungen für ein System linearer Gleichungen gefunden werden. Der Abschnitt Berechnungen enthält vier Methoden, die die Lösung solcher Gleichungen in Abhängigkeit vom Matrixtyp ermöglichen. 

          Funktion

          Aktion

          Solve

          Lösen einer linearen Matrixgleichung oder eines Systems linearer algebraischer Gleichungen

          LstSq

          Rückgabe des Ergebnisses der Lösung einer linearen, algebraischen Gleichungen nach dem Prinzip der kleinsten Quadrate (für nicht quadratische oder entartete Matrizen)

          Inv

          Berechnung der multiplikativen Inversen einer quadratischen invertierbaren Matrix nach der Jordan-Gauss-Methode

          PInv

          Berechnung der Pseudoinverse einer Matrix nach der Moore-Penrose-Methode

          Betrachten Sie ein Beispiel für die Lösung der Gleichung A*x=b.  


          Wir müssen den Lösungsvektor x finden. Da die Matrix A nicht quadratisch ist, kann die Methode Solve hier nicht verwendet werden. 

          Wir werden die Methode LstSq verwenden, die es ermöglicht, nicht quadratische oder entartete Matrizen näherungsweise zu lösen. 

             matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- das System A*x = b lösen
   vector x=a.LstSq(b);
//--- Ergebnisprüfung, x muss gleich [5, -4] sein
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- Prüfung A*x = b1, der resultierende Vektor muss [7, 40, 3] sein
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

          Die Prüfung hat ergeben, dass der gefundene Vektor x die Lösung dieses Gleichungssystems ist.


          Methoden des maschinellen Lernens

          Es gibt drei Matrix- und Vektorverfahren, die beim maschinellen Lernen eingesetzt werden können.

          Funktion

          Aktion

          Activation

          Aktivierungsfunktionswerte berechnen und in den übergebenen Vektor/die Matrix schreiben

          Derivative

          Ableitungswerte der Aktivierungsfunktion berechnen und in den übergebenen Vektor/die Matrix schreiben

          Loss

          Verlustfunktionswerte berechnen und in den übergebenen Vektor/die Matrix schreiben

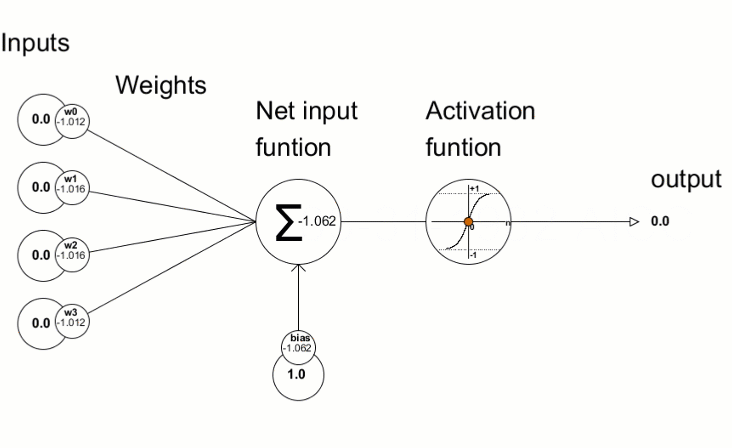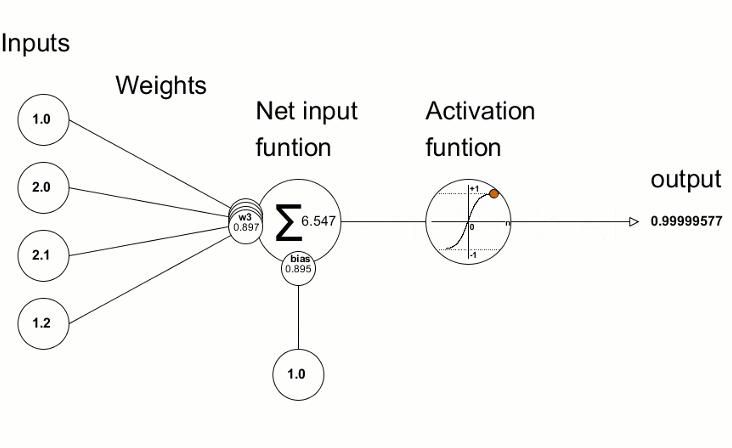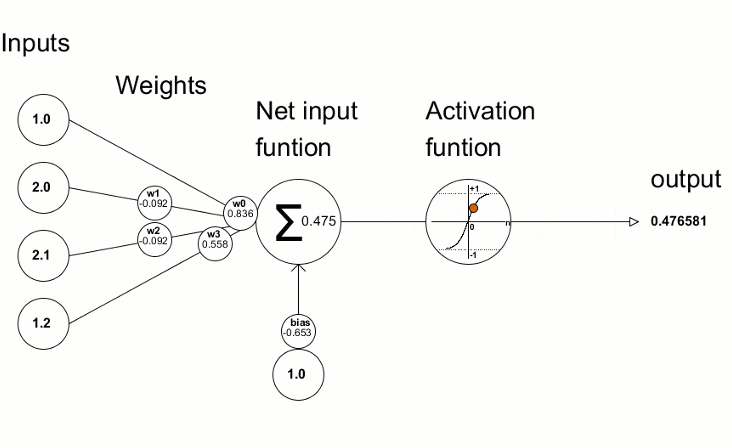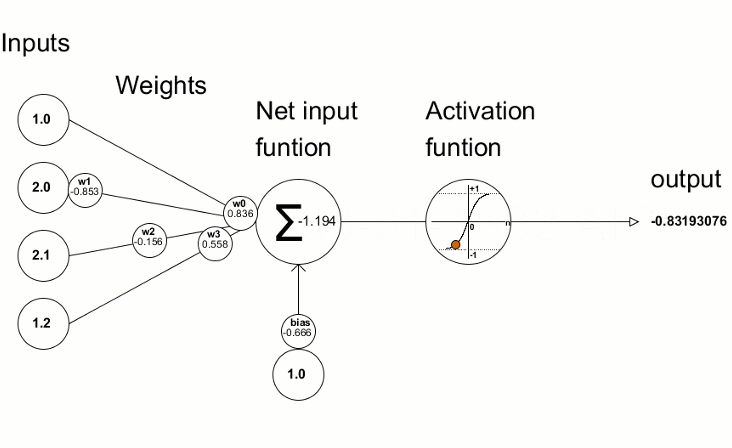
          Aktivierungsfunktionen werden in neuronalen Netzen verwendet, um eine Ausgabe in Abhängigkeit von der gewichteten Summe der Eingaben zu finden. Die Auswahl der Aktivierungsfunktion hat einen großen Einfluss auf die Leistung des neuronalen Netzes.


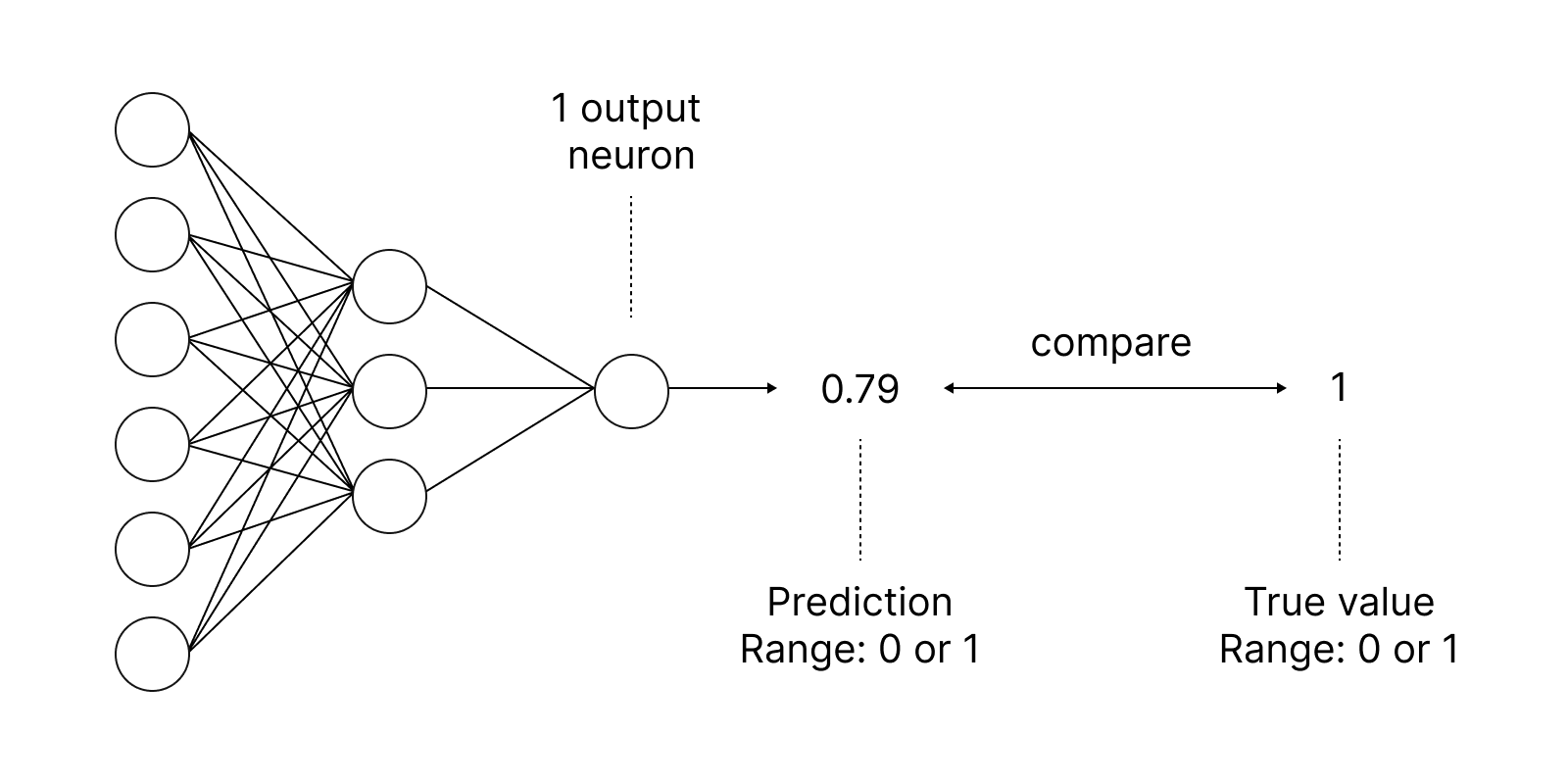
          Eine der beliebtesten Aktivierungsfunktionen ist das Sigmoid.



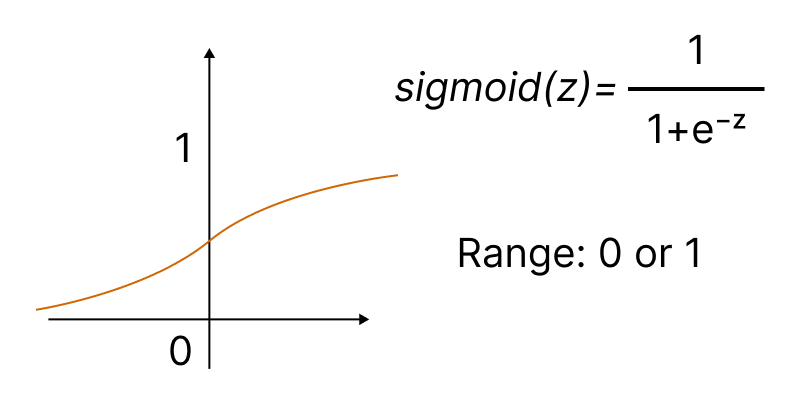
          Die integrierte Methode Activation ermöglicht es, einen der fünfzehn Typen der Aktivierungsfunktion einzustellen. Sie sind alle in der Enumeration ENUM_ACTIVATION_FUNCTION verfügbar.

          ID

          Beschreibung

          AF_ELU                      

          Exponentielle Linear Unit

          AF_EXP                      

          Exponentiell

          AF_GELU                      

          Gaussian Error Linear Unit

          AF_HARD_SIGMOID              

          Hard Sigmoid

          AF_LINEAR                    

          Linear

          AF_LRELU                    

          Leaky Rectified Linear Unit

          AF_RELU                      

          Rectified Linear Unit

          AF_SELU                      

          Skalierte Exponential Linear Unit

          AF_SIGMOID                  

          Sigmoid

          AF_SOFTMAX                  

          Softmax

          AF_SOFTPLUS                  

          Softplus

          AF_SOFTSIGN                  

          Softsign

          AF_SWISH                    

          Swish

          AF_TANH                      

          Die hyperbolische Tangensfunktion

          AF_TRELU                    

          Thresholded Rectified Linear Unit


          Ein neuronales Netz zielt darauf ab, einen Algorithmus zu finden, der den Fehler beim Lernen minimiert, wofür die Verlustfunktion verwendet wird. Die Abweichung wird mit der Methode Loss berechnet, für die Sie einen von vierzehn Typen aus der Enumeration ENUM_LOSS_FUNCTION angeben können.

          Die daraus resultierenden Abweichungswerte werden dann zur Verfeinerung der Parameter des neuronalen Netzes verwendet. Dies geschieht mit der Methode Derivative, die die Werte der Ableitung der Aktivierungsfunktion berechnet und das Ergebnis in den übergebenen Vektor/die Matrix schreibt. Der Trainingsprozess des neuronalen Netzes kann mit der Animation aus dem Artikel „Programmierung eines Tiefen Neuronalen Netzes von Grund auf mit der Sprache MQL“ visuell dargestellt werden.



          Verbesserungen in OpenCL

          Wir haben auch Matrix- und Vektorunterstützung in den Funktionen CLBufferWrite und CLBufferRead implementiert. Für diese Funktionen gibt es entsprechende Überladungen. Das Beispiel einer Matrix ist unten dargestellt.

          Schreiben der Werte aus der Matrix in den Puffer und bei Erfolg Rückgabe von true.

          uint  CLBufferWrite(
   int buffer, // Puffer-Handle für OpenCL
   uint buffer_offset, // Offset im OpenCL-Puffer in Bytes
   matrix<T>&mat // Matrix der in den Puffer zu schreibenden Werte
   );

          Einlesen eines OpenCL-Puffer in eine Matrix und bei Erfolg Rückgabe von true.

          uint  CLBufferRead(
   int buffer, // Puffer-Handle für OpenCL
   uint buffer_offset, // Offset im OpenCL-Puffer in Bytes
   const matrix& mat, // Matrix zum Abrufen von Werten aus dem Puffer
   ulong rows=-1, // Anzahl der Zeilen in der Matrix
   ulong         cols=-1                    // Anzahl der Spalten in der Matrix
   );

          Betrachten wir die Verwendung der neuen Überladungen anhand eines Beispiels für ein Matrixprodukt zweier Matrizen. Lassen Sie uns die Berechnungen nach drei Methoden durchführen:

            • Ein naiver Weg zur Veranschaulichung des Algorithmus zur Matrixmultiplikation
            • Die integrierte Methode MatMul
            • Parallele Berechnung in OpenCL

              Die erhaltenen Matrizen werden mit der Methode Compare überprüft, die die Elemente zweier Matrizen mit der angegebenen Genauigkeit vergleicht.

              #define M  3000 // Anzahl der Zeilen in der ersten Matrix
#define K  2000 // Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix
#define N  3000 // Anzahl der Spalten in der zweiten Matrix
 
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Skript Programm Start Funktion                                   |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- Initialisierung des Zufallszahlengenerators
  MathSrand((int)TimeCurrent());
//--- Matrizen der angegebenen Größe mit Zufallswerten füllen
  matrixf mat1(M, K, MatrixRandom) ; // erste Matrix
  matrixf mat2(K, N, MatrixRandom); // zweite Matrix
 
//--- Berechnung des Produkts von Matrizen auf naive Weise
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// hier wird das Ergebnis der Multiplikation zweier Matrizen wiedergegeben
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- Berechnung des Produkts von Matrizen mit MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- Berechnung des Produkts von Matrizen in OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // Kontext-Handle
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL not found, exit");
    return;
   }
  int cl_prg; // Programm-Handle
  int cl_krn; // Kernel-Handle
  int cl_mem_in1; // Handle des ersten Puffers (Eingang)
  int cl_mem_in2; // Handle des zweiten Puffers (Eingang)
  int cl_mem_out; // Handle des dritten Puffers (Ausgabe)
//--- das Programm und den Kernel erstellen
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- alle drei Puffer für die drei Matrizen erstellen
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- dritte Matrix - Ausgabe
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- Kernel-Argumente setzen
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- Matrizen in Gerätepuffer schreiben
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- Startzeit der Code-Ausführung von OpenCL
  start=GetTickCount();
//--- die Parameter für den Arbeitsbereich der Aufgabe festlegen und das OpenCL-Programm ausführen
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- das Ergebnis in die Matrix einlesen
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl ist fehlgeschlagen. Fehler ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Vergleich der Rechenzeiten der Methoden");
  PrintFormat("Naive Rechenzeit = %d ms",time_naive);
  PrintFormat("MatMul Rechenzeit = %d ms",time_matmul);
  PrintFormat("OpenCl Rechenzeit  = %d ms",time_opencl);  
//--- alle OpenCL-Kontexte freigeben
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- alle erhaltenen Ergebnismatrizen miteinander vergleichen 
  Print("Anzahl der Diskrepanzfehler zwischen den Ergebnismatrizen?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Ergebnis: 
   
   Matrix [3000 x 3000] lesen 
   Vergleich der Rechenzeiten der Methoden
   Naive Rechenzeit = 54750 ms
   MatMul Rechenzeit = 4578 ms
   OpenCl Rechenzeit = 922 ms
   Anzahl der Diskrepanzfehler zwischen den Ergebnismatrizen?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Füllt die Matrix mit Zufallswerten                               |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//--- alle OpenCL-Kontexte freigeben
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- alle erstellten OpenCL-Kontexte in umgekehrter Reihenfolge freigeben
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

              Eine detaillierte Erläuterung des OpenCL-Codes aus diesem Beispiel finden Sie im Artikel „OpenCL: Vom naiven zum aufschlussreicheren Programmieren“.


              Weitere Verbesserungen

              Build 3390 hob zwei Einschränkungen im OpenCL-Betrieb auf, die die GPU-Nutzung beeinträchtigten.

                Die maximale Anzahl von OpenCL-Objekten kann bis zu 65536 betragen, während zuvor eine Grenze von 256 galt. OpenCL-Objekt-Handles werden in einem MQL5-Programm erstellt mit den Funktionen CLContextCreate, CLBufferCreate und CLProgramCreate. Die bisherige Grenze von 256 Handles war für den effizienten Einsatz von Methoden des maschinellen Lernens nicht ausreichend.

                OpenCL kann auch auf Grafikkarten ohne „double“-Unterstützung verwendet werden. Bisher waren in MQL5-Programmen nur GPUs erlaubt, die double unterstützen, obwohl viele Aufgaben Berechnungen mit float erlauben. Der Typ float wird zunächst als nativ für die Parallelverarbeitung angesehen, da er weniger Platz benötigt. Daher wurde die alte Vorschrift aufgehoben.

                Um die obligatorische Verwendung von Grafikprozessoren mit double-Unterstützung für bestimmte Aufgaben festzulegen, verwenden Sie die Option CL_USE_GPU_DOUBLE_ONLY im Aufruf CLContextCreate.
                   int cl_ctx;
//--- Initialisierung des OpenCL-Kontexts
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL nicht gefunden");
      return;
     }

                Obwohl die Änderungen bei den OpenCL-Operationen nicht direkt mit Matrizen und Vektoren zu tun haben, stehen sie im Einklang mit unseren Bemühungen bei der Entwicklung der maschinellen Lernfähigkeiten der Sprache MQL5.


                Die Zukunft von MQL5 im maschinellen Lernen

                In den letzten Jahren haben wir viel getan, um fortschrittliche Technologien in die MQL5-Sprache einzuführen:

                  Die MQL5-Sprache wird sich weiter entwickeln, wobei das maschinelle Lernen eine der wichtigsten Prioritäten ist. Wir haben große Pläne für die weitere Entwicklung. Bleiben Sie uns also treu, unterstützen Sie uns und lernen Sie weiterhin mit uns.

                  Übersetzt aus dem Russischen von MetaQuotes Ltd.
                  Originalartikel: https://www.mql5.com/ru/articles/10922

                  Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

                  Andere Artikel von diesem Autor

                  Zur Diskussion im Händlerforum
                  Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 22): Neues Auftragssystems (V) Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 22): Neues Auftragssystems (V)
                  Heute werden wir die Entwicklung des neuen Auftragssystems fortsetzen. Es ist nicht einfach, ein neues System einzuführen, da wir häufig auf Probleme stoßen, die den Prozess erheblich erschweren. Wenn diese Probleme auftreten, müssen wir innehalten und die Richtung, in die wir uns bewegen, neu analysieren.
                  Techniken des MQL5-Assistenten, die Sie kennen sollten (Teil 03): Shannonsche Entropie Techniken des MQL5-Assistenten, die Sie kennen sollten (Teil 03): Shannonsche Entropie
                  Der Händler von heute ist ein Philomath, der fast immer (entweder bewusst oder unbewusst...) nach neuen Ideen sucht, sie ausprobiert, sich entscheidet, sie zu modifizieren oder zu verwerfen; ein explorativer Prozess, der einiges an Sorgfalt kosten sollte. Diese Artikelserie wird vorschlagen, dass der MQL5-Assistent eine Hauptstütze für Händler sein sollte.
                  Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 23): Neues Auftragssystems (VI) Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 23): Neues Auftragssystems (VI)
                  Wir werden das Auftragssystem flexibler gestalten. Hier werden wir Änderungen am Code in Erwägung ziehen, die ihn flexibler machen, sodass wir die Positionsstopp-Levels viel schneller ändern können.
                  Neuronale Netze leicht gemacht (Teil 20): Autoencoder Neuronale Netze leicht gemacht (Teil 20): Autoencoder
                  Wir untersuchen weiterhin Modelle und Algorithmen für unüberwachtes Lernen. Einige Leser haben vielleicht Fragen zur Relevanz der jüngsten Veröffentlichungen zum Thema neuronale Netze. In diesem neuen Artikel befassen wir uns wieder mit neuronalen Netzen.