MetaTrader 5 / Exemplos
English Русский 中文 Español Deutsch 日本語 한국어 Français Italiano Türkçe
preview
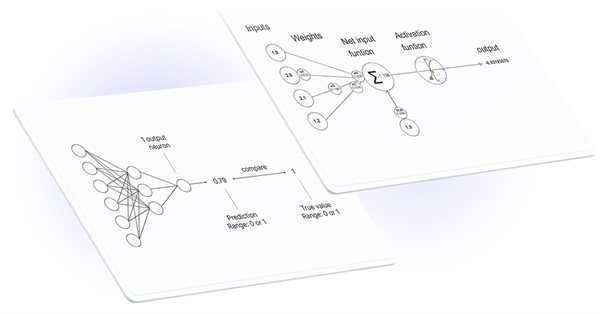
Operações com Matrizes e Vetores em MQL5

Operações com Matrizes e Vetores em MQL5

MetaTrader 5 — Exemplos | 21 novembro 2022, 08:52
712 0
MetaQuotes
MetaQuotes

Tipos de dados especiais — matrizes e vetores — foram adicionados à linguagem MQL5 para resolver uma grande classe de problemas matemáticos. Os novos tipos oferecem métodos integrados para a criação de código conciso e compreensível que se aproxima da notação matemática. Neste artigo, nós fornecemos uma breve descrição dos Métodos matriciais e vetoriais integrados na seção de ajuda.


Conteúdo


Cada linguagem de programação oferece os tipos de array de dados que armazenam os conjuntos de variáveis numéricas, incluindo int, double e outros. Os elementos do array são acessados pelo índice, o que permite realizar as operações vetoriais usando loops. Os vetores mais comumente usados são os unidimensionais e bidimensionais:

int    a[50];       // One-dimensional array of 50 integers
double m[7][50];    // Two-dimensional array of 7 subarrays, each consisting of 50 integers
MyTime t[100];      // Array containing elements of MyTime type

Os recursos dos vetores geralmente são suficientes para as tarefas relativamente simples relacionadas ao armazenamento e processamento de dados. Mas quando se trata de problemas matemáticos complexos, trabalhar com vetores torna-se difícil tanto em termos de programação quanto de leitura de código, devido ao grande número de loops aninhados. Mesmo as operações de álgebra linear mais simples requerem uma codificação excessiva e uma boa compreensão da matemática.

Tecnologias de dados modernas, como aprendizado de máquina, redes neurais e gráficos 3D, usam amplamente as soluções de álgebra linear associadas aos conceitos de vetores e matrizes. Para facilitar as operações com tais objetos, a MQL5 fornece os tipos de dados especiais: matrizes e vetores. Os novos tipos eliminam muitas operações de programação de rotina e melhoram a qualidade do código.


Tipos de matriz e vetor

Resumindo, um vetor é um array do tipo double unidimensional e uma matriz é um array do tipo double bidimensional. Os vetores podem ser verticais e horizontais; no entanto, eles não são separados em MQL5.

Uma matriz pode ser representada como um array de vetores horizontais, em que o primeiro índice é o número da linha e o segundo índice é o número da coluna.


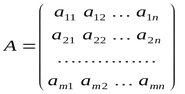
A numeração de linhas e colunas começa em 0, semelhante aos arrays.

Além dos tipos 'matrix' e 'vector' que contêm os dados do tipo double, existem mais quatro tipos para operações com outros tipos de dados relevantes:

  • matrixf — uma matriz contendo elementos do tipo float
  • matrixc — uma matriz contendo elementos do tipo complexo
  • vectorf — um vetor contendo elementos do tipo float
  • vectorc — um vetor contendo elementos do tipo complexo

No momento da escrita deste artigo, o desenvolvimento nos tipos matrixc e vectorc ainda não foram concluídos e, portanto, ainda não é possível usar esses tipos nos métodos integrados.

As funções de modelo suportam notações como matrix<double>, matrix<float>, vector<double>, vector<float> em vez dos tipos correspondentes.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */


Criação e inicialização

Os métodos matrix e vector são divididos em nove categorias de acordo com a sua finalidade. Existem várias maneiras de declarar e inicializar as matrizes e vetores.

O método de criação mais simples é declarar sem a especificação de tamanho, ou seja, sem alocação de memória para os dados. Aqui, nós apenas escrevemos o tipo de dados e o nome da variável:

  matrix         matrix_a;   // double type matrix
  matrix<double> matrix_a1;  // another way to declare a double matrix, suitable for use in templates
  matrix<float>  matrix_a3;  // float type matrix
  vector         vector_a;   // double type vector
  vector<double> vector_a1;  // another notation to create a double vector
  vector<float>  vector_a3;  // float type vector

Então você pode alterar o tamanho dos objetos criados e preenchê-los com os valores desejados. Eles também podem ser usados nos métodos matrix integrados para obter os resultados de cálculo.

Uma matriz ou um vetor pode ser declarado com o tamanho especificado, ao alocar memória para os dados, mas sem inicializar nada. Aqui, após o nome da variável, especificamos o(s) tamanho(s) entre parênteses:

  matrix         matrix_a(128,128);           // the parameters can be either constants
  matrix<double> matrix_a1(InpRows,InpCols);  // or variables
  matrix<float>  matrix_a3(InpRows,1);        // analogue of a vertical vector
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float>  vector_a3(InpSize+16);       // expression can be used as a parameter

A terceira maneira de criar objetos é declarar com a inicialização. Nesse caso, os tamanhos da matriz e do vetor são determinados pela sequência de inicialização indicada entre chaves:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // the matrices must be of the same type
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                     // the vectors must be of the same type


Há também os métodos estáticos para criar matrizes e vetores do tamanho especificado, inicializados de uma certa maneira:  

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Além disso, existem os métodos não estáticos para inicializar uma matriz ou um vetor com os valores dados — Init e Fill:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

Neste exemplo, nós usamos o método Init para alterar os tamanhos de uma matriz já inicializada, pelo que todos os novos elementos foram preenchidos com valores aleatórios.

Uma vantagem importante do método Init é a capacidade de especificar uma função de inicialização nos parâmetros para preencher os elementos da matriz/vetor de acordo com esta regra. Por exemplo:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Execution result
  init = 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Fills the matrix with powers of a number                         |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 }


Cópia das matrizes e vetores

Matrizes e vetores podem ser copiados usando o método Copy. Mas uma maneira mais simples e familiar de copiar esses tipos de dados é usar o operador de atribuição "=". Além disso, você pode usar o método Assign para copiar.

//--- copying matrices
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

A diferença entre Assign e Copy é que ele pode ser usado para matrizes e arrays. O exemplo abaixo mostra a cópia do array de tipo inteiro int_arr em uma matriz do tipo double. A matriz resultante se ajusta automaticamente de acordo com o tamanho da matriz copiada. 

//--- copying an array to a matrix
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

O método Assign permite a transição perfeita de arrays para matrizes, com tamanho automatizado e conversão do tipo.


Cópia de séries temporais para as matrizes ou vetores

A análise do grafico de preços implica nas operações com a matriz de estrutura MqlRates. MQL5 fornece um novo método para trabalhar com tais estruturas de dados de preço.

O método CopyRates copia as séries históricas da estrutura MqlRates diretamente em uma matriz ou vetor. Assim, você pode evitar a necessidade de obter as séries temporais necessárias nas matrizes relevantes usando as funções da seção Acesso a séries temporais e indicadores. Além disso, não há necessidade de transferi-los para uma matriz ou vetor. Com o método CopyRates, você pode receber as cotações em uma matriz ou vetor em apenas uma chamada. Vamos considerar um exemplo de como calcular uma matriz de correlação para uma lista de símbolos: vamos calcular esses valores usando dois métodos diferentes e comparar os resultados.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- list of symbols for calculation
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- matrix and vector to receive Close prices
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- get Close prices to a vector
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- insert the vector to the timeseries matrix
      rates.Col(close, i);
      PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size());
      //--- output the first 20 vector values for debugging
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 Close prices were added to the matrix
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 Close prices were added to the matrix
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 Close prices were added to the matrix
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 Close prices were added to the matrix
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 Close prices were added to the matrix
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- prepare a matrix of correlations between symbols
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Compute pairwise correlation coefficients");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Correlation matrix on vectors: \n", corr_from_vector);
  /*
  Calculate pairwise correlation coefficients
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0.397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0.744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Correlation matrix on vectors:
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- now let's see how a correlation matrix can be calculated in one line
  matrix corr_from_matrix=rates.CorrCoef(false);   // false means that the vectors are in the matrix columns
  Print("Correlation matrix rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- compare the resulting matrices to find discrepancies
  Print("How many discrepancy errors between result matrices?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Correlation matrix rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  How many discrepancy errors between result matrices?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- create a nice output of the correlation matrix
  Print("Output the correlation matrix with headers");
  string header="        ";  // header
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- now rows
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Output the correlation matrix with headers
            EURUSD  GBPUSD  USDJPY  USDCAD  USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Returns a string with vector values                              |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- compose a string
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- add a tail if the vector length exceeds the specified size
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//|  Returns a string with the specified number of spaces            |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

O exemplo mostra como:

    • Obter os preços de fechamento usando o CopyRates
    • Inserir um vetor em uma matriz usando o método col
    • Calcular o coeficiente de correlação entre os dois vetores usando CorrCoef
    • Calcular a matriz de correlação sobre uma matriz com vetores de valor usando CorrCoef
    • Retornar uma matriz triangular superior usando o método TriU
    • Comparar duas matrizes e encontrar discrepâncias usando o método Compare


      Operações matriciais e vetoriais

      Operações matemáticas elementares de adição, subtração, multiplicação e divisão podem ser realizadas em matrizes e vetores. Ambos os objetos em tais operações devem ser do mesmo tipo e devem ter os mesmos tamanhos. Cada elemento da matriz ou vetor opera no elemento correspondente da segunda matriz ou vetor.

      Você também pode usar um escalar do tipo apropriado (duplo, flutuante ou complexo) como segundo termo (multiplicador, subtraendo ou divisor). Nesse caso, cada membro da matriz ou vetor operará no escalar especificado.

        matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // Hadamard product
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- operations in place are possible
  matrix_a+=matrix_b;
  matrix_a/=2;

      Além disso, matrizes e vetores podem ser passados como um segundo parâmetro para a maioria das funções matemáticas, incluindo MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. Tais operações implicam na manipulação de elementos de matrizes ou vetores. Exemplo:

      //---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

      Para o MathMod e MathPow, o segundo elemento pode ser um escalar ou uma matriz/vetor de tamanho apropriado. 

         matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }


      Manipulações

      A MQL5 suporta as seguintes manipulações básicas em matrizes e vetores, que não requerem nenhum cálculo:

      • Transposição
      • Extração de linhas, colunas e diagonais
      • Redimensionamento e remodelação de matrizes
      • Troca de linhas e colunas especificadas
      • Cópia para um novo objeto
      • Comparação de dois objetos
      • Divisão de uma matriz em várias submatrizes
      • Ordenação
      O exemplo a seguir mostra a transposição de matrizes usando o método Transpose:
        matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

      Abaixo estão exemplos mostrando como definir e extrair uma diagonal usando o método diag:

         vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

      Alterar o tamanho de uma matriz usando o método Reshape:

         matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

      Exemplos de uma divisão vertical de uma matriz usando o método Vsplit:

         matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

      O método Col e Row permitem obter os elementos relevantes da matriz, bem como inserir elementos em matrizes não alocadas, ou seja, matrizes sem o tamanho especificado. Aqui está um exemplo:

         vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("col 1 - ",m2.Col(1));
  /*
   col 1 - [8,8,8,8]
  */

   Print("col 2 - ",m2.Col(2));
  /*
   col 1 - [8,8,8,8]  col 2 - [1,2,3,8]
  */


      Produtos

      A multiplicação de matrizes é um dos algoritmos básicos amplamente utilizados nos métodos numéricos. Muitas implementações de algoritmos de retropropagação e propagação direta em rede neural as camadas convolucionais são baseadas nesta operação. Muitas vezes, 90-95% de todo o tempo gasto em aprendizado de máquina é tomado por esta operação. Todos os métodos de produtos são fornecidos sob a seção de ajuda de Produtos de matrizes e vetores.

      O exemplo a seguir mostra a multiplicação de duas matrizes usando o método MatMul:

         matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

      Um exemplo do produto Kronecker de duas matrizes ou uma matriz e um vetor, usando o método Kron.

         matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

      Mais exemplos do artigo Matrizes e Vetores em MQL5:

      //--- initialize matrices
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Product of horizontal vector v[3] and matrix m[3,5]");
   vector v3 = {1,2,3};
   Print("On the left v3 = ",v3);
   Print("On the right m35 = \n",m35);
   Print("v3.MatMul(m35) = horizontal vector v[5] \n",v3.MatMul(m35));
   /*
   1. Product of horizontal vector v[3] and matrix m[3,5]
   On the left v3 = [1,2,3]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = horizontal vector v[5]
   [40,46,52,58,64]
   */

//--- show that this is really a horizontal vector
   Print("\n2. Product of matrix m[1,3] and matrix m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("On the left m13 = \n",m13);
   Print("On the right m35 = \n",m35);
   Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35));
   /*
   2. Product of matrix m[1,3] and matrix m[3,5]
   On the left m13 =
   [[1,2,3]]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = matrix m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Product of matrix m[3,5] and vertical vector v[5]");
   vector v5 = {1,2,3,4,5};
   Print("On the left m35 = \n",m35);
   Print("On the right v5 = ",v5);
   Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5));
   /*
   3. Product of matrix m[3,5] and vertical vector v[5]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vertical vector v[3]
   [40,115,190]
   */

//--- show that this is really a vertical vector
   Print("\n4. Product of matrix m[3,5] and matrix m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("On the left m35 = \n",m35);
   Print("On the right m51 = \n",m51);
   Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51));
   /*
   4. Product of matrix m[3,5] and matrix m[5,1]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = matrix v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Product of matrix m[3,5] and matrix m[5,2]");
   Print("On the left m35 = \n",m35);
   Print("On the right m52 = \n",m52);
   Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52));
   /*
   5. Product of matrix m[3,5] and matrix m[5,2]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = matrix m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Product of horizontal vector v[5] and matrix m[5,2]");
   Print("On the left v5 = \n",v5);
   Print("On the right m52 = \n",m52);
   Print("v5.MatMul(m52) = horizontal vector v[2] \n",v5.MatMul(m52));
   /*
   6. The product of horizontal vector v[5] and matrix m[5,2]
   On the left v5 =
   [1,2,3,4,5]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = horizontal vector v[2]
   [80,95]
   */

   Print("\n7. Outer() product of horizontal vector v[5] and vertical vector v[3]");
   Print("On the left v5 = \n",v5);
   Print("On the right v3 = \n",v3);
   Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3));
   /*
   7. Outer() product of horizontal vector v[5] and vertical vector v[3]
   On the left v5 =
   [1,2,3,4,5]
   On the right v3 =
   [1,2,3]
   v5.Outer(v3) = matrix m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */


      Transformações

      Transformações matriciais são frequentemente usadas em operações de dados. No entanto, muitas operações matriciais complexas não podem ser resolvidas de forma eficiente ou estável devido à precisão limitada dos computadores.

      Transformações de matrizes (ou decomposições) são métodos que reduzem uma matriz em suas partes componentes, o que facilita o cálculo de operações de matrizes mais complexas. Métodos de decomposição de matrizes, também conhecidos como métodos de fatoração de matrizes, são a espinha dorsal da álgebra linear em computadores, mesmo para operações básicas como sistemas de resolução de equações lineares, cálculo da inversa e cálculo do determinante de uma matriz.

      O aprendizado de máquina usa amplamente a Decomposição em Valores Singulares (SVD), que permite a representação da matriz original como o produto de três outras matrizes. A SVD é usada para resolver uma variedade de problemas, desde aproximação dos mínimos quadrados até a compressão e reconhecimento de imagem.

      Um exemplo da Decomposição em Valores Singulares pelo método SVD:

        matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- execute SVD decomposition
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// check block
//--- U * singular diagonal * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- another check
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

      Outra transformação comumente usada é a decomposição de Cholesky, que pode ser usada para resolver um sistema de equações lineares Ax=b se a matriz A for simétrica e positiva definida.

      Em MQL5, a decomposição de Cholesky é executada pelo método Cholesky: 

        matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

      A tabela abaixo mostra a lista de métodos disponíveis:

      Função

      Ação

      Cholesky

      Calcula a decomposição de Cholesky

      Eig

      Calcula os autovalores e autovetores à direita de uma matriz quadrada

      EigVals

      Calcula os autovalores de uma matriz geral

      LU

      Decomposição LU de uma matriz como o produto de uma matriz triangular inferior e uma matriz triangular superior

      LUP

      Decomposição LUP com pivotamento parcial, que se refere à decomposição LU apenas com permutações de linha: PA=LU

      QR

      Calcula a Decomposição QR de uma matriz

      SVD

      Decomposição em Valores Singulares

      Obtenção de estatísticas

        Os métodos da seção Estatisticas são usadas para computar estatísticas descritivas de matrizes e vetores. Use-os para encontrar:
        • Valores máximos e mínimos, juntamente com os seus índices em uma matriz/vetor
        • A soma e o produto dos elementos, bem como a soma e o produto cumulativo
        • Mediana, média, média aritmética e média ponderada dos valores da matriz/vetor
        • Desvio padrão e variância do elemento
        • Percentis e quantis
        • Métrica de regressão como o erro do desvio da linha de regressão construída na matriz de dados especificada

          Um exemplo de cálculo do desvio padrão pelo método Std:

             matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

          Cálculo do quantis pelo método Quantile:

             matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */


          Características da matriz

          Uso dos métodos da seção Características para obter os seguintes valores:

          • O número de linhas e colunas em uma matriz
          • A norma e o número de condicionalidade
          • Determinante, posto, traço e espectro de uma matriz

          Cálculo do posto de uma matriz usando o método Rank:

            matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // matrix deficit
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 size - rank 1, unless all 0
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

          Cálculo da norma usando o método Norm:

            matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */


          Resolução de equações

          Métodos de aprendizado de máquina e problemas de otimização geralmente exigem encontrar as soluções para um sistema de equações lineares. A seção Soluções contém quatro métodos que permitem a solução de tais equações dependendo do tipo de matriz. 

          Função

          Ação

          Solve

          Resolver uma equação de matriz linear ou um sistema de equações algébricas lineares

          LstSq

          Retorna a solução dos mínimos quadrados de equações algébricas lineares (para matrizes não quadradas ou degeneradas)

          Inv

          Cálculo do inverso multiplicativo de uma matriz quadrada invertível pelo método de Jordan-Gauss

          PInv

          Calcula a pseudo-inversa de uma matriz pelo método de Moore-Penrose

          Considere um exemplo de resolução da equação A*x=b.  


          Precisamos encontrar o vetor solução x. A matriz A não é quadrada e, portanto, o método Solve não pode ser usado aqui. 

          Nós usaremos o método LstSq que permite a resolução aproximada de matrizes não quadradas ou degeneradas. 

             matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- solve the system A*x = b
   vector x=a.LstSq(b);
//--- check the solution, x must be equal to [5, -4]
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- check A*x = b1, the resulting vector must be [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

          A verificação mostrou que o vetor encontrado x é a solução desse sistema de equações.


          Métodos de Aprendizado de Máquina

          Existem três métodos de matriz e vetor que podem ser usados no aprendizado de máquina.

          Função

          Ação

          Activation

          Calcula os valores da função de ativação e grava-os no vetor/matriz passado

          Derivative

          Calcula os valores derivados da função de ativação e escreve-os no vetor/matriz passado

          Loss

          Calcula os valores da função de perda e grava-os no vetor/matriz passado

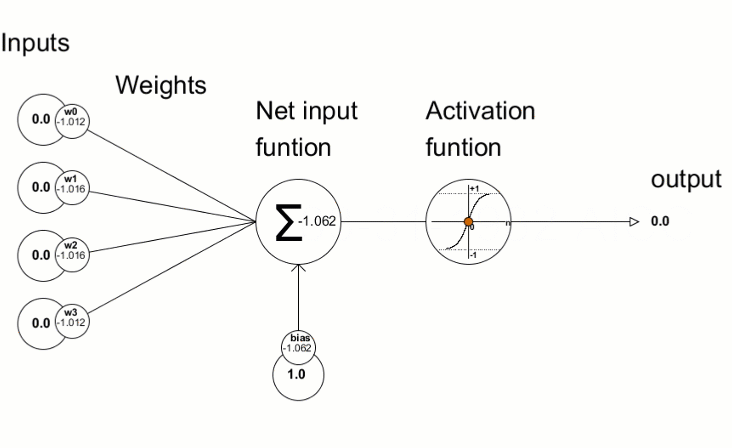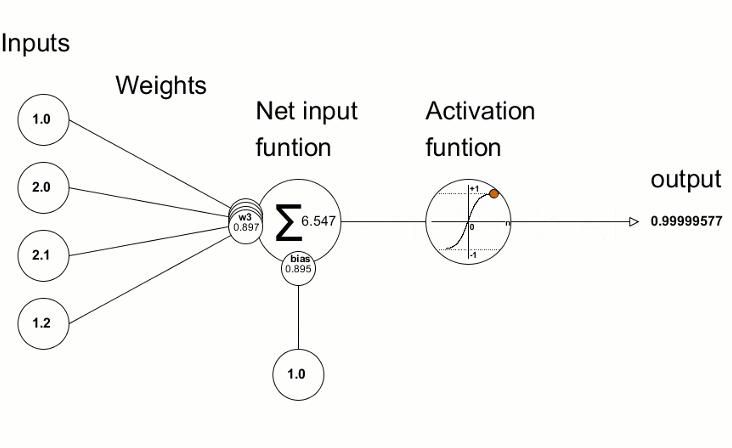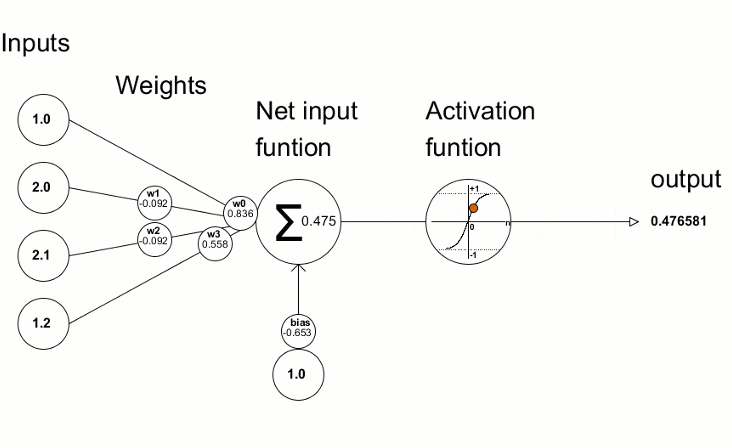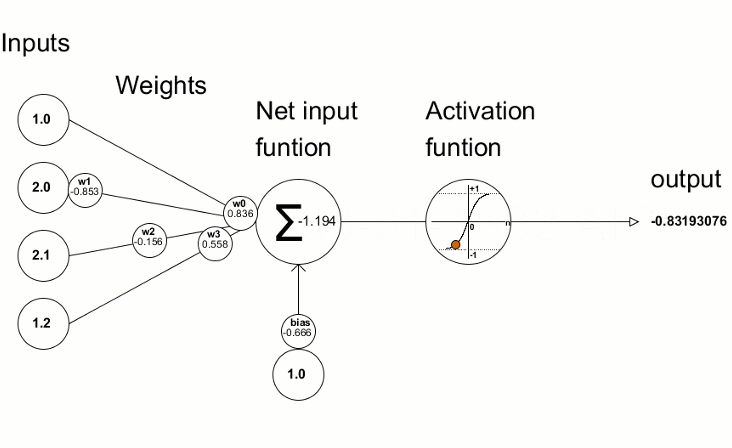
          As funções de ativação são usadas em redes neurais para encontrar uma saída dependendo da soma ponderada das entradas. A seleção da função de ativação tem um grande impacto no desempenho da rede neural.


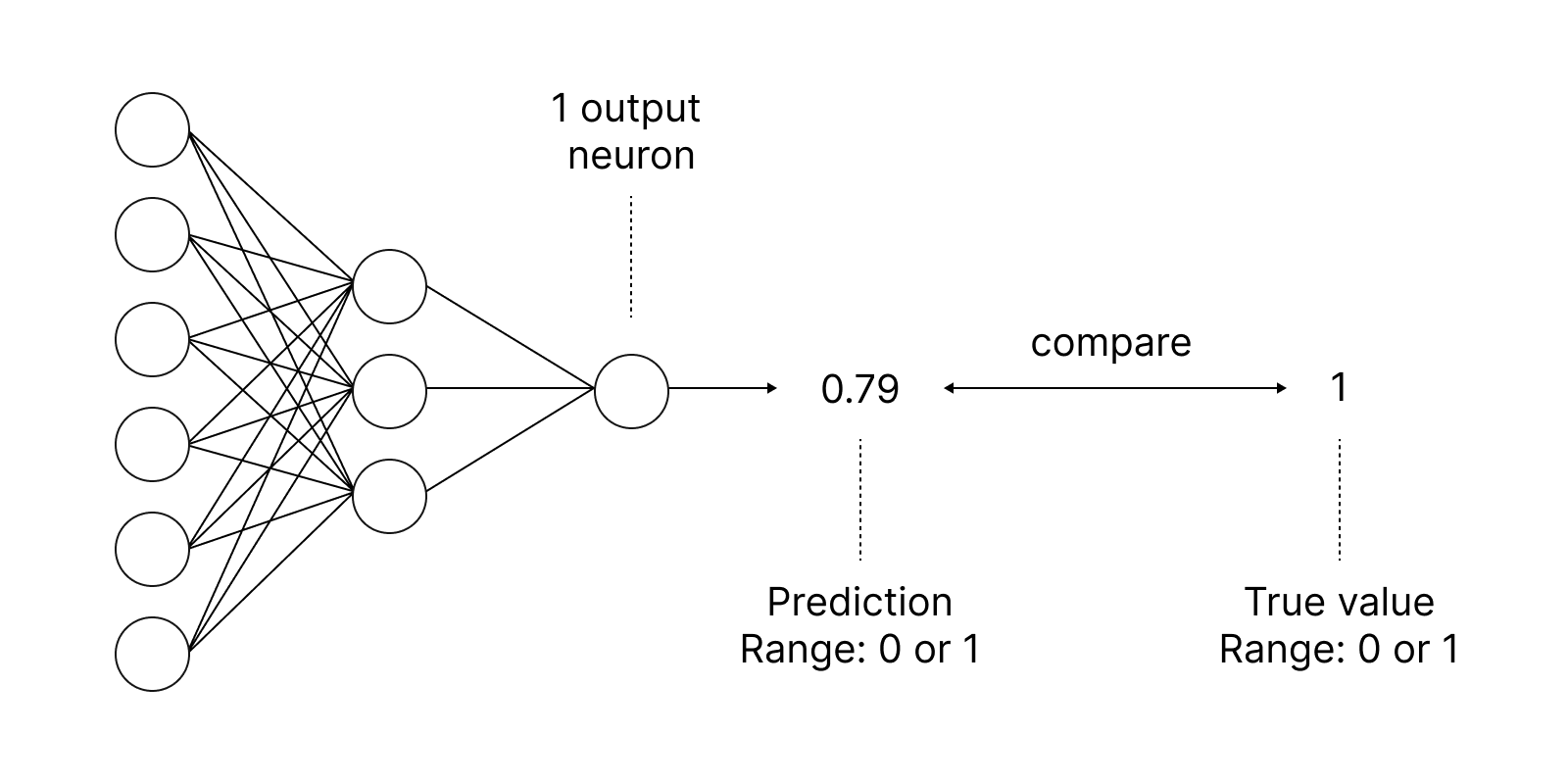
          Uma das funções de ativação mais populares é o sigmóide.



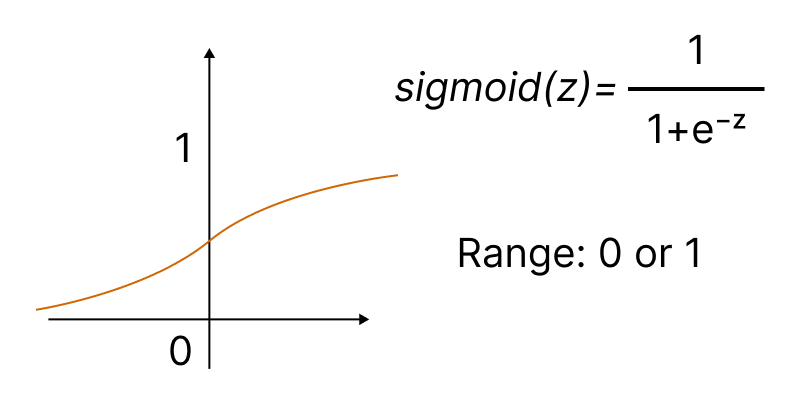
          O método Activation integrado permite definir um dos quinze tipos de função de ativação. Todos eles estão disponíveis na enumeração ENUM_ACTIVATION_FUNCTION.

          ID

          Descrição

          AF_ELU                      

          Unidade Linear Exponencial

          AF_EXP                      

          Exponencial

          AF_GELU                      

          Unidade Linear de Erro Gaussiano

          AF_HARD_SIGMOID              

          Sigmóide rígido

          AF_LINEAR                    

          Linear

          AF_LRELU                    

          Unidade Linear Retificada com Vazamento (Leaky ReLU)

          AF_RELU                      

          Unidade Linear Retificada (ReLU)

          AF_SELU                      

          Unidade Linear Exponencial Escalada

          AF_SIGMOID                  

          Sigmoide

          AF_SOFTMAX                  

          Softmax

          AF_SOFTPLUS                  

          Softplus

          AF_SOFTSIGN                  

          Softsign

          AF_SWISH                    

          Swish

          AF_TANH                      

          A função tangente hiperbólica

          AF_TRELU                    

          Unidade Linear Retificada Limiar


          Uma rede neural visa encontrar um algoritmo que minimize o erro de aprendizado, para o qual é utilizada a função de perda. O desvio é calculado usando o método Loss para o qual você pode especificar um dos 14 tipos da enumeração ENUM_LOSS_FUNCTION.

          Os valores de desvio resultantes são então usados para refinar os parâmetros da rede neural. Isso é feito usando o método Derivative, que calcula os valores da derivada da função de ativação e escreve o resultado no vetor/matriz passado. O processo de treinamento da rede neural pode ser representado visualmente usando a animação do artigo "Construindo uma rede neural profunda do zero em linguagem MQL".



          Melhorias no OpenCL

          Nós também implementamos o suporte matricial e vetorial nas funções CLBufferWrite e CLBufferRead. Sobrecargas correspondentes estão disponíveis para essas funções. Abaixo encontramos um exemplo para uma matriz.

          Grava os valores da matriz no buffer e retorna true em caso de sucesso.

          uint  CLBufferWrite(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   matrix<T>     &mat                       // matrix of values to write to buffer
   );

          Lê um buffer OpenCL para uma matriz e retorna true em caso de sucesso.

          uint  CLBufferRead(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   const matrix& mat,                       // matrix to get values from the buffer
   ulong         rows=-1,                   // number of rows in the matrix
   ulong         cols=-1                    // number of columns in the matrix
   );

          Vamos considerar o uso de novas sobrecargas usando um exemplo do produto matricial de duas matrizes. Vamos fazer os cálculos usando três métodos:

            • Uma maneira ingênua de ilustrar o algoritmo de multiplicação de matrizes
            • O método MatMul integrado
            • Cálculo paralelo em OpenCL

              As matrizes obtidas serão verificadas usando o método Compare que compara os elementos de duas matrizes com a precisão dada.

              #define M       3000      // number of rows in the first matrix
#define K       2000      // number of columns in the first matrix equal to the number of rows in the second one
#define N       3000      // number of columns in the second matrix
 
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- initialize the random number generator
  MathSrand((int)TimeCurrent());
//--- fill matrices of the given size with random values
  matrixf mat1(M, K, MatrixRandom) ;    // first matrix
  matrixf mat2(K, N, MatrixRandom);     // second matrix
 
//--- calculate the product of matrices using the naive way
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// here we rite the result of multiplying two matrices
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- calculate the product of matrices using MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- calculate the product of matrices in OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // context handle
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL not found, exit");
    return;
   }
  int cl_prg;             // program handle
  int cl_krn;             // kernel handle
  int cl_mem_in1;         // handle of the first buffer (input)
  int cl_mem_in2;         // handle of the second buffer (input)
  int cl_mem_out;         // handle of the third buffer (output)
//--- create the program and the kernel
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- create all three buffers for the three matrices
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- third matrix - output
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- set kernel arguments
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- write matrices to device buffers
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- start the OpenCL code execution time
  start=GetTickCount();
//--- set the task workspace parameters and execute the OpenCL program
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- read the result into the matrix
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Compare computation times of the methods");
  PrintFormat("Naive product time = %d ms",time_naive);
  PrintFormat("MatMul product time = %d ms",time_matmul);
  PrintFormat("OpenCl product time = %d ms",time_opencl);  
//--- release all OpenCL contexts
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- compare all obtained result matrices with each other 
  Print("How many discrepancy errors between result matrices?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Result: 
   
   Matrix [3000 x 3000] read 
   Compare computation times of the methods
   Naive product time = 54750 ms
   MatMul product time = 4578 ms
   OpenCl product time = 922 ms
   How many discrepancy errors between result matrices?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Fills the matrix with random values                              |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//| Release all OpenCL contexts                                      |
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- release all created OpenCL contexts in reverse order
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

              Uma explicação detalhada do código OpenCL deste exemplo é fornecida no artigo "OpenCL: Da programação ingênua até a mais perceptível".


              Mais melhorias

              A Build 3390 levantou duas restrições na operação OpenCL que afetavam o uso da GPU.

                O número máximo de objetos OpenCL pode ser de até 65536, enquanto anteriormente havia um limite de 256. Os manipuladores de objetos OpenCL são criados em um programa MQL5 usando a função CLContextCreate, CLBufferCreate e CLProgramCreate. O limite anterior de 256 identificadores não era suficiente para o uso eficiente dos métodos de aprendizado de máquina.

                O OpenCL também pode ser usado em placas gráficas sem suporte ao tipo 'double'. Anteriormente, apenas GPUs com suporte ao tipo double eram permitidos em programas MQL5, embora muitas tarefas permitissem cálculos usando float. O tipo float é inicialmente considerado nativo para computação paralela, pois ocupa menos espaço. Portanto, o antigo requisito foi levantado.

                Para definir o uso obrigatório de GPUs com suporte ao tipo double para tarefas específicas, use o CL_USE_GPU_DOUBLE_ONLY na chamada da CLContextCreate.
                   int cl_ctx;
//--- initialization of OpenCL context
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL not found");
      return;
     }

                Embora as mudanças nas operações OpenCL não estejam diretamente relacionadas a matrizes e vetores, elas estão alinhadas com os nossos esforços no desenvolvimento dos recursos de aprendizado de máquina da linguagem MQL5.


                O futuro da MQL5 no Aprendizado de Máquina

                Nos últimos anos, nós fizemos muito para introduzir tecnologias avançadas na linguagem MQL5:

                  A linguagem MQL5 continuará a se desenvolver, enquanto uma das direções prioritárias é o aprendizado de máquina. Temos grandes planos para um maior desenvolvimento. Portanto, fique conosco, apoie-nos e continue aprendendo conosco.

                  Traduzido do russo pela MetaQuotes Ltd.
                  Artigo original: https://www.mql5.com/ru/articles/10922

                  Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

                  Outros artigos do autor

                  Ir para discussão
                  Redes neurais de maneira fácil (Parte 25): Exercícios práticos de transferência de aprendizado Redes neurais de maneira fácil (Parte 25): Exercícios práticos de transferência de aprendizado
                  Nos dois últimos artigos, criamos uma ferramenta que permite criar e editar modelos de redes neurais. E agora é hora de avaliar o uso potencial da transferência de aprendizado (transfer learning, em inglês) usando exemplos práticos.
                  DoEasy. Controles (Parte 15): Objeto WinForms TabControl - múltiplas fileiras de cabeçalhos de guias, métodos de manuseio de guias DoEasy. Controles (Parte 15): Objeto WinForms TabControl - múltiplas fileiras de cabeçalhos de guias, métodos de manuseio de guias
                  Neste artigo, continuaremos trabalhando no objeto WinForm TabControl, e para tal criaremos a classe do objeto-campo de guia, tornaremos possível colocar cabeçalhos de guias em várias linhas e adicionaremos métodos para trabalhar com as guias do objeto.
                  Redes neurais de maneira fácil (Parte 26): aprendizado por reforço Redes neurais de maneira fácil (Parte 26): aprendizado por reforço
                  Continuamos a estudar métodos de aprendizado de máquina. Com este artigo, começamos outro grande tópico chamado aprendizado por reforço. Essa abordagem permite que os modelos estabeleçam certas estratégias para resolver as tarefas. E esperamos que essa propriedade inerente ao aprendizado de reforço abra novos horizontes para a construção de estratégias de negociação.
                  Redes neurais de maneira fácil (Parte 24): Melhorando a ferramenta para transferência de aprendizado Redes neurais de maneira fácil (Parte 24): Melhorando a ferramenta para transferência de aprendizado
                  No último artigo, elaboramos uma ferramenta para criar e editar a arquitetura de redes neurais. E hoje quero convidá-lo a continuar trabalhando nela, para torná-la mais amigável. De certa forma, ao fazer isso, estamos nos afastando um pouco do nosso tópico. Mas convenhamos que a organização do espaço de trabalho desempenha um papel importante na obtenção do resultado.