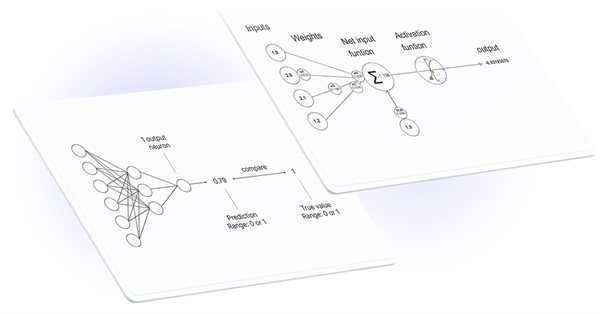
Opérations sur les Matrices et les Vecteurs en MQL5
1 220
0
Des types de données spéciaux - matrices et vecteurs - ont été ajoutés au langage MQL5 pour résoudre de nombreux problèmes mathématiques. De nouvelles méthodes sont intégrées avec ces nouveaux types pour créer un code concis et compréhensible, proche de la notation mathématique. Dans cet article, nous fournissons une brève description de ces nouvelles méthodes tirées de l’aide sur les Méthodes matricielles et vectorielles.
Sommaire
- Types matrix et vector
- Création et initialisation
- Copie de matrices et de tableaux
- Copie de séries temporelles (timeseries) vers des matrices ou des vecteurs
- Opérations sur les matrices et les vecteurs
- Manipulations
- Produits
- Transformations
- Statistiques
- Caractéristiques
- Résolution d’équations
- Méthodes de Machine Learning (Apprentissage Automatique)
- Améliorations en OpenCL
- L'avenir de MQL5 dans le Machine Learning
Chaque langage de programmation propose des types de données de type tableau pour stocker des ensembles de variables numériques: int, double et autres. Les éléments d'un tableau sont accessibles par index, ce qui permet d'effectuer des opérations sur le tableau à l'aide de boucles. Les plus couramment utilisés sont les tableaux à 1 et 2 dimensions :
int a[50]; // One-dimensional array of 50 integers double m[7][50]; // Two-dimensional array of 7 subarrays, each consisting of 50 integers MyTime t[100]; // Array containing elements of MyTime type
Les capacités des tableaux sont généralement suffisantes pour des tâches relativement simples liées au stockage et au traitement des données. Mais lorsqu'il s'agit de problèmes mathématiques complexes, travailler avec des tableaux devient difficile, tant en termes de programmation que de lecture du code, en raison du grand nombre de boucles imbriquées. Même les opérations d'algèbre linéaire les plus simples nécessitent un codage important et une bonne compréhension des mathématiques.
Les technologies de données modernes, telles que l'apprentissage automatique (machine learning), les réseaux de neurones et les graphiques 3D, font largement appel aux solutions d'algèbre linéaire associées aux concepts de vecteurs et de matrices. Pour faciliter les opérations avec ces types d’objets, MQL5 fournit des types de données spéciaux : les matrices et vecteurs. Ces nouveaux types éliminent un grand nombre d'opérations de programmation de routine et améliorent la qualité du code.
Types matrix et vector
Un vecteur, type vector, est un tableau à 1 dimension d’éléments de type double. Une matrice, type matrix, est un tableau à 2 dimensions d’éléments de type double. Les vecteurs peuvent être verticaux et horizontaux. Cependant, ils ne sont pas séparés en MQL5.
Une matrice peut être représentée comme un tableau de vecteurs horizontaux, dans lequel le premier indice est le numéro de la ligne et le deuxième indice le numéro de la colonne.
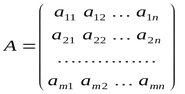
La numérotation des lignes et des colonnes commence à partir de 0, comme pour les tableaux.
Outre les types "matrix" et "vector" qui contiennent des données de type double, il existe 4 autres types pour les opérations avec les types de données correspondants :
- matrixf - une matrice contenant des éléments flottants
- matrixc - une matrice contenant des éléments complexes
- vectorf - un vecteur contenant des éléments flottants
- vectorc - un vecteur contenant des éléments complexes
Au moment de la rédaction de ce document, le travail sur les types matrixc et vectorc n'est pas encore terminé. Il n'est donc pas encore possible d'utiliser ces types dans les méthodes intégrées.
Les modèles de fonctions prennent en charge les notations telles que matrix<double>, matrix<float>, vector<double>, vector<float> au lieu des types correspondants.
vectorf v_f1= {0, 1, 2, 3,}; vector<float> v_f2=v_f1; Print("v_f2 = ", v_f2); /* v_f2 = [0,1,2,3] */
Création et initialisation
Les méthodes matricielles et vectorielles sont divisées en 9 catégories en fonction de leur objectif. Il existe plusieurs façons de déclarer et d'initialiser les matrices et les vecteurs.
La méthode de création la plus simple est la déclaration sans spécification de taille, c'est-à-dire sans allocation préalable de mémoire pour les données. Il suffit simplement d’écrire le type de données et le nom de la variable :
matrix matrix_a; // double type matrix matrix<double> matrix_a1; // another way to declare a double matrix, suitable for use in templates matrix<float> matrix_a3; // float type matrix vector vector_a; // double type vector vector<double> vector_a1; // another notation to create a double vector vector<float> vector_a3; // float type vector
Vous pouvez ensuite modifier la taille des objets créés et les remplir ultérieurement. Ils peuvent également être utilisés dans les méthodes matricielles intégrées pour obtenir des résultats de calcul.
Une matrice ou un vecteur peut être déclaré avec la taille spécifiée, tout en allouant la mémoire pour les données mais sans rien initialiser. Après le nom de la variable, spécifiez ici la ou les tailles entre parenthèses :
matrix matrix_a(128,128); // the parameters can be either constants matrix<double> matrix_a1(InpRows,InpCols); // or variables matrix<float> matrix_a3(InpRows,1); // analogue of a vertical vector vector vector_a(256); vector<double> vector_a1(InpSize); vector<float> vector_a3(InpSize+16); // expression can be used as a parameter
La troisième façon de créer des objets est de les déclarer avec initialisation. Dans ce cas, les tailles des matrices et des vecteurs sont déterminées par la séquence d'initialisation indiquée entre accolades :
matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}}; matrix<double> matrix_a1=matrix_a; // the matrices must be of the same type matrix<float> matrix_a3={{1,2},{3,4}}; vector vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5}; vector<double> vector_a1={1,5,2.4,3.3}; vector<float> vector_a3=vector_a2; // the vectors must be of the same type
Il existe également des méthodes statiques pour créer des matrices et des vecteurs de la taille spécifiée, et initialisés d'une certaine manière :
matrix matrix_a =matrix::Eye(4,5,1); matrix<double> matrix_a1=matrix::Full(3,4,M_PI); matrixf matrix_a2=matrixf::Identity(5,5); matrixf<float> matrix_a3=matrixf::Ones(5,5); matrix matrix_a4=matrix::Tri(4,5,-1); vector vector_a =vector::Ones(256); vectorf vector_a1=vector<float>::Zeros(16); vector<float> vector_a2=vectorf::Full(128,float_value);
Il existe aussi des méthodes non statiques pour initialiser une matrice ou un vecteur avec les valeurs données - Init et Fill :
matrix m(2, 2); m.Fill(10); Print("matrix m \n", m); /* matrix m [[10,10] [10,10]] */ m.Init(4, 6); Print("matrix m \n", m); /* matrix m [[10,10,10,10,0.0078125,32.00000762939453] [0,0,0,0,0,0] [0,0,0,0,0,0] [0,0,0,0,0,0]] */
Dans cet exemple, nous avons utilisé la méthode Init pour modifier la taille d'une matrice déjà initialisée. Du coup, tous les nouveaux éléments ont été remplis de valeurs aléatoires.
Un avantage important de la méthode Init est la possibilité de spécifier une fonction d'initialisation dans les paramètres pour remplir les éléments de la matrice ou du vecteur selon cette règle. Par exemple :
void OnStart() { //--- matrix init(3, 6, MatrixSetValues); Print("init = \n", init); /* Execution result init = [[1,2,4,8,16,32] [64,128,256,512,1024,2048] [4096,8192,16384,32768,65536,131072]] */ } //+------------------------------------------------------------------+ //| Fills the matrix with powers of a number | //+------------------------------------------------------------------+ void MatrixSetValues(matrix& m, double initial=1) { double value=initial; for(ulong r=0; r<m.Rows(); r++) { for(ulong c=0; c<m.Cols(); c++) { m[r][c]=value; value*=2; } } }
Copie de matrices et de tableaux
Les matrices et les vecteurs peuvent être copiés à l'aide de la méthode Copy. Mais une façon plus simple de copier ces types de données est d'utiliser l'opérateur d'affectation "=". Vous pouvez également utiliser la méthode Assign pour la copie.
//--- copying matrices matrix a= {{2, 2}, {3, 3}, {4, 4}}; matrix b=a+2; matrix c; Print("matrix a \n", a); Print("matrix b \n", b); c.Assign(b); Print("matrix c \n", c); /* matrix a [[2,2] [3,3] [4,4]] matrix b [[4,4] [5,5] [6,6]] matrix c [[4,4] [5,5] [6,6]] */
La différence entre Assign et Copy est qu'elle peut être utilisée à la fois pour les matrices et les tableaux. L'exemple ci-dessous montre la copie d’un tableau d'entiers int_arr dans une matrice de doubles. La matrice résultante s'ajuste automatiquement en fonction de la taille du tableau copié.
//--- copying an array to a matrix matrix double_matrix=matrix::Full(2,10,3.14); Print("double_matrix before Assign() \n", double_matrix); int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}}; Print("int_arr: "); ArrayPrint(int_arr); double_matrix.Assign(int_arr); Print("double_matrix after Assign(int_arr) \n", double_matrix); /* double_matrix before Assign() [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14] [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]] int_arr: [,0][,1][,2][,3][,4] [0,] 1 2 0 0 0 [1,] 3 4 0 0 0 [2,] 5 6 0 0 0 [3,] 0 0 0 0 0 [4,] 0 0 0 0 0 double_matrix after Assign(int_arr) [[1,2,0,0,0] [3,4,0,0,0] [5,6,0,0,0] [0,0,0,0,0] [0,0,0,0,0]] */ }
La méthode Assign permet une transition transparente des tableaux aux matrices, avec la définition automatique de la taille et du type.
Copie de séries temporelles (timeseries) vers des matrices ou des vecteurs
L'analyse des graphiques de prix implique des opérations avec les tableaux de la structure MqlRates. MQL5 fournit une nouvelle méthode pour travailler avec ce type de structures de données des prix.
La méthode CopyRates copie les séries historiques de la structure MqlRates directement dans une matrice ou dans un vecteur. Vous pouvez ainsi éviter d'avoir à placer les timeseries requises dans les tableaux correspondants via les fonctions de la section Accès aux séries temporelles et aux indicateurs. De même, il n'est pas nécessaire de les copier dans une matrice ou un vecteur. Avec la méthode CopyRates, vous pouvez récupérer les cotations dans une matrice ou un vecteur en un seul appel. Prenons l’exemple de calcul d'une matrice de corrélation pour une liste de symboles : calculons ces valeurs à l'aide de deux méthodes différentes et comparons les résultats.
input int InBars=100; input ENUM_TIMEFRAMES InTF=PERIOD_H1; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- list of symbols for calculation string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"}; int size=ArraySize(symbols); //--- matrix and vector to receive Close prices matrix rates(InBars, size); vector close; for(int i=0; i<size; i++) { //--- get Close prices to a vector if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars)) { //--- insert the vector to the timeseries matrix rates.Col(close, i); PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size()); //--- output the first 20 vector values for debugging int digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS); Print(VectorToString(close, 20, digits)); } else { Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError()); return; } } /* 1. EURUSD: 100 Close prices were added to the matrix 0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121 1.069 0.99936 1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111 1.079 1.030 ... 2. GBPUSD: 100 Close prices were added to the matrix 1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069 ... 3. USDJPY: 100 Close prices were added to the matrix 143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069 ... 4. USDCAD: 100 Close prices were added to the matrix 1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789 ... 5. USDCHF: 100 Close prices were added to the matrix 0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509 ... */ //--- prepare a matrix of correlations between symbols matrix corr_from_vector=matrix::Zeros(size, size); Print("Compute pairwise correlation coefficients"); for(int i=0; i<size; i++) { for(int k=i; k<size; k++) { vector v1=rates.Col(i); vector v2=rates.Col(k); double coeff = v1.CorrCoef(v2); PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff); corr_from_vector[i][k]=coeff; } } Print("Correlation matrix on vectors: \n", corr_from_vector); /* Calculate pairwise correlation coefficients corr(EURUSD,EURUSD) = 1.000 corr(EURUSD,GBPUSD) = 0.974 corr(EURUSD,USDJPY) = -0.713 corr(EURUSD,USDCAD) = -0.950 corr(EURUSD,USDCHF) = -0.397 corr(GBPUSD,GBPUSD) = 1.000 corr(GBPUSD,USDJPY) = -0.744 corr(GBPUSD,USDCAD) = -0.953 corr(GBPUSD,USDCHF) = -0.362 corr(USDJPY,USDJPY) = 1.000 corr(USDJPY,USDCAD) = 0.736 corr(USDJPY,USDCHF) = 0.083 corr(USDCAD,USDCAD) = 1.000 corr(USDCAD,USDCHF) = 0.425 corr(USDCHF,USDCHF) = 1.000 Correlation matrix on vectors: [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434] [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978] [0,0,1,0.7360546499847362,0.08314381248168941] [0,0,0,0.9999999999999999,0.4247042496841555] [0,0,0,0,1]] */ //--- now let's see how a correlation matrix can be calculated in one line matrix corr_from_matrix=rates.CorrCoef(false); // false means that the vectors are in the matrix columns Print("Correlation matrix rates.CorrCoef(false): \n", corr_from_matrix.TriU()); //--- compare the resulting matrices to find discrepancies Print("How many discrepancy errors between result matrices?"); ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12); Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors); /* Correlation matrix rates.CorrCoef(false): [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434] [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978] [0,0,1,0.7360546499847362,0.08314381248168941] [0,0,0,1,0.4247042496841555] [0,0,0,0,1]] How many discrepancy errors between result matrices? corr_from_vector.Compare(corr_from_matrix,1e-12)=0 */ //--- create a nice output of the correlation matrix Print("Output the correlation matrix with headers"); string header=" "; // header for(int i=0; i<size; i++) header+=" "+symbols[i]; Print(header); //--- now rows for(int i=0; i<size; i++) { string line=symbols[i]+" "; line+=VectorToString(corr_from_vector.Row(i), size, 3, 8); Print(line); } /* Output the correlation matrix with headers EURUSD GBPUSD USDJPY USDCAD USDCHF EURUSD 1.0 0.974 -0.713 -0.950 -0.397 GBPUSD 0.0 1.0 -0.744 -0.953 -0.362 USDJPY 0.0 0.0 1.0 0.736 0.083 USDCAD 0.0 0.0 0.0 1.0 0.425 USDCHF 0.0 0.0 0.0 0.0 1.0 */ } //+------------------------------------------------------------------+ //| Returns a string with vector values | //+------------------------------------------------------------------+ string VectorToString(const vector &v, int length=20, int digits=5, int width=8) { ulong size=(ulong)MathMin(20, v.Size()); //--- compose a string string line=""; for(ulong i=0; i<size; i++) { string value=DoubleToString(v[i], digits); StringReplace(value, ".000", ".0"); line+=Indent(width-StringLen(value))+value; } //--- add a tail if the vector length exceeds the specified size if(v.Size()>size) line+=" ..."; //--- return(line); } //+------------------------------------------------------------------+ //| Returns a string with the specified number of spaces | //+------------------------------------------------------------------+ string Indent(int number) { string indent=""; for(int i=0; i<number; i++) indent+=" "; return(indent); }
Voici comment faire :
- Récupération des prix de Clôture via CopyRates
- Insertion d’un vecteur dans une matrice en utilisant la méthode Col
- Calcul du coefficient de corrélation entre deux vecteurs en utilisant CorrCoef
- Calcul de la matrice de corrélation sur une matrice avec des vecteurs de valeur en utilisant CorrCoef
- Retour d’une matrice triangulaire supérieure en utilisant la méthode TriU
- Comparaison de deux matrices et recherche des divergences à l'aide de Compare
Opérations sur les matrices et les vecteurs
Les opérations mathématiques sur les éléments (addition, soustraction, multiplication et division) peuvent être effectuées sur les matrices et les vecteurs. Pour ces opérations, les deux objets doivent être du même type et avoir les mêmes tailles. Chaque élément de la matrice ou du vecteur opère sur l'élément correspondant de la seconde matrice, ou du second vecteur.
Vous pouvez également utiliser un scalaire du type approprié (double, float ou complex) comme second terme (multiplicateur, soustraction ou diviseur). Dans ce cas, chaque membre de la matrice ou du vecteur opérera sur le scalaire spécifié.
matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}}; matrix matrix_b={{1,2,3},{4,5,6}}; matrix matrix_c1=matrix_a+matrix_b; matrix matrix_c2=matrix_b-matrix_a; matrix matrix_c3=matrix_a*matrix_b; // Hadamard product matrix matrix_c4=matrix_b/matrix_a; matrix_c1=matrix_a+1; matrix_c2=matrix_b-double_value; matrix_c3=matrix_a*M_PI; matrix_c4=matrix_b/0.1; //--- operations in place are possible matrix_a+=matrix_b; matrix_a/=2;
Les matrices et les vecteurs peuvent également être passés comme deuxième paramètre pour la plupart des fonctions mathématiques, notamment MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh et MathTanh. Ces opérations impliquent une gestion par élément des matrices et des vecteurs. Exemple :
//--- matrix a= {{1, 4}, {9, 16}}; Print("matrix a=\n",a); a=MathSqrt(a); Print("MatrSqrt(a)=\n",a); /* matrix a= [[1,4] [9,16]] MatrSqrt(a)= [[1,2] [3,4]] */
Pour les fonctions MathMod et MathPow, le deuxième élément peut être soit un scalaire, soit une matrice/un vecteur de la taille correspondante.
matrix<T> mat1(128,128); matrix<T> mat3(mat1.Rows(),mat1.Cols()); ulong n,size=mat1.Rows()*mat1.Cols(); ... mat2=MathPow(mat1,(T)1.9); for(n=0; n<size; n++) { T res=MathPow(mat1.Flat(n),(T)1.9); if(res!=mat2.Flat(n)) errors++; } mat2=MathPow(mat1,mat3); for(n=0; n<size; n++) { T res=MathPow(mat1.Flat(n),mat3.Flat(n)); if(res!=mat2.Flat(n)) errors++; } ... vector<T> vec1(16384); vector<T> vec3(vec1.Size()); ulong n,size=vec1.Size(); ... vec2=MathPow(vec1,(T)1.9); for(n=0; n<size; n++) { T res=MathPow(vec1[n],(T)1.9); if(res!=vec2[n]) errors++; } vec2=MathPow(vec1,vec3); for(n=0; n<size; n++) { T res=MathPow(vec1[n],vec3[n]); if(res!=vec2[n]) errors++; }
Manipulations
MQL5 supporte les manipulations de base suivantes sur les matrices et les vecteurs, et elles ne nécessitent aucun calcul :
- Transposition
- Extraction de lignes, de colonnes et de diagonales
- Redimensionnement et remodelage des matrices
- Permutation de lignes et de colonnes
- Copie vers un nouvel objet
- Comparaison de deux objets
- Division d'une matrice en plusieurs sous-matrices
- Tri
matrix a= {{0, 1, 2}, {3, 4, 5}}; Print("matrix a \n", a); Print("a.Transpose() \n", a.Transpose()); /* matrix a [[0,1,2] [3,4,5]] a.Transpose() [[0,3] [1,4] [2,5]] */
Les exemples ci-dessous montrent comment définir et extraire une diagonale à l'aide de la méthode Diag :
vector v1={1,2,3}; matrix m1; m1.Diag(v1); Print("m1\n",m1); /* m1 [[1,0,0] [0,2,0] [0,0,3]] m2 */ matrix m2; m2.Diag(v1,-1); Print("m2\n",m2); /* m2 [[0,0,0] [1,0,0] [0,2,0] [0,0,3]] */ matrix m3; m3.Diag(v1,1); Print("m3\n",m3); /* m3 [[0,1,0,0] [0,0,2,0] [0,0,0,3]] */ matrix m4=matrix::Full(4,5,9); m4.Diag(v1,1); Print("m4\n",m4); Print("diag -1 - ",m4.Diag(-1)); Print("diag 0 - ",m4.Diag()); Print("diag 1 - ",m4.Diag(1)); /* m4 [[9,1,9,9,9] [9,9,2,9,9] [9,9,9,3,9] [9,9,9,9,9]] diag -1 - [9,9,9] diag 0 - [9,9,9,9] diag 1 - [1,2,3,9] */
Modification de la taille d'une matrice à l'aide de la méthode Reshape :
matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}}; Print("matrix_a\n",matrix_a); /* matrix_a [[1,2,3] [4,5,6] [7,8,9] [10,11,12]] */ matrix_a.Reshape(2,6); Print("Reshape(2,6)\n",matrix_a); /* Reshape(2,6) [[1,2,3,4,5,6] [7,8,9,10,11,12]] */ matrix_a.Reshape(3,5); Print("Reshape(3,5)\n",matrix_a); /* Reshape(3,5) [[1,2,3,4,5] [6,7,8,9,10] [11,12,0,3,0]] */ matrix_a.Reshape(2,4); Print("Reshape(2,4)\n",matrix_a); /* Reshape(2,4) [[1,2,3,4] [5,6,7,8]] */
Exemples de la division verticale d'une matrice à l'aide de la méthode Vsplit :
matrix matrix_a={{ 1, 2, 3, 4, 5, 6}, { 7, 8, 9,10,11,12}, {13,14,15,16,17,18}}; matrix splitted[]; ulong parts[]={2,3}; matrix_a.Vsplit(2,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2,3] [7,8,9] [13,14,15]] splitted 1 [[4,5,6] [10,11,12] [16,17,18]] */ matrix_a.Vsplit(3,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2] [7,8] [13,14]] splitted 1 [[3,4] [9,10] [15,16]] splitted 2 [[5,6] [11,12] [17,18]] */ matrix_a.Vsplit(parts,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2] [7,8] [13,14]] splitted 1 [[3,4,5] [9,10,11] [15,16,17]] splitted 2 [[6] [12] [18]] */
Les méthodes Col et Row permettent d'obtenir les éléments de la matrice ainsi que d'insérer des éléments dans des matrices non allouées, c'est-à-dire des matrices sans taille spécifiée. Voici un exemple :
vector v1={1,2,3}; matrix m1; m1.Col(v1,1); Print("m1\n",m1); /* m1 [[0,1] [0,2] [0,3]] */ matrix m2=matrix::Full(4,5,8); m2.Col(v1,2); Print("m2\n",m2); /* m2 [[8,8,1,8,8] [8,8,2,8,8] [8,8,3,8,8] [8,8,8,8,8]] */ Print("col 1 - ",m2.Col(1)); /* col 1 - [8,8,8,8] */ Print("col 2 - ",m2.Col(2)); /* col 1 - [8,8,8,8] col 2 - [1,2,3,8] */
Produits
La multiplication matricielle est l'un des algorithmes de base largement utilisé dans les méthodes numériques. De nombreuses implémentations des algorithmes de propagation avant et arrière dans les couches convolutives des réseaux de neurones basées sur cette opération. Souvent, 90 à 95 % du temps consacré au machine learning est consacré à cette opération. Toutes les méthodes de produit sont fournies dans la section Produits de matrices et de vecteurs de la documentation de référence du langage.
L’exemple suivant montre la multiplication de deux matrices à l'aide de la méthode MatMul :
matrix a={{1, 0, 0}, {0, 1, 0}}; matrix b={{4, 1}, {2, 2}, {1, 3}}; matrix c1=a.MatMul(b); matrix c2=b.MatMul(a); Print("c1 = \n", c1); Print("c2 = \n", c2); /* c1 = [[4,1] [2,2]] c2 = [[4,1,0] [2,2,0] [1,3,0]] */
Voici un exemple du produit de Kronecker de deux matrices ou d'une matrice et d'un vecteur, en utilisant la méthode de Kron.
matrix a={{1,2,3},{4,5,6}}; matrix b=matrix::Identity(2,2); vector v={1,2}; Print(a.Kron(b)); Print(a.Kron(v)); /* [[1,0,2,0,3,0] [0,1,0,2,0,3] [4,0,5,0,6,0] [0,4,0,5,0,6]] [[1,2,2,4,3,6] [4,8,5,10,6,12]] */
Vous trouverez plus d'exemples dans l'article Matrices et vecteurs en MQL5 :
//--- initialize matrices matrix m35, m52; m35.Init(3,5,Arange); m52.Init(5,2,Arange); //--- Print("1. Product of horizontal vector v[3] and matrix m[3,5]"); vector v3 = {1,2,3}; Print("On the left v3 = ",v3); Print("On the right m35 = \n",m35); Print("v3.MatMul(m35) = horizontal vector v[5] \n",v3.MatMul(m35)); /* 1. Product of horizontal vector v[3] and matrix m[3,5] On the left v3 = [1,2,3] On the right m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] v3.MatMul(m35) = horizontal vector v[5] [40,46,52,58,64] */ //--- show that this is really a horizontal vector Print("\n2. Product of matrix m[1,3] and matrix m[3,5]"); matrix m13; m13.Init(1,3,Arange,1); Print("On the left m13 = \n",m13); Print("On the right m35 = \n",m35); Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35)); /* 2. Product of matrix m[1,3] and matrix m[3,5] On the left m13 = [[1,2,3]] On the right m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] m13.MatMul(m35) = matrix m[1,5] [[40,46,52,58,64]] */ Print("\n3. Product of matrix m[3,5] and vertical vector v[5]"); vector v5 = {1,2,3,4,5}; Print("On the left m35 = \n",m35); Print("On the right v5 = ",v5); Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5)); /* 3. Product of matrix m[3,5] and vertical vector v[5] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right v5 = [1,2,3,4,5] m35.MatMul(v5) = vertical vector v[3] [40,115,190] */ //--- show that this is really a vertical vector Print("\n4. Product of matrix m[3,5] and matrix m[5,1]"); matrix m51; m51.Init(5,1,Arange,1); Print("On the left m35 = \n",m35); Print("On the right m51 = \n",m51); Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51)); /* 4. Product of matrix m[3,5] and matrix m[5,1] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right m51 = [[1] [2] [3] [4] [5]] m35.MatMul(m51) = matrix v[3] [[40] [115] [190]] */ Print("\n5. Product of matrix m[3,5] and matrix m[5,2]"); Print("On the left m35 = \n",m35); Print("On the right m52 = \n",m52); Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52)); /* 5. Product of matrix m[3,5] and matrix m[5,2] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right m52 = [[0,1] [2,3] [4,5] [6,7] [8,9]] m35.MatMul(m52) = matrix m[3,2] [[60,70] [160,195] [260,320]] */ Print("\n6. Product of horizontal vector v[5] and matrix m[5,2]"); Print("On the left v5 = \n",v5); Print("On the right m52 = \n",m52); Print("v5.MatMul(m52) = horizontal vector v[2] \n",v5.MatMul(m52)); /* 6. The product of horizontal vector v[5] and matrix m[5,2] On the left v5 = [1,2,3,4,5] On the right m52 = [[0,1] [2,3] [4,5] [6,7] [8,9]] v5.MatMul(m52) = horizontal vector v[2] [80,95] */ Print("\n7. Outer() product of horizontal vector v[5] and vertical vector v[3]"); Print("On the left v5 = \n",v5); Print("On the right v3 = \n",v3); Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3)); /* 7. Outer() product of horizontal vector v[5] and vertical vector v[3] On the left v5 = [1,2,3,4,5] On the right v3 = [1,2,3] v5.Outer(v3) = matrix m[5,3] [[1,2,3] [2,4,6] [3,6,9] [4,8,12] [5,10,15]] */
Transformations
Les transformations matricielles sont souvent utilisées dans les opérations sur les données. Cependant, de nombreuses opérations matricielles complexes ne peuvent être résolues de manière efficace ou stable en raison de la précision limitée des ordinateurs.
Les transformations matricielles (ou décompositions) sont des méthodes permettant de réduire une matrice en ses éléments constitutifs, ce qui facilite le calcul d'opérations matricielles plus complexes. Les méthodes de décomposition matricielle, également appelées méthodes de factorisation matricielle, constituent l'épine dorsale de l'algèbre linéaire sur ordinateur, même pour les opérations de base telles que la résolution de systèmes d'équations linéaires, le calcul de l'inverse et le calcul du déterminant d'une matrice.
L'apprentissage automatique (ou machine learning) utilise largement la décomposition en valeurs singulières (SVD - Singular Value Decomposition), qui permet de représenter la matrice d'origine comme le produit de trois autres matrices. La SVD est utilisé pour résoudre une variété de problèmes, de l'approximation des moindres carrés à la compression et à la reconnaissance d'images.
Exemple de décomposition en valeurs singulières par la méthode SVD :
matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}}; a=a-4; Print("matrix a \n", a); a.Reshape(3, 3); matrix b=a; Print("matrix b \n", b); //--- execute SVD decomposition matrix U, V; vector singular_values; b.SVD(U, V, singular_values); Print("U \n", U); Print("V \n", V); Print("singular_values = ", singular_values); // check block //--- U * singular diagonal * V = A matrix matrix_s; matrix_s.Diag(singular_values); Print("matrix_s \n", matrix_s); matrix matrix_vt=V.Transpose(); Print("matrix_vt \n", matrix_vt); matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt); Print("matrix_usvt \n", matrix_usvt); ulong errors=(int)b.Compare(matrix_usvt, 1e-9); double res=(errors==0); Print("errors=", errors); //---- another check matrix U_Ut=U.MatMul(U.Transpose()); Print("U_Ut \n", U_Ut); Print("Ut_U \n", (U.Transpose()).MatMul(U)); matrix vt_V=matrix_vt.MatMul(V); Print("vt_V \n", vt_V); Print("V_vt \n", V.MatMul(matrix_vt)); /* matrix a [[-4,-3,-2,-1,0,1,2,3,4]] matrix b [[-4,-3,-2] [-1,0,1] [2,3,4]] U [[-0.7071067811865474,0.5773502691896254,0.408248290463863] [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256] [0.7071067811865472,0.5773502691896255,0.4082482904638627]] V [[0.5773502691896258,-0.7071067811865474,-0.408248290463863] [0.5773502691896258,1.779939029415334e-16,0.8164965809277258] [0.5773502691896256,0.7071067811865474,-0.408248290463863]] singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17] matrix_s [[7.348469228349533,0,0] [0,2.449489742783175,0] [0,0,3.277709923350408e-17]] matrix_vt [[0.5773502691896258,0.5773502691896258,0.5773502691896256] [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474] [-0.408248290463863,0.8164965809277258,-0.408248290463863]] matrix_usvt [[-3.999999999999997,-2.999999999999999,-2] [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974] [2,2.999999999999999,3.999999999999996]] errors=0 U_Ut [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16] [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17] [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]] Ut_U [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16] [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16] [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]] vt_V [[1,-5.551115123125783e-17,0] [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16] [0,1.110223024625157e-16,0.9999999999999996]] V_vt [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16] [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16] [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996] */ }
Une autre transformation couramment utilisée est la décomposition de Cholesky. Elle peut être utilisée pour résoudre un système d'équations linéaires Ax=b si la matrice A est symétrique et définie positive.
En MQL5, la décomposition de Cholesky est exécutée par la méthode Cholesky :
matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}}; matrix matrix_l; Print("matrix_a\n", matrix_a); matrix_a.Cholesky(matrix_l); Print("matrix_l\n", matrix_l); Print("check\n", matrix_l.MatMul(matrix_l.Transpose())); /* matrix_a [[5.7998084,-2.1825367] [-2.1825367,9.85910595]] matrix_l [[2.408279136645086,0] [-0.9062640068544704,3.006291985133859]] check [[5.7998084,-2.1825367] [-2.1825367,9.85910595]] */
Voici la liste des méthodes disponibles :
| Fonction | Action |
|---|---|
| Calcule la décomposition de Cholesky | |
| Calcule les valeurs propres et les vecteurs propres droits d'une matrice carrée. | |
| Calcule les valeurs propres d'une matrice générale | |
| Factorisation LU d'une matrice comme étant le produit d'une matrice triangulaire inférieure et d'une matrice triangulaire supérieure | |
| Factorisation LUP avec pivotement partiel, qui se réfère à la décomposition LU avec permutations des lignes uniquement : PA = LU | |
| Calculer la factorisation qr d'une matrice | |
| Décomposition en Valeur Singulière (SVD) |
Obtenir des statistiques
- Les valeurs maximales et minimales, ainsi que leurs indices dans une matrice/un vecteur
- La somme et le produit d'éléments, ainsi que la somme et le produit cumulés.
- La médiane, la moyenne, la moyenne arithmétique et la moyenne arithmétique pondérée des valeurs de la matrice/du vecteur
- L’écart-type et la variance de l'élément
- Les percentiles et quantiles
- La métrique de régression comme l'erreur de déviation de la ligne de régression construite sur le tableau de données spécifié.
Exemple de calcul de l'écart-type par la méthode Std :
matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
Print("matrix_a\n",matrix_a);
vectorf cols_std=matrix_a.Std(0);
vectorf rows_std=matrix_a.Std(1);
float matrix_std=matrix_a.Std();
Print("cols_std ",cols_std);
Print("rows_std ",rows_std);
Print("std value ",matrix_std);
/*
matrix_a
[[10,3,2]
[1,8,12]
[6,5,4]
[7,11,9]]
cols_std [3.2403703,3.0310888,3.9607449]
rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
std value 3.452052593231201
*/
Calcul des quantiles par la méthode Quantile :
matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
Print("matrix_a\n",matrix_a);
vectorf cols_percentile=matrix_a.Percentile(50,0);
vectorf rows_percentile=matrix_a.Percentile(50,1);
float matrix_percentile=matrix_a.Percentile(50);
Print("cols_percentile ",cols_percentile);
Print("rows_percentile ",rows_percentile);
Print("percentile value ",matrix_percentile);
/*
matrix_a
[[1,2,3]
[4,5,6]
[7,8,9]
[10,11,12]]
cols_percentile [5.5,6.5,7.5]
rows_percentile [2,5,8,11]
percentile value 6.5
*/
Caractéristiques de la matrice
Utilisez les méthodes de la section Caractéristiques pour obtenir les valeurs suivantes :
- Le nombre de lignes et de colonnes dans une matrice
- Le numéro de norme et de condition
- Le déterminant, le rang, la trace et le spectre d'une matrice
Calcul du rang d'une matrice à l'aide de la méthode Rank :
matrix a=matrix::Eye(4, 4);; Print("matrix a \n", a); Print("a.Rank()=", a.Rank()); matrix I=matrix::Eye(4, 4); I[3, 3] = 0.; // matrix deficit Print("I \n", I); Print("I.Rank()=", I.Rank()); matrix b=matrix::Ones(1, 4); Print("b \n", b); Print("b.Rank()=", b.Rank());;// 1 size - rank 1, unless all 0 matrix zeros=matrix::Zeros(4, 1); Print("zeros \n", zeros); Print("zeros.Rank()=", zeros.Rank()); /* matrix a [[1,0,0,0] [0,1,0,0] [0,0,1,0] [0,0,0,1]] a.Rank()=4 I [[1,0,0,0] [0,1,0,0] [0,0,1,0] [0,0,0,0]] I.Rank()=3 b [[1,1,1,1]] b.Rank()=1 zeros [[0] [0] [0] [0]] zeros.Rank()=0 */
Calcul d'une norme à l'aide de la méthode Norm :
matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}}; a=a-4; Print("matrix a \n", a); a.Reshape(3, 3); matrix b=a; Print("matrix b \n", b); Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS)); Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS)); Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF)); Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF)); Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1)); Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1)); Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2)); Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); /* matrix a [[-4,-3,-2,-1,0,1,2,3,4]] matrix b [[-4,-3,-2] [-1,0,1] [2,3,4]] b.Norm(MATRIX_NORM_P2)=7.745966692414834 b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834 b.Norm(MATRIX_NORM_INF)9.0 b.Norm(MATRIX_NORM_MINUS_INF)2.0 b.Norm(MATRIX_NORM_P1)=)7.0 b.Norm(MATRIX_NORM_MINUS_P1)=6.0 b.Norm(MATRIX_NORM_P2)=7.348469228349533 b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16 */
Résolution d’équations
Les méthodes de machine learning et les problèmes d'optimisation nécessitent souvent de trouver les solutions d'un système d'équations linéaires. La section Solutions contient quatre méthodes permettant de résoudre de telles équations en fonction du type de matrice.
| Fonction | Action |
|---|---|
| Résout une équation matricielle linéaire ou un système d'équations algébriques linéaires. | |
| Renvoie la solution des moindres carrés des équations algébriques linéaires (pour les matrices non carrées ou dégénérées). | |
| Calcule l'inverse multiplicatif d'une matrice carrée inversible par la méthode de Jordan-Gauss | |
| Calcule le pseudo-inverse d'une matrice par la méthode de Moore-Penrose |
Nous devons trouver le vecteur solution x. La matrice A n'est pas carrée et la méthode Solve ne peut donc pas être utilisée ici.
Nous utiliserons la méthode LstSq qui permet de résoudre de manière approximative des matrices non carrées ou dégénérées.matrix a={{3, 2}, {4,-5}, {3, 3}}; vector b={7,40,3}; //--- solve the system A*x = b vector x=a.LstSq(b); //--- check the solution, x must be equal to [5, -4] Print("x=", x); /* x=[5.00000000,-4] */ //--- check A*x = b1, the resulting vector must be [7, 40, 3] vector b1=a.MatMul(x); Print("b11=",b1); /* b1=[7.0000000,40.0000000,3.00000000] */
La vérification a montré que le vecteur trouvé x est la solution à ce système d'équations.
Méthodes de Machine Learning (Apprentissage Automatique)
Il existe trois méthodes matricielles et vectorielles pouvant être utilisées dans l'apprentissage automatique.
| Fonction | Action |
|---|---|
| Calcule les valeurs de la fonction d'activation et les écris dans le vecteur ou la matrice transmise. | |
| Calcule les valeurs dérivées de la fonction d'activation et les écrit dans le vecteur/matrice passé(e). | |
| Calcule les valeurs de la fonction de perte et les écrit dans le vecteur/matrice passé(e) |
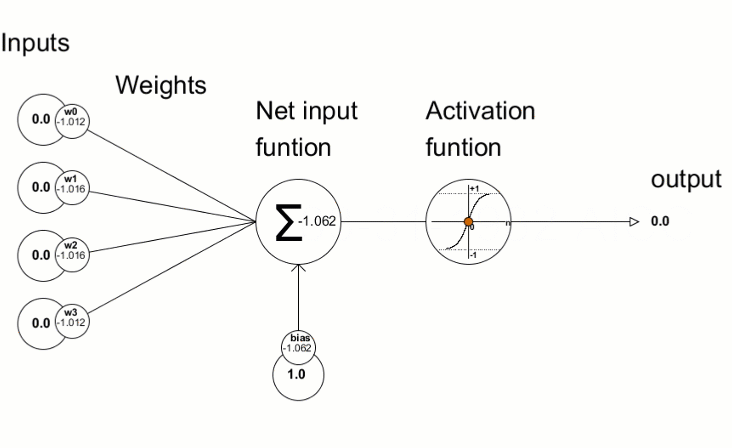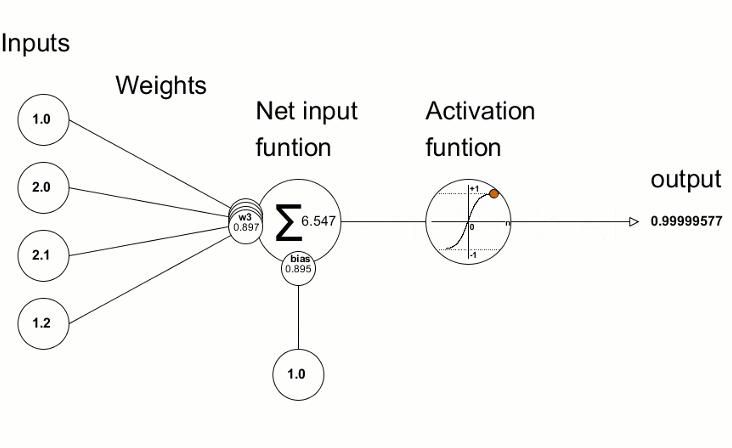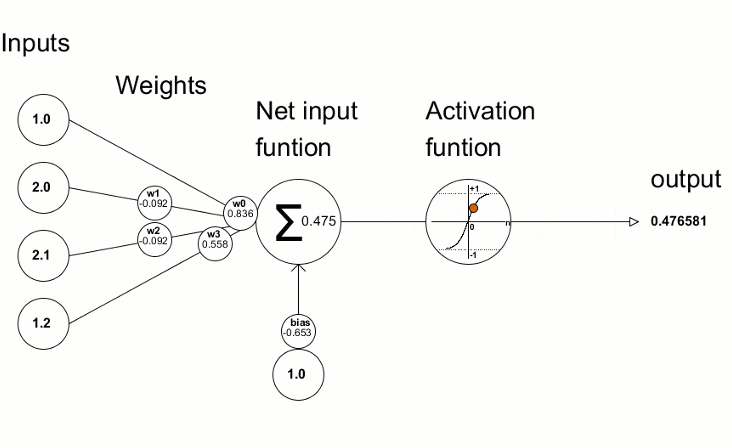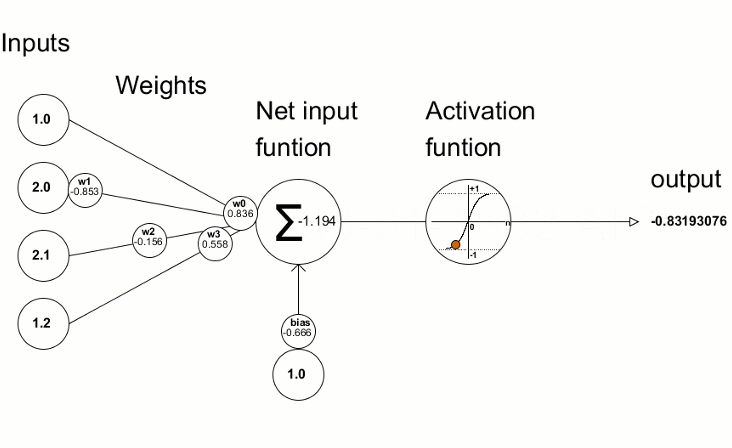
Les fonctions d'activation sont utilisées dans les réseaux de neurones pour trouver une sortie en fonction de la somme pondérée des entrées. La sélection de la fonction d’activation a un grand impact sur la performance du réseau de neurones.
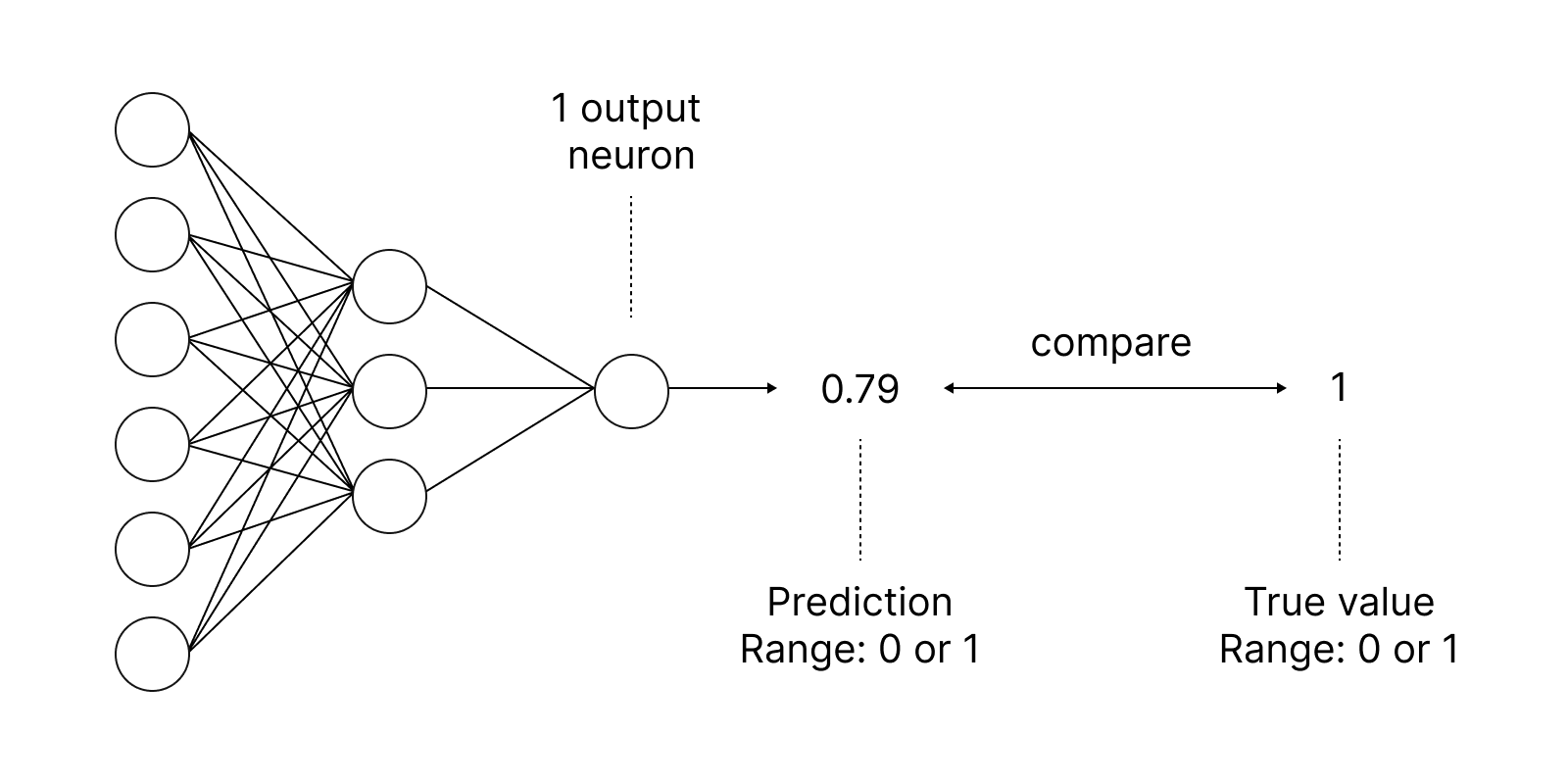
L'une des fonctions d'activation les plus populaires est la sigmoïde.
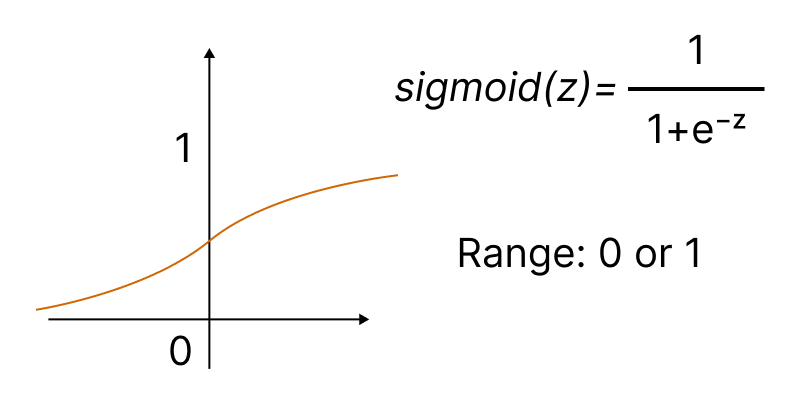
La méthode intégrée Activation permet de définir l'un des quinze types de fonction d'activation. Toutes ces fonctions sont disponibles dans l'énumération ENUM_ACTIVATION_FUNCTION.
| ID | Description |
|---|---|
| AF_ELU | Unité Linéaire Exponentielle |
| AF_EXP | Exponentiel |
| AF_GELU | Unité Linéaire d'Erreur Gaussienne |
| AF_HARD_SIGMOID | Sigmoïde Dure |
| AF_LINEAR | Linéaire |
| AF_LRELU | Unité Linéaire Rectifiée Fuyante (Leaky ReLU) |
| AF_RELU | Unité Linéaire Rectifiée |
| AF_SELU | Unité Linéaire Exponentielle Mise à l'Echelle (SeLU) |
| AF_SIGMOID | Sigmoïde |
| AF_SOFTMAX | Softmax |
| AF_SOFTPLUS | Softplus |
| AF_SOFTSIGN | Softsign |
| AF_SWISH | Bruissement (Swish) |
| AF_TANH | Fonction tangente hyperbolique |
| AF_TRELU | Unité Linéaire Rectifiée à Seuil |
Un réseau de neurones vise à trouver un algorithme minimisant l'erreur d'apprentissage, pour lequel on utilise la fonction de perte. L'écart est calculé à l'aide de la méthode Loss pour laquelle vous pouvez spécifier l'un des quatorze types de l'énumération ENUM_LOSS_FUNCTION.
Les valeurs d'écart résultantes sont ensuite utilisées pour affiner les paramètres du réseau de neurones. Pour ce faire, on utilise la méthode Derivative, qui calcule les valeurs de la dérivée de la fonction d'activation et écrit le résultat dans le vecteur/matrice transmis. Le processus de formation du réseau neuronal peut être représenté visuellement à l'aide de l'animation issue de l'article "Programmer un Réseau de Neurones Profond Depuis Zéro en MQL".
Améliorations en OpenCL
Nous avons également implémenté la prise en charge des matrices et des vecteurs dans les fonctions CLBufferWrite et CLBufferRead. Des surcharges sont disponibles pour ces fonctions. Voici un exemple de matrice ci-dessous.
Écrit les valeurs de la matrice dans le buffer et renvoie true en cas de succès.
uint CLBufferWrite( int buffer, // OpenCL buffer handle uint buffer_offset, // offset in the OpenCL buffer in bytes matrix<T> &mat // matrix of values to write to buffer );
Lit un buffer OpenCL dans une matrice et renvoie true en cas de succès.
uint CLBufferRead( int buffer, // OpenCL buffer handle uint buffer_offset, // offset in the OpenCL buffer in bytes const matrix& mat, // matrix to get values from the buffer ulong rows=-1, // number of rows in the matrix ulong cols=-1 // number of columns in the matrix );
Considérons l'utilisation des nouvelles surcharges à l'aide d'un exemple de produit matriciel de 2 matrices. Faisons les calculs en utilisant 3 méthodes :
- Une manière naïve d'illustrer l'algorithme de multiplication de matrice
- La méthode MatMul intégrée
- Un calcul parallèle en OpenCL
Les matrices obtenues seront vérifiées à l'aide de la méthode Compare, qui compare les éléments de deux matrices avec la précision donnée.
#define M 3000 // number of rows in the first matrix #define K 2000 // number of columns in the first matrix equal to the number of rows in the second one #define N 3000 // number of columns in the second matrix //+------------------------------------------------------------------+ const string clSrc= "#define N "+IntegerToString(N)+" \r\n" "#define K "+IntegerToString(K)+" \r\n" " \r\n" "__kernel void matricesMul( __global float *in1, \r\n" " __global float *in2, \r\n" " __global float *out ) \r\n" "{ \r\n" " int m = get_global_id( 0 ); \r\n" " int n = get_global_id( 1 ); \r\n" " float sum = 0.0; \r\n" " for( int k = 0; k < K; k ++ ) \r\n" " sum += in1[ m * K + k ] * in2[ k * N + n ]; \r\n" " out[ m * N + n ] = sum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- initialize the random number generator MathSrand((int)TimeCurrent()); //--- fill matrices of the given size with random values matrixf mat1(M, K, MatrixRandom) ; // first matrix matrixf mat2(K, N, MatrixRandom); // second matrix //--- calculate the product of matrices using the naive way uint start=GetTickCount(); matrixf matrix_naive=matrixf::Zeros(M, N);// here we rite the result of multiplying two matrices for(int m=0; m<M; m++) for(int k=0; k<K; k++) for(int n=0; n<N; n++) matrix_naive[m][n]+=mat1[m][k]*mat2[k][n]; uint time_naive=GetTickCount()-start; //--- calculate the product of matrices using MatMull start=GetTickCount(); matrixf matrix_matmul=mat1.MatMul(mat2); uint time_matmul=GetTickCount()-start; //--- calculate the product of matrices in OpenCL matrixf matrix_opencl=matrixf::Zeros(M, N); int cl_ctx; // context handle if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE) { Print("OpenCL not found, exit"); return; } int cl_prg; // program handle int cl_krn; // kernel handle int cl_mem_in1; // handle of the first buffer (input) int cl_mem_in2; // handle of the second buffer (input) int cl_mem_out; // handle of the third buffer (output) //--- create the program and the kernel cl_prg = CLProgramCreate(cl_ctx, clSrc); cl_krn = CLKernelCreate(cl_prg, "matricesMul"); //--- create all three buffers for the three matrices cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE); cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE); //--- third matrix - output cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE); //--- set kernel arguments CLSetKernelArgMem(cl_krn, 0, cl_mem_in1); CLSetKernelArgMem(cl_krn, 1, cl_mem_in2); CLSetKernelArgMem(cl_krn, 2, cl_mem_out); //--- write matrices to device buffers CLBufferWrite(cl_mem_in1, 0, mat1); CLBufferWrite(cl_mem_in2, 0, mat2); CLBufferWrite(cl_mem_out, 0, matrix_opencl); //--- start the OpenCL code execution time start=GetTickCount(); //--- set the task workspace parameters and execute the OpenCL program uint offs[2] = {0, 0}; uint works[2] = {M, N}; start=GetTickCount(); bool ex=CLExecute(cl_krn, 2, offs, works); //--- read the result into the matrix if(CLBufferRead(cl_mem_out, 0, matrix_opencl)) PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols()); else Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); uint time_opencl=GetTickCount()-start; Print("Compare computation times of the methods"); PrintFormat("Naive product time = %d ms",time_naive); PrintFormat("MatMul product time = %d ms",time_matmul); PrintFormat("OpenCl product time = %d ms",time_opencl); //--- release all OpenCL contexts CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out); //--- compare all obtained result matrices with each other Print("How many discrepancy errors between result matrices?"); ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12); Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors); errors=matrix_matmul.Compare(matrix_opencl,float(1e-12)); Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors); /* Result: Matrix [3000 x 3000] read Compare computation times of the methods Naive product time = 54750 ms MatMul product time = 4578 ms OpenCl product time = 922 ms How many discrepancy errors between result matrices? matrix_direct.Compare(matrix_matmul,1e-12)=0 matrix_matmul.Compare(matrix_opencl,1e-12)=0 */ } //+------------------------------------------------------------------+ //| Fills the matrix with random values | //+------------------------------------------------------------------+ void MatrixRandom(matrixf& m) { for(ulong r=0; r<m.Rows(); r++) { for(ulong c=0; c<m.Cols(); c++) { m[r][c]=(float)((MathRand()-16383.5)/32767.); } } } //+------------------------------------------------------------------+ //| Release all OpenCL contexts | //+------------------------------------------------------------------+ void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn, int cl_mem_in1, int cl_mem_in2, int cl_mem_out) { //--- release all created OpenCL contexts in reverse order CLBufferFree(cl_mem_in1); CLBufferFree(cl_mem_in2); CLBufferFree(cl_mem_out); CLKernelFree(cl_krn); CLProgramFree(cl_prg); CLContextFree(cl_ctx); }
Une explication détaillée du code OpenCL de cet exemple est fournie dans l'article "OpenCL : Du codage naïf vers un codage plus perspicace".
Nouvelles améliorations
La version 3390 a levé deux restrictions dans le fonctionnement d'OpenCL qui affectaient l'utilisation de la GPU.
Pour forcer l’utilisation des GPU avec le support du type ’double’ pour certaines tâches, utilisez CL_USE_GPU_DOUBLE_ONLY dans l’appel à la fonction CLContextCreate.
int cl_ctx; //--- initialization of OpenCL context if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE) { Print("OpenCL not found"); return; }
Bien que les modifications apportées aux opérations OpenCL ne soient pas directement liées aux matrices et aux vecteurs, elles s'inscrivent dans le cadre de nos efforts pour développer les capacités de machine learning (apprentissage automatique) du langage MQL5.
L'avenir de MQL5 dans le Machine Learning
Au cours des dernières années, nous avons développé de nouvelles fonctionnalités pour introduire des technologies avancées dans le langage MQL5 :
- Portage de la bibliothèque ALGLIB de méthodes numériques vers MQL5
- Mise en œuvre d'une bibliothèque mathématique avec des méthodes de logique floue et de statistiques
- Introduction d’une bibliothèque graphique, analogue à la fonction plot
- Intégration avec le langage Python pour exécuter des scripts Python directement dans le terminal
- Ajout de fonctions DirectX pour créer des graphiques 3D
- Mise en œuvre du support de SQLite de façon native pour les opérations avec les bases de données
- Ajout des nouveaux types de données matrices et vecteurs, ainsi que toutes les méthodes nécessaires.
Le langage MQL5 va continuer à se développer. L’une des orientations prioritaires est l'apprentissage automatique. Nous avons de grands projets pour des développements futurs. Restez donc avec nous, soutenez-nous et continuez à apprendre avec nous.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/10922
Développer un Expert Advisor à partir de zéro (partie 12) : Times et Trade (I)
Apprenez à concevoir un système de trading utilisant l’Accumulation/Distribution (AD)
Développer un Expert Advisor à partir de zéro (partie 13) : Times & Trade (II)
Apprenez à concevoir un système de trading basé sur l’OBV
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation