MetaTrader 5 / Esempi
English Русский 中文 Español Deutsch 日本語 Português 한국어 Français Türkçe
preview
Operazioni con matrici e vettori in MQL5

Operazioni con matrici e vettori in MQL5

MetaTrader 5 — Esempi | 28 novembre 2022, 11:27
799 0
MetaQuotes
MetaQuotes

Al linguaggio MQL5 sono stati aggiunti tipi di dati speciali - matrici e vettori - per risolvere un'ampia classe di problemi matematici. I nuovi tipi offrono metodi integrati per creare codice conciso e comprensibile, vicino alla notazione matematica. In questo articolo viene fornita una breve descrizione dei metodi integrati dalla sezione guida Metodi matriciali e vettoriali.


Contenuto


Ogni linguaggio di programmazione offre tipi di dati array che memorizzano insiemi di variabili numeriche, tra cui int, double e altri. L'accesso agli elementi dell’array avviene per indice, il che consente di eseguire operazioni utilizzando i cicli. I più utilizzati sono gli array monodimensionali e bidimensionali:

int    a[50];       // One-dimensional array of 50 integers
double m[7][50];    // Two-dimensional array of 7 subarrays, each consisting of 50 integers
MyTime t[100];      // Array containing elements of MyTime type

Le capacità degli array sono di solito sufficienti per compiti relativamente semplici legati alla memorizzazione e all'elaborazione dei dati. Ma quando si tratta di problemi matematici complessi, lavorare con gli array diventa difficile sia in termini di programmazione che di lettura del codice, a causa del gran numero di cicli annidati. Anche le operazioni più semplici di algebra lineare richiedono una codifica eccessiva e una buona conoscenza della matematica.

Le moderne tecnologie dei dati, come l'apprendimento automatico, le reti neurali e la grafica 3D, utilizzano ampiamente soluzioni di algebra lineare associate ai concetti di vettori e matrici. Per facilitare le operazioni con tali oggetti, MQL5 fornisce tipi di dati speciali: matrici e vettori. I nuovi tipi eliminano molte routine nelle operazioni di programmazione e migliorano la qualità del codice.


Tipi di matrici e vettori

In breve, un vettore è un array monodimensionale di tipo double e una matrice è un array bidimensionale di tipo double. I vettori possono essere verticali e orizzontali; tuttavia, in MQL5 non sono separati.

Una matrice può essere rappresentata come un array di vettori orizzontali, in cui il primo indice è il numero di riga e il secondo indice è il numero di colonna.


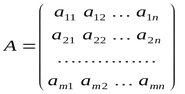
La numerazione delle righe e delle colonne inizia da 0, come per gli array.

Oltre ai tipi "matrice" e "vettore", che contengono dati di tipo double, ne esistono altri quattro tipi per le operazioni con i relativi tipi di dati:

  • matrixf — una matrice contenente elementi float
  • matrixc — una matrice contenente elementi complessi
  • vectorf — un vettore contenente elementi di tipo float
  • vectorc — un vettore contenente elementi complessi

Al momento in cui scriviamo, il lavoro sui tipi matrixc e vectorc non è ancora stato completato e quindi non è ancora possibile utilizzare questi tipi nei metodi integrati.

Le funzioni template supportano notazioni come matrice<double>, matrice<float>, vettore<double>, vettore<float> invece dei tipi corrispondenti.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */


Creazione e inizializzazione

I metodi matriciali e vettoriali sono suddivisi in nove categorie in base al loro scopo. Esistono diversi modi per dichiarare e inizializzare matrici e vettori.

Il metodo di creazione più semplice è la dichiarazione senza specificazione della dimensione, cioè senza allocazione di memoria per i dati. Qui scriviamo solo il tipo di dati e il nome della variabile:

  matrix         matrix_a;   // double type matrix
  matrix<double> matrix_a1;  // another way to declare a double matrix, suitable for use in templates
  matrix<float>  matrix_a3;  // float type matrix
  vector         vector_a;   // double type vector
  vector<double> vector_a1;  // another notation to create a double vector
  vector<float>  vector_a3;  // float type vector

In seguito è possibile modificare le dimensioni degli oggetti creati e riempirli con i valori desiderati. Possono anche essere utilizzati nei metodi matriciali integrati per ottenere risultati di calcolo.

Una matrice o un vettore possono essere dichiarati con la dimensione specificata, allocando la memoria per i dati ma senza inizializzare nulla. Qui, dopo il nome della variabile, specificare le dimensioni tra parentesi:

  matrix         matrix_a(128,128);           // the parameters can be either constants
  matrix<double> matrix_a1(InpRows,InpCols);  // or variables
  matrix<float>  matrix_a3(InpRows,1);        // analogue of a vertical vector
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float>  vector_a3(InpSize+16);       // expression can be used as a parameter

Il terzo modo per creare oggetti è dichiarare con inizializzazione. In questo caso, le dimensioni della matrice e del vettore sono determinate dalla sequenza di inizializzazione indicata tra parentesi graffe:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // the matrices must be of the same type
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                     // the vectors must be of the same type


Esistono anche metodi statici per creare matrici e vettori della dimensione specificata, inizializzati in un certo modo:  

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Inoltre, esistono metodi non statici per inizializzare una matrice o un vettore con i valori dati — Init e Fill:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

In questo esempio, abbiamo usato il metodo Init per modificare le dimensioni di una matrice già inizializzata, per cui tutti i nuovi elementi sono stati riempiti con valori casuali.

Un importante vantaggio del metodo Init è la possibilità di specificare una funzione di inizializzazione nei parametri per riempire gli elementi della matrice/vettore secondo questa regola. Per esempio:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Execution result
  init = 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Fills the matrix with powers of a number                         |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 }


Copiare matrici e array

Le matrici e i vettori possono essere copiati utilizzando il metodo Copy. Ma un modo più semplice e familiare per copiare questi tipi di dati è quello di utilizzare l'operatore di assegnazione "=". Inoltre, è possibile utilizzare il metodo Assign per la copia.

//--- copying matrices
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

La differenza tra Assign e Copy è che può essere utilizzato sia per le matrici che per gli array. L'esempio seguente mostra la copia di un array di interi int_arr in una matrice double. La matrice risultante si adatta automaticamente alle dimensioni della matrice copiata. 

//--- copying an array to a matrix
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

Il metodo Assign consente di passare senza problemi da array a matrici, con la conversione automatica delle dimensioni e del tipo.


Copiare le serie temporali in matrici o vettori

L'analisi dei grafici dei prezzi implica operazioni con gli array della struttura MqlRates. MQL5 fornisce un nuovo metodo per lavorare con queste strutture di dati del prezzo.

Il metodo CopyRates copia le serie storiche della struttura MqlRates direttamente in una matrice o in un vettore. In questo modo, si può evitare di ottenere le serie temporali richieste nei relativi array utilizzando le funzioni della sezione Accesso alle serie temporali e agli indicatori. Inoltre, non è necessario trasferirli in una matrice o in un vettore. Con il metodo CopyRates è possibile ricevere le quotazioni in una matrice o in un vettore con una sola chiamata. Consideriamo un esempio di come calcolare una matrice di correlazione per un elenco di simboli: calcoliamo questi valori utilizzando due metodi differenti e confrontiamo i risultati.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- list of symbols for calculation
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- matrix and vector to receive Close prices
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- get Close prices to a vector
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- insert the vector to the timeseries matrix
      rates.Col(close, i);
      PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size());
      //--- output the first 20 vector values for debugging
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 Close prices were added to the matrix
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 Close prices were added to the matrix
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 Close prices were added to the matrix
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 Close prices were added to the matrix
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 Close prices were added to the matrix
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- prepare a matrix of correlations between symbols
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Compute pairwise correlation coefficients");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Correlation matrix on vectors: \n", corr_from_vector);
  /*
  Calculate pairwise correlation coefficients
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0.397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0.744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Correlation matrix on vectors:
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- now let's see how a correlation matrix can be calculated in one line
  matrix corr_from_matrix=rates.CorrCoef(false);   // false means that the vectors are in the matrix columns
  Print("Correlation matrix rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- compare the resulting matrices to find discrepancies
  Print("How many discrepancy errors between result matrices?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Correlation matrix rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  How many discrepancy errors between result matrices?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- create a nice output of the correlation matrix
  Print("Output the correlation matrix with headers");
  string header="        ";  // header
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- now rows
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Output the correlation matrix with headers
            EURUSD  GBPUSD  USDJPY  USDCAD  USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Returns a string with vector values                              |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- compose a string
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- add a tail if the vector length exceeds the specified size
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//|  Returns a string with the specified number of spaces            |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

L'esempio mostra come:

    • Ottenere i prezzi delle Chiusure utilizzando CopyRates
    • Inserire un vettore in una matrice utilizzando il metodo Col
    • Calcolare il coefficiente di correlazione tra due vettori utilizzando CorrCoef
    • Calcolare la matrice di correlazione su una matrice con valori di vettori usando CorrCoef
    • Restituire una matrice triangolare superiore usando il metodo TriU
    • Confrontare due matrici e trovare le discrepanze usando Compare


      Operazioni con matrici e vettori

      Le operazioni matematiche elementari di addizione, sottrazione, moltiplicazione e divisione possono essere eseguite su matrici e vettori. Entrambi gli oggetti in queste operazioni devono essere dello stesso tipo e avere le stesse dimensioni. Ogni elemento della matrice o del vettore opera sul corrispondente elemento della seconda matrice o del vettore.

      È inoltre possibile utilizzare uno scalare del tipo appropriato (double, float o complex) come secondo termine (moltiplicatore, sottraendo o divisore). In questo caso, ogni membro della matrice o del vettore opererà sullo scalare specificato.

        matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // Hadamard product
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- operations in place are possible
  matrix_a+=matrix_b;
  matrix_a/=2;

      Inoltre, matrici e vettori possono essere passati come secondo parametro alla maggior parte delle funzioni matematiche, tra cui MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. Queste operazioni permettono la gestione di matrici o vettori in base agli elementi. Esempio:

      //---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

      Per MathMod e MathPow, il secondo elemento può essere sia uno scalare o una matrice/vettore di dimensioni appropriate. 

         matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }


      Manipolazioni

      MQL5 supporta le seguenti manipolazioni di base su matrici e vettori, che non richiedono alcun calcolo:

      • Trasposizione
      • Estrazione di righe, colonne e diagonali
      • Ridimensionamento e rimodellamento delle matrici
      • Scambiare le righe e le colonne specificate
      • Copia in un nuovo oggetto
      • Confronto tra due oggetti
      • Suddivisione di una matrice in più sottomatrici
      • Ordinamento
      L'esempio seguente mostra la trasposizione della matrice utilizzando il metodo Transpose:
        matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

      Di seguito sono riportati alcuni esempi che mostrano come impostare ed estrarre una diagonale utilizzando il metodo Diag:

         vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

      Modifica delle dimensioni di una matrice usando il metodo Reshape:

         matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

      Esempi di divisione verticale di una matrice con il metodo Vsplit:

         matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

      I metodi Col e Row consentono di ottenere gli elementi della matrice in questione e di inserire elementi in matrici non allocate, ossia matrici senza la dimensione specificata. Ecco un esempio:

         vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("col 1 - ",m2.Col(1));
  /*
   col 1 - [8,8,8,8]
  */

   Print("col 2 - ",m2.Col(2));
  /*
   col 1 - [8,8,8,8]  col 2 - [1,2,3,8]
  */


      Prodotti

      La moltiplicazione delle matrici è uno degli algoritmi di base ampiamente utilizzati nei metodi numerici. Molte implementazioni degli algoritmi di forward e back-propagation nelle reti neurali convoluzionali si basano su questa operazione. Spesso il 90-95% di tutto il tempo dedicato all'apprendimento automatico è preso da questa operazione. Tutti i metodi sul prodotto sono forniti nella sezione Prodotti di matrici e vettori della guida del linguaggio.

      L'esempio seguente mostra la moltiplicazione di due matrici utilizzando il metodo MatMul:

         matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

      Un esempio del prodotto di Kronecker di due matrici o di una matrice e di un vettore, utilizzando il metodo Kron.

         matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

      Altri esempi tratti dall'articolo Matrici e vettori in MQL5:

      //--- initialize matrices
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Product of horizontal vector v[3] and matrix m[3,5]");
   vector v3 = {1,2,3};
   Print("On the left v3 = ",v3);
   Print("On the right m35 = \n",m35);
   Print("v3.MatMul(m35) = horizontal vector v[5] \n",v3.MatMul(m35));
   /*
   1. Product of horizontal vector v[3] and matrix m[3,5]
   On the left v3 = [1,2,3]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = horizontal vector v[5]
   [40,46,52,58,64]
   */

//--- show that this is really a horizontal vector
   Print("\n2. Product of matrix m[1,3] and matrix m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("On the left m13 = \n",m13);
   Print("On the right m35 = \n",m35);
   Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35));
   /*
   2. Product of matrix m[1,3] and matrix m[3,5]
   On the left m13 =
   [[1,2,3]]
   On the right m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = matrix m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Product of matrix m[3,5] and vertical vector v[5]");
   vector v5 = {1,2,3,4,5};
   Print("On the left m35 = \n",m35);
   Print("On the right v5 = ",v5);
   Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5));
   /*
   3. Product of matrix m[3,5] and vertical vector v[5]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right v5 = [1,2,3,4,5]
   m35.MatMul(v5) = vertical vector v[3]
   [40,115,190]
   */

//--- show that this is really a vertical vector
   Print("\n4. Product of matrix m[3,5] and matrix m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("On the left m35 = \n",m35);
   Print("On the right m51 = \n",m51);
   Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51));
   /*
   4. Product of matrix m[3,5] and matrix m[5,1]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = matrix v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Product of matrix m[3,5] and matrix m[5,2]");
   Print("On the left m35 = \n",m35);
   Print("On the right m52 = \n",m52);
   Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52));
   /*
   5. Product of matrix m[3,5] and matrix m[5,2]
   On the left m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = matrix m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Product of horizontal vector v[5] and matrix m[5,2]");
   Print("On the left v5 = \n",v5);
   Print("On the right m52 = \n",m52);
   Print("v5.MatMul(m52) = horizontal vector v[2] \n",v5.MatMul(m52));
   /*
   6. The product of horizontal vector v[5] and matrix m[5,2]
   On the left v5 =
   [1,2,3,4,5]
   On the right m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = horizontal vector v[2]
   [80,95]
   */

   Print("\n7. Outer() product of horizontal vector v[5] and vertical vector v[3]");
   Print("On the left v5 = \n",v5);
   Print("On the right v3 = \n",v3);
   Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3));
   /*
   7. Outer() product of horizontal vector v[5] and vertical vector v[3]
   On the left v5 =
   [1,2,3,4,5]
   On the right v3 =
   [1,2,3]
   v5.Outer(v3) = matrix m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */


      Trasformazioni

      Le trasformazioni matriciali sono spesso utilizzate nelle operazioni sui dati. Tuttavia, molte operazioni matriciali complesse non possono essere risolte in modo efficiente o stabile a causa della limitata precisione dei computer.

      Le trasformazioni (o scomposizioni) di matrici sono metodi che riducono una matrice nelle sue parti componenti, rendendo facile il calcolo di operazioni matriciali più complesse. I metodi di decomposizione delle matrici, detti anche metodi di fattorizzazione delle matrici, sono la spina dorsale dell'algebra lineare nei computer, anche per operazioni di base come la risoluzione di sistemi di equazioni lineari, il calcolo dell'inversa e il calcolo del determinante di una matrice.

      L'apprendimento automatico utilizza ampiamente la Decomposizione ai Valori Singolari (SVD), che consente di rappresentare la matrice originale come il prodotto di altre tre matrici. La SVD viene utilizzata per risolvere una serie di problemi, dall'approssimazione ai minimi quadrati alla compressione e al riconoscimento delle immagini.

      Un esempio di Decomposizione ai Valori Singolari con il metodo SVD:

        matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- execute SVD decomposition
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// check block
//--- U * singular diagonal * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- another check
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

      Un'altra trasformazione comunemente usata è la decomposizione di Cholesky, che può essere utilizzata per risolvere un sistema di equazioni lineari Ax=b se la matrice A è simmetrica e definita positivamente.

      In MQL5, la decomposizione di Cholesky viene eseguita con il metodo Cholesky: 

        matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

      La tabella seguente mostra l'elenco dei metodi disponibili:

      Funzione

      Azione

      Cholesky

      Calcola la decomposizione di Cholesky

      Eig

      Calcola gli autovalori e gli autovettori destri di una matrice quadrata

      EigVals

      Calcola gli autovalori di una matrice generale

      LU

      Fattorizzazione LU di una matrice come prodotto di una matrice triangolare inferiore e di una matrice triangolare superiore

      LUP

      Fattorizzazione LUP con pivoting parziale, che si riferisce alla decomposizione LU con le sole permutazioni di riga: PA=LU

      QR

      Calcolo della fattorizzazione qr di una matrice

      SVD

      Decomposizione ai Valori Singolari

      Ottenere statistiche

        I metodi della sezione Statistics sono utilizzati per calcolare le statistiche descrittive di matrici e vettori. Utilizzateli per trovare:
        • Valori massimi e minimi, insieme ai relativi indici in una matrice/vettore
        • La somma e il prodotto degli elementi, come la somma e il prodotto cumulativo
        • Mediana, media, media aritmetica e media aritmetica ponderata dei valori della matrice/vettore
        • Deviazione standard e varianza degli elementi
        • Percentili e quantili
        • Metrica dei regressori come errore di deviazione dalla linea di regressione costruita sull'array di dati specificato.

          Un esempio di calcolo della deviazione standard con il metodo Std:

             matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

          Calcolo dei quantili con il metodo dei Quantile:

             matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */


          Caratteristiche della matrice

          Utilizzare i metodi della sezione Caratteristiche per ottenere i seguenti valori:

          • Il numero di righe e colonne di una matrice
          • Numero di norma e condizione
          • Determinante, rango, traccia e spettro di una matrice

          Calcolo del rango di una matrice con il metodo Rank:

            matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // matrix deficit
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 size - rank 1, unless all 0
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

          Calcolo di una norma con il metodo Norm:

            matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */


          Risolvere le equazioni

          I metodi di apprendimento automatico e i problemi di ottimizzazione richiedono spesso di trovare soluzioni a un sistema di equazioni lineari. La sezione Soluzioni contiene quattro metodi che consentono di risolvere queste equazioni a seconda del tipo di matrice. 

          Funzione

          Azione

          Solve

          Risolve un'equazione matriciale lineare o un sistema di equazioni algebriche lineari.

          LstSq

          Restituisce la soluzione ai minimi quadrati di equazioni algebriche lineari (per matrici non quadrate o degenerate)

          Inv

          Calcolo dell'inversa moltiplicativa di una matrice quadrata invertibile con il metodo di Jordan-Gauss

          PInv

          Calcolo della pseudo-inversa di una matrice con il metodo di Moore-Penrose

          Consideriamo un esempio di risoluzione dell'equazione A*x=b.  


          Dobbiamo trovare il vettore di soluzioni x. La matrice A non è quadrata e quindi il metodo Solve non può essere utilizzato qui. 

          Utilizzeremo il metodo LstSq che consente di risolvere approssimativamente matrici non quadrate o degenerate. 

             matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- solve the system A*x = b
   vector x=a.LstSq(b);
//--- check the solution, x must be equal to [5, -4]
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- check A*x = b1, the resulting vector must be [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

          La verifica ha dimostrato che il vettore x trovato è la soluzione di questo sistema di equazioni.


          Metodi di apprendimento automatico

          Esistono tre metodi matriciali e vettoriali che possono essere utilizzati nell'apprendimento automatico.

          Funzione

          Azione

          Activation

          Calcola i valori della funzione di attivazione e li scrive nel vettore/matrice passato

          Derivative

          Calcola i valori della derivata della funzione di attivazione e li scrive nel vettore/matrice passato

          Loss

          Calcola i valori della funzione di perdita e li scrive nel vettore/matrice passato

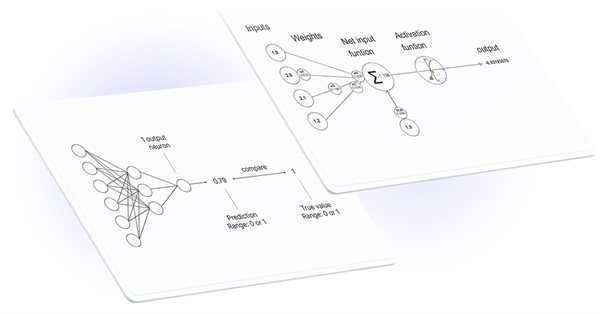
          Le funzioni di attivazione sono utilizzate nelle reti neurali per trovare un'uscita che dipende dalla somma ponderata degli ingressi. La selezione della funzione di attivazione ha un impatto significativo sulle prestazioni della rete neurale.


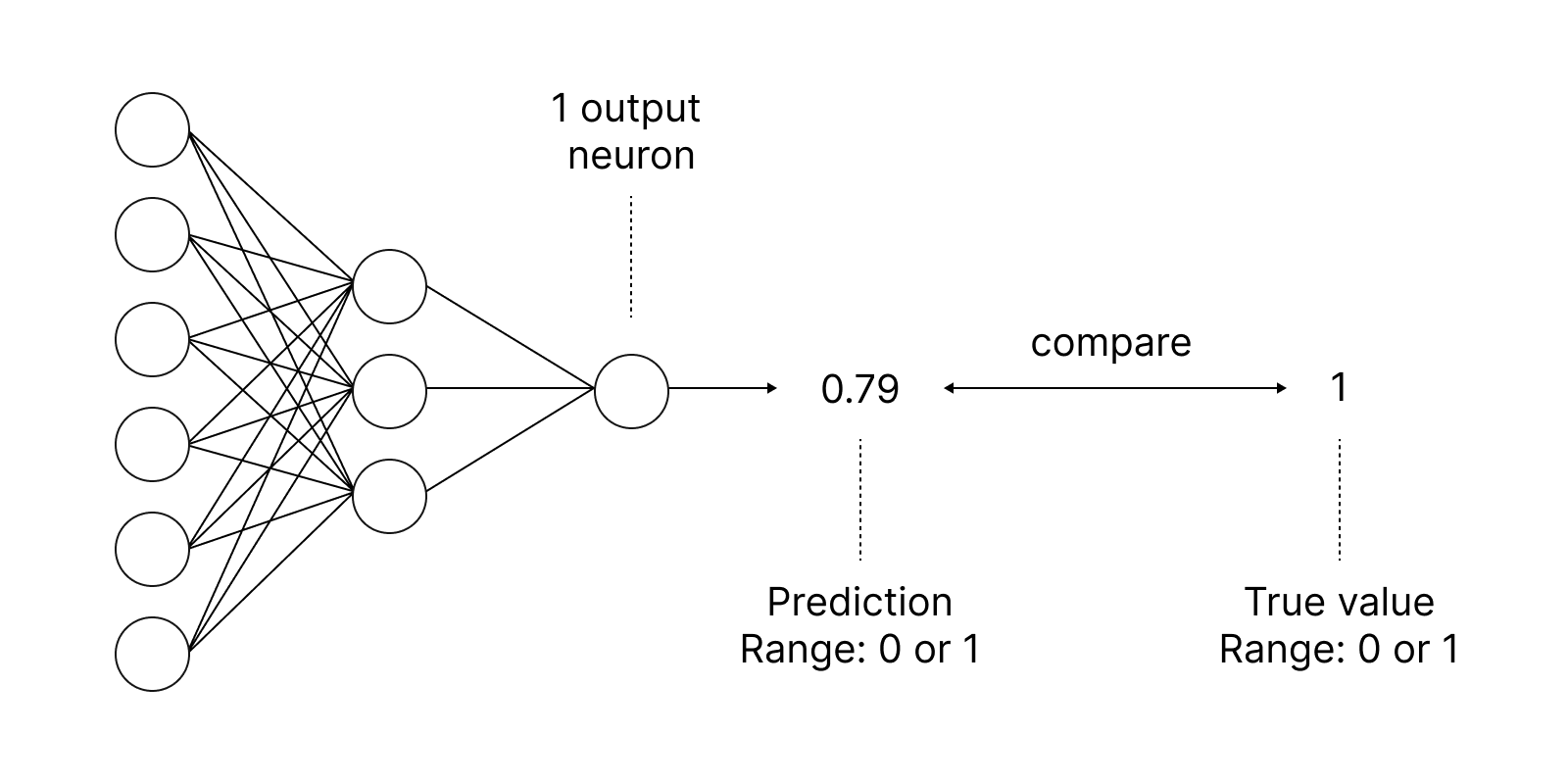
          Una delle funzioni di attivazione più conosciuta è la sigmoide.



          Il metodo integrato Activation consente di impostare uno dei quindici tipi di funzione di attivazione. Sono tutte disponibili nell'enumerazione ENUM_ACTIVATION_FUNCTION.

          ID

          Descrizione

          AF_ELU                      

          Unità Lineare Esponenziale

          AF_EXP                      

          Esponenziale

          AF_GELU                      

          Unità Lineare Errore Gaussiano

          AF_HARD_SIGMOID              

          Sigmoide Rigido

          AF_LINEAR                    

          Lineare

          AF_LRELU                    

          Unità Lineare Rettificata Leaky

          AF_RELU                      

          Unità lineare rettificata

          AF_SELU                      

          Unità Lineare Esponenziale Scalata

          AF_SIGMOID                  

          Sigmoide

          AF_SOFTMAX                  

          Softmax

          AF_SOFTPLUS                  

          Softplus

          AF_SOFTSIGN                  

          Softsign

          AF_SWISH                    

          Swish

          AF_TANH                      

          Funzione tangente iperbolica

          AF_TRELU                    

          Unità Lineare Rettificata con soglia


          Una rete neurale mira a trovare un algoritmo che minimizzi l'errore nell’apprendimento, per il quale viene utilizzata la funzione di perdita. La deviazione viene calcolata con il metodo Loss, per il quale è possibile specificare uno dei quattordici tipi dell'enumerazione ENUM_LOSS_FUNCTION.

          I valori della deviazione risultanti vengono poi utilizzati per affinare i parametri della rete neurale. Questo viene fatto utilizzando il metodo Derivative, che calcola i valori della derivata della funzione di attivazione e scrive il risultato nel vettore/matrice passato. Il processo di addestramento della rete neurale può essere rappresentato visivamente utilizzando l'animazione dell'articolo "Programmazione di una rete neurale profonda da zero utilizzando il linguaggio MQL".



          Miglioramenti in OpenCL

          Abbiamo inoltre implementato il supporto per matrici e vettori nelle funzioni CLBufferWrite e CLBufferRead. Per queste funzioni sono disponibili i corrispondenti sovraccarichi. Di seguito è riportato un esempio per una matrice.

          Scrive i valori dalla matrice al buffer e restituisce true in caso di successo.

          uint  CLBufferWrite(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   matrix<T>     &mat                       // matrix of values to write to buffer
   );

          Legge un buffer OpenCL in una matrice e restituisce true in caso di successo.

          uint  CLBufferRead(
   int           buffer,                    // OpenCL buffer handle
   uint          buffer_offset,             // offset in the OpenCL buffer in bytes
   const matrix& mat,                       // matrix to get values from the buffer
   ulong         rows=-1,                   // number of rows in the matrix
   ulong         cols=-1                    // number of columns in the matrix
   );

          Consideriamo l'uso dei nuovi sovraccarichi con un esempio di prodotto matriciale di due matrici. Eseguiamo i calcoli utilizzando tre metodi:

            • Un modo semplice per illustrare l'algoritmo di moltiplicazione delle matrici
            • Il metodo MatMul integrato
            • Calcolo parallelo in OpenCL

              Le matrici ottenute verranno controllate utilizzando il metodo Compare, che confronta gli elementi di due matrici con la precisione indicata.

              #define M       3000      // number of rows in the first matrix
#define K       2000      // number of columns in the first matrix equal to the number of rows in the second one
#define N       3000      // number of columns in the second matrix
 
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- initialize the random number generator
  MathSrand((int)TimeCurrent());
//--- fill matrices of the given size with random values
  matrixf mat1(M, K, MatrixRandom) ;    // first matrix
  matrixf mat2(K, N, MatrixRandom);     // second matrix
 
//--- calculate the product of matrices using the naive way
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// here we rite the result of multiplying two matrices
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- calculate the product of matrices using MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- calculate the product of matrices in OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // context handle
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL not found, exit");
    return;
   }
  int cl_prg;             // program handle
  int cl_krn;             // kernel handle
  int cl_mem_in1;         // handle of the first buffer (input)
  int cl_mem_in2;         // handle of the second buffer (input)
  int cl_mem_out;         // handle of the third buffer (output)
//--- create the program and the kernel
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- create all three buffers for the three matrices
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- third matrix - output
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- set kernel arguments
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- write matrices to device buffers
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- start the OpenCL code execution time
  start=GetTickCount();
//--- set the task workspace parameters and execute the OpenCL program
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- read the result into the matrix
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Compare computation times of the methods");
  PrintFormat("Naive product time = %d ms",time_naive);
  PrintFormat("MatMul product time = %d ms",time_matmul);
  PrintFormat("OpenCl product time = %d ms",time_opencl);  
//--- release all OpenCL contexts
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- compare all obtained result matrices with each other 
  Print("How many discrepancy errors between result matrices?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Result: 
   
   Matrix [3000 x 3000] read 
   Compare computation times of the methods
   Naive product time = 54750 ms
   MatMul product time = 4578 ms
   OpenCl product time = 922 ms
   How many discrepancy errors between result matrices?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Fills the matrix with random values                              |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//| Release all OpenCL contexts                                      |
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- release all created OpenCL contexts in reverse order
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

              Una spiegazione dettagliata del codice OpenCL di questo esempio è fornito nell'articolo “OpenCL: Da semplice verso una programmazione più perspicace”.


              Ulteriori miglioramenti

              Build 3390 ha eliminato due restrizioni nel funzionamento di OpenCL che influivano sull'utilizzo della GPU.

                Il numero massimo di oggetti OpenCL può arrivare fino a 65536, mentre in precedenza il limite era di 256. Gli handle degli oggetti OpenCL vengono creati in un programma MQL5 utilizzando le funzioni CLContextCreate, CLBufferCreate e CLProgramCreate. Il precedente limite di 256 handle non era sufficiente per un uso efficiente dei metodi di apprendimento automatico.

                OpenCL può essere utilizzato anche su schede grafiche senza supporto 'doppio'. In precedenza, solo le GPU con supporto “doppio” erano consentite nei programmi MQL5, sebbene molti compiti consentissero calcoli utilizzando float. Il tipo float è inizialmente considerato nativo per il calcolo parallelo, in quanto occupa meno spazio. Di conseguenza, il vecchio requisito è stato eliminato.

                Per impostare l'uso obbligatorio di GPU con supporto doppio per compiti specifici, utilizzare CL_USE_GPU_DOUBLE_ONLY nella chiamata CLContextCreate.
                   int cl_ctx;
//--- initialization of OpenCL context
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL not found");
      return;
     }

                Sebbene le modifiche alle operazioni OpenCL non siano direttamente correlate a matrici e vettori, sono in linea con i nostri sforzi nello sviluppo delle capacità di apprendimento automatico del linguaggio MQL5.


                Il futuro di MQL5 nell'Apprendimento Automatico

                Negli ultimi anni abbiamo fatto molto per introdurre tecnologie avanzate nel linguaggio MQL5:

                • Convertendo la libreria di metodi numerici ALGLIB a MQL5
                • Implementando una libreria matematica con logica fuzzy e metodi statistici
                • Introducendo la libreria grafica, analoga della funzione plot
                • Integrando con Python, per eseguire script Python direttamente nel terminale
                • Aggiungendo funzioni DirectX per creare grafica 3D
                • Implementando supporto nativo per SQLite per le operazioni con i database
                • Aggiungendo nuovi tipi di dati: matrici e vettori, con tutti i metodi necessari.

                  Il linguaggio MQL5 continuerà a svilupparsi, mentre una delle principali priorità è l'apprendimento automatico. Abbiamo grandi progetti di sviluppo. Quindi, restate con noi, sosteneteci e continuate ad imparare con noi.

                  Tradotto dal russo da MetaQuotes Ltd.
                  Articolo originale: https://www.mql5.com/ru/articles/10922

                  Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

                  Altri articoli di questo autore

                  Vai alla discussione
                  Sviluppare un Expert Advisor per il trading da zero (Parte 12): Times e Trade (I) Sviluppare un Expert Advisor per il trading da zero (Parte 12): Times e Trade (I)
                  Oggi creeremo Times & Trade con interpretazione rapida per la lettura del flusso degli ordini. È la prima parte in cui costruiremo il sistema. Nel prossimo articolo completeremo il sistema con le informazioni mancanti. Per implementare questa nuova funzionalità, dovremo aggiungere parecchie cose nuove al codice del nostro Expert Advisor.
                  Impara come progettare un sistema di trading tramite Accumulazione/Distribuzione (AD) Impara come progettare un sistema di trading tramite Accumulazione/Distribuzione (AD)
                  Benvenuti nel nuovo articolo della nostra serie sull'apprendimento di come progettare sistemi di trading basati sugli indicatori tecnici più popolari. In questo articolo, impareremo a conoscere un nuovo indicatore tecnico chiamato Indicatore di Accumulazione/Distribuzione e scopriremo come progettare un sistema di trading MQL5 basato su semplici strategie con AD.
                  Sviluppare un Expert Advisor per il trading da zero (Parte 13): Times e Trade (II) Sviluppare un Expert Advisor per il trading da zero (Parte 13): Times e Trade (II)
                  Oggi costruiremo la seconda parte del sistema Times & Trade per l'analisi del mercato. Nel precedente articolo "Times & Trade (I)" abbiamo discusso di un sistema di organizzazione grafica alternativa, che consentirebbe di avere un indicatore per l'interpretazione più rapida possibile delle transazioni eseguite sul mercato.
                  Scopri come progettare un sistema di trading tramite OBV Scopri come progettare un sistema di trading tramite OBV
                  Questo è un nuovo articolo che continua la nostra serie per principianti su come progettare un sistema di trading basato su alcuni degli indicatori popolari. Scopriremo un nuovo indicatore che è On Balance Volume (OBV) e impareremo come usarlo e a progettare un sistema di trading basato su di esso.