OpenCL: De una programación simple a una más intuitiva
4 245
0
Introducción
El primer artículo "OpenCL: El puente hacia mundos paralelos" fue una introducción del tema de OpenCL. En él se trataron los aspectos básicos de la interacción entre el programa OpenCL (también llamado kernel aunque no es muy correcto) y el programa externo (anfitrión) en MQL5. Algunas capacidades de funcionamiento del lenguaje (p.ej. el uso de tipos de datos vector) fueron ilustrados por el cálculo de pi = 3.14159265...
La optimización del funcionamiento del programa fue en algunos casos considerable. Sin embargo, todas estas optimizaciones eran ingenuas ya que no tenían en cuenta las especificaciones del hardware utilizado para realizar todos nuestros cálculos. El conocimiento de estas especificaciones puede, en la mayoría de casos, permitirnos conseguir mejoras de velocidad que van más allá de las capacidades de la CPU.
Para demostrar estas optimizaciones, el autor tuvo que recurrir a un ejemplo nada original que es probablemente uno de los más estudiados en la literatura sobre OpenCL. Es la multiplicación de dos grandes matrices.
Vamos a empezar con los principal: el modelo de memoria de OpenCL junto con peculiaridades de su implementación en la arquitectura de hardware ideal.
1. Jerarquía de memoria en dispositivos de computación modernos
1.1. El modelo de memoria de OpenCL
En general, los sistemas de memoria se diferencian bastante entre sí dependiendo de las plataformas. Por ejemplo, todas las CPU modernas soportan la recogida de datos automática, al contrario de las GPU donde este no es siempre el caso.
Para garantizar la portabilidad del código, se ha adoptado un modelo de memoria abstracto en OpenCL que los programadores y distribuidores que necesitan implementarlo en el hardware real pueden adoptar. La memoria, como se define en OpenCL puede ilustrarse teóricamente como en la Figura siguiente:
Fig. 1. El modelo de memoria de OpenCL
Una vez que los datos son transferidos desde el anfitrión al dispositivo, se almacenan en el dispositivo de memoria global. Cualquier dato transferido en dirección opuesta también se almacena en la memoria global (pero esta vez en la memoria global del anfitrión). La palabra clave _global (¡dos caracteres subrayados!) es un modificador que indica que los datos asociados con un cierto puntero se almacenan en la memoria global:
__kernel void foo( __global float *A ) { /// kernel code }
La memoria global es accesible para todas las unidades de cómputo dentro del dispositivo como la RAM en el sistema anfitrión.
La memoria constante, al contrario de lo que indica su nombre, no almacena datos de solo lectura necesariamente. Este tipo de memoria está diseñada para datos en los que se puede acceder a cada elemento simultáneamente por parte de todas las unidades de trabajo. Las variables con valores constantes por supuesto caen dentro de esta categoría también. La memoria constante en el modelo OpenCL es una parte de la memoria global y los objetos de la memoria transferidos a la memoria global pueden especificarse como __constant.
La memoria local es memoria auxiliar donde el espacio de la dirección es único para cada dispositivo. En el hardware, a menudo viene en la forma de memoria sobre chip pero no hay ningún requisito especial para que sea exactamente el mismo para OpenCL.
El acceso a este tipo de memoria implica un menor tiempo de espera y el ancho de banda es por tanto mucho mayor que el de la memoria global. Intentaremos aprovechar su menor tiempo de respuesta para la optimización del rendimiento del kernel.
La especificación de OpenCL dice que un variable en la memoria local puede declararse en el encabezado del kernel:
__kernel void foo( __local float *sharedData ) { }y en su cuerpo:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Tenga en cuenta que una matriz dinámica no puede declararse en el cuerpo del kernel, siempre debemos especificar su tamaño.
Más abajo, en la optimización del kernel para la multiplicación de dos matrices grandes, veremos cómo gestionar los datos locales y qué peculiaridades de implementación implica en Meta Trader 5 según la experiencia del autor.
Las variables locales y los argumentos del kernel que no contienen punteros son privados por defecto (si se especifican sin el modificador __local). En la práctica, estas variables se encuentran normalmente en los registros. Y viceversa, las matrices privadas y cualquier registro vertido están siempre en una memoria fuera de chip, es decir, una memoria de mayor tiempo de espera. Permítanme citar la información relevante de la Wikipedia:
En muchos lenguajes de programación, el programador tiene la ilusión de asignar arbitrariamente muchas variables. Sin embargo, durante la compilación, el compilador debe decidir cómo asignar estas variables a un conjunto de registros pequeño y finito. No todas las variables se encuentran en uso (o "vivas") al mismo tiempo, por lo que algunos registros pueden ser asignados a más de una variable. Sin embargo, dos variables en uso al mismo tiempo no pueden ser asignadas al mismo registro sin alterar su valor.
Las variables que no pueden asignarse a algunos registros deben mantenerse en la RAM y cargadas/descargadas para cada lectura/escritura, un proceso llamado volcado. El acceso a la RAM es mucho más lento que el acceso a los registros y ralentiza la velocidad de ejecución del programa compilado, por lo que un compilador optimizador intentará asignar tantas variables a los registros como sea posible. La presión del registro es el término usado cuando hay menos registros de hardware disponibles de lo que sería óptimo. Una mayor presión significa que son necesarios más volcados y recargas.
El modelo de memoria de OpenCL que se ha descrito es muy similar a la estructura de memoria de las modernas GPU. La figura a continuación muestra una correlación entre el modelo de memoria de OpenCL y el modelo de memoria de GPU AMD Radeon HD 6970.
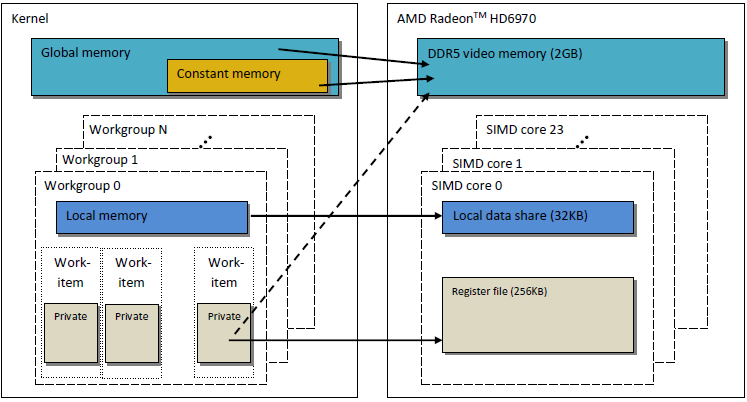
Fig. 2. Correlación entre la estructura de memoria de la Radeon HD 6970 y el modelo de memoria abstracto de OpenCL
Vamos a considerar en mayor detalle los aspectos relacionados con una implementación específica de memoria GPU.
1.2. La memoria en las GPU discretas modernas
1.2.1. Solicitudes de memoria combinadas
Esta información es también importante para la optimización del funcionamiento del kernel ya que el objetivo principal es lograr un ancho de banda de memoria alto.
Vamos a ver la figura a continuación para entender mejor el proceso de direccionamiento de la memoria:
Fig. 3. Esquema de direccionamiento de datos en la memoria de dispositivo global
Supongamos que el puntero a una matriz de variables enteras int es la dirección de X = 0x00001232. Cada int toma 4 bytes de memoria. Suponemos que un hilo (que es un software análogo a una unidad de trabajo que ejecuta el código del kernel) direcciona los datos en Х[ 0 ]:
int tmp = X[ 0 ];
Asumimos que el ancho del bus de memoria es de 32 bytes (256 bits). Este ancho de bus es típico de las potentes GPU, como la Radeon HD 5870. En algunas otras GPU, el ancho del bus de datos puede ser diferente, p. ej. 384 bits o incluso 512 en algunos modelos de NVidia.
El direccionamiento del bus de memoria debe corresponderse con su estructura, es decir, lo primero de todo es el ancho. En otras palabras, los datos en la memoria se almacenan en bloques de 32 bytes (256 bits) cada uno. Con independencia de lo que direccionemos en el rango entre 0x00001220 y 0x0000123F (hay exactamente 32 bytes en este rango, podemos comprobarlo nosotros mismos), obtendremos la dirección 0x00001220 como dirección de inicio para la lectura.
El acceso a la dirección 0x00001232 devolverá todos los datos en las direcciones dentro del rango desde 0x00001220 to 0x0000123F, es decir, 8 números enteros. Por tanto, solo habrá 4 bytes (un número entero) de datos útiles mientras que los restantes 28 bytes (7 números enteros) serán inútiles:
Fig. 4. Esquema de la obtención de los datos requeridos de la memoria
El número que necesitamos localizar en la dirección especificada anteriormente - 0x00001232 - está dentro de un círculo en el esquema.
Para maximizar el uso del bus, la GPU intenta combinar los accesos a la memoria de diferentes hilos en una única solicitud de memoria, cuantos menos accesos a la memoria mejor. La razón detrás de esto es que el acceso a la memoria del dispositivo global nos cuesta tiempo y por ello afecta enormemente a la velocidad de ejecución del programa. Consideremos la siguiente línea del código kernel:
int tmp = X[ get_global_id( 0 ) ];
Supongamos que nuestra matriz X es la matriz del ejemplo anterior. Los primeros 16 hilos (kernels) accederán a direcciones entre 0x00001232 y 0x00001272 (hay 16 números enteros dentro de este rango, es decir, 64 bytes). Si cada solicitud fue enviada por los kernels independientemente, sin haber sido previamente combinada en una sola, cada una de las 16 solicitudes contendrían 4 bytes de datos útiles y 28 bytes de datos inútiles, haciendo un total de 64 bytes usados y 448 no usados.
Este cálculo se basa en el hecho de que cada acceso a una dirección situada dentro del mismo bloque de memoria de 32 bytes devolverá idénticos datos. Este es el clave. Sería más correcto combinar múltiples solicitudes en una sola, para que las solicitudes coherentes economizarán el uso de las inútiles. Esta operación será llamada aquí combinación y las solicitudes combinadas como tales serán denominadas como coherentes.
Fig. 5. Solo son necesarias tres solicitudes de memoria para obtener los datos necesarios
Cada celda en la Figura anterior es de 4 bytes. En nuestro ejemplo, son suficientes 3 solicitudes. Si el comienzo de la matriz estaba alineada con la dirección del principio de cada bloque de memoria de 32 bytes, incluso 2 solicitudes serían suficientes.
En una GPA AMD 64, los hilos son parte de un frente de ola y deben ejecutar la misma instrucción que en la ejecución de SIMD. 16 hilos organizados por get_global_id( 0 ), siendo exactamente un cuarto del frente de ola, se combinan en una solicitud coherente para un uso eficiente del bus.
A continuación se muestra una ilustración del ancho de banda de memoria necesario para las solicitudes incoherentes comparados con las incoherentes, es decir, las solicitudes "espontáneas". Se refiere a la Radeon HD 5870. Puede observarse un resultado similar en las tarjetas NVidia.
Fig. 6. Análisis comparativo del ancho de banda de memoria requerido para las solicitudes coherentes e incoherentes
Puede verse claramente que una solicitud de memoria coherente permite incrementar el ancho de banda de memoria por casi un orden de magnitud.
1.2.2. Bancos de memoria
La memoria está compuesta de bancos donde los datos se almacenan. En las modernas GPU, estos son normalmente palabras de 32 bits (4 bytes). Los datos en serie se almacenan en bancos de memoria adyacentes. Un grupo de hilos accediendo a elementos en serie no producirá ningún conflicto en los bancos.
El efecto negativo máximo de los conflictos de bancos se observa normalmente en la memoria GPU local. Es por tanto aconsejable que los accesos a datos locales desde hilos próximos se dirijan a bancos de memoria distintos.
En el hardware de AMD, el frente de onda que genera conflictos de bancos se atasca hasta que se completan las operaciones de la memoria local. Esto genera una serialización donde los bloques de código que deben ejecutarse en paralelo se ejecutan secuencialmente. Tiene un efecto extremadamente negativo en el rendimiento del kernel.
Fig. 7. Esquemas de acceso a memoria sin conflictos de banco
La figura anterior muestra el acceso a memoria sin conflictos de banco ya que todos los hilos acceden a distintos datos.
Vamos a ilustrar el acceso a memoria con conflictos de banco:
Fig. 8. Acceso a memoria con conflictos de banco
La situación sin embargo tiene una excepción: si todos los accesos son a la misma dirección, el banco puede realizar una publicación para evitar el retraso:
Fig. 9. Todos los hilos acceden a la misma dirección
Ocurrirán eventos similares cuando se accede a la memoria global pero el impacto de estos conflictos es considerablemente menor.
- La memoria de la GPU es distinta de la de la CPU. El principal objetivo a la hora de optimizar el funcionamiento del programa usando OpenCL es garantizar el máximo ancho de banda en lugar de reducir el tiempo de espera, como ocurriría en la CPU.
- La naturaleza del acceso a memoria tiene un gran impacto en la eficiencia del uso del bus. Una eficiencia en el uso del bus baja significa una velocidad de ejecución baja.
- Para mejorar el funcionamiento del código, es aconsejable que el acceso a memoria sea coherente. Además, es mucho mejor para evitar conflictos de banco.
- Las especificaciones del hardware (ancho del bus, el número de bancos de memoria, así como el número de hilos que pueden combinarse para un único acceso coherente) puede encontrarse en la documentación del proveedor.
Las especificaciones de algunas tarjetas gráficas Radeon de las series 5xxx se muestran a continuación como ejemplo:
Fig. 10. Especificaciones técnicas de tarjetas gráficas Radeon HD 58xx de gama media y alta
Vamos ahora a ver la programación.
2. Multiplicación de matrices cuadradas grandes: Del código de CPU en serie al código de GPU en paralelo
2.1. Código de MQL5
La tarea por delante, al contrario que el artículo anterior "OpenCL: el puente hacia mundos paralelos", es estándar, es decir, multiplicar dos matrices. Se ha elegido principalmente debido al hecho de que una gran parte de la información al respecto se encuentra disponible en diferentes fuentes. La mayoría de ellas, de una u otra forma, ofrecen soluciones más o menos coordinadas. Este es el camino que vamos a recorrer, dando aclaraciones paso a paso sobre el significado de las estructuras del modelo mientras tenemos en mente que estamos trabajando con hardware real.
A continuación se muestra un fórmula de multiplicación de matrices conocida en el álgebra lineal, modificada para los cálculos por ordenador. El primer índice es el número de la fila de la matriz y el segundo el número de la columna. Cada elemento de la matriz obtenida se calcula añadiendo cada uno de los sucesivos productos de los elementos en la primera y la segunda matriz a la suma acumulada. Al final, esta suma acumulada es el elemento de la matriz obtenida calculado:
Fig. 11. Fórmula de multiplicación de la matriz
Puede representarse esquemáticamente de esta forma:
Fig. 12. Algoritmo de multiplicación de matrices (ilustrado mediante el cálculo de un elemento de la matriz obtenida) representado algorítmicamente
Puede verse fácilmente que donde ambas matrices tienen las mismas dimensiones iguales a N, el número de adiciones y multiplicaciones puede estimarse por la función O(N^3): para calcular cada elemento de la matriz obtenida, necesitamos obtener el producto escalar e una fila en la primera matriz y una columna en la segunda matriz. Requiere cerca de 2*N adiciones y multiplicaciones. El cálculo necesario se obtiene multiplicando por el número de elementos de la matriz N^2. De esta forma, el tiempo de ejecución del código aproximado depende considerablemente de N al cubo.
El número de filas y columnas para las matrices se establece en 2.000 solo por comodidad, puede ser arbitrario pero no demasiado grande.
El código en MQL5 no es muy complejo:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Listado 1. Programa secuencial inicial en el anfitrión
Resultados utilizando distintos parámetros:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Como puede verse, nuestra dependencia estimada del tiempo de ejecución en los tamaños de la matriz lineal parece haber sido cierta: se ha obtenido un incremento del doble en todas las dimensiones de la matriz en una incremento del tiempo de ejecución de casi 8 veces.
Algunas palabras sobre el algoritmo: el orden del lazo puede cambiarse arbitrariamente en la función de multiplicación mul(). Resulta que tiene un efecto considerable en el tiempo de ejecución: el ratio del tiempo de ejecución más lento sobre el más rápido es de casi 1,73.
El artículo solo muestra la variante más rápida. Las variantes probadas restantes pueden encontrarse en el código adjunto al final del artículo (archivo matr_mul_2dim.mq5). En este sentido, la guía de programación de OpenCL (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) dice lo siguiente (p. 512):
Estas no son obviamente todas las optimizaciones del código "no paralelo" inicial que podemos implementar. Algunas de ellas están relacionadas con el hardware (instrucciones (S)SSEx) mientras otras son puramente algorítmicas, p. ej. el algoritmo Strassen, el algoritmo Coppersmith–Winograd, etc. Tenga en cuenta que el tamaño de las matrices multiplicadas para el algoritmo Strassen que provoquen un aumento de la velocidad considerable con relación al algoritmo clásico es muy pequeño, solo de 64x64. En este artículo vamos a aprender a multiplicar rápidamente matrices cuyo tamaño lineal es de hasta varios millares (aproximadamente hasta 5.000).
2.2. La primera implementación del algoritmo en OpenCL
Vamos ahora a exportar este algoritmo a OpenCL, creando ROWS1*COLS2 hilos, es decir, borrando ambos lazos exteriores del kernel. Cada hilo ejecutará COLSROWS iteraciones por lo que el lazo interior sigue siendo parte del kernel.
Como tendremos que crear tres buffers lineales para el kernel de OpenCL sería razonable volver a recomponer el algoritmo inicial para que sea tan parecido al algoritmo del kernel como sea posible. El código del programa "no paralelo" en una "CPU de un solo núcleo" con buffers lineales será proporcionado junto con el código del kernel. Que el código sea óptimo con matrices de dos dimensiones no significa que su análogo sea también óptimo para los buffers lineales: todas las pruebas deberán repetirse. Por tanto, de nuevo optamos por c-r-cr como la variante inicial que corresponde a la lógica estándar de la multiplicación de matrices en el álgebra lineal.
Dicho esto, para evitar en lo posible la confusión en el direccionamiento de los elementos de la matriz/buffer, responda a la siguiente pregunta: si tenemos una matriz Matr (M filas y N columnas) en una memoria GPU global como buffer lineal, ¿cómo podemos calcular el cambio lineal de un elemento Matr[ fila ][ columna ]?
De hecho no hay orden fijo para disponer una matriz en la memoria de la GPU ya que está determinado por la lógica del propio problema. Por ejemplo, los elementos de ambas matrices pueden disponerse de forma distinta en los buffers ya que en lo que respecta al algoritmo de multiplicación de la matriz, las matrices son asimétricas, es decir, las filas de la primera matriz se multiplican por las columnas de la segunda matriz. Esta nueva disposición puede afectar en gran medida el rendimiento del cálculo en la lectura secuencial de los elementos de la matriz de la memoria de la GPU global en cada iteración del kernel.
La primera implementación del algoritmo tendrá matrices dispuestas de la misma forma, en orden según la fila mayor. Los primeros elementos de la fila serán los primeros en situarse en el buffer seguidos por todos los elementos de la segunda fila, y así sucesivamente. La fórmula de nivelar una representación de dos dimensiones de una matriz Matr[ M (filas) ][ N (columnas) ] en una memoria lineal es de la siguiente forma:
Fig. 13. Algoritmo para convertir un espacio de índice de dos dimensiones en lineal para disponer la matriz en el buffer de la GPU.
La figura anterior es un ejemplo de cómo se nivela una representación de una matriz de dos dimensiones en una memoria lineal en orden según la columna mayor.
A continuación se muestra un código ligeramente reducido de nuestra primera implementación del programa en el dispositivo de OpenCL:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Listado 2. La primera implementación del algoritmo en OpenCL
Las dos últimas funciones se útiles para verificar la precisión de los cálculos. Puede descargar todo el código al final del artículo (matr_mul_1dim.mq5). Tenga en cuenta que las dimensiones no tienen que corresponder necesariamente a matrices cuadradas solo.
Los demás cambios casi siempre tendrán que ver solo con el código del kernel y por tanto en adelante solo se realizarán códigos de modificación del kernel.
El tipo REALTYPE se presenta por comodidad para cambiar la precisión de cálculo de flotante a doble. Debe señalarse que el tipo REALTYPE se declara no solo en el programa anfitrión sino también dentro del kernel. SI es necesario, deberá realizarse cualquier cambio de este tipo en dos lugares al mismo tiempo, en ambos #define del programa anfitrión y en el código kernel.
Los resultados del funcionamiento del código (en adelante, tipo de datos flotantes en todas partes):
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Cuando se ejecuta en una Radeon HD 4870 (_device = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Copo puede verse, la ejecución del kernel en la GPU es mucho más lenta. Sin embargo no hemos abordado la optimización específicamente para la GPU.
Algunas conclusiones:
- El cambio de la representación de la matriz de dos dimensiones a lineal (correspondiente a la representación en el programa ejecutado en el dispositivo) no ha tenido un efecto considerable sobre el tiempo de ejecución total de la versión secuencial del programa.
- El algoritmo de cálculo más intuitivo que coincide con la definición de la multiplicación de matrices en el álgebra lineal ha sido elegida como la variante inicial para mayor optimización Es algo más lento que el más rápido, pero en vista de la futura aceleración de la GPU este factor no es esencial.
- El tiempo de ejecución debe calcularse solo después de la lectura de los buffers en la RAM en vez de después del comando CLExecute(). La razón detrás de esto, señalada por MetaDriver al autor, es probablemente la siguiente:MetaDriver: Antes de leer del buffer, CLBufferRead() simplemente espera la terminación del programa. CLExecute() es de hecho una función de cola de espera asíncrona. Devuelve el resultado inmediatamente, antes de que la operación del código cl se complete.
- Las guías de computación de GPU no suelen calcular el tiempo de ejecución del kernel sino el rendimiento específico relativo a varios objetos, memoria, aritmética, etc. Podemos hacerlo y lo haremos más adelante.
Sabemos que el cálculo de una matriz de tamaño 2.000 requiere cerca de 2*2.000 sumas/multiplicaciones para cada elemento. Al multiplicar por el número de elementos de la matriz (2.000*2000) vemos que el número total de operaciones de datos tipo flotante es de 16.000 millones. Dicho esto, la ejecución en la CPU tarda 115,628 seg. que corresponde a una velocidad de flujo de datos igual a
Por otro lado, recuerde que el cálculo más rápido hasta ahora en una "CPU de un núcleo" con un tamaño de matriz de 2.000 solo tardó 83,663 segundos en completarse (vea nuestro primer código sin OpenCL). Por tanto
Tomemos esta cifra como referencia, punto de inicio para nuestras optimizaciones.
Igualmente, el cálculo usando OpenCL en la CPU arroja:
Finalmente, calculamos el rendimiento específico en la GPU:
2.3. Eliminar accesos a datos incoherentes
Al mirar el código del kernel pueden verse claramente algunos defectos en la optimización.
Veamos el cuerpo del lazo dentro del kernel:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
Es fácil ver que cuando el contador del lazo (cr++) está ejecutándose se toman datos contiguos del primer buffer en 1[]. Mientras que los datos del segundo buffer en 2[] se tomas con "retrasos" iguales a COLS2. En otras palabras, la mayor parte de los datos tomados del segundo buffer serán inútiles ya que las solicitudes de memoria serán incoherentes (véase 1.2.1. Solicitudes de memoria combinadas) Para arreglar esta situación es suficiente modificar el código en tres sitios cambiando la fórmula de cálculo del índice de la matriz 2 [] así como su patrón de generación:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Ahora cuando los valores del contador del lazo (cr++) cambian, los datos de ambas matrices se tomarán secuencialmente, sin ningún "retraso".
- Código de llenado de los buffers en genMatrices(). Ahora debe rellenarse en orden de columna descendiente en lugar de en orden de fila descendente como se usó al principio:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Código de verificación en la función checkRandom():
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Resultados en la CPU:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Como podemos ver, los acceso coherentes a los datos han tenido apenas efecto en el tiempo de ejecución en la GPU, sin embargo mejoró claramente el tiempo de ejecución en la CPU. Es muy probable que tenga que ver con los factores que se optimizarán más tarde, en particular con el tiempo de espera tan prolongado en el acceso a las variables globales de las que deberíamos deshacernos cuanto antes.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
Puede descargar todo el código al final del artículo (matr_mul_1dim_coalesced.mq5).
El código del kernel es el siguiente:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Listado 3. Kernel con acceso a datos de memoria global combinado
Vamos ahora con más optimizaciones.
2.4. Eliminando el acceso a la memoria de GPU global "costoso" de la matriz de salida
Se sabe que el tiempo de espera del acceso a memoria de la GPU global es extremadamente elevado (casi 600-800 ciclos). Por ejemplo, el tiempo de espera para realizar una suma de dos números es aproximadamente de 20 ciclos. El objetivo principal de las optimizaciones al hacer cálculos en la GPU es ocultar el tiempo de espera incrementando el rendimiento específico de los cálculos. En el lazo del kernel desarrollado anteriormente, hemos accedido constantemente a los elementos de memoria global, lo que cuesta mucho tiempo.
Vamos ahora a presentar la suma de la variable local en el kernel (a la que puede accederse muchas veces más rápido ya que es una variable privada del kernel ubicada en la unidad de trabajo del registro) y una vez completado el lazo, asignamos por separado el valor de la suma obtenido al elemento de la matriz de salida:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Listado 4. Introduciendo la variable para calcular la suma acumulada en el lazo de cálculo del producto escalar.
Puede descargar todo el código al final del artículo (matr_mul_sum_local.mq5).
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================¡Esto es un auténtico aumento de productividad !
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
El principio fundamental que intentamos seguir en las optimizaciones secuenciales es el siguiente: primero debemos reorganizar la estructura de los datos de la forma más completa posible para que sea adecuada a una tarea dada y específicamente el hardware subyacente, y solo entonces procederemos a refinar las optimizaciones empleando algoritmos de cálculo rápidos como mad() o fma(). Hay que tener en cuenta que las optimizaciones secuenciales no siempre resultan necesariamente en una disminución del rendimiento, esto no puede garantizarse.
2.5. Aumentando las operaciones ejecutadas por el kernel
En programación paralela es importante organizar los cálculos para minimizar los costes (tiempo invertido) en la organización de la operación paralela. En matrices de dimensión 2.000, una unidad de trabajo calculando un elemento de la matriz de salida realiza una cantidad de trabajo igual a 1 / 4.000.000 de todas las tareas.
Esto es obviamente demasiado y está muy lejos del número real de unidades que realizan cálculos en el hardware. Ahora, en la nueva versión del kernel calcularemos toda la matriz en lugar de un elemento.
Es importante que el espacio de la tarea se cambie ahora de dos dimensiones a una dimensión ya que toda la fila, en lugar de un solo elemento de la matriz se calcula ahora en cada tarea del kernel. Por tanto, el espacio de la tarea se convierte en el número de filas de la matriz.
Fig. 14. Esquema de cálculo de toda la fila de la matriz de salida
El código del kernel se hace más complejo:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 5. El kernel para el cálculo de toda la fila de la matriz de salida
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Los resultados (el código fuente completo está disponible en el archivo matr_mul_row_calc.mq5):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
Podemos ver que el tiempo de ejecución en la CPU ha empeorado claramente y ha sido, aunque no mucho, peor en la GPU. No todo es tan malo: este cambio estratégico que agrava temporalmente la situación a escala local está aquí además para incrementar sustancialmente el rendimiento.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. Transfiriendo la fila de la primera matriz a la memoria privada
La principal peculiaridad del algoritmo de multiplicación de la matriz es un gran número de multiplicaciones con acumulación simultanea de los resultados. Una optimización adecuada de gran calidad de este algoritmo debe suponer la minimización de las transferencias de datos. Pero hasta ahora, en los cálculos en el lazo principal de la acumulación del producto escalar, todas las modificaciones de nuestro kernel han guardado dos de las tres matrices en la memoria global.
Esto significa que todos los datos de entrada para cada producto escalar (siendo de hecho cada elemento de la matriz de salida) fluye constantemente por toda la jerarquía de la memoria, desde la global a la privada, con los tiempos de espera correspondientes. Este tráfico puede reducirse garantizando que cada unidad de trabajo reutilice siempre la misma fila de la primera matriz para cada fila calculada de la matriz de salida.
Fig. 15. Transfiriendo la fila de la primera matriz a la memoria privada de la unidad de trabajo
Esto no conlleva ningún cambio en el código del programa anfitrión. Y los cambios en el kernel son mínimos. Debido al hecho de que una matriz de una dimensión privada se genera dentro del kernel, la GPU intenta ubicarla en la memoria privada de la unidad que ejecuta el kernel. La fila requerida de la primera matriz es simplemente copiada de la memoria global a la privada. Dicho esto, debe señalarse que incluso este copiado será relativamente rápido. El truco está en el hecho de que el copiado más costoso de los elementos de la primera matriz de la memoria global a la privada se hace coherentemente y los costes adicionales de copiado son muy modestos comparados con el tiempo de ejecución del doble lazo principal calculando la fila de la matriz de salida.
El código el kernel (el código comentado en el lazo principal es el mismo de la versión anterior):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 6. Kernel con la fila de la primera matriz a la memoria privada de la unidad de trabajo
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
El rendimiento específico de la CPU sigue siendo del mismo nivel que la última vez, mientras que el rendimiento específico de la GPU volvió al nivel más alto alcanzado, pero en la nueva capacidad. Tenga en cuenta que el rendimiento específico de la CPU es como si se hubiera congelado, siendo solo ligeramente inestable, mientras el rendimiento específico de la GPU sube (aunque no siempre) en saltos muy grandes.
Es preciso señalar que el rendimiento específico real debe ser un poco mayor ya que, debido al copiado de la fila de la primera matriz en la memoria privada, se ejecutan más operaciones ahora que antes. Sin embargo, tiene poco efecto en el rendimiento específico estimado final.
El código fuente puede consultarse en matr_mul_row_in_private.mq5.
2.7. Transfiriendo la columna de la segunda matriz a la memoria local
Ahora es fácil adivinar cuál será el siguiente paso. Ya hemos seguido los pasos para ocultar los tiempos de espera asociados con el resultado y las primeras matrices de entrada. Queda aún una segunda matriz.
Un estudio más detallado de los productos escalares en la multiplicación de matrices muestra que durante el cálculo de la fila de la matriz de salida, todas las unidades de trabajo en el grupo de trabajo refluyen datos de las mismas columnas de la segunda matriz multiplicada a través del dispositivo. Esto se muestra en el esquema a continuación:
Fig. 16. Transfiriendo la columna de la segunda matriz a la cuota de datos local del grupo de trabajo.
Los costes de transferir datos de la memoria global pueden reducirse si las unidades de trabajo que conforman el grupo de trabajo copian las columnas de la segunda matriz en la memoria del grupo de trabajo antes de que comience el cálculo de las filas de la matriz de salida.
Esto requerirá realizar cambios en el kernel así como en el programa anfitrión. El cambio más importante es el establecimiento de la memoria local para cada kernel. Debe ser explícito ya que la asignación de memoria dinámica no está soportada en OpenCL. Por tanto, debe ubicarse primer en el anfitrión un objeto de memoria de tamaño adecuado para que sea posteriormente procesado dentro del kernel.
Y solo entonces, al ejecutar el kernel, las unidades de trabajo copian la columna de la segunda matriz en la memoria local. Esto se hace en paralelo utilizando la distribución cíclica de iteraciones de lazo en todas las unidades del grupo de trabajo. Sin embargo, todo el copiado debe completarse antes de la que la unidad de trabajo comience su operación principal (cálculo de la fila de la matriz de salida).
Por ello se inserta el siguiente comando después del lazo encargado del copiado:
barrier(CLK_LOCAL_MEM_FENCE);
Esta es una "barrera de memoria local" que garantiza que cada unidad de trabajo en el grupo puede "ver" la memoria local en un cierto estado que es coordinado con otras unidades. Todas las unidades de trabajo en el grupo de trabajo deben ejecutar comandos hasta la barrera antes de que cualquiera de ellos pueda proceder con la ejecución del kernel. En otras palabras, la barrera es un mecanismo de sincronización especial entre las unidades de trabajo dentro del grupo de trabajo.
Los mecanismos de sincronización entre los grupos de trabajo no se han previsto en OpenCL.
A continuación se muestra una ilustración de la barrera en acción:
Fig. 17. Ilustración de la barrera en acción
De hecho, solo parece que las unidades de trabajo en el grupo ejecutan el código estrictamente de forma simultánea. Esto es solo una abstracción del modelo de programación de OpenCL.
Hasta ahora, nuestros códigos de kernel ejecutados en diferentes unidades de trabajo no han requerido una sincronización de las operaciones ya que no hubo comunicación explícita entre ellos que estuviera establecida de forma programática en el kernel, y además, no era siquiera necesario. Sin embargo, se requiere la sincronización en este kernel ya que el proceso de llenado de la matriz local se distribuye en paralelo entre todas las unidades del grupo de trabajo.
En otras palabras, cada unidad de trabajo escribe sus valores en cuota de datos local (aquí, en la matriz) sin saber lo lejos que están de otras unidades en este proceso de escritura. La barrera está ahí para que una determinada unidad de trabajo no proceda con la ejecución del kernel antes de que sea necesario, es decir, antes de que una matriz local se haya generado por completo.
Debe entender que esta optimización difícilmente beneficiará al rendimiento de la CPU: La guía de optimización de OpenCL de Intel dice que cuando ejecutamos un kernel en la CPU, todos los objetos de memoria son capturados por el hardware, por lo que el cambio explícito usando la memoria local introduce costes innecesarios (moderados).
Hay otro punto importante que merece destacar aquí y que costó mucho tiempo al autor del artículo. Tiene que ver con el hecho de que una variable local no puede pasarse en el encabezado de la función kernel, es decir, en la etapa de compilación, en la implementación actual por los desarrolladores del terminal. La razón detrás de esto es que para asignar memoria a un objeto de memoria como argumento de la función del kernel, tendríamos primero que crear explícitamente ese objeto en la memoria CPU usando la función CLBufferCreate() y especificar explícitamente su tamaño como función parámetro. Esta función devuelve un controlador de objeto de memoria que será almacenado posteriormente en la memoria de la CPU global ya que este es el único lugar donde puede estar.
La memoria local, sin embargo, es una memoria diferente de la global y por tanto un objeto de memoria creado no puede situarse en la memoria local del grupo de trabajo.
La API de OpenCL permite asignar memoria explícitamente en el tamaño requerido con el puntero NULL al argumento del kernel, incluso sin crear el objeto de memoria como tal (función CLSetKernelArg()). Sin embargo, la sintaxis de la función CLSetKernelArgMem() siendo la análoga de la función API no nos permite pasar en ella el tamaño de la memoria asignada al argumento sin crear el objeto de memoria mismo. Lo que podemos pasar a la función CLSetKernelArgMem() es solo el controlador del buffer ya generado en la memoria de CPU global y pensado para ser transferido a la memoria de la CPU global. Esta es la paradoja.
Por suerte, hay una forma equivalente de trabajar con buffers locales en el kernel. Simplemente declaramos dicho buffer con el modificador __local en el cuerpo del kernel. La memoria local asignada al grupo de trabajo será determinada durante el tiempo de ejecución en lugar de en la etapa de compilación.
Los comandos que lleguen después de la barrera al kernel (la línea de la barrera en el código está marcada en rojo) son, en esencia, los mismo que en la optimización previa. El código del programa anfitrión sigue siendo el mismo (el código fuente está disponible en matr_mul_col_local.mq5).
Este es el nuevo código del kernel:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 7. Transfiriendo la columna de la segunda matriz a la memoria local del grupo de trabajo.
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Ambos casos muestran el deterioro del rendimiento que sin embargo no puede llamarse significativa. Puede ser que el rendimiento mejore en lugar de deteriorarse cambiando el tamaño del grupo de trabajo. El ejemplo anterior servirá además a un propósito diferente: para mostrar cómo usar objetos de la memoria local.
Hay una hipótesis que explica un descenso en el rendimiento cuando se usa la memoria local El artículo comparando OpenCL con CUDA, GLSL y OpenMP (en ruso) publicado en habrahabr.ru hace casi dos años dice:
En otras palabras, ¿significa esto que la memoria local de los productos que salieron al mercado hace dos años no eran más rápidos que la memoria global? La fecha en la que dichos comentarios fueron publicados sugiere que hace dos años la serie de tarjetas gráficas Radeon HD 58xx que salieron, según el autor, eran bastante poco optimistas. Creo que es difícil de creer, especialmente dada la sensacional serie Evergreen de AMD. Sería interesante comprobarlo usando tarjetas más modernas, p. ej. las series HD 69xx.
Adición: inicie el GPU Caps Viewer y verá lo siguiente en la pestaña de OpenCL:
Fig. 18. Parámetros principales de OpenCL soportados por HD 4870
CL_DEVICE_LOCAL_MEM_TYPE: Global
La explicación de este parámetro proporcionada en la especificación del lenguaje (Tabla 4.3, p. 41) es la siguiente:
Tipo de memoria local soportada. Esto puede establecerse a CL_LOCAL implicando el almacenamiento de memoria local dedicada como SRAM o CL_GLOBAL.
De esta forma, la memoria local de la HD 4870 es realmente una parte de la memoria global y cualquier manipulación de la memoria local en esta tarjeta gráfica es por tanto inútil y no dará ningún resultado nada más rápido que la memoria global. Aquí hay otro enlace donde los especialistas de AMD aclaran este punto para las series HD 4xxx. Esto no significa necesariamente que sea tan malo para la tarjeta gráfica que tengamos, era solo para mostrar dónde puede encontrarse dicha información sobre el hardware, en este caso, en CPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Finalmente, vamos a añadir uno toques finales vectorizando el kernel explícitamente. El kernel que se obtuvo en la etapa de transferencia de la fila de la primera matriz a la memoria privada (matr_mul_row_in_private.mq5) servirá como kernel inicial ya que parece que es el más rápido.
2.8. Vectorización del kernel
Esta operación se desglosará mejor en varias etapas, para evitar la confusión. En la modificación inicial, no cambiamos los tipos de datos de los parámetros externos del kernel y solo vectorizamos los cálculos de el lazo interno:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 8. Vectorización parcial del kernel usando float4 (solo lazo interno)
CPU:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Por sorpresa incluso esta primitiva vectorización ha dado buenos resultados en la GPU, aunque no muy significativos, la ganancia parece ser del 10%.
Sigamos vectorizando dentro del kernel: transferimos las costosas operaciones de conversión de tipo vector REALTYPE4 junto con la especificación de los componentes del vector específicos al lazo auxiliar externo rellenando la variable privada rowbuf[]. No hay cambios en el algoritmo:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 9. Deshaciéndonos de las costosas operaciones de conversión de tipo en el lazo principal del kernel
Tenga en cuenta que el valor de recuento máximo del contador del lazo interno (y del auxiliar) ha sido 4 veces más lento ya que las operaciones de lectura que son ahora necesarias para la primera matriz son 4 veces menores que antes, la lectura se ha vuelto claramente una operación de vector.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Resultados específicos aritméticos:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Como puede verse, los cambios en el rendimiento para la CPU son considerables, mientras que son casi revolucionarios para la GPU. El código fuente puede consultarse en matr_mul_vect_v2.mq5.
Vamos a realizar las mismas operaciones con respecto a la última variante del kernel, usando solo el ancho de vector 8. La decisión del autor puede explicarse por el hecho de que el ancho de banda de la memoria de la GPU es 256 bits, es decir, 32 bytes u ocho números de tipo flotante, por tanto, el procesado simultaneo de 8 números flotantes que es equivalente al uso actual de float8 parece ser muy natural.
Tenga en cuenta que en este caso el valor de COLSROWS debe ser divisible por 8. Este es un requisito natural ya que las optimizaciones más precisas establecen requisitos más específicos para los datos.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listado 10. Vectorización del kernel usando un vector de ancho 8.
Tuvimos que insertar en el código del kernel la función en línea dot8() que permite calcular el producto escalar de vectores de ancho 8. En OpenCL, la función estándar dot() puede calcular el producto escalar solo para vectores hasta de ancho 4. El código fuente puede consultarse en matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Los resultados son inesperados: el tiempo de ejecución en la CPU es casi dos veces inferior que antes, donde se ha incrementado ligeramente para la GPU, a pesar del hecho de que float8 es un ancho de bus adecuado para la HD 4870 (siendo igual a 256 bits). Y aquí recurrimos de nuevo a GPU Caps Viewer.
La explicación puede encontrarse en la Fig. 18 en la penúltima línea de la lista del parámetro:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Consulte la especificación de OpenCL y verá el siguiente texto sobre este parámetro en la última columna de la Tabla 4.3 en la página 37:
Se prefiere un ancho de vector nativo para tipos de escalar integrados que puedan ponerse en los vectores. El ancho del vector se define como el número de elementos escalares que pueden almacenarse en el vector.
Por tanto, para la HD 4870 el ancho de vector preferido del vector floatN es float4 en lugar de float8.
Vamos a acabar con el ciclo de optimización del kernel aquí. Podríamos seguir hasta alcanzar mucho más pero la longitud de este artículo no permite dicha profundidad en el análisis.
Conclusión
Este artículo se centra en algunas capacidades de optimización que surgen cuando se tiene en cuenta el hardware subyacente en el que se ejecuta el kernel.
Las cifras obtenidas están lejos de ser un límite pero aún así sugieren que al tener disponibles los recursos existentes aquí y ahora (la API de OpenCL como se implementó por los desarrolladores del terminal no permite el control de algunos parámetros importantes para la optimización, particularmente el tamaño del grupo) la ganancia de rendimiento sobre la ejecución del programa anfitrión es muy sustancial: la ganancia en ejecución en la GPU sobre el programa secuencial en la CPU (aunque no muy optimizado) es de cerca del 200:1.
Mi sincero agradecimiento a MetaDriver por los valiosos consejos y la oportunidad de usar esta GPU discreta cuando la mía no estaba disponible.
Contenido de los archivos adjuntos:
- matr_mul_2dim.mq5 - el programa secuencial inicial en la representación de datos en dos dimensiones del anfitrión;
- matr_mul_1dim.mq5 - la primera implementación del kernel con representación de datos lineal y una relevante validación de la API OpenCL de MQL5;
- matr_mul_1dim_coalesced - el kernel con acceso a memoria global combinado;
- matr_mul_sum_local - una variable privada introducida para el cálculo de un producto escalar, en lugar de acceder a una celda calculada de la matriz de salida almacenada en la memoria global;
- matr_mul_row_calc - el cálculo de toda la fila de la matriz de salida en el kernel;
- matr_mul_row_in_private - la fila de la primera matriz transferida a la memoria privada;
- matr_mul_col_local.mq5 -la columna de la segunda matriz transferida a la memoria local;
- matr_mul_vect.mq5 - la primera vectorización del kernel (usando float4, solo el sublazo interior del lazo principal);
- matr_mul_vect_v2.mq5 - deshaciéndonos de las operaciones costosas de la conversión de datos en el lazo principal;
- matr_mul_vect_v3.mq5 - Vectorización del kernel usando un vector de ancho 8.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/407
Programación basada en autómatas como nuevo enfoque en la creación de sistemas de trading automatizados
OpenCL: El puente hacia mundos paralelos
Los miembros más activos de la comunidad MQL5 ¡han sido premiados con iPhones!
Por qué es el mercado de MQL5 el mejor lugar para vender estrategias de trading e indicadores técnicos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso