Работа с матрицами и векторами в MQL5

MetaTrader 5 — Примеры | 23 сентября 2022, 16:09

2 040

Для решения большого класса математических задач в язык MQL5 были добавлены специальные типы данных — матрицы и векторы. Новые типы имеют встроенные методы для написания краткого и понятного кода, который близок к математической записи. В этой статье мы дадим краткое описание встроенных методов из раздела справки "Методы матриц и векторов".

Содержание

В каждом языке программирования существуют такие типы данных, как массивы, которые позволяют хранить наборы числовых типов — int, double и так далее. Доступ к элементам массива осуществляется по индексу, это позволяет производить операции над массивами с помощью циклов. Чаще всего используются одномерные и двумерные массивы:

int    a[50];       // Одномерный массив из 50 целых чисел
double m[7][50];    // Двумерный массив из 7 подмассивов, каждый из которых состоит из 50 чисел
MyTime t[100];      // Массив, содержащий элементы типа MyTime

Для относительно простых задач хранения и обработки данных возможностей массивов обычно хватает. Но когда дело доходит до комплексных математических задач, из-за большого количества вложенных циклов работа с массивами становится сложной в плане как программирования, так и чтения кода. Даже самые простые операции линейной алгебры требуют большого количества кода и хорошего понимания математики.

Современные технологии работы с данными, такие как машинное обучение, нейронные сети и 3D-графика, широко используют решения задач из линейной алгебры, в которой применяются понятия векторов и матриц. Именно поэтому в MQL5 для нативной работы с такими объектами были добавлены новые типы данных — матрицы и векторы. Это избавляет от множества рутинных операций программирования и улучшает качество кода.

Типы матриц и векторов

Если кратко, то вектор — это одномерный массив типа double, матрица — двумерный массив типа double. Векторы бывают вертикальные и горизонтальные, но в MQL5 они не разделяются.

Матрицы можно представить как массив горизонтальных векторов, где первый индекс матрицы означает номер строки, а второй индекс — номер столбца.

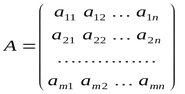
Только нумерация строк и столбцов, в отличие от линейной алгебры, начинается с нуля, как и в массивах.

Помимо типов matrix и vector, которые содержат тип данных double, есть еще 4 типа для работы с соответствующими типами данных:

matrixf — матрица, содержащая элементы типа float
matrixc — матрица, содержащая элементы типа complex
vectorf — вектор, содержащий элементы типа float
vectorc — вектор, содержащий элементы типа complex

На момент написания статьи работа над типами matrixc и vectorc ещё не закончена, использовать эти типы во встроенных методах пока нельзя.

Для применения в шаблонных функциях можно использовать запись matrix<double>, matrix<float>, matrix<complex>, vector<double>, vector<float>, vector<complex> вместо соответствующих типов.

  vectorf       v_f1= {0, 1, 2, 3,};
  vector<float> v_f2=v_f1;
  Print("v_f2 = ", v_f2);

  /*
  v_f2 = [0,1,2,3]
  */

Создание и инициализация

Методы матрицы и векторов разделены на девять категорий по своему назначению. Предусмотрено несколько способов объявления и инициализации матриц и векторов.

Самый простой метод создания — это объявление без указания размера, то есть без распределения памяти для данных. Просто пишем тип данных и имя переменной:

  matrix         matrix_a;   // матрица типа double
  matrix<double> matrix_a1;  // другой способ объявления матрицы типа double, подходит для применения в шаблонах
  matrix<float>  matrix_a3;  // матрица типа float
  vector         vector_a;   // вектор типа double
  vector<double> vector_a1;  // другая запись создания вектора типа double 
  vector<float>  vector_a3;  // вектор типа float

Далее вы можете изменить размер созданных объектов и заполнить нужными значениями. Также их можно использовать во встроенных методах матриц для получения результатов вычислений.

Можно объявить матрицу или вектор с указанием размера, то есть с распределением памяти для данных, но без какой-либо инициализации. Для этого после имени переменной в круглых скобках задаем размер(ы):

  matrix         matrix_a(128,128);           // в качестве параметров можно указывать как константы,
  matrix<double> matrix_a1(InpRows,InpCols);  // так и переменные
  matrix<float>  matrix_a3(InpRows,1);        // аналог вертикального вектора
  vector         vector_a(256);
  vector<double> vector_a1(InpSize);
  vector<float>  vector_a3(InpSize+16);       // в качестве параметра можно использовать выражение

Третий способ создания объектов — объявление с инициализацией. Размеры матриц и векторов в этом случае определяются инициализирующей последовательностью, указанной в фигурных скобках:

  matrix         matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix<double> matrix_a1=matrix_a;                      // должны быть матрицы одного и того же типа
  matrix<float>  matrix_a3={{1,2},{3,4}};
  vector         vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5};
  vector<double> vector_a1={1,5,2.4,3.3};
  vector<float>  vector_a3=vector_a2;                     // должны быть векторы одного и того же типа

Существуют также статические методы создания матриц и векторов указанного размера с инициализацией определённым способом:

  matrix         matrix_a =matrix::Eye(4,5,1);
  matrix<double> matrix_a1=matrix::Full(3,4,M_PI);
  matrixf        matrix_a2=matrixf::Identity(5,5);
  matrixf<float> matrix_a3=matrixf::Ones(5,5);
  matrix         matrix_a4=matrix::Tri(4,5,-1);
  vector         vector_a =vector::Ones(256);
  vectorf        vector_a1=vector<float>::Zeros(16);
  vector<float>  vector_a2=vectorf::Full(128,float_value);

Кроме того, существуют нестатические методы для инициализации матрицы/вектора заданными значениями — Init и Fill:

  matrix m(2, 2);
  m.Fill(10);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10]
  [10,10]]
  */
  m.Init(4, 6);
  Print("matrix m \n", m);
  /*
  matrix m
  [[10,10,10,10,0.0078125,32.00000762939453]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]
  [0,0,0,0,0,0]]
  */

В данном примере метод Init был использован для изменения размеров уже инициализированной матрицы, что привело к заполнению новых элементов случайными значениями.

Важным достоинством метода Init является возможность указать в параметрах инициализирующую функцию для заполнения элементов матрицы/вектора по заданному закону. Например:

void OnStart()
 {
//---
  matrix init(3, 6, MatrixSetValues);  
  Print("init = \n", init);
  /*
  Результат выполнения
  init = 
  [[1,2,4,8,16,32]
   [64,128,256,512,1024,2048]
   [4096,8192,16384,32768,65536,131072]]
  */   
 }
//+------------------------------------------------------------------+
//| Заполняет матрицу степенями числа                                |
//+------------------------------------------------------------------+
void MatrixSetValues(matrix& m, double initial=1)
 {
  double value=initial;
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=value;
      value*=2;
     }
   }
 }

Копирование матриц и массивов

Для копирования матриц и векторов предназначен метод Copy. Но есть и более простой и привычный способ копирование через оператор присвоения "=". Также существует метод Assign.

//--- копирование матриц
  matrix a= {{2, 2}, {3, 3}, {4, 4}};
  matrix b=a+2;
  matrix c;
  Print("matrix a \n", a);
  Print("matrix b \n", b);
  c.Assign(b);
  Print("matrix c \n", c);
  /*
   matrix a
   [[2,2]
    [3,3]
    [4,4]]
   matrix b
   [[4,4]
    [5,5]
    [6,6]]
   matrix c
   [[4,4]
    [5,5]
    [6,6]]
  */

Отличие метода Assign от Copy в том, что он позволяет копировать не только матрицы, но и массивы. Пример ниже показывает, как целочисленный массив int_arr копируется в матрицу типа double. При этом результирующая матрица автоматически подстраивается под размеры копируемого массива.

//--- копирование массива в матрицу
  matrix double_matrix=matrix::Full(2,10,3.14);
  Print("double_matrix before Assign() \n", double_matrix);
  int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}};
  Print("int_arr: ");
  ArrayPrint(int_arr);
  double_matrix.Assign(int_arr);
  Print("double_matrix after Assign(int_arr) \n", double_matrix);  
  /*
   double_matrix before Assign() 
   [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]
    [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]]
    
   int_arr: 
       [,0][,1][,2][,3][,4]
   [0,]   1   2   0   0   0
   [1,]   3   4   0   0   0
   [2,]   5   6   0   0   0
   [3,]   0   0   0   0   0
   [4,]   0   0   0   0   0
   
   double_matrix after Assign(int_arr) 
   [[1,2,0,0,0]
    [3,4,0,0,0]
    [5,6,0,0,0]
    [0,0,0,0,0]
    [0,0,0,0,0]]
  */
 }

Таким образом, метод Assign позволяет бесшовно переходить в коде от массивов к матрицам с автоматическим приведением размера и типа.

Копирование таймсерий в матрицу или вектор

Для анализа ценовых графиков требуется получать и обрабатывать массивы соответствующих структур MqlRates. Но теперь появился еще один способ работы с ними.

Метод CopyRates копирует исторические серии структуры MqlRates прямо в матрицу или вектор. Вам не нужно получать необходимые таймсерии с помощью функций раздела "Доступ к таймсериям и индикаторам" в соответствующие массивы. Кроме того, теперь их не нужно перекладывать в матрицу или вектор. Котировки можно получить в матрицу или вектор за один вызов. Покажем на примере, как вычислить матрицу корреляций для списка символов: вычислим эти значения двумя способами и сравним полученные результаты.

input int             InBars=100;
input ENUM_TIMEFRAMES InTF=PERIOD_H1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- список символов для вычисления
  string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"};
  int size=ArraySize(symbols);
//--- матрица и вектор для получения цен Close
  matrix rates(InBars, size);
  vector close;
  for(int i=0; i<size; i++)
   {
    //--- получим цены Close в вектор
    if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars))
     {
      //--- вставим вектор в матрицу таймсерий
      rates.Col(close, i);
      PrintFormat("%d. %s: %d цен Close добавлено в матрицу", i+1, symbols[i], close.Size());
      //--- выведем для отладки первые 20 значений вектора
      int  digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS);
      Print(VectorToString(close, 20, digits));
     }
    else
     {
      Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError());
      return;
     }
   }
  /*
  1. EURUSD: 100 цен Close добавлено в матрицу
  0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121   1.069 0.99936   1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111   1.079   1.030  ...
  2. GBPUSD: 100 цен Close добавлено в матрицу
  1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069  ...
  3. USDJPY: 100 цен Close добавлено в матрицу
  143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069  ...
  4. USDCAD: 100 цен Close добавлено в матрицу
  1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789  ...
  5. USDCHF: 100 цен Close добавлено в матрицу
  0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509  ...
  */
//--- подготовим матрицу корреляций между символами
  matrix corr_from_vector=matrix::Zeros(size, size);
  Print("Вычислим попарные коэффициенты корреляции");
  for(int i=0; i<size; i++)
   {
    for(int k=i; k<size; k++)
     {
      vector v1=rates.Col(i);
      vector v2=rates.Col(k);
      double coeff = v1.CorrCoef(v2);
      PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff);
      corr_from_vector[i][k]=coeff;
     }
   }
  Print("Матрица корреляций на векторах: \n", corr_from_vector);
  /*
  Вычислим попарные коэффициенты корреляции
  corr(EURUSD,EURUSD) = 1.000
  corr(EURUSD,GBPUSD) = 0.974
  corr(EURUSD,USDJPY) = -0.713
  corr(EURUSD,USDCAD) = -0.950
  corr(EURUSD,USDCHF) = -0.397
  corr(GBPUSD,GBPUSD) = 1.000
  corr(GBPUSD,USDJPY) = -0.744
  corr(GBPUSD,USDCAD) = -0.953
  corr(GBPUSD,USDCHF) = -0.362
  corr(USDJPY,USDJPY) = 1.000
  corr(USDJPY,USDCAD) = 0.736
  corr(USDJPY,USDCHF) = 0.083
  corr(USDCAD,USDCAD) = 1.000
  corr(USDCAD,USDCHF) = 0.425
  corr(USDCHF,USDCHF) = 1.000

  Матрица корреляций на векторах:
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,0.9999999999999999,0.4247042496841555]
   [0,0,0,0,1]]
  */
//--- теперь покажем, как вычислить матрицу корреляций в одну строчку
  matrix corr_from_matrix=rates.CorrCoef(false);   // false означает, что векторы находятся в столбцах матрицы
  Print("Матрица корреляций rates.CorrCoef(false): \n", corr_from_matrix.TriU());
//--- сравним полученные матрицы на расхождения
  Print("Cколько ошибок расхождения между матрицами результатов?");
  ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12);
  Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors);
  /*
  Матрица корреляций rates.CorrCoef(false):
  [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434]
   [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978]
   [0,0,1,0.7360546499847362,0.08314381248168941]
   [0,0,0,1,0.4247042496841555]
   [0,0,0,0,1]]

  Cколько ошибок расхождения между матрицами результатов?
  corr_from_vector.Compare(corr_from_matrix,1e-12)=0
  */
//--- сделаем красивый вывод матрицы корреляций
  Print("Выведем матрицу корреляций с заголовками");
  string header="        ";  // заголовок
  for(int i=0; i<size; i++)
    header+="  "+symbols[i];
  Print(header);
//--- теперь строки
  for(int i=0; i<size; i++)
   {
    string line=symbols[i]+"  ";
    line+=VectorToString(corr_from_vector.Row(i), size, 3, 8);
    Print(line);
   }
  /*
  Выведем матрицу корреляций с заголовками
            EURUSD  GBPUSD  USDJPY  USDCAD  USDCHF
  EURUSD       1.0   0.974  -0.713  -0.950  -0.397
  GBPUSD       0.0     1.0  -0.744  -0.953  -0.362
  USDJPY       0.0     0.0     1.0   0.736   0.083
  USDCAD       0.0     0.0     0.0     1.0   0.425
  USDCHF       0.0     0.0     0.0     0.0     1.0
  */
 }
//+------------------------------------------------------------------+
//| Возвращает строку со значениями вектора                          |
//+------------------------------------------------------------------+
string VectorToString(const vector &v, int length=20, int digits=5, int width=8)
 {
  ulong size=(ulong)MathMin(20, v.Size());
//--- cоставляем строку
  string line="";
  for(ulong i=0; i<size; i++)
   {
    string value=DoubleToString(v[i], digits);
    StringReplace(value, ".000", ".0");
    line+=Indent(width-StringLen(value))+value;
   }
  //--- добавим хвост, если длина вектора превышает заданный размер
  if(v.Size()>size)
    line+="  ...";
//---
  return(line);
 }
//+------------------------------------------------------------------+
//|  Возвращает строку с указанным количеством пробелов              |
//+------------------------------------------------------------------+
string Indent(int number)
 {
  string indent="";
  for(int i=0; i<number; i++)
    indent+=" ";
  return(indent);
 }

В примере показано, как можно:

получить цены Close c помощью CopyRates
вставить в матрицу вектор с помощью метода Col
вычислить коэффициент корреляции между двумя векторами с помощью CorrCoef
с помощью CorrCoef вычислить матрицу корреляций над матрицей с векторами значений
привести матрицу к верхнетреугольному виду с помощью метода TriU
сравнить 2 матрицы на расхождение с помощью Compare

Операции над матрицами и векторами

Над матрицами и векторами можно поэлементно производить математические операции — сложение, вычитание, умножение и деление. Для этого оба объекта должны быть одного и того же типа и должны иметь одинаковые размеры. Каждый член матрицы/вектора оперирует с соответствующим элементом второй матрицы/вектора.

В качестве второго слагаемого (множителя, вычитаемого, делителя) можно также использовать скаляр соответствующего типа (double, float или complex). В этом случае каждый элемент матрицы или вектора будет оперировать с указанным скаляром.

  matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}};
  matrix matrix_b={{1,2,3},{4,5,6}};
  matrix matrix_c1=matrix_a+matrix_b;
  matrix matrix_c2=matrix_b-matrix_a;
  matrix matrix_c3=matrix_a*matrix_b;   // произведение Адамара (Hadamard product) 
  matrix matrix_c4=matrix_b/matrix_a;
  matrix_c1=matrix_a+1;
  matrix_c2=matrix_b-double_value;
  matrix_c3=matrix_a*M_PI;
  matrix_c4=matrix_b/0.1;
//--- возможны операции по месту
  matrix_a+=matrix_b;
  matrix_a/=2;

Кроме того, матрицы и векторы можно передавать в качестве параметра в большинство математических функций — MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. В этом случае матрица или вектор обрабатываются почленно. Пример:

//---
  matrix a= {{1, 4}, {9, 16}};
  Print("matrix a=\n",a);
  a=MathSqrt(a);
  Print("MatrSqrt(a)=\n",a);
  /*
   matrix a=
   [[1,4]
    [9,16]]
   MatrSqrt(a)=
   [[1,2]
    [3,4]]
  */

В случае MathMod и MathPow в качестве второго параметра может быть использован как скаляр, так и матрица или вектор соответствующего размера.

   matrix<T> mat1(128,128);
   matrix<T> mat3(mat1.Rows(),mat1.Cols());
   ulong     n,size=mat1.Rows()*mat1.Cols();
...
   mat2=MathPow(mat1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),(T)1.9);
      if(res!=mat2.Flat(n))
         errors++;
     }

   mat2=MathPow(mat1,mat3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(mat1.Flat(n),mat3.Flat(n));
      if(res!=mat2.Flat(n))
         errors++;
     }
...
   vector<T> vec1(16384);
   vector<T> vec3(vec1.Size());
   ulong     n,size=vec1.Size();
...
   vec2=MathPow(vec1,(T)1.9);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],(T)1.9);
      if(res!=vec2[n])
         errors++;
     }
   vec2=MathPow(vec1,vec3);
   for(n=0; n<size; n++)
     {
      T res=MathPow(vec1[n],vec3[n]);
      if(res!=vec2[n])
         errors++;
     }

Манипуляции

При работе с матрицами и векторами доступны базовые манипуляции без проведения каких-либо вычислений:

транспонирование
извлечение строк, столбцов и диагонали
изменение размера и формы матрицы
перестановка местами указанных строк и столбцов
копирование в новый объект
сравнение двух объектов
разделение матрицы на несколько подматриц
сортировка

Пример транспонирования методом Transpose:

  matrix a= {{0, 1, 2}, {3, 4, 5}};
  Print("matrix a \n", a);
  Print("a.Transpose() \n", a.Transpose());
  /*
  matrix a
  [[0,1,2]
   [3,4,5]]
  a.Transpose()
  [[0,3]
   [1,4]
   [2,5]]
  */

Несколько примеров установки и извлечения диагонали методом Diag:

   vector v1={1,2,3};
   matrix m1;
   m1.Diag(v1);
   Print("m1\n",m1);
  /* 
  m1
  [[1,0,0]
  [0,2,0]
  [0,0,3]]
  m2
  */

   matrix m2;
   m2.Diag(v1,-1);
   Print("m2\n",m2);
  /*
  m2
  [[0,0,0]
  [1,0,0]
  [0,2,0]
  [0,0,3]]
  */

   matrix m3;
   m3.Diag(v1,1);
   Print("m3\n",m3);
  /*
  m3
  [[0,1,0,0]
  [0,0,2,0]
  [0,0,0,3]]
  */

   matrix m4=matrix::Full(4,5,9);
   m4.Diag(v1,1);
   Print("m4\n",m4);
   
   Print("diag -1 - ",m4.Diag(-1));
   Print("diag 0 - ",m4.Diag());
   Print("diag 1 - ",m4.Diag(1)); 
  /*
  m4
  [[9,1,9,9,9]
  [9,9,2,9,9]
  [9,9,9,3,9]
  [9,9,9,9,9]]
  diag -1 - [9,9,9]
  diag 0 - [9,9,9,9]
  diag 1 - [1,2,3,9]
  */

Изменение размера матрицы методом Reshape:

   matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
  /*
  matrix_a
  [[1,2,3]
   [4,5,6]
   [7,8,9]
   [10,11,12]]

  */

   matrix_a.Reshape(2,6);
   Print("Reshape(2,6)\n",matrix_a);
  /*
  Reshape(2,6)
  [[1,2,3,4,5,6]
   [7,8,9,10,11,12]]
  */

   matrix_a.Reshape(3,5);
   Print("Reshape(3,5)\n",matrix_a);
  /*
  Reshape(3,5)
  [[1,2,3,4,5]
   [6,7,8,9,10]
   [11,12,0,3,0]]
  */

   matrix_a.Reshape(2,4);
   Print("Reshape(2,4)\n",matrix_a);
  /*
  Reshape(2,4)
  [[1,2,3,4]
   [5,6,7,8]]
  */

Примеры вертикального разделения матрицы методом Vsplit:

   matrix matrix_a={{ 1, 2, 3, 4, 5, 6},
                    { 7, 8, 9,10,11,12},
                    {13,14,15,16,17,18}};
   matrix splitted[];
   ulong  parts[]={2,3};
 
   matrix_a.Vsplit(2,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /*
     splitted 0
     [[1,2,3]
      [7,8,9]
      [13,14,15]]
     splitted 1
     [[4,5,6]
      [10,11,12]
      [16,17,18]]
  */
 
   matrix_a.Vsplit(3,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4]
      [9,10]
      [15,16]]
     splitted 2
     [[5,6]
      [11,12]
      [17,18]]
*/
 
   matrix_a.Vsplit(parts,splitted);
   for(uint i=0; i<splitted.Size(); i++)
      Print("splitted ",i,"\n",splitted[i]);
  /* 
     splitted 0
     [[1,2]
      [7,8]
      [13,14]]
     splitted 1
     [[3,4,5]
      [9,10,11]
      [15,16,17]]
     splitted 2
     [[6]
      [12]
      [18]]
  */

Методы Col и Row позволяют не только получать соответствующие элементы матрицы, но и вставлять элементы в нераспределенные матрицы, то есть матрицы без заданных размеров. Покажем это на примере:

   vector v1={1,2,3};
   matrix m1;
   m1.Col(v1,1);
   Print("m1\n",m1);
  /*
   m1
   [[0,1]
    [0,2]
    [0,3]]
  */

   matrix m2=matrix::Full(4,5,8);
   m2.Col(v1,2);
   Print("m2\n",m2);
  /*
   m2
   [[8,8,1,8,8]
    [8,8,2,8,8]

    [8,8,3,8,8]
    [8,8,8,8,8]]   
  */

   Print("col 1 - ",m2.Col(1));
  /*
   col 1 - [8,8,8,8]
  */

   Print("col 2 - ",m2.Col(2));
  /*
   col 1 - [8,8,8,8]  col 2 - [1,2,3,8]
  */

Произведения

Умножение матриц является одним из базовых алгоритмов, который широко применяется в различных численных методах. Многие реализации прямого и обратного распространения сигнала в сверточных слоях нейронной сети базируются на этой операции. Зачастую до 90-95% всего времени, затрачиваемого на машинное обучение, приходится именно на эту операцию. Все методы произведений приведены в разделе справки "Произведения матриц и векторов".

Пример матричного произведения двух матриц с помощью метода MatMul:

   matrix a={{1, 0, 0},
             {0, 1, 0}};
   matrix b={{4, 1},
             {2, 2},
             {1, 3}};
   matrix c1=a.MatMul(b);
   matrix c2=b.MatMul(a);
   Print("c1 = \n", c1);
   Print("c2 = \n", c2);
/*
   c1 = 
   [[4,1]
    [2,2]]
   c2 = 
   [[4,1,0]
    [2,2,0]
    [1,3,0]]
*/

Пример произведения Кронекера для двух матриц, а также матрицы и вектора методом Kron:

   matrix a={{1,2,3},{4,5,6}};
   matrix b=matrix::Identity(2,2);
   vector v={1,2};
 
   Print(a.Kron(b));
   Print(a.Kron(v));
 
  /*
   [[1,0,2,0,3,0]
    [0,1,0,2,0,3]
    [4,0,5,0,6,0]
    [0,4,0,5,0,6]]
 
   [[1,2,2,4,3,6]
    [4,8,5,10,6,12]]
  */

Еще больше примеров из статьи "Матрицы и векторы в MQL5":

//--- инициализируем матрицы
   matrix m35, m52;
   m35.Init(3,5,Arange);
   m52.Init(5,2,Arange);
//---
   Print("1. Произведение горизонтального вектора v[3] на матрицу m[3,5]");
   vector v3 = {1,2,3};
   Print("Слева v3 = ",v3);
   Print("Справа m35 = \n",m35);
   Print("v3.MatMul(m35) = горизонтальный вектор v[5] \n",v3.MatMul(m35));
   /*
   1. Произведение горизонтального вектора v[3] на матрицу m[3,5]
   Слева v3 = [1,2,3]
   Справа m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   v3.MatMul(m35) = горизонтальный вектор v[5]
   [40,46,52,58,64]
   */

//--- покажем, что это действительно горизонтальный вектор
   Print("\n2. Произведение матрицы m[1,3] на матрицу m[3,5]");
   matrix m13;
   m13.Init(1,3,Arange,1);
   Print("Слева m13 = \n",m13);
   Print("Справа m35 = \n",m35);
   Print("m13.MatMul(m35) = матрица m[1,5] \n",m13.MatMul(m35));
   /*
   2. Произведение матрицы m[1,3] на матрицу m[3,5]
   Слева m13 =
   [[1,2,3]]
   Справа m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   m13.MatMul(m35) = матрица m[1,5]
   [[40,46,52,58,64]]
   */

   Print("\n3. Произведение матрицы m[3,5] на вертикальный вектор v[5]");
   vector v5 = {1,2,3,4,5};
   Print("Слева m35 = \n",m35);
   Print("Справа v5 = ",v5);
   Print("m35.MatMul(v5) = вертикальный вектор v[3] \n",m35.MatMul(v5));
   /*
   3. Произведение матрицы m[3,5] на вертикальный вектор v[5]
   Слева m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Справа v5 = [1,2,3,4,5]
   m35.MatMul(v5) = вертикальный вектор v[3]
   [40,115,190]
   */

//--- покажем, что это действительно вертикальный вектор
   Print("\n4. Произведение матрицы m[3,5] на матрицу m[5,1]");
   matrix m51;
   m51.Init(5,1,Arange,1);
   Print("Слева m35 = \n",m35);
   Print("Справа m51 = \n",m51);
   Print("m35.MatMul(m51) = матрица v[3] \n",m35.MatMul(m51));
   /*
   4. Произведение матрицы m[3,5] на матрицу m[5,1]
   Слева m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Справа m51 =
   [[1]
    [2]
    [3]
    [4]
    [5]]
   m35.MatMul(m51) = матрица v[3]
   [[40]
    [115]
    [190]]
   */

   Print("\n5. Произведение матрицы m[3,5] на матрицу m[5,2]");
   Print("Слева m35 = \n",m35);
   Print("Справа m52 = \n",m52);
   Print("m35.MatMul(m52) = матрица m[3,2] \n",m35.MatMul(m52));
   /*
   5. Произведение матрицы m[3,5] на матрицу m[5,2]
   Слева m35 =
   [[0,1,2,3,4]
    [5,6,7,8,9]
    [10,11,12,13,14]]
   Справа m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   m35.MatMul(m52) = матрица m[3,2]
   [[60,70]
    [160,195]
    [260,320]]
   */

   Print("\n6. Произведение горизонтального вектора v[5] на матрицу m[5,2]");
   Print("Слева v5 = \n",v5);
   Print("Справа m52 = \n",m52);
   Print("v5.MatMul(m52) = горизонтальный вектор v[2] \n",v5.MatMul(m52));
   /*
   6. Произведение горизонтального вектора v[5] на матрицу m[5,2]
   Слева v5 =
   [1,2,3,4,5]
   Справа m52 =
   [[0,1]
    [2,3]
    [4,5]
    [6,7]
    [8,9]]
   v5.MatMul(m52) = горизонтальный вектор v[2]
   [80,95]
   */

   Print("\n7. Произведение Outer() горизонтального вектора v[5] на вертикальный вектор v[3]");
   Print("Слева v5 = \n",v5);
   Print("Справа v3 = \n",v3);
   Print("v5.Outer(v3) = матрица m[5,3] \n",v5.Outer(v3));
   /*
   7. Произведение Outer() горизонтального вектора v[5] на вертикальный вектор v[3]
   Слева v5 =
   [1,2,3,4,5]
   Справа v3 =
   [1,2,3]
   v5.Outer(v3) = матрица m[5,3]
   [[1,2,3]
    [2,4,6]
    [3,6,9]
    [4,8,12]
    [5,10,15]]
   */

Преобразования

Преобразования матриц являются наиболее востребованными операциями при работе с данными. При этом многие сложные матричные операции не могут быть решены эффективно или со стабильностью, используя ограниченную точность компьютеров.

Матричные преобразования (или по-другому, декомпозиции) — это методы, которые сокращают матрицу на составные части, что облегчает вычисление более сложных матричных операций. Методы матричной декомпозиции, также называемые методами матричной факторизации, являются основой линейной алгебры в компьютерах даже для базовых операций, таких как решение систем линейных уравнений, вычисление обратного и вычисление определителя матрицы.

В машинном обучении широко используется сингулярное разложение (Singular Values Decomposition, SVD), которое позволяет представить исходную матрицу как произведение трех других матриц. SVD-разложение используется при решении самых разных задач — от приближения методом наименьших квадратов до сжатия и распознавания изображений.

Пример сингулярного разложения методом SVD:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
//--- сделаем SVD-разложение
  matrix U, V;
  vector singular_values;
  b.SVD(U, V, singular_values);
  Print("U \n", U);
  Print("V \n", V);
  Print("singular_values = ", singular_values);
 
// блок проверки
//--- U * singular diagonal * V = A
  matrix matrix_s;
  matrix_s.Diag(singular_values);
  Print("matrix_s \n", matrix_s);
  matrix matrix_vt=V.Transpose();
  Print("matrix_vt \n", matrix_vt);
  matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt);
  Print("matrix_usvt \n", matrix_usvt);
 
  ulong errors=(int)b.Compare(matrix_usvt, 1e-9);
  double res=(errors==0);
  Print("errors=", errors);
 
//---- еще проверка
  matrix U_Ut=U.MatMul(U.Transpose());
  Print("U_Ut \n", U_Ut);
  Print("Ut_U \n", (U.Transpose()).MatMul(U));
 
  matrix vt_V=matrix_vt.MatMul(V);
  Print("vt_V \n", vt_V);
  Print("V_vt \n", V.MatMul(matrix_vt)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
   [-1,0,1]
   [2,3,4]]
  U
  [[-0.7071067811865474,0.5773502691896254,0.408248290463863]
   [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256]
   [0.7071067811865472,0.5773502691896255,0.4082482904638627]]
  V
  [[0.5773502691896258,-0.7071067811865474,-0.408248290463863]
   [0.5773502691896258,1.779939029415334e-16,0.8164965809277258]
   [0.5773502691896256,0.7071067811865474,-0.408248290463863]]
  singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17]
 
  matrix_s
  [[7.348469228349533,0,0]
   [0,2.449489742783175,0]
   [0,0,3.277709923350408e-17]]
  matrix_vt
  [[0.5773502691896258,0.5773502691896258,0.5773502691896256]
   [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474]
   [-0.408248290463863,0.8164965809277258,-0.408248290463863]]
  matrix_usvt
  [[-3.999999999999997,-2.999999999999999,-2]
   [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974]
   [2,2.999999999999999,3.999999999999996]]
  errors=0
 
  U_Ut
  [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16]
   [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17]
   [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]]
  Ut_U
  [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16]
   [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16]
   [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]]
  vt_V
  [[1,-5.551115123125783e-17,0]
   [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16]
   [0,1.110223024625157e-16,0.9999999999999996]]
  V_vt
  [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16]
   [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16]
   [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996]
  */
 }

Еще одним часто используемым преобразованием является разложение Холецкого, которое может применяться для решения системы линейных уравнений Ax=b, если матрица A симметрична и положительно определена.

В MQL5 разложение Холецкого выполняется методом Cholesky:

  matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}};
  matrix matrix_l;
  Print("matrix_a\n", matrix_a);
 
  matrix_a.Cholesky(matrix_l);
  Print("matrix_l\n", matrix_l);
  Print("check\n", matrix_l.MatMul(matrix_l.Transpose()));  
  /*
  matrix_a
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  matrix_l
  [[2.408279136645086,0]
   [-0.9062640068544704,3.006291985133859]]
  check
  [[5.7998084,-2.1825367]
   [-2.1825367,9.85910595]]
  */

Список доступных методов представлен в таблице:

Функция	Действие
Cholesky	Вычисляет декомпозицию Холецкого
Eig	Вычисляет собственные значения и правые собственные векторы квадратной матрицы
EigVals	Вычисляет собственные значения общей матрицы
LU	Выполняет LU-факторизацию матрицы как произведения нижнетреугольной матрицы и верхнетреугольной матрицы
LUP	Выполняет LUP-факторизацию с частичным поворотом, которая является LU-факторизацией только с перестановками строк: PA=LU
QR	Вычисляет qr-факторизацию матрицы
SVD	Вычисляет разложение по сингулярным значениям

Получение статистики

Для получения описательной статистики матриц и векторов предназначены методы из раздела "Статистика". Они позволяют получить:

максимальное и минимальное значения и их индексы в матрице/векторе
сумму и произведение элементов, а также кумулятивные сумму и произведение
медиану, среднее, среднеарифметическое и взвешенное среднее арифметическое значений матрицы/вектора
стандартное отклонение и дисперсию элементов
перцентили и квантили
регрессионную метрику как ошибку отклонения от линии регрессии, построенной на указанном массиве данных

Пример вычисления стандартного отклонения методом Std:

   matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_std=matrix_a.Std(0);
   vectorf rows_std=matrix_a.Std(1);
   float matrix_std=matrix_a.Std();
 
   Print("cols_std ",cols_std);
   Print("rows_std ",rows_std);
   Print("std value  ",matrix_std);
   /*
   matrix_a
   [[10,3,2]
    [1,8,12]
    [6,5,4]
    [7,11,9]]
   cols_std [3.2403703,3.0310888,3.9607449]
   rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
   std value  3.452052593231201
   */

Пример вычисления квантилей методом Quantile:

   matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
   Print("matrix_a\n",matrix_a);
 
   vectorf cols_percentile=matrix_a.Percentile(50,0);
   vectorf rows_percentile=matrix_a.Percentile(50,1);
   float matrix_percentile=matrix_a.Percentile(50);
 
   Print("cols_percentile ",cols_percentile);
   Print("rows_percentile ",rows_percentile);
   Print("percentile value  ",matrix_percentile);
   /*
   matrix_a
   [[1,2,3]
    [4,5,6]
    [7,8,9]
    [10,11,12]]
   cols_percentile [5.5,6.5,7.5]
   rows_percentile [2,5,8,11]
   percentile value  6.5
   */

Характеристики матриц

Методы из раздела "Характеристики" позволяют получать следующие значения:

количество строк и столбцов в матрице
норму и число обусловленности
детерминант, ранг, след и спектр матрицы

Пример вычисления ранга матрицы методом Rank:

  matrix a=matrix::Eye(4, 4);;
  Print("matrix a \n", a);
  Print("a.Rank()=", a.Rank());
 
  matrix I=matrix::Eye(4, 4);
  I[3, 3] = 0.;    // дефицит матрицы
  Print("I \n", I);
  Print("I.Rank()=", I.Rank());
 
  matrix b=matrix::Ones(1, 4);
  Print("b \n", b);
  Print("b.Rank()=", b.Rank());;// 1 размерность - ранг 1, если только не все "0"
 
  matrix  zeros=matrix::Zeros(4, 1);
  Print("zeros \n", zeros);
  Print("zeros.Rank()=", zeros.Rank()); 
  /*
  matrix a
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,1]]
  a.Rank()=4
 
  I
  [[1,0,0,0]
  [0,1,0,0]
  [0,0,1,0]
  [0,0,0,0]]
  I.Rank()=3
 
  b
  [[1,1,1,1]]
  b.Rank()=1
 
  zeros
  [[0]
  [0]
  [0]
  [0]]
  zeros.Rank()=0
  */

Пример вычисления нормы матрицы методом Norm:

  matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}};
  a=a-4;
  Print("matrix a \n", a);
  a.Reshape(3, 3);
  matrix b=a;
  Print("matrix b \n", b);
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS));
  Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF));
  Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF));
  Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1));
  Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1));
  Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2));
  Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); 
  /*
  matrix a
  [[-4,-3,-2,-1,0,1,2,3,4]]
  matrix b
  [[-4,-3,-2]
  [-1,0,1]
  [2,3,4]]
  b.Norm(MATRIX_NORM_P2)=7.745966692414834
  b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834
  b.Norm(MATRIX_NORM_INF)9.0
  b.Norm(MATRIX_NORM_MINUS_INF)2.0
  b.Norm(MATRIX_NORM_P1)=)7.0
  b.Norm(MATRIX_NORM_MINUS_P1)=6.0
  b.Norm(MATRIX_NORM_P2)=7.348469228349533
  b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16
  */

Решение уравнений

В методах машинного обучения и задачах оптимизации часто требуется найти решение системы линейных уравнений. Раздел "Решения" содержит 4 метода, которые позволяют решать такие уравнения в зависимости от типа матрицы.

Функция	Действие
Solve	Решает линейное матричное уравнение или систему линейных алгебраических уравнений
LstSq	Решает систему линейных алгебраических уравнений приблизительно (для неквадратных или вырожденных матриц)
Inv	Вычисляет мультипликативную обратную матрицу по отношению к квадратной невырожденной матрице методом Жордана-Гаусса
PInv	Вычисляет псевдообратную матрицу методом Мура-Пенроуза

Рассмотрим пример решения уравнения A*x=b.

Необходимо найти вектор решений x. Матрица A не является квадратной и поэтому здесь не подходит метод Solve.

В данном случае используем метод LstSq, который предназначен для приблизительного решения неквадратных или вырожденных матриц.

   matrix a={{3, 2},
             {4,-5},
             {3, 3}};
   vector b={7,40,3};
//--- решаем систему A*x = b
   vector x=a.LstSq(b);
//--- проверка решения, x должно быть равно [5, -4]
   Print("x=", x);
  /*
  x=[5.00000000,-4]
  */

//--- проверка A*x = b1, полученный вектор должен быть [7, 40, 3]
   vector b1=a.MatMul(x);
   Print("b11=",b1); 
/*
  b1=[7.0000000,40.0000000,3.00000000]
*/

Проверка показала, что найденный вектор x является решением данной системы уравнений.

Методы машинного обучения

Для матриц и векторов предусмотрено 3 метода для использования в машинном обучении.

Функция	Действие
Activation	Вычисляет значения функции активации и записывает в переданный вектор/матрицу
Derivative	Вычисляет значения производной активационной функции и записывает в переданный вектор/матрицу
Loss	Вычисляет значения функции потерь и записывает в переданный вектор/матрицу

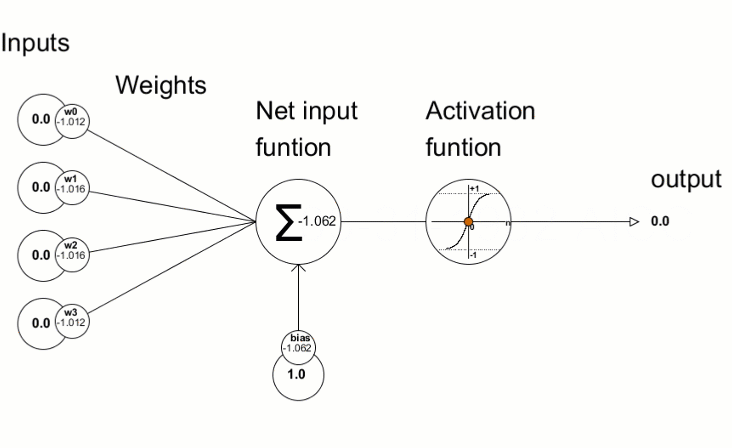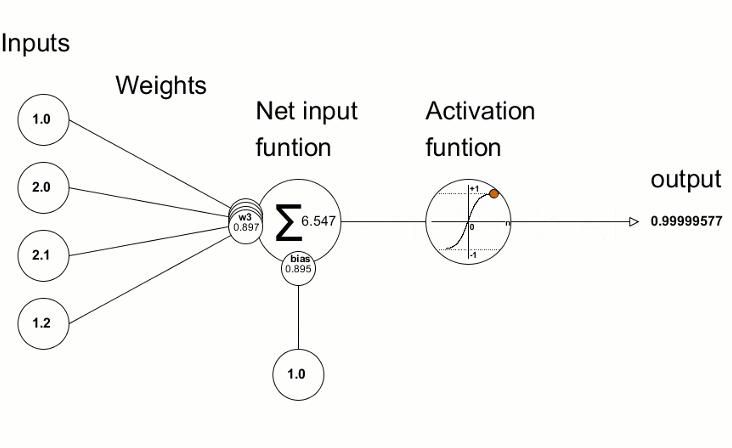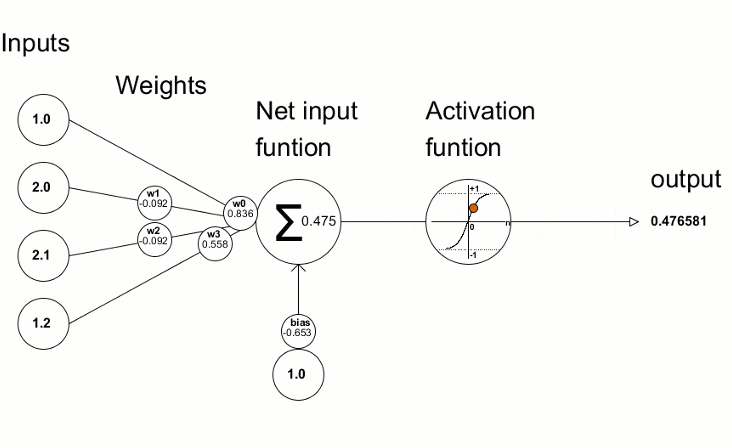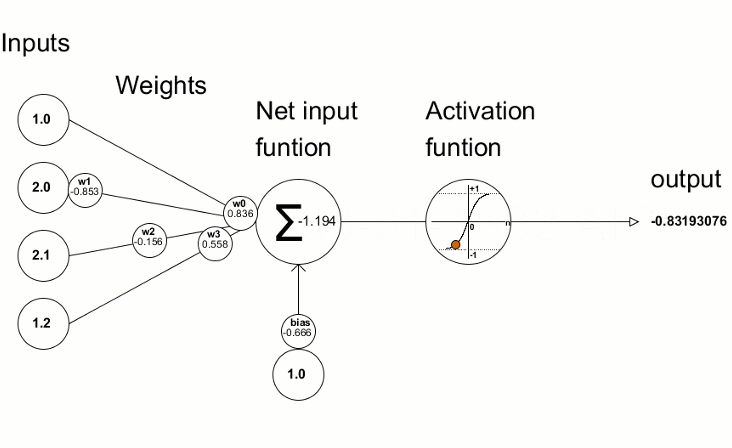
Функции активации используются в нейронных сетях для получения выходного значения в зависимости от результата взвешенной суммы входов. Выбор функции активации имеет большое влияние на возможности и производительность нейронной сети.

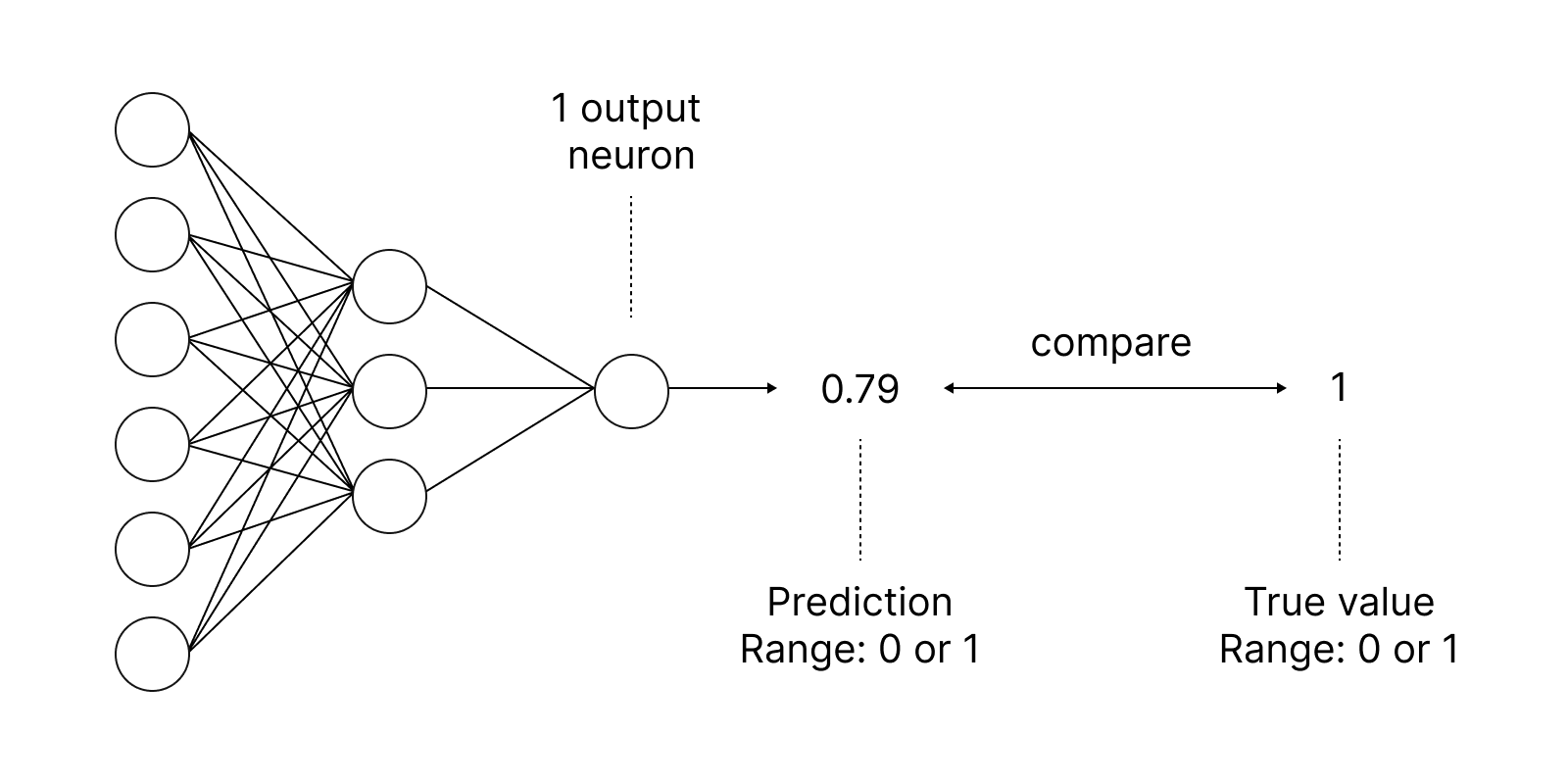
Наиболее известная функция активации — это сигмоид.

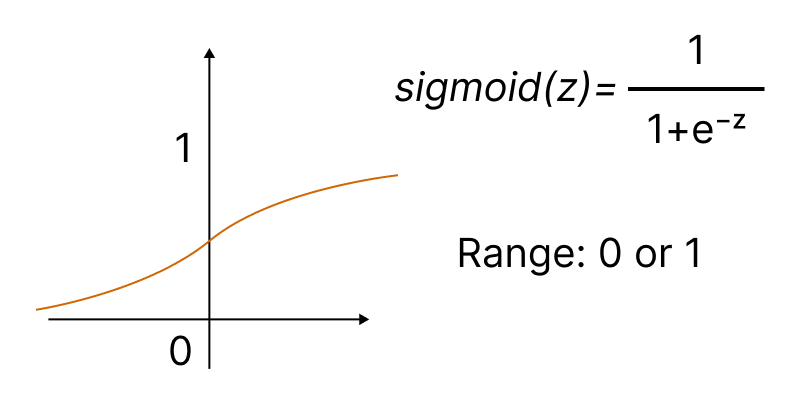
Встроенный метод Activation с помощью перечисления ENUM_ACTIVATION_FUNCTION позволяет задать один из пятнадцати видов функций активации.

Идентификатор	Описание
AF_ELU	Экспоненциальная линейная единица
AF_EXP	Экспоненциальная
AF_GELU	Линейная единица ошибки Гаусса
AF_HARD_SIGMOID	Жесткий сигмоид
AF_LINEAR	Линейная
AF_LRELU	Линейный выпрямитель с "утечкой" (Leaky ReLU)
AF_RELU	Усеченное линейное преобразование ReLU
AF_SELU	Масштабированная экспоненциальная линейная функция (Scaled ELU)
AF_SIGMOID	Сигмоид
AF_SOFTMAX	Softmax
AF_SOFTPLUS	Softplus
AF_SOFTSIGN	Softsign
AF_SWISH	Swish-функция
AF_TANH	Гиперболический тангенс
AF_TRELU	Линейный выпрямитель с порогом

Задача обучения нейронной сети заключается в поиске алгоритма, минимизирующего ошибку на обучающей выборке, для чего используется функция потерь (loss function). Для вычисления отклонения используется метод Loss, который позволяет указать один из видов перечисления ENUM_LOSS_FUNCTION.

Полученные значения отклонений затем используются для уточнений параметров нейронной сети — это делается с помощью метода Derivative, который вычисляет значения производной активационной функции и записывает в переданный вектор/матрицу. Визуально представить процесс обучения сети можно с помощью анимации из статьи "Пишем глубокую нейронную сеть с нуля на языке MQL".

Улучшения в OpenCL

Мы также добавили поддержку матриц и векторов в функции CLBufferWrite и CLBufferRead. Для этих функций появились соответствующие перегрузки, например, для матрицы:

Записывает значения из матрицы в буфер и возвращает true в случае успеха.

uint  CLBufferWrite(
   int           buffer,                    // хэндл на буфер OpenCL
   uint          buffer_offset,             // смещение в OpenCL буфере в байтах
   matrix<T>     &mat                       // матрица значений для записи в буфер
   );

Читает буфер OpenCL в матрицу и возвращает true в случае успеха.

uint  CLBufferRead(
   int           buffer,                    // хэндл на буфер OpenCL
   uint          buffer_offset,             // смещение в OpenCL буфере в байтах
   const matrix& mat,                       // матрица для получения значений  из буфера
   ulong         rows=-1,                   // количество строк в матрице
   ulong         cols=-1                    // количество столбцов в матрице
   );

Покажем использование новых перегрузок на примере матричного произведение двух матриц. Выполним расчеты тремя методами:

наивный метод, который иллюстрирует сам алгоритм умножения матриц
встроенный метод MatMul
параллельные вычисления в OpenCL

Полученные матрицы проверим с помощью метода Compare, который сравнивает элементы двух матриц с заданной точностью.

#define M       3000      // число строк в первой матрице
#define K       2000      // число столбцов в первой матрице равно числу строк во второй 
#define N       3000      // число столбцов во второй матрице
 
//+------------------------------------------------------------------+
const string clSrc=
  "#define N     "+IntegerToString(N)+"                              \r\n"
  "#define K     "+IntegerToString(K)+"                              \r\n"
  "                                                                  \r\n"
  "__kernel void matricesMul( __global float *in1,                   \r\n"
  "                           __global float *in2,                   \r\n"
  "                           __global float *out  )                 \r\n"
  "{                                                                 \r\n"
  "  int m = get_global_id( 0 );                                     \r\n"
  "  int n = get_global_id( 1 );                                     \r\n"
  "  float sum = 0.0;                                                \r\n"
  "  for( int k = 0; k < K; k ++ )                                   \r\n"
  "     sum += in1[ m * K + k ] * in2[ k * N + n ];                  \r\n"
  "  out[ m * N + n ] = sum;                                         \r\n"
  "}                                                                 \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
 {
//--- инициализируем генератор случайных чисел
  MathSrand((int)TimeCurrent());
//--- заполним матрицы заданного размера случайными значениями
  matrixf mat1(M, K, MatrixRandom) ;    // первая матрица
  matrixf mat2(K, N, MatrixRandom);     // вторая матрица
 
//--- посчитаем произведение матриц наивным способом
  uint start=GetTickCount();
  matrixf matrix_naive=matrixf::Zeros(M, N);// сюда запишем результат умножения двух матриц
  for(int m=0; m<M; m++)
    for(int k=0; k<K; k++)
      for(int n=0; n<N; n++)
        matrix_naive[m][n]+=mat1[m][k]*mat2[k][n];
  uint time_naive=GetTickCount()-start;   
     
//--- посчитаем произведение матриц через MatMull
  start=GetTickCount();
  matrixf matrix_matmul=mat1.MatMul(mat2);
  uint time_matmul=GetTickCount()-start;     
  
//--- посчитаем произведение матриц в OpenCL
  matrixf matrix_opencl=matrixf::Zeros(M, N);
  int cl_ctx;             // хэндл контекста
  if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE)
   {
    Print("OpenCL не найдено, выходим");
    return;
   }
  int cl_prg;             // хэндл программы 
  int cl_krn;             // хэндл кернела
  int cl_mem_in1;         // хэндл первого буфера (входного)
  int cl_mem_in2;         // хэндл второго буфера (входного)
  int cl_mem_out;         // хэндл третьего буфера (выходного)
//--- создаем программу и кернел
  cl_prg = CLProgramCreate(cl_ctx, clSrc);
  cl_krn = CLKernelCreate(cl_prg, "matricesMul");
//--- создаем все три буфера для трех матриц
  cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE);
  cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE);
//--- третья матрица - выходная
  cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE);
//--- устанавливаем аргументы кернела
  CLSetKernelArgMem(cl_krn, 0, cl_mem_in1);
  CLSetKernelArgMem(cl_krn, 1, cl_mem_in2);
  CLSetKernelArgMem(cl_krn, 2, cl_mem_out);
//--- пишем матрицы в буферы девайса
  CLBufferWrite(cl_mem_in1, 0, mat1);
  CLBufferWrite(cl_mem_in2, 0, mat2);
  CLBufferWrite(cl_mem_out, 0, matrix_opencl);
//--- старт времени исполнения кода OpenCL
  start=GetTickCount();
//--- устанавливаем параметры рабочего пространства задачи и исполняем программу OpenCL
  uint  offs[2] = {0, 0};
  uint works[2] = {M, N};
  start=GetTickCount();  
  bool ex=CLExecute(cl_krn, 2, offs, works);
//--- считываем результат в матрицу
  if(CLBufferRead(cl_mem_out, 0, matrix_opencl))
    PrintFormat("Прочитана матрица [%d x %d] ", matrix_opencl.Rows(), matrix_opencl.Cols());
   else
      Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); 
  uint time_opencl=GetTickCount()-start;   
  Print("Сравним время вычислений каждым методом");
  PrintFormat("Naive product time = %d ms",time_naive);
  PrintFormat("MatMul product time = %d ms",time_matmul);
  PrintFormat("OpenCl product time = %d ms",time_opencl);  
//--- освободим все OpenCL контексты
  CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out);
 
//--- сравним все полученные матрицы результатов между собой 
  Print("Cколько ошибок расхождения между матрицами результатов?");
  ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12);
  Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors);
  errors=matrix_matmul.Compare(matrix_opencl,float(1e-12));
  Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors);
/*
   Результат: 
   
   Прочитана матрица [3000 x 3000] 
   Сравним время вычислений каждым методом
   Naive product time = 54750 ms
   MatMul product time = 4578 ms
   OpenCl product time = 922 ms
   Cколько ошибок расхождения между матрицами результатов?
   matrix_direct.Compare(matrix_matmul,1e-12)=0
   matrix_matmul.Compare(matrix_opencl,1e-12)=0
*/  
 }
//+------------------------------------------------------------------+
//| Заполняет матрицу случайными значениями                          |
//+------------------------------------------------------------------+
void MatrixRandom(matrixf& m)
 {
  for(ulong r=0; r<m.Rows(); r++)
   {
    for(ulong c=0; c<m.Cols(); c++)
     {
      m[r][c]=(float)((MathRand()-16383.5)/32767.);
     }
   }
 }
//+------------------------------------------------------------------+
//| Освободим все OpenCL контексты                                   |
//+------------------------------------------------------------------+
void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn,
               int cl_mem_in1, int cl_mem_in2, int cl_mem_out)
 {
//--- удаляем в обратной последовательности все созданные OpenCL контексты
  CLBufferFree(cl_mem_in1);
  CLBufferFree(cl_mem_in2);
  CLBufferFree(cl_mem_out);
  CLKernelFree(cl_krn);
  CLProgramFree(cl_prg);
  CLContextFree(cl_ctx);
 }

Детальное объяснение OpenCL-кода из данного примера приведено в статье "OpenCL: от наивного кодирования - к более осмысленному".

Еще немного улучшений

В 3390 билде мы также сняли два ограничения при работе с OpenCL, которые могли затруднять использование GPU.

Теперь максимальное количество объектов OpenCL может достигать 65536, ранее было ограничение в 256. Хэндлы на OpenCL-объекты в MQL5-программе создаются с помощью функций CLContextCreate, CLBufferCreate и CLProgramCreate. Прежнее ограничение в 256 хэндлов не позволяло эффективно работать в методах машинного обучения.

Также теперь разрешено использование OpenCL на картах без поддержки double. Ранее в MQL5-программах безусловно использовались только GPU с поддержкой double, хотя множество задач допускают и предназначены для расчетов с использованием float. Тип float изначально считается родным для проведения параллельных вычислений, так как занимает меньше места. Теперь это требование убрано.

Если для решения задачи требуется использовать только GPU с поддержкой double, то это можно явно указать при вызове CLContextCreate с помощью нового значения CL_USE_GPU_DOUBLE_ONLY (разрешается использовать только устройства, которые поддерживают вычисления с типом double).

   int cl_ctx;
//--- инициализация OpenCL контекста
   if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
     {
      Print("OpenCL not found");
      return;
     }

Хотя данные изменения по работе с OpenCL не связаны напрямую с матрицами и векторами, но они также являются результатом наших усилий по развитию языка MQL5 под нужды машинного обучения.

Будущее MQL5 в машинном обучении

За последние годы мы сделали многое по внедрению передовых технологий в язык MQL5:

Портировали библиотеку численных методов ALGLIB на MQL5
Добавили математическую библиотеку с нечеткой логикой и статистическими функциями
Реализовали графическую библиотеку как аналог функции plot
Сделали интеграцию с Python — теперь питоновские скрипты можно запускать прямо в терминале
Добавили DirectX-функции для создания 3D-графики
Внедрили нативную поддержку SQLite для работы с базами данных
Добавили новые типы данных — матрицы и векторы — с реализацией всех необходимых методов

Язык MQL5 будет продолжать развиваться, и приоритетным направлением является машинное обучение. У нас большие планы, и мы не останавливаемся на достигнутом. Оставайтесь с нами, поддерживайте нас и учитесь новому вместе с нами.

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (63)

Aleksey Vyazmikin | 24 июл. 2023 в 01:56

Прошу разъяснить, как скопировать столбец из одной матрицы в другую!

Пример через копирования в вектор не понимаю.

vector matrix::Col(
  const ulong   ncol      // номер столбца
   );
 
void matrix::Col(
  const vector  v,        // вектор столбец
  const ulong   ncol      // номер столбца
   );

Вот кусок моего кода

   for(P=0; P<Type_Q_Perebor; P++)
   {
      matrixf m_Data_calc;//Матрица с таблицей для вычислений
      vectorf V_Data_calc;//Вектор для передачи массива в матрицу
      switch(P)
      {
      case 0:
         m_Data_calc.Init(Strok_Total_Data*N_1, 1);//Инициализировали матрицу
         m_Data.Reshape(Strok_Total_Data, Stolb_Total_Data);//Имзенили размер матрицы вместе с данными
         break;
      case 1:
         m_Data_calc.Init(Strok_Total_Data*N_0, 1);//Инициализировали матрицу
         m_Data.Reshape(Strok_Total_Data, Stolb_Total_Data);//Имзенили размер матрицы вместе с данными
         break;
      }

      V_Data_calc.Cov(m_Data_calc,0);//Скопировали вектор-столбец из матрицы
      m_Data_calc.Col(V_Data_calc,0);//Скопировали вектор-столбец в матрицу
   }

Получаю ошибку

'Cov' - wrong parameters count  Tree_Analiz_Bi_V_2_4.mq5        219     19
   built-in: matrixf vectorf:Cov(const vectorf&)        Tree_Analiz_Bi_V_2_4.mq5        219     19

Denis Kirichenko | 24 июл. 2023 в 09:18

Это из другой оперы:

V_Data_calc.Cov(m_Data_calc,0);

Наверное нужно как-то так:

V_Data_calc = m_Data_calc.Col(0); //Получили вектор-столбец из матрицы

Aleksey Vyazmikin | 24 июл. 2023 в 15:27

Denis Kirichenko #:

Это из другой оперы:

Наверное нужно как-то так:

Спасибо! А как можно было догадаться, что делать нужно именно так?

Rashid Umarov | 24 июл. 2023 в 16:18

Aleksey Vyazmikin #:

Спасибо! А как можно было догадаться, что делать нужно именно так?

Я тоже не могу понять, как может вычисление ковариации помочь в копировании - Cov

Aleksey Vyazmikin | 24 июл. 2023 в 16:44

Rashid Umarov #:

Я тоже не могу понять, как может вычисление ковариации помочь в копировании - Cov

Вроде понятно, что я описался на форуме - ведь код из справки привёл верно.

Нейросети — это просто (Часть 30): Генетические алгоритмы

Сегодня я хочу познакомить Вас с немного иным методом обучения. Можно сказать, что он заимствован из теории эволюции Дарвина. Наверное, он менее контролируем в сравнении с рассмотренными ранее методами. Но при этом позволяет обучать и недифференцируемые модели.

DoEasy. Элементы управления (Часть 18): Готовим функционал для прокрутки вкладок в TabControl

В статье разместим кнопки управления прокруткой заголовков в WinForms-объекте TabControl на своих местах в случае, если строка заголовков не умещается по размеру элемента управления, и сделаем смещение строки заголовков при щелчке по обрезанному заголовку вкладки.

DoEasy. Элементы управления (Часть 19): Прокрутка вкладок в элементе TabControl, события WinForms-объектов

В статье создадим функционал для прокрутки заголовков вкладок в элементе управления TabControl при помощи кнопок управления прокруткой. Функционал будет работать для расположения заголовков вкладок в одну строку с любой из сторон элемента управления.

Нейросети — это просто (Часть 29): Алгоритм актор-критик с преимуществом (Advantage actor-critic)

В предыдущих статьях данной серии мы познакомились с 2-мя алгоритмами обучения с подкреплением. Каждый из них обладает своими достоинствами и недостатками. Как часто бывает в таких случаях, появляется идея совместить оба метода в некий алгоритм, который бы вобрал в себя лучшее из двух. И тем самым компенсировать недостатки каждого из них. О таком методе мы и поговорим в этой статье.