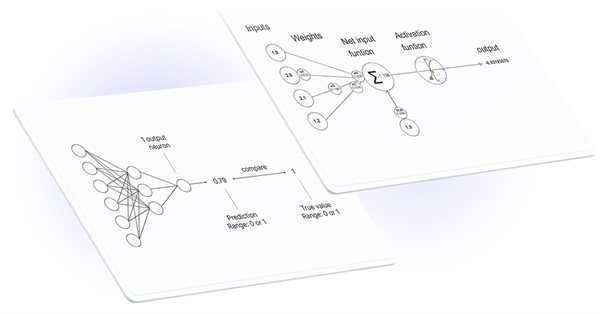
Matrix and Vector operations in MQL5
Special data types — matrices and vectors — have been added to the MQL5 language to solve a large class of mathematical problems. The new types offer built-in methods for creating concise and understandable code that is close to mathematical notation. In this article, we provide a brief description of built-in methods from the Matrix and vector methods help section.
Contents
- Matrix and vector types
- Creation and initialization
- Copying matrices and arrays
- Copying timeseries to matrices or vectors
- Matrix and vector operations
- Manipulations
- Products
- Transformations
- Statistics
- Features
- Solving equations
- Machine Learning methods
- Improvements in OpenCL
- The future of MQL5 in Machine Learning
Every programming language offers array data types which store sets of numeric variables, including int, double and others. Array elements are accessed by index which enables array operations using loops. The most commonly used are one-dimensional and two-dimensional arrays:
int a[50]; // One-dimensional array of 50 integers double m[7][50]; // Two-dimensional array of 7 subarrays, each consisting of 50 integers MyTime t[100]; // Array containing elements of MyTime type
The capabilities of arrays are usually enough for relatively simple tasks related to data storing and processing. But when it comes to complex mathematical problems, working with arrays becomes difficult in terms of both programming and code reading, due to the large number of nested loops. Even the simplest linear algebra operations require excessive coding and a good understanding of mathematics.
Modern data technologies such as machine learning, neural networks and 3D graphics, widely use linear algebra solutions associated with the concepts of vectors and matrices. To facilitate operations with such objects, MQL5 provides special data types: matrices and vectors. The new types eliminate a lot of routine programming operations and improve code quality.
Matrix and vector types
In short, a vector is a one-dimensional double-type array, and a matrix is a two-dimensional double-type array. Vectors can be vertical and horizontal; however, they are not separated in MQL5.
A matrix can be represented as an array of horizontal vectors, in which the first index is the row number, and the second index is the column number.
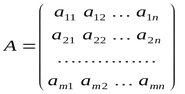
Row and column numbering starts from 0, similar to arrays.
In addition to 'matrix' and 'vector' types which contain double-type data, there are four more types for operations with the relevant data types:
- matrixf — a matrix containing float elements
- matrixc — a matrix containing complex elements
- vectorf — a vector containing float elements
- vectorc — a vector containing complex elements
At the time of this writing, work on the matrixc and vectorc types has not yet been completed, and thus it is not yet possible to use these types in built-in methods.
Template functions support notations like matrix<double>, matrix<float>, vector<double>, vector<float> instead of the corresponding types.
vectorf v_f1= {0, 1, 2, 3,}; vector<float> v_f2=v_f1; Print("v_f2 = ", v_f2); /* v_f2 = [0,1,2,3] */
Creation and initialization
Matrix and vector methods are divided into nine categories according to their purpose. There are several ways to declare and initialize matrices and vectors.
The simplest creation method is declaration without size specification, that is, without memory allocation for the data. Here, we just write the data type and the variable name:
matrix matrix_a; // double type matrix matrix<double> matrix_a1; // another way to declare a double matrix, suitable for use in templates matrix<float> matrix_a3; // float type matrix vector vector_a; // double type vector vector<double> vector_a1; // another notation to create a double vector vector<float> vector_a3; // float type vector
Then you can change the size of the created objects and fill them with the desired values. They can also be used in built-in matrix methods to obtain calculation results.
A matrix or a vector can be declared with the specified size, while allocating memory for the data but not initializing anything. Here, after the variable name, specify the size(s) in parentheses:
matrix matrix_a(128,128); // the parameters can be either constants matrix<double> matrix_a1(InpRows,InpCols); // or variables matrix<float> matrix_a3(InpRows,1); // analogue of a vertical vector vector vector_a(256); vector<double> vector_a1(InpSize); vector<float> vector_a3(InpSize+16); // expression can be used as a parameter
The third way to create objects is to declare with initialization. In this case, matrix and vector sizes are determined by the initialization sequence indicated in curly braces:
matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}}; matrix<double> matrix_a1=matrix_a; // the matrices must be of the same type matrix<float> matrix_a3={{1,2},{3,4}}; vector vector_a={-5,-4,-3,-2,-1,0,1,2,3,4,5}; vector<double> vector_a1={1,5,2.4,3.3}; vector<float> vector_a3=vector_a2; // the vectors must be of the same type
There are also static methods for creating matrices and vectors of the specified size, initialized in a certain way:
matrix matrix_a =matrix::Eye(4,5,1); matrix<double> matrix_a1=matrix::Full(3,4,M_PI); matrixf matrix_a2=matrixf::Identity(5,5); matrixf<float> matrix_a3=matrixf::Ones(5,5); matrix matrix_a4=matrix::Tri(4,5,-1); vector vector_a =vector::Ones(256); vectorf vector_a1=vector<float>::Zeros(16); vector<float> vector_a2=vectorf::Full(128,float_value);
In addition, there are non-static methods for initializing a matrix or a vector with the given values — Init and Fill:
matrix m(2, 2); m.Fill(10); Print("matrix m \n", m); /* matrix m [[10,10] [10,10]] */ m.Init(4, 6); Print("matrix m \n", m); /* matrix m [[10,10,10,10,0.0078125,32.00000762939453] [0,0,0,0,0,0] [0,0,0,0,0,0] [0,0,0,0,0,0]] */
In this example, we used the Init method to change the sizes of an already initialized matrix, due to which all new elements were filled with random values.
An important advantage of the Init method is the ability to specify an initializing function in parameters to fill matrix/vector elements according to this rule. For example:
void OnStart() { //--- matrix init(3, 6, MatrixSetValues); Print("init = \n", init); /* Execution result init = [[1,2,4,8,16,32] [64,128,256,512,1024,2048] [4096,8192,16384,32768,65536,131072]] */ } //+------------------------------------------------------------------+ //| Fills the matrix with powers of a number | //+------------------------------------------------------------------+ void MatrixSetValues(matrix& m, double initial=1) { double value=initial; for(ulong r=0; r<m.Rows(); r++) { for(ulong c=0; c<m.Cols(); c++) { m[r][c]=value; value*=2; } } }
Copying matrices and arrays
Matrices and vectors can be copied using the Copy method. But a simpler and a more familiar way to copy these data types is to use the assignment operator "=". Also, you can use the Assign method for copying.
//--- copying matrices matrix a= {{2, 2}, {3, 3}, {4, 4}}; matrix b=a+2; matrix c; Print("matrix a \n", a); Print("matrix b \n", b); c.Assign(b); Print("matrix c \n", c); /* matrix a [[2,2] [3,3] [4,4]] matrix b [[4,4] [5,5] [6,6]] matrix c [[4,4] [5,5] [6,6]] */
The difference of Assign from Copy is that it can be used for both matrices and arrays. The example below shows copying of the integer array int_arr into a double matrix. The resulting matrix automatically adjusts according to the size of the copied array.
//--- copying an array to a matrix matrix double_matrix=matrix::Full(2,10,3.14); Print("double_matrix before Assign() \n", double_matrix); int int_arr[5][5]= {{1, 2}, {3, 4}, {5, 6}}; Print("int_arr: "); ArrayPrint(int_arr); double_matrix.Assign(int_arr); Print("double_matrix after Assign(int_arr) \n", double_matrix); /* double_matrix before Assign() [[3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14] [3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14,3.14]] int_arr: [,0][,1][,2][,3][,4] [0,] 1 2 0 0 0 [1,] 3 4 0 0 0 [2,] 5 6 0 0 0 [3,] 0 0 0 0 0 [4,] 0 0 0 0 0 double_matrix after Assign(int_arr) [[1,2,0,0,0] [3,4,0,0,0] [5,6,0,0,0] [0,0,0,0,0] [0,0,0,0,0]] */ }
The Assign method enables seamless transition from arrays to matrices, with the automated size and type casting.
Copying timeseries to matrices or vectors
Price chart analysis implies operations with MqlRates structure arrays. MQL5 provides a new method for working with such price data structures.
The CopyRates method copies historical series of the MqlRates structure directly into a matrix or vector. Thus, you can avoid the need to get the required timeseries into the relevant arrays using functions from the Timeseries and indicator access section. Also, there is no need to transfer them to a matrix or vector. With the CopyRates method, you can receive quotes into a matrix or vector in just one call. Let's consider an example of how to calculate a correlation matrix for a list of symbols: let's calculate these values using two different methods and compare the results.
input int InBars=100; input ENUM_TIMEFRAMES InTF=PERIOD_H1; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- list of symbols for calculation string symbols[]= {"EURUSD", "GBPUSD", "USDJPY", "USDCAD", "USDCHF"}; int size=ArraySize(symbols); //--- matrix and vector to receive Close prices matrix rates(InBars, size); vector close; for(int i=0; i<size; i++) { //--- get Close prices to a vector if(close.CopyRates(symbols[i], InTF, COPY_RATES_CLOSE, 1, InBars)) { //--- insert the vector to the timeseries matrix rates.Col(close, i); PrintFormat("%d. %s: %d Close prices were added to matrix", i+1, symbols[i], close.Size()); //--- output the first 20 vector values for debugging int digits=(int)SymbolInfoInteger(symbols[i], SYMBOL_DIGITS); Print(VectorToString(close, 20, digits)); } else { Print("vector.CopyRates(%d,COPY_RATES_CLOSE) failed. Error ", symbols[i], GetLastError()); return; } } /* 1. EURUSD: 100 Close prices were added to the matrix 0.99561 0.99550 0.99674 0.99855 0.99695 0.99555 0.99732 1.00305 1.00121 1.069 0.99936 1.027 1.00130 1.00129 1.00123 1.00201 1.00222 1.00111 1.079 1.030 ... 2. GBPUSD: 100 Close prices were added to the matrix 1.13733 1.13708 1.13777 1.14045 1.13985 1.13783 1.13945 1.14315 1.14172 1.13974 1.13868 1.14116 1.14239 1.14230 1.14160 1.14281 1.14338 1.14242 1.14147 1.14069 ... 3. USDJPY: 100 Close prices were added to the matrix 143.451 143.356 143.310 143.202 143.079 143.294 143.146 142.963 143.039 143.032 143.039 142.957 142.904 142.956 142.920 142.837 142.756 142.928 143.130 143.069 ... 4. USDCAD: 100 Close prices were added to the matrix 1.32840 1.32877 1.32838 1.32660 1.32780 1.33068 1.33001 1.32798 1.32730 1.32782 1.32951 1.32868 1.32716 1.32663 1.32629 1.32614 1.32586 1.32578 1.32650 1.32789 ... 5. USDCHF: 100 Close prices were added to the matrix 0.96395 0.96440 0.96315 0.96161 0.96197 0.96337 0.96358 0.96228 0.96474 0.96529 0.96529 0.96502 0.96463 0.96429 0.96378 0.96377 0.96314 0.96428 0.96483 0.96509 ... */ //--- prepare a matrix of correlations between symbols matrix corr_from_vector=matrix::Zeros(size, size); Print("Compute pairwise correlation coefficients"); for(int i=0; i<size; i++) { for(int k=i; k<size; k++) { vector v1=rates.Col(i); vector v2=rates.Col(k); double coeff = v1.CorrCoef(v2); PrintFormat("corr(%s,%s) = %.3f", symbols[i], symbols[k], coeff); corr_from_vector[i][k]=coeff; } } Print("Correlation matrix on vectors: \n", corr_from_vector); /* Calculate pairwise correlation coefficients corr(EURUSD,EURUSD) = 1.000 corr(EURUSD,GBPUSD) = 0.974 corr(EURUSD,USDJPY) = -0.713 corr(EURUSD,USDCAD) = -0.950 corr(EURUSD,USDCHF) = -0.397 corr(GBPUSD,GBPUSD) = 1.000 corr(GBPUSD,USDJPY) = -0.744 corr(GBPUSD,USDCAD) = -0.953 corr(GBPUSD,USDCHF) = -0.362 corr(USDJPY,USDJPY) = 1.000 corr(USDJPY,USDCAD) = 0.736 corr(USDJPY,USDCHF) = 0.083 corr(USDCAD,USDCAD) = 1.000 corr(USDCAD,USDCHF) = 0.425 corr(USDCHF,USDCHF) = 1.000 Correlation matrix on vectors: [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434] [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978] [0,0,1,0.7360546499847362,0.08314381248168941] [0,0,0,0.9999999999999999,0.4247042496841555] [0,0,0,0,1]] */ //--- now let's see how a correlation matrix can be calculated in one line matrix corr_from_matrix=rates.CorrCoef(false); // false means that the vectors are in the matrix columns Print("Correlation matrix rates.CorrCoef(false): \n", corr_from_matrix.TriU()); //--- compare the resulting matrices to find discrepancies Print("How many discrepancy errors between result matrices?"); ulong errors=corr_from_vector.Compare(corr_from_matrix.TriU(), (float)1e-12); Print("corr_from_vector.Compare(corr_from_matrix,1e-12)=", errors); /* Correlation matrix rates.CorrCoef(false): [[1,0.9736363791537366,-0.7126365191640618,-0.9503129578410202,-0.3968181226230434] [0,1,-0.7440448047501974,-0.9525190338388175,-0.3617774666815978] [0,0,1,0.7360546499847362,0.08314381248168941] [0,0,0,1,0.4247042496841555] [0,0,0,0,1]] How many discrepancy errors between result matrices? corr_from_vector.Compare(corr_from_matrix,1e-12)=0 */ //--- create a nice output of the correlation matrix Print("Output the correlation matrix with headers"); string header=" "; // header for(int i=0; i<size; i++) header+=" "+symbols[i]; Print(header); //--- now rows for(int i=0; i<size; i++) { string line=symbols[i]+" "; line+=VectorToString(corr_from_vector.Row(i), size, 3, 8); Print(line); } /* Output the correlation matrix with headers EURUSD GBPUSD USDJPY USDCAD USDCHF EURUSD 1.0 0.974 -0.713 -0.950 -0.397 GBPUSD 0.0 1.0 -0.744 -0.953 -0.362 USDJPY 0.0 0.0 1.0 0.736 0.083 USDCAD 0.0 0.0 0.0 1.0 0.425 USDCHF 0.0 0.0 0.0 0.0 1.0 */ } //+------------------------------------------------------------------+ //| Returns a string with vector values | //+------------------------------------------------------------------+ string VectorToString(const vector &v, int length=20, int digits=5, int width=8) { ulong size=(ulong)MathMin(20, v.Size()); //--- compose a string string line=""; for(ulong i=0; i<size; i++) { string value=DoubleToString(v[i], digits); StringReplace(value, ".000", ".0"); line+=Indent(width-StringLen(value))+value; } //--- add a tail if the vector length exceeds the specified size if(v.Size()>size) line+=" ..."; //--- return(line); } //+------------------------------------------------------------------+ //| Returns a string with the specified number of spaces | //+------------------------------------------------------------------+ string Indent(int number) { string indent=""; for(int i=0; i<number; i++) indent+=" "; return(indent); }
The example shows how to:
- Get Close prices using CopyRates
- Insert a vector into a matrix using the Col method
- Calculate the correlation coefficient between two vectors using CorrCoef
- Calculate the correlation matrix over a matrix with value vectors using CorrCoef
- Return an upper triangular matrix using the TriU method
- Compare two matrices and find discrepancies using Compare
Matrix and vector operations
Element-wise mathematical operations of addition, subtraction, multiplication and division can be performed on matrices and vectors. Both objects in such operations must be of the same type and must have the same sizes. Each element of the matrix or vector operates on the corresponding element of the second matrix or vector.
You can also use a scalar of the appropriate type (double, float or complex) as the second term (multiplier, subtrahend or divisor). In this case, each member of the matrix or vector will operate on the specified scalar.
matrix matrix_a={{0.1,0.2,0.3},{0.4,0.5,0.6}}; matrix matrix_b={{1,2,3},{4,5,6}}; matrix matrix_c1=matrix_a+matrix_b; matrix matrix_c2=matrix_b-matrix_a; matrix matrix_c3=matrix_a*matrix_b; // Hadamard product matrix matrix_c4=matrix_b/matrix_a; matrix_c1=matrix_a+1; matrix_c2=matrix_b-double_value; matrix_c3=matrix_a*M_PI; matrix_c4=matrix_b/0.1; //--- operations in place are possible matrix_a+=matrix_b; matrix_a/=2;
In addition, matrices and vectors can be passed as a second parameter to most mathematical functions, including MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, MathTanh. Such operations imply element-wise handling of matrices or vectors. Example:
//--- matrix a= {{1, 4}, {9, 16}}; Print("matrix a=\n",a); a=MathSqrt(a); Print("MatrSqrt(a)=\n",a); /* matrix a= [[1,4] [9,16]] MatrSqrt(a)= [[1,2] [3,4]] */
For MathMod and MathPow, the second element can be either a scalar or a matrix/vector of the appropriate size.
matrix<T> mat1(128,128); matrix<T> mat3(mat1.Rows(),mat1.Cols()); ulong n,size=mat1.Rows()*mat1.Cols(); ... mat2=MathPow(mat1,(T)1.9); for(n=0; n<size; n++) { T res=MathPow(mat1.Flat(n),(T)1.9); if(res!=mat2.Flat(n)) errors++; } mat2=MathPow(mat1,mat3); for(n=0; n<size; n++) { T res=MathPow(mat1.Flat(n),mat3.Flat(n)); if(res!=mat2.Flat(n)) errors++; } ... vector<T> vec1(16384); vector<T> vec3(vec1.Size()); ulong n,size=vec1.Size(); ... vec2=MathPow(vec1,(T)1.9); for(n=0; n<size; n++) { T res=MathPow(vec1[n],(T)1.9); if(res!=vec2[n]) errors++; } vec2=MathPow(vec1,vec3); for(n=0; n<size; n++) { T res=MathPow(vec1[n],vec3[n]); if(res!=vec2[n]) errors++; }
Manipulations
MQL5 supports the following basic manipulations on matrices and vectors, which do not require any calculations:
- Transposition
- Extracting rows, columns and diagonals
- Resizing and reshaping matrices
- Swapping the specified rows and columns
- Copying to a new object
- Comparing two objects
- Splitting a matrix into multiple submatrices
- Sorting
matrix a= {{0, 1, 2}, {3, 4, 5}}; Print("matrix a \n", a); Print("a.Transpose() \n", a.Transpose()); /* matrix a [[0,1,2] [3,4,5]] a.Transpose() [[0,3] [1,4] [2,5]] */
Below are examples showing how to set and extract a diagonal using the Diag method:
vector v1={1,2,3}; matrix m1; m1.Diag(v1); Print("m1\n",m1); /* m1 [[1,0,0] [0,2,0] [0,0,3]] m2 */ matrix m2; m2.Diag(v1,-1); Print("m2\n",m2); /* m2 [[0,0,0] [1,0,0] [0,2,0] [0,0,3]] */ matrix m3; m3.Diag(v1,1); Print("m3\n",m3); /* m3 [[0,1,0,0] [0,0,2,0] [0,0,0,3]] */ matrix m4=matrix::Full(4,5,9); m4.Diag(v1,1); Print("m4\n",m4); Print("diag -1 - ",m4.Diag(-1)); Print("diag 0 - ",m4.Diag()); Print("diag 1 - ",m4.Diag(1)); /* m4 [[9,1,9,9,9] [9,9,2,9,9] [9,9,9,3,9] [9,9,9,9,9]] diag -1 - [9,9,9] diag 0 - [9,9,9,9] diag 1 - [1,2,3,9] */
Changing a matrix size using the Reshape method:
matrix matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}}; Print("matrix_a\n",matrix_a); /* matrix_a [[1,2,3] [4,5,6] [7,8,9] [10,11,12]] */ matrix_a.Reshape(2,6); Print("Reshape(2,6)\n",matrix_a); /* Reshape(2,6) [[1,2,3,4,5,6] [7,8,9,10,11,12]] */ matrix_a.Reshape(3,5); Print("Reshape(3,5)\n",matrix_a); /* Reshape(3,5) [[1,2,3,4,5] [6,7,8,9,10] [11,12,0,3,0]] */ matrix_a.Reshape(2,4); Print("Reshape(2,4)\n",matrix_a); /* Reshape(2,4) [[1,2,3,4] [5,6,7,8]] */
Examples of a vertical split of a matrix using the Vsplit method:
matrix matrix_a={{ 1, 2, 3, 4, 5, 6}, { 7, 8, 9,10,11,12}, {13,14,15,16,17,18}}; matrix splitted[]; ulong parts[]={2,3}; matrix_a.Vsplit(2,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2,3] [7,8,9] [13,14,15]] splitted 1 [[4,5,6] [10,11,12] [16,17,18]] */ matrix_a.Vsplit(3,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2] [7,8] [13,14]] splitted 1 [[3,4] [9,10] [15,16]] splitted 2 [[5,6] [11,12] [17,18]] */ matrix_a.Vsplit(parts,splitted); for(uint i=0; i<splitted.Size(); i++) Print("splitted ",i,"\n",splitted[i]); /* splitted 0 [[1,2] [7,8] [13,14]] splitted 1 [[3,4,5] [9,10,11] [15,16,17]] splitted 2 [[6] [12] [18]] */
The Col and Row methods allow getting the relevant matrix elements as well as inserting elements into unallocated matrices, i.e. matrices without the specified size. Here is an example:
vector v1={1,2,3}; matrix m1; m1.Col(v1,1); Print("m1\n",m1); /* m1 [[0,1] [0,2] [0,3]] */ matrix m2=matrix::Full(4,5,8); m2.Col(v1,2); Print("m2\n",m2); /* m2 [[8,8,1,8,8] [8,8,2,8,8] [8,8,3,8,8] [8,8,8,8,8]] */ Print("col 1 - ",m2.Col(1)); /* col 1 - [8,8,8,8] */ Print("col 2 - ",m2.Col(2)); /* col 1 - [8,8,8,8] col 2 - [1,2,3,8] */
Products
Matrix multiplication is one of the basic algorithms which is widely used in numerical methods. Many implementations of forward and back-propagation algorithms in neural network convolutional layers are based on this operation. Often, 90-95% of all time spent on machine learning is taken by this operation. All product methods are provided under the Products of matrices and vectors section of the language reference.
The following example shows the multiplication of two matrices using the MatMul method:
matrix a={{1, 0, 0}, {0, 1, 0}}; matrix b={{4, 1}, {2, 2}, {1, 3}}; matrix c1=a.MatMul(b); matrix c2=b.MatMul(a); Print("c1 = \n", c1); Print("c2 = \n", c2); /* c1 = [[4,1] [2,2]] c2 = [[4,1,0] [2,2,0] [1,3,0]] */
An example of the Kronecker product of two matrices or a matrix and a vector, using the Kron method.
matrix a={{1,2,3},{4,5,6}}; matrix b=matrix::Identity(2,2); vector v={1,2}; Print(a.Kron(b)); Print(a.Kron(v)); /* [[1,0,2,0,3,0] [0,1,0,2,0,3] [4,0,5,0,6,0] [0,4,0,5,0,6]] [[1,2,2,4,3,6] [4,8,5,10,6,12]] */
More examples from the article Matrices and Vectors in MQL5:
//--- initialize matrices matrix m35, m52; m35.Init(3,5,Arange); m52.Init(5,2,Arange); //--- Print("1. Product of horizontal vector v[3] and matrix m[3,5]"); vector v3 = {1,2,3}; Print("On the left v3 = ",v3); Print("On the right m35 = \n",m35); Print("v3.MatMul(m35) = horizontal vector v[5] \n",v3.MatMul(m35)); /* 1. Product of horizontal vector v[3] and matrix m[3,5] On the left v3 = [1,2,3] On the right m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] v3.MatMul(m35) = horizontal vector v[5] [40,46,52,58,64] */ //--- show that this is really a horizontal vector Print("\n2. Product of matrix m[1,3] and matrix m[3,5]"); matrix m13; m13.Init(1,3,Arange,1); Print("On the left m13 = \n",m13); Print("On the right m35 = \n",m35); Print("m13.MatMul(m35) = matrix m[1,5] \n",m13.MatMul(m35)); /* 2. Product of matrix m[1,3] and matrix m[3,5] On the left m13 = [[1,2,3]] On the right m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] m13.MatMul(m35) = matrix m[1,5] [[40,46,52,58,64]] */ Print("\n3. Product of matrix m[3,5] and vertical vector v[5]"); vector v5 = {1,2,3,4,5}; Print("On the left m35 = \n",m35); Print("On the right v5 = ",v5); Print("m35.MatMul(v5) = vertical vector v[3] \n",m35.MatMul(v5)); /* 3. Product of matrix m[3,5] and vertical vector v[5] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right v5 = [1,2,3,4,5] m35.MatMul(v5) = vertical vector v[3] [40,115,190] */ //--- show that this is really a vertical vector Print("\n4. Product of matrix m[3,5] and matrix m[5,1]"); matrix m51; m51.Init(5,1,Arange,1); Print("On the left m35 = \n",m35); Print("On the right m51 = \n",m51); Print("m35.MatMul(m51) = matrix v[3] \n",m35.MatMul(m51)); /* 4. Product of matrix m[3,5] and matrix m[5,1] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right m51 = [[1] [2] [3] [4] [5]] m35.MatMul(m51) = matrix v[3] [[40] [115] [190]] */ Print("\n5. Product of matrix m[3,5] and matrix m[5,2]"); Print("On the left m35 = \n",m35); Print("On the right m52 = \n",m52); Print("m35.MatMul(m52) = matrix m[3,2] \n",m35.MatMul(m52)); /* 5. Product of matrix m[3,5] and matrix m[5,2] On the left m35 = [[0,1,2,3,4] [5,6,7,8,9] [10,11,12,13,14]] On the right m52 = [[0,1] [2,3] [4,5] [6,7] [8,9]] m35.MatMul(m52) = matrix m[3,2] [[60,70] [160,195] [260,320]] */ Print("\n6. Product of horizontal vector v[5] and matrix m[5,2]"); Print("On the left v5 = \n",v5); Print("On the right m52 = \n",m52); Print("v5.MatMul(m52) = horizontal vector v[2] \n",v5.MatMul(m52)); /* 6. The product of horizontal vector v[5] and matrix m[5,2] On the left v5 = [1,2,3,4,5] On the right m52 = [[0,1] [2,3] [4,5] [6,7] [8,9]] v5.MatMul(m52) = horizontal vector v[2] [80,95] */ Print("\n7. Outer() product of horizontal vector v[5] and vertical vector v[3]"); Print("On the left v5 = \n",v5); Print("On the right v3 = \n",v3); Print("v5.Outer(v3) = matrix m[5,3] \n",v5.Outer(v3)); /* 7. Outer() product of horizontal vector v[5] and vertical vector v[3] On the left v5 = [1,2,3,4,5] On the right v3 = [1,2,3] v5.Outer(v3) = matrix m[5,3] [[1,2,3] [2,4,6] [3,6,9] [4,8,12] [5,10,15]] */
Transformations
Matrix transformations are often used in data operations. However, many complex matrix operations cannot be solved efficiently or stably due to the limited accuracy of computers.
Matrix transformations (or decompositions) are methods which reduce a matrix into its component parts, which makes it easier to calculate more complex matrix operations. Matrix decomposition methods, also referred to as matrix factorization methods, are the backbone of linear algebra in computers, even for basic operations such as linear equation solving systems, calculating the inverse, and calculating the determinant of a matrix.
Machine learning widely uses Singular Value Decomposition (SVD), which enables the representation of the original matrix as the product of three other matrices. SVD is used to solve a variety of problems, from least squares approximation to compression and image recognition.
An example of a Singular Value Decomposition by the SVD method:
matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}}; a=a-4; Print("matrix a \n", a); a.Reshape(3, 3); matrix b=a; Print("matrix b \n", b); //--- execute SVD decomposition matrix U, V; vector singular_values; b.SVD(U, V, singular_values); Print("U \n", U); Print("V \n", V); Print("singular_values = ", singular_values); // check block //--- U * singular diagonal * V = A matrix matrix_s; matrix_s.Diag(singular_values); Print("matrix_s \n", matrix_s); matrix matrix_vt=V.Transpose(); Print("matrix_vt \n", matrix_vt); matrix matrix_usvt=(U.MatMul(matrix_s)).MatMul(matrix_vt); Print("matrix_usvt \n", matrix_usvt); ulong errors=(int)b.Compare(matrix_usvt, 1e-9); double res=(errors==0); Print("errors=", errors); //---- another check matrix U_Ut=U.MatMul(U.Transpose()); Print("U_Ut \n", U_Ut); Print("Ut_U \n", (U.Transpose()).MatMul(U)); matrix vt_V=matrix_vt.MatMul(V); Print("vt_V \n", vt_V); Print("V_vt \n", V.MatMul(matrix_vt)); /* matrix a [[-4,-3,-2,-1,0,1,2,3,4]] matrix b [[-4,-3,-2] [-1,0,1] [2,3,4]] U [[-0.7071067811865474,0.5773502691896254,0.408248290463863] [-6.827109697437648e-17,0.5773502691896253,-0.8164965809277256] [0.7071067811865472,0.5773502691896255,0.4082482904638627]] V [[0.5773502691896258,-0.7071067811865474,-0.408248290463863] [0.5773502691896258,1.779939029415334e-16,0.8164965809277258] [0.5773502691896256,0.7071067811865474,-0.408248290463863]] singular_values = [7.348469228349533,2.449489742783175,3.277709923350408e-17] matrix_s [[7.348469228349533,0,0] [0,2.449489742783175,0] [0,0,3.277709923350408e-17]] matrix_vt [[0.5773502691896258,0.5773502691896258,0.5773502691896256] [-0.7071067811865474,1.779939029415334e-16,0.7071067811865474] [-0.408248290463863,0.8164965809277258,-0.408248290463863]] matrix_usvt [[-3.999999999999997,-2.999999999999999,-2] [-0.9999999999999981,-5.977974170712231e-17,0.9999999999999974] [2,2.999999999999999,3.999999999999996]] errors=0 U_Ut [[0.9999999999999993,-1.665334536937735e-16,-1.665334536937735e-16] [-1.665334536937735e-16,0.9999999999999987,-5.551115123125783e-17] [-1.665334536937735e-16,-5.551115123125783e-17,0.999999999999999]] Ut_U [[0.9999999999999993,-5.551115123125783e-17,-1.110223024625157e-16] [-5.551115123125783e-17,0.9999999999999987,2.498001805406602e-16] [-1.110223024625157e-16,2.498001805406602e-16,0.999999999999999]] vt_V [[1,-5.551115123125783e-17,0] [-5.551115123125783e-17,0.9999999999999996,1.110223024625157e-16] [0,1.110223024625157e-16,0.9999999999999996]] V_vt [[0.9999999999999999,1.110223024625157e-16,1.942890293094024e-16] [1.110223024625157e-16,0.9999999999999998,1.665334536937735e-16] [1.942890293094024e-16,1.665334536937735e-16,0.9999999999999996] */ }
Another commonly used transformation is the Cholesky decomposition, which can be used to solve a system of linear equations Ax=b if the matrix A is symmetric and positive definite.
In MQL5, the Cholesky decomposition is executed by the Cholesky method:
matrix matrix_a= {{5.7998084, -2.1825367}, {-2.1825367, 9.85910595}}; matrix matrix_l; Print("matrix_a\n", matrix_a); matrix_a.Cholesky(matrix_l); Print("matrix_l\n", matrix_l); Print("check\n", matrix_l.MatMul(matrix_l.Transpose())); /* matrix_a [[5.7998084,-2.1825367] [-2.1825367,9.85910595]] matrix_l [[2.408279136645086,0] [-0.9062640068544704,3.006291985133859]] check [[5.7998084,-2.1825367] [-2.1825367,9.85910595]] */
The below table shows the list of available methods:
| Function | Action |
|---|---|
| Computes the Cholesky decomposition | |
| Computes the eigenvalues and right eigenvectors of a square matrix | |
| Computes the eigenvalues of a general matrix | |
| LU factorization of a matrix as the product of a lower triangular matrix and an upper triangular matrix | |
| LUP factorization with partial pivoting, which refers to LU decomposition with row permutations only: PA=LU | |
| Compute the qr factorization of a matrix | |
| Singular Value Decomposition |
Obtaining statistics
- Maximum and minimum values, along with their indices in a matrix/vector
- The sum and product of elements, as well as the cumulative sum and product
- Median, mean, arithmetic mean and weighted arithmetic mean of matrix/vector values
- Standard deviation and element variance
- Percentiles and quantiles
- Regression metric as the deviation error from the regression line constructed on the specified data array
An example of calculating the standard deviation by the Std method:
matrixf matrix_a={{10,3,2},{1,8,12},{6,5,4},{7,11,9}};
Print("matrix_a\n",matrix_a);
vectorf cols_std=matrix_a.Std(0);
vectorf rows_std=matrix_a.Std(1);
float matrix_std=matrix_a.Std();
Print("cols_std ",cols_std);
Print("rows_std ",rows_std);
Print("std value ",matrix_std);
/*
matrix_a
[[10,3,2]
[1,8,12]
[6,5,4]
[7,11,9]]
cols_std [3.2403703,3.0310888,3.9607449]
rows_std [3.5590262,4.5460606,0.81649661,1.6329932]
std value 3.452052593231201
*/
Calculating quantiles by the Quantile method:
matrixf matrix_a={{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
Print("matrix_a\n",matrix_a);
vectorf cols_percentile=matrix_a.Percentile(50,0);
vectorf rows_percentile=matrix_a.Percentile(50,1);
float matrix_percentile=matrix_a.Percentile(50);
Print("cols_percentile ",cols_percentile);
Print("rows_percentile ",rows_percentile);
Print("percentile value ",matrix_percentile);
/*
matrix_a
[[1,2,3]
[4,5,6]
[7,8,9]
[10,11,12]]
cols_percentile [5.5,6.5,7.5]
rows_percentile [2,5,8,11]
percentile value 6.5
*/
Matrix characteristics
Use methods from the Characteristics section to obtain the following values:
- The number of rows and columns in a matrix
- Norm and condition number
- Determinant, rank, trace and spectrum of a matrix
Calculating the rank of a matrix using the Rank method:
matrix a=matrix::Eye(4, 4);; Print("matrix a \n", a); Print("a.Rank()=", a.Rank()); matrix I=matrix::Eye(4, 4); I[3, 3] = 0.; // matrix deficit Print("I \n", I); Print("I.Rank()=", I.Rank()); matrix b=matrix::Ones(1, 4); Print("b \n", b); Print("b.Rank()=", b.Rank());;// 1 size - rank 1, unless all 0 matrix zeros=matrix::Zeros(4, 1); Print("zeros \n", zeros); Print("zeros.Rank()=", zeros.Rank()); /* matrix a [[1,0,0,0] [0,1,0,0] [0,0,1,0] [0,0,0,1]] a.Rank()=4 I [[1,0,0,0] [0,1,0,0] [0,0,1,0] [0,0,0,0]] I.Rank()=3 b [[1,1,1,1]] b.Rank()=1 zeros [[0] [0] [0] [0]] zeros.Rank()=0 */
Calculating a norm using the Norm method:
matrix a= {{0, 1, 2, 3, 4, 5, 6, 7, 8}}; a=a-4; Print("matrix a \n", a); a.Reshape(3, 3); matrix b=a; Print("matrix b \n", b); Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_FROBENIUS)); Print("b.Norm(MATRIX_NORM_FROBENIUS)=", b.Norm(MATRIX_NORM_FROBENIUS)); Print("b.Norm(MATRIX_NORM_INF)", b.Norm(MATRIX_NORM_INF)); Print("b.Norm(MATRIX_NORM_MINUS_INF)", b.Norm(MATRIX_NORM_MINUS_INF)); Print("b.Norm(MATRIX_NORM_P1)=)", b.Norm(MATRIX_NORM_P1)); Print("b.Norm(MATRIX_NORM_MINUS_P1)=", b.Norm(MATRIX_NORM_MINUS_P1)); Print("b.Norm(MATRIX_NORM_P2)=", b.Norm(MATRIX_NORM_P2)); Print("b.Norm(MATRIX_NORM_MINUS_P2)=", b.Norm(MATRIX_NORM_MINUS_P2)); /* matrix a [[-4,-3,-2,-1,0,1,2,3,4]] matrix b [[-4,-3,-2] [-1,0,1] [2,3,4]] b.Norm(MATRIX_NORM_P2)=7.745966692414834 b.Norm(MATRIX_NORM_FROBENIUS)=7.745966692414834 b.Norm(MATRIX_NORM_INF)9.0 b.Norm(MATRIX_NORM_MINUS_INF)2.0 b.Norm(MATRIX_NORM_P1)=)7.0 b.Norm(MATRIX_NORM_MINUS_P1)=6.0 b.Norm(MATRIX_NORM_P2)=7.348469228349533 b.Norm(MATRIX_NORM_MINUS_P2)=1.857033188519056e-16 */
Solving equations
Machine learning methods and optimization problems often require finding the solutions to a system of linear equations. The Solutions section contains four methods which allow the solution of such equations depending on the matrix type.
| Function | Action |
|---|---|
| Solve a linear matrix equation or a system of linear algebraic equations | |
| Return the least-squares solution of linear algebraic equations (for non-square or degenerate matrices) | |
| Compute the multiplicative inverse of a square invertible matrix by the Jordan-Gauss method | |
| Compute the pseudo-inverse of a matrix by the Moore-Penrose method |

We need to find the solution vector x. The matrix A is not square and therefore the Solve method cannot be used here.
We will use the LstSq method which enables the approximate solving of non-square or degenerate matrices.matrix a={{3, 2}, {4,-5}, {3, 3}}; vector b={7,40,3}; //--- solve the system A*x = b vector x=a.LstSq(b); //--- check the solution, x must be equal to [5, -4] Print("x=", x); /* x=[5.00000000,-4] */ //--- check A*x = b1, the resulting vector must be [7, 40, 3] vector b1=a.MatMul(x); Print("b11=",b1); /* b1=[7.0000000,40.0000000,3.00000000] */
The check has shown that the found vector x is the solution of this system of equations.
Machine Learning methods
There are three matrix and vector methods which can be used in machine learning.
| Function | Action |
|---|---|
| Compute activation function values and write them to the passed vector/matrix | |
| Compute activation function derivative values and write them to the passed vector/matrix | |
| Compute loss function values and write them to the passed vector/matrix |
Activation functions are used in neural networks to find an output depending on the weighted sum of inputs. The selection of the activation function has a big impact on the neural network performance.
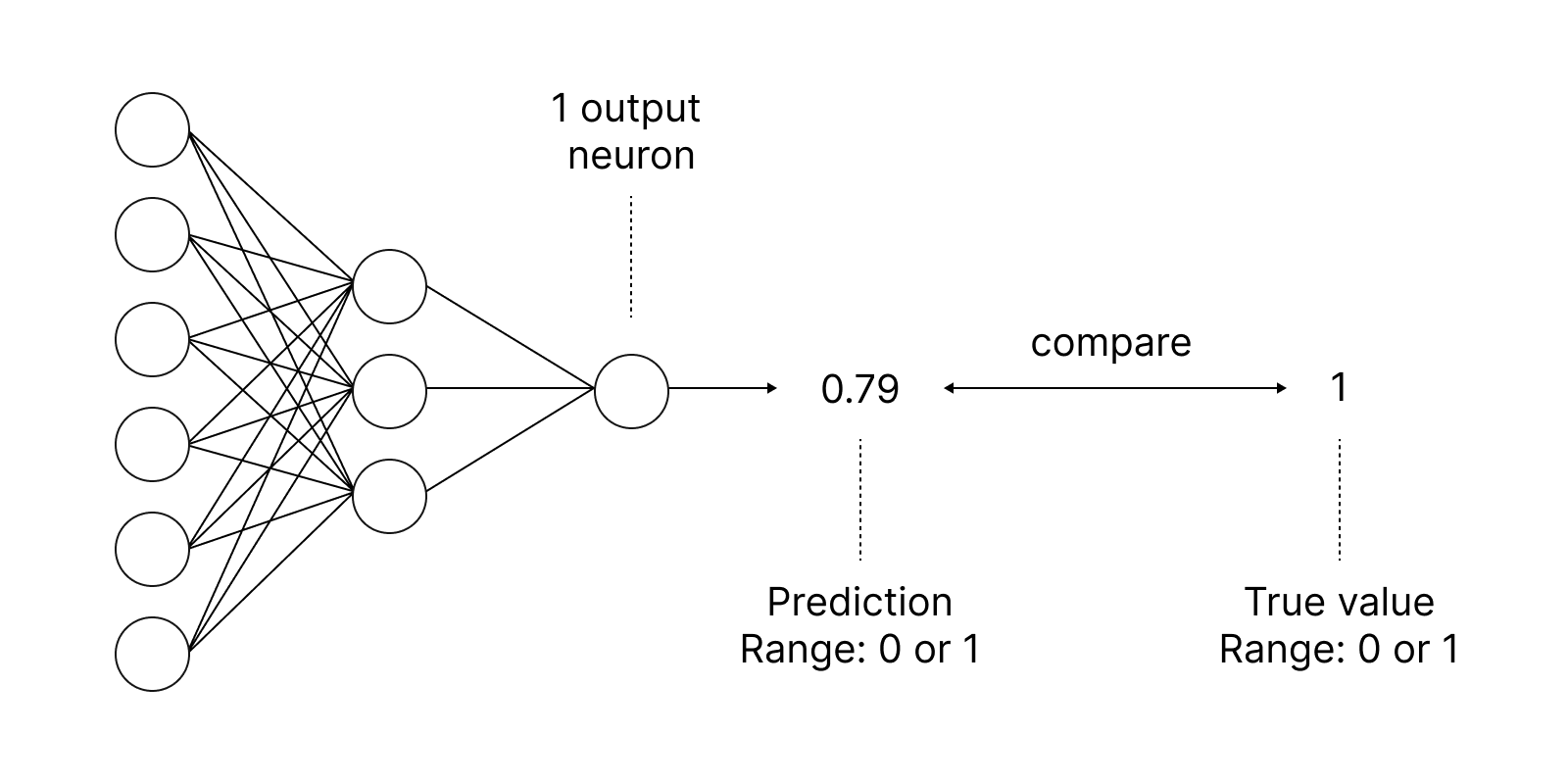
One of the most popular activation functions is the sigmoid.
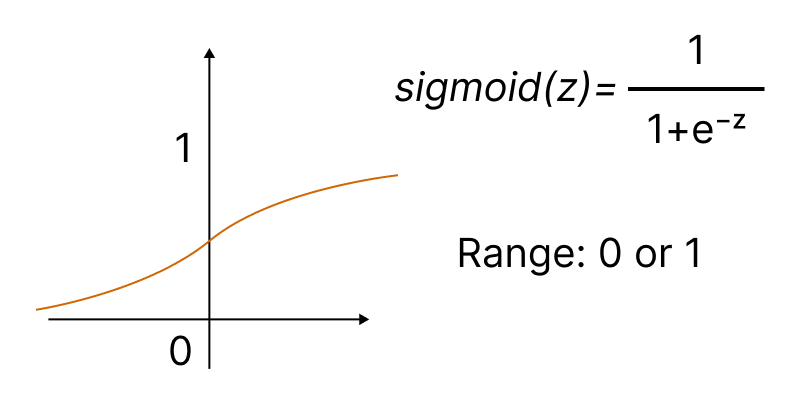
The built-in Activation method allows setting one of the fifteen types of the activation function. All of them are available in the ENUM_ACTIVATION_FUNCTION enumeration.
| ID | Description |
|---|---|
| AF_ELU | Exponential Linear Unit |
| AF_EXP | Exponential |
| AF_GELU | Gaussian Error Linear Unit |
| AF_HARD_SIGMOID | Hard Sigmoid |
| AF_LINEAR | Linear |
| AF_LRELU | Leaky Rectified Linear Unit |
| AF_RELU | Rectified Linear Unit |
| AF_SELU | Scaled Exponential Linear Unit |
| AF_SIGMOID | Sigmoid |
| AF_SOFTMAX | Softmax |
| AF_SOFTPLUS | Softplus |
| AF_SOFTSIGN | Softsign |
| AF_SWISH | Swish |
| AF_TANH | The hyperbolic tangent function |
| AF_TRELU | Thresholded Rectified Linear Unit |
A neural network aims at finding an algorithm that minimizes the error in learning, for which the loss function is used. The deviation is computed using the Loss method for which you can specify one of fourteen types from the ENUM_LOSS_FUNCTION enumeration.
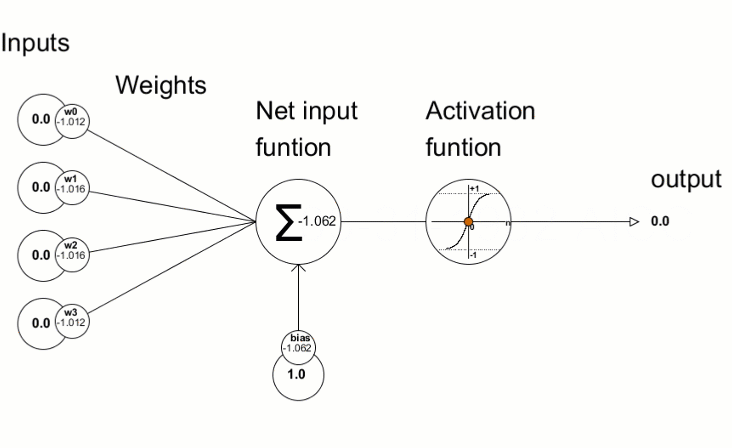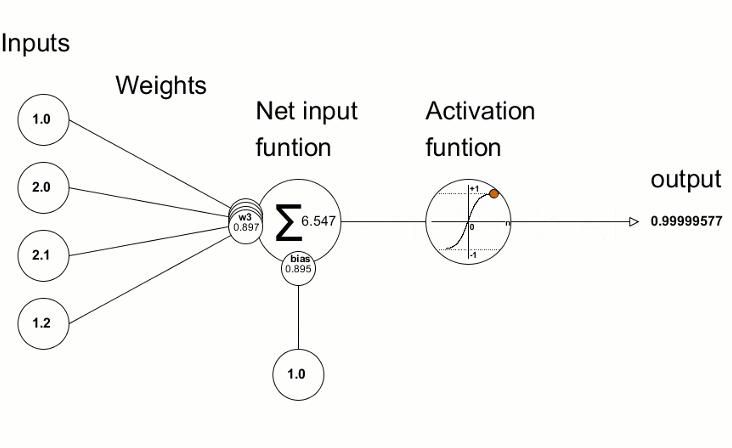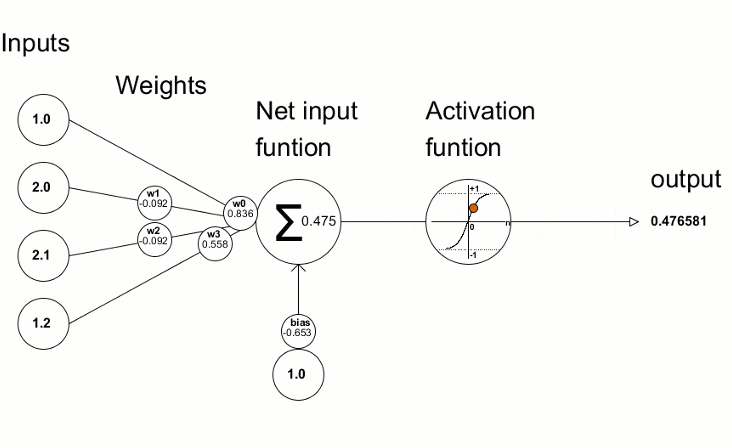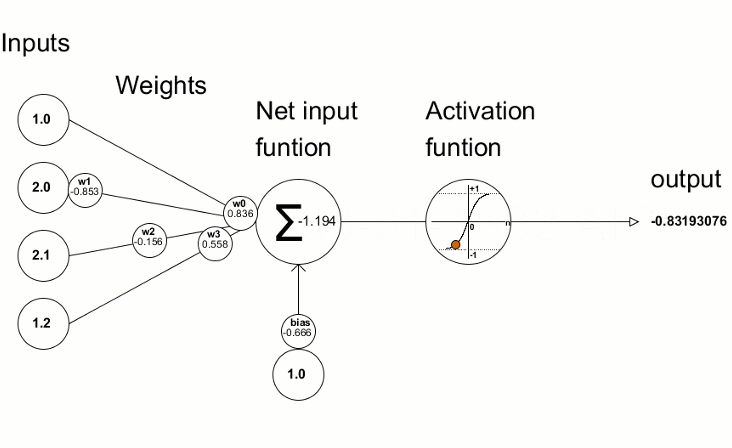
The resulting deviation values are then used to refine the neural network parameters. This is done using the Derivative method, which calculates the values of the derivative of the activation function and writes the result to the passed vector/matrix. The neural network training process can be visually represented using the animation from the article "Programming a Deep Neural Network from Scratch using MQL Language".
Improvements in OpenCL
We have also implemented matrix and vector support in the CLBufferWrite and CLBufferRead functions. Corresponding overloads are available for these functions. An example for a matrix is show below.
Writes values from the matrix to the buffer and returns true on success.
uint CLBufferWrite( int buffer, // OpenCL buffer handle uint buffer_offset, // offset in the OpenCL buffer in bytes matrix<T> &mat // matrix of values to write to buffer );
Reads an OpenCL buffer to a matrix and returns true on success.
uint CLBufferRead( int buffer, // OpenCL buffer handle uint buffer_offset, // offset in the OpenCL buffer in bytes const matrix& mat, // matrix to get values from the buffer ulong rows=-1, // number of rows in the matrix ulong cols=-1 // number of columns in the matrix );
Let's consider the use of new overloads using an example of a matrix product of two matrices. Let's do the calculations using three method:
- A naive way illustrating the matrix multiplication algorithm
- The built-in MatMul method
- Parallel calculation in OpenCL
The obtained matrices will be checked using the Compare method that compares the elements of two matrices with the given precision.
#define M 3000 // number of rows in the first matrix #define K 2000 // number of columns in the first matrix equal to the number of rows in the second one #define N 3000 // number of columns in the second matrix //+------------------------------------------------------------------+ const string clSrc= "#define N "+IntegerToString(N)+" \r\n" "#define K "+IntegerToString(K)+" \r\n" " \r\n" "__kernel void matricesMul( __global float *in1, \r\n" " __global float *in2, \r\n" " __global float *out ) \r\n" "{ \r\n" " int m = get_global_id( 0 ); \r\n" " int n = get_global_id( 1 ); \r\n" " float sum = 0.0; \r\n" " for( int k = 0; k < K; k ++ ) \r\n" " sum += in1[ m * K + k ] * in2[ k * N + n ]; \r\n" " out[ m * N + n ] = sum; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- initialize the random number generator MathSrand((int)TimeCurrent()); //--- fill matrices of the given size with random values matrixf mat1(M, K, MatrixRandom) ; // first matrix matrixf mat2(K, N, MatrixRandom); // second matrix //--- calculate the product of matrices using the naive way uint start=GetTickCount(); matrixf matrix_naive=matrixf::Zeros(M, N);// here we rite the result of multiplying two matrices for(int m=0; m<M; m++) for(int k=0; k<K; k++) for(int n=0; n<N; n++) matrix_naive[m][n]+=mat1[m][k]*mat2[k][n]; uint time_naive=GetTickCount()-start; //--- calculate the product of matrices using MatMull start=GetTickCount(); matrixf matrix_matmul=mat1.MatMul(mat2); uint time_matmul=GetTickCount()-start; //--- calculate the product of matrices in OpenCL matrixf matrix_opencl=matrixf::Zeros(M, N); int cl_ctx; // context handle if((cl_ctx=CLContextCreate(CL_USE_GPU_ONLY))==INVALID_HANDLE) { Print("OpenCL not found, exit"); return; } int cl_prg; // program handle int cl_krn; // kernel handle int cl_mem_in1; // handle of the first buffer (input) int cl_mem_in2; // handle of the second buffer (input) int cl_mem_out; // handle of the third buffer (output) //--- create the program and the kernel cl_prg = CLProgramCreate(cl_ctx, clSrc); cl_krn = CLKernelCreate(cl_prg, "matricesMul"); //--- create all three buffers for the three matrices cl_mem_in1=CLBufferCreate(cl_ctx, M*K*sizeof(float), CL_MEM_READ_WRITE); cl_mem_in2=CLBufferCreate(cl_ctx, K*N*sizeof(float), CL_MEM_READ_WRITE); //--- third matrix - output cl_mem_out=CLBufferCreate(cl_ctx, M*N*sizeof(float), CL_MEM_READ_WRITE); //--- set kernel arguments CLSetKernelArgMem(cl_krn, 0, cl_mem_in1); CLSetKernelArgMem(cl_krn, 1, cl_mem_in2); CLSetKernelArgMem(cl_krn, 2, cl_mem_out); //--- write matrices to device buffers CLBufferWrite(cl_mem_in1, 0, mat1); CLBufferWrite(cl_mem_in2, 0, mat2); CLBufferWrite(cl_mem_out, 0, matrix_opencl); //--- start the OpenCL code execution time start=GetTickCount(); //--- set the task workspace parameters and execute the OpenCL program uint offs[2] = {0, 0}; uint works[2] = {M, N}; start=GetTickCount(); bool ex=CLExecute(cl_krn, 2, offs, works); //--- read the result into the matrix if(CLBufferRead(cl_mem_out, 0, matrix_opencl)) PrintFormat("Matrix [%d x %d] read ", matrix_opencl.Rows(), matrix_opencl.Cols()); else Print("CLBufferRead(cl_mem_out, 0, matrix_opencl failed. Error ",GetLastError()); uint time_opencl=GetTickCount()-start; Print("Compare computation times of the methods"); PrintFormat("Naive product time = %d ms",time_naive); PrintFormat("MatMul product time = %d ms",time_matmul); PrintFormat("OpenCl product time = %d ms",time_opencl); //--- release all OpenCL contexts CLFreeAll(cl_ctx, cl_prg, cl_krn, cl_mem_in1, cl_mem_in2, cl_mem_out); //--- compare all obtained result matrices with each other Print("How many discrepancy errors between result matrices?"); ulong errors=matrix_naive.Compare(matrix_matmul,(float)1e-12); Print("matrix_direct.Compare(matrix_matmul,1e-12)=",errors); errors=matrix_matmul.Compare(matrix_opencl,float(1e-12)); Print("matrix_matmul.Compare(matrix_opencl,1e-12)=",errors); /* Result: Matrix [3000 x 3000] read Compare computation times of the methods Naive product time = 54750 ms MatMul product time = 4578 ms OpenCl product time = 922 ms How many discrepancy errors between result matrices? matrix_direct.Compare(matrix_matmul,1e-12)=0 matrix_matmul.Compare(matrix_opencl,1e-12)=0 */ } //+------------------------------------------------------------------+ //| Fills the matrix with random values | //+------------------------------------------------------------------+ void MatrixRandom(matrixf& m) { for(ulong r=0; r<m.Rows(); r++) { for(ulong c=0; c<m.Cols(); c++) { m[r][c]=(float)((MathRand()-16383.5)/32767.); } } } //+------------------------------------------------------------------+ //| Release all OpenCL contexts | //+------------------------------------------------------------------+ void CLFreeAll(int cl_ctx, int cl_prg, int cl_krn, int cl_mem_in1, int cl_mem_in2, int cl_mem_out) { //--- release all created OpenCL contexts in reverse order CLBufferFree(cl_mem_in1); CLBufferFree(cl_mem_in2); CLBufferFree(cl_mem_out); CLKernelFree(cl_krn); CLProgramFree(cl_prg); CLContextFree(cl_ctx); }
A detailed explanation of the OpenCL code from this example is provided in the article "OpenCL: From naive towards more insightful coding".
More improvements
Build 3390 lifted two restrictions in OpenCL operation which affected the GPU usage.
To set the mandatory use of GPUs with double support for specific tasks, use the CL_USE_GPU_DOUBLE_ONLY in the CLContextCreate call.
int cl_ctx; //--- initialization of OpenCL context if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE) { Print("OpenCL not found"); return; }
Although changes in OpenCL operations are not directly related to matrices and vectors, they are in line with our efforts in developing the MQL5 language machine learning capabilities.
The future of MQL5 in Machine Learning
Over the past years, we have done a lot to introduce advanced technologies into the MQL5 language:
- Porting the ALGLIB library of numerical methods to MQL5
- Implementing a mathematical library with fuzzy logic and statistic methods
- Introducing the graphics library, analogue of the plot function
- Integrating with Python to run Python scripts directly in the terminal
- Adding DirectX functions to create 3D graphics
- Implementing native SQLite support for operations with data bases
- Adding new data types: matrices and vectors, along with all the necessary methods
The MQL5 language will continue to develop, while one of the top priority direction is machine learning. We have big plans for further development. So, stay with us, support us, and keep learning with us.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/10922
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
 MQL5 Wizard techniques you should know (Part 03): Shannon's Entropy
MQL5 Wizard techniques you should know (Part 03): Shannon's Entropy
 Learn how to design a trading system by Awesome Oscillator
Learn how to design a trading system by Awesome Oscillator
 Learn how to design a trading system by Accelerator Oscillator
Learn how to design a trading system by Accelerator Oscillator
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Please clarify how to copy a column from one matrix to another!
I don't understand the example through copy to vector.
Here is a piece of my code
I get an error
That's from another thread:
V_Data_calc.Cov(m_Data_calc,0);It should probably go something like this:
That's from another thread:
It should probably go something like this:
Thank you! How did you know to do it like that?
Thank you! How did you know to do it that way?
I can't understand how covariance calculation can help in copying either - Cov
I can't see how calculating covariance can help with copying either - Cov
It seems clear that I described myself on the forum - after all, the code from the help is correct.