Popülasyon optimizasyon algoritmaları: Elektromanyetizma benzeri algoritma (ElectroMagnetism-like algorithm, ЕМ)

İçindekiler:

1. Giriş
2. Algoritma
3. Test sonuçları

1. Giriş

Son birkaç on yılda, dünyanın dört bir yanındaki araştırmacılar, karmaşık global optimizasyon problemlerini çözmek için birçok metasezgisel arama yöntemi ve bunları iyileştirmenin yollarını buldular.

Elektromanyetizma benzeri algoritma (ЕМ), ilk olarak 2003 yılında I. Birbil ve S.С. Fang tarafından tanıtılan, elektromanyetik parçacıkların fiziksel uzaydaki davranışlarının simülasyonuna dayanan nispeten yeni bir metasezgisel arama algoritmasıdır (https://www.sciencedirect.com/science/article/pii/S0304397516302328#br0040). Yüklü parçacıklar arasındaki elektromanyetik etkileşim kuvvetine dayanan bir popülasyona ve rastgele gürültüye sahip evrimsel bir algoritma olarak tanımlanmaktadır.

Bu algoritma, sürekli bir alanda kısıtlama olmaksızın doğrusal olmayan optimizasyon problemlerini çözmek için elektromanyetizma teorisindeki yüklerin çekme ve itme mekanizmasından esinlenmiştir. Karmaşık global optimizasyon problemlerini çözme kabiliyeti nedeniyle EM, birçok alanda bir optimizasyon aracı olarak yaygın bir şekilde kullanılmaktadır.

Elektromanyetizma ve elektrik yükleri hakkında ilginç gerçekler:

• İki tür elektrik yükü vardır: pozitif ve negatif. Tüm yükler ya pozitif ya da negatiftir.
• Elektromanyetik alan, radyo dalgaları şeklinde bilgi iletmek için kullanılabilir. Bu özelliği her gün radyo dinlerken veya televizyon izlerken kullanıyoruz.
• Bizi güneş rüzgarından ve kozmik ışınlardan koruyan Dünyanın manyetik alanına sahibiz.
• Mıknatıslanabilen çeşitli malzemeler vardır ve bu da elektromıknatısların oluşturulmasını mümkün kılar. Elektromıknatıslar güç jeneratörleri gibi çeşitli uygulamalarda kullanılır.
• Elektromanyetizmaya dayalı birçok uygulama vardır. Örneğin, bilgisayarlar, cep telefonları vb. cihazlar elektromanyetik teknoloji kullanır.
• Tüm ışık saçan nesneler (örneğin ampuller ve araba farları) elektromanyetik radyasyon yayar.
• Elektromanyetizma tıpta da önemli bir rol oynamaktadır. MRI ve CT gibi tıbbi cihazlar vücudun içinde görüntü oluşturmak için elektromanyetik bir alan kullanır.
• Köpekbalıkları ve elektrikli yılan balıkları gibi bazı hayvanlar suda yönlerini bulmak için elektromanyetizmayı kullanabilirler.
• Elektromanyetizma, yerçekimi, zayıf ve güçlü kuvvetlerle birlikte doğanın dört temel kuvvetinden biridir.

2. Algoritma

Elektromanyetizma teorisi tarafından yönlendirilen EM, sınırlı değişkenler kullanarak global bir optimum çözüme ulaşmak için yüklerin çekme-itme mekanizmasını simüle eder. Algoritmada, tüm çözümler arama uzayında yüklü parçacıklar olarak kabul edilir ve her parçacığın yükü amaç fonksiyonunun değeri ile ilişkilendirilir. Daha iyi objektif çıktıya sahip parçacıklar çekici kuvvetler uygularken, daha kötü objektif değerlere sahip parçacıklar diğer parçacıklara itici kuvvetler uygulayacaktır. Amaç fonksiyonunun değeri ne kadar iyi olursa, parçacıklar arasındaki çekme veya itme miktarı da o kadar yüksek olacaktır.

Algoritmanın prensibi, ilk aşamada rastgele çözümlerden oluşan bir popülasyonun oluşturulması ve her çözümün elektromanyetik parçacıklar üzerindeki yüklere karşılık gelen bir koordinat vektörü ile temsil edilmesidir. Ayrıca, algoritmanın her bir yinelemesinde, bu yüklerin uzaydaki hareketi elektromanyetik kuvvetlerin etkisi altında simüle edilir. Hareket halindeyken, her bir yük diğer yüklerle etkileşime girerek hareketin yönünü ve hızını değiştirir. Sonuç olarak, çözümlerin amaç fonksiyonunun optimal değerine kademeli olarak yakınsaması söz konusudur.

EM algoritmasının ana bileşenleri şunlardır:

1. Her bir yükün bir koordinat vektörü ile temsil edildiği ve optimizasyon probleminin belirli bir çözümüne karşılık geldiği ilk çözüm popülasyonunun (yükler) oluşturulması.
2. Yükler arasındaki elektromanyetik etkileşim kuvvetinin hesaplanması. Hesaplama algoritmanın her yinelemesinde gerçekleştirilir ve yükler (çözümler) arasındaki mesafeye bağlıdır.
3. Elektromanyetik etkileşim kuvvetlerinin etkisi altında yüklerin uzaydaki hareketi.
4. Her yinelemede çözüm popülasyonunun amaç fonksiyonu ile güncellenmesi (amaç fonksiyonu, örneğin makine öğrenimi problemlerindeki kayıp fonksiyonu olabilir).
5. Algoritmayı durdurma koşulunun belirlenmesi, örneğin amaç fonksiyonunun belirli bir değerine ulaşılması.

Parçacıklar birbirleriyle etkileşime girer, yüklerine ve aralarındaki mesafeye bağlı olarak birbirlerini çeker veya iterler. Algoritma, her birinde parçacıkların koordinatlarının ve yüklerinin güncellendiği ve uygunluk fonksiyonunun yeni değerlerinin hesaplandığı birkaç yinelemede yürütülür.

EM optimizasyon algoritmasının mantıksal birimi bir parçacıktır. Arama uzayında bir temsilci olan S_Particle yapısı ile tanımlanabilir. Her parçacık, arama uzayındaki konumunu belirleyen c[] koordinatlarının yanı sıra diğer parçacıklarla etkileşimini etkileyen C yüküne sahiptir. Her bir parçacık için, ilgili koordinata karşılık gelen çözümün kalitesini değerlendiren f uygunluk fonksiyonunun değeri hesaplanır. Ayrıca, her bir parçacık için, diğer parçacıklara olan R mesafeleri ve F kuvvet vektörleri hesaplanır, bu da arama uzayında parçacık hareketinin yönünü belirler.

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_EM sınıfı, elektromanyetik optimizasyon algoritmasının bir uygulamasıdır. Bazı reel sayılar kümesinde verilen bir fonksiyonun optimal değerlerini bulmak için kullanılır. Algoritma, fiziksel bir sistemdeki manyetik ve elektriksel parçacıklar arasındaki etkileşim süreçlerinin simüle edilmesine dayanmaktadır.

Sınıf aşağıdaki alanları içerir:

• S_Particle p[] - optimizasyon probleminin potansiyel çözümlerini temsil eden parçacıklar dizisi.
• double rangeMax[] - her koordinat için maksimum arama aralığı değerleri dizisi.
• double rangeMin[] - her koordinat için minimum arama aralığı değerleri dizisi.
• double rangeStep[] - her koordinat için arama adımları dizisi.
• double cB[] - en iyi çözümün koordinatları dizisi.
• double fB - en iyi çözüm fonksiyonunun değeri.

Sınıf aşağıdaki metotları içerir:

• void Init() algoritmayı başlatarak koordinat sayısını, parçacık sayısını, ortam sabitini ve hareket adımını ayarlar.
• void Moving(int iter), parçacıkları manyetik ve elektrik alanların etkileşim kurallarına uygun olarak hareket ettiren algoritmayı yineler.
• void Revision(), parçacıkların arama aralığının dışına çıkıp çıkmadıklarını kontrol ederek ve gerekirse konumlarını ayarlayarak bir revizyon gerçekleştirir.

Sınıf ayrıca private alanlar da içerir:

• int coordinatesNumber - koordinat sayısı.
• int particlesNumber - parçacık sayısı.
• double envConstant - ortam sabiti.
• double movConstant - hareket adımı.
• double exponent - mesafe üssü.
• double vect[] - vektörler dizisi.
• bool revizyon - parçacık revizyonu ihtiyacını gösteren bayrak.

Sınıf ayrıca private metotlar da içerir:

• double SeInDiSp(double In, double InMin, double InMax, double Step) - noktaları tekdüze bir ızgara üzerinde dağıtır.
• double RNDfromCI(double min, double max) - verilen aralıkta rastgele bir sayı üretir.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Elektromanyetizma benzeri optimizasyon algoritması başlatma metodu, rastgele sayı oluşturucusunun sıfırlanması ve bazı değişkenler için başlangıç değerlerinin ayarlanmasıyla başlar. Daha sonra metot girdi olarak birkaç parametre alır: koordinat sayısı, parçacık sayısı, ortamın değeri ve hareket adımı. Ardından, metot gerekli büyüklüklerde birkaç dizi oluşturur ve bunları başlangıç değerleriyle doldurur.

Diziler, her koordinat için aralığın maksimum ve minimum değerlerini, koordinatı değiştirme adımını, vektörü ve her parçacığın mevcut konumunu saklar. Metot daha sonra bir parçacık dizisi oluşturur ve her parçacık için koordinatlarını, diğer parçacıklara olan mesafelerin matrisini, kuvvet vektörünü ve fonksiyonun mevcut en iyi değerini depolamak için diziler oluşturur. Sonunda, metot tüm parçacıkların en iyi koordinatlarını saklamak için bir dizi oluşturur. Böylece metot, elektromanyetizma benzeri optimizasyon algoritmasının çalışması için gerekli tüm değişkenleri ve dizileri başlatır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Moving() metodu, her yinelemede yürütülmesi gereken ilk metottur. Parçacıkların çözüm arama uzayındaki hareketinden sorumludur. İlk olarak, metot parçacıkların halihazırda başlatılıp başlatılmadığını kontrol eder. Başlatılmadıysa, her parçacık verilen sınırlar içinde rastgele koordinatlar alır ve mevcut hesaplamasını ve yükünü sıfıra sıfırlar. Arama uzayının her bir boyutundaki maksimum ve minimum değerler arasındaki farkların vektörü vect[] de hesaplanır.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

Başlatma işlemi zaten gerçekleştirilmişse, metot her bir parçacığın yükünü, tüm parçacıkların global maksimumdan sapmalarının toplamına normalize edilmiş global maksimumdan sapmasına göre hesaplar. Farkların toplamını aşağıdaki gibi hesaplarız:

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

Parçacık yükü şu denklem ile hesaplanır:

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));

Gördüğünüz gibi, denklemdeki yükün değeri pozitiftir. Yükün işareti algoritmanın ilerleyen kısımlarında dikkate alınacaktır. Global maksimumdan sapmalardaki farkların toplamı sıfırsa, parçacığın yükünün sıfır olduğu varsayılır. Parçacığın hesaplanan yükü, kuvvet hesaplama adımı sırasında parçacıktan diğer ilgili parçacıklara etki eden kuvvetin büyüklüğünü belirleyecektir. Bir parçacığın yükünü hesaplamak için kod şu şekilde görünür:

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

Parçacıklar arasındaki mesafeleri hesaplamaya başlamadan önce, parçacıktan diğer parçacıklara olan mesafeler dizisini sıfırlamak ve ayrıca parçacık üzerinde etkili olan kuvvet vektörünü sıfırlamak gerekir:

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

Daha sonra tüm parçacık çiftleri arasındaki mesafeler ve bunlar arasında etki eden kuvvetler hesaplanır. Yüklü parçacıklar arasındaki etkileşimi tanımlayan Coulomb yasasına dayanan bir formül kullanır. Her bir parçacık üzerine etki eden kuvvetler, diğer parçacıklardan üzerine etki eden tüm kuvvetlerin vektörel toplamı olarak hesaplanır.

Elektromanyetik teoriye göre, bir parçacığın diğeri üzerindeki etki kuvveti, iki parçacık arasındaki mesafeyle ters orantılı ve yüklerinin çarpımıyla doğru orantılıdır. Daha düşük hedef değere sahip bir parçacık, nispeten daha yüksek hedef değere sahip bir parçacığa itici bir kuvvet uygular. Benzer şekilde, iyi bir parçacığı kötü bir hedef değeri olan bir bölgeden uzaklaştırır. Öte yandan, daha yüksek bir hedef değere sahip bir parçacık, nispeten daha düşük değerlere sahip parçacıklar üzerinde çekim uygular.

Diğer tüm parçacıklar tarafından üretilen ilgili tüm kuvvetler dikkate alınarak, parçacık için toplam kuvvet vektörü hesaplanır. Bu birleşik kuvvet vektörü, parçacık hareket fazı sırasında parçacığın hareket edeceği yönü belirler. Algoritmanın yazarları, parçacığın kuvvet vektörünün tüm parçacıklar arasındaki kuvvet vektörüne normalleştirilmesini önermektedir. Deneylerim normalleştirme olmadan sonuçların daha iyi olduğunu göstermiştir ve kod normalleştirme olmadan sunulmuştur.

Hangi parçacığın amaç fonksiyonunun daha büyük değerine sahip olduğuna bağlı olarak, kuvvetin yönünü belirleriz (yükün işaretinin taklidi).

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

Son olarak, her bir parçacık için mevcut konumuna ve üzerine etki eden kuvvete bağlı olarak yeni koordinatlar hesaplanır. Parçacıkların kütlesi yoktur, bu da ivme olmadığı anlamına gelir. GSA yerçekimsel arama algoritmasının aksine, parçacıklar anında yeni bir konuma hareket eder. Hareket koordinatları arama aralığı ve değişim adımı ile sınırlıdır.

Yoruma çevrilmiş kod, parçacığın aralık dışında olması durumunda aralığın karşı tarafında ilgili koordinattan uzakta bir parçacık geri döndürür.

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

EM optimizasyon algoritmasında her yinelemede yürütülmesi gereken ikinci metot olan Revision() metodu, parçacığın mevcut yinelemedeki en iyi konumunu kontrol etmekten sorumludur. Metot tüm parçacıklar arasında döngü yapar ve uygunluk fonksiyonlarının değerini fB'nin mevcut en iyi değeriyle karşılaştırır. Mevcut parçacığın uygunluk fonksiyonunun değeri fB'den büyükse, fB güncellenir ve parçacığın konumu cB dizisine kopyalanır.

Böylece Revision() metodu, algoritmanın her yinelemesinde parçacığın en iyi konumunun izlenmesini ve cB dizisinde saklanmasını sağlar. Bu, optimum çözümü bulma sürecinin optimize edilmesine yardımcı olur ve algoritmanın verimliliğini artırır.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Elektromanyetizma benzeri optimizasyon algoritmasındaki SeInDiSp() metodu, In değişkeninin değerlerini Step artışıyla belirli bir aralık [InMin, InMax] içinde sınırlamak için kullanılır. In değeri InMin değerinden küçük veya eşitse, metot InMin değerini geri döndürür. In değeri InMax değerinden büyük veya eşitse, metot InMax değerini geri döndürür. Adım sıfırsa, metot orijinal In değerini geri döndürür. Aksi takdirde, metot şu denklemi kullanarak yeni bir In değeri hesaplar: InMin + Step * (double) MathRound ((In - InMin) / Step), burada MathRound() bir sayıyı en yakın tam sayıya yuvarlama metodudur.

Böylece SeInDiSp() metodu, In değişkeninin değerindeki değişimin belirlenen sınırlar dahilinde ve belirli bir adımla kontrol edilmesine olanak tanıyarak fonksiyonun daha verimli ve hızlı bir şekilde optimize edilmesine yardımcı olur.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————

3. Test sonuçları

EM algoritması test ortamı sonuçları:

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigin's; Func runs 10000 result: 59.939529106561224
2023.03.26 18:27:43.215    Score: 0.74268
2023.03.26 18:27:52.960    25 Rastrigin's; Func runs 10000 result: 59.780143424645416
2023.03.26 18:27:52.960    Score: 0.74071
2023.03.26 18:29:22.856    500 Rastrigin's; Func runs 10000 result: 63.94951378068386
2023.03.26 18:29:22.856    Score: 0.79237
2023.03.26 18:29:22.856    =============================
2023.03.26 18:29:28.901    5 Forest's; Func runs 10000 result: 0.28698617113254693
2023.03.26 18:29:28.901    Score: 0.16233
2023.03.26 18:29:38.103    25 Forest's; Func runs 10000 result: 0.1571444033424823
2023.03.26 18:29:38.103    Score: 0.08889
2023.03.26 18:30:53.341    500 Forest's; Func runs 10000 result: 0.11734383105881332
2023.03.26 18:30:53.341    Score: 0.06638
2023.03.26 18:30:53.341    =============================
2023.03.26 18:30:58.108    5 Megacity's; Func runs 10000 result: 1.3599999999999999
2023.03.26 18:30:58.108    Score: 0.11333
2023.03.26 18:31:08.897    25 Megacity's; Func runs 10000 result: 0.776
2023.03.26 18:31:08.897    Score: 0.06467
2023.03.26 18:32:23.199    500 Megacity's; Func runs 10000 result: 0.34320000000000006
2023.03.26 18:32:23.199    Score: 0.02860
2023.03.26 18:32:23.199    =============================
2023.03.26 18:32:23.199    All score: 2.79996

EM algoritmasının test fonksiyonları üzerindeki animasyonuna dikkat edersek, arama uzayı alanının bir tür “elektriklenmesini” hayal edebiliriz. Parçacıklar, test fonksiyonunun yüzeyinin özelliklerini takip ederek yüksek yük grupları oluşturur. Ne yazık ki, yakınsama kalitesi gözle görülür derecede düşük ancak görüntü inkar edilemeyecek kadar güzeldir.

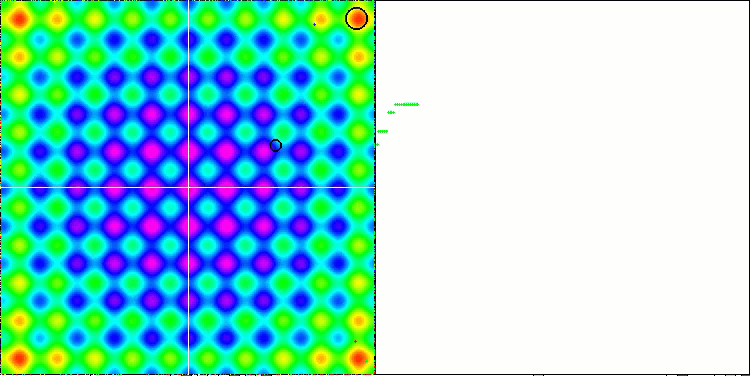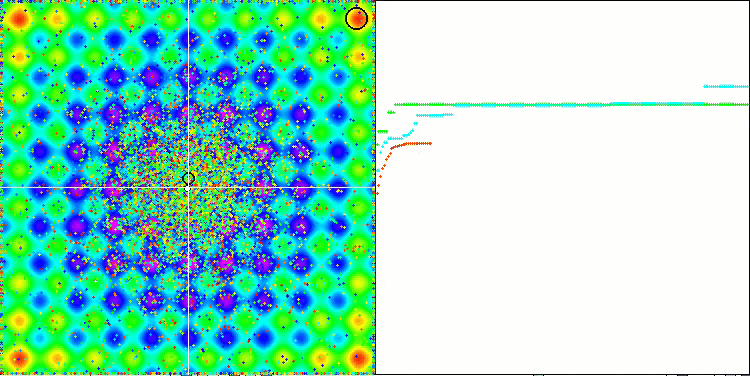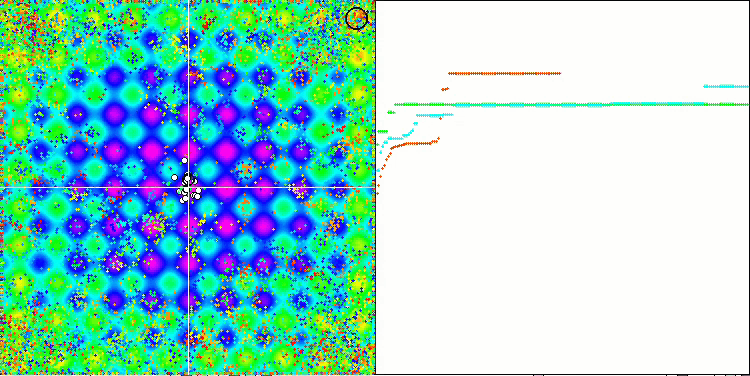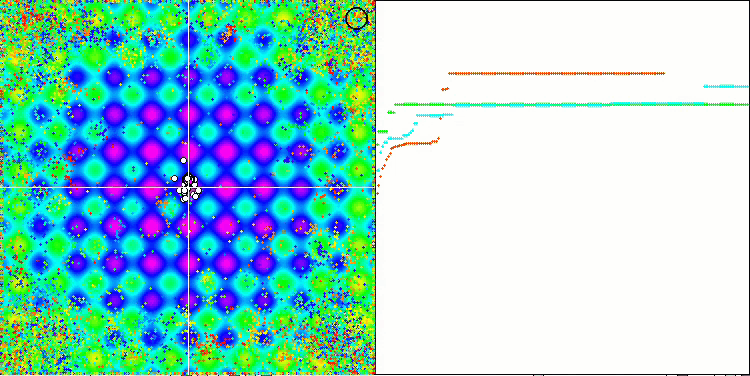
  Rastrigin test fonksiyonu üzerinde EM

  Forest test fonksiyonu üzerinde EM

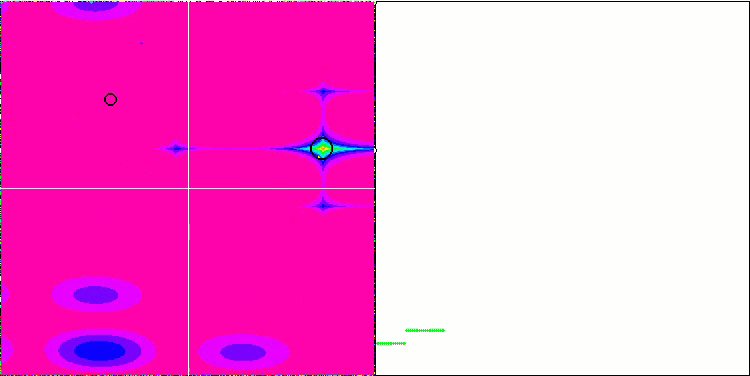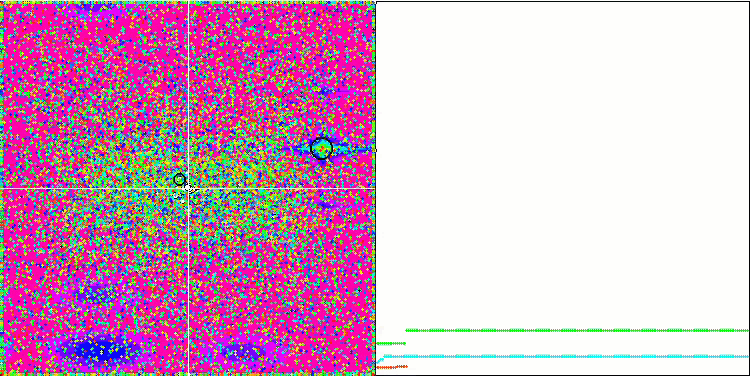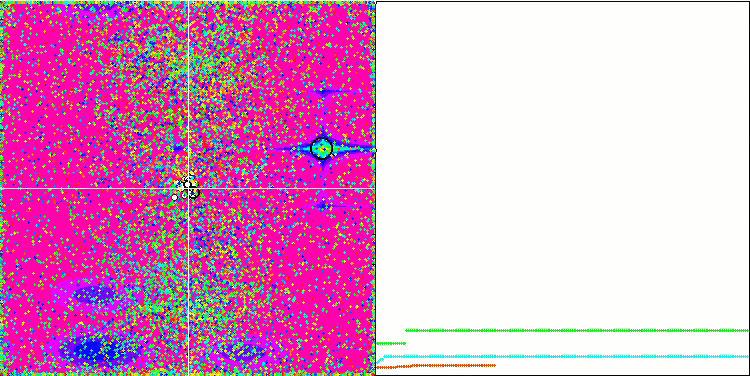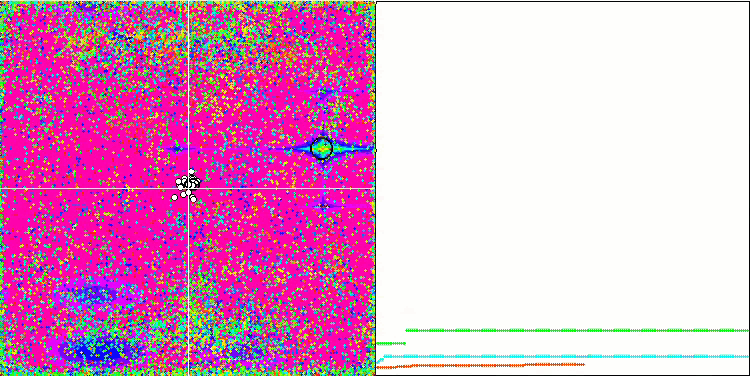
  Megacity test fonksiyonu üzerinde EM

EM optimizasyon algoritmasının test sonuçlarına geçelim. EM, 22 final puanı ile ortalamanın altında bir performans sergilemiştir. Algoritma neredeyse tüm testlerde kötü sonuçlar vermiştir. Bunun istisnası, EM'nin SSG ve BA gibi güçlü algoritmalardan daha iyi olduğu ortaya çıkan 1000 parametreli Rastrigin fonksiyon testidir. Dahası, 1000 parametrede fonksiyonun mutlak değerlerinin 10 ve 50 parametreli testlerden daha yüksek olduğu ortaya çıktı!

Bu, optimize edilen parametrelerin sayısının artmasıyla arama sonuçlarının iyileştiği ilk zamandır. Büyük olasılıkla bu olgu, EM arama stratejisinin kendine has özellikleriyle ilişkilidir. EM'nin bir gradyanın varlığına ve incelenen fonksiyon tanımının tüm alanı üzerinde türevlenebilirliğe olan duyarlılığına dikkat etmek gerekir.

AO	Açıklama	Rastrigin			Rastrigin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
		10 parametre (5 F)	50 params (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 params (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 params (25 F)	1000 parametre (500 F)
SSG	Fidan dikimi ve büyütme	1.00000	1.00000	0.55665	2.55665	0.72740	0.94522	1.00000	2.67262	0.76364	0.85977	1.00000	2.62340	100.000
HS	Armoni araması	0.99676	0.95282	0.48178	2.43136	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	92.329
ACOm	Karınca kolonisi optimizasyonu (m)	0.34611	0.17985	0.17044	0.69640	0.86888	1.00000	0.77362	2.64249	1.00000	0.88930	0.05606	1.94536	65.347
IWO	İstilacı yabancı ot optimizasyonu	0.95828	0.67083	0.29807	1.92719	0.70773	0.46349	0.31773	1.48896	0.80000	0.42067	0.33289	1.55356	61.104
COAm	Guguk kuşu optimizasyon algoritması (m)	0.92400	0.46794	0.26004	1.65199	0.58378	0.34034	0.16526	1.08939	0.72727	0.33025	0.17083	1.22835	47.612
FAm	Ateş böceği algoritması (m)	0.59825	0.33980	0.17135	1.10941	0.51073	0.42299	0.49790	1.43161	0.34545	0.28044	0.35258	0.97847	41.537
ABC	Yapay arı kolonisi	0.78170	0.32715	0.20822	1.31707	0.53837	0.21455	0.13344	0.88636	0.56364	0.26569	0.13926	0.96858	36.849
GSA	Yerçekimsel arama algoritması	0.70167	0.45217	0.00000	1.15384	0.31660	0.36416	0.33204	1.01280	0.59395	0.35054	0.00000	0.94448	36.028
BA	Yarasa algoritması	0.40526	0.63761	0.84451	1.88738	0.20841	0.17477	0.25989	0.64308	0.29698	0.09963	0.17371	0.57032	35.888
BFO	Bakteri yiyecek arama optimizasyonu	0.67203	0.30963	0.11813	1.09979	0.39702	0.26623	0.20652	0.86976	0.52122	0.33211	0.18932	1.04264	34.693
EM	Elektromanyetizma benzeri algoritma	0.12235	0.46278	1.00000	1.58513	0.00000	0.03498	0.34880	0.38377	0.00000	0.00000	0.10924	0.10924	22.091
MA	Maymun algoritması	0.33192	0.33451	0.14644	0.81287	0.10012	0.07891	0.08932	0.26836	0.21818	0.04243	0.10720	0.36781	13.603
FSS	Balık sürüsü arama	0.46812	0.25337	0.11302	0.83451	0.12840	0.05013	0.06516	0.24369	0.16971	0.04796	0.08283	0.30050	12.655
PSO	Parçacık sürüsü optimizasyonu	0.20449	0.08200	0.07160	0.35809	0.18895	0.10486	0.21738	0.51119	0.23636	0.05903	0.01957	0.31496	10.031
RND	Rastgele	0.16826	0.09743	0.08019	0.34589	0.13496	0.04810	0.04715	0.23021	0.16971	0.03875	0.04922	0.25767	5.302
GWO	Gri kurt optimizasyonu	0.00000	0.00000	0.02256	0.02256	0.06570	0.00000	0.00000	0.06570	0.32727	0.07378	0.02557	0.42663	1.000

Özet

1. EM algoritması, çeşitli optimizasyon problemlerini, özellikle de büyük miktarda verinin işlenmesi ve düzgün fonksiyonlar üzerinde yüksek boyutluluk ile ilişkili olanları çözebilen verimli bir optimizasyon yöntemidir.
2. Algoritma, elektromanyetik parçacıkların fiziksel uzaydaki davranışını simüle etmeye dayanır ve bu da karmaşık çok boyutlu fonksiyonlarla çalışırken sonucun yüksek doğruluğunu elde etmesini sağlar.
3. EM algoritması gradyan hesaplamaları gerektirmez, bu da onu çok yönlü ve çeşitli problemlere daha kolay uygulanabilir hale getirir, ancak optimize edilen fonksiyonda bir gradyanın varlığına duyarlıdır.
4. Algoritma, belirli optimizasyon problemine bağlı olarak değiştirilebilir ve özelleştirilebilir, bu da onu çeşitli fonksiyonları optimize etmek için esnek bir araç haline getirir.
5. EM algoritmasının temel versiyonu üzerinde geliştirilebilen ve belirli optimizasyon problemlerine uyarlanabilen çeşitli modifikasyonları vardır.
6. EM algoritması, makine öğrenimi, yapay zeka, finansal piyasa optimizasyonu vb. gibi çeşitli alanlarda kullanılabilir.

Elektromanyetizma benzeri algoritmanın ana avantajı, sonucun yüksek doğruluğunu korurken, çok boyutlu uzaylarda ve büyük boyutlarda optimizasyon problemlerini çözme yeteneğidir.

Dolayısıyla, EM algoritması çeşitli fonksiyonların optimizasyonu için etkili bir araçtır ve özellikle büyük miktarda veri ve/veya yüksek boyutluluğun işlenmesi gerektiğinde geniş bir optimizasyon problemi yelpazesinde kullanılabilir.

Bu derecelendirme, belirli bir optimizasyon problemini çözmek üzere en uygun algoritmayı seçmek için yararlı olabilir. Ancak, algoritmanın verimliliği problemin büyüklüğü, fonksiyonun türü, değişken sayısı vb. gibi birçok faktöre bağlıdır. Bu nedenle, bir algoritma seçimi, belirli bir problemin kapsamlı bir analizine dayanmalıdır.

Şekil 1 algoritmaların test sonuçlarını göstermektedir

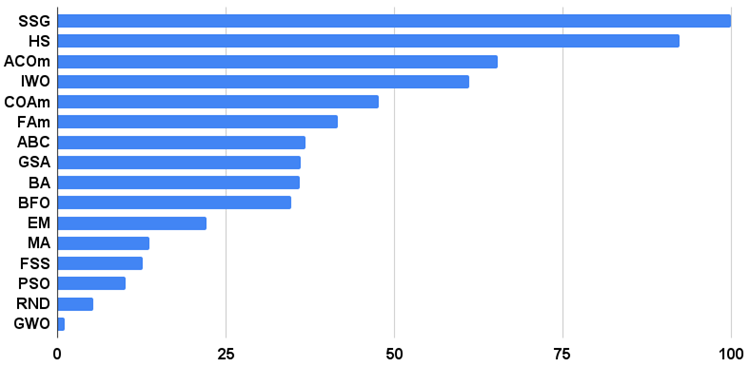
Şekil 1. Algoritmaların test sonuçlarının histogramı

Elektromanyetizma benzeri algoritmanın (EM) avantajları ve dezavantajları:

Avantajları:
1. Kolay uygulama.
2. Düzgün fonksiyonlarda etkileyici ölçeklenebilirlik.
3. Az sayıda harici parametre.

Dezavantajları:
1. Yüksek hesaplama karmaşıklığı.
2. Ayrık fonksiyonlar üzerinde zayıf sonuçlar.
3. Düz yatay "platformlara" sahip fonksiyonlarda takılma.

Her makale, önceki tüm makalelerdeki algoritma kodlarının güncellenmiş sürümlerini içeren bir arşive sahiptir. Makale, yazarın birikmiş deneyimlerine dayanmaktadır ve kişisel görüşünü temsil etmektedir. Sonuçlar ve yargılar deneylere dayanmaktadır.