Popülasyon optimizasyon algoritmaları: Fidan dikimi ve büyütme (Saplings Sowing and Growing up, SSG)

İçindekiler:

1. Giriş
2. Algoritma
3. Test sonuçları

1. Giriş

Doğadaki tüm canlı organizmalar belirli yasalara tabidir. Bu, değişen çevre koşullarında hayatta kalmalarına yardımcı olur. Bitkilerin çevreye uyum sağlayabilmesi için çeşitli seçenekler bulunmaktadır. Bazıları mevsimsel değişiklikleri tolere edebilirken, diğerleri nem eksikliğine, yüksek veya düşük sıcaklıklara ve polen taşıyıcıların yokluğuna uyum sağlayabilir. Bitkiler arasında en istikrarlı organizmalardan biri, bazıları koloniler oluşturarak 50 bin yıldan fazla yaşayabilen ağaçlardır.

Doğa, hesaplama yöntemlerinin geliştirilmesi ve icadında birçok etkili fikir için tükenmez bir ilham alanıdır. Aslında evrimsel hesaplama, evrimin bilgisayar simülasyonlarına yansıtılmasıdır. Evrimsel hesaplama, yapay immünoloji, popülasyon yöntemleri vb. gibi doğada meydana gelen süreçlerden ilham alan birçok optimizasyon yöntemi vardır. SSG temel olarak fidan adı verilen potansiyel çözümlerden oluşan bir bahçe ile çalışan yinelemeli üretim ve kombinasyon süreçleri olarak tanımlanır. Fidan dikimi ve büyütme (Saplings Sowing and Growing up, SSG) algoritması 2002 yılında A. Karcı ve arkadaşları tarafından önerilmiştir. Algoritma, büyüyen ağaçların evriminden ilham alır ve ağaçların büyümesini ve dallanmasını modeller.

2. Algoritma

Algoritma, yazarları tarafından net bir açıklamaya sahip olmayan birkaç algoritmadan biridir (sadece genel hükümler ve fikirler verilmiştir). Yazarlar tarafından sunulan algoritma operatörleri de programın algoritmik uygulaması için hazır talimatlar değildir. Yavru ve ebeveyn ağaçlar ve bunların etkileşimi hakkında net talimatlar yoktur. Operatörlerin yürütüldüğü sıra için herhangi bir gereklilik yoktur ve herhangi bir kullanıcı daha iyi bir fidan elde etmek için sıralarını değiştirebilir.

Geniş anlamda, SSG bir optimizasyon algoritması değildir, optimizasyon kalitesini artırmak için diğer algoritmaları tamamlamak üzere tasarlanmış genel bir kurallar bütünüdür. Başka bir deyişle, SSG herhangi bir evrimsel popülasyon algoritması için bir eklentidir, bu nedenle hayal gücü için yerim ve optimizasyon algoritmasının belirli bir uygulamasını denemek için fırsatım var. Önceki algoritmaları yazarken edindiğim bazı düşünce ve deneyimlerimi SSG ile çalışmak için kullandım. Deneylerimin sonuçlarını aşağıda okuyucunun değerlendirmesine sunuyorum.

Algoritmayı anlamaya başlamak için ağacı bir optimizasyon temsilcisi olarak düşünmemiz gerekir. Ağaç, her bir dalın problemin optimize edilen bir parametresi olduğu bir optimizasyon probleminin çözümüdür. Yavru ve ebeveyn ağaçların soyut ve sanatsal bir çizimi Şekil 1'de verilmiştir. Ağaç gövdesi, optimize edilecek parametreler kümesidir. Her bir dal optimize edilen ayrı bir parametredir ve dalın uzunluğu ilgili parametrenin izin verilen değer aralığı ile sınırlıdır. Dalların yönü önemli değildir ve sadece aralarındaki farkı vurgulamak için şekilde gösterilmiştir.

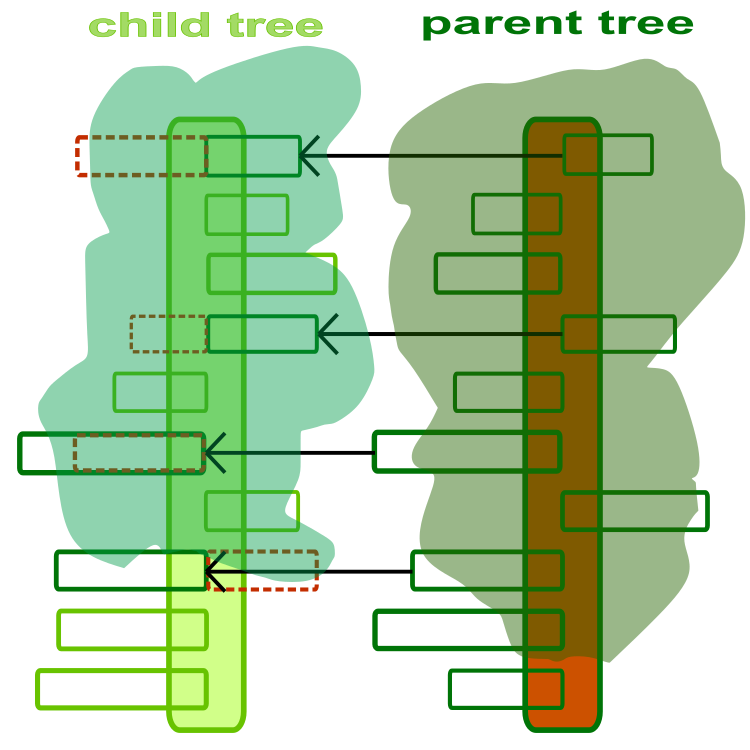
Şekil 1. Yavru ve ebeveyn ağaç. Noktalı çizgiler, ebeveyn dallar tarafından değiştirilen yavru dalları gösterir

Dolayısıyla, ağaç dalları arama uzayındaki ağaçların koordinatlarıdır.

SSG algoritması, ortak çözüm havuzu için aday olan yeni çözümler üreten varyasyon operatörlerinden oluşur. Ana varyasyon operatörleri çaprazlama, dallanma ve aşılamadır. Fidan dikimi birbirinden her yönde (batı, doğu, kuzey, güney) eşit uzaklıkta yapılmalıdır ve bu yöntemin ilk aşamasıdır. Koordinatlar (optimize edilen parametreler) üçten çok daha fazla olduğunda, "tekdüze" dikim, fidanların arama uzayı üzerinde basit bir rastgele dağılımıdır. Daha sonra fidanlar büyür, melezleşir, dallanır ve aşılama süreci gerçekleşir.

SSG algoritmasının adımlarını ve operatörlerini ele alalım:

1) Fidan dikimi.

Arama uzayı bir fidan bahçesi olarak düşünülebilir ve bu nedenle tüm fidanlar bahçeye eşit olarak dağıtılmalıdır. Bir çiftçi fidan dikerken, fidanların birbirine karışmadan daha hızlı büyümesi için onları birbirinden eşit mesafede diker. Fidan yetiştiriciliğini simüle ederek problemi çözmek için, başlangıçta üretilecek rastgele çözümlerin geçerli arama uzayında eşit olarak dağıtılması gerekir.

İki veya üç koordinat olduğunda, fidanları eşit olarak dağıtmak sorun olmaz, ancak üçten çok daha fazla koordinat olduğunda, rastgele bir dağılım kullanmak daha kolaydır. Pratikte, az sayıda koordinatla, görev büyük bir sorun olmadığından ve çözümün yüksek doğrulukla elde edileceği bilindiğinden, fidanların tekdüze dağılımına dikkat etmeye gerek yoktur. Bu nedenle, algoritmadaki koordinat sayısından bağımsız olarak, bahçede rastgele bir fidan dağılımı kullanacağız.

2) Büyüyen fidanlar (ağaçlar), üç operatör sırayla yürütülür.

2.1) Çaprazlama.

"Çaprazlama" operatörünün amacı, aralarında bilgi alışverişi yaparak mevcut fidanlardan yeni bir fidan oluşturmaktır. Çaprazlama esasen bir dalın kopyasının ebeveyn ağaçtan yavru ağaca nakledilmesidir (Şekil 1). Her bir fidan çifti için, çaprazlama olasılığı olan farklı bir çaprazlama katsayısı kullanılır. Çaprazlama olasılığı, bir çiftteki fidanlar arasındaki mesafeye bağlıdır; mesafe arttıkça çaprazlama olasılığı azalır. Çaprazlama operatörü, kombinatoryal mekanizmalar sağlayan algoritmanın çok önemli bir yöntemidir. Temsilciler arasındaki bilgilerin birleştirilmesi, optimizasyon algoritmasının genel kalitesini önemli ölçüde artırabilir.

2.2) Dallanma.

Bu operatör dalların büyümesini modeller. Büyüme pozitif (uzama) ya da negatif (kuruma) olabilir. "Fidanın gövdesindeki herhangi bir noktada bir dalın büyümesi için, yakınlarda daha önce orada filizlenmiş bir dal bulunmayacaktır". Bu, algoritmanın yazarları tarafından operatörün yaklaşık bir tanımıdır. Aslında bu işlem ilk bakışta göründüğünden daha basit ve açıktır ve yavru ağacın mevcut dallarının modifikasyonudur (spesifik modifikasyon yöntemi belirtilmemiştir).

Her bir dalın modifikasyonu, mevcut yineleme ile dalın son modifikasyonunun yapıldığı yineleme arasında ne kadar çok yineleme geçmişse o kadar olasıdır. Deneylerim bu operatörün verimsizliğini gösterdi. Ayrıca, modifikasyon yönteminin kullanıldığına dair doğrudan bir gösterge yoktur ve bu konuda inisiyatif alarak Levy uçuşu dağılımı yasasına göre dal uzunluğu modifikasyonunu uyguladım. Modifikasyon, algoritmanın dış parametreleri olarak belirtilen olasılık ve yoğunluk ile gerçekleştirilecektir.

2.3) Aşılama.

Fidan benzerliği durumunda aşılama işlemi iki farklı fidan arasında gerçekleşir. Fidanların benzerliği aşılama sürecinin başarısını etkiler ve ağırlıklı mesafenin aritmetik ortalaması ile orantılıdır. Operatör, çaprazlama operatörüne benzer ve algoritmaya temsilciler arasındaki bilgileri birleştirmek için ek bir yol sağlayan dalların değişiminden oluşur. Operatör makalede vurgulanacaktır, ancak bu operatör kaynak kodlarında yoruma çevrilmiştir ve aşılama sonuçları kötüleştirdiği için test sonuçları bu operatörün katılımı olmadan sunulmuştur.

3) Ağaçların uygunluğunun hesaplanması.

4) Bahçeye yeni fidanların dikilmesi.

Çaprazlama, dallanma ve aşılama operatörlerinin yardımıyla elde edilen fidanlar geçici çözümlerdir (yavru bahçe). Bu aşamada, n adet en iyi fidanın (algoritmanın harici bir parametresi) seçilmesi ve n adet en kötü ağacın yerine bahçeye yerleştirilmesi gerekmektedir. Bahçedeki en kötü ağaçlardan daha kötü olsalar bile, fidanlarla değiştirmenin her durumda gerçekleşeceği unutulmamalıdır.

Bu, ağaç yetiştirme algoritmasının koduna bakmak için iyi bir zamandır ve bizi bu çalışmanın heyecan verici zirvesine - test sonuçlarının gözden geçirilmesine - giderek daha da yaklaştırmaktadır.

Bu nedenle, her ağacı çiçekli bir bahçe oluşturmak için temel teşkil edecek bir Garden yapısı olarak temsil etmek uygundur. Bu algoritmada sadece iki bileşene ihtiyaç duyan "ağaç" varlığından daha basit bir şey yoktur: c[] koordinatları ve f uygunluk değeri.

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

SSG algoritmasının C_AO_SSG sınıfı özel bir şey değildir. Buradaki her şey, daha önce ele alınan algoritmalardan bize çok tanıdık geliyor. Sınıfta, ebeveyn ve yavru bahçeler üzerinde işlem yapmak için üyeler ve metotlar bildireceğiz. Geçici bir bahçe, sıralama metodunun çalışması içindir, çünkü hem yavru hem de ebeveyn bahçeleri sıralamamız gerekir. Bir bütün olarak çözümün en iyi koordinatlarının dizisini, en iyi uygunluk değerini ve algoritmanın dış parametrelerini saklamak için sabit değişkenleri bildirelim.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

Init() başlatma metodunda, diziler için bellek ayıralım ve sabit parametrelere değerler atayalım. seedlingsReplacementP parametresi, ebeveyn bahçeye dikilecek yavru fidanların sayısından sorumlu olan bahçe büyüklüğünün kesirleri (0.0 ila 1.0 arası) olarak ayarlandığından, bahçe büyüklüğünün tamsayı temsiline dönüştürülmelidir. İlk bahçe fidanı bayrağını sıfırlayalım ve global karar değişkenini mümkün olan en küçük double türü değerle başlatalım.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çağrılan ilk public metot olan Sowing(), fidan dikme işlemidir. İlk yinelemede, algoritma yeni çalışmaya başladığında, fidanları bahçenin (arama uzayı) etrafına tekdüze bir dağılımla rastgele dağıtacağız. Burada koordinatların optimize edilen parametrelerin min. ve maks. değerleri arasında izin verilen aralıkta rastgele üretildiğini görüyoruz, izin verilen aralıktan bir çıkış olup olmadığını kontrol ediyoruz, ardından koordinat değerlerini optimizasyon adımına uygun hale getiriyoruz.

Bu aşamada fidanların adaptasyon kabiliyeti minimum düzeydedir. vec[] vektörünü ayarlıyoruz. Dallanma operatöründeki dalların artışlarını ölçeklendirmek ve ayrıca arama uzayında mümkün olan maksimum Öklid mesafesi r'yi hesaplamak için buna ihtiyacımız olacak. Ağaç çiftleri arasındaki mesafeye bağlı olarak olasılığı belirlemek için çaprazlama operatöründe faydalı olacaktır.

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

Daha sonra, Sowing() metodunda, çaprazlama, dallanma ve aşılama operatörleri ikinci ve sonraki yinelemelerde yürütülür. Operatörler ana döngüde sırayla yürütülür:

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

Operatörleri çalıştırırken, "yavru" ve "ebeveyn" kavramları oldukça gelişigüzeldir. Aslında bunlar, yeni bir fidan oluşturmak için sadece temel bilgi kaynaklarıdır. Yeni fidan tüm dalları (hatırlayacağınız gibi dallar optimize edilen parametrelerdir) yavru ağaçtan kopyalar ve ebeveynden yenilerini alır.

Her yeni fidan için bahçeden iki ağaç ayrı ayrı seçilir; bahçedeki tüm ağaçlar için eşit olasılıkla rastgele bir yavru ağaç ve bir ebeveyn ağaç. Başka bir deyişle, tüm ağaçlar eşit olasılıkla ve uygunluklarına bakılmaksızın yeni bir fidanın yaratılmasında yer alabilir. Böylece, 'child' ve 'parent' basitçe ebeveyn bahçe dizisindeki orijinal iki ağacın indeksleridir.

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

İlk operatör çaprazlamadır (mating). t indeksli bir fidan üzerinde çaprazlama operatörünü çalıştırmak için, 'child' ve 'parent' indekslerine sahip yavru ve ebeveyn ağaçlar arasındaki Öklid uzayını hesaplamak gerekir:

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

Öklid mesafesi, arama uzayında mümkün olan maksimum Öklid mesafesi r'ye normalleştirme yoluyla çaprazlama olasılığını hesaplamak için denklemde yer alır:

eM = 1.0 - (ed / r);

[0.0;1.0] aralığında rastgele bir sayı oluştururuz. Elde edilen sayı hesaplanan eM olasılığı dahilindeyse, çaprazlama gerçekleştiririz - her dal için probabMatingOperator olasılığı ile ebeveyn ağaçtan dalları kopyalarız. eM olasılığı karşılanmazsa, fidan, yavru ağacın tüm orijinal dallarıyla bir sonraki ifadenin yürütülmesine devam edecektir.

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Ardından, dallanma operatörü yürütülür. Dallanma, dalların çeşitlenmesini sağlar - uzama ve kısalma. Bu, yeni uzunlukta dallar oluşturan ana operatördür. Geri kalan operatörler yalnızca kombinatoryal bir rol oynar ve yeni benzersiz dallar oluşturmaz. Her dal için [0.0;1.0] aralığında rastgele bir sayı üretiriz ve probabBranchOperator olasılığı yerine getirilirse, burada dikkate alınan Levy uçuşları dağılım yasasına göre dalın uzunluğunu değiştirerek dallanma gerçekleştiririz.

Gördüğünüz gibi, fidanın tüm dalları değişmeyecektir. Dalın önceki ifadede ebeveyn ağaçtan kopyalanıp kopyalanmadığına veya orijinal yavru dal olup olmadığına bakılmaksızın değiştirilirler. Dalı değiştirdikten sonra, aralık dışı değerleri kontrol eder ve optimizasyon adımıyla uyumlu hale getiririz.

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Üçüncü operatör ise aşılamadır. Aşılama operatörü yazarlar tarafından görünüşe göre kombinatoryal bir operatör olarak düşünülmüştür ve yavru ve ebeveyn ağacın dallarının çiftin tüm dalları arasındaki ortalama farktan daha fazla farklılık gösterdiği durumlarda ebeveyn ağaçtan dalları kopyalamak için gerçekleştirilmelidir. Kulağa çok karmaşık geliyor, ancak bu operatör için çok az kullanım vardır ve bu nedenle bu operatör kaynak dosyalarda yoruma çevrilmiştir. Bu durumda bir uzman olarak hareket edemem ve bu nedenle bu operatör hakkında doğru bir anlayışa sahip olmayabileceğimi kabul ediyorum.

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Algoritmanın son ama önemli bir işlemi olan çimlendirme aşamasına geldik. Her yinelemede çalıştırılması zorunlu olan ikinci public metot Germination()'ı çalıştırıyoruz.

İlk yineleme sona eriyorsa (bunu 'sowing' bayrağından anlayacağız), bu ebeveyn bahçenin boş olduğu anlamına gelir. Yavru bahçedeki tüm fidanları, tüm genç ağaçları tek tek kopyalayarak ebeveyn bahçeye dikiyoruz. Bundan sonra, Sorting() metodunu kullanarak ebeveyn bahçeyi uygunluk değerine göre sıralıyoruz. Ağaçlar sıralandığında, 0. indeksteki ağaç en iyi uygunluğa sahip olacaktır ve halihazırda en iyi değilse en iyi global çözümü güncelleyebiliriz.

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

Kodun ilerleyen kısımlarında, 'sowing' bayrağı temkinli bir şekilde 'true' olarak ayarlandığından, algoritmada yalnızca ikinci ve sonraki yinelemelere ulaşacağız. İkinci ve sonraki yinelemelerde, fidanlar ebeveyn bahçeye aktarılmadan ve en kötü ağaçlar değiştirilmeden önce yavru bahçe sıralanmalıdır. Global çözümün iyileşip iyileşmediğini kontrol ederiz ve ardından en iyi n fidanı ebeveyn bahçenin sonuna kopyalarız.

Sonuç olarak, geriye sadece ebeveyn bahçeyi sıralamak kalıyor. Bahçe topluluğunun yeni üyeleri, eski nesillerin ağaçlarının yerini alabilecek ve optimizasyon görevlerinin sonuçlarıyla çiçek açmalarıyla bizi mutlu edebilecekler.

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);

3. Test sonuçları

SSG test ortamı sonuçları:

2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.7052793572295
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    Score: 0.99998
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    25 Rastrigin's; Func runs 10000 result: 77.3972262608643
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    Score: 0.95900
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    500 Rastrigin's; Func runs 10000 result: 52.24518909141432
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    Score: 0.64735
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    5 Forest's; Func runs 10000 result: 1.331178589711503
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    Score: 0.75298
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    25 Forest's; Func runs 10000 result: 1.019329018074209
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    Score: 0.57658
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    500 Forest's; Func runs 10000 result: 0.25410121872226443
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    Score: 0.14373
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    5 Megacity's; Func runs 10000 result: 6.4
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    Score: 0.53333
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    25 Megacity's; Func runs 10000 result: 4.504
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    Score: 0.37533
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    500 Megacity's; Func runs 10000 result: 1.2336
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Score: 0.10280
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    All score: 5.09109

SSG'nin çok fazla parametresi yoktur, ancak bu, algoritmada yapılan değişikliklerin bir sonucudur (orijinal SSG'nin daha da az parametresi vardır). Bununla birlikte, tüm parametreler ayrıcalıklı bir ilgiyi hak etmektedir. Testlerde aşağıdaki parametreler kullanılmıştır. Hatırlayacağınız gibi, her makalede testlerde mümkün olan en yüksek sonucu veren en iyi algoritma parametrelerini sunuyorum.

C_AO_SSG: 50; 0.3; 0.5; 0.4; 0.1

input int NumberTrees_P = 50; - bahçedeki ağaç sayısı. Bu parametre ile denemeler yapmadım (deneylerimde varsayılan değeri kullandım). Değerin 100 olması durumunda, algoritma toplamda daha iyi sonuçlar üretir, ancak bahçenin büyüklüğü göz önüne alındığında bahçeye göre izin verilen yineleme sayısındaki azalma nedeniyle ölçeklendirme yeteneği azalır. Çok sayıda dalı olan bir bahçenin evrimleşmek için zamanı yoktur.

input double SeedlingsReplacement_P = 0.3; - yavru bahçeden ebeveyn bahçeye aktarılacak fidan oranı.
input double ProbabMatingOperator_P = 0.5; - bir çift ağaç arasındaki mesafeyi dikkate alan olasılık yerine getirilirse çaprazlama (ebeveyn ağaçtan dal kopyalama) olasılığı.
input double ProbabBranchOperator_P = 0.4; - dallanma olasılığı (dalların büyümesi/küçülmesi). Bu, algoritmanın performansını önemli ölçüde etkileyen önemli bir parametredir (genellikle tüm parametreler önemlidir).
input double PowerBranchOperator_P = 0.1; - dallanma gücü. Bu, optimize edilen parametrelerin boyutunda bir ölçeklendirme faktörüdür, 1.0 veya daha fazlası, dalların bahçenin sınırlarına kadar büyümesi anlamına gelecektir, 0.0 - dalların büyümesi yok demektir, yani yeni dal büyüklükleri ortaya çıkmayacak ve algoritma basit bir kombinatorik araca dönüşecektir (bu muhtemelen SSG'yi kullanmak için harika bir fikirdir, ancak burada daha fazla araştırma gereklidir).

SSG algoritmasının test fonksiyonları üzerindeki animasyonuna dikkat ederseniz, bahçede herhangi bir ağaç hareketi modelinin olmadığını fark edeceksiniz, sadece yerel ekstremumlarda bazı "kümelenmeler" fark edilebilir. Bununla birlikte, daha önce ele alınan algoritmalarla karşılaştırıldığında yüksek yakınsama kalitesi hemen fark edilir. Sonuçların istikrarlı bir şekilde tekrarlanabilirliği de dikkat çekicidir.

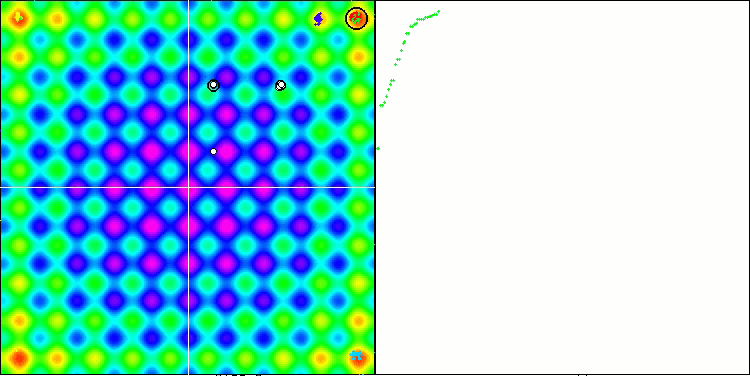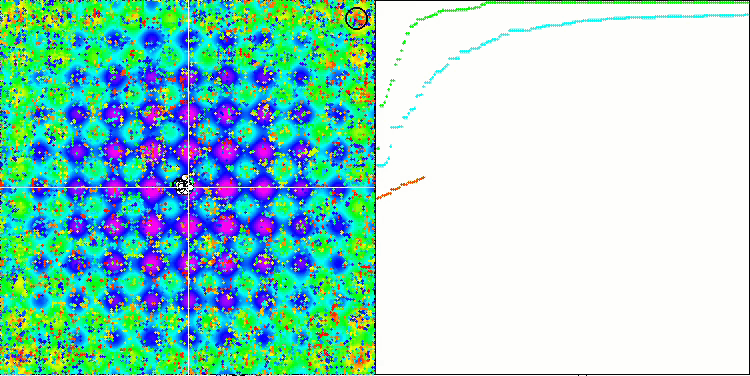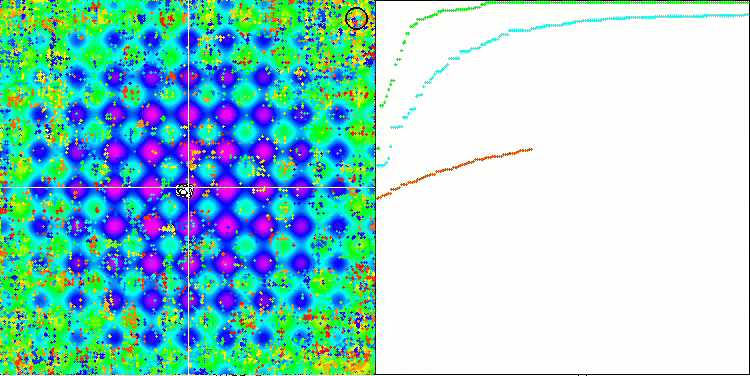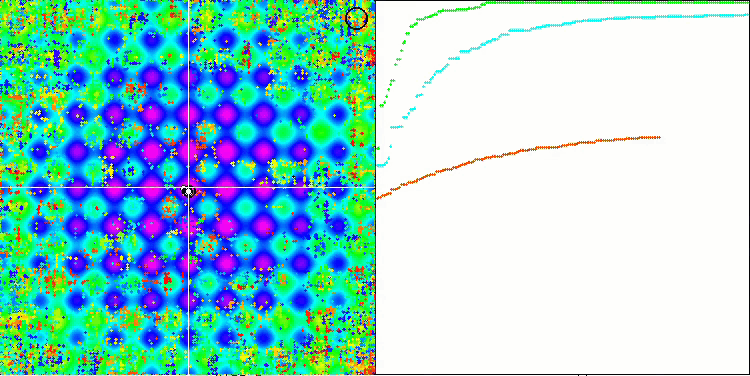
  Rastrigin test fonksiyonu üzerinde SSG

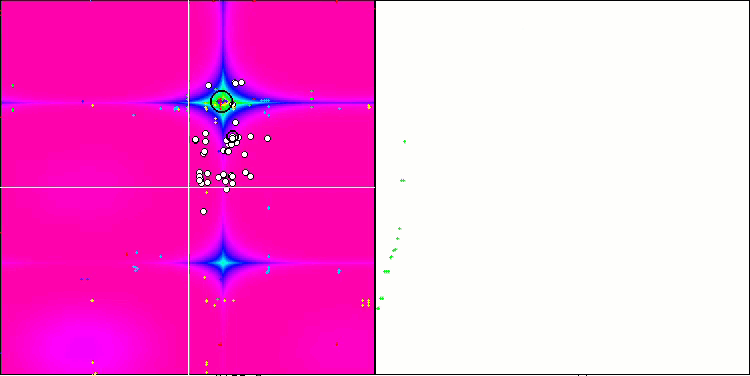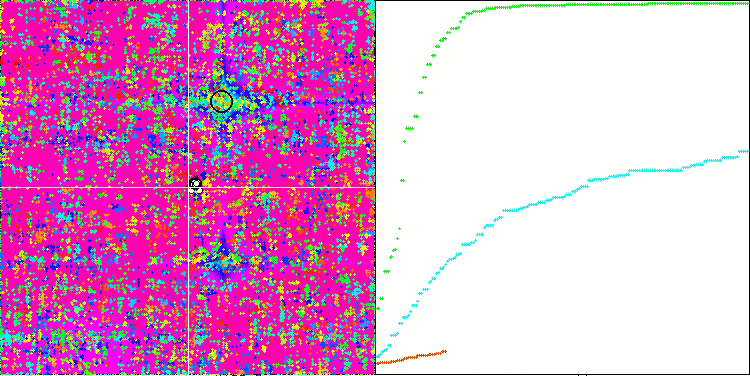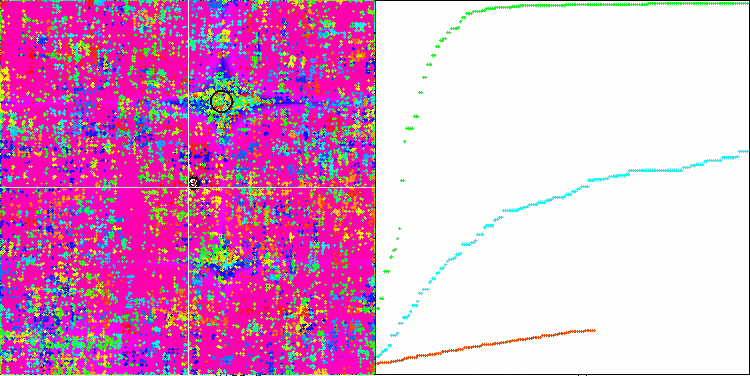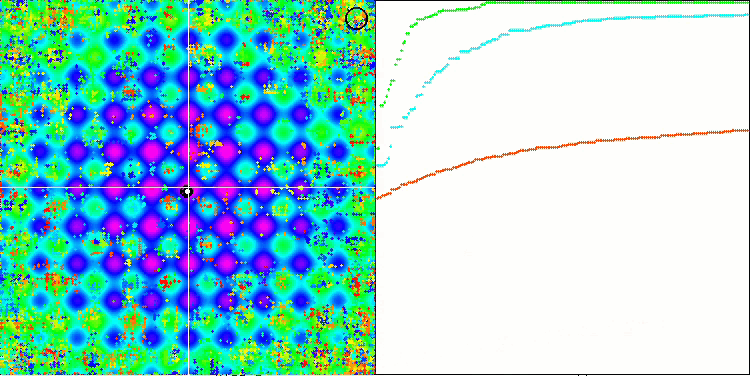
  Forest test fonksiyonu üzerinde SSG

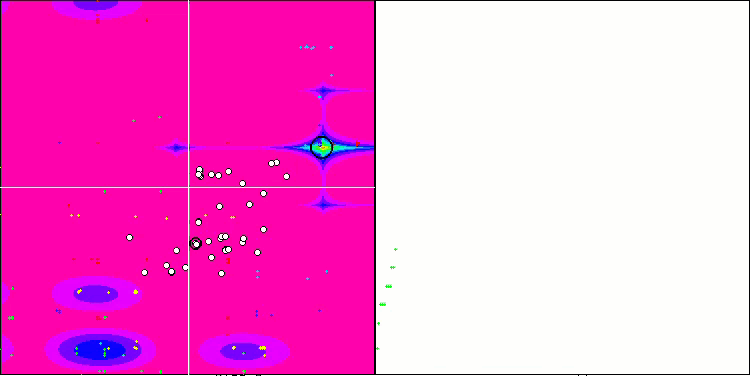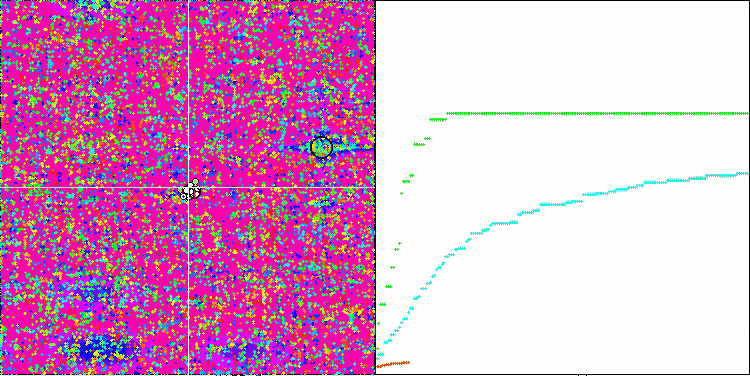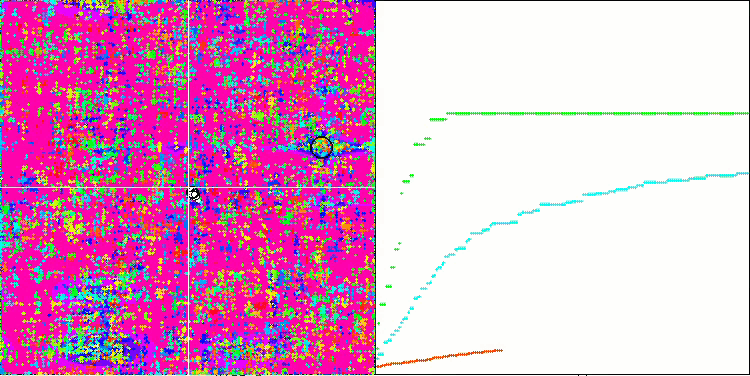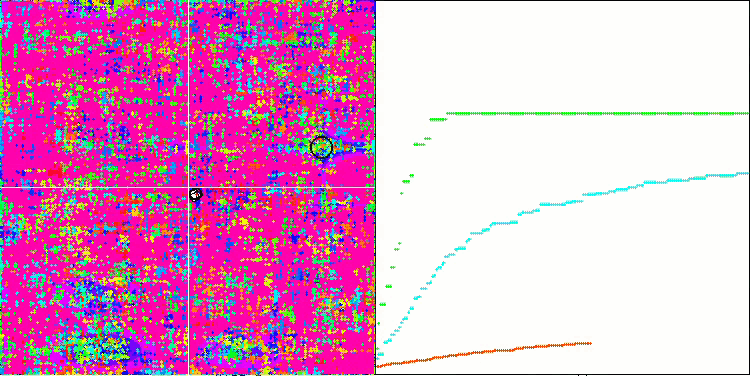
  Megacity test fonksiyonu üzerinde SSG

SSG algoritmasının sonuçlarını tartışmaya geçelim. Kesinlikle konuşulacak bir şeyler var. Algoritma, rakiplerini geride bırakarak derecelendirmenin ilk sırasına zaferle yerleşti! Algoritma, karar ağaçlarını değiştirmek için uygunluk bilgisini doğrudan kullanmaz. Uygunluk sadece yavru bahçeyi ve ebeveyn bahçeyi sıralamak için gereklidir, bu nedenle algoritmanın testlerde bu kadar dikkat çekici sonuçlar gösterebilmesi daha da şaşırtıcıdır.

Bu, oryantiringde körler takımının görenler takımını yenmesiyle aynı şeydir. Algoritma, altı testin dördünde tablodaki katılımcıların önünde yer alırken, lider olmadığı testlerde de çok geride kalmadı. SSG, Megacity ayrık fonksiyonunda rakiplerine karşı en etkileyici liderliği göstererek en yakın rakibi HS'yi neredeyse %60 oranında geride bıraktı! Bu, algoritmanın mükemmel ölçeklenebilirliğini göstermektedir. En iyi ölçeklenebilirlik sonucu da "keskin" Forest test fonksiyonunda gözlemlenmiştir. SSG, bu testteki en iyi rakibinden (ACOm) neredeyse %30 daha iyi performans göstermiştir.

AO	Açıklama	Rastrigin			Rastrigin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)
SSG	Fidan dikimi ve büyütme	1.00000	1.00000	0.65914	2.65914	0.70823	0.94522	1.00000	2.65345	0.71532	0.85412	1.00000	2.56944	100.000
HS	Armoni araması	0.99676	0.95282	0.57048	2.52006	1.00000	0.98931	0.44806	2.43736	1.00000	1.00000	0.41537	2.41537	93.370
ACOm	Karınca kolonisi optimizasyonu (m)	0.34611	0.17985	0.20182	0.72778	0.85966	1.00000	0.77362	2.63327	1.00000	0.88484	0.05606	1.94090	66.407
IWO	İstilacı yabancı ot optimizasyonu	0.95828	0.67083	0.35295	1.98207	0.68718	0.46349	0.31773	1.46840	0.75912	0.39732	0.33289	1.48933	61.691
COAm	Guguk kuşu optimizasyon algoritması (m)	0.92400	0.46794	0.30792	1.69987	0.55451	0.34034	0.16526	1.06012	0.67153	0.30326	0.17083	1.14561	48.226
FAm	Ateş böceği algoritması (m)	0.59825	0.33980	0.20290	1.14095	0.47632	0.42299	0.49790	1.39721	0.21167	0.25143	0.35258	0.81568	41.042
ABC	Yapay arı kolonisi	0.78170	0.32715	0.24656	1.35541	0.50591	0.21455	0.13344	0.85390	0.47444	0.23609	0.13926	0.84979	37.204
BA	Yarasa algoritması	0.40526	0.63761	1.00000	2.04287	0.15275	0.17477	0.25989	0.58741	0.15329	0.06334	0.17371	0.39034	36.703
GSA	Yerçekimsel arama algoritması	0.70167	0.45217	0.00000	1.15384	0.26854	0.36416	0.33204	0.96475	0.51095	0.32436	0.00000	0.83531	35.834
BFO	Bakteri yiyecek arama optimizasyonu	0.67203	0.30963	0.13988	1.12154	0.35462	0.26623	0.20652	0.82736	0.42336	0.30519	0.18932	0.91786	34.700
MA	Maymun algoritması	0.33192	0.33451	0.17340	0.83983	0.03684	0.07891	0.08932	0.20508	0.05838	0.00383	0.10720	0.16941	13.185
FSS	Balık sürüsü arama	0.46812	0.25337	0.13383	0.85532	0.06711	0.05013	0.06516	0.18240	0.00000	0.00959	0.08283	0.09242	12.089
PSO	Parçacık sürüsü optimizasyonu	0.20449	0.08200	0.08478	0.37127	0.13192	0.10486	0.21738	0.45415	0.08028	0.02110	0.01957	0.12095	9.696
RND	Rastgele	0.16826	0.09743	0.09495	0.36065	0.07413	0.04810	0.04715	0.16938	0.00000	0.00000	0.04922	0.04922	4.916
GWO	Gri kurt optimizasyonu	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.02557	0.25179	1.000

Özet

SSG özellikleri: optimize edilen fonksiyonun türevlenebilirliği ve sürekliliği için herhangi bir gereklilik yoktur, uygulanan temsil ve kodlamaların türü üzerinde herhangi bir kısıtlama yoktur. Algoritma, bireysel temsilcilerin uygunluk bilgilerini ve bir bütün olarak en iyi çözümü kullanmaz. Bu özellikleri sayesinde SSG, çok karmaşık olanlar da dahil olmak üzere çeşitli optimizasyon problemlerine kolayca uygulanabilir. SSG, yatırımcıların problemlerinde ve makine öğreniminde kullanım için kesinlikle tavsiye edilebilir. Bu makalenin yazıldığı sırada, fidan dikimi ve büyütme (SSG) algoritması yakınsama kalitesi, sonuçların istikrarı ve ölçeklenebilirlik konularında tartışmasız lider konumdadır.

Şekil 2 algoritmanın test sonuçlarını göstermektedir.

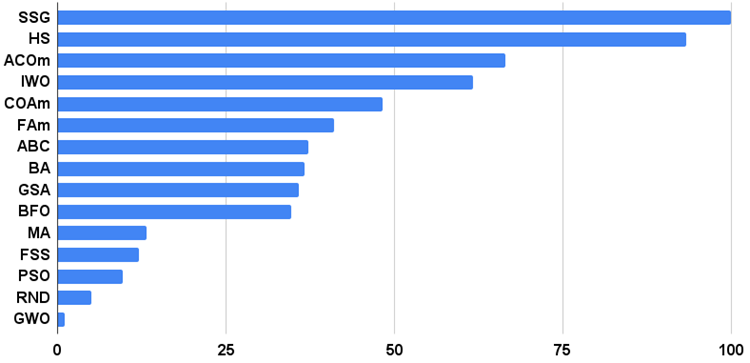
Şekil 2. Algoritmaların test sonuçlarının histogramı

SSG algoritmasının avantajları ve dezavantajları:

Avantajları:
1. Kolay uygulama.
2. İstisnasız tüm fonksiyon türlerinde mükemmel yakınsama.
3. Etkileyici ölçeklenebilirlik.

Dezavantajları:
1. Anlaşılır olmalarına rağmen çok sayıda özelleştirme seçeneği.

Her makale, önceki tüm makalelerdeki algoritma kodlarının güncellenmiş sürümlerini içeren bir arşive sahiptir. Makale, yazarın birikmiş deneyimlerine dayanmaktadır ve kişisel görüşünü temsil etmektedir. Sonuçlar ve yargılar deneylere dayanmaktadır.