OpenCL: Sade Programlamadan Daha Öngörülü Programlamaya Doğru
202
0
Giriş
İlk makale "OpenCL: Paralel Dünyalara Köprü", OpenCL konusuna bir giriş niteliğindeydi. OpenCL'deki program (tam olarak doğru olmasa da çekirdek olarak da adlandırılır) ile MQL5'teki harici (ana bilgisayar) program arasındaki temel etkileşim sorunlarını ele almıştır. Bazı dil performans özellikleri (örneğin vektör veri türlerinin kullanımı) pi = 3.14159265... hesaplaması ile örneklenmiştir.
Program performans optimizasyonu bazı durumlarda önemliydi. Ancak tüm bu optimizasyonlar, tüm hesaplamalarımızı gerçekleştirmek için kullanılan donanım özelliklerini dikkate almadıkları için yetersizdi. Bu özelliklerin bilgisi, çoğu durumda, CPU'nun özelliklerini önemli ölçüde aşan hızlanmaları bilinçli olarak elde etmemizi sağlayabilir.
Bu optimizasyonları göstermek için yazarın artık orijinal olmayan bir örneğe başvurması gerekti ve bu muhtemelen OpenCL literatüründe en kapsamlı şekilde incelenenlerden biridir. İki büyük matrisin çarpımıdır.
Ana meseleyle başlayalım - OpenCL bellek modeli ve gerçek donanım mimarisine uygulanmasının özellikleri.
1. Modern Bilgi İşlem Cihazlarında Bellek Hiyerarşisi
1.1. OpenCL Bellek Modeli
Genel olarak konuşursak, bellek sistemleri bilgisayar platformlarına bağlı olarak birbirinden büyük ölçüde farklılık gösterir. Örneğin, tüm modern CPU'lar, durumun her zaman böyle olmadığı GPU'ların aksine otomatik veri önbelleğe almayı destekler.
Kod taşınabilirliğini sağlamak için, OpenCL'de programcıların yanı sıra bu modeli gerçek donanıma uygulaması gereken satıcılar için kullanabilecekleri soyut bir bellek modeli benimsenmiştir. OpenCL'de tanımlanan bellek, aşağıdaki Şekilde kavramsal olarak gösterilebilir:
Şekil 1. OpenCL Bellek Modeli
Veriler ana bilgisayardan cihaza aktarıldıktan sonra global cihaz belleğinde saklanır. Ters yönde aktarılan herhangi bir veri de global bellekte (ancak bu sefer global ana bilgisayar belleğinde) saklanır. __global (iki alt çizgi!) anahtar sözcüğü, belirli bir işaretçiyle ilişkili verilerin global bellekte depolandığını belirten bir değiştiricidir:
__kernel void foo( __global float *A ) { /// kernel code }
Global belleğe, ana bilgisayar sistemindeki RAM gibi cihaz içindeki tüm bilgi işlem birimleri tarafından erişilebilir.
Sabit bellek, adından farklı olarak salt okunur verileri depolamak zorunda değildir. Bu bellek türü, her öğeye tüm iş birimleri tarafından aynı anda erişilebildiği veriler için tasarlanmıştır. Sabit değerli değişkenler de elbette bu kategoriye girer. OpenCL modelindeki sabit bellek, global belleğin bir parçasıdır ve global belleğe aktarılan bellek nesneleri bu nedenle __constant olarak belirtilebilir.
Yerel bellek, adres alanının her cihaza özgü olduğu bloknot belleğidir. Donanımda, genellikle yonga üstü bellek biçiminde gelir, ancak OpenCL için tam olarak aynı olması için özel bir gereklilik yoktur.
Bu tür belleğe erişim, çok daha düşük gecikme süresine neden olur ve bu nedenle bellek bant genişliği, global belleğe göre çok daha fazladır. Çekirdek performans optimizasyonu için düşük gecikme süresinden yararlanmaya çalışacağız.
OpenCL özelliklerinde, yerel bellekteki bir değişkenin hem çekirdek başlığında
__kernel void foo( __local float *sharedData ) { }hem de gövdesinde bildirilebileceği söylenir:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Çekirdek gövdesinde dinamik bir dizinin bildirilemeyeceğine dikkat edin; her zaman boyutunu belirtmelisiniz.
Aşağıda, iki büyük matrisin çarpımı için çekirdeğin optimizasyonunda, yerel verilerin nasıl ele alınacağını ve yazarın deneyimlediği gibi MetaTrader 5'te hangi uygulama özelliklerini gerektirdiğini göreceksiniz.
İşaretçi içermeyen yerel değişkenler ve çekirdek bağımsız değişkenleri varsayılan olarak özeldir (__local değiştiricisi olmadan belirtilmişse). Uygulamada, bu değişkenler genellikle kayıtlarda bulunur. Ve tam tersi, özel diziler ve taşan kayıtlar genellikle yonga dışı bellekte, yani daha yüksek gecikme süreli bellekte bulunur. İlgili bilgileri Vikipedi’den alıntılayayım:
Birçok programlama dilinde, programcı keyfi olarak birçok değişken tahsis etme yanılsamasına sahiptir. Bununla birlikte, derleme sırasında, derleyici bu değişkenleri küçük, sonlu bir kayıt kümesine nasıl tahsis edeceğine karar vermelidir. Tüm değişkenler aynı anda kullanımda (veya "canlı") değildir, bu nedenle bazı kayıtlar birden fazla değişkene atanabilir. Ancak, aynı anda kullanımda olan iki değişken, değeri bozulmadan aynı kayda atanamaz.
Bazı kayıtlara atanamayan değişkenler RAM'de tutulmalı ve her okuma/yazma işlemi için içeri/dışarı yüklenmelidir, bu işleme taşma denir. RAM'e erişim, kayıtlara erişmekten önemli ölçüde daha yavaştır ve derlenmiş programın yürütme hızını yavaşlatır, bu nedenle bir optimizasyon derleyicisi, kayıtlara mümkün olduğunca çok değişken atamayı amaçlar. Kayıt basıncı, optimal olandan daha az sayıda donanım kaydı olduğunda kullanılan terimdir; daha yüksek basınç, genellikle daha fazla taşma ve yeniden yüklemeye ihtiyaç duyulduğu anlamına gelir.
Açıklandığı gibi OpenCL bellek modeli, modern GPU'ların bellek yapısına çok benzer. Aşağıdaki Şekil, OpenCL bellek modeli ile GPU AMD Radeon HD 6970 bellek modeli arasındaki ilişkiyi göstermektedir.
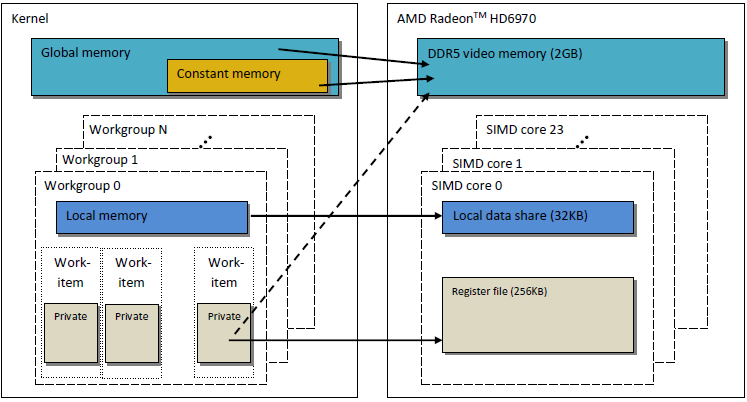
Şekil 2. Radeon HD 6970 bellek yapısı ile soyut OpenCL bellek modeli arasındaki ilişki
Belirli bir GPU bellek uygulamasıyla ilgili sorunları daha ayrıntılı olarak ele alalım.
1.2. Modern Ayrı GPU'larda Bellek
1.2.1. Bellek İsteklerini Birleştirme
Ana amaç yüksek bellek bant genişliği elde etmek olduğundan, bu bilgi çekirdek performans optimizasyonu için de önemlidir.
Bellek adresleme sürecini daha iyi anlamak için aşağıdaki şekle bakın:
Şekil 3. Global cihaz belleğindeki adresleme verilerinin şeması
İnt tamsayı değişkenleri dizisinin işaretçisinin Х = 0x00001232 adresi olduğunu varsayalım. Her int 4 bayt bellek kaplar. Bir iş parçacığının (çekirdek kodunu yürüten bir iş biriminin yazılım analoğudur) Х[ 0 ] konumundaki verileri adreslediğini varsayalım:
int tmp = X[ 0 ];
Bellek veri yolu genişliğinin 32 bayt (256 bit) olduğunu varsayalım. Bu veri yolu genişliği, Radeon HD 5870 gibi güçlü GPU'lar için tipiktir. Diğer bazı GPU'larda, veri yolu genişliği farklı olabilir, örneğin bazı NVidia modellerinde 384 bit veya hatta 512 olabilir.
Bellek veri yolunun adreslenmesi, yapısına, yani her şeyden önce genişliğine uygun olmalıdır. Başka bir deyişle, bellekteki veriler, her biri 32 baytlık (256 bit) bloklarda saklanır. 0x00001220 ile 0x0000123F aralığında neyi adreslediğimize bakılmaksızın (bu aralıkta tam olarak 32 bayt vardır, kendiniz görebilirsiniz), yine de okuma için bir başlangıç adresi olarak 0x00001220 adresini alacağız.
0x00001232 adresinden erişim, 0x00001220 ila 0x0000123F aralığındaki adreslerdeki tüm verileri, yani 8 int sayıyı döndürecektir. Bu nedenle, yalnızca 4 bayt (bir int sayı) yararlı veri olacak ve kalan 28 bayt (7 int sayı) gereksiz olacaktır:
Şekil 4. Gerekli verileri bellekten alma şeması
Daha önce belirtilen adreste bulunmasını istediğimiz numara - 0x00001232 - şemada daire içine alınmıştır.
Veri yolunun kullanımını en üst düzeye çıkarmak için GPU, farklı iş parçacıklarından bellek erişimlerini tek bir bellek isteğinde birleştirmeye çalışır; ne kadar az bellek erişimi olursa o kadar iyidir. Bunun nedeni, global cihaz belleğine erişmenin bize zaman kaybettirmesi ve dolayısıyla programın çalışma hızını büyük ölçüde düşürmesidir. Çekirdek kodunun aşağıdaki satırını göz önünde bulundurun:
int tmp = X[ get_global_id( 0 ) ];
Dizimizin Х, yukarıda verilen önceki örnekteki dizi olduğunu varsayalım. Ardından ilk 16 iş parçacığı (çekirdek) 0x00001232 ile 0x00001272 arasındaki adreslere erişecektir (bu aralıkta 16 int sayı, yani 64 bayt vardır). Her istek, önceden tek birine birleştirilmeden, çekirdekler tarafından bağımsız olarak gönderilseydi, 16 isteğin her biri 4 bayt yararlı veri ve 28 bayt gereksiz veri içerecek ve böylece toplam 64 kullanılmış ve 448 kullanılmayan bayt olacaktı.
Bu hesaplama, bir ve aynı 32 baytlık bellek bloğu içinde bulunan bir adrese her erişimin kesinlikle aynı verileri döndüreceği gerçeğine dayanmaktadır. Bu, kilit noktadır. Yararsız isteklerden tasarruf etmek için birden çok isteği tek, tutarlı isteklerde birleştirmek daha doğru olacaktır. Bu işlem bundan böyle birleştirme olarak adlandırılacak ve birleştirilmiş talepler bu şekilde tutarlı olarak anılacaktır.
Şekil 5. Gerekli verileri elde etmek için yalnızca üç bellek isteği gereklidir
Yukarıdaki Şekildeki her hücre 4 bayttır. Örneğimizde 3 istek yeterli olacaktır. Dizinin başlangıcı, her 32 baytlık bellek bloğunun başındaki adrese göre hizalanmışsa, 2 istek bile yeterli olacaktır.
AMD GPU 64'te, iş parçacıkları bir dalga cephesinin bir parçasıdır ve bu nedenle SIMD yürütmesindekiyle aynı talimatı yürütmelidir. get_global_id( 0 ) tarafından düzenlenen ve dalga cephesinin tam olarak çeyreği olan 16 iş parçacığı, veri yolunun verimli kullanımı için tutarlı bir istekte birleştirilir.
Aşağıda, tutarlı istekler için gerekli olan bellek bant genişliğinin tutarsız, yani "spontane" isteklere kıyasla bir gösterimi bulunmaktadır. Radeon HD 5870 ile ilgilidir. Benzer bir sonuç NVidia kartları için de gözlemlenebilir.
Şekil 6. Tutarlı ve tutarsız istekler için gereken bellek bant genişliğinin karşılaştırmalı analizi
Tutarlı bir bellek talebinin bellek bant genişliğini yaklaşık bir büyüklük sırası kadar artırmaya izin verdiği açıkça görülebilir.
1.2.2. Bellek Bankaları
Bellek, verilerin gerçekte depolandığı bankalardan oluşur. Modern GPU'larda bunlar genellikle 32 bit (4 bayt) kelimedir. Seri veriler bitişik bellek bankalarında saklanır. Seri öğelere erişen bir grup iş parçacığı, herhangi bir banka çakışması oluşturmaz.
Banka çakışmalarının maksimum olumsuz etkisi genellikle yerel GPU belleğinde görülür. Bu nedenle, komşu iş parçacıklarından yerel veri erişimlerinin farklı bellek bankalarını hedeflemesi tavsiye edilir.
AMD donanımında, banka çakışmaları oluşturan dalga cephesi, tüm yerel bellek işlemleri tamamlanana kadar durur. Bu, paralel olarak yürütülmesi gereken kod bloklarının sırayla yürütüldüğü serileştirmeye yol açar. Çekirdeğin performansı üzerinde son derece olumsuz bir etkisi vardır.
Şekil 7. Banka çakışmaları olmadan bellek erişim şemaları
Yukarıdaki Şekil, tüm iş parçacıkları farklı verilere eriştiği için banka çakışmaları olmadan bellek erişimini gösterir.
Banka çakışmaları ile bellek erişimini gösterelim:
Şekil 8. Banka çakışmaları ile bellek erişimi
Ancak bu durumun bir istisnası vardır: tüm erişimler aynı adrese yapılırsa, gecikmeyi önlemek için banka bir yayın yapabilir:
Şekil 9. Tüm iş parçacıkları aynı adrese erişiyor
Benzer olaylar, global belleğe erişirken de meydana gelir, ancak bu tür çakışmaların etkisi oldukça düşüktür.
- GPU belleği CPU belleğinden farklıdır. OpenCL kullanarak program performansını optimize etmenin temel amacı, CPU'da olduğu gibi gecikmeyi azaltmak yerine maksimum bant genişliğini sağlamaktır.
- Bellek erişiminin doğası, veri yolu kullanımının verimliliği üzerinde büyük bir etkiye sahiptir. Düşük veri yolu kullanım verimliliği, düşük çalışma hızı anlamına gelir.
- Kodun performansını artırmak için bellek erişiminin tutarlı olması önerilir. Ayrıca, banka çatışmalarından kaçınmak oldukça tercih edilir.
- Donanım özellikleri (veri yolu genişliği, bellek bankalarının sayısı ve tek bir tutarlı erişim için birleştirilebilecek iş parçacıklarının sayısı) satıcı tarafından sağlanan belgelerde bulunabilir.
Radeon 5xxx serisi video kartlarının bazılarının özellikleri aşağıda örnek olarak verilmiştir:
Şekil 10. Orta ve üst seviye Radeon HD 58xx video kartlarının teknik özellikleri
Şimdi programlamaya geçelim.
2. Büyük Kare Matrislerin Çarpımı: Seri CPU Kodundan Paralel GPU Koduna
2.1. MQL5 Kodu
Önceki "OpenCL: Paralel Dünyalara Köprü" makalesinin aksine, eldeki görev standarttır, yani iki matrisi çarpmak. Öncelikle konuyla ilgili oldukça fazla bilginin farklı kaynaklarda bulunabilmesi nedeniyle seçilmiştir. Çoğu, öyle ya da böyle, az çok koordineli çözümler sunar. Bu, gerçek donanım üzerinde çalıştığımızı unutmadan, model yapılarının anlamını adım adım açıklayarak gideceğimiz yoldur.
Aşağıda, lineer cebirde iyi bilinen, bilgisayar hesaplamaları için değiştirilmiş bir matris çarpım formülü verilmiştir. İlk dizin matris satır numarası, ikinci dizin sütun numarasıdır. Her çıktı matrisi elemanı, birinci ve ikinci matrislerdeki elemanların ardışık her bir ürününün birikmiş toplama sırayla eklenmesiyle hesaplanır. Sonuç olarak, bu birikmiş toplam, hesaplanan çıktı matrisi elemanıdır:
Şekil 11. Matris çarpım formülü
Şematik olarak aşağıdaki gibi gösterilebilir:
Şekil 12. Şekil 12. Şematik olarak gösterilen matris çarpma algoritması (bir çıktı matris elemanının hesaplanmasıyla örneklenmiştir)
Her iki matrisin de N'ye eşit boyutlara sahip olduğu durumlarda, toplama ve çarpma sayısının O(N^3) işleviyle tahmin edilebileceği kolayca görülebilir: her çıktı matrisi öğesini hesaplamak için birinci matristeki bir satır ve ikinci matristeki bir sütunun skaler çarpımını elde etmeniz gerekir. Yaklaşık 2*N toplama ve çarpma işlemi gerektirir. N^2 matris elemanlarının sayısı ile çarpılarak gerekli bir tahmin elde edilir. Bu nedenle, yaklaşık kod çalışma zamanı çok büyük ölçüde N küpüne bağlıdır.
Matrisler için satır ve sütun sayısı bundan sonra yalnızca kolaylık olması amacıyla 2000'e ayarlanmıştır; rastgele olabilirler ama çok büyük olamazlar.
MQL5'teki kod çok karmaşık değildir:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Liste 1. Ana bilgisayardaki ilk sıralı program
Farklı parametreler kullanıldığında performans sonuçları:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Görülebileceği gibi, çalışma zamanının lineer matris boyutlarına olan tahmini bağımlılığımızın doğru olduğu ortaya çıktı: Tüm matris boyutlarında iki katlık bir artış, çalışma zamanında yaklaşık 8 kat artışla sonuçlandı.
Algoritma hakkında birkaç laf edelim: Döngü sırası, çarpma fonksiyonu mul() içinde keyfi olarak değiştirilebilir. Çalışma zamanı üzerinde önemli bir etkisi olduğu ortaya çıkmıştır: En yavaş çalışma zamanı çeşidinin en hızlı çalışma zamanı çeşidine oranı yaklaşık 1,73'tür.
Makale yalnızca en hızlı çeşidi gösterir; kalan test edilmiş varyantlar makalenin sonunda ekli kodda bulunabilir (dosya matr_mul_2dim.mq5). Bu bağlamda OpenCL Programlama Kılavuzu (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) şöyle diyor (s. 512):
Bunlar açıkçası, uygulayabileceğimiz ilk "paralel olmayan" kodun tüm optimizasyonları değildir. Bazıları donanımla ((S)SSEx talimatlarıyla) ilgiliyken diğerleri tamamen algoritmiktir, örneğin Strassen algoritması, Coppersmith–Winograd algoritması, vb. Klasik algoritmaya göre önemli ölçüde hızlanmaya yol açan Strassen Algoritması için çarpılan matrislerin boyutunun oldukça küçük olduğunu, yalnızca 64х64 olduğunu unutmayın. Bu makalemizde, lineer boyutu birkaç bin (yaklaşık 5000) olan matrisleri hızlıca çarpmayı öğreneceğiz.
2.2. Algoritmanın OpenCL'deki İlk Uygulaması
Şimdi bu algoritmayı OpenCL'ye taşıyalım, ROWS1 * COLS2 iş parçacıkları oluşturalım, yani her iki dış döngüyü de çekirdekten silelim. Her iş parçacığı COLSROWS yinelemelerini yürütür, böylece iç döngü çekirdeğin bir parçası olarak kalır.
OpenCL çekirdeği için üç doğrusal arabellek oluşturmamız gerekeceğinden, ilk algoritmayı mümkün olduğunca çekirdek algoritmasına benzer olacağı şekilde yeniden çalışmak mantıklı olacaktır. Lineer arabelleklere sahip bir "tek çekirdekli CPU" üzerindeki "paralel olmayan" programın kodu, çekirdek koduyla birlikte sağlanacaktır. Kodun iki boyutlu dizilerle optimalliği, analoğunun lineer arabellekler için de optimal olacağı anlamına gelmez: tüm testlerin tekrarlanması gerekecektir. Bu nedenle, lineer cebirde standart matris çarpım mantığına karşılık gelen başlangıç çeşidi olarak yine c-r-cr'yi seçiyoruz.
Bununla birlikte, olası bir matris/arabellek öğesini adreslemekle ilgili bir karışıklığı önlemek için ana soruyu yanıtlayın: Bir matris Matr(M satır x N sütun) global GPU belleğinde lineer bir arabellek olarak düzenlenirse, bir Matr[ satır ][ sütun ] elemanının lineer bir kaymasını nasıl hesaplayabiliriz?
Aslında, yalnızca sorunun mantığı tarafından belirlendiğinden, GPU belleğinde bir matris düzenlemenin sabit bir sırası yoktur. Örneğin, matris çarpım algoritması söz konusu olduğunda, matrisler asimetrik olduğundan, yani birinci matrisin satırları ikinci matrisin sütunlarıyla çarpıldığından, her iki matrisin öğeleri arabelleklerde farklı şekilde düzenlenebilir. Bu tür bir yeniden düzenleme, çekirdeğin her yinelemesinde matris öğelerinin global GPU belleğinden sıralı olarak okunmasındaki hesaplama performansını büyük ölçüde etkileyebilir.
Algoritmanın ilk uygulaması, aynı şekilde -ana-satır sıralamasında- düzenlenmiş matrisleri içerecektir. İlk satır öğeleri arabelleğe ilk yerleştirilecek, ardından ikinci satırın tüm öğeleri gelecektir, vb. Bir Matr[ M (satır) ][ N (sütun) ] matrisinin 2 boyutlu temsilini lineer belleğe düzleştirme formülü aşağıdaki gibidir:
Şekil 13. Matrisi GPU arabelleğine yerleştirmek için iki boyutlu bir dizin alanını lineere dönüştürmek için algoritma
Yukarıdaki Şekil ayrıca, 2 boyutlu bir matris gösteriminin, sütun ana düzeninde nasıl düzleştirilip lineer belleğe çevrildiğine dair bir örnek verir.
Aşağıda, OpenCL cihazında yürütülen ilk program uygulamamızın biraz kısaltılmış bir kodu bulunmaktadır:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Liste 2. Programın OpenCL'deki ilk uygulaması
Son iki fonksiyon, hesaplamaların doğruluğunu doğrulamada faydalıdır. Kodun tamamı makalenin sonunda ekte bulunabilir (matr_mul_1dim.mq5). Boyutların mutlaka yalnızca kare matrislere karşılık gelmek zorunda olmadığını unutmayın.
Diğer değişiklikler hemen hemen her zaman yalnızca çekirdek kodunu ilgilendirecektir, dolayısıyla bundan sonra yalnızca çekirdek değişiklik kodları belirtilecektir.
REALTYPE türü, hesaplama hassasiyetini kaydırma türünden çift türe değiştirme kolaylığı için sunulmuştur. REALTYPE türünün sadece ana bilgisayar programında değil aynı zamanda çekirdek içerisinde de bildirildiğini belirtmek gerekir. Gerekirse, bu türle ilgili herhangi bir değişiklik, hem ana bilgisayar programının #define hem de çekirdek kodunda aynı anda iki yerde yapılmalıdır.
Kod performansı sonuçları (bundan böyle, her yerde kayan veri türü):
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Radeon HD 4870'te çalıştırıldığında (_device = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Görüldüğü gibi, çekirdeğin GPU üzerinde yürütülmesi çok daha yavaştır. Ancak, özellikle GPU için optimizasyonu henüz ele almadık.
Birkaç sonuç:
- Matris gösteriminin iki boyutludan lineere değiştirilmesi (cihazda yürütülen programdaki gösterime karşılık gelir), programın sıralı versiyonunun toplam çalışma zamanı üzerinde önemli bir etkiye sahip olmamıştır.
- Lineer cebirdeki matris çarpımının tanımıyla eşleşen en sezgisel hesaplama algoritması, daha fazla optimizasyon için ilk çeşit olarak seçilmiştir. En hızlı olandan biraz daha yavaştır, ancak GPU'da gelecekteki hızlanma göz önüne alındığında bu faktör önemli değildir.
- Çalışma zamanı, CLExecute() komutundan sonra değil, yalnızca arabellekleri RAM'e okuduktan sonra hesaplanmalıdır. MetaDriver tarafından yazara işaret edilen bunun arkasındaki sebep muhtemelen şudur:MetaDriver: Arabellekten okumadan önce, CLBufferRead() sadece programın fiilen tamamlanmasını bekler. CLExecute() aslında asenkron bir kuyruğa alma fonksiyonudur. cl kodu işlemi tamamlanmadan önce, sonucu hemen döndürür.
- GPU hesaplama kılavuzları genellikle çekirdek çalışma zamanını hesaplamaz, bunun yerine çeşitli nesnelerle (bellek, aritmetik vb.) ilgili çıktıyı hesaplar. Bundan sonra da aynısını yapabiliriz ve yapacağız.
2000 boyutunda bir matrisin hesaplanmasının her eleman için yaklaşık 2 * 2000 toplama/çarpma gerektirdiğini biliyoruz. Matris elemanlarının sayısıyla (2000 * 2000) çarparak, kaydırma türü veriler üzerindeki toplam işlem sayısının 16 milyar olduğunu buluyoruz. Bununla birlikte, CPU üzerindeki yürütme 115.628 saniye sürer ve bu da
Öte yandan, 2000 matris boyutuna sahip bir "tek çekirdekli CPU" üzerinde şimdiye kadarki en hızlı hesaplamanın tamamlanmasının yalnızca 83.663 saniye sürdüğünü unutmayın (OpenCL'siz ilk kodumuza bakın). Buradan
Bu rakamı, optimizasyonlarımız için bir referans, başlangıç noktası olarak alalım.
Benzer şekilde, CPU üzerinde OpenCL kullanılarak yapılan hesaplama şu sonuçları verir:
Son olarak, GPU'daki verimi hesaplayalım:
2.3. Tutarsız Veri Erişimlerini Ortadan Kaldırma
Çekirdek koduna baktığınızda, birkaç uygunsuzluğu kolayca fark edebilirsiniz.
Çekirdek içindeki döngünün gövdesine bir göz atın:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
Döngü sayacı (cr++) çalışırken, 1[]'deki ilk arabellekten bitişik verilerin alındığı kolayca görülmektedir. 2[]’deki ikinci arabellekten gelen veriler, COLS2'ye eşit "boşluklar" ile alınır. Diğer bir deyişle, bellek istekleri tutarsız olacağından, ikinci arabellekten alınan verilerin büyük bir kısmı işe yaramaz olacaktır (bakınız 1.2.1. Bellek İsteklerini Birleştirme). Bu durumu düzeltmek için, in2[] dizisinin indeksinin hesaplanması için formülü ve bunun yanı sıra oluşturma modelini değiştirerek kodu üç yerde değiştirmek yeterlidir:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Şimdi, döngü sayacı (cr++) değerleri değiştiğinde, her iki dizideki veriler herhangi bir "boşluk" olmadan sırayla alınacaktır.
- genMatrices() içindeki arabellek doldurma kodu. Şimdi, başlangıçta kullanılan satır ana düzeni yerine sütun ana düzeniyle doldurulmalıdır:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- checkRandom() fonksiyonundaki doğrulama kodu:
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];CPU'daki performans sonuçları:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Gördüğünüz gibi, verilere tutarlı erişimin GPU üzerindeki çalışma zamanı üzerinde neredeyse hiçbir etkisi olmadı; ancak CPU'daki çalışma zamanını açıkça iyileştirdi. Daha sonra optimize edilecek faktörlerle, özellikle de mümkün olan en kısa sürede kurtulmamız gereken global değişkenlere çok yüksek erişim gecikmesi ile ilgili olması çok muhtemeldir.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
Yeni çekirdek kodu, makalenin sonundaki matr_mul_1dim_coalesced.mq5 içinde bulunabilir.
Çekirdek kodu aşağıda belirtilmiştir:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Liste 3. Birleştirilmiş global bellek veri erişimine sahip çekirdek
Daha fazla optimizasyona geçelim.
2.4. Çıktı Matrisinden 'Masraflı' Global GPU Bellek Erişimini Kaldırma
Global GPU bellek erişiminin gecikme süresinin son derece yüksek olduğu bilinmektedir (yaklaşık 600-800 döngü). Örneğin, iki sayının eklenmesinin gecikme süresi yaklaşık 20 döngüdür. GPU'da hesaplama yaparken optimizasyonların temel amacı, hesaplamaların verimini artırarak gecikmeyi gizlemektir. Daha önce geliştirilen çekirdeğin döngüsünde, bize zaman kazandıran global bellek öğelerine sürekli erişiriz.
Şimdi çekirdeğe (çalışma birimi kaydında bulunan çekirdeğin özel bir değişkeni olduğu için kat kat daha hızlı erişilebilen) yerel değişken toplamını girelim ve döngü tamamlandıktan sonra, elde edilen toplam değeri çıktı dizisinin öğesine tek tek atayalım:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Liste 4. Skaler çarpım hesaplama döngüsünde kümülatif toplamı hesaplamak için özel değişkenin girilmesi
Tam kaynak kod dosyası matr_mul_sum_local.mq5, makalenin sonuna eklenmiştir.
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================Bu gerçek bir üretkenlik artışı!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
Sıralı optimizasyonlarda uymaya çalıştığımız ana ilke şudur: Önce veri yapısını, belirli bir göreve ve özellikle temel donanıma uygun olacak şekilde mümkün olan en eksiksiz şekilde yeniden düzenlemelisiniz ve ancak bundan sonra mad() veya fma() gibi hızlı hesaplama algoritmalarını kullanarak ince optimizasyonlara geçmelisiniz. Sıralı optimizasyonların her zaman performansın artmasıyla sonuçlanmayacağını unutmayın - bu garanti edilemez.
2.5. Çekirdek Tarafından Yürütülen İşlemleri Artırma
Paralel programlamada, paralel işlemin organizasyonunda ek yükü (harcanan zamanı) en aza indirecek şekilde hesaplamaları düzenlemek önemlidir. 2000 boyutlu matrislerde, bir çıktı matris elemanını hesaplayan bir çalışma birimi, toplam görevin 1 / 4000000'ine eşit iş miktarını gerçekleştirir.
Bu, açıkçası, donanım üzerinde hesaplamalar yapan gerçek birim sayısından çok fazla ve çok uzaktır. Şimdi, çekirdeğin yeni versiyonunda, bir eleman yerine tüm matris satırını hesaplayacağız.
Tüm boyut olarak görev alanının artık 2 boyutludan tek boyutluya değiştirilmesi önemlidir - artık çekirdeğin her görevinde matrisin tek bir öğesi yerine tüm satır hesaplanır. Bu nedenle, görev alanı matris satırlarının sayısına dönüşür.
Şekil 14. Çıktı matrisinin tüm satırını hesaplama şeması
Çekirdek kodu daha karmaşık hale gelir:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 5. Çıktı matrisinin tüm satırının hesaplanması için çekirdek
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Performans sonuçları (tam kaynak kodu matr_mul_row_calc.mq5'te bulunabilir):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
CPU'daki çalışma zamanının açıkça kötüleştiğini ve GPU'da çok olmasa da biraz daha kötüleştiğini görebiliriz. Her şey o kadar da kötü değil: Yerel düzeyde durumu geçici olarak kötüleştiren bu stratejik değişiklik, yalnızca performansı daha da önemli ölçüde artırmak için burada.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. Birinci Dizinin Satırını Özel Belleğe Aktarma
Matris çarpım algoritmasının ana özelliği, sonuçların eşzamanlı birikimi ile çok sayıda çarpımdır. Bu algoritmanın uygun, yüksek kaliteli bir optimizasyonu, veri aktarımlarının en aza indirilmesi anlamına gelmelidir. Ancak şimdiye kadar, ana skaler çarpım birikimi döngüsü içindeki hesaplamalarda, tüm çekirdek modifikasyonlarımız üç matristen ikisini global bellekte depolamıştır.
Bu, her skaler çarpım için tüm girdi verilerinin (aslında her çıktı matrisi öğelerinin) ilgili gecikmelerle birlikte tüm bellek hiyerarşisi boyunca - globalden özele - sürekli olarak aktığı anlamına gelir. Bu trafik, her çalışma biriminin çıktı matrisinin hesaplanan her satırı için ilk matrisin bir ve aynı satırını yeniden kullanması sağlanarak azaltılabilir.
Şekil 15. İlk matrisin satırının çalışma biriminin özel belleğine aktarılması
Bu, ana bilgisayar program kodunda herhangi bir değişiklik gerektirmez. Ve çekirdekteki değişiklikler minimumdur. Çekirdek içinde bir ara tek boyutlu özel dizi oluşturulduğundan, GPU onu çekirdeği çalıştıran birimin özel belleğine yerleştirmeye çalışır. İlk matrisin gerekli satırı, basitçe globalden özel belleğe kopyalanır. Bununla birlikte, bu kopyalamanın bile nispeten hızlı olacağı belirtilmelidir. İşin püf noktası, ilk dizinin satır öğelerinin globalden özel belleğe en 'maliyetli' kopyalanmasının tutarlı bir şekilde yapılması ve kopyalama üzerindeki ek yükün, çıktı matrisi satırını hesaplayan ana çift döngünün çalışma zamanına kıyasla oldukça mütevazı olmasıdır.
Çekirdek kodu (ana döngüde yorumlanan kod, önceki sürümde bulunan koddur):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 6. Çalışma biriminin özel belleğindeki ilk matrisin satırını içeren çekirdek.
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
CPU çıktısı, geçen seferki ile yaklaşık olarak aynı seviyede kalırken, GPU verimi, ulaşılan en yüksek seviyeye, bu kez yeni kapasiteyle, geri dönmüştür. CPU çıktısının olduğu yerde donmuş gibi olduğunu, sadece biraz kararsız olduğunu, GPU veriminin ise oldukça büyük sıçramalarda arttığını (her zaman olmasa da) unutmayın.
İlk matrisin satırının özel belleğe kopyalanması nedeniyle, şimdi eskisinden daha fazla işlem yürütüldüğünden, gerçek aritmetik çıktının biraz daha yüksek olması gerektiğini belirtelim. Ancak, nihai çıktı tahmini üzerinde çok az etkisi vardır.
Kaynak kodu matr_mul_row_in_private.mq5 içinde bulunabilir.
2.7. İkinci Dizinin Sütununu Yerel Belleğe Aktarma
Şimdi, bir sonraki adımın ne olacağını tahmin etmek kolaydır. Çıktı ve ilk girdi matrisleriyle ilişkili gecikmeleri gizlemek için zaten adımlar attık. Hala kalan ikinci matris var.
Matris çarpımında kullanılan skaler çarpımın daha dikkatli bir incelemesi, çıktı matrisi satırının hesaplanması sırasında, gruptaki tüm çalışma birimlerinin, ikinci çarpılmış matrisin aynı sütunlarından cihaz aracılığıyla verileri yeniden akıttığını göstermektedir. Bu, aşağıdaki şemada gösterilmektedir:
Şekil 16. İkinci matrisin sütununun çalışma grubunun Yerel Veri Paylaşımına aktarılması
Çalışma grubunu oluşturan çalışma birimleri, çıktı matrisi satırlarının hesaplanması başlamadan önce ikinci matrisin sütunlarını çalışma grubu belleğine kopyalarsa global bellekten veri aktarmanın yükü azaltılabilir.
Bu, çekirdekte ve ana bilgisayar programında değişikliklerin yapılmasını gerektirecektir. En önemli değişiklik, her çekirdek için yerel bellek ayarıdır. OpenCL'de dinamik bellek ayırma desteklenmediğinden açık olmalıdır. Bu nedenle, çekirdek içinde daha fazla işlenmek üzere önce ana bilgisayara yeterli boyutta bir bellek nesnesi yerleştirilmelidir.
Ve ancak o zaman, çekirdeği çalıştırırken, çalışma birimleri ikinci matrisin sütununu yerel belleğe kopyalar. Bu, çalışma grubunun tüm çalışma birimleri arasında döngü yinelemelerinin döngüsel dağılımı kullanılarak paralel olarak yapılır. Ancak, tüm kopyalama, çalışma birimi ana işlemine (çıktı matrisi satırının hesaplanması) başlamadan önce tamamlanmalıdır.
Bu nedenle, kopyalamadan sorumlu döngüden sonra aşağıdaki komut eklenir:
barrier(CLK_LOCAL_MEM_FENCE);
Bu, grup içindeki her çalışma biriminin diğer birimlerle koordineli belirli bir durumda yerel belleği "görebilmesini" sağlayan bir "yerel bellek engelidir". Çalışma grubundaki tüm çalışma birimleri, herhangi biri çekirdeğin yürütülmesine devam etmeden önce, bariyere kadar komutları yürütmelidir. Diğer bir deyişle bariyer, çalışma grubu içindeki çalışma birimleri arasında özel bir senkronizasyon mekanizmasıdır.
OpenCL'de çalışma grupları arasındaki senkronizasyon mekanizmaları sağlanmaz.
Aşağıda, hareket halindeki bariyerin resmi verilmiştir:
Şekil 17. Hareket halindeki bariyerin çizimi
Aslında, yalnızca çalışma grubu içindeki çalışma birimlerinin kodu kesinlikle aynı anda yürüttüğü görülüyor. Bu sadece OpenCL programlama modelinin bir soyutlamasıdır.
Şimdiye kadar, farklı çalışma birimlerinde yürütülen çekirdek kodlarımız, aralarında programlı olarak çekirdekte ayarlanacak açık bir iletişim olmadığı için işlemlerin senkronizasyonunu gerektirmedi; ayrıca buna gerek bile yoktu. Ancak, yerel diziyi doldurma işlemi çalışma grubunun tüm birimleri arasında paralel olarak dağıtıldığından, bu çekirdekte senkronizasyon gereklidir.
Diğer bir deyişle, her çalışma birimi, diğer çalışma birimlerinin bu yazma sürecinde ne kadar uzakta olduğunu bilmeden, değerlerini yerel veri paylaşımına (burada, diziye) yazar. Bariyer, belirli bir çalışma biriminin gerekli olmadan, yani yerel bir dizi tamamen oluşturulmadan önce çekirdeğin yürütülmesine devam etmemesi için oradadır.
Bu optimizasyonun CPU'daki performans için pek faydalı olmayacağını anlamalısınız: Intel'in OpenCL Optimizasyon Kılavuzu, CPU'da bir çekirdek yürütülürken, tüm OpenCL bellek nesnelerinin donanım tarafından önbelleğe alındığını, bu nedenle yerel bellek kullanılarak açık önbelleğe almanın gereksiz (orta derecede) ek yük getirdiğini söylüyor.
Burada dikkat edilmesi gereken ve makalenin yazarı için çok zaman alan bir başka önemli nokta daha var. Bu, terminal geliştiricileri tarafından oluşturulan mevcut uygulamada, çekirdek fonksiyon başlığında, yani derleme aşamasında, yerel bir değişkenin iletilememesi gerçeğiyle ilgilidir. Bunun arkasındaki neden, çekirdek fonksiyonu bağımsız değişkeni olarak bir bellek nesnesine bellek tahsis etmek için, önce CLBufferCreate() fonksiyonunu kullanarak böyle bir nesneyi CPU belleğinde açıkça oluşturmamız ve boyutunu bir fonksiyon parametresi olarak açıkça belirtmemiz gerekmesidir. Bu fonksiyon, olabileceği tek yer burası olduğundan, global GPU belleğinde daha sonra saklanacak olan bir bellek nesne tanıtıcısı döndürür.
Ancak yerel bellek, global bellekten farklıdır ve sonuç olarak oluşturulan bir bellek nesnesi, çalışma grubunun yerel belleğine yerleştirilemez.
Tam özellikli OpenCL API, bellek nesnesini bu şekilde oluşturmadan (CLSetKernelArg() fonksiyonu) bile, çekirdeğin bağımsız değişkenine NULL işaretçisiyle gerekli boyutta belleği açıkça atamaya izin verir. Ancak, tam özellikli API fonksiyonunun MQL5 analoğu olan CLSetKernelArgMem() fonksiyonunun sözdizimi, bellek nesnesinin kendisini oluşturmadan bağımsız değişkene ayrılan belleğin boyutunu ona aktarmamıza izin vermez. CLSetKernelArgMem() fonksiyonuna iletebileceğimiz şey, yalnızca global CPU belleğinde zaten oluşturulmuş olan ve global GPU belleğine aktarılması amaçlanan arabellek tanıtıcısıdır. İşte paradoks.
Neyse ki, çekirdekte yerel arabelleklerle çalışmanın eşdeğer bir yolu var. Böyle bir arabelleği, çekirdeğin gövdesinde __local değiştiricisiyle bildirmeniz yeterlidir. Çalışma grubuna ayrılan yerel bellek, bu şekilde derleme aşaması yerine Çalışma Zamanı sırasında belirlenecektir.
Çekirdekteki bariyerden sonra gelen komutlar (koddaki bariyer çizgisi kırmızı ile işaretlenmiştir) özünde önceki optimizasyondakiyle aynıdır. Ana program kodu aynı kaldı (kaynak kodu matr_mul_col_local.mq5'te bulunabilir).
İşte yeni çekirdek kodu:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 7. Çalışma grubunun yerel belleğine aktarılan ikinci dizinin sütunu
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Her iki durum da önemli olarak adlandırılamayan performans düşüşü göstermektedir. Çalışma grubunun büyüklüğü değiştirilerek performans düşürülmek yerine geliştirilebilirse iyi olabilir. Yukarıdaki örnek daha çok, yerel bellek nesnelerinin nasıl kullanılacağını göstermek gibi farklı bir amaca hizmet eder.
Yerel bellek kullanıldığında performans düşüşünü açıklayan bir hipotez vardır. Yaklaşık 2 yıl önce habrahabr.ru'da yayınlanan OpenCL'yi CUDA, GLSL ve OpenMP ile karşılaştırma (Rusça) makalesi şöyle diyor:
Başka bir deyişle, 2 yıl önce piyasaya sürülen ürünlerin yerel belleğinin global bellekten daha hızlı olmadığı anlamına mı geliyor? Yukarıdakilerin yayınlandığı zaman, iki yıl önce Radeon HD 58xx serisi video kartlarının çoktan piyasaya çıktığını gösteriyor, ancak yazara göre durum iyimser olmaktan çok uzaktı. Özellikle AMD'nin sansasyonel Evergreen serisi göz önüne alındığında, buna inanmakta zorlanıyorum. Daha modern kartlar, örneğin HD 69xx serisi kullanarak kontrol etmek ilginç olurdu.
Ekleme: GPU Caps Viewer'ı başlatın ve OpenCL sekmesinde aşağıdakileri göreceksiniz:
Şekil 18. HD 4870 tarafından desteklenen ana OpenCL parametreleri
CL_DEVICE_LOCAL_MEM_TYPE: Global
Dil özelliklerinde (Tablo 4.3, s. 41) sağlanan bu parametrenin açıklaması aşağıdaki gibidir:
Desteklenen yerel bellek türü. Bu, SRAM veya CL_GLOBAL gibi özel olarak ayrılmış yerel bellek depolaması anlamına gelen CL_LOCAL olarak ayarlanabilir.
Bu nedenle, HD 4870 yerel bellek gerçekten global belleğin bir parçasıdır ve bu video kartındaki herhangi bir yerel bellek manipülasyonu bu nedenle işe yaramaz ve global bellekten daha hızlı bir şeyle sonuçlanmaz. Burada bir AMD uzmanının HD 4xxx serisi için bu noktayı açıkladığı başka bir bağlantı yer alıyor. Bu, sahip olduğunuz video kartı için o kadar kötü olacağı anlamına gelmez; donanımla ilgili bu tür bilgilerin nerede bulunabileceğini göstermek içindi - bu durumda GPU Caps Viewer'da.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Son olarak, çekirdeği açıkça vektörleştirerek birkaç son rötuş ekleyelim. İlk dizinin satırının özel belleğe (matr_mul_row_in_private.mq5) aktarılması aşamasında türetilen çekirdek, en hızlı olduğu göründüğü için ilk çekirdek görevi görecektir.
2.8. Çekirdek Vektörleştirme
Karışıklığı önlemek için bu işlem birkaç aşamaya bölünmelidir. İlk modifikasyonda, çekirdeğin harici parametrelerinin veri türlerini değiştirmiyoruz ve sadece iç döngüdeki hesaplamaları vektörleştiriyoruz:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 8. Float4 kullanarak çekirdeğin kısmi vektörleştirilmesi (yalnızca iç döngü)
CPU:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Şaşırtıcı bir şekilde, bu tür ilkel vektörleştirme bile GPU'da iyi sonuçlar verdi; çok önemli olmasa da, kazancın yaklaşık %10 olduğu görüldü.
Çekirdeğin içinde vektörleştirmeye devam edin: 'maliyetli' REALTYPE4 vektör türü dönüştürme işlemlerini açık vektör bileşenlerinin belirtimi ile birlikte özel değişken rowbuf[]'u dolduran dış yardımcı döngüye aktarın. Çekirdekte hala bir değişiklik yok.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 9. Çekirdeğin ana döngüsünde 'maliyetli' tür dönüştürme işlemlerinden kurtulmak
Şu anda ilk dizi için gerekli olan okuma işlemleri öncekinden 4 kat daha az olduğundan, iç (ve yardımcı) döngü sayacının maksimum sayım değerinin 4 kat daha düşük olduğuna dikkat edin - okuma açıkça bir vektör işlemi haline gelmiştir.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Aritmetik çıktı:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Görülebileceği gibi, GPU için neredeyse devrim niteliğinde olurken, CPU için performanstaki değişiklikler dikkate değerdir. Kaynak kodu matr_mul_vect_v2.mq5 içinde bulunabilir.
Çekirdeğin son varyantına göre aynı işlemleri sadece 8 vektör genişliğini kullanarak yapalım. Yazarın kararı, GPU bellek bant genişliğinin 256 bit, yani 32 bayt veya 8 sayı kaydırma türünde olmasıyla açıklanabilir; bu nedenle, float8'in eşzamanlı kullanımına eşdeğer olan 8 float'ın aynı anda işlenmesi oldukça doğal görünmektedir.
Bu durumda COLSROWS değerinin 8'e tam bölünebilmesi gerektiğini unutmayın. Daha hassas optimizasyonlar verilere daha özel gereksinimler belirlediğinden, bu doğal bir gereksinimdir.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Liste 10. 8 vektör genişliğini kullanarak çekirdek vektörleştirme
Çekirdek koduna, genişliği 8 olan vektörler için skaler çarpımı hesaplamaya izin veren satır içi dot8() fonksiyonunu eklemek zorunda kaldık. OpenCL'de, standart dot() fonksiyonu yalnızca 4 genişliğe kadar olan vektörler için skaler çarpımı hesaplayabilir. Kaynak kodu matr_mul_vect_v3.mq5 içinde bulunabilir.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Sonuçlar beklenmedik: float8'in HD 4870 için yeterli bir veri yolu genişliği (256 bite eşittir) olmasına rağmen CPU üzerindeki çalışma zamanı öncekine göre neredeyse iki kat daha az, GPU için ise biraz artmıştır. Ve burada yine GPU Caps Viewer'a başvuruyoruz.
Açıklama, Şekil 18'de, parametre listesinin sondan bir önceki satırında bulunabilir:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
OpenCL Özelliklerine bakın ve bu parametreyle ilgili aşağıdaki metni Tablo 4.3 sayfa 37'nin son sütununda göreceksiniz:
Vektörlere yerleştirilebilen yerleşik skaler türler için tercih edilen yerel vektör genişliği boyutu. Vektör genişliği, vektörde saklanabilecek skaler eleman sayısı olarak tanımlanır.
Bu nedenle, HD 4870 için, floatN vektörünün tercih edilen vektör genişliği, float8 yerine float4'tür.
Çekirdek optimizasyon döngüsünü burada bitirelim. Daha fazlasını elde etmeye devam edebiliriz, ancak bu makalenin uzunluğu bu kadar derin bir tartışmaya izin vermiyor.
Sonuç
Makale, çekirdeğin yürütüldüğü temel donanım az da olsa dikkate alındığında ortaya çıkan bazı optimizasyon özelliklerini göstermiştir.
Elde edilen rakamlar tavan değerler olmaktan uzaktır, ancak bunlar bile şu anda elimizde olan mevcut kaynaklarla (terminal geliştiricileri tarafından uygulanan OpenCL API'si optimizasyon için önemli olan bazı parametreleri -- özellikle çalışma grubu boyutunu kontrol etmeye izin vermez), ana bilgisayar programının yürütülmesi üzerindeki performans kazancının çok önemli olduğunu göstermektedir: CPU üzerindeki sıralı program üzerinden GPU'da yürütme kazancı (çok optimize edilmemiş olsa da) yaklaşık 200:1'dir.
Değerli tavsiyeler ve benimki mevcut değilken farklı GPU'yu kullanma fırsatı için MetaDriver'a içten şükranlarımı sunarım.
Ekli dosyaların içeriği:
- matr_mul_2dim.mq5 - iki boyutlu veri gösterimi ile ana bilgisayardaki ilk sıralı program;
- matr_mul_1dim.mq5 - doğrusal veri gösterimi ve MQL5 OpenCL API için ilgili bir bağlama ile çekirdeğin ilk uygulaması;
- matr_mul_1dim_coalesced - birleşik global bellek erişimini içeren çekirdek;
- matr_mul_sum_local - global bellekte saklanan çıktı dizisinin hesaplanmış bir hücresine erişmek yerine, skaler çarpımın hesaplanması için tanıtılan özel bir değişken;
- matr_mul_row_calc - çekirdekteki çıktı matrisinin tüm satırının hesaplanması;
- matr_mul_row_in_private - özel belleğe aktarılan ilk dizinin satırı;
- matr_mul_col_local.mq5 - yerel belleğe aktarılan ikinci dizinin sütunu;
- matr_mul_vect.mq5 - çekirdeğin ilk vektörleştirilmesi (float4, yalnızca ana döngünün iç alt döngüsü kullanılarak);
- matr_mul_vect_v2.mq5 - ana döngüde 'maliyetli' veri dönüştürme işlemlerinden kurtulmak;
- matr_mul_vect_v3.mq5 - 8 vektör genişliğini kullanarak vektörleştirme.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/407
MQL5 Kodu için Otomatik Oluşturulan Belgeler
Otomatik Alım Satım Sistemleri Oluşturmada Yeni Bir Yaklaşım Olarak Otomat Tabanlı Programlama
MQL5.community - Kullanıcı Notu
En Aktif MQL5.community Üyelerine iPhone Ödülü Verildi!
- Ücretsiz ticaret uygulamaları
- 24 saat boyunca ücretsiz Forex VPS
- Ticaret kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Web sitesi politikasını ve kullanım şartlarını kabul edersiniz