
Scikit-learn kütüphanesinin regresyon modelleri ve bunların ONNX'e aktarılması
ONNX (Open Neural Network Exchange), makine öğrenimi modellerini tanımlamak ve bunları birbirlerine dönüştürmek için kullanılan bir formattır. Modellerin farklı makine öğrenimi çerçeveleri arasında aktarılmasına olanak tanır. Derin öğrenme ve sinir ağlarında float32 gibi veri türleri sıklıkla kullanılır. Derin öğrenme modellerini eğitmek için genellikle kabul edilebilir doğruluk ve verimlilik sağladıkları için yaygın olarak uygulanmaktadırlar.
Bazı klasik makine öğrenimi modellerinin ONNX operatörleri olarak temsil edilmesi zordur. Bu nedenle, ONNX'te bunları uygulamak için ek ML operatörleri (ai.onnx.ml) tanıtılmıştır. ONNX spesifikasyonuna göre, bu setteki anahtar operatörlerin (LinearRegressor, SVMRegressor, TreeEnsembleRegressor) çeşitli girdi veri türlerini (tensor(float), tensor(double), tensor(int64), tensor(int32)) kabul edebildiğini, ancak çıktı olarak her zaman tensor(float) türünü geri döndürdüklerini belirtmek gerekir. Bu operatörlerin parametrelendirilmesi de float sayılar kullanılarak gerçekleştirilir, bu da özellikle orijinal modelin parametrelerini tanımlamak için double hassasiyetli sayılar kullanılmışsa hesaplamaların doğruluğunu sınırlayabilir.
Bu, modelleri dönüştürürken veya ONNX'te veri dönüştürme ve işleme sürecinde farklı veri türleri kullanırken doğruluk kaybına yol açabilir. Daha sonra göreceğimiz gibi, çoğu şey dönüştürücüye bağlıdır; bazı modeller bu sınırlamaları atlamayı başarır ve ONNX modellerinin tam taşınabilirliğini sağlayarak, doğruluğu kaybetmeden onlarla double hassasiyetinde çalışmaya izin verir. Modellerle ve bunların ONNX'te temsiliyle çalışırken, özellikle de veri temsilinin doğruluğunun önemli olduğu durumlarda bu özellikleri göz önünde bulundurmak önemlidir.
Scikit-learn, Python topluluğunda makine öğrenimi için en popüler ve yaygın olarak kullanılan kütüphanelerden biridir. Geniş bir algoritma yelpazesi, kullanıcı dostu bir arayüz ve iyi bir dokümantasyon sunar. "Scikit-learn kütüphanesinin sınıflandırma modelleri ve bunların ONNX'e aktarılması" başlıklı bir önceki makalede sınıflandırma modelleri ele alınmıştı.
Bu makalede ise Scikit-learn paketindeki regresyon modellerinin uygulanmasını inceleyeceğiz, test veri kümesi için parametrelerini double hassasiyetle hesaplayacağız, bunları float ve double hassasiyet için ONNX formatına dönüştürmeye çalışacağız ve elde edilen modelleri MQL5 programlarında kullanacağız. Ayrıca, float ve double hassasiyet için orijinal modellerin ve ONNX versiyonlarının doğruluğunu karşılaştıracağız. Ek olarak, regresyon modellerinin ONNX temsilini inceleyeceğiz, bu da iç yapılarının ve işleyişlerinin daha iyi anlaşılmasını sağlayacaktır.
İçindekiler
- If it bothers you, welcome to contribute
- 1. Test veri kümesi
Test veri kümesini görüntülemek için kod - 2. Regresyon modelleri
2.0. Scikit-learn regresyon modellerinin listesi - 2.1. ONNX float ve double modellerine dönüştürülen Scikit-learn regresyon modelleri
- 2.1.1. sklearn.linear_model.ARDRegression
2.1.1.1. ARDRegression modelini oluşturmak için kod
2.1.1.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.1.3. ard_regression_float.onnx ve ard_regression_double.onnx modellerinin ONNX gösterimi - 2.1.2. sklearn.linear_model.BayesianRidge
2.1.2.1. BayesianRidge modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.2.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.2.3. bayesian_ridge_float.onnx ve bayesian_ridge_double.onnx modellerinin ONNX gösterimi - 2.1.3. sklearn.linear_model.ElasticNet
2.1.3.1. ElasticNet modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.3.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.3.3. elastic_net_float.onnx ve elastic_net_double.onnx modellerinin ONNX gösterimi - 2.1.4. sklearn.linear_model.ElasticNetCV
2.1.4.1. ElasticNet modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.4.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.4.3. elastic_net_cv_float.onnx ve elastic_net_cv_double.onnx modellerinin ONNX gösterimi - 2.1.5. sklearn.linear_model.HuberRegressor
2.1.5.1. HuberRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.5.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.5.3. huber_regressor_float.onnx ve huber_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.6. sklearn.linear_model.Lars
2.1.6.1. Lars modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.6.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.6.3. lars_float.onnx ve lars_double.onnx modellerinin ONNX gösterimi - 2.1.7. sklearn.linear_model.LarsCV
2.1.7.1. LarsCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.7.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.7.3. lars_cv_float.onnx ve lars_cv_double.onnx modellerinin ONNX gösterimi - 2.1.8. sklearn.linear_model.Lasso
2.1.8.1. Lasso modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.8.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.8.3. lasso_float.onnx ve lasso_double.onnx modellerinin ONNX gösterimi - 2.1.9. sklearn.linear_model.LassoCV
2.1.9.1. LassoCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.9.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.9.3. lasso_cv_float.onnx ve lasso_cv_double.onnx modellerinin ONNX gösterimi - 2.1.10. sklearn.linear_model.LassoLars
2.1.10.1. LassoLars modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.10.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.10.3. lasso_lars_float.onnx ve lasso_lars_double.onnx modellerinin ONNX gösterimi - 2.1.11. sklearn.linear_model.LassoLarsCV
2.1.11.1. LassoLarsCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.11.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.11.3. lasso_lars_cv_float.onnx ve lasso_lars_cv_double.onnx modellerinin ONNX gösterimi - 2.1.12. sklearn.linear_model.LassoLarsIC
2.1.12.1. LassoLarsIC modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.12.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.12.3. lasso_lars_ic_float.onnx ve lasso_lars_ic_double.onnx modellerinin ONNX gösterimi - 2.1.13. sklearn.linear_model.LinearRegression
2.1.13.1. LinearRegression modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.13.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.13.3. linear_regression_float.onnx ve linear_regression_double.onnx modellerinin ONNX gösterimi - 2.1.14. sklearn.linear_model.Ridge
2.1.14.1. Ridge modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.14.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.14.3. ridge_float.onnx ve ridge_double.onnx modellerinin ONNX gösterimi - 2.1.15. sklearn.linear_model.RidgeCV
2.1.15.1. RidgeCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.15.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.15.3. ridge_cv_float.onnx ve ridge_cv_double.onnx modellerinin ONNX gösterimi - 2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
2.1.16.1. OrthogonalMatchingPursuit modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.16.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.16.3. orthogonal_matching_pursuit_float.onnx ve orthogonal_matching_pursuit_double.onnx modellerinin ONNX gösterimi - 2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
2.1.17.1. PassiveAggressiveRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.17.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.17.3. passive_aggressive_regressor_float.onnx ve passive_aggressive_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.18. sklearn.linear_model.QuantileRegressor
2.1.18.1. QuantileRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.18.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.18.3. quantile_regressor_float.onnx ve quantile_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.19. sklearn.linear_model.RANSACRegressor
2.1.19.1. RANSACRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.19.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.19.3. ransac_regressor_float.onnx ve ransac_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.20. sklearn.linear_model.TheilSenRegressor
2.1.20.1. TheilSenRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.20.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.20.3. theil_sen_regressor_float.onnx ve theil_sen_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.21. sklearn.linear_model.LinearSVR
2.1.21.1. LinearSVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.21.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.21.3. linear_svr_float.onnx ve linear_svr_double.onnx modellerinin ONNX gösterimi - 2.1.22. sklearn.linear_model.MLPRegressor
2.1.22.1. MLPRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.22.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.22.3. mlp_regressor_float.onnx ve mlp_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.23. sklearn.cross_decomposition.PLSRegression
2.1.23.1. PLSRegression modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.23.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.23.3. pls_regression_float.onnx ve pls_regression_double.onnx modellerinin ONNX gösterimi - 2.1.24. sklearn.linear_model.TweedieRegressor
2.1.24.1. TweedieRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.24.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.24.3. tweedie_regressor_float.onnx ve tweedie_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.25. sklearn.linear_model.PoissonRegressor
2.1.25.1. PoissonRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.25.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.25.3. poisson_regressor_float.onnx ve poisson_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
2.1.26.1. RadiusNeighborsRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.26.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.26.3. radius_neighbors_regressor_float.onnx ve radius_neighbors_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.27. sklearn.neighbors.KNeighborsRegressor
2.1.27.1. KNeighborsRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.27.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.27.3. kneighbors_regressor_float.onnx ve kneighbors_regressor_double.onnx modellerinin ONNX gösterimi
- 2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
2.1.28.1. GaussianProcessRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.28.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.28.3. gaussian_process_regressor_float.onnx ve gaussian_process_regressor_double.onnx modellerinin ONNX gösterimi
- 2.1.29. sklearn.linear_model.GammaRegressor
2.1.29.1. GammaRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.29.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.29.3. gamma_regressor_float.onnx ve gamma_regressor_double.onnx modellerinin ONNX gösterimi - 2.1.30. sklearn.linear_model.SGDRegressor
2.1.30.1. SGDRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.1.30.2. ONNX modellerini yürütmek için MQL5 kodu
2.1.30.3. sgd_regressor_float.onnx ve sgd_rgressor_double.onnx modellerinin ONNX gösterimi
- 2.2. Yalnızca float hassasiyetli ONNX modellerine dönüştürülen Scikit-learn kütüphanesinden regresyon modelleri
- 2.2.1. sklearn.linear_model.AdaBoostRegressor
2.2.1.1. AdaBoostRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.1.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.1.3. adaboost_regressor_float.onnx ve adaboost_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.2. sklearn.linear_model.BaggingRegressor
2.2.2.1. BaggingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.2.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.2.3. bagging_regressor_float.onnx ve bagging_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.3. sklearn.linear_model.DecisionTreeRegressor
2.2.3.1. DecisionTreeRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.3.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.3.3. decision_tree_regressor_float.onnx ve decision_tree_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.4. sklearn.linear_model.ExtraTreeRegressor
2.2.4.1. ExtraTreeRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.4.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.4.3. extra_tree_regressor_float.onnx ve extra_tree_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.5. sklearn.ensemble.ExtraTreesRegressor
2.2.5.1. ExtraTreesRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.5.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.5.3. extra_trees_regressor_float.onnx ve extra_trees_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.6. sklearn.svm.NuSVR
2.2.6.1. NuSVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.6.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.6.3. nu_svr_float.onnx ve nu_svr_double.onnx modellerinin ONNX gösterimi - 2.2.7. sklearn.ensemble.RandomForestRegressor
2.2.7.1. RandomForestRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.7.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.7.3. random_forest_regressor_float.onnx ve random_forest_regressor_double.onnx modellerinin ONNX gösterimi
- 2.2.8. sklearn.ensemble.GradientBoostingRegressor
2.2.8.1. GradientBoostingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.8.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.8.3. gradient_boosting_regressor_float.onnx ve gradient_boosting_regressor_double.onnx modellerinin ONNX gösterimi
- 2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
2.2.9.1. HistGradientBoostingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.9.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.9.3. hist_gradient_boosting_regressor_float.onnx ve hist_gradient_boosting_regressor_double.onnx modellerinin ONNX gösterimi - 2.2.10. sklearn.svm.SVR
2.2.10.1. SVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
2.2.10.2. ONNX modellerini yürütmek için MQL5 kodu
2.2.10.3. svr_float.onnx ve svr_double.onnx modellerinin ONNX gösterimi
- 2.3. ONNX'e dönüştürülürken sorunlarla karşılaşılan regresyon modelleri
- 2.3.1. sklearn.dummy.DummyRegressor
DummyRegressor modelini oluşturmak için kod - 2.3.2. sklearn.kernel_ridge.KernelRidge
KernelRidge modelini oluşturmak için kod - 2.3.3. sklearn.isotonic.IsotonicRegression
IsotonicRegression modelini oluşturmak için kod - 2.3.4. sklearn.cross_decomposition.PLSCanonical
PLSCanonical modelini oluşturmak için kod - 2.3.5. sklearn.cross_decomposition.CCA
CCA modelini oluşturmak için kod - Sonuç
- Özet
If it bothers you, welcome to contribute
ONNX Runtime geliştirici forumunda, kullanıcılardan biri ONNX Runtime aracılığıyla bir model yürütürken karşılaştığı bir hatayı bildirdi: "[ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1)".
Hi all, getting this error when trying to inferance a linear regression model. PLease help me resolve this.
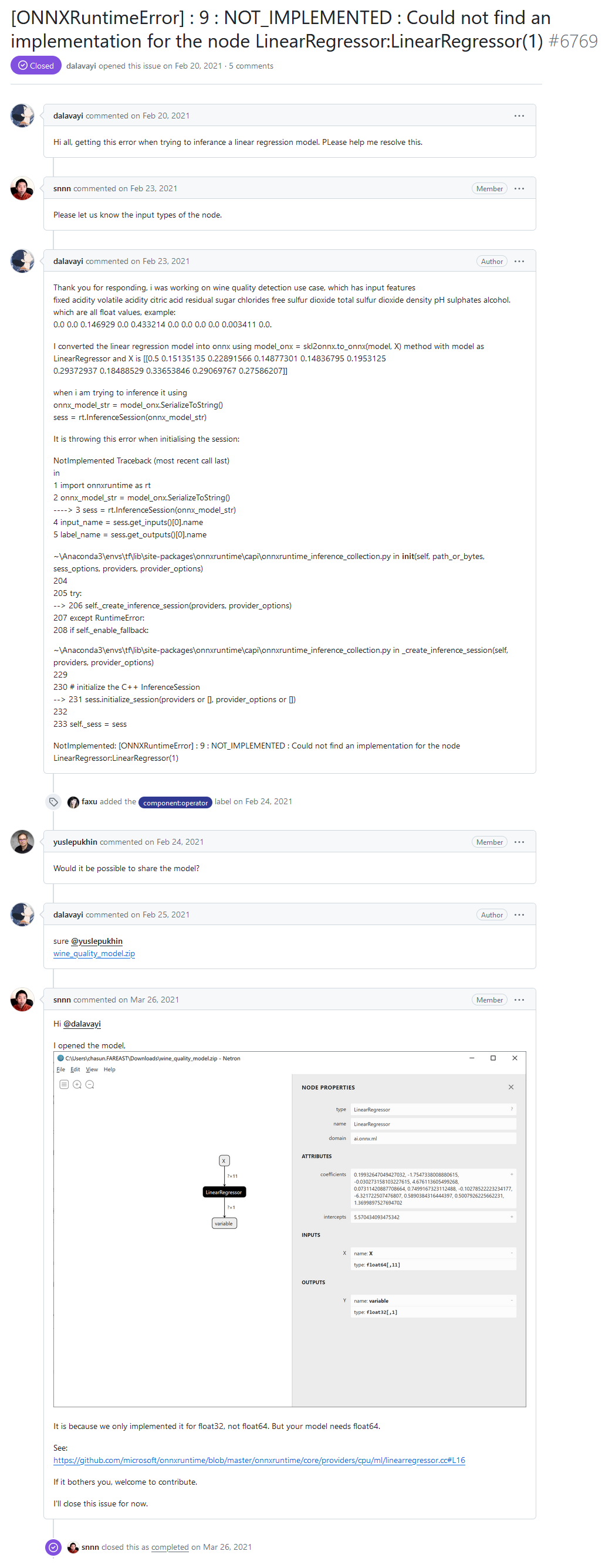
ONNX Runtime geliştirici forumundan hata bildirisi: "NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1)"
Geliştiricinin yanıtı:
It is because we only implemented it for float32, not float64. But your model needs float64.
See:
https://github.com/microsoft/onnxruntime/blob/master/onnxruntime/core/providers/cpu/ml/linearregressor.cc#L16
If it bothers you, welcome to contribute.
Kullanıcının ONNX modelinde, ai.onnx.ml.LinearRegressor operatörü double (float64) veri türüyle çağrılmakta ve hata mesajı, ONNX Runtime’ın double hassasiyetli LinearRegressor() operatörünü desteklememesi nedeniyle ortaya çıkmaktadır.
ai.onnx.ml.LinearRegressor operatörünün özelliklerine göre, double girdi veri türü mümkündür (T: tensor(float), tensor(double), tensor(int64), tensor(int32)); ancak, geliştiriciler kasıtlı olarak bunu uygulamamayı seçmiştir.
Bunun nedeni, çıktının her zaman Y: tensor(float) değerini geri döndürmesidir. Ayrıca, hesaplama parametreleri float sayılardır (coefficients: list of floats, intercepts: list of floats).
Sonuç olarak, hesaplamalar double hassasiyetinde yapıldığında, bu operatör hassasiyeti float'a düşürür ve double hassasiyetli hesaplamalarda uygulanması şüpheli bir değere sahiptir.
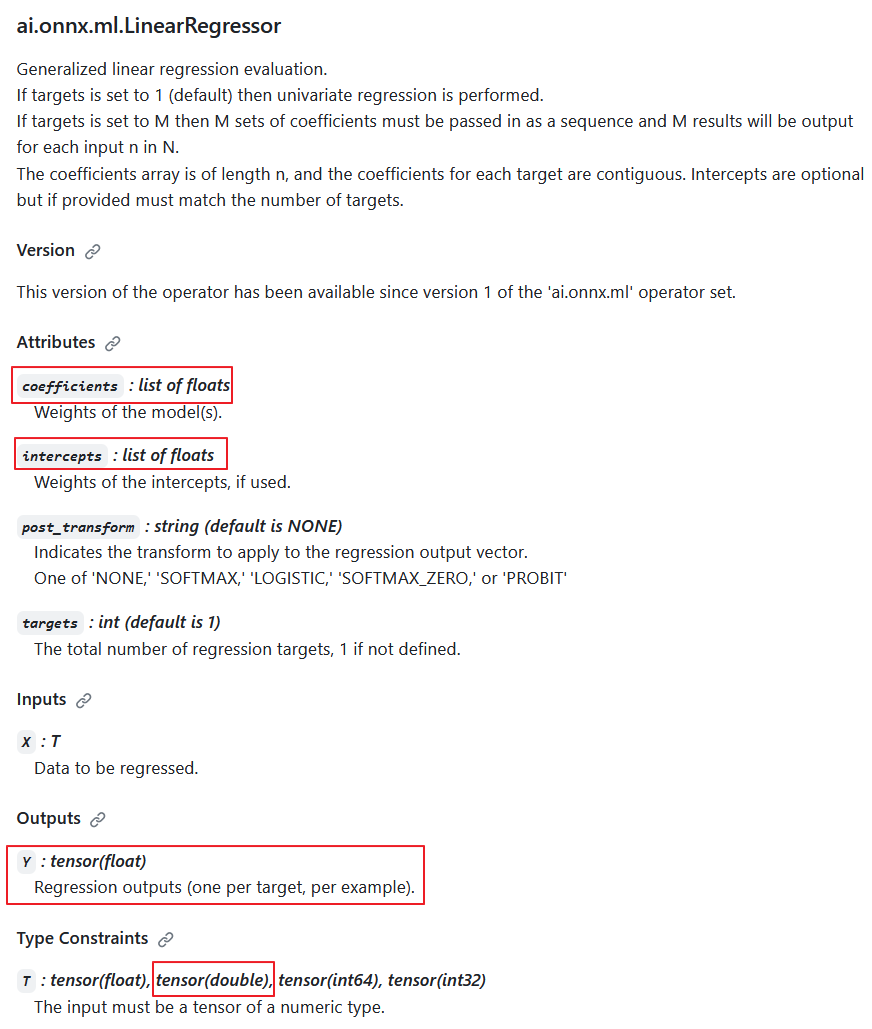
ai.onnx.ml.LinearRegressor operatör açıklaması
Bu nedenle, parametrelerde ve çıktı değerinde hassasiyetin float'a düşürülmesi, ai.onnx.ml.LinearRegressor operatörünün double (float64) sayılarla tam olarak çalışmasını imkansız hale getirir. Muhtemelen, bu nedenle, ONNX Runtime geliştiricileri bunu double türü için uygulamaktan kaçınmaya karar vermiştir.
"double türüne destek ekleme" yöntemi geliştiriciler tarafından kod yorumlarında gösterilmiştir (sarı ile vurgulanmıştır).
ONNX Runtime'da hesaplama LinearRegressor sınıfı kullanılarak gerçekleştirilir (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.h).
Operatörün parametreleri, coefficients_ ve intercepts_, std::vector<float> olarak saklanır:
#pragma once #include "core/common/common.h" #include "core/framework/op_kernel.h" #include "core/util/math_cpuonly.h" #include "ml_common.h" namespace onnxruntime { namespace ml { class LinearRegressor final : public OpKernel { public: LinearRegressor(const OpKernelInfo& info); Status Compute(OpKernelContext* context) const override; private: int64_t num_targets_; std::vector<float> coefficients_; std::vector<float> intercepts_; bool use_intercepts_; POST_EVAL_TRANSFORM post_transform_; }; } // namespace ml } // namespace onnxruntimeLinearRegressor operatörünün uygulanması (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.cc):
// Copyright (c) Microsoft Corporation. All rights reserved. // Licensed under the MIT License. #include "core/providers/cpu/ml/linearregressor.h" #include "core/common/narrow.h" #include "core/providers/cpu/math/gemm.h" namespace onnxruntime { namespace ml { ONNX_CPU_OPERATOR_ML_KERNEL( LinearRegressor, 1, // KernelDefBuilder().TypeConstraint("T", std::vector<MLDataType>{ // DataTypeImpl::GetTensorType<float>(), // DataTypeImpl::GetTensorType<double>()}), KernelDefBuilder().TypeConstraint("T", DataTypeImpl::GetTensorType<float>()), LinearRegressor); LinearRegressor::LinearRegressor(const OpKernelInfo& info) : OpKernel(info), intercepts_(info.GetAttrsOrDefault<float>("intercepts")), post_transform_(MakeTransform(info.GetAttrOrDefault<std::string>("post_transform", "NONE"))) { ORT_ENFORCE(info.GetAttr<int64_t>("targets", &num_targets_).IsOK()); ORT_ENFORCE(info.GetAttrs<float>("coefficients", coefficients_).IsOK()); // use the intercepts_ if they're valid use_intercepts_ = intercepts_.size() == static_cast<size_t>(num_targets_); } // Use GEMM for the calculations, with broadcasting of intercepts // https://github.com/onnx/onnx/blob/main/docs/Operators.md#Gemm // // X: [num_batches, num_features] // coefficients_: [num_targets, num_features] // intercepts_: optional [num_targets]. // Output: X * coefficients_^T + intercepts_: [num_batches, num_targets] template <typename T> static Status ComputeImpl(const Tensor& input, ptrdiff_t num_batches, ptrdiff_t num_features, ptrdiff_t num_targets, const std::vector<float>& coefficients, const std::vector<float>* intercepts, Tensor& output, POST_EVAL_TRANSFORM post_transform, concurrency::ThreadPool* threadpool) { const T* input_data = input.Data<T>(); T* output_data = output.MutableData<T>(); if (intercepts != nullptr) { TensorShape intercepts_shape({num_targets}); onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, intercepts->data(), &intercepts_shape, output_data, threadpool); } else { onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, nullptr, nullptr, output_data, threadpool); } if (post_transform != POST_EVAL_TRANSFORM::NONE) { ml::batched_update_scores_inplace(gsl::make_span(output_data, SafeInt<size_t>(num_batches) * num_targets), num_batches, num_targets, post_transform, -1, false, threadpool); } return Status::OK(); } Status LinearRegressor::Compute(OpKernelContext* ctx) const { Status status = Status::OK(); const auto& X = *ctx->Input<Tensor>(0); const auto& input_shape = X.Shape(); if (input_shape.NumDimensions() > 2) { return ORT_MAKE_STATUS(ONNXRUNTIME, INVALID_ARGUMENT, "Input shape had more than 2 dimension. Dims=", input_shape.NumDimensions()); } ptrdiff_t num_batches = input_shape.NumDimensions() <= 1 ? 1 : narrow<ptrdiff_t>(input_shape[0]); ptrdiff_t num_features = input_shape.NumDimensions() <= 1 ? narrow<ptrdiff_t>(input_shape.Size()) : narrow<ptrdiff_t>(input_shape[1]); Tensor& Y = *ctx->Output(0, {num_batches, num_targets_}); concurrency::ThreadPool* tp = ctx->GetOperatorThreadPool(); auto element_type = X.GetElementType(); switch (element_type) { case ONNX_NAMESPACE::TensorProto_DataType_FLOAT: { status = ComputeImpl<float>(X, num_batches, num_features, narrow<ptrdiff_t>(num_targets_), coefficients_, use_intercepts_ ? &intercepts_ : nullptr, Y, post_transform_, tp); break; } case ONNX_NAMESPACE::TensorProto_DataType_DOUBLE: { // TODO: Add support for 'double' to the scoring functions in ml_common.h // once that is done we can just call ComputeImpl<double>... // Alternatively we could cast the input to float. } default: status = ORT_MAKE_STATUS(ONNXRUNTIME, FAIL, "Unsupported data type of ", element_type); } return status; } } // namespace ml } // namespace onnxruntime
Girdi değerleri olarak double sayılar kullanmak ve operatörün hesaplamasını float parametrelerle gerçekleştirmek için bir seçenek olduğu ortaya çıktı. Başka bir olasılık da girdi verilerinin hassasiyetini float değerine düşürmek olabilir. Ancak bu seçeneklerin hiçbiri uygun bir çözüm olarak kabul edilemez.
ai.onnx.ml.LinearRegressor operatörünün spesifikasyonu, parametreler ve çıktı değeri float türüyle sınırlı olduğundan double sayılarla tam çalışma kapasitesini kısıtlar.
Benzer bir durum ai.onnx.ml.SVMRegressor ve ai.onnx.ml.TreeEnsembleRegressor gibi diğer ONNX ML operatörleri için de geçerlidir.
Sonuç olarak, double hassasiyetli ONNX model yürütmesini kullanan tüm geliştiriciler, spesifikasyonun bu sınırlamasıyla karşı karşıyadır. Bir çözüm, ONNX spesifikasyonunu genişletmeyi (veya parametreleri ve çıktı değerleri double olan LinearRegressor64, SVMRegressor64 ve TreeEnsembleRegressor64 gibi benzer operatörler eklemeyi) içerebilir. Ancak, halihazırda bu mesele çözüme kavuşturulmamıştır.
Çoğu ONNX dönüştürücüsüne bağlıdır. double olarak hesaplanan modeller için bu operatörleri kullanmaktan kaçınmak tercih edilebilir (ancak bu her zaman mümkün olmayabilir). Bu örnek durumda, ONNX dönüştürücüsü kullanıcının modeliyle optimum bir şekilde çalışmamıştır.
Daha sonra göreceğimiz gibi, sklearn-onnx dönüştürücüsü LinearRegressor operatörünün sınırlamasını atlamayı başarıyor: ONNX double modelleri için bunun yerine MatMul() ve Add() ONNX operatörlerini kullanmaktadır. Bu yöntem sayesinde, Scikit-learn kütüphanesindeki çok sayıda regresyon modeli, orijinal double modellerin doğruluğu korunarak, double olarak hesaplanan ONNX modellerine başarıyla dönüştürülebilmektedir.
1. Test veri kümesi
Örnekleri çalıştırmak için Python'ı (biz 3.10.8 sürümünü kullandık), ek kütüphaneleri (pip install -U scikit-learn numpy matplotlib onnx onnxruntime skl2onnx) yüklemeniz ve MetaEditor'da Python yolunu belirtmeniz gerekecektir (Araçlar->Seçenekler->Derleyiciler->Python menüsünde).
Test veri kümesi olarak, y = 4X + 10sin(X*0.5) fonksiyonunun üretilen değerlerini kullanacağız.
Böyle bir fonksiyonun grafiğini görüntülemek için MetaEditor'ı açın, RegressionData.py adında bir dosya oluşturun, kod metnini kopyalayın ve "Derle" düğmesine tıklayarak çalıştırın.
Test veri kümesini görüntülemek için kod
# RegressionData.py # The code plots the synthetic data, used for all regression models # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # import necessary libraries import numpy as np import matplotlib.pyplot as plt # generate synthetic data for regression X = np.arange(0,100,1).reshape(-1,1) y = 4*X + 10*np.sin(X*0.5) # set the figure size plt.figure(figsize=(8,5)) # plot the initial data for regression plt.scatter(X, y, label='Regression Data', marker='o') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Regression data') plt.show()
Sonuç olarak, regresyon yöntemlerini test etmek için kullanacağımız fonksiyonun bir grafiği görüntülenecektir.
Şekil 1. Regresyon modellerini test etme fonksiyonu
2. Regresyon modelleri
Bir regresyon görevinin amacı, yeni veriler için sayısal değerleri tahmin etmek üzere özellikler ve hedef değişken arasındaki ilişkiyi en iyi tanımlayan matematiksel bir fonksiyon veya model bulmaktır. Bu, tahminler yapılmasına, çözümlerin optimize edilmesine ve verilere dayalı bilinçli kararlar alınmasına olanak tanır.
Scikit-learn paketindeki ana regresyon modellerini ele alalım.
2.0. Scikit-learn regresyon modellerinin listesi
Mevcut scikit-learn regresyon modellerinin bir listesini görüntülemek için kodu kullanabilirsiniz:
# ScikitLearnRegressors.py # The script lists all the regression algorithms available inb scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn regression models from sklearn.utils import all_estimators regressors = all_estimators(type_filter='regressor') for index, (name, RegressorClass) in enumerate(regressors, start=1): print(f"Regressor {index}: {name}")
Çıktı:
The scikit-learn version is 1.3.2.
Regressor 1: ARDRegression
Regressor 2: AdaBoostRegressor
Regressor 3: BaggingRegressor
Regressor 4: BayesianRidge
Regressor 5: CCA
Regressor 6: DecisionTreeRegressor
Regressor 7: DummyRegressor
Regressor 8: ElasticNet
Regressor 9: ElasticNetCV
Regressor 10: ExtraTreeRegressor
Regressor 11: ExtraTreesRegressor
Regressor 12: GammaRegressor
Regressor 13: GaussianProcessRegressor
Regressor 14: GradientBoostingRegressor
Regressor 15: HistGradientBoostingRegressor
Regressor 16: HuberRegressor
Regressor 17: IsotonicRegression
Regressor 18: KNeighborsRegressor
Regressor 19: KernelRidge
Regressor 20: Lars
Regressor 21: LarsCV
Regressor 22: Lasso
Regressor 23: LassoCV
Regressor 24: LassoLars
Regressor 25: LassoLarsCV
Regressor 26: LassoLarsIC
Regressor 27: LinearRegression
Regressor 28: LinearSVR
Regressor 29: MLPRegressor
Regressor 30: MultiOutputRegressor
Regressor 31: MultiTaskElasticNet
Regressor 32: MultiTaskElasticNetCV
Regressor 33: MultiTaskLasso
Regressor 34: MultiTaskLassoCV
Regressor 35: NuSVR
Regressor 36: OrthogonalMatchingPursuit
Regressor 37: OrthogonalMatchingPursuitCV
Regressor 38: PLSCanonical
Regressor 39: PLSRegression
Regressor 40: PassiveAggressiveRegressor
Regressor 41: PoissonRegressor
Regressor 42: QuantileRegressor
Regressor 43: RANSACRegressor
Regressor 44: RadiusNeighborsRegressor
Regressor 45: RandomForestRegressor
Regressor 46: RegressorChain
Regressor 47: Ridge
Regressor 48: RidgeCV
Regressor 49: SGDRegressor
Regressor 50: SVR
Regressor 51: StackingRegressor
Regressor 52: TheilSenRegressor
Regressor 53: TransformedTargetRegressor
Regressor 54: TweedieRegressor
Regressor 55: VotingRegressor
Bu regresörler listesinde kolaylık sağlamak için farklı renklerle vurgulanmışlardır. Temel regresyon modeli gerektiren modeller gri renkle vurgulanmıştır, diğer modeller ise bağımsız olarak kullanılabilir. ONNX formatına başarıyla aktarılan modeller yeşil renkle, scikit-learn 1.2.2'nin mevcut sürümünde dönüştürme sırasında hatalarla karşılaşan modeller kırmızı renkle işaretlenmiştir. Söz konusu test görevi için uygun olmayan yöntemler mavi renkle vurgulanmıştır.
Regresyon kalite analizi, gerçek ve tahmin edilen değerlerin fonksiyonları olan regresyon metriklerini kullanır. MQL5 dilinde, "ONNX modellerinin regresyon metrikleri kullanılarak değerlendirilmesi" makalesinde ayrıntılı olarak açıklanan birkaç farklı metrik mevcuttur.
Bu makalede, farklı modellerin kalitesini karşılaştırmak için üç metrik kullanılacaktır:
- Belirleme katsayısı R-kare (R-squared, R2)
- Ortalama mutlak hata (Mean Absolute Error, MAE);
- Ortalama karesel hata (Mean Squared Error, MSE).
2.1. ONNX float ve double modellerine dönüştürülen Scikit-learn regresyon modelleri
Bu bölümde, hem float hem de double hassasiyetlerde ONNX formatlarına başarıyla dönüştürülen regresyon modelleri sunulmaktadır.
Tartışılacak olan tüm regresyon modelleri aşağıdaki formatta sunulmuştur:
- Model tanımı, çalışma prensibi, avantajlar ve sınırlamalar
- Modeli oluşturmak, float ve double formatlarında ONNX dosyalarına aktarmak ve elde edilen modelleri Python'da ONNX Runtime kullanarak çalıştırmak için Python kodu. Orijinal ve ONNX modellerinin kalitesini değerlendirmek için sklearn.metrics kullanılarak hesaplanan R^2, MAE, MSE gibi metrikler kullanılır.
- RegressionMetric() kullanılarak hesaplanan metriklerle ONNX modellerini (float ve double) ONNX Runtime aracılığıyla yürütmek için MQL5 komut dosyası.
- Netron'da float ve double hassasiyet için ONNX model gösterimi.
2.1.1. sklearn.linear_model.ARDRegression
ARDRegression (Automatic Relevance Determination Regression), regresyon problemlerini çözmek için tasarlanmış bir regresyon yöntemidir ve model eğitim sürecinde özelliklerin önemini (alaka düzeyini) otomatik olarak belirler ve ağırlıklarını ayarlar.
ARDRegression, bir regresyon modeli oluşturmak için yalnızca en önemli özelliklerin tespit edilmesini ve kullanılmasını sağlar; bu, çok sayıda özellik ile uğraşırken faydalı olabilir.
ARDRegression'ın çalışma prensibi:
- Lineer regresyon: ARDRegression, bağımsız değişkenler (özellikler) ile hedef değişken arasında doğrusal bir ilişki olduğunu varsayarak lineer regresyona dayanır.
- Otomatik özellik önemi belirleme: ARDRegression'ın temel farkı, hedef değişkeni tahmin etmek için hangi özelliklerin en önemli olduğunu otomatik olarak belirlemesidir. Bu, modelin daha az önemli özellikler için otomatik olarak sıfır ağırlık ayarlamasına olanak tanıyan ağırlıklar üzerinde önsel dağılımlar (düzenlileştirme) getirilerek elde edilir.
- Sonsal olasılıkların hesaplanması: ARDRegression, her özellik için sonsal olasılıkları hesaplayarak önemlerinin belirlenmesini sağlar. Yüksek sonsal olasılıklara sahip özellikler alakalı kabul edilir ve sıfır olmayan ağırlıklar alır, düşük sonsal olasılıklara sahip özellikler ise sıfır ağırlık alır.
- Boyut azaltma: Böylece ARDRegression, önemsiz özellikleri ortadan kaldırarak veri boyutunun azaltılmasını sağlayabilir.
ARDRegression'ın avantajları:
- Önemli özelliklerin otomatik olarak belirlenmesi: Yöntem, yalnızca en önemli özellikleri otomatik olarak tanımlar ve kullanır, bu da potansiyel olarak model performansını artırır ve aşırı uyum riskini azaltır.
- Çoklu eşdoğrusallığa karşı dayanıklılık: ARDRegression, özellikler yüksek oranda ilişkili olsa bile çoklu eşdoğrusallığı iyi bir şekilde yönetir.
ARDRegression'ın sınırlamaları:
- Önsel dağılımların seçilmesini gerektirir: Uygun önsel dağılımların seçilmesi deneysel çalışma gerektirebilir.
- Hesaplama karmaşıklığı: ARDRegression eğitimi, özellikle büyük veri kümeleri için hesaplama açısından maliyetli olabilir.
ARDRegression, özelliklerin önemini otomatik olarak belirleyen ve sonsal olasılıklara dayalı olarak ağırlıklarını oluşturan bir regresyon yöntemidir. Bu yöntem, bir regresyon modeli oluşturmak için yalnızca önemli özellikler dikkate alındığında ve veri boyutunun azaltılması gerektiğinde kullanışlıdır.
2.1.1.1. ARDRegression modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.ARDRegression modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training ARDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"
# create an ARDRegression model
regression_model = ARDRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Kod sklearn.linear_model.ARDRegression modelini oluşturur ve eğitir (orijinal model double olarak kabul edilir), ardından modeli float ve double için ONNX'e aktarır (ard_regression_float.onnx ve ard_regression_double.onnx) ve çalışmasının doğruluğunu karşılaştırır.
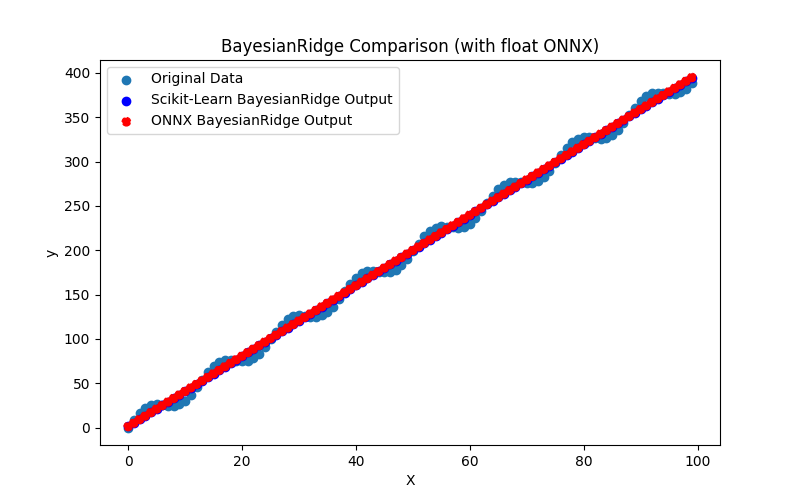
Ayrıca ARDRegression_plot_float.png ve ARDRegression_plot_double.png dosyalarını oluşturarak float ve double için ONNX modellerinin sonuçlarının görsel olarak değerlendirilmesini sağlar (Şekil 2-3).
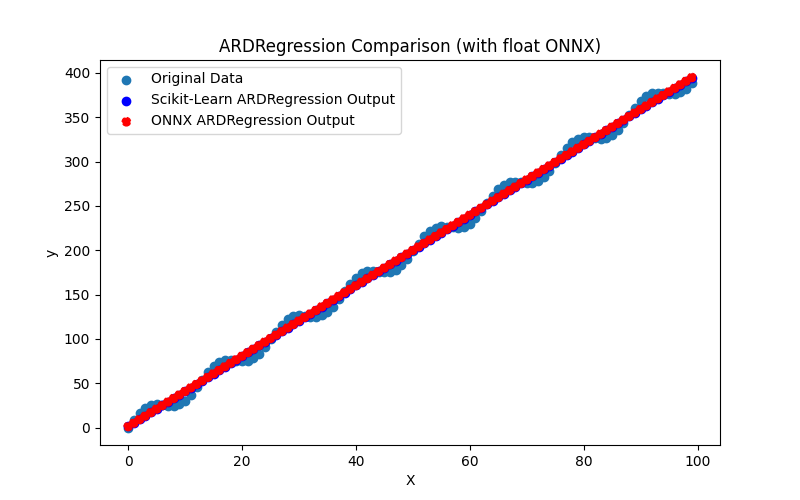
Şekil 2. ARDRegression.py sonuçları (float)
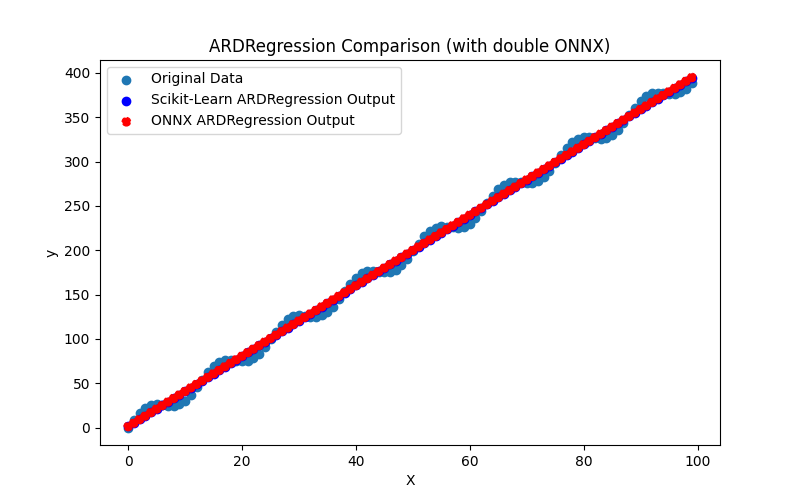
Şekil 3. ARDRegression.py sonuçları (double)
Görsel olarak, float ve double için ONNX modelleri aynı görünmektedir (Şekil 2-3), ayrıntılı bilgi Journal sekmesinden bulunabilir:
Python ARDRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python Python ARDRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python ARDRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
Bu örnekte, orijinal model double olarak ele alınmış, daha sonra sırasıyla float ve double için ard_regression_float.onnx ve ard_regression_double.onnx ONNX modellerine aktarılmıştır.
Modelin doğruluğu MAE ile değerlendirilirse, float için ONNX modelinin doğruluğu 6 ondalık basamağa kadar çıkarken, double kullanan ONNX modeli orijinal modelin hassasiyetine uygun olarak 15 ondalık basamağa kadar doğruluk tutma göstermiştir.
ONNX modellerinin özellikleri MetaEditor'da görüntülenebilir (Şekil 4-5).
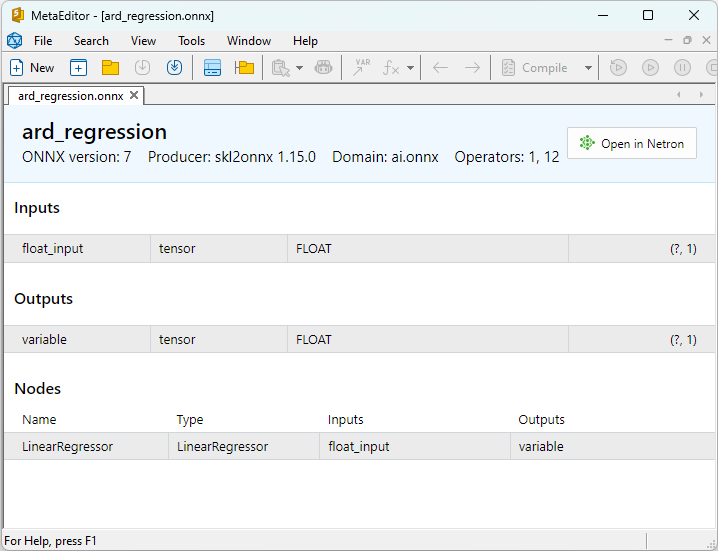
Şekil 4. MetaEditor'da ard_regression_float.onnx ONNX modeli
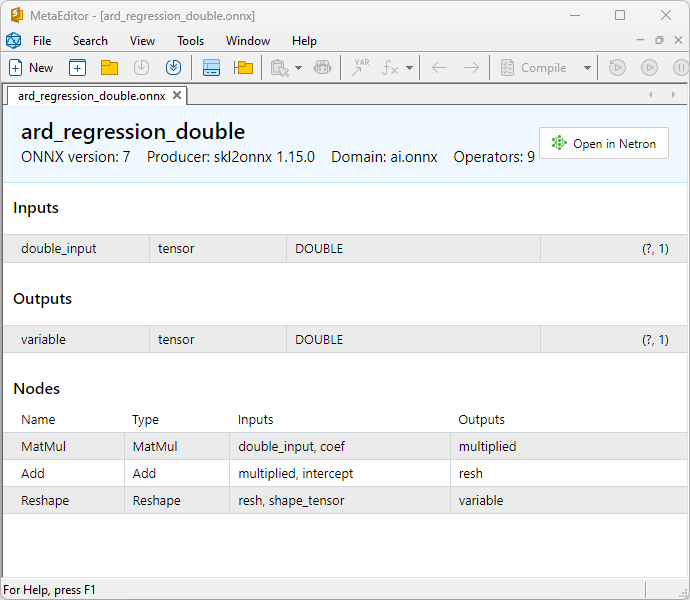
Şekil 5. MetaEditor'da ard_regression_double.onnx ONNX modeli
float ve double ONNX modelleri arasındaki bir karşılaştırma, bu durumda ARDRegresyon için ONNX modellerinin hesaplanmasının farklı şekilde gerçekleştiğini göstermektedir: float sayılar için ONNX-ML'den LinearRegressor() operatörü kullanılırken, double sayılar için MatMul(), Add() ve Reshape() ONNX operatörleri kullanılır.
Modelin ONNX'te uygulanması dönüştürücüye bağlıdır; ONNX'e aktarma örneklerinde skl2onnx kütüphanesindeki skl2onnx.convert_sklearn() fonksiyonu kullanılacaktır.
2.1.1.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen ard_regression_float.onnx ve ard_regression_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| ARDRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ARDRegression" #define ONNXFilenameFloat "ard_regression_float.onnx" #define ONNXFilenameDouble "ard_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
ARDRegression (EURUSD,H1) Testing ONNX float: ARDRegression (ard_regression_float.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 ARDRegression (EURUSD,H1) ARDRegression (EURUSD,H1) Testing ONNX double: ARDRegression (ard_regression_double.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537597 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128795
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: ARDRegression (ard_regression_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: ARDRegression (ard_regression_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537597
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.1.3. ard_regression_float.onnx ve ard_regression_double.onnx modellerinin ONNX gösterimi
Netron (web sürümü), ONNX (Open Neural Network Exchange) formatındaki modeller için kullanılabilen, modelleri görselleştirmeye ve hesaplama grafiklerini analiz etmeye yönelik bir araçtır.
Netron, model grafiklerini ve mimarilerini açık ve etkileşimli bir biçimde sunarak, ONNX kullanılarak oluşturulanlar da dahil olmak üzere derin öğrenme modellerinin yapısının ve parametrelerinin keşfedilmesine olanak tanır.
Netron'un temel özellikleri şunlardır:
- Grafik görselleştirme: Netron, modelin mimarisini bir grafik olarak göstererek katmanları, işlemleri ve bunlar arasındaki bağlantıları görmenizi sağlar. Model içerisindeki yapıyı ve veri akışını kolayca kavrayabilirsiniz.
- Etkileşimli keşif: Her operatör ve parametreleri hakkında ek bilgi edinmek için grafikteki düğümleri seçebilirsiniz.
- Çeşitli formatlar için destek: Netron, ONNX, TensorFlow, PyTorch, CoreML vb. dahil olmak üzere çeşitli derin öğrenme modeli formatlarını destekler.
- Parametre analiz yeteneği: Modelin parametrelerini ve ağırlıklarını görüntüleyebilirsiniz; bu, modelin farklı bölümlerinde kullanılan değerleri anlamak için yararlıdır.
Netron, modellerin görselleştirilmesini ve analizini basitleştirerek karmaşık sinir ağlarının anlaşılmasına ve hatalarının ayıklanmasına yardımcı olduğu için makine öğrenimi ve derin öğrenme alanındaki geliştiriciler ve araştırmacılar için kullanışlıdır.
Bu araç, modellerin hızlı bir şekilde incelenmesine, yapılarının ve parametrelerinin keşfedilmesine olanak tanıyarak derin sinir ağlarıyla çalışmayı kolaylaştırır.
Netron hakkında daha fazla ayrıntı için makalelere bakın: Visualizing your Neural Network with Netron ve Visualize Keras Neural Networks with Netron.
Netron hakkında video:
ard_regression_float.onnx modeli Şekil 6'da gösterilmektedir:
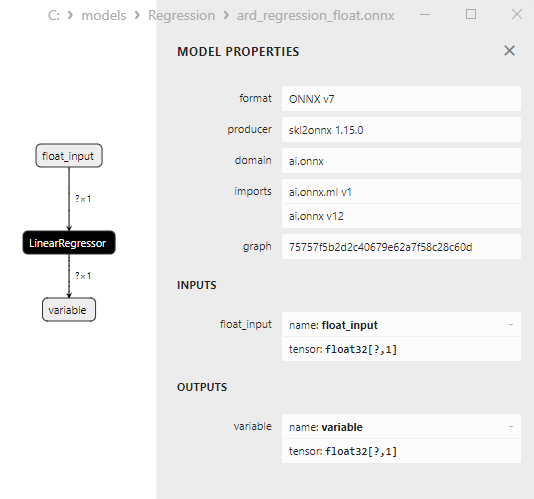
Şekil 6. Netron'da ard_regression_float.onnx modelinin ONNX gösterimi
ai.onnx.ml LinearRegressor() ONNX operatörü, regresyon görevleri için bir model tanımlayan ONNX standardının bir parçasıdır. Bu operatör, girdi özelliklerine dayalı olarak sayısal (sürekli) değerlerin tahmin edilmesini içeren regresyon için kullanılır.
Girdi özellikleri ile birlikte ağırlıklar ve yanlılık gibi model parametrelerini girdi olarak alır ve lineer regresyon yürütür. Lineer regresyon, her bir girdi özelliği için parametreleri (ağırlıkları) hesaplar ve ardından bir tahmin oluşturmak için bu özelliklerin ağırlıklarla doğrusal bir kombinasyonunu gerçekleştirir.
Bu operatör aşağıdaki adımları gerçekleştirir:
- Girdi özellikleriyle birlikte modelin ağırlıklarını ve yanlılığını alır.
- Girdi verilerinin her bir örneği için, ilgili özelliklerle ağırlıkların doğrusal bir kombinasyonunu gerçekleştirir.
- Ortaya çıkan değere yanlılığı ekler.
Sonuç, regresyon görevindeki hedef değişkenin tahminidir.
LinearRegressor() parametreleri Şekil 7'de gösterilmektedir.
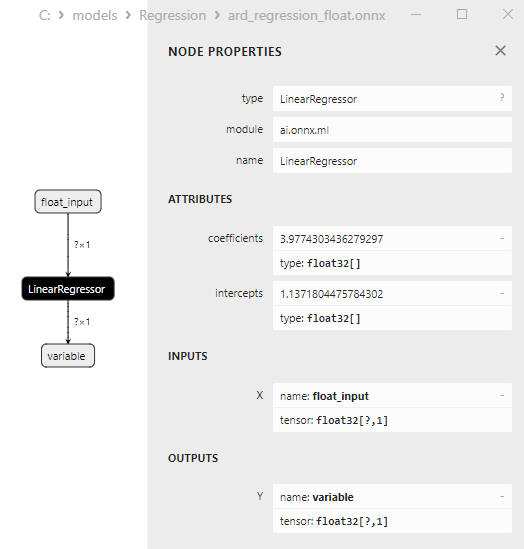
Şekil 7. Netron'da ard_regression_float.onnx modelinin LinearRegressor() operatör özellikleri
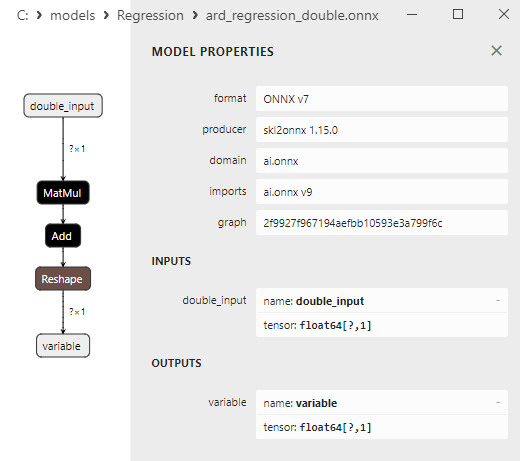
Şekil 8. Netron'da ard_regression_double.onnx modelinin ONNX gösterimi
MatMul(), Add() ve Reshape() ONNX operatörlerinin parametreleri Şekil 9-11'de gösterilmektedir.
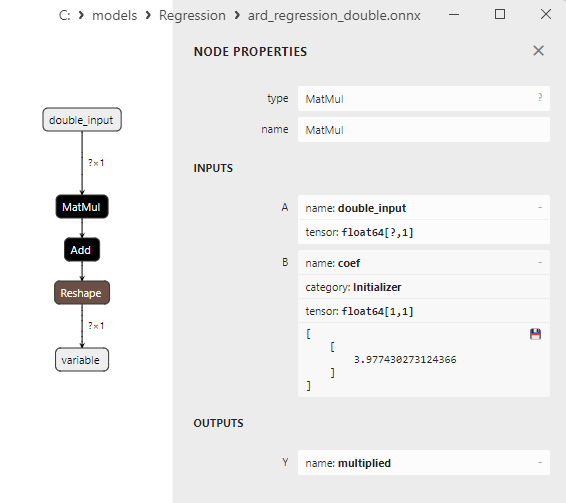
Şekil 9. Netron'da ard_regression_double.onnx modelindeki MatMul operatörünün özellikleri
MatMul (matris çarpımı) ONNX operatörü iki matrisin çarpımını gerçekleştirir.
İki girdi alır: iki matris ve bunların matris çarpımını geri döndürür.
A ve B olmak üzere iki matrisiniz varsa, Matmul(A, B) işleminin sonucu bir C matrisidir; burada her C[i][j] elemanı, A matrisinin i satırındaki elemanlarla B matrisinin j sütunundaki elemanların çarpımlarının toplamı olarak hesaplanır.
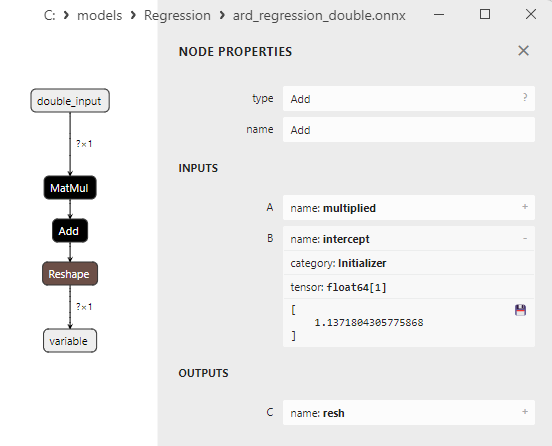
Şek.10. Netron'da ard_regression_double.onnx modelindeki Add operatörünün özellikleri
Add ONNX operatörü, aynı şekle sahip iki tensör veya dizinin eleman bazında toplanmasını gerçekleştirir.
İki girdi alır ve elde edilen tensörün her bir elemanının girdi tensörlerinin karşılık gelen elemanlarının toplamına eşit olduğu sonucu geri döndürür.
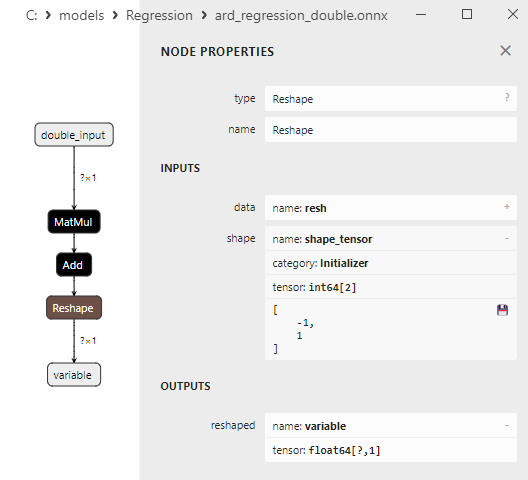
Şekil 11. Netron'da ard_regression_double.onnx modelindeki Reshape operatörünün özellikleri
Reshape(-1,1) ONNX operatörü, girdi verilerinin şeklini (veya boyutunu) değiştirmek için kullanılır. Bu operatörde, boyut için -1 değeri, veri tutarlılığını sağlamak için söz konusu boyutun büyüklüğünün diğer boyutlara göre otomatik olarak hesaplanması gerektiğini belirtir.
İkinci boyuttaki 1 değeri, şekil dönüşümünden sonra her bir elemanın tek bir alt boyuta sahip olacağını belirtir.
2.1.2. sklearn.linear_model.BayesianRidge
BayesianRidge, model parametrelerini hesaplamak için bir Bayes yaklaşımı kullanan bir regresyon yöntemidir. Bu yöntem, parametrelerin önsel dağılımının modellenmesini ve parametrelerin sonsal dağılımını elde etmek için verileri dikkate alarak güncellenmesini sağlar.
BayesianRidge, bir veya birkaç bağımsız değişkene dayalı olarak bağımlı değişkeni tahmin etmek için tasarlanmış bir Bayes regresyon yöntemidir.
BayesianRidge'in çalışma prensibi:
- Parametrelerin önsel dağılımı: Model parametrelerinin önsel dağılımının tanımlanmasıyla başlar. Bu dağılım, verileri dikkate almadan önce model parametreleri hakkındaki ön bilgileri veya varsayımları temsil eder. BayesianRidge durumunda, Gauss şekilli önsel dağılımlar kullanılır.
- Parametre dağılımının güncellenmesi: Önsel parametre dağılımı belirlendikten sonra, verilere göre güncellenir. Bu, parametrelerin sonsal dağılımının veriler dikkate alınarak hesaplandığı Bayes teorisi kullanılarak yapılır. Önemli bir husus, sonsal dağılımın şeklini etkileyen hiperparametrelerin hesaplanmasıdır.
- Tahmin: Parametrelerin sonsal dağılımı hesaplandıktan sonra, yeni gözlemler için tahminler yapılabilir. Bu, tek bir nokta değeri yerine tahminlerin bir dağılımıyla sonuçlanır ve tahminlerdeki belirsizliğin dikkate alınmasına olanak tanır.
BayesianRidge'in avantajları:
- Belirsizlik değerlendirmesi: BayesianRidge, model parametrelerindeki ve tahminlerdeki belirsizliği hesaba katar. Noktasal tahminler yerine güven aralıkları sunulur.
- Düzenlileştirme: Bayes regresyon yöntemi, aşırı uyumu önlemeye yardımcı olarak model düzenlileştirmesi için yararlı olabilir.
- Otomatik özellik seçimi: BayesianRidge, önemsiz özelliklerin ağırlıklarını azaltarak özellik önemini otomatik olarak belirleyebilir.
BayesianRidge'in sınırlamaları:
- Hesaplama karmaşıklığı: Yöntem, parametreleri ve sonsal dağılımı hesaplamak için hesaplama kaynakları gerektirir.
- Yüksek soyutluk seviyesi: BayesianRidge'i anlamak ve kullanmak için Bayes istatistikleri hakkında daha derin bir anlayış gerekebilir.
- Her zaman en iyi seçim değildir: BayesianRidge, bazı regresyon görevlerinde, özellikle de sınırlı verilerle çalışırken en uygun yöntem olmayabilir.
BayesianRidge, parametrelerin ve tahminlerin belirsizliğinin önemli olduğu regresyon görevlerinde ve model düzenlileştirmesinin gerekli olduğu durumlarda kullanışlıdır.
2.1.2.1. BayesianRidge modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.BayesianRidge modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training BayesianRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"
# create a Bayesian Ridge regression model
regression_model = BayesianRidge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python BayesianRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python Python BayesianRidge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python BayesianRidge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
Şekil 12. BayesianRidge.py sonuçları (float ONNX)
2.1.2.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen bayesian_ridge_float.onnx ve bayesian_ridge_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| BayesianRidge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BayesianRidge" #define ONNXFilenameFloat "bayesian_ridge_float.onnx" #define ONNXFilenameDouble "bayesian_ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
BayesianRidge (EURUSD,H1) Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 BayesianRidge (EURUSD,H1) BayesianRidge (EURUSD,H1) Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537624 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128866
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537624
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
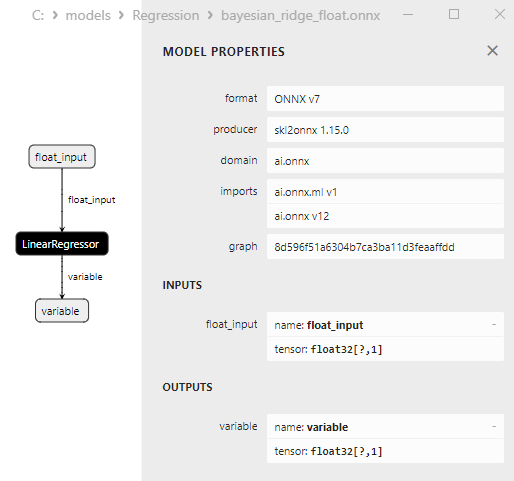
2.1.2.3. bayesian_ridge_float.onnx ve bayesian_ridge_double.onnx modellerinin ONNX gösterimi
Şekil 13. Netron'da bayesian_ridge_float.onnx modelinin ONNX gösterimi
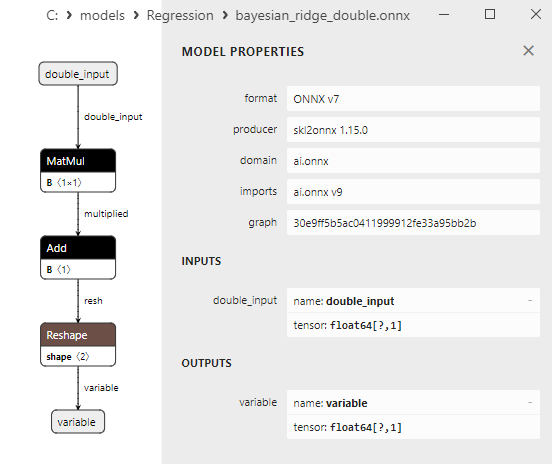
Şekil 14. Netron'da bayesian_ridge_double.onnx modelinin ONNX gösterimi
ElasticNet ve ElasticNetCV yöntemleri hakkında not
ElasticNet ve ElasticNetCV, regresyon modellerini, özellikle lineer regresyonu düzenlileştirmek için kullanılan iki ilgili makine öğrenimi yöntemidir. Ortak işlevselliği paylaşırlar ancak kullanım ve uygulama biçimlerinde farklılık gösterirler.
ElasticNet (Elastic Net Regression):
- Çalışma prensibi: ElasticNet, Lasso (L1 düzenlileştirme) ve Ridge'i (L2 düzenlileştirme) birleştiren bir regresyon yöntemidir. Kayıp fonksiyonuna iki düzenlileştirme bileşeni ekler: biri katsayıların büyük mutlak değerleri için modeli cezalandırır (Lasso gibi), diğeri ise katsayıların büyük kareleri için modeli cezalandırır (Ridge gibi).
- ElasticNet, verilerde çoklu eşdoğrusallık olduğunda (özellikler yüksek oranda ilişkili olduğunda) ve boyut azaltmanın yanı sıra katsayı değerlerinin kontrol edilmesi gerektiğinde yaygın olarak kullanılır.
ElasticNetCV (Elastic Net Cross-Validation):
- Çalışma prensibi: ElasticNetCV, çapraz doğrulama kullanarak alfa (L1 ve L2 düzenlileştirme arasındaki karışım katsayısı) ve lambda (düzenlileştirme gücü) optimum hiperparametrelerini otomatik olarak seçmeyi içeren ElasticNet'in bir uzantısıdır. Çeşitli alfa ve lambda değerlerini yineleyerek çapraz doğrulamada en iyi performansı gösteren kombinasyonu seçer.
- Avantajlar: ElasticNetCV, çapraz doğrulamaya dayalı olarak model parametrelerini otomatik olarak ayarlar ve manuel ayarlamaya gerek kalmadan optimum hiperparametre değerlerinin seçilmesine olanak tanır. Bu, kullanımı daha kolay hale getirir ve modelin aşırı uyumunu önlemeye yardımcı olur.
ElasticNet ve ElasticNetCV arasındaki temel fark, ElasticNet'in verilere uygulanan regresyon yöntemi olması, ElasticNetCV'nin ise çapraz doğrulama kullanarak ElasticNet modeli için en uygun hiperparametre değerlerini otomatik olarak bulan bir araç olmasıdır. ElasticNetCV, en iyi model parametrelerini bulmanız ve ayarlama sürecini daha otomatik hale getirmeniz gerektiğinde yardımcı olur.
2.1.3. sklearn.linear_model.ElasticNet
ElasticNet, L1 (Lasso) ve L2 (Ridge) düzenlileştirmenin bir kombinasyonunu temsil eden bir regresyon yöntemidir.
Bu yöntem, bir dizi özelliğe dayalı olarak hedef değişkenin sayısal değerlerinin tahmin edilmesi anlamına gelen regresyon için kullanılır. ElasticNet aşırı uyumu kontrol etmeye yardımcı olur ve model katsayıları üzerindeki hem L1 hem de L2 cezalarını dikkate alır.
ElasticNet'in çalışma prensibi:
- Girdi verileri: Özelliklere (bağımsız değişkenler) ve hedef değişkenin karşılık gelen değerlerine sahip olduğumuz orijinal veri kümesi ile başlar.
- Amaç fonksiyonu: ElasticNet, iki bileşen içeren kayıp fonksiyonunu en aza indirir - MSE ve iki düzenlileştirme: L1 (Lasso) ve L2 (Ridge). Bu, amaç fonksiyonunun şu şekilde göründüğü anlamına gelir:
Amaç fonksiyonu = MSE + α*L1 + β*L2
Burada α ve β sırasıyla L1 ve L2 düzenlileştirme ağırlıklarını kontrol eden hiperparametrelerdir. - Optimum α ve β'nın bulunması: Çapraz doğrulama yöntemi genellikle α ve β'nın en iyi değerlerini bulmak için kullanılır. Bu, aşırı uyumu azaltmak ve temel özellikleri korumak arasında bir denge kuran değerlerin seçilmesine olanak tanır.
- Model eğitimi: ElasticNet, amaç fonksiyonunu en aza indirerek optimum α ve β'yı dikkate alarak modeli eğitir.
- Tahmin: Model eğitildikten sonra, ElasticNet yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
ElasticNet'in avantajları:
- Özellik seçme yeteneği: ElasticNet, önemsiz özellikler için ağırlıkları sıfıra ayarlayarak (Lasso'ya benzer şekilde) en önemli özellikleri otomatik olarak seçebilir.
- Aşırı uyum kontrolü: ElasticNet, L1 ve L2 düzenlileştirme sayesinde aşırı uyumun kontrol edilmesini sağlar.
- Çoklu eşdoğrusallıkla başa çıkma: Bu yöntem, L2 düzenlileştirme çoklu eşdoğrusal özelliklerin etkisini azaltabileceğinden, çoklu eşdoğrusallığın (özellikler arasında yüksek korelasyon) olduğu durumlarda kullanışlıdır.
ElasticNet'in sınırlamaları:
- Önemsiz bir görev olabilen α ve β hiperparametrelerinin ayarlanmasını gerektirir.
- Parametre seçimlerine bağlı olarak, ElasticNet modelin kalitesini etkileyecek şekilde çok az veya çok fazla özellik tutabilir.
ElasticNet, özellik seçimi ve aşırı uyum kontrolünün çok önemli olduğu görevlerde faydalı olabilecek güçlü bir regresyon yöntemidir.
2.1.3.1. ElasticNet modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.ElasticNet modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training ElasticNet model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"
# create an ElasticNet model
regression_model = ElasticNet()
# fit the model to the data
regression_model.fit(X,y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python ElasticNet Original model (double) Python R-squared (Coefficient of determination): 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python Python ElasticNet ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377032416807 Python Mean Absolute Error: 6.344395027824294 Python Mean Squared Error: 49.78556400887057 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python ElasticNet ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
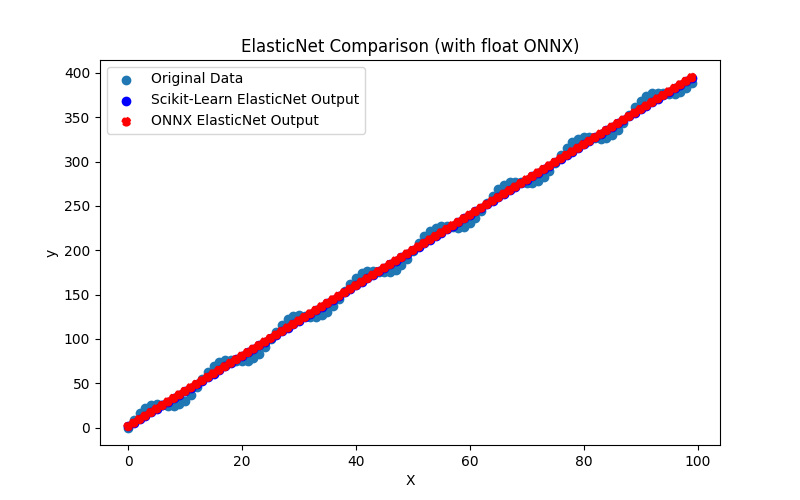
Şekil 15. ElasticNet.py sonuçları (float ONNX)
2.1.3.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen elastic_net_float.onnx ve elastic_net_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| ElasticNet.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNet" #define ONNXFilenameFloat "elastic_net_float.onnx" #define ONNXFilenameDouble "elastic_net_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
ElasticNet (EURUSD,H1) Testing ONNX float: ElasticNet (elastic_net_float.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377032416807 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443950278242944 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855640088705869 ElasticNet (EURUSD,H1) ElasticNet (EURUSD,H1) Testing ONNX double: ElasticNet (elastic_net_double.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377031744798 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443946628765220 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855648981241217
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: ElasticNet (elastic_net_float.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443950278242944 Testing ONNX double: ElasticNet (elastic_net_double.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443946628765220
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.3.3. elastic_net_float.onnx ve elastic_net_double.onnx modellerinin ONNX gösterimi
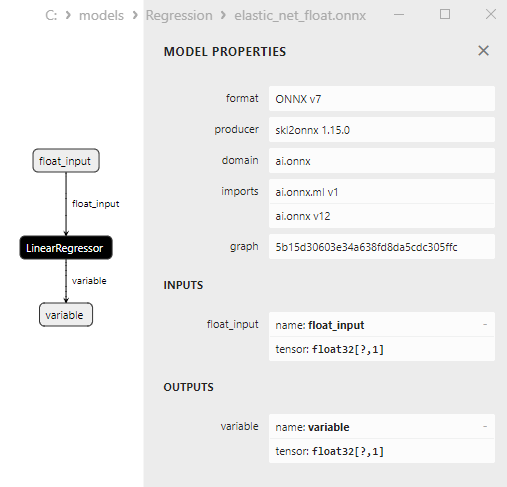
Şekil 16. Netron'da elastic_net_float.onnx modelinin ONNX gösterimi
Şekil 17. Netron'da elastic_net_double.onnx modelinin ONNX gösterimi
2.1.4. sklearn.linear_model.ElasticNetCV
ElasticNetCV, çapraz doğrulama kullanarak α ve β hiperparametrelerinin (L1 ve L2 düzenlileştirme) optimum değerlerini otomatik olarak seçmek için tasarlanmış ElasticNet yönteminin bir uzantısıdır
Bu, manuel parametre ayarlamasına gerek kalmadan ElasticNet modeli için en iyi düzenlileştirme kombinasyonunun bulunmasını sağlar.
ElasticNetCV'nin çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- α ve β aralığının tanımlanması: Kullanıcı, optimizasyon sırasında dikkate alınacak α ve β değer aralığını belirler. Bu değerler tipik olarak logaritmik bir ölçekte seçilir.
- Veri bölme: Veri kümesi çapraz doğrulama için birden fazla kata bölünmüştür. Her bir kat test veri kümesi olarak kullanılırken diğerleri eğitim için kullanılır.
- Çapraz doğrulama: Belirtilen aralıktaki her α ve β kombinasyonu için çapraz doğrulama gerçekleştirilir. ElasticNet modeli eğitim verileri üzerinde eğitilir ve ardından test verileri üzerinde değerlendirilir.
- Performans değerlendirmesi: Çapraz doğrulamada test veri kümelerindeki ortalama hata, her α ve β kombinasyonu için hesaplanır.
- Optimum parametrelerin seçimi: Çapraz doğrulama sırasında elde edilen minimum ortalama hataya karşılık gelen α ve β değerleri belirlenir.
- Optimum parametrelerle model eğitimi: ElasticNetCV modeli, bulunan optimum α ve β değerleri kullanılarak eğitilir.
- Tahmin: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
ElasticNetCV'nin avantajları:
- Otomatik hiperparametre seçimi: ElasticNetCV, α ve β'nın optimum değerlerini otomatik olarak bularak model ayarlamayı basitleştirir.
- Aşırı uyum önleme: Çapraz doğrulama, iyi genelleme kabiliyetine sahip bir modelin seçilmesine yardımcı olur.
- Gürültü dayanıklılığı: Bu yöntem veri gürültüsüne karşı dayanıklıdır ve gürültüyü dikkate alırken en iyi düzenlileştirme kombinasyonunu belirleyebilir.
ElasticNetCV'nin sınırlamaları:
- Hesaplama karmaşıklığı: Geniş bir parametre aralığında çapraz doğrulama yapmak zaman alıcı olabilir.
- Optimum parametreler aralık seçimine bağlıdır: Sonuçlar α ve β aralığının seçimine bağlı olabilir, bu nedenle bu aralığı dikkatlice ayarlamak önemlidir.
ElasticNetCV, ElasticNet modelindeki düzenlileştirmeyi otomatik olarak ayarlamak ve performansını artırmak için güçlü bir araçtır.
2.1.4.1. ElasticNetCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.ElasticNetCV modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# ElasticNetCV.py
# The code demonstrates the process of training ElasticNetCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNetCV"
onnx_model_filename = data_path + "elastic_net_cv"
# create an ElasticNetCV model
regression_model = ElasticNetCV()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python ElasticNetCV Original model (double) Python R-squared (Coefficient of determination): 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python Python ElasticNetCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137770260989 Python Mean Absolute Error: 6.334486542922601 Python Mean Squared Error: 50.10217383894468 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python ElasticNetCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
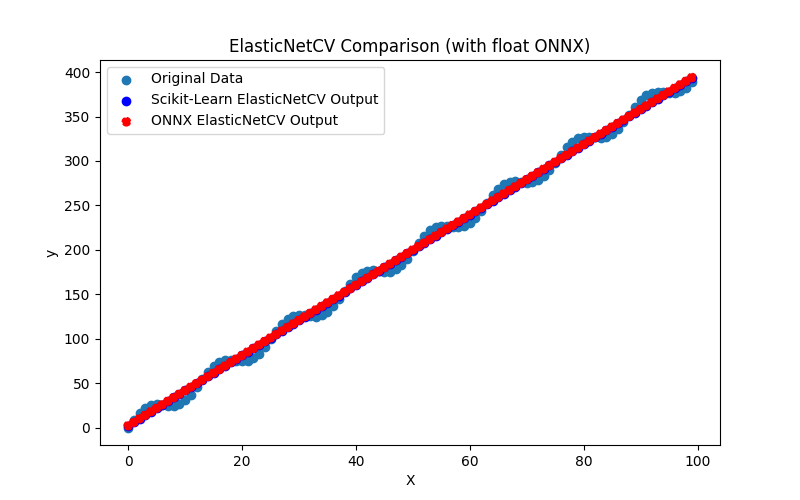
Şekil 18. ElasticNetCV.py sonuçları (float ONNX)
2.1.4.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen elastic_net_cv_float.onnx ve elastic_net_cv_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| ElasticNetCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNetCV" #define ONNXFilenameFloat "elastic_net_cv_float.onnx" #define ONNXFilenameDouble "elastic_net_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
ElasticNetCV (EURUSD,H1) Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137770260989 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344865429226038 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021738389446938 ElasticNetCV (EURUSD,H1) ElasticNetCV (EURUSD,H1) Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137763338385 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344871044232205 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021829994599983
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344865429226038 Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344871044232205
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.4.3. elastic_net_cv_float.onnx ve elastic_net_cv_double.onnx modellerinin ONNX gösterimi
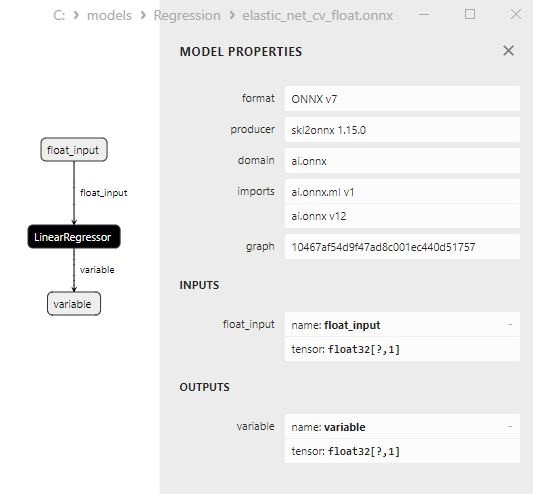
Şekil 19. Netron'da elastic_net_cv_float.onnx modelinin ONNX gösterimi
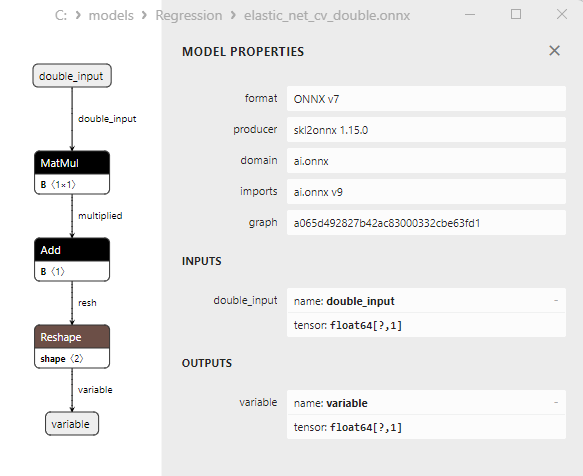
Şekil 20. Netron'da elastic_net_cv_double.onnx modelinin ONNX gösterimi
2.1.5. sklearn.linear_model.HuberRegressor
HuberRegressor, regresyon görevleri için kullanılan, Sıradan En Küçük Kareler (Ordinary Least Squares, OLS) yönteminin bir modifikasyonu olan ve verilerdeki aykırı değerlere karşı sağlam olacak şekilde tasarlanmış bir makine öğrenimi yöntemidir.
Hataların karelerini en aza indiren OLS'nin aksine, HuberRegressor karesel hataların ve mutlak hataların bir kombinasyonunu en aza indirir. Bu, yöntemin verilerdeki aykırı değerlerin varlığında daha sağlam bir şekilde çalışmasını sağlar.
HuberRegressor’ın çalışma prensibi:
- Girdi verileri: Özelliklerin (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerinin bulunduğu orijinal veri kümesi ile başlar.
- Huber kayıp fonksiyonu: HuberRegressor, küçük hatalar için kuadratik bir kayıp fonksiyonunu ve büyük hatalar için lineer bir kayıp fonksiyonunu birleştiren Huber kayıp fonksiyonunu kullanır. Bu, yöntemi aykırı değerlere karşı daha dirençli hale getirir.
- Model eğitimi: Model, Huber kayıp fonksiyonu kullanılarak veriler üzerinde eğitilir. Eğitim sırasında, her bir özellik ve yanlılık için ağırlıkları (katsayıları) ayarlar.
- Tahmin: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
HuberRegressor'ın avantajları:
- Aykırı değerlere karşı dayanıklılık: HuberRegressor, OLS'ye kıyasla verilerdeki aykırı değerlere karşı daha dayanıklıdır, bu da verilerin anormal değerler içerebileceği görevlerde yararlı olmasını sağlar.
- Hata hesaplaması: Huber kayıp fonksiyonu, model sonuçlarını analiz etmek için yararlı olabilecek tahmin hatalarının hesaplanmasına katkıda bulunur.
- Düzenlileştirme seviyesi: HuberRegressor ayrıca aşırı uyumu azaltabilecek bir düzenlileştirme seviyesi de içerebilir.
HuberRegressor'ın sınırlamaları:
- Aykırı değerlerin olmadığı durumlarda OLS kadar doğru değildir: Verilerde aykırı değerlerin bulunmadığı durumlarda, OLS daha doğru sonuçlar sağlayabilir.
- Parametre ayarlama: HuberRegressor, lineer kayıp fonksiyonuna geçmek için "büyük" olarak kabul edilen eşiği tanımlayan bir parametreye sahiptir. Bu parametre ayarlama gerektirir.
HuberRegressor, verilerin aykırı değerler içerebileceği ve bu tür anormalliklere karşı dayanıklı bir modelin gerekli olduğu regresyon görevlerinde değerlidir.
2.1.5.1. HuberRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.HuberRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training HuberRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"
# create a Huber Regressor model
huber_regressor_model = HuberRegressor()
# fit the model to the data
huber_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = huber_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python HuberRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python Python HuberRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363944236795 Python Mean Absolute Error: 6.341633300252807 Python Mean Squared Error: 49.80288328126165 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python HuberRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
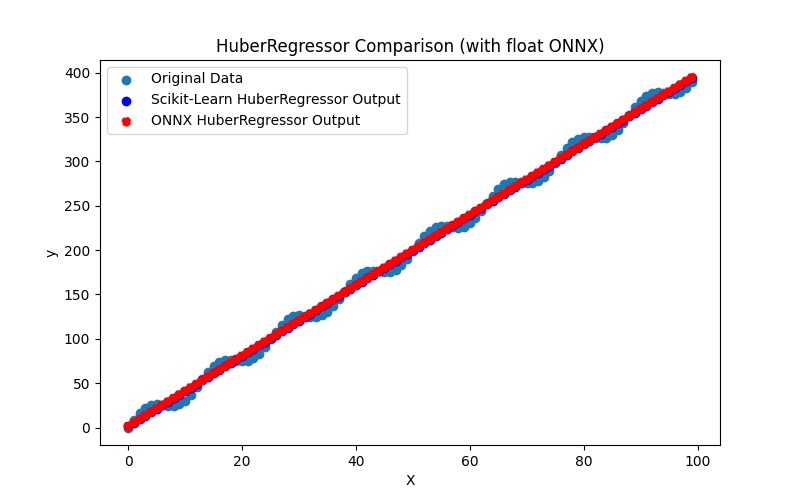
Şekil 21. HuberRegressor.py sonuçları (float ONNX)
2.1.5.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen huber_regressor_float.onnx ve huber_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| HuberRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HuberRegressor" #define ONNXFilenameFloat "huber_regressor_float.onnx" #define ONNXFilenameDouble "huber_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
HuberRegressor (EURUSD,H1) Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363944236795 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416333002528074 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028832812616571 HuberRegressor (EURUSD,H1) HuberRegressor (EURUSD,H1) Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363935647066 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416337085696410 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028946478433525
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416333002528074 Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416337085696410
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.5.3. huber_regressor_float.onnx ve huber_regressor_double.onnx modellerinin ONNX gösterimi
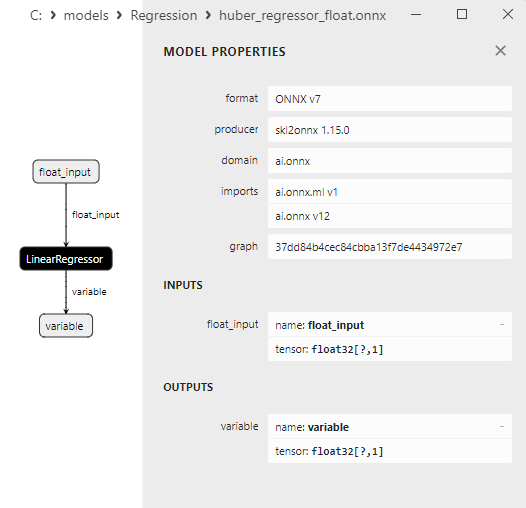
Şekil 22. Netron'da huber_regressor_float.onnx modelinin ONNX gösterimi
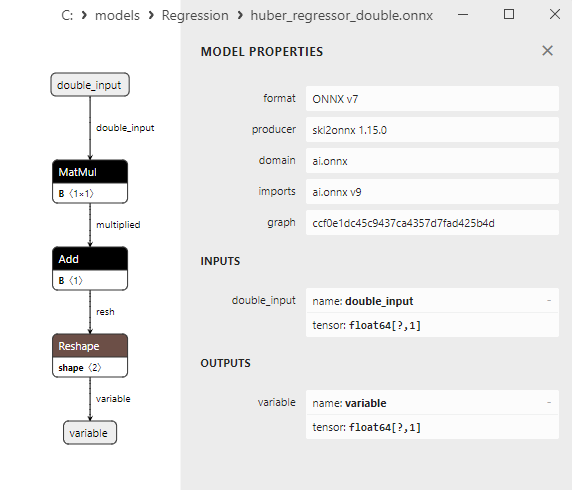
Şekil 23. Netron'da huber_regressor_double.onnx modelinin ONNX gösterimi
2.1.6. sklearn.linear_model.Lars
LARS (Least Angle Regression), regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Öğrenme süreci sırasında aktif özellikleri (değişkenleri) seçerek lineer bir regresyon modeli oluşturan bir algoritmadır
LARS, hedef değişkene en iyi yaklaşımı sağlayan en az sayıda özelliği bulmaya çalışır.
LARS'ın çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Başlatma: Boş bir modelle başlar, yani hiçbir aktif özellik yoktur. Tüm katsayılar sıfıra ayarlanır.
- Özellik seçimi: Her adımda LARS, modelin kalıntılarıyla en çok ilişkili olan özelliği seçer. Bu özellik daha sonra modele eklenir ve karşılık gelen katsayısı en küçük kareler yöntemi kullanılarak ayarlanır.
- Aktif özellikler boyunca regresyon: Özelliği modele ekledikten sonra LARS, yeni modeldeki değişikliklere uyum sağlamak için tüm aktif özelliklerin katsayılarını günceller.
- Tekrarlayan adımlar: Bu süreç, tüm özellikler seçilene veya belirli bir durma kriteri karşılanana kadar devam eder.
- Tahmin: Model eğitiminden sonra, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LARS'ın avantajları:
- Verimlilik: LARS, özellikle çok sayıda özellik olduğunda, ancak yalnızca birkaçı hedef değişkeni önemli ölçüde etkilediğinde verimli bir yöntem olabilir.
- Yorumlanabilirlik: LARS yalnızca en bilgilendirici özellikleri seçmeyi amaçladığından, model nispeten yorumlanabilir kalır.
LARS'ın sınırlamaları:
- Lineer model: LARS, doğrusal olmayan karmaşık ilişkileri modellemek için yetersiz kalabilecek lineer bir model oluşturur.
- Gürültü hassasiyeti: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Çoklu eşdoğrusallığın üstesinden gelememe: Özellikler yüksek oranda korelasyon gösteriyorsa, LARS çoklu eşdoğrusallık sorunlarıyla karşılaşabilir.
LARS, en bilgilendirici özellikleri seçmenin ve minimum sayıda özellik ile lineer bir model oluşturmanın gerekli olduğu regresyon görevlerinde değerlidir.
2.1.6.1. Lars modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.Lars modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training Lars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lars"
onnx_model_filename = data_path + "lars"
# create a Lars Regressor model
lars_regressor_model = Lars()
# fit the model to the data
lars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python Lars Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python Lars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python Lars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
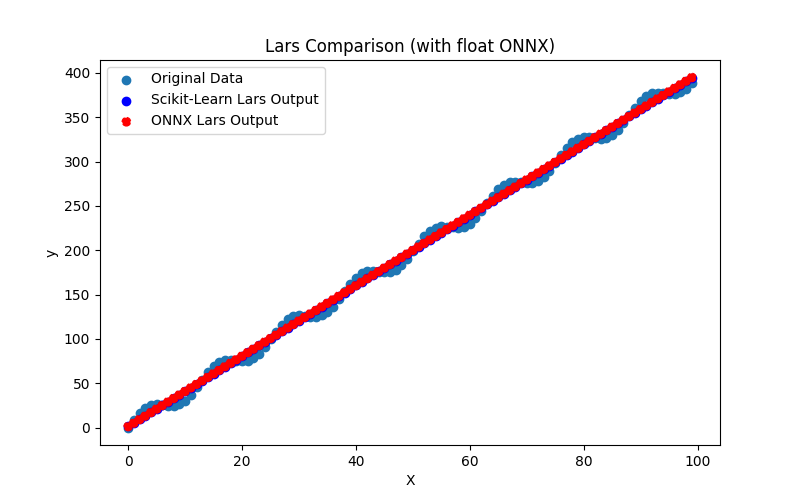
Şekil 24. Lars.py sonuçları (float ONNX)
2.1.6.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lars_float.onnx ve lars_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| Lars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lars" #define ONNXFilenameFloat "lars_float.onnx" #define ONNXFilenameDouble "lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
Lars (EURUSD,H1) Testing ONNX float: Lars (lars_float.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 Lars (EURUSD,H1) Lars (EURUSD,H1) Testing ONNX double: Lars (lars_double.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: Lars (lars_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: Lars (lars_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.6.3. lars_float.onnx ve lars_double.onnx modellerinin ONNX gösterimi
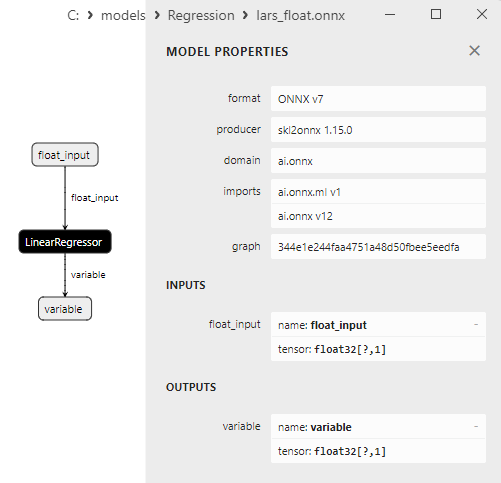
Şekil 25. Netron'da lars_float.onnx modelinin ONNX gösterimi
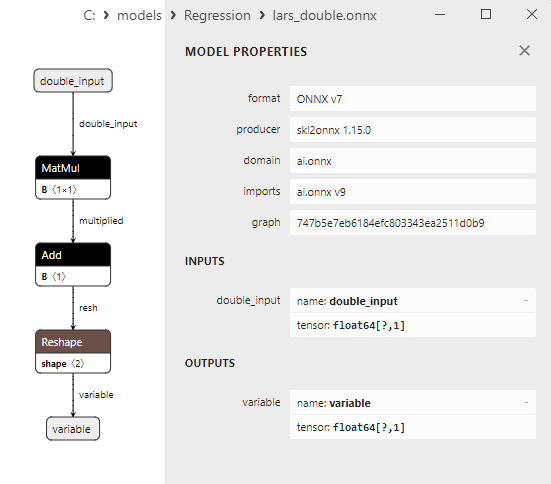
Şekil 26. Netron'da lars_double.onnx modelinin ONNX gösterimi
2.1.7. sklearn.linear_model.LarsCV
LarsCV, çapraz doğrulama kullanarak modele dahil edilecek en uygun özellik sayısını otomatik olarak seçen LARS (Least Angle Regression) yönteminin bir varyasyonudur.
Bu yöntem, verileri etkili bir şekilde genelleştiren bir model ile en az sayıda özellik kullanan bir model arasında bir denge kurulmasına yardımcı olur.
LarsCV'nin çalışma prensibi:
- Girdi verileri: Özelliklerden (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerinden oluşan orijinal veri kümesi ile başlar.
- Başlatma: Boş bir modelle başlar, bu da hiçbir aktif özellik olmadığı anlamına gelir. Tüm katsayılar sıfıra ayarlanır.
- Çapraz doğrulama: LarsCV, dahil edilen özelliklerin farklı miktarları için çapraz doğrulama gerçekleştirir. Bu, modelin performansını farklı özellik setleriyle değerlendirir.
- Optimum özellik sayısının seçilmesi: LarsCV, çapraz doğrulama yoluyla belirlenen en iyi model performansını sağlayan özellik sayısını seçer.
- Model eğitimi: Model, seçilen sayıda özellik ve bunların ilgili katsayıları kullanılarak eğitilir.
- Tahmin: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LarsCV'nin avantajları:
- Otomatik özellik seçimi: LarsCV, en uygun özellik sayısını otomatik olarak seçerek model kurulum sürecini basitleştirir.
- Yorumlanabilirlik: Normal LARS'a benzer şekilde, LarsCV nispeten yüksek model yorumlanabilirliğini korur.
- Verimlilik: Yöntem, özellikle veri kümelerinin çok sayıda özelliğe sahip olduğu, ancak yalnızca birkaçının önemli olduğu durumlarda verimli olabilir.
LarsCV'nin sınırlamaları:
- Lineer model: LarsCV, doğrusal olmayan karmaşık ilişkileri modellemek için yetersiz olabilecek lineer bir model oluşturur.
- Gürültü hassasiyeti: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Çoklu eşdoğrusallığın üstesinden gelememe: Özellikler yüksek oranda korelasyon gösteriyorsa, LarsCV çoklu eşdoğrusallık sorunlarıyla karşılaşabilir.
LarsCV, modelde kullanılan en iyi özellik kümesini otomatik olarak seçmenin ve modelin yorumlanabilirliğini korumanın önemli olduğu regresyon görevlerinde kullanışlıdır.
2.1.7.1. LarsCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LarsCV modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LarsCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"
# create a LarsCV Regressor model
larscv_regressor_model = LarsCV()
# fit the model to the data
larscv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = larscv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
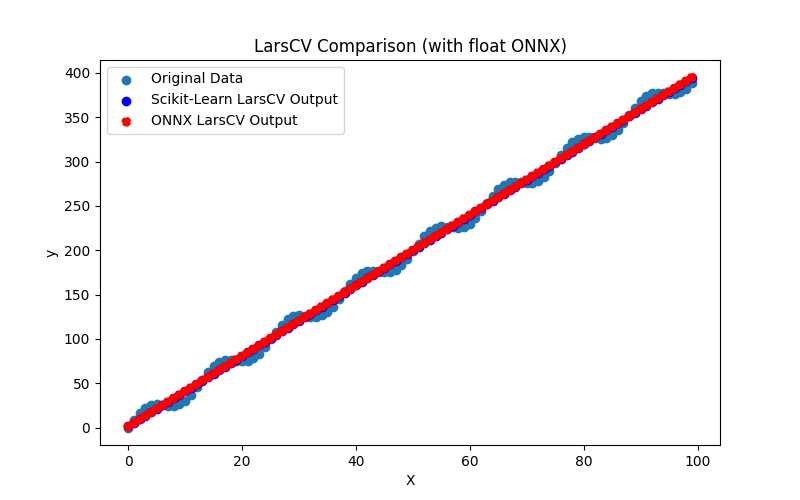
Şekil 27. LarsCV.py sonuçları (float ONNX)
2.1.7.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lars_cv_float.onnx ve lars_cv_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LarsCV" #define ONNXFilenameFloat "lars_cv_float.onnx" #define ONNXFilenameDouble "lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LarsCV (EURUSD,H1) Testing ONNX float: LarsCV (lars_cv_float.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LarsCV (EURUSD,H1) LarsCV (EURUSD,H1) Testing ONNX double: LarsCV (lars_cv_double.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: LarsCV (lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LarsCV (lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.7.3. lars_cv_float.onnx ve lars_cv_double.onnx modellerinin ONNX gösterimi
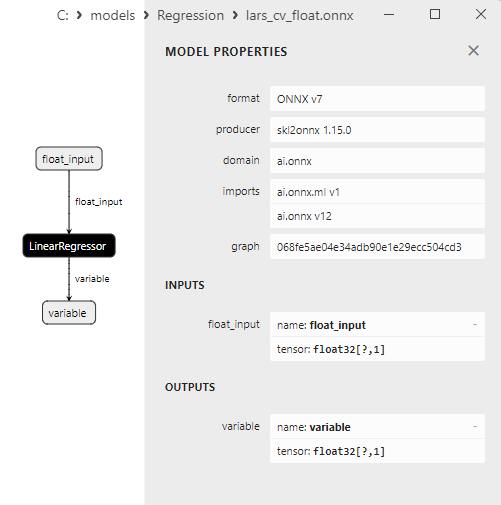
Şekil 28. Netron'da lars_cv_float.onnx modelinin ONNX gösterimi
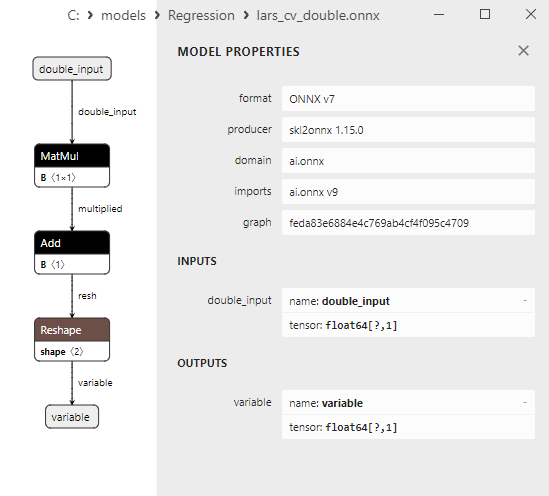
Şekil 29. Netron'da lars_cv_double.onnx modelinin ONNX gösterimi
2.1.8. sklearn.linear_model.Lasso
Lasso (Least Absolute Shrinkage and Selection Operator), en önemli özellikleri seçmek ve model boyutluluğunu azaltmak için kullanılan bir regresyon yöntemidir.
Bunu, lineer regresyon optimizasyon probleminde katsayıların mutlak değerlerinin toplamına bir ceza ekleyerek başarır (L1 düzenlileştirme).
Lasso'nun çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Amaç fonksiyonu: Lasso'daki amaç fonksiyonu, karesel regresyon hatalarının toplamını ve özelliklerle ilişkili katsayıların mutlak değerlerinin toplamı üzerindeki cezayı içerir.
- Optimizasyon: Lasso modeli, amaç fonksiyonunu en aza indirerek eğitilir, bu da bazı katsayıların sıfır olmasıyla sonuçlanır ve ilgili özellikleri modelden etkili bir şekilde hariç tutar.
- Optimum ceza değerinin seçilmesi: Lasso, düzenlileştirmenin gücünü belirleyen bir hiperparametre içerir. Bu hiperparametre için en uygun değerin seçilmesi çapraz doğrulama gerektirebilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
Lasso'nun avantajları:
- Özellik seçimi: Lasso, daha az önemli olanları modelden çıkararak en önemli özellikleri otomatik olarak seçer. Bu, veri boyutluluğunu azaltır ve modeli basitleştirir.
- Düzenlileştirme: Katsayıların mutlak değerlerinin toplamı üzerindeki ceza, modelin aşırı uyumunu önlemeye yardımcı olur ve genelleştirmesini geliştirir.
- Yorumlanabilirlik: Lasso bazı özellikleri hariç tuttuğu için model nispeten yorumlanabilir kalmaktadır.
Lasso'nun sınırlamaları:
- Lineer model: Lasso lineer bir model oluşturur, bu da karmaşık doğrusal olmayan ilişkileri modellemek için yetersiz olabilir.
- Gürültü hassasiyeti: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Çoklu eşdoğrusallığın üstesinden gelememe: Özellikler yüksek oranda korelasyon gösteriyorsa, Lasso çoklu eşdoğrusallık sorunlarıyla karşılaşabilir.
Lasso, en önemli özellikleri seçmenin ve yorumlanabilirliği korurken modelin boyutluluğunu azaltmanın gerekli olduğu regresyon görevlerinde kullanışlıdır.
2.1.8.1. Lasso modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.Lasso modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training Lasso model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lasso"
onnx_model_filename = data_path + "lasso"
# create a Lasso model
lasso_model = Lasso()
# fit the model to the data
lasso_model.fit(X, y)
# predict values for the entire dataset
y_pred = lasso_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python Lasso Original model (double) Python R-squared (Coefficient of determination): 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python Python Lasso ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381720269486 Python Mean Absolute Error: 6.346395056911361 Python Mean Squared Error: 49.77936068668213 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python Lasso ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
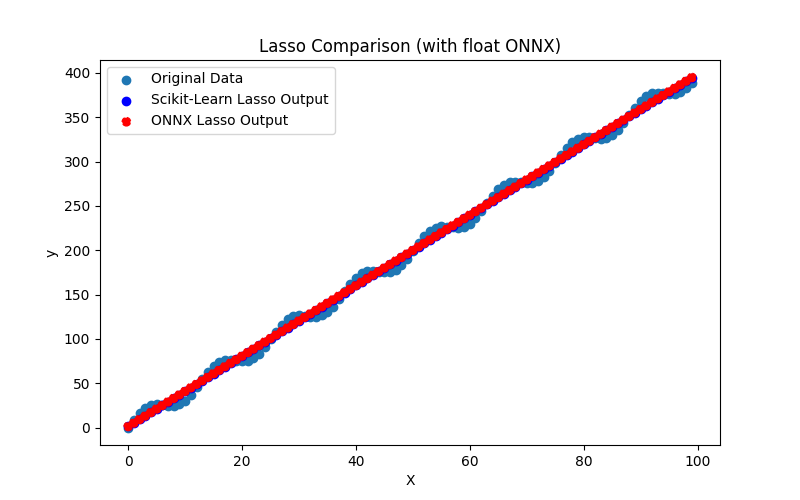
Şekil 30. Lasso.py sonuçları (float ONNX)
2.1.8.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lasso_float.onnx ve lasso_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| Lasso.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lasso" #define ONNXFilenameFloat "lasso_float.onnx" #define ONNXFilenameDouble "lasso_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
Lasso (EURUSD,H1) Testing ONNX float: Lasso (lasso_float.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381720269486 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463950569113612 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793606866821037 Lasso (EURUSD,H1) Lasso (EURUSD,H1) Testing ONNX double: Lasso (lasso_double.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381735682287 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463937919229840 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793402912937850
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: Lasso (lasso_float.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463950569113612 Testing ONNX double: Lasso (lasso_double.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463937919229840
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 15 ondalık basamak.
2.1.8.3. lasso_float.onnx ve lasso_double.onnx modellerinin ONNX gösterimi
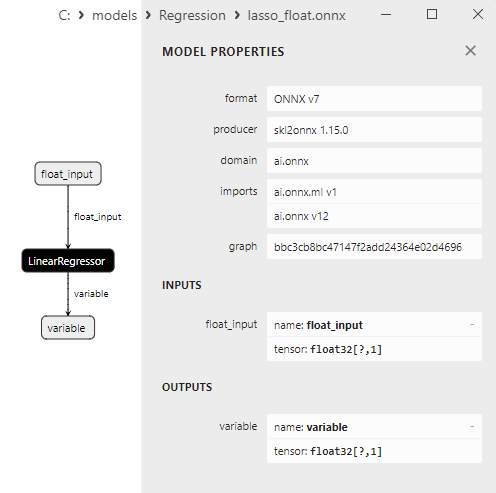
Şekil 31. Netron'da lasso_float.onnx modelinin ONNX gösterimi
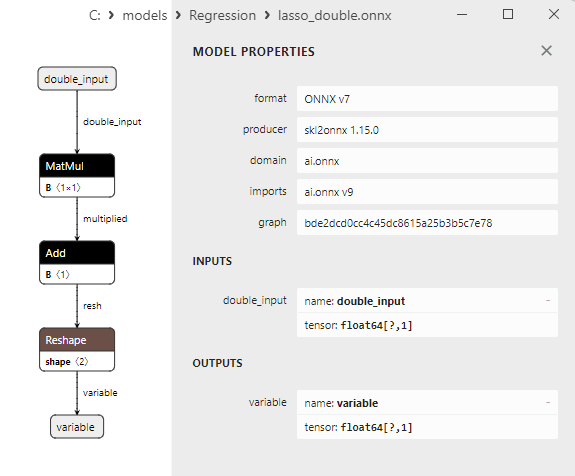
Şekil 32. Netron'da lasso_double.onnx modelinin ONNX gösterimi
2.1.9. sklearn.linear_model.LassoCV
LassoCV, çapraz doğrulama kullanarak düzenlileştirme hiperparametresi (alfa) için en uygun değeri otomatik olarak seçen Lasso yönteminin (Least Absolute Shrinkage and Selection Operator) bir çeşididir.
Bu yöntem, modelin boyutluluğunun azaltılması (önemli özelliklerin seçilmesi) ve aşırı uyumun önlenmesi arasında bir denge bulunmasını sağlayarak regresyon görevleri için kullanışlı hale gelir.
LassoCV'nin çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Başlatma: LassoCV, düşükten yükseğe kadar bir aralığı kapsayan düzenlileştirme hiperparametresinin (alfa) birkaç farklı değerini başlatır.
- Çapraz doğrulama: Her alfa değeri için LassoCV, modelin performansını değerlendirmek için çapraz doğrulama gerçekleştirir. Ortalama karesel hata (MSE) veya belirleme katsayısı (R^2) gibi metrikler yaygın olarak kullanılmaktadır.
- Optimum alfanın seçilmesi: LassoCV, modelin çapraz doğrulama ile belirlenen en iyi performansa ulaştığı alfa değerini seçer.
- Model eğitimi: LassoCV modeli, seçilen alfa değeri kullanılarak, daha az önemli özellikler hariç tutularak ve L1 düzenlileştirme uygulanarak eğitilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LassoCV'nin avantajları:
- Otomatik alfa seçimi: LassoCV, çapraz doğrulamayı kullanarak en uygun alfa değerini otomatik olarak seçer ve model ayarlamasını basitleştirir.
- Özellik seçimi: LassoCV otomatik olarak en önemli özellikleri seçerek modelin boyutluluğunu azaltır ve yorumlanmasını basitleştirir.
- Düzenlileştirme: Yöntem, L1 düzenlileştirme yoluyla modelin aşırı uyumunu önler.
LassoCV'nin sınırlamaları:
- Lineer model: LassoCV lineer bir model oluşturur, bu da karmaşık doğrusal olmayan ilişkileri modellemek için yetersiz olabilir.
- Gürültü hassasiyeti: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Çoklu eşdoğrusallığın üstesinden gelememe: Özellikler yüksek oranda ilişkili olduğunda, LassoCV çoklu eşdoğrusallık sorunlarıyla karşılaşabilir.
LassoCV, en önemli özellikleri seçmenin ve modelin boyutsallığını azaltırken yorumlanabilirliği korumanın ve aşırı uyumu önlemenin önemli olduğu regresyon görevlerinde faydalıdır.
2.1.9.1. LassoCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LassoCV modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LassoCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"
# create a LassoCV Regressor model
lassocv_regressor_model = LassoCV()
# fit the model to the data
lassocv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassocv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LassoCV Original model (double) Python R-squared (Coefficient of determination): 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python Python LassoCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996224142876629 Python Mean Absolute Error: 6.335673221332177 Python Mean Squared Error: 49.96500504333324 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 6 Python float ONNX model precision: 6 Python Python LassoCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
Şekil 33. LassoCV.py sonuçları (float ONNX)
2.1.9.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lasso_cv_float.onnx ve lasso_cv_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LassoCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoCV" #define ONNXFilenameFloat "lasso_cv_float.onnx" #define ONNXFilenameDouble "lasso_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
2023.10.26 22:14:00.736 LassoCV (EURUSD,H1) Testing ONNX float: LassoCV (lasso_cv_float.onnx) 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428766290 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356732213321800 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650050433332211 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) Testing ONNX double: LassoCV (lasso_cv_double.onnx) 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428413416 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356733445381899 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650055102816992
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: LassoCV (lasso_cv_float.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356732213321800 Testing ONNX double: LassoCV (lasso_cv_double.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356733445381899
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.9.3. lasso_cv_float.onnx ve lasso_cv_double.onnx modellerinin ONNX gösterimi
Şekil 34. Netron'da lasso_cv_float.onnx modelinin ONNX gösterimi
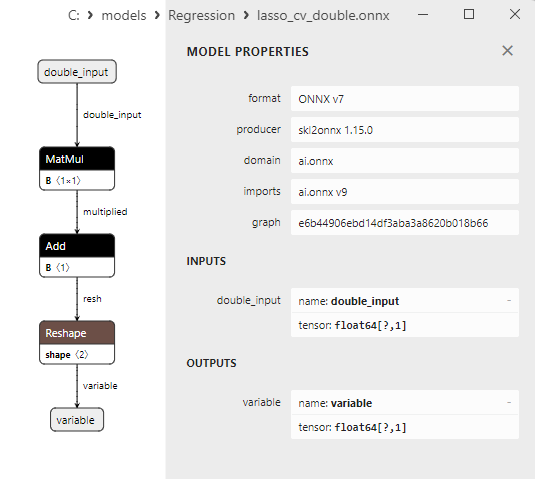
Şekil 35. Netron'da lasso_cv_double.onnx modelinin ONNX gösterimi
2.1.10. sklearn.linear_model.LassoLars
LassoLars iki yöntemin birleşimidir: Lasso (Least Absolute Shrinkage and Selection Operator) ve LARS (Least Angle Regression).
Bu yöntem regresyon görevleri için kullanılır ve her iki algoritmanın avantajlarını birleştirerek eşzamanlı özellik seçimi ve model boyutluluğunun azaltılmasına olanak tanır.
LassoLars'ın çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Başlatma: LassoLars boş bir modelle başlar, yani aktif özellik yoktur. Tüm katsayılar sıfıra ayarlanır.
- Aşamalı özellik seçimi: LARS yöntemine benzer şekilde, LassoLars her adımda model kalıntıları ile en çok korelasyon gösteren özelliği seçer ve modele ekler. Ardından, bu özelliğin katsayısı en küçük kareler yöntemi kullanılarak ayarlanır.
- L1 düzenlileştirme uygulaması: Aşamalı özellik seçimi ile eş zamanlı olarak LassoLars, katsayıların mutlak değerlerinin toplamına bir ceza ekleyerek L1 düzenlileştirme uygular. Bu, karmaşık ilişkilerin modellenmesine ve en önemli özelliklerin seçilmesine olanak tanır.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LassoLars'ın avantajları:
- Özellik seçimi: LassoLars otomatik olarak en önemli özellikleri seçer ve modelin boyutsallığını azaltarak aşırı uyumu önlemeye ve yorumlamayı basitleştirmeye yardımcı olur.
- Yorumlanabilirlik: Yöntem, modelin yorumlanabilirliğini koruyarak hangi özelliklerin dahil edildiğini ve bunların hedef değişkeni nasıl etkilediğini belirlemeyi kolaylaştırır.
- Düzenlileştirme: LassoLars, aşırı uyumu önleyen ve modelin genellemesini artıran L1 düzenlileştirme uygular.
LassoLars'ın sınırlamaları:
- Lineer model: LassoLars lineer bir model oluşturur, ancak bu doğrusal olmayan karmaşık ilişkileri modellemek için yetersiz olabilir.
- Gürültüye karşı hassasiyet: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Hesaplama karmaşıklığı: Her adımda özellik seçimi ve düzenlileştirmenin uygulanması, basit lineer regresyondan daha fazla hesaplama kaynağı gerektirebilir.
LassoLars, en önemli özellikleri seçmenin, modelin boyutluluğunu azaltmanın ve yorumlanabilirliği korumanın önemli olduğu regresyon görevlerinde kullanışlıdır.
2.1.10.1. LassoLars modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LassoLars modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"
# create a LassoLars Regressor model
lassolars_regressor_model = LassoLars(alpha=0.1)
# fit the model to the data
lassolars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LassoLars Original model (double) Python R-squared (Coefficient of determination): 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python Python LassoLars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382635045889 Python Mean Absolute Error: 6.3476034814795375 Python Mean Squared Error: 49.77815018516975 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
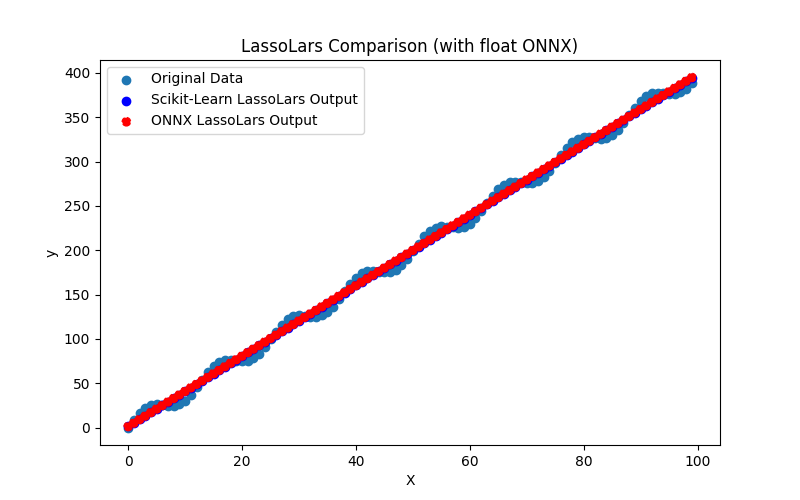
Şekil 36. LassoLars.py sonuçları (float ONNX)
2.1.10.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lasso_lars_float.onnx ve lasso_lars_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LassoLars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLars" #define ONNXFilenameFloat "lasso_lars_float.onnx" #define ONNXFilenameDouble "lasso_lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LassoLars (EURUSD,H1) Testing ONNX float: LassoLars (lasso_lars_float.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382635045889 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476034814795375 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781501851697357 LassoLars (EURUSD,H1) LassoLars (EURUSD,H1) Testing ONNX double: LassoLars (lasso_lars_double.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382633544077 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476035128950858 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781521724819029
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: LassoLars (lasso_lars_float.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476034814795375 Testing ONNX double: LassoLars (lasso_lars_double.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476035128950858
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.10.3. lasso_lars_float.onnx ve lasso_lars_double.onnx modellerinin ONNX gösterimi
Şekil 37. Netron'da lasso_lars_float.onnx modelinin ONNX gösterimi
Şekil 38. Netron'da lasso_lars_double.onnx modelinin ONNX gösterimi
2.1.11. sklearn.linear_model.LassoLarsCV
LassoLarsCV, Lasso (Least Absolute Shrinkage and Selection Operator) ve LARS'ı (Least Angle Regression) çapraz doğrulama kullanarak optimum düzenlileştirme hiperparametresinin (alfa) otomatik seçimi ile birleştiren bir yöntemdir.
Bu yöntem, her iki algoritmanın avantajlarını birleştirir ve özellik seçimi ve düzenlileştirmeyi göz önünde bulundurarak model için en uygun alfa değerinin belirlenmesini sağlar.
LassoLarsCV'nin çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Başlatma: LassoLarsCV, tüm katsayıların sıfır olarak ayarlandığı boş bir modelle başlar.
- Alfa aralığının tanımı: Seçim süreci sırasında dikkate alınacak olan alfa hiperparametresi için bir değer aralığı belirlenir. Genellikle logaritmik bir alfa değeri ölçeği kullanılır.
- Çapraz doğrulama: Seçilen aralıktaki her alfa değeri için LassoLarsCV, modelin performansını bu alfa değeriyle değerlendirmek için çapraz doğrulama gerçekleştirir. Tipik olarak, ortalama karesel hata (MSE) veya belirleme katsayısı (R^2) gibi metrikler kullanılır.
- Optimum alfa seçimi: LassoLarsCV, çapraz doğrulama sonuçlarına göre modelin en iyi performansa ulaştığı alfa değerini seçer.
- Model eğitimi: LassoLarsCV modeli, seçilen alfa değeri kullanılarak, daha az önemli özellikler hariç tutularak ve L1 düzenlileştirme uygulanarak eğitilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LassoLarsCV'nin avantajları:
- Otomatik alfa seçimi: LassoLarsCV, çapraz doğrulamayı kullanarak optimum alfa hiperparametresini otomatik olarak seçer ve model ayarlamasını basitleştirir.
- Özellik seçimi: LassoLarsCV otomatik olarak en önemli özellikleri seçer ve modelin boyutsallığını azaltır.
- Düzenlileştirme: Yöntem, aşırı uyumu önleyen ve modelin genellemesini artıran L1 düzenlileştirme uygular.
LassoLarsCV'nin sınırlamaları:
- Lineer model: LassoLarsCV lineer bir model oluşturur, bu da karmaşık doğrusal olmayan ilişkileri modellemek için yetersiz olabilir.
- Gürültüye karşı hassasiyet: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Hesaplama karmaşıklığı: Her adımda özellik seçimi ve düzenlileştirmenin uygulanması, basit lineer regresyondan daha fazla hesaplama kaynağı gerektirebilir.
LassoLarsCV, en önemli özellikleri seçmenin, modelin boyutluluğunu azaltmanın, aşırı uyumu önlemenin ve modelin hiperparametrelerini otomatik olarak ayarlamanın gerekli olduğu regresyon görevlerinde kullanışlıdır.
2.1.11.1. LassoLarsCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LassoLarsCV modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"
# create a LassoLarsCV Regressor model
lassolars_cv_regressor_model = LassoLarsCV(cv=5)
# fit the model to the data
lassolars_cv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_cv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LassoLarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LassoLarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
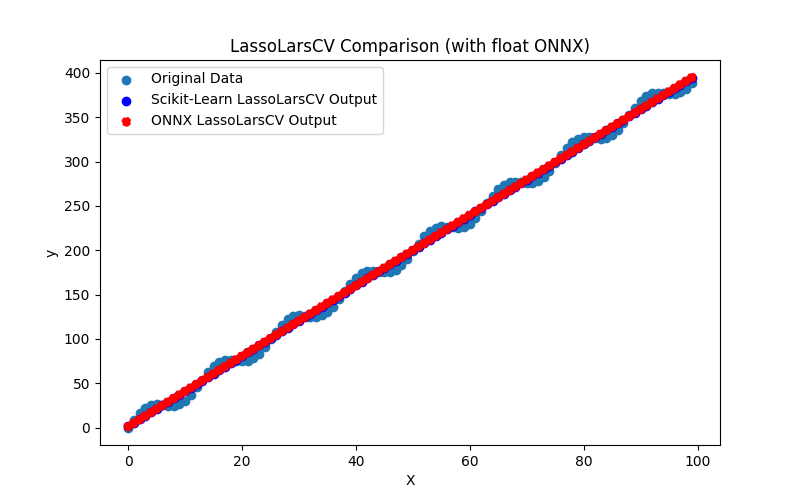
Şekil 39. LassoLarsCV.py sonuçları (float ONNX)
2.1.11.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lasso_lars_cv_float.onnx ve lasso_lars_cv_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LassoLarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsCV" #define ONNXFilenameFloat "lasso_lars_cv_float.onnx" #define ONNXFilenameDouble "lasso_lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LassoLarsCV (EURUSD,H1) Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LassoLarsCV (EURUSD,H1) LassoLarsCV (EURUSD,H1) Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Python'daki orijinal double model ile karşılaştırma:
Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.11.3. lasso_lars_cv_float.onnx ve lasso_lars_cv_double.onnx modellerinin ONNX gösterimi
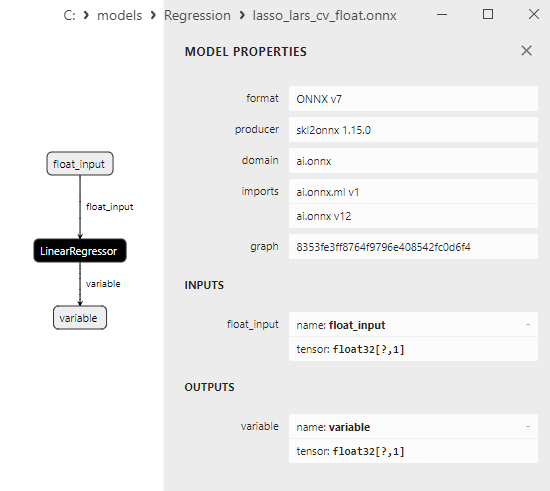
Şekil 40. Netron'da lasso_lars_cv_float.onnx modelinin ONNX gösterimi
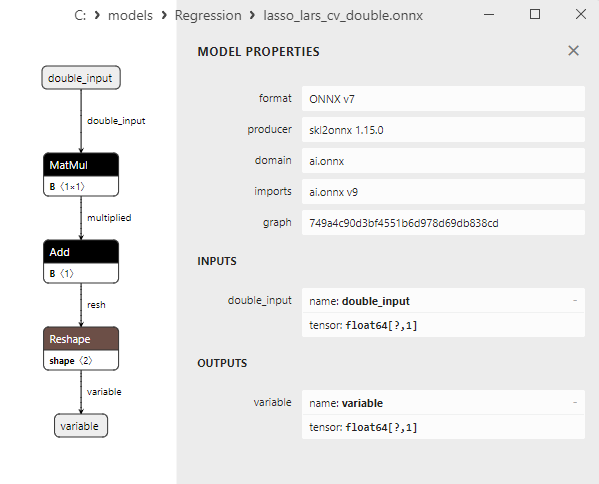
Şekil 41. Netron'da lasso_lars_cv_double.onnx modelinin ONNX gösterimi
2.1.12. sklearn.linear_model.LassoLarsIC
LassoLarsIC, optimum özellik kümesini otomatik olarak seçmek için Lasso (Least Absolute Shrinkage and Selection Operator) ve IC’yi (Information Criterion) birleştiren bir regresyon yöntemidir.
Modele hangi özelliklerin dahil edileceğini belirlemek için AIC (Akaike Information Criterion) ve BIC (Bayesian Information Criterion) gibi bilgi kriterlerini kullanır ve model katsayılarını hesaplamak için L1 düzenlileştirme uygular.
LassoLarsIC'nin çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Başlatma: LassoLarsIC boş bir modelle başlar, yani aktif özellik yoktur. Tüm katsayılar sıfıra ayarlanır.
- Bilgi kriteri kullanılarak özellik seçimi: Yöntem, boş bir modelden başlayarak ve özellikleri kademeli olarak modele dahil ederek farklı özellik setleri için bilgi kriterini (örneğin AIC veya BIC) değerlendirir. Bilgi kriteri, verilere uyum ve model karmaşıklığı arasındaki dengeyi göz önünde bulundurarak modelin kalitesini değerlendirir.
- Optimum özellik setinin seçimi: LassoLarsIC, bilgi kriterinin en iyi değere ulaştığı özellik kümesini seçer. Bu özellik kümesi modele dahil edilecektir.
- L1 düzenlileştirme uygulaması: Seçilen özelliklere L1 düzenlileştirme uygulanarak model katsayılarının hesaplanmasına yardımcı olunur.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
LassoLarsIC'nin avantajları:
- Otomatik özellik seçimi: LassoLarsIC, en uygun özellik kümesini otomatik olarak seçerek modelin boyutluluğunu azaltır ve aşırı uyumu önler.
- Bilgi kriterleri: Bilgi kriterlerinin kullanılması, model kalitesi ve karmaşıklığının dengelenmesine olanak tanır.
- Düzenlileştirme: Yöntem, aşırı uyumu önleyen ve modelin genellemesini artıran L1 düzenlileştirme uygular.
LassoLarsIC'nin sınırlamaları:
- Lineer model: LassoLarsIC lineer bir model oluşturur, bu da karmaşık doğrusal olmayan ilişkileri modellemek için yetersiz olabilir...
- Gürültüye karşı hassasiyet: Yöntem, verilerdeki aykırı değerlere karşı hassas olabilir.
- Hesaplama karmaşıklığı: Çeşitli özellik setleri için bilgi kriterlerinin değerlendirilmesi ek hesaplama kaynakları gerektirebilir.
LassoLarsIC, en iyi özellik kümesini otomatik olarak seçmenin ve bilgi kriterlerine dayalı olarak modelin boyutluluğunu azaltmanın çok önemli olduğu regresyon görevlerinde değerlidir.
2.1.12.1. LassoLarsIC modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LassoLarsIC modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LassoLarsIC model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"
# create a LassoLarsIC Regressor model
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')
# fit the model to the data
lasso_lars_ic_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lasso_lars_ic_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LassoLarsIC Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python LassoLarsIC ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsIC ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
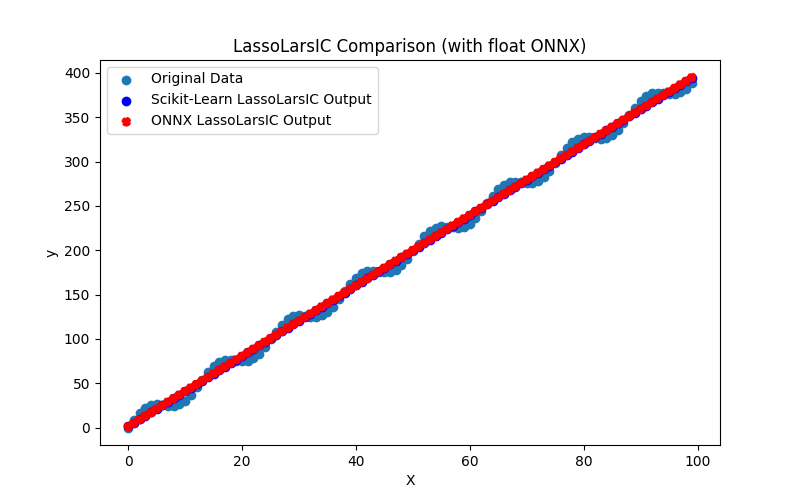
Şekil 42. LassoLarsIC.py sonuçları (float ONNX)
2.1.12.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen lasso_lars_ic_float.onnx ve lasso_lars_ic_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LassoLarsIC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsIC" #define ONNXFilenameFloat "lasso_lars_ic_float.onnx" #define ONNXFilenameDouble "lasso_lars_ic_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LassoLarsIC (EURUSD,H1) Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LassoLarsIC (EURUSD,H1) LassoLarsIC (EURUSD,H1) Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.12.3. lasso_lars_ic_float.onnx ve lasso_lars_ic_double.onnx modellerinin ONNX gösterimi
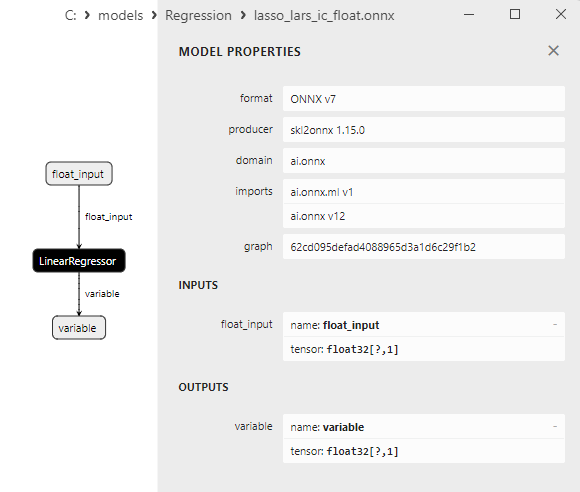
Şekil 43. Netron'da lasso_lars_ic_float.onnx modelinin ONNX gösterimi
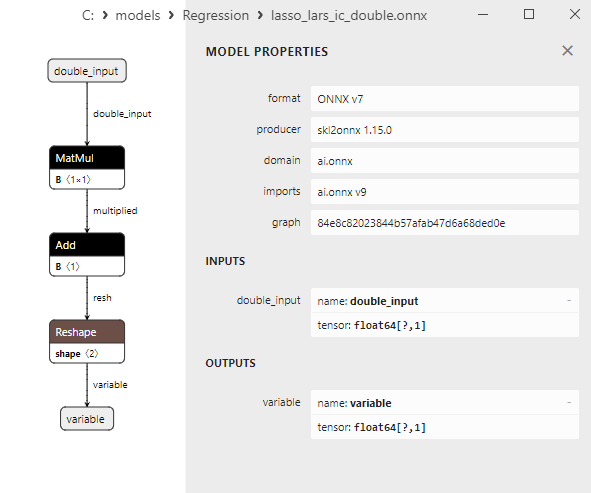
Şekil 44. Netron'da lasso_lars_ic_double.onnx modelinin ONNX gösterimi
2.1.13. sklearn.linear_model.LinearRegression
LinearRegression, regresyon görevleri için makine öğreniminde en basit ve en yaygın kullanılan yöntemlerden biridir.
Girdi özelliklerinin doğrusal bir kombinasyonuna dayalı olarak hedef değişkenin sayısal değerlerini (sürekli) tahmin eden lineer modeller oluşturmak için kullanılır.
LinearRegression’ın çalışma prensibi:
- Lineer model: LinearRegression modeli, bağımsız değişkenler (özellikler) ile hedef değişken arasında doğrusal bir ilişki olduğunu varsayar. Bu ilişki lineer regresyon denklemi ile ifade edilebilir: y = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ, burada y - hedef değişken, β₀ - kesişim katsayısı, β₁, β₂, ... βₚ - özellik katsayıları, x₁, x₂, ... xₚ - özellik değerleridir.
- Parametre hesaplaması: LinearRegression'ın amacı, verilere en iyi uyan β₀, β₁, β₂, ... βₚ katsayılarını hesaplamaktır. Bu, tipik olarak, gerçek ve tahmin edilen değerler arasındaki karesel farkların toplamını en aza indiren OLS (Ordinary Least Squares) yöntemi kullanılarak elde edilir.
- Model değerlendirmesi: LinearRegression modelinin kalitesini değerlendirmek için diğerlerinin yanı sıra ortalama karesel hata (MSE), belirleme katsayısı (R²) gibi çeşitli metrikler kullanılır.
LinearRegression’ın avantajları:
- Basitlik ve yorumlanabilirlik: LinearRegression, her bir özelliğin hedef değişken üzerindeki etkisinin analiz edilmesine olanak tanıyan, kolay yorumlanabilir basit bir yöntemdir.
- Yüksek eğitim ve tahmin hızı: Lineer regresyon modeli yüksek eğitim ve tahmin hızlarına sahiptir, bu da onu büyük veri kümeleri için iyi bir seçim haline getirir.
- Uygulanabilirlik: LinearRegression çeşitli regresyon görevlerine başarıyla uygulanabilir.
LinearRegression’ın sınırlamaları:
- Doğrusallık: Bu yöntem, özellikler ve hedef değişken arasındaki ilişkide doğrusallığı varsayar, bu da karmaşık doğrusal olmayan bağımlılıkları modellemek için yetersiz olabilir.
- Aykırı değerlere hassasiyet: LinearRegression, verilerdeki aykırı değerlere karşı hassastır ve bu da modelin kalitesini etkileyebilir.
LinearRegression, girdi özelliklerinin doğrusal bir kombinasyonuna dayalı olarak hedef değişkenin sayısal değerlerini tahmin etmek için lineer bir model oluşturan basit ve yaygın olarak kullanılan bir regresyon yöntemidir. Doğrusal bir ilişkinin olduğu ve modelin yorumlanabilirliğinin önemli olduğu problemler için çok uygundur.
2.1.13.1. LinearRegression modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LinearRegression modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training LinearRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"
# create a Linear Regression model
linear_model = LinearRegression()
# fit the model to the data
linear_model.fit(X, y)
# predict values for the entire dataset
y_pred = linear_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LinearRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python LinearRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LinearRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
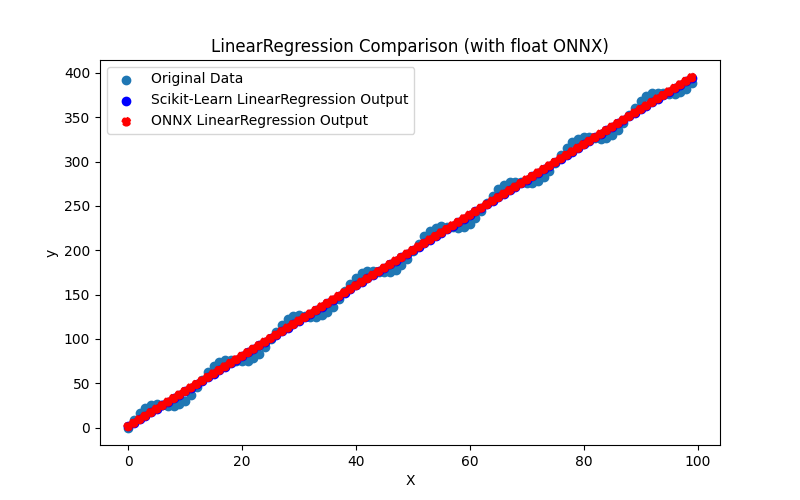
Şekil 45. LinearRegression.py sonuçları (float ONNX)
2.1.13.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen linear_regression_float.onnx ve linear_regression_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LinearRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearRegression" #define ONNXFilenameFloat "linear_regression_float.onnx" #define ONNXFilenameDouble "linear_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LinearRegression (EURUSD,H1) Testing ONNX float: LinearRegression (linear_regression_float.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LinearRegression (EURUSD,H1) LinearRegression (EURUSD,H1) Testing ONNX double: LinearRegression (linear_regression_double.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: LinearRegression (linear_regression_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LinearRegression (linear_regression_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.13.3. linear_regression_float.onnx ve linear_regression_double.onnx modellerinin ONNX gösterimi
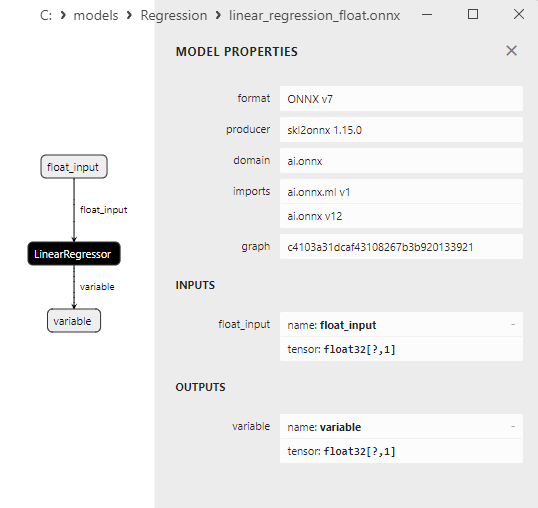
Şekil 46. Netron'da linear_regression_float.onnx modelinin ONNX gösterimi
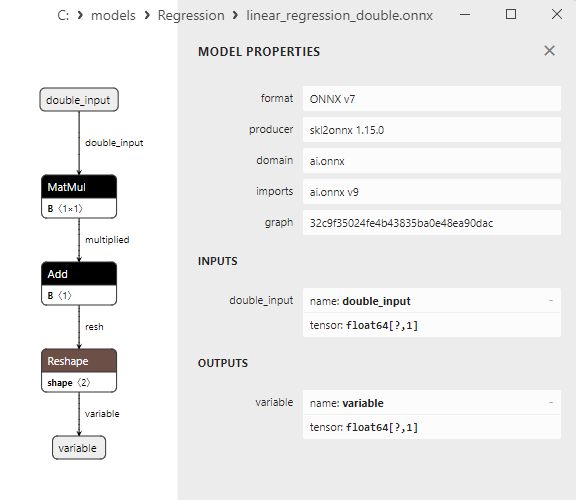
Şekil 47. Netron'da linear_regression_double.onnx modelinin ONNX gösterimi
Ridge ve RidgeCV yöntemleri hakkında not
Ridge ve RidgeCV, Ridge regresyonunda düzenlileştirme için kullanılan makine öğrenimindeki iki ilgili yöntemdir. Benzer işlevselliği paylaşırlar ancak kullanımları ve parametre ayarlamaları bakımından farklılık gösterirler.
Ridge'in çalışma prensibi (Ridge Regression):
- Ridge, L2 düzenlileştirme içeren bir regresyon yöntemidir. Bu, model tarafından minimize edilen kayıp fonksiyonuna karesel katsayıların toplamını (L2 normu) eklediği anlamına gelir. Bu ek düzenlileştirme terimi, modelin katsayılarının büyüklüklerini azaltmaya yardımcı olur ve böylece aşırı uyumu önler.
- Alfa parametresinin kullanımı: Ridge yönteminde, alfa parametresi (düzenlileştirme gücü olarak da bilinir) önceden ayarlanır ve otomatik olarak değiştirilmez. Kullanıcıların veriler ve deneyler hakkındaki bilgilerine dayanarak uygun bir alfa değeri seçmeleri gerekir.
RidgeCV'nin çalışma prensibi (Ridge Cross-Validation):
- RidgeCV, çapraz doğrulama kullanarak alfa parametresi için en uygun değerin otomatik olarak seçilmesini içeren Ridge yönteminin bir uzantısıdır. RidgeCV, alfayı manuel olarak ayarlamak yerine farklı alfa değerleri arasında yineleme yapar ve çapraz doğrulamada en iyi performansı sağlayanı seçer.
- Otomatik ayar yapma avantajı: RidgeCV'nin birincil avantajı, manuel ayar yapmaya gerek kalmadan optimum alfa değerini otomatik olarak belirlemesidir. Bu, ayarlama işlemini daha kolay hale getirir ve alfa seçimindeki olası hataları önler.
Ridge ve RidgeCV arasındaki temel fark, Ridge'in kullanıcıların alfa parametre değerini açıkça belirtmesini gerektirmesi, RidgeCV'nin ise çapraz doğrulamayı kullanarak en uygun alfa değerini otomatik olarak bulmasıdır. RidgeCV, büyük miktarda veri ile çalışırken ve manuel parametre ayarlamasından kaçınmayı amaçlarken tipik olarak daha çok tercih edilen bir seçimdir.
2.1.14. sklearn.linear_model.Ridge
Ridge, regresyon problemlerini çözmek için makine öğreniminde kullanılan bir regresyon yöntemidir. Lineer modeller ailesinin bir parçasıdır ve düzenlileştirilmiş bir lineer regresyonu temsil eder.
Ridge regresyonunun temel özelliği, standart sıradan en küçük kareler (OLS) yöntemine L2 düzenlileştirme eklemesidir.
Ridge regresyonu nasıl çalışır?
- Lineer regresyon: Ridge regresyonu, normal lineer regresyona benzer şekilde, bağımsız değişkenler (özellikler) ile hedef değişken arasında doğrusal bir ilişki bulmayı amaçlar.
- L2 düzenlileştirme: Ridge regresyonunun temel farkı, kayıp fonksiyonuna L2 düzenlileştirme eklemesidir. Bu, regresyon katsayılarının büyük değerleri için gerçek ve tahmin edilen değerler arasındaki karesel farkların toplamına bir ceza eklendiği anlamına gelir.
- Katsayıları cezalandırma: L2 düzenlileştirme regresyon katsayılarının değerlerine bir ceza uygular. Sonuç olarak, bazı katsayılar sıfıra daha yakın olma eğilimindedir, bu da aşırı uyumu azaltır ve model istikrarını artırır.
- α hiperparametresi: Ridge regresyonundaki temel parametrelerden biri, düzenlileştirme derecesini belirleyen α (alfa) hiperparametresidir. Daha yüksek α değerleri daha güçlü düzenlileştirmeye yol açarak daha düşük katsayı değerlerine sahip daha basit modellerle sonuçlanır.
Ridge regresyonunun avantajları:
- Aşırı uyumun azaltılması: Ridge'deki L2 düzenlileştirme, aşırı uyumu azaltmaya yardımcı olarak modeli verilerdeki gürültüye karşı daha sağlam hale getirir.
- Çoklu eşdoğrusallığın yönetimi: Ridge regresyonu, bilhassa özelliklerin yüksek oranda ilişkili olduğu durumlarda çoklu eşdoğrusallık sorunlarıyla iyi başa çıkmaktadır.
- Boyutluluk lanetini çözme: Ridge, OLS'nin kararsız olabileceği birçok özelliğe sahip senaryolarda yardımcı olur.
Ridge regresyonunun sınırlamaları:
- Özellikleri ortadan kaldırmaz: Ridge regresyonu özellik katsayılarını sıfırlamaz, sadece azaltır, yani bazı özellikler hala modelde kalabilir.
- Optimum α'nın seçilmesi: α hiperparametresi için doğru değerin seçilmesi çapraz doğrulama gerektirebilir.
Ridge regresyonu, aşırı uyumu azaltmak, istikrarı artırmak ve çoklu eşdoğrusallık sorunlarını çözmek için standart lineer regresyona L2 düzenlileştirme getiren bir regresyon yöntemidir. Bu yöntem, doğruluk ve model kararlılığının dengelenmesi gerektiğinde kullanışlıdır.
2.1.14.1. Ridge modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.Ridge modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training Ridge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Ridge"
onnx_model_filename = data_path + "ridge"
# create a Ridge model
regression_model = Ridge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python Ridge Original model (double) Python R-squared (Coefficient of determination): 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python Python Ridge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382634837793 Python Mean Absolute Error: 6.347684915729416 Python Mean Squared Error: 49.77815046053819 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python Ridge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
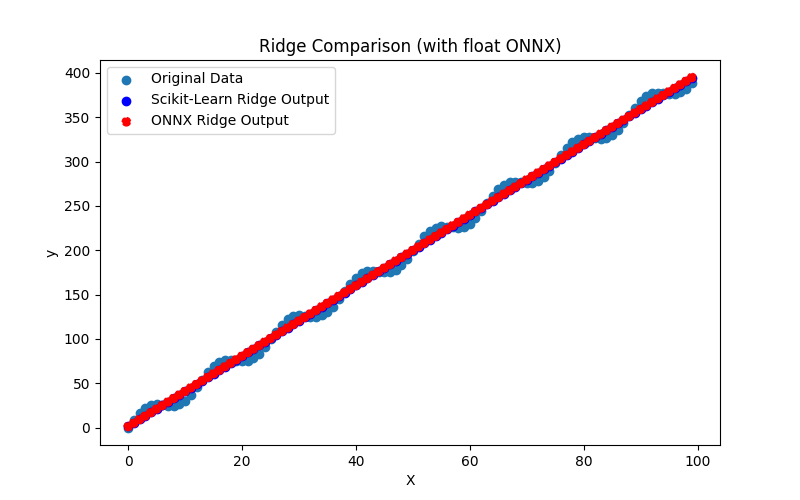
Şekil 49. Ridge.py sonuçları (float ONNX)
2.1.14.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen ridge_float.onnx ve ridge_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| Ridge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Ridge" #define ONNXFilenameFloat "ridge_float.onnx" #define ONNXFilenameDouble "ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
Ridge (EURUSD,H1) Testing ONNX float: Ridge (ridge_float.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382634837793 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476849157294160 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781504605381784 Ridge (EURUSD,H1) Ridge (EURUSD,H1) Testing ONNX double: Ridge (ridge_double.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641178552 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476844629298235 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781420699652131
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: Ridge (ridge_float.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476849157294160 Testing ONNX double: Ridge (ridge_double.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476844629298235
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.14.3. ridge_float.onnx ve ridge_double.onnx modellerinin ONNX gösterimi
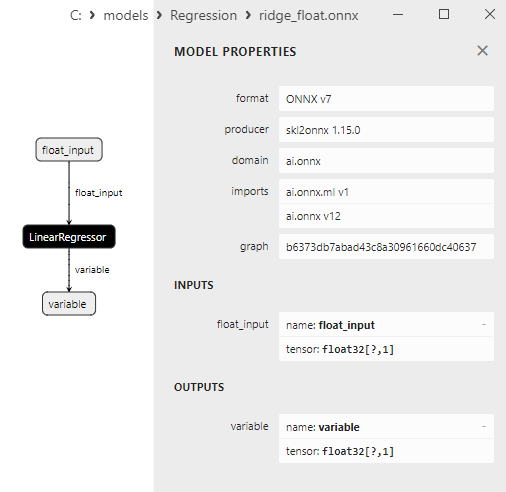
Şekil 50. Netron'da ridge_float.onnx modelinin ONNX gösterimi
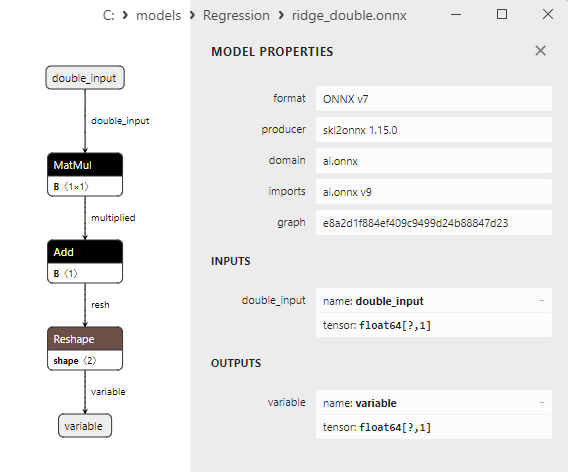
Şekil 51. Netron'da ridge_double.onnx modelinin ONNX gösterimi
2.1.15. sklearn.linear_model.RidgeCV
RidgeCV, Ridge regresyonunda düzenlileştirme derecesini belirleyen en iyi α (alfa) hiperparametresinin otomatik seçimini içeren Ridge regresyonunun bir uzantısıdır. α hiperparametresi, karesel hataların toplamını en aza indirme (sıradan lineer regresyonda olduğu gibi) ile regresyon katsayılarının değerini en aza indirme (düzenlileştirme) arasındaki dengeyi kontrol eder. RidgeCV, belirtilen parametrelere ve kriterlere göre α'nın optimum değerini otomatik olarak seçer.
RidgeCV nasıl çalışır?
- Girdi verileri: RidgeCV, özelliklerden (bağımsız değişkenler) ve hedef değişkenden (sürekli) oluşan girdi verilerini alır.
- α'nın seçilmesi: Ridge regresyonu, düzenlileştirme derecesini belirleyen α hiperparametresinin seçilmesini gerektirir. RidgeCV, verilen aralıktan en uygun α değerini otomatik olarak seçer.
- Çapraz doğrulama: RidgeCV, bağımsız veriler üzerinde hangi α değerinin en iyi model genellemesini sağladığını değerlendirmek için k-kat çapraz doğrulama gibi çapraz doğrulama kullanır.
- Optimum α: RidgeCV, eğitim sürecini tamamladıktan sonra çapraz doğrulamada en iyi performansı sağlayan α değerini seçer ve bu değeri nihai Ridge regresyon modelini eğitmek için kullanır.
RidgeCV'nin avantajları:
- Otomatik α seçimi: RidgeCV, α hiperparametresinin optimum değerinin otomatik olarak seçilmesine olanak tanıyarak model ayarlama sürecini basitleştirir.
- Düzenlileştirme ve performans arasındaki denge: Bu yöntem, düzenlileştirme (aşırı uyumu azaltma) ve model performansı arasındaki optimum dengeyi bulmaya yardımcı olur.
RidgeCV'nin sınırlamaları:
- Hesaplama karmaşıklığı: Çapraz doğrulama, özellikle geniş bir α değeri aralığı kullanıldığında önemli hesaplama kaynakları gerektirebilir.
RidgeCV, çapraz doğrulama kullanarak optimum α hiperparametresinin otomatik olarak seçildiği bir Ridge regresyon yöntemidir. Bu yöntem, hiperparametre seçim sürecini kolaylaştırır ve düzenlileştirme ile model performansı arasındaki en iyi dengeyi bulmayı sağlar.
2.1.15.1. RidgeCV modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.RidgeCV modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training RidgeCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"
# create a RidgeCV model
regression_model = RidgeCV()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python RidgeCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python Python RidgeCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499108485 Python Mean Absolute Error: 6.3472036427935485 Python Mean Squared Error: 49.77833006785168 Python R^2 matching decimal places: 11 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python RidgeCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
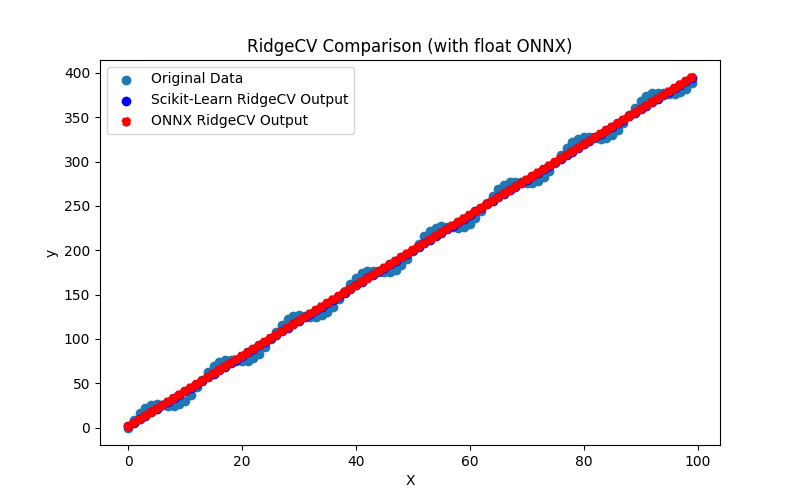
Şekil 52. RidgeCV.py sonuçları (float ONNX)
2.1.15.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen ridge_cv_float.onnx ve ridge_cv_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| RidgeCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RidgeCV" #define ONNXFilenameFloat "ridge_cv_float.onnx" #define ONNXFilenameDouble "ridge_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
RidgeCV (EURUSD,H1) Testing ONNX float: RidgeCV (ridge_cv_float.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499108485 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472036427935485 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783300678516909 RidgeCV (EURUSD,H1) RidgeCV (EURUSD,H1) Testing ONNX double: RidgeCV (ridge_cv_double.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499160807 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472033499935216 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783299986157246
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: RidgeCV (ridge_cv_float.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472036427935485 Testing ONNX double: RidgeCV (ridge_cv_double.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472033499935216
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.15.3. ridge_cv_float.onnx ve ridge_cv_double.onnx modellerinin ONNX gösterimi
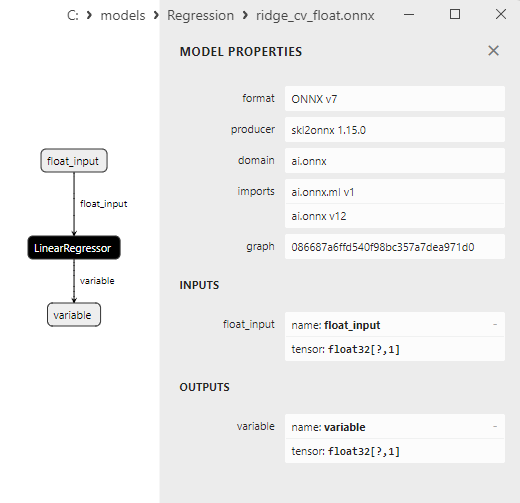
Şekil 53. Netron'da ridge_cv_float.onnx modelinin ONNX gösterimi
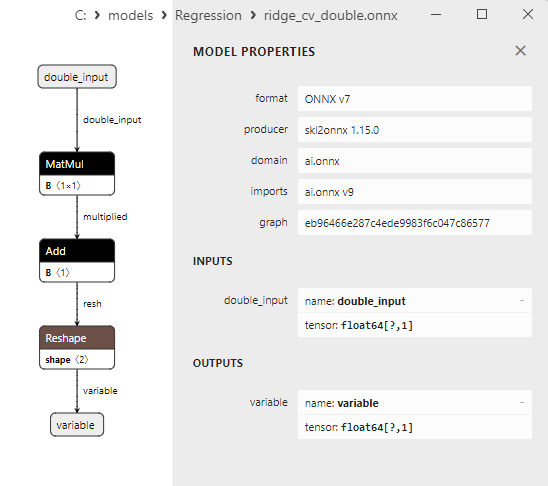
Şekil 54. Netron'da ridge_cv_double.onnx modelinin ONNX gösterimi
2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
OrthogonalMatchingPursuit (OMP), özellik seçimi ve lineer regresyon problemlerini çözmek için kullanılan bir algoritmadır.
Veri boyutluluğunu azaltmada ve modelin genelleme yeteneğini geliştirmede yardımcı olabilecek en önemli özellikleri seçme yöntemlerinden biridir.
OrthogonalMatchingPursuit nasıl çalışır?
- Girdi verileri: Özellikleri (bağımsız değişkenler) ve hedef değişkenin değerlerini (sürekli) içeren bir veri kümesi ile başlar.
- Özellik sayısının seçilmesi: OrthogonalMatchingPursuit kullanırken ilk adımlardan biri, modele dahil etmek istediğiniz özellik sayısını belirlemektir. Bu sayı önceden tanımlanabilir veya Akaike Information Criterion (AIC) ya da minimum hata kriteri gibi kriterler kullanılarak seçilebilir.
- Yinelemeli özellik ekleme: Algoritma boş bir modelle başlar ve modelin kalıntılarını en iyi açıklayan özellikleri yinelemeli olarak ekler. Her yinelemede, daha önce seçilen özelliklere ortogonal olacak şekilde yeni bir özellik seçilir. En uygun özellik, model kalıntıları ile korelasyonuna göre seçilir.
- Model eğitimi: Belirlenen sayıda özellik eklendikten sonra, model sadece bu seçilen özellikler dikkate alınarak veriler üzerinde eğitilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler üzerinde hedef değişkenin değerlerini tahmin edebilir.
OrthogonalMatchingPursuit'in avantajları:
- Boyut azaltma: OMP, yalnızca en bilgilendirici özellikleri seçerek veri boyutluluğunu azaltabilir.
- Yorumlanabilirlik: OMP yalnızca az sayıda özellik seçtiğinden, bu yöntem kullanılarak oluşturulan modeller daha yorumlanabilir olabilir.
OrthogonalMatchingPursuit'in sınırlamaları:
- Seçilen özelliklerin sayısına hassasiyet: Seçilen özelliklerin sayısının uygun şekilde ayarlanması gerekir ve yanlış seçimler aşırı uyum veya yetersiz uyuma yol açabilir.
- Çoklu eşdoğrusallığı dikkate almaz: OMP, özellikler arasındaki çoklu eşdoğrusallığı hesaba katmayabilir ve bu da optimum özelliklerin seçimini etkileyebilir.
- Hesaplama karmaşıklığı: OMP, özellikle büyük veri kümeleri için hesaplama açısından maliyetlidir.
OrthogonalMatchingPursuit, özellik seçimi ve lineer regresyon için bir algoritmadır ve model için en bilgilendirici özelliklerin seçilmesine olanak tanır. Bu yöntem, veri boyutluluğunu azaltmak ve model yorumlanabilirliğini geliştirmek için değerli olabilir.
2.1.16.1. OrthogonalMatchingPursuit modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.OrthogonalMatchingPursuit modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training OrthogonalMatchingPursuit model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"
# create an OrthogonalMatchingPursuit model
regression_model = OrthogonalMatchingPursuit()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python OrthogonalMatchingPursuit Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python Python OrthogonalMatchingPursuit ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python OrthogonalMatchingPursuit ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
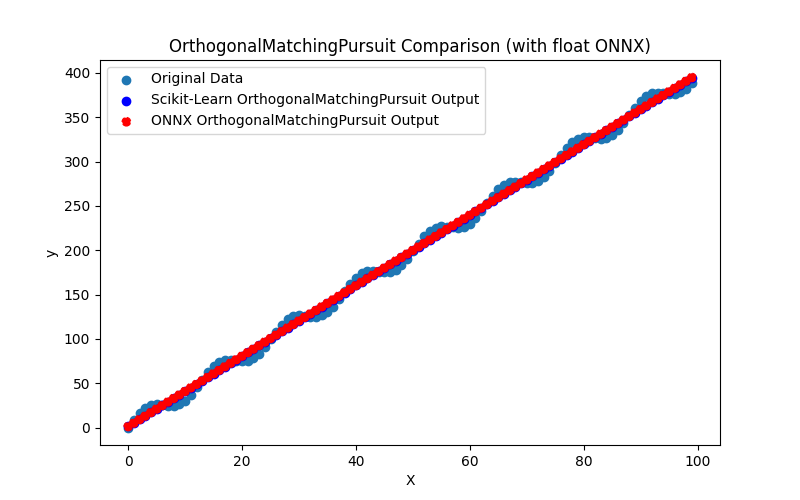
Şekil 55. OrthogonalMatchingPursuit.py sonuçları (float ONNX)
2.1.16.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen orthogonal_matching_pursuit_float.onnx ve orthogonal_matching_pursuit_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| OrthogonalMatchingPursuit.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "OrthogonalMatchingPursuit" #define ONNXFilenameFloat "orthogonal_matching_pursuit_float.onnx" #define ONNXFilenameDouble "orthogonal_matching_pursuit_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 OrthogonalMatchingPursuit (EURUSD,H1) OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.16.3. orthogonal_matching_pursuit_float.onnx ve orthogonal_matching_pursuit_double.onnx modellerinin ONNX gösterimi
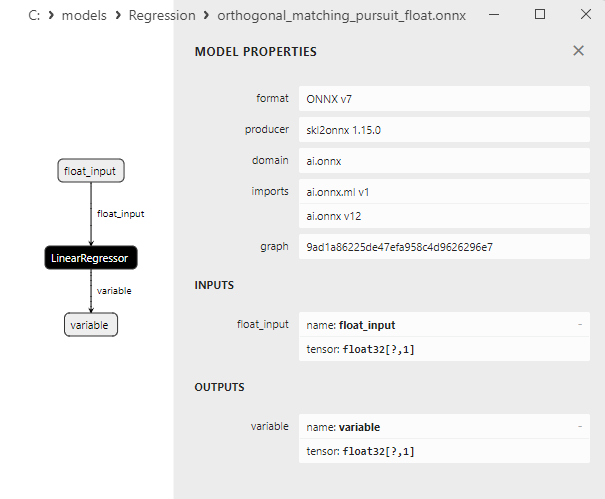
Şekil 56. Netron'da orthogonal_matching_pursuit_float.onnx modelinin ONNX gösterimi
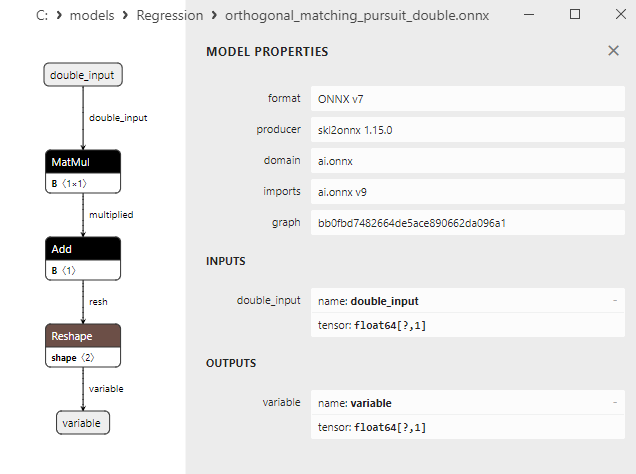
Şekil 57. Netron'da orthogonal_matching_pursuit_double.onnx modelinin ONNX gösterimi
2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
PassiveAggressiveRegressor, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir.
Bu yöntem, hedef değişkenin sürekli değerlerini tahmin edebilen bir modeli eğitmek için kullanılabilen Passive-Aggressive (PA) algoritmasının bir çeşididir.
PassiveAggressiveRegressor nasıl çalışır?
- Girdi verileri: Özelliklerden (bağımsız değişkenler) ve hedef değişkenin değerlerinden (sürekli) oluşan bir veri kümesi ile başlar.
- Denetimli öğrenme PassiveAggressiveRegressor, X'in özellikleri temsil ettiği ve y'nin hedef değişken değerlerine karşılık geldiği (X, y) çiftleri üzerinde eğitilen denetimli bir öğrenme yöntemidir.
- Uyarlanabilir öğrenme: Passive-Aggressive yönteminin arkasındaki temel fikir uyarlanabilir öğrenme yaklaşımıdır. Model, her bir eğitim örneğindeki tahmin hatasını en aza indirerek öğrenir. Tahmin hatasını azaltmak için ağırlıkları düzelterek günceller.
- C parametresi: PassiveAggressiveRegressor, modelin hatalara ne kadar güçlü uyum sağlayacağını kontrol eden bir C hiperparametresine sahiptir. Daha yüksek bir C değeri daha agresif ağırlık güncellemeleri anlamına gelirken, daha düşük bir C değeri modeli daha az agresif hale getirir.
- Tahmin: Model eğitildikten sonra yeni veriler için hedef değişken değerlerini tahmin edebilir.
PassiveAggressiveRegressor'ın avantajları:
- Uyarlanabilirlik: Yöntem, verilerdeki değişikliklere uyum sağlayabilir ve tahmin hatalarını en aza indirmek için modeli güncelleyebilir.
- Büyük veri kümeleri için verimlilik: PassiveAggressiveRegressor, özellikle büyük hacimli veriler üzerinde eğitildiğinde regresyon için etkili bir yöntem olabilir.
PassiveAggressiveRegressor'ın sınırlamaları:
- C parametresi seçimine hassasiyet: C değerinin doğru seçilmesi ayarlama ve deneme gerektirebilir.
- Ek özelliklere ihtiyaç duyulabilir: Bazı durumlarda, başarılı bir model eğitimi için ek mühendislik özellikleri gerekebilir.
PassiveAggressiveRegressor, eğitim verilerindeki tahmin hatalarını en aza indirerek uyarlamalı olarak öğrenen regresyon görevleri için bir makine öğrenimi yöntemidir. Bu yöntem büyük veri kümelerini işlemek için değerli olabilir ve optimum performans için C parametresinin ayarlanmasını gerektirir.
2.1.17.1. PassiveAggressiveRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.PassiveAggressiveRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training PassiveAggressiveRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"
# create a PassiveAggressiveRegressor model
regression_model = PassiveAggressiveRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python PassiveAggressiveRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python Python PassiveAggressiveRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376801868329 Python Mean Absolute Error: 9.645248834431873 Python Mean Squared Error: 139.76862616640122 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python PassiveAggressiveRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
Şekil 58. PassiveAggressiveRegressor.py sonuçları (double ONNX)
2.1.17.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen passive_aggressive_regressor_float.onnx ve passive_aggressive_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| PassiveAggressiveRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PassiveAggressiveRegressor" #define ONNXFilenameFloat "passive_aggressive_regressor_float.onnx" #define ONNXFilenameDouble "passive_aggressive_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376801868329 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452488344318716 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7686261664012761 PassiveAggressiveRegressor (EURUSD,H1) PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376841493092 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452466950654419 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7685737319100667
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452488344318716 Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452466950654419
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.17.3. passive_aggressive_regressor_float.onnx ve passive_aggressive_regressor_double.onnx modellerinin ONNX gösterimi
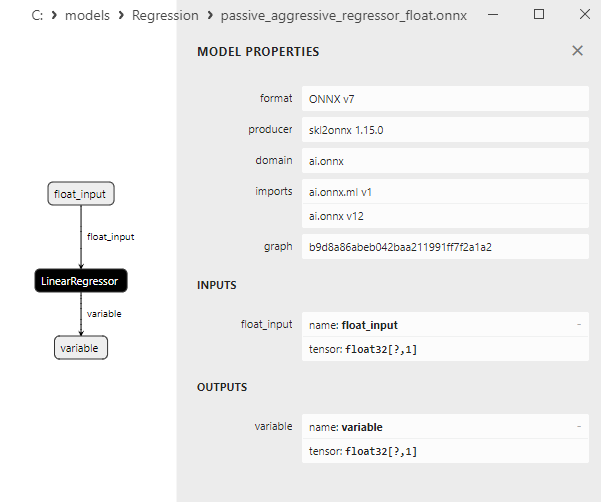
Şekil 59. Netron'da passive_aggressive_regressor_float.onnx modelinin ONNX gösterimi
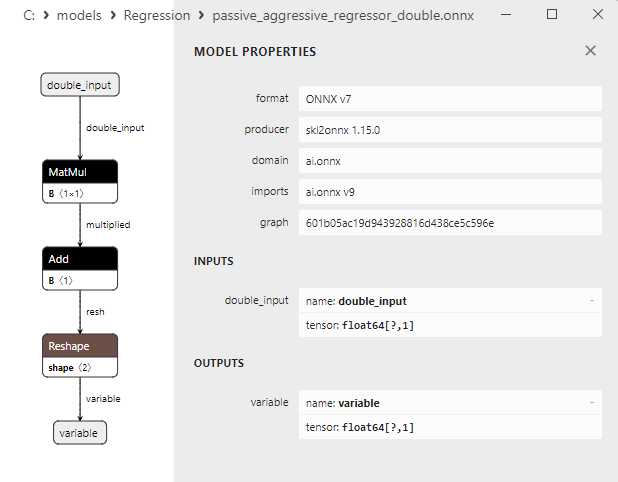
Şekil 60. Netron'da passive_aggressive_regressor_double.onnx modelinin ONNX gösterimi
2.1.18. sklearn.linear_model.QuantileRegressor
QuantileRegressor, regresyon görevlerinde hedef değişkenin niceliklerini (belirli yüzdelik dilimleri) hesaplamak için kullanılan bir makine öğrenimi yöntemidir.
QuantileRegressor, regresyon görevlerinde tipik olarak yapıldığı gibi hedef değişkenin ortalama değerini tahmin etmek yerine, medyan (50. yüzdelik dilim) veya 25. ve 75. yüzdelik dilimler gibi belirtilen niceliklere karşılık gelen değerleri tahmin eder.
QuantileRegressor nasıl çalışır?
- Girdi verileri: Özellikler (bağımsız değişkenler) ve hedef değişkeni (sürekli) içeren bir veri kümesi ile başlar.
- Niceliksel odaklanma: QuantileRegressor, hedef değişkenin tam değerlerini tahmin etmek yerine, hedef değişkenin koşullu dağılımını modeller ve bu dağılımın belirli nicelikleri için değerleri tahmin eder.
- Farklı nicelikler için eğitim: Bir QuantileRegressor modelinin eğitilmesi, istenen her bir nicelik için ayrı modellerin eğitilmesini içerir. Bu modellerin her biri kendi niceliğine karşılık gelen bir değer tahmin eder.
- Nicelik parametresi: Bu yöntem için ana parametre, tahminleri almak istediğiniz istenen niceliklerin seçimidir. Örneğin, medyan için tahminlere ihtiyacınız varsa, modeli 50. yüzdelik dilim üzerinde eğitmeniz gerekir.
- Nicelik tahmini: Eğitimden sonra model, yeni veriler üzerinde belirtilen niceliklere karşılık gelen değerleri tahmin etmek için kullanılabilir.
QuantileRegressor'ın avantajları:
- Esneklik: QuantileRegressor, dağılımın farklı yüzdelik dilimlerinin önemli olduğu görevlerde yararlı olabilecek çeşitli nicelikleri tahmin etmede esneklik sağlar.
- Aykırı değerlere karşı dayanıklılık: Nicelik odaklı bir yaklaşım, uç değerlerden büyük ölçüde etkilenebilen ortalamayı dikkate almadığı için aykırı değerlere karşı sağlam olabilir.
QuantileRegressor'ın sınırlamaları:
- Niceliksel seçim ihtiyacı: En uygun nicelikleri seçmek, görev hakkında biraz bilgi sahibi olmayı gerektirebilir.
- Artan hesaplama karmaşıklığı: Farklı nicelikler için ayrı modeller eğitmek, görevin hesaplama karmaşıklığını artırabilir.
QuantileRegressor, hedef değişkenin belirtilen niceliklerine karşılık gelen değerleri tahmin etmek için tasarlanmış bir makine öğrenimi yöntemidir. Bu yöntem, dağılımın çeşitli yüzdelik dilimlerinin ilgi çekici olduğu görevlerde ve verilerin aykırı değerler içerebileceği durumlarda yararlı olabilir.
2.1.18.1. QuantileRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.QuantileRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training QuantileRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"
# create a QuantileRegressor model
regression_model = QuantileRegressor(solver='highs')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python QuantileRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python Python QuantileRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915739158818 Python Mean Absolute Error: 6.3693091422201125 Python Mean Squared Error: 53.042533910812814 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 5 Python float ONNX model precision: 7 Python Python QuantileRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 13 Python double ONNX model precision: 16
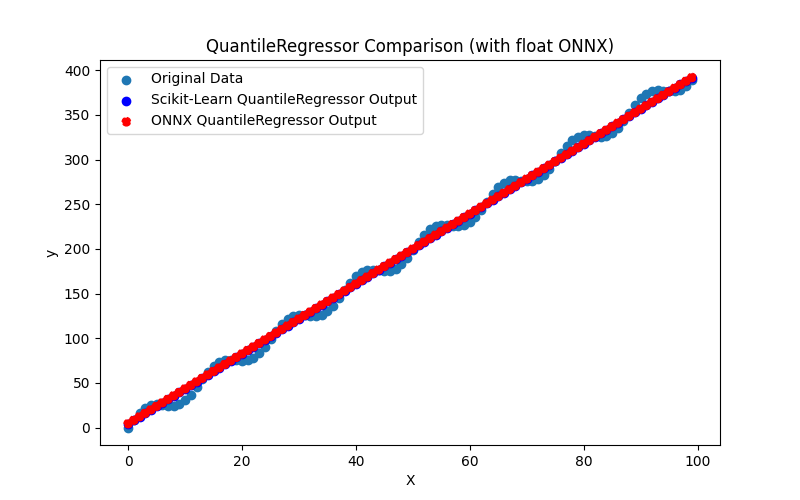
Şekil 61. QuantileRegressor.py sonuçları (float ONNX)
2.1.18.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen quantile_regressor_float.onnx ve quantile_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| QuantileRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "QuantileRegressor" #define ONNXFilenameFloat "quantile_regressor_float.onnx" #define ONNXFilenameDouble "quantile_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
QuantileRegressor (EURUSD,H1) Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915739158818 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091422201169 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425339108128071 QuantileRegressor (EURUSD,H1) QuantileRegressor (EURUSD,H1) Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915738839231 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091850025185 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425343337142721
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091422201169 Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091850025185
ONNX float MAE'nin doğruluğu: 7 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.18.3. quantile_regressor_float.onnx ve quantile_regressor_double.onnx modellerinin ONNX gösterimi
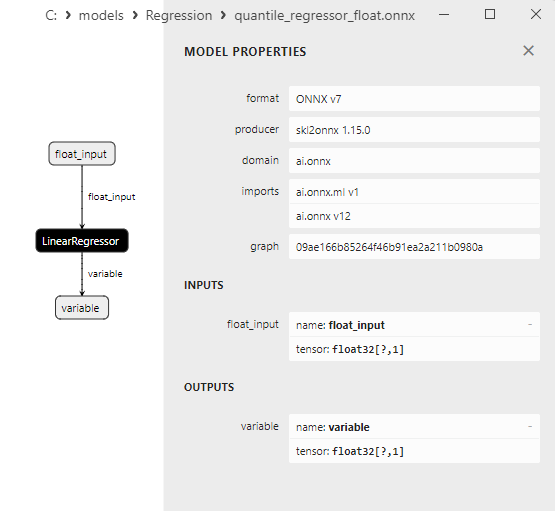
Şekil 62. Netron'da quantile_regressor_float.onnx modelinin ONNX gösterimi
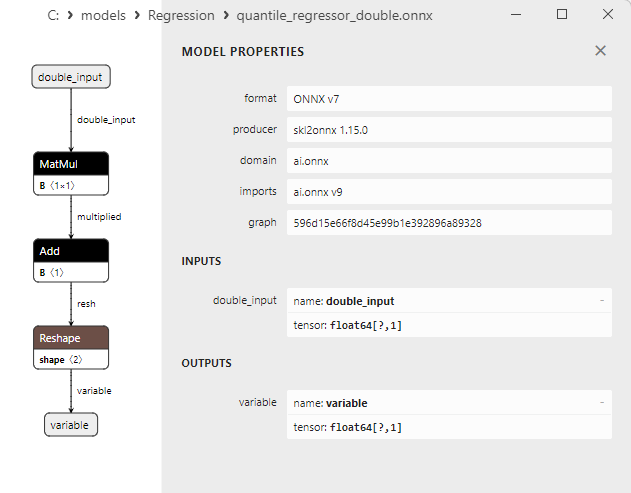
Şekil 63. Netron'da quantile_regressor_double.onnx modelinin ONNX gösterimi
2.1.19. sklearn.linear_model.RANSACRegressor
RANSACRegressor, RANSAC (Random Sample Consensus) yöntemini kullanarak regresyon problemlerini çözmek için kullanılan bir makine öğrenimi yöntemidir.
RANSAC yöntemi, aykırı değerler veya kusurlar içeren verileri işlemek için tasarlanmıştır ve aykırı değerlerin etkisini hariç tutarak daha sağlam bir regresyon modeline olanak tanır.
RANSACRegressor nasıl çalışır?
- Girdi verileri: Özellikler (bağımsız değişkenler) ve hedef değişkeni (sürekli) içeren bir veri kümesi ile başlar.
- Rastgele alt kümelerin seçimi: RANSAC, regresyon modelini eğitmek için kullanılan rastgele veri alt kümelerini seçerek başlar. Bu alt kümeler "hipotez" olarak adlandırılır.
- Hipotezlere model uydurma: Seçilen her hipotez için bir regresyon modeli eğitilir. RANSACRegressor durumunda, genellikle lineer regresyon kullanılır ve model veri alt kümesine uydurulur.
- Aykırı değer değerlendirmesi: Model eğitildikten sonra, tüm verilere uyumu değerlendirilir. Tahmin edilen ve gerçek değerler arasındaki hata her veri noktası için hesaplanır.
- Aykırı değer belirleme: Belirli bir eşiği aşan hatalara sahip veri noktaları aykırı değer olarak kabul edilir. Bu aykırı değerler model eğitimini etkileyebilir ve sonuçları bozabilir.
- Model güncellemesi: Aykırı değer olarak kabul edilmeyen tüm veri noktaları regresyon modelini güncellemek için kullanılır. Bu süreç farklı rastgele hipotezlerle birden çok kez tekrarlanabilir.
- Nihai model: Birkaç yinelemeden sonra, RANSACRegressor veri alt kümesi üzerinde eğitilmiş en iyi modeli seçer ve nihai regresyon modeli olarak geri döndürür.
RANSACRegressor'ın avantajları:
- Aykırı değer sağlamlığı: RANSACRegressor, aykırı değerleri eğitimden çıkardığı için bunlara karşı sağlam bir yöntemdir.
- Sağlam regresyon: Bu yöntem, veriler aykırı değerler veya kusurlar içerdiğinde daha güvenilir bir regresyon modeli oluşturulmasını sağlar.
RANSACRegressor'ın sınırlamaları:
- Hata eşiğine duyarlılık: Hangi noktaların aykırı değer olarak kabul edileceğini belirlemek için bir hata eşiği seçmek denemeler yapmayı gerektirebilir.
- Hipotez seçiminin karmaşıklığı: İlk aşamada iyi hipotezler seçmek kolay bir iş olmayabilir.
RANSACRegressor, RANSAC yöntemine dayalı regresyon problemleri için kullanılan bir makine öğrenimi yöntemidir. Bu yöntem, veriler aykırı değerler veya kusurlar içerdiğinde, bunların model üzerindeki etkilerini hariç tutarak daha sağlam bir regresyon modeli oluşturulmasına olanak tanır.
2.1.19.1. RANSACRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.RANSACRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training RANSACRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"
# create a RANSACRegressor model
regression_model = RANSACRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python RANSACRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python RANSACRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python RANSACRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
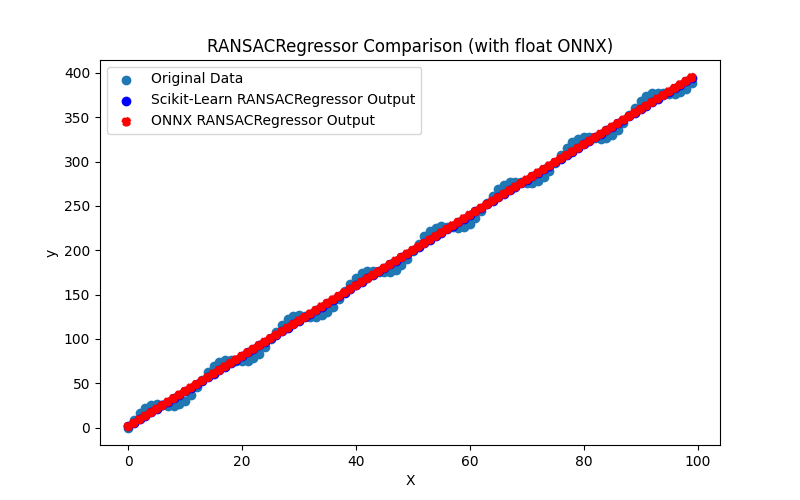
Şekil 64. RANSACRegressor.py sonuçları (float ONNX)
2.1.19.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen ransac_regressor_float.onnx ve ransac_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| RANSACRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RANSACRegressor" #define ONNXFilenameFloat "ransac_regressor_float.onnx" #define ONNXFilenameDouble "ransac_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
RANSACRegressor (EURUSD,H1) Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 RANSACRegressor (EURUSD,H1) RANSACRegressor (EURUSD,H1) Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.19.3. ransac_regressor_float.onnx ve ransac_regressor_double.onnx modellerinin ONNX gösterimi
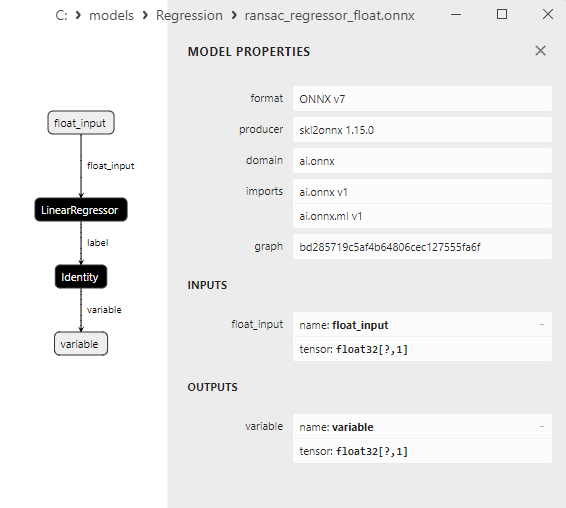
Şekil 65. Netron'da ransac_regressor_float.onnx modelinin ONNX gösterimi
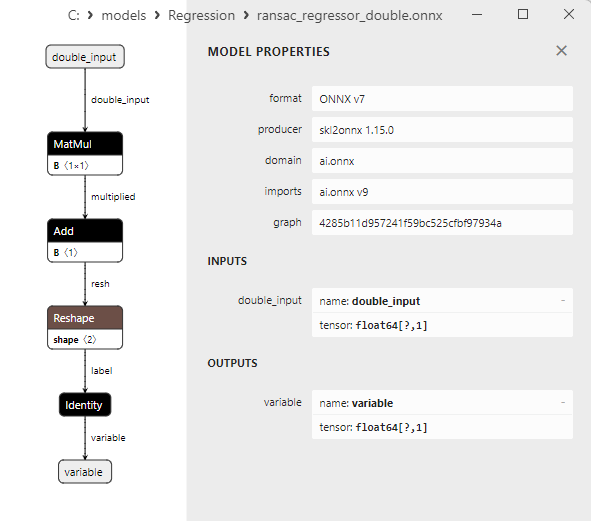
Şekil 66. Netron'da ransac_regressor_double.onnx modelinin ONNX gösterimi
2.1.20. sklearn.linear_model.TheilSenRegressor
Theil-Sen regresyon (Theil-Sen estimator), bağımsız değişkenler ile hedef değişken arasındaki doğrusal ilişkileri yaklaşık olarak tahmin etmek için kullanılan bir regresyon hesaplama yöntemidir.
Verilerdeki aykırı değerlerin ve gürültünün varlığında sıradan lineer regresyona kıyasla daha sağlam bir hesaplama sunar.
Theil-Sen regresyonu nasıl çalışır?
- Nokta seçimi: Başlangıçta, Theil-Sen eğitim veri kümesinden rastgele veri noktası çiftleri seçer.
- Eğim hesaplaması: Yöntem, her bir veri noktası çifti için bu noktalardan geçen doğrunun eğimini hesaplayarak bir eğim kümesi oluşturur.
- Medyan eğim: Ardından, yöntem eğim kümesinden medyan eğimi bulur. Bu medyan eğim, lineer regresyon eğiminin bir hesaplaması olarak kullanılır.
- Medyan sapmalar: Yöntem, her bir veri noktası için sapmayı (gerçek değer ile medyan eğime dayalı olarak tahmin edilen değer arasındaki fark) hesaplar ve bu sapmaların medyanını bulur. Bu, lineer regresyon kesişim katsayısı için bir hesaplama oluşturur.
- Nihai hesaplama: Eğim ve kesişim katsayılarının nihai hesaplamaları lineer regresyon modelini oluşturmak için kullanılır.
Theil-Sen regresyonunun avantajları:
- Aykırı değerlere karşı direnç: Theil-Sen regresyonu, normal lineer regresyona kıyasla aykırı değerlere ve veri gürültüsüne karşı daha dayanıklıdır.
- Daha az katı varsayımlar: Yöntem, veri dağılımı veya bağımlılık biçimi hakkında katı varsayımlar gerektirmez, bu da onu daha çok yönlü hale getirir.
- Çoklu eşdoğrusal veriler için uygundur: Theil-Sen regresyonu, bağımsız değişkenlerin yüksek oranda korelasyon gösterdiği verilerde (çoklu eşdoğrusallık sorunu) iyi performans gösterir.
Theil-Sen regresyonunun sınırlamaları:
- Hesaplama karmaşıklığı: Tüm veri noktası çiftleri için medyan eğimlerinin hesaplanması, özellikle büyük veri kümeleri için zaman alıcı olabilir.
- Kesişim katsayısı hesaplaması: Kesişim katsayısını hesaplamak için medyan sapmalar kullanılır, bu da aykırı değerlerin varlığında yanlılığa yol açabilir.
Theil-Sen regresyonu, özellikle aykırı değerlerin ve veri gürültüsünün varlığında, bağımsız değişkenler ile hedef değişken arasındaki doğrusal ilişkinin istikrarlı bir şekilde değerlendirilmesini sağlayan bir regresyon hesaplama yöntemidir. Bu yöntem, gerçek dünya veri koşulları altında istikrarlı bir hesaplamaya ihtiyaç duyulduğunda kullanışlıdır.
2.1.20.1. TheilSenRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.TheilSenRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training TheilSenRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"
# create a TheilSen Regressor model
regression_model = TheilSenRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python TheilSenRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python Python TheilSenRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996232919516505 Python Mean Absolute Error: 6.338686370832071 Python Mean Squared Error: 49.84886588834327 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python TheilSenRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
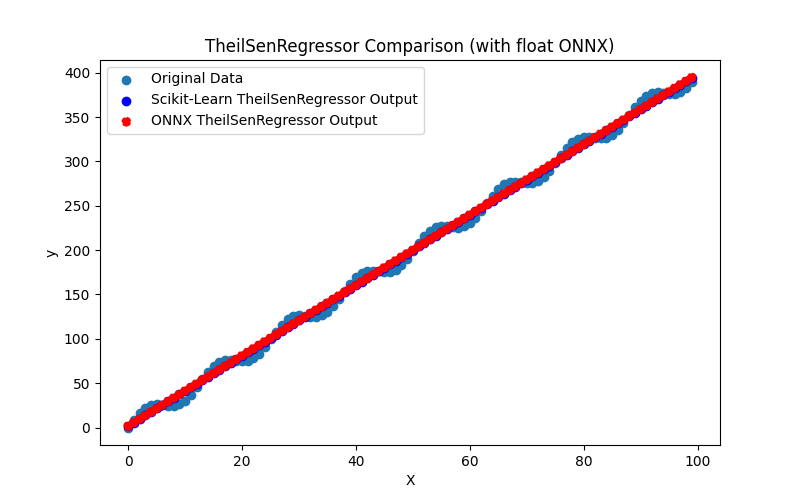
Şekil 67. TheilSenRegressor.py sonuçları (float ONNX)
2.1.20.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen theil_sen_regressor_float.onnx ve theil_sen_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| TheilSenRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TheilSenRegressor" #define ONNXFilenameFloat "theil_sen_regressor_float.onnx" #define ONNXFilenameDouble "theil_sen_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
TheilSenRegressor (EURUSD,H1) Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329195165051 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386863708320735 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488658883432691 TheilSenRegressor (EURUSD,H1) TheilSenRegressor (EURUSD,H1) Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329196940459 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386860045375943 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488635389873735
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386863708320735 Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386860045375943
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 15 ondalık basamak.
2.1.20.3. theil_sen_regressor_float.onnx ve theil_sen_regressor_double.onnx modellerinin ONNX gösterimi
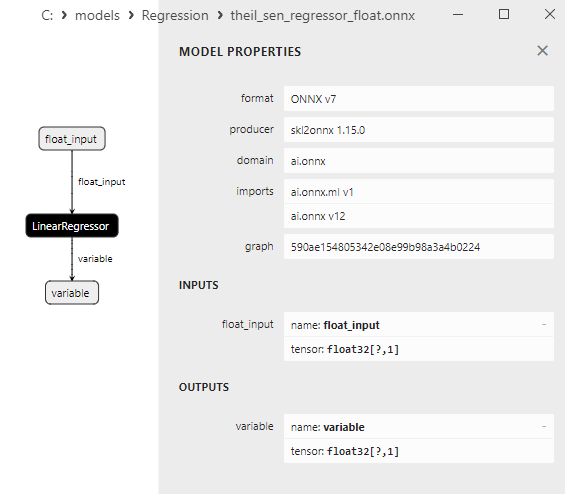
Şekil 68. Netron'da theil_sen_regressor_float.onnx modelinin ONNX gösterimi
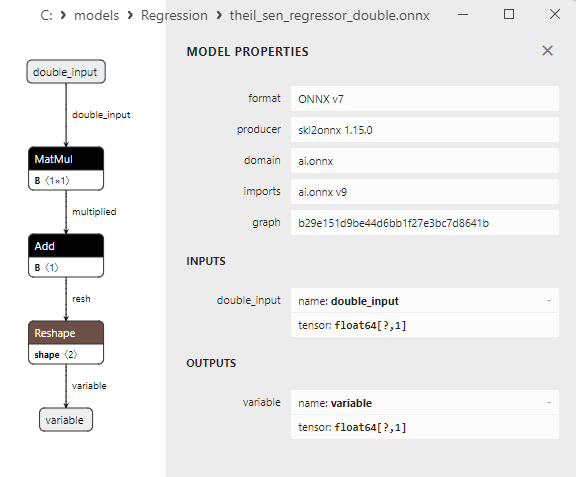
Şekil 69. Netron'da theil_sen_regressor_double.onnx modelinin ONNX gösterimi
2.1.21. sklearn.linear_model.LinearSVR
LinearSVR (Linear Support Vector Regression), destek vektör makineleri (Support Vector Machines, SVM) yöntemine dayanan regresyon görevleri için bir makine öğrenimi modelidir.
Bu yöntem, doğrusal bir çekirdek kullanarak özellikler ve hedef değişken arasındaki doğrusal ilişkileri bulmak için kullanılır.
LinearSVR nasıl çalışır?
- Girdi verileri: LinearSVR, özellikleri (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren bir veri kümesiyle başlar.
- Lineer bir model seçme: Model, özellikler ile hedef değişken arasında doğrusal bir regresyon denklemiyle tanımlanan doğrusal bir ilişki olduğunu varsayar.
- Model eğitimi: LinearSVR, tahmin hatasını ve kabul edilebilir bir hatayı (epsilon) dikkate alan bir kayıp fonksiyonunu en aza indirerek modelin katsayıları için en uygun değerleri bulur.
- Tahmin oluşturma: Eğitimden sonra model, keşfedilen katsayılara dayanarak yeni veriler için hedef değişken değerlerini tahmin edebilir.
LinearSVR'ın avantajları:
- Destek vektör regresyonu: LinearSVR, kabul edilebilir bir hatayı göz önünde bulundurarak veriler arasında en uygun ayrımı bulmayı sağlayan destek vektör makineleri yöntemini kullanır.
- Birden fazla özellik için destek: Model birden fazla özelliği ele alabilir ve yüksek boyutlardaki verileri işleyebilir.
- Düzenlileştirme: LinearSVR, aşırı uyumla mücadeleye yardımcı olan ve daha istikrarlı tahminler sağlayan düzenlileştirme içerir.
LinearSVR'ın sınırlamaları:
- Doğrusallık: LinearSVR, özellikler ve hedef değişken arasındaki doğrusal ilişkiler kullanılarak kısıtlanır. Karmaşık, doğrusal olmayan ilişkiler söz konusu olduğunda, model yeterince esnek olmayabilir.
- Aykırı değerlere hassasiyet: Model, verilerdeki aykırı değerlere ve kabul edilebilir hataya (epsilon) duyarlı olabilir.
- Karmaşık ilişkileri yakalayamama: LinearSVR, diğer lineer modeller gibi, özellikler ve hedef değişken arasındaki karmaşık doğrusal olmayan ilişkileri yakalayamaz.
LinearSVR, özellikler ve hedef değişken arasındaki doğrusal ilişkileri bulmak için destek vektör makineleri yöntemini kullanan bir regresyon makine öğrenimi modelidir. Düzenlileştirmeyi destekler ve kabul edilebilir hatayı kontrol etmenin gerekli olduğu görevlerde kullanılabilir. Bununla birlikte, model doğrusal bağımlılığı ile sınırlıdır ve aykırı değerlere karşı hassas olabilir.
2.1.21.1. LinearSVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.LinearSVR modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# LinearSVR.py
# The code demonstrates the process of training LinearSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearSVR"
onnx_model_filename = data_path + "linear_svr"
# create a Linear SVR model
linear_svr_model = LinearSVR()
# fit the model to the data
linear_svr_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = linear_svr_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_svr_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_svr_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python LinearSVR Original model (double) Python R-squared (Coefficient of determination): 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python Python LinearSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935580726729 Python Mean Absolute Error: 7.026849848037511 Python Mean Squared Error: 72.86541563418206 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 4 Python MSE matching decimal places: 3 Python float ONNX model precision: 4 Python Python LinearSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
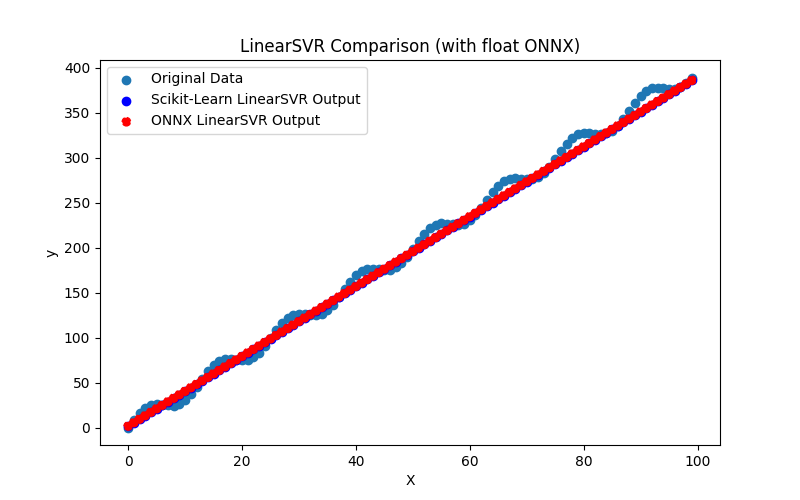
Şekil 70. LinearSVR.py sonuçları (float ONNX)
2.1.21.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen linear_svr_float.onnx ve linear_svr_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| LinearSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearSVR" #define ONNXFilenameFloat "linear_svr_float.onnx" #define ONNXFilenameDouble "linear_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
LinearSVR (EURUSD,H1) Testing ONNX float: LinearSVR (linear_svr_float.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935580726729 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268498480375108 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8654156341820567 LinearSVR (EURUSD,H1) LinearSVR (EURUSD,H1) Testing ONNX double: LinearSVR (linear_svr_double.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935515149387 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268523593819374 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8655024110944680
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: LinearSVR (linear_svr_float.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268498480375108 Testing ONNX double: LinearSVR (linear_svr_double.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268523593819374
ONNX float MAE'nin doğruluğu: 4 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.21.3. linear_svr_float.onnx ve linear_svr_double.onnx modellerinin ONNX gösterimi
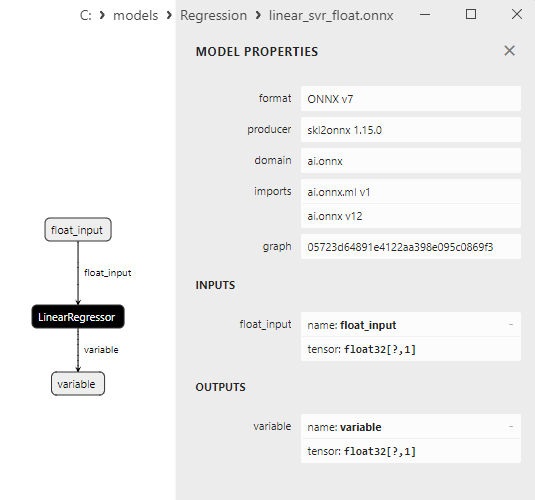
Şekil 71. Netron'da linear_svr_float.onnx modelinin ONNX gösterimi
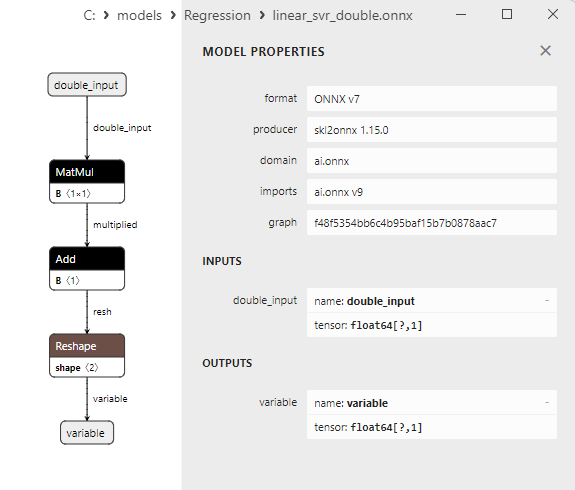
Şekil 72. Netron'da linear_svr_double.onnx modelinin ONNX gösterimi
2.1.22. sklearn.neural_network.MLPRegressor
MLPRegressor (Multi-Layer Perceptron Regressor), regresyon görevleri için yapay sinir ağlarını kullanan bir makine öğrenimi modelidir.
Hedef değişkenin sürekli değerlerini tahmin etmek için eğitilen birkaç nöron katmanından (girdi, gizli ve çıktı katmanları dahil) oluşan çok katmanlı bir sinir ağıdır.
MLPRegressor nasıl çalışır?
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren bir veri kümesi ile başlar.
- Çok katmanlı bir sinir ağı oluşturma: MLPRegressor, birden fazla gizli nöron katmanına sahip çok katmanlı bir sinir ağı kullanır. Bu nöronlar ağırlıklı bağlantılar ve aktivasyon fonksiyonları aracılığıyla birbirine bağlanır.
- Model eğitimi: MLPRegressor, ağın tahminleri ile gerçek hedef değişken değerleri arasındaki uyumsuzluğu ölçen bir kayıp fonksiyonunu en aza indirmek için ağırlıkları ve yanlılıkları ayarlayarak sinir ağını eğitir. Bu, geriye yayılım algoritmaları aracılığıyla gerçekleştirilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin edebilir.
MLPRegressor'ın avantajları:
- Esneklik: Çok katmanlı sinir ağları, özellikler ve hedef değişken arasındaki karmaşık doğrusal olmayan ilişkileri modelleyebilir.
- Çok yönlülük: MLPRegressor, zaman serisi problemleri, fonksiyon yaklaşımı ve daha fazlası dahil olmak üzere çeşitli regresyon görevleri için kullanılabilir.
- Genelleme yeteneği: Sinir ağları verilerden öğrenir ve eğitim verilerinde bulunan bağımlılıkları yeni verilere genelleyebilir.
MLPRegressor'ın sınırlamaları:
- Temel modelin karmaşıklığı: Büyük sinir ağları hesaplama açısından maliyetli olabilir ve eğitim için kapsamlı veri gerektirir.
- Hiperparametre ayarı: Optimum hiperparametrelerin seçilmesi (katman sayısı, her katmandaki nöron sayısı, öğrenme oranı vb.) denemeler yapmayı gerektirebilir.
- Aşırı uyuma yatkınlık: Büyük sinir ağları, yetersiz veri veya yetersiz düzenlileştirme varsa aşırı uyuma eğilimli olabilir.
MLPRegressor, çok katmanlı sinir ağlarına dayanan güçlü bir makine öğrenimi modelini temsil eder ve çok çeşitli regresyon görevleri için kullanılabilir. Bu model esnektir ancak optimum sonuçlar elde etmek için büyük hacimli veriler üzerinde titiz bir ayarlama ve eğitim gerektirir.
2.1.22.1. MLPRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.neural_network.MLPRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training MLPRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"
# create an MLP Regressor model
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)
# fit the model to the data
mlp_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = mlp_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python MLPRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9874070836467945 Python Mean Absolute Error: 10.62249788982753 Python Mean Squared Error: 166.63901957615224 Python Python MLPRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070821340352 Python Mean Absolute Error: 10.62249972216809 Python Mean Squared Error: 166.63903959413219 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python MLPRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070836467945 Python Mean Absolute Error: 10.622497889827532 Python Mean Squared Error: 166.63901957615244 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 12 Python double ONNX model precision: 14
Şekil 73. MLPRegressor.py sonuçları (float ONNX)
2.1.22.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen mlp_regressor_float.onnx ve mlp_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| MLPRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "MLPRegressor" #define ONNXFilenameFloat "mlp_regressor_float.onnx" #define ONNXFilenameDouble "mlp_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
MLPRegressor (EURUSD,H1) Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198695654352 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596681685341309 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1465507645494597 MLPRegressor (EURUSD,H1) MLPRegressor (EURUSD,H1) Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198617341387 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596715833884609 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1466543942046599
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224997221680901 Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224978898275282
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.22.3. mlp_regressor_float.onnx ve mlp_regressor_double.onnx modellerinin ONNX gösterimi
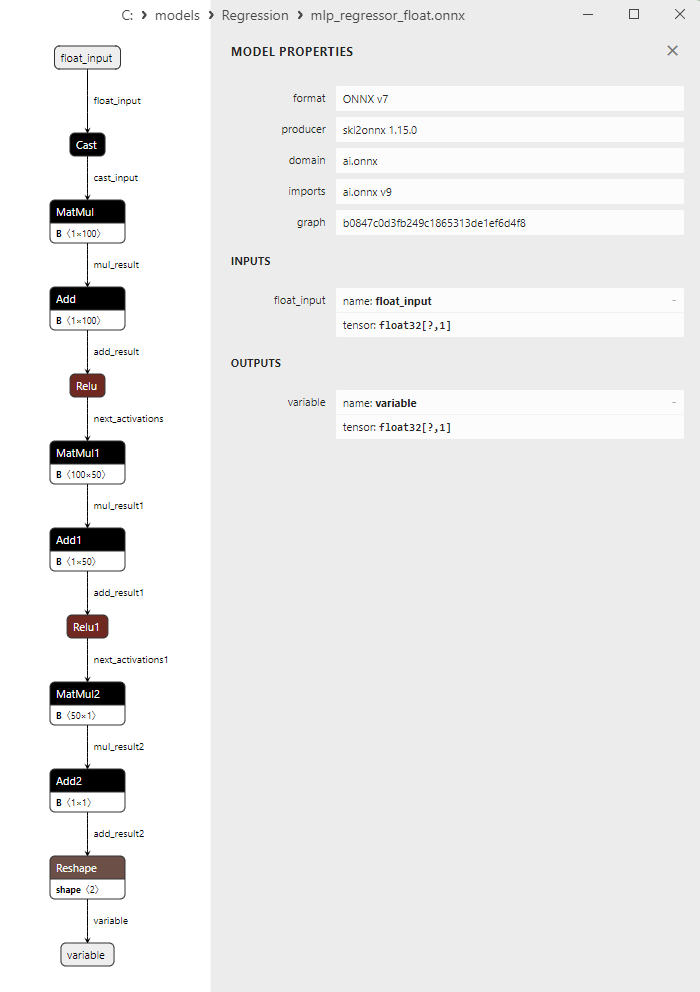
Şekil 74. Netron'da mlp_regressor_float.onnx modelinin ONNX gösterimi
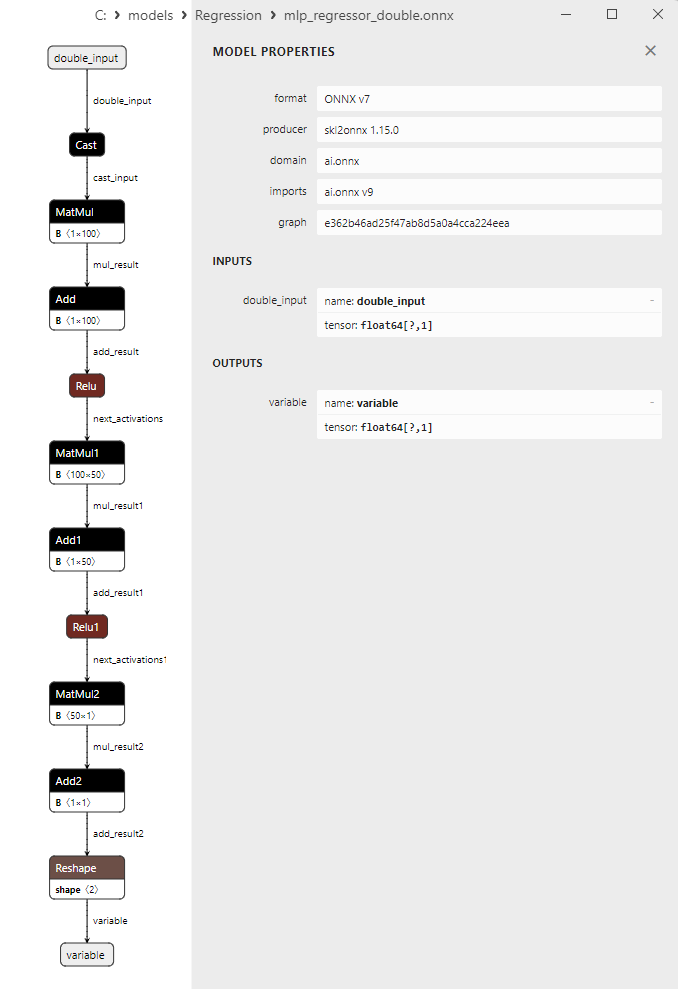
Şekil 75. Netron'da mlp_regressor_double.onnx modelinin ONNX gösterimi
2.1.23. sklearn.cross_decomposition.PLSRegression
PLSRegression (Partial Least Squares Regression), regresyon problemlerini çözmek için kullanılan bir makine öğrenimi yöntemidir.
PLS yöntem ailesinin bir parçasıdır ve bir setin tahmin ediciler olarak hizmet ettiği ve diğer setin hedef değişkenler olduğu iki değişken seti arasındaki ilişkileri analiz etmek ve modellemek için uygulanır.
PLSRegression nasıl çalışır?
- Girdi verileri: X ve Y olarak etiketlenmiş iki veri kümesiyle başlar. X kümesi bağımsız değişkenleri (tahmin ediciler), Y kümesi ise hedef değişkenleri (bağımlı) içerir.
- Doğrusal kombinasyonların seçimi: PLSRegression, X ve Y kümelerinde aralarındaki kovaryansı maksimize eden doğrusal kombinasyonları (bileşenleri) tanımlar. Bu bileşenler PLS bileşenleri olarak adlandırılır.
- Kovaryansın maksimize edilmesi: PLSRegresyonun birincil amacı, X ve Y arasındaki kovaryansı maksimize eden PLS bileşenlerini bulmaktır. Bu, tahmin ediciler ve hedef değişkenler arasındaki en bilgilendirici ilişkilerin çıkarılmasına olanak tanır.
- Model eğitimi: PLS bileşenleri bulunduktan sonra, X'e dayalı olarak Y değerlerini tahmin eden bir model oluşturmak için kullanılabilirler.
- Tahmin oluşturma: Eğitimden sonra model, karşılık gelen X değerlerini kullanarak yeni veriler için Y değerlerini tahmin etmek için kullanılabilir.
PLSRegression’ın avantajları:
- Korelasyon analizi: PLSRegression, iki değişken kümesi arasındaki korelasyonların analiz edilmesini ve modellenmesini sağlar; bu da tahmin ediciler ve hedef değişkenler arasındaki ilişkileri anlamak için yararlı olabilir.
- Boyut azaltma: Yöntem, en önemli PLS bileşenlerini belirleyerek verilerin boyutluluğunu azaltmak için de kullanılabilir.
PLSRegression’ın sınırlamaları:
- Bileşen sayısı seçimine duyarlılık: PLS bileşenlerinin optimum sayısının seçilmesi biraz deneme gerektirebilir.
- Veri yapısına bağımlılık: PLSRegression sonuçları büyük ölçüde verilerin yapısına ve aralarındaki korelasyonlara bağlı olabilir.
PLSRegression, iki değişken kümesi arasındaki korelasyonları analiz etmek ve modellemek için kullanılan bir makine öğrenimi yöntemidir; burada bir küme tahmin ediciler, diğeri ise hedef değişkenler olarak işlev görür. Bu yöntem, veri içerisindeki ilişkilerin incelenmesine olanak tanır ve veri boyutluluğunu azaltmak ve tahmin edicilere dayalı olarak hedef değişken değerlerini tahmin etmek için yararlı olabilir.
2.1.23.1. PLSRegression modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.cross_decomposition.PLSRegression modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training PLSRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"
# create a PLSRegression model
pls_model = PLSRegression(n_components=1)
# fit the model to the data
pls_model.fit(X, y)
# predict values for the entire dataset
y_pred = pls_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python PLSRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python Python PLSRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382638567003 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.778145525764096 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 8 Python MSE matching decimal places: 5 Python float ONNX model precision: 8 Python Python PLSRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
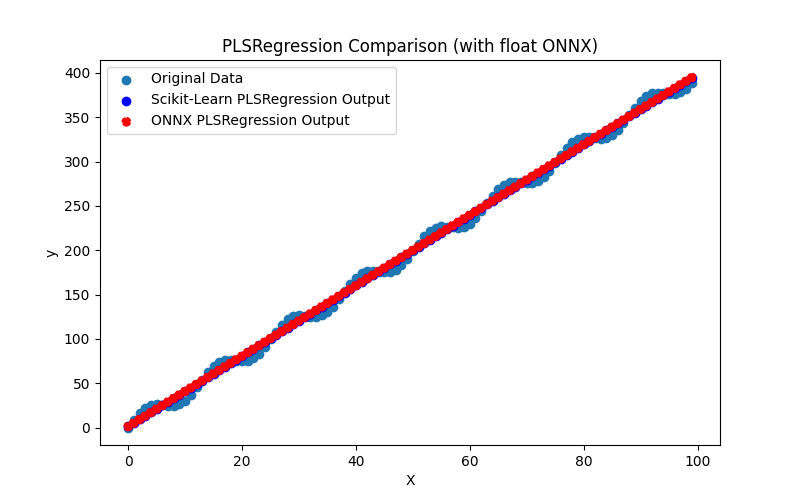
Şekil 76. PLSRegression.py sonuçları (float ONNX)
2.1.23.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen pls_regression_float.onnx ve pls_regression_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| PLSRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PLSRegression" #define ONNXFilenameFloat "pls_regression_float.onnx" #define ONNXFilenameDouble "pls_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
PLSRegression (EURUSD,H1) Testing ONNX float: PLSRegression (pls_regression_float.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382638567003 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781455257640815 PLSRegression (EURUSD,H1) PLSRegression (EURUSD,H1) Testing ONNX double: PLSRegression (pls_regression_double.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817839
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: PLSRegression (pls_regression_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379221400145 Testing ONNX double: PLSRegression (pls_regression_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
ONNX float MAE'nin doğruluğu: 8 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.23.3. pls_regression_float.onnx ve pls_regression_double.onnx modellerinin ONNX gösterimi
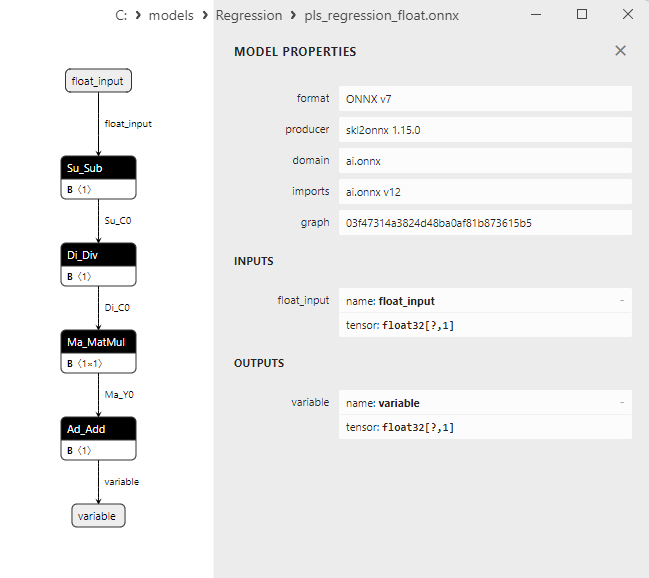
Şekil 77. Netron'da pls_regression_float.onnx modelinin ONNX gösterimi
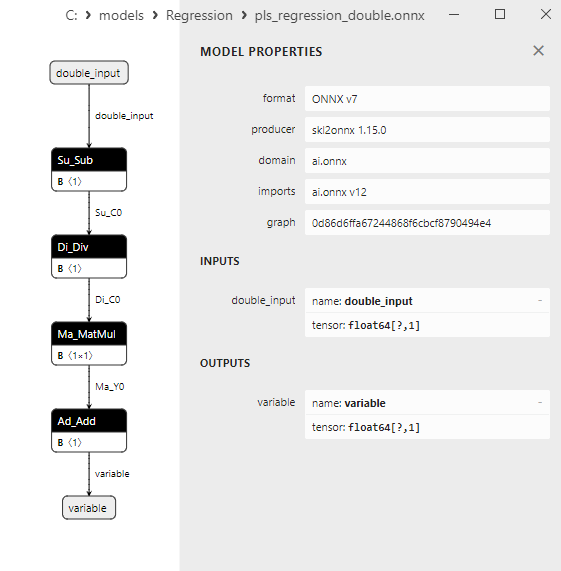
Şekil 78. Netron'da pls_regression_double.onnx modelinin ONNX gösterimi
2.1.24. sklearn.linear_model.TweedieRegressor
TweedieRegressor, Tweedie dağılımını kullanarak regresyon problemlerini çözmek için tasarlanmış bir regresyon yöntemidir. Tweedie dağılımı, değişen varyans yapısına sahip veriler de dahil olmak üzere çok çeşitli verileri tanımlayabilen bir olasılık dağılımıdır. TweedieRegressor, hedef değişkenin Tweedie dağılımı ile uyumlu karakteristiklere sahip olduğu regresyon görevlerinde uygulanır.
TweedieRegressor nasıl çalışır?
- Hedef değişken ve Tweedie dağılımı: TweedieRegressor hedef değişkenin bir Tweedie dağılımı izlediğini varsayar. Tweedie dağılımı, dağılımın şeklini ve varyans derecesini belirleyen 'p' parametresine bağlıdır.
- Model eğitimi: TweedieRegressor, bağımsız değişkenlere (özelliklere) dayalı olarak hedef değişkeni tahmin etmek için bir regresyon modeli eğitir. Model, Tweedie dağılımına karşılık gelen veriler için olasılığı maksimize eder.
- 'p' parametresinin seçilmesi: TweedieRegressor kullanılırken 'p' parametresinin seçilmesi çok önemli bir husustur. Bu parametre dağılımın şeklini ve varyansını tanımlar. Farklı 'p' değerleri farklı veri türlerine karşılık gelir; örneğin, p=1 Poisson dağılımına karşılık gelirken, p=2 normal dağılıma karşılık gelir.
- Yanıtları dönüştürme: Bazen model, eğitimden önce yanıtların (hedef değişkenler) dönüştürülmesini gerektirebilir. Bu dönüşüm 'p' parametresiyle ilgilidir ve Tweedie dağılımına uymak için logaritmik fonksiyonlar veya başka dönüşümler içerebilir.
TweedieRegressor'ın avantajları:
- Değişken varyanslı verileri modelleme becerisi: Tweedie dağılımı, farklı varyans yapılarına sahip verilere uyum sağlayabilir; bu da varyansın değişebildiği gerçek dünya verileri için değerlidir.
- Çeşitli 'p' parametreleri: Farklı 'p' değerlerinin seçilebilmesi, çeşitli veri türlerinin modellenmesine olanak tanır.
TweedieRegressor'ın sınırlamaları:
- 'p' parametresinin seçimindeki karmaşıklık: Doğru 'p' değerini seçmek, veriler hakkında bilgi sahibi olmayı ve denemeler yapmayı gerektirebilir.
- Tweedie dağılımına uygunluk: TweedieRegressor'ın başarılı bir şekilde uygulanması için hedef değişkenin Tweedie dağılımına uygun olması gerekir. Uyumsuzluk zayıf model performansına yol açabilir.
TweedieRegressor, değişen varyans yapılarına sahip verileri modellemek için Tweedie dağılımını kullanan bir regresyon yöntemidir. Bu yöntem, hedef değişkenin Tweedie dağılımına uygun olduğu ve daha iyi veri adaptasyonu için farklı 'p' parametre değerleriyle ayarlanabildiği regresyon görevlerinde kullanışlıdır.
2.1.24.1. TweedieRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.TweedieRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training TweedieRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"
# create a Tweedie Regressor model
regression_model = TweedieRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
2023.10.31 11:39:36.223 Python TweedieRegressor Original model (double) 2023.10.31 11:39:36.223 Python R-squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:39:36.223 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.223 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.223 Python 2023.10.31 11:39:36.223 Python TweedieRegressor ONNX model (float) 2023.10.31 11:39:36.223 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_float.onnx 2023.10.31 11:39:36.253 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python R-squared (Coefficient of determination) 0.9962368338709323 2023.10.31 11:39:36.253 Python Mean Absolute Error: 6.342397072978867 2023.10.31 11:39:36.253 Python Mean Squared Error: 49.797068181938165 2023.10.31 11:39:36.253 Python R^2 matching decimal places: 8 2023.10.31 11:39:36.253 Python MAE matching decimal places: 6 2023.10.31 11:39:36.253 Python MSE matching decimal places: 4 2023.10.31 11:39:36.253 Python float ONNX model precision: 6 2023.10.31 11:39:36.613 Python 2023.10.31 11:39:36.613 Python TweedieRegressor ONNX model (double) 2023.10.31 11:39:36.613 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_double.onnx 2023.10.31 11:39:36.613 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.613 Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.613 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.628 Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.628 Python R-squared (Coefficient of determination) 0.9962368328117072 2023.10.31 11:39:36.628 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.628 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.628 Python R^2 matching decimal places: 16 2023.10.31 11:39:36.628 Python MAE matching decimal places: 15 2023.10.31 11:39:36.628 Python MSE matching decimal places: 15 2023.10.31 11:39:36.628 Python double ONNX model precision: 15
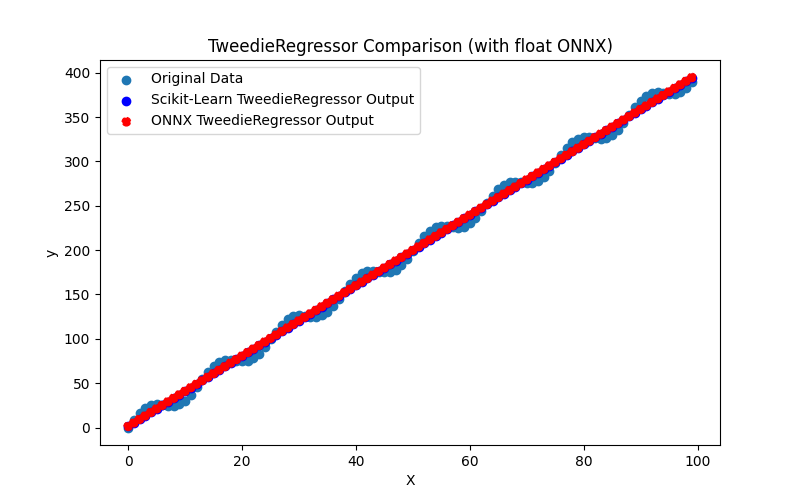
Şekil 79. TweedieRegressor.py sonuçları (float ONNX)
2.1.24.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen tweedie_regressor_float.onnx ve tweedie_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| TweedieRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TweedieRegressor" #define ONNXFilenameFloat "tweedie_regressor_float.onnx" #define ONNXFilenameDouble "tweedie_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
2023.10.31 11:42:20.113 TweedieRegressor (EURUSD,H1) Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368338709323 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423970729788666 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970681819381653 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423978976675608 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970821984087593
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423970729788666 Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423978976675608
ONNX float MAE'nin doğruluğu: 6 ondalık basamak, ONNX double MAE'nin doğruluğu: 14 ondalık basamak.
2.1.24.3. tweedie_regressor_float.onnx ve tweedie_regressor_double.onnx modellerinin ONNX gösterimi
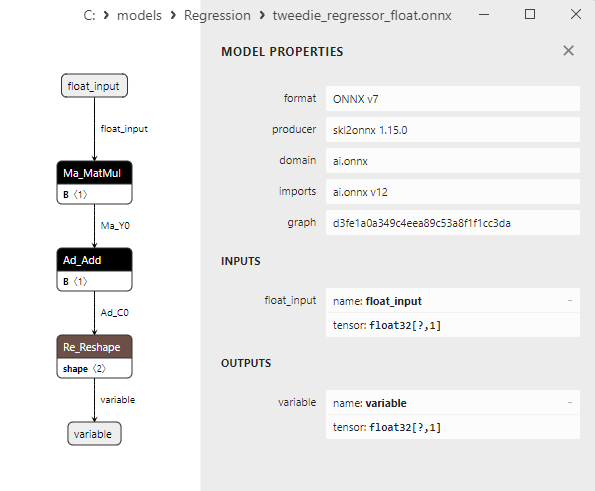
Şekil 80. Netron'da tweedie_regressor_float.onnx modelinin ONNX gösterimi
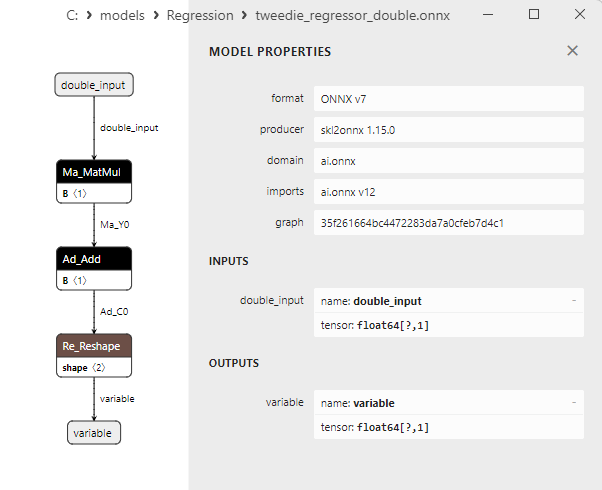
Şekil 81. Netron'da tweedie_regressor_double.onnx modelinin ONNX gösterimi
2.1.25. sklearn.linear_model.PoissonRegressor
PoissonRegressor, Poisson dağılımına dayalı regresyon görevlerini çözmek için uygulanan bir makine öğrenimi yöntemidir.
Bu yöntem, bağımlı değişken (hedef değişken) sayım verisi olduğunda, sabit bir zaman aralığında veya sabit bir uzamsal aralıkta meydana gelen olayların sayısını temsil ettiğinde uygundur. PoissonRegressor, tahmin ediciler (bağımsız değişkenler) ile hedef değişken arasındaki ilişkiyi, bu ilişkinin Poisson dağılımına uygun olduğunu varsayarak modeller.
PoissonRegressor nasıl çalışır?
- Girdi verileri: Özellikleri (bağımsız değişkenler) ve olay sayısını temsil eden hedef değişkeni içeren bir veri kümesi ile başlar.
- Poisson dağılımı: PoissonRegressor yöntemi, hedef değişkeni Poisson dağılımını izlediğini varsayarak modeller. Poisson dağılımı, belirli bir zaman aralığında veya uzamsal aralıkta sabit bir ortalama yoğunlukta meydana gelen olayları modellemek için uygundur.
- Model eğitimi: PoissonRegressor, tahmin edicileri dikkate alarak Poisson dağılımının parametrelerini hesaplayan bir modeli eğitir. Model, Poisson dağılımına uygun olan olabilirlik fonksiyonunu kullanarak gözlemlenen veriler için en iyi uyumu bulmaya çalışır.
- Sayım değerlerini tahmin etme: Eğitimden sonra model, yeni verilerdeki sayım değerlerini (olay sayısı) tahmin etmek için kullanılabilir ve bu tahminler de Poisson dağılımını takip eder.
PoissonRegressor'ın avantajları:
- Sayım verileri için uygundur: PoissonRegressor, hedef değişkenin emir sayısı, çağrı sayısı vb. gibi sayım verilerini temsil ettiği görevler için uygundur.
- Dağılımın özgüllüğü: Model Poisson dağılımına bağlı olduğundan, bu dağılım tarafından iyi tanımlanan veriler için daha doğru olabilir.
PoissonRegressor'ın sınırlamaları:
- Yalnızca sayım verileri için uygundur: PoissonRegressor, hedef değişkenin sürekli ve sayısal olmadığı durumlarda regresyon için uygun değildir.
- Özellik seçimine bağımlılık: Modelin kalitesi büyük ölçüde özelliklerin seçimine ve mühendisliğine bağlı olabilir.
PoissonRegressor, hedef değişken sayım verilerini temsil ettiğinde ve Poisson dağılımı kullanılarak modellendiğinde regresyon görevlerini çözmek için kullanılan bir makine öğrenimi yöntemidir. Bu yöntem, belirli zaman veya uzamsal aralıkta sabit bir yoğunlukta meydana gelen olaylarla ilgili görevler için faydalıdır.
2.1.25.1. PoissonRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.PoissonRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training PoissonRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"
# create a PoissonRegressor model
regression_model = PoissonRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python PoissonRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python Python PoissonRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204305082536851 Python Mean Absolute Error: 27.59790825165078 Python Mean Squared Error: 1052.9238598018305 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 5 Python MSE matching decimal places: 2 Python float ONNX model precision: 5 Python Python PoissonRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
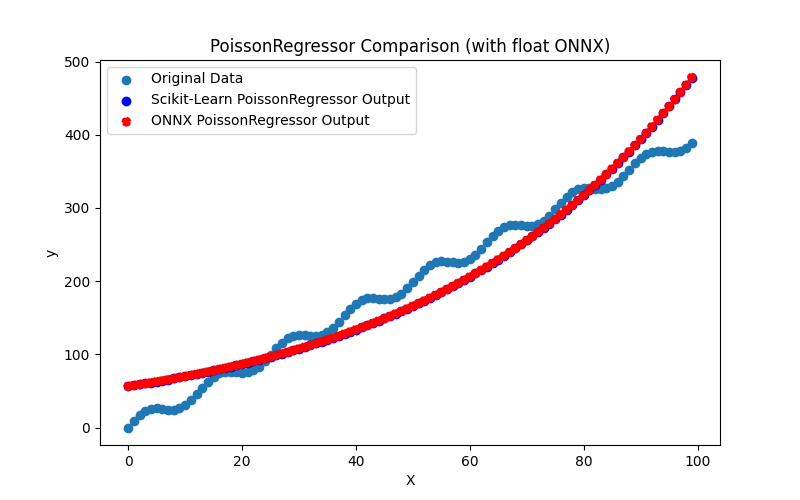
Şekil 82. PoissonRegressor.py sonuçları (float ONNX)
2.1.25.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen poisson_regressor_float.onnx ve poisson_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| PoissonRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PoissonRegressor" #define ONNXFilenameFloat "poisson_regressor_float.onnx" #define ONNXFilenameDouble "poisson_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
PoissonRegressor (EURUSD,H1) Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204305082536851 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979082516507788 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9238598018305311 PoissonRegressor (EURUSD,H1) PoissonRegressor (EURUSD,H1) Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204304782362493 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979046604852343 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9242570153051020
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979082516507788 Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979046604852343
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.25.3. poisson_regressor_float.onnx ve poisson_regressor_double.onnx modellerinin ONNX gösterimi
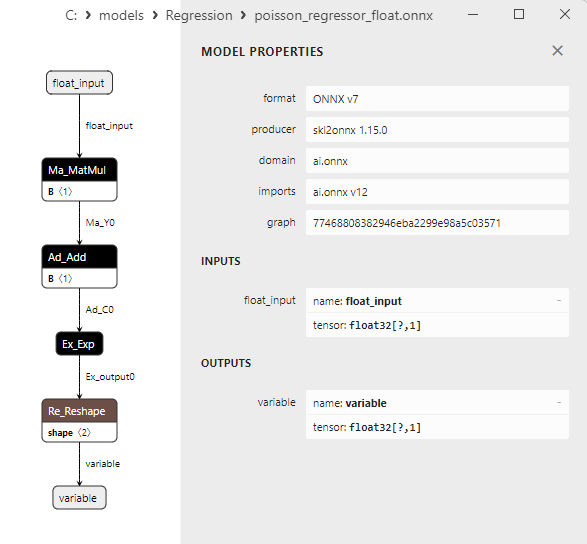
Şekil 83. Netron'da poisson_regressor_float.onnx modelinin ONNX gösterimi
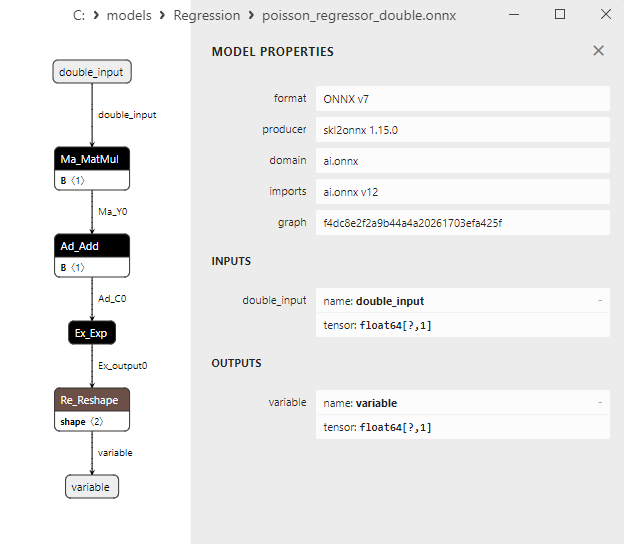
Şekil 84. Netron'da poisson_regressor_double.onnx modelinin ONNX gösterimi
2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
RadiusNeighborsRegressor, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Özellik uzayında en yakın komşulara dayalı olarak hedef değişkenin değerlerini tahmin etmek için tasarlanmış k-Nearest Neighbors (k-NN) yönteminin bir çeşididir. Bununla birlikte, sabit sayıda komşu yerine (k-NN yönteminde olduğu gibi), RadiusNeighborsRegressor her örneklem için komşuları belirlemek üzere sabit bir yarıçap kullanır.RadiusNeighborsRegressor nasıl çalışır?
- Girdi verileri: Özellikleri (bağımsız değişkenler) ve hedef değişkeni (sürekli) içeren bir veri kümesi ile başlar.
- Yarıçapın ayarlanması: RadiusNeighborsRegressor, özellik uzayında her örneklem için en yakın komşuları belirlemek üzere sabit bir yarıçap ayarlanmasını gerektirir.
- Komşu tanımı: Her örneklem için, belirlenen yarıçap içerisindeki tüm veri noktaları belirlenir ve bunlar o örneklemin komşuları haline gelir.
- Ağırlıklı ortalama: Her bir örneklem için hedef değişkenin değerini tahmin etmek amacıyla komşularının hedef değişkenlerinin değerleri kullanılır. Bu genellikle ağırlıkların örneklemler arasındaki mesafeye bağlı olduğu ağırlıklı ortalama kullanılarak yapılır.
- Tahmin: Eğitimden sonra model, özellik uzayında en yakın komşulara dayalı olarak yeni veriler üzerinde hedef değişkenin değerlerini tahmin etmek için kullanılabilir.
- Çok yönlülük: RadiusNeighborsRegressor, özellikle komşu sayısının yarıçapa bağlı olarak önemli ölçüde değişebileceği durumlarda regresyon görevleri için kullanılabilir.
- Aykırı değerlere karşı dayanıklılık: Komşu tabanlı bir yaklaşım aykırı değerlere karşı dirençli olabilir çünkü model yalnızca yakındaki veri noktalarını dikkate alır.
- Yarıçap seçimine bağımlılık: Doğru yarıçapı seçmek ayarlama ve deneme gerektirebilir.
- Hesaplama karmaşıklığı: Büyük veri kümelerinin işlenmesi önemli hesaplama kaynakları gerektirebilir.
2.1.26.1. RadiusNeighborsRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.neighbors.RadiusNeighborsRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training RadiusNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"
# create a RadiusNeighborsRegressor model
regression_model = RadiusNeighborsRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python RadiusNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999521132921395 Python Mean Absolute Error: 0.591458244376554 Python Mean Squared Error: 0.6336732353950723 Python Python RadiusNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 4 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python RadiusNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python double ONNX model precision: 0
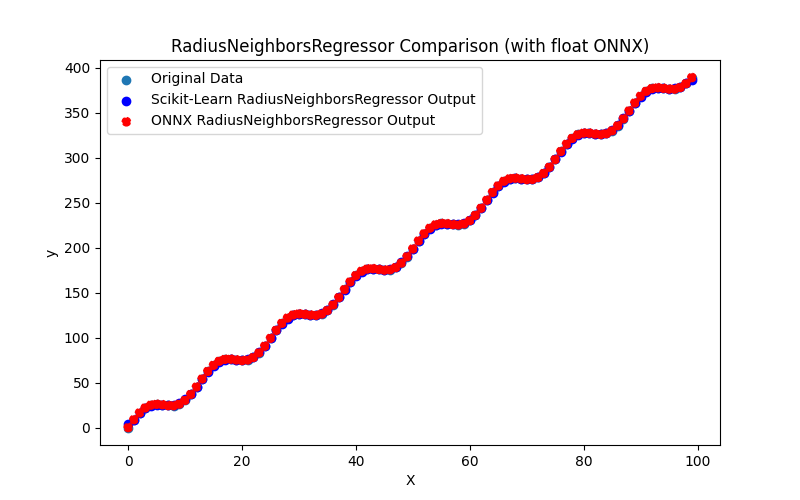
Şekil 85. RadiusNeighborsRegressor.py sonuçları (float ONNX)
2.1.26.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen radius_neighbors_regressor_float.onnx ve radius_neighbors_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| RadiusNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RadiusNeighborsRegressor" #define ONNXFilenameFloat "radius_neighbors_regressor_float.onnx" #define ONNXFilenameDouble "radius_neighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX float: RadiusNeighborsRegressor (radius_neighbors_regressor_float.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 RadiusNeighborsRegressor (EURUSD,H1) RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX double: RadiusNeighborsRegressor (radius_neighbors_regressor_double.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.26.3. radius_neighbors_regressor_float.onnx ve radius_neighbors_regressor_double.onnx modellerinin ONNX gösterimi
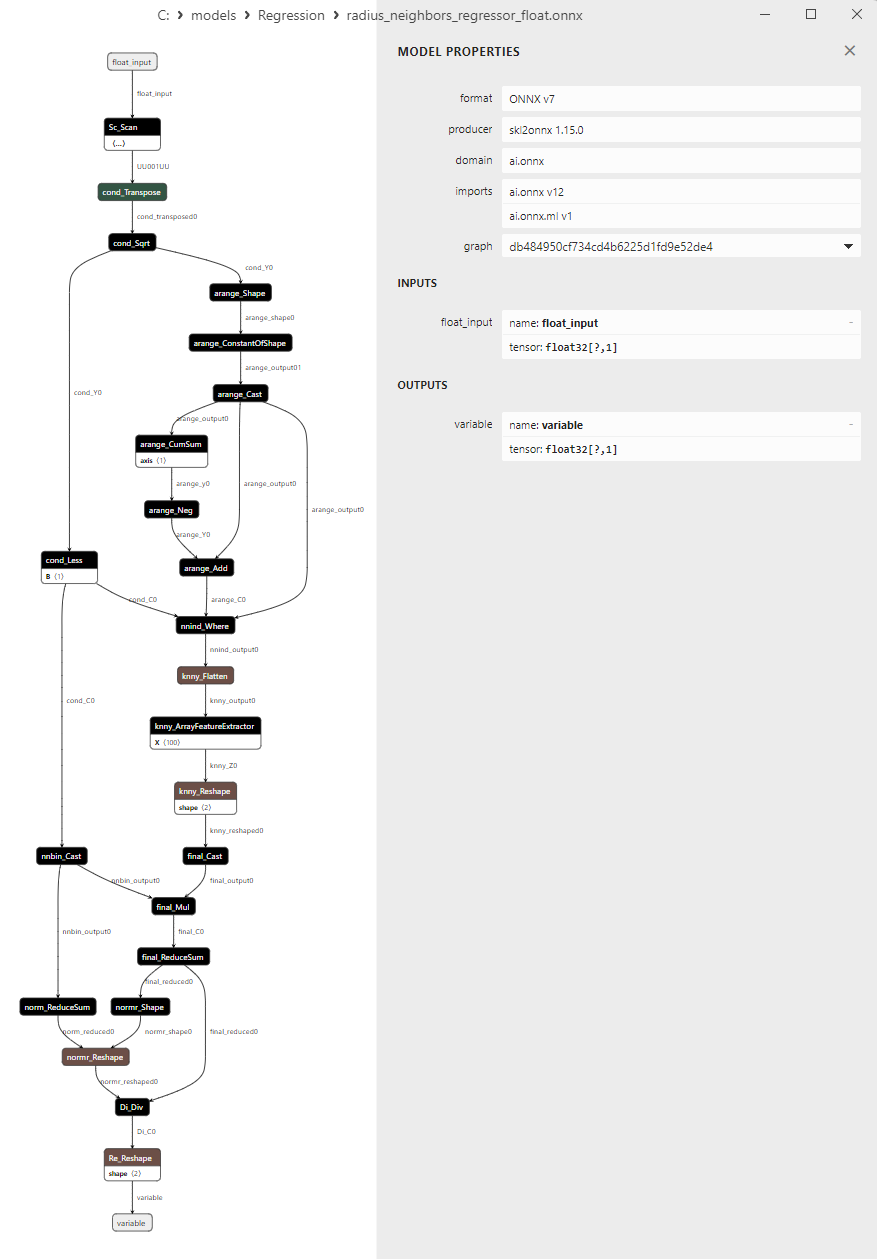
Şekil 86. Netron'da radius_neighbors_regressor_float.onnx modelinin ONNX gösterimi
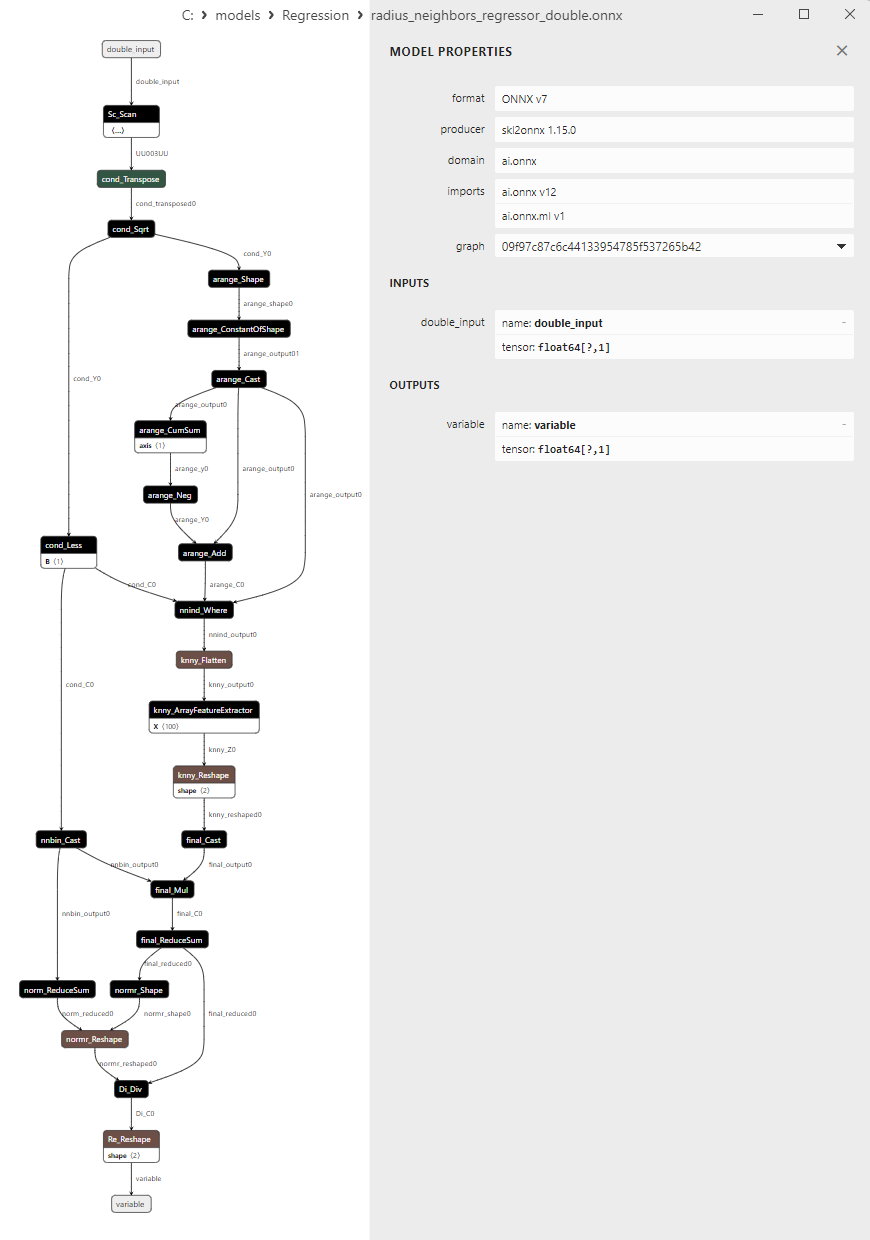
Şekil 87. Netron'da radius_neighbors_regressor_double.onnx modelinin ONNX gösterimi
2.1.27. sklearn.neighbors.KNeighborsRegressor
KNeighborsRegressor, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir.
k-Nearest Neighbors (k-NN) algoritmaları kategorisine aittir ve eğitim veri setindeki nesneler arasındaki yakınlığa (benzerliğe) dayalı olarak hedef değişkenin sayısal değerlerini tahmin etmek için kullanılır.
KNeighborsRegressor nasıl çalışır?
- Girdi verileri: Özellikler (bağımsız değişkenler) ve hedef değişkenin karşılık gelen değerlerini içeren başlangıç veri kümesi ile başlar.
- Komşu sayısının (k) seçilmesi: Tahmin sırasında dikkate alınacak en yakın komşu sayısını (k) seçmeniz gerekir. Bu sayı modelin hiperparametrelerinden biridir.
- Yakınlığı hesaplama: Yeni veriler (tahminlere ihtiyaç duyulan noktalar) için, bu veriler ile eğitim veri kümesindeki tüm nesneler arasındaki mesafe veya benzerlik hesaplanır.
- En yakın k komşunun seçilmesi: Eğitim veri setinden yeni veriye en yakın k nesne seçilir.
- Tahmin: Regresyon görevleri bağlamında, yeni veriler için hedef değişkenin değerinin tahmin edilmesi, k en yakın komşunun hedef değişkenlerinin ortalama değeri olarak hesaplanır.
KNeighborsRegressor'ın avantajları:
- Kullanım kolaylığı: KNeighborsRegressor, verilerin karmaşık bir şekilde ön işlemeye tabi tutulmasını gerektirmeyen basit bir algoritmadır.
- Parametrik olmayan yapı: Yöntem, özellikler ve hedef değişken arasında belirli bir fonksiyonel bağımlılık biçimi varsaymaz ve çeşitli ilişkilerin modellenmesine olanak tanır.
- Yeniden üretilebilirlik: KNeighborsRegressor'dan elde edilen sonuçlar, tahminler veri yakınlığına dayandığından yeniden üretilebilir.
KNeighborsRegressor'ın sınırlamaları:
- Hesaplama karmaşıklığı: Eğitim veri kümesindeki tüm noktalara olan uzaklıkları hesaplamak, büyük hacimli veriler için hesaplama açısından maliyetli olabilir.
- Komşu sayısı seçimine duyarlılık: Optimum k değerinin seçilmesi ayarlama gerektirir ve modelin performansını önemli ölçüde etkileyebilir.
- Gürültüye karşı hassasiyet: Yöntem, veri gürültüsüne ve aykırı değerlere karşı hassas olabilir.
KNeighborsRegressor, hedef değişkeni tahmin etmek için nesnelerin komşuluğunu göz önünde bulundurmanın gerekli olduğu regresyon görevlerinde kullanışlıdır. Özellikler ve hedef değişken arasındaki ilişkinin doğrusal olmadığı ve karmaşık olduğu durumlarda özellikle yararlı olabilir.
2.1.27.1. KNeighborsRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.neighbors.KNeighborsRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training KNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"
# create a KNeighbors Regressor model
kneighbors_model = KNeighborsRegressor(n_neighbors=5)
# fit the model to the data
kneighbors_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = kneighbors_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python KNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117578 Python Mean Squared Error: 5.822594523532273 Python Python KNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599867417418 Python Mean Absolute Error: 1.7414195457976402 Python Mean Squared Error: 5.8225891366283875 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 4 Python MSE matching decimal places: 4 Python float ONNX model precision: 4 Python Python KNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117583 Python Mean Squared Error: 5.822594523532269 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
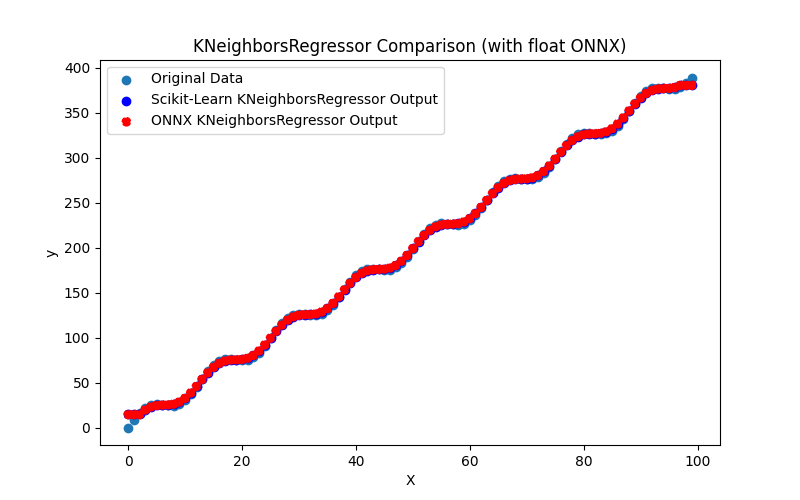
Şekil 88. KNeighborsRegressor.py sonuçları (float ONNX)
2.1.27.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen kneighbors_regressor_float.onnx ve kneighbors_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| KNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "KNeighborsRegressor" #define ONNXFilenameFloat "kneighbors_regressor_float.onnx" #define ONNXFilenameDouble "kneighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
KNeighborsRegressor (EURUSD,H1) Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599860116634 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414200607817711 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225987975798184 KNeighborsRegressor (EURUSD,H1) KNeighborsRegressor (EURUSD,H1) Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599863346534 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414210057117601 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225945235322705
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414200607817711 Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414210057117601
ONNX float MAE'nin doğruluğu: 5 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.27.3. kneighbors_regressor_float.onnx ve kneighbors_regressor_double.onnx modellerinin ONNX gösterimi
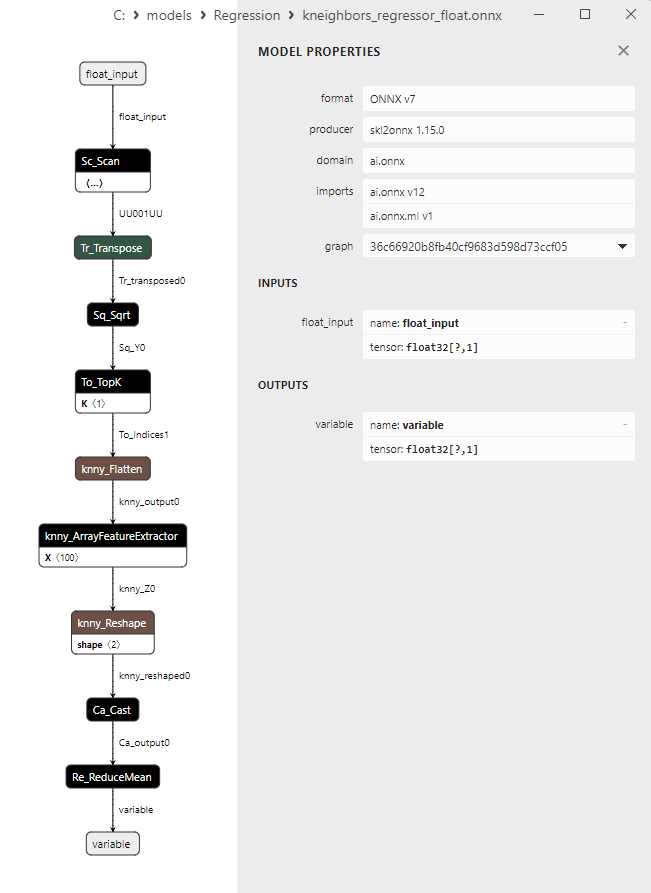
Şekil 89. Netron'da kneighbors_regressor_float.onnx modelinin ONNX gösterimi
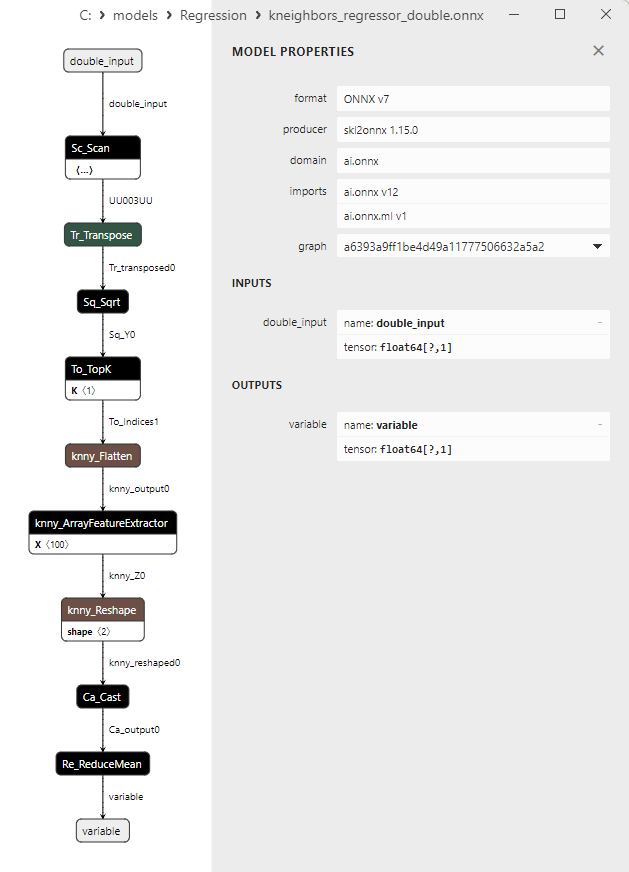
Şekil 90. Netron'da kneighbors_regressor_double.onnx modelinin ONNX gösterimi
2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
GaussianProcessRegressor, regresyon görevleri için kullanılan ve tahminlerdeki belirsizliğin modellenmesini sağlayan bir makine öğrenimi yöntemidir.
Gaussian Process (GP), Bayes makine öğreniminde güçlü bir araçtır ve karmaşık fonksiyonları modellemek ve belirsizliği hesaba katarken hedef değişken değerlerini tahmin etmek için kullanılır.
GaussianProcessRegressor nasıl çalışır?
- Girdi verileri: Özellikler (bağımsız değişkenler) ve hedef değişkenin karşılık gelen değerlerini içeren başlangıç veri kümesi ile başlar.
- Gauss sürecinin modellenmesi: Gaussian Process, bir Gauss (normal) dağılımı tarafından tanımlanan rastgele değişkenler topluluğu olan bir Gauss sürecini kullanır. GP sadece her bir veri noktası için ortalama değerleri değil, aynı zamanda bu noktalar arasındaki kovaryansı (veya benzerliği) da modeller.
- Kovaryans fonksiyonunun seçilmesi: GP'nin önemli bir yönü, veri noktaları arasındaki bağlantıyı ve gücü belirleyen kovaryans fonksiyonunun (veya çekirdeğin) seçilmesidir. Verilerin ve görevin niteliğine bağlı olarak farklı kovaryans fonksiyonları kullanılabilir.
- Model eğitimi: GaussianProcessRegressor, eğitim verilerini kullanarak GP'yi eğitir. Eğitim sırasında model, kovaryans fonksiyonunun parametrelerini ayarlar ve tahminlerdeki belirsizliği değerlendirir.
- Tahmin: Eğitimden sonra model, yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir. GP'nin önemli bir özelliği, yalnızca ortalama değeri değil, aynı zamanda tahminlerdeki güven düzeyini hesaplayan bir güven aralığını da tahmin etmesidir.
GaussianProcessRegressor'ın avantajları:
- Belirsizliğin modellenmesi: GP, tahminlerdeki belirsizliğin hesaba katılmasına olanak tanır; bu da tahmin edilen değerlere duyulan güvenin bilinmesinin çok önemli olduğu görevlerde faydalıdır.
- Esneklik: GP çeşitli fonksiyonları modelleyebilir ve kovaryans fonksiyonları farklı veri türleri için uyarlanabilir.
- Az sayıda hiperparametre: GP'nin nispeten az sayıda hiperparametresi vardır ve bu da modelde ayarlama yapmayı basitleştirir.
GaussianProcessRegressor'ın sınırlamaları:
- Hesaplama karmaşıklığı: GP, özellikle büyük hacimli veriler söz konusu olduğunda hesaplama açısından maliyetli olabilir.
- Yüksek boyutlu uzaylarda verimsizlik: GP, boyutluluk laneti nedeniyle çok sayıda özelliğe sahip görevlerde verimliliğini kaybedebilir.
GaussianProcessRegressor, belirsizliği modellemenin ve güvenilir tahminler sağlamanın çok önemli olduğu regresyon görevlerinde kullanışlıdır. Bu yöntem Bayes makine öğrenimi ve meta analizde sıklıkla kullanılmaktadır.
2.1.28.1. GaussianProcessRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.gaussian_process.GaussianProcessRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training GaussianProcessRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"
# create a GaussianProcessRegressor model
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# fit the model to the data
gp_model.fit(X, y)
# predict values for the entire dataset
y_pred = gp_model.predict(X, return_std=False)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python GaussianProcessRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python Python GaussianProcessRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999936 Python Mean Absolute Error: 6.454076974495848e-06 Python Mean Squared Error: 8.493606782250733e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python GaussianProcessRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python R^2 matching decimal places: 1 Python MAE matching decimal places: 19 Python MSE matching decimal places: 20 Python double ONNX model precision: 19
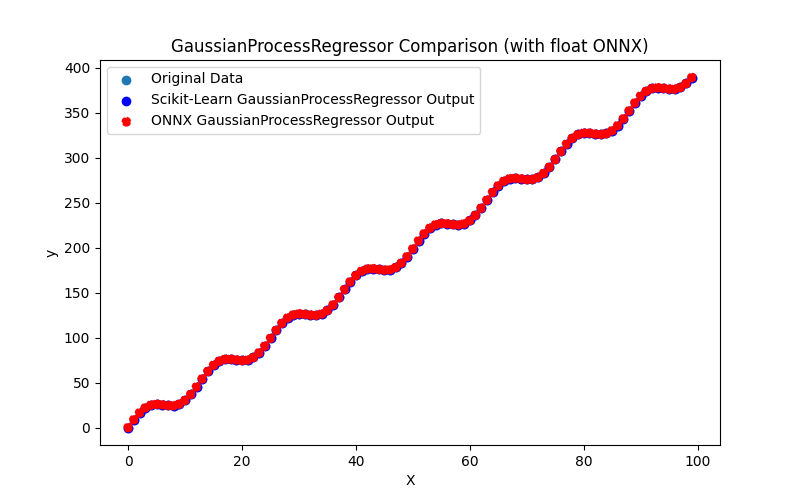
Şekil 91. GaussianProcessRegressor.py sonuçları (float ONNX)
2.1.28.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen gaussian_process_regressor_float.onnx ve gaussian_process_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| GaussianProcessRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GaussianProcessRegressor" #define ONNXFilenameFloat "gaussian_process_regressor_float.onnx" #define ONNXFilenameDouble "gaussian_process_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
GaussianProcessRegressor (EURUSD,H1) Testing ONNX float: GaussianProcessRegressor (gaussian_process_regressor_float.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999936 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000064540769745 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000849361 GaussianProcessRegressor (EURUSD,H1) GaussianProcessRegressor (EURUSD,H1) Testing ONNX double: GaussianProcessRegressor (gaussian_process_regressor_double.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000003504 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.28.3. gaussian_process_regressor_float.onnx ve gaussian_process_regressor_double.onnx modellerinin ONNX gösterimi
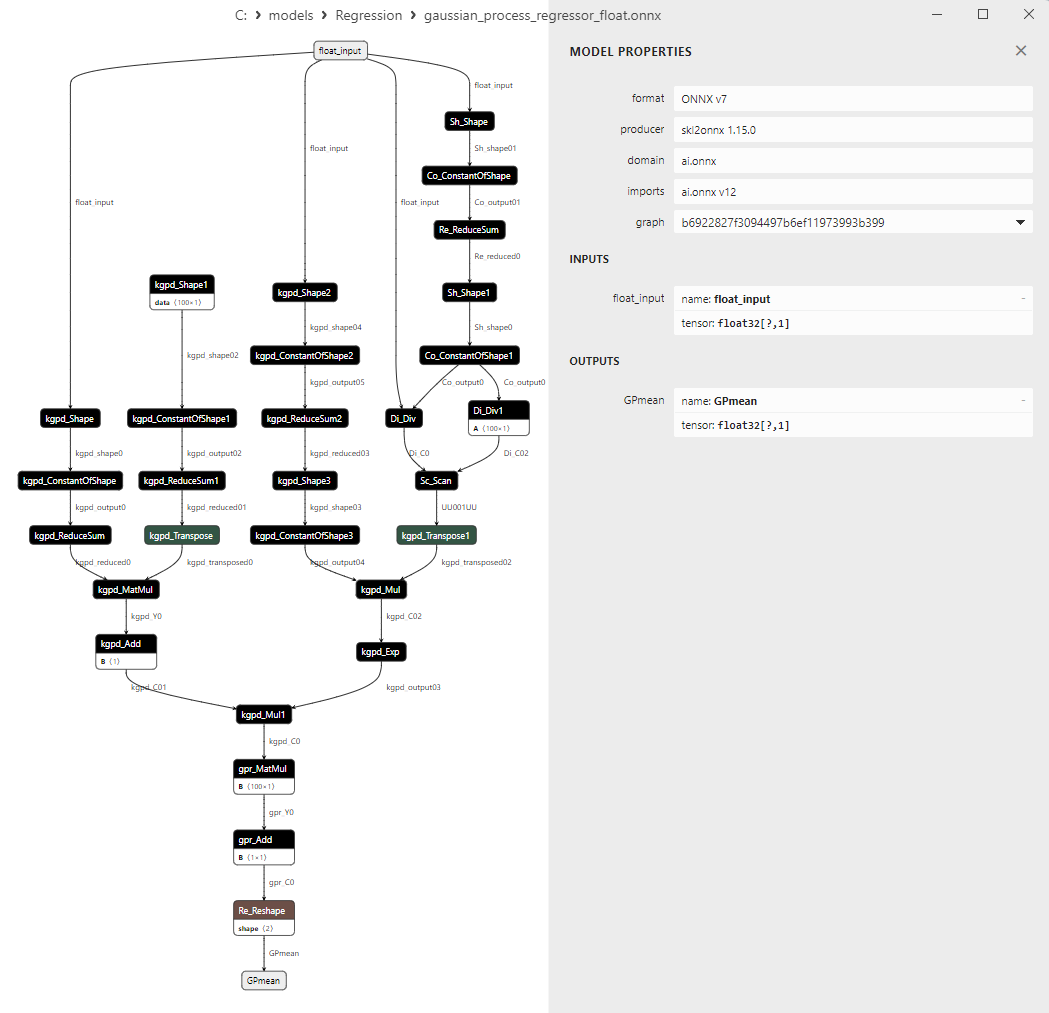
Şekil 92. Netron'da gaussian_process_regressor_float.onnx modelinin ONNX gösterimi
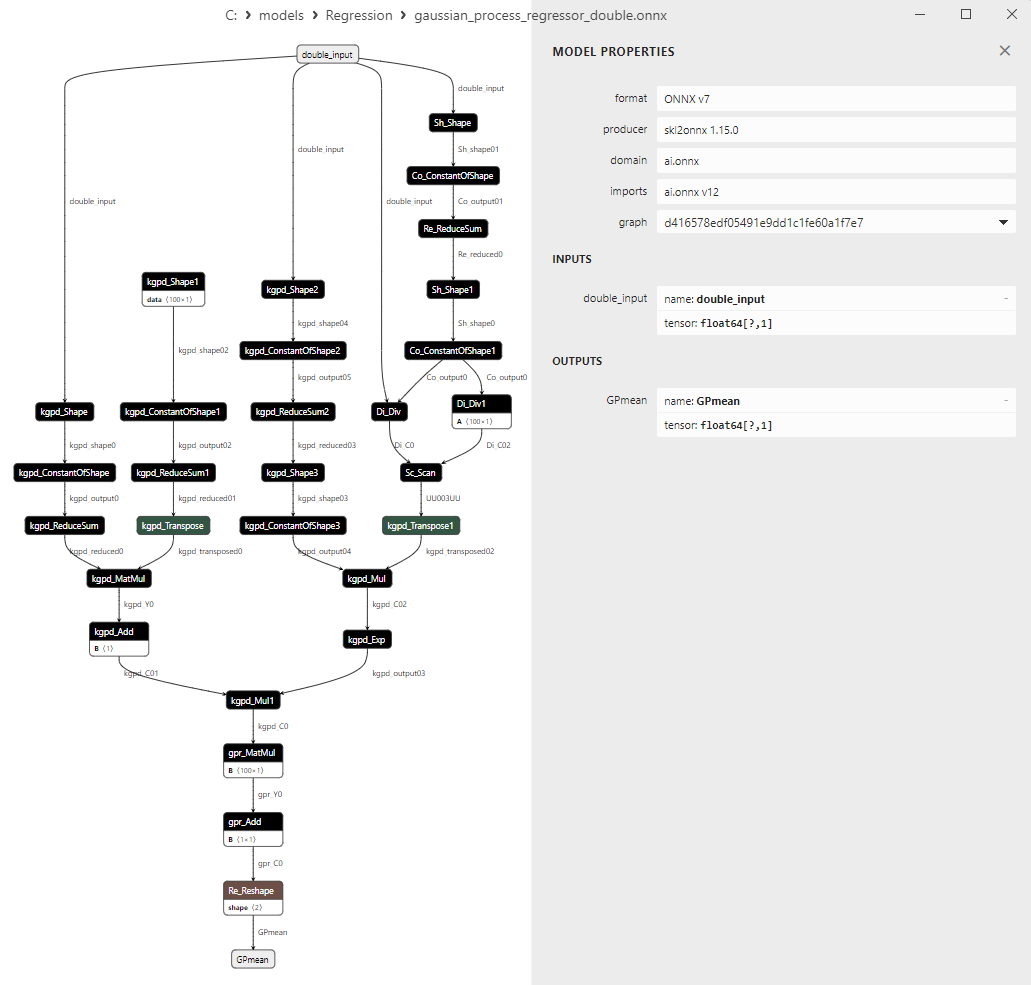
Şekil 93. Netron'da gaussian_process_regressor_double.onnx modelinin ONNX gösterimi
2.1.29. sklearn.linear_model.GammaRegressor
GammaRegressor, hedef değişkenin gama dağılımını takip ettiği regresyon görevleri için tasarlanmış bir makine öğrenimi yöntemidir.
Gama dağılımı, pozitif, sürekli rastgele değişkenleri modellemek için kullanılan bir olasılık dağılımıdır. Bu yöntem maliyet, zaman veya oranlar gibi pozitif sayısal değerlerin modellenmesini ve tahmin edilmesini sağlar.
GammaRegressor nasıl çalışır?
- Girdi verileri: Özelliklerin (bağımsız değişkenler) ve gama dağılımını takip eden hedef değişkenin karşılık gelen değerlerinin bulunduğu başlangıç veri kümesi ile başlar.
- Kayıp fonksiyonu seçimi: GammaRegressor, gamma dağılımına uyan bir kayıp fonksiyonu kullanır ve bu dağılımın özelliklerini dikkate alır. Bu, gamma dağılımının negatif olmamasını ve sağa çarpıklığını göz önünde bulundurarak verilerin modellenmesine olanak tanır.
- Model eğitimi: Model, seçilen kayıp fonksiyonu kullanılarak veriler üzerinde eğitilir. Eğitim sırasında, kayıp fonksiyonunu en aza indirmek için modelin parametrelerini ayarlar.
- Tahmin: Eğitimden sonra model, yeni veriler için hedef değişkenin değerlerini tahmin etmek için kullanılabilir.
GammaRegressor'ın avantajları:
- Pozitif değerlerin modellenmesi: Bu yöntem özellikle pozitif sayısal değerlerin modellenmesi için tasarlanmıştır ve hedef değişkenin alt sınırlı olduğu görevlerde faydalı olabilir.
- Gama dağılım şeklini göz önünde bulundurma: GammaRegressor, gama dağılımının karakteristiğini hesaba katarak bu dağılımı izleyen verilerin daha doğru bir şekilde modellenmesini sağlar.
- Ekonometri ve tıbbi araştırmalarda kullanışlılık: Gama dağılımı, ekonometri ve tıbbi araştırmalarda maliyet, bekleme süresi ve diğer pozitif rastgele değişkenleri modellemek için sıklıkla kullanılır.
GammaRegressor'ın sınırlamaları:
- Veri türünde sınırlama: Bu yöntem yalnızca hedef değişkenin gamma dağılımını veya benzer dağılımları izlediği regresyon görevleri için uygundur. Böyle bir dağılıma uymayan veriler için bu yöntem etkili olmayabilir.
- Bir kayıp fonksiyonu seçilmesini gerektirir: Uygun bir kayıp fonksiyonunun seçilmesi, hedef değişkenin dağılımı ve karakteristiği hakkında bilgi sahibi olmayı gerektirebilir.
GammaRegressor, gama dağılımıyla uyumlu pozitif sayısal değerlerin modellenmesi ve tahmin edilmesinin gerekli olduğu görevlerde kullanışlıdır.
2.1.29.1. GammaRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.GammaRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training GammaRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)
model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"
# create a Gamma Regressor model
regression_model = GammaRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python GammaRegressor Original model (double) Python R-squared (Coefficient of determination): 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python Python GammaRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963795030042045 Python Mean Absolute Error: 37.266211754095956 Python Mean Squared Error: 2694.4608407846144 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 4 Python MSE matching decimal places: 1 Python float ONNX model precision: 4 Python Python GammaRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 12 Python double ONNX model precision: 15
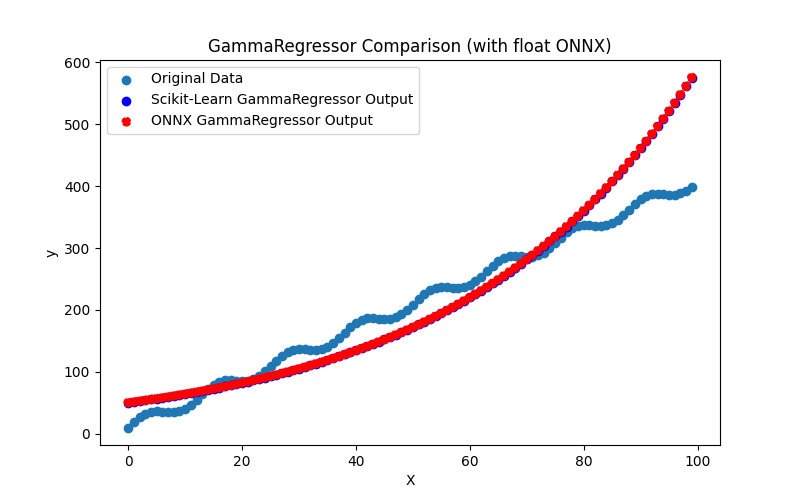
Şekil 94. GammaRegressor.py sonuçları (float ONNX)
2.1.29.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen gamma_regressor_float.onnx ve gamma_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| GammaRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GammaRegressor" #define ONNXFilenameFloat "gamma_regressor_float.onnx" #define ONNXFilenameDouble "gamma_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(10+4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
GammaRegressor (EURUSD,H1) Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963795030042045 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662117540959628 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4608407846144473 GammaRegressor (EURUSD,H1) GammaRegressor (EURUSD,H1) Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963797339354435 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662003194228220 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4577849273218817
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662117540959628 Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662003194228220
ONNX float MAE'nin doğruluğu: 4 ondalık basamak, ONNX double MAE'nin doğruluğu: 13 ondalık basamak.
2.1.29.3. gamma_regressor_float.onnx ve gamma_regressor_double.onnx modellerinin ONNX gösterimi
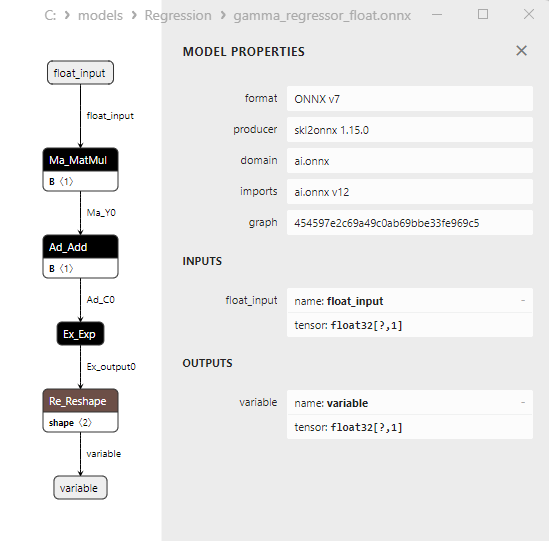
Şekil 95. Netron'da gamma_regressor_float.onnx modelinin ONNX gösterimi
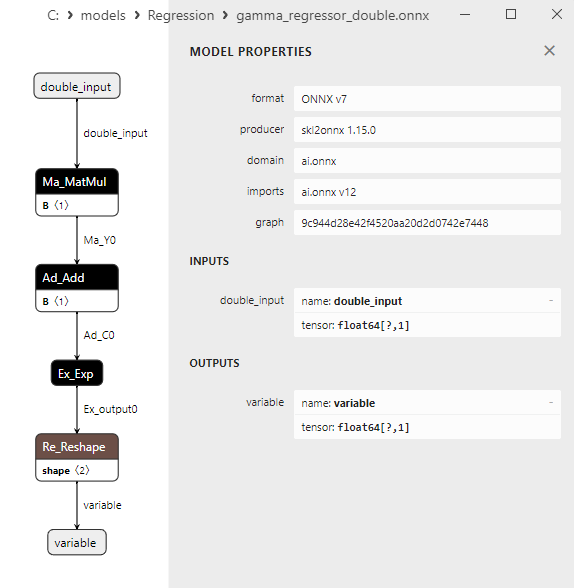
Şekil 96. Netron'da gamma_regressor_double.onnx modelinin ONNX gösterimi
2.1.30. sklearn.linear_model.SGDRegressor
SGDRegressor, bir regresyon modelini eğitmek için stokastik gradyan iniş (Stochastic Gradient Descent, SGD) kullanan bir regresyon yöntemidir. Lineer modeller ailesinin bir parçasıdır ve regresyon görevleri için kullanılabilir. SGDRegressor'ın temel özellikleri verimlilik ve büyük hacimli verileri işleme kabiliyetidir.
SGDRegressor nasıl çalışır?
- Lineer regresyon: Ridge ve Lasso'ya benzer şekilde SGDRegressor, bir regresyon probleminde bağımsız değişkenler (özellikler) ile hedef değişken arasında doğrusal bir ilişki bulmayı amaçlar.
- Stokastik gradyan iniş: SGDRegressor'ın temeli stokastik gradyan iniştir. Tüm eğitim veri kümesi üzerinde gradyanları hesaplamak yerine, rastgele seçilen mini veri gruplarına dayalı olarak modeli günceller. Bu, verimli model eğitimine ve önemli veri kümeleriyle çalışmaya olanak tanır.
- Düzenlileştirme: SGDRegressor L1 ve L2 düzenlileştirmeyi (Lasso ve Ridge) destekler. Bu, aşırı uyumu kontrol etmeye yardımcı olur ve model kararlılığını artırır.
- Hiperparametreler: Ridge ve Lasso'ya benzer şekilde SGDRegressor, düzenlileştirme parametresi (α, alpha) ve düzenlileştirme türü gibi hiperparametrelerin ayarlanmasına izin verir.
SGDRegressor'ın avantajları:
- Verimlilik: SGDRegressor büyük veri kümelerinde iyi performans gösterir ve modelleri kapsamlı veriler üzerinde verimli bir şekilde eğitir.
- Düzenlileştirme yeteneği: L1 ve L2 düzenlileştirme uygulama seçeneği, bu yöntemi aşırı uyum sorunlarını yönetmek için uygun hale getirir.
- Uyarlanabilir gradyan iniş: Stokastik gradyan iniş, değişen verilere adaptasyon ve modelleri hızlı bir şekilde eğitme yeteneği sağlar.
SGDRegressor'ın sınırlamaları:
- Hiperparametre seçimine duyarlılık: Öğrenme oranı ve düzenlileştirme katsayısı gibi hiperparametrelerin ayarlanması denemeler yapmayı gerektirebilir.
- Her zaman global minimuma yakınsamaz: Gradyan inişin stokastik doğası nedeniyle, SGDRegressor her zaman kayıp fonksiyonunun global minimumuna yakınsamaz.
SGDRegressor, bir regresyon modelini eğitmek için stokastik gradyan inişi kullanan bir regresyon yöntemidir. Verimli, büyük veri kümelerini işleyebilen ve aşırı uyumu yönetmek için düzenlileştirmeyi destekleyen bir sistemdir.
2.1.30.1. SGDRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.SGDRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training SGDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)
model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"
# create an SGDRegressor model
regression_model = SGDRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python SGDRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python Python SGDRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197876338647 Python Mean Absolute Error: 0.6405924014799271 Python Mean Squared Error: 0.5169866866963753 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 6 Python float ONNX model precision: 7 Python Python SGDRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 16 Python double ONNX model precision: 16
Şekil 97. SGDRegressor.py sonuçları (float ONNX)
2.1.30.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen sgd_regressor_float.onnx ve sgd_rgressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| SGDRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SGDRegressor" #define ONNXFilenameFloat "sgd_regressor_float.onnx" #define ONNXFilenameDouble "sgd_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i*0.1; y[i]=(double)(4*x[i] + sin(x[i]*10)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
SGDRegressor (EURUSD,H1) Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197876338647 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924014799272 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169866866963754 SGDRegressor (EURUSD,H1) SGDRegressor (EURUSD,H1) Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197872743282 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924406136998 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169867345998348
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924014799272 Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924406136998
ONNX float MAE'nin doğruluğu: 7 ondalık basamak, ONNX double MAE'nin doğruluğu: 16 ondalık basamak.
2.1.30.3. sgd_regressor_float.onnx ve sgd_rgressor_double.onnx modellerinin ONNX gösterimi
Şekil 98. Netron'da sgd_regressor_float.onnx modelinin ONNX gösterimi
Şekil 99. Netron'da sgd_rgressor_double.onnx modelinin ONNX gösterimi
2.2. Yalnızca float hassasiyetli ONNX modellerine dönüştürülen Scikit-learn kütüphanesinden regresyon modelleri
Bu bölüm yalnızca float hassasiyeti ile çalışabilen modelleri kapsar. Bunları double hassasiyetle ONNX'e dönüştürmek, ONNX operatörlerinin ai.onnx.ml alt kümesinin sınırlamalarıyla ilgili hatalara yol açar.
2.2.1. sklearn.linear_model.AdaBoostRegressor
AdaBoostRegressor, sayısal değerlerin (örneğin, emlak fiyatları, satış hacimleri vb.) tahmin edilmesini içeren regresyon için kullanılan bir makine öğrenimi yöntemidir.
Bu yöntem, başlangıçta sınıflandırma görevleri için geliştirilen AdaBoost (Adaptive Boosting) algoritmasının bir varyasyonudur.
AdaBoostRegressor nasıl çalışır?
- Orijinal veri kümesi: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişkenleri (tahmin etmeyi amaçladığımız bağımlı değişkenler) içeren orijinal veri kümesi ile başlar.
- Ağırlık başlatma: Başlangıçta, her bir veri noktası (gözlem) eşit ağırlığa sahiptir ve model bu ağırlıklı veri kümesine dayalı olarak oluşturulur.
- Zayıf öğrenicileri eğitme: AdaBoostRegressor, hedef değişkeni tahmin etmeye çalışan birkaç zayıf regresyon modeli (örn. karar ağaçları) oluşturur. Bu modeller "zayıf öğreniciler" olarak adlandırılır. Her bir zayıf öğrenici, her bir gözlemin ağırlıkları göz önünde bulundurularak veriler üzerinde eğitilir.
- Zayıf öğrenici ağırlıklarının seçimi: AdaBoostRegressor, her bir zayıf öğrenici için o öğrenicinin tahminlerde ne kadar iyi performans gösterdiğine bağlı olarak ağırlıkları hesaplar. Daha doğru tahminler yapan öğreniciler daha yüksek ağırlıklar alır ve bunun tersi de geçerlidir.
- Gözlem ağırlıklarının güncellenmesi: Gözlem ağırlıkları güncellenir, böylece daha önce yanlış tahmin edilen gözlemler daha büyük ağırlıklar alır ve böylece bir sonraki model için önemleri artar.
- Nihai tahmin: AdaBoostRegressor, tüm zayıf öğrenicilerin tahminlerini birleştirerek performanslarına göre ağırlıklar atar. Bu da modelin nihai tahminiyle sonuçlanır.
AdaBoostRegressor'ın avantajları:
- Uyarlanabilirlik: AdaBoostRegressor karmaşık fonksiyonlara uyum sağlar ve doğrusal olmayan ilişkilerle daha iyi başa çıkar.
- Aşırı uyum azaltma: AdaBoostRegressor, gözlem ağırlıklarının güncellenmesi yoluyla düzenlileştirmeyi kullanarak aşırı uyumu önlemeye yardımcı olur.
- Güçlü topluluk: AdaBoostRegressor, birden fazla zayıf modeli birleştirerek hedef değişkeni oldukça doğru bir şekilde tahmin edebilen güçlü modeller oluşturabilir.
AdaBoostRegressor'ın sınırlamaları:
- Aykırı değerlere hassasiyet: AdaBoostRegressor, verilerdeki aykırı değerlere karşı hassastır ve tahmin kalitesini etkiler.
- Yüksek hesaplama maliyetleri: Birden fazla zayıf öğrenici oluşturmak daha fazla hesaplama kaynağı ve zaman gerektirebilir.
- Her zaman en iyi seçim değildir: AdaBoostRegressor her zaman en uygun seçim değildir ve bazı durumlarda diğer regresyon yöntemleri daha iyi performans gösterebilir.
AdaBoostRegressor, özellikle verilerin karmaşık bağımlılıklar içerdiği durumlarda çeşitli regresyon görevlerine uygulanabilen kullanışlı bir makine öğrenimi yöntemidir.
2.2.1.1. AdaBoostRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.AdaBoostRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training AdaBoostRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"
# create an AdaBoostRegressor model
regression_model = AdaBoostRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python AdaBoostRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9991257208809748 Python Mean Absolute Error: 2.3678022748065457 Python Mean Squared Error: 11.569124350863143 Python Python AdaBoostRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9991257199849699 Python Mean Absolute Error: 2.36780399225718 Python Mean Squared Error: 11.569136207480646 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python AdaBoostRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx
Burada model, float ve double için ONNX modellerine aktarılmıştır. ONNX float modeli başarıyla yürütülürken, double modelinde yürütme hatası vardır (Errors sekmesindeki hatalar):
AdaBoostRegressor.py started AdaBoostRegressor.py 1 1 Traceback (most recent call last): AdaBoostRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) AdaBoostRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx failed:Type Error: onnxruntime_inference_collection.py 424 1 AdaBoostRegressor.py finished in 3207 ms 5 1
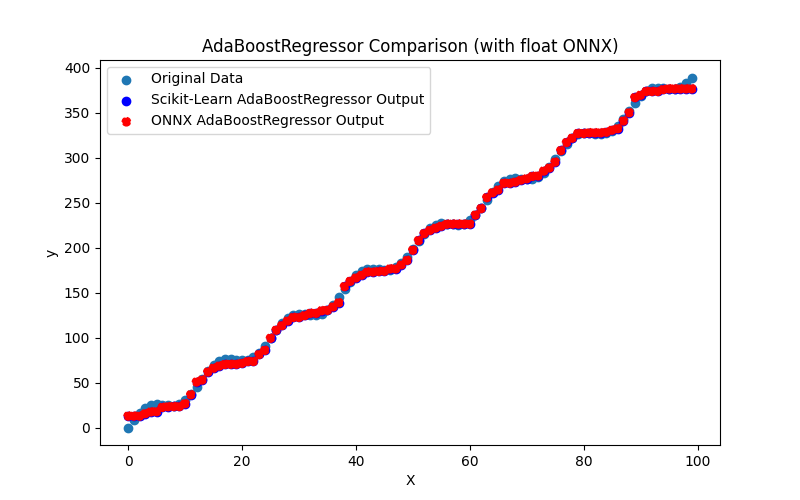
Şekil 100. AdaBoostRegressor.py sonuçları (float ONNX)
2.2.1.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen adaboost_regressor_float.onnx ve adaboost_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| AdaBoostRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "AdaBoostRegressor" #define ONNXFilenameFloat "adaboost_regressor_float.onnx" #define ONNXFilenameDouble "adaboost_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX float: AdaBoostRegressor (adaboost_regressor_float.onnx) AdaBoostRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9991257199849699 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 2.3678039922571803 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Squared Error: 11.5691362074806463 AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX double: AdaBoostRegressor (adaboost_regressor_double.onnx) AdaBoostRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type parameter (T) of Optype (Mul) bound to different types (tensor(float) and tensor(double) in node (Mul).'), inspect code 'Scripts\Regression\AdaBoostRegressor.mq5' (133:16) AdaBoostRegressor (EURUSD,H1) model_name=AdaBoostRegressor OnnxCreate error 5800ONNX float modeli başarıyla yürütülürken, double modelinde yürütme hatası vardır.
2.2.1.3. adaboost_regressor_float.onnx ve adaboost_regressor_double.onnx modellerinin ONNX gösterimi
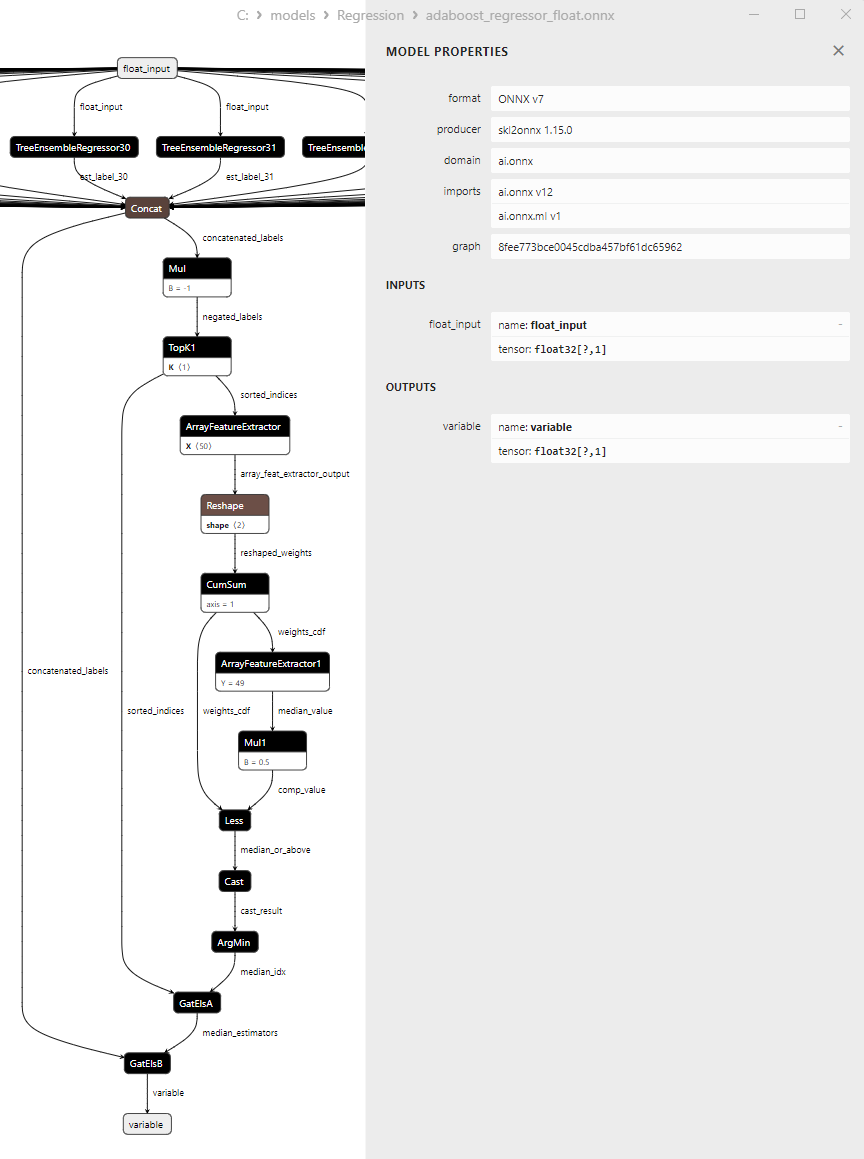
Şekil 101. Netron'da adaboost_regressor_float.onnx modelinin ONNX gösterimi
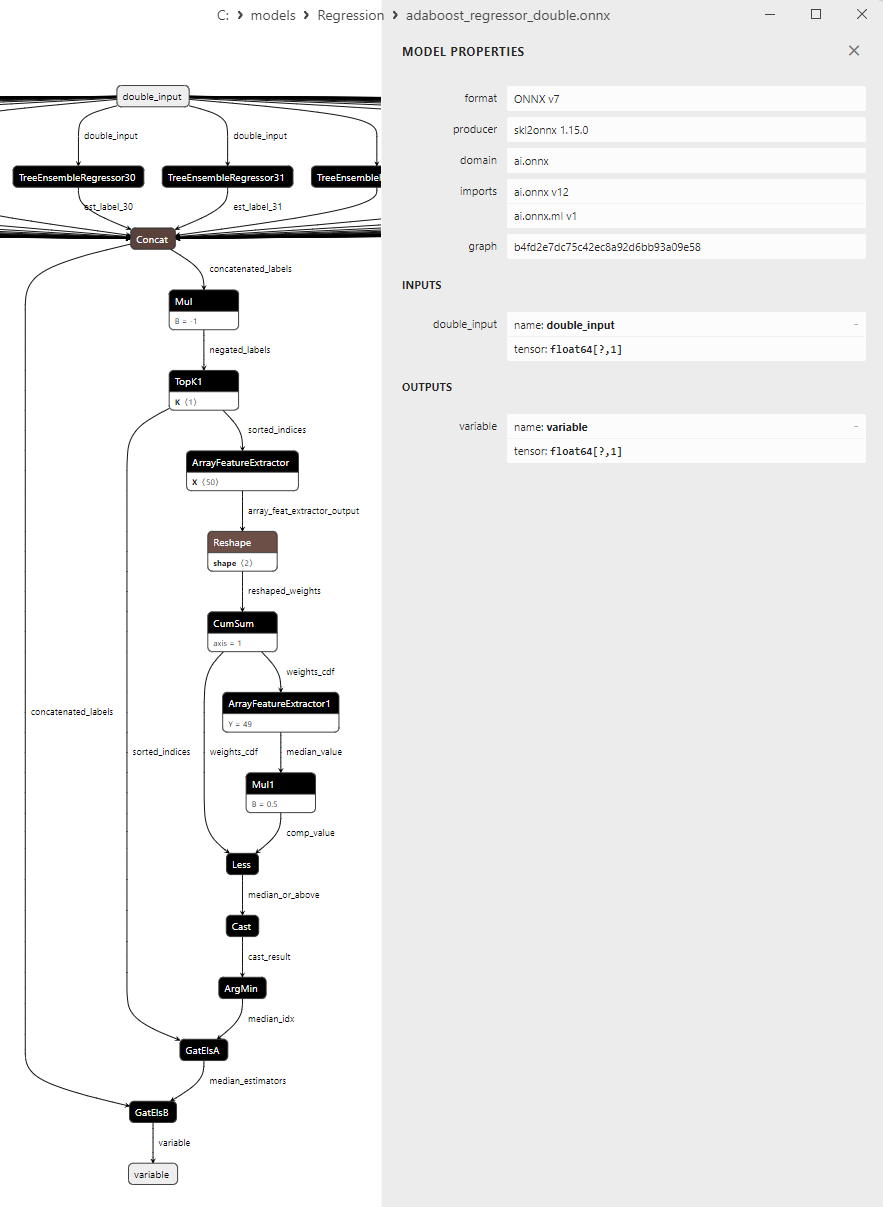
Şekil 102. Netron'da adaboost_regressor_double.onnx modelinin ONNX gösterimi
2.2.2. sklearn.linear_model.BaggingRegressor
BaggingRegressor, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir.
Birden fazla temel regresyon modeli oluşturmayı ve daha istikrarlı ve doğru bir sonuç elde etmek için tahminlerini birleştirmeyi içeren "torbalama" (Bootstrap Aggregating) fikrine dayanan bir topluluk yöntemini temsil eder.
BaggingRegressor nasıl çalışır?
- Orijinal veri kümesi: Özellikleri (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişkenleri (tahmin etmeyi amaçladığımız bağımlı değişkenler) içeren orijinal veri kümesi ile başlar.
- Alt kümelerin oluşturulması: BaggingRegressor, orijinal verilerden rastgele birkaç alt küme (değiştirmeli örneklemler) oluşturur. Her bir alt küme, orijinal verilerden rastgele bir gözlem kümesi içerir.
- Temel regresyon modellerinin eğitimi: Her bir alt küme için BaggingRegressor ayrı bir temel regresyon modeli oluşturur (örneğin, karar ağacı, rastgele orman, lineer regresyon modeli vb.).
- Temel modellerden tahminler: Her bir temel model, ilgili alt kümeye dayalı olarak hedef değişkeni tahmin etmek için kullanılır.
- Ortalama veya kombinasyon: BaggingRegressor, nihai regresyon tahminini elde etmek için tüm temel modellerin tahminlerinin ortalamasını alır veya birleştirir.
BaggingRegressor'ın avantajları:
- Varyans azaltma: BaggingRegressor modelin varyansını azaltarak verilerdeki dalgalanmalara karşı daha dayanıklı olmasını sağlar.
- Aşırı uyum azaltma: Model farklı veri alt kümeleri üzerinde eğitildiğinden, BaggingRegressor genellikle aşırı uyum riskini azaltır.
- Geliştirilmiş genelleme: BaggingRegressor, birden fazla modelden gelen tahminleri birleştirerek tipik olarak daha doğru ve istikrarlı tahminler sağlar.
- Geniş temel model yelpazesi: BaggingRegressor farklı türde temel regresyon modelleri kullanabilir, bu da onu esnek bir yöntem haline getirir.
BaggingRegressor'ın sınırlamaları:
- Temel model veriler üzerinde halihazırda iyi performans gösterdiğinde her zaman performansı artırma yeteneğine sahip değildir.
- BaggingRegressor, tek bir modelin eğitilmesine kıyasla daha fazla hesaplama kaynağı ve zaman gerektirebilir.
BaggingRegressor, özellikle gürültülü veriler ve gelişmiş tahmin kararlılığı ihtiyacı ile regresyon görevlerinde faydalı olabilecek güçlü bir makine öğrenimi yöntemidir.
2.2.2.1. BaggingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.BaggingRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training BaggingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"
# create a Bagging Regressor model
regression_model = BaggingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python Python BaggingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998128324923137 Python Mean Absolute Error: 1.0257279210387649 Python Mean Squared Error: 2.4767424083953005 Python Python BaggingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998128317934672 Python Mean Absolute Error: 1.0257282792130034 Python Mean Squared Error: 2.4767516560614187 Python R^2 matching decimal laces: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python BaggingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx
Errors sekmesi:
BaggingRegressor.py started BaggingRegressor.py 1 1 Traceback (most recent call last): BaggingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) BaggingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx failed:Type Error: T onnxruntime_inference_collection.py 424 1 BaggingRegressor.py finished in 3173 ms 5 1
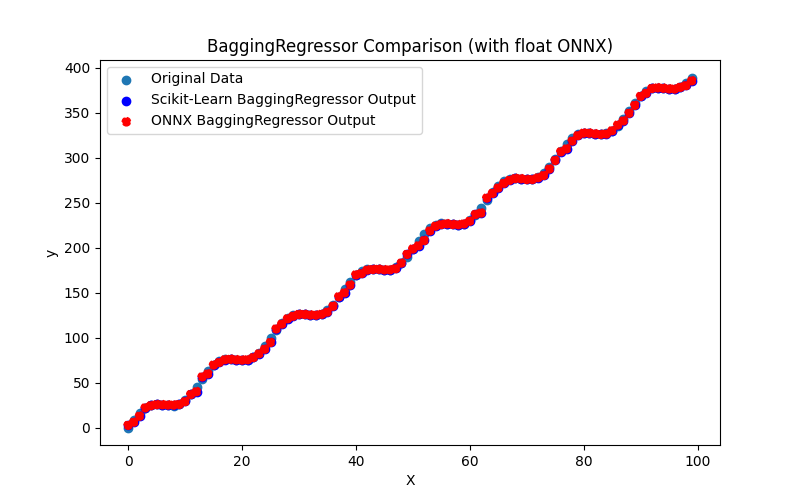
Şekil 103. BaggingRegressor.py sonuçları (float ONNX)
2.2.2.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen bagging_regressor_float.onnx ve bagging_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| BaggingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BaggingRegressor" #define ONNXFilenameFloat "bagging_regressor_float.onnx" #define ONNXFilenameDouble "bagging_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
BaggingRegressor (EURUSD,H1) Testing ONNX float: BaggingRegressor (bagging_regressor_float.onnx) BaggingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998128317934672 BaggingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.0257282792130034 BaggingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2.4767516560614196 BaggingRegressor (EURUSD,H1) BaggingRegressor (EURUSD,H1) Testing ONNX double: BaggingRegressor (bagging_regressor_double.onnx) BaggingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (ReduceMean) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\BaggingRegressor.mq5' (133:16) BaggingRegressor (EURUSD,H1) model_name=BaggingRegressor OnnxCreate error 5800
float cinsinden hesaplanan ONNX modeli normal şekilde yürütüldü, ancak model double cinsinden yürütülürken bir hata oluştu.
2.2.2.3. bagging_regressor_float.onnx ve bagging_regressor_double.onnx modellerinin ONNX gösterimi
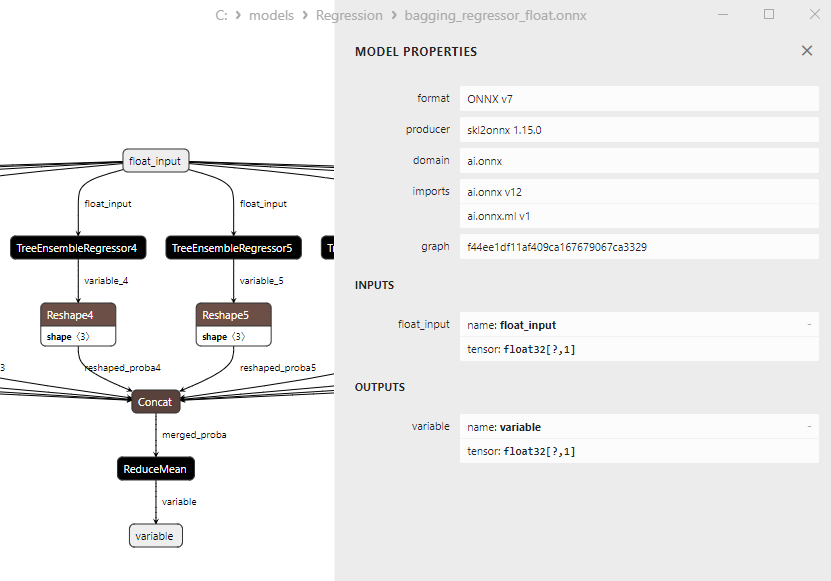
Şekil 104. Netron'da bagging_regressor_float.onnx modelinin ONNX gösterimi
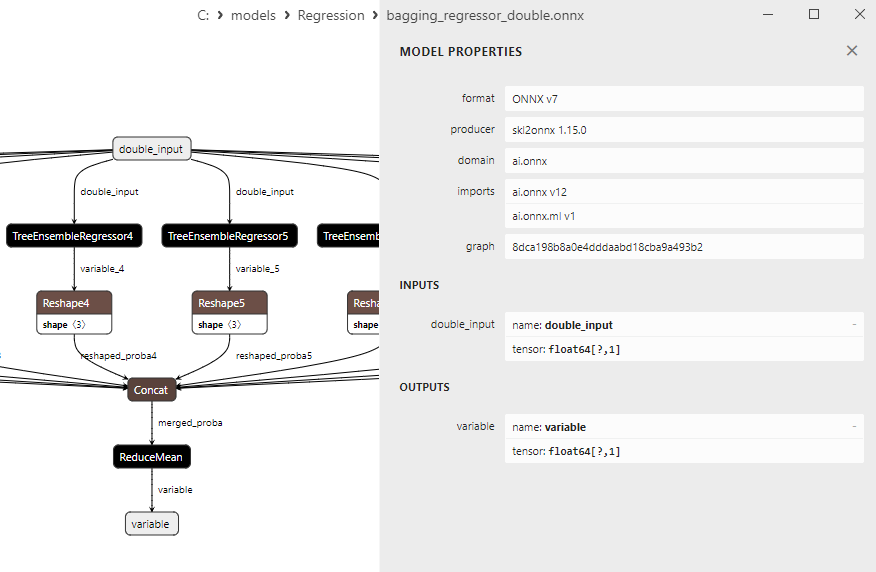
Şekil 105. Netron'da bagging_regressor_double.onnx modelinin ONNX gösterimi
2.2.3. sklearn.linear_model.DecisionTreeRegressor
DecisionTreeRegressor, regresyon görevleri için kullanılan, bir dizi özelliğe (bağımsız değişkenler) dayalı olarak hedef değişkenin sayısal değerlerini tahmin eden bir makine öğrenimi yöntemidir.
Bu yöntem, özellik uzayını aralıklara bölen ve her aralık için hedef değişkenin değerini tahmin eden karar ağaçları oluşturmaya dayanır.
DecisionTreeRegressor'ın çalışma prensibi:
- Yapıma başlama: Özellikleri (bağımsız değişkenler) ve hedef değişkenin karşılık gelen değerlerini içeren başlangıç veri kümesi ile başlar.
- Özellik seçimi ve bölme: Karar ağacı, verileri iki veya daha fazla alt gruba ayıran bir özellik ve bir eşik değeri seçer. Bu bölme işlemi, her bir alt grup içindeki ortalama karesel hatayı (hedef değişkenin tahmin edilen ve gerçek değerleri arasındaki ortalama karesel sapma) en aza indirmek için gerçekleştirilir.
- Yinelemeli yapım: Özellik seçimi ve bölme işlemi her alt grup için tekrarlanarak alt ağaçlar oluşturulur. Bu işlem, maksimum ağaç derinliği veya bir düğümdeki minimum örneklem sayısı gibi belirli durma kriterleri karşılanana kadar yinelemeli olarak gerçekleşir.
- Yaprak düğümleri: Durma kriterleri karşılandığında, belirli bir yaprak düğüme düşen örneklemler için hedef değişkenin sayısal değerlerini tahmin eden yaprak düğümler oluşturulur.
- Tahmin: Yeni veriler için karar ağacı uygulanır ve yeni gözlemler, hedef değişkenin sayısal değerini tahmin eden bir yaprak düğüme ulaşana kadar ağacı dolaşır.
DecisionTreeRegressor'ın avantajları:
- Yorumlanabilirlik: Karar ağaçlarının anlaşılması ve görselleştirilmesi kolaydır, bu da onları model karar verme sürecini açıklamak için kullanışlı hale getirir.
- Aykırı değer sağlamlığı: Karar ağaçları veri aykırı değerlerine karşı dayanıklı olabilir.
- Hem sayısal hem de kategorik verilerin işlenmesi: Karar ağaçları, ek bir ön işlemeye gerek kalmadan hem sayısal hem de kategorik özellikleri işleyebilir.
- Otomatik özellik seçimi: Ağaçlar, daha az ilgili olanları göz ardı ederek önemli özellikleri otomatik olarak seçebilir.
DecisionTreeRegressor'ın sınırlamaları:
- Aşırı uyum zafiyeti: Karar ağaçları, özellikle çok derin olduklarında aşırı uyum sağlamaya eğilimli olabilirler.
- Genelleme sorunları: Karar ağaçları, eğitim setinde yer almayan verilere iyi genelleme yapamayabilir.
- Her zaman optimum bir seçim değildir: Bazı durumlarda, lineer regresyon veya k-Nearest Neighbors gibi diğer regresyon yöntemleri daha iyi performans gösterebilir.
DecisionTreeRegressor, özellikle modelin karar verme mantığını anlamak ve süreci görselleştirmek çok önemli olduğunda, regresyon görevleri için değerli bir yöntemdir.
2.2.3.1. DecisionTreeRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.linear_model.DecisionTreeRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training DecisionTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"
# create a Decision Tree Regressor model
regression_model = DecisionTreeRegressor()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python DecisionTreeRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python Python DecisionTreeRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python DecisionTreeRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx
Errors sekmesi:
DecisionTreeRegressor.py started DecisionTreeRegressor.py 1 1 Traceback (most recent call last): DecisionTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) DecisionTreeRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 DecisionTreeRegressor.py finished in 2957 ms 5 1
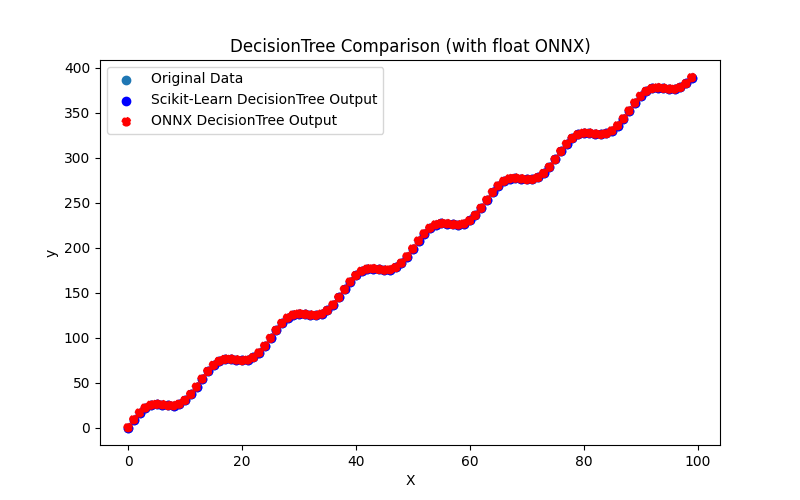
Şekil 106. DecisionTreeRegressor.py sonuçları (float ONNX)
2.2.3.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen decision_tree_regressor_float.onnx ve decision_tree_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| DecisionTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "DecisionTreeRegressor" #define ONNXFilenameFloat "decision_tree_regressor_float.onnx" #define ONNXFilenameDouble "decision_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
DecisionTreeRegressor (EURUSD,H1) Testing ONNX float: DecisionTreeRegressor (decision_tree_regressor_float.onnx) DecisionTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 DecisionTreeRegressor (EURUSD,H1) DecisionTreeRegressor (EURUSD,H1) Testing ONNX double: DecisionTreeRegressor (decision_tree_regressor_double.onnx) DecisionTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\DecisionTreeRegressor.mq5' (133:16) DecisionTreeRegressor (EURUSD,H1) model_name=DecisionTreeRegressor OnnxCreate error 5800
float cinsinden hesaplanan ONNX modeli normal şekilde yürütüldü, ancak model double cinsinden yürütülürken bir hata oluştu.
2.2.3.3. decision_tree_regressor_float.onnx ve decision_tree_regressor_double.onnx modellerinin ONNX gösterimi
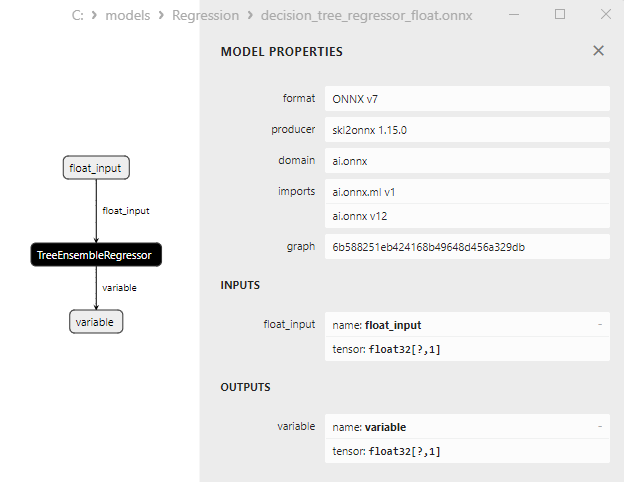
Şekil 107. Netron'da decision_tree_regressor_float.onnx modelinin ONNX gösterimi
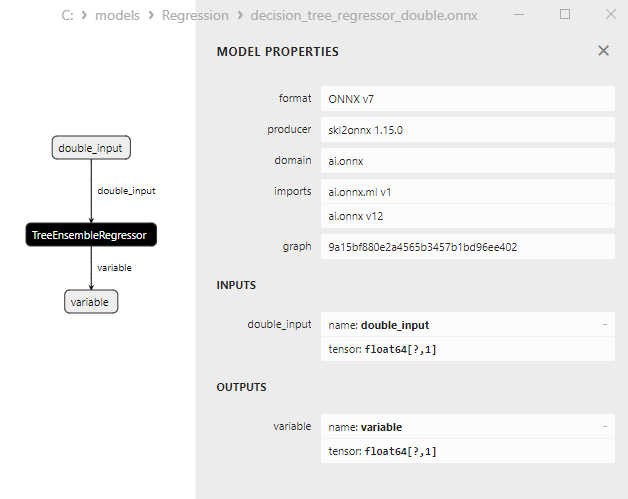
Şekil 108. Netron'da decision_tree_regressor_double.onnx modelinin ONNX gösterimi
2.2.4. sklearn.tree.ExtraTreeRegressor
ExtraTreeRegressor veya Extremely Randomized Trees Regressor, karar ağaçlarına dayalı bir regresyon topluluğu yöntemidir.
Bu yöntem rastgele ormanların bir varyasyonudur ve her ağaç düğümü için en iyi bölünmeyi seçmek yerine, her düğüm için rastgele bölünmeler kullanması bakımından farklılık gösterir. Bu, daha rastgele ve daha hızlı olmasını sağlar, bu da belirli durumlarda avantajlı olabilir.
ExtraTreeRegressor'ın çalışma prensibi:
- Yapıma başlama: Özellikleri (bağımsız değişkenler) ve hedef değişkenin karşılık gelen değerlerini içeren başlangıç veri kümesi ile başlar.
- Bölünmelerde rastgelelik: En iyi bölünmenin seçildiği normal karar ağaçlarının aksine, ExtraTreeRegressor ağaç düğümlerini bölmek için rastgele eşik değerleri kullanır. Bu, bölme işlemini daha rastgele ve aşırı uyuma daha az eğilimli hale getirir.
- Ağaç yapımı: Ağaç, düğümleri rastgele özelliklere ve eşik değerlerine göre bölerek oluşturulur. Bu işlem, maksimum ağaç derinliği veya bir düğümdeki minimum örneklem sayısı gibi belirli durma kriterleri karşılanana kadar devam eder.
- Ağaç topluluğu: ExtraTreeRegressor, sayısı "n_estimators" hiperparametresi tarafından kontrol edilen bu türden birden fazla rastgele ağaç oluşturur.
- Tahmin: Yeni veriler için hedef değişkeni tahmin etmek amacıyla ExtraTreeRegressor, topluluktaki tüm ağaçların tahminlerinin ortalamasını alır.
ExtraTreeRegressor'ın avantajları:
- Aşırı uyumda azalma: Rastgele düğüm bölünmeleri kullanmak, yöntemi normal karar ağaçlarına kıyasla aşırı uyuma daha az eğilimli hale getirir.
- Yüksek paralelleştirme: Ağaçlar bağımsız olarak inşa edildiğinden, ExtraTreeRegressor birden fazla işlemcide eğitim için kolayca paralelleştirilebilir.
- Hızlı eğitim: Gradyan artırma gibi diğer bazı yöntemlerle karşılaştırıldığında, ExtraTreeRegressor daha hızlı eğitilebilir.
ExtraTreeRegressor'ı sınırlamaları:
- Daha az doğru olabilir: Bazı durumlarda, özellikle küçük veri kümelerinde, ExtraTreeRegressor daha karmaşık yöntemlere kıyasla daha az doğru olabilir.
- Daha az yorumlanabilir: Lineer modeller, karar ağaçları ve diğer daha basit yöntemlerle karşılaştırıldığında, ExtraTreeRegressor tipik olarak daha az yorumlanabilirdir.
ExtraTreeRegressor, aşırı uyumu azaltmanın ve hızlı eğitimin gerekli olduğu durumlarda regresyon için yararlı bir yöntem olabilir.
2.2.4.1. ExtraTreeRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.tree.ExtraTreeRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training ExtraTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"
# create an ExtraTreeRegressor model
regression_model = ExtraTreeRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
2023.10.30 14:40:57.665 Python ExtraTreeRegressor Original model (double) 2023.10.30 14:40:57.665 Python R-squared (Coefficient of determination): 1.0 2023.10.30 14:40:57.665 Python Mean Absolute Error: 0.0 2023.10.30 14:40:57.665 Python Mean Squared Error: 0.0 2023.10.30 14:40:57.681 Python 2023.10.30 14:40:57.681 Python ExtraTreeRegressor ONNX model (float) 2023.10.30 14:40:57.681 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_float.onnx 2023.10.30 14:40:57.681 Python Information about input tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python Information about output tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python R-squared (Coefficient of determination) 0.9999999999999971 2023.10.30 14:40:57.681 Python Mean Absolute Error: 4.393654615473253e-06 2023.10.30 14:40:57.681 Python Mean Squared Error: 3.829042036424747e-11 2023.10.30 14:40:57.681 Python R^2 matching decimal places: 0 2023.10.30 14:40:57.681 Python MAE matching decimal places: 0 2023.10.30 14:40:57.681 Python MSE matching decimal places: 0 2023.10.30 14:40:57.681 Python float ONNX model precision: 0 2023.10.30 14:40:58.011 Python 2023.10.30 14:40:58.011 Python ExtraTreeRegressor ONNX model (double) 2023.10.30 14:40:58.011 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx
Errors sekmesi:
ExtraTreeRegressor.py started ExtraTreeRegressor.py 1 1 Traceback (most recent call last): ExtraTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreeRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx failed:Type Error onnxruntime_inference_collection.py 424 1 ExtraTreeRegressor.py finished in 2980 ms 5 1
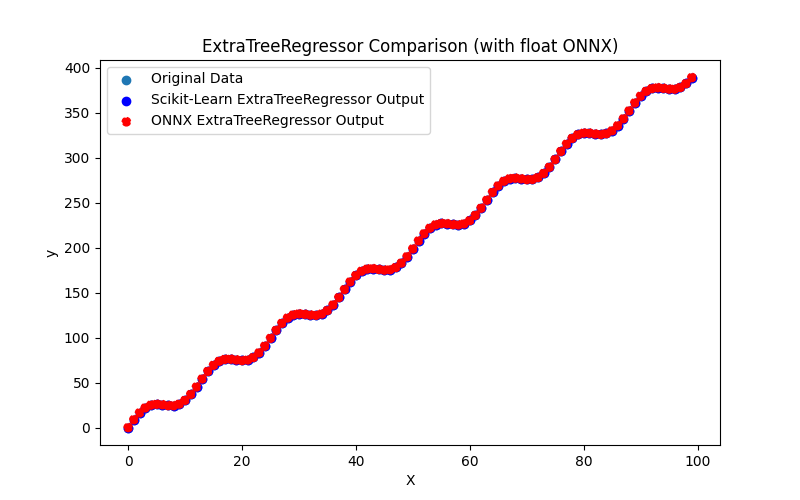
Şekil 109. ExtraTreeRegressor.py sonuçları (float ONNX)
2.2.4.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen extra_tree_regressor_float.onnx ve extra_tree_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| ExtraTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreeRegressor" #define ONNXFilenameFloat "extra_tree_regressor_float.onnx" #define ONNXFilenameDouble "extra_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
ExtraTreeRegressor (EURUSD,H1) Testing ONNX float: ExtraTreeRegressor (extra_tree_regressor_float.onnx) ExtraTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 ExtraTreeRegressor (EURUSD,H1) ExtraTreeRegressor (EURUSD,H1) Testing ONNX double: ExtraTreeRegressor (extra_tree_regressor_double.onnx) ExtraTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreeRegressor.mq5' (133:16) ExtraTreeRegressor (EURUSD,H1) model_name=ExtraTreeRegressor OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
2.2.4.3. extra_tree_regressor_float.onnx ve extra_tree_regressor_double.onnx modellerinin ONNX gösterimi
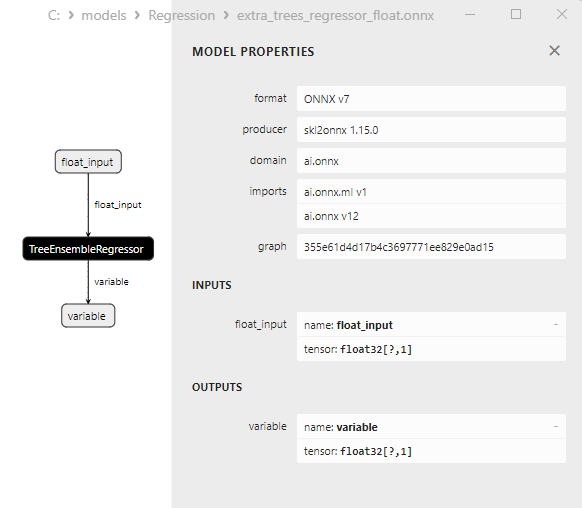
Şekil 110. Netron'da extra_tree_regressor_float.onnx modelinin ONNX gösterimi
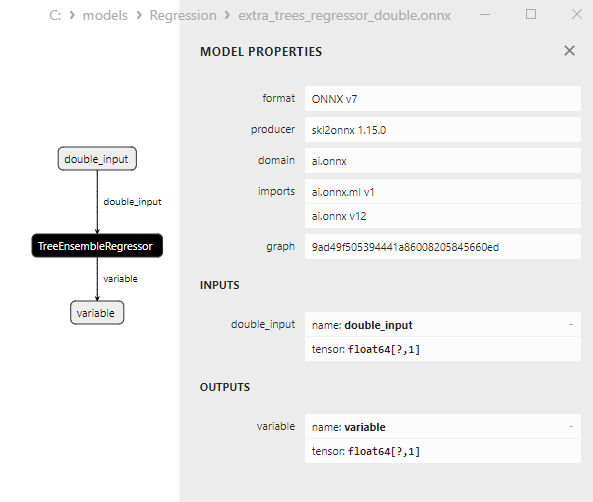
Şekil 111. Netron'da extra_tree_regressor_double.onnx extra_tree_regressor_double ONNX gösterimi
2.2.5. sklearn.ensemble.ExtraTreesRegressor
ExtraTreesRegressor (Extremely Randomized Trees Regressor), regresyon görevleri için rastgele ormanların (Random Forests) bir varyasyonunu temsil eden bir makine öğrenimi yöntemidir.
Bu yöntem, bir dizi özelliğe dayalı olarak hedef değişkenin sayısal değerlerini tahmin etmek için bir karar ağaçları topluluğu kullanır.
ExtraTreesRegressor nasıl çalışır?
- Yapıma başlama: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Bölünmelerde rastgelelik: En iyi bölünmenin seçildiği normal karar ağaçlarının aksine, ExtraTreeRegressor ağaç düğümlerini bölmek için rastgele eşik değerleri kullanır. Bu rastgelelik, bölme işlemini daha değişken ve aşırı uyuma daha az eğilimli hale getirir.
- Ağaç yapımı: ExtraTreesRegressor, toplulukta birden fazla karar ağacı oluşturur. Ağaç sayısı "n_estimators" hiperparametresi tarafından kontrol edilir. Her ağaç, rastgele bir veri alt örneklemi (değiştirme ile) ve rastgele özellik alt kümeleri üzerinde eğitilir.
- Tahmin: Yeni veriler için hedef değişkeni tahmin etmek amacıyla ExtraTreesRegressor, topluluktaki tüm ağaçların tahminlerini bir araya getirir (genellikle ortalama alır).
ExtraTreesRegressor'ın avantajları:
- Aşırı uyumda azalma: Rastgele düğüm bölünmeleri ve veri alt örneklemlerini kullanmak, yöntemi geleneksel karar ağaçlarına kıyasla aşırı uyuma daha az eğilimli hale getirir.
- Yüksek paralelleştirme: Ağaçlar bağımsız olarak oluşturulduğu için ExtraTreesRegressor birden fazla işlemci üzerinde eğitim için kolayca paralelleştirilebilir.
- Aykırı değerlere karşı dayanıklılık: Yöntem tipik olarak verilerdeki aykırı değerlere karşı dayanıklılık gösterir.
- Sayısal ve kategorik verilerin işlenmesi: ExtraTreesRegressor, ek bir ön işleme olmadan hem sayısal hem de kategorik özellikleri işleyebilir.
ExtraTreesRegressor'ın sınırlamaları:
- Hiperparametrelerde ince ayar yapılması gerekebilir: ExtraTreesRegressor genellikle varsayılan parametrelerle iyi çalışsa da, maksimum performans elde etmek için hiperparametrelerde ince ayar yapılması gerekebilir.
- Daha az yorumlanabilirlik: Diğer topluluk yöntemleri gibi, ExtraTreesRegressor da lineer regresyon gibi daha basit modellere kıyasla daha az yorumlanabilirdir.
ExtraTreesRegressor, özellikle aşırı uyumu azaltmak ve modelin genellemesini iyileştirmek gerektiğinde, çeşitli görevlerde regresyon için faydalı bir yöntem olabilir.
2.2.5.1. ExtraTreesRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.ensemble.ExtraTreesRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training ExtraTreesRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"
# create an Extra Trees Regressor model
regression_model = ExtraTreesRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python ExtraTreesRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 2.2302160118670144e-13 Python Mean Squared Error: 8.41048471722451e-26 Python Python ExtraTreesRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999998015 Python Mean Absolute Error: 3.795239380975701e-05 Python Mean Squared Error: 2.627067474763585e-09 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python ExtraTreesRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx
Errors sekmesi:
ExtraTreesRegressor.py started ExtraTreesRegressor.py 1 1 Traceback (most recent call last): ExtraTreesRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreesRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx failed:Type Erro onnxruntime_inference_collection.py 424 1 ExtraTreesRegressor.py finished in 4654 ms 5 1
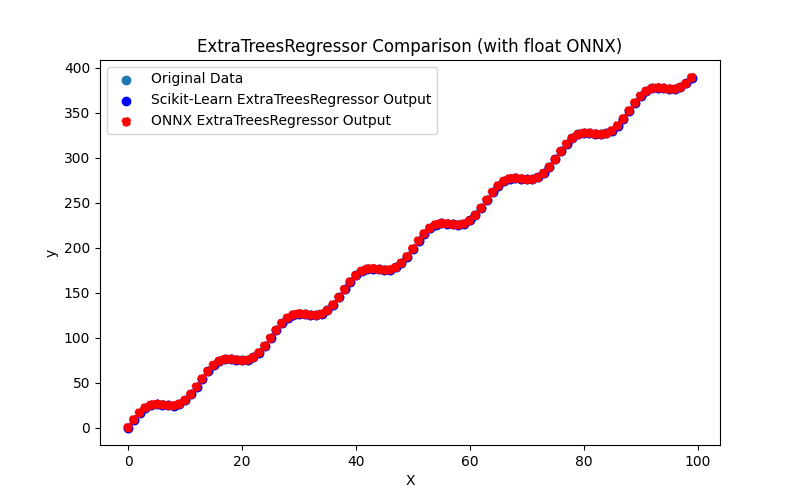
Şekil 112. ExtraTreesRegressor.py sonuçları (float ONNX)
2.2.5.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen extra_trees_regressor_float.onnx ve extra_trees_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| ExtraTreesRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreesRegressor" #define ONNXFilenameFloat "extra_trees_regressor_float.onnx" #define ONNXFilenameDouble "extra_trees_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
ExtraTreesRegressor (EURUSD,H1) Testing ONNX float: ExtraTreesRegressor (extra_trees_regressor_float.onnx) ExtraTreesRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999998015 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000379523938098 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000026270675 ExtraTreesRegressor (EURUSD,H1) ExtraTreesRegressor (EURUSD,H1) Testing ONNX double: ExtraTreesRegressor (extra_trees_regressor_double.onnx) ExtraTreesRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreesRegressor.mq5' (133:16) ExtraTreesRegressor (EURUSD,H1) model_name=ExtraTreesRegressor OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
2.2.5.3. extra_trees_regressor_float.onnx ve extra_trees_regressor_double.onnx modellerinin ONNX gösterimi
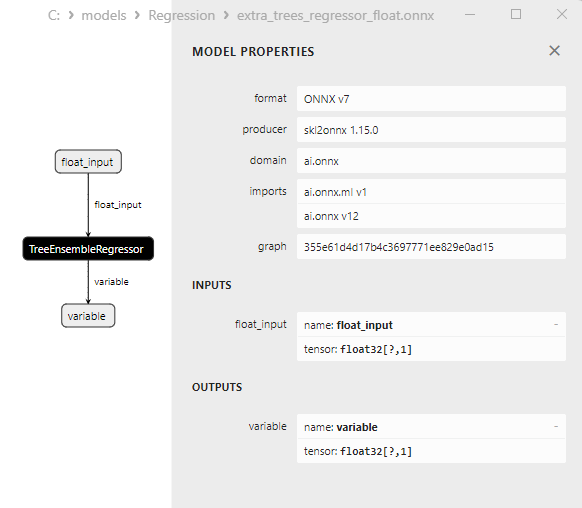
Şekil 113. Netron'da extra_trees_regressor_float.onnx modelinin ONNX gösterimi
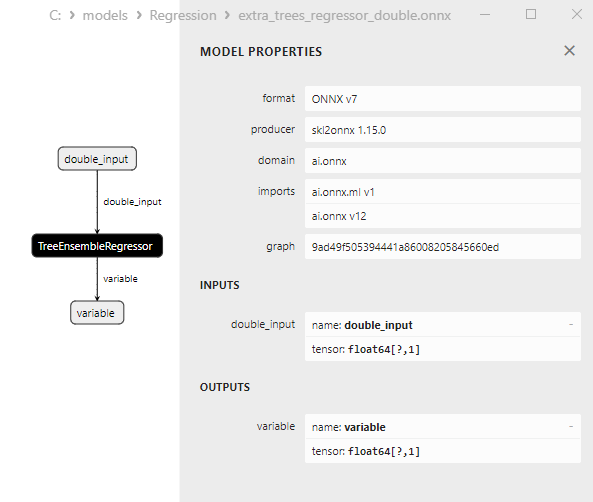
Şekil 114. Netron'da extra_trees_regressor_double.onnx modelinin ONNX gösterimi
2.2.6. sklearn.svm.NuSVR
NuSVR, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Bu yöntem destek vektör makinesine (Support Vector Machine, SVM) dayanır ancak sınıflandırma görevleri yerine regresyon görevlerine uygulanır.
NuSVR, hedef değişkenin sürekli değerlerini tahmin ederek regresyon görevlerini çözmek için tasarlanmış bir SVM varyasyonudur.
NuSVR nasıl çalışır?
- Girdi verileri: Özellikleri (bağımsız değişkenler) ve hedef değişkenin değerlerini (sürekli) içeren bir veri kümesi ile başlar.
- Çekirdek seçimi: NuSVR, verileri doğrusal bir ayırıcı hiperdüzlemin bulunabileceği daha yüksek boyutlu bir uzaya dönüştürmek için lineer, polinom veya radyal temel fonksiyon (Radial Basis Function, RBF) gibi çekirdekler kullanır.
- Nu parametresinin tanımlanması: Nu parametresi model karmaşıklığını kontrol eder ve kaç eğitim örneğinin aykırı değer olarak kabul edileceğini tanımlar. Nu değeri, destek vektörlerinin sayısını etkileyecek şekilde 0 ila 1 arasında olmalıdır.
- Destek vektörü oluşturma: NuSVR, optimum ayırıcı hiperdüzlemi, bu hiperdüzlem ile en yakın örneklem noktaları arasındaki boşluğu en üst düzeye çıkaracak şekilde bulmayı amaçlar.
- Model eğitimi: Model, regresyon hatasını en aza indirecek ve Nu parametresiyle ilişkili kısıtlamaları karşılayacak şekilde eğitilir.
- Tahmin oluşturma: Eğitimden sonra model, yeni veriler üzerinde hedef değişkenin değerlerini tahmin etmek için kullanılabilir.
NuSVR'nin avantajları:
- Aykırı değerlerin yönetilmesi: NuSVR, Nu parametresini kullanarak aykırı değerlerin kontrol edilmesini sağlar ve aykırı değer olarak kabul edilen eğitim örneklerinin sayısını düzenler.
- Çoklu çekirdek: Yöntem, karmaşık doğrusal olmayan ilişkilerin modellenmesini sağlayan çeşitli çekirdek türlerini destekler.
NuSVR'nin sınırlamaları:
- Nu parametresi seçimi: Nu parametresi için doğru değerin seçilmesi denemeler yapmayı gerektirebilir.
- Veri ölçeği hassasiyeti: NuSVR dahil olmak üzere SVM, veri ölçeğine duyarlı olabilir, bu nedenle özellik standardizasyonu veya normalizasyonu gerekli olabilir.
- Hesaplama karmaşıklığı: Büyük veri kümeleri ve karmaşık çekirdekler için NuSVR hesaplama açısından maliyetli olabilir.
NuSVR, destek vektör makinesi (Support Vector Machine, SVM) yöntemine dayalı regresyon görevleri için bir makine öğrenimi yöntemidir. Hedef değişkenin sürekli değerlerinin tahmin edilmesine izin verir ve Nu parametresini kullanarak aykırı değerleri yönetme yeteneği sağlar.
2.2.6.1. NuSVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.svm.NuSVR modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training NuSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"
# create a NuSVR model
nusvr_model = NuSVR()
# fit the model to the data
nusvr_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = nusvr_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python NuSVR Original model (double) Python R-squared (Coefficient of determination): 0.2771437770527445 Python Mean Absolute Error: 83.76666411704255 Python Mean Squared Error: 9565.381751764757 Python Python NuSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_float.onnx Python Information about input tensors in ONNX: 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.27714379657935495 Python Mean Absolute Error: 83.766663385322 Python Mean Squared Error: 9565.381493373838 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python NuSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_double.onnx
Errors sekmesi:
NuSVR.py started NuSVR.py 1 1 Traceback (most recent call last): NuSVR.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) NuSVR.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess.initialize_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 435 1 onnxruntime.capi.onnxruntime_pybind11_state.NotImplemented: [ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for SVMRegressor(1) node with name 'SVM' onnxruntime_inference_collection.py 435 1 NuSVR.py finished in 2925 ms 5 1
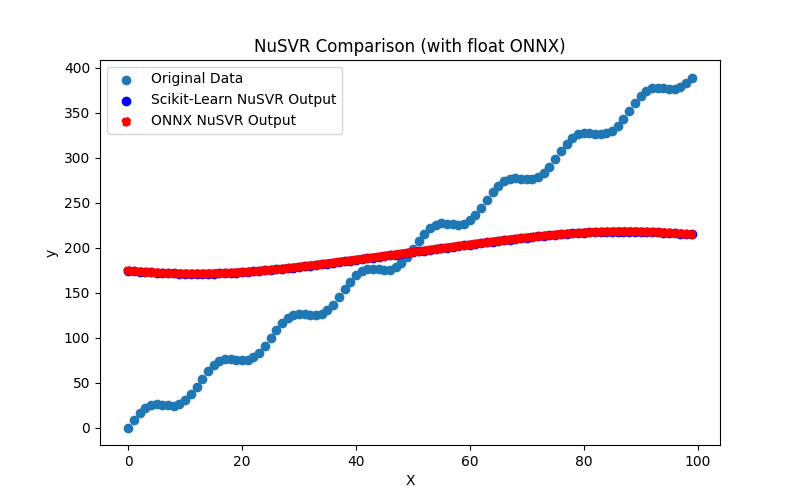
Şekil 115. NuSVR.py sonuçları (float ONNX)
2.2.6.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen nu_svr_float.onnx ve nu_svr_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| NuSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "NuSVR" #define ONNXFilenameFloat "nu_svr_float.onnx" #define ONNXFilenameDouble "nu_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
NuSVR (EURUSD,H1) Testing ONNX float: NuSVR (nu_svr_float.onnx) NuSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.2771437965793548 NuSVR (EURUSD,H1) MQL5: Mean Absolute Error: 83.7666633853219906 NuSVR (EURUSD,H1) MQL5: Mean Squared Error: 9565.3814933738358377 NuSVR (EURUSD,H1) NuSVR (EURUSD,H1) Testing ONNX double: NuSVR (nu_svr_double.onnx) NuSVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\Regression\NuSVR.mq5' (133:16) NuSVR (EURUSD,H1) model_name=NuSVR OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: NuSVR (nu_svr_float.onnx) Python Mean Absolute Error: 83.76666411704255 MQL5: Mean Absolute Error: 83.7666633853219906
2.2.6.3. nu_svr_float.onnx ve nu_svr_double.onnx modellerinin ONNX gösterimi
Şekil 116. Netron'da nu_svr_float.onnx modelinin ONNX gösterimi
Şekil 117. Netron'da nu_svr_double.onnx modelinin ONNX gösterimi
2.2.7. sklearn.ensemble.RandomForestRegressor
RandomForestRegressor, regresyon görevlerini çözmek için kullanılan bir makine öğrenimi yöntemidir.
Topluluk öğrenmesine dayalı en popüler yöntemlerden biridir ve güçlü ve sağlam regresyon modelleri oluşturmak için rastgele orman (Random Forest) algoritmasını kullanır.
RandomForestRegressor şu şekilde çalışır:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bir hedef değişken (sürekli) içeren bir veri kümesi ile başlar.
- Rastgele orman: RandomForestRegressor, regresyon görevini çözmek için bir karar ağaçları topluluğu kullanır. Ormandaki her ağaç, hedef değişken değerlerini tahmin etmek için çalışır.
- Yeniden örnekleme: Her ağaç yeniden örnekleme kullanılarak eğitilir, bu da eğitim veri setinden değiştirme ile rastgele örnekleme anlamına gelir. Bu, her ağacın öğrendiği verilerde çeşitlilik sağlar.
- Rastgele özellik seçimi: Her bir ağaç oluşturulurken, rastgele bir özellik alt kümesi de seçilerek model daha sağlam hale getirilir ve ağaçlar arasındaki korelasyonlar azaltılır.
- Tahminlerin ortalaması: Tüm ağaçlar oluşturulduktan sonra, RandomForestRegressor nihai regresyon tahminini elde etmek için tahminlerinin ortalamasını alır veya birleştirir.
RandomForestRegressor'ın avantajları:
- Güç ve sağlamlık: RandomForestRegressor, genellikle iyi performans sağlayan güçlü bir regresyon yöntemidir.
- Büyük verilerin işlenmesi: Büyük veri kümelerini iyi yönetir ve çok sayıda özelliği işleyebilir.
- Aşırı uyuma karşı direnç: Yeniden örnekleme ve rastgele özellik seçimi sayesinde, rastgele orman tipik olarak aşırı uyuma karşı dayanıklıdır.
- Özellik önemi hesaplaması: Rastgele orman, regresyon görevindeki her bir özelliğin önemi hakkında bilgi sağlayabilir.
RandomForestRegressor'ın sınırlamaları:
- Yorumlanabilirlik eksikliği: Model, lineer modellere kıyasla daha az yorumlanabilir olabilir.
- Her zaman en doğru model değildir: Bazı görevlerde, daha karmaşık topluluklar gereksiz olabilir ve lineer modeller daha uygun olabilir.
RandomForestRegressor, kararlı ve yüksek performanslı bir regresyon modeli oluşturmak için rastgele karar ağaçlarından oluşan bir topluluk kullanan regresyon görevleri için güçlü bir makine öğrenimi yöntemidir. Bu yöntem özellikle büyük veri kümelerine sahip görevler ve özellik öneminin değerlendirilmesi için kullanışlıdır.
2.2.7.1. RandomForestRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.ensemble.RandomForestRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training RandomForestRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"
# create a RandomForestRegressor model
regression_model = RandomForestRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python RandomForestRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998854509605539 Python Mean Absolute Error: 0.9186485980852603 Python Mean Squared Error: 1.5157997632401086 Python Python RandomForestRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998854516013125 Python Mean Absolute Error: 0.9186420704511761 Python Mean Squared Error: 1.515791284236419 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python RandomForestRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx
Errors sekmesi:
RandomForestRegressor.py started RandomForestRegressor.py 1 1 Traceback (most recent call last): RandomForestRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) RandomForestRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 RandomForestRegressor.py finished in 4392 ms 5 1
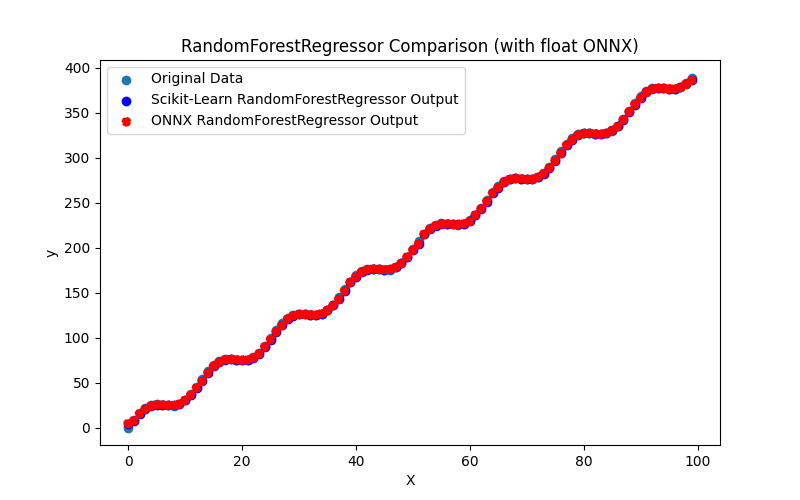
Şekil 118. RandomForestRegressor.py sonuçları (float ONNX)
2.2.7.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen random_forest_regressor_float.onnx ve random_forest_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| RandomForestRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RandomForestRegressor" #define ONNXFilenameFloat "random_forest_regressor_float.onnx" #define ONNXFilenameDouble "random_forest_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX float: RandomForestRegressor (random_forest_regressor_float.onnx) RandomForestRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998854516013125 RandomForestRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.9186420704511761 RandomForestRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1.5157912842364190 RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX double: RandomForestRegressor (random_forest_regressor_double.onnx) RandomForestRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\RandomForestRegressor.mq5' (133:16) RandomForestRegressor (EURUSD,H1) model_name=RandomForestRegressor OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
2.2.7.3. random_forest_regressor_float.onnx ve random_forest_regressor_double.onnx modellerinin ONNX gösterimi
Şekil 119. Netron'da random_forest_regressor_float.onnx modelinin ONNX gösterimi
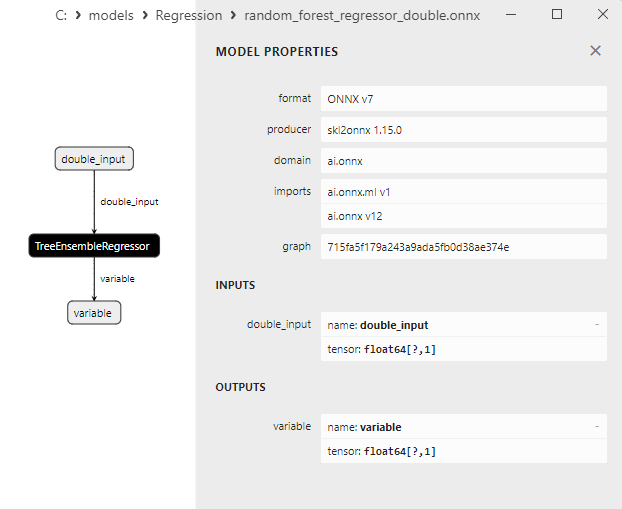
Şekil 120. Netron'da random_forest_regressor_double.onnx modelinin ONNX gösterimi
2.2.8. sklearn.ensemble.GradientBoostingRegressor
GradientBoostingRegressor, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Topluluk yöntemleri ailesinin bir parçasıdır ve zayıf modeller oluşturma ve bunları gradyan artırma kullanarak güçlü bir modelde birleştirme fikrine dayanır.
Gradyan artırma, zayıf modelleri yinelemeli olarak ekleyerek ve önceki modellerin hatalarını düzelterek modelleri iyileştirmek için kullanılan bir tekniktir.
GradientBoostingRegressor şu şekilde çalışır:
- Başlatma: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değerleri içeren orijinal veri kümesi ile başlar.
- İlk model: Genellikle basit bir regresyon modeli (örneğin karar ağacı) olarak seçilen ilk modelin orijinal veriler üzerinde eğitilmesiyle başlar.
- Kalıntılar ve anti-gradyan: Kalıntılar, yani ilk modelin tahmin edilen değerleri ile gerçek hedef değişken değerleri arasındaki fark hesaplanır. Ardından, bu kayıp fonksiyonunun anti-gradyanı hesaplanır, bu da modelin iyileştirileceği yönü gösterir.
- Sonraki modeli oluşturma: Bir sonraki model, anti-gradyanı (ilk modelin hataları) tahmin etmeye odaklanarak oluşturulur. Bu model artıklar üzerinde eğitilir ve ilk modele eklenir.
- Yinelemeler: Yeni modeller oluşturma ve kalıntıları düzeltme süreci birçok kez tekrarlanır. Her yeni model, önceki modellerin kalıntılarını dikkate alır ve tahminleri geliştirmeyi amaçlar.
- Model kombinasyonu: Tüm modellerin tahminleri, önemlerine göre ortalamaları alınarak veya ağırlıklandırılarak nihai tahminde birleştirilir.
GradientBoostingRegressor'ın avantajları:
- Yüksek performans: Gradient boosting, regresyon görevlerinde yüksek performans elde edebilen güçlü bir yöntemdir.
- Aykırı değerlere karşı dayanıklılık: Verilerdeki aykırı değerleri yönetir ve bu belirsizliği göz önünde bulundurarak modeller oluşturur.
- Otomatik özellik seçimi: Hedef değişkeni tahmin etmek için en önemli özellikleri otomatik olarak seçer.
- Çeşitli kayıp fonksiyonlarının işlenmesi: Yöntem, göreve bağlı olarak farklı kayıp fonksiyonlarının kullanılmasına izin verir.
GradientBoostingRegressor'ın sınırlamaları:
- Hiperparametre ayarlaması gerekir: Maksimum performans elde etmek için öğrenme oranı, ağaç derinliği ve model sayısı gibi hiperparametrelerin ayarlanması gerekir.
- Hesaplama açısından maliyetlidir: Gradyan artırma, özellikle büyük hacimli veriler ve çok sayıda ağaç söz konusu olduğunda hesaplama açısından maliyetli olabilir.
GradientBoostingRegressor, doğru hiperparametre ayarlamasıyla yüksek performans elde etmek için pratik görevlerde sıklıkla kullanılan güçlü bir regresyon yöntemidir.
2.2.8.1. GradientBoostingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.ensemble.GradientBoostingRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training GradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"
# create a Gradient Boosting Regressor model
regression_model = GradientBoostingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python GradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999959514652565 Python Mean Absolute Error: 0.15069342754017417 Python Mean Squared Error: 0.053573282108575676 Python Python GradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999959514739537 Python Mean Absolute Error: 0.15069457426101718 Python Mean Squared Error: 0.05357316702127665 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python GradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx
Errors sekmesi:
GradientBoostingRegressor.py started GradientBoostingRegressor.py 1 1 Traceback (most recent call last): GradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) GradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx failed:Typ onnxruntime_inference_collection.py 452 1 GradientBoostingRegressor.py finished in 3073 ms 5 1
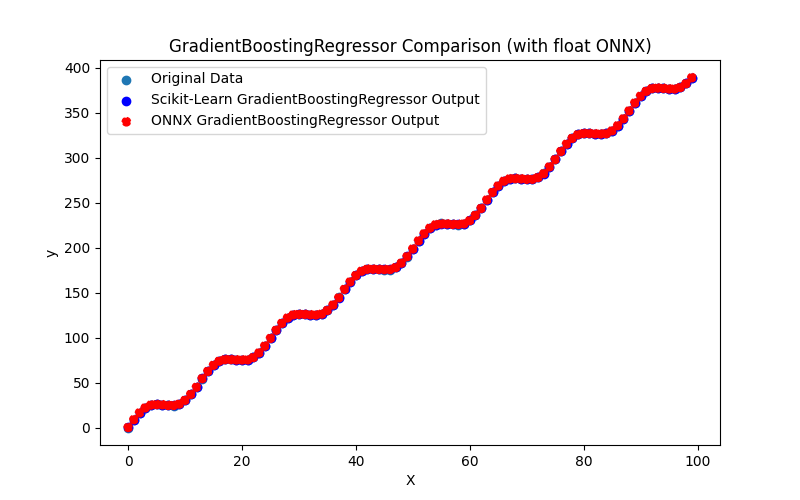
Şekil 121. GradientBoostingRegressor.py sonuçları (float ONNX)
2.2.8.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen gradient_boosting_regressor_float.onnx ve gradient_boosting_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| GradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GradientBoostingRegressor" #define ONNXFilenameFloat "gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
GradientBoostingRegressor (EURUSD,H1) Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) GradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999959514739537 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.1506945742610172 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0535731670212767 GradientBoostingRegressor (EURUSD,H1) GradientBoostingRegressor (EURUSD,H1) Testing ONNX double: GradientBoostingRegressor (gradient_boosting_regressor_double.onnx) GradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\GradientBoostingRegressor.mq5' (133:16) GradientBoostingRegressor (EURUSD,H1) model_name=GradientBoostingRegressor OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 0.15069342754017417 MQL5: Mean Absolute Error: 0.1506945742610172
ONNX float MAE'nin doğruluğu: 5 ondalık basamak.
2.2.8.3. gradient_boosting_regressor_float.onnx ve gradient_boosting_regressor_double.onnx modellerinin ONNX gösterimi
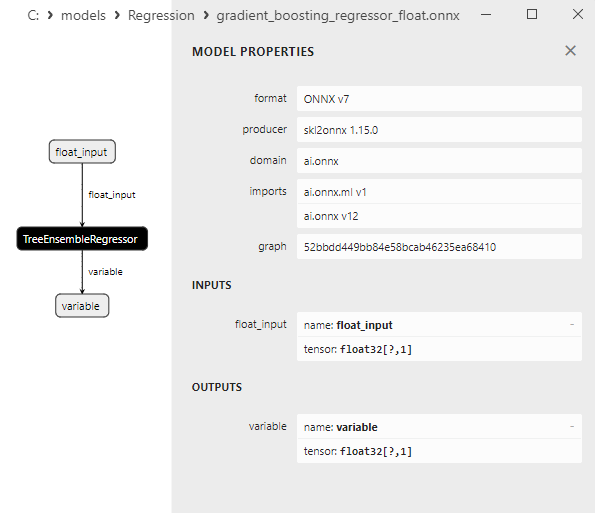
Şekil 122. Netron'da gradient_boosting_regressor_float.onnx modelinin ONNX gösterimi
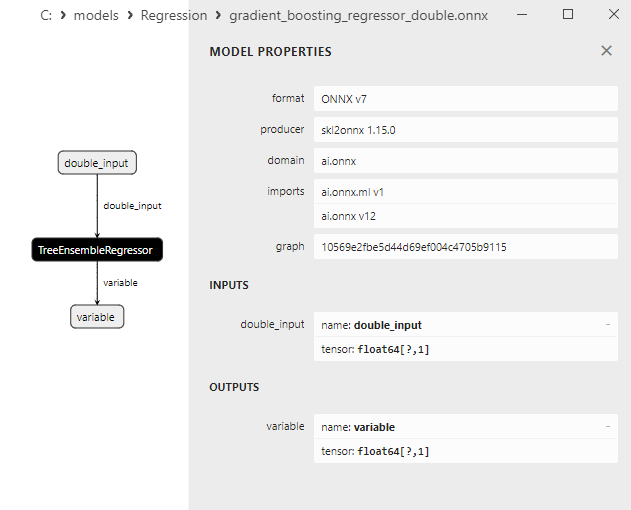
Şekil 123. Netron'da gradient_boosting_regressor_double.onnx modelinin ONNX gösterimi
2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
HistGradientBoostingRegressor, büyük veri kümeleriyle çalışmak için optimize edilmiş bir gradyan artırma varyasyonunu temsil eden bir makine öğrenimi yöntemidir.
Bu yöntem regresyon görevleri için kullanılır ve "Hist" adı, eğitim sürecini hızlandırmak için histogram tabanlı yöntemler kullandığını gösterir.
HistGradientBoostingRegressor nasıl çalışır?
- Başlatma: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değerleri içeren orijinal veri kümesi ile başlar.
- Histogram tabanlı yöntemler: HistGradientBoostingRegressor, ağaç düğümlerinde tam veri bölme yerine, verileri histogramlar şeklinde verimli bir şekilde temsil etmek için histogram tabanlı yöntemler kullanır. Bu, özellikle büyük veri kümelerinde eğitim sürecini önemli ölçüde hızlandırır.
- Temel ağaçlar oluşturma: Yöntem, verilerin histogram temsillerini kullanarak "histogram karar ağaçları" olarak adlandırılan bir dizi temel karar ağacı oluşturur. Bu ağaçlar gradyan artırmaya dayalı olarak oluşturulur ve önceki modelin kalıntılarına göre ayarlanır.
- Kademeli eğitim: HistGradientBoostingRegressor, topluluğa aşamalı olarak yeni ağaçlar ekler ve her ağaç önceki ağaçların kalıntılarını düzeltir.
- Model kombinasyonu: Temel ağaçlar oluşturulduktan sonra, nihai tahmini elde etmek için tüm ağaçlardan gelen tahminler birleştirilir.
HistGradientBoostingRegressor'ın avantajları:
- Yüksek performans: Bu yöntem, büyük hacimli verileri işlemek için optimize edilmiştir ve yüksek performans elde edebilir.
- Gürültü dayanıklılığı: HistGradientBoostingRegressor, verilerde gürültü olsa bile genellikle iyi performans gösterir.
- Yüksek boyutta verimlilik: Yöntem, çok sayıda özelliğe (yüksek boyutlu veri) sahip görevlerin üstesinden gelebilir.
- Mükemmel paralelleştirme: Eğitimi birden fazla işlemci arasında verimli bir şekilde paralelleştirebilir.
HistGradientBoostingRegressor'ın sınırlamaları:
- Hiperparametre ayarlaması gerekir: Maksimum performans elde etmek için ağaç derinliği ve model sayısı gibi hiperparametrelerin ayarlanması gerekir.
- Lineer modellere göre daha az yorumlanabilirlik: Diğer topluluk yöntemleri gibi, HistGradientBoostingRegressor da lineer regresyon gibi daha basit modellere göre daha az yorumlanabilirdir.
HistGradientBoostingRegressor, yüksek performans ve yüksek boyutlu veri verimliliğinin gerekli olduğu büyük veri kümelerini içeren görevler için yararlı bir regresyon yöntemi olabilir.
2.2.9.1. HistGradientBoostingRegressor modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.ensemble.HistGradientBoostingRegressor modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training HistGradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"
# create a Histogram-Based Gradient Boosting Regressor model
hist_gradient_boosting_model = HistGradientBoostingRegressor()
# fit the model to the data
hist_gradient_boosting_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = hist_gradient_boosting_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python HistGradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9833421349506157 Python Mean Absolute Error: 9.070567104488434 Python Mean Squared Error: 220.4295035561544 Python Python HistGradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9833421351962779 Python Mean Absolute Error: 9.07056497799043 Python Mean Squared Error: 220.42950030536645 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python HistGradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx
Errors sekmesi:
HistGradientBoostingRegressor.py started HistGradientBoostingRegressor.py 1 1 Traceback (most recent call last): HistGradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) HistGradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx faile onnxruntime_inference_collection.py 452 1 HistGradientBoostingRegressor.py finished in 3100 ms 5 1
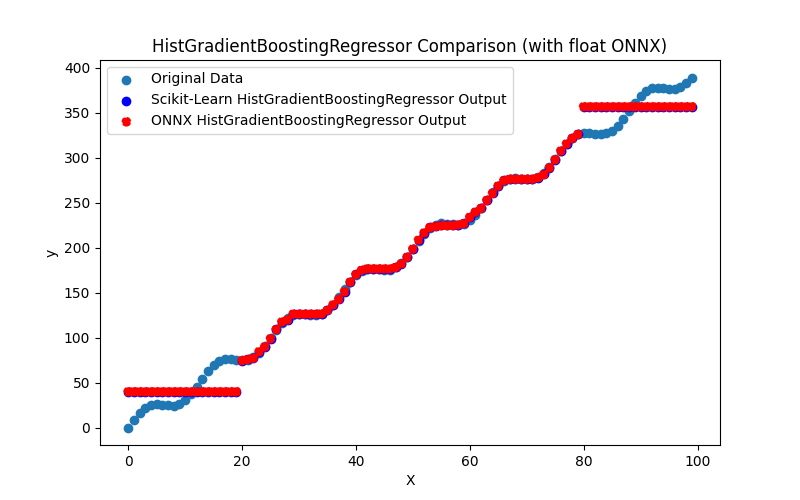
Şekil 124. HistGradientBoostingRegressor.py sonuçları (float ONNX)
2.2.9.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen hist_gradient_boosting_regressor_float.onnx ve hist_gradient_boosting_regressor_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| HistGradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HistGradientBoostingRegressor" #define ONNXFilenameFloat "hist_gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "hist_gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) HistGradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9833421351962779 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.0705649779904292 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 220.4295003053665312 HistGradientBoostingRegressor (EURUSD,H1) HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX double: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_double.onnx) HistGradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\HistGradientBoostingRegressor.mq5' (133:16) HistGradientBoostingRegressor (EURUSD,H1) model_name=HistGradientBoostingRegressor OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 9.070567104488434 MQL5: Mean Absolute Error: 9.0705649779904292
ONNX float MAE'nin doğruluğu: 5 ondalık basamak.
2.2.9.3. hist_gradient_boosting_regressor_float.onnx ve hist_gradient_boosting_regressor_double.onnx modellerinin ONNX gösterimi
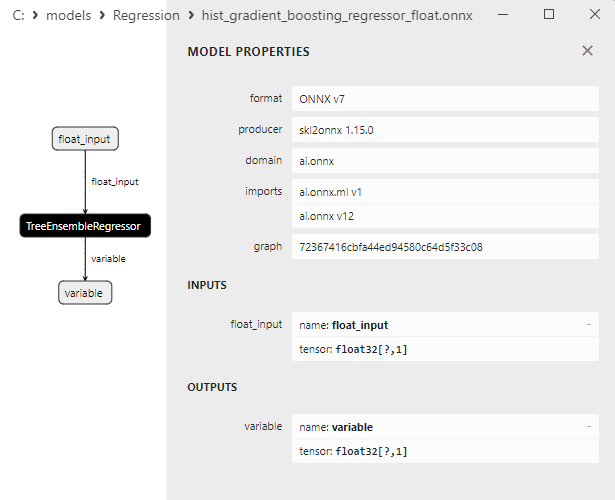
Şekil 125. Netron'da hist_gradient_boosting_regressor_float.onnx modelinin ONNX gösterimi
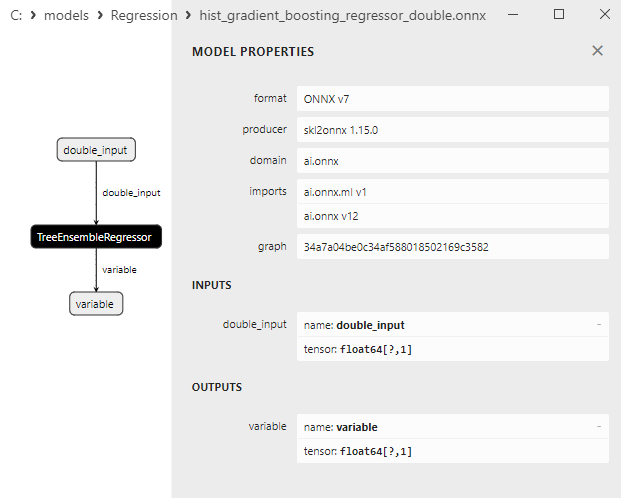
Şekil 126. Netron'da hist_gradient_boosting_regressor_double.onnx modelinin ONNX gösterimi
2.2.10. sklearn.svm.SVR
SVR (Support Vector Regression), regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Sınıflandırma için Support Vector Machine (SVM) ile aynı konsepte dayanır, ancak regresyon için uyarlanmıştır. SVR'nin birincil amacı, veri noktaları ile regresyon doğrusu arasındaki maksimum ortalama mesafeye dayanarak hedef değişkenin sürekli değerlerini tahmin etmektir.
SVR nasıl çalışır?
- Sınır tanımı: SVM'ye benzer şekilde SVR, farklı veri noktası sınıflarını ayıran sınırlar oluşturur. SVR, sınıf ayrımı yerine veri noktalarının etrafında bir "tüp" oluşturmayı amaçlar ve tüpün genişliği bir hiperparametre tarafından kontrol edilir.
- Hedef değişken ve kayıp fonksiyonu: SVR, sınıflandırmada olduğu gibi sınıfları kullanmak yerine hedef değişkenin sürekli değerleriyle ilgilenir. Tahmin edilen ve gerçek değerler arasındaki karesel fark gibi bir kayıp fonksiyonu kullanılarak ölçülen tahmin hatasını en aza indirir.
- Düzenlileştirme: SVR ayrıca model karmaşıklığını kontrol etmeye ve aşırı uyumu önlemeye yardımcı olan düzenlileştirmeyi de destekler.
- Çekirdek fonksiyonları: SVR tipik olarak, özellikler ve hedef değişken arasındaki doğrusal olmayan bağımlılıkları işlemesine izin veren çekirdek fonksiyonlarını kullanır. Popüler çekirdek fonksiyonları arasında radyal temel fonksiyon (RBF), polinom ve lineer fonksiyonlar bulunur.
SVR'nin avantajları:
- Aykırı değerlere karşı dayanıklılık: SVR, tahmin hatasını en aza indirmeyi amaçladığı için verilerdeki aykırı değerlerle başa çıkabilir.
- Doğrusal olmayan bağımlılıklar için destek: Kernel fonksiyonlarının kullanımı, SVR'nin özellikler ve hedef değişken arasındaki karmaşık ve doğrusal olmayan bağımlılıkları modellemesini sağlar.
- Yüksek tahmin kalitesi: Kesin tahminler gerektiren regresyon görevlerinde SVR yüksek kaliteli sonuçlar sağlayabilir.
SVR'nin sınırlamaları:
- Hiperparametrelere duyarlılık: Çekirdek fonksiyonunun ve tüp genişliği (hiperparametreler) gibi model parametrelerinin seçilmesi, dikkatli bir ayarlama ve optimizasyon gerektirebilir.
- Hesaplama karmaşıklığı: SVR modelinin eğitimi, özellikle karmaşık çekirdek fonksiyonları ve büyük veri kümeleri kullanıldığında, hesaplama açısından yoğun olabilir.
SVR, tahmin hatalarını en aza indirmek için veri noktaları etrafında bir "tüp" oluşturma fikrine dayanan regresyon görevleri için bir makine öğrenimi yöntemidir. Aykırı değerlere karşı sağlamlık ve doğrusal olmayan bağımlılıkları işleme yeteneği sergileyerek çeşitli regresyon görevlerinde yararlı olmasını sağlar.
2.2.10.1. SVR modelini oluşturmak ve float ve double için ONNX'e aktarmak için kod
Bu kod sklearn.svm.SVR modelini oluşturur, sentetik veriler üzerinde eğitir, modeli ONNX formatında kaydeder ve hem float hem de double girdi verilerini kullanarak tahminler gerçekleştirir. Ayrıca hem orijinal modelin hem de ONNX'e aktarılan modellerin doğruluğunu değerlendirir.
# The code demonstrates the process of training SVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "SVR"
onnx_model_filename = data_path + "svr"
# create an SVR model
regression_model = SVR()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python SVR Original model (double) Python R-squared (Coefficient of determination): 0.398243655775797 Python Mean Absolute Error: 73.63683696034649 Python Mean Squared Error: 7962.89631509593 Python Python SVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.3982436352100983 Python Mean Absolute Error: 73.63683840363255 Python Mean Squared Error: 7962.896587236852 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python SVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_double.onnx
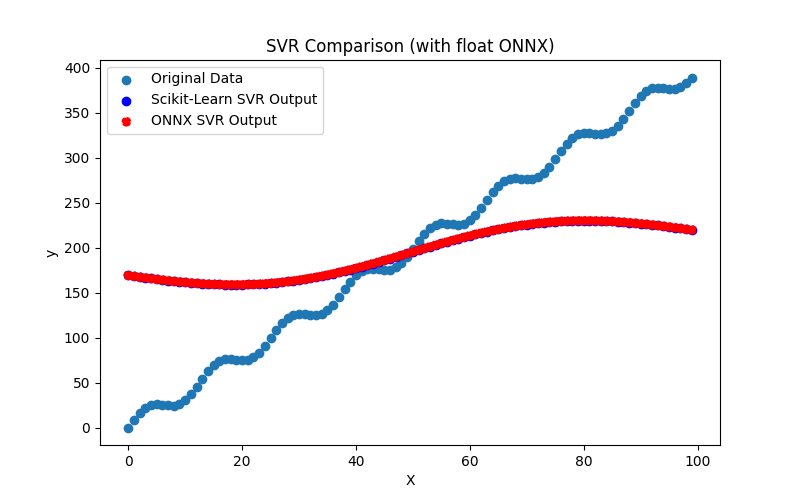
Şekil 127. SVR.py sonuçları (float ONNX)
2.2.10.2. ONNX modellerini yürütmek için MQL5 kodu
Bu kod, kaydedilen svr_float.onnx ve svr_double.onnx ONNX modellerini MQL5'te çalıştırır ve regresyon metriklerinin kullanımını gösterir.
//+------------------------------------------------------------------+ //| SVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SVR" #define ONNXFilenameFloat "svr_float.onnx" #define ONNXFilenameDouble "svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Çıktı:
SVR (EURUSD,H1) Testing ONNX float: SVR (svr_float.onnx) SVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.3982436352100981 SVR (EURUSD,H1) MQL5: Mean Absolute Error: 73.6368384036325523 SVR (EURUSD,H1) MQL5: Mean Squared Error: 7962.8965872368517012 SVR (EURUSD,H1) SVR (EURUSD,H1) Testing ONNX double: SVR (svr_double.onnx) SVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\R\SVR.mq5' (133:16) SVR (EURUSD,H1) model_name=SVR OnnxCreate error 5800
float ONNX modeli normal şekilde yürütüldü, ancak double cinsinden ONNX modeli olarak yürütülürken bir hata oluştu.
Python'daki orijinal double hassasiyetli model ile karşılaştırma:
Testing ONNX float: SVR (svr_float.onnx) Python Mean Absolute Error: 73.63683696034649 MQL5: Mean Absolute Error: 73.6368384036325523
ONNX float MAE'nin doğruluğu: 5 ondalık basamak.
2.2.10.3. svr_float.onnx ve svr_double.onnx modellerinin ONNX gösterimi
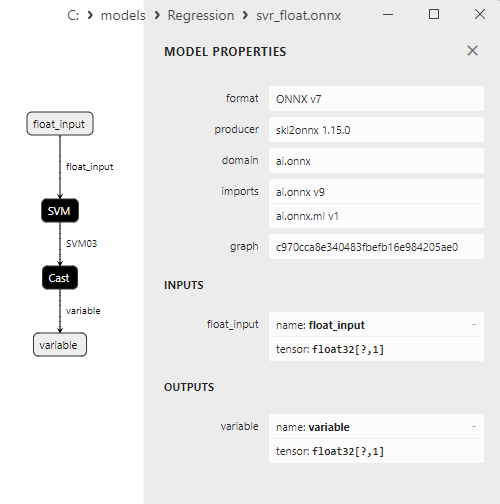
Şekil 128. Netron'da svr_float.onnx modelinin ONNX gösterimi
Şekil 129. Netron'da svr_double.onnx modelinin ONNX gösterimi
2.3. ONNX'e dönüştürülürken sorunlarla karşılaşılan regresyon modelleri
Bazı regresyon modelleri sklearn-onnx dönüştürücü tarafından ONNX formatına dönüştürülememektedir.
2.3.1. sklearn.dummy.DummyRegressor
DummyRegressor, basit kurallar kullanarak hedef değişkeni tahmin eden bir temel model oluşturmak için regresyon görevlerinde kullanılan bir makine öğrenimi yöntemidir. Diğer daha karmaşık modellerle karşılaştırma yapmak ve performanslarını değerlendirmek için değerlidir. Bu yöntem genellikle diğer regresyon modellerinin kalitesinin değerlendirilmesi bağlamında kullanılır.
DummyRegressor tahmin için çeşitli stratejiler sunar:
- "mean" (varsayılan): DummyRegressor, eğitim veri kümesinden hedef değişkenin ortalama değerini tahmin eder. Bu strateji, başka bir modelin sadece ortalamayı tahmin etmeye kıyasla ne kadar daha iyi olduğunu belirlemek için kullanışlıdır.
- "median": DummyRegressor, eğitim veri kümesinden hedef değişkenin medyan değerini tahmin eder.
- "quantile": DummyRegressor, eğitim veri kümesinden hedef değişkenin nicelik değerini (nicelik parametresi tarafından belirtilen) tahmin eder.
- "constant": DummyRegressor, (strateji parametresi kullanılarak) kullanıcı tarafından belirlenen sabit değeri tahmin eder.
DummyRegressor'ın avantajları:
- Performans değerlendirmesi: DummyRegressor, diğer daha karmaşık modellerin performansını değerlendirmek için kullanışlıdır. Modeliniz DummyRegressor tarafından yapılan tahminlerden daha iyi performans gösteremiyorsa, bu durum modeldeki sorunlara işaret edebilir.
- Temel modellerle karşılaştırma: DummyRegressor, daha karmaşık modellerin performansını bir temel değerle (örneğin, ortalama veya medyan değer) karşılaştırmaya olanak tanır.
- Kullanıcı dostudur: DummyRegressor'ın uygulanması ve karşılaştırmalı analiz için kullanılması kolaydır.
DummyRegressor'ın sınırlamaları:
- Doğru tahmin için uygun değildir: DummyRegressor yalnızca basit temel tahminler sağlar ve doğru tahmin için tasarlanmamıştır.
- Karmaşık bağımlılıkları göz ardı eder: DummyRegressor karmaşık veri yapılarını ve özellik bağımlılıklarını göz ardı eder.
- Doğru tahmin gerektiren görevler için uygun değildir: Gerçek dünya tahmin görevlerinde, hedef değişkeni tahmin etmek için DummyRegressor kullanmak yetersizdir.
DummyRegressor, diğer regresyon modellerinin hızlı bir şekilde değerlendirilmesi ve performans karşılaştırması için bir araç olarak değerlidir, ancak tek başına ciddi bir regresyon modeli değildir.
2.3.1.1. DummyRegressor modelini oluşturmak için kod
# The code demonstrates the process of training DummyRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"
# create an Dummy Regressor model
regression_model = DummyRegressor(strategy="mean")
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python DummyRegressor Original model (double) Python R-squared (Coefficient of determination): 0.0 Python Mean Absolute Error: 100.00329851715793 Python Mean Squared Error: 13232.758393867645
Errors sekmesi:
DummyRegressor.py started DummyRegressor.py 1 1 Traceback (most recent call last): DummyRegressor.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) DummyRegressor.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyRegressor'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 DummyRegressor.py finished in 2565 ms 19 1
2.3.2. sklearn.kernel_ridge.KernelRidge
KernelRidge, regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Destek vektör makinelerinin çekirdek yöntemini (Kernel SVM) ve regresyonu birleştirir. KernelRidge, çekirdek fonksiyonlarını kullanarak özellikler ve hedef değişken arasındaki karmaşık, doğrusal olmayan ilişkilerin modellenmesini sağlar.
KernelRidge'in çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Çekirdek fonksiyonları: KernelRidge, verileri yüksek boyutlu bir uzaya dönüştüren ve daha karmaşık doğrusal olmayan ilişkilerin modellenmesine olanak tanıyan çekirdek fonksiyonlarını (polinom, RBF - radyal temel fonksiyon vb.) kullanır.
- Model eğitimi: Model, tahmin edilen değerler ile gerçek hedef değişken değerleri arasındaki ortalama karesel hatayı en aza indirerek veriler üzerinde eğitilir. Çekirdek fonksiyonları karmaşık bağımlılıkları hesaba katmak için kullanılır.
- Tahmin: Eğitimden sonra model, aynı çekirdek fonksiyonlarını kullanarak yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
KernelRidge'in avantajları:
- Karmaşık doğrusal olmayan ilişkilerin modellenmesi: KernelRidge, özellikler ve hedef değişken arasındaki karmaşık ve doğrusal olmayan bağımlılıkların modellenmesine olanak tanır.
- Farklı çekirdeklerin seçimi: Verilerin ve görevin niteliğine bağlı olarak farklı çekirdekler seçebilirsiniz.
- Düzenlileştirme: Yöntem, modelin aşırı uyumunu önlemeye yardımcı olan düzenlileştirmeyi içerir.
KernelRidge'in sınırlamaları:
- Yorumlanabilirlik eksikliği: Birçok lineer olmayan yöntem gibi KernelRidge de lineer modellere göre daha az yorumlanabilirdir.
- Hesaplama karmaşıklığı: Çekirdek fonksiyonlarının kullanılması, büyük hacimli veriler ve/veya yüksek boyutluluk söz konusu olduğunda hesaplama açısından maliyetli olabilir.
- Parametre ayarlama gereksinimi: Uygun çekirdek ve model parametrelerinin seçilmesi ayarlama ve uzmanlık gerektirir.
KernelRidge, verilerin karmaşık, doğrusal olmayan bağımlılıklar sergilediği ve bu ilişkileri dikkate alabilen bir modelin gerekli olduğu regresyon görevlerinde kullanışlıdır. Ayrıca, verileri daha bilgilendirici bir temsile dönüştürmek için çekirdek fonksiyonlarının kullanılabileceği görevlerde de yardımcı olur.
2.3.2.1. KernelRidge modelini oluşturmak için kod
# The code demonstrates the process of training KernelRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"
# create an KernelRidge model
regression_model = KernelRidge(alpha=1.0, kernel='linear')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python KernelRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962137909675411 Python Mean Absolute Error: 6.36977985227399 Python Mean Squared Error: 50.10198935520715
Errors sekmesi:
KernelRidge.py started KernelRidge.py 1 1 Traceback (most recent call last): KernelRidge.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) KernelRidge.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.kernel_ridge.KernelRidge'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 KernelRidge.py finished in 2516 ms 19 1
2.3.3. sklearn.isotonic.IsotonicRegression
IsotonicRegression, özellikler ve hedef değişken arasında monoton bir ilişki modelleyen regresyon görevleri için kullanılan bir makine öğrenimi yöntemidir. Bu bağlamda "monotonluk", özelliklerden birinin değerindeki bir artışın, değişimin yönünü koruyarak hedef değişkenin değerinde bir artışa veya azalmaya yol açması anlamına gelir.
IsotonicRegression’ın çalışma prensibi:
- Girdi verileri: Özellikler (bağımsız değişkenler) ve bunlara karşılık gelen hedef değişken değerlerini içeren orijinal veri kümesi ile başlar.
- Monotonik regresyon: IsotonicRegression, özellikler ile hedef değişken arasındaki ilişkiyi tanımlayan en iyi monotonik fonksiyonu bulmayı amaçlar. Bu fonksiyon doğrusal veya doğrusal olmayan olabilir ancak monotonluğu korumalıdır.
- Model eğitimi: Model, monotonik fonksiyonun parametrelerini belirlemek için veriler üzerinde eğitilir. Eğitim sırasında model, tahminler ile gerçek hedef değişken değerleri arasındaki karesel hataların toplamını en aza indirmeye çalışır.
- Tahmin: Eğitimden sonra model, monotonik ilişkiyi koruyarak yeni veriler için hedef değişken değerlerini tahmin etmek için kullanılabilir.
IsotonicRegression’ın avantajları:
- Monotonik ilişkilerin modellenmesi: Bu yöntem, veriler monotonik bağımlılıklar gösterdiğinde ideal bir seçimdir ve modelde bu karakteristiği korumak önemlidir.
- Yorumlanabilirlik: Monotonik modeller, her bir özelliğin hedef değişken üzerindeki etki yönünün net bir şekilde tanımlanmasına izin verdiği için daha yorumlanabilir olabilir.
IsotonicRegression’ın sınırlamaları:
- Karmaşık, doğrusal olmayan ilişkiler için uygun değildir: Bu yöntem monotonik ilişkilerin modellenmesiyle sınırlıdır ve bu nedenle karmaşık doğrusal olmayan bağımlılıkların modellenmesi için uygun değildir.
- Parametre ayarlama: Bazı IsotonicRegression uygulamalarında optimum performans elde etmek için ayarlama gerektiren parametreler olabilir.
IsotonicRegression, özellikler ve hedef değişken arasındaki ilişkinin monotonluğunun önemli bir faktör olarak kabul edildiği ve bu karakteristiği koruyan bir model oluşturmaya ihtiyaç duyulan görevlerde kullanışlıdır.
2.3.3.1. IsotonicRegression modellerini oluşturmak için kod
# The code demonstrates the process of training IsotonicRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"
# create an IsotonicRegression model
regression_model = IsotonicRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python IsotonicRegression Original model (double) Python R-squared (Coefficient of determination): 0.9999898125037958 Python Mean Absolute Error: 0.20093409873424467 Python Mean Squared Error: 0.13480867590911208
Errors sekmesi:
IsotonicRegression.py started IsotonicRegression.py 1 1 Traceback (most recent call last): IsotonicRegression.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) IsotonicRegression.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.isotonic.IsotonicRegression'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 IsotonicRegression.py finished in 2499 ms 19 1
2.3.4. sklearn.cross_decomposition.PLSCanonical
PLSCanonical (Partial Least Squares Canonical), kanonik korelasyon problemlerini çözmek için kullanılan bir makine öğrenimi yöntemidir. Partial Least Squares (PLS) yönteminin bir uzantısıdır ve iki değişken kümesi arasındaki ilişkileri analiz etmek ve modellemek için uygulanır.
PLSCanonical'ın çalışma prensibi:
- Girdi verileri: Her kümenin bir değişkenler (özellikler) koleksiyonunu temsil ettiği iki veri kümesiyle (X ve Y) başlar. Genellikle, X ve Y birbiriyle ilişkili veriler içerir ve görev, aralarındaki korelasyonu en üst düzeye çıkaran özelliklerin doğrusal kombinasyonlarını bulmaktır.
- Doğrusal kombinasyonların seçimi: PLSCanonical, iki veri kümesinin bileşenleri arasındaki korelasyonu en üst düzeye çıkarmak için hem X hem de Y'de doğrusal kombinasyonlar (bileşenler) bulur. Bu bileşenler kanonik değişkenler olarak adlandırılır.
- Maksimum korelasyon araması: PLSCanonical'ın birincil amacı, iki veri kümesi arasındaki en bilgilendirici ilişkileri vurgulayarak X ve Y arasındaki korelasyonu en üst düzeye çıkaran kanonik değişkenleri bulmaktır.
- Model eğitimi: Kanonik değişkenler bulunduktan sonra, X'e dayalı olarak Y değerlerini tahmin eden bir model oluşturmak için kullanılabilirler.
- Tahmin oluşturma: Eğitimden sonra model, karşılık gelen X değerlerini kullanarak yeni verilerdeki Y değerlerini tahmin etmek için kullanılabilir.
PLSCanonical'ın avantajları:
- Korelasyon analizi: PLSCanonical, değişkenler arasındaki ilişkileri anlamak için yararlı olabilecek iki veri kümesi arasındaki korelasyonların analiz edilmesine ve modellenmesine olanak tanır.
- Boyut azaltma: Bu yöntem, en önemli bileşenleri vurgulayarak veri boyutluluğunu azaltmak için de kullanılabilir.
PLSCanonical'ın sınırlamaları:
- Bileşen sayısı seçimine duyarlılık: En uygun kanonik değişken sayısının seçilmesi biraz deneme gerektirebilir.
- Veri yapısına bağımlılık: PLSCanonical'ın sonuçları büyük ölçüde veri yapısına ve bunlar arasındaki korelasyonlara bağlı olabilir.
PLSCanonical, iki değişken kümesi arasındaki korelasyonları analiz etmek ve modellemek için kullanılan bir makine öğrenimi yöntemidir. Bu yöntem, veriler arasındaki ilişkilerin incelenmesini sağlar ve veri boyutluluğunu azaltmak ve ilişkili bileşenlere dayalı değerleri tahmin etmek için yararlı olabilir.
2.3.4.1. PLSCanonical modelini oluşturmak için kod
# The code demonstrates the process of training PLSCanonical model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"
# create an PLSCanonical model
regression_model = PLSCanonical(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python Python PLSCanonical Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Errors sekmesi:
PLSCanonical.py started PLSCanonical.py 1 1 Traceback (most recent call last): PLSCanonical.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) PLSCanonical.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.PLSCanonical'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 PLSCanonical.py finished in 2513 ms 19 1
2.3.5. sklearn.cross_decomposition.CCA
Canonical Correlation Analysis (CCA), iki değişken kümesi (X kümesi ve Y kümesi) arasındaki ilişkileri incelemek için kullanılan çok değişkenli bir istatistiksel analiz yöntemidir. CCA'nın temel amacı, X ve Y değişkenlerinin aralarındaki korelasyonu en üst düzeye çıkaran doğrusal kombinasyonlarını bulmaktır. Bu doğrusal kombinasyonlara kanonik değişkenler denir.
CCA'nın çalışma prensibi:
- Girdi verileri: Bu kümelerde herhangi bir sayıda değişken olabilir ve CCA bunlar arasındaki korelasyonu en üst düzeye çıkaran doğrusal kombinasyonları bulmaya çalışır.
- Kanonik değişkenlerin oluşturulması: CCA, X ve Y'de korelasyonlarını maksimize eden kanonik değişkenleri tanımlar. Bu kanonik değişkenler, her bir kanonik gösterge için bir tane olmak üzere orijinal değişkenlerin doğrusal kombinasyonlarıdır.
- Korelasyon değerlendirmesi: CCA, kanonik değişken çiftleri arasındaki korelasyonu değerlendirir. Kanonik değişkenler genellikle azalan korelasyona göre sıralanır, bu nedenle ilk çift en yüksek korelasyona sahiptir, ikincisi bir sonraki en yüksek korelasyona sahiptir ve bu böyle devam eder.
- Yorumlama: Kanonik değişkenler, korelasyonları ve değişken ağırlıkları dikkate alınarak yorumlanabilir. Bu, X ve Y kümelerinden hangi değişkenlerin en güçlü şekilde ilişkili olduğunun anlaşılmasını sağlar.
CCA'nın avantajları:
- Gizli bağlantıları ortaya çıkarır: CCA, ilk analiz sırasında belirgin olmayabilecek iki değişken kümesi arasındaki gizli korelasyonları keşfetmeye yardımcı olabilir.
- Gürültüye karşı dayanıklılık: CCA, verilerdeki gürültüyü hesaba katabilir ve en önemli korelasyonlara odaklanabilir.
- Çoklu uygulamalar: CCA, değişken kümeleri arasındaki ilişkileri incelemek için istatistik, biyoinformatik, finans gibi çeşitli alanlarda kullanılabilir.
CCA'nın sınırlamaları:
- Daha fazla veri gerektirir: CCA, korelasyonları güvenilir bir şekilde hesaplamak için diğer analiz yöntemlerine göre daha fazla miktarda veri gerektirebilir.
- Doğrusal ilişkiler: CCA, değişkenler arasında doğrusal ilişkiler olduğunu varsayar ve bu da bazı durumlarda yetersiz kalabilir.
- Yorumlama karmaşıklığı: Kanonik değişkenlerin yorumlanması, özellikle X ve Y kümelerinde çok sayıda değişken olduğunda karmaşık olabilir.
CCA, iki değişken kümesi arasındaki ilişkiyi incelemenin ve gizli korelasyonları ortaya çıkarmanın gerekli olduğu görevlerde faydalıdır.
2.3.5.1. CCA modelini oluşturmak için kod
# The code demonstrates the process of training CCA model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="CCA"
onnx_model_filename = data_path + "cca"
# create an CCA model
regression_model = CCA(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Çıktı:
Python CCA Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Errors sekmesi:
CCA.py started CCA.py 1 1 Traceback (most recent call last): CCA.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) CCA.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.CCA'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 CCA.py finished in 2543 ms 19 1
Sonuç
Makalede Scikit-learn kütüphanesinin 1.3.2 sürümünde bulunan 45 regresyon modelini incelenmiştir.
1. Bu setten 5 model ONNX formatına dönüştürülürken zorluklarla karşılaşmıştır:
- DummyRegressor (Dummy Regressor);
- KernelRidge (Kernel Ridge Regression);
- IsotonicRegression (Isotonic Regression);
- PLSCanonical (Partial Least Squares Canonical Analysis);
- CCA (Canonical Correlation Analysis).
Bu modeller yapıları veya mantıkları bakımından çok karmaşık olabilir ve ONNX formatıyla tam olarak uyumlu olmayan belirli veri yapıları veya algoritmalar kullanabilir.
2. Kalan 40 model, float hassasiyetinde hesaplamalarla başarılı bir şekilde ONNX'e dönüştürülmüştür.
- ARDRegression: Automatic Relevance Determination (ARD) Regression;
- BayesianRidge: Düzenlileştirme ile Bayesian Ridge Regression;
- ElasticNet: Aşırı uyumu azaltmak için L1 ve L2 düzenlileştirme kombinasyonu;
- ElasticNetCV: Otomatik düzenlileştirme parametresi seçimi ile ElasticNet;
- HuberRegressor: Aykırı değerlere duyarlılığı azaltılmış regresyon;
- Lars: Least Angle Regression;
- LarsCV: Çapraz doğrulamalı (Cross-Validated) Least Angle Regression;
- Lasso: Özellik seçimi için L1-düzenlileştirme regresyon;
- LassoCV: Çapraz doğrulamalı Lasso regresyonu;
- LassoLars: Regresyon için Lasso ve LARS kombinasyonu;
- LassoLarsCV: Çapraz doğrulamalı LassoLars regresyonu;
- LassoLarsIC: LassoLars parametre seçimi için bilgi kriterleri;
- LinearRegression: Basit lineer regresyon;
- Ridge: L2 düzenlileştirme ile lineer regresyon;
- RidgeCV: Çapraz doğrulamalı Ridge regresyonu;
- OrthogonalMatchingPursuit: Ortogonal özellik seçimi ile regresyon;
- PassiveAggressiveRegressor: Pasif-agresif öğrenme yaklaşımı ile regresyon;
- QuantileRegressor: Niceliksel regresyon;
- RANSACRegressor: RANdom SAmple Consensus yöntemi ile regresyon;
- TheilSenRegressor: Theil-Sen yöntemine dayalı lineer olmayan regresyon.
- LinearSVR: Lineer destek vektör regresyonu;
- MLPRegressor: Çok katmanlı algılayıcı kullanarak regresyon;
- PLSRegression: Partial Least Squares Regression;
- TweedieRegressor: Tweedie dağılım tabanlı regresyon;
- PoissonRegressor: Poisson dağılımlı verilerin modellenmesi için regresyon;
- RadiusNeighborsRegressor: Yarıçap komşularına dayalı regresyon;
- KNeighborsRegressor: k-en yakın komşulara dayalı regresyon;
- GaussianProcessRegressor: Gauss süreci tabanlı regresyon;
- GammaRegressor: Gama dağılımlı verilerin modellenmesi için regresyon;
- SGDRegressor: Stokastik gradyan inişine dayalı regresyon;
- AdaBoostRegressor: AdaBoost algoritması kullanılarak regresyon;
- BaggingRegressor: Torbalama yöntemi kullanılarak regresyon;
- DecisionTreeRegressor: Karar ağacı tabanlı regresyon;
- ExtraTreeRegressor: Ekstra karar ağacı tabanlı regresyon;
- ExtraTreesRegressor: Ekstra karar ağaçları ile regresyon;
- NuSVR: Sürekli lineer destek vektör regresyonu (SVR);
- RandomForestRegressor: Karar ağaçları topluluğu ile regresyon (Random Forest);
- GradientBoostingRegressor: Gradyan artırma ile regresyon;
- HistGradientBoostingRegressor: Histogram gradyan artırma ile regresyon;
- SVR: Destek vektör regresyonu yöntemi.
3. Regresyon modellerini double hassasiyetli hesaplamalarla ONNX'e dönüştürme olasılığı da araştırılmıştır.
ONNX'te modellerin double hassasiyete dönüştürülmesi sırasında karşılaşılan ciddi bir sorun,ai.onnx.ml.LinearRegressor, ai.onnx.ml.SVMRegressor, ai.onnx.ml.TreeEnsembleRegressor ML operatörlerinin sınırlamasıdır: parametreleri ve çıktı değerleri float türündedir. Esasen, bunlar hassasiyet azaltma bileşenleridir ve double hassasiyetli hesaplamalarda yürütülmeleri şüphelidir. Bu nedenle, ONNX Runtime kütüphanesi, ONNX modelleri için bazı operatörleri double hassasiyetli olarak uygulamamıştır (hatalar oluşabilir: NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1), Could not find an implementation for SVMRegressor(1) node with name 'SVM' vb.). Dolayısıyla, mevcut ONNX spesifikasyonu dahilinde, bu ML operatörleri için tam double hassasiyetli işlem imkansızdır.
Lineer regresyon modelleri için, sklearn-onnx dönüştürücüsü LinearRegressor sınırlamasını atlamayı başarmıştır: Yerine MatMul() ve Add() ONNX operatörleri kullanılır. Bu yaklaşım sayesinde, önceki listedeki ilk 30 model, double hassasiyetli hesaplamalarla başarılı bir şekilde ONNX modellerine dönüştürülmüş ve bu modeller orijinal modellerin double hassasiyetli doğruluğunu korumuştur.
Ancak, SVMRegressor ve TreeEnsembleRegressor gibi daha karmaşık makine öğrenimi operatörleri için bu başarılamamıştır. Bu nedenle, AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor ve SVR gibi modeller şu anda yalnızca float cinsinden hesaplamaları olan ONNX modellerinde mevcuttur.
Özet
Makale, Scikit-learn kütüphanesi sürüm 1.3.2'deki 45 regresyon modelini ve bunların hem float hem de double hassasiyetli hesaplamalar için ONNX formatına dönüştürme sonuçlarını kapsamaktadır.
İncelenen tüm modellerden 5'inin ONNX dönüşümü için karmaşık olduğu kanıtlanmıştır. Bu modeller arasında DummyRegressor, KernelRidge, IsotonicRegression, PLSCanonical ve CCA bulunmaktadır. Karmaşık yapıları veya mantıkları, başarılı bir ONNX dönüşümü için ek uyarlama gerektirebilir.
Kalan 40 regresyon modeli, float için başarılı bir şekilde ONNX formatına dönüştürülmüştür. Bunların arasında 30 model de doğruluklarını koruyarak double hassasiyet için ONNX formatına başarıyla dönüştürülmüştür
SVMRegressor ve TreeEnsembleRegressor için ML operatörlerindeki sınırlama nedeniyle, AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor ve SVR modelleri şu anda yalnızca float cinsinden hesaplamalara sahip ONNX modellerinde mevcuttur.
Makaledeki tüm kodlar MQL5\Shared Projects\Scikit.Regression.ONNX herkese açık projesinde de mevcuttur.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/13538
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hata ne olabilir, log:
Catboost regressor modeli:
Anladığım kadarıyla, çıktı tensörünün (dizi) şekline küfrediyor. Ama doğru ayarlanmış.