OpenCL: From Naive Towards More Insightful Programming
24 690
3
Introduction
The first article "OpenCL: The Bridge to Parallel Worlds" was an introduction to the topic of OpenCL. It addressed the basic issues of interaction between the program in OpenCL (also called a kernel although it is not quite correct) and the external (host) program in MQL5. Some language performance capabilities (e.g. the use of vector data types) were exemplified by the calculation of pi = 3.14159265...
The program performance optimization was in some cases considerable. However all those optimizations were naive as they did not take into account the hardware specifications used to perform all our calculations. The knowledge of these specifications can, in the majority of cases, enable us to knowingly achieve speedups that are significantly beyond the capabilities of the CPU.
To demonstrate these optimizations the author had to resort to a no longer original example which is probably one of the most thoroughly studied in the literature on OpenCL. It is the multiplication of two large matrices.
Let us start with the main thing - the OpenCL memory model along with peculiarities of its implementation on the real hardware architecture.
1. Memory Hierarchy in Modern Compute Devices
1.1. The OpenCL Memory Model
Generally speaking, memory systems differ greatly from each other depending on computer platforms. For example, all modern CPUs support automatic data caching as opposed to GPUs where this is not always the case.
To ensure the code portability, an abstract memory model is adopted in OpenCL that programmers as well as vendors who need to implement this model on real hardware can go by. The memory as defined in OpenCL can be notionally illustrated in Figure below:
Fig. 1. The OpenCL Memory Model
Once the data is transferred from the host to the device, it is stored in global device memory. Any data transferred in the opposite direction is also stored in global memory (but this time, in global host memory). The keyword __global (two underscores!) is a modifier indicating that data associated with a certain pointer is stored in global memory:
__kernel void foo( __global float *A ) { /// kernel code }
Global memory is accessible to all compute units within the device like RAM in the host system.
Constant memory, in contrast to its name, does not necessarily store read-only data. This type of memory is designed for data where each element can be simultaneously accessed by all work units. Variables with constant values of course fall under this category, as well. Constant memory in the OpenCL model is a part of global memory and memory objects transferred to global memory can therefore be specified as __constant.
Local memory is scratchpad memory where address space is unique to each device. In hardware, it often comes in the form of on-chip memory but there is no special requirement to be exactly the same for OpenCL.
Access to this type of memory incurs much lower latency and the memory bandwidth is therefore much greater than that of global memory. We will try to take advantage of its lower latency for the kernel performance optimization.
The OpenCL specification says that a variable in local memory can be declared both in the kernel header:
__kernel void foo( __local float *sharedData ) { }and in its body:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Note that a dynamic array cannot be declared in the kernel body; you should always specify its size.
Below, in the optimization of the kernel for the multiplication of two large matrices, you will see how to handle local data and what implementation peculiarities it entails in MetaTrader 5 as experienced by the author.
Local variables and kernel arguments that do not contain pointers are private by default (if specified without __local modifier). In practice, these variables are usually located in registers. And vice versa, private arrays and any spilled registers are usually located in off-chip memory, i.e. higher latency memory. Let me cite the relevant information from Wikipedia:
In many programming languages, the programmer has the illusion of allocating arbitrarily many variables. However, during compilation, the compiler must decide how to allocate these variables to a small, finite set of registers. Not all variables are in use (or "live") at the same time, so some registers may be assigned to more than one variable. However, two variables in use at the same time cannot be assigned to the same register without corrupting its value.
Variables which cannot be assigned to some register must be kept in RAM and loaded in/out for every read/write, a process called spilling. Accessing RAM is significantly slower than accessing registers and slows down the execution speed of the compiled program, so an optimizing compiler aims to assign as many variables to registers as possible. Register pressure is the term used when there are fewer hardware registers available than would have been optimal; higher pressure usually means that more spills and reloads are needed.
The OpenCL memory model as described is very similar to the memory structure of modern GPUs. The Figure below shows a correlation between the OpenCL memory model and GPU AMD Radeon HD 6970 memory model.
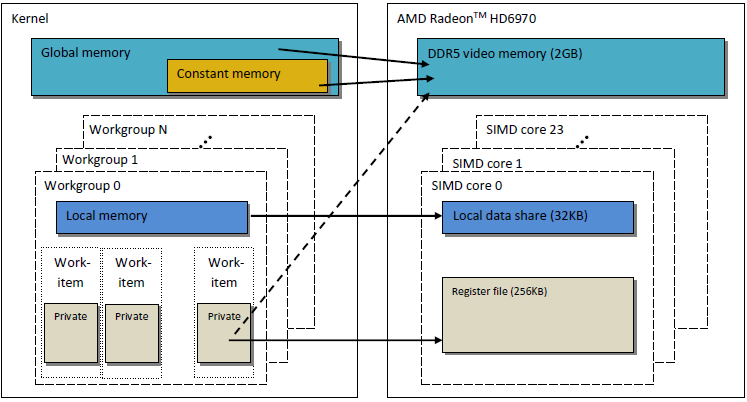
Fig. 2. The correlation between the Radeon HD 6970 memory structure and the abstract OpenCL memory model
Let us proceed to a more detailed consideration of issues related to a specific GPU memory implementation.
1.2. Memory in Modern Discrete GPUs
1.2.1. Coalescing Memory Requests
This information is also important for the kernel performance optimization as the main goal is to achieve high memory bandwidth.
Take a look at the Figure below to better understand the memory addressing process:
Fig. 3. Scheme of addressing data in global device memory
Assume, the pointer to an array of integer variables int is the address of Х = 0x00001232. Every int takes 4 bytes of memory. Assume that a thread (which is a software analogue of a work unit that executes the kernel code) addresses data at Х[ 0 ]:
int tmp = X[ 0 ];
We assume that the memory bus width is 32 bytes (256 bits). This bus width is typical of powerful GPUs, such as Radeon HD 5870. In some other GPUs, the data bus width can be different, e.g. 384 bits or even 512 in some NVidia models.
Addressing of the memory bus should correspond to its structure, i.e. first and foremost, its width. In other words, data in memory is stored in blocks of 32 bytes (256 bits) each. Regardless of what we address within the range from 0x00001220 to 0x0000123F (there is exactly 32 bytes in this range, you can see for yourself), we will still get address 0x00001220 as a start address for reading.
Accessing at address 0x00001232 will return all data at addresses within the range from 0x00001220 to 0x0000123F, i.e. 8 int numbers. Therefore, there will only be 4 bytes (one int number) of useful data while the remaining 28 bytes (7 int numbers) will be useless:
Fig. 4. Scheme of getting required data from memory
The number we need located at the address specified earlier - 0x00001232 - is encircled in the scheme.
To maximize the use of the bus, the GPU tries to coalesce memory accesses from different threads into a single memory request; the less memory accesses, the better. The reason behind that is that accessing global device memory costs us time and thus greatly impairs the program running speed. Consider the following line of the kernel code:
int tmp = X[ get_global_id( 0 ) ];
Assume, our array Х is the array from the previous example given above. Then the first 16 threads (kernels) will access addresses from 0x00001232 to 0x00001272 (there are 16 int numbers within this range, i.e. 64 bytes). If every request was sent by kernels independently, without having being priorly coalesced into a single one, each of 16 requests would contain 4 bytes of useful data and 28 bytes of useless data, thus making a total of 64 used and 448 unused bytes.
This calculation is based on the fact that every access to an address located within one and the same 32-byte memory block will return absolutely identical data. This is the key point. It would be more correct to coalesce multiple requests into single, coherent ones to save on useless requests. This operation will hereinafter be called coalescing and coalesced requests as such will be referred to as coherent.
Fig. 5. Only three memory requests are necessary to obtain the required data
Each cell in the Figure above is 4 bytes. In our example, 3 requests would suffice. If the beginning of the array was address-aligned to the address of the beginning of each 32-byte memory block, even 2 requests would be enough.
In AMD GPU 64, threads are a part of a wavefront and should therefore execute the same instruction as in SIMD execution. 16 threads arranged by get_global_id( 0 ), being exactly a quarter of the wavefront, are coalesced into a coherent request for efficient use of the bus.
Below is an illustration of the memory bandwidth required for coherent requests compared to incoherent, i.e. "spontaneous" requests. It concerns Radeon HD 5870. A similar result can be observed for NVidia cards.
Fig. 6. Comparative analysis of memory bandwidth required for coherent and incoherent requests
It can clearly be seen that a coherent memory request allows to increase memory bandwidth by about one order of magnitude.
1.2.2. Memory Banks
Memory consists of banks where data is actually stored. In modern GPUs, these are usually 32-bit (4-byte) words. Serial data is stored in adjacent memory banks. A group of threads accessing serial elements will not produce any bank conflicts.
The maximum negative effect of bank conflicts is usually observed in local GPU memory. It is therefore advisable that local data accesses from neighboring threads target different memory banks.
On AMD hardware, the wavefront that generates bank conflicts stalls until all local memory operations complete. This leads to serialization whereby blocks of code that should be executed in parallel are sequentially executed. It has an extremely negative effect on performance of the kernel.
Fig. 7. Schemes of memory access without bank conflicts
The Figure above demonstrates memory access without bank conflicts as all threads are accessing different data.
Let us illustrate memory access with bank conflicts:
Fig. 8. Memory access with bank conflicts
This situation however has an exception: if all accesses are to the same address, the bank can perform a broadcast to avoid the delay:
Fig. 9. All threads are accessing the same address
Similar events also occur when accessing global memory but the impact of such conflicts is considerably lower.
- GPU memory is different from CPU memory. The main objective of optimizing the program performance using OpenCL is to ensure the maximum bandwidth instead of reducing latency, as it would be on the CPU.
- The nature of memory access has a great impact on the efficiency of the bus use. Low bus use efficiency means low running speed.
- To improve the performance of the code, it is advisable that the memory access should be coherent. In addition, it is highly preferable to avoid bank conflicts.
- Hardware specifications (bus width, the number of memory banks, as well as the number of threads that can be coalesced for a single coherent access) can be found in vendor-provided documentation.
Specifications of some of the Radeon 5xxx series video cards are set forth below as an example:
Fig. 10. Technical specifications of middle- and high-end Radeon HD 58xx video cards
Let us now proceed to programming.
2. Multiplication of Large Square Matrices: From Serial CPU Code to Parallel GPU Code
2.1. MQL5 Code
The task at hand, in contrast to the previous article "OpenCL: The Bridge to Parallel Worlds", is standard, i.e. to multiply two matrices. It is chosen primarily due to the fact that quite a lot of information on the subject can be found in different sources. Most of them, one way or another, offer more or less coordinated solutions. This is the road that we are going to go down, giving step-by-step clarifications of the meaning of model structures while keeping in mind that we are working on real hardware.
Below is a matrix multiplication formula well-known in linear algebra, modified for computer calculations. The first index is the matrix row number, the second index is the column number. Every output matrix element is calculated by sequentially adding each successive product of elements in the first and second matrices to the accumulated sum. Eventually, this accumulated sum is the calculated output matrix element:
Fig. 11. Matrix multiplication formula
It can schematically be represented as follows:
Fig. 12. Matrix multiplication algorithm (exemplified by the calculation of an output matrix element) represented schematically
It can easily be seen that where both matrices have the same dimensions equal to N, the number of additions and multiplications can be estimated by the function O(N^3): to calculate every output matrix element, you need to get the scalar product of a row in the first matrix and a column in the second matrix. It requires around 2*N additions and multiplications. A required estimate is obtained by multiplying by the number of matrix elements N^2. Thus, the approximate code runtime quite considerably depends on N cubed.
The number of rows and columns for matrices is hereinafter set to 2000 for convenience only; they could be arbitrary but not too large.
The code in MQL5 is not very complicated:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Listing 1. Initial sequential program on the host
Performance results using different parameters:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
As can be seen, our estimated dependence of runtime on linear matrix sizes has appeared to be true: a twofold increase in all matrix dimensions resulted in about 8-fold increase in the runtime.
A few words about the algorithm: the loop order can be changed arbitrarily in the multiplication function mul(). It turns out that it has a considerable effect on the runtime: the ratio of the slowest to the fastest runtime variant is around 1.73.
The article only demonstrates the fastest variant; the remaining tested variants can be found in the code attached at the end of the article (file matr_mul_2dim.mq5). In this connection, OpenCL Programming Guide (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) says as follows (p. 512):
These are obviously not all optimizations of the initial "non-parallel" code that we can implement. Some of them are related to hardware ((S)SSEx instructions) while others are purely algorithmic, e.g. Strassen algorithm, Coppersmith–Winograd algorithm, etc. Note that the size of multiplied matrices for the Strassen Algorithm leading to considerable speedup over the classical algorithm is quite small, only being 64х64. In this article, we are going to learn to quickly multiply matrices whose linear size is up to a few thousand (approximately up to 5000).
2.2. The First Implementation of the Algorithm in OpenCL
Let us now port this algorithm to OpenCL, creating ROWS1 * COLS2 threads, i.e. deleting both outer loops from the kernel. Each thread will execute COLSROWS iterations so that the inner loop remains a part of the kernel.
Since we will have to create three linear buffers for the OpenCL kernel, it would be reasonable to rework the initial algorithm so that it is as similar to the kernel algorithm as possible. The code of the "non-parallel" program on a "single core CPU" with linear buffers will be provided together with the kernel code. The optimality of the code with two-dimensional arrays does not mean that its analog will also be optimal for linear buffers: all tests will have to be repeated. Therefore, we again opt for c-r-cr as the initial variant that corresponds to the standard logic of matrix multiplication in linear algebra.
That said, to avoid a possible matrix/buffer element addressing confusion, answer the main question: if a matrix Matr( M rows by N columns ) is laid out in global GPU memory as a linear buffer, how can we calculate a linear shift of an element Matr[ row ][ column ]?
There is in fact no fixed order of laying out a matrix in GPU memory since it is determined by the logic of the problem alone. For example, elements of both matrices could be laid out differently in buffers because as far as the matrix multiplication algorithm is concerned, matrices are asymmetrical, i.e. the rows of the first matrix are multiplied by the columns of the second matrix. Such rearrangement can greatly affect the calculation performance in sequential reading of matrix elements from global GPU memory in every iteration of the kernel.
The first implementation of the algorithm will feature matrices laid out in the same manner - in row-major order. The first row elements will be first to be placed into the buffer followed by all elements of the second row and so on. The formula of flattening a 2-dimensional representation of a matrix Matr[ M (rows) ][ N (columns) ] onto linear memory is as follows:
Fig. 13. Algorithm for converting a two-dimensional index space into linear for laying the matrix out in the GPU buffer
The Figure above also gives an example of how a 2-dimensional matrix representation is flattened onto linear memory in column-major order.
Below is a slightly reduced code of our first program implementation executed on the OpenCL device:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Listing 2. The first implementation of the program in OpenCL
The last two functions are useful in verifying accuracy of calculations. The complete code can be found attached at the end of the article (matr_mul_1dim.mq5). Note that dimensions do not necessarily have to correspond to square matrices only.
Further changes will almost always concern only the kernel code therefore only the kernel modification codes will hereinafter be set forth.
The REALTYPE type is introduced for convenience of changing the calculation precision from float to double. It should be mentioned that the REALTYPE type is declared not only in the host program but also within the kernel. If necessary, any changes regarding this type will have to be made in two places at the same time, in both #define of the host program and the kernel code.
The code performance results (hereinafter, float data type everywhere):
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
When executed on Radeon HD 4870 (_device = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
As can be seen, the execution of the kernel on the GPU is much slower. However we have not yet tackled the optimization specifically for the GPU.
A few conclusions:
- Changing matrix representation from two-dimensional to linear (corresponding to the representation in the program executed on the device) has not had considerable effect on the total runtime of the sequential version of the program.
- The most intuitive calculation algorithm matching the definition of matrix multiplication in linear algebra has been selected as the initial variant for further optimization. It is somewhat slower than the fastest one but in view of the future speedup on the GPU this factor is not essential.
- The runtime should be calculated only after reading the buffers into RAM rather than after the CLExecute() command. The reason behind that, pointed out by MetaDriver to the author, is probably as follows:MetaDriver: Before reading from the buffer, CLBufferRead() simply waits for the actual completion of the program. CLExecute() is in fact an asynchronous queuing function. It returns the result immediately, well before the cl code operation is completed.
- GPU computing guides do not usually calculate the kernel runtime but rather throughput related to various objects - memory, arithmetic, etc. We can and will hereinafter do the same.
We know that the calculation of a matrix of the size of 2000 requires around 2 * 2000 additions/multiplications for each element. By multiplying by the number of the matrix elements (2000 * 2000), we find that the total number of operations on float type data is 16 billion. That said, the execution on the CPU takes 115.628 sec which corresponds to data streaming speed equal to
On the other hand, remember that the fastest calculation thus far on a "single core CPU" with the matrix size of 2000 only took 83.663 sec to complete (see our first code without OpenCL). Hence
Let us take this figure as a reference, starting point for our optimizations.
Similarly, the calculation using OpenCL on the CPU yields:
Finally, calculate throughput on the GPU:
2.3. Eliminating Incoherent Data Accesses
Looking at the kernel code, you can easily notice a few non-optimalities.
Have a look at the body of the loop within the kernel:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
It is easy to see that when the loop counter (cr++) is running, contiguous data is taken from the first buffer in1[]. While data from the second buffer in2[] is taken with "gaps" equal to COLS2. In other words, the major part of data taken from the second buffer will be useless as memory requests will be incoherent (see 1.2.1. Coalescing Memory Requests). To fix this situation, it is sufficient to modify the code in three places by changing the formula for calculation of the index of array in2[], as well as its generation pattern:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Now, when loop counter (cr++) values change, the data from both arrays will be taken sequentially, without any "gaps".
- Buffer filling code in genMatrices(). It should now be filled in column-major order instead of row-major order used at the beginning:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Verification code in the checkRandom() function:
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Performance results on the CPU:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
As you can see, coherent access to data has had almost no effect on the runtime on the GPU; however it clearly improved the runtime on the CPU. It is very likely that it has to do with factors that will be optimized later, in particular with very high latency of access to global variables that we should get rid of as soon as possible.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
The new kernel code can be found in matr_mul_1dim_coalesced.mq5 at the end of the article.
The kernel code is set forth below:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Listing 3. Kernel with coalesced global memory data access
Let us move on to further optimizations.
2.4. Removing 'Costly' Global GPU Memory Access From the Output Matrix
It is known that the latency of global GPU memory access is extremely high (about 600-800 cycles). For example, the latency of performing an addition of two numbers is approximately 20 cycles. The main objective of optimizations when computing on the GPU is to hide the latency by increasing the throughput of calculations. In the loop of the kernel developed earlier, we constantly access global memory elements which costs us time.
Let us now introduce the local variable sum in the kernel (which can be accessed many times faster as it is a private variable of the kernel located in the work unit register) and upon completion of the loop, singly assign the obtained sum value to the element of the output array:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Listing 4. Introducing the private variable to calculate the cumulative sum in the scalar product calculation loop
The complete source code file, matr_mul_sum_local.mq5, is attached at the end of the article.
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================This is a real productivity boost!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
The main principle we try to stick with in sequential optimizations is as follows: you should first rearrange the data structure in the most complete possible way so that it is appropriate for a given task and specifically the underlying hardware and only then proceed to fine optimizations employing fast calculation algorithms, such as mad() or fma(). Bear in mind that sequential optimizations do not always necessarily result in increased performance - this cannot be guaranteed.
2.5. Increasing the Operations Executed by the Kernel
In parallel programming, it is important to organize calculations so as to minimize overhead (time spent) on the organization of parallel operation. In matrices with dimension of 2000, one work unit calculating one output matrix element performs the amount of work equal to 1 / 4000000 of the total task.
This is obviously too much and too far from the actual number of units performing calculations on the hardware. Now, in the new version of the kernel, we will calculate the whole matrix row instead of one element.
It is important that the task space is now changed from 2-dimensional to one-dimensional as the entire dimension - the whole row, rather than a single element of the matrix, is now calculated in every task of the kernel. Therefore, the task space turns into the number of matrix rows.
Fig. 14. Scheme of calculating the whole row of the output matrix
The kernel code gets more complicated:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 5. The kernel for the calculation of the whole row of the output matrix
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Performance results (the complete source code can be found in matr_mul_row_calc.mq5):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
We can see that the runtime on the CPU has clearly worsened and got slightly, though not much, worse on the GPU. It is not all so bad: this strategic change that temporarily aggravates the situation at the local level is here only to further dramatically increase the performance.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. Transferring the Row of the First Array to Private Memory
The main peculiarity of the matrix multiplication algorithm is a large number of multiplications with concomitant accumulation of the results. A proper, high-quality optimization of this algorithm should imply the minimization of data transfers. But so far, in calculations within the main loop of scalar product accumulation, all our kernel modifications have stored two out of three matrices in global memory.
This means that all input data for every scalar product (being in fact every output matrix element) is constantly streamed through the entire memory hierarchy - from global to private - with associated latencies. This traffic can be reduced by ensuring that every work unit reuses one and the same row of the first matrix for every calculated row of the output matrix.
Fig. 15. Transferring the row of the first matrix to private memory of the work unit
This does not entail any changes in the host program code. And changes in the kernel are minimal. Due to the fact that an intermediate one-dimensional private array is generated within the kernel, the GPU tries to place it in private memory of the unit that executes the kernel. The required row of the first matrix is simply copied from global into private memory. That said, it should be noted that even this copying will be relatively fast. The trick is in the fact that the most 'costly' copying of the row elements of the first array from global into private memory is done coherently and overhead on copying is quite modest compared to the runtime of the main double loop calculating the output matrix row.
The kernel code (the code commented out in the main loop is what there was in the previous version):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 6. Kernel featuring the row of the first matrix in private memory of the work unit.
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
The CPU throughput has remained at about the same level as last time, while the GPU throughput went back to the highest level reached, but in the new capacity. Note that the CPU throughput is as if it had frozen on the spot, only being slightly unsteady, while the GPU throughput goes up (not always, though) in quite large jumps.
Let us point out that the actual arithmetic throughput should be a bit higher as, due to the copying of the row of the first matrix into private memory, more operations are executed now than before. However, it has little effect on the final throughput estimate.
The source code can be found in matr_mul_row_in_private.mq5.
2.7. Transferring the Column of the Second Array to Local Memory
Now, it is easy to guess what the next step will be. We have already taken steps to hide the latencies associated with the output and the first input matrices. There is the second matrix still remaining.
A more careful study of scalar products used in matrix multiplication shows that in the course of calculating the output matrix row, all work units in the group restream data from the same columns of the second multiplied matrix through the device. This is illustrated in the scheme below:
Fig. 16. Transferring the column of the second matrix to the Local Data Share of the work group
The overhead on transferring data from global memory can be reduced if work units making up the work group copy columns of the second matrix into work group memory before the calculation of output matrix rows begins.
This will require changes to be made in the kernel, as well as the host program. The most important change is the setting of local memory for each kernel. It should be explicit as dynamic memory allocation is not supported in OpenCL. Therefore, a memory object of adequate size should first be placed in the host to further be processed within the kernel.
And only then, when executing the kernel, work units copy the column of the second matrix into local memory. This is done in parallel using cyclic distribution of loop iterations across all work units of the work group. However, all copying should be completed before the work unit begins its main operation (calculation of the output matrix row).
That is why the following command is inserted after the loop in charge of copying:
barrier(CLK_LOCAL_MEM_FENCE);
This is a "local memory barrier" ensuring that each work unit within the group can "see" local memory in a certain state that is coordinated with other units. All work units in the work group should execute commands up to the barrier before any of them can proceed with execution of the kernel. In other words, the barrier is a special synchronization mechanism between work units within the work group.
Synchronization mechanisms between work groups are not provided for in OpenCL.
Below is the illustration of the barrier in action:
Fig. 17. Illustration of the barrier in action
In fact, it only seems that work units within the work group execute the code strictly concurrently. This is merely an abstraction of the OpenCL programming model.
So far, our kernel codes executed on different work units have not required synchronization of operations as there was no explicit communication between them that would be programmatically set in the kernel; besides, it was not even needed. However, synchronization is required in this kernel as the process of filling the local array is distributed in parallel between all units of the work group.
In other words, every work unit writes its values into local data share (here, the array) without knowing how far along other work units are in this writing process. The barrier is there so that a certain work unit does not proceed with execution of the kernel before it is necessary, i.e. before a local array has been completely generated.
You should understand that this optimization will hardly be beneficial to performance on the CPU: Intel's OpenCL Optimization Guide says that when executing a kernel on the CPU, all OpenCL memory objects are cached by hardware, so explicit caching by use of local memory just introduces unnecessary (moderate) overhead.
There is another important point worth noting here that cost much time for the author of the article. It has to do with the fact that a local variable cannot be passed in the kernel function header, i.e. at the compilation stage, in the current implementation built by the developers of the terminal. The reason behind it is that in order to allocate memory to a memory object as the kernel function argument, we would have to first explicitly create such object in CPU memory using the CLBufferCreate() function and explicitly specify its size as a function parameter. This function returns a memory object handle which will further be stored in global GPU memory as this is the only place where it can be.
Local memory however is the memory different from global and, consequently, a created memory object cannot be placed in local memory of the work group.
The fully-featured OpenCL API allows to explicitly assign memory of the required size with the pointer NULL to the argument of the kernel, even without creating the memory object as such (CLSetKernelArg() function). However, the syntax of the CLSetKernelArgMem() function being the MQL5 analog of the fully-featured API function does not allow us to pass in it the size of the memory allocated to the argument without creating the memory object itself. What we can pass to the CLSetKernelArgMem() function is only the buffer handle already generated in global CPU memory and intended for transferring to global GPU memory. Here is the paradox.
Fortunately, there is an equivalent way of working with local buffers in the kernel. You simply declare such buffer with the modifier __local in the body of the kernel. Local memory allocated to the work group will, in so doing, be determined during Runtime instead of the compilation stage.
Commands coming after the barrier in the kernel (the barrier line in the code is marked in red) are, in essence, the same as they were in the previous optimization. The host program code has remained the same (the source code can be found in matr_mul_col_local.mq5).
So, here is the new kernel code:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 7. The column of the second array transferred to local memory of the work group
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Both cases demonstrate performance degradation which however cannot be called significant. It may well be that the performance could be improved rather than degraded by changing the size of the work group. The above example would rather serve a different purpose - to show how to use local memory objects.
There is a hypothesis that explains a decrease in performance when local memory is used. The article Comparing OpenCL with CUDA, GLSL and OpenMP (in Russian) published on habrahabr.ru around 2 years ago says:
In other words, does it mean that local memory of the products released 2 years ago is not faster than global memory? The time when the above was posted suggests that two years ago the Radeon HD 58xx series video cards had already been out yet the situation, according to the author, was far from being optimistic. I find that hard to believe, especially given the sensational Evergreen series by AMD. It would be interesting to check it using more modern cards, e.g. the HD 69xx series.
Addition: start GPU Caps Viewer and you will see the following in the OpenCL tab:
Fig. 18. Main OpenCL parameters supported by HD 4870
CL_DEVICE_LOCAL_MEM_TYPE: Global
The explanation of this parameter provided in the language Specification (Table 4.3, p. 41) is as follows:
Type of local memory supported. This can be set to CL_LOCAL implying dedicated local memory storage such as SRAM, or CL_GLOBAL.
Thus, HD 4870 local memory is really a part of global memory and any local memory manipulations in this video card are therefore useless and will not result in anything faster than global memory. Here is another link where an AMD specialist clarifies this point for the HD 4xxx series. It does not necessarily mean that it will be as bad for the video card you have; it was just to show where such information regarding the hardware can be found - in this case, in GPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Finally, let us add a few finishing touches by explicitly vectorizing the kernel. The kernel derived at the stage of transferring the row of the first array to private memory (matr_mul_row_in_private.mq5) will serve as the initial kernel since it has appeared to be the fastest.
2.8. Kernel Vectorization
This operation should better be broken down into several stages, to avoid confusion. In the initial modification, we do not change data types of the external parameters of the kernel and only vectorize calculations in the inner loop:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 8. Partial vectorization of the kernel using float4 (only inner loop)
CPU:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Surprisingly, even such primitive vectorization has yielded good results on the GPU; although not very significant, the gain has appeared to be about 10%.
Keep on vectorizing inside the kernel: transfer 'costly' REALTYPE4 vector type conversion operations along with specification of explicit vector components to the outer auxiliary loop filling the private variable rowbuf[]. There are still no changes in the kernel.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 9. Getting rid of 'costly' operations of type conversion in the main loop of the kernel
Note that the maximum count value of the inner (as well as auxiliary) loop counter has become 4 times lower since the reading operations that are now required for the first array are 4 times less than before - reading has clearly become a vector operation.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Arithmetic throughput:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
As can be seen, the changes in performance for the CPU are considerable, while being almost revolutionary for the GPU. The source code can be found in matr_mul_vect_v2.mq5.
Let us perform the same operations with respect to the last variant of the kernel, only using vector width of 8. The author's decision can be explained by the fact that the GPU memory bandwidth is 256 bits, i.e. 32 bytes or 8 numbers of float type; therefore simultaneous processing of 8 floats which is equivalent to concurrent use of float8, appears to be quite natural.
Bear in mind that in this case the COLSROWS value should be integrally divisible by 8. This is a natural requirement as finer optimizations set more specific requirements to data.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listing 10. Kernel vectorization using vector width of 8
We had to insert in the kernel code the inline function dot8() that allows to calculate scalar product for vectors with width 8. In OpenCL, the standard function dot() can calculate scalar product only for vectors up to width 4. The source code can be found in matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
The results are unexpected: the runtime on the CPU is almost twice as less as before, whereas it has slightly increased for the GPU, despite the fact that float8 is an adequate bus width for HD 4870 (being equal to 256 bits). And here, we again resort to GPU Caps Viewer.
The explanation can be found in Fig. 18, in the last but one line of the parameter list:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Consult the OpenCL Specification and you will see the following text regarding this parameter in the last column of Table 4.3 on page 37:
Preferred native vector width size for built-in scalar types that can be put into vectors. The vector width is defined as the number of scalar elements that can be stored in the vector.
Thus, for HD 4870, the preferred vector width of vector floatN is float4 instead of float8.
Let us finish up the kernel optimization cycle here. We could go on to achieve much more but the length of this article does not allow for that depth of discussion.
Conclusion
The article demonstrated some optimization capabilities that open up when at least some consideration is given to the underlying hardware on which the kernel is executed.
The figures obtained are far from being ceiling values but even they suggest that having the existing resources available here and now (OpenCL API as implemented by the developers of the terminal does not allow to control some parameters important for optimization - - particularly, the work group size), the performance gain over the host program execution is very substantial: the gain in execution on the GPU over the sequential program on the CPU (although not very optimized) is about 200:1.
My sincere gratitude goes to MetaDriver for valuable advice and the opportunity to use the discrete GPU while mine was not available.
Contents of the attached files:
- matr_mul_2dim.mq5 - the initial sequential program on the host with two-dimensional data representation;
- matr_mul_1dim.mq5 - the first implementation of the kernel with linear data representation and a relevant binding for the MQL5 OpenCL API;
- matr_mul_1dim_coalesced - the kernel featuring coalesced global memory access;
- matr_mul_sum_local - a private variable introduced for the calculation of scalar product, instead of accessing a calculated cell of the output array stored in global memory;
- matr_mul_row_calc - the calculation of the whole row of the output matrix in the kernel;
- matr_mul_row_in_private - the row of the first array transferred to private memory;
- matr_mul_col_local.mq5 -the column of the second array transferred to local memory;
- matr_mul_vect.mq5 - the first vectorization of the kernel (using float4, only inner subloop of the main loop);
- matr_mul_vect_v2.mq5 - getting rid of 'costly' operations of data conversion in the main loop;
- matr_mul_vect_v3.mq5 - vectorization using vector width of 8.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/407
MetaTrader 4 on Mac OS
Limitless Opportunities with MetaTrader 5 and MQL5
Why Is MQL5 Market the Best Place for Selling Trading Strategies and Technical Indicators
The Golden Rule of Traders
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Hi there,
Can you provide an example of how OpenCL can speed up an EA backtesting in EveryTick Mode? Currently, it takes me 18 minutes to run 14 years data in EveryTick mode. I believe that lots of traders will be interested if OpenCL can reduce the test time by 50%.
Great article , i did not understand how moving the transfer of the row from within the loop outside to private memory speed it up .
The same transfer operation occurs anyway , i got zero impact on my code but of course each case differs. (but then again 0 impact after adding something means that something sped up but no gain)
This part in the OpenCL source :
Where you move it outside of the crunch loop
Thank you