Görselleştirin! R dilinin plot fonksiyonuna benzer MQL5 grafik kütüphanesi
Ticaret modellerini incelerken grafikler şeklinde görselleştirme büyük önem taşımaktadır. R ve Python gibi bilim topluluğu arasında popüler olan programlama dilleri görselleştirme için özel plot fonksiyonuna sahiptir. Bu fonksiyon, ticaret modellerinin çizgiler, nokta dağılımları ve histogramlar şeklinde görselleştirilmesine olanak sağlar.
plot fonksiyonunun önemli bir avantajı, herhangi bir grafiği çizmek için sadece birkaç satır koda ihtiyacın olmasıdır. Basitçe veri dizisi parametre olarak iletilir, istenilen grafik türü belirtilir ve bu kadar - kullanıma hazır! plot fonksiyonu, ölçeğin hesaplanması, eksenlerin oluşturulması, renklerin seçilmesi gibi tüm rutin işlemleri halleder.
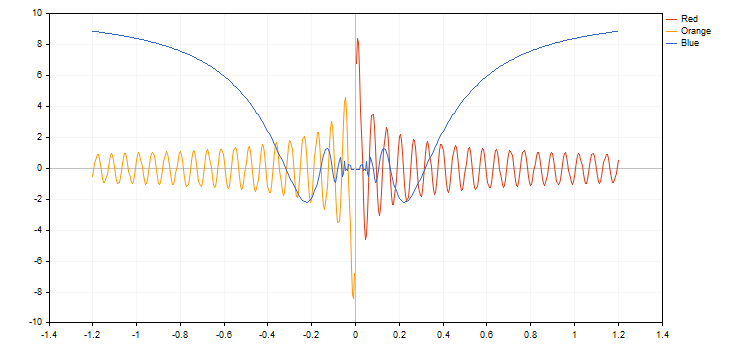
MQL5'te de, bu fonksiyonun tüm yetenekleri, Standart Kütüphanedeki grafik kütüphanesinin metotlarıyla temsil edilir. Örnek kod ve çalıştırılmasının sonucu aşağıda gösterilmektedir:
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- fonksiyonlar
double BlueFunction(double x) { return(RESULT_OR_NAN(x,10*x*sin(1/x))); }
double RedFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//| Komut dosyasını başlatma fonksiyonu |
//+------------------------------------------------------------------+
void OnStart()
{
double from=-1.2;
double to=1.2;
double step=0.005;
CGraphic graphic;
graphic.Create(0,"G",0,30,30,780,380);
//--- renkler
CColorGenerator generator;
uint blue= generator.Next();
uint red = generator.Next();
uint orange=generator.Next();
//--- tüm eğrileri çiz
graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
graphic.CurvePlotAll();
graphic.Update();
}
CCanvas temel sınıfı ve gelişimi
Standart kütüphane, çizimlerin doğrudan fiyat grafiklerinde kolay ve hızlı bir şekilde yapılabilmesi için tasarlanmış CCanvas temel sınıfını içerir. Sınıfın çalışması, bir grafik kaynağı oluşturulmasına ve temel öğelerin (noktalar, doğrular ve çoklu çizgiler, daireler, üçgenler ve çokgenler) tuval üzerine çizilmesine dayanır. Sınıfta ayrıca şekilleri renklerle doldurmak ve metinleri istenilen yazı tipi, renk ve boyutta görüntülemek için fonksiyonlar da bulunur.
Başlangıçta, CCanvas sınıfı, temel öğeleri görüntülemek için yalnızca iki mod içeriyordu - kenar yumuşatmayla (Anti Aliasing, AA) ve kenar yumuşatma olmadan. Ardından, Wu’nun çizgi algoritmasına dayalı olarak temel öğelerin çizilmesi için yeni fonksiyonlar eklenmiştir:
- LineWu - doğru
- PolylineWu - çoklu çizgi
- PolygonWu - çokgen
- TriangleWu - üçgen
- CircleWu - daire
- EllipseWu - elips
Wu’nun çizgi algoritması, Bresenham’ın çizgi algoritmasının hızına yakın şekilde çalışarak onun aksine yüksek kaliteli kenar yumuşatma da uygular. Ayrıca CCanvas'taki standart kenar yumuşatma algoritmasından (AA) görsel olarak da farklıdır. Aşağıda, üç farklı fonksiyon kullanılarak bir dairenin çizilmesine ilişkin örnek yer almaktadır:
CCanvas canvas;
//+------------------------------------------------------------------+
//| Komut dosyasını başlatma fonksiyonu |
//+------------------------------------------------------------------+
void OnStart()
{
int Width=800;
int Height=600;
//--- tuval oluştur
if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
{
Print("Tuval oluşturulurken hata meydana geldi: ",GetLastError());
}
//--- çiz
canvas.Erase(clrWhite);
canvas.Circle(70,70,25,clrBlack);
canvas.CircleAA(120,70,25,clrBlack);
canvas.CircleWu(170,70,25,clrBlack);
//---
canvas.Update();
}
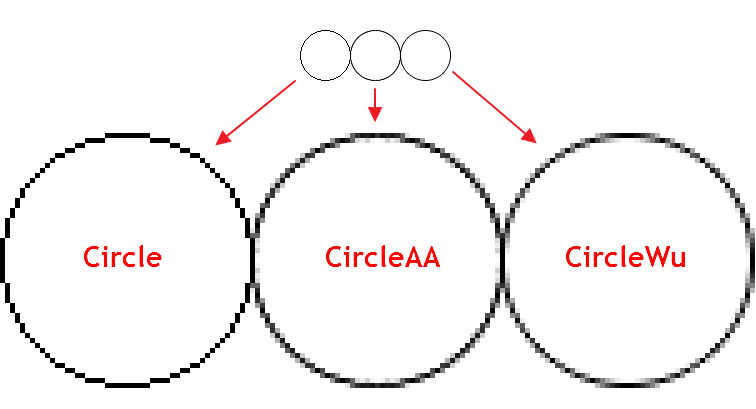
Gördüğümüz gibi, standart kenar yumuşatma algoritmasına sahip CircleAA() fonksiyonu, Wu'nun çizgi algoritmasına sahip CircleWu() fonksiyonuna kıyasla daha kalın bir çizgi çizmektedir. Kalınlığının daha küçük olması ve geçiş gölgelerinin daha iyi hesaplanması nedeniyle CircleWu dairesi daha düzgün ve doğal görünmektedir.
CCanvas sınıfına başka iyileştirmeler de yapılmıştır:
- İki kenar yumuşatma seçeneğine sahip yeni elips temel öğesi eklendi - EllipseAA() ve EllipseWu().
- Doldurma hassasiyetinden sorumlu yeni parametre (eşik parametresi) ile alan doldurma fonksiyonuna overload eklendi.
Kütüphaneyle çalışma algoritması
1. Kütüphaneyi bağladıktan sonra bir CGraphic sınıfı nesnesi oluşturmalıyız. Çizilecek eğriler ona eklenecektir.
Ardından, oluşturulan nesne için Create() metodunu çağırmalıyız. Bu metot, ana grafik parametrelerini içerir:
- Grafik kimliği
- Nesne adı
- Pencere indeksi
- Grafik çapa noktası
- Grafik genişliği ve yüksekliği
Belirtilen parametrelere bağlı olarak metot, grafiğin çizileceği bir grafik kaynağı oluşturacaktır.
CGraphic graphic;
//--- tuval oluştur
graphic.Create(0,"Graphic",0,30,30,830,430);
Böylece bir tuvale sahip olmuş olduk.
2. Şimdi nesnemizi eğrilerle dolduralım. Ekleme, aşağıda belirtilen dört farklı şekilde eğriler çizebilen CurveAdd() metodu kullanılarak gerçekleştirilir:
- double tipinde tek boyutlu diziye dayalı olarak. Bu durumda, dizideki değerler Y ekseninde görüntülenirken, dizi indeksleri ise X koordinatları olarak işlev görür.
- İki x[] ve y[] double tipinde diziye dayalı olarak.
- CPoint2D dizisine dayalı olarak.
- CurveFunction() işaretçisine ve fonksiyon parametrelerini oluşturmak için üç değere dayalı olarak: ilk, son ve artış adımı.
CurveAdd() metodu, yeni oluşturulan eğriye hızlı erişim ve özelliklerini değiştirme olanağı sağlayan CCurve sınıfına bir işaretçi geri döndürür.
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);3. Devamında, eklenen eğrilerden herhangi biri görüntülenebilir. Bu üç şekilde yapılabilir.
- Eklenen tüm eğrileri otomatik olarak çizen CurvePlotAll() metodu kullanılarak. graphic.CurvePlotAll();
- Belirtilen indekse göre eğri çizen CurvePlot() metodu kullanılarak. graphic.CurvePlot(0);
- Redraw() metodu kullanılarak ve eğrinin Visible özelliği 'true' olarak ayarlanarak. curve.Visible(true);
graphic.Redraw();
4. Fiyat grafiği üzerinde grafiğin çizilmesi için de Update() metodunu çağırıyoruz. Sonuç olarak, basit bir grafik çizmek için kodun tamamını elde etmiş oluruz:
//+------------------------------------------------------------------+
//| Komut dosyasını başlatma fonksiyonu |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
graphic.CurvePlotAll();
graphic.Update();
}
Oluşturduğumuz grafik şu şekilde görünmektedir:
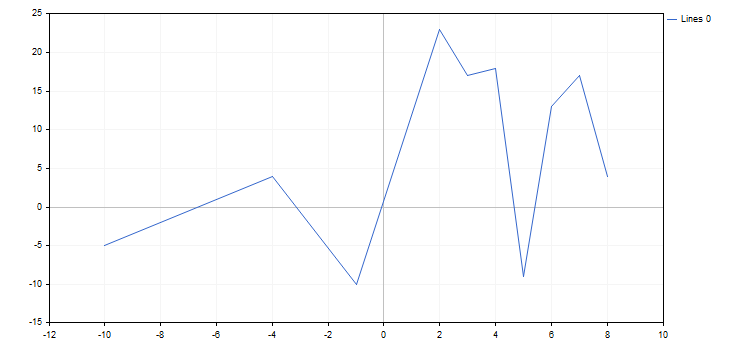
Grafiğin herhangi bir özelliği ve fonksiyonu istenilen herhangi bir zamanda değiştirilebilir. Örneğin, grafik eksenlerine etiketler ekleyebilir, eğrinin adını değiştirebilir ve spline yaklaşımı modunu etkinleştirebiliriz:
//+------------------------------------------------------------------+
//| Komut dosyasını başlatma fonksiyonu |
//+------------------------------------------------------------------+
void OnStart()
{
CGraphic graphic;
graphic.Create(0,"Graphic",0,30,30,780,380);
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
curve.Name("Example");
curve.LinesIsSmooth(true);
graphic.XAxis().Name("X - axis");
graphic.XAxis().NameSize(12);
graphic.YAxis().Name("Y - axis");
graphic.YAxis().NameSize(12);
graphic.YAxis().ValuesWidth(15);
graphic.CurvePlotAll();
graphic.Update();
DebugBreak();
}
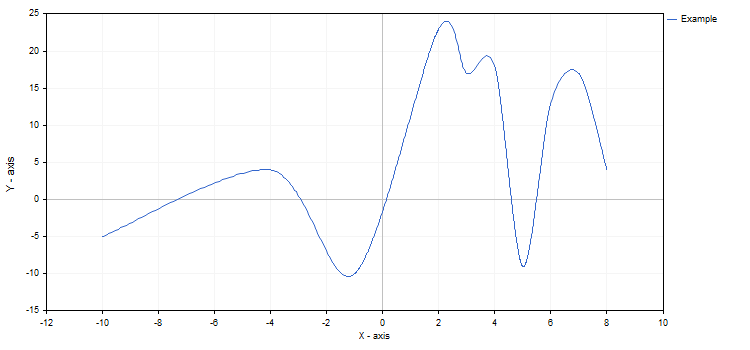
Değişiklikler CurvePlotAll çağrısından sonra olsaydı, onları görmek için ayrıca Redraw metodunu da çağırmamız gerekirdi.
Çoğu modern kütüphane gibi, MQL5 grafik kütüphanesi de grafik çizme sürecini önemli ölçüde basitleştiren çeşitli hazır algoritmalar içerir:
- Kütüphane, açıkça belirtilmediği sürece, eğrilerin kontrast renklerini otomatik olarak üretme yeteneğine sahiptir.
- Grafik eksenleri, istenildiğinde devre dışı bırakılabilen parametrik otomatik ölçeklendirme moduna sahiptir.
- Eğri adları, türlerine ve eklenme sıralarına bağlı olarak otomatik olarak oluşturulur.
- Otomatik olarak grafiğin çalışma alanı çizilir ve eksenler ayarlanır.
- Eğrilerin yumuşatılması mümkündür.
Ek olarak, grafiğe yeni öğeler eklenmesine olanak sağlayan kütüphanedeki şu metotlar da akılda tutulmalıdır:
- TextAdd() - grafik üzerinde rastgele bir yere metin ekler. Koordinatlar gerçek ölçekte ayarlanmalıdır. Görüntülenen metin üzerinde ince ayar yapmak için FontSet metodunu kullanın.
- LineAdd() - grafik üzerinde rastgele bir yere çizgi ekler. Koordinatlar gerçek ölçekte ayarlanmalıdır.
- MarksToAxisAdd() - belirtilen koordinat eksenine yeni yükseklikler ekler.
Bu öğelerin eklenmesine ilişkin veriler hiçbir yerde saklanmaz. Dolayısıyla, grafiğe yeni bir eğri çizildikten veya önceki eğri yeniden çizildikten sonra bu öğeler kaybolacaktır.
Grafik türleri
Grafik kütüphanesi, tümü ENUM_CURVE_TYPE numaralandırmasında belirtilen temel eğri çizim türlerini desteklemektedir:
- CURVE_POINTS - noktalarla eğri çizer
- CURVE_LINES - çizgilerle eğri çizer
- CURVE_POINTS_AND_LINES - hem noktalarla hem de çizgilerle eğri çizer
- CURVE_STEPS - adımlı eğri çizer
- CURVE_HISTOGRAM - histogram olarak eğri çizer
- CURVE_NONE - eğri çizmez
Bu modların her biri, eğrinin grafikte görüntülenmesini etkileyen kendi özelliklerine sahiptir. Eğrinin CCurve işaretçisi, bu özelliklerin hızlı bir şekilde değiştirilmesine olanak sağlar. Bu nedenle, CurveAdd metodu tarafından geri döndürülen tüm işaretçilerin hatırlanması önerilir. Özellik adı her zaman kullanıldığı eğri çizim modunun adıyla başlar.
Şimdi her bir türün özelliklerine daha yakından bakalım.
1. CURVE_POINTS en hızlı ve en basit moddur. Her eğri koordinatı, belirtilen özelliklere sahip bir nokta olarak çizilir:
- PointsSize - nokta boyutu
- PointsFill - dolgunun yapılıp yapılmayacağını ifade eden bayrak
- PointsColor - dolgu rengi
- PointsType - nokta türü
Bu durumda, eğrinin rengi, noktaların sınırlarının rengini tanımlar.
curve.PointsSize(20);
curve.PointsFill(true);
curve.PointsColor(ColorToARGB(clrRed,255));
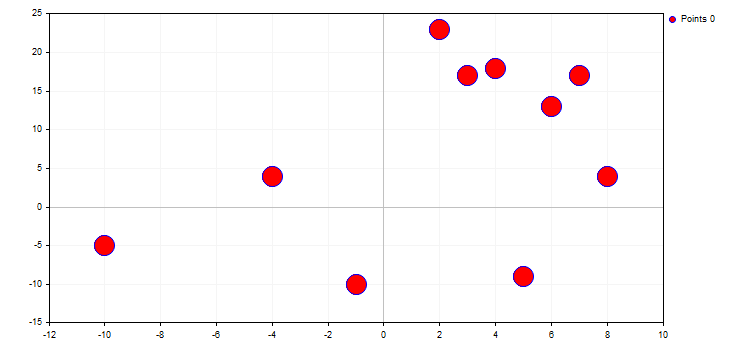
Nokta türü, ENUM_POINT_TYPE numaralandırmasından belirli bir geometrik şekli tanımlar. Bu şekil, eğrinin tüm noktaları görüntülenirken kullanılacaktır. ENUM_POINT_TYPE toplamda on ana geometrik şekil içerir:
- POINT_CIRCLE - daire (varsayılan olarak kullanılır)
- POINT_SQUARE - kare
- POINT_DIAMOND - elmas
- POINT_TRIANGLE - üçgen
- POINT_TRIANGLE_DOWN - ters üçgen
- POINT_X_CROSS - çarpı
- POINT_PLUS - artı
- POINT_STAR - yıldız
- POINT_HORIZONTAL_DASH - yatay çizgi
- POINT_VERTICAL_DASH - dikey çizgi
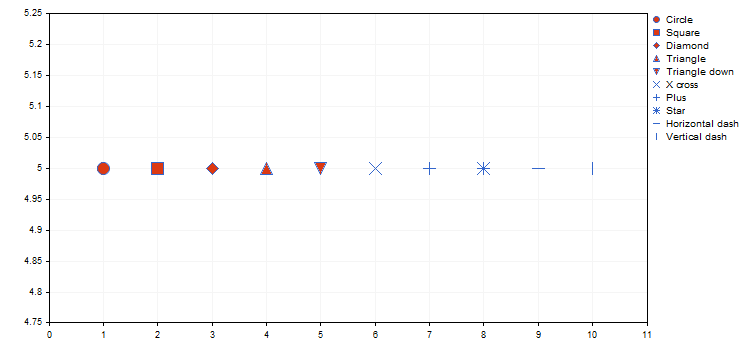
Aşağıda, ekteki IrisSample.mq5 komut dosyasından farklı iris çiçeği türlerinin görsel temsilinin bir örneği bulunmaktadır (daha fazla bilgi için “MetaTrader 5'te kendi kendini düzenleyen özellik haritalarını (Kohonen haritaları) kullanma” adlı makaleye bakabilirsiniz).
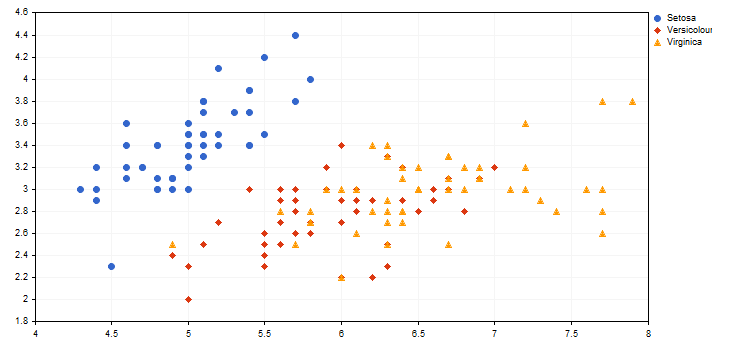
2. CURVE_LINES modu, her nokta çiftinin bir veya birkaç (yumuşatma durumunda) doğru ile bağlandığı, eğrileri görselleştirmek için kullanılan ana eğri çizim modudur. Modun özellikleri şunlardır:
- LinesStyle - ENUM_LINE_STYLE numaralandırmasından çizgi stili
- LinesSmooth - yumuşatma yapılıp yapılmayacağını ifade eden bayrak
- LinesSmoothTension - yumuşatma derecesi
- LinesSmoothStep - yumuşatma sırasında yaklaşma adımı
Grafikler standart parametrik eğri yumuşatma algoritmasına sahiptir. İki aşamadan oluşur:
- Her nokta çifti için türevlerine göre iki referans noktası bulunur.
- Bu dört noktaya dayalı olarak, belirtilen yaklaşma adımıyla Bezier eğrisi çizilir.
LinesSmoothTension parametresi (0.0; 1.0] aralığında değerler alır. Eğer LinesSmoothTension 0,0 olarak ayarlanırsa yumuşatma gerçekleştirilmez. Bu parametre artırıldıkça, giderek daha fazla yumuşatılmış eğri elde edilir.
curve.LinesStyle(STYLE_DOT);
curve.LinesSmooth(true);
curve.LinesSmoothTension(0.8);
curve.LinesSmoothStep(0.2);
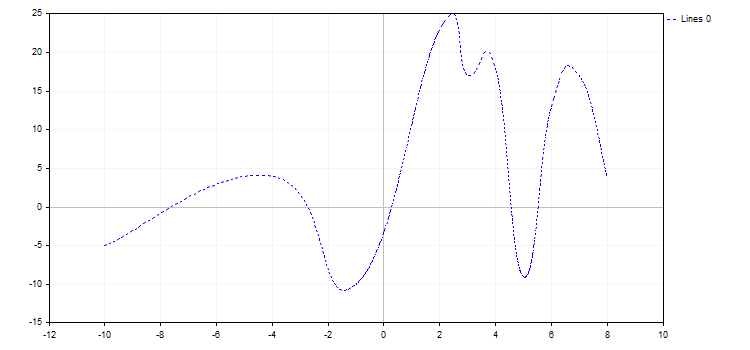
3. CURVE_POINTS_AND_LINES, önceki iki eğri çizim modunu ve özelliklerini birleştirir.
4. CURVE_STEPS modunda, her nokta çifti bir adım olarak iki çizgi ile bağlanır. Modun iki özelliği vardır:
- LinesStyle - bu özellik CURVE_POINTS'ten gelir, çizgi stilini tanımlar
- StepsDimension - adım şekli: 0 - x (yatay çizgi ve ardından dikey çizgi) veya 1 - y (dikey çizgi ve ardından yatay çizgi).
curve.LinesStyle(STYLE_DASH);
curve.StepsDimension(1);

5. CURVE_HISTOGRAM modu, standart çubuk histogram çizer. Mod tek bir özelliğe sahiptir:
- HistogramWidth - çubuk genişliği
Bu değer çok büyük olursa, çubuklar üst üste gelebilir.
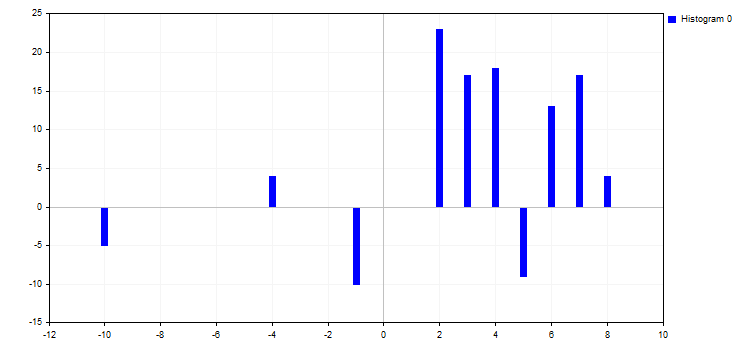
6. CURVE_NONE modu, eğrinin grafiksel gösterimini devre dışı bırakır.
Otomatik ölçeklendirme sırasında, eklenen tüm eğriler belirli değerlere sahip olur. Bu nedenle, eğri çizilmese veya CURVE_NONE moduna sahip olsa bile, değerleri yine de dikkate alınacaktır.
Fonksiyonlarla ilişkili grafikler - birkaç satırda hızlı şekilde oluşturma
Kütüphanenin bir diğer kolaylığı da CurveFunction fonksiyonlarına yönelik işaretçilerle çalışmaktır. MQL5'te, fonksiyon işaretçileri yalnızca global veya statik fonksiyonları kabul eder ve fonksiyon sözdizimi de işaretçi sözdizimine tam olarak uymalıdır. Bizim durumumuzda, CurveFunction işaretçisi, double tipi parametre alan ve ayrıca double geri döndüren fonksiyonlar için yapılandırılmıştır.
Bir fonksiyon işaretçisiyle bir eğri oluşturmak için ayrıca ilk (from), son (to) ve artış adımı (step) parametrelerinin de doğru bir şekilde ayarlanması gerekir. Artış adımı ne kadar küçük olursa, eğriyi oluşturmak için o kadar fazla fonksiyon noktası olacaktır. Bir veri serisi oluşturmak için CurveAdd(), bir fonksiyon çizmek için de CurvePlot() veya CurvePlotAll() kullanın.
Örnek olarak bir parabol fonksiyonu oluşturalım ve onu çeşitli artış adımlarıyla çizelim:
//+------------------------------------------------------------------+
//| Parabol |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| Komut dosyasını başlatma fonksiyonu |
//+------------------------------------------------------------------+
void OnStart()
{
double from1=-5;
double to1=0;
double step1=1;
double from2=0;
double to2=5;
double step2=0.2;
CurveFunction function = Parabola;
CGraphic graph;
graph.Create(0,"Graph",0,30,30,780,380);
graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
graph.CurvePlotAll();
graph.Update();
}
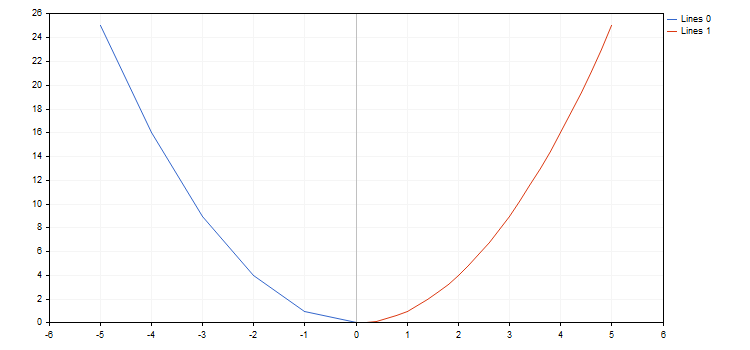
Ek olarak, kütüphane kırılma noktalarına sahip fonksiyonlarla da (koordinatlardan biri artı veya eksi sonsuz değerine sahiptir veya sayısal değildir) çalışabilir. Fonksiyonlardaki artış adımını dikkate almak önemlidir, çünkü kırılma noktası basitçe atlanabilir, ki böyle bir durumda grafik beklentileri karşılamayacaktır. Örneğin, [-5.0; 5.0] aralığında artış adımları 0.7 ve 0.1 olan iki hiperbol fonksiyonu çizelim. Sonuç aşağıda gösterilmektedir:
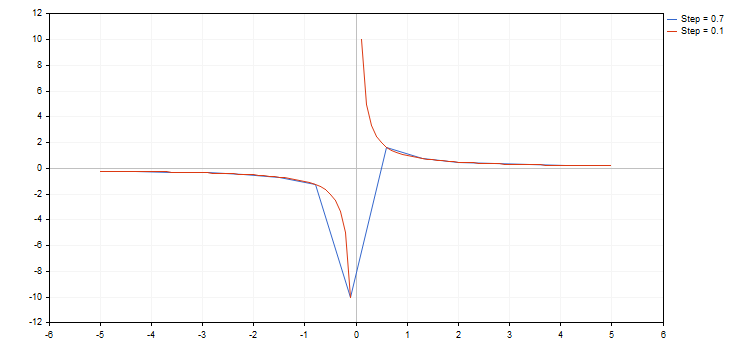
Yukarıdaki görüntüden görebileceğimiz gibi, 0.7'lik artış adımı kullanırken kırılma noktasını atladık. Sonuç olarak, ortaya çıkan eğrinin gerçek hiperbolik fonksiyonla neredeyse hiçbir ilgisi yoktur.
Fonksiyonlar kullanılırken sıfıra bölme hatası oluşabilir. Bu sorunun üstesinden gelmenin iki yolu vardır:
- metaeditor.ini dosyasından sıfıra bölme kontrolünü devre dışı bırakın.
[Experts]
FpNoZeroCheckOnDivision=1 - Veya fonksiyonda kullanılan denklemi analiz edin ve bu tür durumlar için geçerli bir değer geri döndürün. Makro kullanılarak buna örnek, ekteki 3Functions.mq5 ve bat.mq5 dosyalarından bulunabilir.
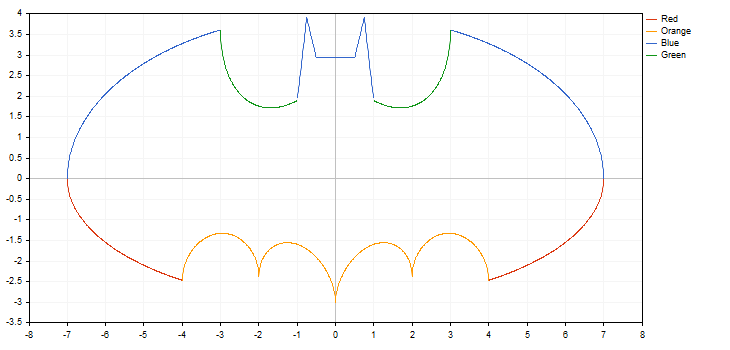
Hızlı çizim fonksiyonları
MQL5 grafik kütüphanesi ayrıca verilere dayalı olarak tüm grafik çizme aşamalarını kendileri gerçekleştiren bir dizi GraphPlot() global fonksiyonu da içerir. Bu fonksiyonlar, R veya Phyton dillerindeki plot fonksiyonuna benzerdir. Mevcut verilerin farklı şekillerde anında görselleştirilmesine olanak sağlarlar.
Bu amaçla GraphPlot fonksiyonu 10 farklı overloada sahiptir. Tek yapılması gereken, eğri için verileri oluşturmaktır. Örneğin, x[] ve y[] dizilerinin hızlı çizimi için kaynak kodu şu şekilde görünür:
{
double x[]={-10,-4,-1,2,3,4,5,6,7,8};
double y[]={-5,4,-10,23,17,18,-9,13,17,4};
GraphPlot(x,y);
}
R dilinde de benzer görünmektedir:
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)
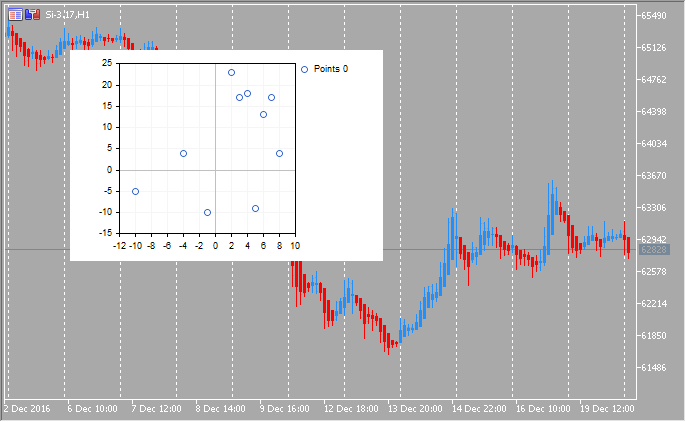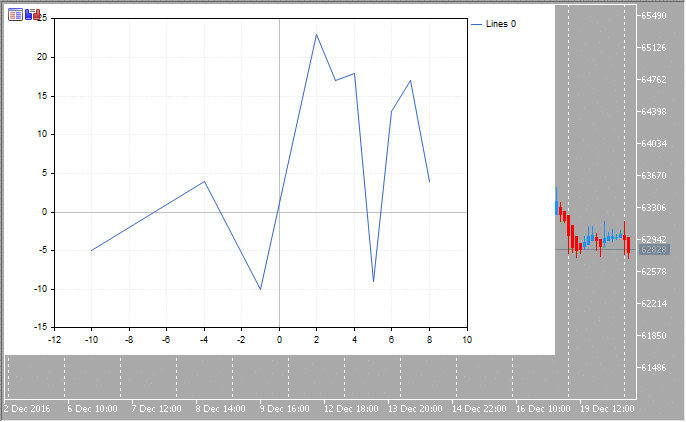
MQL5’teki GraphPlot fonksiyonu ve R’daki plot fonksiyonu tarafından oluşturulan üç çizim modunda grafiklerin karşılaştırılması:
1. Noktalar
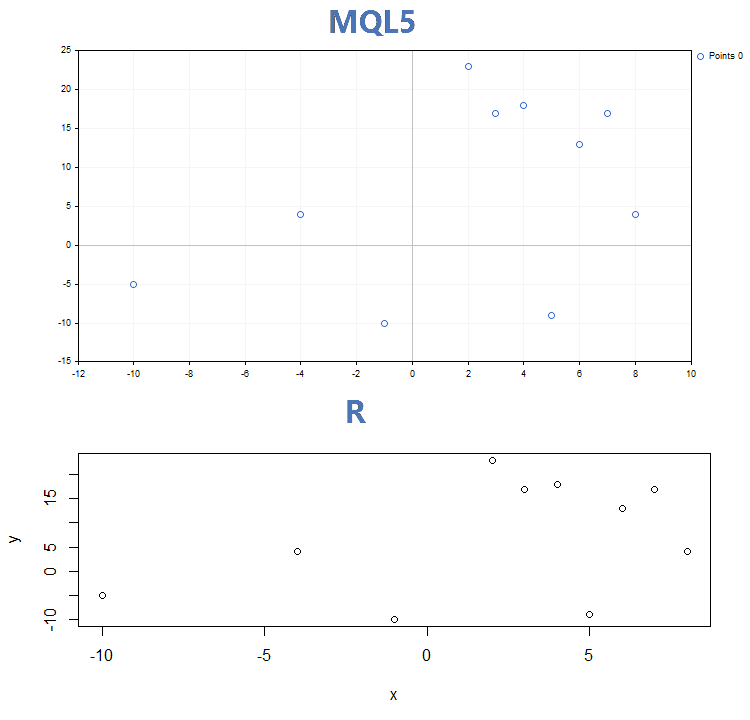
2. Çizgiler
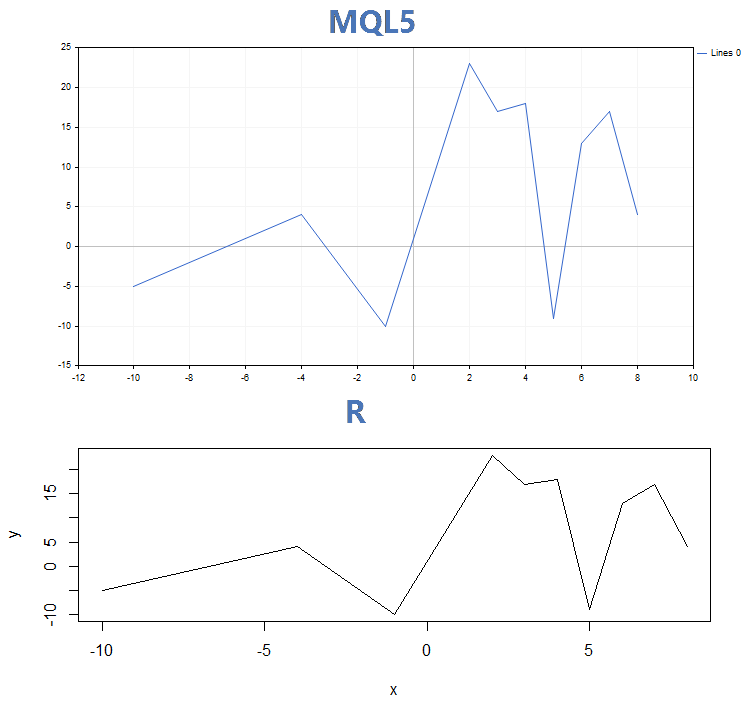
3. Histogram
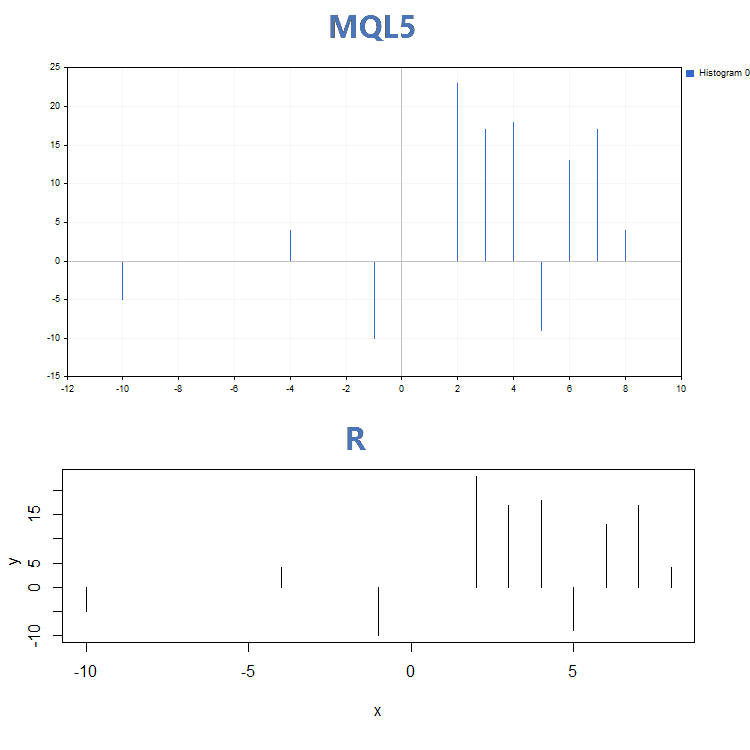
GraphPlot() ve plot() fonksiyonlarının çalışmalarındaki önemli görsel farklılıklara ek olarak, girdi parametrelerinde de farklılık gösterirler. plot() fonksiyonu belirli eğri parametrelerinin (örneğin, çizgi genişliğini değiştiren lwd) ayarlanmasına izin verirken, GraphPlot() fonksiyonu yalnızca verilerin çizilmesi için gerekli olan anahtar parametreleri içerir.
Bu parametreler şunlardır:
- Yukarıda bahsedilmiş olan dört formattan biri olarak eğri verileri
- Çizim türü (varsayılan olarak CURVE_POINTS’tir)
- Nesne adı (varsayılan olarak NULL'dur)
Grafik kütüphanesi kullanılarak oluşturulan her grafik çift şeklindedir: grafik nesnesi ve ona atanan grafik kaynağı. Grafik kaynağının adı, nesnenin adından, basitçe önüne :: eklenerek oluşturulur. Örneğin, nesne adı SomeGraphic ise, grafik kaynağının adı ::SomeGraphic olur.
GraphPlot() fonksiyonu, x=65 ve y=45 olmak üzere fiyat grafiği üzerinde sabit çapa noktasına sahiptir. Grafiğin genişliği ve yüksekliği ise fiyat grafiğinin boyutuna göre hesaplanır: genişlik fiyat grafiğinin genişliğinin %60'ını, yükseklik ise fiyat grafiğinin yüksekliğinin %65'ini oluşturur. Bu nedenle, mevcut fiyat grafiğinin boyutları 65'e 45'ten küçükse, GraphPlot() fonksiyonu düzgün çalışmayacaktır.
Grafik oluştururken önceden oluşturulmuş nesnenin adı kullanılırsa, grafik kütüphanesi kaynak türünü kontrol ettikten sonra grafiği bu nesne üzerinde görüntülemeye çalışır. Eğer kaynak türü OBJ_BITMAP_LABEL ise, çizim aynı nesne-kaynak çifti üzerinde gerçekleştirilir.
Nesne adı açıkça GraphPlot() fonksiyonuna iletilirse, öncelikle bu nesne bulunmaya ve üzerinde grafik görüntülenmeye çalışılır. Nesne bulunamazsa, belirtilen ada göre otomatik olarak yeni bir nesne-kaynak çifti oluşturulur. GraphPlot() fonksiyonu, nesne adı açıkça belirtilmeden kullanılırsa, nesne adı olarak standart “Graphic” adı kullanılır.
Bu durumda, grafiğin çapa noktası ve boyutu bağımsız olarak belirlenebilir. Bu amaçla, Graphic nesne adı iletilerek gerekli parametrelerle nesne-kaynak çifti oluşturulmalıdır. Graphic nesne adıyla nesne-kaynak çifti oluşturarak, GraphPlot() fonksiyonu için standart tuvali yeniden tanımlıyoruz ve onu sabitliyoruz, böylece her çağrıda nesne adını iletme zorunluluğunu ortadan kaldırmış oluyoruz.
Örnek olarak, yukarıdaki örnekteki verileri alalım, 750х350'lik yeni grafik boyutu ayarlayalım ve çapa noktasını sol üst köşeye taşıyalım:
{
//--- nesne ve grafik kaynağı çiftini oluştur
string name="Graphic";
long x=0;
long y=0;
int width=750;
int height=350;
int data[];
ArrayResize(data,width*height);
ZeroMemory(data);
ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- x ve y dizisi oluştur
double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- x ve y dizisini çiz
GraphPlot(arr_x,arr_y,CURVE_LINES);
}
Bilimsel grafik örnekleri
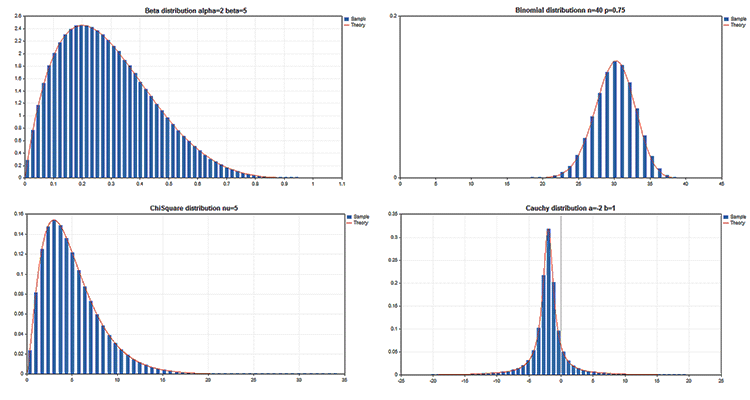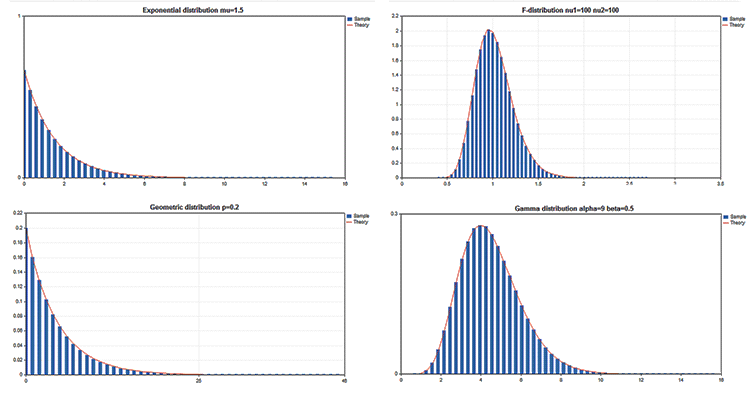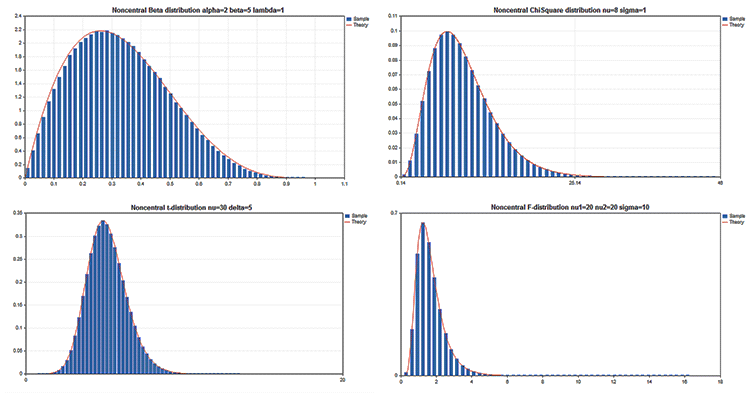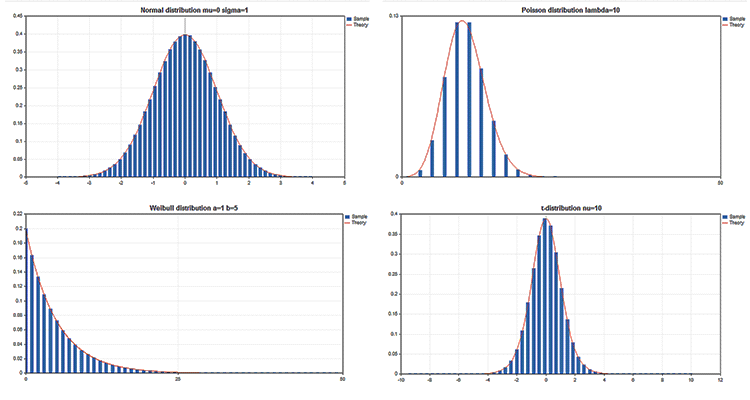
Standart Kütüphane, olasılık teorisindeki çoklu istatistiksel dağılımlarla çalışmaya yönelik fonksiyonlar içeren İstatistik adlı bölüme de sahiptir. Her bir dağılım, grafik örneği ve onu elde etmek için gereken kodla sunulmaktadır. Burada bu grafikleri tek bir GIF’le göstereceğiz. Örneklerin kaynak kodları MQL5.zip dosyasına eklenmiştir. MQL5\Scripts klasörüne açılmaları gerekir.
Tüm bu örneklerde, CHART_SHOW özelliği kullanılarak fiyat grafiğinin görüntülenmesi devre dışı bırakılmıştır:
ChartSetInteger(0,CHART_SHOW,false);
Bu, gerekirse fiyat grafiği penceresini tek bir büyük tuvale dönüştürmemize ve grafik kaynaklarını kullanarak herhangi bir karmaşıklıktaki nesneleri çizmemize olanak tanır.
Grafik kütüphanesinin avantajları
MQL5 dili, geliştiricilerin yalnızca ticaret robotları ve teknik göstergeler oluşturmasına değil, aynı zamanda ALGLIB, Fuzzy ve istatistik kütüphanelerini kullanarak karmaşık matematiksel hesaplamalar yapmasına da olanak sağlar. Elde edilen veriler daha sonra grafik kütüphanesi kullanılarak kolayca görselleştirilebilir. İşlemlerin çoğu otomatikleştirilmiştir ve kütüphane kapsamlı işlevsellik sunar:
- 5 grafik görüntüleme türü
- 10 grafik işaret türü
- X ve Y eksenlerine göre grafikleri otomatik ölçeklendirme yeteneği
- Grafik birkaç yapıya sahip olsa bile otomatik renk seçme yeteneği
- Klasik kenar yumuşatma veya daha gelişmiş Bresenham’ın çizgi algoritmasını kullanarak çizgileri yumuşatma yeteneği
- Çizgiler için spline yaklaşımı parametrelerini ayarlama yeteneği
- x[] ve y[] dizilerine dayalı tek bir kod satırıyla grafik oluşturma yeteneği
- Fonksiyon işaretçilerini kullanarak grafik oluşturma yeteneği
Grafik kütüphanesi, bilimsel grafiklerin oluşturulmasını kolaylaştırır ve ticaret uygulamalarının geliştirilmesini yeni bir seviyeye yükseltir. MetaTrader 5 platformu, herhangi bir karmaşıklıkta matematiksel hesaplamalar yapmanızı ve sonuçları doğrudan terminal penceresinde profesyonel bir şekilde görüntülemenizi mümkün kılar.
Ekteki kodları deneyin. Artık üçüncü taraf paketlere ihtiyacınız yok!
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/2866
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
 SQLite: MQL5'te SQL veritabanlarıyla yerel olarak çalışma
SQLite: MQL5'te SQL veritabanlarıyla yerel olarak çalışma
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 10): Özel göstergelere erişim
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 10): Özel göstergelere erişim
 Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 09): Kavramsal sıçrama (II)
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 09): Kavramsal sıçrama (II)
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
CCanvas'tan daha az fonksiyona sahip yeni bir sınıfa ihtiyacımız var. Tüm BT web'e doğru ilerlerken, öğrenme ve benimseme kolaylığı için bu sınıfı özünde çok fazla işlevi olmayan JS can vas'a olabildiğince yakın yapmak daha iyidir.
ancak bu idealdir.
Muhtemelen böyle bir şeyi kendim yazabilirim, ancak en az yarım yıl tam zamanlı
kişisel olarak JS Canvas'taki her şeyi sevmiyorum, ancak standardizasyon için dize ayrıştırma olmadan yapmak için küçük değişikliklerle benzer bir şey uygulamak doğru olacaktır.
Ancak normal çalışma için MT5 olay modelini yeniden yapmamız gerekiyor, çünkü bu sadece korkunç
Her şeyin "bıçak altında" olduğu açık, ancak yine de soru biraz farklıydı. Mevcut sınıfta neyin değiştirilmesi/iyileştirilmesi isteniyor...
Her şeyin "bıçak altında" olduğu açık, ancak yine de soru biraz farklıydı. Mevcut sınıfta neyin değiştirilmesi/geliştirilmesi isteniyor...
onları hayata geçirmek için pürüzsüz yöntemler. Şimdi düşünüyorum da CCanvas'ta belgelenmemiş fonksiyonlar bile var.
onları hayata geçirmek için yumuşatılmış yöntemler. Şimdi CCanvas'ta belgelenmemiş işlevler bile var gibi görünüyor.
Gerçekten mi? Buna dikkat etmemiştim... Boş zamanıma bir göz atmam gerekecek....
"Bıyıklı çekmeceler" tipi çizelgelere ihtiyacım var, bunları eklemek için herhangi bir plan var mı?
Ayrıca, iki farklı ölçek kullanmak istediğinizde alt pencereleri / bodrumları kullanma yeteneği de eksik.
Merhaba.
CGraphic sınıfının ısı haritaları çizmek için dahili yöntemleri var mı?