OpenCL: от наивного кодирования - к более осмысленному
21 410
14
Введение
Первая статья "OpenCL: Мост в параллельные миры" была вводной в тему OpenCL. Рассматривались базовые вопросы взаимодействия программы, написанной на OpenCL (ее еще называют кернелом, хотя это не совсем точно), и внешней (хостовой) программой на языке MQL5. Также на примере вычисления числа pi = 3.14159265... мы показали некоторые возможности языка (например, использование векторных типов данных).
В некоторых случаях оптимизация быстродействия программы оказалась существенной. Однако все оптимизации были "наивными", т.к. не учитывали данных о "железе", на котором осуществляются все вычисления. Эти данные в большинстве случаев способны дать нам возможность сознательно достичь быстродействия, существенно превышающего возможности CPU.
Для демонстрации этих оптимизаций автор вынужден был воспользоваться теперь уже стандартным примером, который, пожалуй, является одним из самых хорошо изученных в литературе об OpenCL. Это перемножение двух больших матриц.
Начнем с главного - модели памяти, принятой в OpenCL, вместе с особенностями ее отражения на реальное hardware.
1. Иерархия памяти в современных вычислительных устройствах
1.1. Модель памяти в OpenCL
Вообще говоря, системы памяти сильно отличаются друг от друга в зависимости от компьютерной платформы. К примеру, все современные CPU поддерживают автоматическое кэширование данных - в отличие от GPU, в которых это бывает далеко не всегда.
Для переносимости кода (code portability) в OpenCL определяется абстрактная модель памяти, на которую могут ориентироваться кодеры, а также вендоры, которым необходимо поставить эту модель в соответствие с реальным hardware. Память, определяемая в OpenCL, условно показана на рисунке ниже:
Рис. 1. Модель памяти в OpenCL
Как только данные переносятся с хоста на девайс, они остаются в глобальной памяти девайса. Любые данные, переносимые в обратном направлении, также "оседают" в глобальной памяти (но теперь уже памяти хоста). Ключевое слово __global (два подчеркивания!) является модификатором, указывающим на то, что соответствующие указателю данные хранятся в глобальной памяти:
__kernel void foo( __global float *A ) { /// код кернела }
Глобальная память (global memory) доступна всем вычислительным устройствам (units) на девайсе, подобно основной памяти RAM в хостовой системе.
В постоянной памяти (сonstant memory), по контрасту с ее названием, не обязательно хранятся данные, предназначенные только для чтения. Эта память предназначена для данных, в которых к каждому элементу могут получить одновременный доступ все рабочие элементы (work units). Переменные с неизменяемыми значениями, конечно, тоже подпадают под эту категорию. Постоянная память в модели OpenCL является частью глобальной, и поэтому объекты памяти, переносимые в глобальную память, могут быть указаны как __constant.
Локальная память - это "черновая" память (scratchpad memory), адресное пространство которой уникально для каждого девайса. В виде hardware она часто реализуется как внутрикристальная память (on-chip memory), но специального требования, чтобы это было именно так, в OpenCL не существует.
Доступ к этой памяти имеет гораздо меньшую латентность и, следовательно, она обладает гораздо более высокой пропускной способностью, чем глобальная память. Мы попытаемся воспользоваться ее меньшей латентностью для оптимизации быстродействия кернела.
Спецификация OpenCL говорит, что переменную в локальной памяти можно объявить как в шапке кернела:
__kernel void foo( __local float *sharedData ) { }так и в его теле:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Обратите внимание, что в теле кернела нельзя объявить динамический массив; нужно обязательно указывать его размер.
Ниже, при оптимизации кернела для перемножения двух больших матриц, будет показано, как работать с локальными данными и каковы особенности реализации этой работы в терминале MetaTrader 5, с которыми автору пришлось столкнуться.
Локальные переменные и аргументы кернела без указателей приватны по умолчанию (если они указаны без модификатора __local). На практике эти переменные обычно размещаются в регистрах. И, напротив, приватные массивы и любые "выплеснутые" (spilled) регистры обычно располагаются в памяти вне кристалла (off-chip), т.е. в памяти с большой латентностью. Приводим цитату из Вики, относящуюся к делу, и ее перевод:
In many programming languages, the programmer has the illusion of allocating arbitrarily many variables. However, during compilation, the compiler must decide how to allocate these variables to a small, finite set of registers. Not all variables are in use (or "live") at the same time, so some registers may be assigned to more than one variable. However, two variables in use at the same time cannot be assigned to the same register without corrupting its value.
Variables which cannot be assigned to some register must be kept in RAM and loaded in/out for every read/write, a process called spilling. Accessing RAM is significantly slower than accessing registers and slows down the execution speed of the compiled program, so an optimizing compiler aims to assign as many variables to registers as possible. Register pressure is the term used when there are fewer hardware registers available than would have been optimal; higher pressure usually means that more spills and reloads are needed.
Во многих языках программирования у кодера создается иллюзия того, что он может разместить сколько угодно переменных. Однако во время компиляции компилятор должен принять решение о том, как разместить эти переменные в небольшом, конечном множестве регистров. Не все переменные используются ("live") в одно и то же время, и поэтому некоторые регистры можно поставить в соответствие нескольким переменным (более чем одной). Однако две переменные, используемые одновременно, невозможно назначить одному и тому же регистру, не потеряв его правильное значение.
Переменные, которые невозможно поставить в соответствие регистру, придется хранить в RAM и загружать/выгружать для каждой операции чтения/записи. Этот процесс называется "расплескиванием". Доступ к RAM значительно медленнее, чем к регистрам, и поэтому скорость исполнения компилированной программы снижается. Поэтому оптимизирующий компилятор стремится назначить регистрам как можно больше переменных. Существует термин, используемый в таких случаях, когда доступных регистров меньше, чем нужно для оптимального исполнения, - "регистровое давление". Более высокое давление обычно означает, что потребуется больше "расплескиваний" и повторных загрузок данных.
Хранилища памяти, о которых говорят в модели OpenCL, очень близко напоминают строение памяти в современных GPU. На рисунке ниже показана взаимосвязь между хранилищами памяти в OpenCL и их аналогами в GPU AMD Radeon HD 6970.
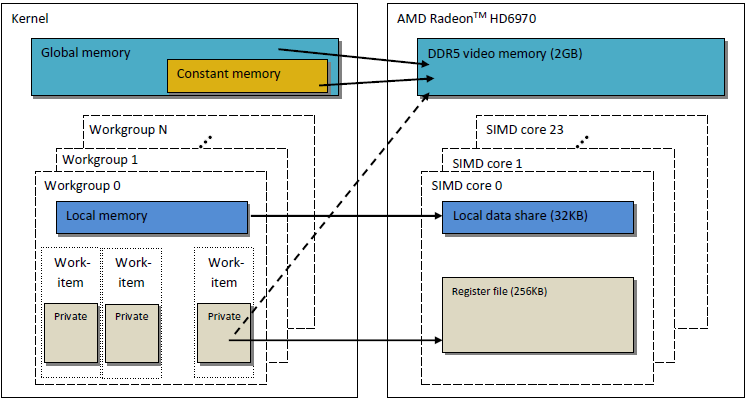
Рис. 2. Строение памяти в видеокарте Radeon HD 6970 и ее связь с абстрактной моделью памяти в OpenCL и ее связь с абстрактной моделью памяти в OpenCL
Перейдем к более подробному рассмотрению вопросов, связанных с конкретной реализацией памяти в GPU.
1.2. Память в современных дискретных GPU
1.2.1. Слияние запросов к памяти
Этот материал также важен для оптимизации быстродействия кернела, т.к. главная цель - достижение высокой пропускной способности памяти.
Рассмотрим рисунок, помогающий понять, как происходит адресация памяти:
Рис. 3. Схема адресации данных в глобальной памяти девайса
Пусть указатель на массив целых переменных int - это адрес Х = 0x00001232. Каждое int занимает в памяти 4 байта. Пусть нить (thread, который является программным аналогом рабочего элемента, исполняющего код кернела) обращается к данным по адресу Х[ 0 ]:
int tmp = X[ 0 ];
Мы предполагаем, что ширина шины памяти составляет 32 байта (256 бит). Такая ширина шины характерна для мощных GPU типа Radeon HD 5870. В некоторых других GPU ширина шины может быть другой - например, 384 бита или даже 512 в некоторых моделях NVidia.
Обращение к шине памяти должно соответствовать ее структуре, т.е. в первую очередь ее ширине. Другими словами, данные в памяти расположены "блоками" по 32 байта (256 бит). Независимо от того, по какому адресу в диапазоне от 0x00001220 до 0x0000123F мы обратились (в этом диапазоне ровно 32 байта, подсчитайте сами), мы все равно получим адрес 0x00001220 как начальный адрес чтения.
В результате обращения по адресу 0x00001232 будут возвращены все данные по адресам в диапазоне от 0x00001220 до 0x0000123F, т.е. 8 int чисел. Поэтому полезными данными окажутся только 4 байта (одно число int), а оставшиеся 28 байт (7 чисел int) будут бесполезными:
Рис. 4. Схема выбора нужных данных из памяти
На рисунке кружочком обведено нужное нам число, находящееся по указанному ранее адресу, - 0x00001232.
Для максимально эффективного использования шины GPU старается комбинировать вместе доступы от разных нитей в единые запросы к памяти, и чем меньше таких доступов, тем лучше. Причина заключается в том, что обращение к глобальной памяти девайса - очень дорогое удовольствие, сильно снижающее быстродействие исполняемой программы. Рассмотрим следующую строку кода кернела:
int tmp = X[ get_global_id( 0 ) ];
Допустим, что наш массив Х - прежний массив из примера раньше. Тогда первые 16 нитей (кернелов) будут обращаться к адресам от 0x00001232 до 0x00001272 (внутри этого диапазона - 16 чисел int, т.е. 64 байта). Если каждый из запросов был послан кернелами независимо, без предварительного объединения в единый, то в каждом из 16 запросов будет по 4 "полезных" байта и 28 "бесполезных", т.е. всего получится соответственно 64 используемых и 448 неиспользуемых байт.
Такая арифметика получается только из-за того, что каждое обращение к адресу, находящемуся внутри одного и того же 32-байтового блока памяти, вернет абсолютно идентичные данные. Это ключевой момент. Правильнее всего объединять многочисленные запросы в единые и согласованные, чтобы сэкономить на "бесполезных" запросах. Это действие будем называть слиянием (coalescing), а сами объединенные запросы - когерентными.
Рис. 5. Для получения нужных нам данных достаточно только трех запросов к памяти
Каждая ячейка на рисунке выше - это 4 байта. В нашем примере вполне достаточно было бы только 3 запросов. А если бы начало массива было выровнено по адресу с адресом начала каждого 32-byte блока в памяти, то достаточно было бы даже 2 запросов.
Для AMD GPU 64 нити являются частью волнового фронта, и поэтому они должны исполнять одну и ту же инструкцию как в SIMD. 16 нитей, последовательных по get_global_id( 0 ), - это ровно четверть волнового фронта, и для эффективного использования шины эти 16 нитей объединяются в когерентный запрос.
Ниже показана пропускная способность памяти при когерентных запросах в сравнении с некогерентными, т.е. "произвольными". Картина относится к Radeon HD 5870. Аналогичная картина наблюдается и для карт от NVidia.
Рис. 6. Сравнительный анализ пропускной способности памяти при когерентных и некогерентных запросах
Легко видеть, что когерентный запрос к памяти позволяет увеличить ее пропускную способность примерно на порядок.
1.2.2. Банки памяти
Память состоит из банков, в которых и хранятся данные. В современных GPU это обычно 32-битовые слова (4-байтовые). Последовательные данные хранятся в соседних банках. Если группа нитей обращается к последовательным элементам, то конфликтов доступа к банкам не будет.
Максимальный негативный эффект от конфликтов банков обычно наблюдается в локальной памяти GPU. Поэтому желательно делать так, чтобы доступ к локальным данным от соседних нитей был к различным банкам памяти.
В случае hardware от AMD волновой фронт, при исполнении которого возникают конфликты доступа к банкам, приостанавливает свое исполнение - до тех пор, пока не заканчиваются операции доступа к локальной памяти. При этом происходит сериализация, т.е. участки кода, которые должны исполняться параллельно, исполняются последовательно. Это крайне негативно отражается на быстродействии кернела.
Рис. 7. Схемы бесконфликтного обращения к банкам памяти
На рисунке выше конфликтов нет, т.к. все нити обращаются к разным данным.
Покажем случай, когда конфликты есть:
Рис. 8. Доступ к банкам данных с конфликтами
Однако из этой ситуации есть исключение: если все запросы относятся к одному адресу, то банк способен передать broadcast (общее сообщение для всех), чтобы исключить задержку:
Рис. 9. Обращение всех нитей по одному адресу
Аналогичные явления в случае обращения к глобальной памяти также наблюдаются, но влияние этих конфликтов значительно меньше.
- Память GPU отличается от памяти CPU. Главная цель оптимизаций быстродействия программы с использованием OpenCL - обеспечение максимальной пропускной способности, а не снижение латентности, как при работе на CPU.
- Характер доступа к памяти оказывает огромное влияние на эффективность использования шины. Низкая эффективность использования шины - это низкое быстродействие.
- Для повышения быстродействия кода желательно, чтобы доступ к памяти был когерентным. Кроме того, крайне желательно избегать конфликтов доступа к банкам.
- Специфичная информация о hardware (ширина шины, количество банков памяти, а также количество нитей, которые можно объединить для разового когерентного доступа) может быть найдена в документации вендора.
В качестве примера приведем данные о некоторых видеокартах семейства Radeon 5xxx:
Рис. 10. Технические параметры middle- и high-end видеокарт Radeon HD 58xx
Давайте теперь приступим к практическим действиям и начнем кодировать.
2. Умножение больших прямоугольных матриц: от последовательного кода на CPU к параллельному на GPU
2.1. Код на MQL5
Теперь задача, в отличие от предыдущей статьи "OpenCL: Мост в параллельные миры", будет стандартной - умножение двух матриц. Выбор задачи обусловлен, прежде всего, достаточно полной информацией о ней в разных источниках. В большинстве из них, в конце концов, предлагаются более-менее согласованные между собой решения. Вот этим путем мы и пойдем, постепенно разъясняя смысл модельных конструкций и не забывая о том, что мы работаем на реальном hardware.
Ниже показана известная в линейной алгебре формула для умножения матриц, модифицированная для компьютерных вычислений. Первый индекс - номер строки матрицы, второй - номер столбца. Каждый элемент выходной матрицы вычисляется путем последовательного прибавления к накопленной сумме очередного произведения элементов первой и второй матрицы. Эта накопленная сумма, в конце концов, и оказывается вычисляемым элементом выходной матрицы:
Рис. 11. Формула умножения матриц
Графически эту формулу можно представить в следующем виде:
Рис. 12. Схема алгоритма умножения матриц (на примере вычисления одного элемента выходной матрицы)
Легко оценить, что при равных размерах обоих измерений у обеих матриц, равного N, количество сложений-умножений оценивается функцией O(N^3): для вычисления каждого элемента результирующей матрицы нужно получить скалярное произведение строки первой матрицы на столбец второй. Это требует около 2*N операций сложения-умножения. Умножая на количество элементов матрицы N^2, получаем искомую оценку. Следовательно, примерное время выполнения кода довольно существенно зависит от N - в кубической степени.
Величины количества строк и столбцов для матриц в дальнейшем выбраны равными 2000 только для удобства, и их можно было бы сделать произвольными, но не слишком большими.
Код на MQL5 очень несложный:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // строк в первой матрице #define COLSROWS 1000 // столбцов в первой = строк во второй #define COLS2 1000 // столбцов во второй float first[ ROWS1 ][ COLSROWS ]; // первая матрица float second[ COLSROWS ][ COLS2 ]; // вторая матрица float third[ ROWS1 ][ COLS2 ]; // результат умножения //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- поехали на CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| генерируем исходные матрицы; при окончательном подсчете | //| времени исполнения эта генерация не отражается | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| генерируем одно значение элемента матрицы: | //| равномерно распределенная величина на отрезке [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Основная функция умножения матриц | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Листинг 1. Исходная последовательная программа на хосте
Результаты исполнения при различных параметрах:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Как видим, наша оценка зависимости времени исполнения от линейных размеров матриц оказалась верной: при увеличении всех размеров матриц вдвое время исполнения увеличивается примерно в 8 раз.
Несколько слов об алгоритме: в функции умножения mul() можно произвольно менять порядок циклов. Оказывается, это существенно влияет на время исполнения: отношение времен исполнения самого медленного к самому быстрому варианту составляет примерно 1.73.
Здесь показан только самый быстрый вариант, а остальные проверенные варианты можно увидеть в коде, приложенном в конце статьи (файл matr_mul_2dim.mq5). Руководство "OpenCL Programming Guide" (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) на сей счет говорит следующее (стр. 512):
Разумеется, это далеко не все оптимизации исходного "непараллельного" кода, которые мы можем осуществить. Некоторые из них связаны с hardware (инструкции (S)SSEx), а некоторые - чисто алгоритмические, например, алгоритм Штрассена, Копперсмита-Винограда и т.п. Отметим, что размеры умножаемых матриц для алгоритма Штрассена, при которых на CPU получается существенное ускорение в сравнении с классическим алгоритмом, совсем невелики и составляют всего 64х64. В этой статье мы намерены научиться быстро умножать матрицы с линейным размером до нескольких тысяч (примерно до 5000).
2.2. Первая реализация алгоритма на OpenCL
Теперь переносим этот алгоритм на OpenCL, создав ROWS1 * COLS2 нитей, т.е. удалив из кернела оба внешних цикла. Каждая нить будет исполнять COLSROWS итераций, так что внутренний цикл останется как часть кернела.
Так как для OpenCL кернела нам придется создавать три линейных буфера, исходный алгоритм было бы справедливо переделать в как можно более близкий к алгоритму кернела. Код "непараллельной" программы "на одном ядре CPU" с линейными буферами будет показан вместе с кодом кернела. Оптимальность кода с двумерными массивами совсем не означает, что его аналог будет тоже оптимальным для случая линейных буферов: все проверки придется проводить заново. Поэтому в качестве исходного варианта мы снова выбираем вариант c-r-cr, который был первоначальным и соответствует обычной логике умножения матриц в линейной алгебре.
При этом, чтобы избавиться от возможной путаницы с адресацией элементов матрицы/буфера, ответим на главный вопрос: если мы разместили матрицу Matr( M строк на N столбцов ) в виде линейного буфера в глобальной памяти GPU, как вычислить линейное смещение элемента Matr[ row ][ column ]?
Какого-то фиксированного порядка размещения матрицы в памяти GPU на самом деле не существует, т.к. это определяется исключительно логикой задачи. Например, элементы обеих матриц можно было бы разместить в буферах по-разному, т.к. с точки зрения алгоритма умножения матрицы несимметричны: строки первой умножаются на столбцы второй. При последовательном считывании элементов матриц из глобальной памяти GPU в каждой итерации кернела такая перестройка может серьезно отразиться на производительности расчета.
В первой реализации алгоритма мы разместим матрицы одинаково - по строкам. В буфере сначала будут размещены элементы первой строки, затем все элементы второй и т.п. При этом формула перевода 2-мерной реализации матрицы Matr[ M (строк) ][ N (столбцов) ] в одномерный вариант выглядит так:
Рис. 13. Алгоритм пересчета двумерного пространства индексов в одномерное для размещения матрицы в буфере GPU
На рисунке также приведен пример того, как пересчитывать двумерное пространство матрицы в одномерное при размещении матриц в буфере по столбцам.
Ниже приведен немного урезанный код нашей первой реализации программы с исполнением на девайсе OpenCL:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // строк в первой матрице #define COLSROWS 2000 // столбцов в первой = строк во второй #define COLS2 2000 // столбцов во второй #define REALTYPE float REALTYPE first[]; // первый одномерный буфер (матрица) rows1 * colsrows REALTYPE second[]; // второй буфер colsrows * cols2 REALTYPE thirdGPU[ ]; // результат умножения - тоже буфер rows1 * cols2 REALTYPE thirdCPU[ ]; // результат умножения - тоже буфер rows1 * cols2 input int _device=1; // тут девайс, можно менять (сейчас 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Основная функция умножения матриц; | //| Входные уже сформированы, выходная инициализирована нулями | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- начинаем работать на непераллельной версии ("голый" CPU, одно ядро) //--- считаем выходную матрицу на одном ядре CPU uint st=GetTickCount(); mulCPUOneCore(); //--- выводим полное время расчетов double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- начинаем работать с OCL int clCtx; // хэндл контекста int clPrg; // хэндл программы на девайсе int clKrn; // хэндл кернела int clMemIn1; // хэндл первого буфера (входного) int clMemIn2; // хэндл второго буфера (входного) int clMemOut; // хэндл третьего буфера (выходного) //--- начинаем считать время исполнения программы на GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- начало подсчета подного времени исполнения кода OCL st=GetTickCount(); executeGPU(clKrn); //--- создаем буфер для чтения и считываем результат; он нам пригодится позднее REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- заканчиваем считать полное время исполнения программы //--- вместе со временем извлечения данных из GPU обратно в RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- подсчитываем прошедшее время Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- отладка: рандомные проверки. Проверяется напрямую корректность умножения //--- на исходных и результирующей матрице на нескольких десятках примеров for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- инициализируем генератор случайных чисел MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- выставляем нужные размеры одномерных представлений входных и выходной матриц ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- генерируем обе входные матрицы и инициализируем выходные нулями genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| размещение по строкам, Matr[ M (строк) ][ N (столбцов) ]: | //| Matr[row][column] = buff[row * N (столбцов в матрице) + column] | //| генерируем исходные матрицы; при окончательном подсчете | //| времени исполнения эта генерация не отражается | //| буферы заполняем по строкам! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| генерируем одно значение элемента матрицы: | //| равномерно распределенная величина на отрезке [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // контекст int& clPrg, // программа на девайсе int& clKrn, // кернел int& clMemIn1, // первый буфер (входной) int& clMemIn2, // второй буфер (входной) int& clMemOut) // третий бфуер (выходной) { //--- записываем код кернела в файл WriteCLProgram(); //--- создаем контекст, программу и кернел clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- создаем все три буфера для трех матриц //--- первая матрица - входная clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- вторая матрица - входная clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- третья матрица - выходная clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- устанавливаем аргументы кернела CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- пишем сгенерированные матрицы в буферы девайса CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 везде return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- устанавливаем параметры рабочего пространства задачи и исполняем программу OpenCL uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - копия того, что записано в буфер thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- уничтожаем в обратной последовательности все созданное для расчета на девайсе OpenCL CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| Рандомная проверка верности вычислений | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- элемент буфера m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- элемент матрицы, вычисленной не на OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Листинг 2. Первая реализация программы на OpenCL
Последние две функции полезны для верификации корректности вычислений. Полный код приложен в конце статьи (matr_mul_1dim.mq5). Отметим, что размерности не обязательно должны соответствовать только квадратным матрицам.
Практически всегда дальнейшие изменения будут относиться только к коду кернела, поэтому далее будут размещены только коды модификаций кернелов.
Тип REALTYPE введен для удобства изменения точности расчетов с float на double. Следует отметить, что тип REALTYPE объявлен не только в хостовой программе, но и внутри кернела. При необходимости изменения этого типа нужно одновременно менять его в двух местах, в обоих #define - в хостовой программе и в коде кернела.
Результаты исполнения кода (везде дальше - данные типа float):
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Исполнение на Radeon HD 4870 (_device = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Как видим, на GPU кернел исполняется немного медленнее. Однако к оптимизации специально для GPU мы еще не приступали.
Несколько выводов:
- Изменение представления матриц с двумерного на одномерное (соответствующее представлению в программе, исполняемой на девайсе) несущественно повлияло на общее время исполнения последовательной версии программы.
- В качестве исходного варианта для дальнейшей оптимизации избран самый интуитивно понятный алгоритм вычисления, соответствующий определению произведения матриц в линейной алгебре. Он немного медленнее самого быстрого, но в свете будущего повышения быстродействия на GPU этот фактор не является существенным.
- Время исполнения необходимо считать только после считывания буферов в память RAM, но не после команды CLExecute(). Причина, которую указал автору статьи MetaDriver, вероятно, заключается в следующем:MetaDriver: Перед чтением из буфера CLBufferRead() просто ждёт реального завершения работы программы. CLExecute() на самом деле асинхронная функция постановки в очередь. Она возвращает результат сразу - задолго до завершения работы cl-кода.
- В руководствах по расчетам на GPU обычно считают не время исполнения кернела, а пропускную способность (throughput), связанную с разными объектами, - памятью, арифметическими вычислениями и т.п. То же самое мы можем сделать здесь и будем делать дальше.
Мы знаем, что для вычисления матрицы с параметром размера 2000 нам нужно выполнить примерно 2 * 2000 сложений/умножений для каждого элемента. Умножая на число элементов матрицы (2000 * 2000), получаем, что общее число операций над данными float равно 16 млрд. При этом CPU выполняет это за 115.628 с, что соответствует "скорости прокачки данных", равной
В то же время вспомним, что до сих пор самое быстрое вычисление на "одноядерном CPU" при параметре матрицы 2000 заняло всего 83.663 с (см. наш первый код без OpenCL). Отсюда
Эту цифру примем за референсную, исходную точку наших оптимизаций.
Вычисление с помощью OpenCL на CPU аналогично дает нам:
Наконец, считаем throughput на GPU:
2.3. Устраняем непоследовательные доступы к данным
В коде кернела можно сразу увидеть несколько неоптимальностей.
Рассмотрим тело цикла внутри кернела:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
Легко видеть, что при движении счетчика цикла (cr++) из первого буфера in1[] извлекаются данные, расположенные рядом. В то же время данные из второго буфера in2[] извлекаются с "дырами" между ними, равными COLS2. Другими словами, для второго буфера большая часть извлекаемых данных будет бесполезной, т.к. запросы к мапяти будут некогерентными (см. раздел 1.2.1. Слияние запросов к памяти). Для исправления этой ситуации достаточно изменить код в трех местах, изменив формулу расчета индекса массива in2[], а также порядок его формирования:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Теперь при изменении счетчика цикла (cr++) данные из обоих массивов будут извлекаться последовательно, без "дырок".
- Код заполнения буфера в genMatrices(). Нам нужно теперь заполнить его по столбцам матрицы, а не по строкам, как сначала:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Проверочный код в функции checkRandom():
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Результаты исполнения на CPU:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Как видим, когерентный доступ к данным практически не повлиял на время исполнения на GPU, но явно улучшил время исполнения на CPU. Очень вероятно, что все дело в факторах, которые будут оптимизированы позднее, - в частности, в очень высоких латентностях доступа к глобальным переменным, от которых нужно скорее избавляться.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
Код с новым кернелом находится в файле matr_mul_1dim_coalesced.mq5 в конце статьи.
Приведем код кернела тут же:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Листинг 3. Кернел с объединенным доступом к глобальным данным (coalescing)
Приступим к дальнейшим оптимизациям.
2.4. Убираем дорогой доступ к глобальной памяти GPU в выходной матрице
Как известно, латентность доступа к глобальной памяти GPU чрезвычайно высока (порядка 600-800 циклов). Например, латентность исполнения операции сложения двух чисел равна примерно 20 циклам. Главной целью оптимизаций при вычислениях на GPU является сокрытие этой латентности за счет увеличения throughput вычислений. В цикле созданного ранее кернела мы постоянно обращаемся к элементам глобальной памяти, и это дорогое удовольствие.
Теперь введем локальную переменную sum внутри кернела (доступ к которой во много раз быстрее, т.к. это приватная переменная кернела, располагающаяся в регистре рабочего элемента), а после окончания цикла одноразово присвоим элементу выходного массива полученное значение sum:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Листинг 4. Вводим приватную переменную для вычисления нарастающей суммы в цикле вычисления скалярного произведения
Полный файл исходного кода - matr_mul_sum_local.mq5, приложен в конце статьи.
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================Вот это настоящий скачок производительности!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
Главный принцип, которого мы стараемся придерживаться при последовательных оптимизациях, звучит так: сначала желательно как можно полнее реорганизовать структуру данных так, чтобы она соответствовала задаче и, в частности, "железу", - и только потом заниматься "тонкими" оптимизациями, использующими "скорострельные" алгоритмы вычислений типа mad() или fma(). Следует помнить, что не всегда оптимизации, расположенные последовательно, будут обязательно увеличивать производительность; никакой гарантии тут не может быть.
2.5. Увеличиваем работу, выполняемую одним кернелом
В параллельном программировании важно организовать вычисления так, чтобы свести оверхед (затраты времени) на организацию параллельной работы к минимуму. При матрицах с параметром порядка 2000 один рабочий элемент, вычисляющий один элемент выходной матрицы, выполняет количество работы, равное 1 / 4000000 части общей задачи.
Это явно многовато и слишком далеко от реального количества элементов, исполняющих вычисления на "железе". Теперь, в новой версии кернела, мы будем вычислять всю строку матрицы - вместо одного элемента.
Важно отметить, что пространство задач теперь изменяется с 2-мерного на одномерное, т.к. в каждой задаче кернела мы теперь вычисляем не один элемент матрицы, а целое измерение - всю строку целиком. Поэтому пространство задач превращается в количество строк матрицы.
Рис. 14. Схема вычисления полной строки результирующей матрицы
Код кернела усложняется:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 5. Кернел для вычисления всей строки результирующей матрицы
void executeGPU( int clKrn ) { //--- устанавливаем параметры рабочего пространства задачи и исполняем программу OpenCL uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Результат исполнения (полный исходный код - в файле matr_mul_row_calc.mq5):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
Как видим, время исполнения на CPU явно ухудшилось, а на GPU тоже стало хуже, но ненамного. Ничего страшного: это стратегическое изменение, временно ухудшающее "локальную" ситуацию - но только для того, чтобы далее кардинально поднять производительность.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2.6. Переносим строку первого массива в приватную память
Главной особенностью алгоритма перемножения матриц является большое количество умножений с сопутствующим накоплением результата. Хорошая, качественная оптимизация этого алгоритма должна предполагать сведение к минимуму операций перемещения данных. Но до сих пор все наши модификации кернелов держали две из трех матриц в глобальной памяти при вычислениях внутри главного цикла накопления скалярного произведения.
Это означает, что для каждого скалярного произведения (которым и является каждый элемент выходной матрицы) все входные данные постоянно "прокачиваются" через всю иерархию памяти - от глобальной к приватной, - с соответствующими латентностями. Этот трафик можно снизить, сделав так, чтобы каждый рабочий элемент повторно использовал одну и ту же строку первой матрицы для каждой вычисляемой строки выходной матрицы.
Рис. 15. Переносим строку первой матрицы в приватную память рабочего элемента
Код хостовой программы никак не меняется. В кернеле изменения тоже минимальны. Благодаря тому, что промежуточный одномерный приватный массив создается внутри кернела, GPU старается разместить его в приватной памяти элемента, исполняющего кернел. Требуемая строка первой матрицы просто копируется из глобальной памяти в приватную. При этом следует отметить, что даже это копирование будет относительно быстрым. Трюк заключается в том, что самое "дорогое" копирование элементов строки первого массива из глобальной памяти в приватную выполняется когерентно, и затраты на это копирование достаточно малы в сравнении со временем исполнения основного двойного цикла, считающего строку выходной матрицы.
Код кернела (закомментированный код в основном цикле - это то, что было в предыдущей версии):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 6. Кернел со строкой первой матрицы в приватной памяти рабочего элемента.
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
Производительность CPU осталась примерно на том же уровне, что и в прошлый раз, однако производительность GPU снова вернулась к высшему достигнутому уровню, но уже в новом качестве. Обратите внимание на то, что производительность CPU как бы застыла на месте, испытывая небольшие колебания, - в то же время производительность GPU движется вверх (не всегда, правда) довольно существенными скачками.
Отметим, что реальная арифметическая производительность должна быть чуть выше, т.к. теперь исполняется больше операций, чем раньше, - за счет копирования строки первой матрицы в приватную память. Но на конечную оценку производительности это влияет незначительно.
Исходный код - в файле matr_mul_row_in_private.mq5.
2.7. Переносим столбец второго массива в локальную память
Теперь уже можно догадаться, каким будет следующий этап. Мы уже предприняли меры, направленные на сокрытие латентностей, связанных с выходной и первой входной матрицей. Осталась вторая.
Более внимательное изучение скалярных произведений, используемых при умножении матриц, показывает, что в процессе вычисления строки выходной матрицы все рабочие элементы в группе повторно "прокачивают" одни и те же столбцы второй умножаемой матрицы через девайс. Это схематически показано на рисунке:
Рис. 16. Переносим столбец второй матрицы в локальное хранилище (Local Data Share) локальной группы
Мы можем снизить затраты на перемещение данных из глобальной памяти, если рабочие элементы, составляющие локальную группу, скопируют столбцы второй матрицы в локальную память группы прежде, чем начнется вычисление строк выходной матрицы.
Для этого потребуется внести изменения не только в кернел, но и в хостовую программу. Самое главное изменение - это задание локальной памяти для каждого кернела. Это необходимо делать явно, т.к. динамическое распределение памяти внутри кернела в OpenCL не поддерживается. Следовательно, сначала нужно разместить на хосте объект памяти соответствующего размера, а затем обработать его внутри кернела.
Уже затем, при исполнении кернела, рабочие элементы копируют столбец второй матрицы в локальную память. Это выполняется параллельно, с помощью циклического распределения итераций цикла по всем рабочим элементам, входящим в локальную группу. Однако до того как рабочий элемент начнет выполнять свою основную работу (вычисление строки выходной матрицы), все копирования уже должны завершиться.
Поэтому после цикла, выполняющего копирование, вставлена команда:
barrier(CLK_LOCAL_MEM_FENCE);
Это "местное ограждение памяти" гарантирует, что каждый рабочий элемент в группе "видит" некоторое согласованное с другими элементами состояние локальной памяти. Все рабочие элементы в локальной группе должны исполнить команды до барьера, прежде чем любой из них сможет продолжать исполнение кернела. Другими словами, барьер - это специальный механизм синхронизации, существующий между рабочими элементами внутри локальной группы.
Механизмов синхронизации между локальными группами в OpenCL не предусмотрено.
Для иллюстрации действия барьера ниже приведена иллюстрация:
Рис. 17. Иллюстрация действия барьера
На самом деле нам только кажется, что внутри рабочей группы рабочие элементы исполняют код строго одновременно. Это всего лишь абстракция программной модели OpenCL.
До сих пор наши коды кернела, исполняемые на разных рабочих элементах, не нуждались в синхронизации операций, т.к. явного общения, заданного программно в кернеле, между ними не было, и оно не было нужно. Но именно в этом кернеле синхронизация необходима, т.к. заполнение локального массива распределяется параллельно между всеми элементами локальной группы.
Другими словами, каждый рабочий элемент записывает свои несколько значений в локальное хранилище (здесь - массив), но он не знает, на какой стадии этот же процесс записи находится у других рабочих элементов. Для того, чтобы какой-нибудь рабочий элемент не продолжил исполнение кернела раньше, чем нужно, т.е. до полного формирования локального массива, этот барьер и нужен.
Нужно понимать, что на скорости на CPU эта оптимизация вряд ли скажется позитивно: из руководства по оптимизации на OpenCL от корпорации Intel известно, что при исполнении кернела на CPU все объекты памяти OpenCL кэшируются на уровне "железа", и поэтому явное программное кэширование промежуточных результатов через локальную память лишь вносит умеренную задержку при исполнении кернела на CPU.
Следут отметить одно важное обстоятельство, из-за которого автор статьи потерял много времени. Оно связано с тем, что в реализации разработчиков терминала не существует возможности передать локальную переменную через заголовок функции кернела, т.е. на этапе компиляции. Причина заключается в том, что для выделения памяти объекту памяти как аргументу функции кернела нам пришлось бы сначала явно создавать этот объект в памяти CPU с помощью функции CLBufferCreate(), явно указывая его размер в качестве параметра функции. Эта функция возвращает хэндл объекта памяти, который в дальнейшем будет находиться в глобальной памяти GPU и может находиться только там.
Однако локальная память - это другая память, не глобальная, и поэтому созданный объект памяти невозможно разместить в локальной памяти локальной группы.
В полноценном OpenCL API существует возможность явного назначения памяти нужного размера с указателем NULL аргументу кернела - даже без создания самого объекта памяти (функция CLSetKernelArg()). Однако синтаксис функции CLSetKernelArgMem(), являющейся MQL5-аналогом полноценной функции API, не позволяет нам передать в нее количество размещаемой под аргумент памяти, не создавая сам объект памяти. В функцию CLSetKernelArgMem() можно только передать хэндл буфера, уже созданного в глобальной памяти CPU и предназначенного для переноса в глобальную память GPU. Получается парадокс.
К счастью, существует эквивалентный способ работы с локальными буферами в кернеле. Достаточно просто объявить такой буфер с модификатором __local в теле кернела. При этом локальная память, выделяемая локальной группе, будет определяться на этапе Runtime, а не при компиляции.
Команды, следующие после барьера в кернеле (строка барьера выделена красным в коде), - это по сути то же самое, что было при предыдущей оптимизации. Код хостовой программы не изменился (исходный код - в файле matr_mul_col_local.mq5).
Итак, новый код кернела:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 7. Столбец второй матрицы - в локальную память локальной группы
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
В обоих случаях произошли ухудшения, но назвать их существенными, пожалуй, нельзя. Вполне возможно, что, варьируя размер локальной группы, можно было бы добиться улучшения производительности вместо ее ухудшения. Этот пример скорее служит другой цели - показать, как использовать объекты локальной памяти.
Есть гипотеза, объясняющая снижение производительности при использовании локальной памяти. Обратимся к статье Сравнение OpenCL с CUDA, GLSL и OpenMP на habrahabr.ru, написанной примерно 2 года назад:
Другими словами, локальная память для продуктов 2-летней давности - не быстрее глобальной? Судя по времени написания этого поста, два года назад уже были выпущены видеокарты семейства Radeon HD 58xx - и ситуация, по словам автора, была такой же печальной. Не слишком в это верится, особенно для великолепной серии Evergreen от AMD. Было бы интересно проверить это на более современных картах - например, семейства HD 69xx.
Дополнение: запускаем утилиту GPU Caps Viewer и видим в закладке OpenCL следующее:
Рис. 18. Основные параметры OpenCL, поддерживаемые видеокартой HD 4870
CL_DEVICE_LOCAL_MEM_TYPE: Global
В Спецификации языка (Таблица 4.3, стр. 41) этому параметру дается следующее пояснение:
Type of local memory supported. This can be set to CL_LOCAL implying dedicated local memory storage such as SRAM, or CL_GLOBAL.
Тип поддерживаемой локальной памяти. Его можно установить в CL_LOCAL, подразумевая специальное локальное хранилище памяти типа SRAM, - или в CL_GLOBAL.
Таким образом, локальная память в видеокарте HD 4870 действительно является частью глобальной, и поэтому манипуляции с локальной памятью на этой видеокарте бесполезны и будут не быстрее работы с глобальной памятью. Здесь - еще одна ссылка, где специалист от AMD разъясняет этот момент для серии HD 4xxx. Совершенно не обязательно, что все будет так же плохо на видеокарте, имеющейся у вас, но мы просто показали, где искать подобную информацию, относящуюся к "железу", - в данном случае в GPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Наконец, добавим несколько завершающих штрихов, явно векторизовав кернел. В качестве исходного возьмем кернел, полученный на этапе размещения строки первого массива в приватную память (matr_mul_row_in_private.mq5), т.к. именно он оказался самым быстрым.
2.8. Векторизация кернела
Эту операцию лучше провести в несколько этапов, чтобы не запутаться. В первоначальной модификации мы не меняем типы данных внешних параметров кернела и векторизуем только вычисления во внутреннем цикле:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 8. Частичная векторизация кернела на float4 (только внутренний цикл)
CPU:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Удивительно, но даже такая примитивная векторизация принесла эффект на GPU - правда, не слишком значительный, в районе 10%.
Продолжаем распространять векторизацию вглубь кода: перенесем дорогие операции преобразования типа в векторный REALTYPE4, вместе с указанием явных компонент вектора, во внешний служебный цикл, заполняющий приватную переменную rowbuf[]. В кернеле изменений по-прежнему нет.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 9. Избавляемся от дорогих операций преобразования типов в главном цикле кернела
Отметим, что максимальный счетчик внутреннего цикла (и вспомогательного тоже) уменьшился в 4 раза, т.к. для первого массива нам теперь нужно в 4 раза меньше операций чтения: чтение стало явно векторным.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Пропускная способность (арифметическая):
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Изменения производительности, как видим, существенны для CPU и почти революционны для GPU. Исходный код - в файле matr_mul_vect_v2.mq5.
Проведем аналогичные манипуляции для последнего варианта кернела, но теперь с шириной векторизации, равной 8. Такое намерение автора обусловлено тем, что ширина шины памяти в GPU равна 256 бит, т.е. 32 байта, или 8 чисел типа float; поэтому одновременная обработка 8 float, эквивалентная одновременной работе с float8, представляется вполне естественной.
Следует помнить, что при этом величина COLSROWS должна нацело делиться на 8. Это нормальное требование: чем "тоньше" оптимизации, тем более специфичны требования к данным.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Листинг 10. Векторизация кернела с шириной векторных данных, равной 8
Нам пришлось добавить в код кернела inline функцию dot8(), позволяющую вычислять скалярное произведение для векторов шириной 8. В OpenCL стандартная функция dot() умеет вычислять скалярное произведение только для векторов до ширины 4. Исходный код - в файле matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Результат неожиданный: время исполнения на CPU сократилось чуть ли не в 2 раза, зато на GPU оно слегка увеличилось - несмотря на то, что float8 является "естественной" шириной шины для HD 4870 (она равна 256 бит). И снова нам на помощь приходит GPU Caps Viewer.
Объяснение можно найти на рис. 18, в предпоследней строке списка параметров:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Заглядываем в Спецификацию OpenCL и видим следующий текст в крайней колонке Таблицы 4.3 на стр. 37, относящийся к этому параметру:
Preferred native vector width size for built-in scalar types that can be put into vectors. The vector width is defined as the number of scalar elements that can be stored in the vector.
Предпочтительная нативная ширина вектора для встроенных скалярных типов, которая может быть установлена для векторов. Ширина вектора определяется как количество скалярных элементов, которые можно сохранить в векторе.
Таким образом, именно для видеокарты HD 4870 предпочтительная ширина вектора floatN равна float4, а не float8.
На этом мы закончим цикл оптимизаций кернела. Можно было бы достичь и большего, но объем статьи этого уже не позволяет.
Заключение
В статье продемонстрированы некоторые возможности оптимизации, открывающиеся при хотя бы поверхностном учете особенностей "железа", на котором исполняется кернел.
Полученные цифры весьма далеки от предельных, но даже они показывают, что при том наборе возможностей, который имеется здесь и сейчас (OpenCL API в реализации разрaботчиков терминала не позволяет контролировать некоторые важные для оптимизации параметры - в частности, размер локальной группы), выигрыш в производительности в сравнении с исполнением хостовой программы очень существенен: выигрыш по времени исполнения на GPU в сравнении с последовательной программой на CPU (правда, не слишком оптимизированной) близок к 200:1.
Выражаю огромную признательность MetaDriver'у за ценные советы и возможность пользоваться дискретным GPU на тот момент, пока у автора его не было в наличии.
Содержимое приложенных файлов:
- matr_mul_2dim.mq5 - исходная последовательная программа на хосте с двумерным представлением данных;
- matr_mul_1dim.mq5 - первая реализация кернела с одномерным представлением данных и соответствующей "обвязкой" MQL5 OpenCL API;
- matr_mul_1dim_coalesced - кернел с когерентным доступом к глобальной памяти;
- matr_mul_sum_local - введена приватная переменная вычисления скалярного произведения - вместо обращения к вычисляемой ячейке выходного массива, хранящейся в глобальной памяти;
- matr_mul_row_calc - вычисление полной строки выходного массива в кернеле;
- matr_mul_row_in_private - строка первого массива - в приватной памяти;
- matr_mul_col_local.mq5 - столбец второго массива - в локальной памяти;
- matr_mul_vect.mq5 - первая векторизация кернела (float4, только внутренний подцикл главного цикла);
- matr_mul_vect_v2.mq5 - избавление от дорогих операций преобразования данных в главном цикле;
- matr_mul_vect_v3.mq5 - векторизация с шириной вектора, равной 8.
200 usd за вашу статью по алготрейдингу!
MetaTrader 5 - больше, чем можно представить!
Визуализируй стратегию в тестере MetaTrader 5
Создай торгового робота за 6 шагов!
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Можно было бы сразу начать с нервосетки. Она явно связана с трейдерским делом. Правда, сам в нервосетках ничего не понимаю, но, потратив несколько дней, разобрался бы в основах.
Как Вы думаете, это было бы проще, чем простенькое вычисление числа pi - даже без входных буферов?
Сомневаюсь что-то...
Mathemat, не считаю нейросеть простым примером :-))
Пример с ПИ очень удачен, имхо...
Можно было добавить например какой-нибудь статистический расчёт. Условно. Взять историю котировок по всем инструментам в терминале. Допустим минутную. Синхронизировать котировки. Это будет двумерный массив. Строк там наверное будет несколько тысяч... Посчитать мувинги разных периодов по каждому инструменту. Массив уже вырастет в несколько раз. И посмотреть, как быстро OpenCL справиться с расчётом... такая пока что мысль...
Уже собираюсь сделать это, (скорее всего) будет как раз сбор статистики на большой истории. К мувам, правда, не имеет никакого отношения. Ненавижу мувы - имею на это право :)
Синхронизировать котировки.
Это задача скорее для CPU, а не GPU. Для GPU ведь явно не каждая задачка подходит, так ведь? А лучше выбрать такую, чтобы подходила, т.к. GPU именно для этого и нужен.
Это будет двумерный массив.
Предполагаю, что в будущей статье будет трехмерный. Заодно станет понятно, как работать с буфером GPU, отображающим массив любой размерности.
Уже собираюсь сделать это, (скорее всего) будет как раз сбор статистики на большой истории...
Предполагаю, что в будущей статье будет трехмерный. Заодно станет понятно, как записывать в буфер GPU массив любой размерности и как с ним работать.
здОрово! Будем ждать...
А что, их еще и синхронизировать надо?
P.S. Почитал справку, вижу, что надо.
Пересчитал результаты статьи с учетом обновления железа.
Было год назад: CPU Intel Pentium G840 (2 ядра @ 2.8 GHz) + видеокарта AMD HD4870
Стало недавно: CPU Intel Xeon E3-1230v2 (4 ядра/8 потоков @ 3.3 GHz; чуть отстает по производительности от i7-3770) + видеокарта AMD HD6870.
Результаты расчетов в OpenCL показаны на графике (по горизонтали - номер оптимизации, примененной в статье):
Время вычислений показано по вертикали в секундах. Время исполнения скрипта "в одно дуло на ЦПУ" (на одном ядре, без OpenCL) колебалось в зависимости от изменений алгоритма в пределах 95 плюс-минус 25 сек.
Как видим, все вроде понятно, но все же не очень очевидно.
Явный аутсайдер - двухъядерник G840. Ну так оно и ожидалось. Дальнейшие оптимизации не слишком изменяли время исполнения, которое колебалось в районе от 4 до 5.5 секунд. Отметим, что даже в этом случае ускорение исполнения скрипта достигало значений свыше 20 раз.
В соревновании между двумя видеокартами разных поколений - древней HD4870 и более современной HD6870 - можно почти считать, что победа за 6870. Не считая последнего этапа оптимизации, на котором древний монстр 4870 все же вырвал номинальную победу (хотя почти все время отставал). Причины, откровенно говоря, неясны: и шейдеров поменьше, и частота их тоже ниже - а все же выиграла.
Будем считать, что это капризы развития поколений видеокарт. Или ошибка в моем алгоритме :)
Откровенно порадовал Xeon, который умудрился на всех оптимизациях быть лучше древней 4870, да и с 6870 сражался практически на равных, а в конце умудрился даже победить всех. Я не говорю, что так будет всегда, на любых задачах. Но ведь и задача была вычислительно совсем непростой - все-таки это умножение двух матриц размером 2000 х 2000!
Вывод прост: если у вас уже есть приличный CPU типа i7, а вычисления на OpenCL не слишком долгие, то, может, в дополнительной мощной грелке (видеокарте) и нет особой необходимости? С другой стороны, загрузка камня на 100% в течение десятков секунд (при долгих вычислениях) - это не очень приятно, т.к. компьютер на это время "теряет отзывчивость".