Нейросети — это просто (Часть 30): Генетические алгоритмы
1 971
4
Содержание
- Введение
- 1. Эволюционные методы оптимизации
- 2. Реализация средствами MQL5
- 3. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Мы продолжаем изучение алгоритмов обучения моделей. Как вы помните, все ранее рассмотренные методы использовали аналитический метод определения направления и силы изменения параметров модели в процессе обучения. Отсюда и основное требование ко всем обучаемым моделям — функция модели должна быть дифференцируемая на всем протяжении области допустимых значений. Именно благодаря этому свойству мы использовали метод градиентного спуска и аналитическим путем определяли влияние каждого параметра модели на общий результат, а также корректировали весовые коэффициенты в сторону снижения ошибки.
Однако, существует довольно много задач, когда не представляется возможность дифференцировать исходную функцию. Это могут быть недифференцируемые функции или модель, склонная к проявлению проблем взрывного или затухающего градиента, а методы борьбы с указанными проявлениями оказываются неэффективными. В таких случаях мы прибегаем к эволюционным методам оптимизации.
1. Эволюционные методы оптимизации
Эволюционные методы оптимизации относятся к безградиентными методами и позволяют оптимизировать модели, которые невозможно оптимизировать ранее рассмотренными методами. Хотя и не ограничиваются ими. Порой даже интересно наблюдать за ходом обучения одной модели эволюционным методом и с помощью одного из методов с использованием алгоритма распределения градиента ошибки.
Из названия можно уже догадаться, что основные идеи метода заимствованы из естествознания. И, в частности, из теории эволюции Дарвина. Согласно данной теории, любая популяция живых организмов достаточно плодовита для создания потомства и роста популяции. Но ограниченность доступных ресурсов для жизни ограничивают рост популяции. И здесь ключевую роль играет естественный отбор. Благодаря которому выживает сильнейший. Или наиболее приспособленный к выживанию в окружающей среде обитания. Таким образом, с каждым поколением популяция развивается и все больше приспосабливается к среде обитания. При этом у членов популяции развиваются новые свойства и способности, помогающие выжить. А все, что больше неактуально, забывается.
Как можно заметить, в представленном выше сильно сжатом описании теории абсолютно отсутствует математика. Конечно, можно посчитать максимально возможный размер популяции исходя из общего числа доступных ресурсов и их потребления одним членом популяции. Тем не менее, это не влияет на общие принципы теории.
И, как бы ни показалось странным, именно эта теория послужила прототипом создания целого семейства эволюционных методов. В данной статье я предлагаю познакомиться с генетическим алгоритмом оптимизации. Который является одним из базовых алгоритмов эволюционных методов. Алгоритм основа на двух основных постулата теории эволюции Дарвина: наследственность и естественный отбор.
Суть метода заключается в наблюдении за каждым поколением популяции и отборе лучших её представителей. Но обо всем по порядку.
Так как мы наблюдаем за популяцией в целом, то вытекает основное требование конечности жизни каждого поколения. То есть, как и в рассмотренных ранее алгоритмах обучения с подкреплением, становится требование к конечности процесса. И здесь мы будем использовать те же подходы. В частности, временное ограничение одной сессии.
Как уже было сказано выше, мы будем наблюдать за целой популяцией. Следовательно, в отличии от рассмотренных ранее алгоритмов, мы создаем не одну модель, а целую популяцию. Которая "живет" одновременно в одних и тех же условиях. Размер популяции является гиперпараметром и определяет способность популяции к изучению среды. Каждый член популяции совершает действия в соответствии со своей индивидуальной политикой. Соответственно, чем больше наблюдаемая популяция, тем больше различных стратегий мы наблюдаем. И тем лучше изучается среда обитания.
Данный процесс можно сравнить с повторяющимся случайным выбором действия агента в одном и том же состоянии при обучении с подкреплением. Только сейчас мы используем одновременно несколько агентов, каждый из которых сделает свой выбор.
Использование независимых членов популяции является удобным для распараллеливания процесса оптимизации. Очень часто, для сокращения времени нахождения оптимальной модели процесс оптимизации параллельно запускают на нескольких машинах, задействовав все доступные ресурсы. При этом каждый член популяции "живет" в своём потоке микропроцессора. А весь процесс оптимизации контролируется и обрабатывается узловой машиной. В которой оцениваются результаты каждого агента и генерируется новая популяция.
После окончания сессии одного поколения популяции в работу вступает естественный отбор. В процессе которого из всей популяции выбираются лучшие представители, которые и дадут потомство. Новое поколение популяции. Количество отбираемых лучших представителей является гиперпараметром и, чаще всего, указывается долей от общего размера популяции.
Критерии отбора лучших представителей зависят от архитектора процесса оптимизации. Здесь могут быть вознаграждения, как при обучении с подкреплением. Или вводится функция потерь, как в обучении с учителем. Соответственно, мы будем выбирать агентов с максимальным суммарным вознаграждением или минимальным значением функции потерь.
Заметьте, что мы не используем градиент ошибки. Поэтому функция отбора лучших представителей может быть не дифференцируема.
После отбора родителей для будущего потомства нам предстоит создать новое поколение популяции. Для этого мы случайным образом выбираем пару моделей из отобранных лучших представителей, которые будут родителями новой модели. Согласитесь, символично выбирать пару для создания новой модели.
В процессе создания новой модели все её параметры рассматриваются в качестве хромосомы. А каждый отдельный весовой коэффициент является отдельным геном, который наследуется от одного из родителей.
Алгоритмы наследования могут быть разные, но все они основаны на 2-х правилах:
- каждый ген не изменяет своё место;
- случайности выбора родителя для каждого гена.
При этом мы можем выбирать случайным образом родителей для каждого члена популяции нового поколения. А можем сразу создавать пару агентов с зеркальным наследованием генов.
Процесс циклично повторяется до полного заполнения нового поколения популяции. Отобранные ранее родители не входят в новое поколение популяции и после производства потомства удаляются.
Для нового поколения мы запускаем новую сессию и процесс оптимизации повторяется.
Заметьте, я намеренно говорю "оптимизация", а не "обучение". Описанный выше процесс мало чем напоминает обучение. Это в чистом виде естественный отбор в процессе эволюции. И, как вы знаете, в процессе эволюции не очень часто, но встречаются различные мутации, которые являются неотъемлемой частью процесса эволюции. Поэтому и мы введем в наш процесс оптимизации долю неопределенности.
Наверное, звучит странно. В процессе оптимизации практически все построено на случайном выборе: сначала мы случайным образом генерируем первую совокупность, затем случайным образом выбираем родителей и, наконец, случайным образом копируем параметры моделей. Но за всей этой случайностью нет новизны. Именно её мы и добавим за счет мутации.
В процесс оптимизации мы вводим ещё один гиперпараметр, отвечающий за долю мутации. Он будет указывать вероятность, с которой мы вместо копирования будем добавлять случайные гены в создаваемое потомство. Иными словами, каждый новый член популяции вместо наследования от родителей получает случайный ген с вероятностью параметра мутации. Таким образом, в каждое новое поколение помимо наследования от родителей будет вноситься и что-то новое. Так сказать, максимальное подобие нашему развитию.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов алгоритмов мы переходим к практической части нашей статьи. И реализуем рассмотренный алгоритм средствами MQL5. Конечно, в представленном алгоритме практически нет математики. Но есть главное — четкий выстроенный алгоритм действий. Его мы и реализуем.
Сразу скажем, что выстроенная нами ранее модель не приспособлена для решения подобных задач. При построении нашего класса работы с нейронными сетями CNet предполагалось использование только единичных линейных моделей. Сейчас же нам предстоит реализовать параллельную работу нескольких линейных моделей. И здесь есть 2 пути решения этой задачи.
Первый, менее трудозатратный для программиста, но более ресурсоемкий — мы просто создаем динамический массив объектов, в котором создаем несколько одинаковых моделей. И далее мы будем поочередно извлекать из массива модели одну за другой и последовательно их обрабатывать. В таком варианте вся работа каждой отдельной модели будет реализована в рамках уже существующего функционала. Нам остаётся лишь реализовать методы отбора родителей и генерации нового поколения, а также процесс перебора агентов.
К минусам этого метода можно отнести большую ресурсоемкость и создание большого количества излишних объектов. Так для каждого агента мы создаем отдельный экземпляр класса работы с контекстом OpenCL. А вместе с тем создается отдельный контекст, копия программы и объекты всех кернелов. Это допустимо при использовании нескольких вычислительных устройств параллельно. В противном случае создание излишних объектов ведет к нерациональному использованию ресурсов и сильно ограничивает размеры популяции, что отрицательно сказывается на результатах процесса оптимизации.
Поэтому было принято решение «закатить рукава» и внести изменения в наш класс работы с моделями нейронных сетей. Однако, чтобы не ломать рабочий процесс я создал новый класс CNetGenetic с публичным наследованием от класса CNet.
class CNetGenetic : public CNet { protected: uint i_PopulationSize; vector v_Probability; vector v_Rewards; matrixf m_Weights; matrixf m_WeightsConv; //--- bool CreatePopulation(void); int GetAction(CBufferFloat * probability); bool GetWeights(uint layer); float NextGenerationWeight(matrixf &array, uint shift, vector &probability); float GenerateWeight(uint total); public: CNetGenetic(); ~CNetGenetic(); //--- bool Create(CArrayObj *Description, uint population_size); bool SetPopulationSize(uint size); bool feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true); bool Rewards(CArrayFloat *targetVals); bool NextGeneration(double quantile, double mutation, double &average, double &mamximum); bool Load(string file_name, uint population_size, bool common = true); bool SaveModel(string file_name, int model, bool common = true); //--- bool CopyModel(CArrayLayer *source, uint model); bool Detach(void); };
С назначением методов класса мы познакомимся по мере реализации функционала. Сейчас посмотрим на переменные:
- i_PopulationSize — размер популяции;
- v_Probability — вектор вероятностей выбора модели в качестве "родителя";
- v_Rewards — вектор суммарных вознаграждений, накопленных каждой отдельной моделью;
- m_Weights — матрица для записи параметров всех моделей;
- m_WeightsConv — аналогичная матрица для записи всех параметров сверточных нейронных слоёв.
В конструкторе класса мы лишь инициализируем указанные выше переменные. Здесь мы зададим размер популяции по умолчанию и вызовем метод изменения соответствующих переменных.
CNetGenetic::CNetGenetic() : i_PopulationSize(100)
{
SetPopulationSize(i_PopulationSize);
}
Данный класс не использует экземпляры других объектов. Поэтому деструктор класса остается пустым.
Выше мы упомянули метод указания размера популяции SetPopulationSize, алгоритм которого довольно банален и прост. В параметрах метод получает размер популяции. В теле метода мы сохраним полученное значение в соответствующую переменную и инициализируем нулевыми значениями вектора вероятностей и вознаграждений.
bool CNetGenetic::SetPopulationSize(uint size) { i_PopulationSize = size; v_Probability = vector::Zeros(i_PopulationSize); v_Rewards = vector::Zeros(i_PopulationSize); //--- return true; }
Далее я предлагаю посмотреть на метод инициализации объекта класса Create. По аналогии с аналогичным методом родительского класса, в параметрах метод получает указатель на объект описания одного агента. И добавляем размер популяции.
bool CNetGenetic::Create(CArrayObj *Description, uint population_size) { if(CheckPointer(Description) == POINTER_INVALID) return false; //--- if(!SetPopulationSize(population_size)) return false; CNet::Create(Description); return CreatePopulation(); }
В теле метода мы сначала проверяем действительность полученного указателя на объект описания архитектуры модели. И только после успешного прохождения проверки мы вызываем уже известный нам метод указания размера популяции.
Затем мы вызываем аналогичный метод родительского класса, в котором будет создан один агент по полученному описанию и инициализированы все дополнительные объекты.
И в завершении мы вызовем метод создания популяции CreatePopulation, в котором осуществляется заполнение популяции путем копирования созданной ранее модели. Давайте детальнее посмотрим на алгоритм этого метода.
В начале метода мы проверяем количество нейронных слоев в созданной модели. Их должно быть не менее 2-х.
bool CNetGenetic::CreatePopulation(void) { if(!layers || layers.Total() < 2) return false;
Далее мы сохраним в локальную переменную указатель нейронного слоя исходных данных.
CLayer *layer = layers.At(0); if(!layer || !layer.At(0)) return false; //--- CNeuronBaseOCL *neuron_ocl = layer.At(0); int prev_count = neuron_ocl.Neurons();
Здесь следует обратить внимание, что первый нейронный слой используется только для записи исходных данных. И все агенты нашей популяции будут работать с одними исходными данными. Поэтому нам нет смысла копировать слой исходных данных по числу агентов популяции. И дублирование нейронных слоев осуществляется начиная со следующего нейронного слоя. Индекс которого равен "1".
Давайте вспомнить структуру объектов хранения наших нейронных слоев. За организацию работы модели на верхнем уровне отвечает класс CNet. Он содержит экземпляр объекта динамического массива нейронных слоёв CArrayLayer. В данном динамическом массиве мы сохраняем указатели на объекты вложенных динамических массивов непосредственно нейронного слоя CLayer. И уже в него мы записываем указатели на объекты нейронов CNeuronBaseOCL и других.
CNet -> CArrayLayer -> CLayer -> CNeuronBaseOCL
Хочу напомнить, что такая структура была создана изначально при организации процесса вычислений средствами MQL5 на CPU. Тогда каждый отдельный нейрон был отдельным объектом. Позже, при переносе вычислений на GPU с использованием технологии OpenCL, мы были вынуждены перейти на использование буферов данных. И, по существу, каждый нейронный слой стал выражаться в одном нейроне CNeuronBaseOCL, который выполнял функционал нейронного слоя. Аналогично и в части использования других типов нейронов.
Таким образом каждый объект нейронного слоя CLayer сейчас содержит только один объект нейрона. Ранее мы не меняли архитектуру хранения данных для сохранения совместимости с предыдущими наработками. Сейчас же нам это сослужит ещё одну роль. Мы просто добавим в динамический массив CLayer необходимое количество объектов для хранения полной популяции наших агентов. Таким образом в рамках одной модели мы получим параллельные объекты нейронных слоёв всех агентов нашей популяции. И нам достаточно будет организовать их работу по соответствующему индексу агента.
Следуя этой логике, далее мы организовываем цикл дублирования нейронных слоёв. В нем мы будем последовательно перебирать все нейронные слои нашей модели и добавлять необходимое количество нейронов, аналогичных созданному ранее первому нейрону в каждом слое.
В теле цикла мы сначала проверяем действительность указателя на созданный ранее нейронный слой.
for(int i = 1; i < layers.Total(); i++) { layer = layers.At(i); if(!layer || !layer.At(0)) return false; //---
Затем мы получаем описание архитектуры нейрона.
neuron_ocl = layer.At(0); CLayerDescription *desc = neuron_ocl.GetLayerInfo(); int outputs = neuron_ocl.getConnections();
И создаем аналогичные объекты, дополняя нейронный слой до необходимого размера популяции. Для чего мы создаем ещё один вложенный цикл.
for(uint n = layer.Total(); n < i_PopulationSize; n++) { CNeuronConvOCL *neuron_conv_ocl = NULL; CNeuronProofOCL *neuron_proof_ocl = NULL; CNeuronAttentionOCL *neuron_attention_ocl = NULL; CNeuronMLMHAttentionOCL *neuron_mlattention_ocl = NULL; CNeuronDropoutOCL *dropout = NULL; CNeuronBatchNormOCL *batch = NULL; CVAE *vae = NULL; CNeuronLSTMOCL *lstm = NULL; switch(layer.At(0).Type()) {
case defNeuron: case defNeuronBaseOCL: neuron_ocl = new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl) == POINTER_INVALID) return false; if(!neuron_ocl.Init(outputs, n, opencl, desc.count, desc.optimization, desc.batch)) { delete neuron_ocl; return false; } neuron_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_ocl)) { delete neuron_ocl; return false; } neuron_ocl = NULL; break;
case defNeuronConvOCL: neuron_conv_ocl = new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl) == POINTER_INVALID) return false; if(!neuron_conv_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.window_out, desc.count, desc.optimization, desc.batch)) { delete neuron_conv_ocl; return false; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; return false; } neuron_conv_ocl = NULL; break;
case defNeuronProofOCL: neuron_proof_ocl = new CNeuronProofOCL(); if(!neuron_proof_ocl) return false; if(!neuron_proof_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.count, desc.optimization, desc.batch)) { delete neuron_proof_ocl; return false; } neuron_proof_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_proof_ocl)) { delete neuron_proof_ocl; return false; } neuron_proof_ocl = NULL; break;
case defNeuronAttentionOCL: neuron_attention_ocl = new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID) return false; if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch)) { delete neuron_attention_ocl; return false; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; return false; } neuron_attention_ocl = NULL; break;
case defNeuronMHAttentionOCL: neuron_attention_ocl = new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID) return false; if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch)) { delete neuron_attention_ocl; return false; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; return false; } neuron_attention_ocl = NULL; break;
case defNeuronMLMHAttentionOCL: neuron_mlattention_ocl = new CNeuronMLMHAttentionOCL(); if(CheckPointer(neuron_mlattention_ocl) == POINTER_INVALID) return false; if(!neuron_mlattention_ocl.Init(outputs, n, opencl, desc.window, desc.window_out, desc.step, desc.count, desc.layers, desc.optimization, desc.batch)) { delete neuron_mlattention_ocl; return false; } neuron_mlattention_ocl.SetActivationFunction(desc.activation); if(!layer.Add(neuron_mlattention_ocl)) { delete neuron_mlattention_ocl; return false; } neuron_mlattention_ocl = NULL; break;
Алгоритм добавления объектов аналогичен созданию нового объекта в родительском классе.
После добавления всех элементов популяции одного нейронного слоя выровняем размер слоя с размером популяции и удалим объект описания нейрона.
} if(layer.Total() > (int)i_PopulationSize) layer.Resize(i_PopulationSize); delete desc; } //--- return true; }
После завершения всех итераций системы циклов мы получим полную популяции в рамках нашего одного экземпляра модели и выходим из метода с положительным результатом.
С полным кодом этого метода и всего класса можно ознакомиться во вложении к статье.
После завершения работы с методами инициализации объекта класса CNetGenetic мы переходим к описанию метода прямого прохода. Его наименование и параметры аналогичны методу родительского класса. Здесь можно увидеть указатель на объект динамического массива исходных данных. А также параметры для создания временных меток исходных данных.
В теле метода мы проверим действительность полученного указателя и используемых внутренних объектов.
bool CNetGenetic::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true) { if(CheckPointer(layers) == POINTER_INVALID || CheckPointer(inputVals) == POINTER_INVALID || layers.Total() <= 1) return false;
И подготовим локальные переменные.
CLayer *previous = NULL; CLayer *current = layers.At(0); int total = MathMin(current.Total(), inputVals.Total()); CNeuronBase *neuron = NULL; if(CheckPointer(opencl) == POINTER_INVALID) return false; CNeuronBaseOCL *neuron_ocl = current.At(0); CBufferFloat *inputs = neuron_ocl.getOutput(); int total_data = inputVals.Total(); if(!inputs.Resize(total_data)) return false;
Перенесем исходные данные в буфер нейронного слоя исходных данных и запишем их в контекст OpenCL. Одновременно, при необходимости, мы добавляем временные метки.
for(int d = 0; d < total_data; d++) { int pos = d; int dim = 0; if(window > 1) { dim = d % window; pos = (d - dim) / window; } float value = pos / pow(10000, (2 * dim + 1) / (float)(window + 1)); value = (float)(tem ? (dim % 2 == 0 ? sin(value) : cos(value)) : 0); value += inputVals.At(d); if(!inputs.Update(d, value)) return false; } if(!inputs.BufferWrite()) return false;
После чего организуем систему циклов для непосредственной реализации прямого прохода всех агентов анализируемой популяции. Внешний цикл будет перебирать нейронные слои по возрастанию. А вложенный цикл будет перебирать агентов.
Обратите внимание, что при указании нейрона предыдущего слоя мы должны четко контролировать соответствие агентов. Каждый агент работает в своей вертикали нейронов, которая определяется порядковым номером нейрона в слое. Но в то же время, мы не дублировали слой исходных данных. Поэтому, при указании индекса соответствующего нейрона предыдущего слоя мы сначала проверяем порядковый номер самого нейронного слоя. И для слоя исходных данных порядковый номер нейрона предыдущего слоя всегда будет "0". А для всех последующих слоев он будет соответствовать порядковому номеру агента.
Так как все агенты у нас абсолютно независимы, то мы можем осуществлять операции для всех агентов одновременно.
for(int l = 1; l < layers.Total(); l++) { previous = current; current = layers.At(l); if(CheckPointer(current) == POINTER_INVALID) return false; //--- for(uint n = 0; n < i_PopulationSize; n++) { CNeuronBaseOCL *current_ocl = current.At(n); if(!current_ocl.FeedForward(previous.At(l == 1 ? 0 : n))) return false; continue; } } //--- return true; }
Конечно, использование цикла не дает полный параллелизм вычислений. Но в то же время, мы будем последовательно одну за другой осуществлять аналогичные итерации для всех агентов. Что позволит нам однажды сформированные исходные данные эксплуатировать для всех агентов. И тем самым сократить затраты на подготовку исходных данных для каждого отдельного агента.
И обязательно не забываем контролировать процесс выполнения операций на каждом шагу. А после полного завершения итераций системы вложенных циклов выходим из метода.
Обратного прохода с распределением градиента ошибки генетическим алгоритмом не предусматривается. Тем не менее, нам необходимо оценивать работу моделей. В данной статье я буду оптимизировать агента из предыдущей статьи, который мы обучали алгоритмом policy gradient. И для оптимизации работы моделей мы будет максимизировать суммарное вознаграждение модели за сессию. Следовательно, после очередного действия мы должны вернуть каждому агенту его вознаграждение. Как вы помните, вознаграждение зависит от выбранного действия. А каждый агент совершает свое действие. Раньше мы получали от агента вероятностное распределения совершения действий. Семплировали из полученного распределения одно действие и возвращали агенту соответствующее вознаграждением. Сейчас у нас много таких агентов. И чтобы не повторять данные итерации для каждого отдельного агента во внешней программе, мы просто обернем это все в отдельный метод Rewards. В параметры которого внешняя программа (среда) передаст вознаграждение для всех возможных действий. Такой подход позволяет нам оценить каждое действие только один раз вне зависимости от числа используемых агентов.
В теле метода мы сначала проверяем действительность указателей на полученный в параметрах вектор вознаграждений и динамический массив наших нейронных слоёв.
bool CNetGenetic::Rewards(CArrayFloat *rewards) { if(!rewards || !layers || layers.Total() < 2) return false;
Далее мы извлекаем из динамического массива указатель на слой результатов работы агентов и сразу проверяем действительность полученного указателя.
CLayer *output = layers.At(layers.Total() - 1); if(!output) return false;
После чего организуем цикл с перебором и опросом всех агентов нашей популяции. Для каждого агента мы семплируем одно действие из соответствующего распределения. В зависимости от выбранного действия агент получает свое вознаграждение, которое суммируется с полученными ранее в векторе v_Rewards под индексом агента.
for(int i = 0; i < output.Total(); i++) { CNeuronBaseOCL *neuron = output.At(i); if(!neuron) return false; int action = GetAction(neuron.getOutput()); if(action < 0) return false; v_Rewards[i] += rewards.At(action); }
По результатам оценки агентов мы можем составить вероятностное распределение попадания агентов в число родителей будущего поколения.
v_Probability = v_Rewards - v_Rewards.Min(); if(!v_Probability.Clip(0, v_Probability.Max())) return false; v_Probability = v_Probability / v_Probability.Sum(); //--- return true; }
И выходим из метода с положительным результатом. А с полным кодом всех используемых методов и классов вы можете познакомиться во вложении.
Созданного функционала достаточно для осуществления каждой отдельной сессии для анализируемой популяции и оценки действий агентов. Но после завершения сессии нам необходимо выбрать лучших представителей и сгенерировать новое поколение нашей популяции. Данный функционал мы реализуем в методе NextGeneration. В параметрах данного метода мы передадим 2 гиперпараметра: долю отсеиваемых особей и параметр мутации. Кроме того, параметры метода содержат 2 переменные, в которые мы вернем среднее и максимальное вознаграждение отобранных агентов.
В теле метода мы сначала обнуляем вероятности выбора агентов, не входящих в число избранных. И сразу подсчитаем максимальное вознаграждение и средневзвешенное для отобранных кандидатов.
bool CNetGenetic::NextGeneration(double quantile, double mutation, double &average, double &maximum) { maximum = v_Rewards.Max(); v_Probability = v_Rewards - v_Rewards.Quantile(quantile); if(!v_Probability.Clip(0, v_Probability.Max())) return false; v_Probability = v_Probability / v_Probability.Sum(); average = v_Rewards.Average(v_Probability);
Обратите внимание, что здесь мы используем недавно добавленные векторные операции. Это позволило нам отказаться от использования циклов и сократить код нашей программы. Метод vector::Max() позволяет в одной строке кода определить максимальное значение всего вектора. Метод vector::Quantile(...) возвращает значение указанного квантиля для вектора. Мы используем данное значение для отсеивания слабых агентов. И после векторной операции вычитания их вероятности станут отрицательными.
С помощью функций vector::Clip(0, vector::Max()) мы обнулим все отрицательные значения вектора.
И также изящно в рамках одной строки мы нормализуем все значения вектора в диапазоне от 0 до 1 с суммарным значением всех элементов равным 1.
v_Probability = v_Probability / v_Probability.Sum();
А операция vector::Average(weights) позволяет определить средневзвешенное значение вектора. Вектор weights содержит веса каждого элемента вектора. Выше мы обнулили вероятности слабых агентов, поэтому их значения не будут учитываться при расчете средневзвешенного значения вектора.
Таким образом, использование векторных операций сильно сокращает код программы и облегчает работу программиста. За что отдельное спасибо команде MetaQuotes. Подробно изучить матричные и векторные операции вам поможет раздел Документации.
Но вернемся к нашему методу. Мы определили кандидатов и их вероятности. Теперь мы добавим в распределение долю мутаций и пересчитаем вероятности.
if(!v_Probability.Resize(i_PopulationSize + 1)) return false; v_Probability[i_PopulationSize] = mutation; v_Probability = (v_Probability / (1 + mutation)).CumSum();
На данном этапе у нас есть вероятностное распределение использования агентов в качестве родителей будущего поколения. И мы можем перейти непосредственно к генерации новой популяции. Для этого мы организуем цикл, в котором будем генерировать каждый нейронный слой новой популяции. Надо сказать, что мы на каждом уровне нейронного слоя будем генерировать матрицы весов сразу всех агентов. И так слой за слоем.
Но чтобы не создавать новые объекты мы просто будем перезаписывать матрицы весов уже существующих агентов. Поэтому, прежде чем приступить к обновлению весов очередного нейронного слоя мы сначала вызовем метод GetWeights, в котором скопируем параметры текущего нейронного слоя всех агентов в специально созданные матрицы m_Weights и m_WeightsConv. Здесь указаны только матрицы весов полносвязного и сверточного слоев, так как только они используются в архитектуре оптимизируемой модели. При использовании других архитектур нейронных слоёв нужно будет добавить соответствующие матрицы для временного хранения параметров.
for(int l = 1; l < layers.Total(); l++) { if(!GetWeights(l)) { PrintFormat("Error of load weights from layer %d", l); return false; }
После получения копии параметров моделей мы можем безболезненно начинать правку параметров в объектах. Сначала мы получаем указатель на объект нейронного слоя. А затем организовываем вложенный цикл перебора всех наших агентов. В нем мы извлекаем указатель на матрицу весов соответствующего агента.
CLayer* layer = layers.At(l); for(uint i = 0; i < i_PopulationSize; i++) { CNeuronBaseOCL* neuron = layer.At(i); CBufferFloat* weights = neuron.getWeights();
И при действительности полученного указателя организовываем ещё один вложенный цикл, в котором будем перебирать все элементы матрицы весов и заменять их соответствующими параметрами родителей.
if(!!weights) { for(int w = 0; w < weights.Total(); w++) if(!weights.Update(w, NextGenerationWeight(m_Weights, w, v_Probability))) { Print("Error of update weights"); return false; } weights.BufferWrite(); }
Здесь надо сказать, что мы сделали небольшое отступление от базового алгоритма. Мы не стали случайным образом извлекать пару родителей. Вместо этого, мы случайным образом будем брать веса сразу у всех отобранных агентов в соответствии с их вероятностным распределением. Непосредственно семплирование весовых коэффициентов осуществляется в методе NextGenerationWeight.
После генерации значений очередного буфера данных скопируем его значения в контекст OpenCL.
При необходимости повторяем операции для матрицы сверточного слоя.
if(neuron.Type() != defNeuronConvOCL) continue; CNeuronConvOCL* temp = neuron; weights = temp.GetWeightsConv(); for(int w = 0; w < weights.Total(); w++) if(!weights.Update(w, NextGenerationWeight(m_WeightsConv, w, v_Probability))) { Print("Error of update weights"); return false; } weights.BufferWrite(); } }
После обновления параметров всех агентов мы обнуляем значение вектора накопления наград для корректного определения доходности нового поколения и выходим из метода с положительным результатом.
v_Rewards.Fill(0); //--- return true; }
Мы с вами рассмотрели алгоритм основных методов класса, которые составляют основу организации генетического алгоритма. Однако есть и несколько вспомогательных методов. Их алгоритм не сложен, и вы можете ознакомиться с ними во вложении. Однако, хотелось бы ещё обратить ваше внимание на метод сохранения модели. Дело в том, что метод сохранения родительского класса сохранит всех агентов. И им можно воспользоваться для последующего продолжения оптимизации. Но он не применим для сохранения отдельно взятого агента. А ведь цель оптимизации — нахождения оптимального агента. Поэтому, для сохранения одного лучшего агента мы создадим метод SaveModel. В параметрах метода мы будем передавать имя файла для сохранения модели, порядковый номер агента и флаг записи в Common каталог.
В теле метода мы сначала проверяем порядковый номер агента. Если он не удовлетворяет количеству активных агентов, мы заменяем его номером агента с максимальной вероятностью. Он же агент с максимальной доходностью.
bool CNetGenetic::SaveModel(string file_name, int model, bool common = true) { if(model < 0 || model >= (int)i_PopulationSize) model = (int)v_Probability.ArgMax();
Далее мы создаем экземпляр объекта новой модели и копируем в неё параметры необходимой модели.
CNetGenetic *new_model = new CNetGenetic(); if(!new_model) return false; if(!new_model.CopyModel(layers, model)) { new_model.Detach(); delete new_model; return false; }
Теперь мы можем просто вызвать метод сохранения родительского класса для новой модели.
bool result = new_model.Save(file_name, 0, 0, 0, 0, common);
После сохранения модели, перед выходом из метода мы должны удалить вновь созданный объект. Однако при копировании данных мы не создавали новых объектов нейронных слоёв, а просто использовали указатели на них. Поэтому, при удалении объекта модели, мы удалим и все объекты сохраненного агента в нашей общей модели. Чтобы этого не произошло, мы сначала воспользуемся методом Detach, который позволит открепить объекты нейронных слоёв от сохраненной модели. После этого мы можем безболезненно удалить созданный в данном методе объект модели.
new_model.Detach(); delete new_model; //--- return result; }
С полным кодом всех методов данного класса вы можете ознакомиться во вложении. А мы переходим к созданию советника "Genetic.mq5", в котором и организуем непосредственный процесс оптимизации модели. Новый советник мы создаем на базе советника "Actor_Critic.mq5" из предыдущей статьи.
Во внешних параметрах советника добавим гиперпараметры для организации нового процесса.
input int PopulationSize = 50; input int Generations = 1000; input double Quantile = 0.5; input double Mutation = 0.01;
Также мы заменим рабочий объект модели.
CNetGenetic Models;
Инициализация модели в советнике организована аналогично инициализации родительской модели в ранее рассмотренных советниках.
int OnInit() { //--- ............. ............. //--- if(!Models.Load(MODEL + ".nnw", PopulationSize, false)) return INIT_FAILED; //--- if(!Models.GetLayerOutput(0, TempData)) return INIT_FAILED; HistoryBars = TempData.Total() / 12; Models.getResults(TempData); if(TempData.Total() != Actions) return INIT_PARAMETERS_INCORRECT; //--- bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init"); //--- return(INIT_SUCCEEDED); }
Непосредственно процесс оптимизации, как всегда, организован в функции Train. В начале функции, по аналогии с ранее рассмотренными советниками, мы определяем период оптимизации (обучения).
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time);
И загружаем обучающую выборку.
int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh();
После формирования исходных данных мы подготовим локальные переменные. При этом исключим последний месяц из обучающей выборки для тестирования работы оптимизированной модели на новых данных.
CBufferFloat* State = new CBufferFloat(); float loss = 0; uint count = 0; uint total = bars - HistoryBars - 1; ulong ticks = GetTickCount64(); uint test_size=22*24;
Далее мы создаем систему вложенных циклов для организации процесса оптимизации. Внешний цикл отвечает за отсчет поколений оптимизации. Во вложенном цикле мы будем отсчитывать итерации оптимизации. В данном случае я организовал полный перебор обучающей выборки всеми агентами. Однако, для сокращения времени прохождения одной сессии вы можете воспользоваться случайной выборкой. Надо лишь позаботиться о её достаточности для оценки главных тенденций обучающей выборки. Конечно, в таком случае возможно снижение точности оптимизации. Но здесь важен баланс между точностью результатов и затратами на оптимизацию модели.
for(int gen = 0; (gen < Generations && !IsStopped()); gen ++) { for(uint i = total; i > test_size; i--) { uint r = i + HistoryBars; if(r > (uint)bars) continue;
В теле вложенного цикла мы определяем границы текущего паттерна и создаем буфер исходных данных.
State.Clear(); for(uint b = 0; b < HistoryBars; b++) { uint bar_t = r - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) || !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) || !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign)) break; } if(IsStopped()) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } if(State.Total() < (int)HistoryBars * 12) continue;
И вызываем метод прямого прохода для нашей оптимизируемой популяции.
if(!Models.feedForward(State, 12, true)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Как можно заметить, этот процесс практически не отличается от выполняемых ранее операций при обучении моделей. Ведь все отличие процессов организовано в библиотеках. А интерфейс работы методов остался без изменений. И сейчас мы вызываем прямой проход для одной модели. А в теле класса CNetGenetic организован прямой проход для всех активных агентов популяции.
Далее нам предстоит передать текущее вознаграждение агентам. Как уже было сказано выше, здесь мы не будем осуществлять опрос всех агентов. Вместо этого мы создадим буфер, в котором укажем вознаграждение для каждого действия в данном состоянии. И передадим этот буфер в параметрах следующего метода.
double reward = Rates[i - 1].close - Rates[i - 1].open; TempData.Clear(); if(!TempData.Add((float)(reward < 0 ? 20 * reward : reward)) || !TempData.Add((float)(reward > 0 ? -reward * 20 : -reward)) || !TempData.Add((float) - fabs(reward))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } if(!Models.Rewards(TempData)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Политику вознаграждений мы используем в оригинальном виде без изменений. Это позволит нам оценить влияние именно процесса оптимизации на общий результат.
В завершении итераций цикла обработки одного состояния системы мы выведем на график информацию о её прохождении для визуального контроля процесса и перейдем к следующей итерации цикла.
if(GetTickCount64() - ticks > 250) { uint x = total - i; double perc = x * 100.0 / (total - test_size); Comment(StringFormat("%d from %d -> %.2f%% from %.2f%%", x, total - test_size, perc, 100)); ticks = GetTickCount64(); } }
После завершения очередной сессии мы сохраним параметры лучшего агента.
Models.SaveModel(MODEL+".nnw", -1, false);
И перейдем к генерации нового поколения. Для этого нам достаточно вызвать один метод CNetGenetic::NextGeneration. При этом не забываем контролировать процесс выполнения операций.
double average, maximum; if(!Models.NextGeneration(Quantile, Mutation, average, maximum)) { PrintFormat("Error of create next generation: %d", GetLastError()); PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } //--- PrintFormat("Genegation %d, Average Cummulative reward %.5f, Max Reward %.5f", gen, average, maximum); }
В завершении выведем в журнал информации о достигнутых результатах и перейдем к оценке нового поколения анализируемой популяции на новой итерации цикла.
После окончания процесса оптимизации мы очистим данные и завершим работу советника.
delete State; Comment(""); //--- ExpertRemove(); }
Как можно заметить, благодаря подобной организации класса мы максимально упростили работу на стороне основной программы. Практически, организация процесса оптимизации заключается в последовательном вызове 3-х методов класса. Что сравнимо с обучением моделей при использовании градиентных методов. При этом мы значительно сокращаем общее количество операций в рамках одного агента.
3. Тестирование
Тестирование процесса оптимизации осуществлялось с сохранением всех ранее используемых параметров. Обучающая выборка взята из истории инструмента EURUSD, таймфрейм H1. Для процесса оптимизации взята история за последние 2 года. Все внешние параметры советника использовались по умолчанию. В качестве модели для тестирования мы взяли архитектуры из предыдущей статьи с поиском оптимального вероятностного распределения принятия решений. Такой подход позволяет нам подставить оптимизированную модель в используемый ранее советник "REINFORCE-test.mq5". Как можно заметить, это уже третий подход в процессе обучения модели одной архитектуры. Ранее мы уже обучали аналогичную модель алгоритмами Policy Gradient и Актер-Критик. Тем интереснее становится наблюдать за результатами оптимизации.
Как вы помните, при оптимизации модели мы не использовали данные последнего месяца. Тем самым мы оставили немного данных для тестирования оптимизированной модели. Запустив оптимизированную модель в тестере стратегий на данных последнего месяца, мы получили ниже следующий результат её работы.
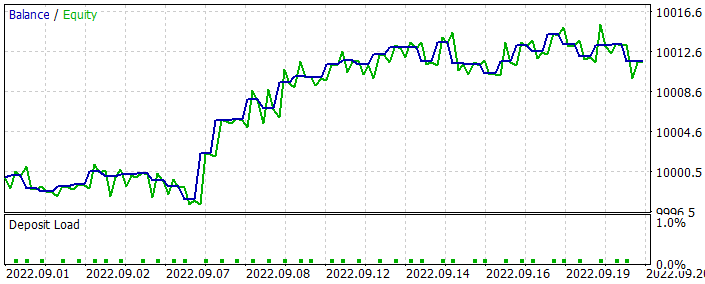
Как можно заметить из представленного графика, мы получили график растущего баланса. Но его доходность несколько ниже, полученной при обучении аналогичной модели методом Актер-Критик. При этом можно заметить и снижение количества торговых операций. Действительно, число трейдов сократилось в 2 раза.
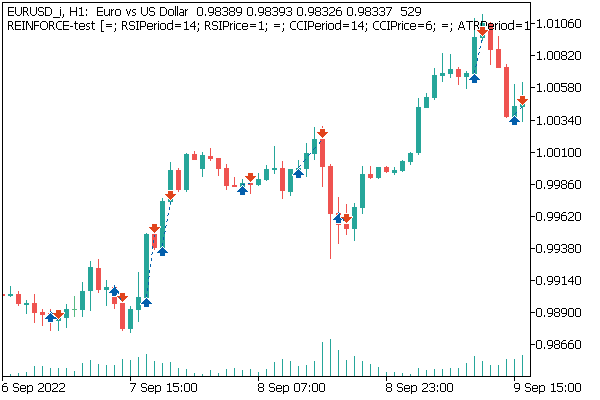
Если вы посмотрите на график инструмента с совершенными торговыми операциями, то можно заметить явную попытку торговли по тренду. Мне кажется это интересным результатом. Если при обучении аналогичной модели градиентными методами, она пыталась совершить сделку на большинстве движений. И довольно часто это имело хаотичный вид. То здесь мы можем заметить некую логику, созвучную с общеизвестными постулатами торговли.
Или мне это только кажется? И все мои выводы "притянуты за уши"? Проведите свои эксперименты и будет интересно понаблюдать за их результатами.
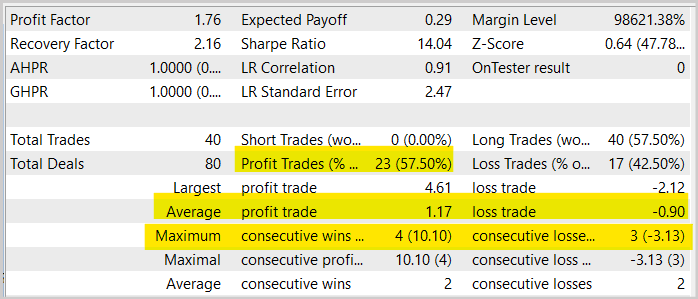
В целом же мы видим увеличение доли прибыльных сделок почти на 1,5% по сравнению с аналогичным тестом модели, обученной методом Актер-Критик. Но при этом наблюдается сокращение количества сделок в 2 раза. В то же время мы видим и снижение средних прибыли и убытков на одну операцию. Все это ведет к общему снижению торгового оборота. А вместе с ним и общей доходности за период. Однако, стоит отметить, что тестирование на протяжении 1-го месяца не может быть оценено как презентабельное для работы советника на длительном временном отрезке. Поэтому, ещё раз призываю к тщательному и всестороннему тестированию ваших моделей перед использованием для реальной торговли.
Заключение
В данной статье мы познакомились с генетическим методом оптимизации моделей. Он может быть использован для оптимизации любых параметрических моделей. Одно из основных преимуществ данного метода, это возможность его использования для оптимизации не дифференцируемых моделей. Что абсолютно не возможно при обучении моделей градиентными методами. И, в частности, методом градиентного спуска во всех его вариациях.
В статье также предложен вариант реализации алгоритма средствами MQL5. Мы даже провели оптимизацию тестовой модели. И просмотрели на её результаты в тестере стратегий.
По результатам тестирования можно сказать, что модель показала достойные результаты. И метод может быть использован для оптимизации торговых моделей. Но прежде, чем поставить модель работать на реальном счету, её необходимо протестировать тщательно и всесторонне.
Ссылки
- Нейросети — это просто (Часть 26): Обучение с подкреплением
- Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
- Нейросети — это просто (Часть 28): Policy gradient алгоритм
- Нейросети — это просто (Часть 29): Алгоритм актер-критик с преимуществом (Advantage actor-critic)
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Genetic.mq5 | Советник | Советник для оптимизации модели |
| 2 | NetGenetic.mqh | Библиотека класса | Библиотека для организации генетического алгоритма |
| 3 | REINFORCE-test.mq5 | Советник | Советник для тестирования модели в тестере стратегий |
| 4 | NeuroNet.mqh | Библиотека классов | Библиотека для организации моделей нейронных сетей |
| 5 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL для организации моделей нейронных сетей |
DoEasy. Элементы управления (Часть 19): Прокрутка вкладок в элементе TabControl, события WinForms-объектов
Работа с матрицами и векторами в MQL5
Разработка торгового советника с нуля (Часть 22): Новая система ордеров (V)
DoEasy. Элементы управления (Часть 18): Готовим функционал для прокрутки вкладок в TabControl
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Любопытно, почему в результате именно трендовая направленность. Обычно, если стоит задача найти закономерности, то, учитывая зигзагообразный рост практически любого тренда, нейросеть должна находить прибыльной и использовать параллельно контртрендовую стратегию, открываясь на предполагаемых экстремумах, особенно при затяжном росте. У предыдущего опыта (ст. 29) как раз что-то похожее, там и кривая баланса растёт на протяжении всего периода, а здесь постепенно затухает.
Dmitriy Gizlyk
Проведите свои эксперименты и будет интересно понаблюдать за их результатами.
Замечательно, что есть возможность покрутить реализацию в руках.
К сожалению, не тестируется. Попробовал зайти в редактор, при компиляции ругается. Вроде копировал все файлы при просмотре всех статей.
Подскажите, пожалуйста, что мне нужно сделать.
Удалил namespace Math и фигурные скобки в одном из включаемых файлов,
Для обучения в статье я использовал модель аналогичную обучаемой в статье актер-критик и policy gradient. Вы просто даете советнику обычную модель. А он дополняет её аналогичными по архитектуре моделями до заполнения популяции.