Визуализируй это! Графическая библиотека в MQL5 как аналог plot из R

При исследовании и изучении закономерностей важную роль играет визуальное отображение с помощью графиков. В популярных среди научного сообщества языках программирования, таких как R и Python, для визуализации предназначена специальная функция plot,  с помощью которой можно рисовать линии, точечные распределения и гистограммы для наглядного представления закономерностей.

Важным достоинством функции plot является то, что для построения любого графика требуется всего несколько строк кода. Достаточно передать в качестве параметров массив данных, указать тип желаемого графика — и готово!  Всю рутинную работу по расчету масштаба, построению осей, выбору цвета и многому другому функция plot берет на себя.

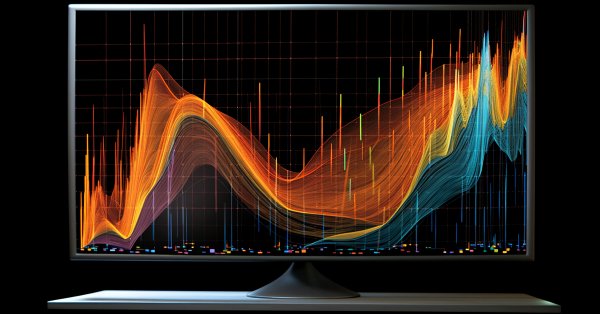
В языке MQL5 все возможности этой функции представлены методами графической библиотеки из Стандартной библиотеки. Вот пример кода и результат его выполнения:

#include <Graphics\Graphic.mqh>
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- Functions
double BlueFunction(double x)   { return(RESULT_OR_NAN(x,10*x*sin(1/x)));      }
double RedFunction(double x)    { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from=-1.2;
   double to=1.2;
   double step=0.005;
   CGraphic graphic;
   graphic.Create(0,"G",0,30,30,780,380);
//--- colors
   CColorGenerator generator;
   uint blue= generator.Next();
   uint red = generator.Next();
   uint orange=generator.Next();
//--- plot all curves
   graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
   graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
   graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
   graphic.CurvePlotAll();
   graphic.Update();
  }

Базовый класс CCanvas и его развитие

Стандартная библиотека содержит базовый класс CCanvas, предназначенный для удобного и быстрого создания рисунков прямо на ценовых графиках. В основе работы класса лежит создание графического ресурса и дальнейшее рисование на холсте простых примитивов: точек, прямых и ломанных линий, окружностей, треугольников и полигонов. В классе также реализованы функции по заполнению фигур цветом и вывод текстовой информации в нужном шрифте, цвете и размере.

Изначально класс CCanvas содержал только два режима отрисовки графических примитивов —  со сглаживанием (antialiasing, AA) и без него. Затем были добавлены новые функции для создания примитивов на основе алгоритма Ву:

• LineWu — прямая линия
• PolylineWu — ломаная линия
  
• PolygonWu — многоугольник
  
• TriangleWu — треугольник
  
• CircleWu — окружность
• EllipseWu — эллипс

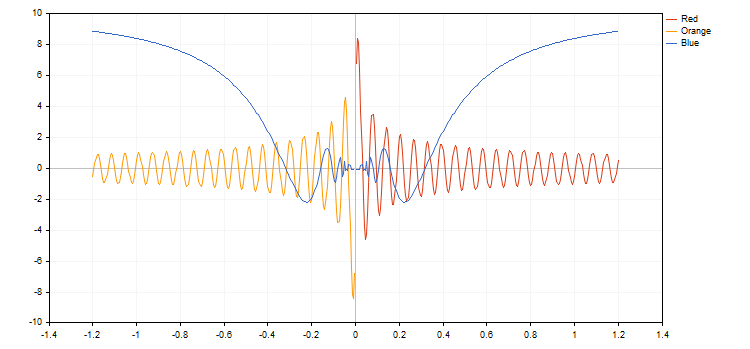
Алгоритм Ву сочетает высококачественное устранение ступенчатости и скорость работы близкую к скорости алгоритма Брезенхема без сглаживания. Есть в нем и визуальное отличие от стандартного алгоритма сглаживания (AA), реализованного в CCanvas. Вот пример отрисовки окружности тремя разными функциями:

#include<Canvas\Canvas.mqh>
CCanvas canvas;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int      Width=800;
   int      Height=600;
//--- create canvas
   if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
     {
      Print("Error creating canvas: ",GetLastError());
     }
//--- draw
   canvas.Erase(clrWhite);
   canvas.Circle(70,70,25,clrBlack);
   canvas.CircleAA(120,70,25,clrBlack);
   canvas.CircleWu(170,70,25,clrBlack);
//---
   canvas.Update();  
  }

Как видно из рисунка, CircleAA() со стандартным алгоритмом сглаживания рисует более толстую линию, чем функция CircleWu() по алгоритму Ву. За счет меньшей толщины и лучшего расчета переходных оттенков окружность CircleWu выглядит более аккуратно и естественно.

Были сделаны и другие улучшения в классе CCanvas:

1. Добавлен новый примитив эллипc с двумя вариантами сглаживания — EllipseAA() и EllipseWu()
   
2. Добавлена перегрузка функции заливки области с новым параметром, отвечающим за "чувствительность заливки" (параметр threshould).

Алгоритм работы с библиотекой

1. После подключения библиотеки необходимо создать объект класса CGraphic. Именно в него будут добавляться кривые, которые необходимо нарисовать.

Затем для созданного объекта нужно вызвать метод Create(), в котором указываются основные параметры графика:

1. Идентификатор графика
2. Имя объекта
3. Индекс окна
   
4. Точка привязки графика
5. Ширина и высота графика

Этот метод создаст на основе введенных параметров объект на чарте и графический ресурс, на котором и будет построен график.

   //--- объект для создания графиков
   CGraphic graphic;
   //--- создание холста
   graphic.Create(0,"Graphic",0,30,30,830,430);

В итоге мы уже имеем готовое полотно для рисования.

2. Теперь наполним наш объект кривыми. Добавление реализуется методом CurveAdd(), который, в свою очередь, имеет возможность создавать кривые четырьмя различными способами:

1. На основе одномерного массива типа double. В этом случае значения из массива будут отображаться на оси Y, а индексы массива — служить координатами X.
2. На основе двух массивов x[] и y[] типа double.
3. На основе массива CPoint2D.
4. На основе указателя на функцию CurveFunction() и трех значений для построения аргументов функции: начального, конечного и приращения по аргументу.

Метод CurveAdd() возвращает указатель на класс CCurve, таким образом мы имеем быстрый доступ к только что созданной кривой и можем изменять её свойства.

   double x[]={-10,-4,-1,2,3,4,5,6,7,8};

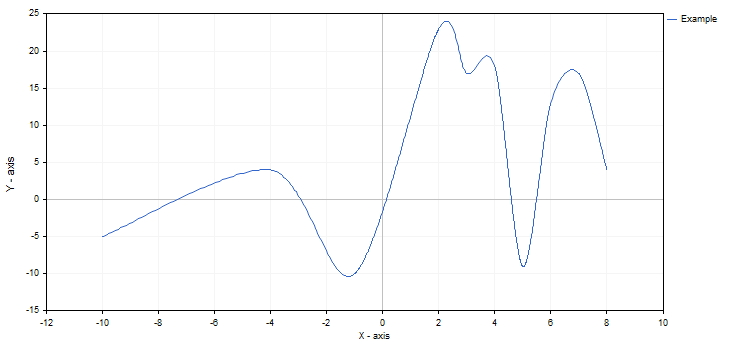
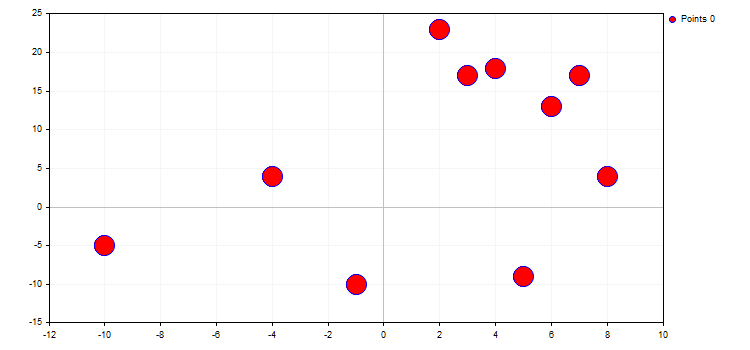
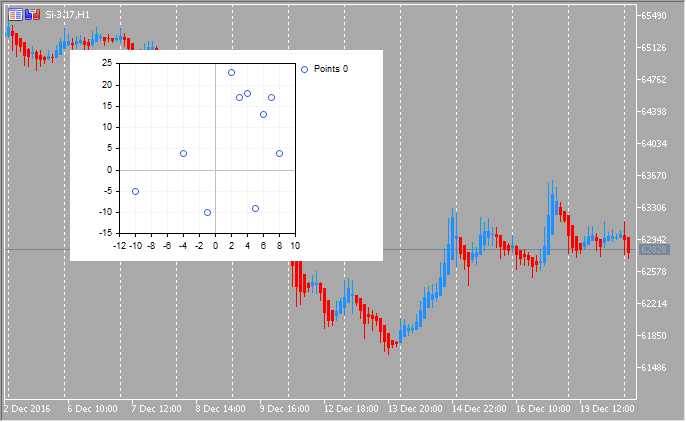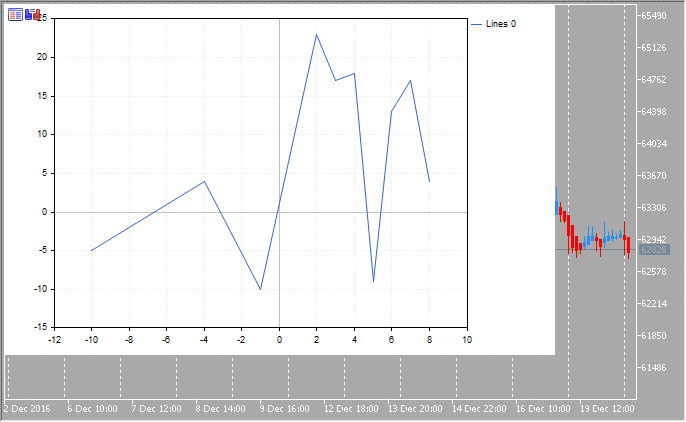
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};

   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);

3. Далее любую из добавленных кривых можно можно отобразить на графике. Это можно сделать тремя способами.

1. Используя метод CurvePlotAll() — который автоматически нарисует все кривые, добавленные на график.
   graphic.CurvePlotAll();
2. Используя метод CurvePlot() — который нарисует кривую по указанному индексу.
   graphic.CurvePlot(0);
3. Используя метод Redraw() и выставив свойству Visible у кривой значение true.
   curve.Visible(true);
   graphic.Redraw();

4. Чтобы непосредственно нарисовать график на чарте, остаётся вызвать метод Update(). В итоге получим полный код скрипта для создания простейшего графика:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   graphic.CurvePlotAll();
   graphic.Update();
  }

Вот так выглядит этот график:

Изменять свойства самого графика и каждой из его функций можно в любой момент. К примеру, добавим подписи осей графика, сменим имя кривой и включим для неё режим сплайн-аппроксимации:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   curve.Name("Example");                
   curve.LinesIsSmooth(true);            
   graphic.XAxis().Name("X - axis");      
   graphic.XAxis().NameSize(12);          
   graphic.YAxis().Name("Y - axis");      
   graphic.YAxis().NameSize(12);
   graphic.YAxis().ValuesWidth(15);
   graphic.CurvePlotAll();
   graphic.Update();
   DebugBreak();
  }

Если бы изменения стояли после вызова CurvePlotAll, то нам бы дополнительно пришлось вызвать метод Redraw, чтобы увидеть их.

Как и большинство современных библиотек, Graphics реализует в себе различные готовые алгоритмы, которые значительно облегчают процесс построения графиков:

1. Библиотека способна сама генерировать контрастные цвета кривых, если те явно не указаны.
2. Оси графика имеют параметрический режим автомасштабирования, который при желании можно отключить.
3. Имена кривых автоматически генерируются в зависимости от их типа и порядка добавления.
4. Идет автоматическая разлиновка рабочей области графика и выделение реальных координатных осей.
5. Есть возможность сглаживать кривые при рисовании линиями.

Также среди дополнительных возможностей библиотеки Graphics нужно отметить методы, которые позволяют добавлять на график новые элементы:

1. TextAdd() — добавляет текст в произвольное место на графике, координаты необходимо задавать в реальном масштабе. Для точной настройки выводимого текста используйте метод FontSet.
   
2. LineAdd() — добавляет линию в произвольное место на графике, координаты необходимо задавать в реальном масштабе.
3. MarksToAxisAdd() — добавляет новые отметки на указанную координатную ось.

Важно отметить, что данные о добавлении этих элементов нигде не хранятся, следовательно, после отрисовки новой кривой на графике или его перерисовки все они будут затёрты.

Типы графиков

Библиотека Graphics поддерживает основные типы отрисовки кривых, все они указаны в перечислении ENUM_CURVE_TYPE:

1. CURVE_POINTS — рисует кривую точками
2. CURVE_LINES — рисует кривую линиями
3. CURVE_POINTS_AND_LINES — рисует кривую и точками, и линиями
4. CURVE_STEPS — рисует ступенчатую кривую
   
5. CURVE_HISTOGRAM — рисует кривую в виде гистограммы
6. CURVE_NONE — не рисует кривую
   

Каждый из указанных режимов имеет свои свойства, изменение которых качественно влияет на отображение кривой на графике. Имея указатель CCurve на кривую, можно быстро менять эти свойства. Именно поэтому рекомендуется запоминать все указатели, которые возвращает метод CurveAdd. Имя свойства всегда начинается с названия режима отрисовки кривой, в котором оно используется.

Рассмотрим подробнее свойства для каждого из типов.

1. Режим отрисовки точками CURVE_POINTS — самый быстрый и простой, который каждую координату кривой рисует точкой с заданными свойствами:

• PointsSize — размер точек
• PointsFill — флаг, указывающий на наличие заливки
  
• PointsColor — цвет заливки
  
• PointsType — тип точек
  

Цвет самой кривой в данном случае определяет внешний цвет точек.

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_POINTS);
   curve.PointsSize(20);
   curve.PointsFill(true);
   curve.PointsColor(ColorToARGB(clrRed,255));

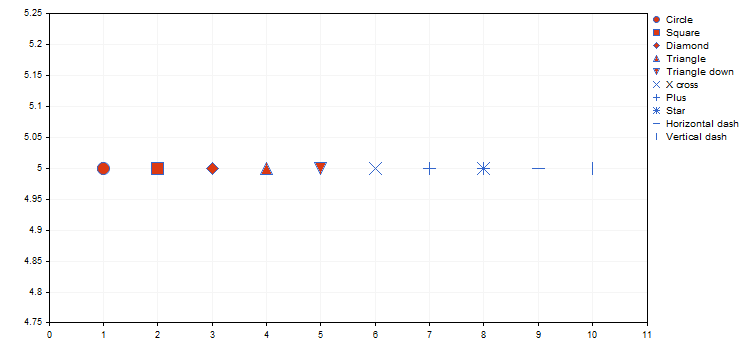
Тип точек определяет конкретную геометрическую фигуру из перечисления ENUM_POINT_TYPE, которой будут отображаться все точки кривой. Всего ENUM_POINT_TYPE включает десять основных геометрических фигур:

1. POINT_CIRCLE — круг (используется по умолчанию)
   
2. POINT_SQUARE — квадрат
   
3. POINT_DIAMOND — ромб
   
4. POINT_TRIANGLE — треугольник
   
5. POINT_TRIANGLE_DOWN — перевернутый треугольник
   
6. POINT_X_CROSS — крестик
   
7. POINT_PLUS — плюс
   
8. POINT_STAR — звездочка
   
9. POINT_HORIZONTAL_DASH — горизонтальная линия
   
10. POINT_VERTICAL_DASH — вертикальная линия
    

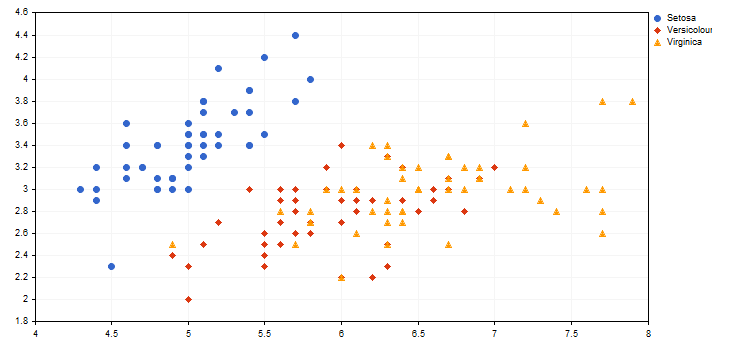
Пример визуального отображения различных видов ириса (см. статью Использование самоорганизующихся карт Кохонена в трейдинге) из приложенного скрипта IrisSample.mq5.

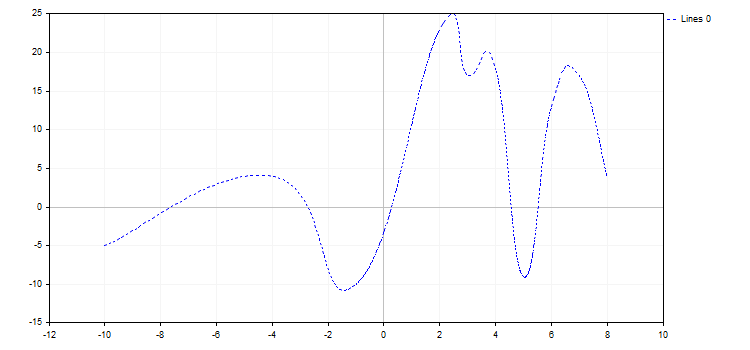
2. Режим отрисовки линиями CURVE_LINES — основной режим для визуализации кривых, в котором каждая пара точек соединяется одной или несколькими (в случае сглаживания) прямыми. Свойства этого режима такие:

• LinesStyle — стиль линии из перечисления ENUM_LINE_STYLE
  
• LinesSmooth — флаг, указывающий, нужно ли выполнять сглаживание
  
• LinesSmoothTension — степень сглаживания
  
• LinesSmoothStep — длина аппроксимирующих линий при сглаживании
  

В Graphics реализован стандартный параметрический алгоритм сглаживания кривых. Он состоит из двух этапов:

1. Для каждой пары точек на основе их производной находятся две контрольные точки
2. На основе этих четырех точек строится кривая Безье с заданным шагом аппроксимации

Параметр LinesSmoothTension принимает значения (0.0; 1.0]. Если LinesSmoothTension установлен на значение 0.0, сглаживания не происходит, при увеличении этого параметра мы будем получать все более и более сглаженную кривую.

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_LINES);
   curve.LinesStyle(STYLE_DOT);
   curve.LinesSmooth(true);
   curve.LinesSmoothTension(0.8);
   curve.LinesSmoothStep(0.2);

3. Режим отрисовки точками и линия CURVE_POINTS_AND_LINES — совмещает в себе первые два режима отрисовки и их свойства.

4. Режим отрисовки ступенчатой кривой CURVE_STEPS — режим, когда каждая пара точек соединяется двумя линиями в виде ступеньки. У этого режима два свойства:

• LinesStyle — это свойство позаимствовано из CURVE_POINTS и характеризует стиль линий
• StepsDimension — измерение, по которому делается шаг: 0 — x (сначала горизонтальная линия, затем вертикальная) или 1 — y (сначала вертикальная линия, затем горизонтальная).
  

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_STEPS);
   curve.LinesStyle(STYLE_DASH);
   curve.StepsDimension(1);

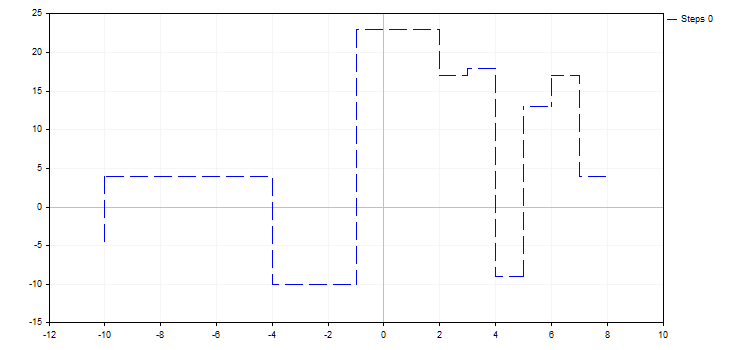
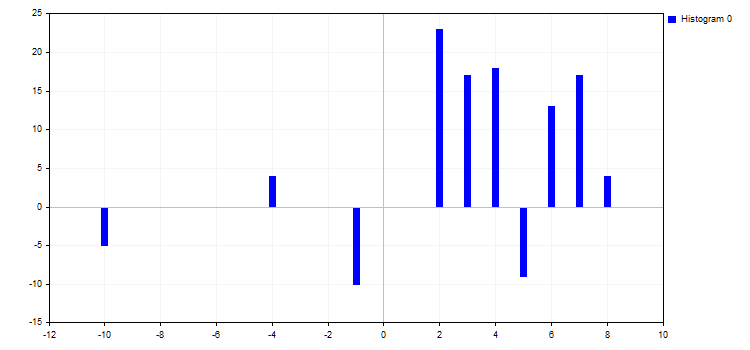
5. Режим отрисовки гистограммой CURVE_HISTOGRAM — рисует стандартную столбчатую гистограмму. Данный режим имеет всего одно свойство:

• HistogramWidth — ширина каждого столбца гистограммы

При большом значении ширины данные начинают сливаться, и столбцы с большим значением Y будут "поглощать" соседние столбцы с меньшими значениями.

6. Последний режим CURVE_NONE не предполагает никакого графического отображения кривой, вне зависимости от её видимости.

Следует отметить, что при автоматическом масштабировании все добавленные к графику кривые имеют значения, следовательно, если даже кривая не отрисована или имеет режим CURVE_NONE, её значения будут учитываться.

Графики на функциях — быстрая генерация в несколько строчек

Еще одно удобство библиотеки — работа с указателями на функции CurveFunction. Указатели на функции в MQL5 принимают только глобальные или статические функции, при этом синтаксис функции должен полностью соответствовать синтаксису указателя. В нашем случае указатель CurveFunction настраивается на функции, которые получают один параметр типа double, и возвращает также double.

Для построения кривой по указателю на функцию нам также потребуется точно задать начальное (from), конечное (to) значение аргумента и его приращение (step). Следовательно, чем меньше значение приращения, тем больше точек функции у нас будет для её построения. Для создания датасерии используйте CurveAdd(), а для отрисовки функции — CurvePlot() или CurvePlotAll().

Для примера создадим функцию параболы и нарисуем её при различных приращениях:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Parabola                                                         |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from1=-5;
   double to1=0;
   double step1=1;
  
   double from2=0;
   double to2=5;
   double step2=0.2;
  
   CurveFunction function = Parabola;
  
   CGraphic graph;
   graph.Create(0,"Graph",0,30,30,780,380);
   graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
   graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
   graph.CurvePlotAll();
   graph.Update();
  }

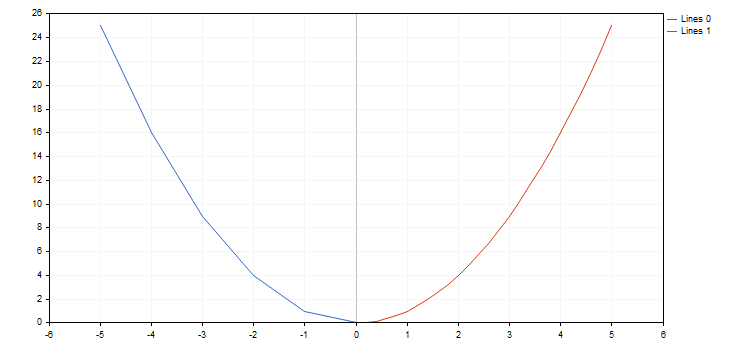
При этом библиотека способна работать с функциями, имеющими точки разрыва (одна из координат имеет значение плюс или минус бесконечность, либо является нечисловой). Важно учитывать при этом приращение по функции, т.к. в некоторых случаях мы можем просто пропустить точку разрыва, и тогда график не будет соответствовать ожиданиям. Например, нарисуем две функции гипербол на отрезке [-5.0; 5.0], первую — с шагом 0.7, а вторую — с 0.1. Получим следующий результат:

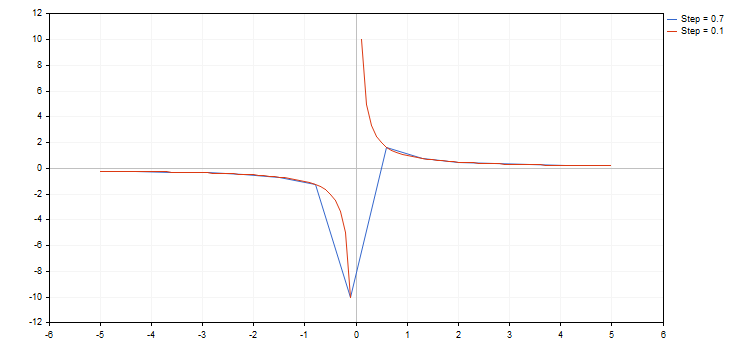
Из рисунка выше видно, что с шагом 0.7 мы просто проскочили точку разрыва, и в итоге график полученной кривой имеет мало общего с реальной функцией гиперболы.

При использовании функций может возникать ошибка "деление на ноль". Решить эту проблему можно двумя способами:

• отключить в  файле metaeditor.ini контроль деления на ноль
  
  [Experts]
  FpNoZeroCheckOnDivision=1
• либо анализировать используемую в функции формулу и возвращать для таких случаев валидное значение. Пример такой обработки с помощью макроса вы найдете в приложенных файлах 3Functions.mq5 и bat.mq5.

  
  
  
  

  
  

Функции быстрой отрисовки

Также библиотека Graphics включает в себя ряд глобальных функций GraphPlot(), которые на основе данных сами будут выполнять все этапы по созданию графика и в качестве результата возвращать имя объекта на чарте. Эти функции схожи с функцией plot из R или Phyton, и позволяют мгновенно визуализировать имеющиеся данные в различных форматах.

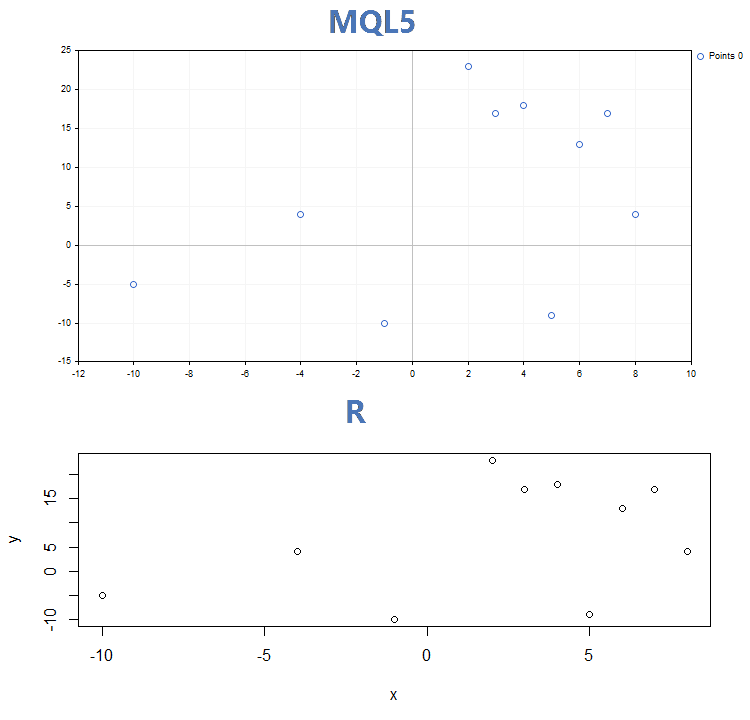
Всего функция GraphPlot имеет 10 различных перегрузок, которые позволяют рисовать различное количество кривых на одном графике и задавать их разными способами. Все, что необходимо сделать пользователю — это сформировать данные для построения кривой одним из способов. Для примера, исходный код для быстрой отрисовки двух массивов x[] и y[] будет выглядеть так:

void OnStart()
  {
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   GraphPlot(x,y);
  }

Аналогично это будет выглядеть на R:

> x<-c(-10,-4,-1,2,3,4,5,6,7,8)
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)

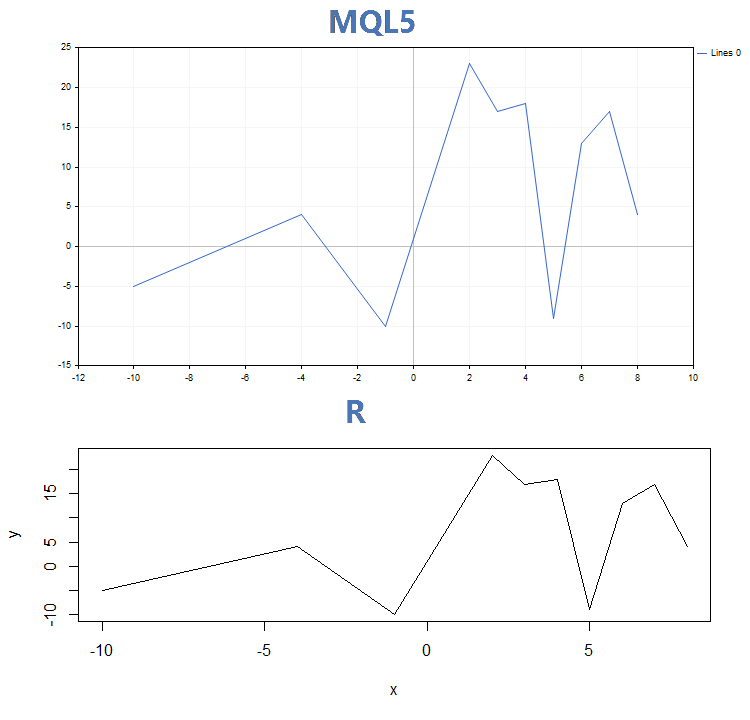
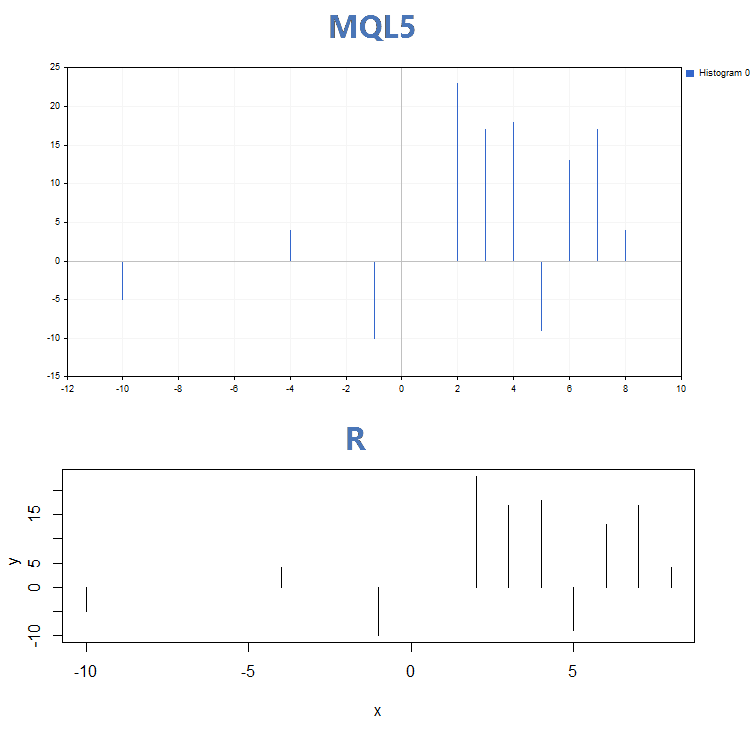
Сравнение графиков по трем основным режимам отображения отрисовки, построенных функцией GraphPlot на MQL5 и функцией plot на R:

1. Отрисовка кривых точками

2. Отрисовка линиями

3. Отрисовка гистограммой

Кроме весьма существенных визуальных различий результатов работы функций GraphPlot() на MQL5 и plot() на R, они отличаются и по входным параметрам. В отличие от функции plot(), в которой можно указывать конкретные параметры кривой (например, lwd, изменяющий ширину линий), функция GraphPlot() включает в себя только ключевые параметры, необходимые для построения данных.

Перечислим их:

1. Данные о кривой в одном из четырех форматов, описанных выше.
   
2. Тип отрисовки (по умолчанию это CURVE_POINTS).
   
3. Имя объекта (по умолчанию NULL).

Каждый график, созданный библиотекой Graphics, представляет из себя пару: объект на чарте и графический ресурс, привязанный к объекту. Имя графического ресурса создается на основе имени объекта путем простого добавления "::" перед именем. Таким образом, если имя объекта было "SomeGraphic", то имя его графического ресурса будет "::SomeGraphic".

Функция GraphPlot() имеет фиксированную точку привязки на чарте x=65 и y=45. Ширина и высота графика вычисляются на основе размеров самого чарта: ширина составит 60% от ширины чарта, высота — 65% от его высоты. Следовательно, если размеры вашего текущего чарта меньше 65 на 45, то функция GraphPlot() не сможет корректно на нем отработать.

Если вы пытаетесь создать график и используете имя уже созданного объекта, то библиотека Graphics будет пытаться отобразить график на этом объекте, предварительно проверив тип его ресурса. Если тип ресурса OBJ_BITMAP_LABEL, то отрисовка будет происходить на этой же паре объект-ресурс.

Если в  функцию GraphPlot() явно передаётся имя объекта, то сначала происходит попытка найти этот объект и отобразить график на нем.  Если же объект не найден, то будет автоматически создана новая пара объект-ресурс на основе указанного имени. При использовании функции GraphPlot() без явного указания имени объекта будет использоваться стандартное имя "Graphic". 

При этом открывается новая возможность: можно самостоятельно указывать точку привязки графика и его размер. Для этого необходимо самостоятельно создать пару объект-ресурс с нужными параметрами и передать в функцию GraphPlot() имя созданного объекта. Очевидно, что создав пару, где имя объекта будет "Graphic", мы, можно сказать, переопределили и зафиксировали стандартное полотно для функции GraphPlot, избавив себя от необходимости при каждом вызове передавать имя объекта.

Для примера возьмем данные из примера выше и установим новый размер графика 750х350, а точку привязки перенесем в верхний левый угол:

void OnStart()
  {
//--- create object on chart and dynamic resource
   string name="Graphic";
   long x=0;
   long y=0;
   int width=750;
   int height=350;
   int data[];
   ArrayResize(data,width*height);
   ZeroMemory(data);
   ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
   ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
   ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
   ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
   ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- create x and y array
   double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- plot x and y array
   GraphPlot(arr_x,arr_y,CURVE_LINES);
  }

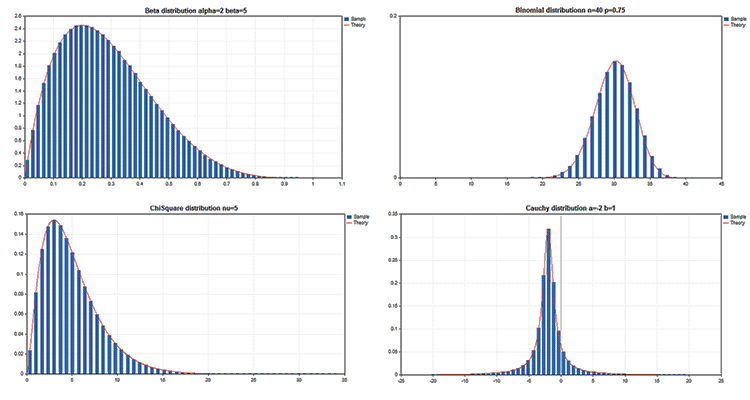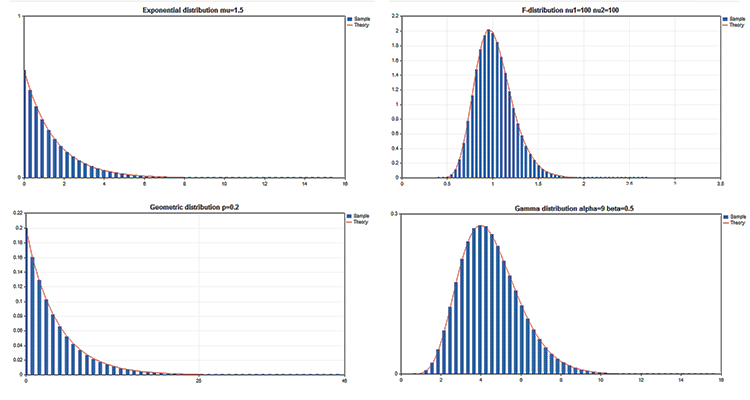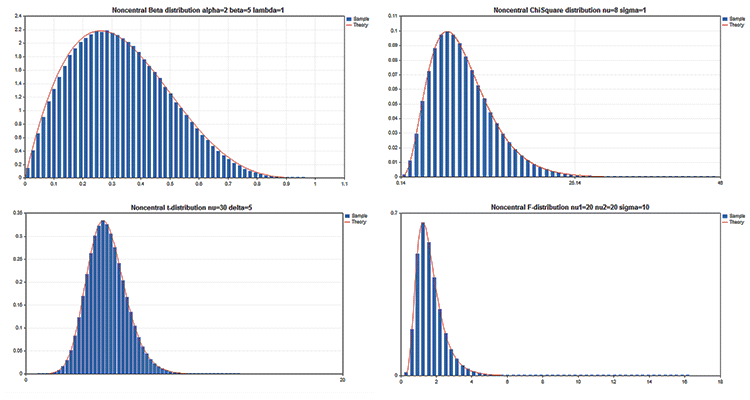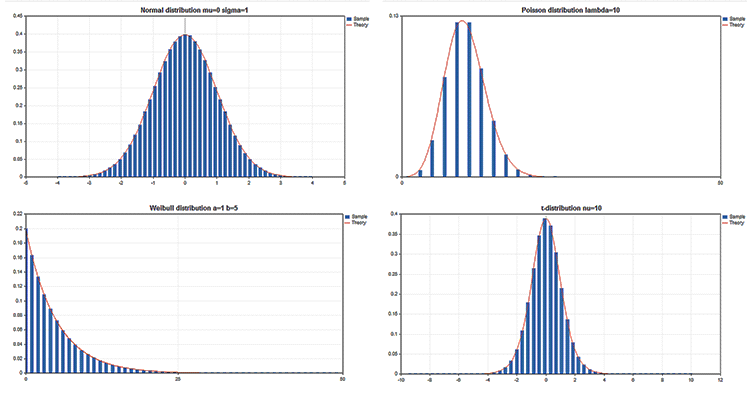
Примеры научных графиков

В состав Стандартной библиотеки входит раздел Статистика, в котором представлены функции для работы со множеством статистических распределений из теории вероятности. Для каждого распределения дается пример графика и код для его получения. Здесь мы просто покажем эти графики одной GIF-картинкой. Исходные коды примеров также приложены в файле MQL5.zip, их нужно распаковать в папку MQL5\Scripts.

Во всех этих примерах используется отключение показа ценового графика с помощью свойства CHART_SHOW:

//--- отключим показ ценового графика
   ChartSetInteger(0,CHART_SHOW,false);

Это позволяет при необходимости превратить окно чарта в один большой холст и рисовать на нем объекты любой сложности с использованием графических ресурсов.

Посмотрите также статью Пример разработки спредовой стратегии на фьючерсах Московской биржи, в которой показывается использование графической библиотеки для отображения обучающей выборки и результатов линейной регрессии, полученных библиотекой Alglib.

Ключевые достоинства графической библиотеки

На языке MQL5 разработчики могут не только создавать торговых роботов и технические индикаторы, но также и производить сложные математические расчеты с помощью библиотек ALGLIB, Fuzzy и Статистика. Полученные данные затем легко визуализируются с помощью представленной графической библиотеки. При этом большинство операций автоматизировано, библиотека предлагает обширный функционал:

• 5 типов отрисовки графика
• 10 типов маркеров для графика
  
• автоматическое масштабирование графиков по осям X и Y
• автоматический выбор цвета, даже если на график выводится несколько построений
  
• сглаживание линий с помощью классического антиальясинга или более продвинутого алгоритма Брезенхема
• возможность установки параметров сплайн-аппроксимации для вывода линий
  
• возможность создавать график одной строчкой кода на основе двух массивов x[] и y[]
• возможность создания графиков с помощью указателей на функции
  

Использование графической библиотеки не только облегчает создание научных графиков, но и позволяет поднять разработку торговых приложений на новый уровень. Платформа MetaTrader 5 позволяет не только провести математические вычисления любой сложности, но и вывести результаты прямо в окно терминала в профессиональном виде.

Попробуйте приложенные к статье коды и убедитесь, что сторонние пакеты больше не нужны!