OpenCL: Da programação ingênua até a mais perceptível
2 337
0
Introdução
O primeiro artigo "OpenCL: A ponte para mundos paralelos" foi uma introdução ao tópico do OpenCL. Ele dirigiu as questões básicas de interação entre o programa no OpenCL (também chamado de núcleo, embora não seja muito correto) e o programa externo no MQL5. Algumas capacidades de desempenho de linguagem (por exemplo, o uso de tipos de dados vetoriais) foram exemplificadas pelo cálculo do pi = 3,14159265 ...
A otimização de desempenho do programa foi em alguns casos considerável. Entretanto, todas essas otimizações foram ingênuas, pois, não levaram em conta as especificações de hardware utilizadas para realizar todos os nossos cálculos. O conhecimento dessas especificações pode, na maioria dos casos, nos permitir alcançar conscientemente speedups que estão muito além das capacidades da CPU.
Para demonstrar essas otimizações o autor teve de recorrer a um exemplo já não mais original, que é provavelmente um dos mais bem estudados na literatura no OpenCL. é a multiplicação de duas grandes matrizes.
Vamos começar com a coisa principal - o modelo de memória OpenCL, juntamente com as peculiaridades de sua implementação na arquitetura de hardware real.
1. Hierarquia de memória em dispositivos de computação moderna
1,1. O modelo de memória OpenCL
De um modo geral, os sistemas de memória diferem muito entre si dependendo das plataformas de computador. Por exemplo, todas as CPUs modernas suportam cachê de dados automático, ao invés de GPUs, onde nem sempre é o caso.
Para garantir a portabilidade do código, um modelo abstrato de memória é adotado no OpenCL, que programadores, bem como fornecedores que precisem implementar este modelo em hardware real possam guiar-se. A memória, tal como definida no OpenCL pode ser teoricamente ilustrada na figura abaixo:
Fig. 1. O modelo de memória OpenCL
Uma vez que os dados são transferidos do anfitrião para o dispositivo, são armazenados na memória do dispositivo global. Todos os dados transferidos na direção oposta são também armazenados na memória global (mas, desta vez, na memória anfitriã global). A palavra-chave __global (dois underlines!) é um modificador que indica que os dados associados com um determinado ponteiro é armazenado na memória global:
__kernel void foo( __global float *A ) { /// kernel code }
Memória global é acessível a todas as unidades de computação dentro do dispositivo como memória RAM no sistema anfitrião.
Memória constante, em contraste com o seu nome, não necessariamente armazena dados somente de leitura. Este tipo de memória é projetada para dados onde cada elemento possa ser acessado simultaneamente por todas as unidades de trabalho. As variáveis com valores constantes de curso também se enquadram nesta categoria. O modelo de memória constante no modelo OpenCL é uma parte da memória global e objetos de memória transferidos para a memória global, pode portanto ser especificado como __constante.
Memória local é a memória de rascunho, onde o espaço de endereço é exclusivo para cada dispositivo. Em hardware, ela, muitas vezes, vem na forma de memória on-chip, mas não há nenhuma exigência especial para ser exatamente o mesmo para OpenCL.
O acesso a este tipo de memória incorre em uma latência muito baixa e a largura de banda de memória é, portanto, muito maior do que a da memória global. Vamos tentar tirar proveito de sua menor latência para a otimização do desempenho do núcleo.
A especificação OpenCL diz que uma variável em memória local pode ser declarada tanto no cabeçalho do núcleo:
__kernel void foo( __local float *sharedData ) { }como em seu corpo:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Observe que um banco de dados dinâmico não pode ser declarado no corpo do núcleo, você sempre deve especificar o seu tamanho.
Abaixo, na otimização do núcleo para a multiplicação de duas grandes matrizes, você verá como lidar com dados locais e quais as peculiaridades de implementação que acarreta no MetaTrader 5 como experimentado pelo autor.
As variáveis locais e argumentos do núcleo que não contenham ponteiros são privadas por padrão (se especificado sem __modificador local). Na prática, essas variáveis estão normalmente localizadas em registros. E vice-versa, bancos de dados privados e quaisquer registros espalhados geralmente estão localizados na memória off-chip, ou seja, memória de latência superior. Permitam-me citar a informação relevante do Wikipédia:
Em muitas linguagens de programação, o programador tem a ilusão de alocar arbitrariamente muitas variáveis. No entanto, durante a compilação, o compilador deve decidir como alocar essas variáveis para um conjunto pequeno, limitado de registros. Nem todas as variáveis estão em uso (ou "existem") ao mesmo tempo, então alguns registros podem ser atribuídos a mais do que uma variável. Entretanto, duas variáveis em utilização, ao mesmo tempo, não podem ser atribuídas ao mesmo registro sem danificar os seus valores.
Variáveis que não podem ser atribuídas a nenhum registro devem ser mantidas em RAM e carregadas dentro/fora para cada leitura/gravação, um processo chamado de derramamento. Acessar a RAM é significativamente mais lento do que acessar os registros e diminui a velocidade de execução do programa compilado, portanto, um compilador de otimização tem como objetivo atribuir tantas variáveis aos registros quanto possível. Alocação de registro é o termo usado quando há menos registro de hardware disponível do que teria sido ideal, maior alocação geralmente significa que são necessários mais derramamentos e recargas.
O modelo de memória OpenCL como descrito, é muito semelhante à estrutura da memória das GPUs modernas. A figura abaixo mostra uma correlação entre o modelo de memória OpenCL e modelo GPU AMD Radeon HD 6970.
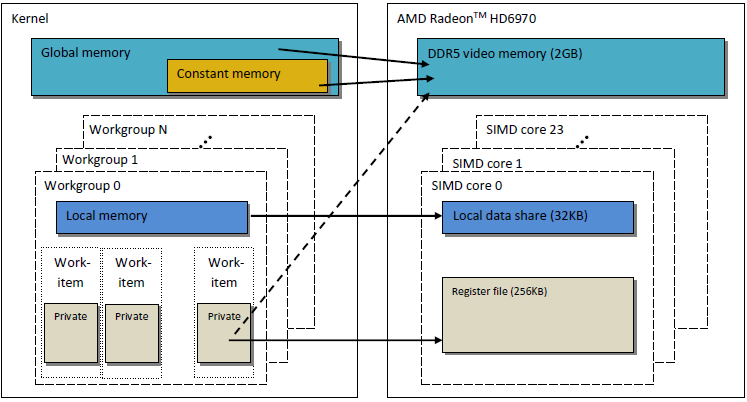
Fig. 2. A correlação entre a estrutura de memória do HD Radeon 6970 e o modelo de memória abstrato OpenCL
Vamos proceder a uma análise mais detalhada das questões relacionadas com a implementação específica da memória GPU.
1,2. Memória em GPUs discretas modernas
1.2.1. Pedidos de memória coalescente
Esta informação também é importante para a otimização do desempenho do núcleo, na medida que o objetivo principal é alcançar alta largura de banda de memória.
Dê uma olhada na figura abaixo para entender melhor o processo de endereçamento de memória:
Fig. 3. Esquema de endereçamento de dados na memória do dispositivo global
Suponha que, o ponteiro para um banco de dados de variáveis de números inteiros int é o endereço de Х = 0x00001232. Cada int ocupa 4 bytes de memória. Suponhamos que um encadeamento de execução (que é um software analógico de uma unidade de trabalho, que executa o código núcleo) endereça dados em Х [0]:
int tmp = X[ 0 ];
Suponhamos que a largura do barramento de memória seja de 32 bytes (256 bits). Esta largura de barramento é típica de GPUs poderosas, como a Radeon HD 5870. Em algumas outras GPUs, a largura de barramento de dados pode ser diferente, por exemplo, 384 bits ou até 512 em alguns modelos NVidia.
O endereçamento do barramento de memória deve corresponder à sua estrutura, por exemplo, em primeiro lugar, a sua largura. Em outras palavras, os dados são armazenados na memória em blocos de 32 bytes (256 bits) cada uma. Independentemente do que endereçarmos no intervalo de 0x00001220 a 0x0000123F (há exatamente 32 bytes nesta faixa, você mesmo pode ver), ainda obteremos o endereçamento 0x00001220 como um endereço de partida para a leitura.
Acessando no endereçamento 0x00001232 retornará todos os dados a endereços no intervalo de 0x00001220 a 0x0000123F, ou seja, 8 números int. Portanto, haverá apenas 4 bytes (um número int) de dados úteis, enquanto os restantes 28 bytes (7 números int) serão inúteis:
Fig. 4. Esquema de obtenção de dados requeridos da memória
O número que nós precisamos localizado no endereço especificado anteriormente - 0x00001232 - é cercado no esquema.
Para maximizar o uso barramento, a GPU tenta aglutinar acessos à memória de encadeamentos de execução diferentes em uma única solicitação de memória, quanto menos acessos à memória, melhor. A razão por trás disso é que o acesso a memória do dispositivo global nos custa tempo e, portanto, prejudica muito a velocidade do programa em execução. Considere a seguinte linha de código do núcleo:
int tmp = X[ get_global_id( 0 ) ];
Suponha que, nossa matriz Х é a matriz a partir do exemplo anterior dado acima. Em seguida, os primeiros 16 encadeamentos de execução (núcleos) irão acessar os endereços de 0x00001232 para 0x00001272 (existem 16 números int dentro deste intervalo, ou seja, 64 bytes). Se cada pedido foi enviado por núcleos de forma independente, sem terem de ser previamente fundidos em um só, cada um dos 16 pedidos conteriam 4 bytes de dados úteis e 28 bytes de dados inúteis, fazendo assim um total de 64 usados e 448 bytes não usados.
Este cálculo baseia-se no fato de que todos os acessos a um endereço localizado no interior de um mesmo bloco de memória de 32 bytes retornará dados absolutamente idênticos. Este é o ponto-chave. Seria mais correto fundir vários pedidos em pedidos únicos e coerentes, para economizar em pedidos inúteis. Esta operação será a seguir chamada de coalescente e pedidos fundidos, como tais, serão referidos como coerentes.
Fig. 5. Apenas três pedidos de memória são necessárias obter os dados necessários
Cada célula na figura acima é de 4 bytes. No nosso exemplo, três pedidos seriam suficientes. Se o início da matriz foi endereçado alinhadamente ao endereço do início de cada bloco de memória de 32 bytes, até dois pedidos seriam suficientes.
Na GPU AMD 64, os encadeamentos de execução são uma parte de uma frente de onda e devem, então, executar as mesmas instruções como na execução SIMD. 16 encadeamentos de execução organizados por get_global_id (0), sendo exatamente um quarto da frente de onda, são fundidos em um pedido coerente para o uso eficiente do barramento.
Abaixo está uma ilustração da largura de banda de memória necessária para pedidos coerentes em relação a pedidos incoerentes, ou seja, "espontâneos". Trata-se de Radeon HD 5870. Um resultado semelhante pode ser observado para placas NVidia.
Fig. 6. Análise comparativa da largura de banda de memória necessária para pedidos coerentes e incoerentes
Pode claramente ser visto que uma solicitação de memória coerente permite aumentar a largura de banda de memória por aproximadamente uma ordem de magnitude.
1.2.2. Bancos de Memória
A Memória consiste em bancos onde os dados são realmente armazenados. Em GPUs modernas, estes são normalmente de palavras de 32 bits (4 bytes). Dados seriais são armazenados em bancos de memória adjacentes. Um grupo de encadeamento de execução acessando elementos seriais não produzirá quaisquer conflitos bancários.
O efeito máximo negativo de conflitos bancários é geralmente observado na memória da GPU local. Portanto, é aconselhável que os dados locais acessem a partir de bancos de memória diferentes de alvo de encadeamento de execução vizinhos.
No hardware AMD, a frente de onda que gera conflitos bancários para, até que todas as operações de memória locais estejam completas. Isto leva a serialização, pela qual blocos de código que devem ser executados em paralelo, sejam executados sequencialmente. Isso tem um efeito extremamente negativo sobre o desempenho do núcleo.
Fig. 7. Esquemas de acesso à memória, sem conflitos bancários
A figura acima mostra o acesso à memória sem conflitos bancários como os tópicos estão acessando dados diferentes.
Vamos ilustrar o acesso à memória com os conflitos bancários:
Fig. 8. Acesso à memória com os conflitos bancários
Essa situação, entretanto, tem uma exceção: se todos os acessos são para o mesmo endereço, o banco pode realizar uma transmissão para evitar o atraso:
Fig. 9. Todos os encadeamentos de execução estão acessando o mesmo endereço
Eventos similares também ocorrem ao acessar a memória global, mas o impacto de tais conflitos é consideravelmente menor.
- Memória GPU é diferente da memória CPU. O principal objetivo de otimizar o desempenho do programa usando OpenCL é garantir a largura de banda máxima em vez de reduzir a latência, como seria na CPU.
- A natureza do acesso à memória tem um grande impacto sobre a eficácia do uso do barramento. Baixa eficiência de uso do barramento significa baixa velocidade de execução.
- Para melhorar o desempenho do código, é aconselhável que o acesso à memória deve ser coerente. Além disso, é altamente preferível, para evitar conflitos de bancos.
- Especificações de hardware (largura do barramento, o número de bancos de memória, bem como o número de encadeamentos de execução que podem ser fundidas para um único acesso coerente) podem ser encontradas na documentação fornecida pelo fornecedor.
Especificações de algumas das placas de vídeo Radeon de série 5xxx são indicados a seguir como um exemplo:
Fig. 10. Especificações técnicas de placas de vídeo Radeon HD 58xx de média e elevada capacidade
Vamos agora proceder à programação.
2. A multiplicação de grandes matrizes quadradas: Do código serial CPU para o código paralelo GPU
2,1. Código MQL5
A tarefa em mãos, em contraste com o artigo anterior "OpenCL: A ponte para mundos paralelos", é padrão, isto é, para multiplicar duas matrizes. é escolhido principalmente devido ao fato de que um monte de informações sobre o assunto podem ser encontrados em diferentes fontes. A maioria delas, de um jeito ou de outro, oferecem mais ou menos soluções coordenadas. Este é o caminho que estamos indo para ir para baixo, fornecendo explicações passo a passo sobre o significado de estruturas de modelos, mantendo em mente que estamos trabalhando em hardware real.
Abaixo está uma fórmula de multiplicação de matrizes bem conhecida na álgebra linear, modificada por cálculos de computador. O primeiro índice é o número de linhas da matriz, o segundo índice é o número de colunas. Cada elemento da matriz de saída é calculado adicionando sequencialmente cada produto sucessivo de elementos na primeira e na segunda matriz à soma acumulada. Eventualmente, esta soma acumulada é o elemento de matriz de saída calculado:
Fig. 11. Fórmula de multiplicação de matriz
Ela pode ser esquematicamente representada como segue:
Fig. 12. Algoritmo de multiplicação de matriz (exemplificado pelo cálculo de um elemento da matriz de saída), representado esquematicamente
Ele pode ser facilmente visto, onde ambas matrizes tenham as mesmas dimensões iguais a N, o número de adições e multiplicações pode ser estimado pela função de O (n^3): para calcular cada elemento da matriz de saída, você precisa obter o produto escalar de uma linha da primeira matriz e uma coluna na segunda matriz. Ele requer cerca de adições e multiplicações 2*N. A estimativa necessária é obtida multiplicando-se pelo número de elementos da matriz N^2. Assim, o código de tempo de execução aproximado depende consideravelmente em N ao cubo.
O número de linhas e colunas para matrizes é a seguir definido para 2000, apenas por conveniência, elas poderiam ser arbitrárias, mas não muito grande.
O código em MQL5 não é muito complicado:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Listagem 1. Programa sequencial inicial no anfitrião
Resultados de desempenho usando diferentes parâmetros:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Como pode ser visto, a nossa dependência estimada de tempo de execução em matrizes de tamanho lineares, apareceu para ser verdade: um aumento de duas vezes em todas as dimensões da matriz resultou em cerca de aumento de 8 vezes no tempo de execução.
Algumas palavras sobre o algoritmo: a ordem de loop pode ser alterada arbitrariamente na função de multiplicação mul(). Acontece que ele tem um efeito considerável sobre o tempo de execução: a relação entre a variante mais lenta para a mais rápida no tempo de execução é de cerca de 1,73.
O artigo demonstra apenas a variante mais rápida, as variantes restantes testadas podem ser encontradas no código anexado no fim do artigo (arquivo matr_mul_2dim.mq5). Neste contexto, o Guia de programação OpenCL (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) diz o seguinte (p. 512):
Estas, obviamente, não são todas as otimizações do código inicial "não-paralelo" que podemos implementar. Alguns deles estão relacionados ao hardware ((S) instruções SSEX), enquanto outros são puramente algorítmicos, por exemplo, algoritmo Strassen, algoritmo Coppersmith–Winograd, etc. Observe que o tamanho das matrizes multiplicadas para o algoritmo Strassen levando a um speedup considerável sobre o algoritmo clássico é bem pequeno, apenas sendo de 64х64. Neste artigo, vamos aprender a multiplicar rapidamente matrizes cujo tamanho linear é até alguns milhares (aproximadamente até 5000).
2,2. A primeira implementação do algoritmo no OpenCL
Vamos agora portar este algoritmo para OpenCL, criando tópicos ROWS1 * COLS2, ou seja, a exclusão de ambos os loops exteriores do núcleo. Cada encadeamento de execução executará repetições COLSROWS para que o loop interno continue a ser uma parte do núcleo.
Uma vez que teremos que criar três buffers lineares para o núcleo do OpenCL, seria razoável retrabalhar o algoritmo inicial para que seja o mais semelhante ao algoritmo do núcleo quanto possível. O código do programa "não-paralelo" em um "CPU de núcleo único " com buffers lineares será fornecido juntamente com o código do núcleo. A otimização do código com matrizes bidimensionais não significa que seu análogo também será ideal para buffers lineares: todos os testes terão de ser repetidos. Portanto, mais uma vez optamos por c-r-cr como a variante inicial, que corresponde ao padrão lógica de multiplicação de matrizes em álgebra linear.
Dito isso, para evitar uma possível confusão de endereçamento de elemento de matriz/buffer, responda à pergunta principal: se uma matriz Matr (linhas M por colunas N) é apresentada na memória da GPU global como um buffer linear, como podemos calcular um deslocamento linear de um elemento Matr[ linha ] [ coluna ]?
De fato, não há nenhuma ordem fixa de colocar para fora uma matriz na memória da GPU, uma vez que ela é determinada pela lógica do problema sozinho. Por exemplo, os elementos de ambas as matrizes podem ser estabelecido de forma diferente nos buffers até porque tanto o algoritmo como a multiplicação de matrizes estão em questão, as matrizes são assimétricas, por exemplo, as linhas da primeira matriz são multiplicadas pelas colunas da segunda matriz. Essa reorganização pode afetar significativamente o desempenho de cálculo na leitura sequencial dos elementos da matriz da memória global da GPU em cada iteração do núcleo.
A primeira implementação do algoritmo contará com matrizes dispostas da mesma maneira - na ordem da maior linha. Os primeiros elementos da linha serão os primeiros a serem colocados no buffer, seguido por todos os elementos da segunda linha e assim por diante. A fórmula de aplanar uma representação 2-dimensional de uma matriz Matr[ (linhas) M ][ (colunas) N ] na memória linear é como se segue:
Fig. 13. Algoritmo para converter um espaço de índice bidimensional em linear para colocar a matriz no buffer da GPU
A figura acima também dá um exemplo de como uma representação de matriz 2-dimensional é achatada na memória linear na ordem da maior coluna.
Abaixo está um código ligeiramente reduzido da nossa primeira implementação do programa executado no dispositivo OpenCL:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Listagem 2. A primeira implementação do programa no OpenCL
As duas últimas funções são úteis na verificação de precisão dos cálculos. O código completo pode ser encontrado no anexo no final do artigo (matr_mul_1dim.mq5). Observe que as dimensões não têm necessariamente que corresponder somente a matrizes quadradas.
Mudanças adicionais quase sempre se referirão apenas ao código do núcleo, portanto, apenas os códigos de modificação do núcleo serão a seguir estabelecidos.
O tipo REALTYPE é introduzido por conveniência de alterar a precisão do cálculo de flutuante para duplo. Deve ser mencionado que o tipo REALTYPE é declarado, não só no programa hospedeiro, mas também dentro do núcleo. Se necessárias, as alterações em relação a este tipo terão de ser feitas em dois lugares ao mesmo tempo, em ambos os #define do programa anfitrião e do código do núcleo.
Os resultados de desempenho de código (em seguida, o tipo de dados flutuantes em todos os lugares):
CPU (OpenCL, _device = 0) :
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Quando executado em HD Radeon 4870 (_dispositivo = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Como pode ser visto, a execução do núcleo na GPU é mais lenta. No entanto, nós ainda não abordamos a otimização especifica para a GPU.
Algumas conclusões:
- Alterando representação matricial da bidimensional para a linear (correspondente à representação do programa executado no dispositivo) não teve efeito sobre o tempo de execução considerável total da versão sequencial do programa.
- O algoritmo de cálculo mais intuitivo em combinação com a definição de multiplicação de matrizes em álgebra linear foi selecionado como a variante inicial para uma maior otimização. Ele é um pouco mais lento do que os mais rápidos, mas, levando em conta o aumento de velocidade (speedup) futuro na GPU, este fator não é essencial.
- O tempo de execução deve ser calculado somente depois de ler os buffers na memória RAM em vez de depois do comando CLExecute(). A razão por trás disso, apontado pelo MetaDriver ao autor, é, provavelmente, como a seguir:MetaDriver: Antes de ler a partir do buffer, CLBufferRead() simplesmente aguarda a conclusão real do programa. CLExecute() é na verdade uma função de enfileiramento assíncrona. Ela retorna o resultado imediatamente, bem antes da operação de código cl estar concluída.
- Guias de computação GPU não costumam calcular o tempo de execução do núcleo, mas sim o resultado relacionado a vários objetos - memória, aritmética, etc. Podemos e vamos a seguir fazer o mesmo.
Sabemos que o cálculo de uma matriz do tamanho de 2000 requer cerca de 2 * 2000 adições/multiplicações para cada elemento. Multiplicando pelo número de elementos da matriz (2000 * 2000), verificamos que o número total de operações de dados do tipo flutuante é de 16 bilhões. Dito isso, a execução na CPU leva 115,628 seg., o que corresponde a velocidade de transmissão de dados igual a
Por outro lado, lembre-se que o cálculo, até agora o mais rápido, em uma "CPU de núcleo único" com o tamanho da matriz de 2000 levou apenas 83,663 segundos para completar (consulte o nosso primeiro código sem OpenCL). Por isso
Vamos pegar esta figura como referência, ponto de partida para nossas otimizações.
Da mesma forma, o cálculo usando OpenCL sobre os rendimentos da CPU:
Finalmente, calcule o resultado na GPU:
2,3. Eliminação de acessos a dados incoerentes
Olhando para o código do núcleo, você pode facilmente notar alguns não otimizáveis.
Dê uma olhada no corpo do loop dentro do núcleo:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
é fácil ver que, quando o contador do loop (cr++) está em execução, os dados contíguos são feitos a partir do primeiro buffer in1[]. Enquanto os dados do segundo buffer in2[] é feito com "lacunas" igual à COLS2. Em outras palavras, a maior parte dos dados obtidos a partir do segundo buffer serão inúteis, assim como as solicitações de memória serão incoerentes (consultar 1.2.1. Pedidos de memória coalescente). Para corrigir esta situação, é suficiente modificar o código em três lugares, alterando a fórmula para o cálculo do índice da variável in2[], bem como o seu padrão de geração:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Agora, quando os valores do contador de loop (cr++) mudarem, os dados de ambas as matrizes serão tomados sequencialmente, sem quaisquer "lacunas".
Código de preenchimento buffer na genMatrices(). Ele agora deve ser preenchido na ordem da maior coluna, ao invés da ordem da maior linha utilizada no início:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Código de verificação na função checkRandom():
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Os resultados de desempenho da CPU:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Como você pode ver, o acesso aos dados coerentes obteve quase nenhum efeito sobre o tempo de execução na GPU, no entanto melhorou claramente o tempo de execução na CPU. é muito provável que isso tenha a ver com fatores que serão otimizados depois, em particular, com a alta latência de acesso a variáveis globais que devemos nos livrar o mais rapidamente possível.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
O novo código de núcleo pode ser encontrado em matr_mul_1dim_coalesced.mq5 no final do artigo.
O código do núcleo está descrito abaixo:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Listagem 3. Núcleo com acesso a dados de memória global coalescente
Vamos seguir em frente para novas otimizações.
2,4. Remoção do acesso de memória GPU global 'cara' a partir da matriz de saída
Sabe-se que a latência de acesso de memória global GPU é extremamente elevada (cerca de 600-800 ciclos). Por exemplo, a latência de realizar uma adição de dois números é de aproximadamente 20 ciclos. O principal objetivo de otimizações no cálculo na GPU é esconder a latência, aumentando a taxa de transferência de cálculos. No loop do núcleo desenvolvido anteriormente, nós acessamos elementos da memória global, o que nos custa tempo.
Vamos agora introduzir a soma da variável local no núcleo (que pode ser acessada muitas vezes mais rápido, pois é uma variável privada do núcleo localizado no registro da unidade de trabalho) e após a conclusão do loop, atribua individualmente o valor da soma obtido ao elemento da matriz de saída:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Listagem 4. A introdução da variável particular para calcular a soma acumulada no loop de cálculo do produto escalar
O arquivo de código-fonte completo, matr_mul_sum_local.mq5, está anexo no final do artigo.
CPU:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================Este é um aumento de produtividade real!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
O princípio fundamental que tentamos aderir com otimizações sequenciais é o seguinte: primeiro você deve reorganizar a estrutura de dados da forma mais completa possível, de modo que seja apropriado para uma determinada tarefa e, especificamente, o hardware subjacente e só depois avançar a otimizações delicadas, empregando algoritmos de cálculo rápido, tais como mad() ou fma(). Tenha em mente que as otimizações sequenciais nem sempre resultam necessariamente em maior desempenho - isto não pode ser garantido.
2,5. O aumento das operações realizadas pelo núcleo
Na programação paralela, é importante organizar os cálculos de modo a diminuir a sobrecarga (gasto de tempo) na organização de operação paralela. Em matrizes com dimensão de 2000, uma unidade de trabalho calculando elementos de uma matriz de saída executa uma quantidade de trabalho igual a 1 / 4000000 da tarefa total.
Este é, obviamente, um número bem longe de ser o número real de unidades que realizam cálculos no hardware. Agora, na nova versão do núcleo, vamos calcular toda a linha da matriz em vez de um elemento.
é importante que o espaço de trabalho seja agora alterado de bidimensional para unidimensional como toda a dimensão - a linha inteira, em vez de um único elemento da matriz, agora é calculada em cada tarefa do núcleo. Portanto, o espaço de trabalho torna-se o número de linhas da matriz.
Fig. 14. Esquema de cálculo de toda a linha da matriz de saída
O código do núcleo fica mais complicado:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 5. O núcleo para o cálculo de toda a linha da matriz de saída
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Os resultados de desempenho (o código-fonte completo pode ser encontrado em matr_mul_row_calc.mq5):
CPU:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
Podemos ver que o tempo de execução na CPU claramente piorou e ficou um pouco, mas não muito, pior na GPU. Nem tudo é tão ruim: essa mudança estratégica que agrava temporariamente a situação a nível local está aqui apenas para aumentar ainda mais drasticamente o desempenho.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2,6. Transferindo a linha da primeira matriz à memória privada
A principal característica do algoritmo de multiplicação de matrizes é um grande número de multiplicações com uma acumulação concomitante dos resultados. A otimização adequada e de alta qualidade deste algoritmo deve implicar a minimização de transferências de dados. Mas, até agora, em cálculos dentro do loop principal de acumulação do produto escalar, todas as nossas modificações do núcleo armazenaram duas das três matrizes da memória global.
Isto significa que todos os dados de entrada para cada produto escalar (sendo, de fato, todos os elementos da matriz de saída) são constantemente transmitidos pela hierarquia da memória inteira - do global ao privado - com latências associadas. Este tráfego pode ser reduzido, assegurando que cada unidade de trabalho reutiliza uma e a mesma linha da primeira matriz para cada linha calculado da matriz de saída.
Fig. 15. Transferência da linha da primeira matriz à memória particular da unidade de trabalho
Isto não implica qualquer alteração no código do programa anfitrião. E mudanças no núcleo são mínimas. Devido ao fato de que uma matriz privada unidimensional intermediária é gerada dentro do núcleo, a GPU tenta colocá-la na memória privada da unidade que executa o núcleo. A linha necessária da primeira matriz é simplesmente copiada do global para a memória privada. Dito isso, deve ser observado que, mesmo esta cópia será relativamente rápida. O truque está no fato de que a cópia mais "cara" dos elementos de linha da primeira matriz de global à memória privada é feita de forma coerente e a sobrecarga na cópia é bastante modesta em comparação com o tempo de execução do principal loop duplo ao calcular a linha da matriz de saída.
O código do núcleo (o código anulado no loop principal é o que havia na versão anterior):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 6. Núcleo com a linha da primeira matriz na memória privada da unidade de trabalho.
CPU:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
A taxa de transferência da CPU se manteve mais ou menos no mesmo nível que da última vez, enquanto a taxa de transferência da GPU voltou ao nível mais alto alcançado, mas na nova capacidade. Observe que a taxa de transferência de CPU é como se estivesse sido congelada no local, estando apenas um pouco instável, enquanto a taxa de transferência da GPU sobe (embora, nem sempre) em grandes saltos.
Vamos ressaltar que a taxa de transferência aritmética real deve ser um pouco maior, pois, devido à cópia da linha da primeira matriz na memória privada, mais operações agora são executadas do que antes. No entanto, isso tem pouco efeito sobre a estimativa da taxa de transferência final.
O código-fonte pode ser encontrado em matr_mul_row_in_private.mq5.
2,7. Transferência da coluna da segunda matriz para a memória local
Agora, é fácil adivinhar qual será o próximo passo. Nós já tomamos medidas para ocultar as latências associadas à saída e às primeiras matrizes de entrada. Há a segunda matriz ainda restante.
Um estudo mais cuidadoso dos produtos escalares utilizados na multiplicação de matrizes mostra que, no decurso de cálculo da linha da matriz de saída, todas as unidades de trabalho no grupo retransmitem dados das mesmas colunas da segunda matriz multiplicada através do dispositivo. Isto está ilustrado no esquema abaixo:
Fig. 16. Transferência da coluna da segunda matriz ao Compartilhamento de dados locais do grupo de trabalho
A sobrecarga na transferência de dados da memória global pode ser reduzida se as unidades de trabalho que integrarem as colunas de cópia do grupo de trabalho da segunda matriz na memória do grupo de trabalho antes do cálculo das linhas da matriz de saída começarem.
Isso exigirá mudanças a serem feitas no núcleo, assim como o programa anfitrião. A mudança mais importante é a configuração da memória local para cada núcleo. Deveria ser explícita que a alocação dinâmica de memória não é suportada no OpenCL. Portanto, um objeto de memória de tamanho adequado deve primeiro ser colocado no anfitrião para ainda ser processado dentro do núcleo.
E, só então, ao executar o núcleo, que as unidades de trabalho copiam a coluna da segunda matriz na memória local. Isso é feito em paralelo usando distribuição cíclica de repetições do loop em todas as unidades de trabalho do grupo de trabalho. No entanto, todas as cópias devem ser concluídas antes da unidade de trabalho começar a sua principal operação (cálculo da matriz da linha de saída).
Por isso, o seguinte comando é inserido após o loop no comando de cópia:
barrier(CLK_LOCAL_MEM_FENCE);
Esta é uma "barreira de memória local" garantindo que cada unidade de trabalho dentro do grupo possa "ver" memória local em um determinado estado, que é coordenada com outras unidades. Todas as unidades de trabalho do grupo de trabalho devem executar comandos até a barreira, antes que qualquer uma delas possa prosseguir com a execução do núcleo. Em outras palavras, a barreira é um mecanismo especial de sincronização entre unidades de trabalho dentro do grupo de trabalho.
Mecanismos de sincronização entre os grupos de trabalho não são fornecidos no OpenCL.
Abaixo está a ilustração da barreira em ação:
Fig. 17. Ilustração da barreira em ação
Na verdade, parece que somente as unidades de trabalho dentro do grupo de trabalho executam o código estritamente ao mesmo tempo. Esta é apenas uma abstração do modelo de programação OpenCL.
Até agora, os nossos códigos do núcleo executados em diferentes unidades de trabalho não exigiram a sincronização das operações, pois não houve comunicação explícita entre eles, isso seria definido programaticamente no núcleo; além disso ele nem sequer foi necessário. No entanto, a sincronização é necessária neste núcleo como o processo de preenchimento da matriz local é distribuído paralelamente entre todas as unidades do grupo de trabalho.
Em outras palavras, cada unidade de trabalho, grava os seus valores em Compartilhamento de dados locais (aqui, a matriz) sem saber o até que ponto outras unidades de trabalho estão neste processo de gravação. A barreira existe para que uma determinada unidade de trabalho não prossiga com a execução do núcleo, antes que seja necessário, por exemplo, antes de uma matriz local for totalmente gerada.
Você deve entender que essa otimização dificilmente será benéfica para o desempenho na CPU: O Guia Otimização OpenCL da Intel diz que ao executar um núcleo da CPU, todos os objetos de memória OpenCL são armazenados em cachê pelo hardware, então o cachê explícito pelo uso de memória local apenas introduz sobrecarga (moderada) desnecessária.
Há um outro ponto importante a observar aqui que custa muito tempo para o autor do artigo. Tem a ver com o fato de que uma variável local não pode ser passada no cabeçalho da função de núcleo, por exemplo, no estágio de compilação, na implementação atual construída pelos desenvolvedores do terminal. A razão por trás disso é que, a fim de alocar memória a um objeto de memória como argumento da função núcleo, teríamos que primeiro criar explicitamente tal objeto na memória da CPU usando a função CLBufferCreate() e especificar explicitamente seu tamanho como um parâmetro de função. Esta função retorna um manuseio de objeto de memória que ainda será armazenado na memória global da GPU,pois este é o único lugar onde ele pode ser armazenado.
A memória local, porém, é uma memória diferente da global e, consequentemente, um objeto de memória criado não pode ser colocado na memória local do grupo de trabalho.
O recurso completo de OpenCL API permite atribuir explicitamente memória do tamanho necessário com o ponteiro NULL ao argumento do núcleo, mesmo sem a criação do objeto de memória tal como (funçãoCLSetKernelArg() ). Porém, a sintaxe da função CLSetKernelArgMem() sendo o MQL5 analógico da função API de recurso completo não nos permite a passagem do tamanho da memória alocada para o argumento, sem criar o próprio objeto de memória. O que podemos passar para a função CLSetKernelArgMem() é apenas o identificador de buffer já gerado na memória da CPU global e destina-se a transferir à memória da GPU.global. Aqui está o paradoxo.
Felizmente, há uma maneira equivalente de trabalhar com buffers locais no núcleo. Você simplesmente declara tal buffer com o modificador __local no corpo do núcleo. A memória local alocada ao grupo de trabalho será, deste modo, determinada durante a execução em vez da fase de compilação.
Os comandos que chegam após a barreira no núcleo (a linha da barreira no código é marcada em vermelho) são, em essência, os mesmos anteriores à otimização. O código de programa anfitrião permaneceu o mesmo (o código-fonte pode ser encontrado em matr_mul_col_local.mq5).
Então, aqui está o novo código do núcleo:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 7. A coluna da segunda matriz transferida à memória local do grupo de trabalho
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Ambos os casos demonstram a degradação do desempenho que, contudo, não pode ser considerada significativa. Pode muito bem acontecer que o desempenho possa ser melhorado ao invés de degradado, alterando o tamanho do grupo de trabalho. O exemplo acima deveria servir a um propósito diferente - mostrar como usar objetos de memória locais.
Há uma hipótese que explica uma diminuição no desempenho quando a memória local é usada. O artigo Comparação de OpenCL com CUDA, GLSL e OpenMP (em russo) publicado em habrahabr.ru há cerca de 2 anos atrás, diz:
Em outras palavras, isso significa que a memória local dos produtos lançados há 2 anos atrás não e mais rápida do que a memória global? O momento em que o acima foi publicado sugere que há dois anos a série de placas de vídeo Radeon HD 58xx já tinha, no entanto, saído da situação, de acordo com o autor, estava longe de ser otimista. Acho isso difícil de acreditar, especialmente levando em conta a série sensacional Evergreen da AMD. Seria interessante verificar isso usando placas mais modernas, por exemplo, a série HD 69xx.
Adição: comece o GPU Caps Viewer e você verá o seguinte na aba OpenCL:
Fig. 18. Principais parâmetros OpenCL suportados pelo HD 4870
CL_DEVICE_LOCAL_MEM_TYPE: Global
A explicação deste parâmetro previsto na especificação da linguagem (tabela 4.3, p.41) é a seguinte:
Tipo de memória local suportada. Isso pode ser configurado para CL_LOCAL implicando o armazenamento de memória local comprometida, tal como SRAM, ou CL_GLOBAL.
Assim, a memória local do HD 4870 é realmente uma parte da memória global e quaisquer manipulações de memória local nesta placa de vídeo são, portanto, inúteis e não resultarão em nada mais rápido do que a memória global. Aqui está outro link onde um especialista AMD esclarece este ponto para a série HD 4xxx. Não significa necessariamente que ele será tão ruim para a placa de vídeo que você tem, foi apenas para mostrar onde as informações relativas ao hardware podem ser encontradas - neste caso, no GPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Finalmente, vamos adicionar alguns toques finais ao vetorizar o núcleo de forma explícita. O núcleo obtido na fase de transferência da linha da primeira matriz para a memória privada (matr_mul_row_in_private.mq5) servirá como o núcleo inicial, uma vez que se verificou ser a mais rápido.
2,8. Vetorização do núcleo
Esta operação deveria ser dividida em várias etapas, para evitar confusão. Na modificação inicial, nós não alteramos os tipos de dados dos parâmetros externos do núcleo e apenas vetorizamos cálculos no loop interno:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 8. Vetorização parcial do núcleo usando float4 (apenas loop interno)
CPU:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Surpreendentemente, mesmo que tal vetorização primitiva tenha mostrado bons resultados na GPU, embora não muito significativos, o ganho já apareceu ser algo em torno de 10%.
Continue a vetorização dentro do núcleo: transferir operações de tipo de conversão de vetor REALTYPE4 'caras', juntamente com a especificação de componentes de vetor explícita ao loop auxiliar externo preenchendo a variável privada rowbuf[]. Ainda não existem alterações no núcleo.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 9. Livrar-se de operações 'caras' de conversão de tipo no loop principal do núcleo
Observe que o valor máximo de contagem do contador do loop interior (bem como o auxiliar) tornou-se 4 vezes mais baixo uma vez que as operações de leitura, que agora são necessárias para a primeira matriz é 4 vezes menor do que anteriormente - a leitura tornou-se claramente uma operação de vetor.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Taxa de transferência aritmética:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Como pode ser visto, as mudanças no desempenho para a CPU são consideráveis, sendo quase revolucionárias para a GPU. O código-fonte pode ser encontrado em matr_mul_vect_v2.mq5.
Vamos realizar as mesmas operações com relação à última variante do núcleo, usando apenas vetores de largura 8. A decisão do autor pode ser explicada pelo fato de que a largura de banda de memória da GPU é de 256 bits, por exemplo, 32 bytes ou 8 números de tipo flutuante e, portanto, o processamento simultâneo de 8 flutuações, que é equivalente à utilização simultânea de float8, parece ser muito natural.
Tenha em mente que, neste caso, o valor COLSROWS deve ser integralmente divisível por 8. Esta é uma exigência natural, na medida em que otimizações mais delicadas estabelecem mais exigências específicas aos dados.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Listagem 10. Vetorização do núcleo usando vetor de largura 8
Tivemos de inserir no código do núcleo a função dot8() alinhada, que permite calcular o produto escalar para vetores com largura 8. Em OpenCL, a função padrão dot() pode calcular o produto escalar apenas para vetores com largura acima de 4. O código-fonte pode ser encontrado em matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Os resultados são inesperados: o tempo de execução na CPU é quase duas vezes menor do que antes, enquanto que aumentou ligeiramente para a GPU, apesar do fato da float8 ser uma largura de barramento adequada para HD 4870 (igual a 256 bits). E aqui, mais uma vez recorremos ao GPU Caps Viewer.
A explicação pode ser encontrada na fig. 18, na penúltima linha da lista de parâmetros:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Consulte a especificação OpenCL e você verá o seguinte texto em relação a este parâmetro na última coluna da tabela 4.3 na página 37:
Prefira tamanho de largura de vetor nativo para montagem em tipos escalares embutidos que podem ser colocados em vetores. A largura do vetor é definida pelo número de elementos escalares que podem ser armazenados no vetor.
Assim, para HD 4870, a largura de vetor preferida de vetor floatN é float4 em vez de float8.
Vamos terminar o ciclo de otimização do núcleo aqui. Poderíamos continuar a conseguir muito mais, mas o comprimento deste artigo não permite essa profundidade de discussão.
Conclusão
O artigo demonstrou alguns recursos de otimização que se abrem quando pelo menos alguma consideração é dada ao hardware subjacente em que o núcleo é executado.
Os valores obtidos estão longe de serem os valores de teto, mas eles mesmos sugerem que tendo os recursos existentes disponíveis aqui e agora (OpenCL API como implementado pelos desenvolvedores do terminal não permite controlar alguns parâmetros importantes para otimização - particularmente, o tamanho do grupo de trabalho), o ganho de desempenho ao longo da execução do programa anfitrião é muito importante: o ganho em execução na GPU no programa sequencial na CPU (embora não muito otimizado) é de cerca de 200:1.
Meu sincero agradecimento vai para MetaDriver pelo conselho valioso e a oportunidade de usar a GPU discreta enquanto a minha não estava disponível.
Conteúdo dos arquivos anexados:
- matr_mul_2dim.mq5 - o programa sequencial inicial no anfitrião com representação de dados em duas dimensões;
- matr_mul_1dim.mq5 - a primeira implementação do núcleo com representação de dados lineares e uma relevante ligação para com o API MQL5 OpenCL;
- matr_mul_1dim_coalesced - o núcleo apresentando o acesso de memória global coalescente;
- matr_mul_sum_local -uma variável privada introduzida para o cálculo do produto escalar, em vez de acessar uma célula calculada do banco de dados da saída armazenada na memória global;
- matr_mul_row_calc - o cálculo de toda a linha do banco de dados da saída no núcleo;
- matr_mul_row_in_private - a linha da primeira matriz transferida à memória privada;
- matr_mul_col_local.mq5 -a coluna da segunda matriz transferida à memória global;
- matr_mul_vect.mq5 - a primeira vetorização do núcleo (usando float4, somente subloop interno do loop principal);
- matr_mul_vect_v2.mq5 - livrar-se de operações 'caras' da conversão de dados no loop principal;
- matr_mul_vect_v3.mq5 -vetorização usando vetor de largura 8
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/407
Oportunidades ilimitadas com o MetaTrader 5 e MQL5
OpenCL: A ponte para mundos paralelos
Programação baseada em autômatos como nova abordagem para criação de sistemas de negociação automatizados
Por que o mercado de MQL5 é o melhor lugar para vender estratégias de negociação e indicadores técnicos
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso