Modelos de regressão da biblioteca Scikit-learn e sua exportação para ONNX
MetaTrader 5
—
Integração
| 9 julho 2024, 15:51
266
0
ONNX (Open Neural Network Exchange) é um formato para descrever e trocar modelos de aprendizado de máquina, proporcionando a capacidade de transferir modelos entre diferentes frameworks de aprendizado de máquina. Em aprendizado profundo e redes neurais, tipos de dados como float32 são frequentemente usados. Eles são amplamente aplicados porque geralmente oferecem precisão e eficiência aceitáveis para o treinamento de modelos de aprendizado profundo.
Alguns modelos clássicos de aprendizado de máquina são difíceis de representar como operadores ONNX. Portanto, operadores adicionais ML operators (ai.onnx.ml) foram introduzidos para implementá-los no ONNX. Vale notar que, de acordo com a especificação ONNX, os operadores chave nesse conjunto (LinearRegressor, SVMRegressor, TreeEnsembleRegressor) podem aceitar vários tipos de dados de entrada (tensor(float), tensor(double), tensor(int64), tensor(int32)), mas sempre retornam o tipo tensor(float) como saída. A parametrização desses operadores também é realizada usando números de ponto flutuante, o que pode limitar a precisão dos cálculos, especialmente se números de precisão dupla forem usados para definir os parâmetros do modelo original.
Isso pode levar a uma perda de precisão ao converter modelos ou usar diferentes tipos de dados no processo de conversão e processamento de dados em ONNX. Muito depende do conversor, como veremos mais adiante; alguns modelos conseguem contornar essas limitações e garantir total portabilidade dos modelos ONNX, permitindo trabalhar com eles em precisão dupla sem perder precisão. É importante considerar essas características ao trabalhar com modelos e sua representação em ONNX, especialmente em casos onde a precisão da representação de dados é importante.
Scikit-learn é uma das bibliotecas mais populares e amplamente utilizadas para aprendizado de máquina na comunidade Python. Ela oferece uma ampla gama de algoritimos, uma inrterface amigável e uma boa documentação O artigo anterior, "Modelos de Classificação da Biblioteca Scikit-learn e Sua Exportação para ONNX", abordou modelos de classificação.
Neste artigo, exploraremos a aplicação de modelos de regressão no pacote Scikit-learn, calcularemos seus parâmetros com precisão dupla para o conjunto de dados de teste, tentaremos convertê-los para o formato ONNX para precisão float e double, e usaremos os modelos obtidos em programas no MQL5. Além disso, compararemos a precisão dos modelos originais e suas versões ONNX para precisão float e double. Além disso, examinaremos a representação ONNX dos modelos de regressão, o que proporcionará uma melhor compreensão de sua estrutura interna e operação.
Conteúdo
- Se isso te incomoda, sinta-se à vontade para contribuir
- 1. Conjunto de Dados de Teste
O script para exibir o conjunto de dados de teste - 2. Modelo de Regressão
2.0. Lista de Modelos de Regressão do Scikit-learn - 2.1. Modelos de Regressão do Scikit-learn que se convertem para modelos ONNX float e double
- 2.1.1. sklearn.linear_model.ARDRegression
2.1.1.1. Código para criar o ARDRegression
2.1.1.2. Código MQL5 para executar Modelos ONNX
2.1.1.3. Representação ONNX do ard_regression_float.onnx e ard_regression_double.onnx - 2.1.2. sklearn.linear_model.BayesianRidge
2.1.2.1. Código para criar o modelo BayesianRidge e exportá-lo para ONNX em float e double
2.1.2.2. Código MQL5 para executar Modelos ONNX
2.1.2.3. Representação ONNX do bayesian_ridge_float.onnx e bayesian_ridge_double.onnx - 2.1.3. sklearn.linear_model.ElasticNet
2.1.3.1. Código para criar o modelo ElasticNet e exportá-lo para ONNX em float e double
2.1.3.2. Código MQL5 para executar Modelos ONNX
2.1.3.3. Representação ONNX do elastic_net_float.onnx e elastic_net_double.onnx - 2.1.4. sklearn.linear_model.ElasticNetCV
2.1.4.1. Código para criar o modelo ElasticNet e exportá-lo para ONNX em float e double
2.1.4.2. Código MQL5 para executar Modelos ONNX
2.1.4.3. Representação ONNX do elastic_net_cv_float.onnx e elastic_net_cv_double.onnx - 2.1.5. sklearn.linear_model.HuberRegressor
2.1.5.1. Código para criar o modelo HuberRegressor e exportá-lo para ONNX em float e double
2.1.5.2. Código MQL5 para executar Modelos ONNX
2.1.5.3. Representação ONNX do huber_regressor_float.onnx e huber_regressor_double.onnx - 2.1.6. sklearn.linear_model.Lars
2.1.6.1. Código para criar o modelo Lars e exportá-lo para ONNX em float e double
2.1.6.2. Código MQL5 para executar Modelos ONNX
2.1.6.3. Representação ONNX do lars_float.onnx e lars_double.onnx - 2.1.7. sklearn.linear_model.LarsCV
2.1.7.1. Código para criar o modelo LarsCV e exportá-lo para ONNX em float e double
2.1.7.2. Código MQL5 para executar Modelos ONNX
2.1.7.3. Representação ONNX do lars_cv_float.onnx e lars_cv_double.onnx - 2.1.8. sklearn.linear_model.Lasso
2.1.8.1. Código para criar o modelo Lasso e exportá-lo para ONNX em float e double
2.1.8.2. Código MQL5 para executar Modelos ONNX
2.1.8.3. Representação ONNX do lasso_float.onnx e lasso_double.onnx - 2.1.9. sklearn.linear_model.LassoCV
2.1.9.1. Código para criar o modelo LassoCV e exportá-lo para ONNX em float e double
2.1.9.2. Código MQL5 para executar Modelos ONNX
2.1.9.3. Representação ONNX do lasso_cv_float.onnx e lasso_cv_double.onnx - 2.1.10. sklearn.linear_model.LassoLars
2.1.10.1. Código para criar o modelo LassoLars e exportá-lo para ONNX em float e double
2.1.10.2. Código MQL5 para executar Modelos ONNX
2.1.10.3. Representação ONNX do lasso_lars_float.onnx e lasso_lars_double.onnx - 2.1.11. sklearn.linear_model.LassoLarsCV
2.1.11.1. Código para criar o modelo LassoLarsCV e exportá-lo para ONNX em float e double
2.1.11.2. Código MQL5 para executar Modelos ONNX
2.1.11.3. Representação ONNX do lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx - 2.1.12. sklearn.linear_model.LassoLarsIC
2.1.12.1. Código para criar o modelo LassoLarsIC e exportá-lo para ONNX em float e double
2.1.12.2. Código MQL5 para executar Modelos ONNX
2.1.12.3. Representação ONNX do lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx - 2.1.13. sklearn.linear_model.LinearRegression
2.1.13.1. Código para criar o modelo LinearRegressione exportá-lo para ONNX em float e double
2.1.13.2. Código MQL5 para executar Modelos ONNX
2.1.13.3. Representação ONNX do linear_regression_float.onnx e linear_regression_double.onnx - 2.1.14. sklearn.linear_model.Ridge
2.1.14.1. Código para criar o modelo Ridge e exportá-lo para ONNX em float e double
2.1.14.2. Código MQL5 para executar Modelos ONNX
2.1.14.3. Representação ONNX do ridge_float.onnx e ridge_double.onnx - 2.1.15. sklearn.linear_model.RidgeCV
2.1.15.1. Código para criar o modelo RidgeCV e exportá-lo para ONNX em float e double
2.1.15.2. Código MQL5 para executar Modelos ONNX
2.1.15.3. Representação ONNX doridge_cv_float.onnx e ridge_cv_double.onnx - 2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
2.1.16.1. Código para criar o modelo OrthogonalMatchingPursuit e exportá-lo para ONNX em float e double
2.1.16.2. Código MQL5 para executar Modelos ONNX
2.1.16.3. Representação ONNX do orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx - 2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
2.1.17.1. Código para criar o modelo PassiveAggressiveRegressor e exportá-lo para ONNX em float e double
2.1.17.2. Código MQL5 para executar Modelos ONNX
2.1.17.3. Representação ONNX do passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx - 2.1.18. sklearn.linear_model.QuantileRegressor
2.1.18.1. Código para criar o modelo QuantileRegressor e exportá-lo para ONNX em float e double
2.1.18.2. Código MQL5 para executar Modelos ONNX
2.1.18.3. Representação ONNX do quantile_regressor_float.onnx e quantile_regressor_double.onnx - 2.1.19. sklearn.linear_model.RANSACRegressor
2.1.19.1. Código para criar o modelo RANSACRegressor e exportá-lo para ONNX em float e double
2.1.19.2. Código MQL5 para executar Modelos ONNX
2.1.19.3. Representação ONNX do ransac_regressor_float.onnx e ransac_regressor_double.onnx - 2.1.20. sklearn.linear_model.TheilSenRegressor
2.1.20.1. Código para criar o modelo TheilSenRegressor e exportá-lo para ONNX em float e double
2.1.20.2. Código MQL5 para executar Modelos ONNX
2.1.20.3. Representação ONNX do theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx - 2.1.21. sklearn.linear_model.LinearSVR
2.1.21.1. Código para criar o modelo LinearSVR e exportá-lo para ONNX em float e double
2.1.21.2. Código MQL5 para executar Modelos ONNX
2.1.21.3. Representação ONNX do linear_svr_float.onnx e linear_svr_double.onnx - 2.1.22. sklearn.linear_model.MLPRegressor
2.1.22.1. Código para criar o modelo MLPRegressor e exportá-lo para ONNX em float e double
2.1.22.2. Código MQL5 para executar Modelos ONNX
2.1.22.3. Representação ONNX do mlp_regressor_float.onnx e mlp_regressor_double.onnx - 2.1.23. sklearn.cross_decomposition.PLSRegression
2.1.23.1. Código para criar o modelo PLSRegression e exportá-lo para ONNX em float e double
2.1.23.2. Código MQL5 para executar Modelos ONNX
2.1.23.3. Representação ONNX do pls_regression_float.onnx e pls_regression_double.onnx - 2.1.24. sklearn.linear_model.TweedieRegressor
2.1.24.1. Código para criar o modelo TweedieRegressor e exportá-lo para ONNX em float e double
2.1.24.2. Código MQL5 para executar Modelos ONNX
2.1.24.3. Representação ONNX do tweedie_regressor_float.onnx e tweedie_regressor_double.onnx - 2.1.25. sklearn.linear_model.PoissonRegressor
2.1.25.1. Código para criar o modelo PoissonRegressor e exportá-lo para ONNX em float e double
2.1.25.2. Código MQL5 para executar Modelos ONNX
2.1.25.3. Representação ONNX do poisson_regressor_float.onnx e poisson_regressor_double.onnx - 2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
2.1.26.1. Código para criar o modelo RadiusNeighborsRegressor e exportá-lo para ONNX em float e double
2.1.26.2. Código MQL5 para executar Modelos ONNX
2.1.26.3. Representação ONNX do radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx - 2.1.27. sklearn.neighbors.KNeighborsRegressor
2.1.27.1. Código para criar o modelo KNeighborsRegressor e exportá-lo para ONNX em float e double
2.1.27.2. Código MQL5 para executar Modelos ONNX
2.1.27.3. Representação ONNX do kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx
- 2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
2.1.28.1. Código para criar o modelo GaussianProcessRegressor e exportá-lo para ONNX em float e double
2.1.28.2. Código MQL5 para executar Modelos ONNX
2.1.28.3. Representação ONNX do gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx
- 2.1.29. sklearn.linear_model.GammaRegressor
2.1.29.1. Código para criar o modelo GammaRegressor e exportá-lo para ONNX em float e double
2.1.29.2. Código MQL5 para executar Modelos ONNX
2.1.29.3. Representação ONNX do gamma_regressor_float.onnx e gamma_regressor_double.onnx - 2.1.30. sklearn.linear_model.SGDRegressor
2.1.30.1. Código para criar o modelo SGDRegressor e exportá-lo para ONNX em float e double
2.1.30.2. Código MQL5 para executar Modelos ONNX
2.1.30.3. Representação ONNX do sgd_regressor_float.onnx e sgd_rgressor_double.onnx
- 2.2. Modelos de regressão da biblioteca Scikit-learn que são convertidos apenas em modelos ONNX de precisão float
- 2.2.1. sklearn.linear_model.AdaBoostRegressor
2.2.1.1. Código para criar o modelo AdaBoostRegressor e exportá-lo para ONNX em float e double
2.2.1.2. Código MQL5 para executar Modelos ONNX
2.2.1.3. Representação ONNX do adaboost_regressor_float.onnx e adaboost_regressor_double.onnx - 2.2.2. sklearn.linear_model.BaggingRegressor
2.2.2.1. Código para criar o modelo BaggingRegressor e exportá-lo para ONNX em float e double
2.2.2.2. Código MQL5 para executar Modelos ONNX
2.2.2.3. Representação ONNX do bagging_regressor_float.onnx e bagging_regressor_double.onnx - 2.2.3. sklearn.linear_model.DecisionTreeRegressor
2.2.3.1. Código para criar o modelo DecisionTreeRegressor e exportá-lo para ONNX em float e double
2.2.3.2. Código MQL5 para executar Modelos ONNX
2.2.3.3. Representação ONNX do decision_tree_regressor_float.onnx e decision_tree_regressor_double.onnx - 2.2.4. sklearn.linear_model.ExtraTreeRegressor
2.2.4.1. Código para criar o modelo ExtraTreeRegressor e exportá-lo para ONNX em float e double
2.2.4.2. Código MQL5 para executar Modelos ONNX
2.2.4.3. Representação ONNX do extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx - 2.2.5. sklearn.ensemble.ExtraTreesRegressor
2.2.5.1. Código para criar o modelo ExtraTreesRegressor e exportá-lo para ONNX em float e double
2.2.5.2. Código MQL5 para executar Modelos ONNX
2.2.5.3. Representação ONNX do extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx - 2.2.6. sklearn.svm.NuSVR
2.2.6.1. Código para criar o modelo NuSVR e exportá-lo para ONNX em float e double
2.2.6.2. Código MQL5 para executar Modelos ONNX
2.2.6.3. Representação ONNX do nu_svr_float.onnx e nu_svr_double.onnx - 2.2.7. sklearn.ensemble.RandomForestRegressor
2.2.7.1. Código para criar o modelo RandomForestRegressor e exportá-lo para ONNX em float e double
2.2.7.2. Código MQL5 para executar Modelos ONNX
2.2.7.3. Representação ONNX do random_forest_regressor_float.onnx e random_forest_regressor_double.onnx
- 2.2.8. sklearn.ensemble.GradientBoostingRegressor
2.2.8.1. Código para criar o modelo GradientBoostingRegressor e exportá-lo para ONNX em float e double
2.2.8.2. Código MQL5 para executar Modelos ONNX
2.2.8.3. Representação ONNX do gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx
- 2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
2.2.9.1. Código para criar o modelo HistGradientBoostingRegressor e exportá-lo para ONNX em float e double
2.2.9.2. Código MQL5 para executar Modelos ONNX
2.2.9.3. Representação ONNX do hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx - 2.2.10. sklearn.svm.SVR
2.2.10.1. Código para criar o modelo SVR e exportá-lo para ONNX em float e double
2.2.10.2. Código MQL5 para executar Modelos ONNX
2.2.10.3. Representação ONNX do svr_float.onnx and svr_double.onnx
- 2.3. Modelos de Regressão que encontraram problemas ao serem convertidos para ONNX
- 2.3.1. sklearn.dummy.DummyRegressor
Código para criar o DummyRegressor - 2.3.2. sklearn.kernel_ridge.KernelRidge
Código para criar o KernelRidge - 2.3.3. sklearn.isotonic.IsotonicRegression
Código para criar o IsotonicRegression - 2.3.4. sklearn.cross_decomposition.PLSCanonical
Código para criar o PLSCanonical - 2.3.5. sklearn.cross_decomposition.CCA
Código para criar o CCA - Conclusão
- Resumo
Se isso te incomoda, sinta-se à vontade para contribuir
No fórum de desenvolvedores do ONNX Runtime, um dos usuários relatou um erro "[ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1)" ao executar um modelo através do ONNX Runtime.
Olá a todos, estou recebendo este erro ao tentar inferir um modelo de regressão linear. Por favor, me ajudem a resolver isso.
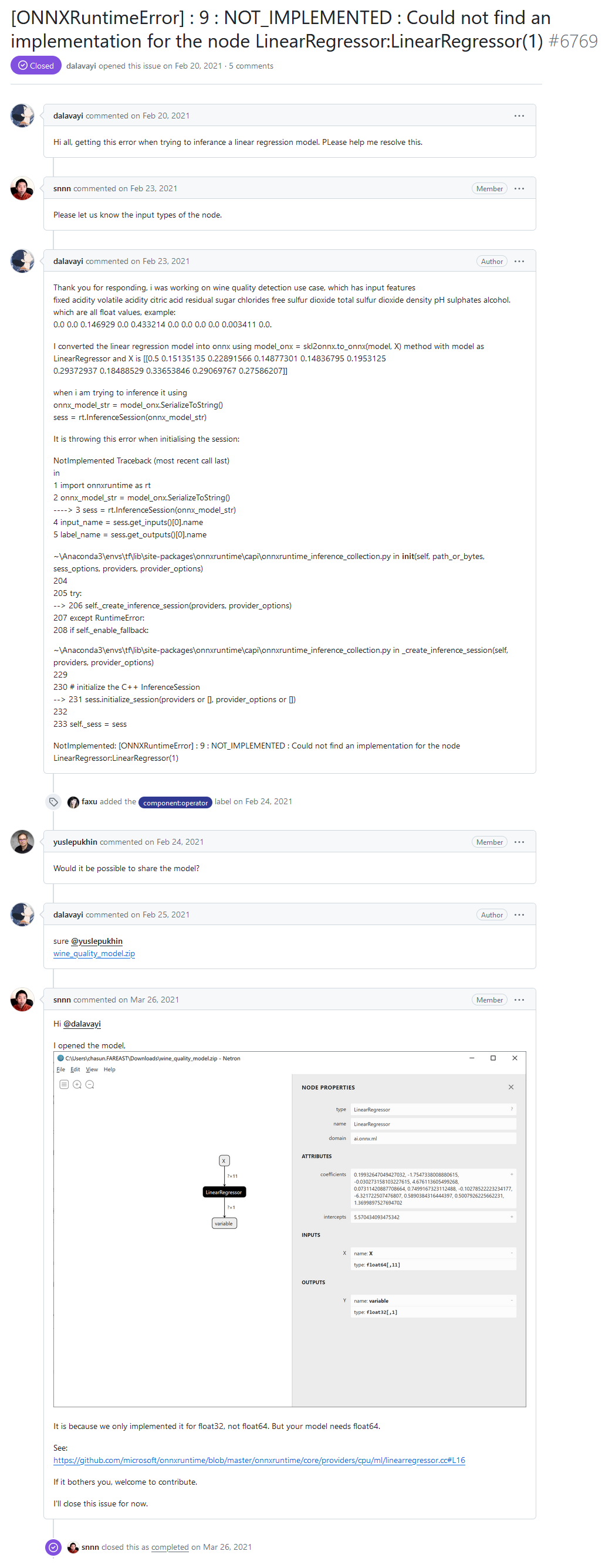
Erro "NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor (1)" do fórum de desenvolvedores do ONNX Runtime
Resposta do desenvolvedor:
Isso acontece porque nós implementamos apenas para float32, não para float64. Mas o seu modelo precisa de float64.
See:
https://github.com/microsoft/onnxruntime/blob/master/onnxruntime/core/providers/cpu/ml/linearregressor.cc#L16
Se isso te incomoda, sinta-se à vontade para contribuir
No modelo ONNX do usuário, o operador ai.onnx.ml.LinearRegressor é chamado com o tipo de dado double (float64), e a mensagem de erro surge porque o ONNX Runtime não tem suporte para o operador LinearRegressor() com precisão double.
De acordo com a especificação do operador ai.onnx.ml.LinearRegressor, o tipo de dado de entrada double é possível (T: tensor(float), tensor(double), tensor(int64), tensor(int32)); no entanto, os desenvolvedores optaram por não implementá-lo intencionalmente.
A razão para isso é que a saída sempre retorna o valor Y: tensor(float). Além disso, os parâmetros computacionais são números float (coeficientes: lista de floats, interceptos: lista de floats).
Consequentemente, quando os cálculos são realizados em precisão double, este operador reduz a precisão para float, e sua implementação em cálculos de precisão double tem valor questionável.
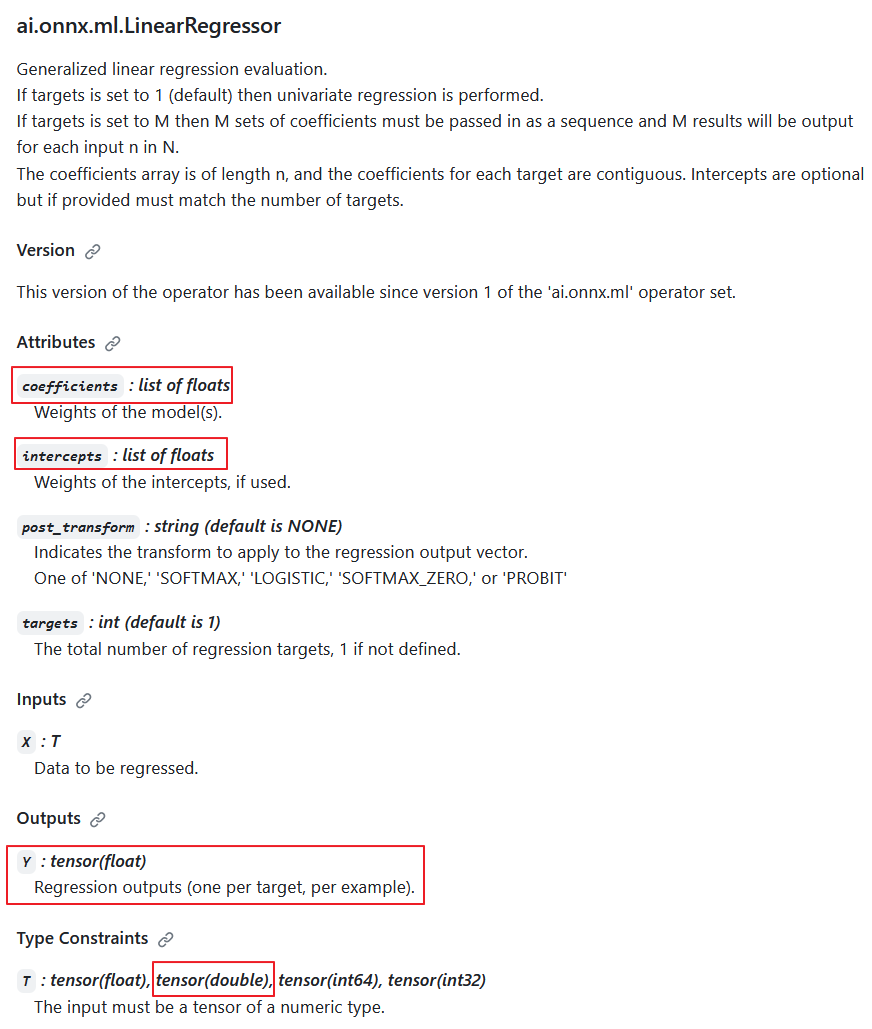
ai.onnx.ml.LinearRegressor operator description
Assim, a redução da precisão para float nos parâmetros e no valor de saída torna impossível para o ai.onnx.ml.LinearRegressor operar totalmente com números double (float64). Presumivelmente, por essa razão, os desenvolvedores do ONNX Runtime decidiram abster-se de implementá-lo para o tipo double.
O método de "adicionar suporte para double" foi demonstrado pelos desenvolvedores nos comentários do código (destacado em amarelo).
No ONNX Runtime, seu cálculo é realizado usando a classe LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.h).
Os parâmetros do operador, coefficients_ e intercepts_, são armazenados como std::vector<float>:
#pragma once #include "core/common/common.h" #include "core/framework/op_kernel.h" #include "core/util/math_cpuonly.h" #include "ml_common.h" namespace onnxruntime { namespace ml { class LinearRegressor final : public OpKernel { public: LinearRegressor(const OpKernelInfo& info); Status Compute(OpKernelContext* context) const override; private: int64_t num_targets_; std::vector<float> coefficients_; std::vector<float> intercepts_; bool use_intercepts_; POST_EVAL_TRANSFORM post_transform_; }; } // namespace ml } // namespace onnxruntimeA implementação do operador LinearRegressor (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.cc)
// Copyright (c) Microsoft Corporation. All rights reserved. // Licensed under the MIT License. #include "core/providers/cpu/ml/linearregressor.h" #include "core/common/narrow.h" #include "core/providers/cpu/math/gemm.h" namespace onnxruntime { namespace ml { ONNX_CPU_OPERATOR_ML_KERNEL( LinearRegressor, 1, // KernelDefBuilder().TypeConstraint("T", std::vector<MLDataType>{ // DataTypeImpl::GetTensorType<float>(), // DataTypeImpl::GetTensorType<double>()}), KernelDefBuilder().TypeConstraint("T", DataTypeImpl::GetTensorType<float>()), LinearRegressor); LinearRegressor::LinearRegressor(const OpKernelInfo& info) : OpKernel(info), intercepts_(info.GetAttrsOrDefault<float>("intercepts")), post_transform_(MakeTransform(info.GetAttrOrDefault<std::string>("post_transform", "NONE"))) { ORT_ENFORCE(info.GetAttr<int64_t>("targets", &num_targets_).IsOK()); ORT_ENFORCE(info.GetAttrs<float>("coefficients", coefficients_).IsOK()); // use the intercepts_ if they're valid use_intercepts_ = intercepts_.size() == static_cast<size_t>(num_targets_); } // Use GEMM for the calculations, with broadcasting of intercepts // https://github.com/onnx/onnx/blob/main/docs/Operators.md#Gemm // // X: [num_batches, num_features] // coefficients_: [num_targets, num_features] // intercepts_: optional [num_targets]. // Output: X * coefficients_^T + intercepts_: [num_batches, num_targets] template <typename T> static Status ComputeImpl(const Tensor& input, ptrdiff_t num_batches, ptrdiff_t num_features, ptrdiff_t num_targets, const std::vector<float>& coefficients, const std::vector<float>* intercepts, Tensor& output, POST_EVAL_TRANSFORM post_transform, concurrency::ThreadPool* threadpool) { const T* input_data = input.Data<T>(); T* output_data = output.MutableData<T>(); if (intercepts != nullptr) { TensorShape intercepts_shape({num_targets}); onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, intercepts->data(), &intercepts_shape, output_data, threadpool); } else { onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans, num_batches, num_targets, num_features, 1.f, input_data, coefficients.data(), 1.f, nullptr, nullptr, output_data, threadpool); } if (post_transform != POST_EVAL_TRANSFORM::NONE) { ml::batched_update_scores_inplace(gsl::make_span(output_data, SafeInt<size_t>(num_batches) * num_targets), num_batches, num_targets, post_transform, -1, false, threadpool); } return Status::OK(); } Status LinearRegressor::Compute(OpKernelContext* ctx) const { Status status = Status::OK(); const auto& X = *ctx->Input<Tensor>(0); const auto& input_shape = X.Shape(); if (input_shape.NumDimensions() > 2) { return ORT_MAKE_STATUS(ONNXRUNTIME, INVALID_ARGUMENT, "Input shape had more than 2 dimension. Dims=", input_shape.NumDimensions()); } ptrdiff_t num_batches = input_shape.NumDimensions() <= 1 ? 1 : narrow<ptrdiff_t>(input_shape[0]); ptrdiff_t num_features = input_shape.NumDimensions() <= 1 ? narrow<ptrdiff_t>(input_shape.Size()) : narrow<ptrdiff_t>(input_shape[1]); Tensor& Y = *ctx->Output(0, {num_batches, num_targets_}); concurrency::ThreadPool* tp = ctx->GetOperatorThreadPool(); auto element_type = X.GetElementType(); switch (element_type) { case ONNX_NAMESPACE::TensorProto_DataType_FLOAT: { status = ComputeImpl<float>(X, num_batches, num_features, narrow<ptrdiff_t>(num_targets_), coefficients_, use_intercepts_ ? &intercepts_ : nullptr, Y, post_transform_, tp); break; } case ONNX_NAMESPACE::TensorProto_DataType_DOUBLE: { // TODO: Add support for 'double' to the scoring functions in ml_common.h // once that is done we can just call ComputeImpl<double>... // Alternatively we could cast the input to float. } default: status = ORT_MAKE_STATUS(ONNXRUNTIME, FAIL, "Unsupported data type of ", element_type); } return status; } } // namespace ml } // namespace onnxruntime
Acontece que há uma opção de usar números double como valores de entrada e realizar o cálculo do operador com parâmetros float. Outra possibilidade poderia ser reduzir a precisão dos dados de entrada para float. No entanto, nenhuma dessas opções pode ser considerada uma solução adequada.
A especificação do operador ai.onnx.ml.LinearRegressor restringe a capacidade de operação total com números double, já que os parâmetros e o valor de saída são limitados ao tipo float.
Uma situação semelhante ocorre com outros operadores ML do ONNX, como ai.onnx.ml.SVMRegressor e ai.onnx.ml.TreeEnsembleRegressor.
Como resultado, todos os desenvolvedores que utilizam a execução de modelos ONNX em precisão double enfrentam essa limitação da especificação. Uma solução poderia envolver a extensão da especificação ONNX (ou a adição de operadores semelhantes como LinearRegressor64, SVMRegressor64 e TreeEnsembleRegressor64 com parâmetros e valores de saída em double). No entanto, no momento, essa questão permanece sem solução.
Muito depende do conversor ONNX. Para modelos calculados em double, pode ser preferível evitar o uso desses operadores (embora isso nem sempre seja possível). Neste caso específico, o conversor para ONNX não funcionou de maneira ideal com o modelo do usuário.
Como veremos mais adiante, o conversor sklearn-onnx consegue contornar a limitação do LinearRegressor: para modelos ONNX double, ele usa os operadores ONNX MatMul() e Add() em vez disso. Graças a esse método, inúmeros modelos de regressão da biblioteca Scikit-learn são convertidos com sucesso em modelos ONNX calculados em double, preservando a precisão dos modelos double originais.
1. Conjunto de Dados de Teste
Para executar os exemplos, você precisará instalar o Python (usamos a versão 3.10.8), bibliotecas adicionais (pip install -U scikit-learn numpy matplotlib onnx onnxruntime skl2onnx) e especificar o caminho para o Python no MetaEditor (no menu Ferramentas->Opções->Compiladores->Python).
Como conjunto de dados de teste, usaremos valores gerados da função y = 4X + 10sin(X*0.5).
Para exibir um gráfico dessa função, abra o MetaEditor, crie um arquivo chamado RegressionData.py, copie o texto do script e execute-o clicando no botão "Compilar".
O script para exibir o conjunto de dados de teste
# RegressionData.py # The code plots the synthetic data, used for all regression models # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # import necessary libraries import numpy as np import matplotlib.pyplot as plt # generate synthetic data for regression X = np.arange(0,100,1).reshape(-1,1) y = 4*X + 10*np.sin(X*0.5) # set the figure size plt.figure(figsize=(8,5)) # plot the initial data for regression plt.scatter(X, y, label='Regression Data', marker='o') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Regression data') plt.show()
Como resultado, será exibido um gráfico da função, que usaremos para testar os métodos de regressão.
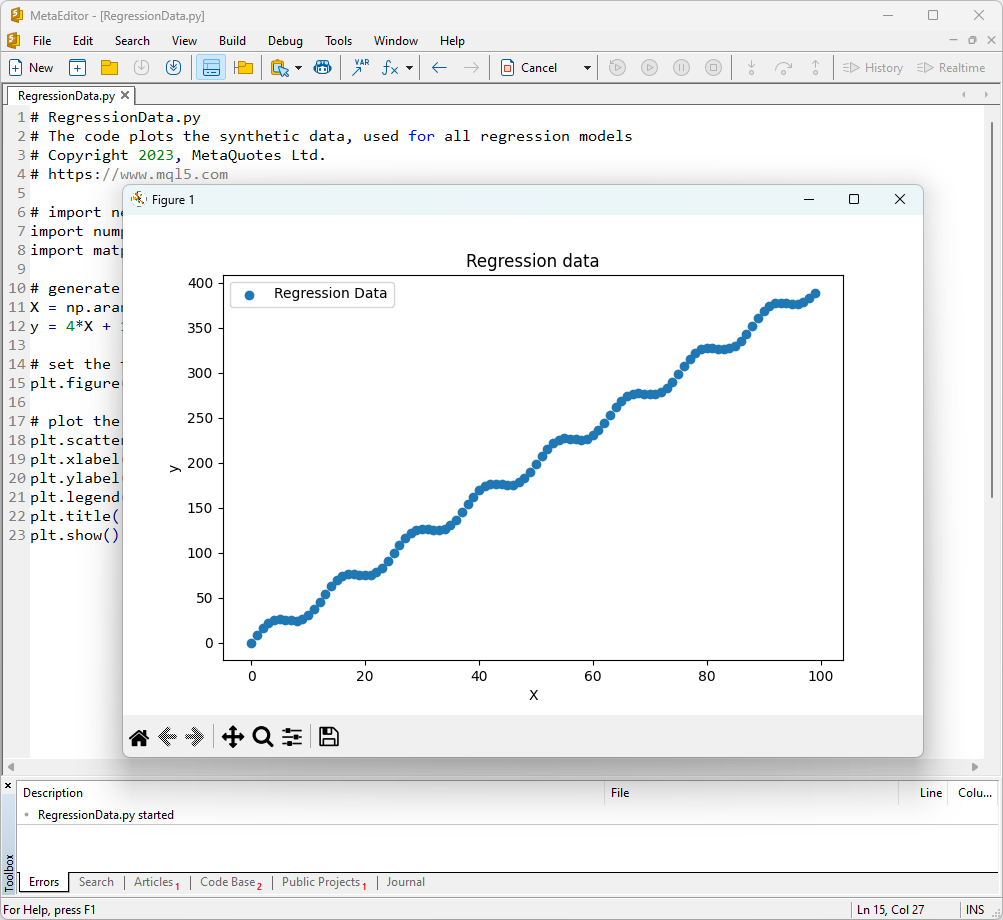
Fig.1. Função para testar modelos de regressão
2. Modelo de Regressão
O objetivo de uma tarefa de regressão é encontrar uma função ou modelo matemático que melhor descreva a relação entre as características e a variável alvo para prever valores numéricos para novos dados. Isso permite fazer previsões, otimizar soluções e tomar decisões informadas com base em dados.
Vamos considerar os principais modelos de regressão no pacote scikit-learn.
2.0. Lista de Modelos de Regressão do Scikit-learn
Para exibir uma lista dos modelos de regressão disponíveis no scikit-learn, você pode usar o script:
# ScikitLearnRegressors.py # The script lists all the regression algorithms available inb scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn regression models from sklearn.utils import all_estimators regressors = all_estimators(type_filter='regressor') for index, (name, RegressorClass) in enumerate(regressors, start=1): print(f"Regressor {index}: {name}")
Saída:
The Python version is 3.10.8
The scikit-learn version is 1.3.2.
Regressor 1: ARDRegression
Regressor 2: AdaBoostRegressor
Regressor 3: BaggingRegressor
Regressor 4: BayesianRidge
Regressor 5: CCA
Regressor 6: DecisionTreeRegressor
Regressor 7: DummyRegressor
Regressor 8: ElasticNet
Regressor 9: ElasticNetCV
Regressor 10: ExtraTreeRegressor
Regressor 11: ExtraTreesRegressor
Regressor 12: GammaRegressor
Regressor 13: GaussianProcessRegressor
Regressor 14: GradientBoostingRegressor
Regressor 15: HistGradientBoostingRegressor
Regressor 16: HuberRegressor
Regressor 17: IsotonicRegression
Regressor 18: KNeighborsRegressor
Regressor 19: KernelRidge
Regressor 20: Lars
Regressor 21: LarsCV
Regressor 22: Lasso
Regressor 23: LassoCV
Regressor 24: LassoLars
Regressor 25: LassoLarsCV
Regressor 26: LassoLarsIC
Regressor 27: LinearRegression
Regressor 28: LinearSVR
Regressor 29: MLPRegressor
Regressor 30: MultiOutputRegressor
Regressor 31: MultiTaskElasticNet
Regressor 32: MultiTaskElasticNetCV
Regressor 33: MultiTaskLasso
Regressor 34: MultiTaskLassoCV
Regressor 35: NuSVR
Regressor 36: OrthogonalMatchingPursuit
Regressor 37: OrthogonalMatchingPursuitCV
Regressor 38: PLSCanonical
Regressor 39: PLSRegression
Regressor 40: PassiveAggressiveRegressor
Regressor 41: PoissonRegressor
Regressor 42: QuantileRegressor
Regressor 43: RANSACRegressor
Regressor 44: RadiusNeighborsRegressor
Regressor 45: RandomForestRegressor
Regressor 46: RegressorChain
Regressor 47: Ridge
Regressor 48: RidgeCV
Regressor 49: SGDRegressor
Regressor 50: SVR
Regressor 51: StackingRegressor
Regressor 52: TheilSenRegressor
Regressor 53: TransformedTargetRegressor
Regressor 54: TweedieRegressor
Regressor 55: VotingRegressor
The scikit-learn version is 1.3.2.
Regressor 1: ARDRegression
Regressor 2: AdaBoostRegressor
Regressor 3: BaggingRegressor
Regressor 4: BayesianRidge
Regressor 5: CCA
Regressor 6: DecisionTreeRegressor
Regressor 7: DummyRegressor
Regressor 8: ElasticNet
Regressor 9: ElasticNetCV
Regressor 10: ExtraTreeRegressor
Regressor 11: ExtraTreesRegressor
Regressor 12: GammaRegressor
Regressor 13: GaussianProcessRegressor
Regressor 14: GradientBoostingRegressor
Regressor 15: HistGradientBoostingRegressor
Regressor 16: HuberRegressor
Regressor 17: IsotonicRegression
Regressor 18: KNeighborsRegressor
Regressor 19: KernelRidge
Regressor 20: Lars
Regressor 21: LarsCV
Regressor 22: Lasso
Regressor 23: LassoCV
Regressor 24: LassoLars
Regressor 25: LassoLarsCV
Regressor 26: LassoLarsIC
Regressor 27: LinearRegression
Regressor 28: LinearSVR
Regressor 29: MLPRegressor
Regressor 30: MultiOutputRegressor
Regressor 31: MultiTaskElasticNet
Regressor 32: MultiTaskElasticNetCV
Regressor 33: MultiTaskLasso
Regressor 34: MultiTaskLassoCV
Regressor 35: NuSVR
Regressor 36: OrthogonalMatchingPursuit
Regressor 37: OrthogonalMatchingPursuitCV
Regressor 38: PLSCanonical
Regressor 39: PLSRegression
Regressor 40: PassiveAggressiveRegressor
Regressor 41: PoissonRegressor
Regressor 42: QuantileRegressor
Regressor 43: RANSACRegressor
Regressor 44: RadiusNeighborsRegressor
Regressor 45: RandomForestRegressor
Regressor 46: RegressorChain
Regressor 47: Ridge
Regressor 48: RidgeCV
Regressor 49: SGDRegressor
Regressor 50: SVR
Regressor 51: StackingRegressor
Regressor 52: TheilSenRegressor
Regressor 53: TransformedTargetRegressor
Regressor 54: TweedieRegressor
Regressor 55: VotingRegressor
Para conveniência, nesta lista de regressoras, elas estão destacadas em diferentes cores. Modelos que requerem um modelo de regressão base estão destacados em cinza, enquanto outros modelos podem ser usados de forma independente. Note que os modelos exportados com sucesso para o formato ONNX estão marcados em verde, e os modelos que encontram erros durante a conversão na versão atual do scikit-learn 1.2.2 estão marcados em vermelho. Métodos inadequados para a tarefa de teste considerada estão destacados em azul.
A análise da qualidade da regressão usa métricas de regressão, que são funções dos valores reais e previstos. Na linguagem MQL5, várias métricas diferentes estão disponíveis, detalhadas no artigo "Avaliando modelos ONNX usando métricas de regressão".
Neste artigo, três métricas serão usadas para comparar a qualidade de diferentes modelos:
- Coeficiente de determinação R-quadrado (R2);
- Erro Médio Absoluto (MAE);
- Erro Médio Quadrático (MSE).
2.1. Modelos de Regressão do Scikit-learn que se convertem para modelos ONNX float e double
Esta seção apresenta modelos de regressão que são convertidos com sucesso para formatos ONNX em ambas as precisões float e double.
Todos os modelos de regressão discutidos a seguir são apresentados no seguinte formato:
- Descrição do modelo, princípio de funcionamento, vantagens e limitações
- Script Python para criar o modelo, exportá-lo para arquivos ONNX em formatos float e double, e executar os modelos obtidos usando o ONNX Runtime em Python. Métricas como R^2, MAE, MSE, calculadas usando sklearn.metrics, são usadas para avaliar a qualidade dos modelos originais e ONNX.
- Script MQL5 para executar modelos ONNX (float e double) via ONNX Runtime, com métricas calculadas usando RegressionMetric().
- Representação do modelo ONNX no Netron para precisão float e double.
2.1.1. sklearn.linear_model.ARDRegression
ARDRegression (Regressão por Determinação Automática de Relevância) é um método de regressão projetado para abordar problemas de regressão enquanto determina automaticamente a importância (relevância) das características e estabelece seus pesos durante o processo de treinamento do modelo.
ARDRegression permite a detecção e uso apenas das características mais importantes para construir um modelo de regressão, o que pode ser benéfico ao lidar com um grande número de características.
Princípio de Funcionamento do ARDRegression:
- Regressão Linear: ARDRegression é baseado em regressão linear, assumindo uma relação linear entre as variáveis independentes (características) e a variável alvo.
- Determinação Automática da Importância das Características: A principal distinção do ARDRegression é sua determinação automática de quais características são mais importantes para prever a variável alvo. Isso é alcançado introduzindo distribuições prévias (regularização) sobre os pesos, permitindo que o modelo defina automaticamente pesos zero para características menos significativas.
- Estimativa das Probabilidades Posteriores: ARDRegression calcula probabilidades posteriores para cada característica, permitindo determinar sua importância. Características com altas probabilidades posteriores são consideradas relevantes e recebem pesos não zero, enquanto características com baixas probabilidades posteriores recebem pesos zero.
- Redução de Dimensionalidade: Assim, ARDRegression pode levar à redução da dimensionalidade dos dados removendo características insignificantes.
Vantagens do ARDRegression:
- Determinação Automática das Características Importantes: O método identifica e usa automaticamente apenas as características mais importantes, potencialmente melhorando o desempenho do modelo e reduzindo o risco de overfitting.
- Resiliência à Multicolinearidade: ARDRegression lida bem com a multicolinearidade, mesmo quando as características são altamente correlacionadas.
Limitações do ARDRegression:
- Requer Seleção de Distribuições Prévias: A escolha de distribuições prévias adequadas pode requerer experimentação.
- Complexidade Computacional: Treinar ARDRegression pode ser computacionalmente caro, especialmente para grandes conjuntos de dados.
ARDRegression é um método de regressão que determina automaticamente a importância das características e estabelece seus pesos com base nas probabilidades posteriores. Este método é útil quando é necessário considerar apenas as características significativas para construir um modelo de regressão e reduzir a dimensionalidade dos dados.
2.1.1.1. Código para criar o modelo ARDRegression e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.ARDRegression, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# ARDRegression.py
# The code demonstrates the process of training ARDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"
# create an ARDRegression model
regression_model = ARDRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training ARDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"
# create an ARDRegression model
regression_model = ARDRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
O script cria e treina o modelo sklearn.linear_model.ARDRegression (o modelo original é considerado em double), exporta o modelo para ONNX em float e double (ard_regression_float.onnx e ard_regression_double.onnx) e compara a precisão de sua operação.
Ele também gera os arquivos ARDRegression_plot_float.png e ARDRegression_plot_double.png, permitindo uma avaliação visual dos resultados dos modelos ONNX para float e double (Fig. 2-3).
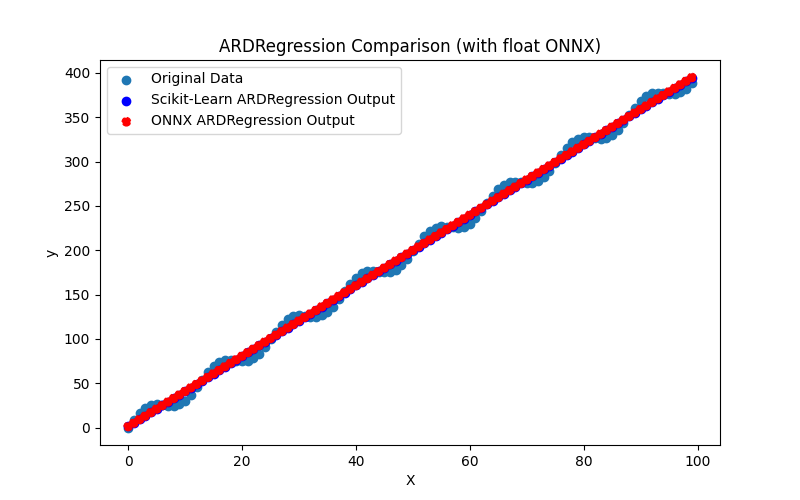
Fig.2. Resultados do ARDRegression.py (float)
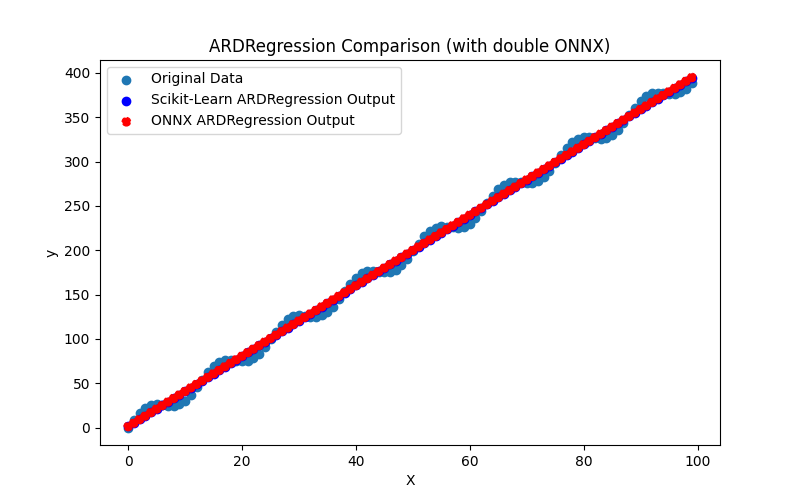
Fig.3. Resultados do ARDRegression.py (double)
Visualmente, os modelos ONNX para float e double parecem os mesmos (Fig. 2-3), informações detalhadas podem ser encontradas na aba Journal:
Python ARDRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python Python ARDRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python ARDRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891289 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
Neste exemplo, o modelo original foi considerado em double, e depois foi exportado para os modelos ONNX ard_regression_float.onnx e ard_regression_double.onnx para float e double, respectivamente.
Se a precisão do modelo for avaliada pelo Erro Médio Absoluto (MAE), a precisão do modelo ONNX para float é de até 6 casas decimais, enquanto o modelo ONNX usando double mostrou retenção de precisão de até 15 casas decimais, em conformidade com a precisão do modelo original.
As propriedades dos modelos ONNX podem ser visualizadas no MetaEditor (Fig. 4-5).
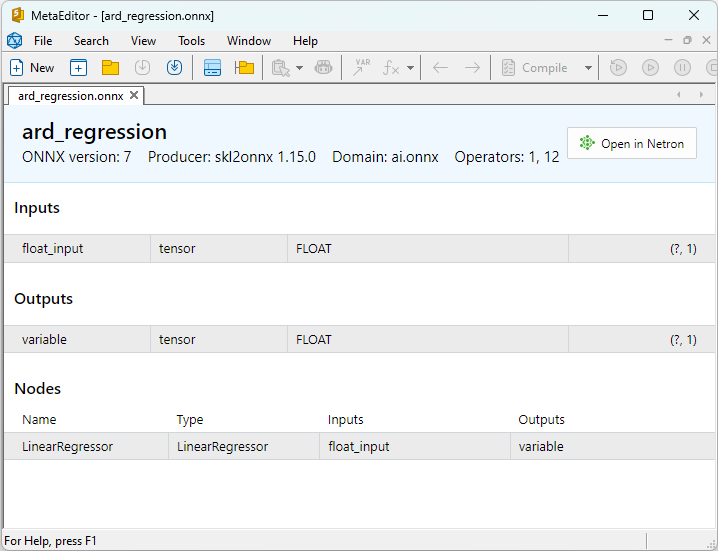
Fig.4. ard_regression_float.onnx modelo ONNX no MetaEditor
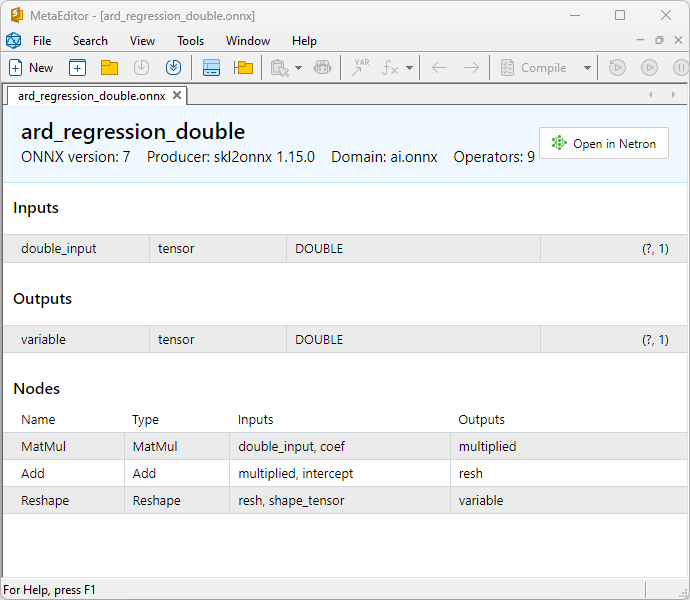
Fig.5. ard_regression_double.onnx modelo ONNX no MetaEditor
Uma comparação entre os modelos ONNX em float e double mostra que, neste caso, o cálculo dos modelos ONNX para ARDRegression ocorre de maneira diferente: para números float, o operador LinearRegressor() do ONNX-ML é usado, enquanto para números double, são utilizados os operadores ONNX MatMul(), Add() e Reshape().
A implementação do modelo em ONNX depende do conversor; nos exemplos para exportação para ONNX, a função skl2onnx.convert_sklearn() da biblioteca skl2onnx será usada.
2.1.1.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos ONNX salvos ard_regression_float.onnx e ard_regression_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| ARDRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ARDRegression" #define ONNXFilenameFloat "ard_regression_float.onnx" #define ONNXFilenameDouble "ard_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
ARDRegression (EURUSD,H1) Testing ONNX float: ARDRegression (ard_regression_float.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 ARDRegression (EURUSD,H1) ARDRegression (EURUSD,H1) Testing ONNX double: ARDRegression (ard_regression_double.onnx) ARDRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 ARDRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537597 ARDRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128795
Comparação com o modelo original em double no Python:
Testing ONNX float: ARDRegression (ard_regression_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: ARDRegression (ard_regression_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537597
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.1.3. As representações ONNX dos modelos ard_regression_float.onnx e ard_regression_double.onnx
Netron (versão web) é uma ferramenta para visualização de modelos e análise de gráficos de computação, que pode ser usada para modelos no formato ONNX (Open Neural Network Exchange).
Netron apresenta gráficos de modelos e sua arquitetura de forma clara e interativa, permitindo a exploração da estrutura e dos parâmetros de modelos de aprendizado profundo, incluindo aqueles criados usando ONNX.
Principais características do Netron incluem:
- Visualização de Gráficos: Netron exibe a arquitetura do modelo como um gráfico, permitindo ver as camadas, operações e conexões entre elas. Você pode compreender facilmente a estrutura e o fluxo de dados dentro do modelo.
- Exploração Interativa: Você pode selecionar nós no gráfico para obter informações adicionais sobre cada operador e seus parâmetros.
- Suporte para Vários Formatos: Netron suporta uma variedade de formatos de modelos de aprendizado profundo, incluindo ONNX, TensorFlow, PyTorch, CoreML e outros.
- Capacidade de Análise de Parâmetros: Você pode visualizar os parâmetros e pesos do modelo, o que é útil para entender os valores usados em diferentes partes do modelo.
Netron é conveniente para desenvolvedores e pesquisadores na área de aprendizado de máquina e aprendizado profundo, pois simplifica a visualização e análise de modelos, auxiliando na compreensão e depuração de redes neurais complexas.
Esta ferramenta permite uma inspeção rápida do modelo, explorando sua estrutura e parâmetros, facilitando o trabalho com redes neurais profundas.
Para mais detalhes sobre o Netron, consulte os artigos: Visualizing your Neural Network with Netron e Visualize Keras Neural Networks with Netron.
Vídeo sobre o Netron::
O modelo ard_regression_float.onnx é mostrado na Fig.6:
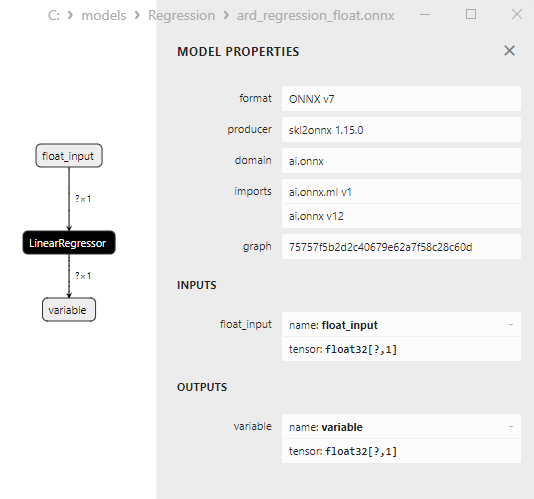
Fig.6. Representação ONNX do modelo ard_regression_float.onnx no Netron
O operador ONNX LinearRegressor() da ai.onnx.ml é parte do padrão ONNX, descrevendo um modelo para tarefas de regressão. Este operador é usado para regressão, que envolve a previsão de valores numéricos (contínuos) com base em características de entrada.
Ele recebe os parâmetros do modelo como entrada, tais como pesos e bias, junto com as características de entrada, e executa a regressão linear. A regressão linear estima os parâmetros (pesos) para cada característica de entrada e, em seguida, realiza uma combinação linear dessas características com os pesos para gerar uma previsão.
Este operador realiza os seguintes passos:
- Recebe os pesos e bias do modelo, juntamente com as características de entrada.
- Para cada exemplo de dados de entrada, realiza uma combinação linear dos pesos com as características correspondentes.
- Adiciona o bias ao valor resultante.
O resultado é a previsão da variável alvo na tarefa de regressão.
Os parâmetros do LinearRegressor() são mostrados na Fig.7.
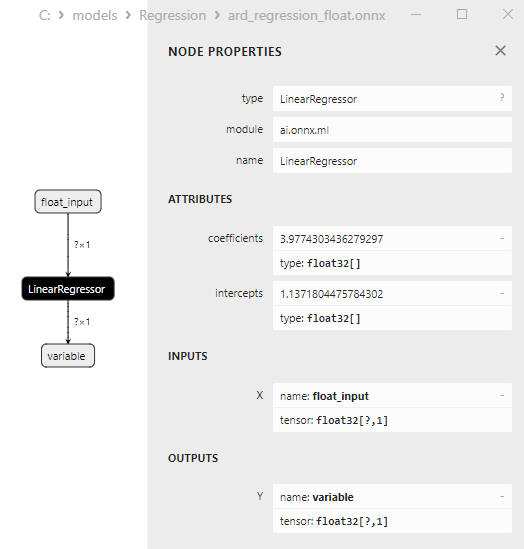
Fig.7. As propriedades do operador LinearRegressor() do modelo ard_regression_float.onnx no Netron
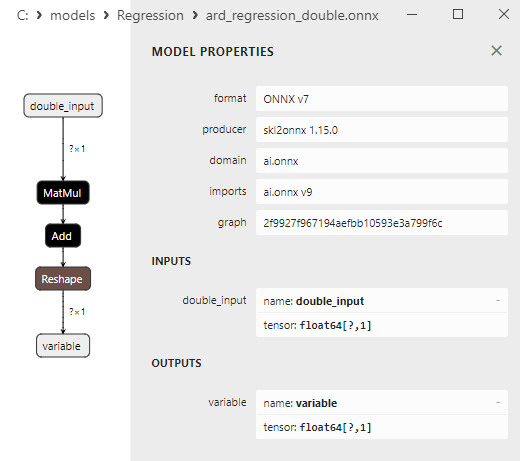
Fig.8. Representação ONNX do modelo ard_regression_double.onnx no Netron
Os parâmetros dos operadores ONNX MatMul(), Add() e Reshape() são mostrados nas Fig.9-11.
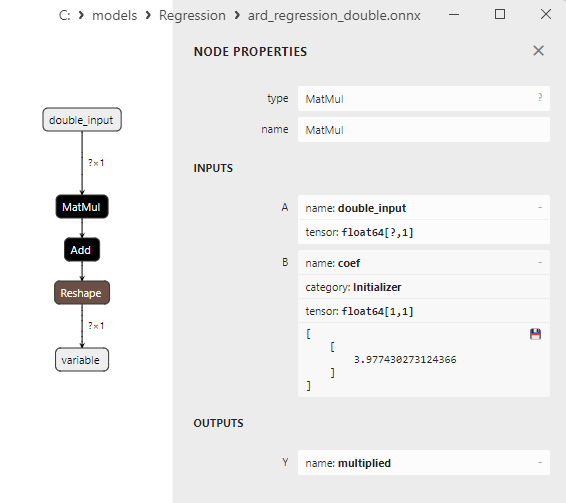
Fig.9. Propriedades do operador MatMul no modelo ard_regression_double.onnx no Netron
O operador ONNX MatMul (multiplicação de matrizes) realiza a multiplicação de duas matrizes.
Ele recebe duas entradas: duas matrizes e retorna seu produto matricial.
Se você tiver duas matrizes, A e B, o resultado de Matmul(A, B) é uma matriz C, onde cada elemento C[i][j] é calculado como a soma dos produtos dos elementos da linha i da matriz A pelos elementos da coluna j da matriz B.
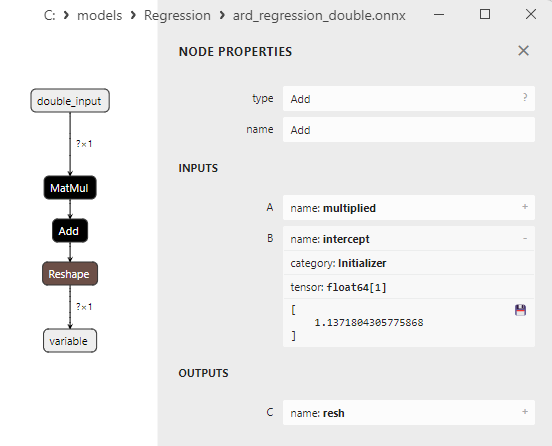
Fig.10. Propriedades do operador Add no modelo ard_regression_double.onnx no Netron
O operador ONNX Add() realiza a adição elemento a elemento de dois tensores ou matrizes de mesma forma.
Ele recebe duas entradas e retorna o resultado, onde cada elemento do tensor resultante é igual à soma dos elementos correspondentes dos tensores de entrada.
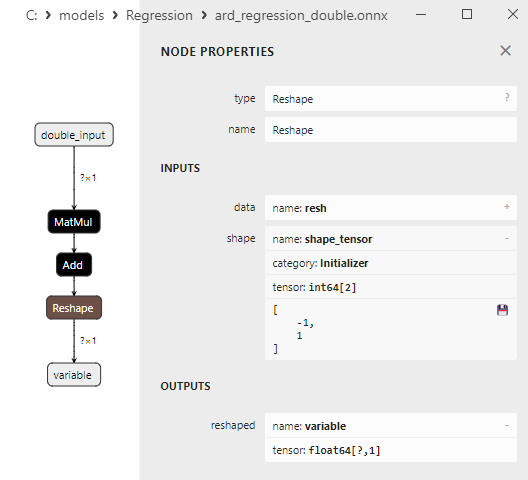
Fig.11. Propriedades do operador Reshape no modelo ard_regression_double.onnx no Netron
O operador ONNX Reshape(-1,1) é usado para modificar a forma (ou dimensão) dos dados de entrada. Neste operador, o valor -1 para a dimensão indica que o tamanho dessa dimensão deve ser calculado automaticamente com base nas outras dimensões para garantir a consistência dos dados.
O valor 1 na segunda dimensão especifica que, após a transformação da forma, cada elemento terá uma única subdimensão.
2.1.2. sklearn.linear_model.BayesianRidge
BayesianRidge é um método de regressão que utiliza uma abordagem bayesiana para estimar os parâmetros do modelo. Este método permite modelar a distribuição a priori dos parâmetros e atualizá-la considerando os dados para obter a distribuição a posteriori dos parâmetros.
BayesianRidge é um método de regressão bayesiana projetado para prever a variável dependente com base em uma ou várias variáveis independentes.
Princípio de Funcionamento do BayesianRidge:
- Distribuição a priori dos parâmetros: Começa com a definição da distribuição a priori dos parâmetros do modelo. Esta distribuição representa o conhecimento prévio ou suposições sobre os parâmetros do modelo antes de considerar os dados. No caso do BayesianRidge, distribuições a priori em forma de Gaussianas são usadas.
- Atualizando a distribuição dos parâmetros: Uma vez que a distribuição a priori dos parâmetros é definida, ela é atualizada com base nos dados. Isso é feito usando a teoria bayesiana, onde a distribuição a posteriori dos parâmetros é calculada considerando os dados. Um aspecto essencial é a estimativa dos hiperparâmetros, que influenciam a forma da distribuição a posteriori.
- Previsão: Após a estimativa da distribuição a posteriori dos parâmetros, previsões podem ser feitas para novas observações. Isso resulta em uma distribuição de previsões, em vez de um único valor pontual, permitindo que a incerteza nas previsões seja considerada.
Vantagens do BayesianRidge:
- Consideração da incerteza: O BayesianRidge leva em conta a incerteza nos parâmetros do modelo e nas previsões. Em vez de previsões pontuais, são fornecidos intervalos de confiança.
- Regularização: O método de regressão bayesiana pode ser útil para a regularização do modelo, auxiliando na prevenção do overfitting.
- Seleção automática de características: O BayesianRidge pode determinar automaticamente a importância das características, reduzindo os pesos das características insignificantes.
Limitações do BayesianRidge:
- Complexidade computacional: O método requer recursos computacionais para estimar os parâmetros e calcular a distribuição a posteriori.
- Alto nível de abstração: Pode ser necessário um entendimento mais profundo de estatísticas bayesianas para compreender e usar o BayesianRidge.
- Nem sempre a melhor escolha: O BayesianRidge pode não ser o método mais adequado em certas tarefas de regressão, especialmente ao lidar com dados limitados.
BayesianRidge é útil em tarefas de regressão onde a incerteza dos parâmetros e previsões é importante e em casos onde a regularização do modelo é necessária.
2.1.2.1. Código para criar o modelo BayesianRidge e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.BayesianRidge, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# BayesianRidge.py
# The code demonstrates the process of training BayesianRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"
# create a Bayesian Ridge regression model
regression_model = BayesianRidge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training BayesianRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"
# create a Bayesian Ridge regression model
regression_model = BayesianRidge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python BayesianRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python Python BayesianRidge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382627587808 Python Mean Absolute Error: 6.347568283744705 Python Mean Squared Error: 49.778160054267204 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python BayesianRidge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382628120845 Python Mean Absolute Error: 6.347568012853758 Python Mean Squared Error: 49.77815934891288 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
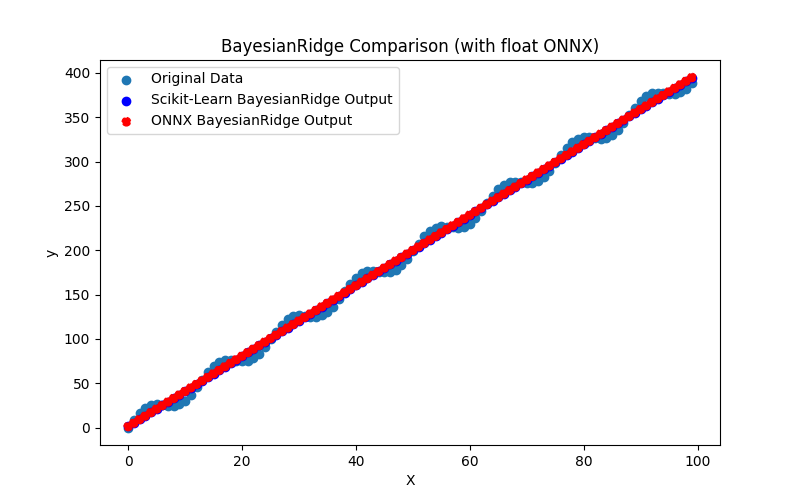
Fig.12. Resultados do BayesianRidge.py (float ONNX)
2.1.2.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos ONNX salvos bayesian_ridge_float.onnx e bayesian_ridge_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| BayesianRidge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BayesianRidge" #define ONNXFilenameFloat "bayesian_ridge_float.onnx" #define ONNXFilenameDouble "bayesian_ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
BayesianRidge (EURUSD,H1) Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382627587808 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475682837447049 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781600542671896 BayesianRidge (EURUSD,H1) BayesianRidge (EURUSD,H1) Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) BayesianRidge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382628120845 BayesianRidge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3475680128537624 BayesianRidge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781593489128866
Comparação com o modelo original em double no Python:
Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475682837447049 Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx) Python Mean Absolute Error: 6.347568012853758 MQL5: Mean Absolute Error: 6.3475680128537624
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.2.3. Representação ONNX do bayesian_ridge_float.onnx e bayesian_ridge_double.onnx
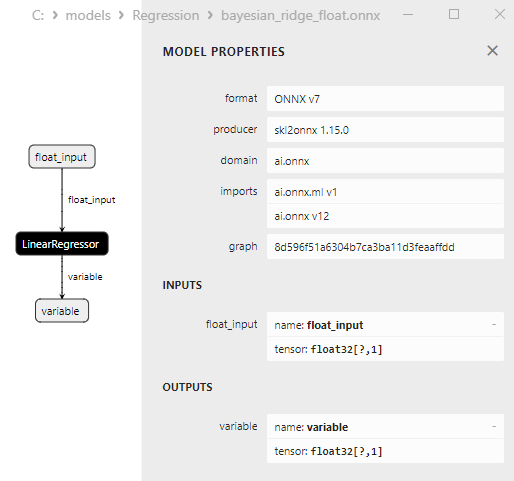
Fig.13. Representação ONNX do bayesian_ridge_float.onnx no Netron
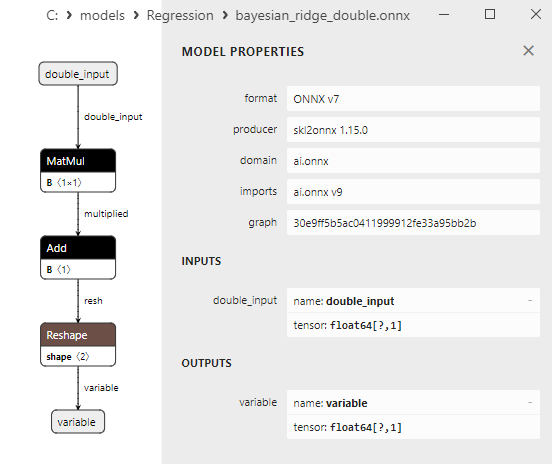
Fig.14. Representação ONNX do bayesian_ridge_double.onnx no Netron
Nota sobre os Métodos ElasticNet e ElasticNetCV
ElasticNet e ElasticNetCV são dois métodos de aprendizado de máquina relacionados, usados para regularizar modelos de regressão, especialmente a regressão linear. Eles compartilham funcionalidades comuns, mas diferem na maneira de uso e aplicação.
ElasticNet (Regressão Elastic Net):
- Princípio de Funcionamento: ElasticNet é um método de regressão que combina Lasso (regularização L1) e Ridge (regularização L2). Ele adiciona dois componentes de regularização à função de perda: um penaliza o modelo por valores absolutos grandes dos coeficientes (como o Lasso), e o outro penaliza o modelo por grandes quadrados dos coeficientes (como o Ridge).
- ElasticNet é comumente usado quando há multicolinearidade nos dados (quando as características são altamente correlacionadas) e quando a redução de dimensionalidade é necessária, além de controlar os valores dos coeficientes.
ElasticNetCV (Validação Cruzada Elastic Net):
- Princípio de Funcionamento: ElasticNetCV é uma extensão do ElasticNet que envolve a seleção automática dos hiperparâmetros ótimos alpha (o coeficiente de mistura entre regularização L1 e L2) e lambda (a força da regularização) usando validação cruzada. Ele itera por vários valores de alpha e lambda, escolhendo a combinação que apresenta o melhor desempenho na validação cruzada.
- Vantagens: ElasticNetCV ajusta automaticamente os parâmetros do modelo com base na validação cruzada, permitindo a seleção dos valores ótimos dos hiperparâmetros sem a necessidade de ajuste manual. Isso o torna mais conveniente de usar e ajuda a prevenir o overfitting do modelo.
Assim, a principal diferença entre ElasticNet e ElasticNetCV é que ElasticNet é o método de regressão aplicado aos dados, enquanto ElasticNetCV é uma ferramenta que encontra automaticamente os valores ótimos dos hiperparâmetros para o modelo ElasticNet usando validação cruzada. ElasticNetCV é útil quando você precisa encontrar os melhores parâmetros do modelo e tornar o processo de ajuste mais automatizado.
2.1.3. sklearn.linear_model.ElasticNet
ElasticNet é um método de regressão que representa uma combinação de regularização L1 (Lasso) e L2 (Ridge).
Este método é usado para regressão, o que significa prever valores numéricos de uma variável alvo com base em um conjunto de características. ElasticNet ajuda a controlar o overfitting e considera penalidades L1 e L2 nos coeficientes do modelo.
Princípio de Funcionamento do ElasticNet:
- Dados de Entrada: Ele começa com o conjunto de dados original, onde temos características (variáveis independentes) e os valores correspondentes da variável alvo.
- Função Objetivo: ElasticNet minimiza a função de perda que inclui dois componentes - erro quadrático médio (MSE) e duas regularizações: L1 (Lasso) e L2 (Ridge). Isso significa que a função objetivo é assim:
Função Objetivo = MSE + α * L1 + β * L2
Onde α e β são hiperparâmetros que controlam os pesos das regularizações L1 e L2, respectivamente. - Encontrando α e β Ótimos: O método da validação cruzada é geralmente usado para encontrar os melhores valores de α e β. Isso permite selecionar valores que equilibram a redução do overfitting e a preservação das características essenciais.
- Treinamento do Modelo: ElasticNet treina o modelo considerando os valores ótimos de α e β, minimizando a função objetivo.
- Previsão: Após o treinamento do modelo, ElasticNet pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do ElasticNet:
- Capacidade de Seleção de Características: ElasticNet pode selecionar automaticamente as características mais importantes, definindo pesos zero para características insignificantes (semelhante ao Lasso)
- Controle do Overfitting: ElasticNet permite controlar o overfitting devido às regularizações L1 e L2.
- Tratamento da Multicolinearidade: Este método é útil quando existe multicolinearidade (alta correlação entre as características), pois a regularização L2 pode reduzir a influência das características multicolineares.
Limitações do ElasticNet:
- Requer ajuste dos hiperparâmetros α e β, o que pode ser uma tarefa não trivial.
- Dependendo das escolhas dos parâmetros, ElasticNet pode reter poucas ou muitas características, afetando a qualidade do modelo.
ElasticNet é um método de regressão poderoso que pode ser benéfico em tarefas onde a seleção de características e o controle do overfitting são cruciais.
2.1.3.1. Código para criar o modelo ElasticNet e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.ElasticNet, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# ElasticNet.py
# The code demonstrates the process of training ElasticNet model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"
# create an ElasticNet model
regression_model = ElasticNet()
# fit the model to the data
regression_model.fit(X,y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training ElasticNet model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"
# create an ElasticNet model
regression_model = ElasticNet()
# fit the model to the data
regression_model.fit(X,y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python ElasticNet Original model (double) Python R-squared (Coefficient of determination): 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python Python ElasticNet ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377032416807 Python Mean Absolute Error: 6.344395027824294 Python Mean Squared Error: 49.78556400887057 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python ElasticNet ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962377031744798 Python Mean Absolute Error: 6.344394662876524 Python Mean Squared Error: 49.78556489812415 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
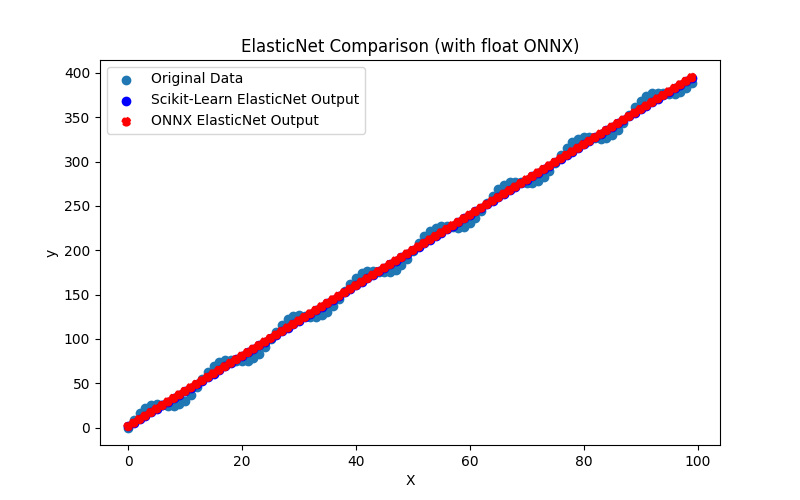
Fig.15. Resultados do ElasticNet.py (float ONNX)
2.1.3.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos elastic_net_double.onnx e elastic_net_float.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| ElasticNet.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNet" #define ONNXFilenameFloat "elastic_net_float.onnx" #define ONNXFilenameDouble "elastic_net_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
ElasticNet (EURUSD,H1) Testing ONNX float: ElasticNet (elastic_net_float.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377032416807 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443950278242944 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855640088705869 ElasticNet (EURUSD,H1) ElasticNet (EURUSD,H1) Testing ONNX double: ElasticNet (elastic_net_double.onnx) ElasticNet (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962377031744798 ElasticNet (EURUSD,H1) MQL5: Mean Absolute Error: 6.3443946628765220 ElasticNet (EURUSD,H1) MQL5: Mean Squared Error: 49.7855648981241217
Comparação com o modelo original em double no Python:
Testing ONNX float: ElasticNet (elastic_net_float.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443950278242944 Testing ONNX double: ElasticNet (elastic_net_double.onnx) Python Mean Absolute Error: 6.344394662876524 MQL5: Mean Absolute Error: 6.3443946628765220
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.3.3. Representação ONNX do modelo elastic_net_float.onnx e elastic_net_double.onnx
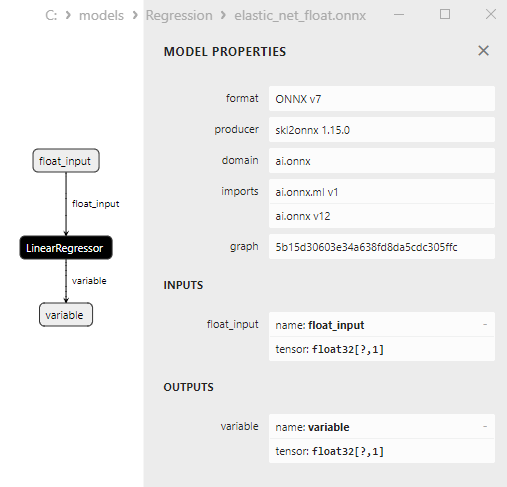
Fig.16. Representação ONNX do elastic_net_float.onnx no Netron
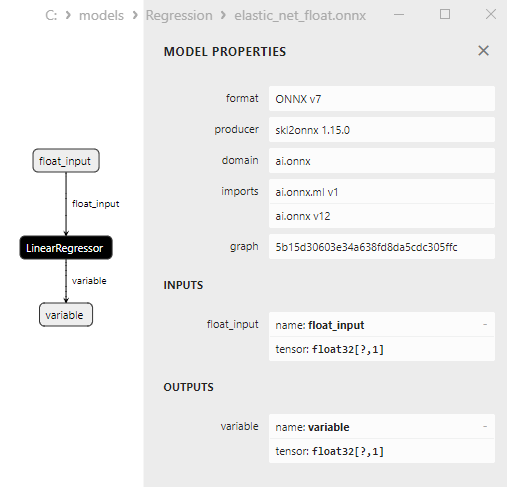
Fig.17. Representação ONNX do elastic_net_double.onnx no Netron
2.1.4. sklearn.linear_model.ElasticNetCV
ElasticNetCV é uma extensão do método ElasticNet projetada para selecionar automaticamente os valores ótimos dos hiperparâmetros α e β (regularização L1 e L2) usando validação cruzada.
Isso permite encontrar a melhor combinação de regularizações para o modelo ElasticNet sem a necessidade de ajuste manual dos parâmetros.
Princípio de Funcionamento do ElasticNetCV:
- Dados de Entrada: Começa com o conjunto de dados original contendo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Definindo o Intervalo de α e β: O usuário especifica o intervalo de valores para α e β a serem considerados durante a otimização. Esses valores são tipicamente escolhidos em uma escala logarítmica.
- Divisão dos Dados: O conjunto de dados é dividido em múltiplos folds para validação cruzada. Cada fold é usado como conjunto de dados de teste enquanto os outros são usados para treinamento.
- Validação Cruzada: Para cada combinação de α e β dentro do intervalo especificado, a validação cruzada é realizada. O modelo ElasticNet é treinado nos dados de treinamento e depois avaliado nos dados de teste.
- Avaliação de Desempenho: O erro médio nos conjuntos de dados de teste na validação cruzada é calculado para cada combinação de α e β.
- Seleção dos Parâmetros Ótimos: Valores de α e β correspondentes ao erro médio mínimo obtido durante a validação cruzada são determinados.
- Treinamento do Modelo com Parâmetros Ótimos: O modelo ElasticNetCV é treinado usando os valores ótimos de α e β encontrados.
- Previsão: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do ElasticNetCV:
- Seleção Automática de Hiperparâmetros: ElasticNetCV encontra automaticamente os valores ótimos de α e β, simplificando o ajuste do modelo.
- Prevenção de Overfitting: A validação cruzada ajuda a selecionar um modelo com boa capacidade de generalização.
- Robustez ao Ruído: Este método é robusto contra ruído nos dados e pode identificar a melhor combinação de regularizações considerando o ruído.
Limitações do ElasticNetCV:
- Complexidade Computacional: Realizar validação cruzada em um grande intervalo de parâmetros pode ser demorado.
- Parâmetros Ótimos Dependem da Escolha do Intervalo: Os resultados podem depender da escolha do intervalo de α e β, então é importante ajustar cuidadosamente esse intervalo.
ElasticNetCV é uma ferramenta poderosa para ajustar automaticamente a regularização no modelo ElasticNet e melhorar seu desempenho.
2.1.4.1. Código para criar o modelo ElasticNetCV e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.ElasticNetCV, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# ElasticNetCV.py
# The code demonstrates the process of training ElasticNetCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ElasticNetCV"
onnx_model_filename = data_path + "elastic_net_cv"
# create an ElasticNetCV model
regression_model = ElasticNetCV()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python ElasticNetCV Original model (double) Python R-squared (Coefficient of determination): 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python Python ElasticNetCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137770260989 Python Mean Absolute Error: 6.334486542922601 Python Mean Squared Error: 50.10217383894468 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python ElasticNetCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962137763338385 Python Mean Absolute Error: 6.334487104423225 Python Mean Squared Error: 50.10218299945999 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
< 
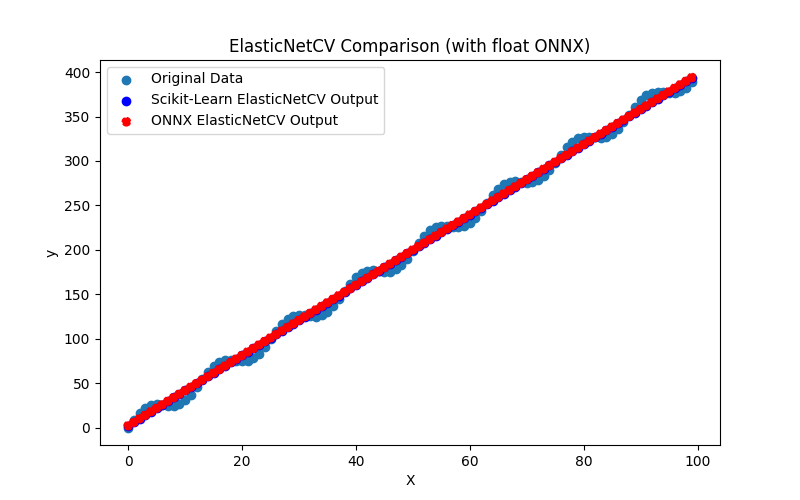
Fig.18. Resultados do ElasticNetCV.py (float ONNX)
2.1.4.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos elastic_net_cv_float.onnx e elastic_net_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| ElasticNetCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ElasticNetCV" #define ONNXFilenameFloat "elastic_net_cv_float.onnx" #define ONNXFilenameDouble "elastic_net_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
ElasticNetCV (EURUSD,H1) Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137770260989 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344865429226038 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021738389446938 ElasticNetCV (EURUSD,H1) ElasticNetCV (EURUSD,H1) Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) ElasticNetCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962137763338385 ElasticNetCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3344871044232205 ElasticNetCV (EURUSD,H1) MQL5: Mean Squared Error: 50.1021829994599983
Comparação com o modelo original em double no Python:
Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344865429226038 Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx) Python Mean Absolute Error: 6.334487104423225 MQL5: Mean Absolute Error: 6.3344871044232205
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.4.3. Representação ONNX do elastic_net_cv_float.onnx e elastic_net_cv_double.onnx
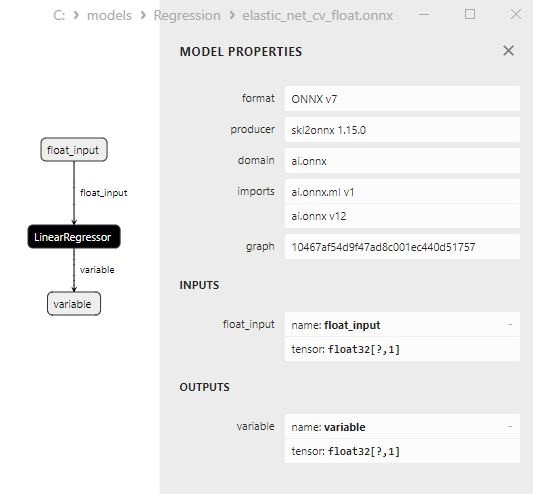
Fig.19. Representação ONNX do elastic_net_cv_float.onnx no Netron
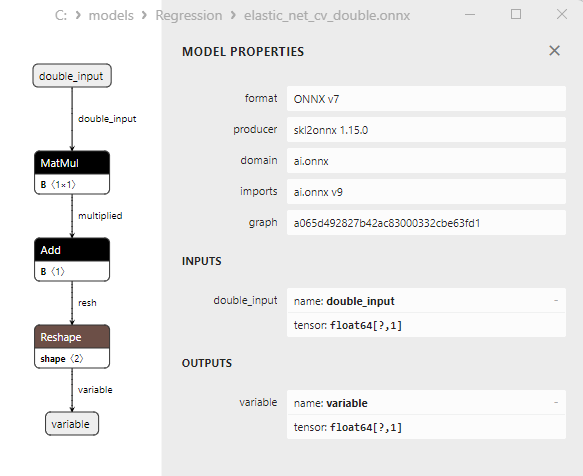
Fig.20. Representação ONNX do elastic_net_cv_double.onnx no Netron
2.1.5. sklearn.linear_model.HuberRegressor
HuberRegressor é um método de aprendizado de máquina usado para tarefas de regressão, sendo uma modificação do método de Mínimos Quadrados Ordinários (OLS) e projetado para ser robusto a outliers nos dados.
Ao contrário do OLS, que minimiza os quadrados dos erros, o HuberRegressor minimiza uma combinação de erros quadráticos e erros absolutos. Isso permite que o método funcione de maneira mais robusta na presença de outliers nos dados.
Princípio de Funcionamento do HuberRegressor:
- Dados de Entrada: Começa com o conjunto de dados original, onde há características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Função de Perda de Huber: O HuberRegressor utiliza a função de perda de Huber, que combina uma função de perda quadrática para erros pequenos e uma função de perda linear para erros grandes. Isso torna o método mais resistente a outliers.
- Treinamento do Modelo: O modelo é treinado nos dados usando a função de perda de Huber. Durante o treinamento, ajusta os pesos (coeficientes) para cada característica e o bias.
- Previsão: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do HuberRegressor:
- Robustez a Outliers: O HuberRegressor é mais robusto a outliers nos dados em comparação com OLS, tornando-o útil em tarefas onde os dados podem conter valores anômalos.
- Estimativa de Erros: A função de perda de Huber contribui para a estimativa de erros de previsão, o que pode ser útil para analisar os resultados do modelo.
- Nível de Regularização: O HuberRegressor também pode incorporar um nível de regularização, o que pode reduzir o overfitting.
Limitações do HuberRegressor:
- Menos Preciso que OLS na Ausência de Outliers: Em casos onde não há outliers nos dados, OLS pode fornecer resultados mais precisos.
- Ajuste de Parâmetros: O HuberRegressor possui um parâmetro que define o limite para o que é considerado "grande" para mudar para a função de perda linear. Este parâmetro requer ajuste.
HuberRegressor é valioso em tarefas de regressão onde os dados podem conter outliers e um modelo que seja robusto a tais anomalias é necessário.
2.1.5.1. Código para criar o modelo HuberRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.HuberRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. precisão tanto do modelo original quanto dos modelos exportados para ONNX.
# HuberRegressor.py
# The code demonstrates the process of training HuberRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"
# create a Huber Regressor model
huber_regressor_model = HuberRegressor()
# fit the model to the data
huber_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = huber_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training HuberRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"
# create a Huber Regressor model
huber_regressor_model = HuberRegressor()
# fit the model to the data
huber_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = huber_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python HuberRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python Python HuberRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363944236795 Python Mean Absolute Error: 6.341633300252807 Python Mean Squared Error: 49.80288328126165 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python HuberRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962363935647066 Python Mean Absolute Error: 6.341633708569641 Python Mean Squared Error: 49.80289464784336 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
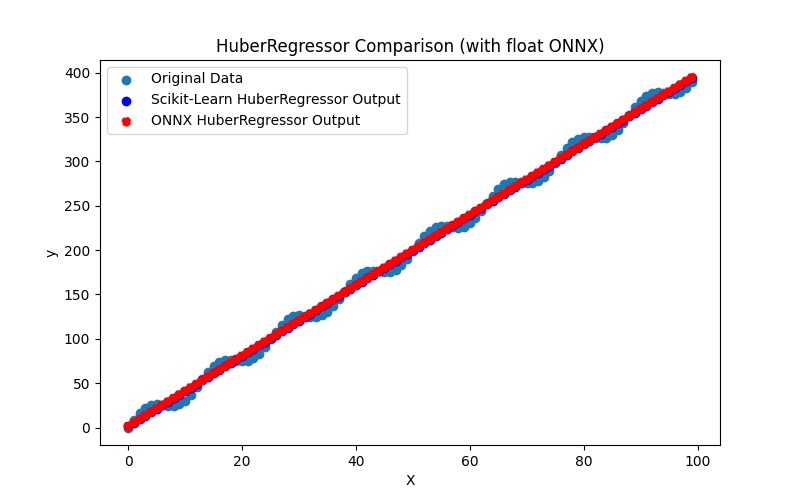
Fig.21. Resultados do HuberRegressor.py (float ONNX)
2.1.5.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos huber_regressor_float.onnx e huber_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| HuberRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HuberRegressor" #define ONNXFilenameFloat "huber_regressor_float.onnx" #define ONNXFilenameDouble "huber_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
HuberRegressor (EURUSD,H1) Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363944236795 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416333002528074 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028832812616571 HuberRegressor (EURUSD,H1) HuberRegressor (EURUSD,H1) Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) HuberRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962363935647066 HuberRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3416337085696410 HuberRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8028946478433525
Comparação com o modelo original em double no Python:
Testing ONNX float: HuberRegressor (huber_regressor_float.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416333002528074 Testing ONNX double: HuberRegressor (huber_regressor_double.onnx) Python Mean Absolute Error: 6.341633708569641 MQL5: Mean Absolute Error: 6.3416337085696410
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.5.3. Representação ONNX do huber_regressor_float.onnx e huber_regressor_double.onnx
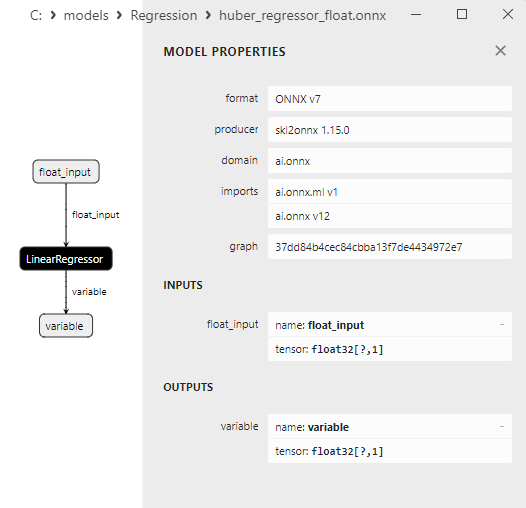
Fig.22. Representação ONNX do huber_regressor_float.onnx no Netron
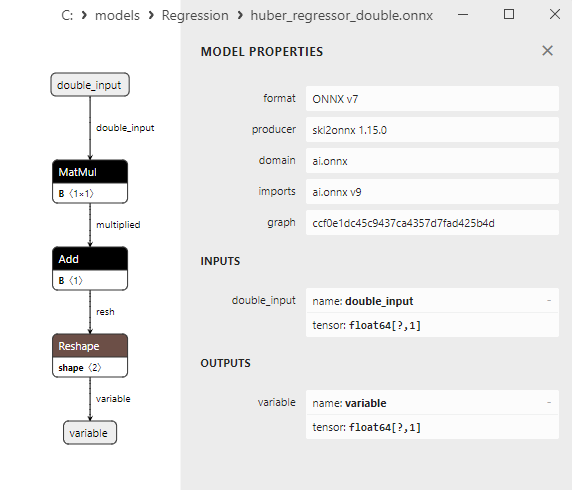
Fig.23. Representação ONNX do huber_regressor_double.onnx no Netron
2.1.6. sklearn.linear_model.Lars
LARS (Least Angle Regression) é um método de aprendizado de máquina usado para tarefas de regressão. É um algoritmo que constrói um modelo de regressão linear selecionando características ativas (variáveis) durante o processo de aprendizado.
LARS tenta encontrar o menor número de características que forneçam a melhor aproximação para a variável alvo.
Princípio de Funcionamento do LARS:
- Dados de Entrada: Começa com o conjunto de dados original, compreendendo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: Começa com um modelo nulo, o que significa que não há características ativas. Todos os coeficientes são definidos como zero.
- Seleção de Características: A cada passo, LARS seleciona a característica mais correlacionada com os resíduos do modelo. Essa característica é então adicionada ao modelo e seu coeficiente correspondente é ajustado usando o método dos mínimos quadrados.
- Regressão ao Longo das Características Ativas: Após adicionar a característica ao modelo, LARS atualiza os coeficientes de todas as características ativas para acomodar as mudanças no novo modelo.
- Passos Repetitivos: Esse processo continua até que todas as características sejam selecionadas ou um critério de parada especificado seja atingido.
- Previsão: Após o treinamento do modelo, ele pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LARS:
- Eficiência: LARS pode ser um método eficiente, especialmente quando há muitas características, mas apenas algumas afetam significativamente a variável alvo.
- Interpretabilidade: Como LARS visa selecionar apenas as características mais informativas, o modelo permanece relativamente interpretável.
Limitações do LARS:
- Modelo Linear: LARS constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Incapacidade de Lidar com Multicolinearidade: Se as características forem altamente correlacionadas, LARS pode enfrentar problemas de multicolinearidade.
LARS é valioso em tarefas de regressão onde a seleção das características mais informativas e a construção de um modelo linear com um número mínimo de características é essencial.
2.1.6.1. Código para criar o modelo Lars e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.Lars, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# Lars.py
# The code demonstrates the process of training Lars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lars"
onnx_model_filename = data_path + "lars"
# create a Lars Regressor model
lars_regressor_model = Lars()
# fit the model to the data
lars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training Lars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lars"
onnx_model_filename = data_path + "lars"
# create a Lars Regressor model
lars_regressor_model = Lars()
# fit the model to the data
lars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python Lars Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python Lars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python Lars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
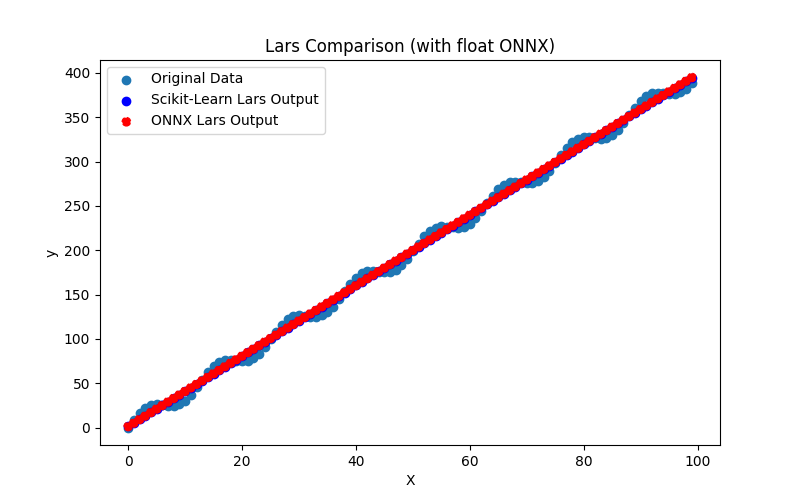
Fig.24. Resultados do Lars.py (float ONNX)
2.1.6.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lars_cv_float.onnx e lars_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| Lars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lars" #define ONNXFilenameFloat "lars_float.onnx" #define ONNXFilenameDouble "lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
Lars (EURUSD,H1) Testing ONNX float: Lars (lars_float.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 Lars (EURUSD,H1) Lars (EURUSD,H1) Testing ONNX double: Lars (lars_double.onnx) Lars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 Lars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 Lars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Comparação com o modelo original em double no Python:
Testing ONNX float: Lars (lars_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: Lars (lars_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.6.3. Representação ONNX do lars_float.onnx e lars_double.onnx
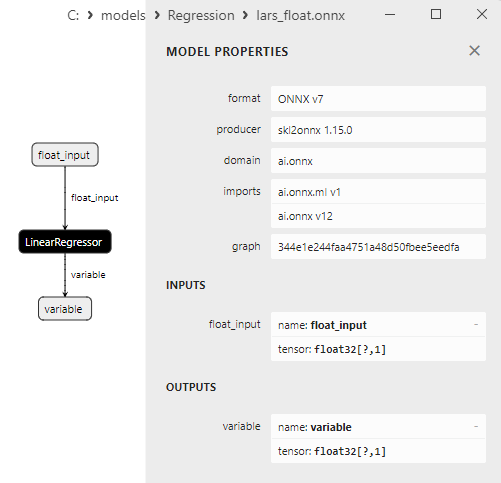
Fig.25. Representação ONNX do lars_float.onnx no Netron
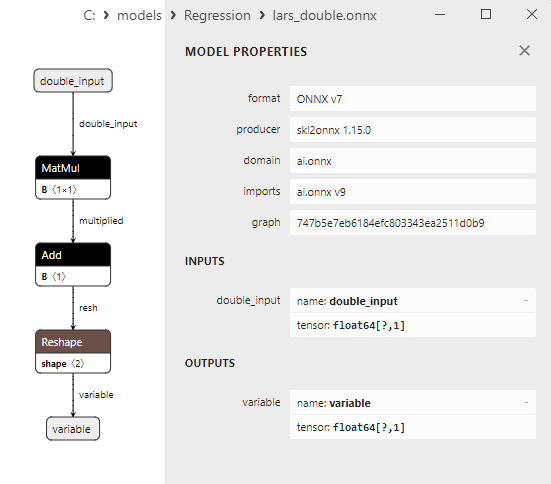
Fig.26. Representação ONNX do lars_double.onnx no Netron
2.1.7. sklearn.linear_model.LarsCV
LarsCV é uma variação do método LARS (Least Angle Regression) que seleciona automaticamente o número ideal de características a serem incluídas no modelo usando validação cruzada.
Este método ajuda a equilibrar entre um modelo que generaliza os dados de forma eficaz e um que utiliza o número mínimo de características.
Princípio de Funcionamento do LarsCV:
- Dados de Entrada: Começa com o conjunto de dados original, compreendendo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: Começa com um modelo nulo, o que significa que não há características ativas. Todos os coeficientes são definidos como zero.
- Validação Cruzada: LarsCV realiza validação cruzada para diferentes quantidades de características incluídas. Isso avalia o desempenho do modelo com diferentes conjuntos de características.
- Seleção do Número Ótimo de Características: LarsCV escolhe o número de características que produz o melhor desempenho do modelo, conforme determinado pela validação cruzada.
- Treinamento do Modelo: O modelo é treinado usando o número escolhido de características e seus respectivos coeficientes.
- Previsão: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LarsCV:
- Seleção Automática de Características: LarsCV escolhe automaticamente o número ideal de características, simplificando o processo de configuração do modelo.
- Interpretabilidade: Semelhante ao LARS regular, LarsCV mantém uma alta interpretabilidade do modelo.
- Eficiência: O método pode ser eficiente, especialmente quando conjuntos de dados têm muitas características, mas apenas algumas são significativas.
Limitações do LarsCV:
- Modelo Linear: LarsCV constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Incapacidade de Lidar com Multicolinearidade: Se as características forem altamente correlacionadas, LarsCV pode enfrentar problemas de multicolinearidade.
LarsCV é útil em tarefas de regressão onde escolher automaticamente o melhor conjunto de características usadas no modelo e manter a interpretabilidade do modelo são importantes.
2.1.7.1. Código para criar o modelo LarsCV e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LarsCV, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LarsCV.py
# The code demonstrates the process of training LarsCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"
# create a LarsCV Regressor model
larscv_regressor_model = LarsCV()
# fit the model to the data
larscv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = larscv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training LarsCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"
# create a LarsCV Regressor model
larscv_regressor_model = LarsCV()
# fit the model to the data
larscv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = larscv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
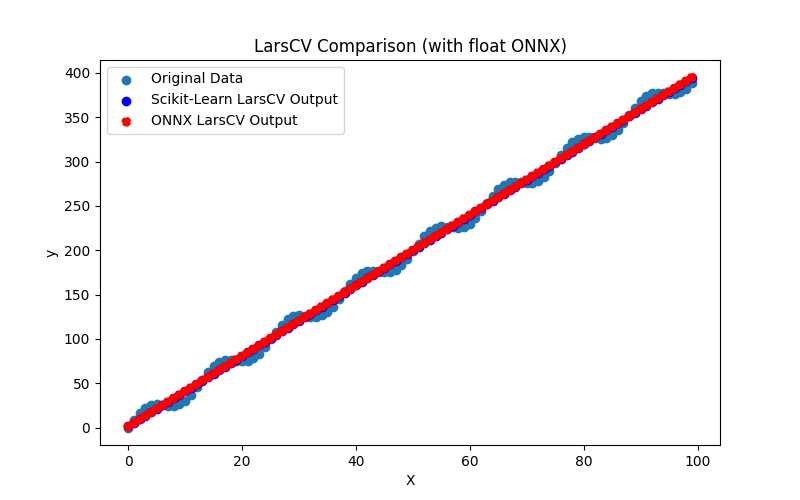
Fig.27. Resultados do LarsCV.py (float ONNX)
2.1.7.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lars_cv_float.onnx e lars_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LarsCV" #define ONNXFilenameFloat "lars_cv_float.onnx" #define ONNXFilenameDouble "lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LarsCV (EURUSD,H1) Testing ONNX float: LarsCV (lars_cv_float.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LarsCV (EURUSD,H1) LarsCV (EURUSD,H1) Testing ONNX double: LarsCV (lars_cv_double.onnx) LarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Comparação com o modelo original em double no Python:
Testing ONNX float: LarsCV (lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LarsCV (lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.7.3. Representação ONNX do lars_cv_float.onnx e lars_cv_double.onnx
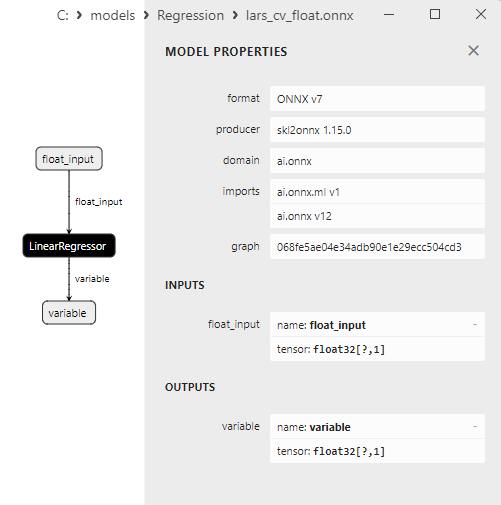
Fig.28. Representação ONNX do lars_cv_float.onnx no Netron
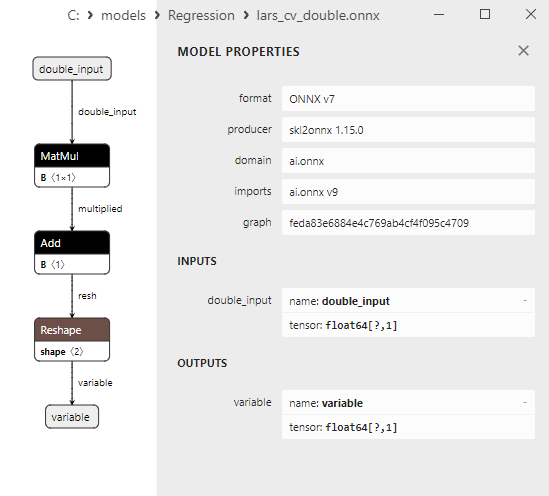
Fig.29. Representação ONNX do lars_cv_double.onnx no Netron
2.1.8. sklearn.linear_model.Lasso
Lasso (Least Absolute Shrinkage and Selection Operator) é um método de regressão usado para selecionar as características mais importantes e reduzir a dimensionalidade do modelo.
Ele consegue isso adicionando uma penalidade pela soma dos valores absolutos dos coeficientes (regularização L1) no problema de otimização da regressão linear.
Princípio de Funcionamento do Lasso:
- Dados de Entrada: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Função Objetivo: A função objetivo no Lasso inclui a soma dos erros quadrados de regressão e uma penalidade na soma dos valores absolutos dos coeficientes associados às características.
- Otimização: O modelo Lasso é treinado minimizando a função objetivo, resultando em alguns coeficientes se tornando zero, excluindo efetivamente as características correspondentes do modelo.
- Seleção do Valor de Penalidade Ótimo: O Lasso inclui um hiperparâmetro que determina a força da regularização. A escolha do valor ótimo para esse hiperparâmetro pode exigir validação cruzada.
- Geração de Previsões: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do Lasso:
- Seleção de Características: O Lasso seleciona automaticamente as características mais importantes, excluindo as menos significativas do modelo. Isso reduz a dimensionalidade dos dados e simplifica o modelo.
- Regularização: A penalidade na soma dos valores absolutos dos coeficientes ajuda a prevenir o overfitting do modelo e melhora sua generalização.
- Interpretabilidade: Como o Lasso exclui algumas características, o modelo permanece relativamente interpretável.
Limitações do Lasso:
- Modelo Linear: O Lasso constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Incapacidade de Lidar com Multicolinearidade: Se as características forem altamente correlacionadas, o Lasso pode enfrentar problemas de multicolinearidade.
O Lasso é útil em tarefas de regressão onde a seleção das características mais importantes e a redução da dimensionalidade do modelo, mantendo a interpretabilidade, são essenciais.
2.1.8.1. Código para criar o modelo Lasso e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.Lasso, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. precisão tanto do modelo original quanto dos modelos exportados para ONNX.
# Lasso.py
# The code demonstrates the process of training Lasso model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lasso"
onnx_model_filename = data_path + "lasso"
# create a Lasso model
lasso_model = Lasso()
# fit the model to the data
lasso_model.fit(X, y)
# predict values for the entire dataset
y_pred = lasso_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training Lasso model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Lasso"
onnx_model_filename = data_path + "lasso"
# create a Lasso model
lasso_model = Lasso()
# fit the model to the data
lasso_model.fit(X, y)
# predict values for the entire dataset
y_pred = lasso_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python Lasso Original model (double) Python R-squared (Coefficient of determination): 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python Python Lasso ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381720269486 Python Mean Absolute Error: 6.346395056911361 Python Mean Squared Error: 49.77936068668213 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python Lasso ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962381735682287 Python Mean Absolute Error: 6.346393791922984 Python Mean Squared Error: 49.77934029129379 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
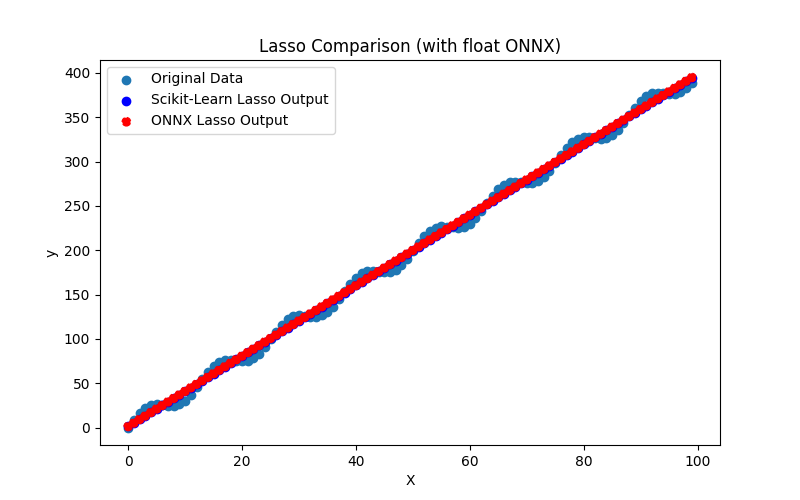
Fig.30. Resultados do Lasso.py (float ONNX)
2.1.8.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lasso_float.onnx e lasso_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| Lasso.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Lasso" #define ONNXFilenameFloat "lasso_float.onnx" #define ONNXFilenameDouble "lasso_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
Lasso (EURUSD,H1) Testing ONNX float: Lasso (lasso_float.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381720269486 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463950569113612 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793606866821037 Lasso (EURUSD,H1) Lasso (EURUSD,H1) Testing ONNX double: Lasso (lasso_double.onnx) Lasso (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962381735682287 Lasso (EURUSD,H1) MQL5: Mean Absolute Error: 6.3463937919229840 Lasso (EURUSD,H1) MQL5: Mean Squared Error: 49.7793402912937850
Comparação com o modelo original em double no Python:
Testing ONNX float: Lasso (lasso_float.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463950569113612 Testing ONNX double: Lasso (lasso_double.onnx) Python Mean Absolute Error: 6.346393791922984 MQL5: Mean Absolute Error: 6.3463937919229840
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 15 casas decimais.
2.1.8.3. Representação ONNX do lasso_float.onnx e lasso_double.onnx
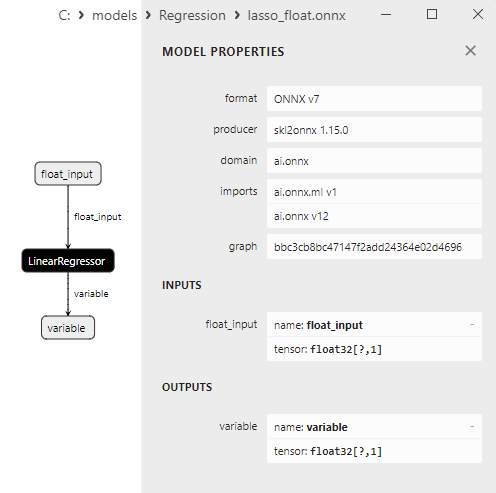
Fig.31. Representação ONNX do lasso_float.onnx no Netron
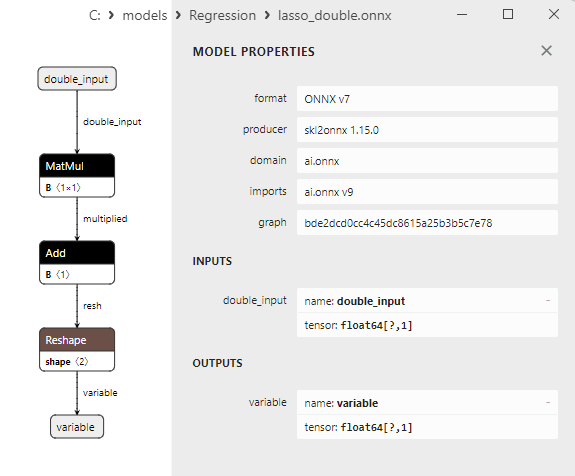
Fig.32. Representação ONNX do lasso_double.onnx no Netron
2.1.9. sklearn.linear_model.LassoCV
LassoCV é uma variante do método Lasso (Least Absolute Shrinkage and Selection Operator) que seleciona automaticamente o valor ideal para o hiperparâmetro de regularização (alpha) usando validação cruzada.
Este método permite encontrar um equilíbrio entre reduzir a dimensionalidade do modelo (selecionando características importantes) e prevenir o overfitting, tornando-o útil para tarefas de regressão.
Princípio de Funcionamento do LassoCV:
- Dados de Entrada: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: LassoCV inicializa vários valores diferentes do hiperparâmetro de regularização (alpha) que cobrem uma faixa de baixo a alto.
- Validação Cruzada: Para cada valor de alpha, LassoCV realiza validação cruzada para avaliar o desempenho do modelo. Métricas como erro quadrático médio (MSE) ou coeficiente de determinação (R^2) são comumente usadas.
- Seleção do Alpha Ótimo: LassoCV seleciona o valor de alpha onde o modelo atinge o melhor desempenho conforme determinado pela validação cruzada.
- Treinamento do Modelo: O modelo Lasso é treinado usando o valor de alpha escolhido, excluindo características menos importantes e aplicando a regularização L1.
- Geração de Previsões: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LassoCV:
- Seleção Automática de Alpha: LassoCV seleciona automaticamente o valor ideal de alpha usando validação cruzada, simplificando o ajuste do modelo.
- Seleção de Características: LassoCV escolhe automaticamente as características mais importantes, reduzindo a dimensionalidade do modelo e simplificando sua interpretação.
- Regularização: O método previne o overfitting do modelo através da regularização L1.
Limitações do LassoCV:
- Modelo Linear: LassoCV constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Incapacidade de Lidar com Multicolinearidade: Quando as características são altamente correlacionadas, LassoCV pode enfrentar problemas de multicolinearidade.
LassoCV é benéfico em tarefas de regressão onde a seleção das características mais importantes e a redução da dimensionalidade do modelo, mantendo a interpretabilidade e prevenindo o overfitting, são importantes.
2.1.9.1. Código para criar o modelo LassoCV e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LassoCV, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LassoCV.py
# The code demonstrates the process of training LassoCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"
# create a LassoCV Regressor model
lassocv_regressor_model = LassoCV()
# fit the model to the data
lassocv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassocv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training LassoCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"
# create a LassoCV Regressor model
lassocv_regressor_model = LassoCV()
# fit the model to the data
lassocv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassocv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LassoCV Original model (double) Python R-squared (Coefficient of determination): 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python Python LassoCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996224142876629 Python Mean Absolute Error: 6.335673221332177 Python Mean Squared Error: 49.96500504333324 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 6 Python float ONNX model precision: 6 Python Python LassoCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962241428413416 Python Mean Absolute Error: 6.33567334453819 Python Mean Squared Error: 49.96500551028169 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
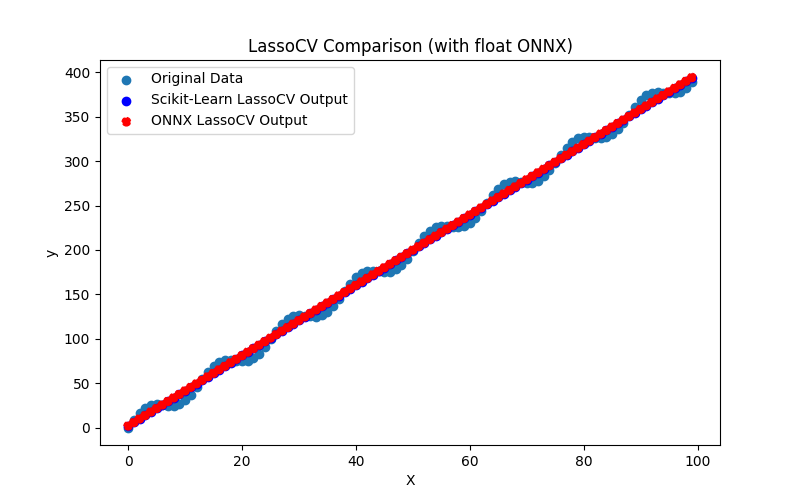
Fig.33. Resultados do LassoCV.py (float ONNX)
2.1.9.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lasso_cv_float.onnx e lasso_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LassoCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoCV" #define ONNXFilenameFloat "lasso_cv_float.onnx" #define ONNXFilenameDouble "lasso_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
2023.10.26 22:14:00.736 LassoCV (EURUSD,H1) Testing ONNX float: LassoCV (lasso_cv_float.onnx) 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428766290 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356732213321800 2023.10.26 22:14:00.739 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650050433332211 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) 2023.10.26 22:14:00.748 LassoCV (EURUSD,H1) Testing ONNX double: LassoCV (lasso_cv_double.onnx) 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962241428413416 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3356733445381899 2023.10.26 22:14:00.753 LassoCV (EURUSD,H1) MQL5: Mean Squared Error: 49.9650055102816992
Comparação com o modelo original em double no Python:
Testing ONNX float: LassoCV (lasso_cv_float.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356732213321800 Testing ONNX double: LassoCV (lasso_cv_double.onnx) Python Mean Absolute Error: 6.33567334453819 MQL5: Mean Absolute Error: 6.3356733445381899
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.9.3. Representação ONNX do lasso_cv_float.onnx e lasso_cv_double.onnx
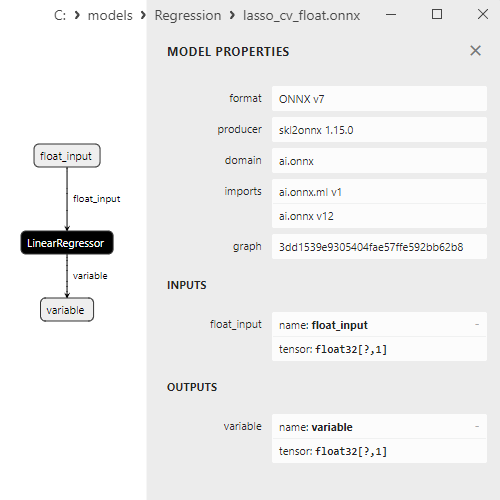
Fig.34. Representação ONNX do lasso_cv_float.onnx no Netron
Fig.35. Representação ONNX do lasso_cv_double.onnx no Netron
2.1.10. sklearn.linear_model.LassoLars
LassoLars é uma combinação de dois métodos: Lasso (Least Absolute Shrinkage and Selection Operator) e LARS (Least Angle Regression).
Este método é usado para tarefas de regressão e combina as vantagens de ambos os algoritmos, permitindo a seleção simultânea de características e a redução da dimensionalidade do modelo.
Princípio de Funcionamento do LassoLars:
- Dados de Entrada: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: LassoLars começa com um modelo nulo, o que significa que não há características ativas. Todos os coeficientes são definidos como zero.
- Seleção de Características em Etapas: Semelhante ao método LARS, LassoLars seleciona, em cada etapa, a característica mais correlacionada com os resíduos do modelo e a adiciona ao modelo. Em seguida, o coeficiente dessa característica é ajustado usando o método dos mínimos quadrados.
- Aplicação da Regularização L1: Simultaneamente com a seleção de características em etapas, LassoLars aplica a regularização L1, adicionando uma penalidade pela soma dos valores absolutos dos coeficientes. Isso permite modelar relações complexas e escolher as características mais importantes.
- Geração de Previsões: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LassoLars:
- Seleção de Características: LassoLars seleciona automaticamente as características mais importantes e reduz a dimensionalidade do modelo, ajudando a evitar o overfitting e simplificando a interpretação.
- Interpretabilidade: O método mantém a interpretabilidade do modelo, facilitando a determinação de quais características estão incluídas e como elas influenciam a variável alvo.
- Regularização: LassoLars aplica a regularização L1, prevenindo o overfitting e melhorando a generalização do modelo.
Limitações do LassoLars:
- Modelo Linear: LassoLars constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Complexidade Computacional: A seleção de características em cada etapa e a aplicação da regularização podem exigir mais recursos computacionais do que a regressão linear simples.
LassoLars é útil em tarefas de regressão onde é importante escolher as características mais importantes, reduzir a dimensionalidade do modelo e manter a interpretabilidade.
2.1.10.1. Código para criar o modelo LassoLars e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LassoLars, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LassoLars.py
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"
# create a LassoLars Regressor model
lassolars_regressor_model = LassoLars(alpha=0.1)
# fit the model to the data
lassolars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"
# create a LassoLars Regressor model
lassolars_regressor_model = LassoLars(alpha=0.1)
# fit the model to the data
lassolars_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LassoLars Original model (double) Python R-squared (Coefficient of determination): 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python Python LassoLars ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382635045889 Python Mean Absolute Error: 6.3476034814795375 Python Mean Squared Error: 49.77815018516975 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLars ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382633544077 Python Mean Absolute Error: 6.3476035128950805 Python Mean Squared Error: 49.778152172481896 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
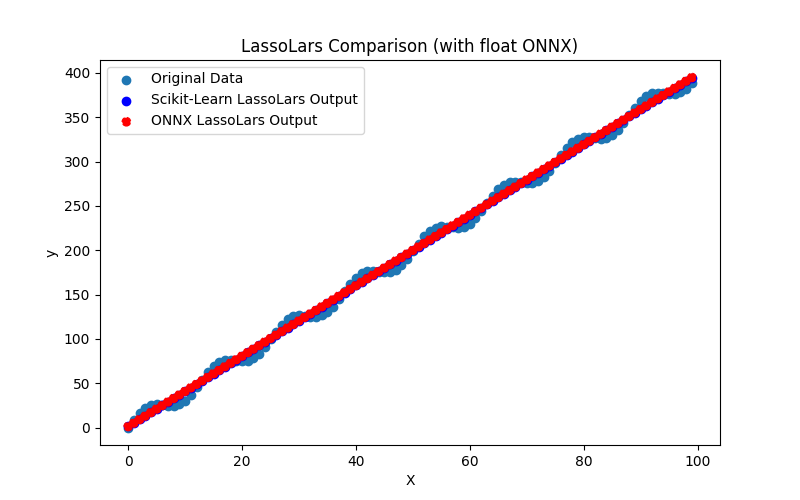
Fig.36. Resultados do LassoLars.py (float)
2.1.10.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lasso_lars_float.onnx e lasso_lars_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LassoLars.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLars" #define ONNXFilenameFloat "lasso_lars_float.onnx" #define ONNXFilenameDouble "lasso_lars_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LassoLars (EURUSD,H1) Testing ONNX float: LassoLars (lasso_lars_float.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382635045889 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476034814795375 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781501851697357 LassoLars (EURUSD,H1) LassoLars (EURUSD,H1) Testing ONNX double: LassoLars (lasso_lars_double.onnx) LassoLars (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382633544077 LassoLars (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476035128950858 LassoLars (EURUSD,H1) MQL5: Mean Squared Error: 49.7781521724819029
Comparação com o modelo original em double no Python:
Testing ONNX float: LassoLars (lasso_lars_float.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476034814795375 Testing ONNX double: LassoLars (lasso_lars_double.onnx) Python Mean Absolute Error: 6.3476035128950805 MQL5: Mean Absolute Error: 6.3476035128950858
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.10.3. Representação ONNX do lasso_lars_float.onnx e lasso_lars_double.onnx
Fig.37. Representação ONNX do lasso_lars_float.onnx no Netron
Fig.38. Representação ONNX do lasso_lars_double.onnx no Netron
2.1.11. sklearn.linear_model.LassoLarsCV
LassoLarsCV é um método que combina Lasso (Least Absolute Shrinkage and Selection Operator) e LARS (Least Angle Regression) com a seleção automática do hiperparâmetro de regularização ideal (alpha) usando validação cruzada.
Este método combina as vantagens de ambos os algoritmos e permite determinar o valor ideal de alpha para o modelo, considerando a seleção de características e a regularização.
Princípio de Funcionamento do LassoLarsCV:
- Dados de Entrada: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: LassoLarsCV começa com um modelo nulo, onde todos os coeficientes são definidos como zero.
- Definição do Intervalo de Alpha: Um intervalo de valores para o hiperparâmetro alpha é determinado, que será considerado durante o processo de seleção. Normalmente, uma escala logarítmica de valores de alpha é usada.
- Validação Cruzada: Para cada valor de alpha do intervalo escolhido, LassoLarsCV realiza validação cruzada para avaliar o desempenho do modelo com esse valor de alpha. Normalmente, são usadas métricas como erro quadrático médio (MSE) ou coeficiente de determinação (R^2).
- Seleção do Alpha Ótimo: LassoLarsCV escolhe o valor de alpha onde o modelo atinge o melhor desempenho com base nos resultados da validação cruzada.
- Treinamento do Modelo: O modelo LassoLars é treinado usando o valor de alpha selecionado, excluindo características menos importantes e aplicando a regularização L1.
- Geração de Previsões: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LassoLarsCV:
- Seleção Automática de Alpha: LassoLarsCV seleciona automaticamente o hiperparâmetro alpha ideal usando validação cruzada, simplificando o ajuste do modelo.
- Seleção de Características: LassoLarsCV escolhe automaticamente as características mais importantes e reduz a dimensionalidade do modelo.
- Regularização: O método aplica a regularização L1, prevenindo o overfitting e melhorando a generalização do modelo.
Limitações do LassoLarsCV:
- Modelo Linear: LassoLarsCV constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas.
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Complexidade Computacional: A seleção de características em cada etapa e a aplicação da regularização podem exigir mais recursos computacionais do que a regressão linear simples.
LassoLarsCV é útil em tarefas de regressão onde é essencial escolher as características mais importantes, reduzir a dimensionalidade do modelo, prevenir o overfitting e ajustar automaticamente os hiperparâmetros do modelo.
2.1.11.1. Código para criar o modelo LassoLarsCV e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LassoLarsCV, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LassoLarsCV.py
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"
# create a LassoLarsCV Regressor model
lassolars_cv_regressor_model = LassoLarsCV(cv=5)
# fit the model to the data
lassolars_cv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_cv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"
# create a LassoLarsCV Regressor model
lassolars_cv_regressor_model = LassoLarsCV(cv=5)
# fit the model to the data
lassolars_cv_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lassolars_cv_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LassoLarsCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python Python LassoLarsCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382640824089 Python Mean Absolute Error: 6.347737845846069 Python Mean Squared Error: 49.778142539016564 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642612767 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.77814017210321 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 14 Python double ONNX model precision: 16
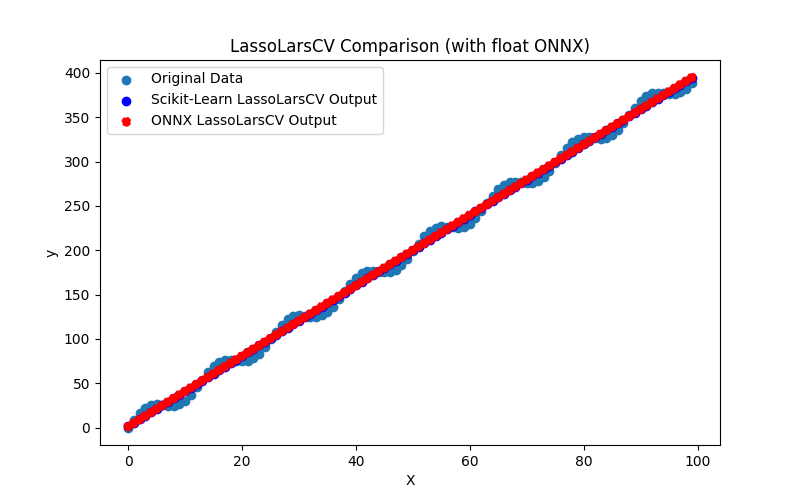
Fig.39. Resultados do LassoLarsCV.py (float ONNX)
2.1.11.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LassoLarsCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsCV" #define ONNXFilenameFloat "lasso_lars_cv_float.onnx" #define ONNXFilenameDouble "lasso_lars_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LassoLarsCV (EURUSD,H1) Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382640824089 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477378458460691 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781425390165566 LassoLarsCV (EURUSD,H1) LassoLarsCV (EURUSD,H1) Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) LassoLarsCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642612767 LassoLarsCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 LassoLarsCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401721031642
Comparação com o modelo original em double no Python:
Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477378458460691 Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx) Python Mean Absolute Error: 6.3477379221400145 MQL5: Mean Absolute Error: 6.3477379221400145
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.11.3. Representação ONNX do lasso_lars_cv_float.onnx e lasso_lars_cv_double.onnx
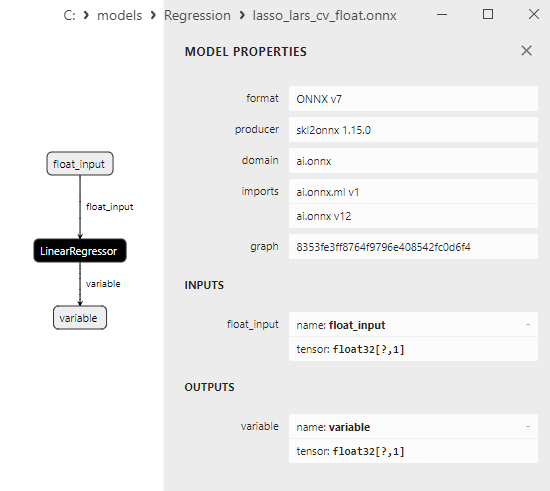
Fig.40. Representação ONNX do lasso_lars_cv_float.onnx no Netron
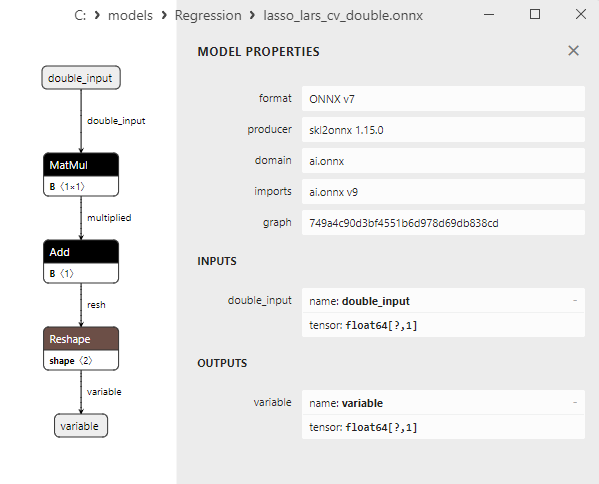
Fig.41. Representação ONNX do lasso_lars_cv_double.onnx no Netron
2.1.12. sklearn.linear_model.LassoLarsIC
LassoLarsIC é um método de regressão que combina Lasso (Least Absolute Shrinkage and Selection Operator) e Critério de Informação (IC) para selecionar automaticamente o conjunto ideal de características.
Ele utiliza critérios de informação, como AIC (Critério de Informação de Akaike) e BIC (Critério de Informação Bayesiano), para determinar quais características incluir no modelo e aplica a regularização L1 para estimar os coeficientes do modelo.
Princípio de Funcionamento do LassoLarsIC:
- Dados de Entrada: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Inicialização: LassoLarsIC começa com um modelo nulo, o que significa que não há características ativas. Todos os coeficientes são definidos como zero.
- Seleção de Características usando Critério de Informação: O método avalia o critério de informação (por exemplo, AIC ou BIC) para diferentes conjuntos de características, começando de um modelo vazio e gradualmente incorporando características ao modelo. O critério de informação avalia a qualidade do modelo, considerando o equilíbrio entre ajustar os dados e a complexidade do modelo.
- Seleção do Conjunto de Características Ótimo: LassoLarsIC escolhe o conjunto de características para o qual o critério de informação atinge o melhor valor. Este conjunto de características será incluído no modelo.
- Aplicação da Regularização L1: A regularização L1 é aplicada às características selecionadas, auxiliando na estimativa dos coeficientes do modelo.
- Geração de Previsões: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados.
Vantagens do LassoLarsIC:
- Seleção Automática de Características: LassoLarsIC escolhe automaticamente o conjunto ideal de características, reduzindo a dimensionalidade do modelo e prevenindo o overfitting.
- Critérios de Informação: O uso de critérios de informação permite equilibrar a qualidade e a complexidade do modelo.
- Regularização: O método aplica a regularização L1, prevenindo o overfitting e melhorando a generalização do modelo.
Limitações do LassoLarsIC:
- Modelo Linear: LassoLarsIC constrói um modelo linear, que pode ser insuficiente para modelar relações não lineares complexas..
- Sensibilidade ao Ruído: O método pode ser sensível a outliers nos dados.
- Complexidade Computacional: Avaliar critérios de informação para vários conjuntos de características pode exigir recursos computacionais adicionais.
LassoLarsIC é valioso em tarefas de regressão onde a seleção automática do melhor conjunto de características e a redução da dimensionalidade do modelo com base em critérios de informação são cruciais.
2.1.12.1. Código para criar o modelo LassoLarsIC e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LassoLarsIC, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LassoLarsIC.py
# The code demonstrates the process of training LassoLarsIC model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"
# create a LassoLarsIC Regressor model
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')
# fit the model to the data
lasso_lars_ic_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lasso_lars_ic_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training LassoLarsIC model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"
# create a LassoLarsIC Regressor model
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')
# fit the model to the data
lasso_lars_ic_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = lasso_lars_ic_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LassoLarsIC Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python Python LassoLarsIC ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LassoLarsIC ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336425 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 15 Python double ONNX model precision: 15
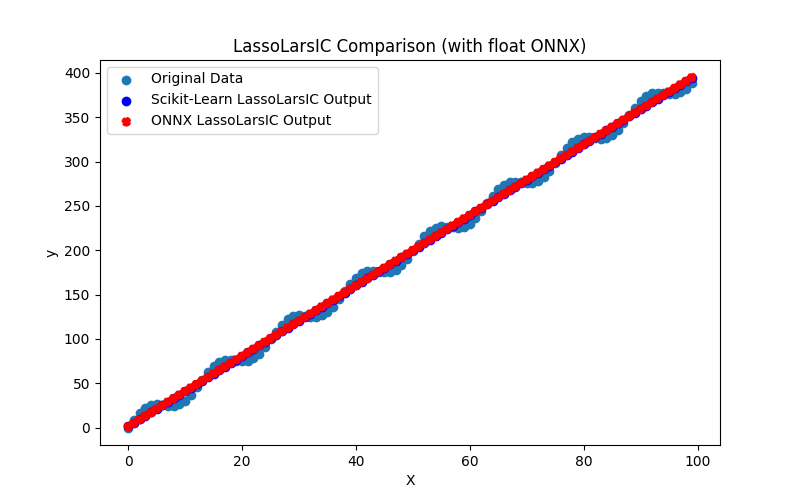
Fig.42. Resultados do LassoLarsIC.py (float ONNX)
2.1.12.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LassoLarsIC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LassoLarsIC" #define ONNXFilenameFloat "lasso_lars_ic_float.onnx" #define ONNXFilenameDouble "lasso_lars_ic_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LassoLarsIC (EURUSD,H1) Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LassoLarsIC (EURUSD,H1) LassoLarsIC (EURUSD,H1) Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) LassoLarsIC (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LassoLarsIC (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364302 LassoLarsIC (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Comparação com o modelo original em double no Python:
Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx) Python Mean Absolute Error: 6.347737926336425 MQL5: Mean Absolute Error: 6.3477379263364302
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.12.3. Representação ONNX do lasso_lars_ic_float.onnx e lasso_lars_ic_double.onnx
Fig.43. Representação ONNX do lasso_lars_ic_float.onnx no Netron
Fig.44. Representação ONNX do lasso_lars_ic_double.onnx no Netron
2.1.13. sklearn.linear_model.LinearRegression
LinearRegression é um dos métodos mais simples e amplamente utilizados em aprendizado de máquina para tarefas de regressão.
É usado para construir modelos lineares que preveem valores numéricos (contínuos) da variável alvo com base em uma combinação linear de características de entrada.
Princípio de Funcionamento do LinearRegression:
- Modelo Linear: O modelo LinearRegression assume que existe uma relação linear entre as variáveis independentes (características) e a variável alvo. Essa relação pode ser expressa pela equação de regressão linear: y = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ, onde y é a variável alvo, β₀ é o coeficiente de intercepto, β₁, β₂, ... βₚ são os coeficientes das características, e x₁, x₂, ... xₚ são os valores das características.
- Estimativa de Parâmetros: O objetivo do LinearRegression é estimar os coeficientes β₀, β₁, β₂, ... βₚ que melhor se ajustem aos dados. Isso é tipicamente alcançado usando o método dos Mínimos Quadrados Ordinários (OLS), minimizando a soma dos quadrados das diferenças entre os valores reais e previstos.
- Avaliação do Modelo: Várias métricas, como Erro Quadrático Médio (MSE), Coeficiente de Determinação (R²), entre outras, são usadas para avaliar a qualidade do modelo LinearRegression.
Vantagens do LinearRegression:
- Simplicidade e Interpretabilidade: LinearRegression é um método simples com fácil interpretabilidade, permitindo a análise da influência de cada característica na variável alvo.
- Alta Velocidade de Treinamento e Previsão: O modelo de regressão linear tem altas velocidades de treinamento e previsão, tornando-o uma boa escolha para grandes conjuntos de dados.
- Aplicabilidade: LinearRegression pode ser aplicado com sucesso em diversas tarefas de regressão.
Limitações do LinearRegression:
- Linearidade: Este método assume linearidade na relação entre as características e a variável alvo, o que pode ser insuficiente para modelar dependências não lineares complexas.
- Sensibilidade a Outliers: LinearRegression é sensível a outliers nos dados, o que pode afetar a qualidade do modelo.
LinearRegression é um método de regressão simples e amplamente utilizado que constrói um modelo linear para prever valores numéricos da variável alvo com base em uma combinação linear de características de entrada. É bem adequado para problemas com uma relação linear e quando a interpretabilidade do modelo é importante.
2.1.13.1. Código para criar o modelo LinearRegressione exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LinearRegression, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# The code demonstrates the process of training LinearRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"
# create a Linear Regression model
linear_model = LinearRegression()
# fit the model to the data
linear_model.fit(X, y)
# predict values for the entire dataset
y_pred = linear_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"
# create a Linear Regression model
linear_model = LinearRegression()
# fit the model to the data
linear_model.fit(X, y)
# predict values for the entire dataset
y_pred = linear_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LinearRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python LinearRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python LinearRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
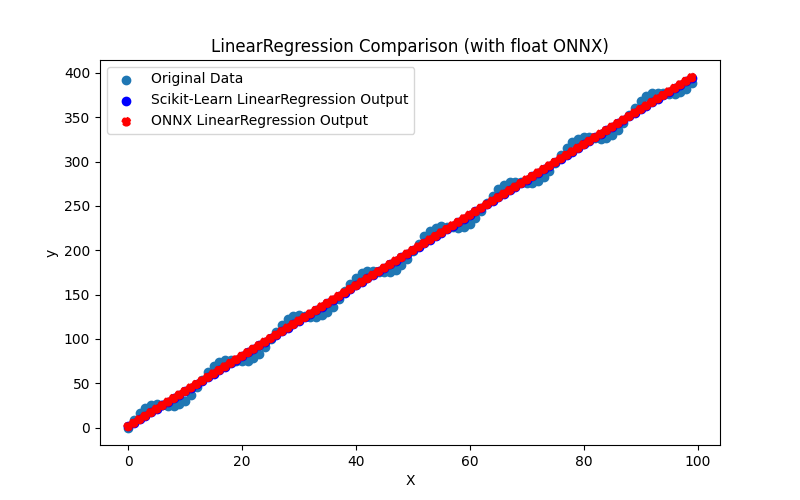
Fig.45. Resultados do LinearRegression.py (float ONNX)
2.1.13.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos linear_regression_float.onnx e linear_regression_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LinearRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearRegression" #define ONNXFilenameFloat "linear_regression_float.onnx" #define ONNXFilenameDouble "linear_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LinearRegression (EURUSD,H1) Testing ONNX float: LinearRegression (linear_regression_float.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 LinearRegression (EURUSD,H1) LinearRegression (EURUSD,H1) Testing ONNX double: LinearRegression (linear_regression_double.onnx) LinearRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 LinearRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 LinearRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Comparação com o modelo original em double no Python:
Testing ONNX float: LinearRegression (linear_regression_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: LinearRegression (linear_regression_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.13.3. Representação ONNX do linear_regression_float.onnx e linear_regression_double.onnx
Fig.46. Representação ONNX do linear_regression_float.onnx no Netron
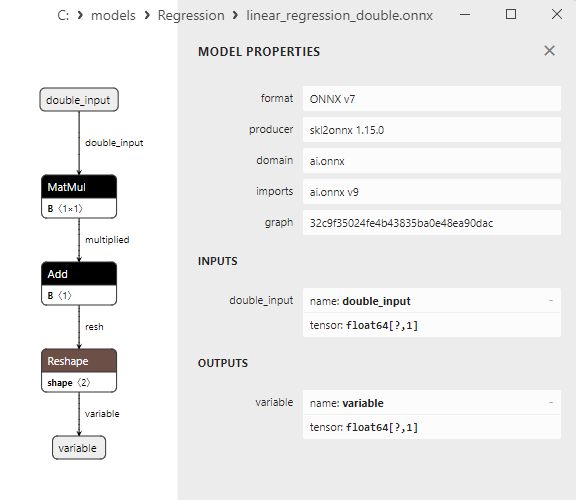
Fig.47. Representação ONNX do linear_regression_double.onnx no Netron
Nota sobre os Métodos Ridge e RidgeCV
Ridge e RidgeCV são dois métodos relacionados em aprendizado de máquina usados para regularização na regressão Ridge. Eles compartilham funcionalidades semelhantes, mas diferem no uso e ajuste de parâmetros.
Princípio de Funcionamento do Ridge (Regressão Ridge):
- Ridge é um método de regressão que envolve a regularização L2. Isso significa que ele adiciona a soma dos coeficientes quadrados (norma L2) à função de perda minimizada pelo modelo. This additional regularization term helps reduce the magnitudes of the model's coefficients, thus preventing overfitting.
- Uso do parâmetro alpha: No método Ridge, o parâmetro alpha (também conhecido como força de regularização) é pré-definido e não é alterado automaticamente. Os usuários precisam selecionar um valor adequado para alpha com base em seu conhecimento dos dados e experimentos.
Princípio de Funcionamento do RidgeCV (Validação Cruzada Ridge):
- RidgeCV é uma extensão do método Ridge, que envolve a seleção automática do valor ideal para o parâmetro alpha usando validação cruzada. Em vez de definir manualmente o alpha, o RidgeCV itera por diferentes valores de alpha e escolhe aquele que fornece o melhor desempenho na validação cruzada.
- Vantagem do ajuste automático: A principal vantagem do RidgeCV é sua determinação automática do valor ideal de alpha sem a necessidade de ajuste manual. Isso torna o processo de ajuste mais conveniente e previne possíveis erros na seleção do alpha.
A principal diferença entre Ridge e RidgeCV é que Ridge exige que os usuários especifiquem explicitamente o valor do parâmetro alpha, enquanto RidgeCV encontra automaticamente o valor ideal de alpha usando validação cruzada. RidgeCV é tipicamente a escolha preferida ao lidar com uma grande quantidade de dados e visando evitar o ajuste manual de parâmetros.
2.1.14. sklearn.linear_model.Ridge
Ridge é um método de regressão usado em aprendizado de máquina para resolver problemas de regressão. Faz parte da família de modelos lineares e representa uma regressão linear regularizada.
A principal característica da regressão Ridge é a adição de regularização L2 ao método padrão dos mínimos quadrados ordinários (OLS).
Como funciona a regressão Ridge:
- Regressão linear: Semelhante à regressão linear regular, a regressão Ridge visa encontrar uma relação linear entre as variáveis independentes (características) e a variável alvo.
- Regularização L2: A principal distinção da regressão Ridge é a adição de regularização L2 à função de perda. Isso significa que uma penalidade para grandes valores dos coeficientes de regressão é adicionada à soma das diferenças quadradas entre os valores reais e previstos.
- Penalizando coeficientes: A regularização L2 impõe uma penalidade aos valores dos coeficientes de regressão. Como resultado, alguns coeficientes tendem a ficar mais próximos de zero, reduzindo o overfitting e melhorando a estabilidade do modelo.
- Hiperparâmetro α: Um dos parâmetros essenciais na regressão Ridge é o hiperparâmetro α (alpha), que determina o grau de regularização. Valores mais altos de α levam a uma regularização mais forte, resultando em modelos mais simples com valores de coeficiente mais baixos.
Vantagens da regressão Ridge:
- Redução do overfitting: A regularização L2 no Ridge ajuda a reduzir o overfitting, tornando o modelo mais robusto contra ruídos nos dados.
- Tratamento da multicolinearidade: A regressão Ridge lida bem com problemas de multicolinearidade, particularmente quando as características são altamente correlacionadas.
- Abordagem da maldição da dimensionalidade: O Ridge ajuda em cenários com muitas características, onde o OLS pode ser instável.
Limitações da regressão Ridge:
- Não elimina características: A regressão Ridge não zera os coeficientes das características, apenas os reduz, significando que algumas características ainda podem permanecer no modelo.
- Escolha do α ótimo: Selecionar o valor correto para o hiperparâmetro α pode exigir validação cruzada.
A regressão Ridge é um método de regressão que introduz a regularização L2 na regressão linear padrão para reduzir o overfitting, melhorar a estabilidade e lidar com problemas de multicolinearidade. Este método é útil quando é necessário equilibrar precisão e estabilidade do modelo.
2.1.14.1. Código para criar o modelo Ridge e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.Ridge, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. precisão tanto do modelo original quanto dos modelos exportados para ONNX.
# Ridge.py
# The code demonstrates the process of training Ridge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Ridge"
onnx_model_filename = data_path + "ridge"
# create a Ridge model
regression_model = Ridge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training Ridge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "Ridge"
onnx_model_filename = data_path + "ridge"
# create a Ridge model
regression_model = Ridge()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python Ridge Original model (double) Python R-squared (Coefficient of determination): 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python Python Ridge ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382634837793 Python Mean Absolute Error: 6.347684915729416 Python Mean Squared Error: 49.77815046053819 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python Ridge ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641178552 Python Mean Absolute Error: 6.347684462929819 Python Mean Squared Error: 49.77814206996523 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
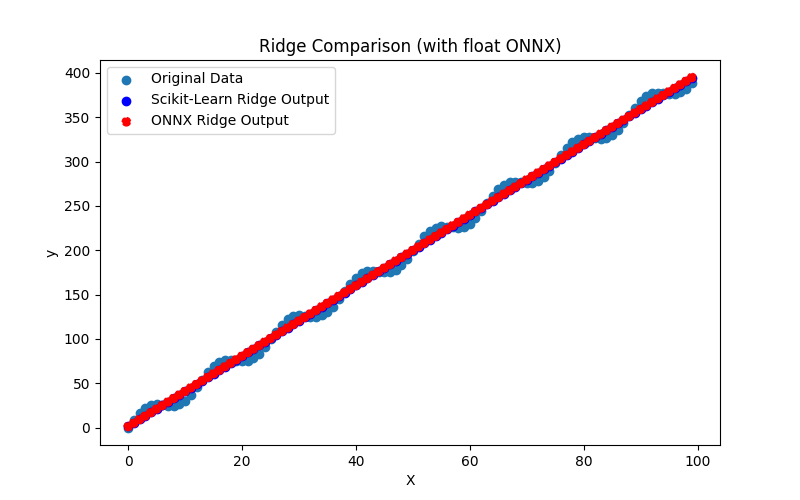
Fig.49. Resultados do Ridge.py (float ONNX)
2.1.14.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos ridge_float.onnx e ridge_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| Ridge.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "Ridge" #define ONNXFilenameFloat "ridge_float.onnx" #define ONNXFilenameDouble "ridge_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
Ridge (EURUSD,H1) Testing ONNX float: Ridge (ridge_float.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382634837793 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476849157294160 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781504605381784 Ridge (EURUSD,H1) Ridge (EURUSD,H1) Testing ONNX double: Ridge (ridge_double.onnx) Ridge (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641178552 Ridge (EURUSD,H1) MQL5: Mean Absolute Error: 6.3476844629298235 Ridge (EURUSD,H1) MQL5: Mean Squared Error: 49.7781420699652131
Comparação com o modelo original em double no Python:
Testing ONNX float: Ridge (ridge_float.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476849157294160 Testing ONNX double: Ridge (ridge_double.onnx) Python Mean Absolute Error: 6.347684462929819 MQL5: Mean Absolute Error: 6.3476844629298235
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.14.3. Representação ONNX do ridge_float.onnx e ridge_double.onnx
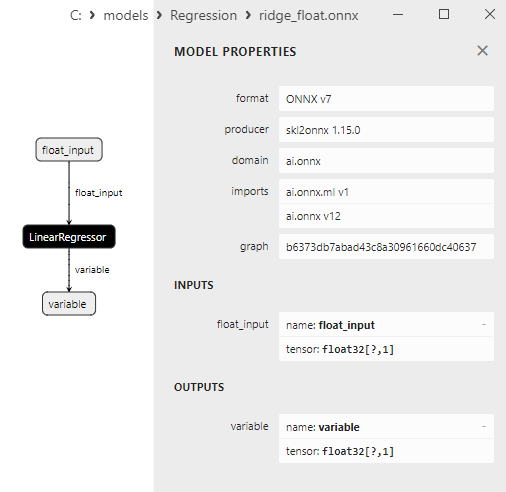
Fig.50. Representação ONNX do ridge_float.onnx no Netron
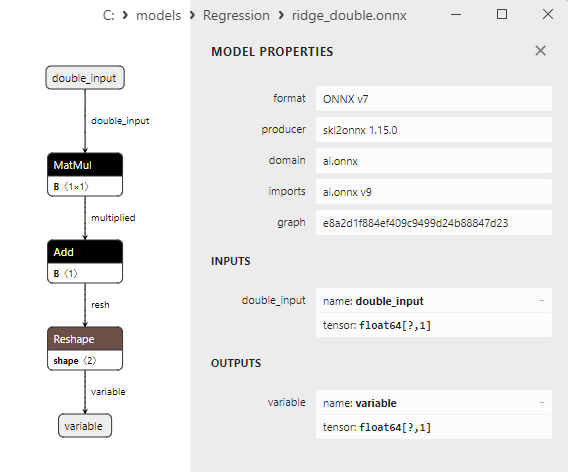
Fig.51. Representação ONNX do ridge_double.onnx no Netron
2.1.15. sklearn.linear_model.RidgeCV
RidgeCV é uma extensão da regressão Ridge que inclui a seleção automática do melhor hiperparâmetro α (alpha), que determina o grau de regularização na regressão Ridge. O hiperparâmetro α controla o equilíbrio entre minimizar a soma dos erros quadráticos (como na regressão linear ordinária) e minimizar o valor dos coeficientes de regressão (regularização). O RidgeCV seleciona automaticamente o valor ideal de α com base em parâmetros e critérios especificados.
Como funciona o RidgeCV:
- Dados de entrada: O RidgeCV recebe dados de entrada consistindo de características (variáveis independentes) e a variável alvo (contínua).
- Escolha de α: A regressão Ridge requer a seleção do hiperparâmetro α, que determina o grau de regularização. O RidgeCV seleciona automaticamente o valor ideal de α a partir do intervalo fornecido.
- Validação cruzada: O RidgeCV usa validação cruzada, como k-fold cross-validation, para avaliar qual valor de α fornece a melhor generalização do modelo em dados independentes.
- α Ótimo: Ao concluir o processo de treinamento, o RidgeCV escolhe o valor de α que apresenta o melhor desempenho na validação cruzada e usa esse valor para treinar o modelo final de regressão Ridge.
Vantagens do RidgeCV:
- Seleção automática de α: O RidgeCV permite a seleção automática do valor ideal do hiperparâmetro α, simplificando o processo de ajuste do modelo.
- Equilíbrio entre regularização e desempenho: Este método ajuda a encontrar o equilíbrio ideal entre regularização (redução do overfitting) e desempenho do modelo.
Limitações do RidgeCV:
- Complexidade computacional: A validação cruzada pode exigir recursos computacionais significativos, especialmente ao usar um grande intervalo de valores de α.
RidgeCV é um método de regressão Ridge com seleção automática do hiperparâmetro α ideal usando validação cruzada. Este método simplifica o processo de seleção de hiperparâmetros e permite encontrar o melhor equilíbrio entre regularização e desempenho do modelo.
2.1.15.1. Código para criar o modelo RidgeCV e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.RidgeCV, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# RidgeCV.py
# The code demonstrates the process of training RidgeCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"
# create a RidgeCV model
regression_model = RidgeCV()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training RidgeCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"
# create a RidgeCV model
regression_model = RidgeCV()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python RidgeCV Original model (double) Python R-squared (Coefficient of determination): 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python Python RidgeCV ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499108485 Python Mean Absolute Error: 6.3472036427935485 Python Mean Squared Error: 49.77833006785168 Python R^2 matching decimal places: 11 Python MAE matching decimal places: 6 Python MSE matching decimal places: 4 Python float ONNX model precision: 6 Python Python RidgeCV ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382499160807 Python Mean Absolute Error: 6.34720334999352 Python Mean Squared Error: 49.77832999861571 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
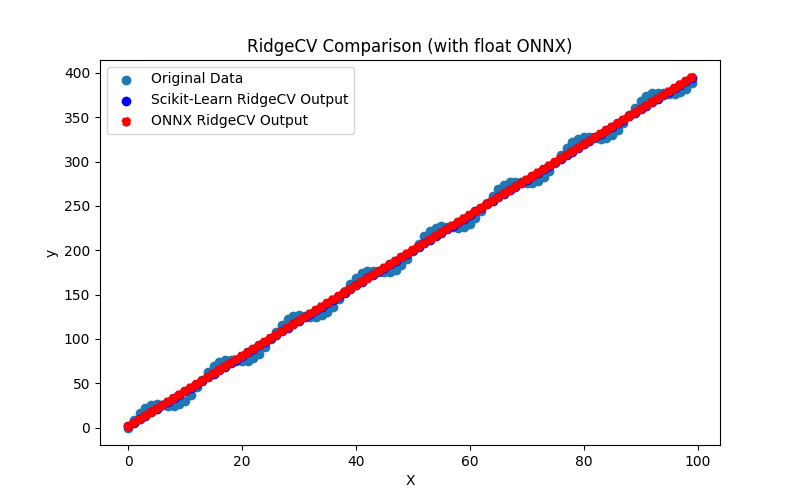
Fig.52. Resultados do RidgeCV.py (float ONNX)
2.1.15.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos ridge_cv_float.onnx e ridge_cv_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| RidgeCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RidgeCV" #define ONNXFilenameFloat "ridge_cv_float.onnx" #define ONNXFilenameDouble "ridge_cv_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
RidgeCV (EURUSD,H1) Testing ONNX float: RidgeCV (ridge_cv_float.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499108485 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472036427935485 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783300678516909 RidgeCV (EURUSD,H1) RidgeCV (EURUSD,H1) Testing ONNX double: RidgeCV (ridge_cv_double.onnx) RidgeCV (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382499160807 RidgeCV (EURUSD,H1) MQL5: Mean Absolute Error: 6.3472033499935216 RidgeCV (EURUSD,H1) MQL5: Mean Squared Error: 49.7783299986157246
Comparação com o modelo original em double no Python:
Testing ONNX float: RidgeCV (ridge_cv_float.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472036427935485 Testing ONNX double: RidgeCV (ridge_cv_double.onnx) Python Mean Absolute Error: 6.34720334999352 MQL5: Mean Absolute Error: 6.3472033499935216
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.15.3. Representação ONNX doridge_cv_float.onnx e ridge_cv_double.onnx
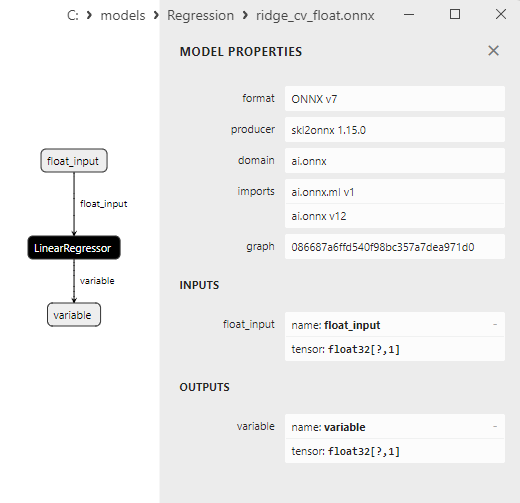
Fig.53. Representação ONNX do ridge_cv_float.onnx no Netron
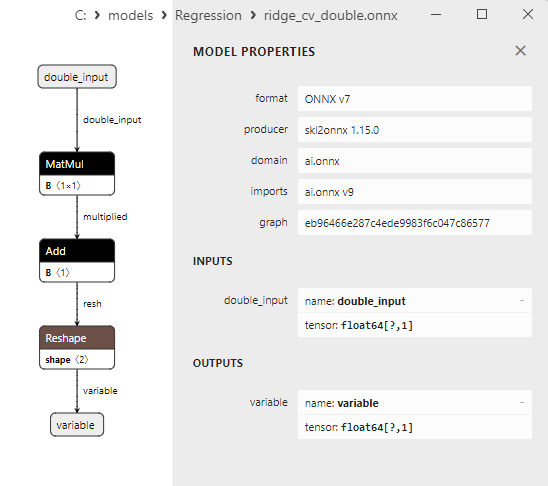
Fig.54. Representação ONNX do ridge_cv_double.onnx no Netron
2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
OrthogonalMatchingPursuit (OMP) é um algoritmo usado para resolver problemas de seleção de características e regressão linear.
É um dos métodos para selecionar as características mais significativas, o que pode ser útil para reduzir a dimensionalidade dos dados e melhorar a capacidade de generalização do modelo.
Como funciona o OrthogonalMatchingPursuit:
- Dados de entrada: Começa com um conjunto de dados contendo características (variáveis independentes) e valores da variável alvo (contínua).
- Seleção do número de características: Um dos passos iniciais ao usar o OrthogonalMatchingPursuit é determinar o número de características que você deseja incluir no modelo. Esse número pode ser pré-definido ou escolhido usando critérios como o Critério de Informação de Akaike (AIC) ou critérios de erro mínimo.
- Adição iterativa de características: O algoritmo começa com um modelo vazio e adiciona iterativamente características que melhor explicam os resíduos do modelo. Em cada iteração, uma nova característica é escolhida para ser ortogonal às características selecionadas anteriormente. A característica ótima é selecionada com base na sua correlação com os resíduos do modelo.
- Treinamento do modelo: Após adicionar o número especificado de características, o modelo é treinado nos dados considerando apenas essas características selecionadas.
- Geração de previsões: Após o treinamento, o modelo pode prever os valores da variável alvo em novos dados.
Vantagens do OrthogonalMatchingPursuit:
- Redução da dimensionalidade: OMP pode reduzir a dimensionalidade dos dados selecionando apenas as características mais informativas.
- Interpretabilidade: Como o OMP seleciona apenas um pequeno número de características, os modelos criados usando-o podem ser mais interpretáveis.
Limitações do OrthogonalMatchingPursuit:
- Sensibilidade ao número de características selecionadas: O número de características selecionadas precisa ser ajustado corretamente, e escolhas incorretas podem levar ao overfitting ou underfitting.
- Não considera multicolinearidade: OMP pode não considerar a multicolinearidade entre as características, o que pode impactar a seleção das características ótimas.
- Complexidade computacional: OMP é computacionalmente caro, especialmente para grandes conjuntos de dados.
OrthogonalMatchingPursuit é um algoritmo para seleção de características e regressão linear, permitindo a seleção das características mais informativas para o modelo. Este método pode ser valioso para reduzir a dimensionalidade dos dados e melhorar a interpretabilidade do modelo.
2.1.16.1. Código para criar o modelo OrthogonalMatchingPursuit e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.OrthogonalMatchingPursuit, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# OrthogonalMatchingPursuit.py
# The code demonstrates the process of training OrthogonalMatchingPursuit model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"
# create an OrthogonalMatchingPursuit model
regression_model = OrthogonalMatchingPursuit()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training OrthogonalMatchingPursuit model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"
# create an OrthogonalMatchingPursuit model
regression_model = OrthogonalMatchingPursuit()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python OrthogonalMatchingPursuit Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python Python OrthogonalMatchingPursuit ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python OrthogonalMatchingPursuit ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281784 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
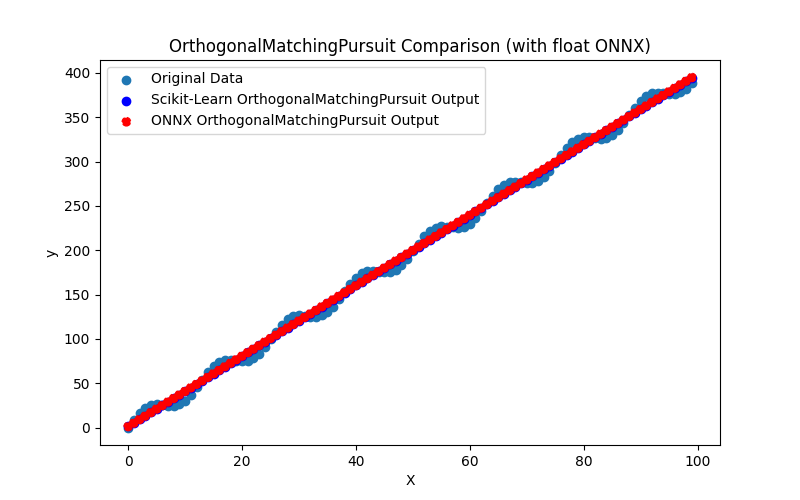
Fig.55. Resultados do OrthogonalMatchingPursuit.py (float ONNX)
2.1.16.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| OrthogonalMatchingPursuit.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "OrthogonalMatchingPursuit" #define ONNXFilenameFloat "orthogonal_matching_pursuit_float.onnx" #define ONNXFilenameDouble "orthogonal_matching_pursuit_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 OrthogonalMatchingPursuit (EURUSD,H1) OrthogonalMatchingPursuit (EURUSD,H1) Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) OrthogonalMatchingPursuit (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 OrthogonalMatchingPursuit (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Comparação com o modelo original em double no Python:
Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.16.3. Representação ONNX do orthogonal_matching_pursuit_float.onnx e orthogonal_matching_pursuit_double.onnx
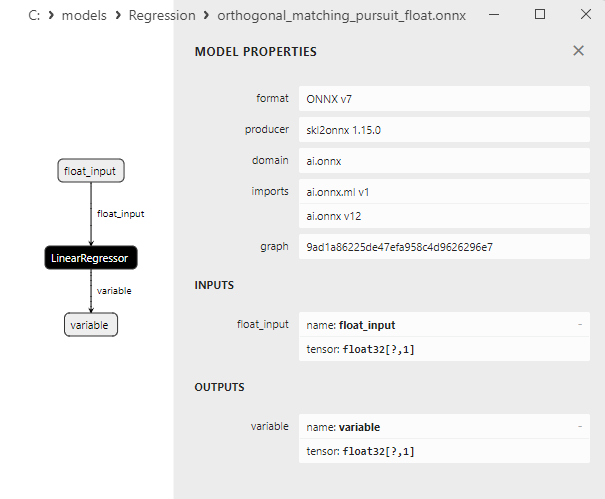
Fig.56. Representação ONNX do orthogonal_matching_pursuit_float.onnx no Netron
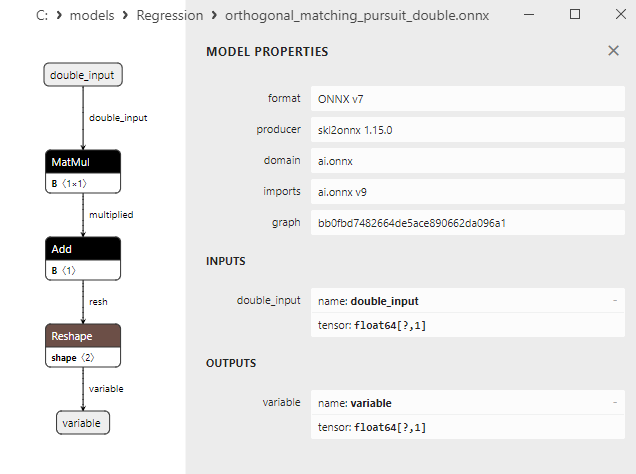
Fig.57. Representação ONNX do orthogonal_matching_pursuit_double.onnx no Netron
2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
PassiveAggressiveRegressor é um método de aprendizado de máquina usado para tarefas de regressão.
Este método é uma variante do algoritmo Passive-Aggressive (PA) que pode ser empregado para treinar um modelo capaz de prever valores contínuos da variável alvo.
Como funciona o PassiveAggressiveRegressor:
- Dados de entrada: Começa com um conjunto de dados que compreende características (variáveis independentes) e valores da variável alvo (contínua).
- Aprendizado supervisionado: PassiveAggressiveRegressor é um método de aprendizado supervisionado treinado em pares (X, y), onde X representa as características e y corresponde aos valores da variável alvo.
- Aprendizado adaptativo: A ideia principal por trás do método Passive-Aggressive é a abordagem de aprendizado adaptativo. O modelo aprende minimizando o erro de previsão em cada exemplo de treinamento. Ele se atualiza corrigindo os pesos para reduzir o erro de previsão.
- Parâmetro C: PassiveAggressiveRegressor possui um hiperparâmetro C, que controla o quão fortemente o modelo se adapta aos erros. Um valor mais alto de C significa atualizações de peso mais agressivas, enquanto um valor mais baixo de C torna o modelo menos agressivo.
- Previsão: Uma vez treinado, o modelo pode prever valores da variável alvo para novos dados.
Vantagens do PassiveAggressiveRegressor:
- Adaptabilidade: O método pode se adaptar às mudanças nos dados e atualizar o modelo para minimizar os erros de previsão.
- Eficiência para grandes conjuntos de dados: PassiveAggressiveRegressor pode ser um método eficaz para regressão, particularmente quando treinado em grandes volumes de dados.
Limitações do PassiveAggressiveRegressor:
- Sensibilidade à escolha do parâmetro C: Selecionar adequadamente o valor de C pode exigir ajustes e experimentação.
- Características adicionais podem ser necessárias: Em alguns casos, características adicionais projetadas podem ser necessárias para o treinamento bem-sucedido do modelo.
PassiveAggressiveRegressor é um método de aprendizado de máquina para tarefas de regressão que aprende adaptativamente minimizando erros de previsão nos dados de treinamento. Este método pode ser valioso para lidar com grandes conjuntos de dados e requer ajustes do parâmetro C para desempenho ideal.
2.1.17.1. Código para criar o modelo PassiveAggressiveRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.PassiveAggressiveRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# PassiveAggressiveRegressor.py
# The code demonstrates the process of training PassiveAggressiveRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"
# create a PassiveAggressiveRegressor model
regression_model = PassiveAggressiveRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training PassiveAggressiveRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"
# create a PassiveAggressiveRegressor model
regression_model = PassiveAggressiveRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python PassiveAggressiveRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python Python PassiveAggressiveRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376801868329 Python Mean Absolute Error: 9.645248834431873 Python Mean Squared Error: 139.76862616640122 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python PassiveAggressiveRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9894376841493092 Python Mean Absolute Error: 9.64524669506544 Python Mean Squared Error: 139.76857373191007 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 14 Python double ONNX model precision: 14
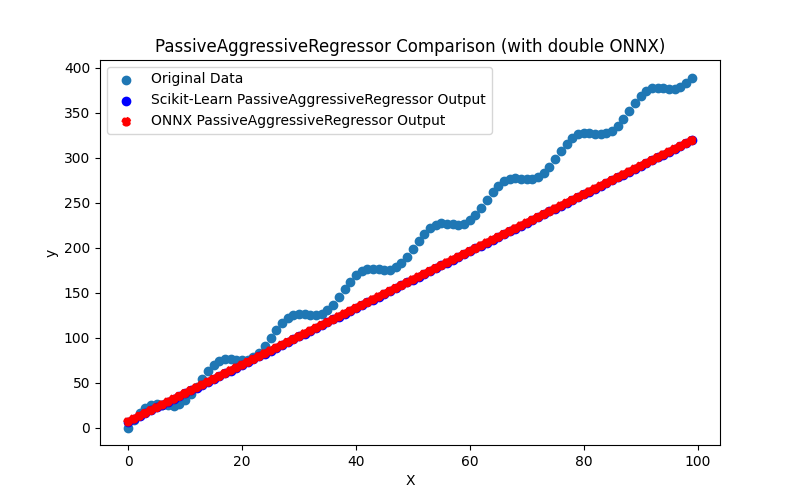
Fig.58. Resultados do PassiveAggressiveRegressor.py (double ONNX)
2.1.17.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| PassiveAggressiveRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PassiveAggressiveRegressor" #define ONNXFilenameFloat "passive_aggressive_regressor_float.onnx" #define ONNXFilenameDouble "passive_aggressive_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376801868329 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452488344318716 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7686261664012761 PassiveAggressiveRegressor (EURUSD,H1) PassiveAggressiveRegressor (EURUSD,H1) Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) PassiveAggressiveRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9894376841493092 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.6452466950654419 PassiveAggressiveRegressor (EURUSD,H1) MQL5: Mean Squared Error: 139.7685737319100667
Comparação com o modelo original em double no Python:
Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452488344318716 Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx) Python Mean Absolute Error: 9.64524669506544 MQL5: Mean Absolute Error: 9.6452466950654419
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.17.3. Representação ONNX do passive_aggressive_regressor_float.onnx e passive_aggressive_regressor_double.onnx
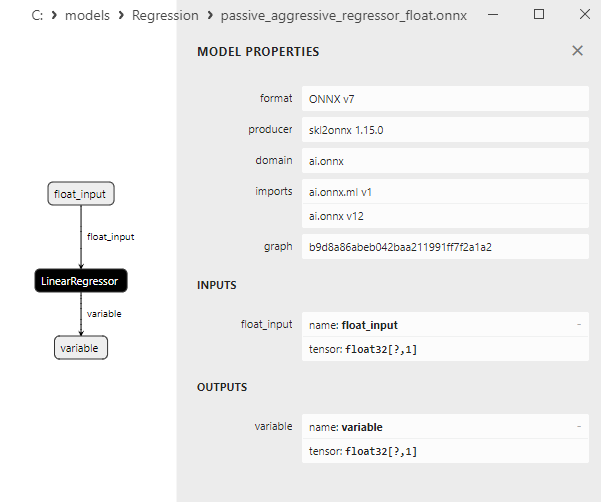
Fig.59. Representação ONNX do passive_aggressive_regressor_float.onnx no Netron
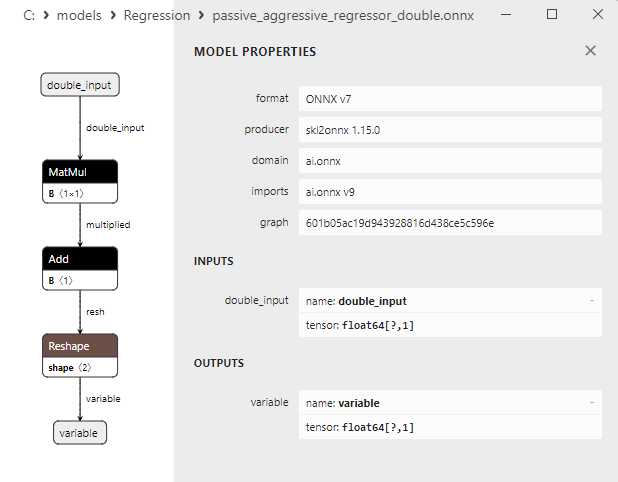
Fig.60. Representação ONNX do passive_aggressive_regressor_double.onnx no Netron
2.1.18. sklearn.linear_model.QuantileRegressor
QuantileRegressor é um método de aprendizado de máquina usado para estimar quantis (percentis específicos) da variável alvo em tarefas de regressão.
Em vez de prever o valor médio da variável alvo, como normalmente feito em tarefas de regressão, o QuantileRegressor prevê valores correspondentes a quantis especificados, como a mediana (percentil 50) ou os percentis 25 e 75.
Como funciona o QuantileRegressor:
- Dados de entrada: Começa com um conjunto de dados contendo características (variáveis independentes) e a variável alvo (contínua).
- Foco no quantil: Em vez de prever valores exatos da variável alvo, o QuantileRegressor modela a distribuição condicional da variável alvo e prevê valores para certos quantis dessa distribuição.
- Treinamento para diferentes quantis: Treinar um modelo QuantileRegressor envolve treinar modelos separados para cada quantil desejado. Cada um desses modelos prevê um valor correspondente ao seu quantil.
- Parâmetro do quantil: O principal parâmetro para este método é a escolha dos quantis desejados para os quais você deseja obter previsões. Por exemplo, se você precisar de previsões para a mediana, precisará treinar o modelo no percentil 50.
- Previsão do quantil: Após o treinamento, o modelo pode ser usado para prever valores correspondentes a quantis especificados em novos dados.
Vantagens do QuantileRegressor:
- Flexibilidade: O QuantileRegressor fornece flexibilidade na previsão de vários quantis, o que pode ser útil em tarefas onde diferentes percentis da distribuição são importantes.
- Robustez a outliers: Uma abordagem orientada a quantis pode ser robusta contra outliers, pois não considera a média, que pode ser fortemente influenciada por valores extremos.
Limitações do QuantileRegressor:
- Necessidade de seleção de quantis: Escolher os quantis ótimos pode exigir algum conhecimento sobre a tarefa.
- Aumento da complexidade computacional: Treinar modelos separados para diferentes quantis pode aumentar a complexidade computacional da tarefa.
QuantileRegressor é um método de aprendizado de máquina projetado para prever valores correspondentes a quantis especificados da variável alvo. Este método pode ser útil em tarefas onde vários percentis da distribuição são de interesse e em casos onde os dados podem conter outliers.
2.1.18.1. Código para criar o modelo QuantileRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.QuantileRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# QuantileRegressor.py
# The code demonstrates the process of training QuantileRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"
# create a QuantileRegressor model
regression_model = QuantileRegressor(solver='highs')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training QuantileRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"
# create a QuantileRegressor model
regression_model = QuantileRegressor(solver='highs')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python QuantileRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python Python QuantileRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915739158818 Python Mean Absolute Error: 6.3693091422201125 Python Mean Squared Error: 53.042533910812814 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 5 Python float ONNX model precision: 7 Python Python QuantileRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9959915738839231 Python Mean Absolute Error: 6.3693091850025185 Python Mean Squared Error: 53.0425343337143 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 13 Python double ONNX model precision: 16
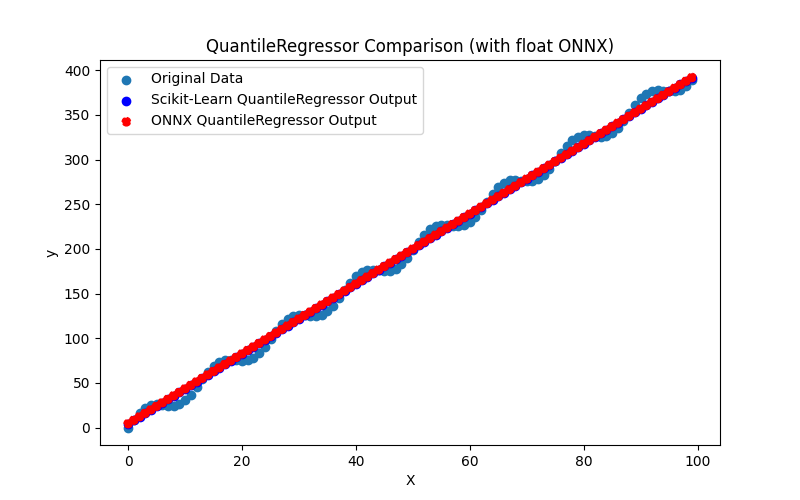
Fig.61. Resultados do QuantileRegressor.py (float ONNX)
2.1.18.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos quantile_regressor_float.onnx e quantile_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| QuantileRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "QuantileRegressor" #define ONNXFilenameFloat "quantile_regressor_float.onnx" #define ONNXFilenameDouble "quantile_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
QuantileRegressor (EURUSD,H1) Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915739158818 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091422201169 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425339108128071 QuantileRegressor (EURUSD,H1) QuantileRegressor (EURUSD,H1) Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) QuantileRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9959915738839231 QuantileRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3693091850025185 QuantileRegressor (EURUSD,H1) MQL5: Mean Squared Error: 53.0425343337142721
Comparação com o modelo original em double no Python:
Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091422201169 Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx) Python Mean Absolute Error: 6.3693091850025185 MQL5: Mean Absolute Error: 6.3693091850025185
Precisão do ONNX float MAE: 7 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.18.3. Representação ONNX do quantile_regressor_float.onnx e quantile_regressor_double.onnx
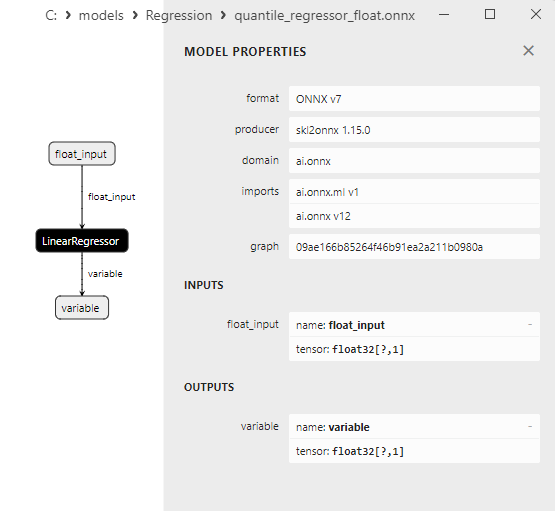
Fig.62. Representação ONNX do quantile_regressor_float.onnx no Netron
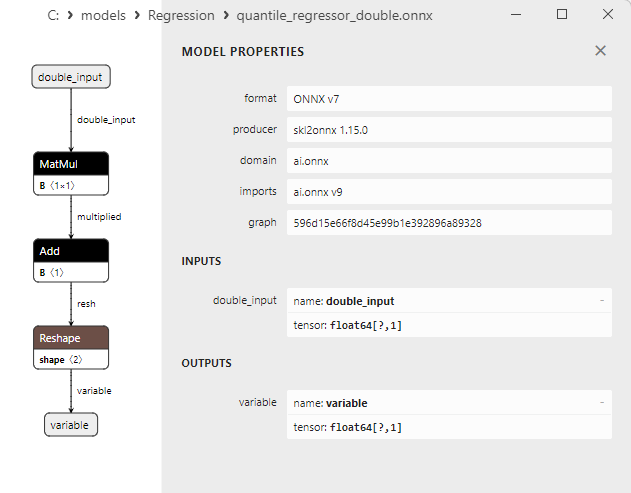
Fig.63. Representação ONNX do quantile_regressor_double.onnx no Netron
2.1.19. sklearn.linear_model.RANSACRegressor
RANSACRegressor é um método de aprendizado de máquina usado para resolver problemas de regressão utilizando o método RANSAC (Random Sample Consensus).
O método RANSAC é projetado para lidar com dados que contêm outliers ou imperfeições, permitindo um modelo de regressão mais robusto ao excluir a influência dos outliers.
Como funciona o RANSACRegressor:
- Dados de entrada: Começa com um conjunto de dados contendo características (variáveis independentes) e a variável alvo (contínua).
- Seleção de subconjuntos aleatórios: O RANSAC começa escolhendo subconjuntos aleatórios de dados usados para treinar o modelo de regressão. Esses subconjuntos são chamados de "hipóteses".
- Ajuste do modelo às hipóteses: Para cada hipótese escolhida, um modelo de regressão é treinado. No caso do RANSACRegressor, geralmente é utilizada a regressão linear, e o modelo é ajustado ao subconjunto de dados.
- Avaliação de outliers: Após o treinamento do modelo, seu ajuste a todos os dados é avaliado. O erro entre os valores previstos e reais é calculado para cada ponto de dados.
- Identificação de outliers: Pontos de dados com erros que excedem um limite especificado são considerados outliers. Esses outliers podem influenciar o treinamento do modelo e distorcer os resultados.
- Atualização do modelo: Todos os pontos de dados que não são considerados outliers são usados para atualizar o modelo de regressão. Esse processo pode ser repetido várias vezes com diferentes hipóteses aleatórias.
- Modelo final: Após várias iterações, o RANSACRegressor seleciona o melhor modelo treinado no subconjunto de dados e o retorna como o modelo de regressão final.
Vantagens do RANSACRegressor:
- Robustez a outliers: O RANSACRegressor é um método robusto contra outliers, pois os exclui do treinamento.
- Regressão robusta: Este método permite a criação de um modelo de regressão mais confiável quando os dados contêm outliers ou imperfeições.
Limitações do RANSACRegressor:
- Sensibilidade ao limite de erro: Escolher um limite de erro para determinar quais pontos são considerados outliers pode exigir experimentação.
- Complexidade na seleção de hipóteses: Escolher boas hipóteses na fase inicial pode não ser uma tarefa simples.
RANSACRegressor é um método de aprendizado de máquina usado para problemas de regressão com base no método RANSAC. Este método permite a criação de um modelo de regressão mais robusto quando os dados contêm outliers ou imperfeições, excluindo sua influência no modelo.
2.1.19.1. Código para criar o modelo RANSACRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.RANSACRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# RANSACRegressor.py
# The code demonstrates the process of training RANSACRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"
# create a RANSACRegressor model
regression_model = RANSACRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training RANSACRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"
# create a RANSACRegressor model
regression_model = RANSACRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python RANSACRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python Python RANSACRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382641628886 Python Mean Absolute Error: 6.3477377671679385 Python Mean Squared Error: 49.77814147404787 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python ONNX: MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python RANSACRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.347737926336427 Python Mean Squared Error: 49.77814017128179 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
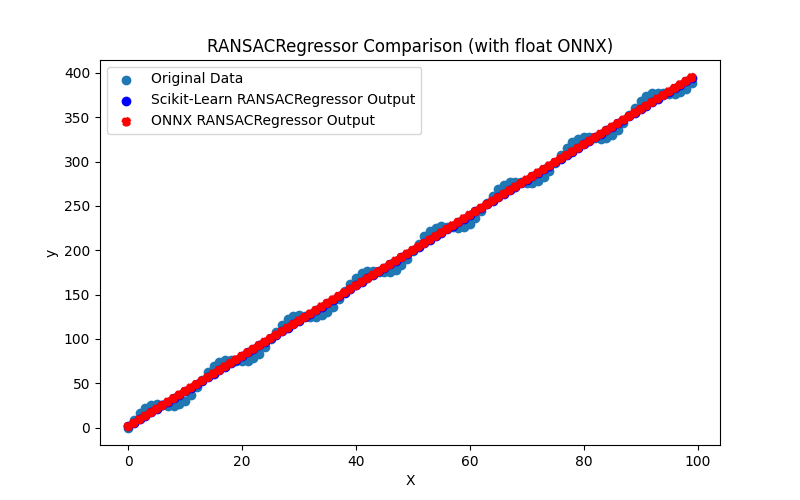
Fig.64. Resultados do RANSACRegressor.py (float ONNX)
2.1.19.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos ransac_regressor_float.onnx e ransac_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| RANSACRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RANSACRegressor" #define ONNXFilenameFloat "ransac_regressor_float.onnx" #define ONNXFilenameDouble "ransac_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
RANSACRegressor (EURUSD,H1) Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382641628886 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477377671679385 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781414740478638 RANSACRegressor (EURUSD,H1) RANSACRegressor (EURUSD,H1) Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) RANSACRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 RANSACRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364266 RANSACRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817768
Comparação com o modelo original em double no Python:
Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477377671679385 Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx) Python Mean Absolute Error: 6.347737926336427 MQL5: Mean Absolute Error: 6.3477379263364266
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.19.3. Representação ONNX do ransac_regressor_float.onnx e ransac_regressor_double.onnx
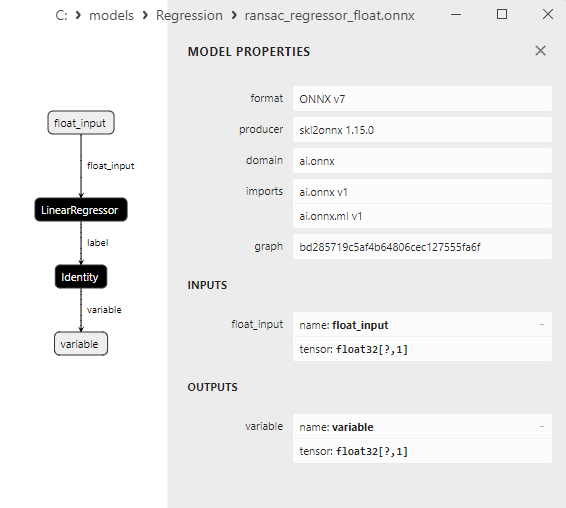
Fig.65. Representação ONNX do ransac_regressor_float.onnx no Netron
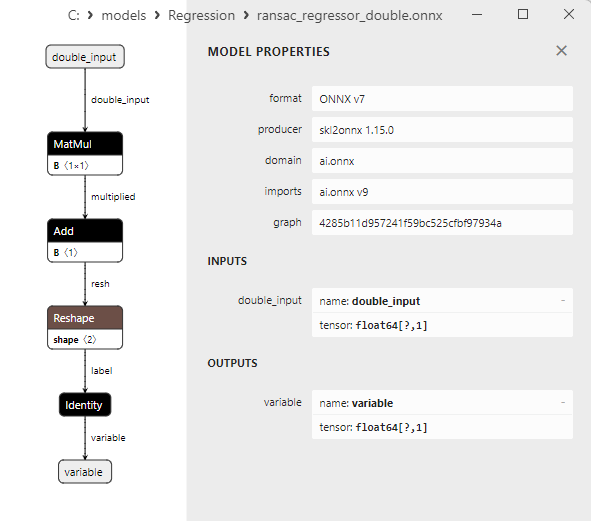
Fig.66. Representação ONNX do ransac_regressor_double.onnx no Netron
2.1.20. sklearn.linear_model.TheilSenRegressor
Theil-Sen regression (Estimador de Theil-Sen) é um método de estimativa de regressão usado para aproximar relações lineares entre variáveis independentes e a variável alvo.
Ele oferece uma estimativa mais robusta em comparação com a regressão linear ordinária na presença de outliers e ruídos nos dados.
Como funciona a regressão Theil-Sen:
- Seleção de pontos: Inicialmente, o Theil-Sen seleciona pares aleatórios de pontos de dados do conjunto de treinamento.
- Cálculo da inclinação: Para cada par de pontos de dados, o método calcula a inclinação da linha que passa por esses pontos, criando um conjunto de inclinações.
- Inclinação mediana: Em seguida, o método encontra a inclinação mediana do conjunto de inclinações. Esta inclinação mediana é usada como uma estimativa da inclinação da regressão linear.
- Desvios medianos: Para cada ponto de dados, o método calcula o desvio (diferença entre o valor real e o valor previsto com base na inclinação mediana) e encontra a mediana desses desvios. Isso cria uma estimativa para o coeficiente de intercepto da regressão linear.
- Estimativa final: As estimativas finais dos coeficientes de inclinação e intercepto são usadas para construir o modelo de regressão linear.
Vantagens da regressão Theil-Sen:
- Resiliência a outliers: A regressão Theil-Sen é mais robusta contra outliers e ruídos nos dados em comparação com a regressão linear regular.
- Assumptions menos rigorosos: O método não requer suposições rigorosas sobre a distribuição dos dados ou a forma de dependência, tornando-o mais versátil.
- Adequado para dados multicolineares: A regressão Theil-Sen funciona bem com dados onde as variáveis independentes são altamente correlacionadas (problema de multicolinearidade).
Limitações da regressão Theil-Sen:
- Complexidade computacional: Calcular inclinações medianas para todos os pares de pontos de dados pode ser demorado, especialmente para grandes conjuntos de dados.
- Estimativa do coeficiente de intercepto: Desvios medianos são usados para estimar o coeficiente de intercepto, o que pode levar a vieses na presença de outliers.
A regressão Theil-Sen é um método de estimativa para regressão que fornece uma avaliação estável da relação linear entre variáveis independentes e a variável alvo, particularmente na presença de outliers e ruídos nos dados. Este método é útil quando é necessária uma estimativa estável sob condições de dados do mundo real.
2.1.20.1. Código para criar o TheilSenRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.TheilSenRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. precisão tanto do modelo original quanto dos modelos exportados para ONNX.
# TheilSenRegressor.py
# The code demonstrates the process of training TheilSenRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"
# create a TheilSen Regressor model
regression_model = TheilSenRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training TheilSenRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"
# create a TheilSen Regressor model
regression_model = TheilSenRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python TheilSenRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python Python TheilSenRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.996232919516505 Python Mean Absolute Error: 6.338686370832071 Python Mean Squared Error: 49.84886588834327 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 6 Python MSE matching decimal places: 5 Python float ONNX model precision: 6 Python Python TheilSenRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962329196940459 Python Mean Absolute Error: 6.338686004537594 Python Mean Squared Error: 49.84886353898735 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
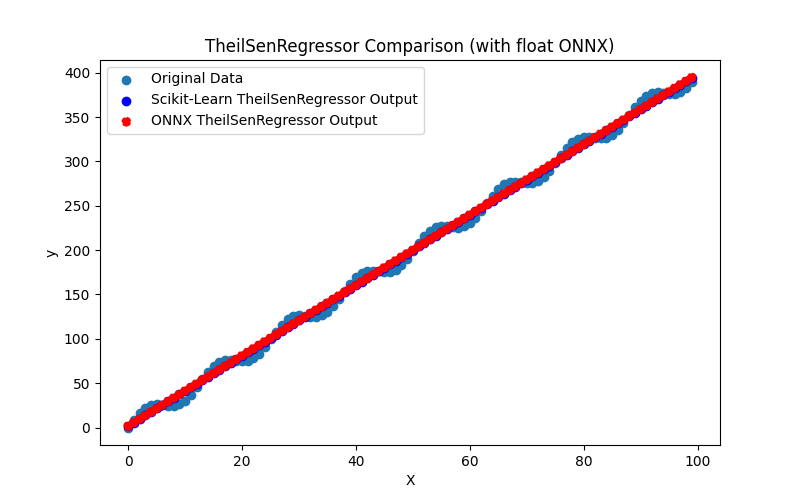
Fig.67. Resultados do TheilSenRegressor.py (float ONNX)
2.1.20.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| TheilSenRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TheilSenRegressor" #define ONNXFilenameFloat "theil_sen_regressor_float.onnx" #define ONNXFilenameDouble "theil_sen_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
TheilSenRegressor (EURUSD,H1) Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329195165051 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386863708320735 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488658883432691 TheilSenRegressor (EURUSD,H1) TheilSenRegressor (EURUSD,H1) Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) TheilSenRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962329196940459 TheilSenRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3386860045375943 TheilSenRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.8488635389873735
Comparação com o modelo original em double no Python:
Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386863708320735 Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx) Python Mean Absolute Error: 6.338686004537594 MQL5: Mean Absolute Error: 6.3386860045375943
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 15 casas decimais.
2.1.20.3. Representação ONNX do theil_sen_regressor_float.onnx e theil_sen_regressor_double.onnx
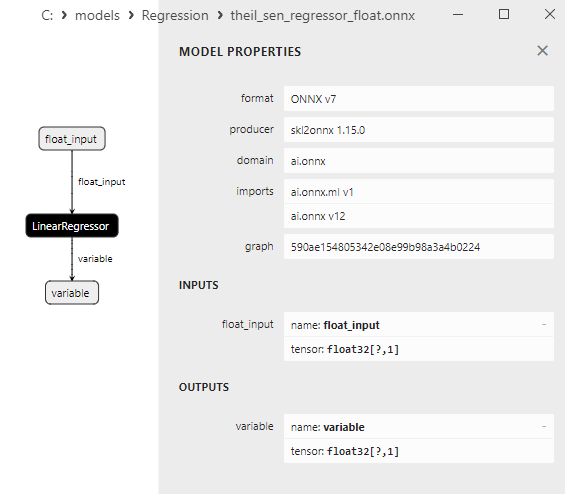
Fig.68. Representação ONNX do theil_sen_regressor_float.onnx no Netron
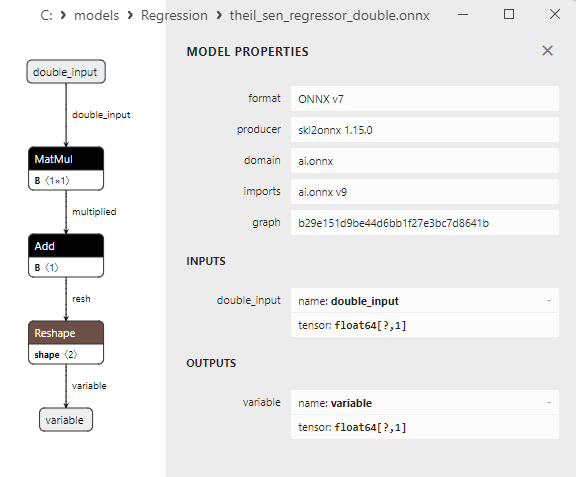
Fig.69. Representação ONNX do theil_sen_regressor_double.onnx no Netron
2.1.21. sklearn.linear_model.LinearSVR
LinearSVR (Linear Support Vector Regression) é um modelo de aprendizado de máquina para tarefas de regressão baseado no método de Máquinas de Vetores de Suporte (SVM).
Este método é usado para encontrar relações lineares entre características e a variável alvo usando um kernel linear.
Como funciona o LinearSVR:
- Dados de entrada: O LinearSVR começa com um conjunto de dados que inclui características (variáveis independentes) e seus respectivos valores da variável alvo.
- Seleção de um modelo linear: O modelo assume que existe uma relação linear entre as características e a variável alvo, descrita por uma equação de regressão linear.
- Treinamento do modelo: O LinearSVR encontra os valores ótimos para os coeficientes do modelo minimizando uma função de perda que considera o erro de previsão e um erro aceitável (epsilon).
- Geração de previsões: Após o treinamento, o modelo pode prever os valores da variável alvo para novos dados com base nos coeficientes descobertos.
Vantagens do LinearSVR:
- Regressão de Vetores de Suporte: O LinearSVR emprega o método de Máquinas de Vetores de Suporte, o que permite encontrar a separação ótima entre os dados enquanto considera um erro aceitável.
- Suporte para múltiplas características: O modelo pode lidar com múltiplas características e processar dados em altas dimensões.
- Regularização: O LinearSVR envolve regularização, auxiliando no combate ao overfitting e garantindo previsões mais estáveis.
Limitações do LinearSVR:
- Linearidade: O LinearSVR é limitado ao uso de relações lineares entre características e a variável alvo. No caso de relações complexas e não lineares, o modelo pode ser insuficientemente flexível.
- Sensibilidade a outliers: O modelo pode ser sensível a outliers nos dados e ao erro aceitável (epsilon).
- Incapacidade de capturar relações complexas: O LinearSVR, como outros modelos lineares, é incapaz de capturar relações não lineares complexas entre características e a variável alvo.
LinearSVR é um modelo de aprendizado de máquina para regressão que utiliza o método de Máquinas de Vetores de Suporte para encontrar relações lineares entre características e a variável alvo. Ele suporta regularização e pode ser usado em tarefas onde controlar o erro aceitável é essencial. No entanto, o modelo é limitado por sua dependência linear e pode ser sensível a outliers.
2.1.21.1. Código para criar o modelo LinearSVR e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.LinearSVR, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# LinearSVR.py
# The code demonstrates the process of training LinearSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "LinearSVR"
onnx_model_filename = data_path + "linear_svr"
# create a Linear SVR model
linear_svr_model = LinearSVR()
# fit the model to the data
linear_svr_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = linear_svr_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_svr_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_svr_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python LinearSVR Original model (double) Python R-squared (Coefficient of determination): 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python Python LinearSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935580726729 Python Mean Absolute Error: 7.026849848037511 Python Mean Squared Error: 72.86541563418206 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 4 Python MSE matching decimal places: 3 Python float ONNX model precision: 4 Python Python LinearSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9944935515149387 Python Mean Absolute Error: 7.026852359381935 Python Mean Squared Error: 72.86550241109444 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 14 Python double ONNX model precision: 15
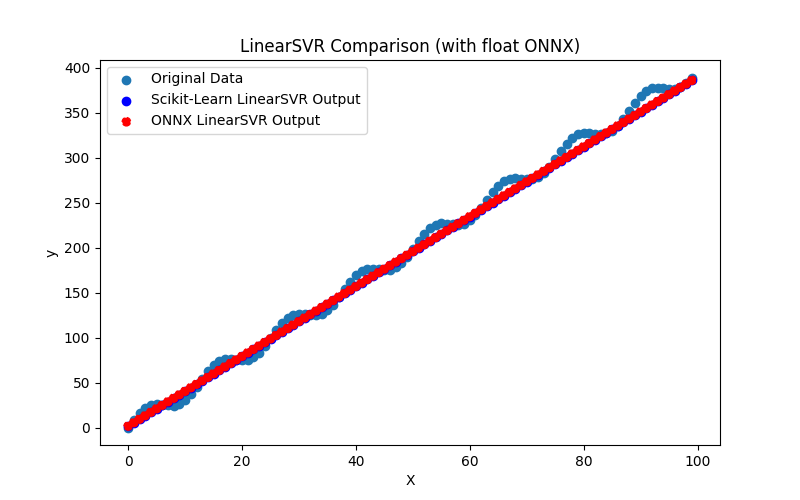
Fig.70. Resultados do LinearSVR.py (float ONNX)
2.1.21.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos linear_svr_float.onnx e linear_svr_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| LinearSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "LinearSVR" #define ONNXFilenameFloat "linear_svr_float.onnx" #define ONNXFilenameDouble "linear_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
LinearSVR (EURUSD,H1) Testing ONNX float: LinearSVR (linear_svr_float.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935580726729 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268498480375108 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8654156341820567 LinearSVR (EURUSD,H1) LinearSVR (EURUSD,H1) Testing ONNX double: LinearSVR (linear_svr_double.onnx) LinearSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9944935515149387 LinearSVR (EURUSD,H1) MQL5: Mean Absolute Error: 7.0268523593819374 LinearSVR (EURUSD,H1) MQL5: Mean Squared Error: 72.8655024110944680
Comparação com o modelo original em double no Python:
Testing ONNX float: LinearSVR (linear_svr_float.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268498480375108 Testing ONNX double: LinearSVR (linear_svr_double.onnx) Python Mean Absolute Error: 7.026852359381935 MQL5: Mean Absolute Error: 7.0268523593819374
Precisão do ONNX float MAE: 4 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.21.3. Representação ONNX do linear_svr_float.onnx e linear_svr_double.onnx
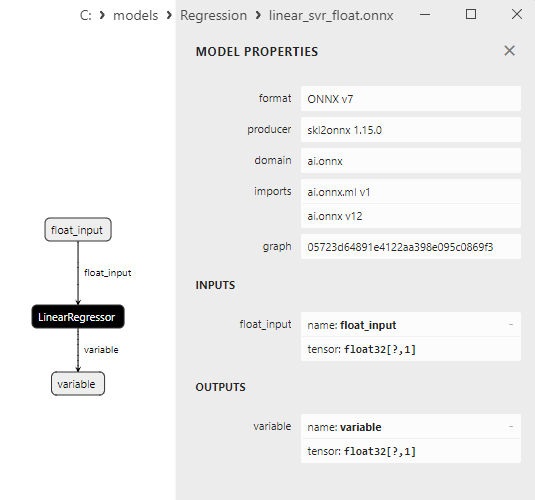
Fig.71. Representação ONNX do linear_svr_float.onnx no Netron
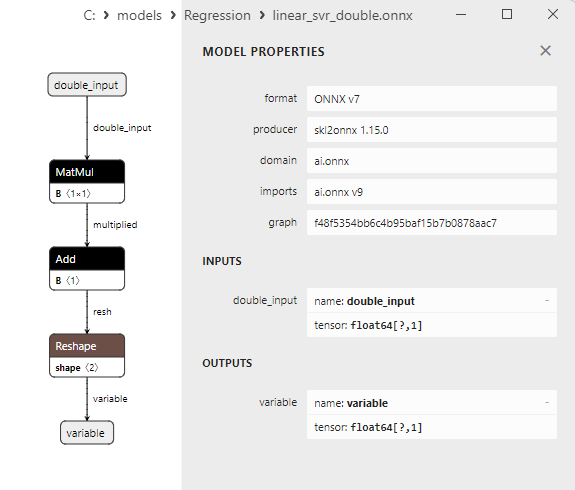
Fig.72. Representação ONNX do linear_svr_double.onnx no Netron
2.1.22. sklearn.neural_network.MLPRegressor
MLPRegressor (Multi-Layer Perceptron Regressor) é um modelo de aprendizado de máquina que utiliza redes neurais artificiais para tarefas de regressão.
É uma rede neural de múltiplas camadas que compreende várias camadas de neurônios (incluindo camadas de entrada, ocultas e de saída) que são treinadas para prever valores contínuos da variável alvo.
Como funciona o MLPRegressor:
- Dados de entrada: Começa com um conjunto de dados contendo características (variáveis independentes) e seus respectivos valores da variável alvo.
- Criação de uma rede neural de múltiplas camadas: O MLPRegressor emprega uma rede neural de múltiplas camadas com várias camadas ocultas de neurônios. Esses neurônios são conectados por conexões ponderadas e funções de ativação.
- Treinamento do modelo: O MLPRegressor treina a rede neural ajustando pesos e vieses para minimizar uma função de perda que mede a disparidade entre as previsões da rede e os valores reais da variável alvo. Isso é alcançado por meio de algoritmos de retropropagação.
- Geração de previsões: Após o treinamento, o modelo pode prever os valores da variável alvo para novos dados.
Vantagens do MLPRegressor:
- Flexibilidade: Redes neurais de múltiplas camadas podem modelar relações não lineares complexas entre características e a variável alvo.
- Versatilidade: O MLPRegressor pode ser usado para várias tarefas de regressão, incluindo problemas de séries temporais, aproximação de funções e mais.
- Capacidade de generalização: Redes neurais aprendem com os dados e podem generalizar as dependências encontradas nos dados de treinamento para novos dados.
Limitações do MLPRegressor:
- Complexidade do modelo base: Grandes redes neurais podem ser computacionalmente caras e exigir extensos dados para treinamento.
- Ajuste de hiperparâmetros: Escolher hiperparâmetros ótimos (número de camadas, número de neurônios em cada camada, taxa de aprendizado, etc.) pode exigir experimentação.
- Susceptibilidade ao overfitting: Grandes redes neurais podem ser propensas ao overfitting se houver dados insuficientes ou regularização insuficiente.
O MLPRegressor representa um poderoso modelo de aprendizado de máquina baseado em redes neurais de múltiplas camadas e pode ser usado para uma ampla gama de tarefas de regressão. Este modelo é flexível, mas requer ajustes meticulosos e treinamento em grandes volumes de dados para alcançar resultados ótimos.
2.1.22.1. Código para criar o modelo MLPRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.neural_network.MLPRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# MLPRegressor.py
# The code demonstrates the process of training MLPRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"
# create an MLP Regressor model
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)
# fit the model to the data
mlp_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = mlp_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training MLPRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"
# create an MLP Regressor model
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)
# fit the model to the data
mlp_regressor_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = mlp_regressor_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python MLPRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9874070836467945 Python Mean Absolute Error: 10.62249788982753 Python Mean Squared Error: 166.63901957615224 Python Python MLPRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070821340352 Python Mean Absolute Error: 10.62249972216809 Python Mean Squared Error: 166.63903959413219 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python MLPRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9874070836467945 Python Mean Absolute Error: 10.622497889827532 Python Mean Squared Error: 166.63901957615244 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 12 Python double ONNX model precision: 14
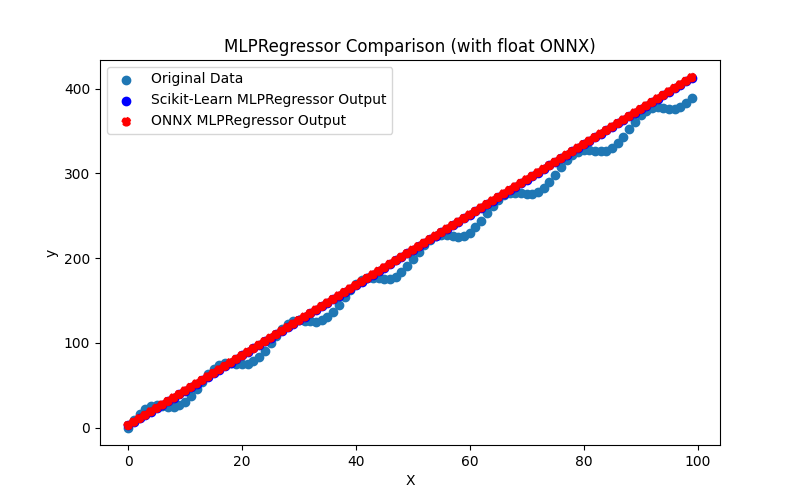
Fig.73. Resultados do MLPRegressor.py (float ONNX)
2.1.22.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos mlp_regressor_float.onnx e mlp_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| MLPRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "MLPRegressor" #define ONNXFilenameFloat "mlp_regressor_float.onnx" #define ONNXFilenameDouble "mlp_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
MLPRegressor (EURUSD,H1) Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198695654352 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596681685341309 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1465507645494597 MLPRegressor (EURUSD,H1) MLPRegressor (EURUSD,H1) Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) MLPRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9875198617341387 MLPRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 10.5596715833884609 MLPRegressor (EURUSD,H1) MQL5: Mean Squared Error: 165.1466543942046599
Comparação com o modelo original em double no Python:
Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224997221680901 Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx) Python Mean Absolute Error: 10.62249788982753 MQL5: Mean Absolute Error: 10.6224978898275282
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.22.3. Representação ONNX do mlp_regressor_float.onnx e mlp_regressor_double.onnx
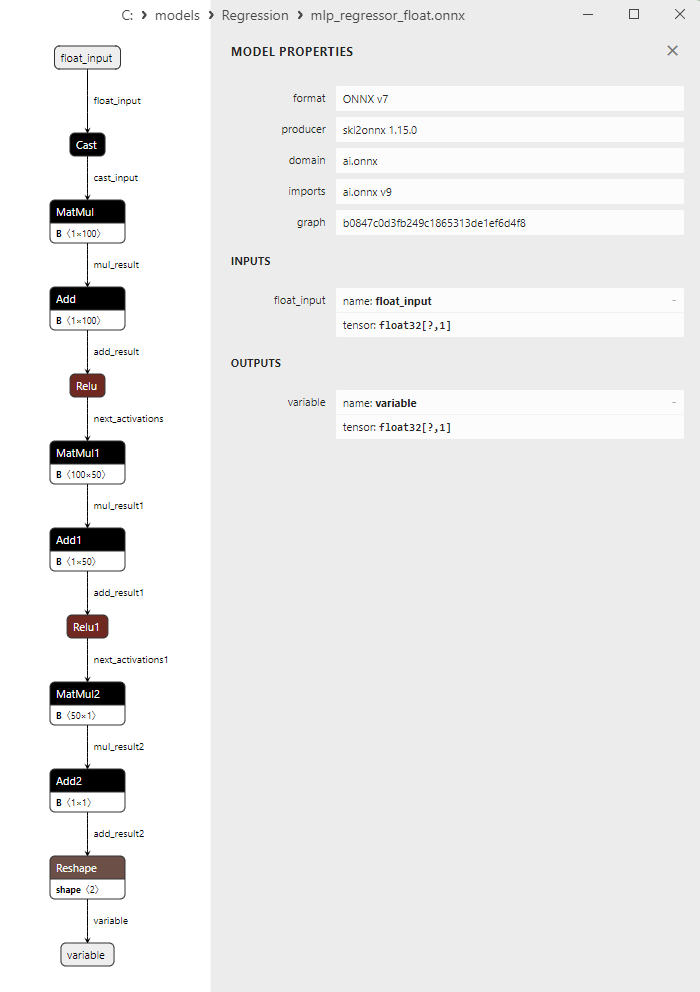
Fig.74. Representação ONNX do mlp_regressor_float.onnx no Netron
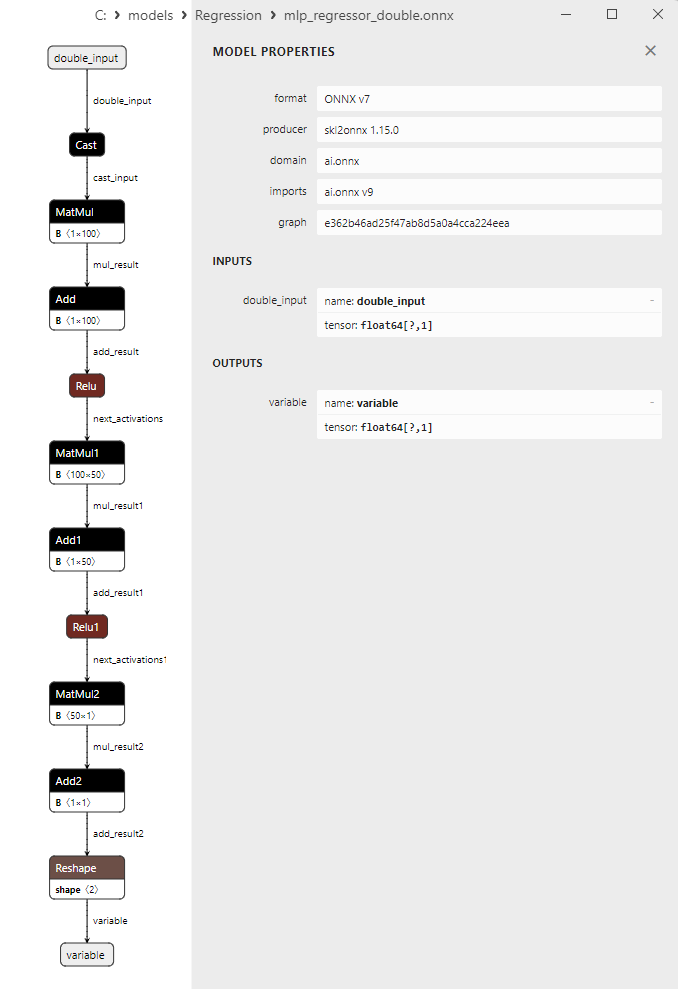
Fig.75. representação ONNX do mlp_regressor_double.onnx no Netron
2.1.23. sklearn.cross_decomposition.PLSRegression
PLSRegression (Partial Least Squares Regression) é um método de aprendizado de máquina usado para resolver problemas de regressão.
Ele faz parte da família de métodos PLS e é aplicado para analisar e modelar relações entre dois conjuntos de variáveis, onde um conjunto serve como preditores e o outro conjunto são as variáveis alvo.
Como funciona o PLSRegression:
- Dados de entrada: Começa com dois conjuntos de dados, rotulados como X e Y. O conjunto X contém variáveis independentes (preditores), e o conjunto Y contém variáveis alvo (dependentes).
- Seleção de combinações lineares: O PLSRegression identifica combinações lineares (componentes) nos conjuntos X e Y que maximizam a covariância entre eles. Esses componentes são chamados de componentes PLS.
- Maximização da covariância: O objetivo principal do PLSRegression é encontrar componentes PLS que maximizem a covariância entre X e Y. Isso permite a extração das relações mais informativas entre preditores e variáveis alvo.
- Treinamento do modelo: Uma vez encontrados os componentes PLS, eles podem ser usados para criar um modelo que prevê os valores de Y com base em X.
- Geração de previsões: Após o treinamento, o modelo pode ser usado para prever os valores de Y para novos dados usando os valores correspondentes de X.
Vantagens do PLSRegression:
- Análise de correlação: O PLSRegression permite a análise e modelagem de correlações entre dois conjuntos de variáveis, o que pode ser útil para entender as relações entre preditores e variáveis alvo.
- Redução de dimensionalidade: O método também pode ser usado para reduzir a dimensionalidade dos dados, identificando os componentes PLS mais importantes.
Limitações do PLSRegression:
- Sensibilidade à escolha do número de componentes: Selecionar o número ideal de componentes PLS pode exigir alguma experimentação.
- Dependência da estrutura dos dados: Os resultados do PLSRegression podem depender fortemente da estrutura dos dados e das correlações entre eles.
PLSRegression é um método de aprendizado de máquina usado para analisar e modelar correlações entre dois conjuntos de variáveis, onde um conjunto atua como preditores e o outro são as variáveis alvo. Este método permite estudar as relações dentro dos dados e pode ser útil para reduzir a dimensionalidade dos dados e prever valores de variáveis alvo com base nos preditores.
2.1.23.1. Código para criar o modelo PLSRegression e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.cross_decomposition.PLSRegression, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# PLSRegression.py
# The code demonstrates the process of training PLSRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"
# create a PLSRegression model
pls_model = PLSRegression(n_components=1)
# fit the model to the data
pls_model.fit(X, y)
# predict values for the entire dataset
y_pred = pls_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training PLSRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"
# create a PLSRegression model
pls_model = PLSRegression(n_components=1)
# fit the model to the data
pls_model.fit(X, y)
# predict values for the entire dataset
y_pred = pls_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python PLSRegression Original model (double) Python R-squared (Coefficient of determination): 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python Python PLSRegression ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382638567003 Python Mean Absolute Error: 6.3477379221400145 Python Mean Squared Error: 49.778145525764096 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 8 Python MSE matching decimal places: 5 Python float ONNX model precision: 8 Python Python PLSRegression ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9962382642613388 Python Mean Absolute Error: 6.3477379263364275 Python Mean Squared Error: 49.778140171281805 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 15 Python double ONNX model precision: 16
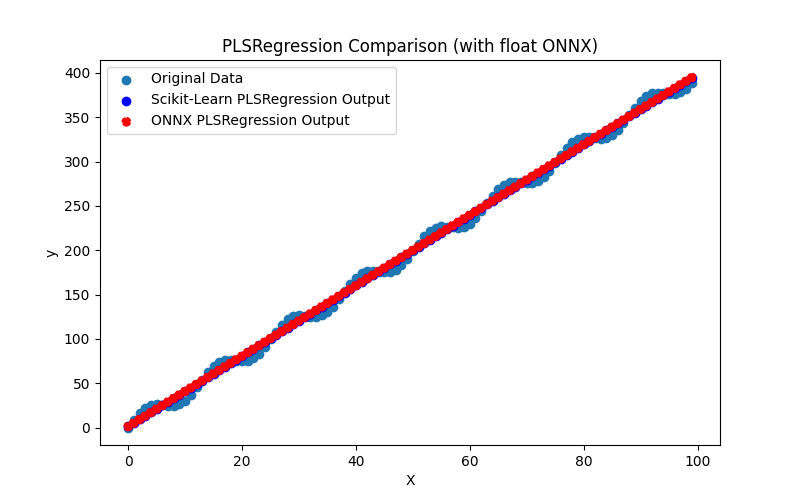
Fig.76. Resultados do PLSRegression.py (float ONNX)
2.1.23.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos pls_regression_float.onnx e pls_regression_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| PLSRegression.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PLSRegression" #define ONNXFilenameFloat "pls_regression_float.onnx" #define ONNXFilenameDouble "pls_regression_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
PLSRegression (EURUSD,H1) Testing ONNX float: PLSRegression (pls_regression_float.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382638567003 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379221400145 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781455257640815 PLSRegression (EURUSD,H1) PLSRegression (EURUSD,H1) Testing ONNX double: PLSRegression (pls_regression_double.onnx) PLSRegression (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962382642613388 PLSRegression (EURUSD,H1) MQL5: Mean Absolute Error: 6.3477379263364275 PLSRegression (EURUSD,H1) MQL5: Mean Squared Error: 49.7781401712817839
Comparação com o modelo original em double no Python:
Testing ONNX float: PLSRegression (pls_regression_float.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379221400145 Testing ONNX double: PLSRegression (pls_regression_double.onnx) Python Mean Absolute Error: 6.3477379263364275 MQL5: Mean Absolute Error: 6.3477379263364275
Precisão do ONNX float MAE: 8 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.23.3. Representação ONNX do pls_regression_float.onnx e pls_regression_double.onnx
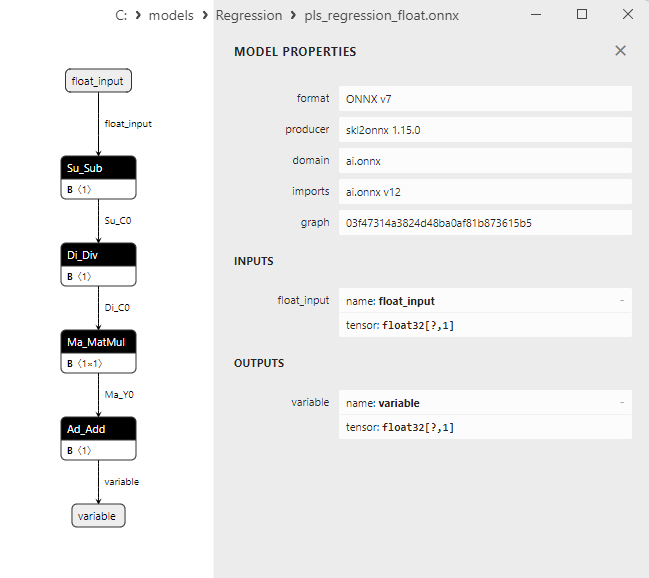
Fig.77. Representação ONNX do pls_regression_float.onnx no Netron
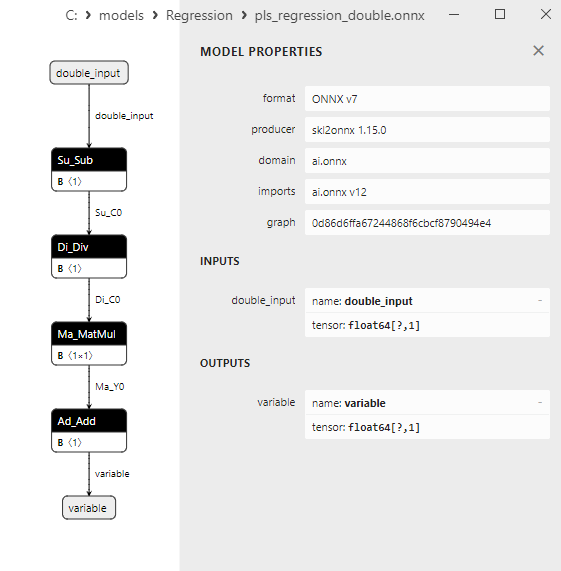
Fig.78. Representação ONNX do pls_regression_double.onnx no Netron
2.1.24. sklearn.linear_model.TweedieRegressor
TweedieRegressor é um método de regressão projetado para resolver problemas de regressão usando a distribuição de Tweedie. A distribuição de Tweedie é uma distribuição de probabilidade que pode descrever uma ampla gama de dados, incluindo dados com estrutura de variância variável. O TweedieRegressor é aplicado em tarefas de regressão onde a variável alvo possui características que se alinham com a distribuição de Tweedie.
Como funciona o TweedieRegressor:
- Variável alvo e distribuição de Tweedie: O TweedieRegressor assume que a variável alvo segue uma distribuição de Tweedie. A distribuição de Tweedie depende do parâmetro 'p', que determina a forma da distribuição e o grau de variância.
- Treinamento do modelo: O TweedieRegressor treina um modelo de regressão para prever a variável alvo com base nas variáveis independentes (características). O modelo maximiza a verossimilhança para dados correspondentes à distribuição de Tweedie.
- Escolha do parâmetro 'p': Selecionar o parâmetro 'p' é um aspecto crucial ao usar o TweedieRegressor. Esse parâmetro define a forma da distribuição e a variância. Diferentes valores de 'p' correspondem a diferentes tipos de dados; por exemplo, p=1 corresponde à distribuição de Poisson, enquanto p=2 corresponde à distribuição normal.
- Transformação das respostas: Às vezes, o modelo pode exigir transformações das respostas (variáveis alvo) antes do treinamento. Essa transformação se relaciona com o parâmetro 'p' e pode envolver funções logarítmicas ou outras transformações para se conformar à distribuição de Tweedie.
Vantagens do TweedieRegressor:
- Capacidade de modelar dados com variância variável: A distribuição de Tweedie pode se adaptar a dados com diferentes estruturas de variância, o que é valioso para dados do mundo real onde a variância pode variar.
- Variedade de parâmetros 'p': A capacidade de escolher diferentes valores de 'p' permite modelar vários tipos de dados.
Limitações do TweedieRegressor:
- Complexidade na escolha do parâmetro 'p': Selecionar o valor correto de 'p' pode exigir conhecimento sobre os dados e experimentação.
- Conformidade com a distribuição de Tweedie: Para a aplicação bem-sucedida do TweedieRegressor, a variável alvo deve corresponder à distribuição de Tweedie. A não conformidade pode levar a um desempenho ruim do modelo.
TweedieRegressor é um método de regressão que usa a distribuição de Tweedie para modelar dados com estruturas de variância variáveis. Este método é útil em tarefas de regressão onde a variável alvo se conforma à distribuição de Tweedie e pode ser ajustado com diferentes valores do parâmetro 'p' para melhor adaptação aos dados.
2.1.24.1. Código para criar o modelo TweedieRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.TweedieRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# TweedieRegressor.py
# The code demonstrates the process of training TweedieRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"
# create a Tweedie Regressor model
regression_model = TweedieRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training TweedieRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"
# create a Tweedie Regressor model
regression_model = TweedieRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
2023.10.31 11:39:36.223 Python TweedieRegressor Original model (double) 2023.10.31 11:39:36.223 Python R-squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:39:36.223 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.223 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.223 Python 2023.10.31 11:39:36.223 Python TweedieRegressor ONNX model (float) 2023.10.31 11:39:36.223 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_float.onnx 2023.10.31 11:39:36.253 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.253 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.31 11:39:36.253 Python R-squared (Coefficient of determination) 0.9962368338709323 2023.10.31 11:39:36.253 Python Mean Absolute Error: 6.342397072978867 2023.10.31 11:39:36.253 Python Mean Squared Error: 49.797068181938165 2023.10.31 11:39:36.253 Python R^2 matching decimal places: 8 2023.10.31 11:39:36.253 Python MAE matching decimal places: 6 2023.10.31 11:39:36.253 Python MSE matching decimal places: 4 2023.10.31 11:39:36.253 Python float ONNX model precision: 6 2023.10.31 11:39:36.613 Python 2023.10.31 11:39:36.613 Python TweedieRegressor ONNX model (double) 2023.10.31 11:39:36.613 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_double.onnx 2023.10.31 11:39:36.613 Python Information about input tensors in ONNX: 2023.10.31 11:39:36.613 Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.613 Python Information about output tensors in ONNX: 2023.10.31 11:39:36.628 Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] 2023.10.31 11:39:36.628 Python R-squared (Coefficient of determination) 0.9962368328117072 2023.10.31 11:39:36.628 Python Mean Absolute Error: 6.342397897667562 2023.10.31 11:39:36.628 Python Mean Squared Error: 49.797082198408745 2023.10.31 11:39:36.628 Python R^2 matching decimal places: 16 2023.10.31 11:39:36.628 Python MAE matching decimal places: 15 2023.10.31 11:39:36.628 Python MSE matching decimal places: 15 2023.10.31 11:39:36.628 Python double ONNX model precision: 15
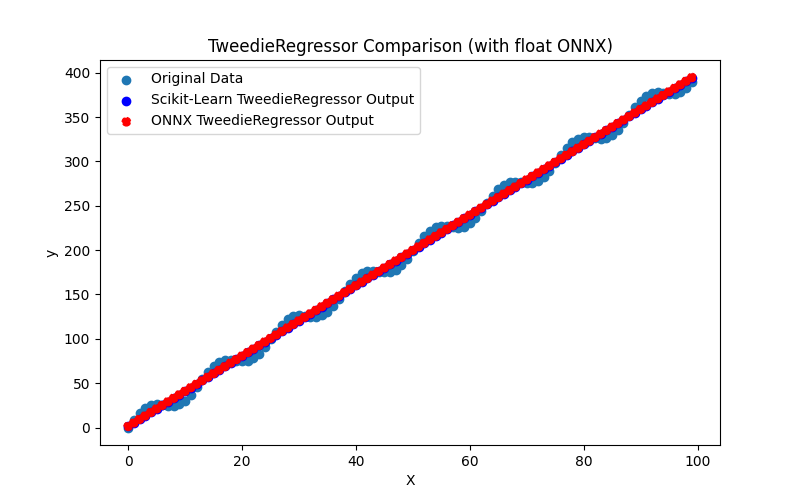
Fig.79. Resultados do TweedieRegressor.py (float ONNX)
2.1.24.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos tweedie_regressor_float.onnx e tweedie_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| TweedieRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "TweedieRegressor" #define ONNXFilenameFloat "tweedie_regressor_float.onnx" #define ONNXFilenameDouble "tweedie_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
2023.10.31 11:42:20.113 TweedieRegressor (EURUSD,H1) Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368338709323 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423970729788666 2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970681819381653 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) 2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1) Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9962368328117072 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 6.3423978976675608 2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1) MQL5: Mean Squared Error: 49.7970821984087593
Comparação com o modelo original em double no Python:
Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423970729788666 Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx) Python Mean Absolute Error: 6.342397897667562 MQL5: Mean Absolute Error: 6.3423978976675608
Precisão do ONNX float MAE: 6 casas decimais, Precisão do ONNX double MAE: 14 casas decimais.
2.1.24.3. Representação ONNX do tweedie_regressor_float.onnx e tweedie_regressor_double.onnx
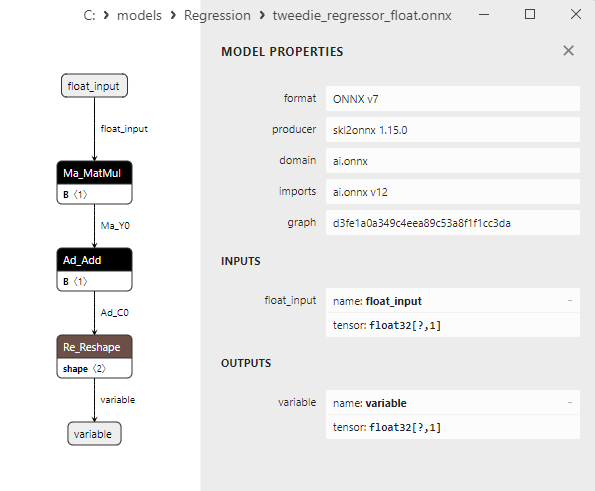
Fig.80. Representação ONNX do tweedie_regressor_float.onnx no Netron
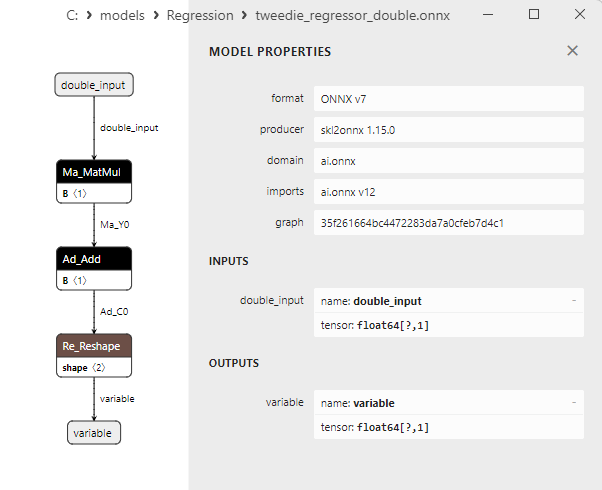
Fig.81. Representação ONNX do tweedie_regressor_double.onnx no Netron
2.1.25. sklearn.linear_model.PoissonRegressor
PoissonRegressor é um método de aprendizado de máquina aplicado para resolver tarefas de regressão com base na distribuição de Poisson.
Este método é adequado quando a variável dependente (variável alvo) é um dado de contagem, representando o número de eventos que ocorreram dentro de um período de tempo fixo ou em um intervalo espacial fixo. O PoissonRegressor modela a relação entre preditores (variáveis independentes) e a variável alvo assumindo que essa relação se conforma à distribuição de Poisson.
Como funciona o PoissonRegressor:
- Dados de entrada: Começando com um conjunto de dados que inclui características (variáveis independentes) e a variável alvo, representando a contagem de eventos.
- Distribuição de Poisson: O método PoissonRegressor modela a variável alvo assumindo que ela segue a distribuição de Poisson. A distribuição de Poisson é adequada para modelar eventos que ocorrem a uma intensidade média fixa dentro de um intervalo de tempo ou espaço determinado.
- Treinamento do modelo: O PoissonRegressor treina um modelo que estima os parâmetros da distribuição de Poisson, considerando os preditores. O modelo tenta encontrar o melhor ajuste para os dados observados usando a função de verossimilhança correspondente à distribuição de Poisson.
- Previsão de valores de contagem: Após o treinamento, o modelo pode ser usado para prever valores de contagem (o número de eventos) em novos dados, e essas previsões também seguem a distribuição de Poisson.
Vantagens do PoissonRegressor:
- Adequado para dados de contagem: O PoissonRegressor é adequado para tarefas onde a variável alvo representa dados de contagem, como o número de pedidos, chamadas, etc.
- Especificidade da distribuição: Como o modelo segue a distribuição de Poisson, ele pode ser mais preciso para dados bem descritos por essa distribuição.
Limitações do PoissonRegressor:
- Apenas adequado para dados de contagem: O PoissonRegressor não é adequado para regressão onde a variável alvo é contínua e não é de contagem.
- Dependência da seleção de características: A qualidade do modelo pode depender muito da seleção e engenharia das características.
O PoissonRegressor é um método de aprendizado de máquina usado para resolver tarefas de regressão quando a variável alvo representa dados de contagem e é modelada usando a distribuição de Poisson. Este método é benéfico para tarefas relacionadas a eventos que ocorrem a uma intensidade fixa dentro de intervalos de tempo ou espaço específicos.
2.1.25.1. Código para criar o modelo PoissonRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.PoissonRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# PoissonRegressor.py
# The code demonstrates the process of training PoissonRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"
# create a PoissonRegressor model
regression_model = PoissonRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training PoissonRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"
# create a PoissonRegressor model
regression_model = PoissonRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python PoissonRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python Python PoissonRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204305082536851 Python Mean Absolute Error: 27.59790825165078 Python Mean Squared Error: 1052.9238598018305 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 5 Python MSE matching decimal places: 2 Python float ONNX model precision: 5 Python Python PoissonRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9204304782362495 Python Mean Absolute Error: 27.59790466048524 Python Mean Squared Error: 1052.9242570153044 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
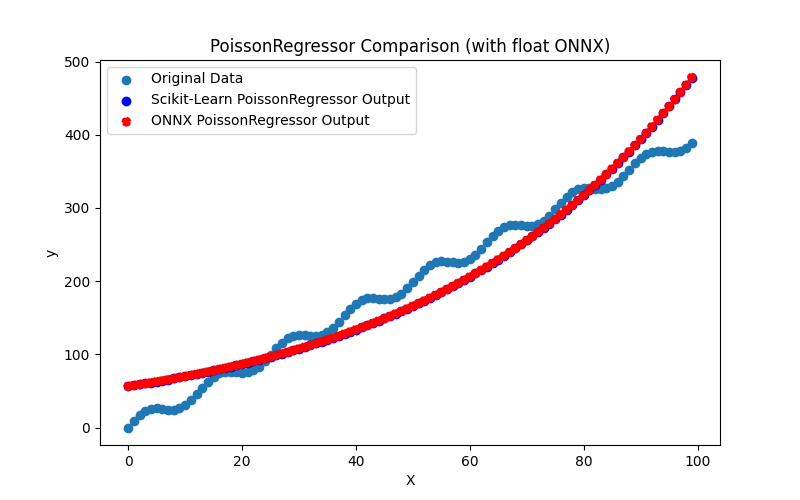
Fig.82. Resultados do PoissonRegressor.py (float ONNX)
2.1.25.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos poisson_regressor_float.onnx e poisson_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| PoissonRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "PoissonRegressor" #define ONNXFilenameFloat "poisson_regressor_float.onnx" #define ONNXFilenameDouble "poisson_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
PoissonRegressor (EURUSD,H1) Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204305082536851 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979082516507788 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9238598018305311 PoissonRegressor (EURUSD,H1) PoissonRegressor (EURUSD,H1) Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) PoissonRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9204304782362493 PoissonRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 27.5979046604852343 PoissonRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1052.9242570153051020
Comparação com o modelo original em double no Python:
Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979082516507788 Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx) Python Mean Absolute Error: 27.59790466048524 MQL5: Mean Absolute Error: 27.5979046604852343
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.25.3. Representação ONNX do poisson_regressor_float.onnx e poisson_regressor_double.onnx
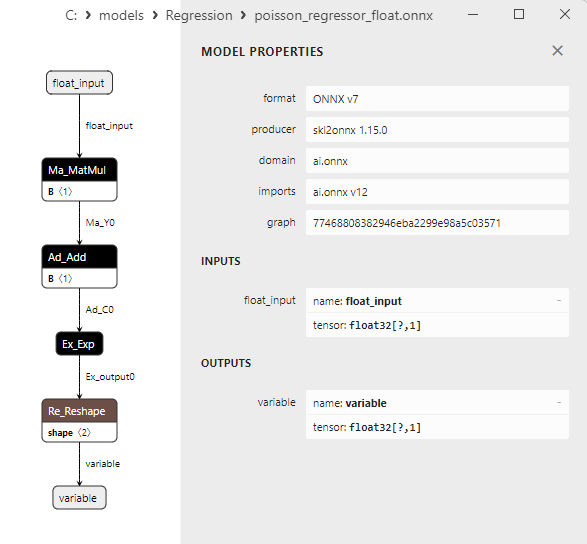
Fig.83. Representação ONNX do poisson_regressor_float.onnx no Netron
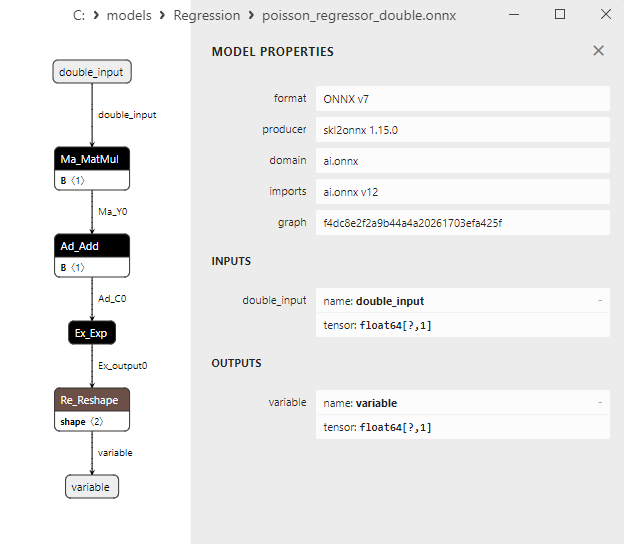
Fig.84. Representação ONNX do poisson_regressor_double.onnx no Netron
2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
RadiusNeighborsRegressor é um método de aprendizado de máquina usado para tarefas de regressão. É uma variante do método k-Nearest Neighbors (k-NN) projetada para prever valores da variável alvo com base nos vizinhos mais próximos no espaço das características. No entanto, em vez de um número fixo de vizinhos (como no método k-NN), o RadiusNeighborsRegressor usa um raio fixo para determinar os vizinhos para cada amostra.Como funciona o RadiusNeighborsRegressor:
- Dados de entrada: Começa com um conjunto de dados que inclui características (variáveis independentes) e a variável alvo (contínua).
- Configuração do raio: O RadiusNeighborsRegressor requer a configuração de um raio fixo para determinar os vizinhos mais próximos para cada amostra no espaço das características.
- Definição de vizinhos: Para cada amostra, todos os pontos de dados dentro do raio especificado são determinados, tornando-se vizinhos dessa amostra.
- Média ponderada: Para prever o valor da variável alvo para cada amostra, são usados os valores das variáveis alvo de seus vizinhos. Isso é frequentemente feito usando média ponderada, onde os pesos dependem da distância entre as amostras.
- Previsão: Após o treinamento, o modelo pode ser usado para prever os valores da variável alvo em novos dados com base nos vizinhos mais próximos no espaço das características.
- Versatilidade: O RadiusNeighborsRegressor pode ser usado para tarefas de regressão, particularmente quando o número de vizinhos pode variar significativamente dependendo do raio.
- Resiliência a outliers: Uma abordagem baseada em vizinhos pode ser resiliente a outliers porque o modelo considera apenas pontos de dados próximos.
- Dependência da seleção do raio: Escolher o raio certo pode exigir ajuste e experimentação.
- Complexidade computacional: Lidar com grandes conjuntos de dados pode exigir recursos computacionais substanciais.
2.1.26.1. Código para criar o modelo RadiusNeighborsRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.neighbors.RadiusNeighborsRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# RadiusNeighborsRegressor.py
# The code demonstrates the process of training RadiusNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"
# create a RadiusNeighborsRegressor model
regression_model = RadiusNeighborsRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training RadiusNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"
# create a RadiusNeighborsRegressor model
regression_model = RadiusNeighborsRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python RadiusNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999521132921395 Python Mean Absolute Error: 0.591458244376554 Python Mean Squared Error: 0.6336732353950723 Python Python RadiusNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 4 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python RadiusNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python double ONNX model precision: 0
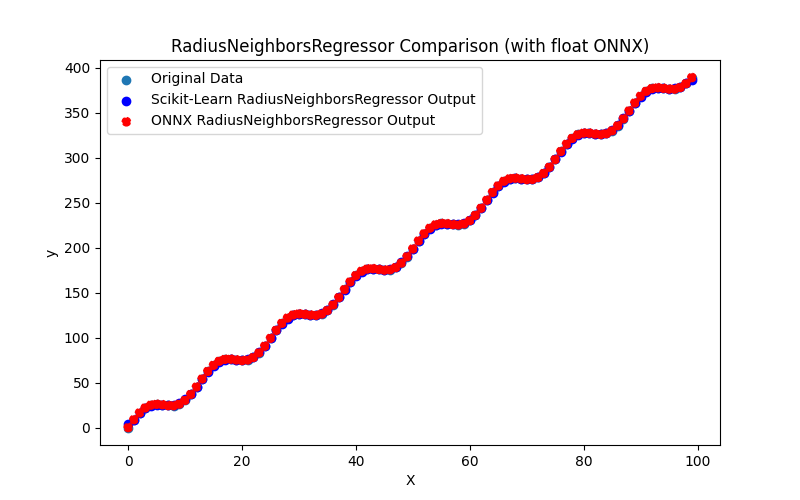
Fig.85. Resultados do RadiusNeighborsRegressor.py (float ONNX)
2.1.26.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| RadiusNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RadiusNeighborsRegressor" #define ONNXFilenameFloat "radius_neighbors_regressor_float.onnx" #define ONNXFilenameDouble "radius_neighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX float: RadiusNeighborsRegressor (radius_neighbors_regressor_float.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 RadiusNeighborsRegressor (EURUSD,H1) RadiusNeighborsRegressor (EURUSD,H1) Testing ONNX double: RadiusNeighborsRegressor (radius_neighbors_regressor_double.onnx) RadiusNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000000000 RadiusNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.26.3. Representação ONNX do radius_neighbors_regressor_float.onnx e radius_neighbors_regressor_double.onnx
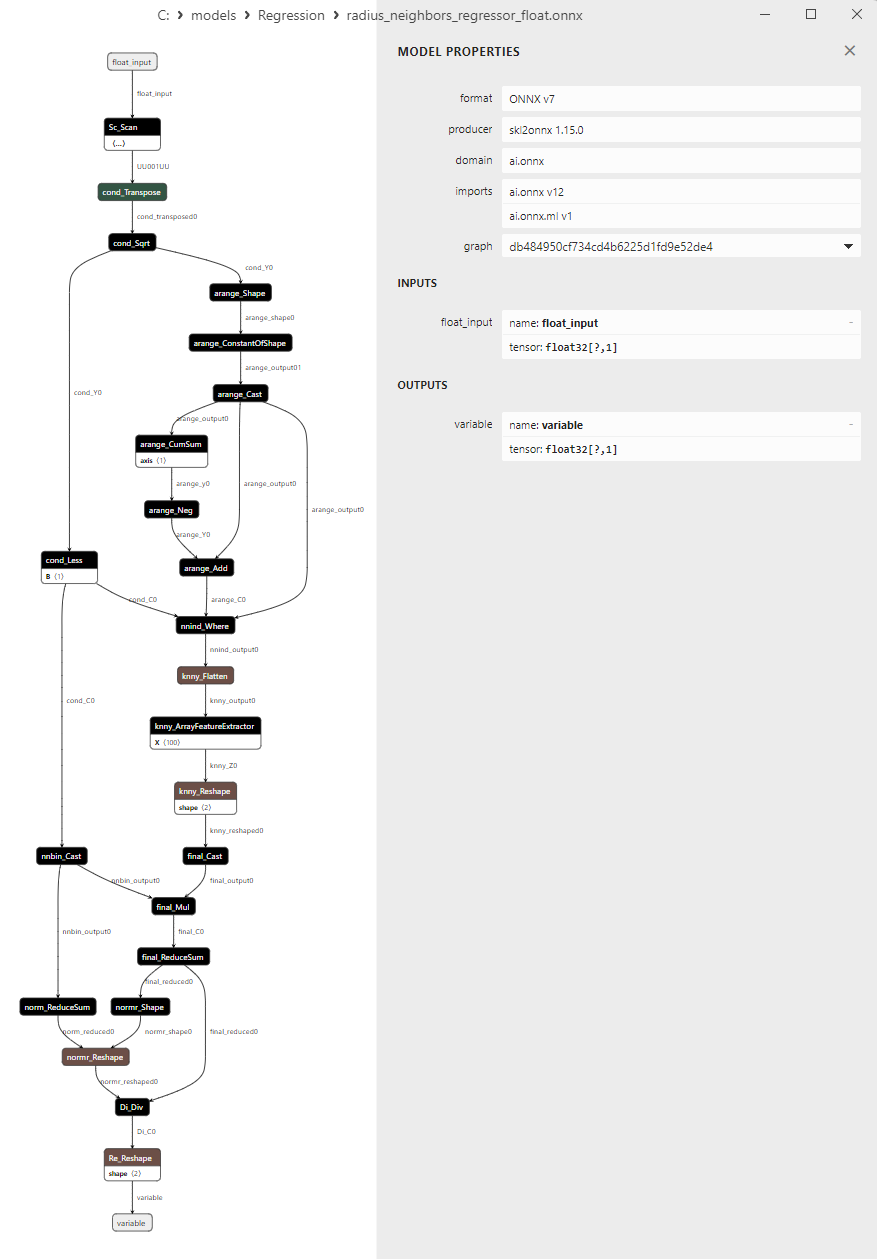
Fig.86. Representação ONNX do radius_neighbors_regressor_float.onnx no Netron
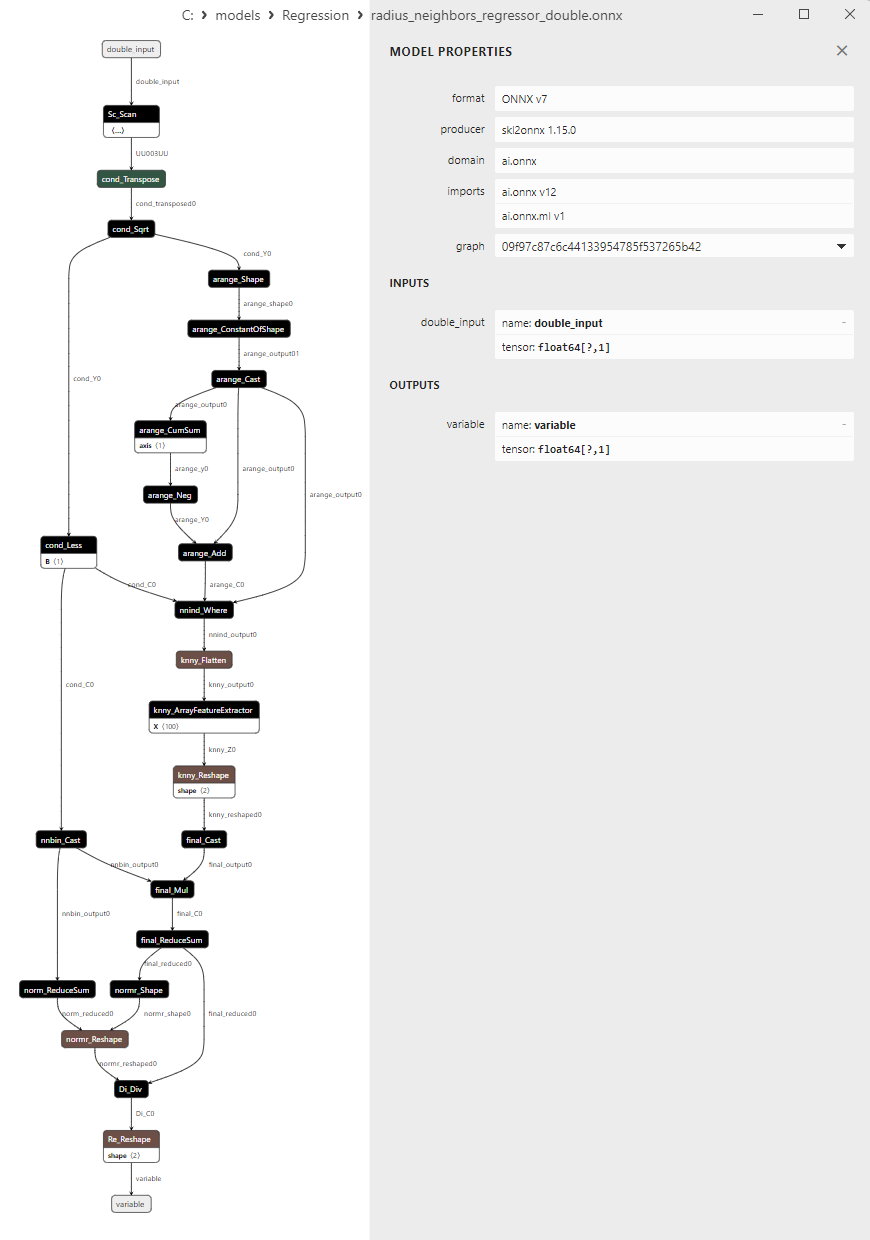
Fig.87. Representação ONNX do radius_neighbors_regressor_double.onnx no Netron
2.1.27. sklearn.neighbors.KNeighborsRegressor
KNeighborsRegressor é um método de aprendizado de máquina usado para tarefas de regressão.
Pertence à categoria de algoritmos k-Nearest Neighbors (k-NN) e é usado para prever valores numéricos da variável alvo com base na proximidade (similaridade) entre objetos no conjunto de dados de treinamento.
Como funciona o KNeighborsRegressor:
- Dados de entrada: Começa com o conjunto de dados inicial, incluindo características (variáveis independentes) e valores correspondentes da variável alvo.
- Selecionando o número de vizinhos (k): É necessário escolher o número de vizinhos mais próximos (k) a serem considerados durante a previsão. Esse número é um dos hiperparâmetros do modelo.
- Calculando a proximidade: Para novos dados (pontos para os quais são necessárias previsões), a distância ou similaridade entre esses dados e todos os objetos no conjunto de dados de treinamento é calculada.
- Escolhendo k vizinhos mais próximos: São selecionados k objetos do conjunto de dados de treinamento que estão mais próximos dos novos dados.
- Previsão: Para tarefas de regressão, a previsão do valor da variável alvo para novos dados é calculada como a média dos valores das variáveis alvo dos k vizinhos mais próximos.
Vantagens do KNeighborsRegressor:
- Facilidade de uso: KNeighborsRegressor é um algoritmo simples que não requer pré-processamento complexo dos dados.
- Natureza não paramétrica: O método não assume uma forma funcional específica de dependência entre características e a variável alvo, permitindo modelar relações diversas.
- Reprodutibilidade: Os resultados do KNeighborsRegressor podem ser reproduzidos, pois as previsões são baseadas na proximidade dos dados.
Limitações do KNeighborsRegressor:
- Complexidade computacional: Calcular distâncias para todos os pontos no conjunto de dados de treinamento pode ser computacionalmente caro para grandes volumes de dados.
- Sensibilidade à escolha do número de vizinhos: Selecionar o valor ótimo de k requer ajuste e pode impactar significativamente o desempenho do modelo.
- Sensibilidade ao ruído: O método pode ser sensível ao ruído nos dados e a outliers.
KNeighborsRegressor é útil em tarefas de regressão onde considerar a vizinhança de objetos para prever a variável alvo é essencial. Pode ser particularmente útil em situações onde a relação entre características e a variável alvo é não linear e complexa.
2.1.27.1. Código para criar o modelo KNeighborsRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.neighbors.KNeighborsRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada tanto em float quanto em double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# KNeighborsRegressor.py
# The code demonstrates the process of training KNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"
# create a KNeighbors Regressor model
kneighbors_model = KNeighborsRegressor(n_neighbors=5)
# fit the model to the data
kneighbors_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = kneighbors_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training KNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"
# create a KNeighbors Regressor model
kneighbors_model = KNeighborsRegressor(n_neighbors=5)
# fit the model to the data
kneighbors_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = kneighbors_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python KNeighborsRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117578 Python Mean Squared Error: 5.822594523532273 Python Python KNeighborsRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599867417418 Python Mean Absolute Error: 1.7414195457976402 Python Mean Squared Error: 5.8225891366283875 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 4 Python MSE matching decimal places: 4 Python float ONNX model precision: 4 Python Python KNeighborsRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9995599863346534 Python Mean Absolute Error: 1.7414210057117583 Python Mean Squared Error: 5.822594523532269 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 14 Python MSE matching decimal places: 13 Python double ONNX model precision: 14
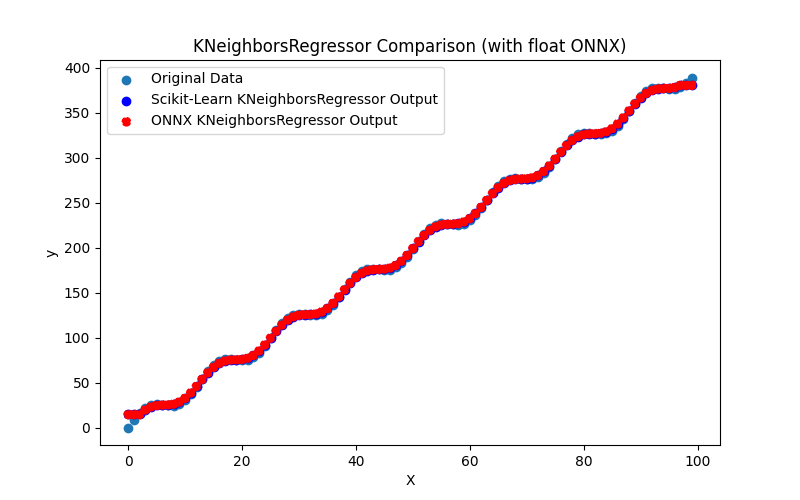
Fig.88. Resultados do KNeighborsRegressor.py (float ONNX)
2.1.27.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx e demonstra o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| KNeighborsRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "KNeighborsRegressor" #define ONNXFilenameFloat "kneighbors_regressor_float.onnx" #define ONNXFilenameDouble "kneighbors_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
KNeighborsRegressor (EURUSD,H1) Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599860116634 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414200607817711 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225987975798184 KNeighborsRegressor (EURUSD,H1) KNeighborsRegressor (EURUSD,H1) Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) KNeighborsRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9995599863346534 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.7414210057117601 KNeighborsRegressor (EURUSD,H1) MQL5: Mean Squared Error: 5.8225945235322705
Comparação com o modelo original em double no Python:
Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414200607817711 Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx) Python Mean Absolute Error: 1.7414210057117578 MQL5: Mean Absolute Error: 1.7414210057117601
Precisão do ONNX float MAE: 5 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.27.3. Representação ONNX do kneighbors_regressor_float.onnx e kneighbors_regressor_double.onnx
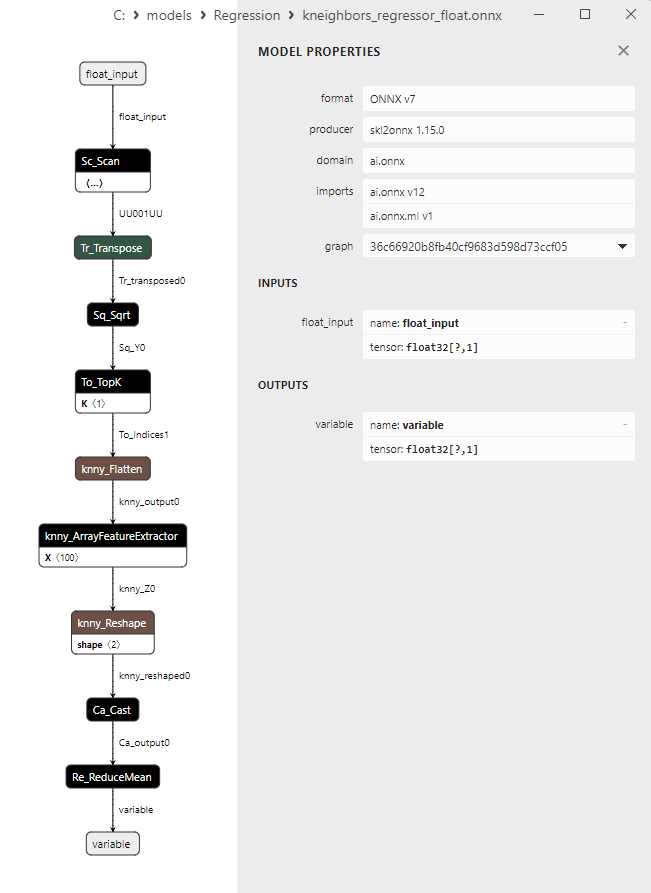
Fig.89. Representação ONNX do kneighbors_regressor_float.onnx no Netron
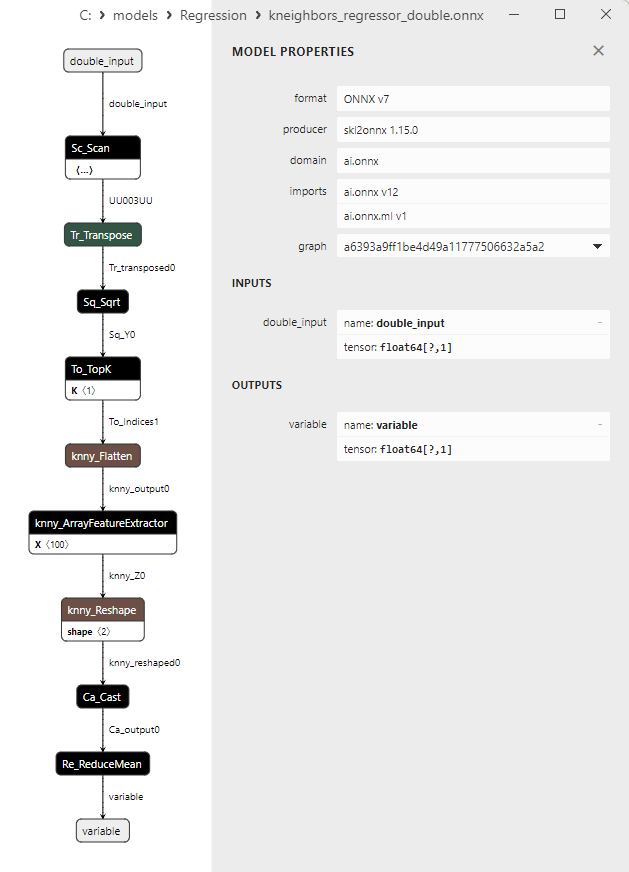
Fig.90. Representação ONNX do kneighbors_regressor_double.onnx no Netron
2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
GaussianProcessRegressor é um método de aprendizado de máquina usado para tarefas de regressão que permite modelar a incerteza nas previsões.
O Processo Gaussiano (GP) é uma ferramenta poderosa no aprendizado de máquina Bayesiano e é usado para modelar funções complexas e prever valores da variável alvo, considerando a incerteza.
Como funciona o GaussianProcessRegressor:
- Dados de entrada: Começa com o conjunto de dados inicial, incluindo características (variáveis independentes) e valores correspondentes da variável alvo.
- Modelando o processo Gaussiano: O Processo Gaussiano emprega um processo gaussiano, que é uma coleção de variáveis aleatórias descritas por uma distribuição Gaussiana (normal). O GP modela não apenas os valores médios para cada ponto de dados, mas também a covariância (ou similaridade) entre esses pontos.
- Escolhendo a função de covariância: Um aspecto crucial do GP é a seleção da função de covariância (ou kernel) que determina a interconexão e a força entre os pontos de dados. Diferentes funções de covariância podem ser usadas com base na natureza dos dados e da tarefa.
- Treinamento do modelo: O GaussianProcessRegressor treina o GP usando os dados de treinamento. Durante o treinamento, o modelo ajusta os parâmetros da função de covariância e avalia a incerteza nas previsões.
- Previsão: Após o treinamento, o modelo pode ser usado para prever valores da variável alvo para novos dados. Uma característica importante do GP é que ele prevê não apenas o valor médio, mas também um intervalo de confiança que estima o nível de confiança nas previsões.
Vantagens do GaussianProcessRegressor:
- Modelagem da incerteza: O GP permite considerar a incerteza nas previsões, o que é benéfico em tarefas onde saber a confiança nos valores previstos é crucial.
- Flexibilidade: O GP pode modelar várias funções, e suas funções de covariância podem ser adaptadas para diferentes tipos de dados.
- Poucos hiperparâmetros: O GP possui um número relativamente pequeno de hiperparâmetros, simplificando a configuração do modelo.
Limitações do GaussianProcessRegressor:
- Complexidade computacional: O GP pode ser computacionalmente caro, especialmente com um grande volume de dados.
- Ineficácia em espaços de alta dimensão: O GP pode perder eficiência em tarefas com muitas características devido à maldição da dimensionalidade.
O GaussianProcessRegressor é útil em tarefas de regressão onde modelar a incerteza e fornecer previsões confiáveis são cruciais. Este método é frequentemente usado em aprendizado de máquina Bayesiano e meta-análise.
2.1.28.1. Código para criar o modelo GaussianProcessRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.gaussian_process.GaussianProcessRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# GaussianProcessRegressor.py
# The code demonstrates the process of training GaussianProcessRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"
# create a GaussianProcessRegressor model
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# fit the model to the data
gp_model.fit(X, y)
# predict values for the entire dataset
y_pred = gp_model.predict(X, return_std=False)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training GaussianProcessRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"
# create a GaussianProcessRegressor model
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)
# fit the model to the data
gp_model.fit(X, y)
# predict values for the entire dataset
y_pred = gp_model.predict(X, return_std=False)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python GaussianProcessRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python Python GaussianProcessRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999936 Python Mean Absolute Error: 6.454076974495848e-06 Python Mean Squared Error: 8.493606782250733e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python GaussianProcessRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: GPmean, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 1.0 Python Mean Absolute Error: 3.504041501400934e-13 Python Mean Squared Error: 1.6396606443650807e-25 Python R^2 matching decimal places: 1 Python MAE matching decimal places: 19 Python MSE matching decimal places: 20 Python double ONNX model precision: 19
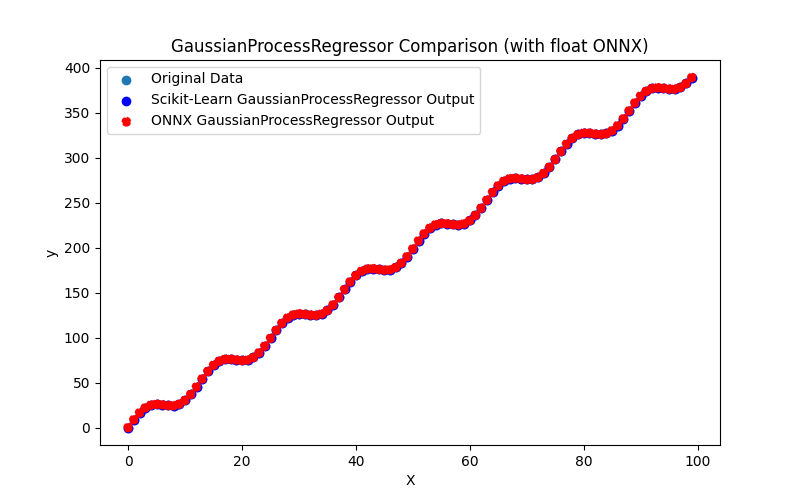
Fig.91. Resultados do GaussianProcessRegressor.py (float ONNX)
2.1.28.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx e demonstra o uso de métricas de regressão no MQL5.
//+------------------------------------------------------------------+ //| GaussianProcessRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GaussianProcessRegressor" #define ONNXFilenameFloat "gaussian_process_regressor_float.onnx" #define ONNXFilenameDouble "gaussian_process_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
GaussianProcessRegressor (EURUSD,H1) Testing ONNX float: GaussianProcessRegressor (gaussian_process_regressor_float.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999936 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000064540769745 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000849361 GaussianProcessRegressor (EURUSD,H1) GaussianProcessRegressor (EURUSD,H1) Testing ONNX double: GaussianProcessRegressor (gaussian_process_regressor_double.onnx) GaussianProcessRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 1.0000000000000000 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000000000003504 GaussianProcessRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000000000
2.1.28.3. Representação ONNX do gaussian_process_regressor_float.onnx e gaussian_process_regressor_double.onnx
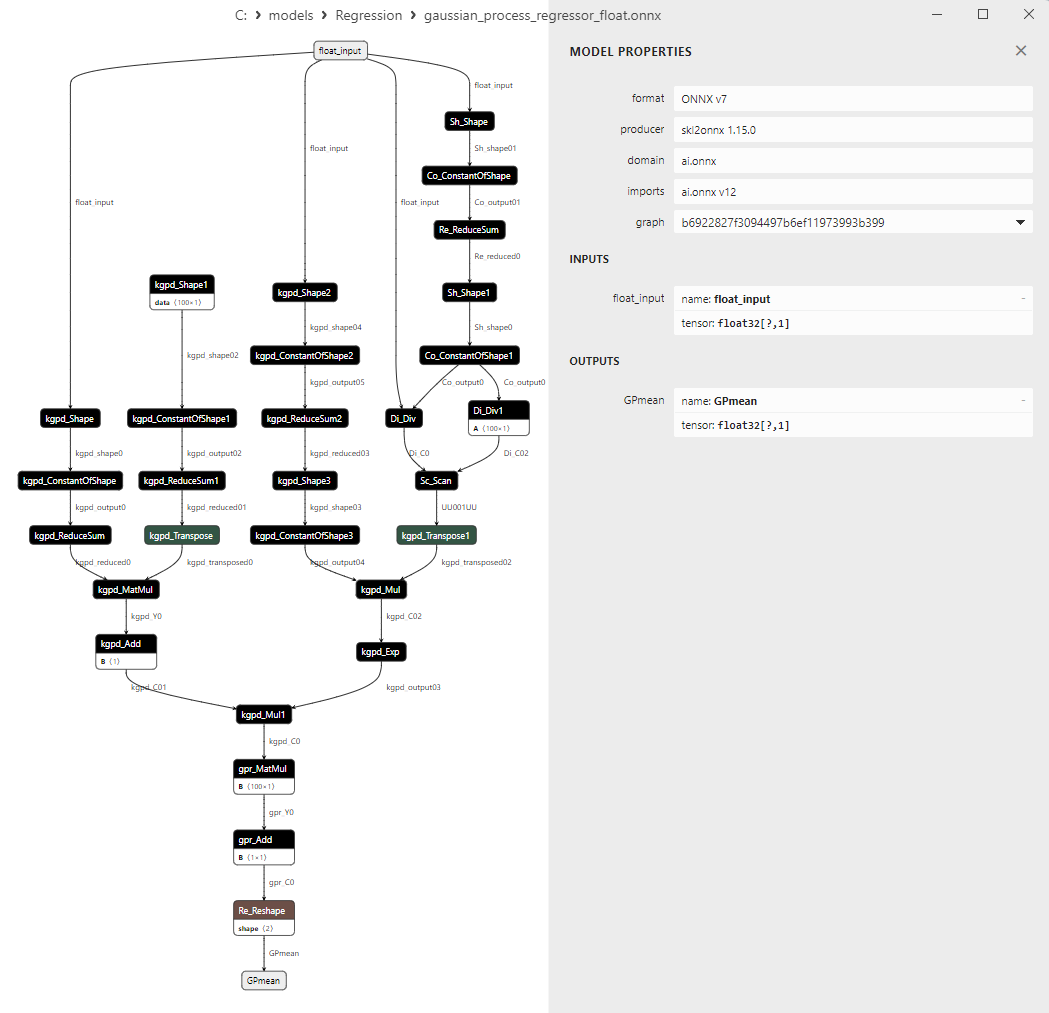
Fig.92. Representação ONNX do gaussian_process_regressor_float.onnx no Netron
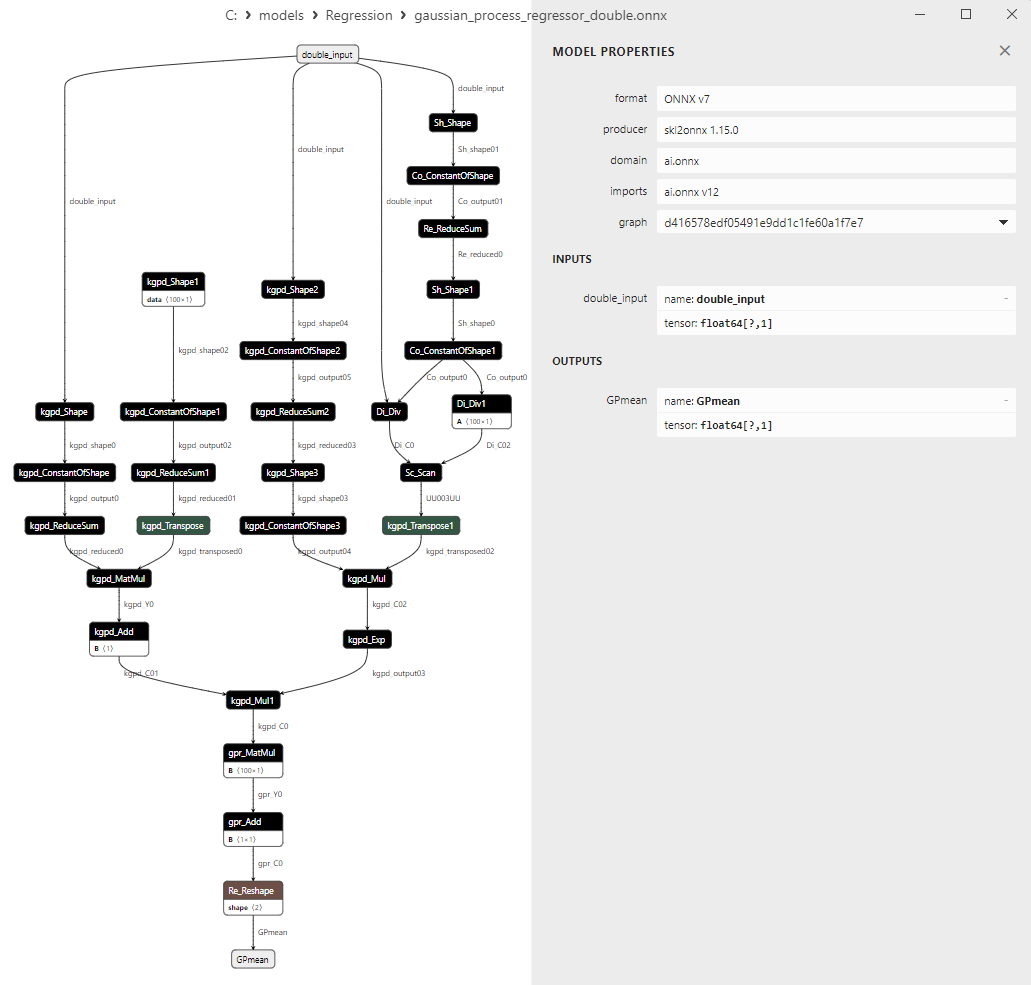
Fig.93. Representação ONNX do gaussian_process_regressor_double.onnx no Netron
2.1.29. sklearn.linear_model.GammaRegressor
GammaRegressor é um método de aprendizado de máquina projetado para tarefas de regressão onde a variável alvo segue uma distribuição gama.
A distribuição gama é uma distribuição de probabilidade usada para modelar variáveis aleatórias contínuas e positivas. Este método permite modelar e prever valores numéricos positivos, como custo, tempo ou proporções.
Como o GammaRegressor funciona:
- Dados de entrada: Começa com o conjunto de dados inicial, onde há características (variáveis independentes) e valores correspondentes da variável alvo seguindo a distribuição gama.
- Seleção da função de perda: O GammaRegressor utiliza uma função de perda que corresponde à distribuição gama e considera as peculiaridades dessa distribuição. Isso permite modelar os dados enquanto considera a não negatividade e a assimetria à direita da distribuição gama.
- Treinamento do modelo: O modelo é treinado nos dados usando a função de perda escolhida. Durante o treinamento, ajusta os parâmetros do modelo para minimizar a função de perda.
- Previsão: Após o treinamento, o modelo pode ser usado para prever os valores da variável alvo para novos dados.
Vantagens do GammaRegressor:
- Modelagem de valores positivos: Este método é especificamente projetado para modelar valores numéricos positivos, o que pode ser útil em tarefas onde a variável alvo é limitada inferiormente.
- Considerando a forma da distribuição gama: O GammaRegressor leva em conta as características da distribuição gama, permitindo uma modelagem mais precisa dos dados que seguem essa distribuição.
- Utilidade em econometria e pesquisa médica: A distribuição gama é frequentemente usada para modelar custos, tempo de espera e outras variáveis aleatórias positivas em econometria e pesquisa médica.
Limitações do GammaRegressor:
- Limitação no tipo de dados: Este método é adequado apenas para tarefas de regressão onde a variável alvo segue a distribuição gama ou distribuições similares. Para dados que não se conformam a tal distribuição, este método pode não ser eficaz.
- Requer a escolha de uma função de perda: Escolher uma função de perda apropriada pode exigir conhecimento sobre a distribuição da variável alvo e suas características.
GammaRegressor é útil em tarefas onde é necessário modelar e prever valores numéricos positivos que se alinham com a distribuição gama.
2.1.29.1. Código para criar o modelo GammaRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.GammaRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# GammaRegressor.py
# The code demonstrates the process of training GammaRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)
model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"
# create a Gamma Regressor model
regression_model = GammaRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training GammaRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)
model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"
# create a Gamma Regressor model
regression_model = GammaRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python GammaRegressor Original model (double) Python R-squared (Coefficient of determination): 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python Python GammaRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963795030042045 Python Mean Absolute Error: 37.266211754095956 Python Mean Squared Error: 2694.4608407846144 Python R^2 matching decimal places: 6 Python MAE matching decimal places: 4 Python MSE matching decimal places: 1 Python float ONNX model precision: 4 Python Python GammaRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.7963797339354436 Python Mean Absolute Error: 37.266200319422815 Python Mean Squared Error: 2694.457784927322 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 15 Python MSE matching decimal places: 12 Python double ONNX model precision: 15
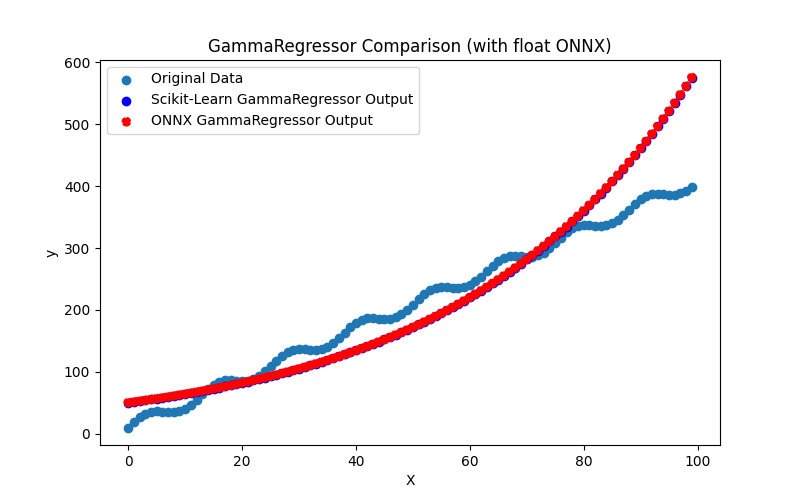
Fig.94. Resultados do GammaRegressor.py (float ONNX)
2.1.29.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos gamma_regressor_float.onnx e gamma_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| GammaRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GammaRegressor" #define ONNXFilenameFloat "gamma_regressor_float.onnx" #define ONNXFilenameDouble "gamma_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(10+4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
GammaRegressor (EURUSD,H1) Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963795030042045 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662117540959628 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4608407846144473 GammaRegressor (EURUSD,H1) GammaRegressor (EURUSD,H1) Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) GammaRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.7963797339354435 GammaRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 37.2662003194228220 GammaRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2694.4577849273218817
Comparação com o modelo original em double no Python:
Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662117540959628 Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx) Python Mean Absolute Error: 37.266200319422815 MQL5: Mean Absolute Error: 37.2662003194228220
Precisão do ONNX float MAE: 4 casas decimais, Precisão do ONNX double MAE: 13 casas decimais.
2.1.29.3. Representação ONNX do gamma_regressor_float.onnx e gamma_regressor_double.onnx
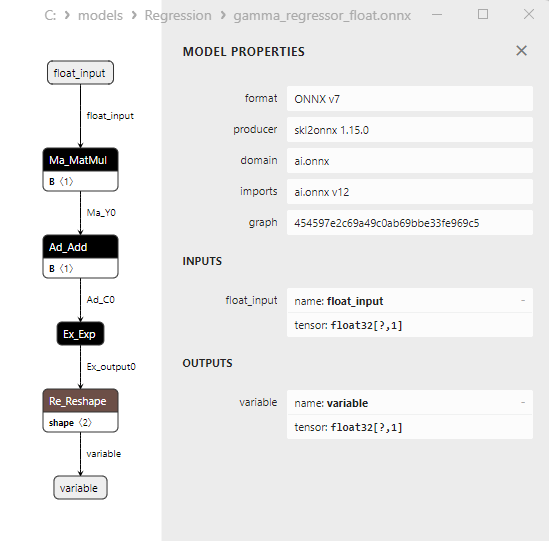
Fig.95. Representação ONNX do gamma_regressor_float.onnx no Netron
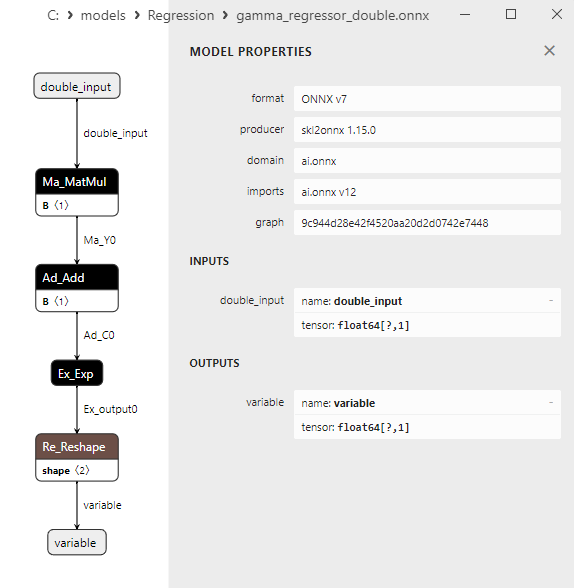
Fig.96. Representação ONNX do gamma_regressor_double.onnx no Netron
2.1.30. sklearn.linear_model.SGDRegressor
SGDRegressor é um método de regressão que utiliza o Gradiente Descendente Estocástico (SGD) para treinar um modelo de regressão. Ele faz parte da família de modelos lineares e pode ser empregado para tarefas de regressão. Os principais atributos do SGDRegressor são sua eficiência e sua capacidade de lidar com grandes volumes de dados.
Como o SGDRegressor funciona:
- Regressão linear: Semelhante ao Ridge e Lasso, o SGDRegressor visa encontrar uma relação linear entre variáveis independentes (características) e a variável alvo em um problema de regressão.
- Gradiente Descendente Estocástico: A base do SGDRegressor é o gradiente descendente estocástico. Em vez de calcular gradientes em todo o conjunto de dados de treinamento, ele atualiza o modelo com base em mini-lotes de dados selecionados aleatoriamente. Isso permite um treinamento eficiente do modelo e o trabalho com conjuntos de dados substanciais.
- Regularização: O SGDRegressor suporta regularização L1 e L2 (Lasso e Ridge). Isso ajuda a controlar o overfitting e a melhorar a estabilidade do modelo.
- Hiperparâmetros: Semelhante ao Ridge e Lasso, o SGDRegressor permite ajustar hiperparâmetros como o parâmetro de regularização (α, alfa) e o tipo de regularização.
Vantagens do SGDRegressor:
- Eficiência: O SGDRegressor tem um bom desempenho com grandes conjuntos de dados e treina modelos de forma eficiente em dados extensos.
- Capacidade de regularização: A opção de aplicar regularização L1 e L2 torna este método adequado para gerenciar problemas de overfitting.
- Gradiente descendente adaptativo: O gradiente descendente estocástico permite adaptação a dados em mudança e a capacidade de treinar modelos em tempo real.
Limitações do SGDRegressor:
- Sensibilidade à escolha de hiperparâmetros: Ajustar hiperparâmetros como a taxa de aprendizado e o coeficiente de regularização pode exigir experimentação.
- Nem sempre convergindo para o mínimo global: Devido à natureza estocástica do gradiente descendente, o SGDRegressor nem sempre converge para o mínimo global da função de perda.
SGDRegressor é um método de regressão que usa o gradiente descendente estocástico para treinar um modelo de regressão. É eficiente, capaz de lidar com grandes conjuntos de dados e suporta regularização para gerenciar o overfitting.
2.1.30.1. Código para criar o modelo SGDRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.SGDRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# SGDRegressor2.py
# The code demonstrates the process of training SGDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)
model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"
# create an SGDRegressor model
regression_model = SGDRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training SGDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)
model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"
# create an SGDRegressor model
regression_model = SGDRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python SGDRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python Python SGDRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197876338647 Python Mean Absolute Error: 0.6405924014799271 Python Mean Squared Error: 0.5169866866963753 Python R^2 matching decimal places: 9 Python MAE matching decimal places: 7 Python MSE matching decimal places: 6 Python float ONNX model precision: 7 Python Python SGDRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_double.onnx Python Information about input tensors in ONNX: Python 1. Name: double_input, Data Type: tensor(double), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(double), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9961197872743282 Python Mean Absolute Error: 0.6405924406136998 Python Mean Squared Error: 0.5169867345998348 Python R^2 matching decimal places: 16 Python MAE matching decimal places: 16 Python MSE matching decimal places: 16 Python double ONNX model precision: 16
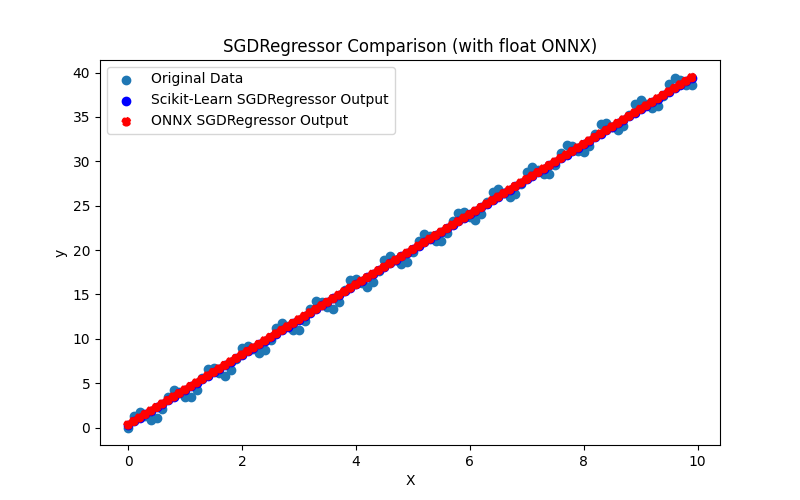
Fig.97. Resultados do SGDRegressor.py (float ONNX)
2.1.30.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos sgd_regressor_float.onnx e sgd_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| SGDRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SGDRegressor" #define ONNXFilenameFloat "sgd_regressor_float.onnx" #define ONNXFilenameDouble "sgd_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i*0.1; y[i]=(double)(4*x[i] + sin(x[i]*10)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
SGDRegressor (EURUSD,H1) Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197876338647 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924014799272 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169866866963754 SGDRegressor (EURUSD,H1) SGDRegressor (EURUSD,H1) Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) SGDRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9961197872743282 SGDRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.6405924406136998 SGDRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.5169867345998348
Comparação com o modelo original em double no Python:
Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924014799272 Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx) Python Mean Absolute Error: 0.6405924406136998 MQL5: Mean Absolute Error: 0.6405924406136998
Precisão do ONNX float MAE: 7 casas decimais, Precisão do ONNX double MAE: 16 casas decimais.
2.1.30.3. Representação ONNX do sgd_rgressor_float.onnx e sgd_regressor_double.onnx
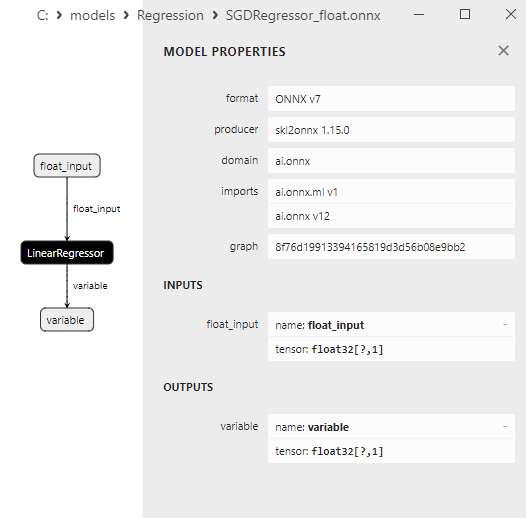
Fig.98. Representação ONNX do sgd_regressor_float.onnx no Netron
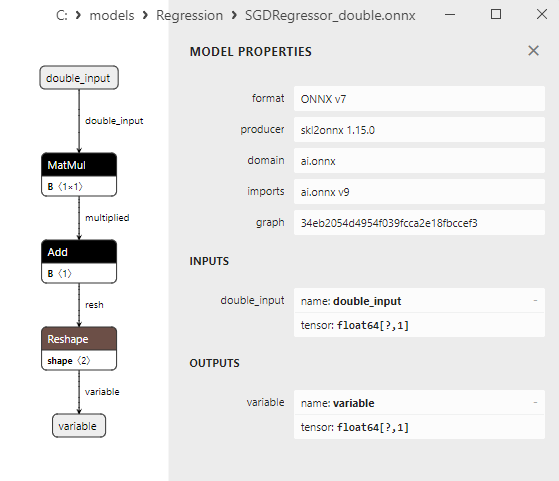
Fig.99. Representação ONNX do sgd_regressor_double.onnx no Netron
2.2. Modelos de regressão da biblioteca Scikit-learn que são convertidos apenas em modelos ONNX de precisão float
Esta seção cobre modelos que só podem funcionar com precisão em float. Convertê-los para ONNX com precisão em double leva a erros relacionados às limitações do subconjunto ai.onnx.ml de operadores ONNX.
2.2.1. sklearn.linear_model.AdaBoostRegressor
AdaBoostRegressor é um método de aprendizado de máquina usado para regressão, que envolve a previsão de valores numéricos (por exemplo, preços de imóveis, volumes de vendas, etc.).
Este método é uma variação do algoritmo AdaBoost (Adaptive Boosting), inicialmente desenvolvido para tarefas de classificação.
Como o AdaBoostRegressor funciona:
- Conjunto de dados original: Começa com o conjunto de dados original contendo características (variáveis independentes) e suas respectivas variáveis alvo (variáveis dependentes que desejamos prever).
- Inicialização de pesos: Inicialmente, cada ponto de dados (observação) tem pesos iguais, e o modelo é construído com base nesse conjunto de dados ponderado.
- Treinamento de aprendizes fracos: O AdaBoostRegressor constrói vários modelos de regressão fracos (por exemplo, árvores de decisão) que tentam prever a variável alvo. Esses modelos são chamados de "aprendizes fracos". Cada aprendiz fraco é treinado nos dados considerando os pesos de cada observação.
- Seleção de pesos dos aprendizes fracos: O AdaBoostRegressor calcula os pesos para cada aprendiz fraco com base no desempenho de suas previsões. Aprendizes que fazem previsões mais precisas recebem pesos maiores, e vice-versa.
- Atualização dos pesos das observações: Os pesos das observações são atualizados para que observações anteriormente previstas incorretamente recebam pesos maiores, aumentando assim sua importância para o próximo modelo.
- Previsão final: O AdaBoostRegressor combina as previsões de todos os aprendizes fracos, atribuindo pesos com base no desempenho deles. Isso resulta na previsão final do modelo.
Vantagens do AdaBoostRegressor:
- Adaptabilidade: O AdaBoostRegressor se adapta a funções complexas e lida melhor com relações não lineares.
- Redução de overfitting: O AdaBoostRegressor usa regularização através da atualização dos pesos das observações, ajudando a prevenir o overfitting.
- Conjunto poderoso: Ao combinar múltiplos modelos fracos, o AdaBoostRegressor pode criar modelos fortes que podem prever a variável alvo de forma bastante precisa.
Limitações do AdaBoostRegressor:
- Sensibilidade a outliers: O AdaBoostRegressor é sensível a outliers nos dados, afetando a qualidade da previsão.
- Altos custos computacionais: Construir múltiplos aprendizes fracos pode exigir mais recursos computacionais e tempo.
- Nem sempre é a melhor escolha: O AdaBoostRegressor nem sempre é a escolha ideal, e em alguns casos, outros métodos de regressão podem ter um desempenho melhor.
O AdaBoostRegressor é um método útil de aprendizado de máquina aplicável a várias tarefas de regressão, especialmente em situações onde os dados contêm dependências complexas.
2.2.1.1. Código para criar o modelo AdaBoostRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.AdaBoostRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# AdaBoostRegressor.py
# The code demonstrates the process of training AdaBoostRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"
# create an AdaBoostRegressor model
regression_model = AdaBoostRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training AdaBoostRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"
# create an AdaBoostRegressor model
regression_model = AdaBoostRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python AdaBoostRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9991257208809748 Python Mean Absolute Error: 2.3678022748065457 Python Mean Squared Error: 11.569124350863143 Python Python AdaBoostRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9991257199849699 Python Mean Absolute Error: 2.36780399225718 Python Mean Squared Error: 11.569136207480646 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python AdaBoostRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx
Aqui, o modelo foi exportado para modelos ONNX para float e double. O modelo ONNX float foi executado com sucesso, enquanto houve um erro de execução com o modelo double (erros na aba Erros):
AdaBoostRegressor.py started AdaBoostRegressor.py 1 1 Traceback (most recent call last): AdaBoostRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) AdaBoostRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx failed:Type Error: onnxruntime_inference_collection.py 424 1 AdaBoostRegressor.py finished in 3207 ms 5 1
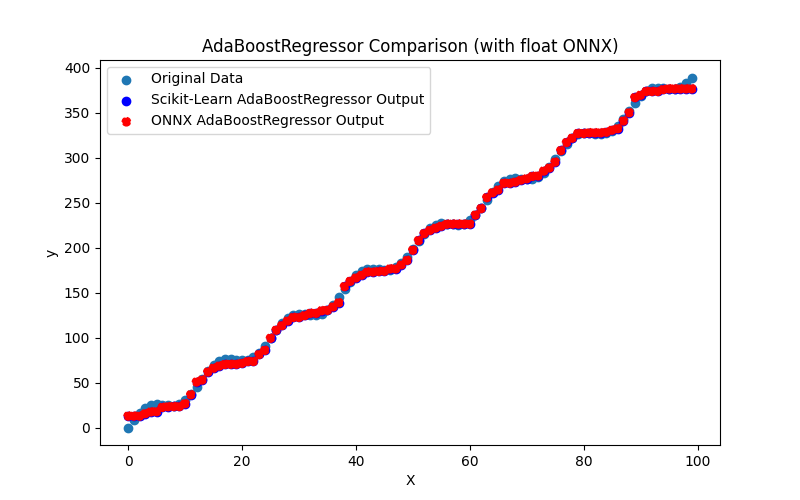
Fig.100. Resultados do AdaBoostRegressor.py (float ONNX)
2.2.1.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos adaboost_regressor_float.onnx e adaboost_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| AdaBoostRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "AdaBoostRegressor" #define ONNXFilenameFloat "adaboost_regressor_float.onnx" #define ONNXFilenameDouble "adaboost_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX float: AdaBoostRegressor (adaboost_regressor_float.onnx) AdaBoostRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9991257199849699 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 2.3678039922571803 AdaBoostRegressor (EURUSD,H1) MQL5: Mean Squared Error: 11.5691362074806463 AdaBoostRegressor (EURUSD,H1) AdaBoostRegressor (EURUSD,H1) Testing ONNX double: AdaBoostRegressor (adaboost_regressor_double.onnx) AdaBoostRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type parameter (T) of Optype (Mul) bound to different types (tensor(float) and tensor(double) in node (Mul).'), inspect code 'Scripts\Regression\AdaBoostRegressor.mq5' (133:16) AdaBoostRegressor (EURUSD,H1) model_name=AdaBoostRegressor OnnxCreate error 5800O modelo ONNX float foi executado com sucesso, enquanto houve um erro de execução com o modelo double.
2.2.1.3. Representação ONNX do adaboost_regressor_float.onnx e adaboost_regressor_double.onnx
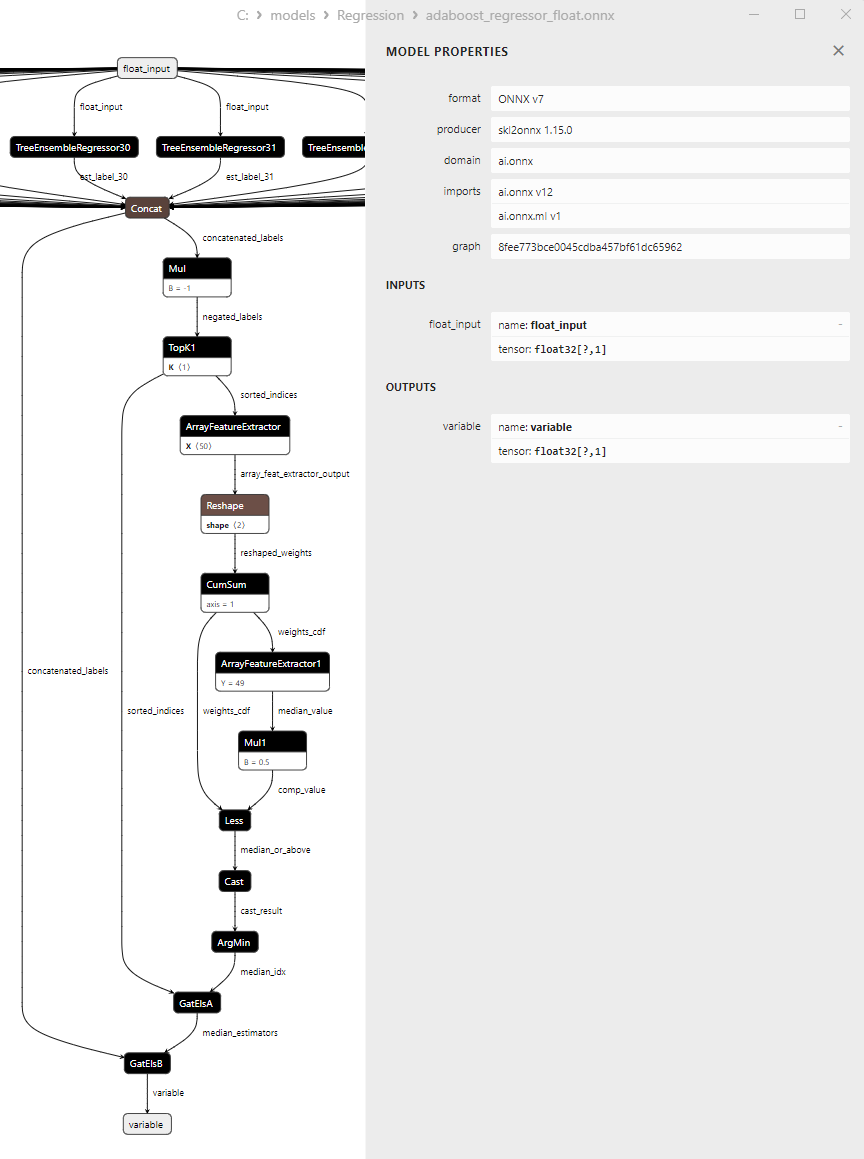
Fig.101. Representação ONNX do adaboost_regressor_float.onnx no Netron
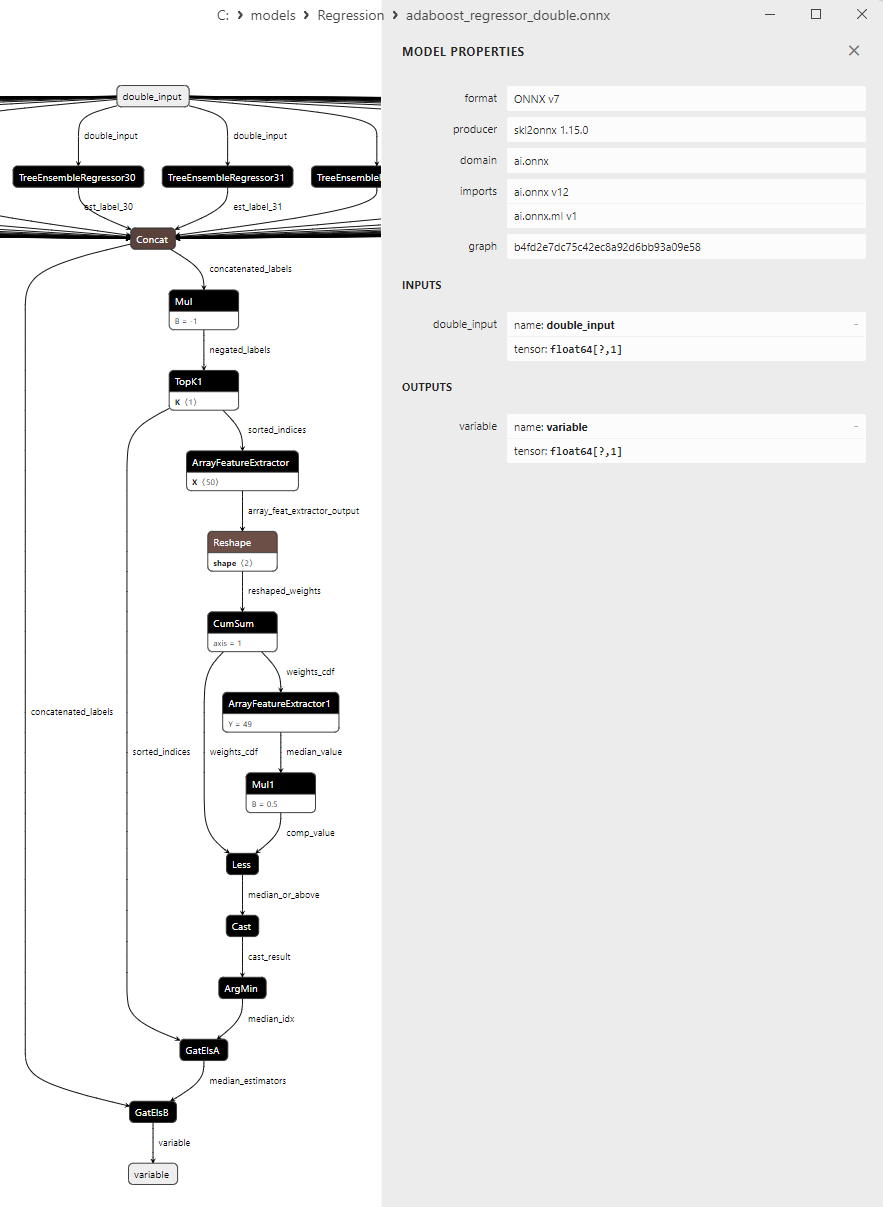
Fig.102. Representação ONNX do adaboost_regressor_double.onnx no Netron
2.2.2. sklearn.linear_model.BaggingRegressor
BaggingRegressor é um método de aprendizado de máquina usado para tarefas de regressão.
Representa um método de conjunto baseado na ideia de "bagging" (Bootstrap Aggregating), que envolve a construção de múltiplos modelos de regressão base e a combinação de suas previsões para obter um resultado mais estável e preciso.
Como o BaggingRegressor funciona:
- Conjunto de dados original: Começa com o conjunto de dados original contendo características (variáveis independentes) e suas respectivas variáveis alvo (variáveis dependentes que desejamos prever).
- Geração de subconjuntos: O BaggingRegressor cria aleatoriamente vários subconjuntos (amostras com reposição) dos dados originais. Cada subconjunto contém um conjunto aleatório de observações dos dados originais.
- Treinamento de modelos de regressão base: Para cada subconjunto, o BaggingRegressor constrói um modelo de regressão base separado (por exemplo, árvore de decisão, floresta aleatória, modelo de regressão linear, etc.).
- Previsões dos modelos base: Cada modelo base é usado para prever a variável alvo com base no subconjunto correspondente.
- Média ou combinação: O BaggingRegressor faz a média ou combina as previsões de todos os modelos base para obter a previsão final de regressão.
Vantagens do BaggingRegressor:
- Redução da variância: O BaggingRegressor reduz a variância do modelo, tornando-o mais robusto às flutuações nos dados.
- Redução do overfitting: Como o modelo é treinado em diferentes subconjuntos de dados, o BaggingRegressor geralmente reduz o risco de overfitting.
- Melhoria na generalização: Ao combinar previsões de múltiplos modelos, o BaggingRegressor geralmente fornece previsões mais precisas e estáveis.
- Ampla gama de modelos base: O BaggingRegressor pode usar diferentes tipos de modelos de regressão base, tornando-o um método flexível.
Limitações do BaggingRegressor:
- Nem sempre é capaz de melhorar o desempenho quando o modelo base já apresenta um bom desempenho nos dados.
- O BaggingRegressor pode exigir mais recursos computacionais e tempo em comparação com o treinamento de um único modelo.
O BaggingRegressor é um método poderoso de aprendizado de máquina que pode ser benéfico em tarefas de regressão, especialmente com dados ruidosos e a necessidade de melhorar a estabilidade da previsão.
2.2.2.1. Código para criar o modelo BaggingRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.linear_model.BaggingRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# BaggingRegressor.py
# The code demonstrates the process of training BaggingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"
# create a Bagging Regressor model
regression_model = BaggingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training BaggingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"
# create a Bagging Regressor model
regression_model = BaggingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python Python BaggingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998128324923137 Python Mean Absolute Error: 1.0257279210387649 Python Mean Squared Error: 2.4767424083953005 Python Python BaggingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998128317934672 Python Mean Absolute Error: 1.0257282792130034 Python Mean Squared Error: 2.4767516560614187 Python R^2 matching decimal laces: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 4 Python float ONNX model precision: 5 Python Python BaggingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx
Aba de Erros:
BaggingRegressor.py started BaggingRegressor.py 1 1 Traceback (most recent call last): BaggingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) BaggingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx failed:Type Error: T onnxruntime_inference_collection.py 424 1 BaggingRegressor.py finished in 3173 ms 5 1
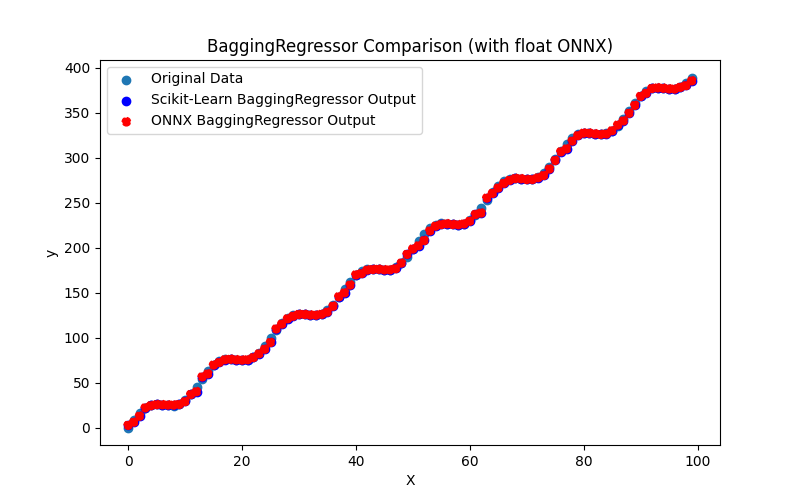
Fig.103. Resultados do BaggingRegressor.py (float ONNX)
2.2.2.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos bagging_regressor_float.onnx e bagging_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| BaggingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "BaggingRegressor" #define ONNXFilenameFloat "bagging_regressor_float.onnx" #define ONNXFilenameDouble "bagging_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
BaggingRegressor (EURUSD,H1) Testing ONNX float: BaggingRegressor (bagging_regressor_float.onnx) BaggingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998128317934672 BaggingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 1.0257282792130034 BaggingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 2.4767516560614196 BaggingRegressor (EURUSD,H1) BaggingRegressor (EURUSD,H1) Testing ONNX double: BaggingRegressor (bagging_regressor_double.onnx) BaggingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (ReduceMean) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\BaggingRegressor.mq5' (133:16) BaggingRegressor (EURUSD,H1) model_name=BaggingRegressor OnnxCreate error 5800
O modelo ONNX calculado em float foi executado normalmente, mas ocorreu um erro ao executar o modelo em double.
2.2.2.3. Representação ONNX dos modelos bagging_regressor_float.onnx e bagging_regressor_double.onnx
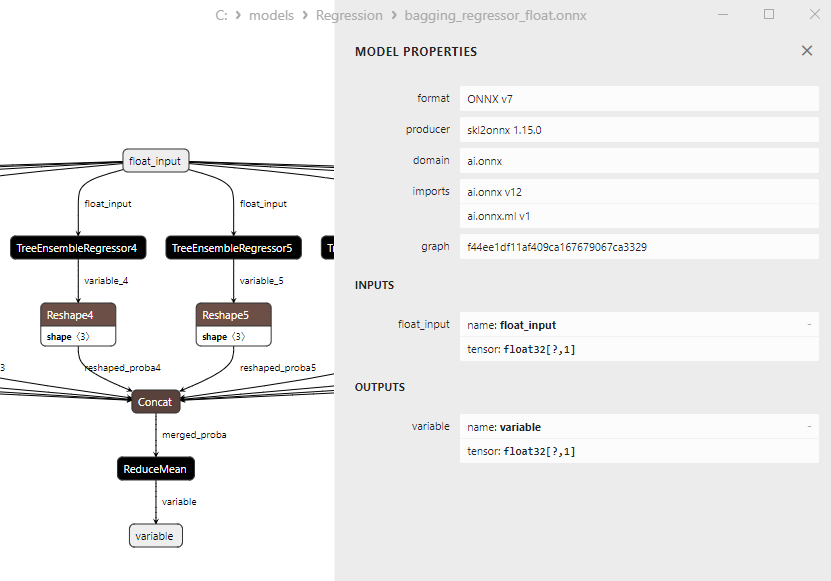
Fig.104. Representação ONNX do bagging_regressor_float.onnx no Netron
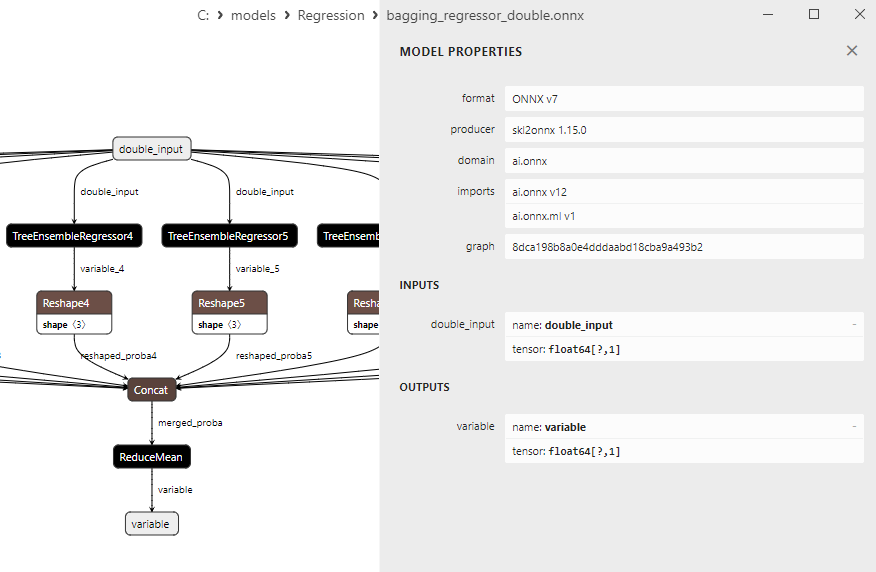
Fig.105. Representação ONNX do bagging_regressor_double.onnx no Netron
2.2.3. sklearn.linear_model.DecisionTreeRegressor
DecisionTreeRegressor é um método de aprendizado de máquina usado para tarefas de regressão, prevendo valores numéricos da variável alvo com base em um conjunto de características (variáveis independentes).
Este método baseia-se na construção de árvores de decisão que particionam o espaço de características em intervalos e preveem o valor da variável alvo para cada intervalo.
Princípio de funcionamento do DecisionTreeRegressor:
- Início da construção: Começando com o conjunto de dados inicial contendo características (variáveis independentes) e valores correspondentes da variável alvo.
- Seleção de características e divisão: A árvore de decisão seleciona uma característica e um valor de limiar que divide os dados em dois ou mais subgrupos. Essa divisão é realizada para minimizar o erro quadrático médio (a média dos desvios quadráticos entre os valores previstos e reais da variável alvo) dentro de cada subgrupo.
- Construção recursiva: O processo de seleção de características e divisão é repetido para cada subgrupo, criando subárvores. Esse processo é feito recursivamente até que certos critérios de parada sejam atendidos, como profundidade máxima da árvore ou número mínimo de amostras em um nó.
- Nós folha: Quando os critérios de parada são atendidos, nós folha são criados, prevendo valores numéricos da variável alvo para amostras que caem em um determinado nó folha.
- Previsão: Para novos dados, a árvore de decisão é aplicada, e novas observações percorrem a árvore até chegarem a um nó folha que prevê o valor numérico da variável alvo.
Vantagens do DecisionTreeRegressor:
- Interpretabilidade: Árvores de decisão são fáceis de entender e visualizar, tornando-as úteis para explicar a tomada de decisão do modelo.
- Robustez a outliers: Árvores de decisão podem ser robustas a outliers nos dados.
- Tratamento de dados numéricos e categóricos: Árvores de decisão podem processar tanto características numéricas quanto categóricas sem pré-processamento adicional.
- Seleção automática de características: Árvores podem selecionar automaticamente características importantes, ignorando as menos relevantes.
Limitações do DecisionTreeRegressor:
- Vulnerabilidade ao overfitting: Árvores de decisão podem ser propensas ao overfitting, especialmente se forem muito profundas.
- Problemas de generalização: Árvores de decisão podem não generalizar bem para dados que não foram incluídos no conjunto de treinamento.
- Nem sempre é a escolha ideal: Em alguns casos, outros métodos de regressão, como regressão linear ou k-vizinhos mais próximos, podem ter um desempenho melhor.
O DecisionTreeRegressor é um método valioso para tarefas de regressão, especialmente quando entender a lógica de tomada de decisão do modelo e visualizar o processo é crucial.
2.2.3.1. Código para criar o modelo DecisionTreeRegressor e exportá-lo para ONNX para float e double
Este código cria o modelo sklearn.linear_model.DecisionTreeRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# DecisionTreeRegressor.py
# The code demonstrates the process of training DecisionTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"
# create a Decision Tree Regressor model
regression_model = DecisionTreeRegressor()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training DecisionTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"
# create a Decision Tree Regressor model
regression_model = DecisionTreeRegressor()
# fit the model to the data
regression_model.fit(X, y)
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python DecisionTreeRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 0.0 Python Mean Squared Error: 0.0 Python Python DecisionTreeRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999999971 Python Mean Absolute Error: 4.393654615473253e-06 Python Mean Squared Error: 3.829042036424747e-11 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python DecisionTreeRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx
Aba de Erros:
DecisionTreeRegressor.py started DecisionTreeRegressor.py 1 1 Traceback (most recent call last): DecisionTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) DecisionTreeRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 DecisionTreeRegressor.py finished in 2957 ms 5 1
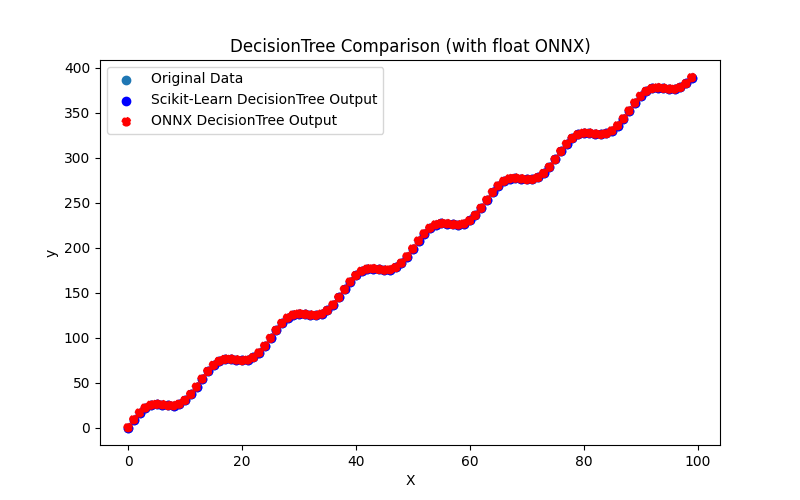
Fig.106. Resultados do DecisionTreeRegressor.py (float ONNX)
2.2.3.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos decision_tree_regressor_float.onnx e decision_tree_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| DecisionTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "DecisionTreeRegressor" #define ONNXFilenameFloat "decision_tree_regressor_float.onnx" #define ONNXFilenameDouble "decision_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
DecisionTreeRegressor (EURUSD,H1) Testing ONNX float: DecisionTreeRegressor (decision_tree_regressor_float.onnx) DecisionTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 DecisionTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 DecisionTreeRegressor (EURUSD,H1) DecisionTreeRegressor (EURUSD,H1) Testing ONNX double: DecisionTreeRegressor (decision_tree_regressor_double.onnx) DecisionTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\DecisionTreeRegressor.mq5' (133:16) DecisionTreeRegressor (EURUSD,H1) model_name=DecisionTreeRegressor OnnxCreate error 5800
O modelo ONNX calculado em float foi executado normalmente, mas ocorreu um erro ao executar o modelo em double.
2.2.3.3. Representação ONNX do decision_tree_regressor_float.onnx e decision_tree_regressor_double.onnx
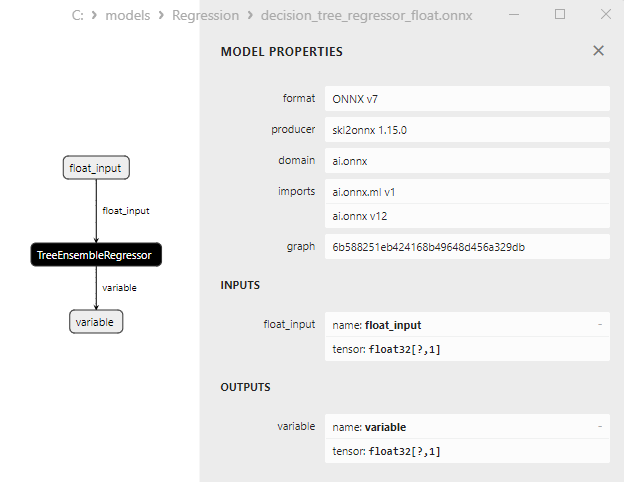
Fig.107. Representação ONNX do decision_tree_regressor_float.onnx no Netron
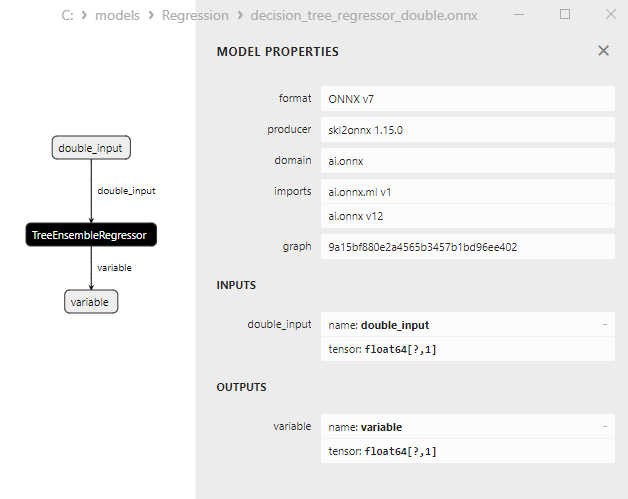
Fig.108. Representação ONNX do decision_tree_regressor_double.onnx no Netron
2.2.4. sklearn.tree.ExtraTreeRegressor
ExtraTreeRegressor, ou Extremely Randomized Trees Regressor, é um método de regressão em conjunto baseado em árvores de decisão.
Este método é uma variação das florestas aleatórias e difere no fato de que, em vez de escolher a melhor divisão para cada nó da árvore, ele usa divisões aleatórias para cada nó. Isso o torna mais aleatório e rápido, o que pode ser vantajoso em certas situações.
Princípio de funcionamento do ExtraTreeRegressor:
- Início da construção: Começando com o conjunto de dados inicial contendo características (variáveis independentes) e valores correspondentes da variável alvo.
- Aleatoriedade nas divisões: Ao contrário das árvores de decisão regulares, onde a melhor divisão é escolhida, o ExtraTreeRegressor usa valores de limiar aleatórios para dividir os nós da árvore. Isso torna o processo de divisão mais aleatório e menos propenso ao overfitting.
- Construção da árvore: A árvore é construída dividindo os nós com base em características e valores de limiar aleatórios. Esse processo continua até que certos critérios de parada sejam atendidos, como profundidade máxima da árvore ou número mínimo de amostras em um nó.
- Conjunto de árvores: O ExtraTreeRegressor constrói múltiplas dessas árvores aleatórias, cujo número é controlado pelo hiperparâmetro "n_estimators".
- Previsão: Para prever a variável alvo para novos dados, o ExtraTreeRegressor simplesmente faz a média das previsões de todas as árvores no conjunto.
Vantagens do ExtraTreeRegressor:
- Redução do overfitting: Usar divisões aleatórias nos nós torna o método menos propenso ao overfitting em comparação com árvores de decisão regulares.
- Alta paralelização: Como as árvores são construídas independentemente, o ExtraTreeRegressor pode ser facilmente paralelizado para treinamento em múltiplos processadores.
- Treinamento rápido: Comparado a alguns outros métodos, como boosting de gradiente, o ExtraTreeRegressor pode ser treinado mais rapidamente.
Limitações do ExtraTreeRegressor:
- Pode ser menos preciso: Em alguns casos, especialmente com conjuntos de dados pequenos, o ExtraTreeRegressor pode ser menos preciso em comparação com métodos mais complexos.
- Menos interpretável: Comparado a modelos lineares, árvores de decisão e outros métodos mais simples, o ExtraTreeRegressor é tipicamente menos interpretável.
O ExtraTreeRegressor pode ser um método útil para regressão em situações onde a redução do overfitting e o rápido treinamento são necessários.
2.2.4.1. Código para criar o modelo ExtraTreeRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.tree.ExtraTreeRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# ExtraTreeRegressor.py
# The code demonstrates the process of training ExtraTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"
# create an ExtraTreeRegressor model
regression_model = ExtraTreeRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training ExtraTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"
# create an ExtraTreeRegressor model
regression_model = ExtraTreeRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
2023.10.30 14:40:57.665 Python ExtraTreeRegressor Original model (double) 2023.10.30 14:40:57.665 Python R-squared (Coefficient of determination): 1.0 2023.10.30 14:40:57.665 Python Mean Absolute Error: 0.0 2023.10.30 14:40:57.665 Python Mean Squared Error: 0.0 2023.10.30 14:40:57.681 Python 2023.10.30 14:40:57.681 Python ExtraTreeRegressor ONNX model (float) 2023.10.30 14:40:57.681 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_float.onnx 2023.10.30 14:40:57.681 Python Information about input tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python Information about output tensors in ONNX: 2023.10.30 14:40:57.681 Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] 2023.10.30 14:40:57.681 Python R-squared (Coefficient of determination) 0.9999999999999971 2023.10.30 14:40:57.681 Python Mean Absolute Error: 4.393654615473253e-06 2023.10.30 14:40:57.681 Python Mean Squared Error: 3.829042036424747e-11 2023.10.30 14:40:57.681 Python R^2 matching decimal places: 0 2023.10.30 14:40:57.681 Python MAE matching decimal places: 0 2023.10.30 14:40:57.681 Python MSE matching decimal places: 0 2023.10.30 14:40:57.681 Python float ONNX model precision: 0 2023.10.30 14:40:58.011 Python 2023.10.30 14:40:58.011 Python ExtraTreeRegressor ONNX model (double) 2023.10.30 14:40:58.011 Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx
Aba de Erros:
ExtraTreeRegressor.py started ExtraTreeRegressor.py 1 1 Traceback (most recent call last): ExtraTreeRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreeRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx failed:Type Error onnxruntime_inference_collection.py 424 1 ExtraTreeRegressor.py finished in 2980 ms 5 1
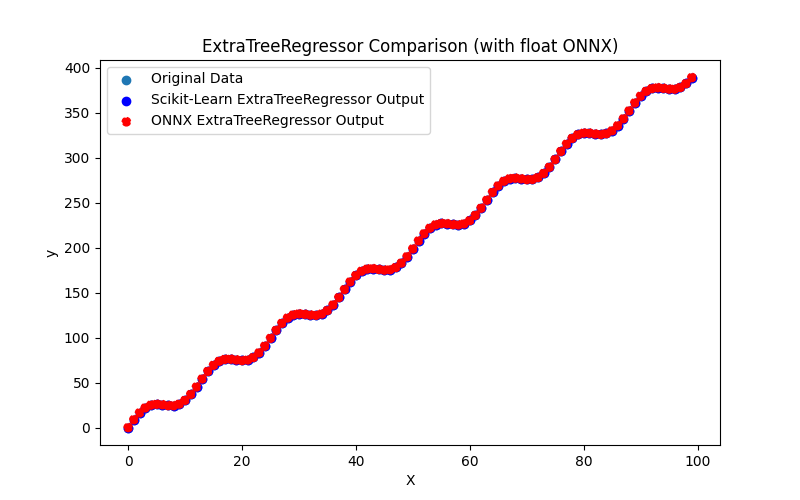
Fig.109. Resultados do ExtraTreeRegressor.py (float ONNX)
2.2.4.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| ExtraTreeRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreeRegressor" #define ONNXFilenameFloat "extra_tree_regressor_float.onnx" #define ONNXFilenameDouble "extra_tree_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
ExtraTreeRegressor (EURUSD,H1) Testing ONNX float: ExtraTreeRegressor (extra_tree_regressor_float.onnx) ExtraTreeRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999999971 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000043936546155 ExtraTreeRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000000382904 ExtraTreeRegressor (EURUSD,H1) ExtraTreeRegressor (EURUSD,H1) Testing ONNX double: ExtraTreeRegressor (extra_tree_regressor_double.onnx) ExtraTreeRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreeRegressor.mq5' (133:16) ExtraTreeRegressor (EURUSD,H1) model_name=ExtraTreeRegressor OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
2.2.4.3. Representação ONNX do extra_tree_regressor_float.onnx e extra_tree_regressor_double.onnx
Fig.110. Representação ONNX do extra_tree_regressor_float.onnx no Netron
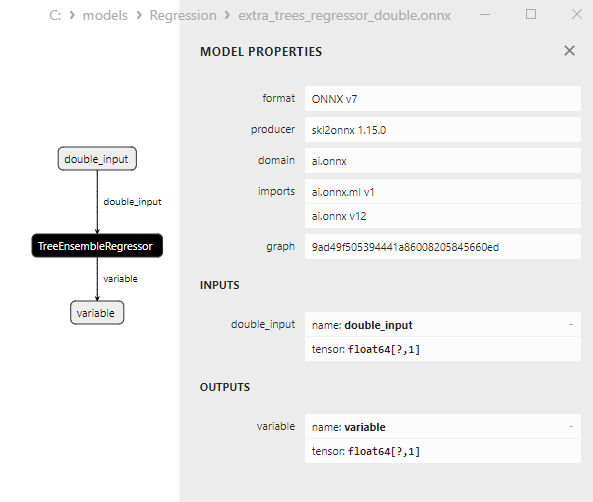
Fig.111. Representação ONNX do extra_tree_regressor_double.onnx no Netron
2.2.5. sklearn.ensemble.ExtraTreesRegressor
ExtraTreesRegressor (Extremely Randomized Trees Regressor) é um método de aprendizado de máquina que representa uma variação das Florestas Aleatórias para tarefas de regressão.
Este método emprega um conjunto de árvores de decisão para prever valores numéricos da variável alvo com base em um conjunto de características.
Como o ExtraTreesRegressor funciona:
- Início da construção: Começa com o conjunto de dados original, incluindo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Aleatoriedade nas divisões: Ao contrário das árvores de decisão regulares, onde a melhor divisão é selecionada para dividir os nós, o ExtraTreesRegressor usa valores de limiar aleatórios para dividir os nós da árvore. Essa aleatoriedade torna o processo de divisão mais arbitrário e menos propenso ao overfitting.
- Construção da árvore: O ExtraTreesRegressor constrói múltiplas árvores de decisão no conjunto. O número de árvores é controlado pelo hiperparâmetro "n_estimators". Cada árvore é treinada em uma amostra aleatória de dados (com reposição) e subconjuntos aleatórios de características.
- Previsão: Para prever a variável alvo para novos dados, o ExtraTreesRegressor agrega as previsões de todas as árvores no conjunto (geralmente pela média).
Vantagens do ExtraTreeRegressor:
- Redução do Overfitting: Usar divisões de nós aleatórias e amostragem de dados torna o método menos propenso ao overfitting em comparação com árvores de decisão convencionais.
- Alta Paralelização: Como as árvores são construídas independentemente, o ExtraTreesRegressor pode ser facilmente paralelizado para treinamento em múltiplos processadores.
- Robustez a Outliers: O método geralmente mostra resiliência a outliers nos dados.
- Tratamento de Dados Numéricos e Categóricos: O ExtraTreesRegressor pode lidar com características numéricas e categóricas sem pré-processamento adicional.
Limitações do ExtraTreesRegressor:
- Pode Requerer Ajuste Fino dos Hiperparâmetros: Embora o ExtraTreesRegressor geralmente funcione bem com os parâmetros padrão, o ajuste fino dos hiperparâmetros pode ser necessário para alcançar o desempenho máximo.
- Menor Interpretabilidade: Como outros métodos de conjunto, o ExtraTreesRegressor é menos interpretável em comparação com modelos mais simples, como a regressão linear.
O ExtraTreesRegressor pode ser um método benéfico para regressão em várias tarefas, particularmente quando reduzir o overfitting e melhorar a generalização do modelo é necessário.
2.2.5.1. Código para criar o modelo ExtraTreesRegressor e exportá-lo para ONNX para float e double
Este código cria o modelo sklearn.ensemble.ExtraTreesRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# ExtraTreesRegressor.py
# The code demonstrates the process of training ExtraTreesRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"
# create an Extra Trees Regressor model
regression_model = ExtraTreesRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training ExtraTreesRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"
# create an Extra Trees Regressor model
regression_model = ExtraTreesRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python ExtraTreesRegressor Original model (double) Python R-squared (Coefficient of determination): 1.0 Python Mean Absolute Error: 2.2302160118670144e-13 Python Mean Squared Error: 8.41048471722451e-26 Python Python ExtraTreesRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999999999998015 Python Mean Absolute Error: 3.795239380975701e-05 Python Mean Squared Error: 2.627067474763585e-09 Python R^2 matching decimal places: 0 Python MAE matching decimal places: 0 Python MSE matching decimal places: 0 Python float ONNX model precision: 0 Python Python ExtraTreesRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx
Aba de Erros:
ExtraTreesRegressor.py started ExtraTreesRegressor.py 1 1 Traceback (most recent call last): ExtraTreesRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) ExtraTreesRegressor.py 160 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx failed:Type Erro onnxruntime_inference_collection.py 424 1 ExtraTreesRegressor.py finished in 4654 ms 5 1
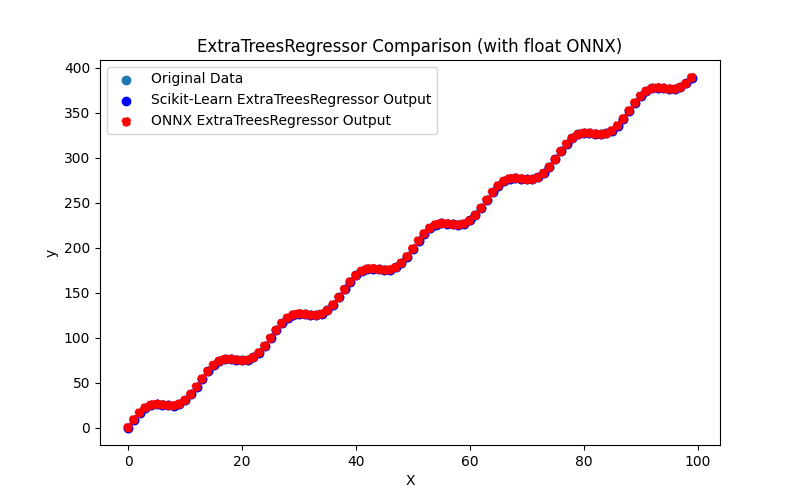
Fig.112. Resultados do ExtraTreesRegressor.py (float ONNX)
2.2.5.2. Código MQL5 para executar Modelos ONNX
Este código cria os modelos extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| ExtraTreesRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "ExtraTreesRegressor" #define ONNXFilenameFloat "extra_trees_regressor_float.onnx" #define ONNXFilenameDouble "extra_trees_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
ExtraTreesRegressor (EURUSD,H1) Testing ONNX float: ExtraTreesRegressor (extra_trees_regressor_float.onnx) ExtraTreesRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999999999998015 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.0000379523938098 ExtraTreesRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0000000026270675 ExtraTreesRegressor (EURUSD,H1) ExtraTreesRegressor (EURUSD,H1) Testing ONNX double: ExtraTreesRegressor (extra_trees_regressor_double.onnx) ExtraTreesRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreesRegressor.mq5' (133:16) ExtraTreesRegressor (EURUSD,H1) model_name=ExtraTreesRegressor OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
2.2.5.3. Representação ONNX do extra_trees_regressor_float.onnx e extra_trees_regressor_double.onnx
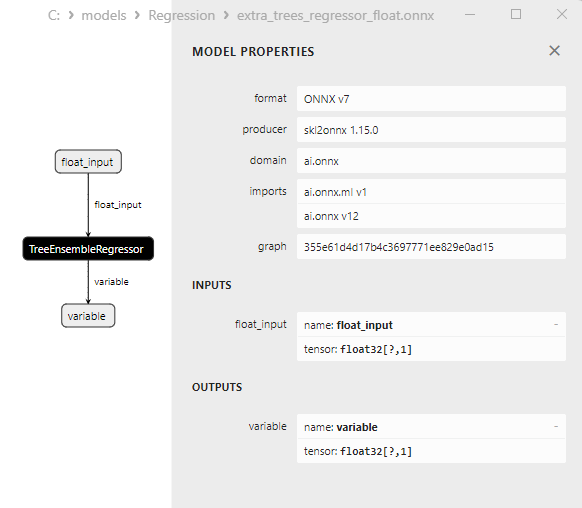
Fig.113. Representação ONNX do extra_trees_regressor_float.onnx no Netron
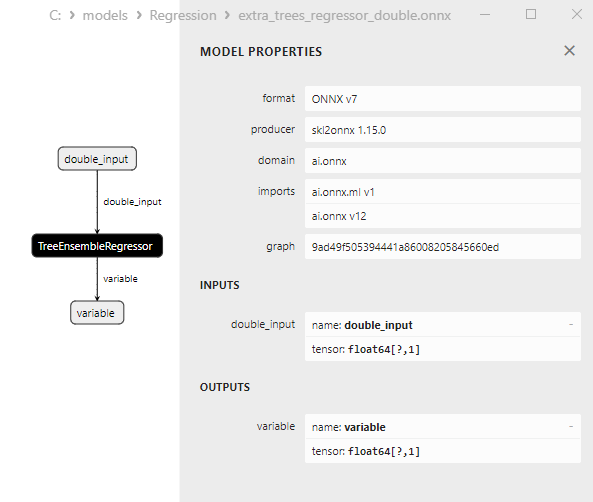
Fig.114. Representação ONNX do extra_trees_regressor_double.onnx no Netron
2.2.6. sklearn.svm.NuSVR
NuSVR é um método de aprendizado de máquina usado para tarefas de regressão. Este método é baseado em Support Vector Machine (SVM), mas é aplicado a tarefas de regressão em vez de tarefas de classificação.
NuSVR é uma variação do SVM projetada para resolver tarefas de regressão, prevendo valores contínuos da variável alvo.
Como o NuSVR funciona:
- Dados de Entrada: Começa com um conjunto de dados que inclui características (variáveis independentes) e valores da variável alvo (contínuos).
- Seleção de Kernel: NuSVR usa kernels como linear, polinomial ou função de base radial (RBF) para transformar os dados em um espaço de alta dimensão onde um hiperplano separador linear pode ser encontrado.
- Definição do parâmetro Nu: O parâmetro Nu controla a complexidade do modelo e define quantos exemplos de treinamento serão considerados outliers. O valor de Nu deve variar de 0 a 1, influenciando o número de vetores de suporte.
- Construção do Vetor de Suporte: O NuSVR busca encontrar um hiperplano separador ótimo que maximize a lacuna entre esse hiperplano e os pontos de amostra mais próximos.
- Treinamento do Modelo: O modelo é treinado para minimizar o erro de regressão e atender às restrições associadas ao parâmetro Nu.
- Fazendo Previsões: Após o treinamento, o modelo pode ser usado para prever os valores da variável alvo em novos dados.
Vantagens do NuSVR:
- Manipulação de Outliers: O NuSVR permite controlar outliers usando o parâmetro Nu, regulando o número de exemplos de treinamento considerados outliers.
- Múltiplos Kernels: O método suporta vários tipos de kernels, permitindo a modelagem de relações não lineares complexas.
Limitações do NuSVR:
- Seleção do Parâmetro Nu: Escolher o valor correto para o parâmetro Nu pode exigir alguma experimentação.
- Sensibilidade à Escala dos Dados: SVM, incluindo NuSVR, pode ser sensível à escala dos dados, portanto, a padronização ou normalização das características pode ser necessária.
- Complexidade Computacional: Para grandes conjuntos de dados e kernels complexos, o NuSVR pode ser computacionalmente caro.
O NuSVR é um método de aprendizado de máquina para tarefas de regressão baseado no método Support Vector Machine (SVM). Permite a previsão de valores contínuos da variável alvo e oferece a capacidade de gerenciar outliers usando o parâmetro Nu.
2.2.6.1. Código para criar o modelo NuSVR e exportá-lo para ONNX para float e double
Este código cria o modelo sklearn.svm.NuSVR, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# NuSVR.py
# The code demonstrates the process of training NuSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"
# create a NuSVR model
nusvr_model = NuSVR()
# fit the model to the data
nusvr_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = nusvr_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training NuSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"
# create a NuSVR model
nusvr_model = NuSVR()
# fit the model to the data
nusvr_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = nusvr_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python NuSVR Original model (double) Python R-squared (Coefficient of determination): 0.2771437770527445 Python Mean Absolute Error: 83.76666411704255 Python Mean Squared Error: 9565.381751764757 Python Python NuSVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_float.onnx Python Information about input tensors in ONNX: 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.27714379657935495 Python Mean Absolute Error: 83.766663385322 Python Mean Squared Error: 9565.381493373838 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python NuSVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_double.onnx
Aba de Erros:
NuSVR.py started NuSVR.py 1 1 Traceback (most recent call last): NuSVR.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) NuSVR.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess.initialize_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 435 1 onnxruntime.capi.onnxruntime_pybind11_state.NotImplemented: [ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for SVMRegressor(1) node with name 'SVM' onnxruntime_inference_collection.py 435 1 NuSVR.py finished in 2925 ms 5 1
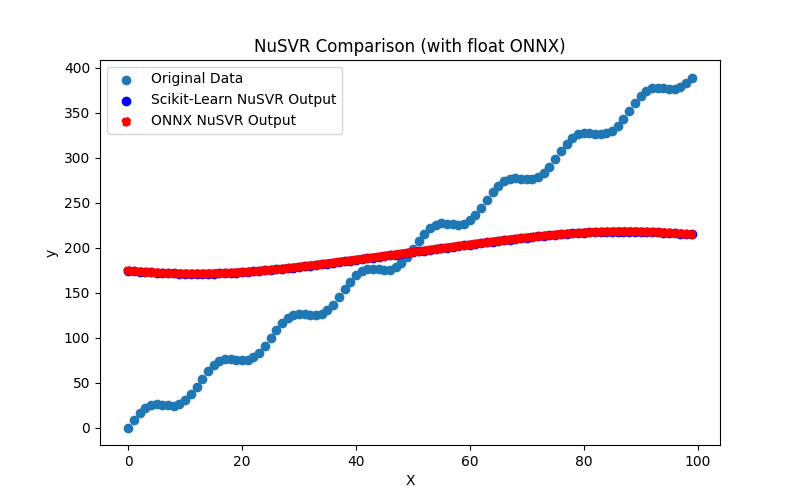
Fig.115. Resultados do NuSVR.py (float ONNX)
2.2.6.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos nu_svr_float.onnx e nu_svr_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| NuSVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "NuSVR" #define ONNXFilenameFloat "nu_svr_float.onnx" #define ONNXFilenameDouble "nu_svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
NuSVR (EURUSD,H1) Testing ONNX float: NuSVR (nu_svr_float.onnx) NuSVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.2771437965793548 NuSVR (EURUSD,H1) MQL5: Mean Absolute Error: 83.7666633853219906 NuSVR (EURUSD,H1) MQL5: Mean Squared Error: 9565.3814933738358377 NuSVR (EURUSD,H1) NuSVR (EURUSD,H1) Testing ONNX double: NuSVR (nu_svr_double.onnx) NuSVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\Regression\NuSVR.mq5' (133:16) NuSVR (EURUSD,H1) model_name=NuSVR OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
Comparação com o modelo original em double no Python:
Testing ONNX float: NuSVR (nu_svr_float.onnx) Python Mean Absolute Error: 83.76666411704255 MQL5: Mean Absolute Error: 83.7666633853219906
2.2.6.3. Representação ONNX do nu_svr_float.onnx e nu_svr_double.onnx
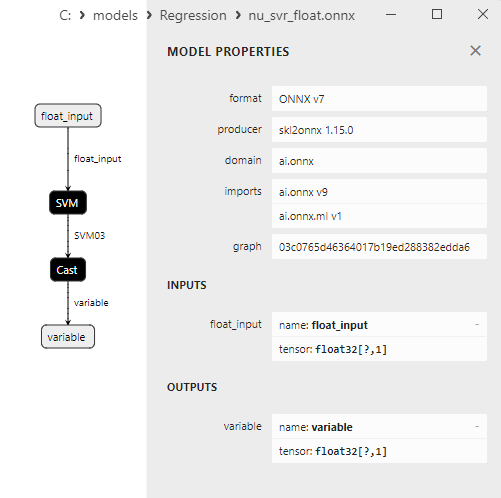
Fig.116. representação ONNX do nu_svr_float.onnx no Netron
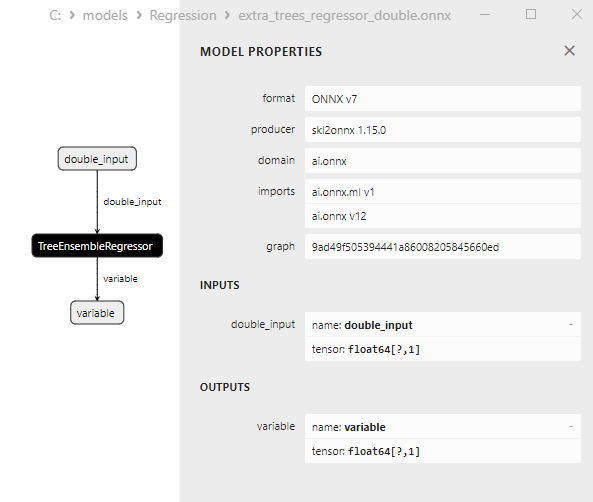
Fig.117. Representação ONNX do nu_svr_double.onnx no Netron
2.2.7. sklearn.ensemble.RandomForestRegressor
RandomForestRegressor é um método de aprendizado de máquina usado para resolver tarefas de regressão.
É um dos métodos mais populares baseados em aprendizado em conjunto e emprega o algoritmo Random Forest para criar modelos de regressão poderosos e robustos.
Veja como o RandomForestRegressor funciona:
- Dados de Entrada: Começa com um conjunto de dados que inclui características (variáveis independentes) e uma variável alvo (contínua).
- Random Forest: O RandomForestRegressor usa um conjunto de árvores de decisão para resolver a tarefa de regressão. Cada árvore na floresta trabalha para prever os valores da variável alvo.
- Amostragem Bootstrap: Cada árvore é treinada usando amostras bootstrap, o que significa amostragem aleatória com reposição do conjunto de dados de treinamento. Isso permite diversidade nos dados que cada árvore aprende.
- Seleção Aleatória de Características: Ao construir cada árvore, um subconjunto aleatório de características também é selecionado, tornando o modelo mais robusto e reduzindo as correlações entre as árvores.
- Média das Previsões: Uma vez que todas as árvores são construídas, o RandomForestRegressor faz a média ou combina suas previsões para obter a previsão final de regressão.
Vantagens do RandomForestRegressor:
- Poder e Robustez: O RandomForestRegressor é um método de regressão poderoso que geralmente oferece bom desempenho.
- Manipulação de Grandes Dados: Lida bem com grandes conjuntos de dados e pode lidar com uma multitude de características.
- Resiliência ao Overfitting: Devido à amostragem bootstrap e à seleção aleatória de características, a floresta aleatória é tipicamente robusta contra overfitting.
- Estimativa da Importância das Características: O Random Forest pode fornecer informações sobre a importância de cada característica na tarefa de regressão.
Limitações do RandomForestRegressor:
- Falta de Interpretabilidade: O modelo pode ser menos interpretável em comparação com modelos lineares.
- Nem Sempre o Modelo Mais Preciso: Em algumas tarefas, conjuntos mais complexos podem ser desnecessários, e modelos lineares podem ser mais adequados.
O RandomForestRegressor é um poderoso método de aprendizado de máquina para tarefas de regressão que usa um conjunto de árvores de decisão aleatórias para criar um modelo de regressão estável e de alto desempenho. Este método é particularmente útil para tarefas com grandes conjuntos de dados e para avaliar a importância das características.
2.2.7.1. Código para criar o modelo RandomForestRegressor e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.ensemble.RandomForestRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# RandomForestRegressor.py
# The code demonstrates the process of training RandomForestRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"
# create a RandomForestRegressor model
regression_model = RandomForestRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training RandomForestRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"
# create a RandomForestRegressor model
regression_model = RandomForestRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python RandomForestRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9998854509605539 Python Mean Absolute Error: 0.9186485980852603 Python Mean Squared Error: 1.5157997632401086 Python Python RandomForestRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9998854516013125 Python Mean Absolute Error: 0.9186420704511761 Python Mean Squared Error: 1.515791284236419 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python RandomForestRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx
Aba de Erros:
RandomForestRegressor.py started RandomForestRegressor.py 1 1 Traceback (most recent call last): RandomForestRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) RandomForestRegressor.py 159 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx failed:Type Er onnxruntime_inference_collection.py 424 1 RandomForestRegressor.py finished in 4392 ms 5 1
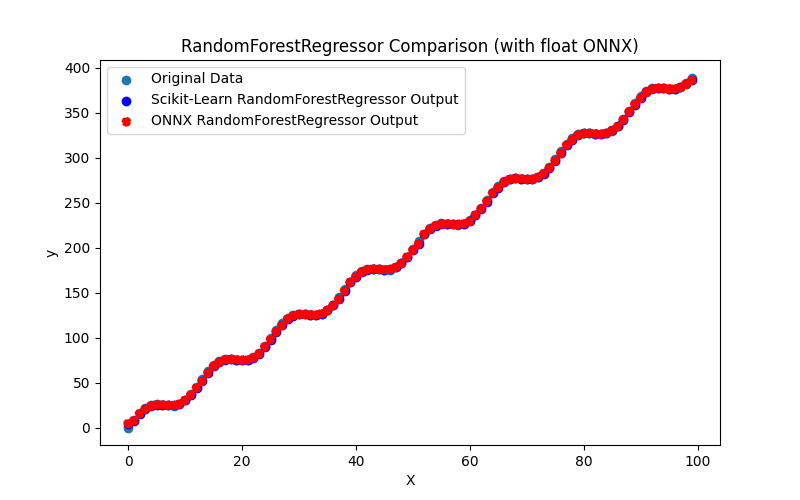
Fig.118. Resultados do RandomForestRegressor.py (float ONNX)
2.2.7.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos random_forest_regressor_float.onnx e random_forest_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| RandomForestRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "RandomForestRegressor" #define ONNXFilenameFloat "random_forest_regressor_float.onnx" #define ONNXFilenameDouble "random_forest_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX float: RandomForestRegressor (random_forest_regressor_float.onnx) RandomForestRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9998854516013125 RandomForestRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.9186420704511761 RandomForestRegressor (EURUSD,H1) MQL5: Mean Squared Error: 1.5157912842364190 RandomForestRegressor (EURUSD,H1) RandomForestRegressor (EURUSD,H1) Testing ONNX double: RandomForestRegressor (random_forest_regressor_double.onnx) RandomForestRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\RandomForestRegressor.mq5' (133:16) RandomForestRegressor (EURUSD,H1) model_name=RandomForestRegressor OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
2.2.7.3. Representação ONNX do random_forest_regressor_float.onnx e random_forest_regressor_double.onnx
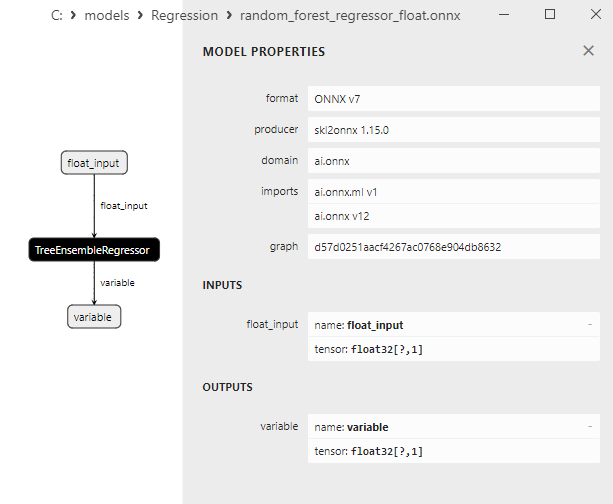
Fig.119. Representação ONNX do random_forest_regressor_float.onnx no Netron
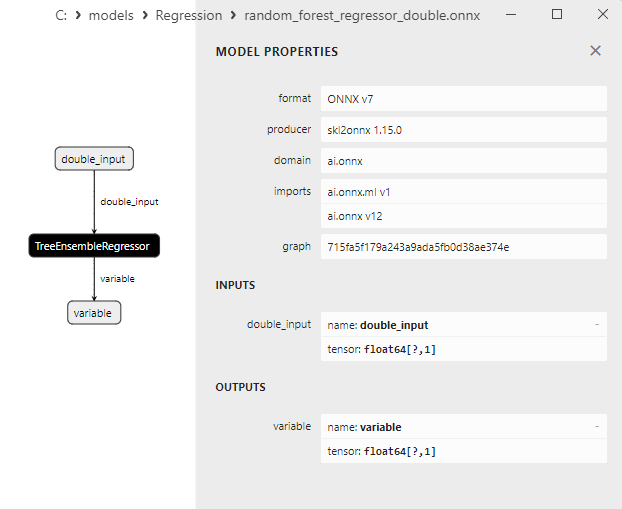
Fig.120. Representação ONNX do random_forest_regressor_double.onnx no Netron
2.2.8. sklearn.ensemble.GradientBoostingRegressor
GradientBoostingRegressor é um método de aprendizado de máquina usado para tarefas de regressão. Faz parte da família de métodos de conjunto e é baseado na ideia de construir modelos fracos e combiná-los em um modelo forte usando boosting de gradiente.
O boosting de gradiente é uma técnica para aprimorar modelos adicionando iterativamente modelos fracos e corrigindo os erros dos modelos anteriores.
Veja como o GradientBoostingRegressor funciona:
- Inicialização: Começa com o conjunto de dados original contendo características (variáveis independentes) e seus valores alvo correspondentes.
- Primeiro Modelo: Inicia treinando o primeiro modelo, frequentemente escolhido como um modelo de regressão simples (por exemplo, árvore de decisão) nos dados originais.
- Resíduos e Anti-Gradiente: Os resíduos, a diferença entre os valores previstos pelo primeiro modelo e os valores reais da variável alvo, são calculados. Em seguida, o anti-gradiente dessa função de perda é calculado, indicando a direção para melhorar o modelo.
- Construção do Próximo Modelo: O próximo modelo é construído, focando em prever o anti-gradiente (erros do primeiro modelo). Este modelo é treinado nos resíduos e adicionado ao primeiro modelo.
- Iterações: O processo de construção de novos modelos e correção de resíduos é repetido várias vezes. Cada novo modelo leva em consideração os resíduos dos modelos anteriores e visa melhorar as previsões.
- Combinação de Modelos: As previsões de todos os modelos são combinadas na previsão final através de média ou ponderação de acordo com sua importância.
Vantagens do GradientBoostingRegressor:
- Alto Desempenho: O boosting de gradiente é um método poderoso capaz de alcançar alto desempenho em tarefas de regressão.
- Robustez a Outliers: Lida com outliers nos dados e constrói modelos considerando essa incerteza.
- Seleção Automática de Características: Seleciona automaticamente as características mais importantes para prever a variável alvo.
- Manipulação de Várias Funções de Perda: O método permite o uso de diferentes funções de perda, dependendo da tarefa.
Limitações do GradientBoostingRegressor:
- Necessidade de Ajuste de Hiperparâmetros: Alcançar o desempenho máximo requer ajuste de hiperparâmetros como taxa de aprendizado, profundidade da árvore e número de modelos.
- Computacionalmente Caro: O boosting de gradiente pode ser computacionalmente caro, especialmente com grandes volumes de dados e um alto número de árvores.
O GradientBoostingRegressor é um método de regressão poderoso, frequentemente usado em tarefas práticas para alcançar alto desempenho com o ajuste correto dos hiperparâmetros.
2.2.8.1. Código para criar o modelo GradientBoostingRegressor e exportá-lo para ONNX para float e double
Este código cria o modelo sklearn.ensemble.GradientBoostingRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# GradientBoostingRegressor.py
# The code demonstrates the process of training GradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"
# create a Gradient Boosting Regressor model
regression_model = GradientBoostingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training GradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"
# create a Gradient Boosting Regressor model
regression_model = GradientBoostingRegressor()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python GradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9999959514652565 Python Mean Absolute Error: 0.15069342754017417 Python Mean Squared Error: 0.053573282108575676 Python Python GradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9999959514739537 Python Mean Absolute Error: 0.15069457426101718 Python Mean Squared Error: 0.05357316702127665 Python R^2 matching decimal places: 10 Python MAE matching decimal places: 5 Python MSE matching decimal places: 6 Python float ONNX model precision: 5 Python Python GradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx
Aba de Erros:
GradientBoostingRegressor.py started GradientBoostingRegressor.py 1 1 Traceback (most recent call last): GradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) GradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx failed:Typ onnxruntime_inference_collection.py 452 1 GradientBoostingRegressor.py finished in 3073 ms 5 1
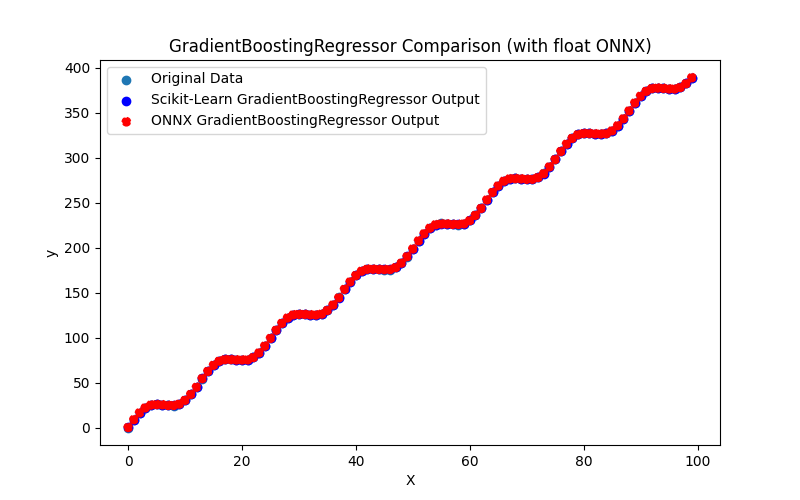
Fig.121. Resultados do GradientBoostingRegressor.py (float ONNX)
2.2.8.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| GradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "GradientBoostingRegressor" #define ONNXFilenameFloat "gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
GradientBoostingRegressor (EURUSD,H1) Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) GradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9999959514739537 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 0.1506945742610172 GradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 0.0535731670212767 GradientBoostingRegressor (EURUSD,H1) GradientBoostingRegressor (EURUSD,H1) Testing ONNX double: GradientBoostingRegressor (gradient_boosting_regressor_double.onnx) GradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\GradientBoostingRegressor.mq5' (133:16) GradientBoostingRegressor (EURUSD,H1) model_name=GradientBoostingRegressor OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
Comparação com o modelo original em double no Python:
Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 0.15069342754017417 MQL5: Mean Absolute Error: 0.1506945742610172
Acurácia do ONNX float MAE: 5 casas decimais.
2.2.8.3. Representação ONNX dos modelos gradient_boosting_regressor_float.onnx e gradient_boosting_regressor_double.onnx
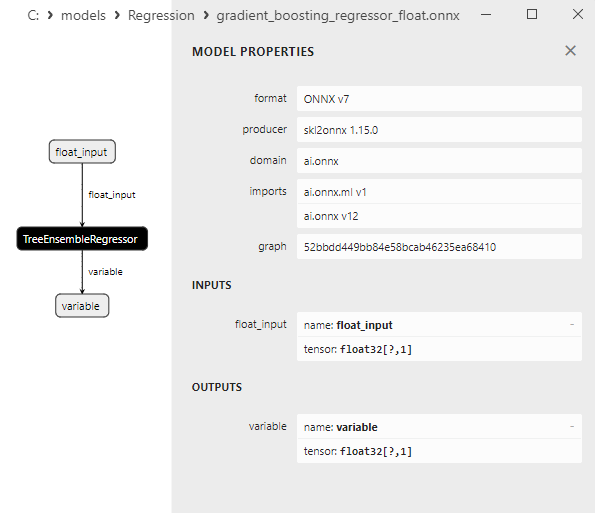
Fig.122. Representação ONNX do gradient_boosting_regressor_float.onnx no Netron
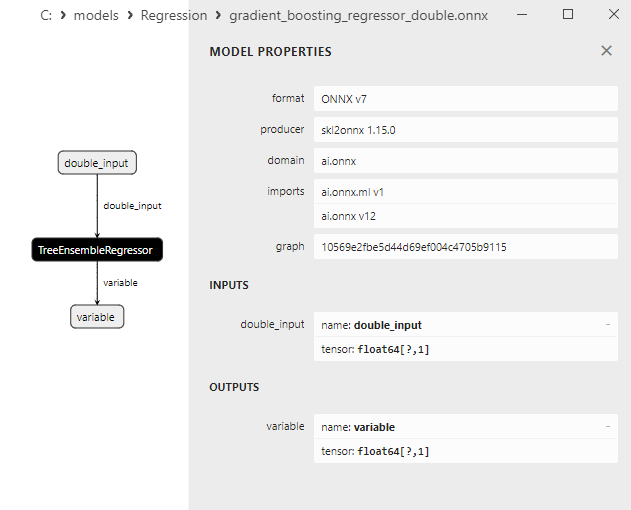
Fig.123. Representação ONNX do gradient_boosting_regressor_double.onnx no Netron
2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
HistGradientBoostingRegressor é um método de aprendizado de máquina que representa uma variação do boosting de gradiente otimizada para trabalhar com grandes conjuntos de dados.
Este método é usado para tarefas de regressão, e seu nome "Hist" significa que emprega métodos baseados em histogramas para acelerar o processo de treinamento.
Como o HistGradientBoostingRegressor Funciona:
- Inicialização: Começa com o conjunto de dados original contendo características (variáveis independentes) e seus valores alvo correspondentes.
- Métodos Baseados em Histogramas: Em vez de dividir os dados exatamente nos nós da árvore, o HistGradientBoostingRegressor usa métodos baseados em histogramas para representar os dados de forma eficiente em forma de histogramas. Isso acelera significativamente o processo de treinamento, especialmente em grandes conjuntos de dados.
- Construção de Árvores Base: O método constrói um conjunto de árvores de decisão base, referidas como "árvores de decisão histograma", usando as representações dos histogramas dos dados. Essas árvores são construídas com base no boosting de gradiente e ajustadas aos resíduos do modelo anterior.
- Treinamento Gradual: O HistGradientBoostingRegressor adiciona incrementamente novas árvores ao conjunto, com cada árvore corrigindo os resíduos das árvores anteriores.
- Combinação de Modelos: Após a construção das árvores base, as previsões de todas as árvores são combinadas para obter a previsão final.
Vantagens do HistGradientBoostingRegressor:
- Alto Desempenho: Este método é otimizado para lidar com grandes volumes de dados e pode alcançar alto desempenho.
- Robustez ao Ruído: O HistGradientBoostingRegressor geralmente tem um bom desempenho mesmo na presença de ruído nos dados.
- Eficiência em Alta Dimensionalidade: O método pode lidar com tarefas com um grande número de características (dados de alta dimensionalidade).
- Excelente Paralelização: Pode paralelizar o treinamento de forma eficiente em múltiplos processadores.
Limitações do HistGradientBoostingRegressor:
- Requer Ajuste de Hiperparâmetros: Alcançar o desempenho máximo exige ajuste de hiperparâmetros como profundidade da árvore e número de modelos.
- Menos Interpretável que Modelos Lineares: Como outros métodos de conjunto, o HistGradientBoostingRegressor é menos interpretável do que modelos mais simples, como a regressão linear.
O HistGradientBoostingRegressor pode ser um método útil de regressão para tarefas envolvendo grandes conjuntos de dados, onde alto desempenho e eficiência em dados de alta dimensionalidade são essenciais.
2.2.9.1. Código para criar o modelo HistGradientBoostingRegressor e exportá-lo para ONNX para float e double
Este código cria o modelo sklearn.ensemble.HistGradientBoostingRegressor, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# HistGradientBoostingRegressor.py
# The code demonstrates the process of training HistGradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"
# create a Histogram-Based Gradient Boosting Regressor model
hist_gradient_boosting_model = HistGradientBoostingRegressor()
# fit the model to the data
hist_gradient_boosting_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = hist_gradient_boosting_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training HistGradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"
# create a Histogram-Based Gradient Boosting Regressor model
hist_gradient_boosting_model = HistGradientBoostingRegressor()
# fit the model to the data
hist_gradient_boosting_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = hist_gradient_boosting_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python HistGradientBoostingRegressor Original model (double) Python R-squared (Coefficient of determination): 0.9833421349506157 Python Mean Absolute Error: 9.070567104488434 Python Mean Squared Error: 220.4295035561544 Python Python HistGradientBoostingRegressor ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.9833421351962779 Python Mean Absolute Error: 9.07056497799043 Python Mean Squared Error: 220.42950030536645 Python R^2 matching decimal places: 8 Python MAE matching decimal places: 5 Python MSE matching decimal places: 5 Python float ONNX model precision: 5 Python Python HistGradientBoostingRegressor ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx
Aba de Erros:
HistGradientBoostingRegressor.py started HistGradientBoostingRegressor.py 1 1 Traceback (most recent call last): HistGradientBoostingRegressor.py 1 1 onnx_session = ort.InferenceSession(onnx_filename) HistGradientBoostingRegressor.py 161 1 self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 419 1 sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 452 1 onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx faile onnxruntime_inference_collection.py 452 1 HistGradientBoostingRegressor.py finished in 3100 ms 5 1
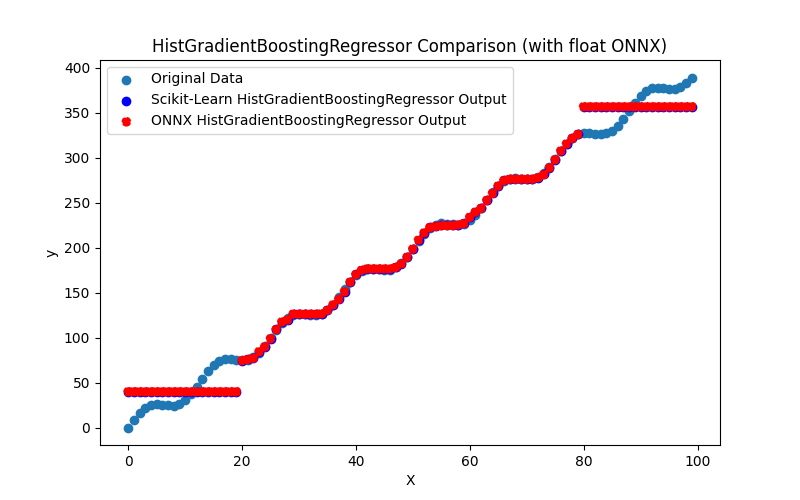
Fig.124. Resultados do HistGradientBoostingRegressor.py (float ONNX)
2.2.9.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| HistGradientBoostingRegressor.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "HistGradientBoostingRegressor" #define ONNXFilenameFloat "hist_gradient_boosting_regressor_float.onnx" #define ONNXFilenameDouble "hist_gradient_boosting_regressor_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) HistGradientBoostingRegressor (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.9833421351962779 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Absolute Error: 9.0705649779904292 HistGradientBoostingRegressor (EURUSD,H1) MQL5: Mean Squared Error: 220.4295003053665312 HistGradientBoostingRegressor (EURUSD,H1) HistGradientBoostingRegressor (EURUSD,H1) Testing ONNX double: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_double.onnx) HistGradientBoostingRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\HistGradientBoostingRegressor.mq5' (133:16) HistGradientBoostingRegressor (EURUSD,H1) model_name=HistGradientBoostingRegressor OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
Comparação com o modelo original em double no Python:
Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx) Python Mean Absolute Error: 9.070567104488434 MQL5: Mean Absolute Error: 9.0705649779904292
Acurácia do ONNX float MAE: 5 casas decimais.
2.2.9.3. Representação ONNX do hist_gradient_boosting_regressor_float.onnx e hist_gradient_boosting_regressor_double.onnx
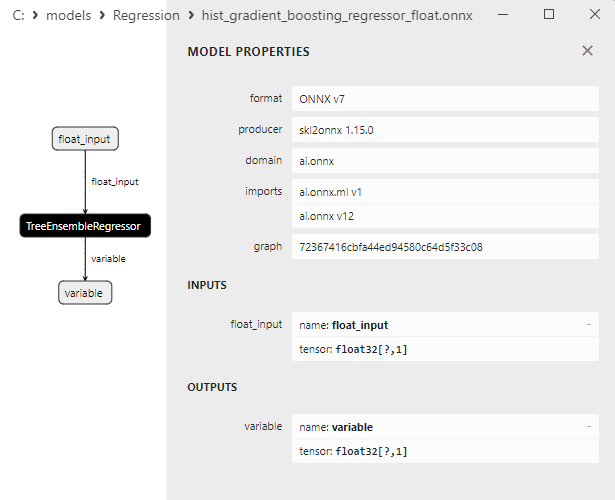
Fig.125. Representação ONNX do hist_gradient_boosting_regressor_float.onnx no Netron
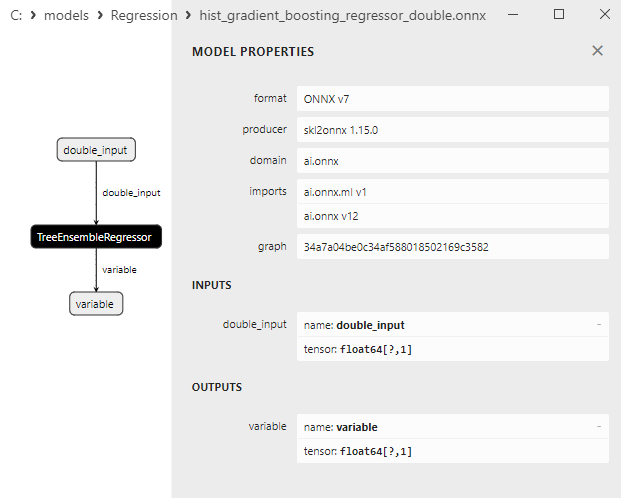
Fig.126. Representação ONNX do hist_gradient_boosting_regressor_double.onnx no Netron
2.2.10. sklearn.svm.SVR
SVR (Support Vector Regression) é um método de aprendizado de máquina usado para tarefas de regressão. É baseado no mesmo conceito do Support Vector Machine (SVM) para classificação, mas é adaptado para regressão. O objetivo principal do SVR é prever valores contínuos da variável alvo, baseando-se na máxima distância média entre os pontos de dados e a linha de regressão.
Como o SVR Funciona:
- Definição de Limites: Semelhante ao SVM, o SVR constrói limites que separam diferentes classes de pontos de dados. Em vez de separação de classes, o SVR visa construir um "tubo" ao redor dos pontos de dados, onde a largura do tubo é controlada por um hiperparâmetro.
- Variável Alvo e Função de Perda: Em vez de usar classes como na classificação, o SVR lida com valores contínuos da variável alvo. Minimiza o erro de previsão medido usando uma função de perda, como a diferença quadrada entre os valores previstos e reais.
- Regularização: O SVR também suporta regularização, ajudando a controlar a complexidade do modelo e a prevenir overfitting.
- Funções de Kernel: O SVR tipicamente emprega funções de kernel que permitem lidar com dependências não lineares entre as características e a variável alvo. As funções de kernel populares incluem a função de base radial (RBF), polinomial e funções lineares.
Vantagens do SVR:
- Robustez a Outliers: O SVR pode lidar com outliers nos dados, pois visa minimizar o erro de previsão.
- Suporte a Dependências Não Lineares: O uso de funções de kernel permite que o SVR modele dependências complexas e não lineares entre as características e a variável alvo.
- Alta Qualidade de Previsão: Em tarefas de regressão que requerem previsões precisas, o SVR pode fornecer resultados de alta qualidade.
Limitações do SVR:
- Sensibilidade a Hiperparâmetros: Escolher a função de kernel e os parâmetros do modelo, como a largura do tubo (hiperparâmetros), pode exigir ajuste e otimização cuidadosos.
- Complexidade Computacional: Treinar o modelo SVR, especialmente ao usar funções de kernel complexas e grandes conjuntos de dados, pode ser intensivo em termos computacionais.
O SVR é um método de aprendizado de máquina para tarefas de regressão baseado na ideia de construir um "tubo" ao redor dos pontos de dados para minimizar os erros de previsão. Ele apresenta robustez a outliers e a capacidade de lidar com dependências não lineares, tornando-o útil em várias tarefas de regressão.
2.2.10.1. Código para criar o modelo SVR e exportá-lo para ONNX em float e double
Este código cria o modelo sklearn.svm.SVR, treina-o em dados sintéticos, salva o modelo no formato ONNX e realiza previsões usando dados de entrada em float e double. Ele também avalia a precisão do modelo original e dos modelos exportados para ONNX.
# SVR.py
# The code demonstrates the process of training SVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "SVR"
onnx_model_filename = data_path + "svr"
# create an SVR model
regression_model = SVR()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training SVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "SVR"
onnx_model_filename = data_path + "svr"
# create an SVR model
regression_model = SVR()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python SVR Original model (double) Python R-squared (Coefficient of determination): 0.398243655775797 Python Mean Absolute Error: 73.63683696034649 Python Mean Squared Error: 7962.89631509593 Python Python SVR ONNX model (float) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_float.onnx Python Information about input tensors in ONNX: Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 1] Python Information about output tensors in ONNX: Python 1. Name: variable, Data Type: tensor(float), Shape: [None, 1] Python R-squared (Coefficient of determination) 0.3982436352100983 Python Mean Absolute Error: 73.63683840363255 Python Mean Squared Error: 7962.896587236852 Python R^2 matching decimal places: 7 Python MAE matching decimal places: 5 Python MSE matching decimal places: 3 Python float ONNX model precision: 5 Python Python SVR ONNX model (double) Python ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_double.onnx
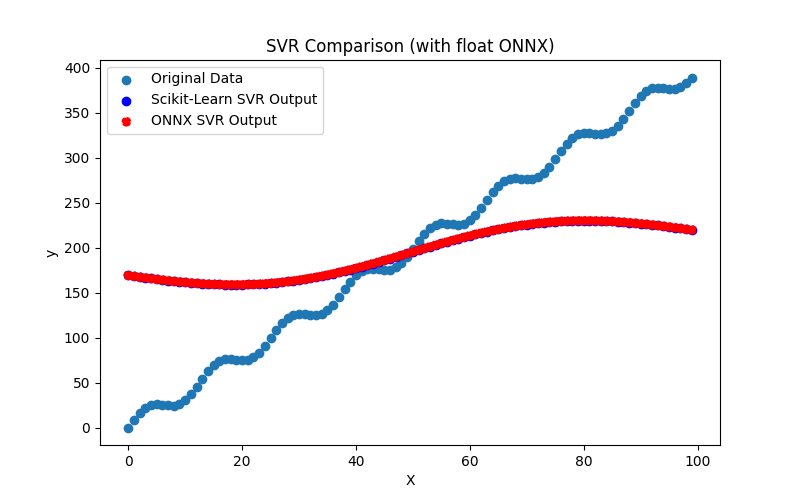
Fig.127. Resultados do SVR.py (float ONNX)
2.2.10.2. Código MQL5 para executar Modelos ONNX
Este código executa os modelos salvos svr_float.onnx e svr_double.onnx, demonstrando o uso de métricas de regressão em MQL5.
//+------------------------------------------------------------------+ //| SVR.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #define ModelName "SVR" #define ONNXFilenameFloat "svr_float.onnx" #define ONNXFilenameDouble "svr_double.onnx" #resource ONNXFilenameFloat as const uchar ExtModelFloat[]; #resource ONNXFilenameDouble as const uchar ExtModelDouble[]; #define TestFloatModel 1 #define TestDoubleModel 2 //+------------------------------------------------------------------+ //| Calculate regression using float values | //+------------------------------------------------------------------+ bool RunModelFloat(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor float input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=(float)input_vector[k]; //--- prepare output tensor float output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Calculate regression using double values | //+------------------------------------------------------------------+ bool RunModelDouble(long model,vector &input_vector, vector &output_vector) { //--- check number of input samples ulong batch_size=input_vector.Size(); if(batch_size==0) return(false); //--- prepare output array output_vector.Resize((int)batch_size); //--- prepare input tensor double input_data[]; ArrayResize(input_data,(int)batch_size); //--- set input shape ulong input_shape[]= {batch_size, 1}; OnnxSetInputShape(model,0,input_shape); //--- copy data to the input tensor for(int k=0; k<(int)batch_size; k++) input_data[k]=input_vector[k]; //--- prepare output tensor double output_data[]; ArrayResize(output_data,(int)batch_size); //--- set output shape ulong output_shape[]= {batch_size,1}; OnnxSetOutputShape(model,0,output_shape); //--- run the model bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data); //--- copy output to vector if(res) { for(int k=0; k<(int)batch_size; k++) output_vector[k]=output_data[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Generate synthetic data | //+------------------------------------------------------------------+ bool GenerateData(const int n,vector &x,vector &y) { if(n<=0) return(false); //--- prepare arrays x.Resize(n); y.Resize(n); //--- for(int i=0; i<n; i++) { x[i]=(double)1.0*i; y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5)); } //--- return(true); } //+------------------------------------------------------------------+ //| TestRegressionModel | //+------------------------------------------------------------------+ bool TestRegressionModel(const string model_name,const int model_type) { //--- long model=INVALID_HANDLE; ulong flags=ONNX_DEFAULT; if(model_type==TestFloatModel) { PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat); model=OnnxCreateFromBuffer(ExtModelFloat,flags); } else if(model_type==TestDoubleModel) { PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble); model=OnnxCreateFromBuffer(ExtModelDouble,flags); } else { PrintFormat("Model type is not incorrect."); return(false); } //--- check if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError()); return(false); } //--- vector x_values= {}; vector y_true= {}; vector y_predicted= {}; //--- int n=100; GenerateData(n,x_values,y_true); //--- bool run_result=false; if(model_type==TestFloatModel) { run_result=RunModelFloat(model,x_values,y_predicted); } else if(model_type==TestDoubleModel) { run_result=RunModelDouble(model,x_values,y_predicted); } //--- if(run_result) { PrintFormat("MQL5: R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2)); PrintFormat("MQL5: Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE)); PrintFormat("MQL5: Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE)); } else PrintFormat("Error %d",GetLastError()); //--- release model OnnxRelease(model); //--- return(true); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { //--- test ONNX regression model for float TestRegressionModel(ModelName,TestFloatModel); //--- test ONNX regression model for double TestRegressionModel(ModelName,TestDoubleModel); //--- return(0); } //+------------------------------------------------------------------+
Saída:
SVR (EURUSD,H1) Testing ONNX float: SVR (svr_float.onnx) SVR (EURUSD,H1) MQL5: R-Squared (Coefficient of determination): 0.3982436352100981 SVR (EURUSD,H1) MQL5: Mean Absolute Error: 73.6368384036325523 SVR (EURUSD,H1) MQL5: Mean Squared Error: 7962.8965872368517012 SVR (EURUSD,H1) SVR (EURUSD,H1) Testing ONNX double: SVR (svr_double.onnx) SVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\R\SVR.mq5' (133:16) SVR (EURUSD,H1) model_name=SVR OnnxCreate error 5800
O modelo ONNX em float foi executado normalmente, mas ocorreu um erro ao executar o modelo ONNX em double.
Comparação com o modelo original em double no Python:
Testing ONNX float: SVR (svr_float.onnx) Python Mean Absolute Error: 73.63683696034649 MQL5: Mean Absolute Error: 73.6368384036325523
Acurácia do ONNX float MAE: 5 casas decimais.
2.2.10.3. Representação ONNX do svr_float.onnx and svr_double.onnx
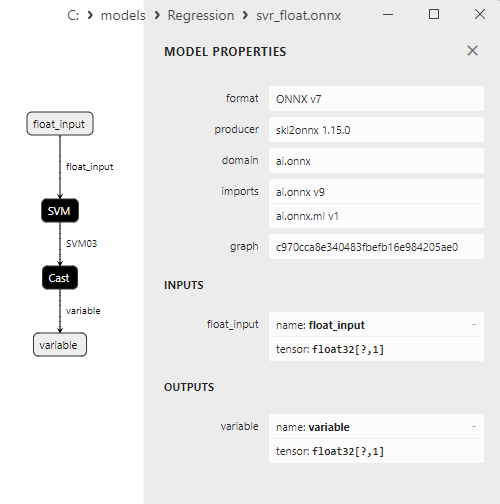
Fig.128. Representação ONNX do svr_float.onnx no Netron
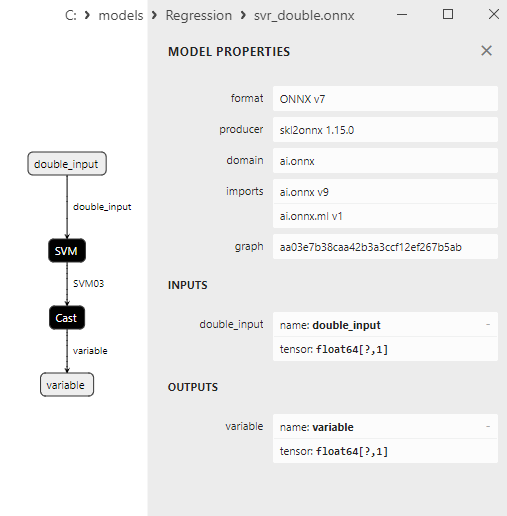
Fig.129. Representação ONNX do svr_double.onnx no Netron
2.3. Modelos de Regressão que Encontraram Problemas ao Serem Convertidos para ONNX
Alguns modelos de regressão não puderam ser convertidos para o formato ONNX pelo conversor sklearn-onnx.
2.3.1. sklearn.dummy.DummyRegressor
DummyRegressor é um método de aprendizado de máquina usado em tarefas de regressão para criar um modelo de referência que prediz a variável alvo usando regras simples. É valioso para comparação com outros modelos mais complexos e para avaliar seu desempenho. Este método é frequentemente usado no contexto de avaliação da qualidade de outros modelos de regressão.
O DummyRegressor oferece várias estratégias de previsão:
- "mean" (padrão): O DummyRegressor prediz o valor médio da variável alvo a partir do conjunto de dados de treinamento. Esta estratégia é útil para determinar o quanto outro modelo é melhor em comparação a simplesmente prever a média.
- "median": O DummyRegressor prediz o valor mediano da variável alvo a partir do conjunto de dados de treinamento.
- "quantile": O DummyRegressor prediz o valor do quantil da variável alvo (especificado pelo parâmetro quantile) a partir do conjunto de dados de treinamento.
- "constant": O DummyRegressor prediz um valor constante definido pelo usuário (usando o parâmetro strategy).
Vantagens do DummyRegressor:
- Avaliação de Desempenho: O DummyRegressor é útil para avaliar o desempenho de outros modelos mais complexos. Se o seu modelo não conseguir superar as previsões feitas pelo DummyRegressor, isso pode indicar problemas no modelo.
- Comparação com Modelos de Referência: O DummyRegressor permite comparar o desempenho de modelos mais complexos com uma linha de base (por exemplo, valor médio ou mediano).
- Fácil de Usar: O DummyRegressor é fácil de implementar e usar para análise comparativa.
Limitações do DummyRegressor:
- Não é para Previsão Precisa: O DummyRegressor fornece apenas previsões básicas de referência e não é destinado a previsões precisas.
- Ignora Dependências Complexas: O DummyRegressor desconsidera estruturas de dados complexas e dependências de características.
- Não Adequado para Tarefas que Requerem Previsão Precisa: Em tarefas reais de previsão, usar o DummyRegressor para prever a variável alvo é insuficiente.
O DummyRegressor é valioso como uma ferramenta para avaliação rápida e comparação de desempenho de outros modelos de regressão, mas não é um modelo de regressão sério e autônomo.
2.3.1.1. Código para criar o modelo DummyRegressor:
# DummyRegressor.py
# The code demonstrates the process of training DummyRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"
# create an Dummy Regressor model
regression_model = DummyRegressor(strategy="mean")
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training DummyRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"
# create an Dummy Regressor model
regression_model = DummyRegressor(strategy="mean")
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python DummyRegressor Original model (double) Python R-squared (Coefficient of determination): 0.0 Python Mean Absolute Error: 100.00329851715793 Python Mean Squared Error: 13232.758393867645
Aba de Erros:
DummyRegressor.py started DummyRegressor.py 1 1 Traceback (most recent call last): DummyRegressor.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) DummyRegressor.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyRegressor'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 DummyRegressor.py finished in 2565 ms 19 1
2.3.2. sklearn.kernel_ridge.KernelRidge
KernelRidge é um método de aprendizado de máquina usado para tarefas de regressão. Combina o método de kernel das Máquinas de Vetores de Suporte (Kernel SVM) e regressão. KernelRidge permite a modelagem de relações complexas e não lineares entre características e a variável alvo usando funções de kernel.
Princípio de funcionamento do KernelRidge:
- Dados de entrada: Começa com o conjunto de dados original contendo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Funções de kernel: KernelRidge usa funções de kernel (como polinomial, RBF - função de base radial, entre outras) que transformam os dados em um espaço de alta dimensão, permitindo a modelagem de relações não lineares mais complexas.
- Treinamento do modelo: O modelo é treinado nos dados minimizando o erro quadrático médio entre os valores previstos e os valores reais da variável alvo. As funções de kernel são usadas para levar em conta dependências complexas.
- Previsão: Após o treinamento, o modelo pode ser usado para prever os valores da variável alvo para novos dados, usando as mesmas funções de kernel.
Vantagens do KernelRidge:
- Modelagem de relações não lineares complexas: KernelRidge permite a modelagem de dependências complexas e não lineares entre características e a variável alvo.
- Seleção de diferentes kernels: Você pode escolher diferentes kernels dependendo da natureza dos dados e da tarefa.
- Regularização: O método inclui regularização, ajudando a prevenir o overfitting do modelo.
Limitações do KernelRidge:
- Falta de interpretabilidade: Como muitos métodos não lineares, o KernelRidge é menos interpretável do que os modelos lineares.
- Complexidade computacional: Usar funções de kernel pode ser computacionalmente caro com grandes volumes de dados e/ou alta dimensionalidade.
- Necessidade de ajuste de parâmetros: Escolher o kernel apropriado e os parâmetros do modelo requer ajuste e expertise.
KernelRidge é útil em tarefas de regressão onde os dados exibem dependências complexas e não lineares, e um modelo capaz de considerar essas relações é necessário. Também é útil em tarefas onde as funções de kernel podem ser utilizadas para transformar os dados em uma representação mais informativa.
2.3.2.1. Código para criar o modelo KernelRidge
# KernelRidge.py
# The code demonstrates the process of training KernelRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"
# create an KernelRidge model
regression_model = KernelRidge(alpha=1.0, kernel='linear')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training KernelRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"
# create an KernelRidge model
regression_model = KernelRidge(alpha=1.0, kernel='linear')
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python KernelRidge Original model (double) Python R-squared (Coefficient of determination): 0.9962137909675411 Python Mean Absolute Error: 6.36977985227399 Python Mean Squared Error: 50.10198935520715
Aba de Erros:
KernelRidge.py started KernelRidge.py 1 1 Traceback (most recent call last): KernelRidge.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) KernelRidge.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.kernel_ridge.KernelRidge'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 KernelRidge.py finished in 2516 ms 19 1
2.3.3. sklearn.isotonic.IsotonicRegression
IsotonicRegression - é um método de aprendizado de máquina usado para tarefas de regressão que modela uma relação monotônica entre as características e a variável alvo. Neste contexto, "monotonicidade" significa que um aumento no valor de uma das características leva a um aumento ou diminuição no valor da variável alvo, mantendo a direção da mudança.
Princípio de funcionamento do IsotonicRegression:
- Dados de entrada: Começa com o conjunto de dados original contendo características (variáveis independentes) e seus valores correspondentes da variável alvo.
- Regressão monotônica: O IsotonicRegression visa encontrar a melhor função monotônica que descreve a relação entre as características e a variável alvo. Esta função pode ser linear ou não linear, mas deve manter a monotonicidade.
- Treinamento do modelo: O modelo é treinado nos dados para determinar os parâmetros da função monotônica. Durante o treinamento, o modelo tenta minimizar a soma dos erros quadráticos entre as previsões e os valores reais da variável alvo.
- Previsão: Após o treinamento, o modelo pode ser usado para prever os valores da variável alvo para novos dados, mantendo a relação monotônica.
Vantagens do IsotonicRegression:
- Modelagem de relações monotônicas: Este método é uma escolha ideal quando os dados demonstram dependências monotônicas, e é importante manter essa característica no modelo.
- Interpretabilidade: Modelos monotônicos podem ser mais interpretáveis, pois permitem uma definição clara da direção da influência de cada característica na variável alvo.
Limitações do IsotonicRegression:
- Não é adequado para relações complexas e não lineares: Este método é limitado a modelar relações monotônicas e, portanto, não é adequado para modelar dependências não lineares complexas.
- Ajuste de parâmetros: Algumas implementações do IsotonicRegression podem ter parâmetros que requerem ajuste para alcançar o desempenho ideal.
IsotonicRegression é útil em tarefas onde a monotonicidade da relação entre as características e a variável alvo é considerada um fator importante e há a necessidade de construir um modelo que preserve essa característica.
2.3.3.1. Código para criar os modelos IsotonicRegression
# IsotonicRegression.py
# The code demonstrates the process of training IsotonicRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"
# create an IsotonicRegression model
regression_model = IsotonicRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training IsotonicRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"
# create an IsotonicRegression model
regression_model = IsotonicRegression()
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python IsotonicRegression Original model (double) Python R-squared (Coefficient of determination): 0.9999898125037958 Python Mean Absolute Error: 0.20093409873424467 Python Mean Squared Error: 0.13480867590911208
Aba de Erros:
IsotonicRegression.py started IsotonicRegression.py 1 1 Traceback (most recent call last): IsotonicRegression.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) IsotonicRegression.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.isotonic.IsotonicRegression'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 IsotonicRegression.py finished in 2499 ms 19 1
2.3.4. sklearn.cross_decomposition.PLSCanonical
PLSCanonical (Partial Least Squares Canonical) é um método de aprendizado de máquina usado para resolver problemas de correlação canônica. É uma extensão do método Partial Least Squares (PLS) e é aplicado para analisar e modelar relações entre dois conjuntos de variáveis.
Princípio de funcionamento do PLSCanonical:
- Dados de entrada: Começa com dois conjuntos de dados (X e Y), onde cada conjunto representa uma coleção de variáveis (características). Geralmente, X e Y contêm dados correlacionados, e a tarefa é encontrar combinações lineares de características que maximizem a correlação entre eles.
- Seleção de combinações lineares: O PLSCanonical encontra combinações lineares (componentes) tanto em X quanto em Y para maximizar a correlação entre os componentes dos dois conjuntos de dados. Esses componentes são chamados de variáveis canônicas.
- Busca de correlação máxima: O objetivo principal do PLSCanonical é encontrar variáveis canônicas que maximizem a correlação entre X e Y, destacando as relações mais informativas entre os dois conjuntos de dados.
- Treinamento do modelo: Uma vez encontradas as variáveis canônicas, elas podem ser usadas para criar um modelo que prevê os valores de Y com base em X.
- Geração de previsões: Após o treinamento, o modelo pode ser usado para prever os valores de Y em novos dados usando os valores correspondentes de X.
Vantagens do PLSCanonical:
- Análise de correlação: O PLSCanonical permite a análise e modelagem de correlações entre dois conjuntos de dados, o que pode ser útil para entender as relações entre variáveis.
- Redução de dimensionalidade: O método também pode ser usado para reduzir a dimensionalidade dos dados, destacando os componentes mais importantes.
Limitações do PLSCanonical:
- Sensibilidade à escolha do número de componentes: Selecionar o número ótimo de variáveis canônicas pode exigir alguma experimentação.
- Dependência da estrutura dos dados: Os resultados do PLSCanonical podem depender fortemente da estrutura dos dados e das correlações entre eles.
PLSCanonical é um método de aprendizado de máquina usado para analisar e modelar correlações entre dois conjuntos de variáveis. Este método permite estudar relações entre dados e pode ser útil para reduzir a dimensionalidade dos dados e prever valores com base em componentes correlacionados.
2.3.4.1. Código para criar o PLSCanonical
# PLSCanonical.py
# The code demonstrates the process of training PLSCanonical model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"
# create an PLSCanonical model
regression_model = PLSCanonical(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training PLSCanonical model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"
# create an PLSCanonical model
regression_model = PLSCanonical(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python Python PLSCanonical Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Aba de Erros:
PLSCanonical.py started PLSCanonical.py 1 1 Traceback (most recent call last): PLSCanonical.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) PLSCanonical.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.PLSCanonical'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 PLSCanonical.py finished in 2513 ms 19 1
2.3.5. sklearn.cross_decomposition.CCA
Canonical Correlation Analysis (CCA) é um método de análise estatística multivariada usado para estudar as relações entre dois conjuntos de variáveis (conjunto X e conjunto Y). O principal objetivo do CCA é encontrar combinações lineares de variáveis X e Y que maximizem a correlação entre elas. Essas combinações lineares são chamadas de variáveis canônicas.
Princípio de funcionamento do CCA:
- Dados de entrada: Começa com dois conjuntos de variáveis X e Y. Pode haver qualquer número de variáveis nesses conjuntos, e o CCA tenta encontrar combinações lineares que maximizem a correlação entre elas.
- Construção de variáveis canônicas: O CCA identifica variáveis canônicas em X e Y que maximizam a correlação entre elas. Essas variáveis canônicas são combinações lineares das variáveis originais, uma para cada indicador canônico.
- Avaliação da correlação: O CCA avalia a correlação entre pares de variáveis canônicas. As variáveis canônicas são geralmente ordenadas por correlação decrescente, então o primeiro par tem a maior correlação, o segundo tem a próxima maior, e assim por diante.
- Interpretação: As variáveis canônicas podem ser interpretadas considerando sua correlação e pesos das variáveis. Isso permite entender quais variáveis dos conjuntos X e Y estão mais fortemente relacionadas.
Vantagens do CCA:
- Revela conexões ocultas: O CCA pode ajudar a descobrir correlações ocultas entre dois conjuntos de variáveis que podem não ser óbvias durante a análise inicial.
- Robusto ao ruído: O CCA pode considerar o ruído nos dados e focar nas correlações mais significativas.
- Múltiplas aplicações: O CCA pode ser usado em vários campos, incluindo estatística, bioinformática, finanças, entre outros, para estudar relações entre conjuntos de variáveis.
Limitações do CCA:
- Requer mais dados: O CCA pode exigir uma quantidade maior de dados do que outros métodos de análise para estimar correlações de forma confiável.
- Relações lineares: O CCA assume relações lineares entre as variáveis, o que pode ser insuficiente em alguns casos.
- Complexidade de interpretação: Interpretar variáveis canônicas pode ser complexo, especialmente quando há muitas variáveis nos conjuntos X e Y.
O CCA é benéfico em tarefas onde é necessário estudar a relação entre dois conjuntos de variáveis e descobrir correlações ocultas.
2.3.5.1. Código para criar o modelo CCA
# CCA.py
# The code demonstrates the process of training CCA model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="CCA"
onnx_model_filename = data_path + "cca"
# create an CCA model
regression_model = CCA(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
# The code demonstrates the process of training CCA model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# function to compare matching decimal places
def compare_decimal_places(value1, value2):
# convert both values to strings
str_value1 = str(value1)
str_value2 = str(value2)
# find the positions of the decimal points in the strings
dot_position1 = str_value1.find(".")
dot_position2 = str_value2.find(".")
# if one of the values doesn't have a decimal point, return 0
if dot_position1 == -1 or dot_position2 == -1:
return 0
# calculate the number of decimal places
decimal_places1 = len(str_value1) - dot_position1 - 1
decimal_places2 = len(str_value2) - dot_position2 - 1
# find the minimum of the two decimal places counts
min_decimal_places = min(decimal_places1, decimal_places2)
# initialize a count for matching decimal places
matching_count = 0
# compare characters after the decimal point
for i in range(1, min_decimal_places + 1):
if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
matching_count += 1
else:
break
return matching_count
# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)
model_name="CCA"
onnx_model_filename = data_path + "cca"
# create an CCA model
regression_model = CCA(n_components=1)
# fit the model to the data
regression_model.fit(X, y.ravel())
# predict values for the entire dataset
y_pred = regression_model.predict(X)
# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)
# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)
print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')
# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]
# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)
# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)
print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)
# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]
# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))
# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')
Saída:
Python CCA Original model (double) Python R-squared (Coefficient of determination): 0.9962347199278333 Python Mean Absolute Error: 6.3561407034365995 Python Mean Squared Error: 49.82504148022689
Aba de Erros:
CCA.py started CCA.py 1 1 Traceback (most recent call last): CCA.py 1 1 onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12) CCA.py 87 1 onnx_model = convert_topology( convert.py 208 1 topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1 self.call_shape_calculator(operator) _topology.py 1348 1 operator.infer_types() _topology.py 1163 1 raise MissingShapeCalculator( _topology.py 629 1 skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.CCA'>'. _topology.py 629 1 It usually means the pipeline being converted contains a _topology.py 629 1 transformer or a predictor with no corresponding converter _topology.py 629 1 implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1 in another library, you need to register _topology.py 629 1 the converted so that it can be used by sklearn-onnx (function _topology.py 629 1 update_registered_converter). If the model is not yet covered _topology.py 629 1 by sklearn-onnx, you may raise an issue to _topology.py 629 1 https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1 to get the converter implemented or even contribute to the _topology.py 629 1 project. If the model is a custom model, a new converter must _topology.py 629 1 be implemented. Examples can be found in the gallery. _topology.py 629 1 CCA.py finished in 2543 ms 19 1
Conclusão
O artigo revisou 45 modelos de regressão disponíveis na biblioteca Scikit-learn versão 1.3.2.
1. Deste conjunto, 5 modelos enfrentaram dificuldades ao serem convertidos para o formato ONNX:
- DummyRegressor (Regressor Dummy);
- KernelRidge (Regressão Kernel Ridge);
- IsotonicRegression (Regressão Isotônica);
- PLSCanonical (Análise Canônica de Mínimos Quadrados Parciais);
- CCA (Análise de Correlação Canônica).
Esses modelos podem ser muito complexos em sua estrutura ou lógica e podem usar estruturas de dados ou algoritmos específicos que não são totalmente compatíveis com o formato ONNX.
2. Os 40 modelos restantes foram convertidos com sucesso para ONNX com cálculos em precisão float.
- ARDRegression: Regressão de Determinação Automática de Relevância (ARD);
- BayesianRidge: Regressão Bayesiana Ridge com regularização;
- ElasticNet: Combinação de regularização L1 e L2 para mitigar overfitting;
- ElasticNetCV: Elastic Net com seleção automática de parâmetro de regularização;
- HuberRegressor: Regressão com sensibilidade reduzida a outliers;
- Lars: Regressão de Ângulo Mínimo;
- LarsCV: Regressão de Ângulo Mínimo com validação cruzada;
- Lasso: Regressão regularizada L1 para seleção de características;
- LassoCV: Regressão Lasso com validação cruzada;
- LassoLars: Combinação de Lasso e LARS para regressão;
- LassoLarsCV: Regressão LassoLars com validação cruzada;
- LassoLarsIC: Critérios de informação para seleção de parâmetros LassoLars;
- LinearRegression: Regressão linear simples;
- Ridge: Regressão linear com regularização L2;
- RidgeCV: Regressão Ridge com validação cruzada;
- OrthogonalMatchingPursuit: Regressão com seleção ortogonal de características;
- PassiveAggressiveRegressor: Regressão com abordagem de aprendizado passivo-agressivo;
- QuantileRegressor: Regressão quantílica;
- RANSACRegressor: Regressão com o método RANdom SAmple Consensus;
- TheilSenRegressor: Regressão não linear baseada no método Theil-Sen.
- LinearSVR: Regressão linear de vetores de suporte;
- MLPRegressor: Regressão usando perceptron multicamadas;
- PLSRegression: Regressão de Mínimos Quadrados Parciais;
- TweedieRegressor: Regressão baseada na distribuição de Tweedie;
- PoissonRegressor: Regressão para modelar dados distribuídos de Poisson;
- RadiusNeighborsRegressor: Regressão baseada em vizinhos de raio;
- KNeighborsRegressor: Regressão baseada em k-vizinhos mais próximos;
- GaussianProcessRegressor: Regressão baseada em processos gaussianos;
- GammaRegressor: Regressão para modelar dados distribuídos de gama;
- SGDRegressor: Regressão baseada em gradiente descendente estocástico;
- AdaBoostRegressor: Regressão usando o algoritmo AdaBoost;
- BaggingRegressor: Regressão usando o método Bagging;
- DecisionTreeRegressor: Regressão baseada em árvore de decisão;
- ExtraTreeRegressor: Regressão baseada em árvore de decisão extra;
- ExtraTreesRegressor: Regressão com árvores de decisão extra;
- NuSVR: Regressão contínua de vetores de suporte linear (SVR);
- RandomForestRegressor: Regressão com um conjunto de árvores de decisão (Random Forest);
- GradientBoostingRegressor: Regressão com boosting de gradiente;
- HistGradientBoostingRegressor: Regressão com boosting de gradiente histograma;
- SVR: Método de regressão de vetores de suporte.
3. A possibilidade de converter modelos de regressão em ONNX com cálculos em precisão dupla também foi explorada.
Um problema sério encontrado durante a conversão de modelos para precisão dupla em ONNX é a limitação dos operadores ML ai.onnx.ml.LinearRegressor, ai.onnx.ml.SVMRegressor, ai.onnx.ml.TreeEnsembleRegressor: seus parâmetros e valores de saída são do tipo float. Essencialmente, esses são componentes de redução de precisão e sua execução em cálculos de precisão dupla é duvidosa. Por essa razão, a biblioteca ONNX Runtime não implementou alguns operadores para modelos ONNX em precisão dupla (podem ocorrer erros de natureza NOT_IMPLEMENTED: 'Could not find an implementation for the node LinearRegressor (1)', 'Could not find an implementation for SVMRegressor(1) node with name 'SVM', e assim por diante). Assim, dentro da especificação atual do ONNX, a operação completa em precisão dupla para esses operadores ML é impossível.
Para modelos de regressão linear, o conversor sklearn-onnx conseguiu contornar a limitação do LinearRegressor: são usados os operadores ONNX MatMul() e Add(). Graças a essa abordagem, os primeiros 30 modelos da lista anterior foram convertidos com sucesso em modelos ONNX com cálculos em precisão dupla, e esses modelos mantiveram a precisão dos modelos originais em precisão dupla.
No entanto, para operadores de ML mais complexos, como SVMRegressor e TreeEnsembleRegressor, isso não foi alcançado. Portanto, modelos como AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor e SVR estão atualmente disponíveis apenas em modelos ONNX com cálculos em float.
Resumo
O artigo abordou 45 modelos de regressão da versão 1.3.2 da biblioteca Scikit-learn e seus resultados de conversão para o formato ONNX para cálculos em precisão float e dupla.
De todos os modelos revisados, 5 se mostraram complexos para conversão em ONNX. Esses modelos incluem DummyRegressor, KernelRidge, IsotonicRegression, PLSCanonical e CCA. Sua estrutura ou lógica complexa pode exigir adaptação adicional para uma conversão ONNX bem-sucedida.
Os 40 modelos de regressão restantes foram transformados com sucesso para o formato ONNX em float. Entre eles, 30 modelos também foram convertidos com sucesso para o formato ONNX em precisão dupla, mantendo sua precisão.
Devido à limitação nos operadores ML para SVMRegressor e TreeEnsembleRegressor, os modelos AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor e SVR estão atualmente disponíveis apenas em modelos ONNX com cálculos em float.
Todos os scripts do artigo também estão disponíveis no projeto público MQL5\Shared Projects\Scikit.Regression.ONNX.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/13538
Arquivos anexados |
Scikit.Regression.ONNX.zip
(563.48 KB)
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Ir para discussão
Redes neurais de maneira fácil (Parte 75): aumentando a produtividade dos modelos de previsão de trajetórias
Os modelos que estamos criando estão se tornando cada vez maiores e mais complexos. Com isso, aumentam os custos não apenas para o treinamento, mas também para a operação. Além disso, muitas vezes nos deparamos com situações em que o tempo de tomada de decisão é crítico. E, por isso, voltamos nossa atenção para métodos de otimização de desempenho dos modelos sem perder qualidade.
Desenvolvendo um sistema de Replay (Parte 55): Módulo de controle
Neste artigo iremos implementar o indicador de controle de forma que ele possa o sistema de mensagens que está sendo implementado. Apesar de não ser algo muito complexo de ser feito, você precisa entender alguns detalhes referentes a como fazer a inicialização deste módulo. O conteúdo exposto aqui, visa e tem como objetivo, pura e simplesmente a didática. De modo algum deve ser encarado como sendo, uma aplicação cuja finalidade não venha a ser o aprendizado e estudo dos conceitos mostrados.
Desenvolvendo um EA multimoeda (Parte 2): Transição para posições virtuais de estratégias de trading
Vamos continuar a desenvolver o EA multimoeda com várias estratégias funcionando paralelamente. Tentaremos transferir todo o trabalho relacionado à abertura de posições a mercado do nível das estratégias para o nível do expert que gerencia as estratégias. As próprias estratégias irão negociar apenas virtualmente, sem abrir posições a mercado.
Algoritmos de otimização populacionais: objetos de busca multissociais artificiais (artificial Multi-Social search Objects, MSO)
Continuação do artigo anterior como desenvolvimento da ideia de grupos sociais. No novo artigo, explora-se a evolução dos grupos sociais utilizando algoritmos de movimentação e memória. Os resultados ajudarão a entender a evolução dos sistemas sociais e aplicá-los na otimização e busca de soluções.
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se