Visualize isto! Biblioteca gráfica em linguagem MQL5 como equivalente a plot de R

A exibição visual usando gráficos desempenha um importante papel na exploração e estudo de padrões regulares. Nas populares linguagens de programação entre a comunidade científica, tais como R e Python, a função especial plot é destinada para visualização, com ela você pode desenhar linhas, gráficos de dispersão e histogramas para visualizar padrões.

A vantagem mais importante da função plot é que a plotagem de qualquer gráfico requer apenas algumas cadeias de caracteres de código. Basta passar - como parâmetros - uma matriz de dados, especificar o tipo de gráfico desejado, e já está! Todo o trabalho de rotina no cálculo de escala, a plotagem de eixos, a escolha de cores e muito mais é assumido pela função plot.

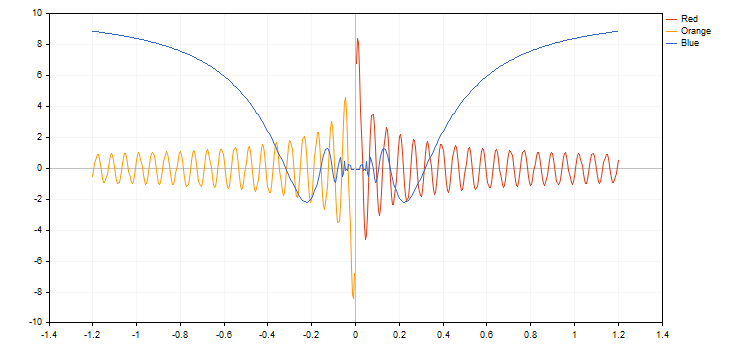
Na linguagem MQL5, todas as possibilidades desta função são apresentadas pelos métodos da biblioteca gráfica a partir da Biblioteca padrão. Aqui está um exemplo do código e o resultado de sua execução:

#include <Graphics\Graphic.mqh>
#define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression)
//--- Functions
double BlueFunction(double x)   { return(RESULT_OR_NAN(x,10*x*sin(1/x)));      }
double RedFunction(double x)    { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); }
double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));}
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from=-1.2;
   double to=1.2;
   double step=0.005;
   CGraphic graphic;
   graphic.Create(0,"G",0,30,30,780,380);
//--- colors
   CColorGenerator generator;
   uint blue= generator.Next();
   uint red = generator.Next();
   uint orange=generator.Next();
//--- plot all curves
   graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red");
   graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange");
   graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue");
   graphic.CurvePlotAll();
   graphic.Update();
  }

Classe base CCanvas e seu desenvolvimento

A biblioteca padrão contém a classe base CCanvas, ela é projetada para criação rápida e fácil de imagens diretamente nos gráficos de preço. A criação do recurso gráfico e o desenho futuro sobre a tela de primitivas simples - pontos, linhas e linhas quebradas, círculos, triângulos e polígonos - são baseados no trabalho desta classe. Nela também são implementadas funções para o preenchimento colorido de formas e saída de informações na fonte, cor e tamanho corretos.

Inicialmente a classe CCanvas continha apenas dois modos de renderização de primitivas gráficas, isto é, com suavização (antialiasing, AA) e sem ela. Logo foram adicionadas novas funções para construir primitivas com base no algoritmo Wu:

• LineWu — linha reta
• PolylineWu — linha poligonal
  
• PolygonWu — polígono
  
• TriangleWu — triângulo
  
• CircleWu — círculo
• EllipseWu — elipse

O algoritmo Wu combina a correção de alta qualidade do serrilhamento (aliasing) e uma velocidade próxima do algoritmo de Bresenham sem suavização (antialiasing). Nele existe um contraste visual em relação ao algoritmo padrão de suavização (AA), implementado na CCanvas. Aqui está um exemplo de uma renderização de uma circunferência usando três funções diferentes:

#include<Canvas\Canvas.mqh>
CCanvas canvas;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int      Width=800;
   int      Height=600;
//--- create canvas
   if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height))
     {
      Print("Error creating canvas: ",GetLastError());
     }
//--- draw
   canvas.Erase(clrWhite);
   canvas.Circle(70,70,25,clrBlack);
   canvas.CircleAA(120,70,25,clrBlack);
   canvas.CircleWu(170,70,25,clrBlack);
//---
   canvas.Update();  
  }

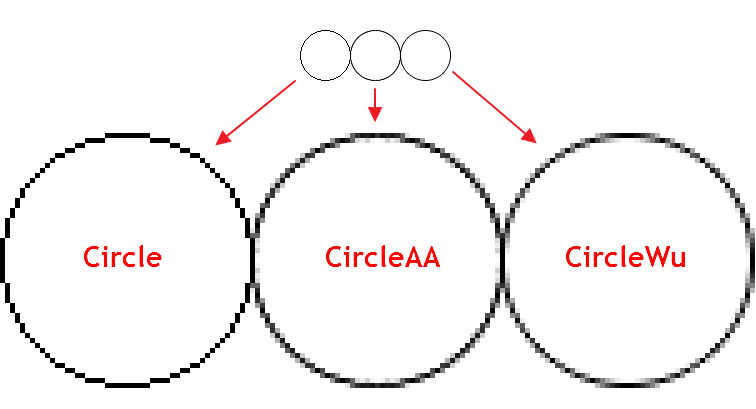
Como pode ser visto a partir da figura, a CircleAA() - com algoritmo padrão de suavização - desenha uma linha mais grossa do que a função CircleWu() segundo o algoritmo de Wu. A CircleWu parece mais precisa e natural, graças a uma espessura menor e melhor cálculo da gradação da circunferência.

Também foram feitas outras melhorias na classe CCanvas:

1. Foi adicionada uma nova primitiva gráfica, trata-se da elipse com dois variantes de suavização, isto é, EllipseAA() e EllipseWu()
   
2. Foi adicionada a sobrecarga da função de preenchimento de área com um novo parâmetro que responde pela "sensibilidade do preenchimento" (parâmetro threshould).

Algoritmo de trabalho com a biblioteca

1. Após ligar a biblioteca, é necessário criar o objeto de classe CGraphic. É precisamente nele onde serão incluídas as curvas que devem ser desenhadas.

Em seguida, para o objeto criado, é preciso chamar o método Create(), nele são definidos os parâmetros básicos do gráfico:

1. Identificador de gráfico
2. Nome de objeto
3. Índice de janela
   
4. Ponto de âncora de gráfico
5. Largura e altura de gráfico

Este método criará - com base nos parâmetros inseridos - o objeto no gráfico e o recurso gráfico em que será construído o gráfico.

   //--- objeto para criar gráficos
   CGraphic graphic;
   //--- criação da área de desenho
   graphic.Create(0,"Graphic",0,30,30,830,430);

Como resultado, nós já temos uma tela pronta para desenho.

2. Agora preenchemos com curvas nosso objeto. A adição é realizada pelo método CurveAdd(), que, por sua vez, tem a capacidade de criar curvas de quatro maneiras diferentes:

1. Com base na matriz unidimensional do tipo double. Neste caso, os valores a partir da matriz serão exibidos no eixo Y, enquanto os índices da matriz servirão como coordenadas X.
2. Com base nas duas matrizes x[] e y[] do tipo double.
3. Com base na matriz CPoint2D.
4. Com base no ponteiro para a função CurveFunction() e três valores para construção dos argumentos da função: inicial, final e incremento do argumento.

O método CurveAdd() retorna o ponteiro para a classe CCurve, desse modo nós temos um acesso rápido à curva recém-criada e podemos alterar suas propriedades.

   double x[]={-10,-4,-1,2,3,4,5,6,7,8};

   double y[]={-5,4,-10,23,17,18,-9,13,17,4};

   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);

3. Além disso, qualquer das curvas adicionadas pode ser exibida no gráfico. Isto pode ser realizado de três maneiras.

1. Usando o método CurvePlotAll() — ele desenha automaticamente todas as curvas adicionadas no gráfico.
   graphic.CurvePlotAll();
2. Usando o método CurvePlot() — ele desenha a curva de acordo com o índice especificado.
   graphic.CurvePlot(0);
3. Usando o método Redraw() e colocando o valor true para a propriedade Visible na curva.
   curve.Visible(true);
   graphic.Redraw();

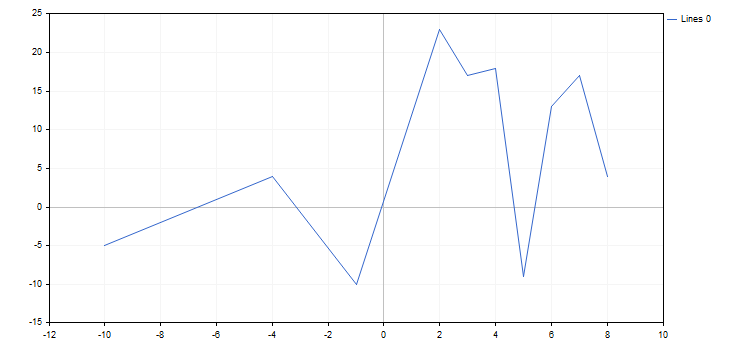
4. Para desenhar o traçado no gráfico, resta chamar o método Update(). Como resultado, obtemos o código completo do script para criar um gráfico simples:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   graphic.CurvePlotAll();
   graphic.Update();
  }

Aqui está uma imagem deste gráfico:

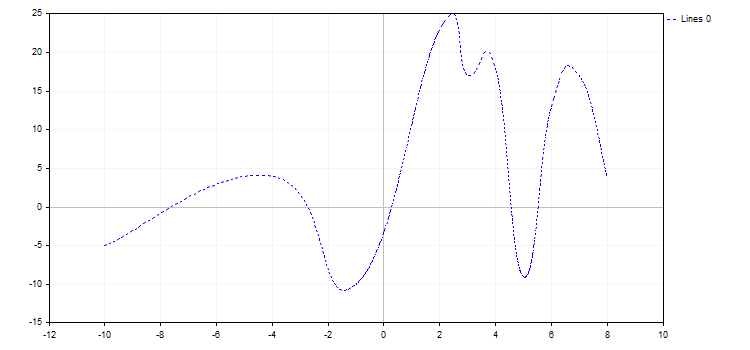
É possível a qualquer momento alterar as propriedades do gráfico e cada uma de suas funções. Por exemplo, adicionamos os rótulos dos eixos do gráfico, alteramos o nome da curva e ativamos para ele o modo curva de aproximação:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CGraphic graphic;
   graphic.Create(0,"Graphic",0,30,30,780,380);
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
   curve.Name("Example");                
   curve.LinesIsSmooth(true);            
   graphic.XAxis().Name("X - axis");      
   graphic.XAxis().NameSize(12);          
   graphic.YAxis().Name("Y - axis");      
   graphic.YAxis().NameSize(12);
   graphic.YAxis().ValuesWidth(15);
   graphic.CurvePlotAll();
   graphic.Update();
   DebugBreak();
  }

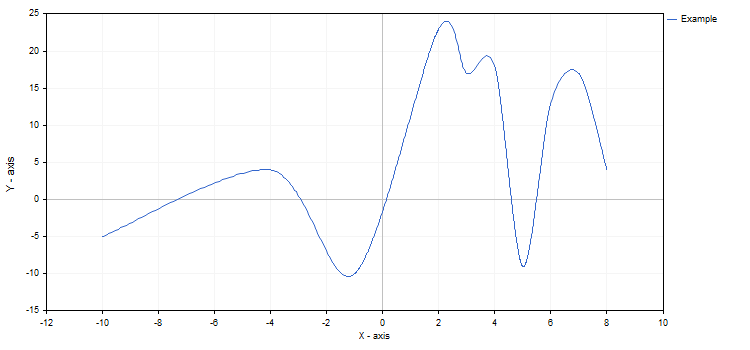
Se houvesse alterações após a chamada da CurvePlotAll, deveríamos adicionalmente chamar o método Redraw, para vê-las.

Como a maioria das bibliotecas atuais, a Graphics implementa uma variedade de algoritmos que facilitam significativamente o processo de plotagem de gráficos:

1. A biblioteca em si é capaz de gerar cores contrastantes de curvas, se elas não são definidas explicitamente.
2. Os eixos do gráfico têm o modo paramétrico de dimensionamento automático, ele pode ser desativado se desejar.
3. Os nomes das curvas são gerados automaticamente, dependendo de seu tipo e ordem de adição.
4. O espaço de trabalho do gráfico é riscado automaticamente e os eixos reais são selecionados.
5. É possível suavizar as curvas ao desenhar usando linhas.

Além disso, entre as características adicionais da biblioteca Graphics é necessário referir os métodos que permitem adicionar novos elementos ao gráfico:

1. TextAdd() — adiciona o texto num lugar arbitrário, no gráfico, é necessário definir as coordenadas na escala real. Para uma configuração exata do texto a ser exibido, use o método FontSet.
   
2. LineAdd() — adiciona a linha num lugar arbitrário, no gráfico, é necessário definir as coordenadas na escala real.
3. MarksToAxisAdd() — adicionas novos marcadores para o eixo de coordenadas especificado.

É importante notar que os dados sobre a adição destes elementos não são armazenados em nenhum lugar, de modo que, após desenhar ou redesenhar uma nova curva, no gráfico, todos os desenhos serão removidos.

Tipos de gráficos

A biblioteca Graphics suporta os tipos básicos de processamento básico de curvas, todos eles são listados na enumeração ENUM_CURVE_TYPE:

1. CURVE_POINTS — desenha curvas usando pontos
2. CURVE_LINES — desenha curvas usando linhas
3. CURVE_POINTS_AND_LINES — desenha curvas usando pontos e usando linhas
4. CURVE_STEPS — desenha curvas em escada
   
5. CURVE_HISTOGRAM — desenha curvas em forma de histograma
6. CURVE_NONE — não desenha curvas
   

Cada um destes modos tem propriedades particulares que ao serem alteradas afetam a qualidade da exibição da curva no gráfico. Tendo o ponteiro CCurve para a curva, é possível alterar rapidamente estas propriedades. É por isso que é recomendado memorizar todos os ponteiros que retorna o método CurveAdd. O nome da propriedade começa sempre com o nome do modo de desenho de curva em que é usado.

Consideremos em detalhe as propriedades de cada tipo.

1. O modo de renderização usando pontos CURVE_POINTS é o mais simples e rápido que desenha cada coordenada da curva usando o ponto com as propriedades definidas:

• PointsSize — tamanho dos pontos
• PointsFill — sinalizador que indica a presença de preenchimento
  
• PointsColor — cor de preenchimento
  
• PointsType — tipo de pontos
  

A cor da própria curva, neste caso, define a cor exterior dos pontos.

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_POINTS);
   curve.PointsSize(20);
   curve.PointsFill(true);
   curve.PointsColor(ColorToARGB(clrRed,255));

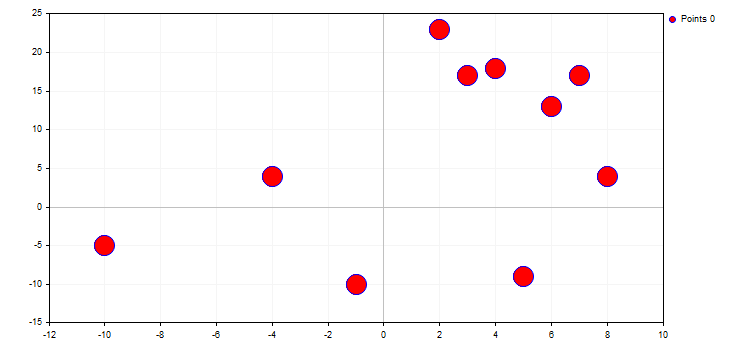
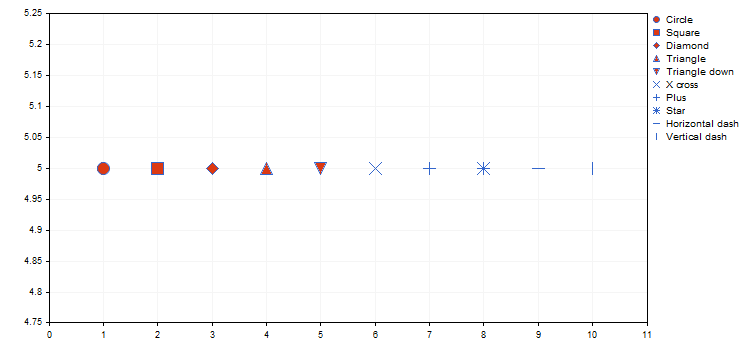
O tipo de pontos define uma forma geométrica específica a partir da enumeração ENUM_POINT_TYPE, com a qual serão exibidos todos os pontos da curva. Em total, ENUM_POINT_TYPE inclui dez formas geométricas básicas:

1. POINT_CIRCLE — círculo (é usado por padrão)
   
2. POINT_SQUARE — quadrado
   
3. POINT_DIAMOND — diamante
   
4. POINT_TRIANGLE — triângulo
   
5. POINT_TRIANGLE_DOWN — triângulo invertido
   
6. POINT_X_CROSS — cruz
   
7. POINT_PLUS — sinal de mais
   
8. POINT_STAR — estrela
   
9. POINT_HORIZONTAL_DASH — linha horizontal
   
10. POINT_VERTICAL_DASH — linha vertical
    

Exemplo de exibição visual de diferentes tipos de íris (veja o artigo Usar mapas auto-organizáveis (mapas de Kohonen) no MetaTrader 5 ) a partir do script anexado IrisSample.mq5.

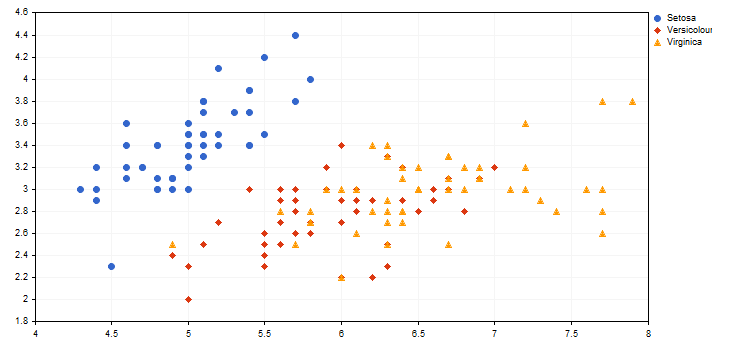
2. O modo de renderização usando linhas CURVE_LINES é o principal modo para visualização de curvas, nele cada par de pontos é conectado por uma ou mais retas (em caso de suavização). As propriedades deste modo são:

• LinesStyle — estilo de linha a partir da enumeração ENUM_LINE_STYLE
  
• LinesSmooth — sinalizador que indica se é necessário executar a suavização
  
• LinesSmoothTension — grau de suavização
  
• LinesSmoothStep — comprimento das linhas que se aproximam durante a suavização
  

Na Graphics é implementado o algoritmo paramétrico padrão de suavização de curvas. Consiste em duas fases:

1. Para cada par de pontos, com base em sua derivada há dois pontos de controle
2. Com base nestes quatro pontos, é construída a curva de Bezier com incrementos predeterminados

O parâmetro LinesSmoothTension aceita valores (0.0; 1.0]. Se LinesSmoothTension for definido como 0.0, não haverá suavização, ao aumentar este parâmetro, mais suavizada é a curva.

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_LINES);
   curve.LinesStyle(STYLE_DOT);
   curve.LinesSmooth(true);
   curve.LinesSmoothTension(0.8);
   curve.LinesSmoothStep(0.2);

3. O modo de renderização usando pontos e linha CURVE_POINTS_AND_LINES combina os dois primeiros modos e suas propriedades.

4 O modo de renderização da curva em escada CURVE_STEPS é o modo em que cada par de pontos é ligado por dois linas em forma de escada. Este modo tem duas propriedades:

• LinesStyle — esta propriedade é tomada a partir do CURVE_POINTS e é caraterizada pelo estilo das linhas
• StepsDimension — dimensão segundo a qual é feito o passo: 0 — x (primeiro, linha horizontal, em seguida, linha vertical) ou 1 — y (primeiro, linha vertical, em seguida, linha horizontal).
  

   CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_STEPS);
   curve.LinesStyle(STYLE_DASH);
   curve.StepsDimension(1);

5. O modo de renderização de histograma CURVE_HISTOGRAM desenha um gráfico de colunas padrão. Este modo tem apenas uma propriedade:

• HistogramWidth — largura de cada coluna do histograma

Se a largura adotar valores grandes, por um lado, os dados começarão a se fundir e, por outro lado, as colunas com valores grandes Y "engolirão" as colunas vizinhas com valores menores.

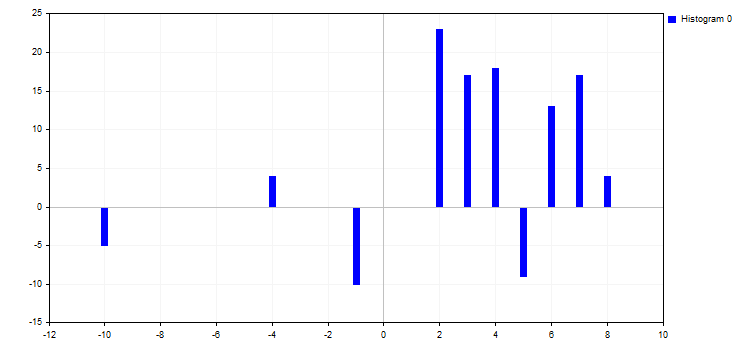
6 O último modo CURVE_NONE não implica qualquer representação gráfica da curva, independentemente da sua visibilidade.

Deve notar-se que, durante o dimensionamento automático, todas as curvas adicionadas ao gráfico têm valores, por conseguinte, mesmo se a curva não for renderizada ou tiver o modo CURVE_NONE, seus valores serão tidos em conta.

Gráficos nas funções, geração rápida em várias cadenas de caracteres

Outra vantagem da biblioteca é o trabalho com ponteiros para a função CurveFunction. Os ponteiros para a função em linguagem MQL5 aceitam apenas funções globais ou estáticas, além disso, a sintaxe da função deve coincidir com a sintaxe do ponteiro. No nosso caso, o ponteiro CurveFunction é configurado paras as funções que recebem um parâmetro do tipo double, e também retorna double.

Para plotar a curva de acordo com o ponteiro para a função, também precisamos especificar exatamente os valores inicial (from), final (to) do argumento e seu incremento (step). Assim, quanto menor o incremento, mais pontos de função teremos para sua plotagem. Para criar data de série, utilize CurveAdd(),, enquanto, para plotagem da função, utilize CurvePlot() ou CurvePlotAll().

Por exemplo, criamos uma função de parábola e consideramos vários incrementos:

#include <Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Parabola                                                         |
//+------------------------------------------------------------------+
double Parabola(double x) { return MathPow(x,2); }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   double from1=-5;
   double to1=0;
   double step1=1;
  
   double from2=0;
   double to2=5;
   double step2=0.2;
  
   CurveFunction function = Parabola;
  
   CGraphic graph;
   graph.Create(0,"Graph",0,30,30,780,380);
   graph.CurveAdd(function,from1,to1,step1,CURVE_LINES);
   graph.CurveAdd(function,from2,to2,step2,CURVE_LINES);
   graph.CurvePlotAll();
   graph.Update();
  }

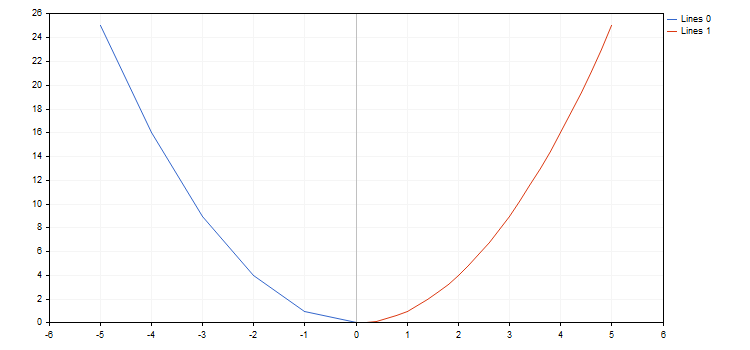
Ao fazer isto, a biblioteca é capaz de trabalhar com as funções com pontos de interrupção (uma das coordenadas quer tem o valor mais ou menos infinito quer é não-numérica). É importante ter em mente que, ao acontecer isto, o incremento é segundo a função, uma vez que, em alguns casos, podemos simplesmente ignorar o ponto de interrupção e, consequentemente, o gráfico não atenderá às expectativas. Por exemplo, plotamos duas funções hipérbole no intervalo [-5,0; 5,0], a primeira tem incrementos de 0,7, e a segunda, de 0,1. Obtemos o seguinte resultado:

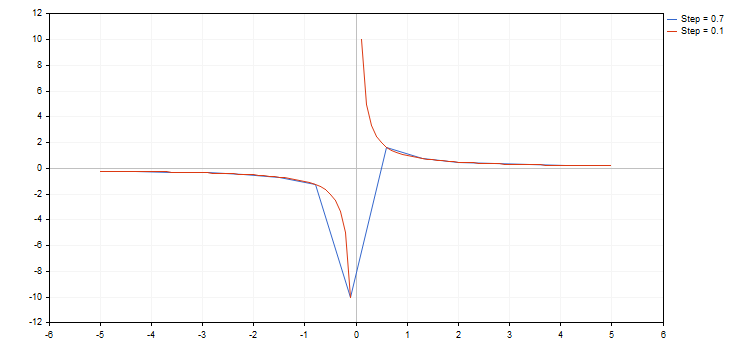
A figura acima mostra que com o incremento 0,7 apenas passamos o ponto de interrupção e, como resultado, o gráfico da curva obtida tem pouco a ver com a função real da hipérbole.

Ao utilizar as funções, pode ocorrer o erro "divisão por zero". Você pode resolver este problema de duas maneiras:

• desativar - no arquivo metaeditor.ini - o controle da divisão por zero
  
  [Experts]
  FpNoZeroCheckOnDivision=1
• ou analisar a fórmula a ser utilizada na função e retornar para tais casos um valor válido. Nos arquivos 3Functions.mq5 e bat.mq5 do apêndice, você encontrará um exemplo de tal processamento com ajuda de uma macro.

  
  
  
  

  
  

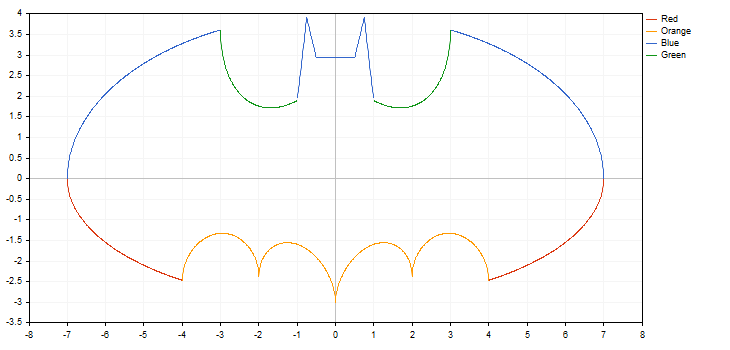
Funções de plotagem rápida

A biblioteca Graphics também inclui uma série de funções globais GraphPlot() que por si mesmas e com base em dados executarão todas as etapas para criação do gráfico e, como resultado, retornarão o nome do objeto no gráfico. Estas funções são semelhantes com as funções plot a partir de R ou Phyton, e permitem visualizar instantaneamente os dados disponíveis em diferentes formatos.

A função GraphPlot tem só 10 sobrecargas diferentes, elas permitem plotar um número diferente de curvas, no mesmo gráfico, e defini-las de maneiras diferentes. Tudo o que o usuário precisa fazer é gerar os dados para a plotagem da curva usando uma das maneiras possíveis. Por exemplo, este é o código-fonte para plotagem rápida de duas matrizes x[] e y[]:

void OnStart()
  {
   double x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double y[]={-5,4,-10,23,17,18,-9,13,17,4};
   GraphPlot(x,y);
  }

Da mesma forma, R ficaria:

> x<-c(-10,-4,-1,2,3,4,5,6,7,8)
> y<-c(-5,4,-10,23,17,18,-9,13,17,4)
> plot(x,y)

Nos três modos principais de exibição, comparação de gráficos de renderização de funções plotadas GraphPlot, em linguagem MQL5, e de funções plot em linguagem R:

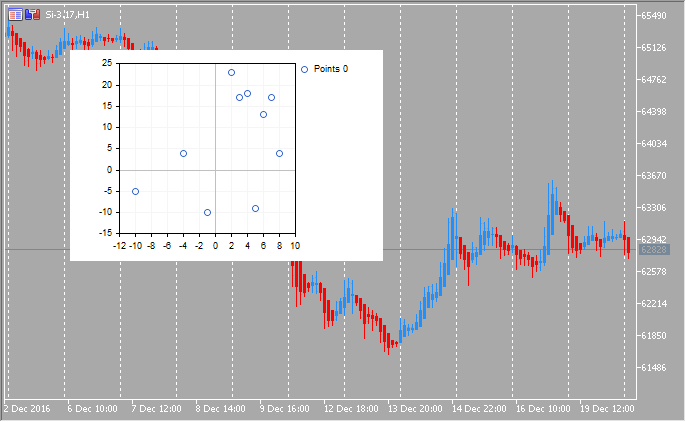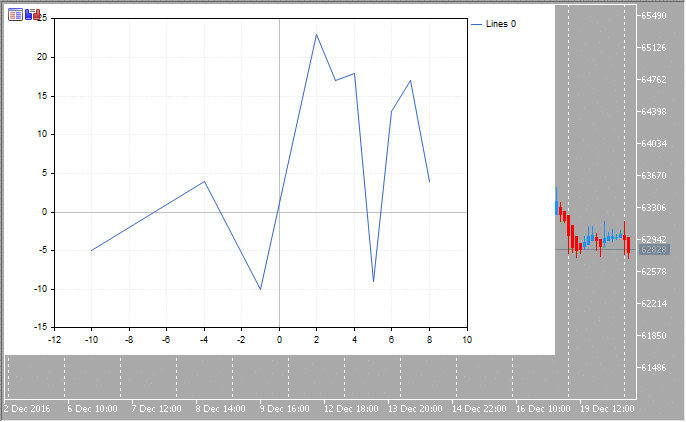
1. Renderização de curvas usando pontos

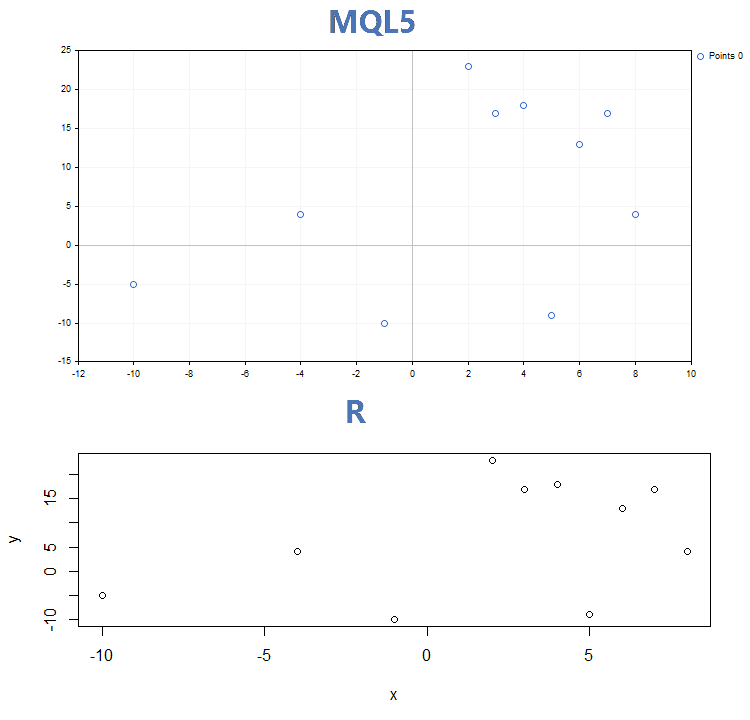
2. Renderização usando linhas

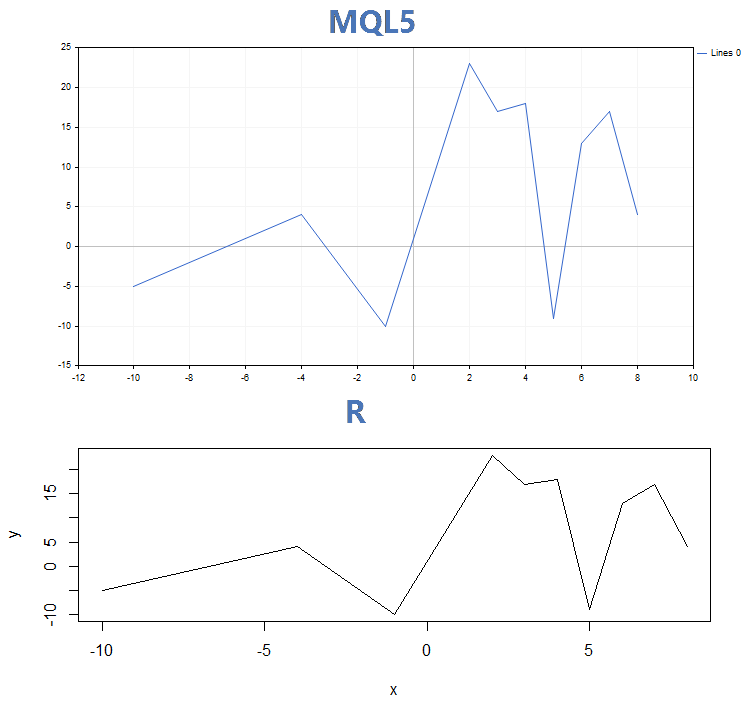
3. Renderização usando gráfico de colunas

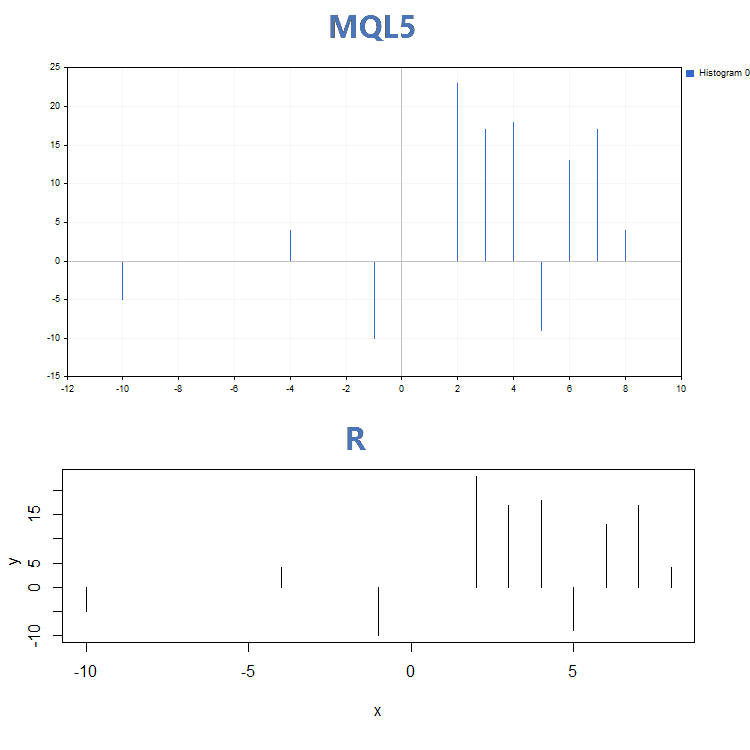
Além das significativas diferenças visuais entre os resultados das funções GraphPlot() em MQL5 e plot() em R, elas diferem nos parâmetros de entrada. Ao contrário da função plot(), na qual é possível definir parâmetros específicos de curva (por exemplo, lwd, para alterar a largura das linhas), a função GraphPlot() inclui apenas os parâmetros chave necessários para construção de dados.

Aqui estão eles:

1. Dados da curva de um dos quatro formatos descritos acima.
   
2. Tipo de renderização (por padrão, CURVE_POINTS).
   
3. Nome do objeto (por padrão, NULL).

Cada gráfico criado pela biblioteca Graphics é um par: um objeto no gráfico e um recurso gráfico vinculado a um objeto. O nome do recurso gráfico é criado com base no nome do objeto simplesmente adicionando "::" antes do nome. Assim, se o nome do objeto for "SomeGraphic", o nome do recurso gráfico será "::SomeGraphic".

A função GraphPlot() tem um ponto de ancoragem fixo no gráfico x=65 e y=45. A largura e a altura do gráfico são calculados com base nas dimensões do gráfico: a largura é 60% da largura do gráfico, enquanto a altura do gráfico é 65% de sua altura. Portanto, se o tamanho de seu gráfico atual estiver entre 65 e 45, a função GraphPlot() não funcionará adequadamente nele.

Se você tentar criar um gráfico e usar o nome do objeto já criado, a biblioteca Graphics tentará exibir o gráfico neste objeto, após verificar o tipo de seu recurso. Se o tipo de recurso for OBJ_BITMAP_LABEL, a renderização ocorrerá neste par objeto-recurso.

Se, para a função GraphPlot(), for enviado explicitamente o nome do objeto, primeiro, haverá uma tentativa de encontrar o objeto e exibi-lo num gráfico. Se o objeto não for encontrado, será criado automaticamente um novo par objeto-recurso com base no nome especificado. Ao utilizar a função GraphPlot() sem especificar o nome do objeto, será usado o nome padrão "Graphic". 

Ao fazer isto, abre-se uma nova possibilidade, isto é: especificar manualmente o ponto de ancoragem e seu tamanho. Para fazer isto, é necessário criar manualmente o objeto-recurso com os parâmetros necessários e transferir para a função GraphPlot() o nome do objeto criado. Obviamente, após criar o par onde o nome do objeto será "Graphic", podemos dizer que redefinimos e fixamos o tecido padrão para a função GraphPlot, a fim de nos livrar da necessidade de transferir o nome do objeto sempre que é realizada uma chamada.

Como exemplo tomamos os dados a partir do exemplo acima e definimos o novo tamanho do gráfico como 750x350, enquanto transferimos o ponto de ancoragem para o canto superior esquerdo:

void OnStart()
  {
//--- create object on chart and dynamic resource
   string name="Graphic";
   long x=0;
   long y=0;
   int width=750;
   int height=350;
   int data[];
   ArrayResize(data,width*height);
   ZeroMemory(data);
   ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0);
   ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA);
   ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x);
   ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y);
   ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name);
//--- create x and y array
   double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8};
   double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4};
//--- plot x and y array
   GraphPlot(arr_x,arr_y,CURVE_LINES);
  }

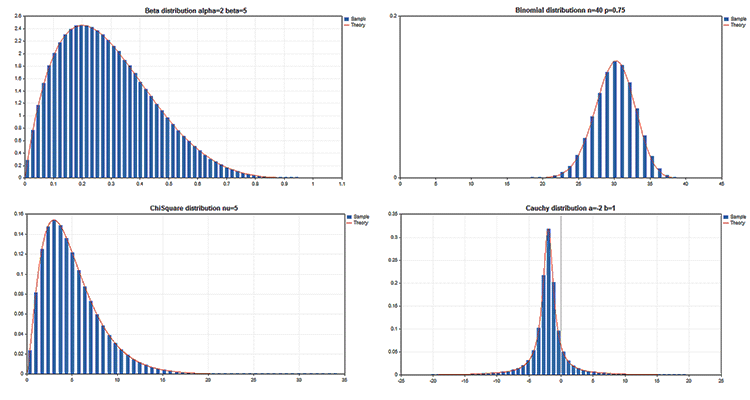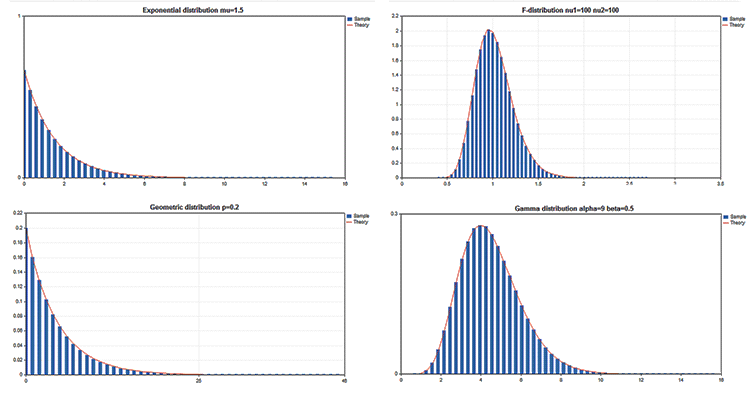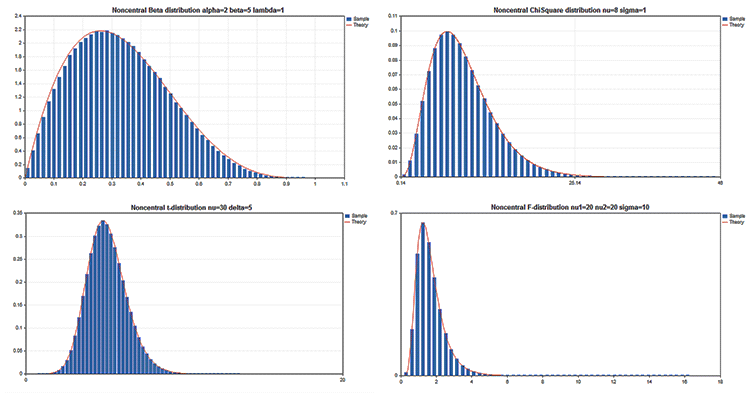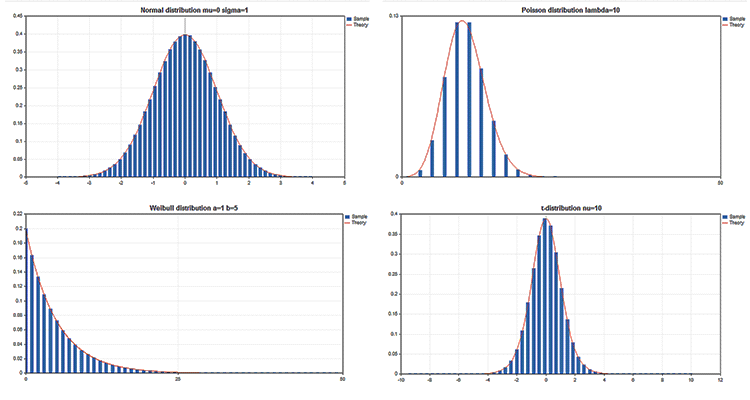
Exemplos de gráficos científicos

A Biblioteca padrão inclui a seção Estatística, nela são apresentadas funções para trabalhar com o conjunto de distribuições estatísticas a partir da teoria de probabilidades. Para cada distribuição é fornecido um exemplo de gráfico e código para sua obtenção. Aqui nós apenas mostramos estes gráficos numa imagem GIF. Os códigos-fontes dos exemplos também estão anexados ao arquivo MQL5.zip, eles devem ser descompactados na pasta MQL5\\Scripts.

Em todos estes exemplos, é escondido o gráfico de preço usando a propriedade CHART_SHOW:

//--- escondemos o gráfico de preço
   ChartSetInteger(0,CHART_SHOW,false);

Isto permite se necessário tornar a janela do gráfico numa área de desenho grande e desenhar nela objetos de qualquer complexidade usando recursos gráficos.

Veja também o artigo Exemplo de desenvolvimento de uma estratégia de spread nos futuros da MICEX-RTS, nele é mostrado como usar a biblioteca gráfica para exibir a amostragem de treinamento e os resultados da regressão linear obtidos pela biblioteca Alglib.

Principais virtudes da biblioteca gráfica

Na linguagem MQL5 os desenvolvedores podem não só criar robôs de negociação e indicadores técnicos, mas também realizar cálculos matemáticos complexos usando as bibliotecas ALGLIB, Fuzzy e Estatística. Os dados obtidos são facilmente visualizados usando a biblioteca gráfica fornecida. Além disso, a maioria de operações é automatizada, a biblioteca oferece ampla funcionalidade:

• 5 tipos de renderizações de gráfico
• 10 tipos de marcadores para o gráfico
  
• dimensionamento automático de gráficos nos eixos X e Y
• seleção automática de cor, mesmo se no gráfico forem mostradas várias construções
  
• suavização de linhas usando a antialiasing clássica ou o algoritmo Bresenham mais avançado
• possibilidade de definir os parâmetros da curva-aproximação para exibir linhas
  
• possibilidade de criar o gráfico usando um código de cadeia com base em duas matrizes x[] e y[]
• possibilidade de criar os gráficos usando ponteiros para funções
  

O uso da biblioteca gráfica não só facilita a criação de gráficos científicos, mas também permite levar o desenvolvimento de aplicativos de negociação para um novo nível. A plataforma MetaTrader 5 permite não só realizar cálculos matemáticos de qualquer complexidade, mas também exibir os resultados direito na janela do terminal de uma forma profissional.

Experimente os códigos anexos ao artigo e certifique-se de que os pacotes de terceiros não são mais necessários!