Resampling-Techniken für die Bewertung von Vorhersagen und Klassifizierungen in MQL5

Einführung

Die Leistung von Modellen des maschinellen Lernens wird in der Regel in zwei verschiedenen Phasen bewertet: Training mit einem Datensatz und Testen mit einem anderen Datensatz. In Situationen, in denen die Erfassung mehrerer Datensätze aufgrund von Ressourcenknappheit oder logistischen Beschränkungen nicht praktikabel ist, müssen jedoch alternative Ansätze gewählt werden.

Eine dieser Methoden ist die Verwendung von Resampling-Techniken zur Bewertung der Leistung von Vorhersage- oder Klassifizierungsmodellen. Es hat sich gezeigt, dass dieser Ansatz trotz seiner potenziellen Nachteile zuverlässige Ergebnisse liefert. In diesem Artikel wird eine neuartige Methode zur Bewertung der Modellqualität vorgestellt, bei der ein einziger Datensatz sowohl als Trainings- als auch als Validierungssatz verwendet wird. Der Hauptgrund für die Anwendung dieser Methoden ist die begrenzte Verfügbarkeit von Daten für Testzwecke.

Daher müssen Praktiker ausgefeilte Resampling-Algorithmen einsetzen, um Leistungskennzahlen zu erhalten, die mit denen vergleichbar sind, die mit einfacheren Ansätzen erzielt werden. Diese Techniken erfordern beträchtliche Rechenressourcen und können den Modellentwicklungsprozess verkomplizieren. Trotz dieses Zielkonflikts kann der Einsatz von Bewertungsstrategien auf der Grundlage von Stichproben in bestimmten Kontexten, in denen die Vorteile die Kosten überwiegen, sinnvoll sein.

Zerlegung der Fehler

Um die Darstellung der in diesem Text vorgestellten algorithmischen Konzepte zu erleichtern, wird ein Notationssystem eingeführt. Dieser Notationsrahmen befasst sich in erster Linie mit der Zerlegung von Modellfehlern in ihre einzelnen Bestandteile. Dieser Datensatz umfasst n Beobachtungen, die jeweils aus einer Prädiktorvariablen x, die entweder skalar oder vektoriell sein kann, und einer skalaren Prädiktorvariablen y bestehen. Um die inhärente Interdependenz von Prädiktor und vorhergesagter Variable zu betonen, wird der zusammengesetzte Term t (für Training) verwendet, um das Paar (x, y) darzustellen. Die i-te Beobachtung im Datensatz wird also als t_i = (x_i, y_i) dargestellt. Diese Notation schlägt einen numerischen Vorhersagerahmen vor. Klassifizierungsprobleme können gelöst werden, indem y_i als die Klassenzugehörigkeit der i-ten Beobachtung interpretiert wird.

Der vollständige Datensatz wird mit T bezeichnet. Wenn ein Modell mit T als Trainingssatz trainiert wird, wird das resultierende trainierte Modell als M_T bezeichnet. Die Anwendung dieses trainierten Modells, M_T, auf einen bestimmten Wert der Prädiktorvariablen x, um eine Schätzung der entsprechenden vorhergesagten Variablen zu erzeugen, ergibt die Vorhersage des Modells, bezeichnet als M_T(x). Der Einfachheit halber kann eine allgemeine Modellvorhersage mit M abgekürzt werden. Bei der Bewertung der Wirksamkeit eines Vorhersagemodells ist es oft notwendig, die Diskrepanz zwischen der Modellvorhersage M und dem beobachteten Wert y der vorhergesagten Variablen zu quantifizieren. Diese Diskrepanz wird formal als Fehlermaß definiert, das als Ef[y, M] bezeichnet wird. Ein in Regressionszusammenhängen häufig verwendetes Fehlermaß ist der mittlere quadratische Fehler, bei dem die quadrierte Differenz wie in der nachstehenden Gleichung dargestellt verwendet wird. Bei Klassifizierungsproblemen kann Ef[y, M] als binäre Funktion definiert werden, die den Wert Null annimmt, wenn y gleich M ist, und andernfalls Eins.

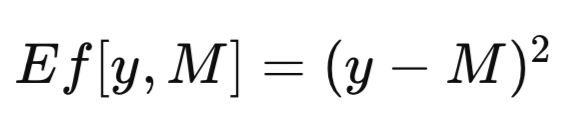
Wenn das trainierte Modell auf denselben Datensatz angewendet wird, der für das Training verwendet wurde, wird der mittlere Fehler über alle Trainingsinstanzen als scheinbarer Fehler bezeichnet. Während der herkömmliche Ansatz darin besteht, das Modell so zu trainieren, dass dieser offensichtliche Fehler minimiert wird, gibt es bei der hier vorgestellten Methode keine solche Einschränkung. Die Optimierung eines beliebigen Maßes ist zulässig, gefolgt von der Bewertung der Qualität des trainierten Modells anhand eines bestimmten Kriteriums. Der nachstehend definierte offensichtliche Fehler ist ausschließlich eine Funktion der Leistung des Modells bei den Trainingsdaten und der Anwendung der Funktion Ef[] auf jede Vorhersage; die Trainingsmethodik ist unerheblich.

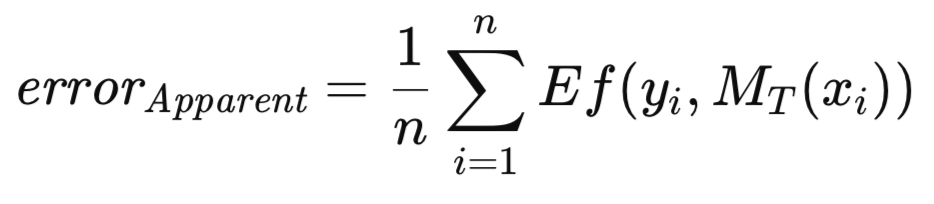
Es ist bekannt, dass der offensichtliche Fehler eine optimistische Verzerrung aufweist, ein Phänomen, das manchmal als Trainingsverzerrung bezeichnet wird und darauf zurückzuführen ist, dass die Bewertung des Modells auf denselben Daten beruht, die für sein Training verwendet wurden. Um diese Verzerrung abzuschwächen, wird das trainierte Modell, wenn genügend Daten vorhanden sind, an einem unabhängigen Datensatz bewertet. Dieses Verfahren erleichtert die Schätzung des erwarteten Fehlers des trainierten Modells bei Anwendung auf die allgemeine Population. Dieser erwartete Fehler, der voraussetzt, dass das Modell mit der Trainingsmenge trainiert wurde, wird als Vorhersagefehler bezeichnet. Der Schwerpunkt liegt hier auf der Bewertung der voraussichtlichen künftigen Leistung eines bestimmten trainierten Modells. Der Vorhersagefehler wird formal durch die folgende Gleichung ausgedrückt.

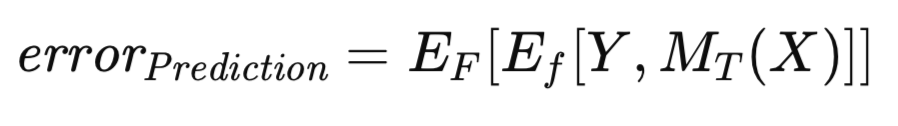
Ein verwandtes, aber konzeptionell unterschiedliches Fehlermaß ist zu berücksichtigen. Der Vorhersagefehler, wie zuvor definiert, ist abhängig von einem bestimmten realisierten Modell, das auf einem bestimmten Datensatz trainiert wurde. Es ist jedoch möglich, die Erwartung so zu erweitern, dass sie die Gesamtheit aller möglichen Trainingssätze umfasst. Da der Trainingssatz aus n Beobachtungen besteht, die einer unbekannten Verteilung entnommen wurden, kann man den Vorhersagefehler bewerten, der mit dem Modell verbunden ist, das auf diesem speziellen Trainingsdatensatz trainiert wurde, und ihn möglicherweise durch einen unabhängigen Validierungssatz annähern. Betrachten wir nun das Szenario, in dem eine neue Trainingsmenge gezogen und das Trainingsverfahren wiederholt wird. Dies würde zwangsläufig zu einem leicht abweichenden Vorhersagefehler führen. Folglich ist es notwendig, ein Maß zu formulieren, das den erwarteten Vorhersagefehler über das gesamte Spektrum möglicher Trainingssätze erfasst. Dieses Maß, der so genannte Populationsfehler, wird im Folgenden formal definiert.

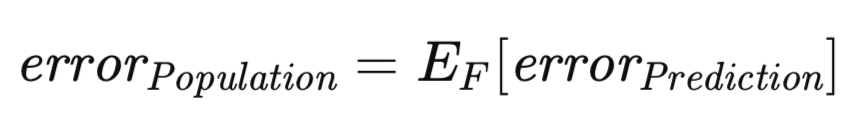
Es ist ein wohlbekannter Grundsatz, dass bei einem gegebenen Trainingssatz der scheinbare Fehler mit hoher Wahrscheinlichkeit den Vorhersagefehler unterschätzt. Diese Diskrepanz ergibt sich aus der Tendenz des Modells, sich zu sehr an die spezifischen Merkmale der Trainingsdaten anzupassen, wodurch seine Verallgemeinerbarkeit auf die breitere Population beeinträchtigt wird. Der Betrag der Differenz zwischen dem Vorhersagefehler und dem offensichtlichen Fehler wird als Exzess-Fehler definiert.

Von besonderer Bedeutung ist in diesem Zusammenhang der erwartete Exzess-Fehler. Da sowohl der Vorhersagefehler als auch der offensichtliche Fehler von einem bestimmten Trainingssatz abhängen, muss der Erwartungswert des Exzess-Fehlers über die Gesamtheit aller möglichen Trainingssätze betrachtet werden, analog zur Ableitung des Populationsfehlers. Dies wird in der nachstehenden Gleichung formell dargestellt.

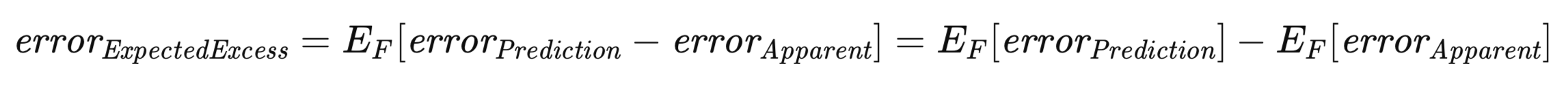
Die obige Gleichung unterstreicht die Dualität des Konzepts des erwarteten Exzess-Fehlers. Sie kann als die Erwartung der Differenz zwischen dem Vorhersagefehler und dem offensichtlichen Fehler für jeden einzelnen Trainingssatz über alle möglichen Trainingssätze hinweg betrachtet werden. Diese Interpretation entspricht einem intuitiven Verständnis des Konzepts. Alternativ kann er auch als Differenz zwischen dem Fehler der Grundgesamtheit und dem erwarteten offensichtlichen Fehler ausgedrückt werden.

Kreuzvalidierung: Methodik und Grenzen

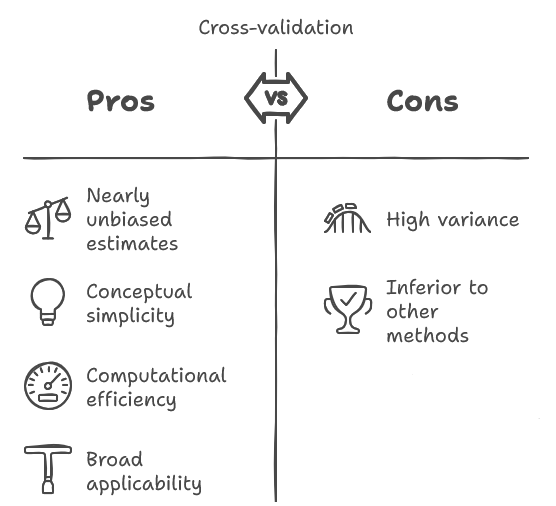
Die Kreuzvalidierung ist eine in der Forschung gut etablierte Technik. Unter den in diesem Text besprochenen Algorithmen zeichnet sich die Kreuzvalidierung durch ihre konzeptionelle Einfachheit und ihre leichte Implementierung aus, die oft auch rechnerisch effizient ist. Sie besitzt die vorteilhafte Eigenschaft, eine nahezu unverzerrte Schätzung der erwarteten zukünftigen Leistung eines Modells zu liefern.

Darüber hinaus ist sie für eine Vielzahl von Algorithmen zur Modellbildung geeignet, was bei anderen Methoden nicht immer der Fall ist. Die Kreuzvalidierung unterliegt jedoch einer erheblichen Einschränkung: Die ihr innewohnende Varianz ist häufig beträchtlich, möglicherweise in einem unannehmbaren Ausmaß. Dies bedeutet eine erhöhte Empfindlichkeit gegenüber den stochastischen Schwankungen, die durch die Zufallsstichprobe des ursprünglichen Datensatzes entstehen.

Insbesondere kann ein Experimentator, der eine Stichprobe erhebt, ein Modell trainiert und anschließend eine Kreuzvalidierung durchführt, um die erwartete künftige Leistung des Modells zu bewerten, bei der Wiederholung des Verfahrens mit einer unabhängigen Stichprobe ein deutlich anderes Ergebnis feststellen. Während die nahezu unverzerrte Natur der Schätzung eine wünschenswerte Eigenschaft ist, wird sie oft von der Größe der Varianz überschattet. Entscheidend ist, dass diese Variabilität von Praktikern häufig unterschätzt wird.

Trotz der Existenz besserer Methoden für analoge Aufgaben wird die Kreuzvalidierung nach wie vor häufig eingesetzt, da sie einfach ist und in Szenarien angewendet werden kann, in denen alternative Ansätze nicht durchführbar sind. Angesichts der weiten Verbreitung und der gelegentlichen Notwendigkeit ist es jedoch gerechtfertigt, das Verfahren der Kreuzvalidierung ausführlich zu erläutern.

Das Grundprinzip der Kreuzvalidierung ist konzeptionell einfach. Dabei wird der Datensatz in zwei getrennte Teilmengen aufgeteilt: eine Trainingsmenge, die für die Schätzung der Modellparameter verwendet wird, und eine Validierungsmenge, die für die unabhängige Bewertung des Modells eingesetzt wird, was dem Verfahren entspricht, das angewandt wird, wenn die Datenfülle keine Einschränkung darstellt.

Im Gegensatz zur Zuweisung eines großen Teils der Daten zum Validierungssatz für eine robuste Leistungseinschätzung wird bei der Kreuzvalidierung jedoch ein minimaler Validierungssatz verwendet, wobei die Mehrheit der Beobachtungen dem Trainingssatz zugewiesen wird. Insbesondere ist es gängige Praxis, eine einzige Beobachtung als Validierungssatz zu verwenden.

Nach dem Training und der Evaluierung des Modells mit dieser Partition wird die Validierungsmenge wieder in den Datensatz integriert und eine andere Beobachtung als Validierungsmenge bezeichnet. Dieser Vorgang wird so lange wiederholt, bis jede Beobachtung einmal als Validierungspunkt gedient hat. Der mittlere Testfehler über alle Iterationen hinweg bildet die Kreuzvalidierungsfehlerschätzung.

Die am weitesten verbreitete Variante der Kreuzvalidierung beinhaltet den sequentiellen Ausschluss einzelner Beobachtungen. Die Anpassung dieser Algorithmen für den Ausschluss von Mehrfachbeobachtungen sollte einfach genug sein. Da M_T das Modell darstellt, das auf dem gesamten Datensatz T trainiert wurde, soll M_T(i) das Modell bezeichnen, das auf dem Datensatz T ohne die i-te Beobachtung trainiert wurde. Die Kreuzvalidierungsschätzung des erwarteten zukünftigen Fehlers des Modells wird dann formell wie folgt ausgedrückt.

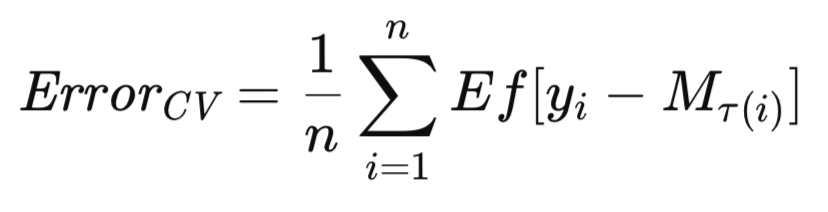
In diesem Abschnitt wird der Algorithmus für die Kreuzvalidierung vorgestellt und mit Erklärungen versehen. Vergleichende Leistungsbewertungen finden Sie am Ende dieses Artikels. Alle Algorithmen, die zur Schätzung der erwarteten Fehler verwendet werden, sind in der Header-Datei error_variance_estimation.mqh aufgeführt. Der Kreuzvalidierungsalgorithmus ist in der Methode cross_validation() implementiert. Diese Routine und die zur Implementierung anderer Fehlerschätzungsalgorithmen verwendeten Routinen haben eine ähnliche Struktur und ähnliche Funktionsparameter. Diese Parameter sind:

• Die ersten beiden erforderlichen Argumente für die Methode sind Matrizen des Trainingsdatensatzes. Die erste Matrix enthält die Prädiktoren und die zweite die entsprechenden Ziele.
  
• Das dritte Argument der Routine ist eine Instanz eines Modells, das die IModel-Schnittstelle implementiert. Dies stellt das zu bewertende Vorhersagemodell dar.
• Das letzte Argument, das an die Funktion cross_validation() übergeben wird, enthält das endgültige Fehlermaß, das sich aus der Berechnung ergibt. Wenn ein Fehler auftritt, gibt die Methode den booleschen Wert false zurück.

//+------------------------------------------------------------------+
//| estimate error variance using cross validation testing           |
//+------------------------------------------------------------------+
bool CErrorVar::cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   vector test;
   double test_target;
   matrix preds,targs;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      test = predictors.Row(i);
      test_target = targets[i][0];
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
      
      preds = np::sliceMatrixRows(predictors,0,long(predictors.Rows()-1));
      targs = np::sliceMatrixRows(targets,0,long(targets.Rows()-1));

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ");
         return false;
        }

      out_err += error_fun(test_target,model.forecast(test));
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
     }

   out_err/=double(predictors.Rows());

   return true;
  }

Der Aufruf von cross_validation() löst den Beginn einer Schleife aus, die den Trainingsdatensatz durchläuft. Die letzte Position im Trainingsdatensatz wird immer als Testpunkt verwendet. In der Schleife werden nacheinander andere Stichproben an dieser Stelle in der Prädiktor- und der Zielmatrix ausgetauscht. Sobald die Daten aufgeteilt sind, wird das Modell trainiert und dann an der einzigen Probe getestet, die vom Training ausgeschlossen wurde. Der Fehler wird kumuliert und schließlich als Ergebnis des Durchlaufs der gesamten Schleife zurückgegeben.

Bootstrap-Schätzung des Populationsfehlers

In diesem Abschnitt wird ein grundlegender Bootstrap-Algorithmus für die Schätzung des Populationsfehlers beschrieben. Es wird eingeräumt, dass dieser Algorithmus nicht allgemein für praktische Anwendungen empfohlen wird, da die Algorithmen E0 und E632, die in den folgenden Abschnitten beschrieben werden, in der Regel eine bessere Leistung bieten. Dennoch dient die hier vorgestellte direkte Bootstrap-Methode als Grundprinzip, auf dem anspruchsvollere Algorithmen aufgebaut werden. Daher ist ein umfassendes Verständnis seiner Funktionsweise unerlässlich, um seine Nachfolger verstehen zu können.

Im vorliegenden Szenario gehen wir von einer Grundgesamtheit F aus, aus der die Beobachtungen, die unseren Trainingssatz bilden, nach dem Zufallsprinzip gezogen werden. Das Modell wird auf T trainiert und ausgewertet, wodurch sich der offensichtliche Fehler ergibt. Dieser Fehler ist von Natur aus optimistisch, und es wird erwartet, dass der Populationsfehler den offensichtlichen Fehler um den Exzess-Fehler übersteigt. In Ermangelung eines unabhängigen Validierungssatzes sind jedoch weder der Exzess-Fehler noch der Fehler der Grundgesamtheit, die Größen von primärem Interesse, direkt beobachtbar. Wir beschränken uns auf den optimistischen offensichtlichen Fehler. Dennoch kann die Bootstrap-Methode angewandt werden, um den Exzess-Fehler zu schätzen, der dann zum offensichtlichen Fehler addiert werden kann, um eine grobe Schätzung des Populationsfehlers zu erhalten.

Die Verwendung des Bootstraps für die Schätzung des Exzess-Fehlers spiegelt das Verfahren zur Schätzung der Parameterverzerrung wider. Die unbekannte Populationsverteilung wird durch eine empirische Verteilungsfunktion ersetzt, und es werden zahlreiche Bootstrap-Stichproben gezogen. Für jede Bootstrap-Stichprobe wird das Modell trainiert. Der Fehler des Modells in der Bootstrap-Stichprobe stellt den offensichtlichen Fehler für diese Stichprobe dar. Der Fehler des Modells auf dem gesamten Datensatz stellt den Vorhersagefehler dar, da die empirische Verteilung effektiv als die gesamte Population fungiert. Die Differenz zwischen diesen beiden Fehlern ergibt den Exzess-Fehler für diese Bootstrap-Stichprobe. Der Durchschnitt dieses Exzess-Fehlers über zahlreiche Bootstrap-Replikationen liefert einen Schätzwert für den erwarteten Exzess-Fehler.

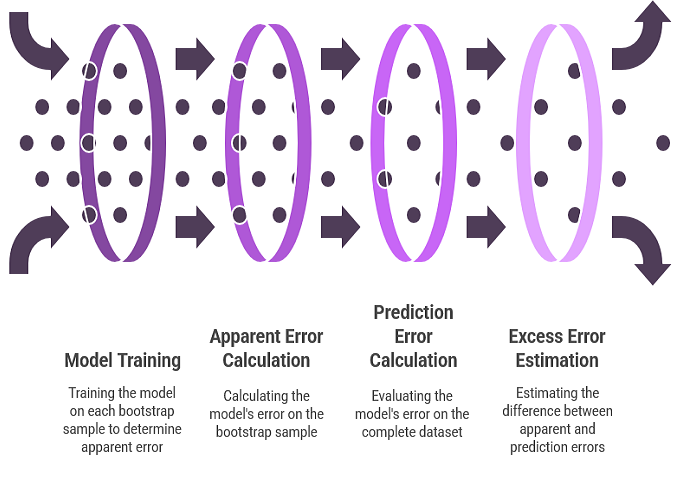
Um die Strenge des oben erwähnten Algorithmus zu verbessern, werden eine Reihe von Definitionen und Gleichungen eingeführt. B steht für einen Trainingssatz, der durch Bootstrap-Sampling aus dem ursprünglichen Datensatz generiert wurde. Konkret wird B durch eine zufällige Auswahl von n Beobachtungen aus T mit Ersetzung konstruiert. Das Modell wird anschließend mit B trainiert. Der Vorhersagefehler dieses Modells wird ermittelt, indem sein Fehler über alle Beobachtungen in der Grundgesamtheit gemittelt wird, aus der die Bootstrap-Stichprobe gezogen wurde, was in diesem Zusammenhang der ursprüngliche Datensatz ist. Dies wird in der nachstehenden Gleichung formell dargestellt.

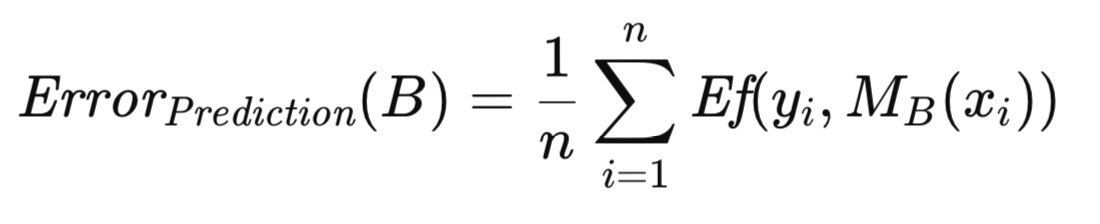
k_i steht für die Häufigkeit, mit der die i-te Beobachtung aus T in B erscheint. Der mit B verbundene offensichtliche Fehler wird durch Mittelung des Modellfehlers über die in B enthaltenen Beobachtungen berechnet, wie in der nachstehenden Gleichung dargestellt.

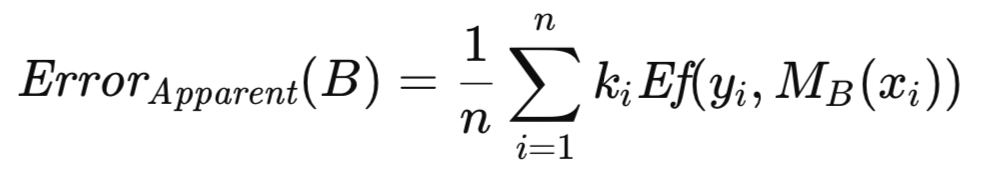
Der mit B verbundene Exzess-Fehler ist definiert als die Differenz zwischen seinem Vorhersagefehler und seinem offensichtlichen Fehler. Anstatt sie getrennt zu berechnen und dann zu subtrahieren, was aufgrund des Vorhandenseins gemeinsamer Fehlerterme rechnerisch redundant wäre, erhält man eine effizientere Formulierung, indem man die gemeinsame Größe ausklammert. Dies führt zu einem Ausdruck, der für jede der zahlreichen (in der Größenordnung von Hunderten bis Tausenden) Bootstrap-Replikationen ausgewertet werden muss. Der durchschnittliche Exzess-Fehler über diese Wiederholungen hinweg liefert eine Schätzung des erwarteten Exzess-Fehler, der dann zum offensichtlichen Fehler der vollständigen Stichprobe addiert wird, um einen Näherungswert für den Populationsfehler zu erhalten.

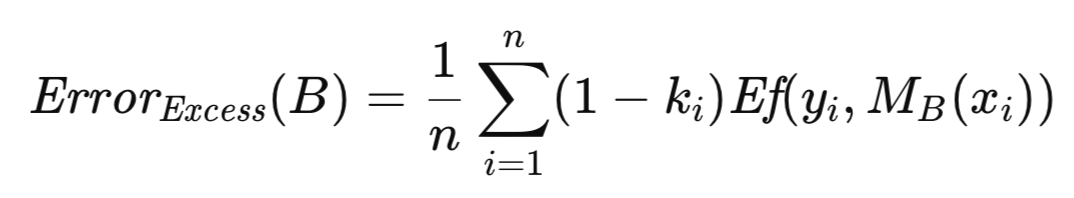
Die Bootstrap-Technik für die Fehlerschätzung ist in der Methode boot_strap() implementiert. Zusätzlich zu den Parametern, die für die Implementierung der Kreuzvalidierung aufgeführt sind, enthält diese Methode einen zusätzlichen Parameter, der die Anzahl der Bootstrap-Replikationen angibt. Die Routine beginnt mit der Initialisierung einer Instanz eines Zufallszahlengenerators, der von der MQL5-Implementierung der Alglib-Bibliothek zur Verfügung gestellt wird. Der Zufallszahlengenerator wird verwendet, um einen zufälligen Zeilenindex als Bootstrap-Stichprobe auszuwählen, der in die Matrixvariablen „preds“ und „targs“ aus dem ursprünglichen Trainingssatz eingesetzt wird. Der Bootstrap-Stichprobensatz wird verwendet, um das Modell zu trainieren und anschließend zu testen, um den Exzess-Fehler zu akkumulieren.

//+------------------------------------------------------------------+
//| estimate error variance using ordinary bootstrap                 |
//+------------------------------------------------------------------+
bool CErrorVar::boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double err,apparent,excess;
   excess = 0.0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         predicted[i] = model.forecast(predictors.Row(i));
         err = error_fun(targets[i][0],predicted[i]);
         excess+=(1.0 - double(count[i]))*err;
        }
     }

   excess/=double(nsize*nboot);

Sobald der Bootstrap-Vorgang abgeschlossen ist. Der ursprüngliche Trainingsdatensatz wird zur Berechnung des offensichtlichen Fehlers verwendet. Die endgültige Fehlerschätzung ergibt sich aus dem kombinierten Wert des übermäßigen und des scheinbaren Fehlers.

if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }
   apparent = 0.0;
   for(ulong i=0; i<nsize; i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      err = error_fun(targets[i][0],predicted[i]);
      apparent+=err;
     }
   apparent/=double(nsize);
   out_err = apparent+excess;
   return true;
  }

Efrons E0-Schätzer für den Populationsfehler

Eine bemerkenswerte Herausforderung, die sich aus der Duplizierung von Trainingsfällen innerhalb der Bootstrap-Stichproben ergibt, ist die Möglichkeit, dass bestimmte Modellklassen unbrauchbar werden. Insbesondere probabilistische und verallgemeinerte neuronale Regressionsnetze sind dafür besonders anfällig. Wenn die Glättungskonstante nicht ausreichend groß ist, führt ein Testfall, der mit einem Trainingsfall identisch ist, zu einer nahezu perfekten Vorhersage, was das Problem der optimistischen Verzerrung noch verschärft. Um dieses Problem zu entschärfen, schlug Bradley Efron eine unkomplizierte Lösung vor: die Vermeidung von artifiziellen Dubletten. Dies beinhaltet die Erzeugung von Bootstrap-Trainingsmengen durch Standard-Resampling-Verfahren. Bei jeder Bootstrap-Replikation wird das Modell jedoch nur anhand der ursprünglichen Beobachtungen bewertet, die nicht in der Trainingsmenge enthalten sind. Der mittlere Fehler über diese ausgeschlossenen Beobachtungen wird dann als Schätzung des Fehlers der Grundgesamtheit verwendet. Diese Methodik wird als E0-Schätzer des Populationsfehlers bezeichnet.

In der Fachliteratur werden zwei verschiedene Ansätze zur Berechnung von E0 vorgestellt. Bei der ursprünglichen Methode werden alle Fehler addiert und durch die Gesamtzahl der bewerteten Fälle geteilt. Dieser Ansatz wird hier verfolgt. Nachfolgende theoretische Untersuchungen zu den Eigenschaften von E0 schlagen einen alternativen Algorithmus vor, der den Mittelwertbildungsprozess in zwei Stufen unterteilt. Zunächst werden für jede ursprüngliche Beobachtung die Fehler aus allen Bootstrap-Replikationen, bei denen diese Beobachtung fehlt, summiert und durch die Anzahl dieser Replikationen geteilt, was einen mittleren Fehler für diese Beobachtung ergibt. Anschließend werden diese mittleren Fehler über alle Beobachtungen summiert und durch die Gesamtzahl der Beobachtungen geteilt, um einen Gesamtmittelwert zu erhalten. Die letztgenannte Methode weist zwar einen höheren Rechenaufwand auf, ist aber asymptotisch gleichwertig mit der erstgenannten Methode, und empirische Bewertungen zeigen vernachlässigbare Leistungsunterschiede. Daher wird die ursprüngliche Methode wegen ihrer Einfachheit gewählt.

Um den Algorithmus besser beschreiben zu können, wird eine zusätzliche Notation eingeführt. Wie zuvor steht T für den ursprünglichen Datensatz und B für eine Bootstrap-Stichprobe. C sei die Menge der Beobachtungen in T, die nicht in B enthalten sind. count(C) sei die Kardinalität (Anzahl der Beobachtungen) von C. Dann wird Efrons ursprüngliche E0-Schätzung des Populationsfehlers wie folgt formuliert.

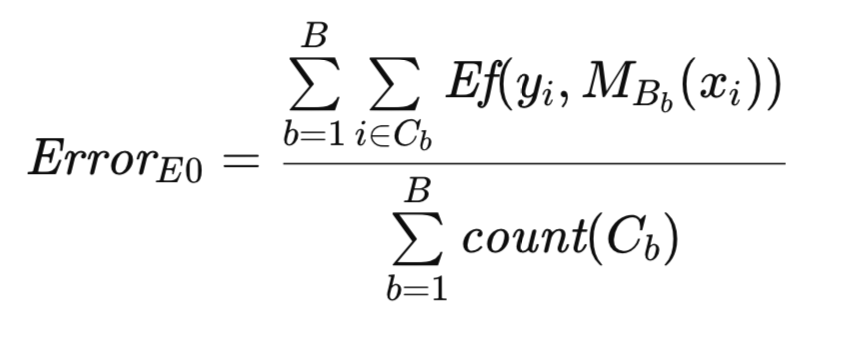
Die algorithmische Implementierung des E0-Schätzers hat Ähnlichkeit mit der zuvor beschriebenen Bootstrap-Routine. Die Erzeugung und Verwendung von Bootstrap-Stichproben für das Modelltraining ist bei beiden Methoden gleich. In diesem Zusammenhang dient das Zählfeld jedoch als binärer Indikator, der das Vorhandensein oder Nichtvorhandensein einer Beobachtung anzeigt, und nicht als Häufigkeitszähler wie in der vorangegangenen Routine. Der Algorithmus ist in der Methode efrons_0() implementiert. 

//+------------------------------------------------------------------+
//| estimate error variance using efron's E0 bootstrap               |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   ulong tot = 0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         continue;//return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         if(count[i])
            continue;
         predicted[i] = model.forecast(predictors.Row(i));
         out_err+= error_fun(targets[i][0],predicted[i]);
         ++tot;
        }
     }

   if(tot)
      out_err/=double(tot);
   else
     {
      Print(__FUNCTION__, " zero denominator ");
      return false;
     }
   return true;
  }

Efrons E632-Schätzer für den Populationsfehler

Der zuvor beschriebene E0-Schätzer weist wünschenswerte Eigenschaften auf und wird allgemein für die praktische Anwendung empfohlen. Durch den Verzicht auf die Auswertung von Beobachtungen aus dem Trainingssatz ist die Kompatibilität mit verschiedenen Modellklassen gewährleistet. Darüber hinaus ist die Varianz relativ gering, was den derzeitigen Stand der methodischen Entwicklung widerspiegelt.

Der E0-Schätzer ist jedoch durch eine mäßig konservative Verzerrung gekennzeichnet, die dazu neigt, den tatsächlichen Populationsfehler zu überschätzen. Es sei darauf hingewiesen, dass diese Verzerrung, sofern sie nicht zu groß ist, im Allgemeinen als weniger problematisch angesehen wird als eine Unterschätzung. Eine Unterschätzung, wie sie beim gewöhnlichen Bootstrap zu beobachten ist, ist eher schädlich, da sie zu ungerechtfertigtem Optimismus verleitet. Die Anwendung der E0-Methode bietet in der Regel die Gewissheit, dass der tatsächliche Populationsfehler mit größerer Wahrscheinlichkeit niedriger ist als der berechnete Wert. Dieser inhärente Konservatismus ist zwar im Allgemeinen von Vorteil, kann aber auch dazu führen, dass ein Modell aufgrund eines unangemessenen Pessimismus fälschlicherweise abgelehnt wird. Der E632-Schätzer wurde entwickelt, um dieses Problem zu lösen, indem er die konservative Verzerrung von E0 abschwächt.

Bedenken Sie die inhärenten Grenzen der Verwendung des offensichtlichen Fehlers (des Fehlers, der sich aus der Auswertung des Trainingssatzes ergibt) als Schätzung des Populationsfehlers. Das Bewertungsverfahren ist von Natur aus voreingenommen, da nur Beobachtungen, die in der Ausbildung verwendet wurden, bewertet werden. Diese Untergruppe ist nicht repräsentativ für die gesamte Population und weist eine übermäßige Ähnlichkeit mit der Trainingsgruppe auf, was zu einer optimistischen Verzerrung führt.

Umgekehrt weist der E0-Schätzer die entgegengesetzte Verzerrung auf. Durch den absichtlichen Ausschluss von Trainingsbeobachtungen von der Auswertung wird die Testmenge nicht repräsentativ für die Grundgesamtheit und weist eine übermäßige Unähnlichkeit zur Trainingsmenge auf. In realen Szenarien wird es unweigerlich zu Beobachtungen kommen, die mit den Trainingsbeobachtungen identisch oder nahezu identisch sind. Der Ausschluss dieser Beobachtungen durch E0 führt zu einer pessimistischen Verzerrung.

Der E632-Algorithmus versucht, einen Kompromiss zwischen diesen beiden Extremen zu finden. Ein gerechterer Ansatz könnte darin bestehen, das Modell anhand von Stichproben sowohl innerhalb als auch außerhalb des Trainingssatzes zu bewerten, wobei die Wahrscheinlichkeiten ihr reales Auftreten widerspiegeln. Alternativ können Anpassungen vorgenommen werden, um Diskrepanzen bei den Stichproben zu berücksichtigen. Mit zunehmendem Stichprobenumfang konvergiert die Wahrscheinlichkeit, dass eine bestimmte Beobachtung in einer Bootstrap-Stichprobe vorkommt, gegen 1 - 1/e ≈ 0,632. Die Heuristik von Efron schlägt vor, den Fehler der Grundgesamtheit als gewichtete Summe von E0 und dem offensichtlichen Fehler zu schätzen, wobei die Gewichte durch diese Stichprobenwahrscheinlichkeiten bestimmt werden. Sein Schätzer mit der Bezeichnung E632 wird in der nachstehenden Gleichung formal dargestellt.

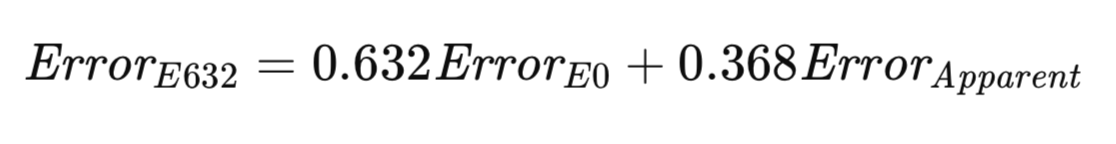
Die Implementierung des E632-Algorithmus erfolgt mit der Methode efrons_632(), die im Folgenden dargestellt wird.

//+------------------------------------------------------------------+
//| estimate error variance using efron's E632 bootstrap             |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double apparent;

   if(!efrons_0(nboot,predictors,targets,model,out_err))
      return false;


   if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }

   apparent = 0.0;
   
   vector predicted(predictors.Rows());

   for(ulong i=0; i<predictors.Rows(); i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      apparent+= error_fun(targets[i][0],predicted[i]);
     }

   apparent/=double(predictors.Rows());

   out_err = 0.632*out_err + 0.368*apparent;

   return true;
  }

Alle bisher in diesem Text besprochenen Algorithmen sind als Mitglieder der Klasse CErrorVar implementiert. Diese Klasse definiert auch die Methode error_fun(), mit der der Fehler zwischen einem vorhergesagten Wert, der als zweiter Parameter angegeben wird, und dem entsprechenden Zielwert, der als erster Parameter der Methode angegeben wird, berechnet wird.

//+------------------------------------------------------------------+
//|  class for estimating error variance                             |
//+------------------------------------------------------------------+
class CErrorVar
  {
public:
                     CErrorVar(void);
                    ~CErrorVar(void);

   virtual double    error_fun(const double truevalue,const double predictedvalue);
   virtual bool      cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CErrorVar::CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CErrorVar::~CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| calculate the error                                              |
//+------------------------------------------------------------------+
double CErrorVar::error_fun(const double truevalue,const double predictedvalue)
  {
   return pow(truevalue-predictedvalue,2.0);
  }

Im nächsten Abschnitt wird gezeigt, wie diese Algorithmen zur Schätzung des Fehlers eines trainierten Modells verwendet werden, wobei nur der Trainingsdatensatz verwendet wird.

Vergleichende Analyse von Schätzern für Vorhersagefehler

In diesem Text wurde eine Reihe von Methoden zur Schätzung des Populationsfehlers eines Vorhersagemodells vorgestellt. Die folgenden wichtigen Überlegungen sollten beachtet werden:

• Kreuzvalidierung: Diese Technik zeichnet sich durch ihre einfache Implementierung und Recheneffizienz aus. Sie ist für verschiedene Modellklassen geeignet und liefert eine nahezu unverzerrte Schätzung. Es ist jedoch anfällig für eine hohe Varianz, insbesondere in Szenarien mit instabilen Trainingsverfahren. Daher wird die Kreuzvalidierung im Allgemeinen nicht als primäre Methode empfohlen, es sei denn, alternative Ansätze sind nicht verfügbar. Sie ist zwar wirksam, wird aber nicht als optimal angesehen.
• Straight Bootstrap: Diese Methode wird im Allgemeinen als die am wenigsten wünschenswerte Option angesehen. Es ist nicht kompatibel mit Modellen, die keine doppelten Trainingsbeobachtungen aufnehmen können oder die durch das Vorhandensein von Testbeobachtungen innerhalb des Trainingssatzes beeinträchtigt werden. Außerdem wird der tatsächliche Populationsfehler deutlich unterschätzt. Daher hat sie keine zwingenden Vorteile.
• E0 Schätzer: In Szenarien, in denen der Trainingsprozess doppelte Beobachtungen zulässt, ist der E0-Schätzer im Allgemeinen die bevorzugte Wahl. Die Anwendbarkeit erstreckt sich auf eine breite Palette von Modellen, da die Auswertung von Trainingsbeobachtungen vermieden wird. Es zeigt sich robust gegenüber instabilen Lernbedingungen, wie z.B. bei Modellen mit stochastischen Trainingsverfahren. Empirisch gesehen nähert sich die Varianz der Kreuzvalidierung in stabilen Lernumgebungen an, während sie in instabilen Umgebungen eine deutlich geringere Varianz aufweist. Außerdem ist sie rechnerisch effizient, da der für den E632-Schätzer erforderliche scheinbare Fehler gleichzeitig mit der E0-Schätzung berechnet werden kann. Es ist jedoch zu beachten, dass Praktiker möglicherweise die konservative Verzerrung von E0 gegenüber der potenziell höheren Varianz des weniger verzerrten E632-Schätzers bevorzugen.

Um diese Schätzer empirisch zu bewerten, wurde eine Simulationsstudie mit künstlichen Daten durchgeführt, die nach dem folgenden Modell erzeugt wurden: y = x_1 - x_2 + Fehler. In diesem Modell folgen die Vorhersagevariablen x_1 und x_2 einer Standardnormalverteilung, und der Fehlerterm ist normalverteilt mit einem Mittelwert von Null und einer vom Nutzer angegebenen Varianz. Ein gewöhnliches lineares Modell wurde an den Datensatz angepasst, und der mittlere quadratische Fehler der Population wurde mit den in diesem Artikel vorgestellten Algorithmen geschätzt. Das angepasste Modell wurde auch anhand unabhängiger Testdaten bewertet, um seinen tatsächlichen Fehler zu ermitteln. Dieser Vorgang wurde für eine vom Nutzer festgelegte Anzahl von Versuchen wiederholt, und es wurden der Durchschnitt und die Standardabweichung der Fehlerschätzungen berechnet. Dies ist in dem Skript ErrorVarianceEstimation_NumericalPredictionDemo.mq5 implementiert.

//+------------------------------------------------------------------+
//|              ErrorVarianceEstimation_NumericalPredictionDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     Variance = 1.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = Variance ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVar errorvar;
   COrdReg regmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = normal(rngstate);
         xdata[i][2] = xdata[i][0] - xdata[i][1] + std * normal(rngstate);
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = normal(rngstate);
         testdata[j][2] = testdata[j][0] - testdata[j][1] + std *normal(rngstate);
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!regmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = regmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,regmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,regmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,regmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,regmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
      //---
     }
//---
   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf      std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+------------------------------------------------------------------+

Mit einer Varianz von 1,0, einem Stichprobenumfang von 15 Beobachtungen und 1.000 Bootstrap-Iterationen. Die Ergebnisse waren wie folgt:

MJ      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    Number of Iterations 100   Observed error = 1.18380
RF      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.18825      std=   0.53117
PK      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.12521      std=   0.48780
IR      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.38168      std=   0.63579
NO      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.18647      std=   0.52380

Wie erwartet, zeigte die Standard-Bootstrap-Methode eine Unterschätzung des wahren Fehlers. Umgekehrt überschätzte der E0-Schätzer den Fehler erheblich. Während diese Überschätzung als Einschränkung empfunden werden kann, ist es wichtig zu beachten, dass der E0-Schätzer auch die höchste Standardabweichung aufwies. Dieser Grad der Überschätzung ist in erster Linie auf den geringen Stichprobenumfang zurückzuführen. Die Entscheidung über ihre Akzeptanz bleibt jedoch subjektiv. Um die Leistung der Fehlerschätzer weiter zu bewerten, wurde die Simulationsstudie mit einem größeren Stichprobenumfang von 100 Beobachtungen wiederholt, was für viele praktische Anwendungen repräsentativer ist. Hier sind die Ergebnisse:

KG      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.01810      std=   0.24132
LH      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.01672      std=   0.14194
PS      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.01989      std=   0.14441
IP      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.01855      std=   0.14099

Die Ergebnisse dieses Experiments zeigen eine zufriedenstellende Leistung aller vier Methoden. Vor allem der E0-Schätzer überschätzt den Fehler leicht. Die übrigen drei Algorithmen wiesen eine vernachlässigbare Unterschätzung auf. Der E0-Schätzer wies zwar die höchste Standardabweichung auf, aber der Unterschied war minimal. In Szenarien, die sich durch eine hohe Gesamtqualität der Schätzung auszeichnen, ist die geringfügige Überschätzung des Fehlers durch den E0-Schätzer wahrscheinlich der trivialen Unterschätzung vorzuziehen, die bei den anderen Methoden beobachtet wird, insbesondere angesichts der Auswirkungen der Unterschätzung auf die Modellauswahl und -bewertung.

Das vorangegangene Beispiel veranschaulicht bestimmte Unterscheidungen zwischen den verschiedenen Methoden zur Schätzung des Populationsfehlers. Möglicherweise wurde jedoch versehentlich der Eindruck erweckt, dass die Kreuzvalidierung im Hinblick auf ihre Wirksamkeit durchweg mit anderen Methoden vergleichbar ist. Diese Wahrnehmung ist auf die Verwendung einer glatten Fehlerfunktion zurückzuführen, insbesondere des mittleren quadratischen Fehlers eines einfachen Modells, das ein stabiles Lernumfeld begünstigt.

Klassifizierungsaufgaben hingegen sind im Allgemeinen durch eine inhärente Instabilität gekennzeichnet. Geringfügige Störungen in den Daten können zu abrupten und erheblichen Schwankungen der Fehlerquote führen. In diesem Abschnitt wird ein Beispiel vorgestellt, das dieses Phänomen untersucht. Die Algorithmen, die zur Schätzung des Populationsfehlers verwendet werden, entsprechen denen, die zuvor diskutiert wurden. Die wichtigsten Änderungen betreffen die Definition der Vorhersagefehlerfunktion und die Struktur des für die vergleichende Bewertung verwendeten Hauptprogramms.

Das Testskript ErrorVarianceEstimation_ClassificationDemo.mq5 erzeugt bivariate Daten, die eine moderate positive Korrelation aufweisen.

//+------------------------------------------------------------------+
//|                   ErrorVarianceEstimation_ClassificationDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     PredictionDifficultyLevel = 0.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//+------------------------------------------------------------------+
//| error variance for classification models                         |
//+------------------------------------------------------------------+
class CErrorVarC:public CErrorVar
  {
public:
                     CErrorVarC(void)
     {
     }
                    ~CErrorVarC(void)
     {
     }

   virtual double    error_fun(const double truevalue,const double predictedvalue)
     {
      if(truevalue*predictedvalue>0.0)
         return 0.0;
      else
         return 1.0;
     }


  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = PredictionDifficultyLevel ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVarC errorvar;
   COrdReg olsmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = 0.7071 * xdata[i][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            xdata[i][0] -=dfactor;
            xdata[i][1] +=dfactor;
            xdata[i][2] = 1.0;
           }
         else
           {
            xdata[i][0] +=dfactor;
            xdata[i][1] -=dfactor;
            xdata[i][2] = -1.0;
           }
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = 0.7071 * testdata[j][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            testdata[j][0] -=dfactor;
            testdata[j][1] +=dfactor;
            testdata[j][2] = 1.0;
           }
         else
           {
            testdata[j][0] +=dfactor;
            testdata[j][1] -=dfactor;
            testdata[j][2] = -1.0;
           }
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!olsmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = olsmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,olsmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,olsmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,olsmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,olsmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
     }

   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf    std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf    std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+--------------------------------------------------------------------+

Ein Streudiagramm der Daten für einen gegebenen „PredictionDifficultyLevel“ von 1,0 würde eine elliptische Verteilung zeigen, deren Hauptachse diagonal nach oben und rechts ausgerichtet ist. Der Parameter „PredictionDifficultyLevel“ im Skript steuert den Grad der Trennung zwischen den Clustern und ermöglicht so eine einfachere Klassenidentifizierung. Je niedriger dieser Parameter ist, desto schwieriger wird es für das Modell, die Klassenzugehörigkeit abzuleiten.

Es werden zwei unterschiedliche Klassen erzeugt, deren jeweilige Datenverteilungen um eine vom Nutzer festgelegte Größe ungefähr senkrecht zur Hauptachse verschoben sind. Ein lineares Modell wird an die Daten angepasst, wobei die vorhergesagte Variable einen Wert von -1,0 für die eine Klasse und +1,0 für die andere Klasse erhält. Der Vorhersagefehler ist mit 0,0 definiert, wenn der wahre und der vorhergesagte Wert das gleiche Vorzeichen haben, und mit 1,0, wenn sie entgegengesetzte Vorzeichen aufweisen. Diese binäre Fehlermetrik spiegelt die inhärente Natur von Klassifizierungsproblemen wider.

Es wurden zwei verschiedene experimentelle Bewertungen durchgeführt. Das erste Experiment verwendete eine Stichprobengröße von 15 Beobachtungen, 1.000 Bootstrap-Wiederholungen, 100 Versuche und eine Trennung von Null. Diese Konfiguration simulierte effektiv ein Szenario ohne diskriminierende Informationen, da die beiden Klassen identische Verteilungen aufwiesen. Wie erwartet, lag der beobachtete mittlere Fehler bei etwa 0,5. Die Ergebnisse dieses Experiments werden im Folgenden vorgestellt:

OO      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.50267
PS      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.50267      std=   0.18389
KM      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.45214    std=   0.11748
EQ      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.50517      std=   0.10845
RF      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.45196    std=   0.09941

Die Kreuzvalidierung hat einmal mehr gezeigt, dass sie nahezu unvoreingenommen ist. Dieses Ergebnis ist in diesem Szenario zu erwarten, da die mangelnde Vorhersagekraft des Modells zu einer 50 %igen Wahrscheinlichkeit einer Fehlklassifizierung für eine bestimmte Beobachtung führt. Entsprechende Überlegungen gelten für den E0-Schätzer. Während bei E0 in der Regel eine pessimistische Verzerrung zu erwarten ist, zeigt sich diese Eigenschaft nur, wenn das Modell einen gewissen Grad an Effektivität aufweist. In diesem Fall hat der von E0 erzwungene Ausschluss von Testbeobachtungen aus der Trainingsmenge eine neutrale Wirkung.

Diese Neutralität gilt jedoch auch für den E632-Schätzer. Aufgrund der Kombination einer wirklich unverzerrten Komponente und einer stark optimistisch verzerrten Komponente weist E632 eine erhebliche optimistische Verzerrung auf. Diese mögliche Verzerrung muss sorgfältig geprüft werden. Dieses Experiment verdeutlicht auch den Hauptkritikpunkt der Kreuzvalidierung: ihre hohe Varianz. Die Standardabweichung des Kreuzvalidierungsschätzers ist wesentlich höher als die des E0-Schätzers. Wie häufig zu beobachten ist, weist der E632-Schätzer die geringste Standardabweichung auf. Dieser Vorteil wird jedoch durch die starke optimistische Tendenz von E632 geschmälert.

Ein zweites Experiment, bei dem das Modell eine gewisse Vorhersagefähigkeit besaß, wurde ebenfalls durchgeführt (der Parameter PredictionDifficultyLevel wurde auf 1,0 erhöht). Die Ergebnisse dieses Experiments werden im Folgenden vorgestellt:

GM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.00747
NM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.00533      std=   0.01909
RO      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.00716    std=   0.01766
OG      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.01012      std=   0.01878
FD      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.00820    std=   0.01869

Dieses Experiment zeigt, dass der E632-Schätzer am effektivsten ist. Sie weist eine geringe Verzerrung und die niedrigste Standardabweichung auf. Der E0-Schätzer hat jedoch eine etwas höhere Standardabweichung und weist seine charakteristische und oft wünschenswerte pessimistische Verzerrung auf. In Anbetracht der Ergebnisse des vorangegangenen Experiments sollte dieser Faktor bei der Auswahl zwischen den Schätzern E0 und E632 sorgfältig geprüft werden. Auch hier weist die Kreuzvalidierung die höchste Standardabweichung auf, und der reine Bootstrap weist eine potenziell gefährliche optimistische Verzerrung auf.

Ein Hinweis zur Verwendung der vorgestellten Algorithmen zur Einschätzung der Klassifizierungsleistung. Bei der Erstellung von Bootstrap-Klassifizierungsdatensätzen gibt es eine erhebliche Einschränkung. Manchmal kann eine Bootstrap-Stichprobe Exemplare einer einzigen Klasse enthalten, wodurch der Klassifizierungsalgorithmus Probleme bekommt oder in manchen Fällen sogar komplett versagt. Leser, die die beschriebenen Techniken anwenden wollen, sollten sich dieser möglichen Fallstricke bewusst sein.

Schlussfolgerung

Eine flüchtige Betrachtung des Inhalts dieses Artikels könnte zu dem Eindruck führen, dass Resampling-Techniken zur Schätzung des Populationsfehlers eines Modells zwar konzeptionell faszinierend, aber übermäßig komplex und von begrenztem praktischen Nutzen sind. Eine solche Schlussfolgerung wäre bedauerlich, da die hier vorgestellten Methoden der Wiederholungsstichproben erhebliche Vorteile bieten und ernsthaft in Betracht gezogen werden sollten.

Diese Methoden gehen insbesondere auf eine grundlegende Herausforderung bei der Modellbewertung ein: die Notwendigkeit eines unabhängigen Datensatzes. Der herkömmliche Ansatz erfordert die Beschaffung eines separaten Datensatzes, was häufig logistisch aufwändig und in einigen Fällen nicht durchführbar ist.

Die in diesem Text erörterten Resampling-Techniken machen diese Anforderung überflüssig. Der gesamte Datensatz kann sowohl für das Training des Modells als auch für die Schätzung seiner zukünftigen Leistung verwendet werden, wodurch die Datennutzung maximiert wird. Diese Fähigkeit stellt einen bedeutenden methodischen Fortschritt dar und sollte nicht auf die leichte Schulter genommen werden.

Dateiname	Beschreibung der Datei
MQL5/include/error_variance_estimation.mqh	Eine Header-Datei mit Definitionen der im Artikel beschriebenen Fehlerschätzungsalgorithmen.
MQL5/include/imodel.mqh	Die Header-Datei enthält die Definition von Schnittstellen, die für die Interaktion mit Modellen des maschinellen Lernens verwendet werden.
MQL5/include/np.mqh	Eine Header-Datei mit verschiedenen Hilfsfunktionen für Vektoren und Matrizen.
MQL5/include/OLS.mqh	Die Include-Datei definiert die OLS-Klasse, die Modelle der gewöhnlichen kleinsten Quadrate implementiert.
MQL5/scripts/ErrorVarianceEstimation_NumericalPredictionDemo.mq5	Demonstrationsskript, das die Nützlichkeit von Fehlerschätzungsalgorithmen bei numerischen Vorhersagen zeigt.
MQL5/scripts/ErrorVarianceEstimation_ClassificationDemo.mq5	Demonstrationsskript, das den Nutzen von Fehlerschätzungsalgorithmen bei der Datenklassifizierung zeigt.