
Eine Einführung in die Kurven von Receiver Operating Characteristic
Einführung
Das Diagramm von Receiver Operating Characteristic (ROC) dient als Methode zur Visualisierung, Organisation und Auswahl von Klassifikatoren auf der Grundlage ihrer Leistung. Ursprünglich aus der Signaldetektionstheorie stammend, wurden ROC-Diagramme verwendet, um den Kompromiss zwischen Wahr-Positiv und Falsch-Positiv von Klassifikatoren zu veranschaulichen. Neben ihrer allgemeinen Nützlichkeit als Leistungsdiagramm-Methode weisen ROC-Kurven Eigenschaften auf, die sie in Bereichen mit schiefen Klassenverteilung und ungleichen Klassifizierungsfehlerkosten besonders wertvoll machen. Dies ist vor allem für Klassifikatoren relevant, die auf Finanzzeitreihendaten angewandt werden.
Während der konzeptionelle Rahmen der ROC-Diagramme einfach ist, weist die praktische Anwendung komplexe Aspekte auf, die eine sorgfältige Prüfung erfordern. Darüber hinaus gibt es häufige Missverständnisse und potenzielle Fallstricke bei ihrer empirischen Anwendung. Dieser Artikel soll eine grundlegende Einführung in die ROC-Kurven bieten und als praktischer Leitfaden für ihre Anwendung bei der Bewertung der Klassifikatorleistung dienen.
Formulierung der binären Klassifizierung
Viele reale Anwendungen beinhalten binäre Klassifizierungsprobleme, bei denen Instanzen zu einer von zwei sich gegenseitig ausschließenden und gemeinsam erschöpfenden Klassen gehören. Ein häufiger Fall dieses Szenarios tritt auf, wenn eine einzige Zielklasse definiert wird und jede Instanz entweder als Mitglied dieser Klasse oder als ihr Komplement kategorisiert wird. Nehmen wir zum Beispiel die Klassifizierung von Radarsignalen, bei der ein erkannter Umriss auf dem Bildschirm entweder als Panzer (die Zielklasse) oder als Nicht-Panzer-Objekt eingestuft wird. In ähnlicher Weise kann eine Kreditkartentransaktion entweder als betrügerisch (die Zielklasse) oder als rechtmäßig eingestuft werden.
Diese spezifische Formulierung des binären Klassifikationsproblems, das durch die Identifizierung einer einzigen Zielklasse gekennzeichnet ist, bildet die Grundlage für die nachfolgende Analyse. Anstatt Instanzen explizit einer von zwei verschiedenen Klassen zuzuordnen, konzentriert sich der hier gewählte Ansatz auf die Feststellung, ob eine Instanz zu der vorgesehenen Zielklasse gehört. Auch wenn die verwendete Terminologie, die sich auf das „Ziel“ und seine Ergänzung bezieht, militärische Konnotationen hervorrufen mag, ist das Konzept allgemein anwendbar. Die Zielklasse kann verschiedene Entitäten darstellen, z. B. einen bösartigen Tumor, einen erfolgreichen Finanzhandel oder, wie bereits erwähnt, eine betrügerische Kreditkartentransaktion. Das wesentliche Merkmal ist die Dualität zwischen der Klasse von primärem Interesse und allen anderen Möglichkeiten.
Die Konfusionsmatrix
Für einen bestimmten Klassifikator, der auf einen Testdatensatz angewendet wird, sind vier verschiedene Ergebnisse möglich. Wenn eine Instanz, die zur positiven Klasse gehört, als positiv eingestuft wird, wird sie als wahr Positiv (TP) bezeichnet. Wird es hingegen als negativ eingestuft, spricht man von einem falsch Negativ (FN). Wird eine Instanz, die zur negativen Klasse gehört, als negativ eingestuft, wird sie als wahr Negativ (TN) bezeichnet; wird sie als positiv eingestuft, wird sie als falsch Positiv (FP) bezeichnet. Diese vier Werte bilden eine zwei-mal-zwei Konfusionsmatrix, die auch als Kontingenztabelle bezeichnet wird.
Diese Matrix fasst die Verteilung der Instanzen auf diese vier Ergebnisse zusammen und dient als Grundlage für zahlreiche allgemein verwendete Leistungskennzahlen, von denen einige zu nennen sind:
- Trefferquote oder Empfindlichkeit oder Rückruf: Der Anteil der Zielinstanzen, die korrekt als Ziele klassifiziert wurden, berechnet als TP / (TP + FN).
- Rate der Falschalarme (Typ-I-Fehlerrate): Der Anteil der fälschlicherweise als Ziel eingestuften Nicht-Ziel-Instanzen, berechnet als FP / (TN + FP).
- Miss-Rate (Typ-II-Fehlerrate): Der Anteil der fälschlicherweise als Nicht-Ziele eingestuften Zielinstanzen, berechnet als FN / (TP + FN).
- Spezifität: Der Anteil der Nicht-Ziel-Instanzen, die korrekt als Nicht-Ziele klassifiziert wurden, berechnet als TN / (TN + FP).
Wikipedia hat eine nützliche Grafik, die eine umfangreiche Liste von Leistungskennzahlen anzeigt, die von einer Konfusionsmatrix abgeleitet sind.
ROC-Kurven
Das Innenleben der meisten binären Klassifizierungsmodelle erstellt eine numerische Vorhersage und vergleicht diese anschließend mit einem vorgegebenen Schwellenwert. Wenn die Vorhersage diesen Schwellenwert erreicht oder überschreitet, wird die Instanz als Ziel eingestuft; andernfalls wird sie als Nicht-Ziel eingestuft. Es ist offensichtlich, dass der Schwellenwert alle vorgenannten Leistungskennzahlen beeinflusst. Wird der Schwellenwert auf oder unter das Minimum der möglichen Vorhersage gesetzt, werden alle Instanzen als Ziele klassifiziert, was zu einer perfekten Trefferquote, aber einer entsprechend niedrigen Fehlalarmquote führt.
Umgekehrt führt eine Einstellung des Schwellenwerts über die maximal mögliche Vorhersage dazu, dass alle Instanzen als Nicht-Ziele eingestuft werden, was zu einer Trefferquote von Null und einer Fehlalarmquote von perfekt Null führt. Der optimale Schwellenwert liegt zwischen diesen beiden Extremen. Durch systematisches Variieren des Schwellenwerts über den gesamten Bereich hinweg durchlaufen sowohl die Trefferquote als auch die Falschalarmquote ihren jeweiligen Bereich von 0 bis 1, wobei sich eine Kennzahl auf Kosten der anderen verbessert. Die Kurve, die durch das Auftragen dieser beiden Raten gegeneinander entsteht (wobei der Schwellenwert als latenter Parameter fungiert), wird als Receiver Operating Characteristic-Kurve bezeichnet.
Die ROC-Kurve wird üblicherweise mit der Fehlalarmrate auf der horizontalen Achse und der Trefferquote auf der vertikalen Achse dargestellt. Betrachten wir ein Klassifizierungsmodell, das zufällige numerische Vorhersagen liefert, die nicht mit der wahren Klasse eines Falles korreliert sind.
In einem solchen Szenario sind die Trefferquote und die Falschalarmquote im Durchschnitt über alle Schwellenwerte hinweg gleich, was zu einer ROC-Kurve führt, die sich einer diagonalen Linie annähert, die von der unteren linken zur oberen rechten Ecke des Diagramms verläuft. Wenn beispielsweise ein Klassifikator eine Instanz mit einer Wahrscheinlichkeit von 50 % zufällig der positiven Klasse zuordnet, wird erwartet, dass er sowohl 50 % der positiven als auch der negativen Instanzen korrekt klassifiziert, was zu dem Koordinatenpunkt (0,5, 0,5) innerhalb des ROC-Raums führt.
Wenn der Klassifikator eine Instanz mit einer Wahrscheinlichkeit von 90 % der positiven Klasse zuordnet, wird er voraussichtlich 90 % der positiven Instanzen richtig klassifizieren; die Falsch-Positiv-Rate wird jedoch gleichzeitig auf 90 % steigen, was den Koordinatenpunkt (0,9, 0,9) ergibt. Folglich wird ein zufälliger Klassifikator einen ROC-Punkt erzeugen, der entlang der Diagonale verläuft, wobei seine Position durch die Häufigkeit bestimmt wird, mit der er die positive Klasse vorhersagt. Um eine Leistung zu erzielen, die über die des zufälligen Ratens hinausgeht, was durch eine Position im oberen dreieckigen Bereich des ROC-Raums angezeigt wird, muss der Klassifikator informative Muster in den Daten nutzen.
Umgekehrt weist ein perfektes Modell, das durch das Vorhandensein eines Schwellenwerts gekennzeichnet ist, der Ziele (Vorhersagen, die dem Schwellenwert entsprechen oder ihn überschreiten) von Nicht-Zielen (Vorhersagen unterhalb des Schwellenwerts) genau trennt, eine eindeutige ROC-Kurve auf. Wenn der parametrische Schwellenwert von seinem Minimum zum optimalen Schwellenwert übergeht, sinkt die Fehlalarmrate von 1 auf 0, während die Trefferquote konstant bei 1 bleibt. Nachfolgende Erhöhungen des parametrischen Schwellenwerts führen dazu, dass die Trefferquote von 1 auf 0 sinkt, wobei die Fehlalarmquote bei 0 bleibt. Daraus ergibt sich eine ROC-Kurve, die einen Pfad von der oberen rechten Ecke zur oberen linken Ecke und dann zur unteren linken Ecke bildet.
Modelle mit mittlerer Leistung, die eine Genauigkeit zwischen diesen Extremen aufweisen, ergeben ROC-Kurven, die zwischen der Diagonale und der oberen linken Ecke liegen. Das Ausmaß, in dem die Kurve von der Diagonale in Richtung der oberen linken Ecke abweicht, zeigt die Leistung des Modells an. Generell gilt ein Punkt auf einem ROC-Diagramm als besser als ein anderer, wenn er eine höhere Rate an echten positiven Ergebnissen, eine niedrigere Rate an falschen positiven Ergebnissen oder beides aufweist. Klassifikatoren, die sich auf der linken Seite eines ROC-Diagramms, nahe der Abszisse, befinden, können als konservativ bezeichnet werden.
Diese Klassifikatoren neigen dazu, nur dann positive Klassifizierungen vorzunehmen, wenn sie über umfangreiche Beweise verfügen, was zu einer niedrigen Falsch-Positiv-Rate führt, die jedoch häufig mit einer geringeren Rate an echten Positivmeldungen einhergeht. Umgekehrt neigen Klassifikatoren, die sich auf der oberen rechten Seite des ROC-Diagramms befinden und als weniger konservativ charakterisiert werden, dazu, selbst bei minimaler Evidenz positive Klassifizierungen vorzunehmen, was zu einer hohen Rate an echten positiven Ergebnissen führt, die jedoch häufig mit einer hohen Rate an falschen positiven Ergebnissen einhergeht. In zahlreichen realen Bereichen, in denen negative Instanzen überwiegen, wird die Leistung von Klassifikatoren im linken Bereich des ROC-Diagramms immer relevanter.
Klassifikatoren, die im unteren rechten Dreiecksbereich des ROC-Raums angesiedelt sind, zeigen eine schlechtere Leistung als die des zufälligen Ratens. Folglich gibt es in diesem Bereich in der Regel keine Datenpunkte in den ROC-Diagrammen. Die Negation eines Klassifikators, definiert als die Umkehrung seiner Klassifizierungsentscheidungen für alle Instanzen, führt dazu, dass seine echten positiven Klassifizierungen zu falsch negativen Fehlern und seine falsch positiven Klassifizierungen zu echten negativen Klassifizierungen werden. Daher kann jeder Klassifikator, der einen Punkt im unteren rechten Dreieck ergibt, durch Negation so umgewandelt werden, dass ein entsprechender Punkt im oberen linken Dreieck entsteht. Ein Klassifikator, der sich entlang der Diagonale befindet, besitzt keine erkennbaren Informationen über die Klassenzugehörigkeit. Umgekehrt kann ein Klassifikator, der sich unterhalb der Diagonale befindet, so interpretiert werden, dass er über informative Muster verfügt, diese aber falsch anwendet.
ROC-Leistungskennzahlen
Während die visuelle Inspektion eines ROC-Kurvendiagramms erste Einblicke bieten kann, wird ein umfassenderes Verständnis der Modellleistung durch die Analyse relevanter Leistungsmaße erreicht. Vor einer detaillierten Analyse ist es notwendig, die Datenkonstrukte zu erläutern, die eine ROC-Kurve charakterisieren. Um das Verständnis zu erleichtern, wird ein anschauliches Beispiel angeführt.
Die folgende Tabelle enthält ein hypothetisches Beispiel für ROC-Leistungskennzahlen, die von einem Klassifikationsmodell abgeleitet wurden. In diesem Beispiel wird der Iris-Datensatz verwendet, der über die Python-Bibliothek Sklearn zugänglich ist. In Anlehnung an das Paradigma Ziel/Nicht-Ziel wurde das Klassifizierungsziel auf die Identifizierung einer einzelnen Irisvariante beschränkt. Wenn Setosa als Ziel bestimmt wird, werden alle anderen Varianten als Nicht-Ziele eingestuft. In Übereinstimmung mit konventionellen Klassifizierungsmethoden wurde das Modell so trainiert, dass es eine Ausgabe von 0 für Nicht-Ziele und 1 für Ziele erzeugt. Die Probenkennzeichnung wurden entsprechend transformiert. Es sei darauf hingewiesen, dass auch alternative Kennzeichnungssysteme in Frage kommen.
Für jeden Schwellenwert innerhalb des Entscheidungsschwellenbereichs wird eine Konfusionsmatrix erstellt, um die Rate der echten positiven und der falschen positiven Ergebnisse zu berechnen. Bei diesen Berechnungen wird die Ausgabewahrscheinlichkeit oder der Wert der Entscheidungsfunktion aus dem trainierten Vorhersagemodell verwendet, wobei der entsprechende Schwellenwert die Klassenzugehörigkeit bestimmt. Die hier vorgestellte Tabelle wurde mit Hilfe des Skripts ROC_curves_table_demo.mq5 erstellt.
KG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) TPR FPR FNR TNR PREC NPREC M_E ACC B_ACC THRESH NF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.038 0.000 0.962 1.000 1.000 0.000 0.481 0.667 0.519 0.98195 DI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.077 0.000 0.923 1.000 1.000 0.000 0.462 0.680 0.538 0.97708 OI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.115 0.000 0.885 1.000 1.000 0.000 0.442 0.693 0.558 0.97556 GI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.154 0.000 0.846 1.000 1.000 0.000 0.423 0.707 0.577 0.97334 GH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.192 0.000 0.808 1.000 1.000 0.000 0.404 0.720 0.596 0.97221 RH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.231 0.000 0.769 1.000 1.000 0.000 0.385 0.733 0.615 0.97211 IK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.269 0.000 0.731 1.000 1.000 0.000 0.365 0.747 0.635 0.96935 CK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.308 0.000 0.692 1.000 1.000 0.000 0.346 0.760 0.654 0.96736 NK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.346 0.000 0.654 1.000 1.000 0.000 0.327 0.773 0.673 0.96715 EJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.385 0.000 0.615 1.000 1.000 0.000 0.308 0.787 0.692 0.96645 DJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.423 0.000 0.577 1.000 1.000 0.000 0.288 0.800 0.712 0.96552 HJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.462 0.000 0.538 1.000 1.000 0.000 0.269 0.813 0.731 0.96534 NM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.500 0.000 0.500 1.000 1.000 0.000 0.250 0.827 0.750 0.96417 GM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.538 0.000 0.462 1.000 1.000 0.000 0.231 0.840 0.769 0.96155 CL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.577 0.000 0.423 1.000 1.000 0.000 0.212 0.853 0.788 0.95943 LL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.615 0.000 0.385 1.000 1.000 0.000 0.192 0.867 0.808 0.95699 NL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.654 0.000 0.346 1.000 1.000 0.000 0.173 0.880 0.827 0.95593 KO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.692 0.000 0.308 1.000 1.000 0.000 0.154 0.893 0.846 0.95534 NO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.731 0.000 0.269 1.000 1.000 0.000 0.135 0.907 0.865 0.95258 NO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.769 0.000 0.231 1.000 1.000 0.000 0.115 0.920 0.885 0.94991 EN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.808 0.000 0.192 1.000 1.000 0.000 0.096 0.933 0.904 0.94660 CN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.846 0.000 0.154 1.000 1.000 0.000 0.077 0.947 0.923 0.94489 OQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.885 0.000 0.115 1.000 1.000 0.000 0.058 0.960 0.942 0.94420 NQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.923 0.000 0.077 1.000 1.000 0.000 0.038 0.973 0.962 0.93619 GQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 0.962 0.000 0.038 1.000 1.000 0.000 0.019 0.987 0.981 0.92375 PP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.000 0.000 1.000 1.000 0.000 0.000 1.000 1.000 0.92087 OP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.020 0.000 0.980 0.963 0.037 0.010 0.987 0.990 0.12257 RP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.041 0.000 0.959 0.929 0.071 0.020 0.973 0.980 0.07124 RS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.061 0.000 0.939 0.897 0.103 0.031 0.960 0.969 0.05349 KS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.082 0.000 0.918 0.867 0.133 0.041 0.947 0.959 0.04072 KR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.102 0.000 0.898 0.839 0.161 0.051 0.933 0.949 0.03502 KR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.122 0.000 0.878 0.812 0.188 0.061 0.920 0.939 0.02523 JR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.143 0.000 0.857 0.788 0.212 0.071 0.907 0.929 0.02147 HE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.163 0.000 0.837 0.765 0.235 0.082 0.893 0.918 0.01841 QE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.184 0.000 0.816 0.743 0.257 0.092 0.880 0.908 0.01488 DE 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.204 0.000 0.796 0.722 0.278 0.102 0.867 0.898 0.01332 PD 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.224 0.000 0.776 0.703 0.297 0.112 0.853 0.888 0.01195 PD 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.245 0.000 0.755 0.684 0.316 0.122 0.840 0.878 0.01058 MG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.265 0.000 0.735 0.667 0.333 0.133 0.827 0.867 0.00819 JG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.286 0.000 0.714 0.650 0.350 0.143 0.813 0.857 0.00744 EG 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.306 0.000 0.694 0.634 0.366 0.153 0.800 0.847 0.00683 LF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.327 0.000 0.673 0.619 0.381 0.163 0.787 0.837 0.00635 CF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.347 0.000 0.653 0.605 0.395 0.173 0.773 0.827 0.00589 KF 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.367 0.000 0.633 0.591 0.409 0.184 0.760 0.816 0.00578 JI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.388 0.000 0.612 0.578 0.422 0.194 0.747 0.806 0.00556 JI 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.408 0.000 0.592 0.565 0.435 0.204 0.733 0.796 0.00494 NH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.429 0.000 0.571 0.553 0.447 0.214 0.720 0.786 0.00416 PH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.449 0.000 0.551 0.542 0.458 0.224 0.707 0.776 0.00347 LH 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.469 0.000 0.531 0.531 0.469 0.235 0.693 0.765 0.00244 KK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.490 0.000 0.510 0.520 0.480 0.245 0.680 0.755 0.00238 HK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.510 0.000 0.490 0.510 0.490 0.255 0.667 0.745 0.00225 LK 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.531 0.000 0.469 0.500 0.500 0.265 0.653 0.735 0.00213 PJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.551 0.000 0.449 0.491 0.509 0.276 0.640 0.724 0.00192 CJ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.571 0.000 0.429 0.481 0.519 0.286 0.627 0.714 0.00189 EM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.592 0.000 0.408 0.473 0.527 0.296 0.613 0.704 0.00177 IM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.612 0.000 0.388 0.464 0.536 0.306 0.600 0.694 0.00157 HM 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.633 0.000 0.367 0.456 0.544 0.316 0.587 0.684 0.00132 EL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.653 0.000 0.347 0.448 0.552 0.327 0.573 0.673 0.00127 DL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.673 0.000 0.327 0.441 0.559 0.337 0.560 0.663 0.00119 KL 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.694 0.000 0.306 0.433 0.567 0.347 0.547 0.653 0.00104 DO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.714 0.000 0.286 0.426 0.574 0.357 0.533 0.643 0.00102 RO 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.735 0.000 0.265 0.419 0.581 0.367 0.520 0.633 0.00085 DN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.755 0.000 0.245 0.413 0.587 0.378 0.507 0.622 0.00082 EN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.776 0.000 0.224 0.406 0.594 0.388 0.493 0.612 0.00069 HN 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.796 0.000 0.204 0.400 0.600 0.398 0.480 0.602 0.00062 HQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.816 0.000 0.184 0.394 0.606 0.408 0.467 0.592 0.00052 DQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.837 0.000 0.163 0.388 0.612 0.418 0.453 0.582 0.00048 FQ 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.857 0.000 0.143 0.382 0.618 0.429 0.440 0.571 0.00044 MP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.878 0.000 0.122 0.377 0.623 0.439 0.427 0.561 0.00028 LP 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.898 0.000 0.102 0.371 0.629 0.449 0.413 0.551 0.00026 NS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.918 0.000 0.082 0.366 0.634 0.459 0.400 0.541 0.00015 ES 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.939 0.000 0.061 0.361 0.639 0.469 0.387 0.531 0.00012 MS 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.959 0.000 0.041 0.356 0.644 0.480 0.373 0.520 0.00007 QR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 0.980 0.000 0.020 0.351 0.649 0.490 0.360 0.510 0.00004 CR 0 17:13:16.458 ROC_curves_table_demo (Crash 1000 Index,M5) 1.000 1.000 0.000 0.000 0.347 0.653 0.500 0.347 0.500 0.00002
Eine Untersuchung der tabellierten Daten der ROC-Kurven zeigt einen erkennbaren Trend: Sowohl die TPR als auch die FPR zeigen einen Rückgang von 1 auf 0, wenn die Entscheidungsschwelle steigt. In Anbetracht der dem Modell innewohnenden Vorhersagefähigkeit zeigt die FPR einen schnelleren Rückgang als die TPR. Es fällt auf, dass die FPR den Wert Null erreicht, während die TPR einen Wert von 1 behält. Sofern die relativen Kosten von Fehlern des Typs I und des Typs II nicht erheblich voneinander abweichen, dürfte der optimale Schwellenwert innerhalb des durch diese Extrema definierten Intervalls liegen. Es ist auch wichtig zu beachten, dass die Tabelle die Spezifität enthält, die der True Negative Rate (TNR) entspricht und das Komplement der FPR darstellt.
In vielen Fällen kann der optimale Schwellenwert durch direkte Betrachtung der Spalten „True Positive Rate“ und „False Positive Rate“ ermittelt werden. Die Interpretierbarkeit dieses Prozesses wird durch die Einbeziehung von Ziel- und Nicht-Ziel-Stichprobengrößen verbessert. Wenn die mit Fehlern des Typs I und des Typs II verbundenen Kosten annähernd gleich hoch sind, dient der mittlere Fehler als geeigneter skalarer Leistungsmaßstab. Diese Kennzahl, in der Tabelle als M_E bezeichnet, wird als arithmetisches Mittel der Falschalarmrate und der Fehlalarmrate berechnet.
In Szenarien, in denen die Kosten dieser Fehlerarten erheblich voneinander abweichen, verliert die Metrik des mittleren Fehlers jedoch an Bedeutung. Insbesondere die Präzision ist bei verschiedenen Anwendungen ein wichtiger Leistungsindikator. In der Regel ist die Genauigkeit der Zielerfassung von vorrangigem Interesse. In bestimmten Kontexten kann auch die Genauigkeit der Identifizierung als Nicht-Ziel von Bedeutung sein. Für eine genaue Zielerfassung liefert die Spalte mit der Aufschrift PREC relevante Informationen. Umgekehrt ist die Spalte mit der Bezeichnung NPREC für die genaue Identifizierung von Nicht-Zielen relevant.
Die Tabelle enthält zusätzliche Leistungskennzahlen, darunter Genauigkeit (ACC) und ausgewogene Genauigkeit (B_ACC). Die Genauigkeit ist definiert als der Anteil der korrekt klassifizierten Instanzen, die sowohl wahr-positive als auch wahr-negative Instanzen innerhalb des gesamten Datensatzes umfassen. Ein ausgewogene Genauigkeit, berechnet als arithmetisches Mittel von Sensitivität und Spezifität, wird verwendet, um die Auswirkungen eines Klassenungleichgewichts abzuschwächen, das durch eine erhebliche Diskrepanz zwischen den Stichprobengrößen von Ziel- und Nicht-Zielklassen gekennzeichnet ist. Vor der Erörterung der Fläche unter der ROC-Kurve ist eine Untersuchung der Berechnungsverfahren, die zur Erstellung der oben genannten Tabelle der ROC-Kennzahlen verwendet wurden, gerechtfertigt. Insbesondere wird der Code, der für die Berechnung dieser ROC-bezogenen Metriken verantwortlich ist, analysiert werden.
Der entsprechende Code ist in der Header-Datei roc_curves.mqh gekapselt, die eine Reihe von Funktionen und die Datenstruktur conf_stats definiert. Die Struktur conf_stats dient als Container für die Speicherung verschiedener Parameter, die aus der Konfusionsmatrix abgeleitet werden.
//+------------------------------------------------------------------+ //| confusion matrix stats | //+------------------------------------------------------------------+ struct conf_stats { double tn; //true negatives double tp; //true positives double fn; //false negatives double fp; //false positives double num_targets; //number of actual positive labels(target) double num_non_targets; //number of acutal negative labels(non targets) double tp_rate; //true positives rate - hit rate - recall - sensitivity double fp_rate; //false positives rate - fall out - type 1 error double fn_rate; //false negatives rate - miss rate - type 2 error double tn_rate; //true negatives rate - specificity double precision; //precision - positive predictve value double null_precision; //null precision - false discovery rate double prevalence; //prevalence double lr_plus; //positive likelihood ratio double lr_neg; //negative likelihood ratio double for_rate; //false omission rate double npv; //negative predictive value double acc; //accuracy double b_acc; //balanced accuracy double f1_score; //f1 score double mean_error; //mean error };
Die Struktur conf_stats fungiert als primärer Parameter innerhalb der Funktion roc_stats() und erleichtert die Speicherung der aus der Konfusionsmatrix abgeleiteten Bewertungsergebnisse. Diese Bewertung erfolgt anhand eines Datensatzes, der wahre Kennzeichnungen, entsprechende Vorhersagen und einen festgelegten Schwellenwert enthält. Die wahren Kennzeichnungen werden als Vektor bereitgestellt, der als zweiter Parameter dient und als Ziele bezeichnet wird. Das dritte Argument, probas, stellt den Vektor der vorhergesagten Wahrscheinlichkeiten oder Entscheidungsvariablen dar.
//+------------------------------------------------------------------+ //| defines | //+------------------------------------------------------------------+ bool roc_stats(conf_stats &cmat, vector &targets, vector &probas, double threshold, long target_label = 1, long non_target_label= 0) { vector all_labels = np::unique(targets); if(all_labels.Size()!=2 || long(all_labels[all_labels.ArgMin()])!=non_target_label || long(all_labels[all_labels.ArgMax()])!=target_label || target_label<=non_target_label) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return false; } //--- cmat.tp=cmat.fn=cmat.tn=cmat.fp = 0.0; //--- for(ulong i = 0; i<targets.Size(); i++) { if(probas[i]>=threshold && long(targets[i]) == target_label) cmat.tp++; else if(probas[i]>=threshold && long(targets[i]) == non_target_label) cmat.fp++; else if(probas[i]<threshold && long(targets[i]) == target_label) cmat.fn++; else cmat.tn++; } //--- cmat.num_targets = cmat.tp+cmat.fn; cmat.num_non_targets = cmat.fp+cmat.tn; //--- cmat.tp_rate = (cmat.tp+cmat.fn>0.0)?(cmat.tp/(cmat.tp+cmat.fn)):double("na"); cmat.fp_rate = (cmat.tn+cmat.fp>0.0)?(cmat.fp/(cmat.tn+cmat.fp)):double("na"); cmat.fn_rate = (cmat.tp+cmat.fn>0.0)?(cmat.fn/(cmat.tp+cmat.fn)):double("na"); cmat.tn_rate = (cmat.tn+cmat.fp>0.0)?(cmat.tn/(cmat.tn+cmat.fp)):double("na"); cmat.precision = (cmat.tp+cmat.fp>0.0)?(cmat.tp/(cmat.tp+cmat.fp)):double("na"); cmat.null_precision = 1.0 - cmat.precision; cmat.for_rate = (cmat.tn+cmat.fn>0.0)?(cmat.fn/(cmat.tn+cmat.fn)):double("na"); cmat.npv = 1.0 - cmat.for_rate; cmat.lr_plus = (cmat.fp_rate>0.0)?(cmat.tp_rate/cmat.fp_rate):double("na"); cmat.lr_neg = (cmat.tn_rate>0.0)?(cmat.fn_rate/cmat.tn_rate):double("na"); cmat.prevalence = (cmat.num_non_targets+cmat.num_targets>0.0)?(cmat.num_targets/(cmat.num_non_targets+cmat.num_targets)):double("na"); cmat.acc = (cmat.num_non_targets+cmat.num_targets>0.0)?((cmat.tp+cmat.tn)/(cmat.num_non_targets+cmat.num_targets)):double("na"); cmat.b_acc = ((cmat.tp_rate+cmat.tn_rate)/2.0); cmat.f1_score = (cmat.tp+cmat.fp+cmat.fn>0.0)?((2.0*cmat.tp)/(2.0*cmat.tp+cmat.fp+cmat.fn)):double("na"); cmat.mean_error = ((cmat.fp_rate+cmat.fn_rate)/2.0); //--- return true; //--- }
Der Schwellenwertparameter definiert den kritischen Wert, der zur Abgrenzung der Klassenzugehörigkeit verwendet wird. Die beiden letzten Parameter ermöglichen die explizite Angabe der Ziel- bzw. Nicht-Ziel-Kennzeichnungen. Die Funktion gibt einen booleschen Wert zurück, der die erfolgreiche Ausführung mit true und das Auftreten eines Fehlers mit false angibt.
//+------------------------------------------------------------------+ //| roc table | //+------------------------------------------------------------------+ matrix roc_table(vector &true_targets,matrix &probas,ulong target_probs_col = 1, long target_label = 1, long non_target_label= 0) { matrix roctable(probas.Rows(),10); conf_stats mts; vector probs = probas.Col(target_probs_col); if(!np::quickSort(probs,false,0,probs.Size()-1)) return matrix::Zeros(1,1); for(ulong i = 0; i<roctable.Rows(); i++) { if(!roc_stats(mts,true_targets,probas.Col(target_probs_col),probs[i],target_label,non_target_label)) return matrix::Zeros(1,1); roctable[i][0] = mts.tp_rate; roctable[i][1] = mts.fp_rate; roctable[i][2] = mts.fn_rate; roctable[i][3] = mts.tn_rate; roctable[i][4] = mts.precision; roctable[i][5] = mts.null_precision; roctable[i][6] = mts.mean_error; roctable[i][7] = mts.acc; roctable[i][8] = mts.b_acc; roctable[i][9] = probs[i]; } //--- return roctable; }
Die Funktion roc_table() erzeugt eine Matrix, die die Daten der ROC-Kurve enthält. Zu den Eingabeparametern gehören ein Vektor wahrer Klassenbezeichnungen, eine Matrix vorhergesagter Wahrscheinlichkeiten oder Entscheidungsvariablen und eine lange Ganzzahl ohne Vorzeichen, die den Spaltenindex für die Bestimmung der Klassenzugehörigkeit in mehrspaltigen Matrizen angibt. Die letzten beiden Parameter definieren die Ziel- und Nicht-Ziel-Kennzeichnungen. Im Falle eines Fehlers gibt die Funktion eine 1x1-Matrix aus Nullen zurück. Es ist unbedingt zu beachten, dass sowohl roc_stats() als auch roc_table() speziell für binäre Klassifizierungsmodelle konzipiert sind. Die Nichteinhaltung dieser Anforderung führt zu einer Fehlermeldung.
//+------------------------------------------------------------------+ //| roc curve table display | //+------------------------------------------------------------------+ string roc_table_display(matrix &out) { string output,temp; if(out.Rows()>=10) { output = "TPR FPR FNR TNR PREC NPREC M_E ACC B_ACC THRESH"; for(ulong i = 0; i<out.Rows(); i++) { temp = StringFormat("\n%5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.3lf %5.5lf", out[i][0],out[i][1],out[i][2],out[i][3],out[i][4],out[i][5],out[i][6],out[i][7],out[i][8],out[i][9]); StringAdd(output,temp); } } return output; }
Die Funktion roc_table_display() akzeptiert einen einzelnen Matrixparameter, idealerweise die Ausgabe eines vorherigen Aufrufs von roc_table(), und formatiert die Daten in eine tabellarische Zeichenkettendarstellung.
Die Fläche unter einer ROC-Kurve
Die Fläche unter der ROC-Kurve (Area Under the ROC Curve, AUC) bietet eine prägnante, einwertige Metrik für die Klassifizierungsleistung, die die übermäßige Detailgenauigkeit der vollständigen ROC-Kurve vermeidet. Während die ROC-Kurve den Kompromiss zwischen den Richtig- und Falsch-Positiv-Raten visuell darstellt, quantifiziert der AUC die allgemeine Fähigkeit des Modells, zwischen Klassen zu unterscheiden. Ein unbrauchbares Modell, dargestellt durch eine diagonale Linie im ROC-Diagramm, ergibt einen AUC von 0,5, was auf eine zufällige Leistung hinweist. Umgekehrt erreicht ein perfektes Modell mit einer ROC-Kurve, die sich in der oberen linken Ecke befindet, einen AUC von 1,0. Daher bedeutet ein höherer AUC eine bessere Modellleistung. Die Berechnung der AUC beinhaltet die Bestimmung der Fläche unter der ROC-Kurve, und aufgrund der inhärenten statistischen Schwankungen in den Testdatensätzen ist eine einfache Summierung in der Regel für eine genaue Schätzung ausreichend, so dass auf eine komplexe numerische Integration verzichtet werden kann.
Der AUC hat eine signifikante statistische Bedeutung: Er stellt die Wahrscheinlichkeit dar, dass ein Klassifikator einem zufällig ausgewählten positiven Fall einen höheren Rang zuweist als einem zufällig ausgewählten negativen Fall. Dieses Merkmal stellt eine Gleichwertigkeit zwischen der AUC und dem Wilcoxon-Rangsummentest, auch bekannt als Mann-Whitney-U-Test, her.
Der Wilcoxon-Rangsummentest, ein nichtparametrisches statistisches Verfahren, bewertet den Unterschied zwischen zwei unabhängigen Gruppen, ohne dass Normalität vorausgesetzt wird. Dabei werden alle Beobachtungen in eine Rangfolge gebracht und die Rangsummen zwischen den Gruppen verglichen, wodurch die Unterschiede in den Medianen bewertet werden.
Außerdem ist der AUC untrennbar mit dem Gini-Koeffizienten verbunden. Der Gini-Koeffizient ist das Doppelte der Fläche zwischen der Diagonale des Zufalls und der ROC-Kurve. Der Gini-Koeffizient, ein Maß für die Verteilungsungleichheit, quantifiziert den Grad der Streuung innerhalb einer Verteilung und reicht von 0 (perfekte Gleichheit) bis 1 (maximale Ungleichheit). Im Zusammenhang mit der Einkommensverteilung spiegelt es die Ungleichheit der Einkommensniveaus wider. Grafisch gesehen ist der Gini-Koeffizient definiert als das Verhältnis zwischen der Fläche zwischen der Lorenzkurve und der Linie der vollkommenen Gleichheit und der Fläche unter der Linie der vollkommenen Gleichheit.
Die Funktion roc_auc(), die in roc_curves.mqh definiert ist, berechnet den AUC für ein binäres Klassifikationsproblem mit der Option, die Berechnung auf einen bestimmten maximalen FPR zu beschränken. Es nimmt die wahren Klassenbezeichnungen und die vorhergesagten Wahrscheinlichkeiten als Eingabe, zusammen mit einer optionalen Zielbezeichnung und der maximalen FPR. Wenn die maximale FPR 1,0 beträgt, wird die Standard-AUC berechnet. Andernfalls wird die ROC-Kurve berechnet, der Punkt auf der Kurve, der der maximalen FPR entspricht, mit Hilfe der Suchfunktion gefunden, die TPR an diesem Punkt interpoliert und dann die partielle AUC bis zu dieser maximalen FPR mit Hilfe der Trapezregel berechnet. Schließlich wird dieser partielle AUC auf einen Wert zwischen 0,5 und 1,0 normiert, wodurch ein Maß für die Klassifizierungsleistung innerhalb des angegebenen FPR-Bereichs entsteht.
//+------------------------------------------------------------------+ //| area under the curve | //+------------------------------------------------------------------+ double roc_auc(vector &true_classes, matrix &predicted_probs,long target_label=1,double max_fpr=1.0) { vector all_labels = np::unique(true_classes); if(all_labels.Size()!=2|| max_fpr<=0.0 || max_fpr>1.0) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return EMPTY_VALUE; } if(max_fpr == 1.0) { vector auc = true_classes.ClassificationScore(predicted_probs,CLASSIFICATION_ROC_AUC,AVERAGE_BINARY); return auc[0]; } matrix tpr,fpr,threshs; if(!true_classes.ReceiverOperatingCharacteristic(predicted_probs,AVERAGE_BINARY,fpr,tpr,threshs)) { Print(__FUNCTION__, " ", __LINE__, " invalid inputs "); return EMPTY_VALUE; } vector xp(1); xp[0] = max_fpr; vector stop; if(!np::searchsorted(fpr.Row(0),xp,true,stop)) { Print(__FUNCTION__, " ", __LINE__, " searchsorted failed "); return EMPTY_VALUE; } vector xpts(2); vector ypts(2); xpts[0] = fpr[0][long(stop[0])-1]; xpts[1] = fpr[0][long(stop[0])]; ypts[0] = tpr[0][long(stop[0])-1]; ypts[1] = tpr[0][long(stop[0])]; vector vtpr = tpr.Row(0); vtpr = np::sliceVector(vtpr,0,long(stop[0])); vector vfpr = fpr.Row(0); vfpr = np::sliceVector(vfpr,0,long(stop[0])); if(!vtpr.Resize(vtpr.Size()+1) || !vfpr.Resize(vfpr.Size()+1)) { Print(__FUNCTION__, " ", __LINE__, " error ", GetLastError()); return EMPTY_VALUE; } vfpr[vfpr.Size()-1] = max_fpr; vector yint = np::interp(xp,xpts,ypts); vtpr[vtpr.Size()-1] = yint[0]; double direction = 1.0; vector dx = np::diff(vfpr); if(dx[dx.ArgMin()]<0.0) direction = -1.0; double partial_auc = direction*np::trapezoid(vtpr,vfpr); if(partial_auc == EMPTY_VALUE) { Print(__FUNCTION__, " ", __LINE__, " trapz failed "); return EMPTY_VALUE; } double minarea = 0.5*(max_fpr*max_fpr); double maxarea = max_fpr; return 0.5*(1+(partial_auc-minarea)/(maxarea-minarea)); }
Der Parameter max_fpr erleichtert die Berechnung der partiellen Fläche unter der ROC-Kurve (AUC) und ermöglicht so die Bewertung der Klassifikatorleistung innerhalb eines bestimmten Bereichs von FPR-Werten. Diese Funktion ist besonders in Szenarien von Bedeutung, in denen die Leistung bei niedrigeren FPR-Schwellenwerten im Vordergrund steht. Darüber hinaus erweist es sich als vorteilhaft, wenn unausgewogene Datensätze analysiert werden, bei denen die ROC-Kurve durch eine beträchtliche Anzahl echter Negative unverhältnismäßig stark beeinflusst werden kann. Die Verwendung dieses Parameters ermöglicht eine gezielte Bewertung des entsprechenden Bereichs der Kurve.
ROC-Kurven (Receiver Operating Characteristic) bieten zwar einen nützlichen Rahmen für die Bewertung von Klassifizierern, ihre Anwendung zur Bestimmung der endgültigen Überlegenheit von Klassifizierern muss jedoch sorgfältig geprüft werden, insbesondere wenn die Kosten von Fehlklassifizierungen berücksichtigt werden. Obwohl der AUC ein Maß für die Bewertung der Klassifikatorqualität ist, erfordern vergleichende Leistungsbewertungen einen differenzierteren Ansatz. Um Kostenerwägungen angemessen zu berücksichtigen, ist eine Rückkehr zur grundlegenden Konfusionsmatrix erforderlich.
Herkömmliche Klassifizierungsparadigmen stellen häufig die Maximierung der Genauigkeit in den Vordergrund und gehen implizit von einheitlichen Kosten für alle Fehlklassifizierungen aus. Im Gegensatz dazu werden bei der kostensensitiven Klassifizierung die mit den verschiedenen Fehlertypen verbundenen unterschiedlichen Kosten berücksichtigt, wobei das Ziel darin besteht, die Gesamtkosten der Fehler zu minimieren, anstatt nur die Genauigkeit zu optimieren. Bei einem Klassifikator, der vielversprechende Anlagewerte identifizieren soll, können beispielsweise die Kosten einer verpassten Chance (falsch negativ) als weniger folgenreich angesehen werden als die Kosten eines falsch positiven Ergebnisses. Die Zuordnung der Kosten zu den einzelnen Fehlklassifizierungsarten ergibt eine Kostenmatrix. In dieser Matrix werden die mit verschiedenen Vorhersageergebnissen verbundenen Kosten dargelegt, wobei die Strafen oder Verluste für falsche Vorhersagen, wie z. B. falsch-positive und falsch-negative Vorhersagen, angegeben werden und möglicherweise auch die Kosten für richtige Vorhersagen einbezogen werden. Eine hypothetische Konfusionsmatrix mit der dazugehörigen Kostenmatrix ist unten dargestellt.
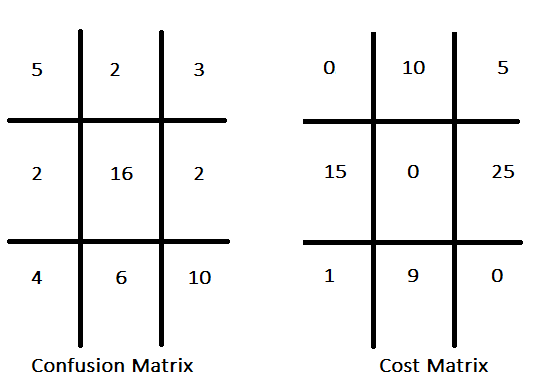
Die Kostenmatrix weist in der Regel Nullwerte entlang ihrer Diagonale auf, was bedeutet, dass die Kosten für korrekte Vorhersagen gleich Null sind. Diese Konvention ist zwar weit verbreitet, aber nicht zwingend erforderlich. Bei einer definierten Kostenstruktur für alle Fehlklassifizierungsarten kann die in der Konfusionsmatrix enthaltene Information zu einer singulären Leistungskennzahl aggregiert werden. Ein rudimentärer Ansatz besteht darin, die Häufigkeit jeder Art von Fehlklassifizierung mit den entsprechenden Kosten zu multiplizieren und diese Produkte anschließend zu addieren. Die Wirksamkeit dieser Metrik hängt jedoch davon ab, dass die Klassenproportionen des Datensatzes die in realen Anwendungen vorkommenden Proportionen genau widerspiegeln.
Ein robusteres Maß für die kostenorientierte Leistung sind die erwarteten Kosten je Probe. Diese Metrik wird abgeleitet, indem die Anzahl der Stichproben in der Konfusionsmatrix durch ihre jeweiligen Zeilensummen normalisiert wird, was die bedingten Wahrscheinlichkeiten der klassifizierten Klassen bei gegebenen wahren Klassen ergibt. Diese Wahrscheinlichkeiten werden dann mit den entsprechenden Kosten aus der Kostenmatrix multipliziert, und die Produkte werden über jede Zeile summiert, was die erwarteten Kosten für ein Mitglied jeder Klasse ergibt. Anschließend werden diese klassenspezifischen Kosten mit dem erwarteten Anteil der Proben in jeder Klasse gewichtet und summiert, was die erwarteten Gesamtkosten pro Probe ergibt. Die Schätzung der erwarteten Klassenanteile in realen Szenarien erfordert ein umfassendes Verständnis der zugrunde liegenden Datenverteilung in der Einsatzumgebung. Zu den Methoden für diese Schätzung gehören:
- Analyse historischer Daten, wobei vorhandene Aufzeichnungen untersucht werden, um zuverlässige Schätzungen der Klassenanteile zu erhalten. In der medizinischen Diagnostik zum Beispiel können Patientenakten Aufschluss über die Verbreitung von Krankheiten geben.
- Konsultation von Fachleuten, deren Spezialwissen die auf anderem Wege gewonnenen Schätzungen verfeinern oder bestätigen kann.
- Anwendung repräsentativer Stichprobenverfahren, wenn eine neue Datenerhebung möglich ist, um sicherzustellen, dass die Stichprobe die reale Verteilung genau widerspiegelt, insbesondere bei unausgewogenen Datensätzen. Durch geschichtete Stichproben kann auch bei ungleichmäßiger Verteilung eine angemessene Vertretung aller Klassen gewährleistet werden.
Die erwarteten Proportionen der Stichproben innerhalb einer Klasse sind formal äquivalent zu vorherigen Wahrscheinlichkeiten. Im spezifischen Kontext der binären Klassifikation sei
q bezeichnet die vorherige Wahrscheinlichkeit, dass eine Stichprobe zur Zielklasse gehört. Definieren Sie ferner p1 als die Wahrscheinlichkeit eines Fehlers vom Typ I (falsch positiv), wobei c1 die damit verbundenen Kosten darstellt, und p2 als die Wahrscheinlichkeit eines Fehlers vom Typ II (falsch negativ), wobei c2 die damit verbundenen Kosten darstellt. In zahlreichen Anwendungen ist q mit theoretischen oder empirischen Mitteln ermittelbar, und die Kosten c1 und c2 sind entweder genau oder in angemessener Näherung bekannt. Folglich können diese drei Größen als feste Parameter behandelt werden. Die Fehlerwahrscheinlichkeiten p1 und p2 werden durch die Klassifizierungsschwelle bestimmt. Die erwarteten Kosten werden durch die folgende Gleichung ausgedrückt.
Wenn man diese Gleichung umstellt, erhält man.
Nachweis einer linearen Beziehung zwischen p1 und p2 bei gegebenen erwarteten Kosten. Wird diese lineare Beziehung auf der ROC-Kurve grafisch dargestellt, wird ihre Steigung durch die Vorwahrscheinlichkeit q und das Kostenverhältnis c2/c1 bestimmt. Die Variation der erwarteten Kosten führt zu einer Reihe von parallelen Linien, wobei Linien, die niedriger und weiter rechts liegen, höhere Kosten bedeuten. Der Schnittpunkt dieser Linie mit der ROC-Kurve an zwei Punkten zeigt zwei Schwellenwerte an, die gleichwertige, wenn auch suboptimale Kosten ergeben. Linien, die sich vollständig oberhalb und links der ROC-Kurve befinden, stellen eine Leistung dar, die vom Modell nicht erreicht werden kann. Die Linie, die die ROC-Kurve tangiert, stellt die optimalen erreichbaren Kosten dar.
Diese Analyse unterstreicht, dass der AUC nicht unbedingt ein endgültiges Maß für die praktische Leistung eines Klassifikationsmodells ist. Der AUC ist zwar ein gültiger Maßstab für die Gesamtqualität, sein Nutzen wird jedoch geschmälert, wenn die Betriebskosten berücksichtigt werden, da er bei kostensensiblen Anwendungen zu irreführenden Schlussfolgerungen führen kann.
Entscheidungsprobleme mit mehr als zwei Klassen
Die Ausweitung des ROC-Kurven-Rahmens auf die Mehrklassen-Klassifikation erfordert die Anwendung spezifischer Anpassungsstrategien. Überwiegend werden zwei Methoden angewandt: der One-vs-Rest (OvR), auch bekannt als One-vs-All (OvA), und der One-vs-One (OvO) Ansatz. Bei der OvR-Strategie wird das Mehrklassenproblem in mehrere binäre Klassifizierungsaufgaben umgewandelt, indem jede Klasse als die positive Klasse gegenüber den kombinierten verbleibenden Klassen behandelt wird, was zu n ROC-Kurven für n Klassen führt. Umgekehrt werden bei der OvO-Methode binäre Klassifizierungsprobleme für alle möglichen Klassenpaare konstruiert, was zu n(n-1)/2 ROC-Kurven führt.
Um die aus diesen binären Klassifizierungen abgeleiteten Leistungskennzahlen zu aggregieren, werden Mittelungstechniken eingesetzt. Die Mikro-Mittelung berechnet die globale TPR und FPR, indem sie alle Instanzen über alle Klassen hinweg berücksichtigt und somit jeder Instanz das gleiche Gewicht zuweist. Bei der Makro-Mittelwertbildung hingegen werden TPR und FPR für jede Klasse unabhängig voneinander berechnet und dann gemittelt, wodurch jeder Klasse das gleiche Gewicht zugewiesen wird - eine Methode, die besonders nützlich ist, wenn die klassenspezifische Leistung im Vordergrund steht. Folglich hängt die Interpretation von Mehrklassen-ROC-Kurven von der gewählten Zerlegungsstrategie (OvR oder OvO) und Mittelungsmethode (Mikro oder Makro) ab, da diese Entscheidungen die resultierende Leistungsbewertung erheblich beeinflussen.
In MQL5 integrierte Funktionen für ROC-Kurven und AUC
In MQL5 wird die Berechnung der Kurven von „Receiver Operating Characteristic“ (ROC) und „Area Under the Curve“ (AUC) durch eine spezielle Funktion erleichtert. Die Sprache
Die Vektormethode ReceiverOperatingCharacteristic() wird verwendet, um die erforderlichen Werte für die Visualisierung der ROC-Kurve zu erzeugen. Diese Methode arbeitet mit einem Vektor, der die wahren Klassenbezeichnungen darstellt. Das erste Argument ist eine Matrix von Wahrscheinlichkeiten oder Entscheidungswerten, deren Spalten entsprechend der Anzahl der Klassen strukturiert sind. Das zweite Argument, eine Variable der Enumeration ENUM_AVERAGE_MODE, gibt die Methode der Mittelwertbildung an. Insbesondere unterstützt diese Funktion nur AVERAGE_NONE, AVERAGE_BINARY und AVERAGE_MICRO. Nach erfolgreicher Ausführung werden die Falsch-Positiv-Rate (FPR), die Wahr-Positiv-Rate (TPR) und die zugehörigen Schwellenwerte in die entsprechenden Matrizen, die letzten drei Parameter, geschrieben. Die Methode gibt einen booleschen Wert zurück, der den Erfolg der Ausführung anzeigt.
Die AUC-Berechnung wird über die Vektormethode ClassificationScore() durchgeführt. Ähnlich wie die ROC-Methode wird sie auf den Vektor der wahren Klassenbezeichnungen angewandt und erfordert eine Matrix der vorhergesagten Wahrscheinlichkeiten oder Entscheidungswerte. Der zweite Parameter, vom Typ der Enumeration ENUM_CLASSIFICATION_METRIC, muss auf CLASSIFICATION_ROC_AUC gesetzt werden, um die AUC-Berechnung festzulegen. Anders als bei der ROC-Methode werden bei dieser Funktion alle Werte von ENUM_AVERAGE_MODE berücksichtigt. Die Methode gibt einen Vektor der berechneten Flächen zurück, dessen Kardinalität vom Mittelungsmodus und der Anzahl der im Datensatz vorhandenen Klassen abhängt.
Um die Auswirkungen verschiedener Mittelungsmodi zu verdeutlichen, wurde das Skript ROC_Demo.mq5 entwickelt. Dieses Skript verwendet den Iris-Datensatz und ein logistisches Regressionsmodell, um nutzerkonfigurierbare binäre oder Mehrklassen-Klassifizierungsprobleme zu lösen. Der vollständige Skriptcode ist unten aufgeführt.
//+------------------------------------------------------------------+ //| ROC_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<logistic.mqh> #include<ErrorDescription.mqh> #include<Generic/SortedSet.mqh> //--- enum CLASSIFICATION_TYPE { BINARY_CLASS = 0,//binary classification problem MULITI_CLASS//multiclass classification problem }; //--- input parameters input double Train_Test_Split = 0.5; input int Random_Seed = 125; input CLASSIFICATION_TYPE classification_problem = BINARY_CLASS; input ENUM_AVERAGE_MODE av_mode = AVERAGE_BINARY; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- CHighQualityRandStateShell rngstate; CHighQualityRand::HQRndSeed(Random_Seed,Random_Seed+Random_Seed,rngstate.GetInnerObj()); //--- matrix data = np::readcsv("iris.csv"); data = np::sliceMatrixCols(data,1); //--- if(classification_problem == BINARY_CLASS) data = np::sliceMatrixRows(data,0,100); //--- ulong rindices[],trainset[],testset[]; np::arange(rindices,int(data.Rows())); //--- //--- if(!np::shuffleArray(rindices,GetPointer(rngstate)) || ArrayCopy(trainset,rindices,0,0,int(ceil(Train_Test_Split*rindices.Size())))<0 || !ArraySort(trainset)) { Print(__LINE__, " error ", ErrorDescription(GetLastError())); return; } //--- CSortedSet<ulong> test_set(rindices); //--- test_set.ExceptWith(trainset); //--- test_set.CopyTo(testset); //--- matrix testdata = np::selectMatrixRows(data,testset); matrix test_predictors = np::sliceMatrixCols(testdata,0,4); vector test_targets = testdata.Col(4); matrix traindata = np::selectMatrixRows(data,trainset); matrix train_preditors = np::sliceMatrixCols(traindata,0,4); vector train_targets = traindata.Col(4); //--- logistic::Clogit logit; //-- if(!logit.fit(train_preditors,train_targets)) { Print(" error training logistic model "); return; } //--- matrix y_probas = logit.probas(test_predictors); vector y_preds = logit.predict(test_predictors); //--- vector auc = test_targets.ClassificationScore(y_probas,CLASSIFICATION_ROC_AUC,av_mode); //--- if(auc.Size()>0) Print(" AUC ", auc); else Print(" AUC error ", ErrorDescription(GetLastError())); //--- matrix fpr,tpr,threshs; if(!test_targets.ReceiverOperatingCharacteristic(y_probas,av_mode,fpr,tpr,threshs)) { Print(" ROC error ", ErrorDescription(GetLastError())); return; } //--- string legend; for(ulong i = 0; i<auc.Size(); i++) { string temp = (i!=int(auc.Size()-1))?StringFormat("%.3lf,",auc[i]):StringFormat("%.3lf",auc[i]); StringAdd(legend,temp); } CGraphic* roc = np::plotMatrices(fpr, tpr,"ROC",false,"FPR","TPR",legend,true,0,0,10,10,600,500); if(CheckPointer(roc)!=POINTER_INVALID) { Sleep(7000); roc.Destroy(); delete roc; ChartRedraw(); } } //+------------------------------------------------------------------+
Zunächst wird ein binäres Klassifikationsproblem untersucht, wobei der Mittelungsmodus auf AVERAGE_BINARY eingestellt ist. In diesem Modus werden die ROC-Kurve und die AUC unter der Annahme berechnet, dass die Zielklasse mit 1 gekennzeichnet ist, was dem grundlegenden Ziel/Nicht-Ziel-Paradigma entspricht, das der Erstellung von ROC-Kurven zugrunde liegt. Die Ausgabe, die sich aus der Ausführung des Skripts mit diesen Konfigurationen ergibt, zeigt, dass der AUC-Wertvektor ein einziges Element enthält. Außerdem bestehen die FPR-, TPR- und Schwellenwertmatrizen jeweils aus einer einzigen Zeile.
MK 0 12:45:28.930 ROC_Demo (Crash 1000 Index,M5) AUC [1]
Um die ROC-Kurve und die zugehörige AUC für andere Zielklassen als der Kennzeichnung 1 zu untersuchen, sollte der Mittelungsmodus auf AVERAGE_NONE gesetzt werden. In diesem Modus werten die Funktionen ReceiverOperatingCharacteristic() und ClassificationScore() jede Klasse unabhängig als Ziel aus und liefern entsprechende Ergebnisse. Wenn Sie das Skript mit AVERAGE_NONE und einem binären Klassifikationsproblem ausführen, erhalten Sie die folgende Ausgabe. In diesem Fall zeigt das ROC-Diagramm zwei Kurven an, die die Diagramme der jeweiligen Zeilen in den FPR- und TPR-Matrizen darstellen. Es werden auch zwei AUC-Werte berechnet.
CK 0 16:42:43.249 ROC_Demo (Crash 1000 Index,M5) AUC [1,1]
Die Ergebnisse werden in Übereinstimmung mit der Reihenfolge der Klassenbezeichnungen dargestellt. Bei dem im oben genannten Skript dargestellten binären Klassifizierungsproblem, bei dem die Labels 0 und 1 sind, stellen die ersten Zeilen der TPR-, FPR- und Schwellenwertmatrizen die Werte der ROC-Kurve dar, wenn Label 0 als Zielklasse betrachtet wird, während die zweiten Zeilen sich auf Label 1 als Ziel beziehen. Diese Ordnungskonvention gilt auch für die AUC-Werte. Es sei darauf hingewiesen, dass dieses Ergebnisformat bei ROC-Statistiken, die aus Mehrklassendatensätzen berechnet werden, konsistent ist. In binären Klassifizierungsszenarien führt die Verwendung anderer Mittelungsoptionen als AVERAGE_NONE und AVERAGE_BINARY zu Berechnungsmethoden, die der Handhabung von Mehrklassendatensätzen entsprechen. Umgekehrt löst AVERAGE_BINARY bei der Mehrklassen-Klassifikation einen Fehler aus. AVERAGE_MICRO, AVERAGE_MACRO und AVERAGE_WEIGHTED ergeben jedoch alle einen einzigen, aggregierten AUC-Wert.
LL 0 17:27:13.673 ROC_Demo (Crash 1000 Index,M5) AUC [1,0.9965694682675815,0.9969135802469137]
Der Mittelungsmodus AVERAGE_MICRO berechnet ROC-Kurven und AUC global, indem er jedes Element der One-Hot-codierten wahren Klassenmatrix als ein eigenes Label behandelt. Bei diesem Ansatz wird das Mehrklassenproblem in ein binäres Klassifizierungsproblem umgewandelt, und zwar durch anfängliche One-Hot-Codierung der wahren Klassenbezeichnungen, wobei eine Matrix mit Spalten erzeugt wird, die der Anzahl der Klassen entsprechen. Diese Matrix wird dann zusammen mit den vorhergesagten Entscheidungswerten oder der Wahrscheinlichkeitsmatrix in eine einspaltige Struktur umgewandelt. Die anschließenden ROC-Kurven- und AUC-Berechnungen werden auf diesen abgeflachten Containern durchgeführt. Diese Methodik führt zu umfassenden Leistungskennzahlen, die alle Klassen umfassen und jeder Instanz das gleiche Gewicht zuweisen. Dies ist besonders vorteilhaft in Szenarien mit erheblichem Klassenungleichgewicht, da es die Voreingenommenheit gegenüber der Mehrheitsklasse abschwächt. Die empirischen Ergebnisse des Demonstrationsskripts veranschaulichen dieses Verhalten.
RG 0 17:26:51.955 ROC_Demo (Crash 1000 Index,M5) AUC [0.9984000000000001]
Der Mittelungsmodus AVERAGE_MACRO wendet eine andere Strategie an, um das Ungleichgewicht zwischen den Klassen zu beseitigen. Jede Klasse wird unabhängig bewertet, wobei der AUC auf der Grundlage der jeweiligen Klassenwahrscheinlichkeiten berechnet wird. Die endgültige AUC ergibt sich dann als arithmetisches Mittel dieser einzelnen AUC-Werte. In der MQL5-Dokumentation wird darauf hingewiesen, dass AVERAGE_MACRO von der Methode ReceiverOperatingCharacteristic() nicht unterstützt wird. Die Methode ClassificationScore() implementiert die OvR-Technik für die AUC-Berechnung in Mehrklassen-Datensätzen. Die Skriptausführung mit AVERAGE_MACRO bestätigt die erfolgreiche AUC-Berechnung, während die Erstellung der ROC-Kurve erwartungsgemäß fehlschlägt.
ER 0 17:26:09.341 ROC_Demo (Crash 1000 Index,M5) AUC [0.997827682838166] NF 0 17:26:09.341 ROC_Demo (Crash 1000 Index,M5) ROC error Wrong parameter when calling the system function
Der Mittelungsmodus AVERAGE_WEIGHTED funktioniert analog zu AVERAGE_MACRO, mit Ausnahme des letzten Aggregationsschritts. Anstelle eines einfachen arithmetischen Mittels wird ein gewichteter Durchschnitt berechnet, wobei die Gewichte durch die Klassenverteilung der wahren Klassenbezeichnungen bestimmt werden. Dieser Ansatz führt zu einem endgültigen AUC-Wert, der die dominanten Klassen innerhalb des Datensatzes berücksichtigt. Ähnlich wie AVERAGE_MACRO unterstützt auch ReceiverOperatingCharacteristic() nicht AVERAGE_WEIGHTED. Die Skriptausgabe veranschaulicht dieses Verhalten.
IN 0 17:26:28.465 ROC_Demo (Crash 1000 Index,M5) AUC [0.9978825995807129] HO 0 17:26:28.465 ROC_Demo (Crash 1000 Index,M5) ROC error Wrong parameter when calling the system function
Schlussfolgerung
ROC-Kurven sind wirksame Instrumente zur Visualisierung und Bewertung von Klassifikatoren. Sie ermöglichen eine umfassendere Bewertung der Klassifizierungsleistung im Vergleich zu skalaren Metriken wie Genauigkeit, Fehlerrate oder Fehlerkosten. Durch die Entkopplung der Klassifikatorleistung von der Klassenschiefe und den Fehlerkosten bieten sie Vorteile gegenüber alternativen Evaluierungsmethoden, einschließlich Präzisions- und Recall-Kurven. Wie bei jeder Bewertungsmetrik erfordert jedoch auch die vernünftige Anwendung von ROC-Diagrammen ein gründliches Verständnis ihrer inhärenten Merkmale und Grenzen. Es wird erwartet, dass dieser Artikel zur Erweiterung des allgemeinen Wissens über ROC-Kurven beiträgt und die Annahme verbesserter Bewertungspraktiken innerhalb der Gemeinschaft fördert.
| Dateiname | Beschreibung der Datei |
|---|---|
| MQL5/Scripts/ROC_Demo.mq5 | Das verwendete Skript demonstriert die eingebauten MQL5-Funktionen in Bezug auf ROC-Kurven. |
| MQL5/Scripts/ ROC_curves_table_demo.mq5 | Skript, das die Erstellung verschiedener ROC-basierter Leistungskennzahlen demonstriert. |
| MQL5/Include/logisitc.mqh | Header-Datei mit der Definition der Clogit-Klasse, die die logistische Regression implementiert. |
| MQL5/Include/roc_curves.mqh | Header der nutzerdefinierten Funktionen, die verschiedene Dienstprogramme für die Leistungsbewertung der Binärklassifikation implementieren. |
| MQL5/Include/np.mqh | Header-Datei mit verschiedenen Vektor- und Matrixfunktionen. |
| MQL5/Files/iris.csv | CSV-Datei des Iris-Datensatzes. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/17390
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 MQL5 Handels-Toolkit (Teil 8): Implementierung und Verwendung der EX5-Bibliothek History Manager in Ihrer Codebasis
MQL5 Handels-Toolkit (Teil 8): Implementierung und Verwendung der EX5-Bibliothek History Manager in Ihrer Codebasis
 Einführung in MQL5 (Teil 13): Ein Anfängerleitfaden zur Erstellung nutzerdefinierter Indikatoren (II)
Einführung in MQL5 (Teil 13): Ein Anfängerleitfaden zur Erstellung nutzerdefinierter Indikatoren (II)
 Entwicklung eines Toolkit zur Analyse von Preisaktionen (Teil 18): Einführung in die Quarters-Theorie (III) - Quarters Board
Entwicklung eines Toolkit zur Analyse von Preisaktionen (Teil 18): Einführung in die Quarters-Theorie (III) - Quarters Board
 Datenwissenschaft und ML (Teil 34): Zeitreihenzerlegung, den Aktienmarkt auf den Kern herunterbrechen.
Datenwissenschaft und ML (Teil 34): Zeitreihenzerlegung, den Aktienmarkt auf den Kern herunterbrechen.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.