Visualisierung! Eine grafische MQL5 Bibliothek ähnlich 'plot' der Sprache R
Der wesentliche Vorteil der 'plot'-Funktion ist, dass Sie nur ein paar Codezeilen zum Zeichnen beliebiger Grafiken benötigen. Die Daten werden einfach in Form eines Arrays übergeben und der Grafiktyp angegeben, das war's! Die 'plot'-Funktion berechnet alles Notwendige wie den Maßstab, die Achsen, die Auswahl der Farben etc.
In MQL5 werden alle Merkmale der Funktion durch die Methoden aus der Grafikbibliothek aus der Standardbibliothek bereitgestellt. Ein Codebeispiel und dessen ausgeführtes Ergebnis ist unten angeführt:
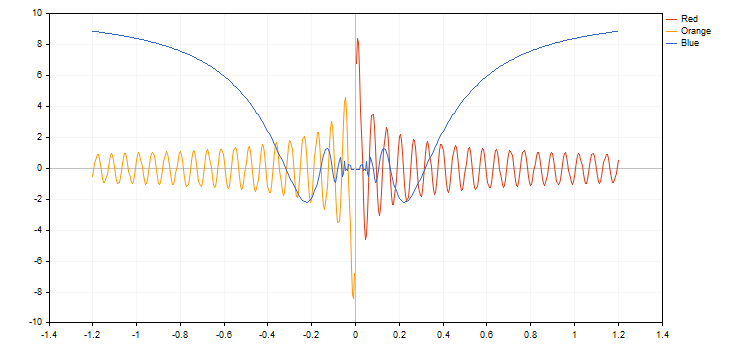
#include <Graphics\Graphic.mqh> #define RESULT_OR_NAN(x,expression) ((x==0)?(double)"nan":expression) //--- Functions double BlueFunction(double x) { return(RESULT_OR_NAN(x,10*x*sin(1/x))); } double RedFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(x))); } double OrangeFunction(double x) { return(RESULT_OR_NAN(x,sin(100*x)/sqrt(-x)));} //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { double from=-1.2; double to=1.2; double step=0.005; CGraphic graphic; graphic.Create(0,"G",0,30,30,780,380); //--- Farben CColorGenerator generator; uint blue= generator.Next(); uint red = generator.Next(); uint orange=generator.Next(); //--- Zeichnen aller Kurven graphic.CurveAdd(RedFunction,from,to,step,red,CURVE_LINES,"Red"); graphic.CurveAdd(OrangeFunction,from,to,step,orange,CURVE_LINES,"Orange"); graphic.CurveAdd(BlueFunction,from,to,step,blue,CURVE_LINES,"Blue"); graphic.CurvePlotAll(); graphic.Update(); }
CCanvas Basisklasse und ihre Entwicklung
Die Standardbibliothek beinhaltet die Klasse CCanvas für ein schnelles und einfaches Zeichnen von Grafiken direkt auf dem Chart. Die Klasse basiert auf dem Erstellen grafischer Ressourcen und zeichnet Grafikprimitive (Punkte, Geraden Linien, Linienzüge, Kreise, Dreiecke und Polygone) auf den Hintergrund. Die Klasse implementiert Funktionen für das Ausfüllen von Formen und das Anzeigen von Texten in gewünschtem Schrifttyp, Farbe und Größe.
Anfangs verfügte CCanvas nur über zwei Modi zur Anzeige der Grafikprimitive — mit und ohne Kantenglättung (antialiasing: AA). Dann wurden neue Funktionen ergänzt, um die Grafikprimitive auf Basis von Wu's Algorithmus zu zeichnen:
- LineWu — Gerade
- PolylineWu — Linienzüge
- PolygonWu — Polygon
- TriangleWu — Dreieck
- CircleWu — Kreis
- EllipseWu — Ellipse
Wus Algorithmus vereint hochwertige Kantenglättung mit einer Geschwindigkeit nahe des Bresenhams Algorithmus ohne Kantenglättung. Er unterscheidet sich auch visuell von der normalen Kantenglättung (AA) aus CCanvas. Unten ist das Beispiel von Kreisen, gezeichnet von drei verschiedenen Funktionen:
#include<Canvas\Canvas.mqh> CCanvas canvas; //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { int Width=800; int Height=600; //--- Erstellen des Hintergrundes if(!canvas.CreateBitmapLabel(0,0,"CirclesCanvas",30,30,Width,Height)) { Print("Error creating canvas: ",GetLastError()); } //--- Zeichnen canvas.Erase(clrWhite); canvas.Circle(70,70,25,clrBlack); canvas.CircleAA(120,70,25,clrBlack); canvas.CircleWu(170,70,25,clrBlack); //--- canvas.Update(); }
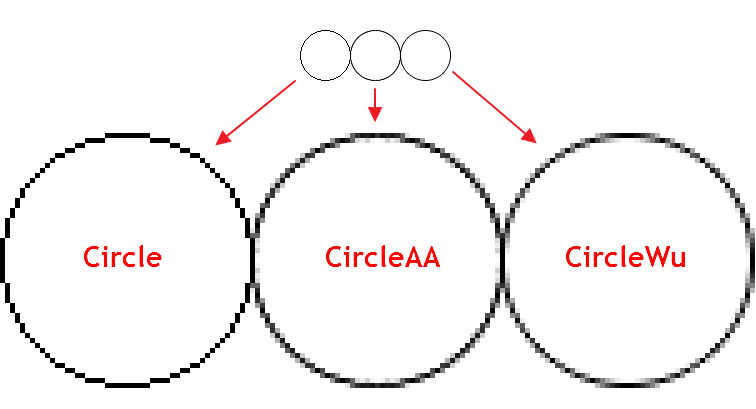
Wie man sieht zeichnet CircleAA() mit der normalen Kantenglättung eine dickere Linie im Vergleich zur Funktion CircleWu() mit dem Algorithmus von Wu. Wegen der geringen Strichstärke und der besseren Berechnung der Übergangsschattierungen schaut CircleWu sauberer und natürlicher aus.
Es gibt auch andere Verbesserungen in der Klasse CCanvas:
- Hinzugefügt wurde die neue Grafikprimitive Ellipse mit zwei Optionen zur Kantenglättung — EllipseAA() und EllipseWu()
- Hinzugefügt wurden neue Überladungen der Funktion Flächen ausfüllen mit neuen Parametern für die "Füll-Sensitivität" (ein Schwellenwertparameter).
Das Verwenden der Bibliothek
1. Nach dem laden der Bibliothek erstellen wir ein Klassenobjekt der CGraphic. Das erstellt uns die zu zeichnenden Kurven.
Danach rufen wir die Methode Create() auf, um das Objekt zu erzeugen. Diese Methode hat zwei Hauptparameter der Grafik:
- Grafikkennung
- Objektname
- Fensterindex
- Grafik Ankerpunkt
- Höhe und Breite der Grafik
Die Methode verwendet diese Parameter zum Erstellen der Grafik und der zum Zeichen benötigten grafischen Ressourcen.
//--- Objekt zum Erstellen der Grafik CGraphic graphic; //--- Erstellen des Hintergrundes graphic.Create(0,"Graphic",0,30,30,830,430);
Im Ergebnis erhalten wir einen fertigen Hintergrund.
2. Jetzt bevölkern wir unsere Objekt mit Kurven. Eine neue Kurve wird mit der Methode CurveAdd() hinzugefügt, die Kurven auf 4 Arten zeichnen kann:
- Auf Basis einen eindimensionalen Array vom Typ double. In diesem Fall werden die Werte des Arrays auf der Y-Koordinate platziert und der Indices dient als X-Koordinate.
- Auf Basis von zwei Arrays vom Typ double x[] und y[].
- Auf Basis des Arrays CPoint2D.
- Auf Basis der Pointer-Funktion CurveFunction() und den drei Argumenten der Funktion: Anfangs-, Endwert und Inkrement.
Die Methode CurveAdd() liefert den Pointer auf die Klasse CCurve, wodurch ein schneller Zugriff auf die Kurve möglich ist und ihre Eigenschaften geändert werden können.
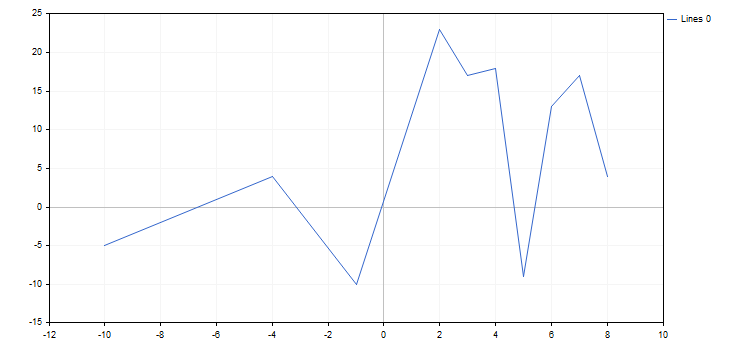
double x[]={-10,-4,-1,2,3,4,5,6,7,8};double y[]={-5,4,-10,23,17,18,-9,13,17,4};
CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES);
3. Jeder der zusätzlichen Kurven kann auf dem Chart gezeigt werden. Dies kann auf drei Arten erfolgen.
- Durch die Methode CurvePlotAll(), die automatisch alle Kurven auf den Chart zeichnet.
graphic.CurvePlotAll();
- Durch die Methode CurvePlot(), die die Kurve des angegebenen Index anzeigt.
graphic.CurvePlot(0);
- Durch die Methode Redraw() und dem Setzen des Parameters Visible auf 'true'.
curve.Visible(true); graphic.Redraw();
4. Um eine Grafik auf den Chart zu zeichnen, muss die Methode Update() aufgerufen werden. Im Ergebnis schaut der gesamten Code zum Zeichnen einer einfachen Grafik so aus:
#include <Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { CGraphic graphic; graphic.Create(0,"Graphic",0,30,30,780,380); double x[]={-10,-4,-1,2,3,4,5,6,7,8}; double y[]={-5,4,-10,23,17,18,-9,13,17,4}; CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES); graphic.CurvePlotAll(); graphic.Update(); }
Unten ist die resultierende Grafik:
Die Eigenschaften der Grafik und jede ihrer Funktionen kann in jedem Augenblick geändert werden. Zum Beispiel können wir der Grafik Kennzeichnungen der Achsen hinzufügen, den Namen der Kurve ändern und eine Spline-Approximation aktivieren:
#include <Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { CGraphic graphic; graphic.Create(0,"Graphic",0,30,30,780,380); double x[]={-10,-4,-1,2,3,4,5,6,7,8}; double y[]={-5,4,-10,23,17,18,-9,13,17,4}; CCurve *curve=graphic.CurveAdd(x,y,CURVE_LINES); curve.Name("Example"); curve.LinesIsSmooth(true); graphic.XAxis().Name("X - axis"); graphic.XAxis().NameSize(12); graphic.YAxis().Name("Y - axis"); graphic.YAxis().NameSize(12); graphic.YAxis().ValuesWidth(15); graphic.CurvePlotAll(); graphic.Update(); DebugBreak(); }
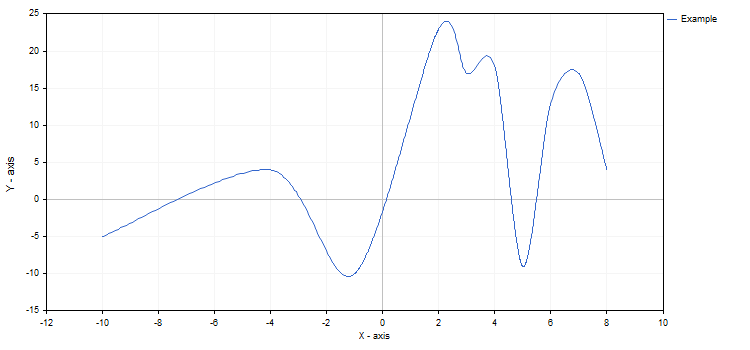
Wird nach dem Aufruf von CurvePlotAll etwas geändert, muss die Methode Redraw aufgerufen werden, um das zu sehen.
Wie viele moderne Bibliotheken verfügt auch Graphics verschiedene fertige Algorithmen, um das Zeichnen auf dem Chart zu erleichtern:
- Die Bibliothek ermöglicht das automatische Erstellen von kontrastreichen Farben der Kurven, wenn diese nicht explizit angegeben wurden.
- Die Achsen der Grafiken können, wenn aktiviert, automatisch ihren Maßstab ermitteln.
- Die Namen der Kurven werden auch in Abhängigkeit von ihrem Typ und der Reihung automatisch bestimmt.
- Der Darstellungsbereich der Grafik wird automatisch mit festgelegten Achsen angeordnet.
- Linien können geglättet werden.
Die Bibliothek Graphics hat auch noch ein paar weitere Methoden, um neue Elemente auf dem Chart zu platzieren:
- TextAdd() — Schreibt Sie einen Text an einer beliebigen Stelle auf den Chart. Die Koordinaten sollten im realen Maßstab angegeben werden. Mit der Methode FontSet kann der anzuzeigende Text genau angepasst werden.
- LineAdd() — Fügt eine Linie an einer beliebigen Position auf dem Chart hinzu. Die Koordinaten sollten im realen Maßstab angegeben werden.
- MarksToAxisAdd() — Fügt eine neue Kennzeichnung an den angegebenen Koordinaten der Achsen hinzu.
Die Daten über hinzugefügte Elemente werden nirgendwo gesichert. Nach dem Zeichnen einer neuen Kurve auf dem Chart oder dem Neuzeichnen einer Vorherigen verschwinden sie.
Grafiktypen
Die Bibliothek Graphics unterstützt die Basistypen zeichenbarer Kurven. Sie alle sind in der Enumeration ENUM_CURVE_TYPE aufgelistet:
- CURVE_POINTS — Zeichnen einer Kurve aus Punkten
- CURVE_LINES — Zeichnen einer Linie
- CURVE_POINTS_AND_LINES — Zeichnen einer Kurve mit Punkten und Strichen
- CURVE_STEPS — Zeichnen einer stufenartigen Kurve
- CURVE_HISTOGRAM — Zeichnen eines Histogramms
- CURVE_NONE — Keine Kurve zeichnen
Jeder dieser Möglichkeiten hat eigene Eigenschaften, die die Darstellung der Kurve auf dem Chart beeinflussen. Der Pointer CCurve auf eine Kurve erlaubt ein schnelles Ändern ihrer Eigenschaften. Daher ist zu empfehlen, den Pointer, den die Methode CurveAdd liefert, zu sichern. Die Eigenschaftsnamen beginnen immer mit der Zeichenart der Kurve.
Betrachten wir die Eigenschaften jeden Typs genauer.
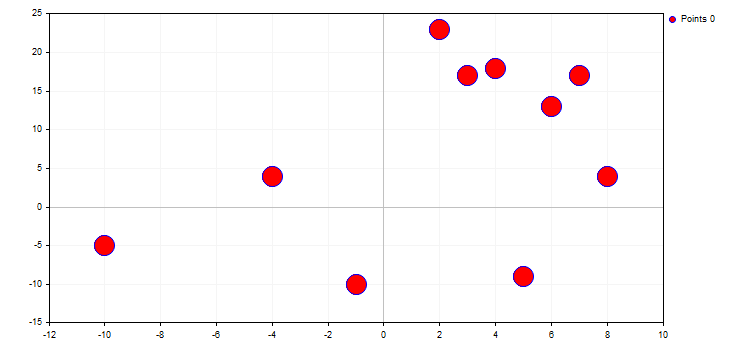
1. CURVE_POINTS ist die einfachste und schnellste Art. Jede Kurvenkoordinate wird als Punkt mit den angegebenen Eigenschaften angezeigt:
- PointsSize — Punktgröße
- PointsFill — Ausfüllen der Punkte aktivieren oder nicht
- PointsColor — Füllfarbe
- PointsType — Typ des Punktes
In diesem Fall ist die Kurvenfarbe die Farbe der Umrandung des Punktes.
CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_POINTS); curve.PointsSize(20); curve.PointsFill(true); curve.PointsColor(ColorToARGB(clrRed,255));
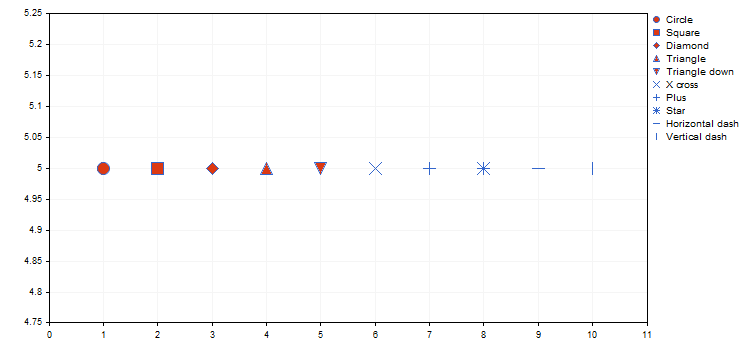
Die Art des Punktes bestimmt eine spezifische, geometrische Form aus der Enumeration ENUM_POINT_TYPE. Diese Form wird zur Darstellung aller Punkte verwendet. Insgesamt verfügt ENUM_POINT_TYPE über zehn geometrische Hauptformen:
- POINT_CIRCLE — Kreis (standardmäßig verwendet)
- POINT_SQUARE — Quadrat
- POINT_DIAMOND — Raute
- POINT_TRIANGLE — Dreieck
- POINT_TRIANGLE_DOWN — umgekehrtes Dreieck
- POINT_X_CROSS — Kreuz
- POINT_PLUS — Plus
- POINT_STAR — Stern
- POINT_HORIZONTAL_DASH — horizontaler Strich
- POINT_VERTICAL_DASH — vertikaler Strich
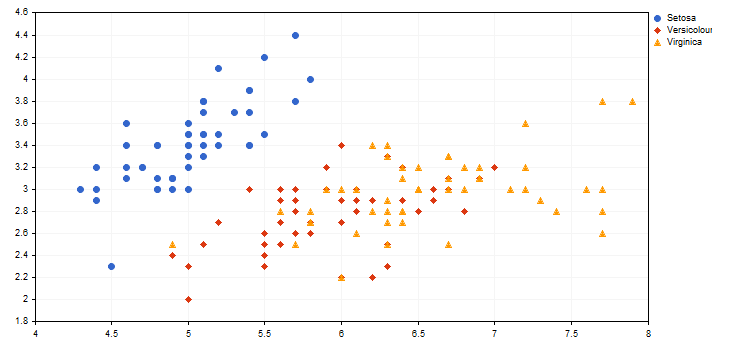
Beispiel der Darstellung verschiedene Arten von Iris (siehe im Artikel "Verwendung von selbstorganisierenden Karten (Kohonenkarten) in MetaTrader 5") aus dem beigefügten Skript IrisSample.mq5.
2. CURVE_LINES ist der Darstellungstyp für das Zeichnen von Kurven, dergestalt, dass jedes Punktepaar mit einer oder (im Falle einer Glättung) mehreren geraden Linien verbunden wird. Die Eigenschaften des Typs sind wie folgt:
- LinesStyle — Stil der Linie aus der Enumeration ENUM_LINE_STYLE
- LinesSmooth — Kurvenglättung aktivieren oder nicht
- LinesSmoothTension — Grad der Glättung
- LinesSmoothStep — Länge der Näherungsgeraden im Falle einer Glättung
Graphics verfügt über einen standardmäßigen Glättungsalgorithmus für Kurven. Er bietet zwei Phasen:
- Für jedes Punktepaar werden zwei Referenzpunkte auf Basis ihrer Derivate definiert.
- Eine Bezierkurve mit der angegebenen Näherungsstufe wird auf Basis dieser vier Punkte gezeichnet.
Der Parameter LinesSmoothTension akzeptiert die Werte (0.0; 1.0]. Ist LinesSmoothTension gleich 0.0, findet keine Glättung statt. Wird dieser Parameter erhöht, erhalten wir eine mehr und mehr geglättete Kurve.
CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_LINES); curve.LinesStyle(STYLE_DOT); curve.LinesSmooth(true); curve.LinesSmoothTension(0.8); curve.LinesSmoothStep(0.2);
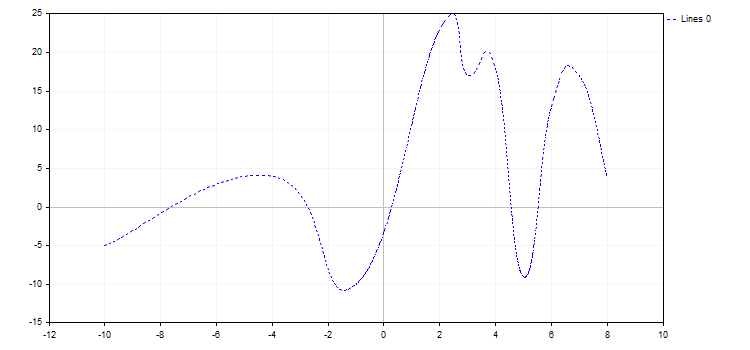
3. CURVE_POINTS_AND_LINES kombiniert beide oben erläuterte Anzeigeformen mit ihren Eigenschaften.
4. Im Modus CURVE_STEPS wird jedes Punktepaar durch zwei Linien in Stufenform verbunden. Dieser Modus hat zwei Eigenschaften:
- LinesStyle — diese Eigenschaft wird von CURVE_POINTS übernommen und bestimmt den Linienstil
- StepsDimension — Stufendimension: 0 — x (horizontale Striche gefolgt von vertikalen) oder 1 — y (vertikale Striche gefolgt von horizontalen).
CCurve *curve=graphic.CurveAdd(x,y,ColorToARGB(clrBlue,255),CURVE_STEPS); curve.LinesStyle(STYLE_DASH); curve.StepsDimension(1);

5. Der Modus CURVE_HISTOGRAM zeichnet Histogramme. Dieser Modus hat eine einzige Eigenschaft:
- HistogramWidth — die Breite der Balken
Wird dieser Wert zu groß, könnten sich die Balken überlappen und die Balken mit einem höheren Y-Wert "absorbieren" die benachbarten Balken mit kleineren Werten.
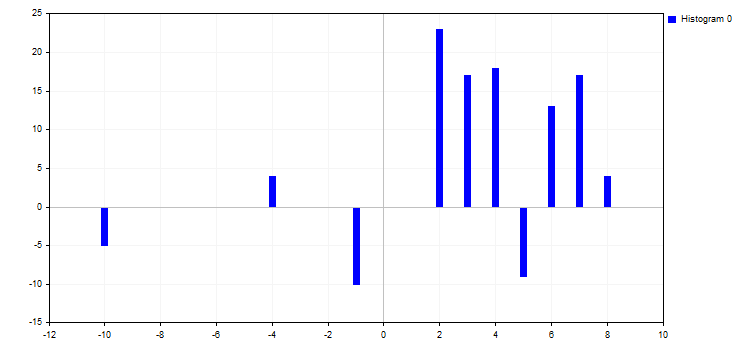
6. Der Modus CURVE_NONE deaktiviert die grafische Darstellung der Kurven unabhängig von ihrer Sichtbarkeit.
Bei einer automatischen Skalierung, erhalten alle Kurven, die dem Diagramm hinzugefügt werden, bestimmte Werte. Daher, auch wenn eine Kurven nicht gezeichnet wird, oder ihr Modus auf CURVE_NONE gesetzt wurde, werden ihre Werte berücksichtigt.
Funktionen als Grafik — Schnellerzeugung mit ein paar Linien
Ein weiterer Vorteil der Bibliothek ist die Arbeit mit CurveFunction und Pointer auf Funktionen. In MQL5 akzeptieren Pointers auf Funktionen nur globale oder statische Funktionen, während die Syntax der Funktion voll der des Pointers entsprechen soll. In unserem Fall ist die Funktion CurveFunction für Funktionen konfiguriert, denen auch double Werte als Parameter übergeben werden.
Um ein Kurve durch einen Pointer auf eine Funktion zu erstellen, müssen wir den genauen ersten (from) und letzten (to) Wert als Argument übergeben zusammen mit dem Inkrement (step). Je kleiner das Inkrement, desto mehr Funktionspunkte werden erstellt. Um eine Datenreihe zu erstellen, verwenden wir CurveAdd(), und, um die Funktion zu zeichnen, CurvePlot() oder CurvePlotAll().
Als Beispiel erstellen wir mal eine Parabel und zeichnen sie mit unterschiedlichen Schrittweiten:
#include <Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| Parabola | //+------------------------------------------------------------------+ double Parabola(double x) { return MathPow(x,2); } //+------------------------------------------------------------------+ //| Script Programm Start Funktion | //+------------------------------------------------------------------+ void OnStart() { double from1=-5; double to1=0; double step1=1; double from2=0; double to2=5; double step2=0.2; CurveFunction function = Parabola; CGraphic graph; graph.Create(0,"Graph",0,30,30,780,380); graph.CurveAdd(function,from1,to1,step1,CURVE_LINES); graph.CurveAdd(function,from2,to2,step2,CURVE_LINES); graph.CurvePlotAll(); graph.Update(); }
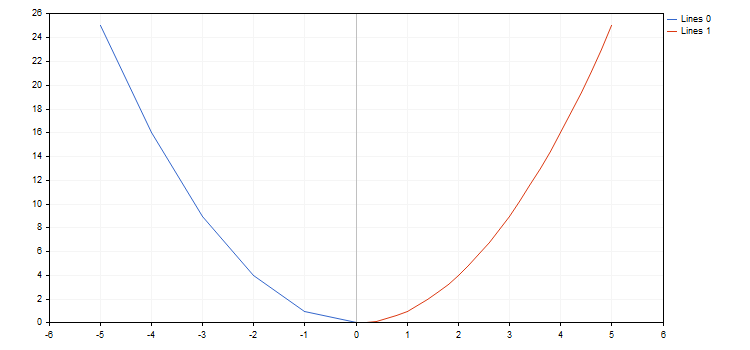
Die Bibliothek arbeitet auch mit Unterbrechungen innerhalb von Funktionen (eine der Koordinaten hat einen Wert von plus oder minus Unendlich oder ist nicht numerisch). Das Inkrement muss bei diesen Unterbrechungen beachtet werden, da sie sonst "verpasst" werden könnten. In diesem Fall wird die Grafik nicht wie erwartet aussehen. Zeichnen wir zum Beispiel zwei Hyperbel im Intervall [-5.0; 5.0], wobei die erste eine Schrittweite von 0.7, die zweite eine von 0.1 hat. Das Ergebnis sieht man unten:
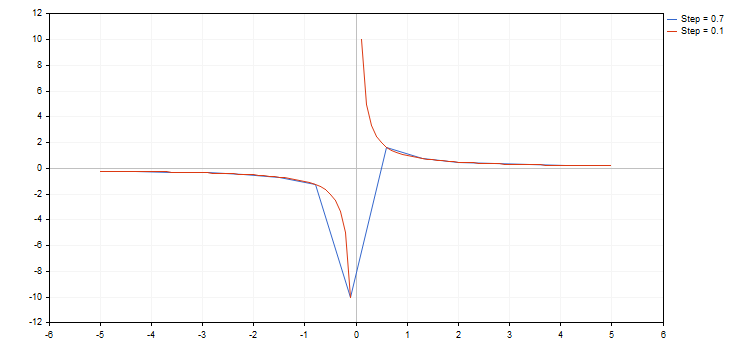
Wie man sieht, wurde wurde der Unterbrechungspunkt bei einer Schrittweite von 0.7 nicht erkannt. Als Ergebnis entsteht eine Kurve, die mit einer wirklichen Hyperbel nicht viel zu tun hat.
Es könnte der Fehler Division durch Null bei dieser Funktion entstehen. Es gibt zwei Wege dieses Problem abzufangen:
- deaktivieren der Überprüfung einer Division durch Null im metaeditor.ini
[Experts] FpNoZeroCheckOnDivision=1 - oder eine Analyse der Gleichung, die von der Funktion verwendet werden soll, und die Rückgabe eines gültigen Wertes in diesem Fall. Ein Beispiel für den Umgang damit findet sich in den beigefügten Dateien 3Functions.mq5 und bat.mq5 Dateien.
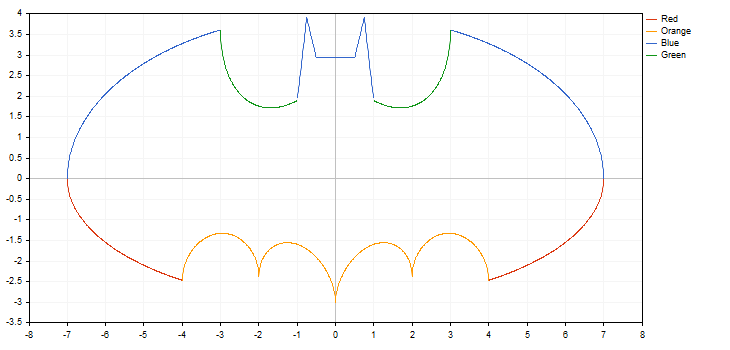
Funktionen zum Schnellzeichnen
Die Bibliothek Graphics beinhaltet eine Reihe von globalen Funktionen GraphPlot(), die jede Form der Darstellung von Grafiken auf Basis der übergebenen Daten durchführen und den Namen des Charts als Ergebnis zurückgeben. Diese Funktionen sind ähnlich 'plot' von R oder Phyton und erlaubt Ihnen die sofortige visuelle Umsetzung der Daten in den verschiedenen Formen.
Die Funktion GraphPlot hat 10 verschiedene Überladungen, die alle verschiedene Arten von Kurven auf einem Chart zeichnen. Alles, was Sie tun müssen, ist die Daten der zu zeichnenden Kurve für die verfügbaren Methoden anzupassen. So sieht zum Beispiel der Quellcode zum Schnellzeichnen der Daten von x[] und y[] wie folgt aus:
void OnStart() { double x[]={-10,-4,-1,2,3,4,5,6,7,8}; double y[]={-5,4,-10,23,17,18,-9,13,17,4}; GraphPlot(x,y); }
Ganz ähnlich wie in R:
> x<-c(-10,-4,-1,2,3,4,5,6,7,8) > y<-c(-5,4,-10,23,17,18,-9,13,17,4) > plot(x,y)
Ergebnis des Vergleiches der Grafiken in den drei wichtigsten Anzeigemodi durch die Funktion GraphPlot von MQL5 und der Funktion plot aus R:
1. Punkte
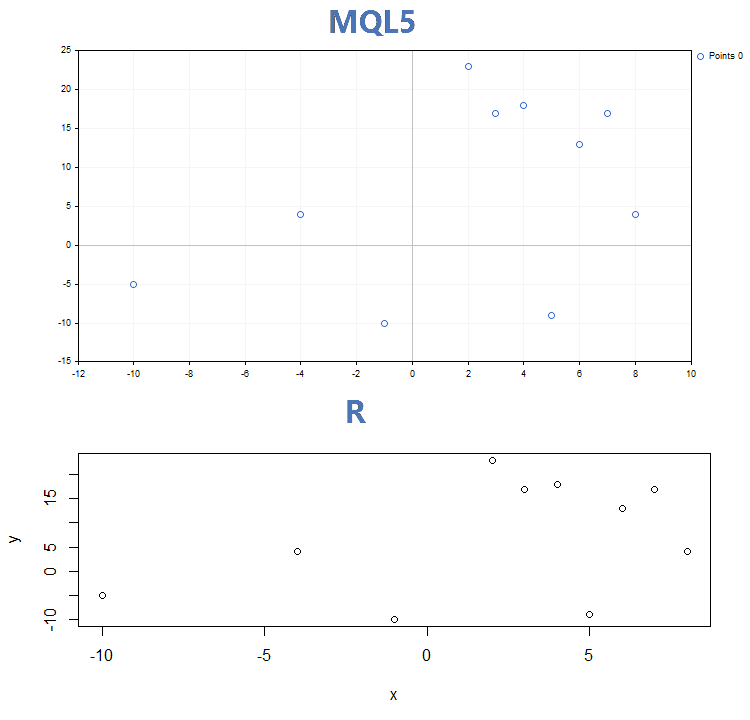
2. Linie
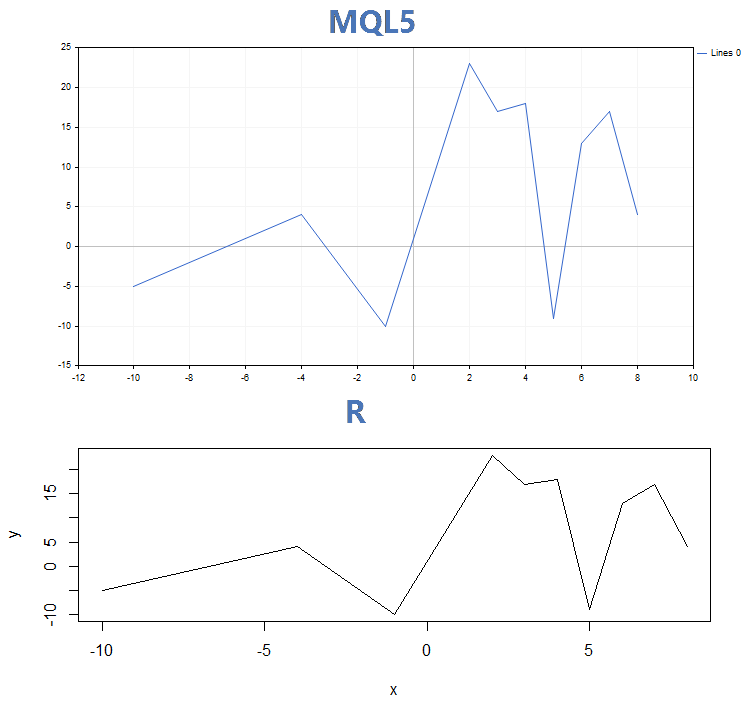
3. Histogramme
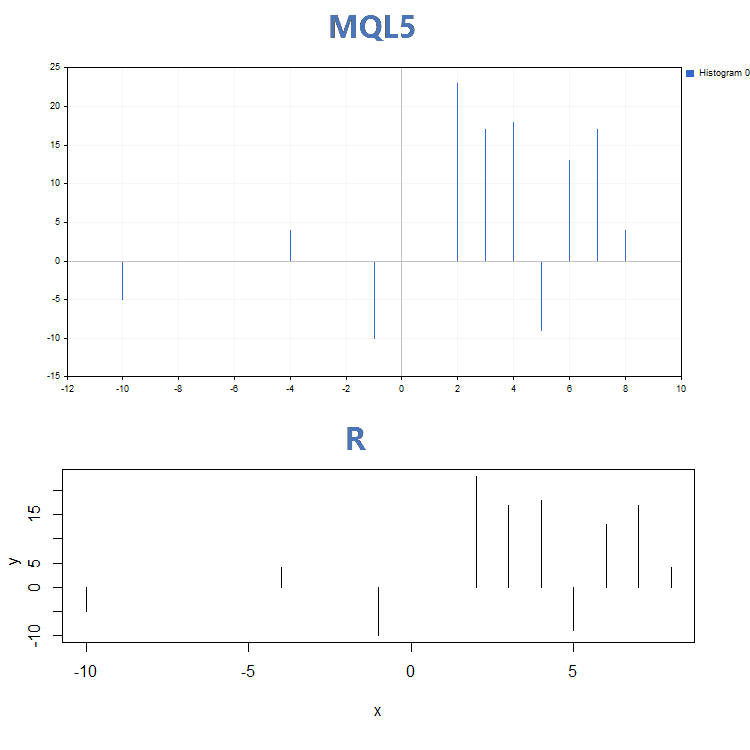
Abgesehen von dem deutlichen, optischen Unterschied zwischen GraphPlot() und plot(), haben beide unterschiedliche Eingabeparameter. Während die Funktion plot() die Übergabe spezieller Parameter für die Kurve erlaubt (zum Beispiel 'lwd', das die Linienbreite ändert), kann die Funktion GraphPlot() nur die Schlüsselparameter für die Daten akzeptieren.
Nennen wir sie beim Namen:
- Die Daten der Kurve in eine der oben beschriebenen vier Formaten.
- Zeichentyp (standardmäßig CURVE_POINTS).
- Objectname (standardmäßig NULL).
Jeder Grafik, die über die Bibliothek Graphics erstellt wurde, enthält ein Chartobjekt und eine zugehörige, grafische Ressource. Der Name der grafischen Ressource wird auf Basis des Objektnamens und der einfachen Ergänzung von "::" davor gebildet. Ist der Objektname zum Beispiel "SomeGraphic", wird der Name der grafischen Ressource "::SomeGraphic".
Die Funktion GraphPlot() hat einen festen Ankerpunkt an den Chartk x=65 und y=45. Die Breite und Höhe der Grafik wird auf Basis der Größe des Chart berechnet: die Breite beträgt 60% des Chart, die Höhe 65% seiner Höhe. Wenn also die aktuellen Dimensionen des Chart Chart weniger als 65 zu 45 sind, kann die Funktion GraphPlot() nicht korrekt arbeiten.
Wenn man den Namen eines bereits bestehenden Objektes einem entstehenden Objekt übergibt, versucht die Bibliothek Graphics die Grafik auf diesem Objekt nach der Überprüfung des Typs der Ressource. Wenn der Typ der Ressource ein OBJ_BITMAP_LABEL ist, erfolgt die Zeichnung auf demselben Paar Objekt-Ressource.
Wenn ein Objektname ausdrücklich der Funktion GraphPlot() übergeben wird, wird versucht, das Objekt zu finden und auf ihm die Grafik anzuzeigen. Wird das Objekt nicht gefunden, wird automatisch ein neues Ressource-Objekt mit diesem Namen erstellt. Wird die Funktion GraphPlot() verwendet, ohne explizit einen Namen anzugeben, wird der Standardname "Graphic" eingesetzt.
In diesem Fall können Sie den Ankerpunkt und die Größe der Grafik angeben. Dafür erstellen Sie ein Ressource-Objekt-Paar mit den notwendigen Parametern und übergeben Sie den Namen des erstellten Objektes der Funktion GraphPlot(). Wird eine Grafik mit Namen erstellt, wird der Standardhintergrund für die Funktion GraphPlot neu definiert und angepasst, in dem die Notwendigkeit, bei jedem Aufruf den Namen übergeben zu müssen, ausgeschaltet wird.
Nehmen wir beispielsweise die Daten von oben und setzen die Größe der Grafik auf 750х350. Weiters verschieben wir den Ankerpunkt in die obere, linke Ecke:
void OnStart() { //--- create object on chart and dynamic resource string name="Graphic"; long x=0; long y=0; int width=750; int height=350; int data[]; ArrayResize(data,width*height); ZeroMemory(data); ObjectCreate(0,name,OBJ_BITMAP_LABEL,0,0,0); ResourceCreate("::"+name,data,width,height,0,0,0,COLOR_FORMAT_XRGB_NOALPHA); ObjectSetInteger(0,name,OBJPROP_XDISTANCE,x); ObjectSetInteger(0,name,OBJPROP_YDISTANCE,y); ObjectSetString(0,name,OBJPROP_BMPFILE,"::"+name); //--- create x and y array double arr_x[]={-10,-4,-1,2,3,4,5,6,7,8}; double arr_y[]={-5,4,-10,23,17,18,-9,13,17,4}; //--- plot x and y array GraphPlot(arr_x,arr_y,CURVE_LINES); }
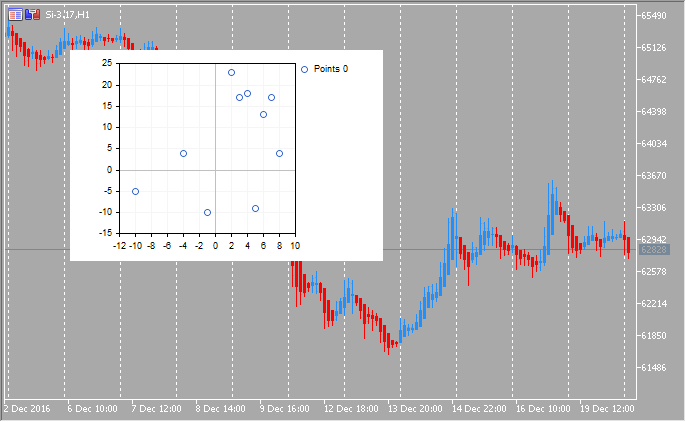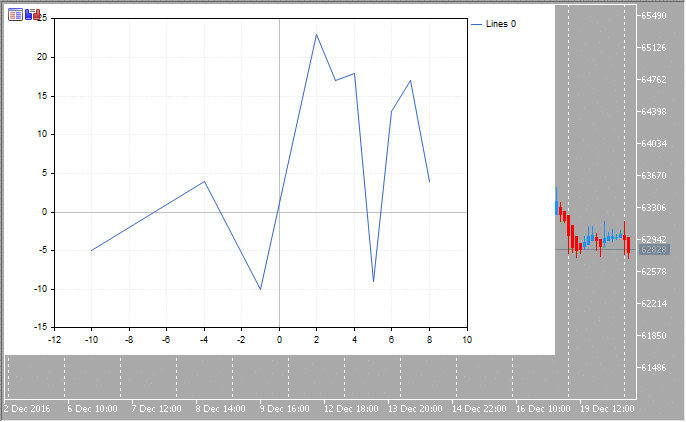
Beispiele wissenschaftlicher Grafiken
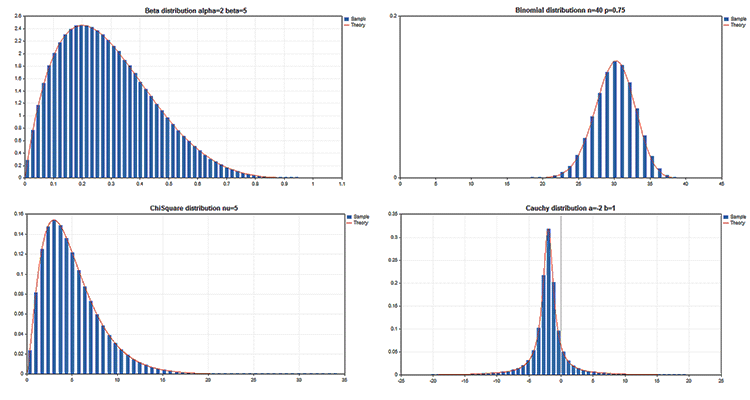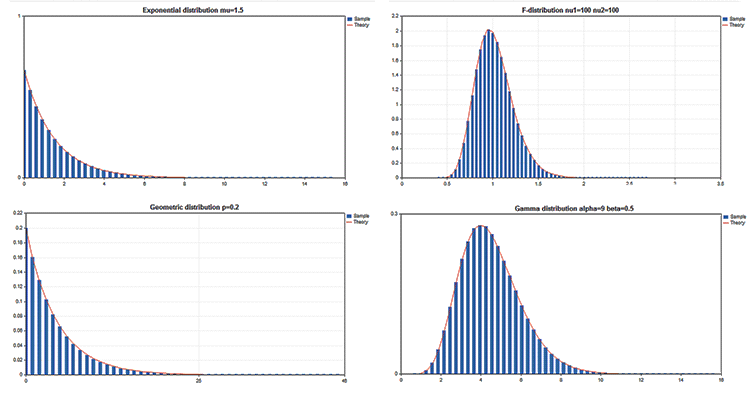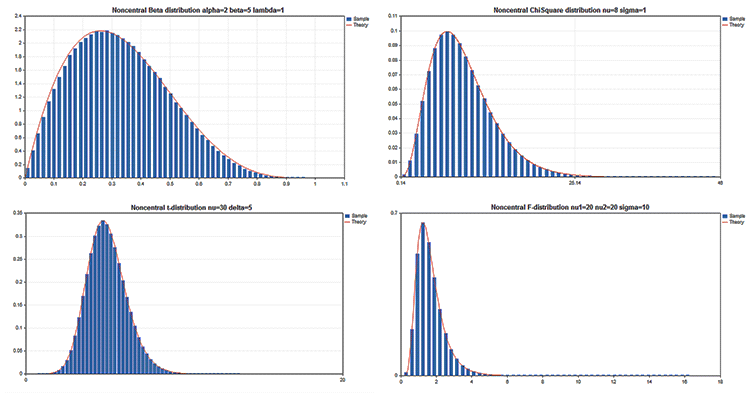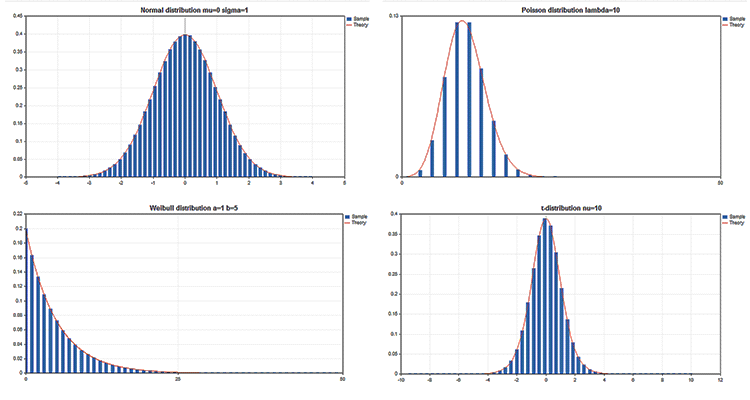
In der Standardbibliothek gibt es Statistics mit Funktionen für mehrere statistische Verteilungen aus der Wahrscheinlichkeitstheorie. Zu jeder Verteilung gibt es Beispielgrafiken und den Code, mit dem man sie erhält. Hier zeigen wir einfach nur die Diagramme als einzelne GIF-Bilder. Der Quellcode der Beispiele befindet sich in der Datei MQL5.zip. Entpacken Sie sie in das Verzeichnis MQL5\Scripts.
Alle diese Beispiele haben einen Kurschart, der durch die Eigenschaft CHART_SHOW deaktiviert wurde:
//--- Deaktivieren des Kurscharts ChartSetInteger(0,CHART_SHOW,false);
Das erlaubt uns, das Chartfenster in einen einzigen, großen Hintergrund zu wandeln und Objekte jeder Komplexität unter Anwendung der grafischen Ressourcen zu zeichnen.
Die entscheidenden Vorteile der Grafikbibliothek
Die Sprache MQL5 erlaubt es den Entwicklern nicht nur Handelsroboter und technische Indikatoren zu erstellen, sondern auch komplexe mathematische Berechnungen unter Verwendung der Bibliotheken ALGLIB, Fuzzy und Statistics durchzuführen. Die erhaltenen Daten können mit der grafischen Bibliothek ganz leicht dargestellt werden. Die meisten Vorgänge sind automatisiert, und die Bibliothek bietet eine umfangreiche Funktionalität:
- 5 grafische Anzeigearten
- 10 Arten grafischer Markierungen
- automatische Skalierung der Diagramme durch die X- und Y-Achsen
- automatische Farbauswahl auch bei mehreren Elementen
- Linienglättung mittels der standardmäßigen Kantenglättung oder des fortgeschrittenen Bresenham-Algorithmus
- Fähigkeit zum Festlegen der Parameter für eine Spline-Approximation der Linien
- Fähigkeit eine Grafik zu zeichnen mit nur eine Codezeile auf Basis der x[]- und y[]-Arrays
- Fähigkeit zum Zeichnen von Grafiken mittels Pointer auf Funktionen
Die Grafikbibliothek vereinfacht das Zeichnen wissenschaftlicher Grafiken und hebt die Entwicklung von Handelsprogrammen auf eine neue Ebene. Die Plattform MetaTrader 5 ermöglicht das Durchführen von mathematischen Berechnungen von beliebiger Komplexität und zeigt die Ergebnisse direkt in das Fenster des Terminals auf professionelle Art und Weise.
Versuchen Sie den beigefügten Code. Keine Notwendigkeit mehr für Programme Dritter!
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2866
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
 Die Berechnung des Hurst-Exponenten
Die Berechnung des Hurst-Exponenten
 Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil II.
Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil II.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wir brauchen eine neue Klasse mit weniger Funktionen als CCanvas. Es ist besser, diese Klasse so nah wie möglich an JS Canvas zu machen, das im Wesentlichen nicht viele Funktionen hat, um das Erlernen und die Übernahme zu erleichtern, da sich die gesamte IT in Richtung Web bewegt.
aber das ist ideal.
Ich könnte so etwas wahrscheinlich selbst schreiben, aber es würde mindestens ein halbes Jahr Vollzeit dauern
obwohl ich persönlich nicht alles in JS Canvas mag, aber für die Standardisierung wäre es richtig, etwas Ähnliches mit kleinen Änderungen zu implementieren, um auf String-Parsing zu verzichten.
Aber für die normale Arbeit müssen wir das MT5-Ereignismodell überarbeiten, da es einfach furchtbar ist
Es ist klar, dass alles "unter dem Messer" ist, aber die Frage war doch etwas anders. Was ist es wünschenswert, in der bestehenden Klasse zu ändern/verfeinern...
Es ist klar, dass alles "unter dem Messer" ist, aber trotzdem war die Frage ein bisschen anders. Was ist es wünschenswert, in der bestehenden Klasse zu ändern/verbessern...
glatte Methoden, um sie zum Leben zu erwecken. Jetzt denke ich, es gibt sogar Funktionen in CCanvas, die undokumentiert sind.
geglättete Methoden, um sie zum Leben zu erwecken. Jetzt scheint es sogar Funktionen in CCanvas zu geben , die undokumentiert sind.
Echt jetzt? Darauf habe ich nicht geachtet... Ich muss mal einen Blick auf mein leisure.... werfen.
Ich brauche die "Schubladen mit Schnurrbart"-Diagramme. Ist geplant, sie hinzuzufügen?
Außerdem fehlt die Möglichkeit, Unterfenster/Unterschichten zu verwenden, z. B. wenn man zwei verschiedene Skalen verwenden möchte.
Hallo.
Hat die Klasse CGraphic eingebaute Methoden zum Zeichnen von Heatmaps?