Klassifizierungsmodelle in der Bibliothek Scikit-Learn und ihr Export nach ONNX
MetaTrader 5
—
Beispiele
| 18 April 2024, 16:37
401
0
Die Entwicklung der Technologie hat zur Entstehung eines grundlegend neuen Ansatzes für die Entwicklung von Datenverarbeitungsalgorithmen geführt. Bisher waren für die Lösung jeder spezifischen Aufgabe eine klare Formalisierung und die Entwicklung entsprechender Algorithmen erforderlich.
Beim maschinellen Lernen lernt der Computer, selbständig die besten Wege zur Verarbeitung von Daten zu finden. Modelle des maschinellen Lernens können Klassifizierungsaufgaben (bei denen es einen festen Satz von Klassen gibt und das Ziel darin besteht, die Wahrscheinlichkeiten für die Zugehörigkeit eines bestimmten Satzes von Merkmalen zu jeder Klasse zu ermitteln) und Regressionsaufgaben (bei denen das Ziel darin besteht, einen numerischen Wert der Zielvariablen auf der Grundlage eines bestimmten Satzes von Merkmalen zu schätzen) erfolgreich lösen. Auf der Grundlage dieser grundlegenden Komponenten können komplexere Datenverarbeitungsmodelle aufgebaut werden.
Die Bibliothek Scikit-Learn bietet eine Vielzahl von Werkzeugen für Klassifizierung und Regression. Die Wahl speziFisher Methoden und Modelle hängt von den Merkmalen der Daten ab, da verschiedene Methoden je nach Aufgabe unterschiedlich effektiv sein und unterschiedliche Ergebnisse liefern können.
In der Pressemitteilung „Runtime is now open source“ wird erklärt, dass ONNX Runtime auch das ONNX-ML Profil unterstützt:
ONNX Runtime ist die erste öffentlich verfügbare Inferenzmaschine mit vollständiger Unterstützung für ONNX 1.2 und höher, einschließlich des ONNX-ML-Profils.
Das Profil ONNX-ML ist ein Teil von ONNX, der speziell für Modelle für maschinelles Lernen (ML) entwickelt wurde. Es ist für die Beschreibung und Darstellung verschiedener Arten von ML-Modellen, wie Klassifizierung, Regression, Clustering und andere, in einem praktischen Format gedacht, das auf verschiedenen Plattformen und Umgebungen, die ONNX unterstützen, verwendet werden kann. Das ONNX-ML-Profil vereinfacht die Übertragung, Bereitstellung und Ausführung von Modellen des maschinellen Lernens und macht sie leichter zugänglich und portabel.
In diesem Artikel werden wir die Anwendung aller Klassifizierungsmodelle des Scikit-Learn-Pakets zur Lösung der Klassifizierungsaufgabe von Fishers Schwertlilien, den Iris-Daten, untersuchen. Wir werden auch versuchen, diese Modelle in das ONNX-Format zu konvertieren und die resultierenden Modelle in MQL5-Programmen zu verwenden.
Darüber hinaus werden wir die Genauigkeit der ursprünglichen Modelle mit ihren ONNX-Versionen auf dem kompletten Iris-Datensatz vergleichen.
Inhaltsverzeichnis
- 1. Fishers Schwertlilien (Iris-Daten)
- 2. Modelle für die Klassifizierung
Liste der Klassifikatoren von Scikit-Learn
Verschiedene Darstellungen der Ausgabe von Modellen iris.mqh - 2.1. SVC Classifier
2.1.1. Code zur Erstellung des Klassifizierungsmodells SVC
2.1.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell SVC
2.1.3. ONNX-Darstellung des Klassifizierungsmodells SVC - 2.2. LinearSVC Classifier
2.2.1. Code zur Erstellung des Klassifizierungsmodells von LinearSVC
2.2.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell LinearSVC
2.2.3. ONNX-Darstellung des Klassifizierungsmodells LinearSVC - 2.3. NuSVC Classifier
2.3.1. Code zur Erstellung des Klassifizierungsmodells von NuSVC
2.3.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell NuSVC
2.3.3. ONNX-Darstellung des Klassifizierungsmodells NuSVC - 2.4. Radius Neighbors Classifier
2.4.1. Code zur Erstellung des Klassifizierungsmodells von Radius Neighbors
2.4.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Radius Neighbors
2.3.3. ONNX-Darstellung des Klassifizierungsmodells Radius Neighbors - 2.5. Ridge Classifier
2.5.1. Code zur Erstellung des Klassifizierungsmodells von Ridge Classifier
2.5.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Ridge
2.5.3. ONNX-Darstellung des Klassifizierungsmodells Ridge - 2.6. RidgeClassifierCV
2.6.1. Code zur Erstellung des Klassifizierungsmodells von Ridge ClassifierCV
2.6.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Ridge ClassifierCV
2.6.3. ONNX-Darstellung des Klassifizierungsmodells Ridge ClassifierCV - 2.7. Random Forest Classifier
2.7.1. Code für die Erstellung des Klassifizierungsmodells Random-Forest
2.7.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Random Forest
2.7.3. ONNX-Darstellung des Klassifizierungsmodells Random-Forest - 2.8. Gradient Boosting Classifier
2.8.1. Code für die Erstellung des Klassifizierungsmodells Gradient-Boosting
2.8.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Gradient Boosting
2.8.3. ONNX-Darstellung des Klassifizierungsmodells Gradient-Boosting - 2.9. Adaptive Boosting Classifier
2.9.1. Code für die Erstellung des Klassifizierungsmodells Adaptive Boosting
2.9.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Adaptive Boosting
2.9.3. ONNX-Darstellung des Klassifizierungsmodells Adaptive Boosting - 2.10. Bootstrap Aggregating Classifier
2.10.1. Code für die Erstellung des Bootstrap Aggregating Classifier Model
2.10.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Bootstrap Aggregating
2.10.3. ONNX-Darstellung des Klassifizierungsmodells Bootstrap Aggregating - 2.11. K-Nearest Neighbors (K-NN) Classifier
2.11.1. Code zur Erstellung des Klassifizierungsmodells von K-Nearest Neighbors (K-NN)
2.11.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell K-Nächste-Nachbarn (K-NN)
2.11.3. ONNX-Darstellung des Klassifizierungsmodells K-Nächste-Nachbarn (K-NN) - 2.12. Decision Tree Classifier
2.12.1. Code für die Erstellung des Klassifizierungsmodells Decision Tree
2.12.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Decision Tree
2.12.3. ONNX-Darstellung des Klassifizierungsmodells Decision Tree - 2.13. Logistic Regression Classifier
2.13.1. Code für die Erstellung des Klassifizierungsmodells Logistic Regression
2.13.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Logistic Regression
2.13.3. ONNX-Darstellung des Klassifizierungsmodells Logistic Regression - 2.14. LogisticRegressionCV Classifier
2.14.1. Code zur Erstellung des Klassifizierungsmodells von LogisticRegressionCV
2.14.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell LogisticRegressionCV
2.14.3. ONNX-Darstellung des Klassifizierungsmodells LogisticRegressionCV - 2.15. Passive-Aggressive (PA) Classifier
2.15.1. Code zur Erstellung des Klassifizierungsmodells von Passive-Aggressive (PA)
2.15.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Passive-Aggressive (PA)
2.15.3. ONNX-Darstellung des Klassifizierungsmodells Passive-Aggressive (PA) - 2.16. Perceptron Classifier
2.16.1. Code zur Erstellung des Klassifizierungsmodells von Perceptron
2.16.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Perceptron
2.16.3. ONNX-Darstellung des Klassifizierungsmodells Perceptron - 2.17. Stochastic Gradient Descent Classifier
2.17.1. Code für die Erstellung des Klassifizierungsmodells mit stochastischem Gradientenabstieg
2.17.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Stochastic Gradient Descent
2.17.3. ONNX-Darstellung des Klassifizierungsmodells mit stochastischem Gradientenabstieg - 2.18. Gaussian Naive Bayes (GNB) Klassifikator
2.18.1. Code für die Erstellung des Klassifizierungsmodells Gaussian Naive Bayes (GNB)
2.18.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Gaussian Naive Bayes (GNB)
2.18.3. ONNX-Darstellung des Klassifizierungsmodells Gaussian Naive Bayes (GNB) - 2.19. Multinomial Naive Bayes (MNB) Classifier
2.19.1. Code zur Erstellung des Klassifizierungsmodells von Multinomial Naive Bayes (MNB)
2.19.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Multinomial Naive Bayes (MNB)
2.19.3. ONNX-Darstellung des Klassifizierungsmodells Multinomial Naive Bayes (MNB) - 2.20. Complement Naive Bayes (CNB) Classifier
2.20.1. Code zur Erstellung des Klassifizierungsmodells von Complement Naive Bayes (CNB)
2.20.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Complement Naive Bayes (CNB)
2.20.3. ONNX-Darstellung des Klassifizierungsmodells Complement Naive Bayes (CNB) - 2.21. Bernoulli Naive Bayes (BNB) Classifier
2.21.1. Code zur Erstellung des Klassifizierungsmodells von Bernoulli Naive Bayes (BNB)
2.21.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Bernoulli Naive Bayes (BNB)
2.21.3. ONNX-Darstellung des Klassifizierungsmodells Bernoulli Naive Bayes (BNB) - 2.22. Multilayer Perceptron Classifier
2.22.1. Code zur Erstellung des Klassifizierungsmodells von Multilayer Perceptron
2.22.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Multilayer Perceptron
2.22.3. ONNX-Darstellung des Klassifizierungsmodells Multilayer Perceptron - 2.23. Linear Discriminant Analysis (LDA) Classifier
2.23.1. Code zur Erstellung des Klassifizierungsmodells der linearen Diskriminanzanalyse (LDA)
2.23.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell der linearen Diskriminanzanalyse (LDA)
2.23.3. ONNX-Darstellung des Klassifizierungsmodells der linearen Diskriminanzanalyse (LDA) - 2.24. Hist Gradient Boosting
2.24.1. Code zur Erstellung des Klassifizierungsmodells des Histogram-basierten Gradient-Boosting
2.24.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Histogramm-basierten Gradient Boosting
2.24.3. ONNX-Darstellung des Klassifizierungsmodells Histogramm-basierten Gradient-Boosting - 2.25. CategoricalNB Classifier
2.25.1. Code zur Erstellung des Klassifizierungsmodells von CategoricalNB
2.25.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell CategoricalNB
2.25.3. ONNX-Darstellung des Klassifizierungsmodells CategoricalNB - 2.26. ExtraTreeClassifier
2.26.1. Code zur Erstellung des Modells von ExtraTreeClassifier
2.26.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell ExtraTreeClassifier
2.26.3. ONNX-Darstellung des Klassifizierungsmodells ExtraTreeClassifier - 2.27. ExtraTreesClassifier
2.27.1. Code zur Erstellung des Modells von ExtraTreesClassifier
2.27.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell ExtraTreesClassifier
2.27.3. ONNX-Darstellung des Klassifizierungsmodells ExtraTreesClassifier - 2.28. Vergleich der Genauigkeit aller Modelle
2.28.1. Code für die Berechnung aller Modelle und die Erstellung eines Genauigkeitsvergleichsdiagramms
2.28.2. MQL5-Code für die Ausführung aller ONNX-Modelle - 2.29. Scikit-Learn-Klassifikationsmodelle, die nicht in ONNX konvertiert werden konnten
- 2.29.1. DummyClassifier
2.29.1.1. Code zum Erstellen des Klassifizierungsmodells DummyClassifier - 2.29.2. GaussianProcessClassifier
2.29.2.1. Code zur Erstellung des Modells von GaussianProcessClassifier - 2.29.3. LabelPropagation Klassifikator
2.29.3.1. Code zur Erstellung des Modells von LabelPropagationClassifier - 2.29.4. LabelSpreading-Klassifikator
2.29.4.1. Code zur Erstellung des Modells von LabelSpreadingClassifier - 2.29.5. NearestCentroid-Klassifikator
2.29.5.1. Code zur Erstellung Modells von NearestCentroid - 2.29.6. Quadratische Diskriminanzanalyse Klassifikator
2.29.6.1. Code zur Erstellung des Modells der quadratischen Diskriminanzanalyse - Schlussfolgerungen
1. Fishers Schwertlilien
Der Iris-Datensatz, Bilder von Schwertlilien, ist einer der bekanntesten und am häufigsten verwendeten Datensätze im Bereich des maschinellen Lernens. Sie wurde erstmals 1936 von dem Statistiker und Biologen R.A. Fisher und ist seitdem zu einem klassischen Datensatz für Klassifizierungsaufgaben geworden.
Der Iris-Datensatz besteht aus Messungen von Kelch- (sepal) und Blütenblätter (petal) von drei Schwertlilienarten - Iris setosa, Iris virginica und Iris versicolor.
Abbildung 1. Iris setosa
Abbildung 2. Schwertlilie (Iris virginica)
Abbildung 3. Iris versicolor
Der Iris-Datensatz umfasst 150 Instanzen von Schwertlilien, davon 50 Instanzen von jeder der drei Arten. Jede Instanz hat vier numerische Merkmale (gemessen in Zentimetern):
- Länge des Kelchblatts
- Breite des Kelchblatts
- Länge des Blütenblatts
- Breite des Blütenblatts
Jede Instanz hat auch eine entsprechende Klasse, die die Art der Schwertlilie angibt (Iris setosa, Iris virginica oder Iris versicolor). Diese Klassifizierungseigenschaft macht den Iris-Datensatz zu einem idealen Datensatz für maschinelle Lernaufgaben wie Klassifizierung und Clustering.
MetaEditor ermöglicht die Arbeit mit Python-Skripten. Um ein Python-Skript zu erstellen, wählen Sie in MetaEditor im Menü „Datei“ die Option „Neu“, woraufhin ein Dialog zur Auswahl des zu erstellenden Objekts erscheint (siehe Abbildung 4).
Abbildung 4. Erstellen eines Python-Skripts im MQL5-Assistenten - Schritt 1
Als Nächstes muss ein Namen für das Skript ein, z. B. „IRIS.py“ eingegeben werden (siehe Abbildung 5).
Abbildung 5. Erstellen eines Python-Skripts im MQL5-Assistenten - Schritt 2 - Skriptname
Danach können Sie angeben, welche Bibliotheken verwendet werden sollen. In unserem Fall werden wir diese Felder leer lassen (siehe Abbildung 6).
Abbildung 6: Erstellen eines Python-Skripts im MQL5-Assistenten - Schritt 3
Eine Möglichkeit, mit der Analyse des Iris-Datensatzes zu beginnen, besteht darin, die Daten zu visualisieren. Eine grafische Darstellung ermöglicht es uns, die Struktur der Daten und die Beziehungen zwischen den Merkmalen besser zu verstehen.
Sie können z. B. ein Streudiagramm erstellen, um zu sehen, wie die verschiedenen Schwertlilienarten im Merkmalsraum verteilt sind.
Python-Skript-Code:
# The script shows the scatter plot of the Iris dataset features # Copyright 2023, MetaQuotes Ltd. # https://mql5.com import matplotlib.pyplot as plt from sklearn import datasets # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # extract sepal length and sepal width (the first two features) sepal_length = X[:, 0] sepal_width = X[:, 1] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(sepal_length, sepal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Sepal Length (cm)') plt.ylabel('Sepal Width (cm)') plt.title('Scatter Plot for Sepal Length and Sepal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_sepal_length_width.png') # Extract petal length and petal width (the third and fourth features) petal_length = X[:, 2] petal_width = X[:, 3] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(petal_length, petal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Petal Length (cm)') plt.ylabel('Petal Width (cm)') plt.title('Scatter Plot for Petal Length and Petal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_petal_length_width.png')
Um dieses Skript auszuführen, müssen Sie es in MetaEditor kopieren (siehe Abbildung 7) und auf „Kompilieren“ klicken.
Abbildung 7: Skript IRIS.py in MetaEditor
Danach erscheinen die Diagramme auf dem Bildschirm:
Abbildung 8: Skript IRIS.py in MetaEditor mit Darstellung der Kelchblattlänge/Kelchblattbreite (Sepal Length/Sepal Width)
Abbildung 9: Skript IRIS.py in MetaEditor mit der Darstellung von Blütenblattlänge/Blütenblattbreite
Schauen wir sie uns genauer an.
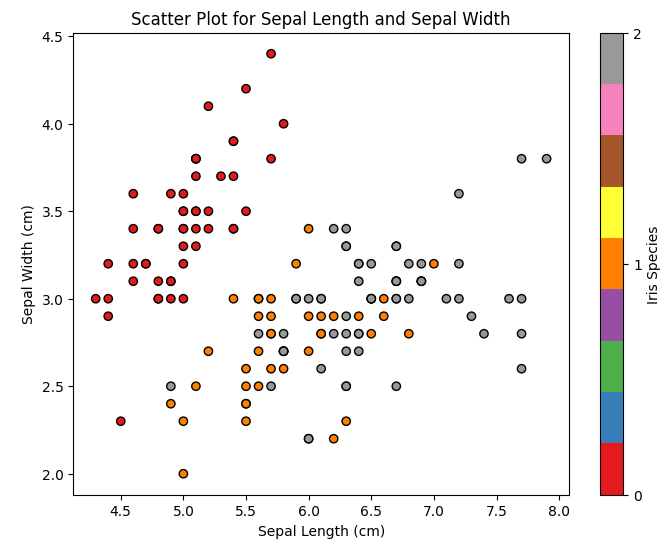
Abbildung 10: Streuungsdiagramm Kelchblattlänge vs. Kelchblattbreite
In diesem Diagramm sehen wir, wie sich die verschiedenen Schwertlilienarten nach Kelchblattlänge und Kelchblattbreite verteilen. Wir können feststellen, dass Iris setosa im Vergleich zu den anderen beiden Arten kürzere und breitere Kelchblätter hat.
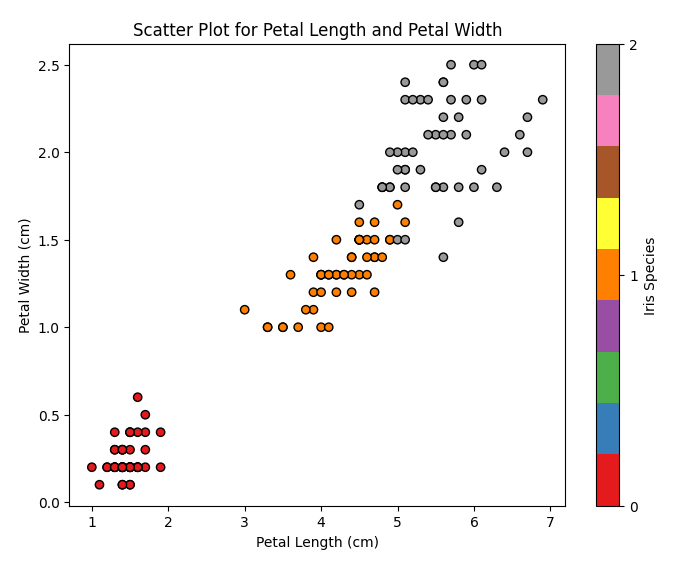
Abbildung 11: Streudiagramm Blütenblattlänge vs. Blütenblattbreite
In diesem Diagramm können wir die verschiedenen Schwertlilienarten auf Basis der Verteilung von Blütenblattlänge und -breite sehen. Wir können feststellen, dass Iris setosa die kürzesten und schmalsten Blütenblätter hat, Iris virginica hat die längsten und breitesten Blütenblätter, und Iris versicolor liegt dazwischen.
Der Iris-Datensatz ist ein idealer Datensatz zum Trainieren und Testen von Modellen für maschinelles Lernen. Wir werden es verwenden, um die Effektivität von maschinellen Lernmodellen für eine Klassifizierungsaufgabe zu analysieren.
2. Modelle für die Klassifizierung
Die Klassifizierung ist eine der grundlegenden Aufgaben des maschinellen Lernens, deren Ziel es ist, Daten anhand bestimmter Merkmale in verschiedene Kategorien oder Klassen einzuteilen.
Schauen wir uns die wichtigsten Modelle für maschinelles Lernen im Scikit-Learn-Paket an.
Liste der Klassifikatoren von Scikit-Learn
Um eine Liste der verfügbaren Klassifikatoren in Scikit-Learn anzuzeigen, können Sie das folgende Skript verwenden:
# ScikitLearnClassifiers.py # The script lists all the classification algorithms available in scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn classifiers from sklearn.utils import all_estimators classifiers = all_estimators(type_filter='classifier') for index, (name, ClassifierClass) in enumerate(classifiers, start=1): print(f"Classifier {index}: {name}")
Ausgabe:
Python The Python version is 3.10.0
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV-Klassifikator
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV-Klassifikator
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Der Einfachheit halber sind sie in dieser Liste der Klassifikatoren farblich hervorgehoben. Modelle, die einen Basisklassifikator erfordern, sind gelb hervorgehoben, während andere Modelle unabhängig davon verwendet werden können.
Mit Blick auf die Zukunft ist es erwähnenswert, dass grün gefärbte Modelle erfolgreich in das ONNX-Format exportiert wurden, während rot gefärbte Modelle bei der Konvertierung in der aktuellen Version von Scikit-Learn 1.2.2 Fehler aufweisen.
Unterschiedliche Darstellung von Ausgabedaten in Modellen
Es ist zu beachten, dass verschiedene Modelle die Ausgabedaten unterschiedlich darstellen, sodass man bei der Arbeit mit Modellen, die in ONNX konvertiert wurden, aufmerksam sein sollte.
Für die Klassifizierungsaufgabe der Schwertlilien von Fisher haben die Eingabetensoren für alle diese Modelle das gleiche Format:
Informationen über Eingabe-Tensoren in ONNX:
1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Die Output-Tensoren der ONNX-Modelle sind unterschiedlich.
1. Modelle, die nicht nachbearbeitet werden müssen:
- SVC Classifier;
- LinearSVC Classifier;
- NuSVC Classifier;
- Radius Neighbors Classifier;
- Ridge Classifier;
- Ridge Classifier CV.
Informationen über Ausgangstensoren in ONNX:
1. Name: label, Data Type: tensor(int64), Shape: [None]
2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
1. Name: label, Data Type: tensor(int64), Shape: [None]
2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Diese Modelle geben das Ergebnis (Klassennummer) explizit im ersten ganzzahligen Ausgabetensor „label“ zurück, ohne dass eine Nachbearbeitung erforderlich ist.
2. Modelle, deren Ergebnisse nachbearbeitet werden müssen:
- Random Forest Classifier;
- Gradient Boosting Classifier;
- AdaBoost Classifier;
- Bagging Classifier;
- K-NN_Classifier;
- Decision Tree Classifier;
- Logistic Regression Classifier;
- Logistic Regression CV Classifier;
- Passive-Aggressive Classifier;
- Perceptron Classifier;
- SGD Classifier;
- Gaussian Naive Bayes Classifier;
- Multinomial Naive Bayes Classifier;
- Complement Naive Bayes Classifier;
- Bernoulli Naive Bayes Classifier;
- Multilayer Perceptron Classifier;
- Linear Discriminant Analysis Classifier;
- Hist Gradient Boosting Classifier;
- Categorical Naive Bayes Classifier;
- ExtraTree Classifier;
- ExtraTrees Classifier.
Informationen über Ausgangstensoren in ONNX:
1. Name: output_label, Data Type: tensor(int64), Shape: [None]
2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
1. Name: output_label, Data Type: tensor(int64), Shape: [None]
2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Diese Modelle liefern eine Liste von Klassen und Wahrscheinlichkeiten der Zugehörigkeit zu jeder Klasse.
Um das Ergebnis in diesen Fällen zu erhalten, ist eine Nachbearbeitung erforderlich, wie z. B. seq(map(int64, tensor(float)) (Suche nach dem Element mit der höchsten Wahrscheinlichkeit).
Daher ist es wichtig, bei der Arbeit mit ONNX-Modellen aufmerksam zu sein und diese Aspekte zu berücksichtigen. Ein Beispiel für eine andere Ergebnisverarbeitung ist im Skript in 2.28.2 dargestellt.
iris.mqh
Um Modelle mit dem vollständigen Iris-Datensatz in MQL5 zu testen, ist eine Datenaufbereitung erforderlich. Zu diesem Zweck wird die Funktion PrepareIrisDataset() verwendet.
Es ist praktisch, diese Funktionen in die Datei iris.mqh zu verschieben.
//+------------------------------------------------------------------+ //| Iris.mqh | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" //+------------------------------------------------------------------+ //| Structure for the IRIS Dataset sample | //+------------------------------------------------------------------+ struct sIRISsample { int sample_id; // sample id (1-150) double features[4]; // SepalLengthCm,SepalWidthCm,PetalLengthCm,PetalWidthCm string class_name; // class ("Iris-setosa","Iris-versicolor","Iris-virginica") int class_id; // class id (0,1,2), calculated by function IRISClassID }; //--- Iris dataset sIRISsample ExtIRISDataset[]; int Exttotal=0; //+------------------------------------------------------------------+ //| Returns class id by class name | //+------------------------------------------------------------------+ int IRISClassID(string class_name) { //--- if(class_name=="Iris-setosa") return(0); else if(class_name=="Iris-versicolor") return(1); else if(class_name=="Iris-virginica") return(2); //--- return(-1); } //+------------------------------------------------------------------+ //| AddSample | //+------------------------------------------------------------------+ bool AddSample(const int Id,const double SepalLengthCm,const double SepalWidthCm,const double PetalLengthCm,const double PetalWidthCm, const string Species) { //--- ExtIRISDataset[Exttotal].sample_id=Id; //--- ExtIRISDataset[Exttotal].features[0]=SepalLengthCm; ExtIRISDataset[Exttotal].features[1]=SepalWidthCm; ExtIRISDataset[Exttotal].features[2]=PetalLengthCm; ExtIRISDataset[Exttotal].features[3]=PetalWidthCm; //--- ExtIRISDataset[Exttotal].class_name=Species; ExtIRISDataset[Exttotal].class_id=IRISClassID(Species); //--- Exttotal++; //--- return(true); } //+------------------------------------------------------------------+ //| Prepare Iris Dataset | //+------------------------------------------------------------------+ bool PrepareIrisDataset(sIRISsample &iris_samples[]) { ArrayResize(ExtIRISDataset,150); Exttotal=0; //--- AddSample(1,5.1,3.5,1.4,0.2,"Iris-setosa"); AddSample(2,4.9,3.0,1.4,0.2,"Iris-setosa"); AddSample(3,4.7,3.2,1.3,0.2,"Iris-setosa"); AddSample(4,4.6,3.1,1.5,0.2,"Iris-setosa"); AddSample(5,5.0,3.6,1.4,0.2,"Iris-setosa"); AddSample(6,5.4,3.9,1.7,0.4,"Iris-setosa"); AddSample(7,4.6,3.4,1.4,0.3,"Iris-setosa"); AddSample(8,5.0,3.4,1.5,0.2,"Iris-setosa"); AddSample(9,4.4,2.9,1.4,0.2,"Iris-setosa"); AddSample(10,4.9,3.1,1.5,0.1,"Iris-setosa"); AddSample(11,5.4,3.7,1.5,0.2,"Iris-setosa"); AddSample(12,4.8,3.4,1.6,0.2,"Iris-setosa"); AddSample(13,4.8,3.0,1.4,0.1,"Iris-setosa"); AddSample(14,4.3,3.0,1.1,0.1,"Iris-setosa"); AddSample(15,5.8,4.0,1.2,0.2,"Iris-setosa"); AddSample(16,5.7,4.4,1.5,0.4,"Iris-setosa"); AddSample(17,5.4,3.9,1.3,0.4,"Iris-setosa"); AddSample(18,5.1,3.5,1.4,0.3,"Iris-setosa"); AddSample(19,5.7,3.8,1.7,0.3,"Iris-setosa"); AddSample(20,5.1,3.8,1.5,0.3,"Iris-setosa"); AddSample(21,5.4,3.4,1.7,0.2,"Iris-setosa"); AddSample(22,5.1,3.7,1.5,0.4,"Iris-setosa"); AddSample(23,4.6,3.6,1.0,0.2,"Iris-setosa"); AddSample(24,5.1,3.3,1.7,0.5,"Iris-setosa"); AddSample(25,4.8,3.4,1.9,0.2,"Iris-setosa"); AddSample(26,5.0,3.0,1.6,0.2,"Iris-setosa"); AddSample(27,5.0,3.4,1.6,0.4,"Iris-setosa"); AddSample(28,5.2,3.5,1.5,0.2,"Iris-setosa"); AddSample(29,5.2,3.4,1.4,0.2,"Iris-setosa"); AddSample(30,4.7,3.2,1.6,0.2,"Iris-setosa"); AddSample(31,4.8,3.1,1.6,0.2,"Iris-setosa"); AddSample(32,5.4,3.4,1.5,0.4,"Iris-setosa"); AddSample(33,5.2,4.1,1.5,0.1,"Iris-setosa"); AddSample(34,5.5,4.2,1.4,0.2,"Iris-setosa"); AddSample(35,4.9,3.1,1.5,0.2,"Iris-setosa"); AddSample(36,5.0,3.2,1.2,0.2,"Iris-setosa"); AddSample(37,5.5,3.5,1.3,0.2,"Iris-setosa"); AddSample(38,4.9,3.6,1.4,0.1,"Iris-setosa"); AddSample(39,4.4,3.0,1.3,0.2,"Iris-setosa"); AddSample(40,5.1,3.4,1.5,0.2,"Iris-setosa"); AddSample(41,5.0,3.5,1.3,0.3,"Iris-setosa"); AddSample(42,4.5,2.3,1.3,0.3,"Iris-setosa"); AddSample(43,4.4,3.2,1.3,0.2,"Iris-setosa"); AddSample(44,5.0,3.5,1.6,0.6,"Iris-setosa"); AddSample(45,5.1,3.8,1.9,0.4,"Iris-setosa"); AddSample(46,4.8,3.0,1.4,0.3,"Iris-setosa"); AddSample(47,5.1,3.8,1.6,0.2,"Iris-setosa"); AddSample(48,4.6,3.2,1.4,0.2,"Iris-setosa"); AddSample(49,5.3,3.7,1.5,0.2,"Iris-setosa"); AddSample(50,5.0,3.3,1.4,0.2,"Iris-setosa"); AddSample(51,7.0,3.2,4.7,1.4,"Iris-versicolor"); AddSample(52,6.4,3.2,4.5,1.5,"Iris-versicolor"); AddSample(53,6.9,3.1,4.9,1.5,"Iris-versicolor"); AddSample(54,5.5,2.3,4.0,1.3,"Iris-versicolor"); AddSample(55,6.5,2.8,4.6,1.5,"Iris-versicolor"); AddSample(56,5.7,2.8,4.5,1.3,"Iris-versicolor"); AddSample(57,6.3,3.3,4.7,1.6,"Iris-versicolor"); AddSample(58,4.9,2.4,3.3,1.0,"Iris-versicolor"); AddSample(59,6.6,2.9,4.6,1.3,"Iris-versicolor"); AddSample(60,5.2,2.7,3.9,1.4,"Iris-versicolor"); AddSample(61,5.0,2.0,3.5,1.0,"Iris-versicolor"); AddSample(62,5.9,3.0,4.2,1.5,"Iris-versicolor"); AddSample(63,6.0,2.2,4.0,1.0,"Iris-versicolor"); AddSample(64,6.1,2.9,4.7,1.4,"Iris-versicolor"); AddSample(65,5.6,2.9,3.6,1.3,"Iris-versicolor"); AddSample(66,6.7,3.1,4.4,1.4,"Iris-versicolor"); AddSample(67,5.6,3.0,4.5,1.5,"Iris-versicolor"); AddSample(68,5.8,2.7,4.1,1.0,"Iris-versicolor"); AddSample(69,6.2,2.2,4.5,1.5,"Iris-versicolor"); AddSample(70,5.6,2.5,3.9,1.1,"Iris-versicolor"); AddSample(71,5.9,3.2,4.8,1.8,"Iris-versicolor"); AddSample(72,6.1,2.8,4.0,1.3,"Iris-versicolor"); AddSample(73,6.3,2.5,4.9,1.5,"Iris-versicolor"); AddSample(74,6.1,2.8,4.7,1.2,"Iris-versicolor"); AddSample(75,6.4,2.9,4.3,1.3,"Iris-versicolor"); AddSample(76,6.6,3.0,4.4,1.4,"Iris-versicolor"); AddSample(77,6.8,2.8,4.8,1.4,"Iris-versicolor"); AddSample(78,6.7,3.0,5.0,1.7,"Iris-versicolor"); AddSample(79,6.0,2.9,4.5,1.5,"Iris-versicolor"); AddSample(80,5.7,2.6,3.5,1.0,"Iris-versicolor"); AddSample(81,5.5,2.4,3.8,1.1,"Iris-versicolor"); AddSample(82,5.5,2.4,3.7,1.0,"Iris-versicolor"); AddSample(83,5.8,2.7,3.9,1.2,"Iris-versicolor"); AddSample(84,6.0,2.7,5.1,1.6,"Iris-versicolor"); AddSample(85,5.4,3.0,4.5,1.5,"Iris-versicolor"); AddSample(86,6.0,3.4,4.5,1.6,"Iris-versicolor"); AddSample(87,6.7,3.1,4.7,1.5,"Iris-versicolor"); AddSample(88,6.3,2.3,4.4,1.3,"Iris-versicolor"); AddSample(89,5.6,3.0,4.1,1.3,"Iris-versicolor"); AddSample(90,5.5,2.5,4.0,1.3,"Iris-versicolor"); AddSample(91,5.5,2.6,4.4,1.2,"Iris-versicolor"); AddSample(92,6.1,3.0,4.6,1.4,"Iris-versicolor"); AddSample(93,5.8,2.6,4.0,1.2,"Iris-versicolor"); AddSample(94,5.0,2.3,3.3,1.0,"Iris-versicolor"); AddSample(95,5.6,2.7,4.2,1.3,"Iris-versicolor"); AddSample(96,5.7,3.0,4.2,1.2,"Iris-versicolor"); AddSample(97,5.7,2.9,4.2,1.3,"Iris-versicolor"); AddSample(98,6.2,2.9,4.3,1.3,"Iris-versicolor"); AddSample(99,5.1,2.5,3.0,1.1,"Iris-versicolor"); AddSample(100,5.7,2.8,4.1,1.3,"Iris-versicolor"); AddSample(101,6.3,3.3,6.0,2.5,"Iris-virginica"); AddSample(102,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(103,7.1,3.0,5.9,2.1,"Iris-virginica"); AddSample(104,6.3,2.9,5.6,1.8,"Iris-virginica"); AddSample(105,6.5,3.0,5.8,2.2,"Iris-virginica"); AddSample(106,7.6,3.0,6.6,2.1,"Iris-virginica"); AddSample(107,4.9,2.5,4.5,1.7,"Iris-virginica"); AddSample(108,7.3,2.9,6.3,1.8,"Iris-virginica"); AddSample(109,6.7,2.5,5.8,1.8,"Iris-virginica"); AddSample(110,7.2,3.6,6.1,2.5,"Iris-virginica"); AddSample(111,6.5,3.2,5.1,2.0,"Iris-virginica"); AddSample(112,6.4,2.7,5.3,1.9,"Iris-virginica"); AddSample(113,6.8,3.0,5.5,2.1,"Iris-virginica"); AddSample(114,5.7,2.5,5.0,2.0,"Iris-virginica"); AddSample(115,5.8,2.8,5.1,2.4,"Iris-virginica"); AddSample(116,6.4,3.2,5.3,2.3,"Iris-virginica"); AddSample(117,6.5,3.0,5.5,1.8,"Iris-virginica"); AddSample(118,7.7,3.8,6.7,2.2,"Iris-virginica"); AddSample(119,7.7,2.6,6.9,2.3,"Iris-virginica"); AddSample(120,6.0,2.2,5.0,1.5,"Iris-virginica"); AddSample(121,6.9,3.2,5.7,2.3,"Iris-virginica"); AddSample(122,5.6,2.8,4.9,2.0,"Iris-virginica"); AddSample(123,7.7,2.8,6.7,2.0,"Iris-virginica"); AddSample(124,6.3,2.7,4.9,1.8,"Iris-virginica"); AddSample(125,6.7,3.3,5.7,2.1,"Iris-virginica"); AddSample(126,7.2,3.2,6.0,1.8,"Iris-virginica"); AddSample(127,6.2,2.8,4.8,1.8,"Iris-virginica"); AddSample(128,6.1,3.0,4.9,1.8,"Iris-virginica"); AddSample(129,6.4,2.8,5.6,2.1,"Iris-virginica"); AddSample(130,7.2,3.0,5.8,1.6,"Iris-virginica"); AddSample(131,7.4,2.8,6.1,1.9,"Iris-virginica"); AddSample(132,7.9,3.8,6.4,2.0,"Iris-virginica"); AddSample(133,6.4,2.8,5.6,2.2,"Iris-virginica"); AddSample(134,6.3,2.8,5.1,1.5,"Iris-virginica"); AddSample(135,6.1,2.6,5.6,1.4,"Iris-virginica"); AddSample(136,7.7,3.0,6.1,2.3,"Iris-virginica"); AddSample(137,6.3,3.4,5.6,2.4,"Iris-virginica"); AddSample(138,6.4,3.1,5.5,1.8,"Iris-virginica"); AddSample(139,6.0,3.0,4.8,1.8,"Iris-virginica"); AddSample(140,6.9,3.1,5.4,2.1,"Iris-virginica"); AddSample(141,6.7,3.1,5.6,2.4,"Iris-virginica"); AddSample(142,6.9,3.1,5.1,2.3,"Iris-virginica"); AddSample(143,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(144,6.8,3.2,5.9,2.3,"Iris-virginica"); AddSample(145,6.7,3.3,5.7,2.5,"Iris-virginica"); AddSample(146,6.7,3.0,5.2,2.3,"Iris-virginica"); AddSample(147,6.3,2.5,5.0,1.9,"Iris-virginica"); AddSample(148,6.5,3.0,5.2,2.0,"Iris-virginica"); AddSample(149,6.2,3.4,5.4,2.3,"Iris-virginica"); AddSample(150,5.9,3.0,5.1,1.8,"Iris-virginica"); //--- ArrayResize(iris_samples,150); for(int i=0; i<Exttotal; i++) { iris_samples[i]=ExtIRISDataset[i]; } //--- return(true); } //+------------------------------------------------------------------+
Anmerkung zu den Klassifizierungsmethoden: SVC, LinearSVC und NuSVC
Vergleichen wir drei gängige Klassifizierungsmethoden: SVC (Support Vector Classification), LinearSVC (Linear Support Vector Classification), und NuSVC (Nu Support Vector Classification).
Funktionsprinzipien:
SVC (Support Vector Classification)
Arbeitsprinzip: SVC ist eine Klassifizierungsmethode, die auf der Maximierung der Spanne zwischen den Klassen basiert. Es wird eine optimale Trennungshyperfläche gesucht, die die Klassen maximal trennt und die Supportvektoren - Punkte, die der Hyperfläche am nächsten liegen - unterstützt.
Kernel-Funktionen: SVC kann verschiedene Kernel-Funktionen verwenden, z. B. lineare, radiale Basisfunktion (RBF), Polynom und andere. Die Kernel-Funktion bestimmt, wie die Daten transformiert werden, um die optimale Hyperebene zu finden.
LinearSVC (Linear Support Vector Classification)
Arbeitsprinzip: LinearSVC ist eine Variante von SVC, die auf lineare Klassifizierung spezialisiert ist. Es sucht nach einer optimalen linearen Trennhyperebene ohne Verwendung von Kernel-Funktionen. Das macht die Arbeit mit großen Datenmengen schneller und effizienter.
NuSVC (Nu Support Vector Classification)
Arbeitsprinzip: NuSVC basiert ebenfalls auf Support-Vector-Methoden, führt aber einen Parameter Nu (nu) ein, der die Komplexität des Modells und den Anteil der Support-Vektoren steuert. Der Nu-Wert liegt im Bereich von 0 bis 1 und bestimmt, wie viele der Daten für Stützvektoren und Fehler verwendet werden können.
Vorteile:
SVC
Leistungsstarker Algorithmus: SVC kann dank der Verwendung von Kernel-Funktionen komplexe Klassifizierungsaufgaben bewältigen und mit nichtlinearen Daten arbeiten.
Robustheit gegenüber Ausreißern: SVC ist robust gegenüber Datenausreißern, da es Unterstützungsvektoren verwendet, um die trennende Hyperebene zu erstellen.
LinearSVC
Hoher Wirkungsgrad: LinearSVC ist schneller und effizienter im Umgang mit großen Datensätzen, vor allem wenn die Daten groß sind und die lineare Trennung für die Aufgabe geeignet ist.
Lineare Klassifizierung: Wenn das Problem gut linear trennbar ist, kann LinearSVC gute Ergebnisse liefern, ohne dass komplexe Kernel-Funktionen erforderlich sind.
NuSVC
Kontrolle der Modellkomplexität: Mit dem Nu-Parameter in NuSVC können Sie die Komplexität des Modells und den Kompromiss zwischen Anpassung an die Daten und Verallgemeinerung steuern.
Robustheit gegenüber Ausreißern: Ähnlich wie SVC ist NuSVC robust gegenüber Ausreißern, wodurch es sich für Aufgaben mit verrauschten Daten eignet.
Einschränkungen:
SVC
Berechnungskomplexität: SVC kann bei großen Datensätzen und/oder bei Verwendung komplexer Kernel-Funktionen langsam sein.
Kernel-Empfindlichkeit: Die Wahl der richtigen Kernel-Funktion kann eine schwierige Aufgabe sein und die Modellleistung erheblich beeinflussen.
LinearSVC
Linearitätsbeschränkung: LinearSVC ist durch eine lineare Datentrennung eingeschränkt und kann in Fällen mit nichtlinearen Abhängigkeiten zwischen Merkmalen und der Zielvariablen schlecht abschneiden.
NuSVC
Nu-Parameter-Abstimmung: Die Abstimmung des Parameters Nu kann einige Zeit und Experimente erfordern, um optimale Ergebnisse zu erzielen.
Je nach den Merkmalen der Aufgabe und dem Datenvolumen kann jede dieser Methoden die beste Wahl sein. Es ist wichtig, Experimente durchzuführen und die Methode auszuwählen, die am besten zu den spezifischen Anforderungen der Klassifizierungsaufgabe passt.
Vergleichen wir drei gängige Klassifizierungsmethoden: SVC (Support Vector Classification), LinearSVC (Linear Support Vector Classification), und NuSVC (Nu Support Vector Classification).
Funktionsprinzipien:
SVC (Support Vector Classification)
Arbeitsprinzip: SVC ist eine Klassifizierungsmethode, die auf der Maximierung der Spanne zwischen den Klassen basiert. Es wird eine optimale Trennungshyperfläche gesucht, die die Klassen maximal trennt und die Supportvektoren - Punkte, die der Hyperfläche am nächsten liegen - unterstützt.
Kernel-Funktionen: SVC kann verschiedene Kernel-Funktionen verwenden, z. B. lineare, radiale Basisfunktion (RBF), Polynom und andere. Die Kernel-Funktion bestimmt, wie die Daten transformiert werden, um die optimale Hyperebene zu finden.
LinearSVC (Linear Support Vector Classification)
Arbeitsprinzip: LinearSVC ist eine Variante von SVC, die auf lineare Klassifizierung spezialisiert ist. Es sucht nach einer optimalen linearen Trennhyperebene ohne Verwendung von Kernel-Funktionen. Das macht die Arbeit mit großen Datenmengen schneller und effizienter.
NuSVC (Nu Support Vector Classification)
Arbeitsprinzip: NuSVC basiert ebenfalls auf Support-Vector-Methoden, führt aber einen Parameter Nu (nu) ein, der die Komplexität des Modells und den Anteil der Support-Vektoren steuert. Der Nu-Wert liegt im Bereich von 0 bis 1 und bestimmt, wie viele der Daten für Stützvektoren und Fehler verwendet werden können.
Vorteile:
SVC
Leistungsstarker Algorithmus: SVC kann dank der Verwendung von Kernel-Funktionen komplexe Klassifizierungsaufgaben bewältigen und mit nichtlinearen Daten arbeiten.
Robustheit gegenüber Ausreißern: SVC ist robust gegenüber Datenausreißern, da es Unterstützungsvektoren verwendet, um die trennende Hyperebene zu erstellen.
LinearSVC
Hoher Wirkungsgrad: LinearSVC ist schneller und effizienter im Umgang mit großen Datensätzen, vor allem wenn die Daten groß sind und die lineare Trennung für die Aufgabe geeignet ist.
Lineare Klassifizierung: Wenn das Problem gut linear trennbar ist, kann LinearSVC gute Ergebnisse liefern, ohne dass komplexe Kernel-Funktionen erforderlich sind.
NuSVC
Kontrolle der Modellkomplexität: Mit dem Nu-Parameter in NuSVC können Sie die Komplexität des Modells und den Kompromiss zwischen Anpassung an die Daten und Verallgemeinerung steuern.
Robustheit gegenüber Ausreißern: Ähnlich wie SVC ist NuSVC robust gegenüber Ausreißern, wodurch es sich für Aufgaben mit verrauschten Daten eignet.
Einschränkungen:
SVC
Berechnungskomplexität: SVC kann bei großen Datensätzen und/oder bei Verwendung komplexer Kernel-Funktionen langsam sein.
Kernel-Empfindlichkeit: Die Wahl der richtigen Kernel-Funktion kann eine schwierige Aufgabe sein und die Modellleistung erheblich beeinflussen.
LinearSVC
Linearitätsbeschränkung: LinearSVC ist durch eine lineare Datentrennung eingeschränkt und kann in Fällen mit nichtlinearen Abhängigkeiten zwischen Merkmalen und der Zielvariablen schlecht abschneiden.
NuSVC
Nu-Parameter-Abstimmung: Die Abstimmung des Parameters Nu kann einige Zeit und Experimente erfordern, um optimale Ergebnisse zu erzielen.
Je nach den Merkmalen der Aufgabe und dem Datenvolumen kann jede dieser Methoden die beste Wahl sein. Es ist wichtig, Experimente durchzuführen und die Methode auszuwählen, die am besten zu den spezifischen Anforderungen der Klassifizierungsaufgabe passt.
2.1. SVC Classifier
Die Klassifizierungsmethode Support Vector Classification (SVC) ist ein leistungsfähiger Algorithmus für maschinelles Lernen, der häufig zur Lösung von Klassifizierungsaufgaben eingesetzt wird.
Funktionsprinzipien:
- Optimale Trennungshyperebene
Arbeitsprinzip: Die Hauptidee hinter SVC ist es, die optimale trennende Hyperebene im Merkmalsraum zu finden. Diese Hyperebene sollte die Trennung zwischen Objekten verschiedener Klassen und Unterstützungsvektoren maximieren, d. h. Datenpunkte, die der Hyperebene am nächsten liegen.
Maximierung der Gewinnspanne: SVC zielt darauf ab, die Spanne zwischen den Klassen zu maximieren, d. h. den Abstand der Support-Vektoren zur Hyperebene. Dadurch ist die Methode robust gegenüber Ausreißern und lässt sich gut auf neue Daten verallgemeinern. - Nutzung von Kernel-Funktionen
Kernel-Funktionen: SVC kann verschiedene Kernel-Funktionen verwenden, z. B. lineare, radiale Basisfunktion (RBF), Polynom und andere. Die Kernel-Funktion ermöglicht es, Daten in einen höherdimensionalen Raum zu projizieren, in dem die Aufgabe linear wird, auch wenn es im ursprünglichen Datenraum keine lineare Trennbarkeit gibt.
Kernel-Auswahl: Die Wahl der richtigen Kernel-Funktion kann die Leistung des SVC-Modells erheblich beeinflussen. Eine lineare Hyperebene ist nicht immer die optimale Lösung.
Vorteile:
- Leistungsstarker Algorithmus. Bewältigung komplexer Aufgaben: SVC kann komplexe Klassifizierungsaufgaben lösen, einschließlich solcher mit nicht-linearen Abhängigkeiten zwischen Merkmalen und der Zielvariablen.
- Robustheit gegenüber Ausreißern: Die Verwendung von Stützvektoren macht die Methode robust gegenüber Datenausreißern. Sie hängt von Stützvektoren und nicht vom gesamten Datensatz ab.
- Kernel-Flexibilität. Anpassungsfähigkeit an Daten: Die Möglichkeit, verschiedene Kernel-Funktionen zu verwenden, erlaubt es SVC, sich an spezifische Daten anzupassen und nicht-lineare Beziehungen zu entdecken.
- Gute Verallgemeinerung. Verallgemeinerung auf neue Daten: Das SVC-Modell kann gut auf neue Daten verallgemeinert werden, was es für Vorhersageaufgaben nützlich macht.
Einschränkungen:
- Berechnungskomplexität: Trainingszeit: SVC kann langsam trainiert werden, insbesondere bei großen Datenmengen oder komplexen Kernel-Funktionen.
- Kernel-Auswahl. Die Wahl der richtigen Kernel-Funktion: Die Auswahl der richtigen Kernel-Funktion erfordert möglicherweise Experimente und hängt von den Datenmerkmalen ab.
- Empfindlichkeit gegenüber Merkmalsskalierung. Normalisierung der Daten: SVC reagiert empfindlich auf die Skalierung von Merkmalen, daher wird empfohlen, die Daten vor dem Training zu normalisieren oder zu standardisieren.
- Interpretierbarkeit des Modells. Komplexität der Interpretation: SVC-Modelle können aufgrund der Verwendung nichtlinearer Kernel und einer Vielzahl von Support-Vektoren komplex zu interpretieren sein.
Je nach Aufgabenstellung und Datenmenge kann die SVC-Methode ein leistungsfähiges Werkzeug zur Lösung von Klassifikationsaufgaben sein. Es ist jedoch wichtig, seine Grenzen zu beachten und die Parameter so einzustellen, dass optimale Ergebnisse erzielt werden.
2.1.1. Code zur Erstellung des Klassifizierungsmodells von SVC
Dieser Code demonstriert den Prozess des Trainings eines SVC-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_SVCClassifier.py # The code demonstrates the process of training SVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import SVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SVC Classifier model with a linear kernel svc_model = SVC(kernel='linear', C=1.0) # train the model on the entire dataset svc_model.fit(X, y) # predict classes for the entire dataset y_pred = svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SVC Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SVC Classifier model in ONNX format:", accuracy_onnx)
Nachdem Sie das Skript in MetaEditor mit Hilfe der Schaltfläche „Kompilieren“ ausgeführt haben, können Sie die Ergebnisse der Ausführung auf der Registerkarte „Journal“ einsehen.
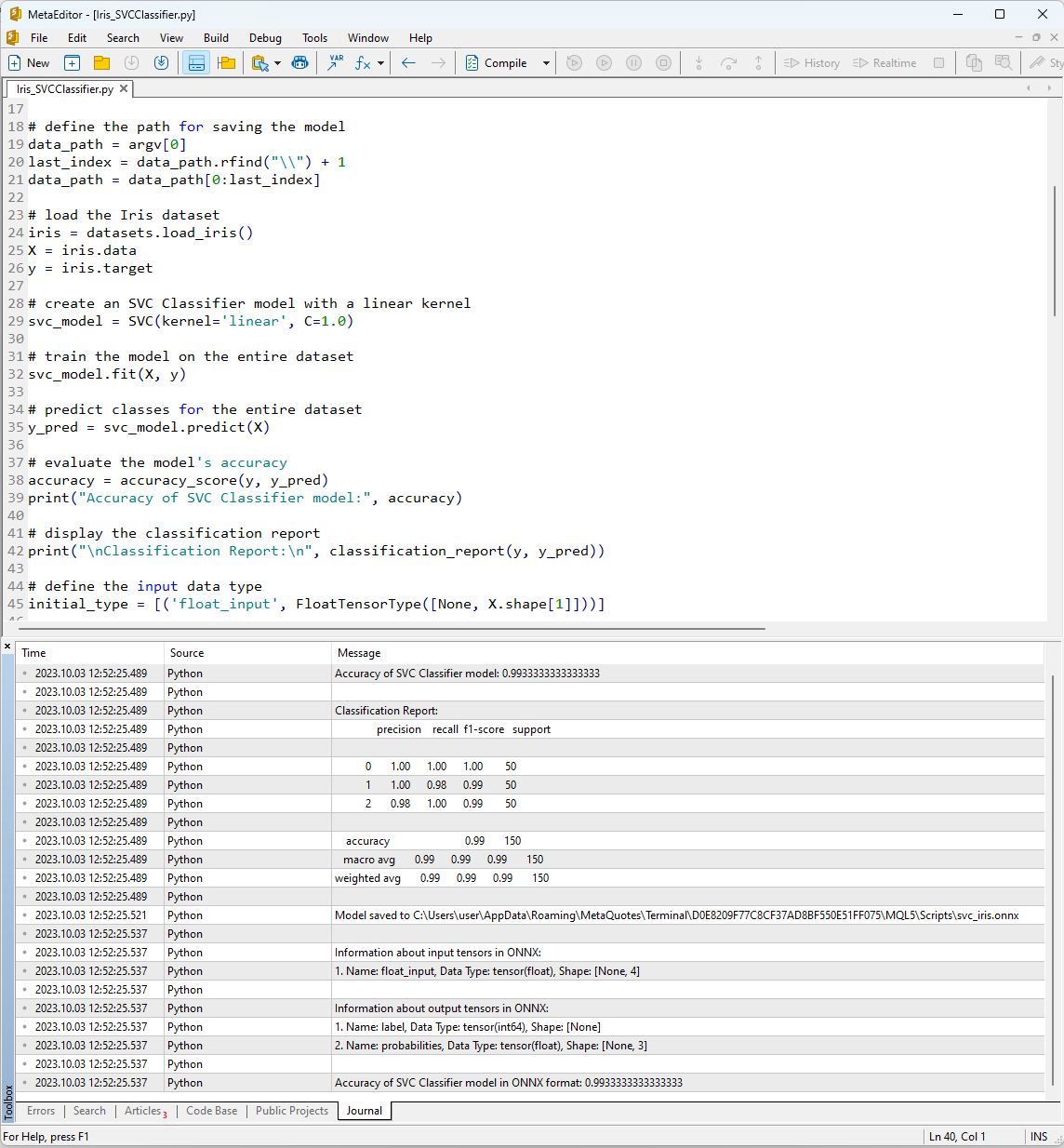
Abbildung 12. Ergebnisse des Skripts Iris_SVMClassifier.py in MetaEditor
Ausgabe des Skripts Iris_SVCClassifier.py:
Python Accuracy of SVC Classifier model: 0.9933333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.98 0.99 50
Python 2 0.98 1.00 0.99 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.9933333333333333
Hier finden Sie Informationen über den Pfad, in dem das ONNX-Modell gespeichert wurde, die Arten der Eingabe- und Ausgabeparameter des ONNX-Modells sowie die Genauigkeit bei der Beschreibung des Iris-Datensatzes.
Die Genauigkeit der Beschreibung des Datensatzes mit dem SVM-Klassifikator liegt bei 99 %, und das in das ONNX-Format exportierte Modell weist die gleiche Genauigkeit auf.
Nun werden wir diese Ergebnisse in MQL5 verifizieren, indem wir das konstruierte Modell für jede der 150 Datenproben ausführen. Außerdem enthält das Skript ein Beispiel für die Stapelverarbeitung von Daten.
2.1.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell SVC
//+------------------------------------------------------------------+ //| Iris_SVCClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SVCClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Die Ergebnisse der Ausführung des Skripts werden auf der Registerkarte „Experten“ des MetaTrader 5-Terminals angezeigt.
Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier correct results: 99.33% Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier all samples accuracy=0.993333 Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier batch test accuracy=1.000000
Das SVC-Modell hat 149 von 150 Proben richtig klassifiziert, was ein ausgezeichnetes Ergebnis ist. Das Modell machte nur einen Klassifizierungsfehler im Iris-Datensatz, indem es für die Probe Nr. 84 die Klasse 2 (versicolor) statt der Klasse 1 (virginica) vorhersagte.
Es ist erwähnenswert, dass die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz 99,33 % beträgt, was der Genauigkeit des Originalmodells entspricht.
2.1.3. ONNX-Darstellung des Klassifizierungsmodells SVC
Sie können das erstellte ONNX-Modell in MetaEditor anzeigen.
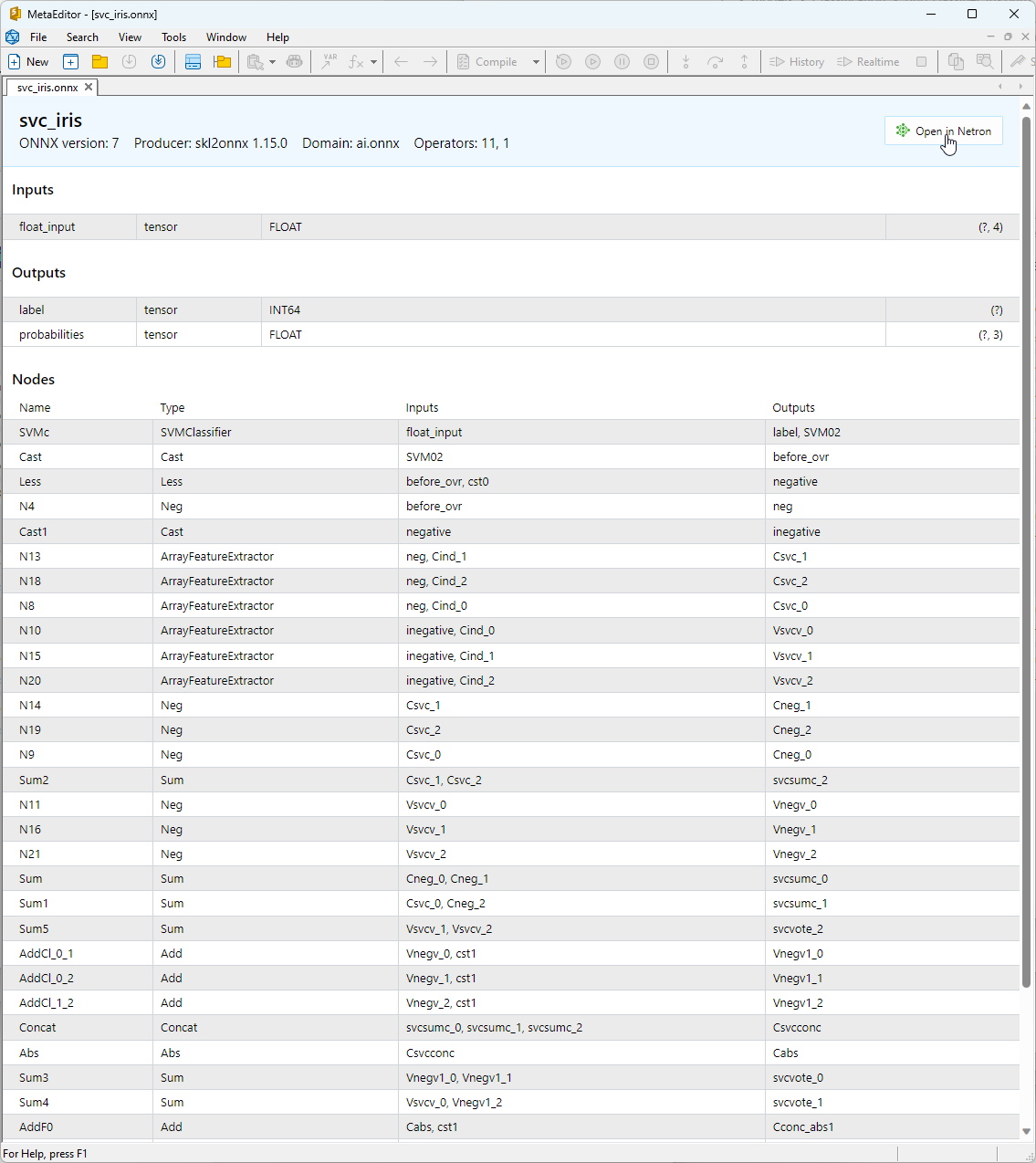
Abbildung 13. ONNX-Modell svc_iris.onnx in MetaEditor
Detailliertere Informationen über die Architektur des Modells erhalten Sie mit Netron. Klicken Sie dazu in der Beschreibung des Modells im MetaEditor auf die Schaltfläche „Open in Netron“.
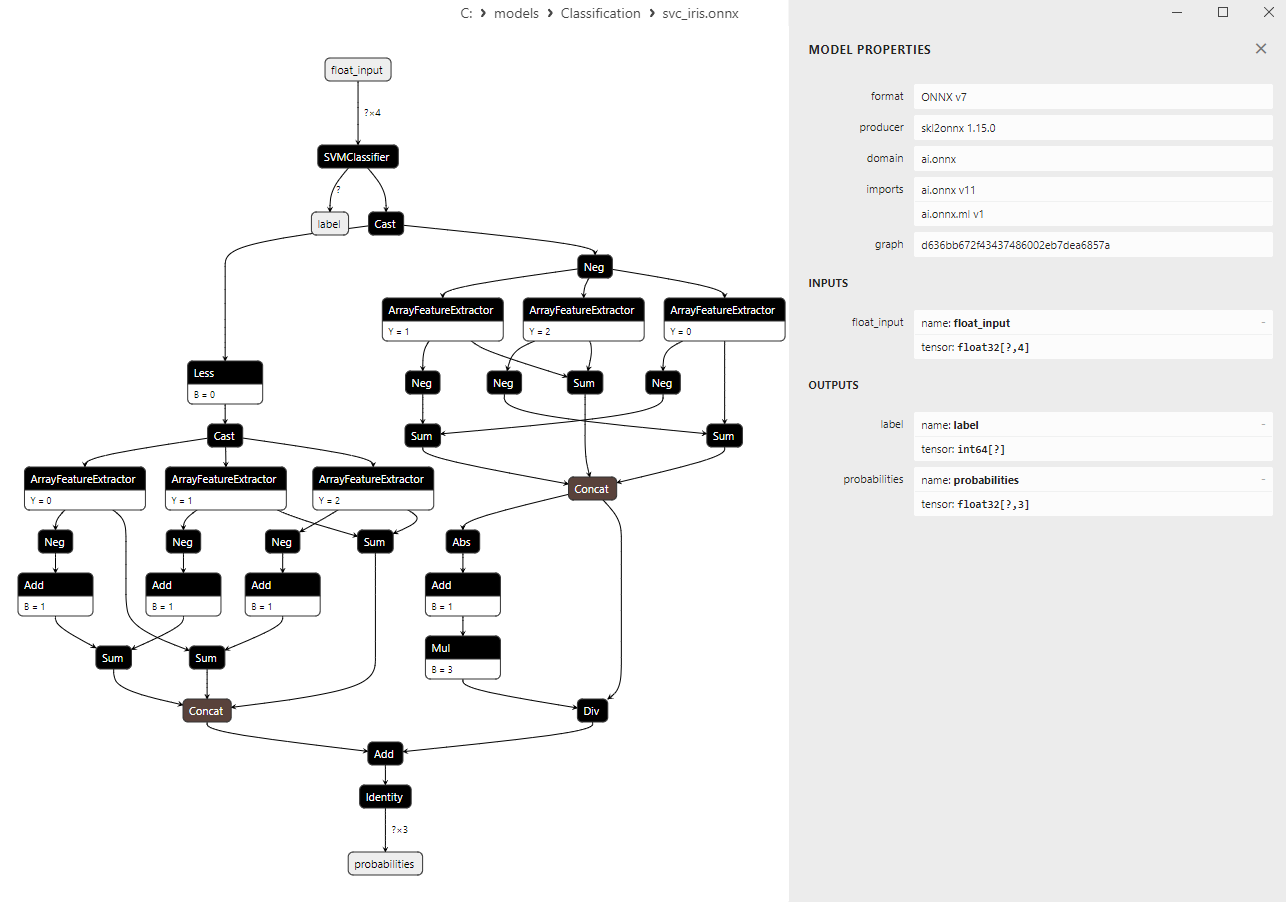
Abbildung 14. ONNX-Modell svc_iris.onnx in Netron
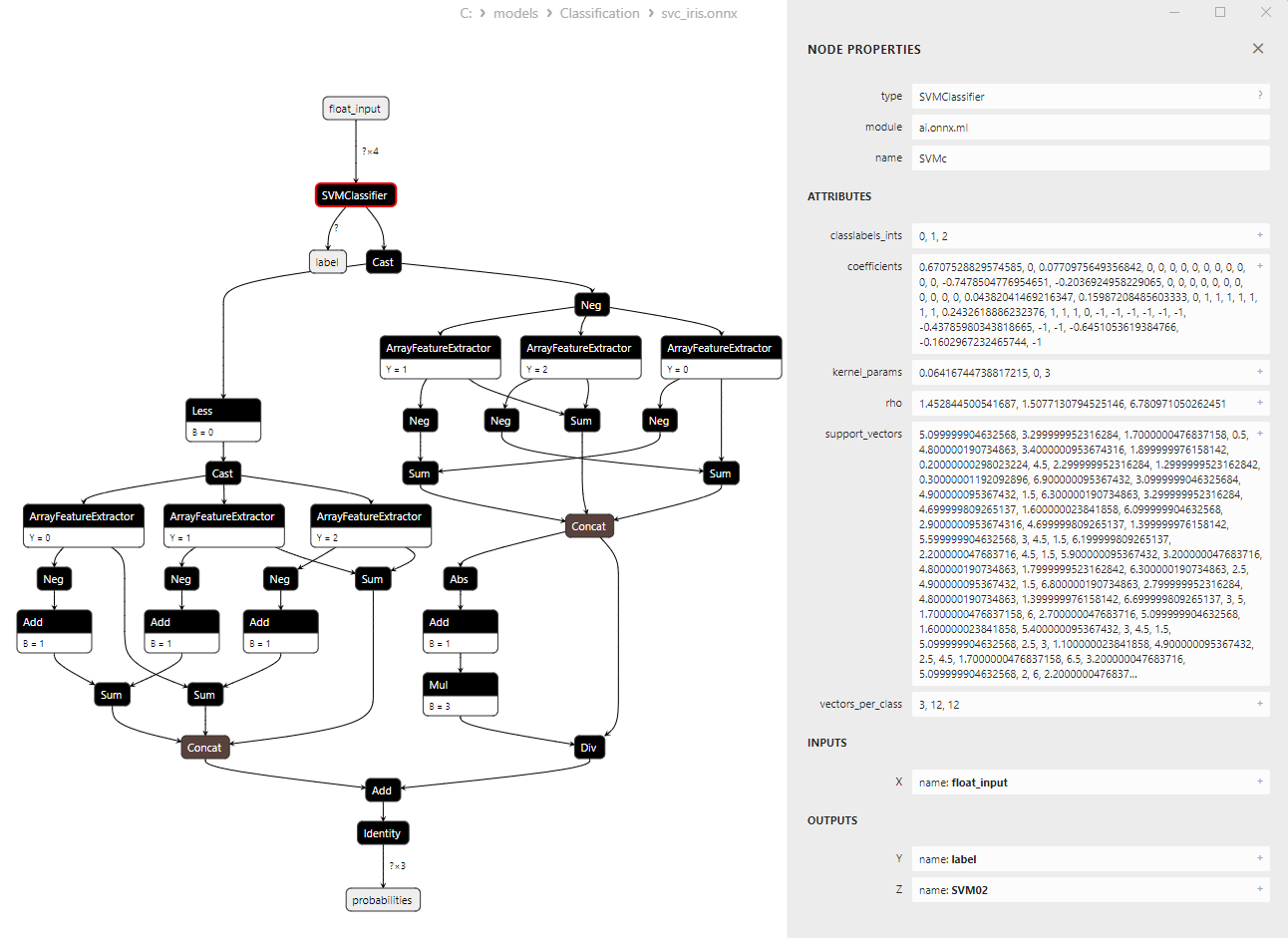
Abbildung 15. ONNX-Modell svc_iris.onnx in Netron (SVMClassifier ONNX-Operator-Parameter)
2.2. LinearSVC Classifier
LinearSVC (Linear Support Vector Classification) ist ein leistungsfähiger Algorithmus für maschinelles Lernen, der für binäre und Multiklassen-Klassifizierungsaufgaben verwendet wird. Es basiert auf der Idee, eine Hyperebene zu finden, die die Daten am besten trennt.
Grundsätze der LinearSVC:
- Suche nach der optimalen Hyperebene: Die Hauptidee von LinearSVC ist es, die optimale Hyperebene zu finden, die die beiden Datenklassen maximal trennt. Eine Hyperebene ist eine mehrdimensionale Ebene, die durch eine lineare Gleichung definiert ist.
- Einrückungen minimieren: LinearSVC zielt darauf ab, die Einrückungen (Abstände von Datenpunkten zur Hyperebene) zu minimieren. Je größer die Einrückungen sind, desto zuverlässiger trennt die Hyperebene die Klassen.
- Handhabung linear nicht trennbarer Daten: LinearSVC kann mit Daten arbeiten, die im ursprünglichen Merkmalsraum nicht linear getrennt werden können, dank der Verwendung von Kernel-Funktionen (Kernel-Trick), die die Daten in einen höherdimensionalen Raum projizieren, wo sie linear getrennt werden können.
Vorteile von LinearSVC:
- Gute Verallgemeinerung: LinearSVC hat eine gute Verallgemeinerungsfähigkeit und kann bei neuen, ungesehenen Daten gute Ergebnisse erzielen.
- Effizienz: LinearSVC arbeitet schnell mit großen Datensätzen und benötigt relativ wenig Rechenressourcen.
- Handhabung linear nicht trennbarer Daten: Mit Hilfe von Kernel-Funktionen kann LinearSVC Klassifizierungsaufgaben mit linear nicht trennbaren Daten lösen.
- Skalierbarkeit: LinearSVC kann bei Aufgaben mit einer großen Anzahl von Merkmalen und großen Datenmengen effizient eingesetzt werden.
Einschränkungen von LinearSVC:
- Nur linear trennende Hyperebenen: LinearSVC konstruiert nur lineare Trennebenen, was für komplexe Klassifikationsaufgaben mit nichtlinearen Abhängigkeiten unzureichend sein kann.
- Auswahl der Parameter: Die Wahl der richtigen Parameter (z. B. der Regularisierungsparameter) kann Expertenwissen oder eine Kreuzvalidierung erfordern.
- Empfindlichkeit gegenüber Ausreißern: LinearSVC kann empfindlich auf Ausreißer in den Daten reagieren, was die Klassifizierungsqualität beeinträchtigen kann.
- Interpretierbarkeit des Modells: Mit LinearSVC erstellte Modelle könnten im Vergleich zu einigen anderen Methoden weniger gut zu interpretieren sein.
LinearSVC ist ein leistungsstarker Klassifizierungsalgorithmus, der sich durch Verallgemeinerung, Effizienz und den Umgang mit linear nicht trennbaren Daten auszeichnet. Sie findet Anwendung bei verschiedenen Klassifizierungsaufgaben, insbesondere wenn Daten durch eine lineare Hyperebene getrennt werden können. Für komplexe Aufgaben, die die Modellierung nichtlinearer Abhängigkeiten erfordern, kann LinearSVC jedoch weniger geeignet sein, und in solchen Fällen sollten alternative Methoden mit komplexeren Entscheidungsgrenzen in Betracht gezogen werden.
2.2.1. Code für die Erstellung des Klassifizierungsmodells LinearSVC
Dieser Code veranschaulicht den Prozess des Trainings eines LinearSVC-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_LinearSVC.py # The code demonstrates the process of training LinearSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import LinearSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LinearSVC model linear_svc_model = LinearSVC(C=1.0, max_iter=10000) # train the model on the entire dataset linear_svc_model.fit(X, y) # predict classes for the entire dataset y_pred = linear_svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LinearSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(linear_svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "linear_svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LinearSVC model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of LinearSVC model: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
2.2.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell LinearSVC
//+------------------------------------------------------------------+ //| Iris_LinearSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "linear_svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LinearSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC correct results: 96.67% Iris_LinearSVC (EURUSD,H1) model=LinearSVC all samples accuracy=0.966667 Iris_LinearSVC (EURUSD,H1) model=LinearSVC batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 96,67 %, was der Genauigkeit des Originalmodells entspricht.
2.2.3. ONNX-Darstellung des Klassifizierungsmodells LinearSVC
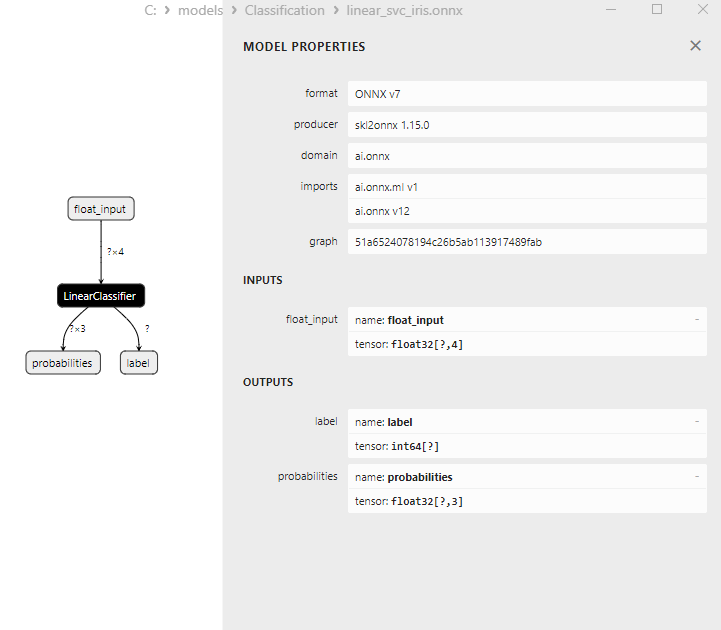
Abbildung 16. ONNX-Darstellung des Klassifizierungsmodells LinearSVC in Netron
2.3. NuSVC Classifier
Die Nu-Support Vector Classification (NuSVC)-Methode ist ein leistungsstarker Algorithmus für maschinelles Lernen, der auf dem Ansatz der Support Vector Machine (SVM) basiert.
Grundsätze der NuSVC:
- Support-Vektor-Maschine (SVM): NuSVC ist eine Variante der SVM, die für binäre und Mehrklassen-Klassifikationsaufgaben verwendet wird. Das Grundprinzip der SVM besteht darin, die optimale Trennhyperebene zu finden, die die Klassen maximal trennt und gleichzeitig den maximalen Spielraum beibehält.
- Der Nu-Parameter: Ein Schlüsselparameter in NuSVC ist der Nu-Parameter (nu), der die Komplexität des Modells steuert und den Anteil der Stichprobe definiert, der als Stützvektoren und Fehler verwendet werden kann. Der Wert von Nu reicht von 0 bis 1, wobei 0,5 bedeutet, dass etwa die Hälfte der Stichprobe als Stützvektoren und Fehler verwendet wird.
- Abstimmung der Parameter: Die Bestimmung der optimalen Werte für den Nu-Parameter und andere Hyperparameter kann eine Kreuzvalidierung und eine Suche nach den besten Werten in den Trainingsdaten erfordern.
- Kernel-Funktionen: NuSVC kann verschiedene Kernel-Funktionen verwenden, z. B. lineare, radiale Basisfunktion (RBF), Polynom und andere. Die Kernel-Funktion bestimmt, wie der Merkmalsraum transformiert wird, um die trennende Hyperebene zu finden.
Vorteile von NuSVC:
- Effizienz in hochdimensionalen Räumen: NuSVC kann effizient in hochdimensionalen Räumen arbeiten und eignet sich daher für Aufgaben mit einer großen Anzahl von Merkmalen.
- Robustheit gegenüber Ausreißern: SVM und insbesondere NuSVC sind aufgrund der Verwendung von Support-Vektoren robust gegenüber Ausreißern in den Daten.
- Kontrolle der Modellkomplexität: Der Nu-Parameter ermöglicht es, die Modellkomplexität zu steuern und ein Gleichgewicht zwischen Datenanpassung und Verallgemeinerung herzustellen.
- Gute Verallgemeinerung: Insbesondere SVM und NuSVC weisen eine gute Generalisierung auf, was zu einer ausgezeichneten Leistung bei neuen, zuvor ungesehenen Daten führt.
Einschränkungen von NuSVC:
- Ineffizienz bei großen Datenvolumina: NuSVC kann aufgrund der Rechenkomplexität ineffizient sein, wenn es auf großen Datenmengen trainiert wird.
- Parameterabstimmung erforderlich: Die Abstimmung der Nu-Parameter und der Kernel-Funktion kann Zeit und Rechenressourcen erfordern.
- Linearität der Kernel-Funktion: Die Effektivität von NuSVC kann in erheblichem Maße von der Wahl der Kernel-Funktion abhängen, und für einige Aufgaben kann es notwendig sein, mit verschiedenen Funktionen zu experimentieren.
- Interpretierbarkeit des Modells: SVM und NuSVC liefern hervorragende Ergebnisse, aber ihre Modelle können komplex zu interpretieren sein, insbesondere wenn nichtlineare Kernel verwendet werden.
Nu-Support Vector Classification (NuSVC) ist eine leistungsstarke Klassifizierungsmethode auf der Grundlage von SVM mit mehreren Vorteilen, darunter Robustheit gegenüber Ausreißern und gute Generalisierung. Ihre Effektivität hängt jedoch von der Wahl der Parameter und Kernel-Funktionen ab, und sie kann bei großen Datenmengen ineffizient sein. Es ist wichtig, die Parameter sorgfältig auszuwählen und die Methode an spezifische Klassifizierungsaufgaben anzupassen.
2.3.1. Code zur Erstellung des Klassifizierungsmodells von NuSVC
Dieser Code demonstriert den Prozess des Trainings eines NuSVC-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_NuSVC.py # The code demonstrates the process of training NuSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import NuSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a NuSVC model nusvc_model = NuSVC(nu=0.5, kernel='linear') # train the model on the entire dataset nusvc_model.fit(X, y) # predict classes for the entire dataset y_pred = nusvc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of NuSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(nusvc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "nusvc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of NuSVC model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of NuSVC model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of NuSVC model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of NuSVC model in ONNX format: 0.9733333333333334
2.3.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell NuSVC
//+------------------------------------------------------------------+ //| Iris_NuSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "nusvc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="NuSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_NuSVC (EURUSD,H1) model:NuSVC sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_NuSVC (EURUSD,H1) model:NuSVC correct results: 97.33% Iris_NuSVC (EURUSD,H1) model=NuSVC all samples accuracy=0.973333 Iris_NuSVC (EURUSD,H1) model=NuSVC batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 97,33 %, was der Genauigkeit des Originalmodells entspricht.
2.3.3. ONNX-Darstellung des Klassifizierungsmodells NuSVC
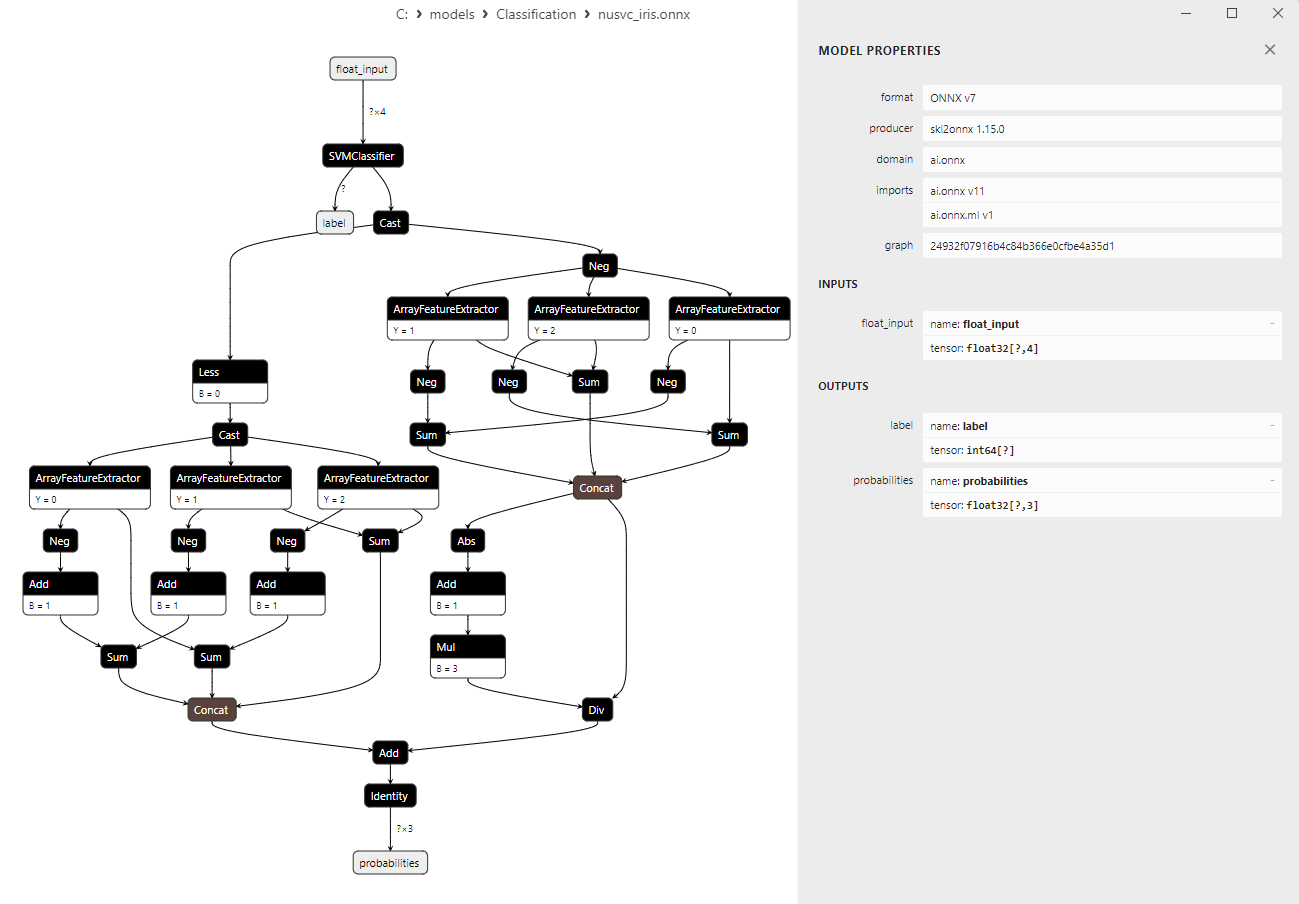
Abbildung 17. ONNX-Darstellung des Klassifizierungsmodells NuSVC in Netron
2.4. Radius Neighbors Classifier
Der Radius Neighbors Classifier (Radius der Nachbarn) ist ein maschinelles Lernverfahren, das für Klassifizierungsaufgaben verwendet wird, die auf dem Prinzip der Nähe zwischen Objekten basieren. Im Gegensatz zum klassischen K-Nearest Neighbors-Klassifikator (K-NN), bei dem eine feste Anzahl von nächsten Nachbarn (K) gewählt wird, werden beim Radius Neighbor-Klassifikator die Objekte auf der Grundlage der Entfernung zu den nächsten Nachbarn innerhalb eines bestimmten Radius klassifiziert.Grundsätze des Radius Neighbors:
- Bestimmung des Radius: Der wichtigste Parameter des Radius Neighbors Classifier ist der Radius, der den maximalen Abstand zwischen einem Objekt und seinen Nachbarn festlegt, damit es als nahe an der Klasse der Nachbarn angesehen wird.
- Suche nach den nächsten Nachbarn: Für jedes Objekt wird der Abstand zu allen anderen Objekten im Trainingsdatensatz berechnet. Die Objekte, die sich innerhalb des angegebenen Radius befinden, werden als Nachbarn des Objekts betrachtet.
- Abstimmung: Der Radius Neighbors Classifier verwendet die Mehrheitsentscheidung unter den Nachbarn, um die Klasse des Objekts zu bestimmen. Wenn zum Beispiel die Mehrheit der Nachbarn zur Klasse A gehört, wird das Objekt auch der Klasse A zugeordnet.
- Anpassungsfähigkeit an die Datendichte: Der Radius Neighbors Classifier eignet sich für Aufgaben, bei denen die Datendichte in verschiedenen Regionen des Merkmalsraums variieren kann.
- Fähigkeit, mit verschiedenen Klassenformen zu arbeiten: Diese Methode eignet sich gut für Aufgaben, bei denen die Klassen komplexe und nichtlineare Formen aufweisen.
- Geeignet für Daten mit Ausreißern: Der Radius Neighbors Classifier ist robuster gegenüber Ausreißern als K-NN, da er Nachbarn, die sich außerhalb des angegebenen Radius befinden, außer Acht lässt.
- Empfindlichkeit gegenüber der Wahl des Radius: Die Auswahl des optimalen Radiuswertes kann eine nicht triviale Aufgabe sein und erfordert eine Anpassung.
- Ineffizienz bei großen Datensätzen: Bei großen Datensätzen kann die Berechnung der Entfernungen zu allen Objekten sehr rechenintensiv sein.
- Abhängigkeit von der Datendichte: Diese Methode kann weniger effizient sein, wenn die Daten eine ungleichmäßige Dichte im Merkmalsraum aufweisen.
Der Radius Neighbors Classifier ist eine wertvolle Methode des maschinellen Lernens in Situationen, in denen die Nähe von Objekten wichtig ist und die Klassenformen komplex sein können. Sie kann in verschiedenen Bereichen eingesetzt werden, z. B. bei der Bildanalyse und der Verarbeitung natürlicher Sprache.
2.4.1. Code zur Erstellung des Klassifizierungsmodells von Radius Neighbor
Dieser Code veranschaulicht den Prozess des Trainings eines Radius Neighbors Klassifizierungsmodells mit dem Iris-Datensatz, den Export im ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_RadiusNeighborsClassifier.py # The code demonstrates the process of training an Radius Neughbors model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023 MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import RadiusNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Radius Neighbors Classifier model radius_model = RadiusNeighborsClassifier(radius=1.0) # train the model on the entire dataset radius_model.fit(X, y) # predict classes for the entire dataset y_pred = radius_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Radius Neighbors Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(radius_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "radius_neighbors_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Radius Neighbors Classifier model in ONNX format:", accuracy_onnx)
Ergebnisse des Skripts Iris_RadiusNeighbors.py:
Python Accuracy of Radius Neighbors Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
Die Genauigkeit des Originalmodells und die Genauigkeit des im ONNX-Format exportierten Modells sind identisch.
2.4.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Radius Neighbor
//+------------------------------------------------------------------+ //| Iris_RadiusNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "radius_neighbors_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RadiusNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier correct results: 97.33% Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier all samples accuracy=0.973333 Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier batch test accuracy=1.000000
Die Klassifizierung durch Radius Neighbors zeigte eine Genauigkeit von 97,33% mit 4 Klassifikationsfehlern (Proben 78, 107, 127 und 139).
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 97,33 % und entspricht damit der Genauigkeit des Originalmodells.
2.4.3.ONNX-Darstellung des Klassifizierungsmodells Radius Neighbor
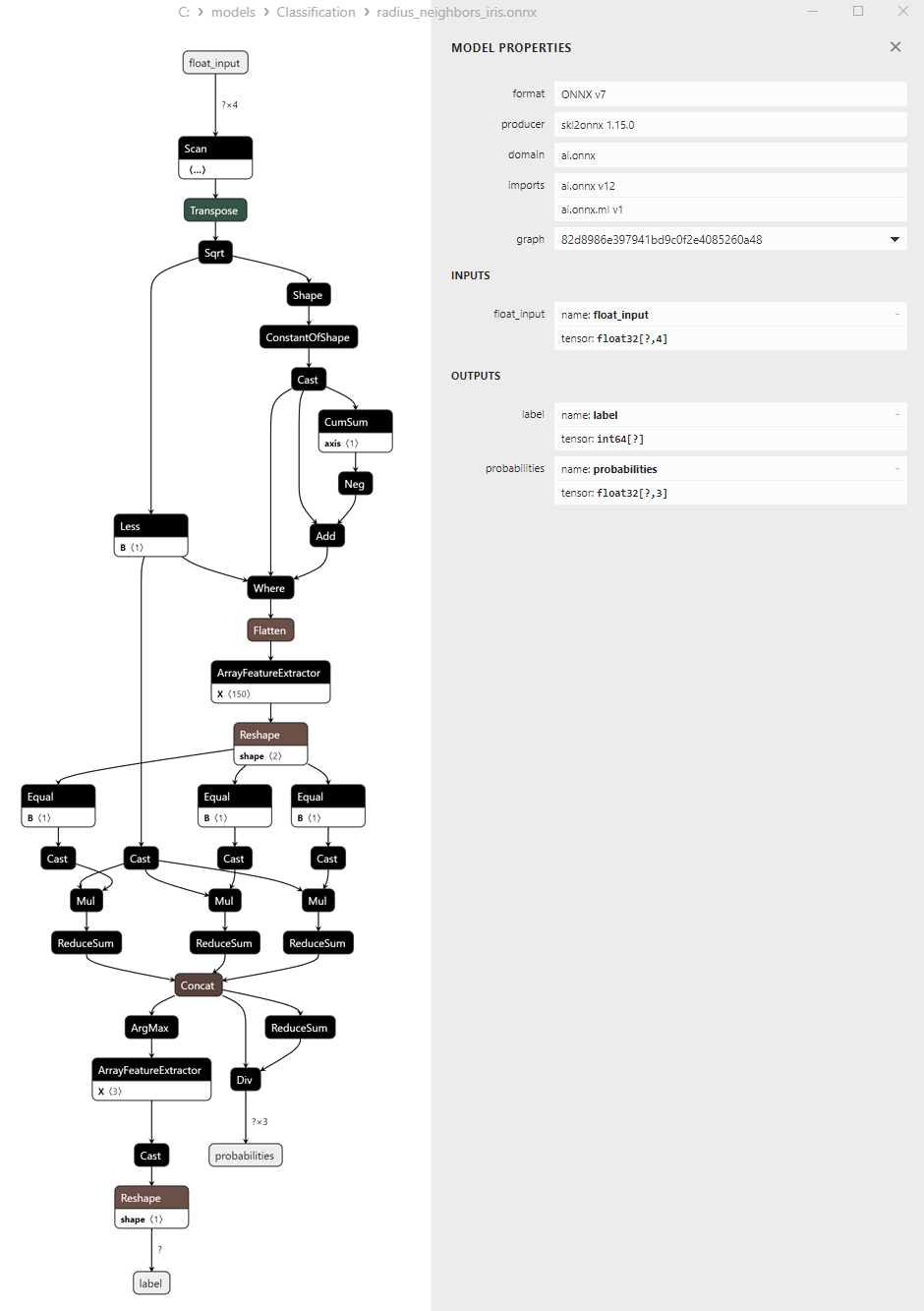
Abbildung 18. ONNX-Darstellung des Klassifizierungsmodells Radius Neighbor in Netron
Hinweis zu den Methoden RidgeClassifier und RidgeClassifierCV
RidgeClassifier und RidgeClassifierCV sind zwei Klassifizierungsmethoden, die auf der Ridge-Regression beruhen, sich aber in der Art und Weise unterscheiden, wie die Parameter abgestimmt und die Hyperparameter automatisch ausgewählt werden:
RidgeClassifier:
- RidgeClassifier ist eine auf Ridge-Regression basierende Klassifizierungsmethode, die für binäre und Multiklassen-Klassifizierungsaufgaben verwendet wird.
- Im Falle einer Multiklassenklassifizierung wandelt RidgeClassifier die Aufgabe in mehrere binäre Aufgaben um (eine vs. alle) und erstellt für jede ein Modell.
- Der Regularisierungsparameter Alpha muss vom Nutzer manuell eingestellt werden, d. h. Sie müssen den optimalen Alpha-Wert durch Experimente oder die Analyse von Validierungsdaten auswählen.
RidgeClassifierCV:
- RidgeClassifierCV ist eine Erweiterung von RidgeClassifier, die integrierte Unterstützung für Kreuzvalidierung und automatische Auswahl des optimalen Regularisierungsparameters Alpha bietet.
- Anstatt Alpha manuell zu setzen, können Sie RidgeClassifierCV eine Liste von Alpha-Werten zur Untersuchung übergeben und die Methode der Kreuzvalidierung angeben (z. B. über den Parameter cv).
- RidgeClassifierCV wählt automatisch den optimalen Alpha-Wert, der bei der Kreuzvalidierung am besten abschneidet.
Der Hauptunterschied zwischen ihnen liegt also im Grad der Automatisierung bei der Auswahl des optimalen Werts für den Regularisierungsparameter alpha. RidgeClassifier erfordert eine manuelle Einstellung von Alpha, während RidgeClassifierCV die automatische Auswahl des optimalen Alpha-Werts durch Kreuzvalidierung ermöglicht. Die Wahl zwischen beiden hängt von Ihren Bedürfnissen und Ihrem Wunsch nach Automatisierung des Modelloptimierungsprozesses ab.
2.5. Ridge Classifier
Der Ridge Classifier ist eine Variante der logistischen Regression, die eine L2-Regularisierung (Ridge Regression) in das Modell einschließt. Die L2-Regularisierung fügt den großen Koeffizienten des Modells einen Malus hinzu und hilft so, die Überanpassung zu reduzieren und die Generalisierungsfähigkeit des Modells zu verbessern.
Grundsätze des Ridge Classifiers:
- Vorhersage von Wahrscheinlichkeiten: Wie die Logistic Regression modelliert der Ridge Classifier die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu einer bestimmten Klasse anhand einer logistischen (sigmoiden) Funktion.
- L2-Regularisierung: Ridge Classifier fügt einen L2-Regularisierungsterm hinzu, der große Koeffizienten des Modells bestraft. Dies geschieht, um die Komplexität des Modells zu kontrollieren und eine Überanpassung zu vermeiden.
- Training der Parameter: Das Ridge Klassifizierungsmodell wird auf dem Trainingsdatensatz trainiert, um die Gewichte (Koeffizienten) für Merkmale und den Regularisierungsparameter anzupassen.
Vorteile des Ridge Classifiers:
- Reduzierung der Überanpassung: Die L2-Regularisierung trägt dazu bei, die Tendenz des Modells zur Überanpassung zu verringern, was besonders bei begrenzten Daten nützlich ist.
- Umgang mit Multikollinearität: Der Ridge Classifier kann gut mit Multikollinearitätsproblemen umgehen, bei denen die Merkmale stark miteinander korreliert sind.
Einschränkungen des Ridge Classifiers:
- Empfindlichkeit gegenüber der Wahl der Regularisierungsparameter: Wie bei anderen Regularisierungsmethoden ist es auch hier erforderlich, den richtigen Wert für den Regularisierungsparameter (Alpha) zu wählen und zu bewerten.
- Multiklassen-Klassifizierung Constraint: Ridge Classifier wurde ursprünglich für die binäre Klassifizierung entwickelt, kann aber mit Ansätzen wie One-vs-All an die Multiklassenklassifizierung angepasst werden.
Ridge Classifier ist eine leistungsstarke Methode des maschinellen Lernens, die die Vorteile der logistischen Regression mit einer Regularisierung kombiniert, um eine Überanpassung zu verhindern und die Generalisierungsfähigkeit des Modells zu verbessern. Sie findet Anwendung in verschiedenen Bereichen, in denen probabilistische Klassifizierung und Modellkomplexitätskontrolle wichtig sind.
2.5.1. Der Code zur Erstellung des Klassifizierungsmodells von Ridge
Dieser Code demonstriert den Prozess des Trainings des Ridge Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_RidgeClassifier.py # The code demonstrates the process of training Ridge Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Ridge Classifier model ridge_model = RidgeClassifier() # train the model on the entire dataset ridge_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Ridge Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Ridge Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Ridge Classifier model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Ridge Classifier model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Ridge Classifier model in ONNX format: 0.8533333333333334
2.5.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Ridge
//+------------------------------------------------------------------+ //| Iris_RidgeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier correct results: 85.33% Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier all samples accuracy=0.853333 Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier batch test accuracy=0.000000
Auf dem vollständigen Iris-Datensatz zeigte das Modell eine Genauigkeit von 85,33 %, was der Genauigkeit des Originals entspricht.
2.5.3. ONNX-Darstellung des Klassifizierungsmodells Ridge
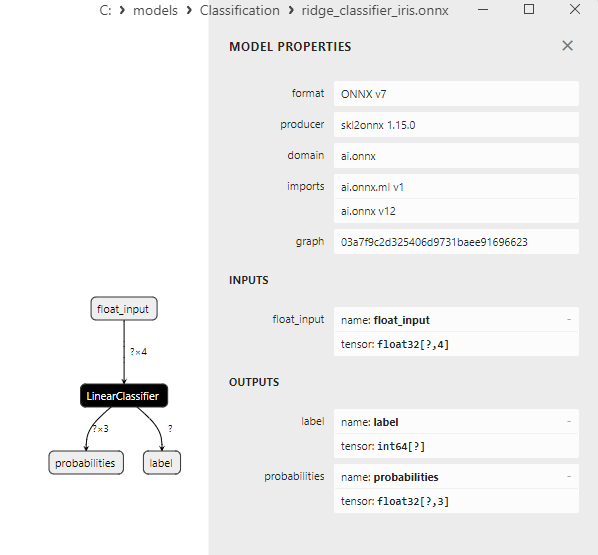
Abbildung 19. ONNX-Darstellung des Klassifizierungsmodells Ridge in Netron
2.6. RidgeClassifierCV
Die Klassifizierungsmethode RidgeClassifierCV ist ein leistungsstarker Algorithmus für die binäre und Multiklassenklassifizierung auf der Grundlage der Ridge-Regression.
Grundsätze von RidgeClassifierCV:
- Lineare Ridge-Regression: Der RidgeClassifierCV basiert auf der linearen Ridge-Regression. Diese Methode ist eine Modifikation der linearen Regression, bei der eine L2-Regularisierung hinzugefügt wird. Die Regularisierung hilft, die Überanpassung zu kontrollieren, indem sie die Größe der Merkmalsgewichte reduziert.
- Binäre und Multiklassen-Klassifizierung: RidgeClassifierCV kann sowohl für die binäre Klassifizierung (wenn es nur zwei Klassen gibt) als auch für die Multiklassenklassifizierung (wenn es mehr als zwei Klassen gibt) verwendet werden. Bei der Multiklassenklassifizierung wird die Aufgabe in mehrere binäre Aufgaben (eine gegen alle) umgewandelt und für jede ein Modell erstellt.
- Automatische Auswahl der Regularisierungsparameter: Einer der Hauptvorteile von RidgeClassifierCV ist die eingebaute Unterstützung für Kreuzvalidierung und die automatische Auswahl des optimalen Regularisierungsparameters Alpha. Anstatt Alpha manuell einzustellen, iteriert die Methode über verschiedene Alpha-Werte und wählt den besten auf der Grundlage einer Kreuzvalidierung aus.
- Umgang mit Multikollinearität: Die Ridge-Regression kann gut mit Multikollinearitätsproblemen umgehen, wenn die Merkmale stark miteinander korreliert sind. Die Regularisierung ermöglicht es, den Beitrag jedes Merkmals zu kontrollieren und macht das Modell robust gegenüber korrelierten Daten.
Vorteile von RidgeClassifierCV:
- Automatische Auswahl der Hyperparameter: Einer der wesentlichen Vorteile von RidgeClassifierCV ist seine Fähigkeit, automatisch den optimalen Alpha-Wert durch Kreuzvalidierung auszuwählen. Dadurch entfällt die Notwendigkeit, mit verschiedenen Alphawerten zu experimentieren, und die Wahrscheinlichkeit, dass gute Ergebnisse erzielt werden, steigt.
- Kontrolle der Überanpassung: Die von RidgeClassifierCV bereitgestellte L2-Regularisierung hilft bei der Kontrolle der Modellkomplexität und reduziert das Risiko einer Überanpassung. Dies ist besonders wichtig für Aufgaben mit begrenzten Daten.
- Transparenz und Interpretierbarkeit: RidgeClassifierCV bietet interpretierbare Merkmalsgewichte, die eine Analyse des Beitrags jedes Merkmals zu den Vorhersagen und Schlussfolgerungen zur Merkmalsbedeutung ermöglichen.
- Effizienz: Die Methode ist sehr effizient und kann auf große Datensätze angewendet werden.
Einschränkungen von RidgeClassifierCV:
- Linearität: RidgeClassifierCV geht von linearen Beziehungen zwischen Merkmalen und der Zielvariablen aus. Weisen die Daten starke nichtlineare Beziehungen auf, ist die Methode möglicherweise nicht genau genug.
- Empfindlichkeit der Merkmalsskalierung: Die Methode reagiert empfindlich auf die Skalierung der Merkmale. Es wird empfohlen, die Merkmale vor der Anwendung von RidgeClassifierCV zu standardisieren oder zu normalisieren.
- Optimale Auswahl der Merkmale: RidgeClassifierCV führt keine automatische Merkmalsauswahl durch, sodass Sie manuell entscheiden müssen, welche Merkmale in das Modell aufgenommen werden sollen.
Die RidgeClassifierCV-Klassifizierungsmethode ist ein leistungsfähiges Werkzeug für die binäre und Multiklassenklassifizierung mit automatischer Auswahl des optimalen Regularisierungsparameters. Die Kontrolle der Überanpassung, die Interpretierbarkeit und die Effizienz machen es zu einer beliebten Wahl für verschiedene Klassifizierungsaufgaben. Es ist jedoch wichtig, seine Grenzen zu beachten, insbesondere die Annahme linearer Beziehungen zwischen Merkmalen und der Zielvariablen.
2.6.1. Der Code zur Erstellung des Modells von RidgeClassifierCV
Dieser Code demonstriert den Prozess des Trainings des RidgeClassifierCV-Modells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_RidgeClassifierCV.py # The code demonstrates the process of training RidgeClassifierCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifierCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a RidgeClassifierCV model ridge_classifier_cv_model = RidgeClassifierCV() # train the model on the entire dataset ridge_classifier_cv_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_classifier_cv_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of RidgeClassifierCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_classifier_cv_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_cv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of RidgeClassifierCV model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of RidgeClassifierCV model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of RidgeClassifierCV model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of RidgeClassifierCV model in ONNX format: 0.8533333333333334
2.6.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell RidgeClassifierCV
//+------------------------------------------------------------------+ //| Iris_RidgeClassifierCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_cv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifierCV"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV correct results: 85.33% Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV all samples accuracy=0.853333 Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV batch test accuracy=0.000000
Die Leistung des ONNX-Modells entspricht auch perfekt der Leistung des ursprünglichen Scikit-Learn-Modells (85,33 %).
2.6.3. ONNX-Darstellung des Klassifizierungsmodells RidgeClassifierCV
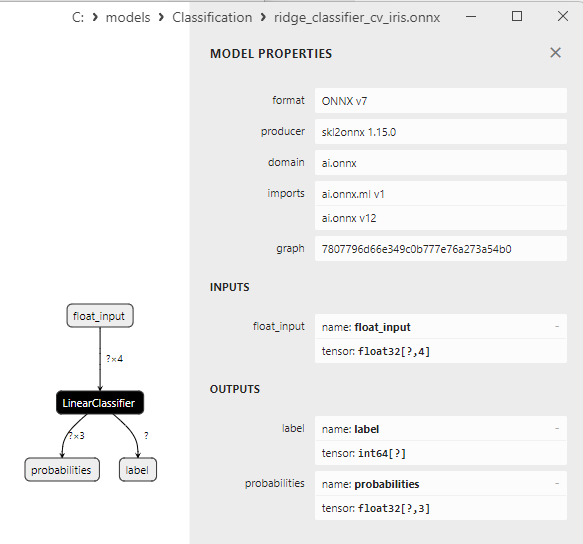
Abbildung 20. ONNX-Darstellung des Klassifizierungsmodells RidgeClassifierCV in Netron
2.7. Random Forest Classifier
Der Random Forest Classifier ist eine maschinelle Lernmethode, die auf der Konstruktion mehrerer Entscheidungsbäume (decision trees) und der Kombination ihrer Ergebnisse zur Verbesserung der Klassifizierungsqualität beruht. Diese Methode ist aufgrund ihrer Effizienz und ihrer Fähigkeit, mit unterschiedlichen Daten zu arbeiten, äußerst beliebt.
Prinzipien des Random Forest:
- Bagging (Bootstrap Aggregating): Random Forest verwendet die Bagging-Methode, bei der mehrere Teilstichproben (Bootstrap-Stichproben) aus den Trainingsdaten mit Ersetzung erstellt werden. Für jede Teilstichprobe wird ein eigener Entscheidungsbaum erstellt.
- Zufällige Auswahl von Merkmalen: Bei der Erstellung jedes Baums wird eine zufällige Teilmenge von Merkmalen aus dem gesamten Satz von Merkmalen ausgewählt. Dies fördert die Vielfalt unter den Bäumen und verringert die Korrelationen zwischen ihnen.
- Abstimmung: Bei der Klassifizierung eines Objekts gibt jeder Baum seine eigene Vorhersage ab, und die Klasse, die von allen Bäumen die meisten Stimmen erhält, wird als endgültige Modellvorhersage ausgewählt.
Vorteile des Random Fores:
- Hohe Genauigkeit: Random Forest erreicht in der Regel eine hohe Klassifizierungsgenauigkeit, indem er die Ergebnisse mehrerer Bäume mittelt.
- Fähigkeit zum Umgang mit unterschiedlichen Daten: Es funktioniert gut mit numerischen und kategorialen Merkmalen sowie mit Daten unterschiedlicher Struktur.
- Widerstand gegen Überanpassung: Random Forest verfügt über eine eingebaute Regularisierung, die ihn resistent gegen Überanpassung macht.
- Merkmal Wichtigkeit: Random Forest kann die Wichtigkeit von Merkmalen bewerten und so Datenwissenschaftlern und Merkmalstechnikern helfen, die Daten besser zu verstehen.
Einschränkungen des Random Forest:
- Berechnungskomplexität: Das Training eines Random Forest kann zeitaufwändig sein, insbesondere bei einer großen Anzahl von Bäumen und Merkmalen.
- Herausforderungen an die Interpretierbarkeit: Aufgrund der großen Anzahl von Bäumen und der zufälligen Auswahl der Merkmale kann die Interpretation des Modells schwierig sein.
- Keine garantierte Ausreißer-Robustheit: Random Forest bietet nicht immer Robustheit gegenüber Datenausreißern.
Der Random Forest Classifier ist ein leistungsfähiger Algorithmus für maschinelles Lernen, der in verschiedenen Bereichen wie Biomedizin, Finanzanalyse und Textdatenanalyse eingesetzt wird. Es eignet sich hervorragend zur Lösung von Klassifizierungs- und Regressionsaufgaben und hat eine hohe Generalisierungsfähigkeit.
2.7.1. Code für die Erstellung des Modells eines Random Forest Classifier
Dieser Code demonstriert den Prozess des Trainings des Random Forest Classifier Modells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_RandomForestClassifier.py # The code demonstrates the process of training Random Forest Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023,2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Random Forest Classifier model rf_model = RandomForestClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset rf_model.fit(X, y) # predict classes for the entire dataset y_pred = rf_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Random Forest Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(rf_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "rf_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Random Forest Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Random Forest Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
Das Klassifizierungsmodell Random Forest(und seine ONNX-Version) löst das Iris-Klassifizierungsproblem von Fisher mit 100%iger Genauigkeit.
2.7.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Random Forest
//+------------------------------------------------------------------+ //| Iris_RandomForestClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "rf_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RandomForestClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_RandomForestClassifier (EURUSD,H1) model:RandomForestClassifier correct results: 100.00% Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier all samples accuracy=1.000000 Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 100 % und entspricht damit der Genauigkeit des Originalmodells.
2.7.3. ONNX-Darstellung des Klassifizierungsmodells Random Forest
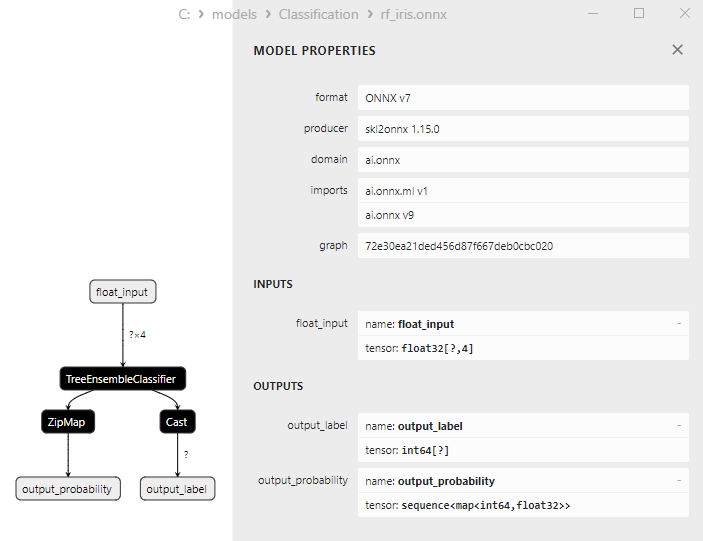
Abbildung 21. ONNX-Darstellung des Klassifizierungsmodells Random Forest Classifier Modells in Netron
2.8. Gradient Boosting Klassifikator
Gradient Boosting ist eine der leistungsfähigsten Methoden des maschinellen Lernens und findet dank seiner hohen Genauigkeit und seiner Fähigkeit, mit unterschiedlichen Daten zu arbeiten, in verschiedenen Bereichen Anwendung, darunter Datenanalyse, Computer Vision, Verarbeitung natürlicher Sprache und Finanzanalyse. Der Gradient Boosting Classifier (Gradientenverstärkung Klassifikator) ist eine maschinelle Lernmethode, die eine Komposition von Entscheidungsbäumen zur Lösung von Klassifizierungsaufgaben erstellt. Diese Methode ist wegen ihrer hohen Genauigkeit und ihrer Widerstandsfähigkeit gegen Überanpassung beliebt.
Prinzipien des Gradient Boosting:
- Ensemble von Entscheidungsbäumen: Der Gradient Boosting Classifier konstruiert ein Ensemble von Entscheidungsbäumen, wobei jeder Baum darauf abzielt, die Vorhersagen des vorherigen Baums zu verbessern.
- Gradientenabstieg: Beim Gradient Boosting wird die Verlustfunktion durch Gradientenabstieg optimiert. Es minimiert den Klassifikationsfehler, indem es den Gradienten der Verlustfunktion berechnet und die Vorhersagen auf der Grundlage dieses Gradienten aktualisiert.
- Baum-Gewichtung: Jeder Baum in der Zusammensetzung hat ein Gewicht, und am Ende werden die Vorhersagen aller Bäume unter Berücksichtigung ihrer Gewichte kombiniert.
Vorteile des Gradient Boosting:
- Hohe Genauigkeit: Der Gradient Boosting Classifier bietet in der Regel eine hohe Klassifizierungsgenauigkeit und ist eine der leistungsfähigsten Methoden des maschinellen Lernens.
- Widerstand gegen Überanpassung: Dank der Verwendung von Regularisierung und Gradientenabstieg ist diese Methode resistent gegen Überanpassung, insbesondere bei der Abstimmung der Hyperparameter.
- Fähigkeit, mit verschiedenen Datentypen zu arbeiten: Der Gradient Boosting Classifier kann verschiedene Datentypen verarbeiten, darunter numerische und kategoriale Merkmale.
Einschränkungen des Gradient Boosting:
- Berechnungskomplexität: Das Training des Gradient-Boosting-Klassifikators kann rechenintensiv sein, insbesondere bei einer großen Anzahl von Bäumen oder tiefen Bäumen.
- Herausforderungen an die Interpretierbarkeit: Aufgrund der Komplexität der Zusammensetzung mehrerer Bäume kann die Interpretation der Ergebnisse schwierig sein.
- Nicht immer für kleine Datensätze geeignet: Gradient Boosting erfordert in der Regel eine beträchtliche Menge an Daten für einen effektiven Betrieb und kann bei kleinen Datensätzen zu einer Überanpassung führen.
Der Gradient-Boosting-Klassifikator ist eine leistungsstarke Methode des maschinellen Lernens, die häufig in Datenanalyse-Wettbewerben eingesetzt wird und verschiedene Klassifizierungsaufgaben effektiv löst. Es kann komplexe nichtlineare Beziehungen in Daten entdecken und zeigt eine gute Generalisierung, wenn die Hyperparameter richtig eingestellt sind.
2.8.1. Der Code zur Erstellung des Klassifizierungsmodells von Gradient Boosting
Dieser Code veranschaulicht den Prozess des Trainings des Gradient Boosting Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_GradientBoostingClassifier.py # The code demonstrates the process of training Gradient Boostring Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import GradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gradient Boosting Classifier model gb_model = GradientBoostingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset gb_model.fit(X, y) # predict classes for the entire dataset y_pred = gb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 100 % und entspricht damit der Genauigkeit des Originalmodells.
2.8.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Gradient Boostingl
//+------------------------------------------------------------------+ //| Iris_GradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_GradientBoostingClassifier (EURUSD,H1) model:GradientBoostingClassifier correct results: 100.00% Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier all samples accuracy=1.000000 Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 100 % und entspricht damit der Genauigkeit des Originalmodells.
2.8.3. ONNX-Darstellung des Klassifizierungsmodells Gradient Boosting
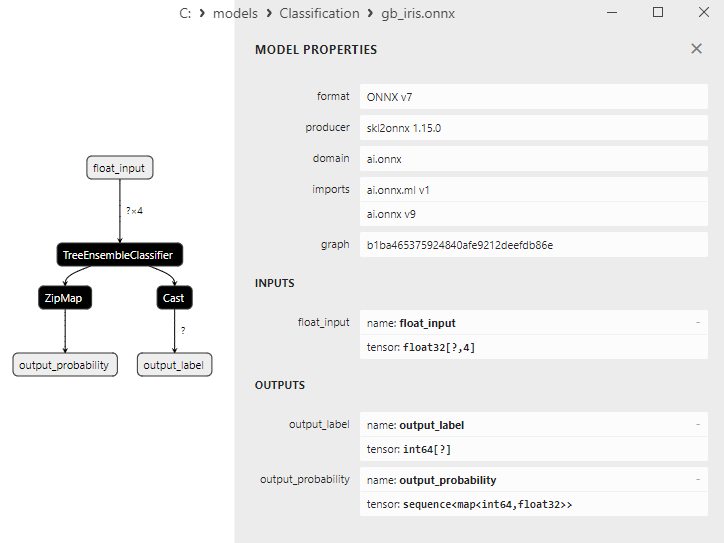
Abbildung 22. ONNX-Darstellung des Klassifizierungsmodells Gradient Boosting in Netron
2.9. Adaptive Boosting Classifier
Der AdaBoost (Adaptive Boosting) Klassifikator ist eine Methode des maschinellen Lernens, die zur Verbesserung der Klassifizierung verwendet wird, indem die Ergebnisse mehrerer schwacher Klassifikatoren (z. B. Entscheidungsbäume) kombiniert werden, um einen stärkeren Algorithmus zu schaffen.
Grundsätze des AdaBoost-Klassifikators:
- Ensemble von schwachen Klassifikatoren: AdaBoost beginnt mit der Initialisierung der Gewichte jeder Probe in der Trainingsmenge, wobei ihnen gleiche Anfangswerte zugewiesen werden.
- Training schwacher Klassifikatoren: AdaBoost trainiert dann einen schwachen Klassifikator (z. B. einen Decision Tree) auf der Trainingsmenge unter Berücksichtigung der Probengewichte. Dieser Klassifikator versucht, die Proben korrekt zu klassifizieren.
- Gewichtsumverteilung: AdaBoost passt die Gewichte der Proben an, indem es die Gewichte der falsch klassifizierten Proben erhöht und die Gewichte der richtig klassifizierten Proben verringert.
- Erstellung der Komposition: AdaBoost wiederholt den Prozess des Trainings schwacher Klassifikatoren und der Neuverteilung der Gewichte mehrfach. Die Ergebnisse dieser schwachen Klassifikatoren werden dann zu einer Komposition kombiniert, wobei jeder Klassifikator entsprechend seiner Genauigkeit beiträgt.
Vorteile des AdaBoost-Klassifikators:
- Hohe Genauigkeit: AdaBoost bietet in der Regel eine hohe Klassifizierungsgenauigkeit durch die Kombination mehrerer schwacher Klassifikatoren.
- Widerstand gegen Überanpassung: AdaBoost verfügt über eine eingebaute Regularisierung, die es resistent gegen Überanpassung macht.
- Fähigkeit, mit verschiedenen Klassifikatoren zu arbeiten: AdaBoost kann verschiedene Basisklassifikatoren verwenden, die eine Anpassung an spezifische Aufgaben ermöglichen.
Einschränkungen des AdaBoost-Klassifikators:
- Empfindlichkeit gegenüber Ausreißern: AdaBoost kann empfindlich auf Ausreißer in den Daten reagieren, da diese ein erhebliches Gewicht haben können.
- Nicht immer für komplexe Aufgaben geeignet: Bei einigen komplexen Aufgaben kann AdaBoost eine große Anzahl von Basisklassifikatoren erfordern, um gute Ergebnisse zu erzielen.
- Abhängigkeit von der Qualität der Basisklassifikatoren: AdaBoost schneidet besser ab, wenn die Basisklassifikatoren besser sind als zufälliges Raten.
AdaBoost Classifier ist ein leistungsstarker Algorithmus für maschinelles Lernen, der in der Praxis häufig zur Lösung von Klassifizierungsaufgaben eingesetzt wird. Es eignet sich sowohl für binäre als auch für Mehrklassenprobleme und kann an verschiedene Basisklassifikatoren angepasst werden.
2.9.1. Codeerstellung für den Adaptive Boosting Classifier
Dieser Code demonstriert den Prozess des Trainings des Adaptive Boosting Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_AdaBoostClassifier.py # The code demonstrates the process of training AdaBoost Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import AdaBoostClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an AdaBoost Classifier model adaboost_model = AdaBoostClassifier(n_estimators=50, random_state=42) # train the model on the entire dataset adaboost_model.fit(X, y) # predict classes for the entire dataset y_pred = adaboost_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of AdaBoost Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(adaboost_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "adaboost_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of AdaBoost Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of AdaBoost Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
2.9.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Adaptive Boostingl
//+------------------------------------------------------------------+ //| Iris_AdaBoostClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "adaboost_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="AdaBoostClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier correct results: 96.00% Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier all samples accuracy=0.960000 Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 96 %, was der Genauigkeit des Originalmodells entspricht.
2.9.3. ONNX-Darstellung des Klassifizierungsmodells Adaptive Boosting
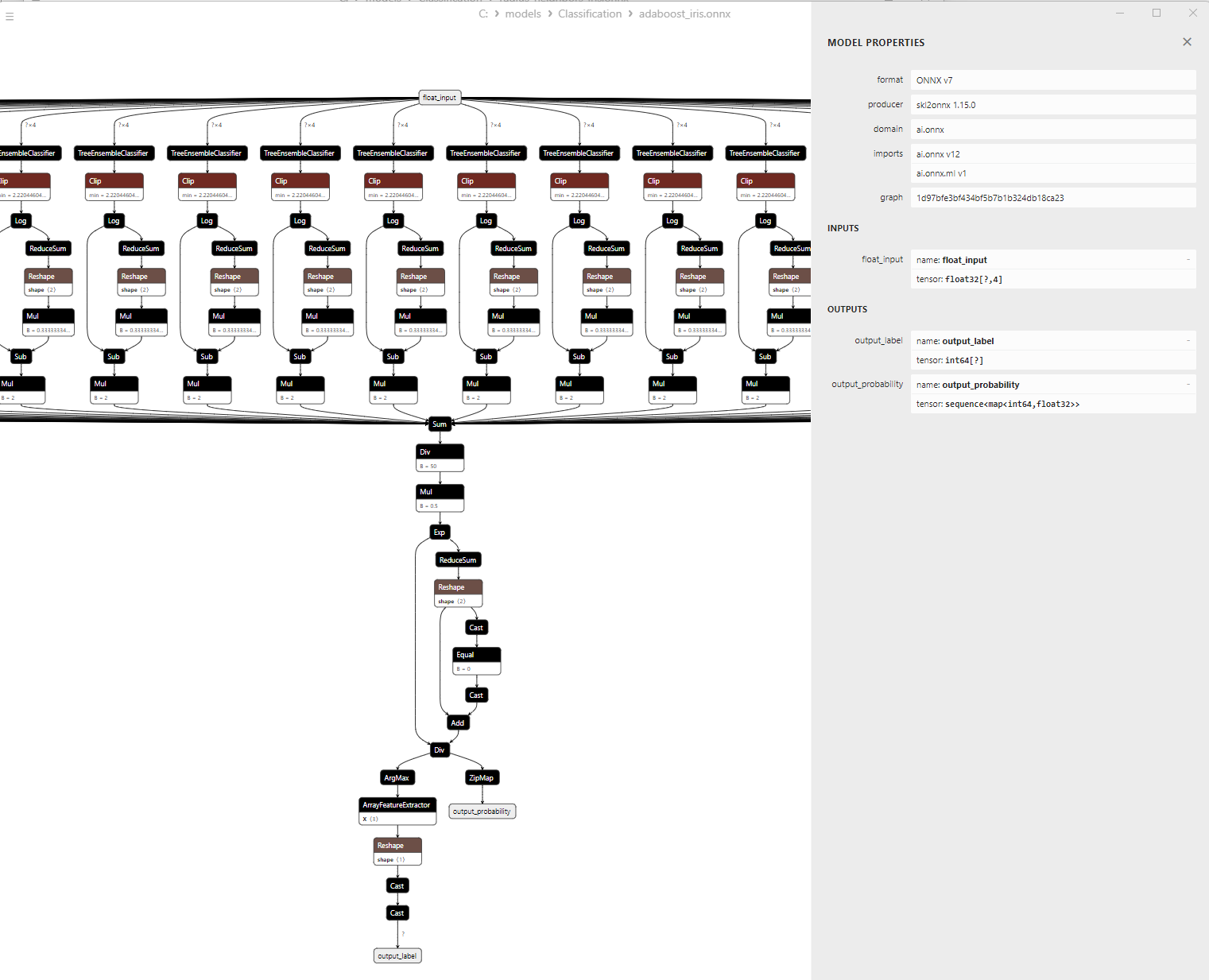
Abbildung 23. ONNX-Darstellung des Klassifizierungsmodells Adaptive Boosting Classifier in Netron
2.10. Bootstrap Aggregating Classifier
Der Bagging-Klassifikator (Bootstrap Aggregating Classifier) ist eine Ensemble-Methode des maschinellen Lernens, die auf der Erstellung mehrerer zufälliger Teilstichproben (Bootstrap-Stichproben) aus den Trainingsdaten und der Erstellung separater Modelle für jede dieser Teilstichproben beruht. Die Ergebnisse werden dann kombiniert, um die Generalisierungsfähigkeit des Modells zu verbessern.
Grundsätze des Bagging-Klassifikators:
- Erstellen von Teilstichproben: Beim Bagging werden zunächst mehrere zufällige Teilstichproben (Bootstrap-Stichproben) aus den Trainingsdaten mit Ersetzung erstellt. Das bedeutet, dass dieselben Proben in mehreren Teilstichproben vorkommen können und dass einige Proben ausgelassen werden können.
- Training von Basismodellen: Für jede Teilstichprobe wird ein eigenes Basismodell (z. B. ein Decision Tree) trainiert. Jedes Modell wird unabhängig von den anderen trainiert.
- Aggregation der Ergebnisse: Nachdem alle Basismodelle trainiert wurden, werden die Ergebnisse ihrer Vorhersagen kombiniert, um die endgültige Vorhersage zu erhalten. Bei der binären Klassifizierung kann dies durch Mehrheitsentscheidungen geschehen.
Vorteile des Bagging Classifiers:
- Reduzierte Varianz: Das Bagging reduziert die Varianz des Modells, indem es die Ergebnisse mehrerer Basismodelle mittelt, was zu stabileren und zuverlässigeren Vorhersagen führen kann.
- Reduzierung der Überanpassung: Da jedes Basismodell auf verschiedenen Teilstichproben trainiert wird, kann Bagging die Tendenz des Modells zur Überanpassung verringern.
- Vielseitigkeit: Beim Bagging können verschiedene Basismodelle verwendet werden, die eine Anpassung an unterschiedliche Datentypen und Aufgaben ermöglichen.\
Einschränkungen des Bagging-Klassifikators:
- Verbessert die Voreingenommenheit nicht: Durch Bagging wird die Varianz verringert, aber die Verzerrung des Modells wird nicht behoben. Wenn die Basismodelle dazu neigen, verzerrt zu sein (z. B. unzureichend trainiert), wird Bagging dieses Problem nicht korrigieren.
- Nicht immer für komplexe Aufgaben geeignet: Bei einigen komplexen Aufgaben kann das Bagging eine große Anzahl von Basismodellen erfordern, um gute Ergebnisse zu erzielen.
Bagging Classifier ist eine effektive Methode des maschinellen Lernens, die die Generalisierungsfähigkeit des Modells verbessern und die Überanpassung reduzieren kann. Es wird häufig in Kombination mit verschiedenen Basismodellen verwendet, um verschiedene Klassifizierungs- und Regressionsaufgaben zu lösen.
2.10.1. Code für die Erstellung des Model von Bootstrap Aggregating Classifier Model
Dieser Code demonstriert den Prozess des Trainings des Klassifizierungsmodells von Bootstrap Aggregating mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_BootstrapAggregatingClassifier.py # The code demonstrates the process of training Bagging Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import BaggingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bagging Classifier model with a Decision Tree base estimator bagging_model = BaggingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset bagging_model.fit(X, y) # predict classes for the entire dataset y_pred = bagging_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bagging Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bagging_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bagging_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bagging Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Bagging Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
Das Klassifizierungsmodell von Bootstrap Aggregating (und seine ONNX-Version) erreichte eine 100%ige Genauigkeit bei der Klassifizierung des Iris-Datensatzes.
2.10.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Bootstrap Aggregating
//+------------------------------------------------------------------+ //| Iris_BootstrapAggregatingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bagging_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BootstrapAggregatingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_BootstrapAggregatingClassifier (EURUSD,H1) model:BootstrapAggregatingClassifier correct results: 100.00% Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier all samples accuracy=1.000000 Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 100 %, was mit der Genauigkeit des ursprünglichen Modells übereinstimmt.
2.10.3. ONNX-Darstellung des Klassifizierungsmodells Bootstrap Aggregating
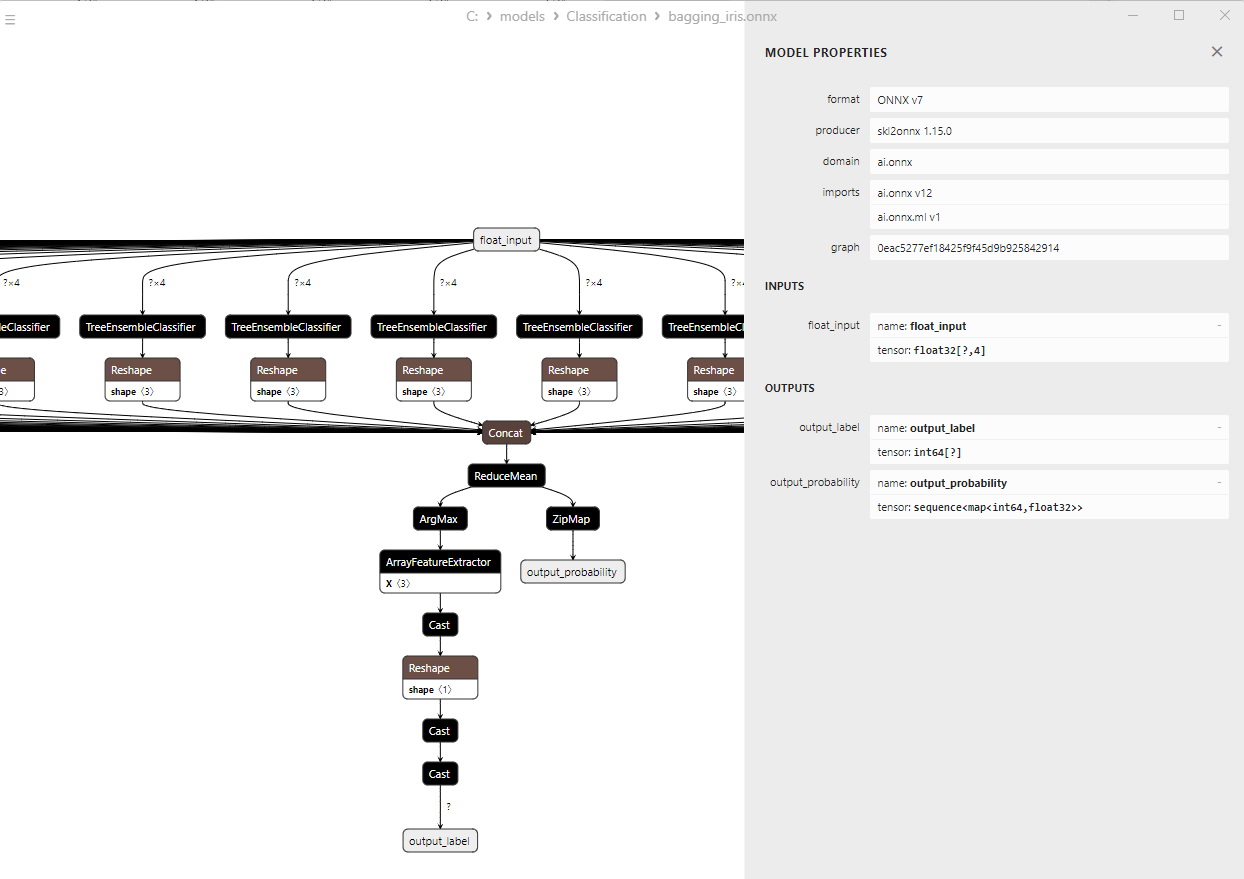
Abbildung 24. ONNX-Darstellung des Klassifizierungsmodells Bootstrap Aggregating in Netron
2.11. K-Nearest Neighbors (K-NN) Classifier
K-Nearest Neighbors (K-NN) Klassifikator ist eine Methode des maschinellen Lernens, die zur Lösung von Klassifizierungs- und Regressionsaufgaben auf der Grundlage der Ähnlichkeit zwischen Datenpunkten verwendet wird. Es beruht auf dem Prinzip, dass Objekte, die in einem mehrdimensionalen Merkmalsraum nahe beieinander liegen, ähnliche Merkmale aufweisen und daher auch ähnliche Klassenbezeichnungen haben können.
Grundsätze des K-NN-Klassifikators:
- Bestimmung der Nähe: Der K-NN-Klassifikator berechnet die Nähe zwischen dem zu klassifizierenden Objekt und anderen Objekten im Trainingsdatensatz. Dazu wird häufig eine Abstandsmetrik verwendet, z. B. der euklidische Abstand oder der Manhattan-Abstand.
- Auswahl der Anzahl der Nachbarn: Der Parameter K bestimmt die Anzahl der nächsten Nachbarn, die für die Klassifizierung eines Objekts verwendet werden. In der Regel wird K auf der Grundlage der Aufgabe und der Daten gewählt.
- Abstimmung: K-NN verwendet eine Mehrheitsentscheidung unter den K nächsten Nachbarn, um die Klasse des Objekts zu bestimmen. Wenn zum Beispiel die Mehrheit der K Nachbarn zur Klasse A gehört, wird das Objekt auch als Klasse A eingestuft.
Vorteile des K-NN-Klassifikators:
- Einfachheit und Intuitivität: K-NN ist eine einfache und intuitive Methode, die leicht zu verstehen und anzuwenden ist.
- Fähigkeit, mit verschiedenen Datentypen zu arbeiten: K-NN kann für verschiedene Datentypen verwendet werden, darunter numerische, kategoriale und Textdaten.
- Anpassungsfähigkeit an sich ändernde Daten: K-NN kann sich schnell an Veränderungen in den Daten anpassen und eignet sich daher für Aufgaben mit dynamischen Daten.
Einschränkungen des K-NN-Klassifikators:
- Empfindlichkeit gegenüber der Wahl von K: Die Auswahl des optimalen K-Wertes kann eine nicht triviale Aufgabe sein. Ein kleines K kann zu einer Überanpassung führen, während ein großes K zu einer Unteranpassung führen kann.
- Empfindlichkeit gegenüber der Skalierung von Merkmalen: K-NN reagiert empfindlich auf die Skalierung von Merkmalen, sodass eine Normalisierung der Daten wichtig sein kann.
- Berechnungskomplexität: Bei großen Datensätzen und einer hohen Anzahl von Merkmalen kann die Berechnung von Entfernungen zwischen allen Objektpaaren sehr rechenintensiv sein.
- Mangelnde Interpretierbarkeit: K-NN-Ergebnisse können schwierig zu interpretieren sein, vor allem wenn K groß ist und es viele Daten gibt.
Der K-NN-Klassifikator ist eine Methode des maschinellen Lernens, die bei Aufgaben nützlich sein kann, bei denen die Objektnähe von entscheidender Bedeutung ist, z. B. bei Empfehlungssystemen, Textklassifizierung und Mustererkennung. Es eignet sich gut für erste Datenanalysen und die schnelle Erstellung von Modellprototypen.
2.11.1. K-Nearest Neighbors (K-NN) Klassifikator Modellerstellungscode
Dieser Code demonstriert den Prozess des Trainings eines K-Nearest Neighbors (K-NN)-Klassifizierungsmodells mit dem Iris-Datensatz, den Export im ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_KNearestNeighborsClassifier.py # The code uses the K-Nearest Neighbors (KNN) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a K-Nearest Neighbors (KNN) Classifier model knn_model = KNeighborsClassifier(n_neighbors=3) # train the model on the entire dataset knn_model.fit(X, y) # predict classes for the entire dataset y_pred = knn_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of KNN Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(knn_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "knn_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of KNN Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of KNN Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
2.11.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell K-Nächste-Nachbarn (K-NN)
//+------------------------------------------------------------------+ //| Iris_KNearestNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "knn_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="KNearestNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier correct results: 96.00% Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier all samples accuracy=0.960000 Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 96 %, was mit der Genauigkeit des ursprünglichen Modells übereinstimmt.
2.11.3. ONNX-Darstellung des Klassifizierungsmodells K-Nächste-Nachbarn (K-NN)
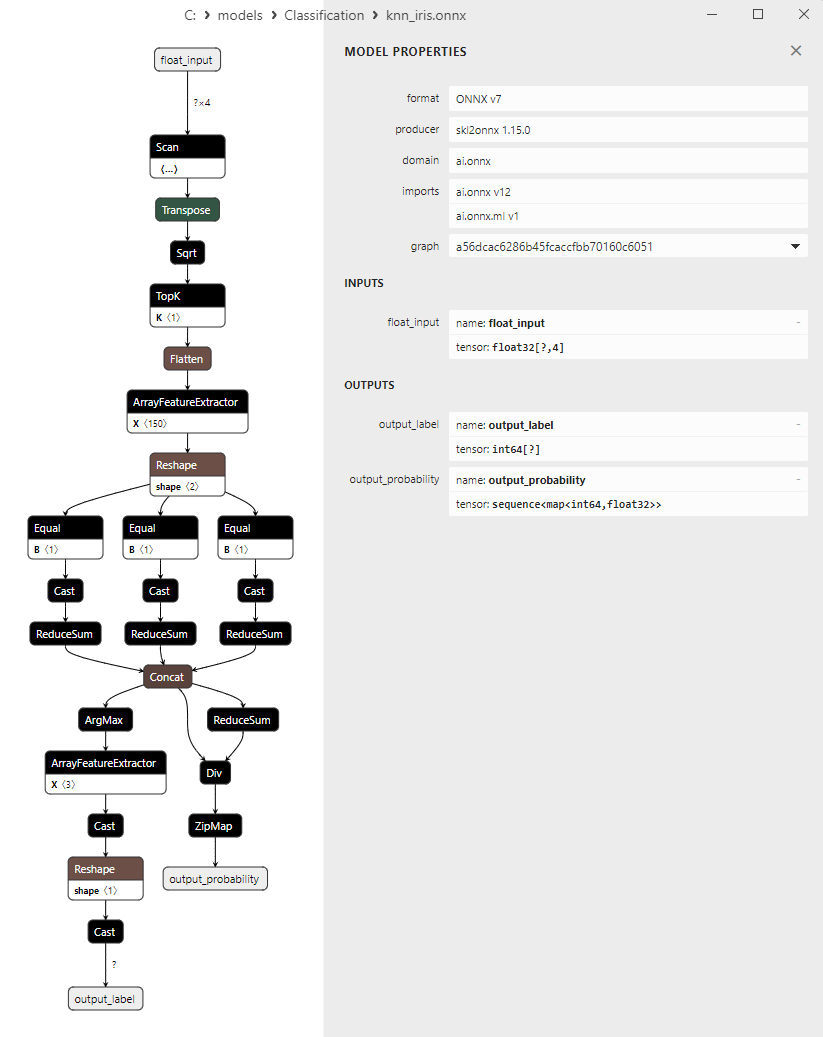
Abbildung 25. ONNX-Darstellung der K-Nächsten Nachbarn in Netron
2.12. Decision Tree Classifier
Der Decision Tree-Klassifikator ist eine maschinelle Lernmethode, die für Klassifizierungsaufgaben verwendet wird und auf der Konstruktion eines Entscheidungsbaums (Decision Tree) basiert. Diese Methode unterteilt den Datensatz in kleinere Untergruppen, indem sie eine Reihe von bedingten Tests auf Merkmale durchführt und die Klasse eines Objekts auf der Grundlage des Pfads des Baumes bestimmt
Prinzipien des Decision Tree-Klassifikators:
- Aufbau des Entscheidungsbaums: Zu Beginn werden alle Daten an der Wurzel des Baums dargestellt. Für jeden Knoten des Baums werden die Daten auf der Grundlage der Werte eines Merkmals in zwei oder mehr Untergruppen aufgeteilt, wobei versucht wird, die Unsicherheit (z. B. Entropie oder Gini-Index) in jeder Untergruppe zu minimieren.
- Rekursive Konstruktion: Der Prozess der Datenaufteilung wird rekursiv durchgeführt, bis der Baum seine Blätter erreicht. Die Blätter stellen die endgültigen Klassen von Objekten dar.
- Entscheidungsfindung: Wenn ein Objekt den Baum betritt, folgt es einem Pfad von der Wurzel zu einem der Blätter, wo seine Klasse auf der Grundlage der Mehrheit der Objekte in diesem Blatt bestimmt wird.
Vorteile des Entscheidungsbaums:
- Interpretierbarkeit: Entscheidungsbäume sind leicht zu interpretieren und zu visualisieren. Die für die Klassifizierung verwendeten Entscheidungsregeln sind verständlich.
- Handhabung verschiedener Datentypen: Der Entscheidungsbaum-Klassifikator kann sowohl mit numerischen als auch mit kategorialen Merkmalen arbeiten.
- Bedeutung der Funktion: Entscheidungsbäume können die Bedeutung von Merkmalen bewerten und so Datenanalysten und Merkmalstechnikern helfen, die Daten zu verstehen.
Einschränkungen der Entscheidungsbäume:
- Überanpassung: Große und tiefe Bäume können zu einer Überanpassung neigen, was ihre Verallgemeinerbarkeit für neue Daten verringert.
- Empfindlichkeit gegenüber Rauschen: Entscheidungsbäume können empfindlich auf Rauschen und Ausreißer in den Daten reagieren.
- Gierige Konstruktion: Entscheidungsbäume werden mit einem gierigen Algorithmus erstellt, der zu suboptimalen Gesamtlösungen führen kann.
- Instabilität bei Datenänderungen: Geringfügige Änderungen in den Daten können zu erheblichen Änderungen in der Baumstruktur führen.
Der Entscheidungsbaum-Klassifikator ist eine nützliche Methode des maschinellen Lernens für Klassifizierungsaufgaben, insbesondere in Situationen, in denen die Interpretierbarkeit des Modells wichtig ist und Sie verstehen müssen, welche Merkmale die Entscheidung beeinflussen. Diese Methode kann auch in Ensemble-Methoden wie Random Forest und Gradient Boosting verwendet werden.
2.12.1. Code für die Erstellung des Klassifizierungsmodells von Entscheidungsbäume
Dieser Code veranschaulicht den Prozess des Trainings eines Entscheidungsbaum-Klassifizierungsmodells mit dem Iris-Datensatz, den Export im ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_DecisionTreeClassifier.py # The code uses the Decision Tree Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Decision Tree Classifier model decision_tree_model = DecisionTreeClassifier(random_state=42) # train the model on the entire dataset decision_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = decision_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Decision Tree Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(decision_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "decision_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Decision Tree Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Decision Tree Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
Das Entscheidungsbaum-Klassifizierungsmodell (und seine ONNX-Version) zeigte eine 100%ige Genauigkeit bei der Klassifizierung des gesamten Fisher-Iris-Datensatzes.
2.12.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Entscheidungsbaum
//+------------------------------------------------------------------+ //| Iris_DecisionTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "decision_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="DecisionTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_DecisionTreeClassifier (EURUSD,H1) model:DecisionTreeClassifier correct results: 100.00% Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier all samples accuracy=1.000000 Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells für den gesamten Iris-Datensatz beträgt 100 % und entspricht damit der Genauigkeit des Originalmodells.
2.12.3. ONNX-Darstellung des Klassifizierungsmodells Entscheidungsbaum
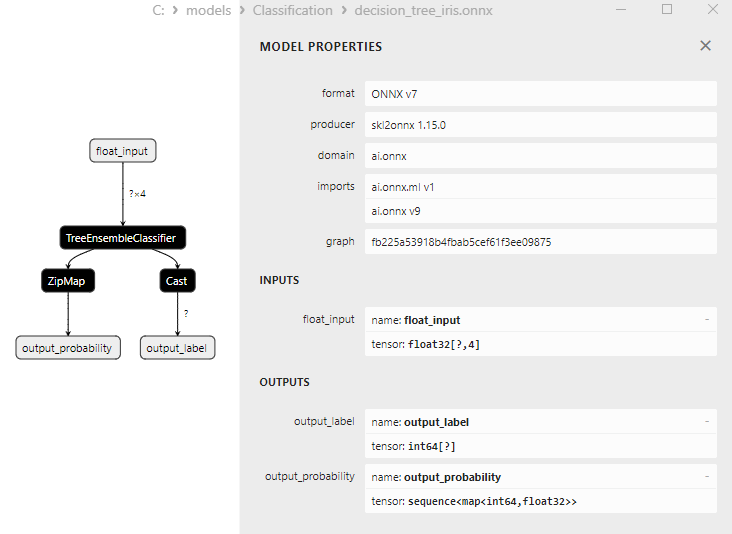
Abbildung 26. ONNX-Darstellung des Klassifizierungsmodells Entscheidungsbaum in Netron
Hinweis zu LogisticRegression und LogisticRegressionCV:
LogisticRegression und LogisticRegressionCV sind zwei Klassifikatoren, die für die binäre Klassifizierung mit logistischer Regression verwendet werden, aber sie unterscheiden sich darin, wie die Modellparameter eingestellt werden:
LogistischeRegression:
- LogisticRegression ist ein Klassifikator, der die logistische Funktion verwendet, um die Wahrscheinlichkeit der Zugehörigkeit zu einer von zwei Klassen zu modellieren (binäre Klassifizierung).
- Es bietet grundlegende Parameter zur Anpassung, wie C (Stärke der inversen Regularisierung), Strafe (Art der Regularisierung, z. B. L1 oder L2), Solver (Optimierungsalgorithmus) und andere.
- Bei der Verwendung von LogisticRegression wählen Sie in der Regel manuell Parameterwerte und deren Kombinationen aus und trainieren dann das Modell anhand der Daten.
LogistischeRegressionCV:
- LogisticRegressionCV ist eine Erweiterung von LogisticRegression, die integrierte Unterstützung für die Kreuzvalidierung und die Auswahl des optimalen Werts des Regularisierungsparameters C bietet.
- Anstatt C manuell auszuwählen, können Sie LogisticRegressionCV eine Liste von C-Werten übergeben, die untersucht werden sollen, und die Methode der Kreuzvalidierung angeben (z. B. über den Parameter cv).
- LogisticRegressionCV wählt automatisch den optimalen C-Wert, der bei der Kreuzvalidierung am besten abschneidet.
- Dies ist praktisch, wenn Sie die Regularisierung automatisch abstimmen müssen, insbesondere wenn Sie viele Daten haben oder unsicher sind, welchen C-Wert Sie wählen sollen.
Der Hauptunterschied zwischen ihnen liegt also im Grad der Automatisierung der Parametereinstellung. LogisticRegression erfordert eine manuelle Abstimmung von C, während LogisticRegressionCV die automatische Auswahl des optimalen C-Wertes durch Kreuzvalidierung ermöglicht. Die Wahl zwischen beiden hängt von Ihren Bedürfnissen und dem Wunsch nach Automatisierung des Modellabstimmungsprozesses ab.
2.13. Logistic Regression Classifier
Der logistischen Regressions-Klassifikator ist eine maschinelle Lernmethode, die für binäre und mehrklassige Klassifizierungsaufgaben verwendet wird. Trotz ihres Namens „Regression“ prognostiziert die Logistic Regression die Wahrscheinlichkeit, dass ein Objekt einer der Klassen angehört. Auf der Grundlage dieser Wahrscheinlichkeiten wird dann die endgültige Klassifizierungsentscheidung getroffen.
Grundsätze des logistischen Regression Klassifikators:
- Wahrscheinlichkeitsvorhersage: Die Logistic Regression modelliert die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu einer bestimmten Klasse unter Verwendung der logistischen (sigmoiden) Funktion.
- Grenze der Entscheidung: Auf der Grundlage der vorhergesagten Wahrscheinlichkeiten bestimmt die logistischen Regression die Entscheidungsgrenze, die die Klassen voneinander trennt. Wenn die Wahrscheinlichkeit einen bestimmten Schwellenwert (in der Regel 0,5) übersteigt, wird das Objekt einer Klasse zugeordnet, andernfalls einer anderen Klasse.
- Parameter-Lernen: Das Logistic Regression-Modell wird auf einem Trainingsdatensatz trainiert, indem die den Merkmalen zugeordneten Gewichte (Koeffizienten) angepasst werden, um die Verlustfunktion zu minimieren.
Vorteile des logistischen Regressions-Klassifikators:
- Einfachheit und Interpretierbarkeit: Die logistische Regression ist ein einfaches Modell mit leicht interpretierbaren Ergebnissen hinsichtlich des Einflusses von Merkmalen auf Klassenvorhersagen.
- Effizienz bei großen Datensätzen: Die logistischen Regression kann große Datensätze effizient verarbeiten und schnell trainieren.
- Verwendung in Ensemble-Methoden: Die logistischen Regression kann als Basis-Klassifikator in Ensemble-Methoden wie dem Stacking dienen.
Einschränkungen der logistischen Regression Klassifikator:
- Linearität: Die logistischen Regression geht von einer linearen Beziehung zwischen den Merkmalen und dem Logarithmus der Quoten aus, was für komplexe Aufgaben unzureichend sein kann.
- Multi-Klassen Bedingung: In ihrer ursprünglichen Form ist die Logistic Regression für die binäre Klassifizierung konzipiert, aber es gibt Methoden wie Eine-vs-Alle (Eine-vs-Rest), um sie auf die Mehrklassenklassifizierung zu erweitern.
- Empfindlichkeit gegenüber Ausreißern: Die Logistic Regression kann empfindlich auf Ausreißer in den Daten reagieren.
Die Logistic Regression ist eine klassische Methode des maschinellen Lernens, die in der Praxis häufig für Klassifizierungsaufgaben verwendet wird, insbesondere wenn die Interpretierbarkeit des Modells wichtig ist und die Daten eine lineare oder nahezu lineare Struktur aufweisen. Sie wird auch in der Statistik und der medizinischen Datenanalyse verwendet, um die Auswirkungen von Faktoren auf die Wahrscheinlichkeit von Ereignissen zu bewerten.
2.13.1. Code zur Erstellung eines Klassifizierungsmodells mit logistischer Regression
Dieser Code veranschaulicht den Prozess des Trainings eines logistischen Regressionsklassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_LogisticRegressionClassifier.py # The code uses the Logistic Regression Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Logistic Regression Classifier model logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Logistic Regression Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regression_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Logistic Regression Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Logistic Regression Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
2.13.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell der Regression
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regression_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Ausgabe:
Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier correct results: 97.33% Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier all samples accuracy=0.973333 Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 97,33 %, was der Genauigkeit des Originalmodells entspricht.
2.13.3. ONNX-Darstellung des Klassifizierungsmodells Logistic Regression
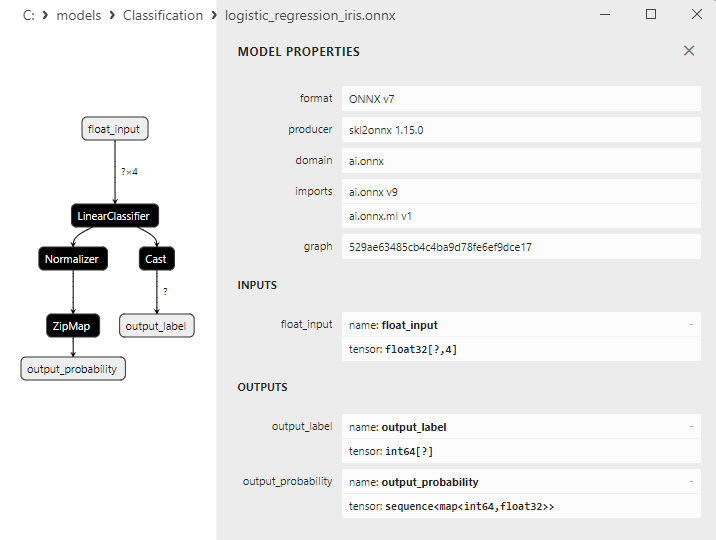
Abbildung 27. ONNX-Darstellung des Klassifizierungsmodells logistischen Regression in Netron
2.14. LogisticRegressionCV Classifier
Die Klassifizierung durch LogisticRegressionCV (logistischen Regression mit Kreuzvalidierung) ist eine leistungsstarke und flexible Methode zur binären Klassifizierung. Mit dieser Methode können Sie nicht nur Klassifizierungsmodelle auf der Grundlage der logistischen Regression erstellen, sondern auch die Parameter automatisch abstimmen, um die beste Leistung zu erzielen.
Arbeitsprinzipien der logistischen RegressionCV:
- logistischen Regression: LogisticRegressionCV basiert im Wesentlichen auf der logistischen Regression. Die Logistic Regression ist eine statistische Methode zur Modellierung der Wahrscheinlichkeit, dass ein Objekt zu einer von zwei Klassen gehört. Dieses Modell wird angewendet, wenn die abhängige Variable binär ist (zwei Klassen) oder in eine binäre Variable umgewandelt werden kann.
- Kreuzvalidierung: Der Hauptvorteil von LogisticRegressionCV ist seine integrierte Kreuzvalidierung. Das bedeutet, dass die Methode den optimalen Wert für den Regularisierungsparameter C nicht manuell auswählt, sondern automatisch verschiedene C-Werte ausprobiert und denjenigen auswählt, der in der Kreuzvalidierung am besten abschneidet.
- Die Wahl des optimalen C: LogisticRegressionCV wendet eine Kreuzvalidierungsstrategie an, um die Leistung des Modells bei verschiedenen C-Werten zu bewerten. C ist der Regularisierungsparameter, der das Ausmaß der Modellregularisierung steuert. Ein kleiner C-Wert weist auf eine starke Regularisierung hin, während ein großer C-Wert eine schwache Regularisierung anzeigt. Die Kreuzvalidierung hilft bei der Auswahl des optimalen C-Werts, um ein Gleichgewicht zwischen Unteranpassung und Überanpassung herzustellen.
- Regulierung: LogisticRegressionCV unterstützt auch verschiedene Arten der Regularisierung, einschließlich L1 (Lasso) und L2 (Ridge) Regularisierung. Diese Regularisierungsarten tragen dazu bei, die Generalisierung des Modells zu verbessern und eine Überanpassung zu verhindern.
Vorteile von LogisticRegressionCV:
Automatische Parameterabstimmung: Einer der Hauptvorteile von LogisticRegressionCV ist seine Fähigkeit, den optimalen C-Wert automatisch durch Kreuzvalidierung zu wählen. Dadurch entfällt die Notwendigkeit einer manuellen Modellabstimmung und Sie können sich auf die Daten und die Aufgabe konzentrieren.
Robustheit der Überanpassung: Die von LogisticRegressionCV unterstützte Regularisierung hilft dabei, die Komplexität des Modells zu kontrollieren und das Risiko einer Überanpassung zu verringern, insbesondere bei begrenzten Daten.
Transparenz: Die logistischen Regression ist eine interpretierbare Methode. Der Beitrag jedes Merkmals zur Vorhersage analysiert werden, was für das Verständnis der Bedeutung der Merkmale nützlich ist.
Hohe Leistung: Die logistischen Regression kann schnell und effizient arbeiten, insbesondere bei einer großen Datenmenge.
Einschränkungen von LogisticRegressionCV:
Lineare Abhängigkeiten: LogisticRegressionCV eignet sich für die Lösung linearer und nahezu linearer Klassifikationsprobleme. Wenn die Beziehung zwischen den Merkmalen und der Zielvariablen stark nichtlinear ist, kann das Modell nicht gut funktionieren.
Handhabung einer großen Anzahl von Merkmalen: Bei einer großen Anzahl von Merkmalen kann die logistischen Regression umfangreiche Daten oder Techniken zur Dimensionalitätsreduktion erfordern, um eine Überanpassung zu verhindern.
Abhängigkeit von der Datendarstellung: Die Wirksamkeit der logistischen Regression kann davon abhängen, wie die Daten dargestellt und welche Merkmale ausgewählt werden.
LogisticRegressionCV ist ein leistungsfähiges Werkzeug für die binäre Klassifikation mit automatischer Parameterabstimmung und Robustheit gegen Überanpassung. Es ist besonders nützlich, wenn Sie schnell ein interpretierbares Klassifikationsmodell erstellen müssen. Es ist jedoch zu bedenken, dass sie am besten funktioniert, wenn die Daten lineare oder nahezu lineare Abhängigkeiten aufweisen.
2.14.1. Code zur Erstellung des Klassifizierungsmodells von LogisticRegressionCV
Dieser Code demonstriert den Prozess des Trainings eines Klassifizierungsmodells von LogisticRegressionCV mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_LogisticRegressionCVClassifier.py # The code demonstrates the process of training LogisticRegressionCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegressionCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LogisticRegressionCV model logistic_regression_model = LogisticRegressionCV(cv=5, max_iter=1000) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LogisticRegressionCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regressioncv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LogisticRegressionCV model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of LogisticRegressionCV model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
2.14.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell der LogisticRegressionCV
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionCVClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regressioncv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionCVClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier correct results: 98.00% Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier all samples accuracy=0.980000 Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 98 %, was der Genauigkeit des Originalmodells entspricht.
2.14.3. ONNX-Darstellung des Klassifikators LogisticRegressionCV
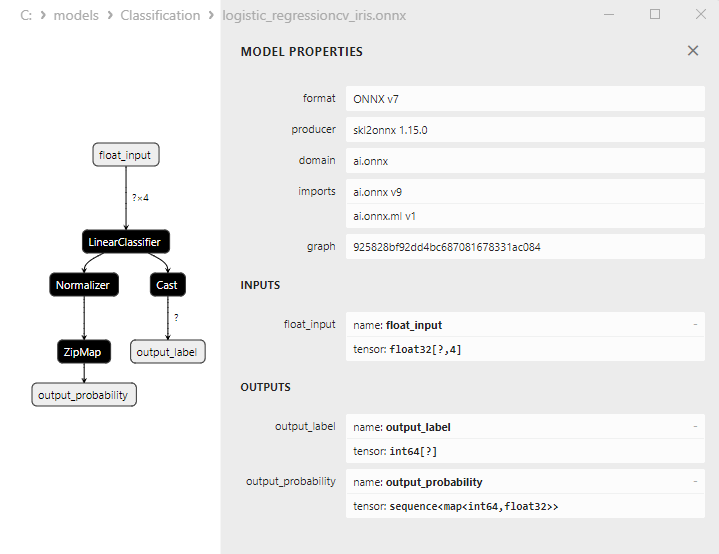
Abbildung 28. ONNX-Darstellung des Klassifizierungsmodells LogisticRegressionCV in Netron
2.15. Passive-Aggressive (PA) Classifier
Der Passiv-Aggressiv (PA)-Klassifikator ist eine maschinelle Lernmethode, die für Klassifizierungsaufgaben verwendet wird. Der Kerngedanke dieser Methode besteht darin, die Gewichte (Koeffizienten) des Modells während des Trainings anzupassen, um die Klassifizierungsfehler zu minimieren. Der Passive-Aggressive-Klassifikator kann in Online-Lernszenarien und in Situationen, in denen sich Daten im Laufe der Zeit ändern, nützlich sein.
Funktionsprinzipien des Passive-Aggressive-Klassifikators:
- Gewichtsanpassung: Anstatt die Gewichte des Modells in Richtung der Minimierung der Verlustfunktion zu aktualisieren, wie es beim stochastischen Gradientenabstieg geschieht, passt der Passive-Aggressive Klassifikator die Gewichte in der Richtung an, die den Klassifizierungsfehler für das aktuelle Beispiel minimiert.
- Aufrechterhaltung der Aggressivität: Die Methode verfügt über einen Parameter namens Aggressivität (C), der bestimmt, wie stark die Gewichte des Modells angepasst werden sollen. Größere C-Werte machen die Methode aggressiver in der Anpassung, während kleinere Werte sie weniger aggressiv machen.
Vorteile des Passive-Aggressive-Klassifikators:
- Geeignet für Online-Lernen: Der Passive-Aggressive-Klassifikator kann aktualisiert werden, wenn neue Daten eintreffen, wodurch er sich für Online-Lernaufgaben eignet, bei denen die Daten in einem Strom eintreffen.
- Anpassungsfähigkeit an Datenänderungen: Die Methode funktioniert gut bei sich ändernden Daten, da sie das Modell an neue Umstände anpasst.
Einschränkungen des Passive-Aggressive-Klassifikators:
- Empfindlichkeit gegenüber der Wahl der Aggressivitätsparameter: Die Auswahl des optimalen Werts für den Aggressivitätsparameter C kann eine Abstimmung erfordern und hängt von den Datenmerkmalen ab.
- Nicht immer für komplexe Aufgaben geeignet: Der Passive-Aggressive-Klassifikator bietet möglicherweise keine hohe Genauigkeit bei komplexen Aufgaben, bei denen komplizierte Merkmalsabhängigkeiten berücksichtigt werden müssen.
- Interpretation der Gewichte: Die mit dieser Methode erhaltenen Modellgewichte können im Vergleich zu den mit linearer oder logistischer Regression erhaltenen Gewichten weniger interpretierbar sein.
Der Passive-Aggressive Klassifikator ist eine Methode des maschinellen Lernens, die sich für Klassifizierungsaufgaben mit sich verändernden Daten und für Situationen eignet, in denen eine schnelle Anpassung des Modells an neue Umstände entscheidend ist. Es findet in verschiedenen Bereichen Anwendung, darunter Textdatenanalyse, Bildklassifizierung und andere Aufgaben.
2.15.1. Code zur Erstellung des Klassifizierungsmodells von Passive-Aggressive (PA)
Dieser Code demonstriert den Prozess des Trainings eines Passive-Aggressive (PA) Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_PassiveAgressiveClassifier.py # The code uses the Passive-Aggressive (PA) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import PassiveAggressiveClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Passive-Aggressive (PA) Classifier model pa_classifier_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset pa_classifier_model.fit(X, y) # predict classes for the entire dataset y_pred = pa_classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Passive-Aggressive (PA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(pa_classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "pa_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Passive-Aggressive (PA) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Passive-Aggressive (PA) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
2.15.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Passive-Aggressive (PA)
//+------------------------------------------------------------------+ //| Iris_PassiveAgressiveClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "pa_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PassiveAgressiveClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier correct results: 96.00% Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier all samples accuracy=0.960000 Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 96 %, was der Genauigkeit des Originalmodells entspricht.
2.15.3. ONNX-Darstellung des Klassifizierungsmodells Passive-Aggressive (PA) Klassifikators
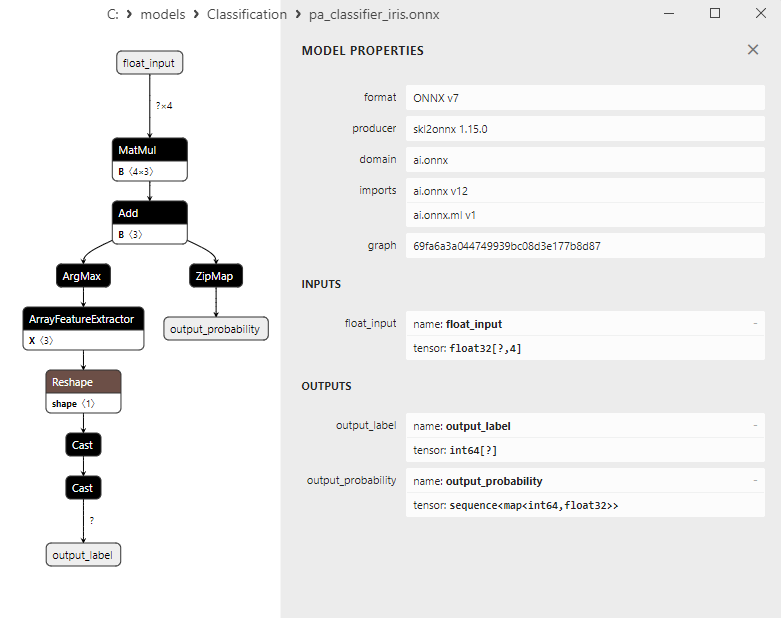
Abbildung 29. ONNX-Darstellung des Klassifizierungsmodells Passive-Aggressive (PA) in Netron
2.16. Perceptron Classifier
Der Perceptron-Klassifikator ist ein linearer binärer Klassifikator, der zur Trennung zweier Klassen auf der Grundlage einer linearen Trennhyperebene verwendet wird. Es handelt sich um eine der einfachsten und ältesten Methoden des maschinellen Lernens, deren Kernprinzip darin besteht, die Gewichte (Koeffizienten) des Modells so zu trainieren, dass die Klassifizierungsgenauigkeit auf dem Trainingsdatensatz maximiert wird.
Funktionsprinzipien des Perceptron-Klassifikators:
- Lineare Hyperebene: Das Perceptron konstruiert eine lineare Hyperebene im Merkmalsraum, die zwei Klassen trennt. Diese Hyperebene wird durch die Gewichte (Koeffizienten) des Modells bestimmt.
- Training der Gewichte: Zu Beginn werden die Gewichte zufällig oder mit Nullen initialisiert. Dann sagt das Modell für jedes Objekt im Trainingsdatensatz die Klasse auf der Grundlage der aktuellen Gewichte voraus und passt sie im Falle eines Fehlers an. Das Training wird so lange fortgesetzt, bis alle Objekte richtig klassifiziert sind oder bis eine maximale Anzahl von Iterationen erreicht ist.
Vorteile des Perceptron-Klassifikators:
- Einfachheit: Das Perceptron ist ein sehr einfacher Algorithmus, der leicht zu verstehen und zu implementieren ist.
- Hohe Trainingsgeschwindigkeit: Das Perceptron kann schnell trainiert werden, insbesondere auf großen Datensätzen, und kann bei Online-Lernaufgaben eingesetzt werden.
Einschränkungen des Perceptron-Klassifikators:
- Lineare Trennbarkeitsbeschränkung: Das Perceptron funktioniert nur dann gut, wenn die Daten linear trennbar sind. Wenn Daten nicht linear getrennt werden können, erreicht das Perceptron möglicherweise keine hohe Genauigkeit.
- Empfindlichkeit gegenüber Anfangsgewichten: Die anfängliche Wahl der Gewichte kann die Konvergenz des Algorithmus beeinflussen. Eine ungünstige Wahl der Anfangsgewichte kann zu einer langsamen Konvergenz oder zu einem Neuron führen, das die Klassen nicht korrekt trennen kann.
- Unfähigkeit, Wahrscheinlichkeiten zu bestimmen: Das Perceptron liefert keine Wahrscheinlichkeitsschätzungen der Klassenzugehörigkeit, was für bestimmte Aufgaben wichtig sein kann.
Der Perceptron-Klassifikator ist ein grundlegender Algorithmus für die binäre Klassifizierung, der in einfachen Fällen nützlich sein kann, wenn die Daten linear trennbar sind. Sie kann auch als Grundlage für komplexere Methoden, wie z. B. mehrschichtige neuronale Netze, dienen. Es ist wichtig, daran zu denken, dass bei komplexeren Aufgaben, bei denen die Daten komplizierte Strukturen aufweisen, andere Methoden wie logistische Regression oder Support Vector Machines (SVM) eine höhere Klassifizierungsgenauigkeit bieten können.
2.16.1. Code zur Erstellung des Klassifizierungsmodells von Perceptron
Dieser Code demonstriert den Prozess des Trainings eines Perceptron-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_PerceptronClassifier.py # The code demonstrates the process of training Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import Perceptron from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Perceptron Classifier model perceptron_model = Perceptron(max_iter=1000, random_state=42) # train the model on the entire dataset perceptron_model.fit(X, y) # predict classes for the entire dataset y_pred = perceptron_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Perceptron Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(perceptron_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "perceptron_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Perceptron Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Genauigkeit des Perceptron-Klassifizierungsmodells: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
2.16.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Perceptron
//+------------------------------------------------------------------+ //| Iris_PerceptronClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "perceptron_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PerceptronClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier correct results: 61.33% Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier all samples accuracy=0.613333 Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80) Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 61,33 %, was der Genauigkeit des Originalmodells entspricht.
2.16.3. ONNX-Darstellung des Klassifizierungsmodells Perceptron
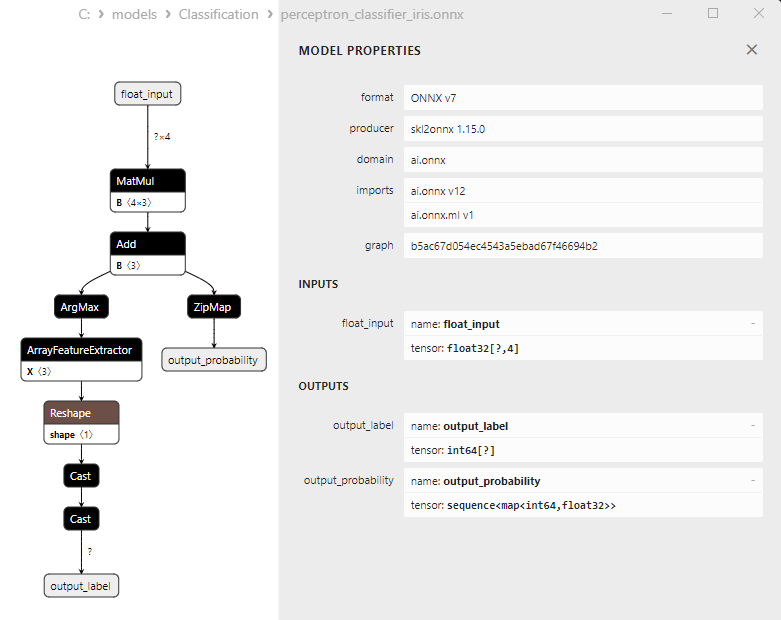
Abbildung 30. ONNX-Darstellung des Klassifizierungsmodells Perceptron in Netron
2.17. Stochastic Gradient Descent Classifier
Der SGD-Klassifikator (Stochastischer Gradientenabstieg) ist ein maschinelles Lernverfahren, das für Klassifizierungsaufgaben verwendet wird. Es ist ein Sonderfall der linearen Modelle und ist ein linearer Klassifikator, der mittels stochastischem Gradientenabstieg trainiert wird.
Grundsätze des SGD-Klassifikators:
- Lineare Hyperebene: Der SGD Classifier konstruiert eine lineare Hyperebene im mehrdimensionalen Merkmalsraum, die zwei Klassen trennt. Diese Hyperebene wird durch die Gewichte (Koeffizienten) des Modells bestimmt.
- Stochastic Gradient Descent: Die Methode wird mit Hilfe des stochastischen Gradientenabstiegs trainiert, was bedeutet, dass die Aktualisierung der Gewichte für jedes Objekt im Trainingsdatensatz (oder einer zufällig ausgewählten Teilmenge) und nicht für den gesamten Datensatz durchgeführt wird. Dadurch ist die Klassifizierung durch SGD für große Datenmengen und Online-Lernen geeignet.
- Verlustfunktion: Die Klassifizierung durch SGD optimiert eine Verlustfunktion, z. B. die logistische Verlustfunktion für die binäre Klassifikation oder die Softmax-Verlustfunktion für die Mehrklassenklassifikation.
Vorteile des SGD-Klassifizierung:
- Trainingsgeschwindigkeit: Der SGD-Klassifikator trainiert dank des stochastischen Gradientenabstiegs schnell, insbesondere bei großen Datenmengen.
- Geeignet für Online-Lernen: Die Methode eignet sich gut für Online-Lernaufgaben, bei denen die Daten in „streams“ eintreffen und das Modell aktualisiert werden muss, sobald neue Daten eintreffen.
Einschränkungen des SGD-Klassifikators:
- Empfindlichkeit gegenüber Parametern: Der SGD-Klassifikator verfügt über zahlreiche Hyperparameter, wie z. B. die Lernrate und den Regularisierungsparameter, die sorgfältig abgestimmt werden müssen.
- Gewicht Initialisierung: Die anfängliche Wahl der Gewichte kann die Konvergenz und die Modellqualität beeinflussen.
- Konvergenz zu lokalen Minima: Aufgrund der stochastischen Natur der SGD-Methode kann sie zu lokalen Minima der Verlustfunktion konvergieren, was die Modellqualität beeinträchtigen kann.
Der SGD-Klassifikator ist ein vielseitiges maschinelles Lernverfahren, das für binäre und mehrklassige Klassifizierungsaufgaben eingesetzt werden kann, insbesondere bei großen Datenmengen, die eine schnelle Verarbeitung erfordern. Um eine hohe Klassifizierungsgenauigkeit zu erreichen, ist es wichtig, die Hyperparameter richtig einzustellen und die Konvergenz zu überwachen.
2.17.1. Code für die Erstellung des Klassifizierungsmodells mit stochastischem Gradientenabstieg
Dieser Code veranschaulicht den Prozess des Trainings eines SGD-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_SGDClassifier.py # The code demonstrates the process of training Stochastic Gradient Descent Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import SGDClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SGD Classifier model sgd_model = SGDClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset sgd_model.fit(X, y) # predict classes for the entire dataset y_pred = sgd_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SGD Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(sgd_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "sgd_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SGD Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of SGD Classifier model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
2.17.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Stochastic Gradient Descent
//+------------------------------------------------------------------+ //| Iris_SGDClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "sgd_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SGDClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier correct results: 93.33% Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier all samples accuracy=0.933333 Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 93,33 %, was der Genauigkeit des Originalmodells entspricht.
2.17.3. ONNX-Darstellung des Klassifizierungsmodells Stochastic Gradient Descent
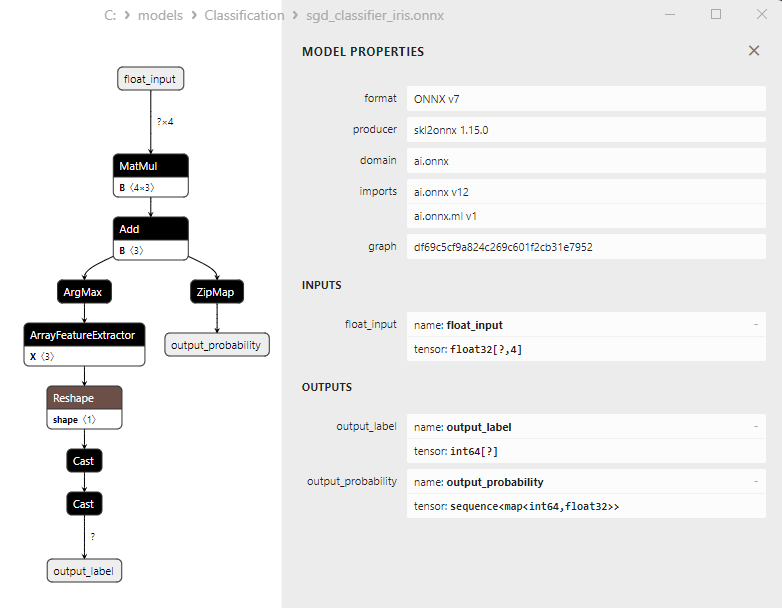
Abbildung 31. ONNX-Darstellung des Klassifizierungsmodells stochastischen Gradientenabstiegs in Netron
2.18. Gaussian Naive Bayes (GNB) Classifier
Der gaußsche Naive Bayes (GNB)-Klassifikator ist eine maschinelle Lernmethode, die auf einem bayesschen probabilistischen Modell basiert und für Klassifizierungsaufgaben verwendet wird. Er gehört zur Familie der Naive-Bayes-Klassifikatoren und geht davon aus, dass alle Merkmale unabhängig sind und eine Normalverteilung haben.
Prinzipien des Gaußschen Naive Bayes Klassifikators:
- Bayesscher Ansatz: GNB basiert auf dem bayesschen Klassifizierungsansatz, der das bayessche Theorem verwendet, um die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu den einzelnen Klassen zu berechnen.
- Naive Vermutung: Die Hauptannahme bei GNB ist, dass alle Merkmale unabhängig sind und einer normalen (Gaußschen) Verteilung folgen. Diese Annahme wird als naiv angesehen, da in realen Daten die Merkmale oft miteinander korrelieren.
- Schätzung der Parameter: Das GNB-Modell wird mit dem Trainingsdatensatz trainiert, indem die Parameter der Verteilung (Mittelwert und Standardabweichung) für jedes Merkmal innerhalb jeder Klasse berechnet werden.
Vorteile des Gaußschen Naive Bayes Klassifikator:
- Einfachheit und Trainingsgeschwindigkeit: GNB ist ein sehr einfacher Algorithmus, der selbst bei großen Datensätzen schnell trainiert.
- Effektivität bei kleinen und mittleren Daten: GNB kann für Klassifizierungsaufgaben mit einer kleinen oder mittleren Anzahl von Merkmalen effektiv sein, insbesondere wenn die Annahme einer normalen Merkmalsverteilung gilt.
Einschränkungen des Gaußschen Naive-Bayes-Klassifikators:
- Naive Vermutung: Die Annahme der Unabhängigkeit von Merkmalen und der Normalverteilung kann bei realen Daten zu stark vereinfacht und falsch sein, was zu einer geringeren Klassifizierungsgenauigkeit führt.
- Empfindlichkeit gegenüber Ausreißern: GNB kann empfindlich auf Ausreißer in den Daten reagieren, da diese die Parameter der Normalverteilung erheblich verzerren können.
- Unfähigkeit zur Erfassung von Feature-Abhängigkeiten: Aufgrund der Annahme der Unabhängigkeit berücksichtigt GNB nicht die Abhängigkeiten zwischen den Merkmalen.
Der gaußsche Naive-Bayes-Klassifikator ist eine gute Wahl für einfache Klassifikationsaufgaben, insbesondere wenn die Annahme normaler Merkmalsverteilungen annähernd erfüllt ist. Bei komplexeren Aufgaben, bei denen die Merkmale korreliert sind oder nicht einer Normalverteilung folgen, können jedoch andere Methoden wie Support Vector Machines (SVM) oder Gradient Boosting genauere Ergebnisse liefern.
2.18.1. Code für die Erstellung des Klassifizierungsmodells Gaussian Naive Bayes (GNB)
Dieser Code demonstriert den Prozess des Trainings eines Gaussian Naive Bayes (GNB) Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_GaussianNaiveBayesClassifier.py # The code demonstrates the process of training Gaussian Naive Bayes Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import GaussianNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gaussian Naive Bayes (GNB) Classifier model gnb_model = GaussianNB() # train the model on the entire dataset gnb_model.fit(X, y) # predict classes for the entire dataset y_pred = gnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gaussian Naive Bayes (GNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
2.18.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Gaußschen Naive Bayes (GNB)
//+------------------------------------------------------------------+ //| Iris_GaussianNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GaussianNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier correct results: 96.00% Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier all samples accuracy=0.960000 Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 96 %, was der Genauigkeit des Originalmodells entspricht.
2.18.3. ONNX-Darstellung des Klassifizierungsmodells Gaußschen Naive Bayes (GNB)
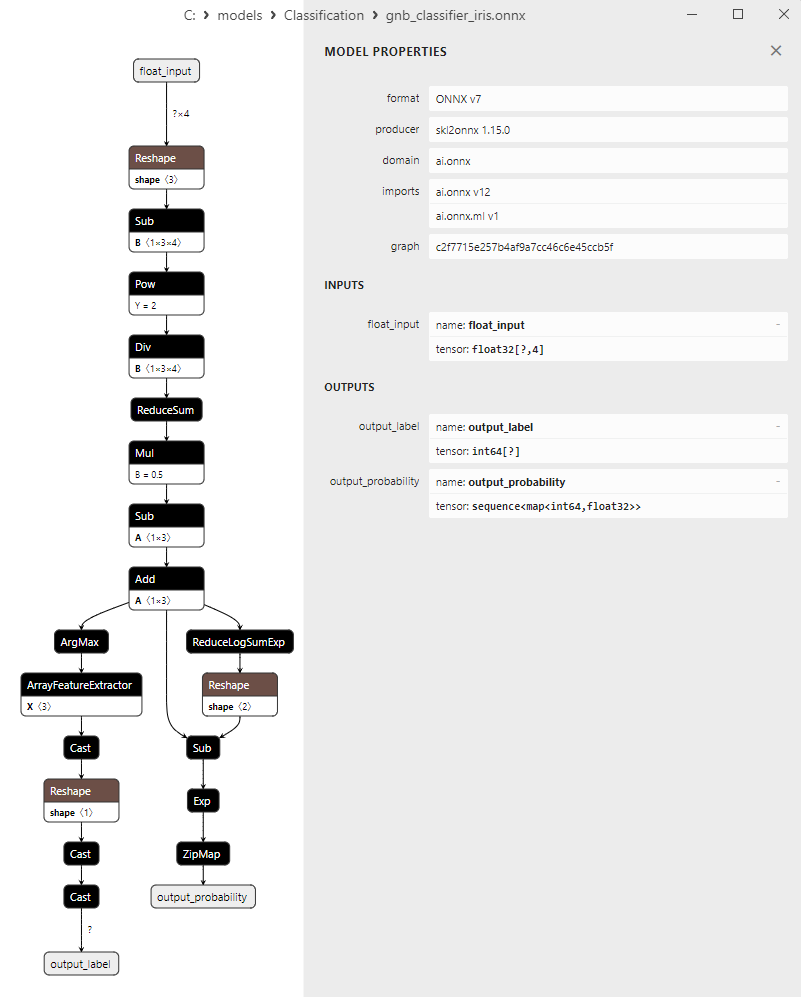
Abbildung 32. ONNX-Darstellung des Klassifizierungsmodells Gaussian Naive Bayes (GNB) in Netron
2.19. Multinomial Naive Bayes (MNB) Classifier
Der Multinomial Naive Bayes (MNB)-Klassifikator ist ein maschinelles Lernverfahren, das auf einem bayesschen probabilistischen Modell basiert und für Klassifizierungsaufgaben, insbesondere in der Textverarbeitung, eingesetzt wird. Es ist eine der Varianten der Naive-Bayes-Klassifikatoren und geht davon aus, dass die Merkmale Zählungen darstellen, wie z. B. die Anzahl der Wortvorkommen im Text.
Prinzipien des Multinomial Naive Bayes:
- Bayesscher Ansatz: MNB folgt ebenfalls dem bayesschen Klassifizierungsansatz und verwendet das bayessche Theorem, um die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu den einzelnen Klassen zu berechnen.
- Annahme einer Multinomialverteilung: Die Hauptannahme bei MNB ist, dass Merkmale Zählungen darstellen, wie z. B. die Anzahl der Wortvorkommen im Text, und einer multinomialen Verteilung folgen. Diese Annahme gilt häufig für Textdaten.
- Schätzung der Parameter: Das MNB-Modell wird anhand des Trainingsdatensatzes trainiert, indem die Parameter der Verteilung für jedes Merkmal innerhalb jeder Klasse berechnet werden.
Vorteile des Multinomial Naive Bayes Klassifikator:
- Effektivität in der Textverarbeitung: MNB eignet sich gut für Aufgaben im Zusammenhang mit der Analyse von Textdaten, wie z. B. Textklassifizierung oder Spam-Filterung, dank der Annahme, dass die Merkmale gezählt werden.
- Einfachheit und Trainingsgeschwindigkeit: Wie andere Naive-Bayes-Klassifikatoren ist MNB ein unkomplizierter Algorithmus, der selbst bei großen Mengen an Textdaten schnell trainiert.
Einschränkungen des Klassifikators Multinomial Naive-Bayes:
- Naive Vermutung: Die Annahme einer multinomialen Verteilung von Merkmalen kann für reale Daten zu vereinfachend und ungenau sein, insbesondere wenn die Merkmale komplexe Strukturen aufweisen.
- Unfähigkeit, die Wortfolge zu berücksichtigen: MNB berücksichtigt nicht die Reihenfolge der Wörter im Text, was bei bestimmten Textanalyseaufgaben wichtig sein kann.
- Empfindlichkeit gegenüber seltenen Wörtern: MNB kann empfindlich auf seltene Wörter reagieren, und eine unzureichende Anzahl von Vorkommen kann die Klassifizierungsgenauigkeit verringern.
Der Multinomial-Naive-Bayes-Klassifikator ist eine nützliche Methode für Textanalyseaufgaben, insbesondere dann, wenn sich die Merkmale auf die Anzahl der Wörter im Text beziehen. Sie wird häufig in der natürlichen Sprachverarbeitung (NLP) für die Klassifizierung von Texten, die Kategorisierung von Dokumenten und andere Textanalysen verwendet.
2.19.1. Code zur Erstellung des Klassifizierungsmodells von Multinomial Naive Bayes (MNB)
Dieser Code demonstriert den Prozess des Trainings eines Multinomial Naive Bayes (MNB)-Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_MultinomialNaiveBayesClassifier.py # The code demonstrates the process of training Multinomial Naive Bayes (MNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import MultinomialNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multinomial Naive Bayes (MNB) Classifier model mnb_model = MultinomialNB() # train the model on the entire dataset mnb_model.fit(X, y) # predict classes for the entire dataset y_pred = mnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multinomial Naive Bayes (MNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "mnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
2.19.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Multinomial Naive Bayes (MNB)
//+------------------------------------------------------------------+ //| Iris_MultinomialNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MultinomialNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier correct results: 95.33% Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier all samples accuracy=0.953333 Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 95,33 %, was der Genauigkeit des Originalmodells entspricht.
2.19.3. ONNX-Darstellung des Klassifizierungsmodells Multinomial Naive Bayes (MNB)
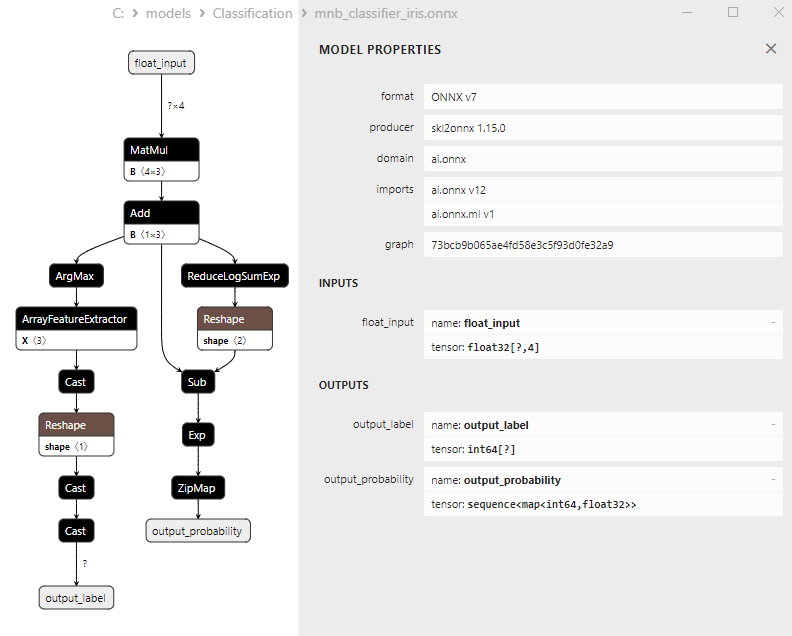
Abbildung 33. ONNX-Darstellung des Klassifizierungsmodells Multinomial Naive Bayes (MNB) in Netron
2.20. Complement Naive Bayes (CNB) Classifier
Der Complement Naive Bayes (CNB)-Klassifikator ist eine Variante des Naive Bayes-Klassifikators, die speziell für die Arbeit mit unausgewogenen Daten entwickelt wurde, bei denen eine Klasse deutlich häufiger vorkommt als die andere. Dieser Klassifikator passt die klassische Naive-Bayes-Methode an, um ein Ungleichgewicht der Klassen zu vermeiden.
Prinzipien des Complement Naive Bayes:
- Bayesscher Ansatz: Wie andere bayessche Klassifikatoren folgt der CNB dem bayesschen Klassifizierungsansatz und verwendet das bayessche Theorem, um die Wahrscheinlichkeit der Zugehörigkeit eines Objekts zu den einzelnen Klassen zu berechnen.
- Bekämpfung des Klassenungleichgewichts: Der Hauptzweck der CNB besteht darin, das Ungleichgewicht zwischen den Klassen zu korrigieren. Anstatt die Wahrscheinlichkeit von Merkmalen in der Klasse zu berücksichtigen, wie es bei der Standardmethode von Naive Bayes der Fall ist, versucht CNB, die Wahrscheinlichkeit von Merkmalen außerhalb der Klasse zu berücksichtigen. Dies ist besonders nützlich, wenn eine Klasse deutlich weniger vertreten ist als die andere.
- Schätzung der Parameter: Das CNB-Modell wird mit dem Trainingsdatensatz trainiert, indem die Parameter der Verteilung für jedes Merkmal außerhalb der Klasse berechnet werden.
Vorteile des Complement Naive Bayes Klassifikators:
- Eignung für unausgewogene Daten: CNB eignet sich gut für Klassifizierungsaufgaben mit unausgewogenen Daten, bei denen die Klassen unterschiedlich häufig vorkommen.
- Einfachheit und Trainingsgeschwindigkeit: Wie andere Naive-Bayes-Klassifikatoren ist CNB ein einfacher Algorithmus, der selbst bei großen Datenmengen schnell trainiert.
Einschränkungen des Complement Naive Bayes:
- Empfindlichkeit gegenüber der Wahl der Regularisierungsparameter: Wie bei anderen bayesschen Methoden kann die Auswahl des richtigen Wertes für den Regularisierungsparameter eine Abstimmung und Bewertung erfordern.
- Naive Vermutung: Wie andere Naive-Bayes-Klassifikatoren geht auch der CNB von der Annahme aus, dass die Merkmale unabhängig sind, was bei einigen Aufgaben zu einfach sein kann.
Der Complement Naive Bayes Classifier ist eine gute Wahl für Klassifizierungsaufgaben mit unausgewogenen Daten, insbesondere wenn eine Klasse deutlich weniger vertreten ist als die andere. Sie kann besonders bei Textklassifizierungsaufgaben nützlich sein, bei denen die Wörter zwischen den Klassen stark unausgewogen sein können, z. B. bei der Stimmungsanalyse oder der Spam-Filterung.
2.20.1. Code zur Erstellung des Klassifizierungsmodells von Complement Naive Bayes (CNB)
Dieser Code demonstriert den Prozess des Trainings eines Complement Naive Bayes (CNB) Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_CNBClassifier.py # The code demonstrates the process of training Complement Naive Bayes (CNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import ComplementNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Complement Naive Bayes (CNB) Classifier model cnb_model = ComplementNB() # train the model on the entire dataset cnb_model.fit(X, y) # predict classes for the entire dataset y_pred = cnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Complement Naive Bayes (CNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(cnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "cnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Complement Naive Bayes (CNB) Classifier model: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
2.20.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Complement Naive Bayes (CNB)
//+------------------------------------------------------------------+ //| Iris_CNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "cnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier correct results: 66.67% Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier all samples accuracy=0.666667 Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier batch test accuracy=0.000000Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 66,67 %, was der Genauigkeit des Originalmodells entspricht.
2.20.3. ONNX-Darstellung des Klassifizierungsmodells Complement Naive Bayes (CNB)
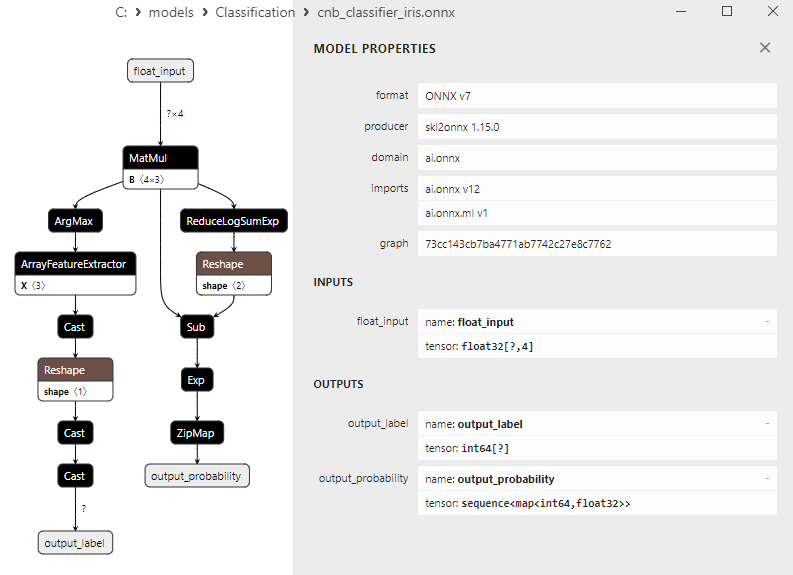
Abbildung 34. ONNX-Darstellung des Klassifizierungsmodells Complement Naive Bayes (CNB) in Netron
2.21. Bernoulli Naive Bayes (BNB) Klassifikator
Der Klassifikator Bernoulli-Naive-Bayes (BNB) ist eine weitere Variante des Naive-Bayes, der für binäre Klassifikationsaufgaben verwendet wird. Dieser Klassifikator ist besonders nützlich in Situationen, in denen Merkmale als binäre Daten dargestellt werden, wie z. B. bei der Textanalyse, wo Merkmale das Vorhandensein oder Fehlen von Wörtern im Text sein können.
Prinzipien des Bernoulli Naive Bayes Klassifikators:
- Bayesscher Ansatz: Wie andere bayessche Klassifikatoren folgt der BNB dem bayesschen Klassifizierungsansatz und verwendet das bayessche Theorem zur Berechnung der Wahrscheinlichkeit, dass ein Objekt zu einer Klasse gehört.
- Annahme von binären Merkmalen: Die Grundannahme von BNB ist, dass Merkmale als binäre Daten dargestellt werden, d. h. sie können nur zwei Werte annehmen, z. B. 1 und 0, wobei 1 für das Vorhandensein des Merkmals steht und 0 für sein Fehlen.
- Schätzung der Parameter: Das BNB-Modell wird mit dem Trainingsdatensatz trainiert, indem die Parameter der Verteilung für jedes Merkmal in jeder Klasse berechnet werden.
Vorteile des Bernoulli Naive Bayes Klassifikators:
- Effektivität für binäre Daten: BNB eignet sich gut für Aufgaben, bei denen Merkmale als binäre Daten dargestellt werden, und kann besonders bei der Textanalyse oder Ereignisklassifizierung nützlich sein.
- Einfachheit und Trainingsgeschwindigkeit: Wie andere Naive-Bayes-Klassifikatoren ist auch BNB ein einfacher Algorithmus, der schnell trainiert.
Einschränkungen des Bernoulli Naive Bayes Klassifikators:
- Beschränkung auf binäre Merkmale: BNB ist nicht für Aufgaben geeignet, bei denen die Merkmale nicht binär sind. Wenn Merkmale mehr als zwei Werte haben, berücksichtigt BNB diese Information nicht.
- Naive Vermutung: Wie andere Naive-Bayes-Klassifikatoren geht BNB von der Annahme aus, dass die Merkmale unabhängig sind, was für einige Aufgaben zu einfach sein kann.
Der Bernoulli-Naive-Bayes-Klassifikator ist eine gute Wahl für binäre Klassifizierungsaufgaben mit binären Merkmalen, wie z. B. die Stimmungsanalyse von Texten oder die Spam-Klassifizierung. Es ist einfach zu bedienen und funktioniert gut mit dieser Art von Daten.
2.21.1. Code zur Erstellung des Klassifizierungsmodells von Bernoulli Naive Bayes (BNB)
Dieser Code demonstriert den Prozess des Trainings eines Bernoulli Naive Bayes (BNB) Klassifizierungsmodells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_BNBClassifier.py # The code demonstrates the process of training Bernoulli Naive Bayes (BNB) Classifier on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import BernoulliNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bernoulli Naive Bayes (BNB) Classifier model bnb_model = BernoulliNB() # train the model on the entire dataset bnb_model.fit(X, y) # predict classes for the entire dataset y_pred = bnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bernoulli Naive Bayes (BNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
2.21.2. MQL5 Code für die Arbeit mit dem Klassifizierungsmodell Bernoulli Naive Bayes (BNB)
//+------------------------------------------------------------------+ //| Iris_BNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier correct results: 33.33% Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier all samples accuracy=0.333333 Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80) Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 33,33 %, was der Genauigkeit des Originalmodells entspricht.
2.21.3. ONNX-Darstellung des Klassifizierungsmodells Bernoulli Naive Bayes (BNB)
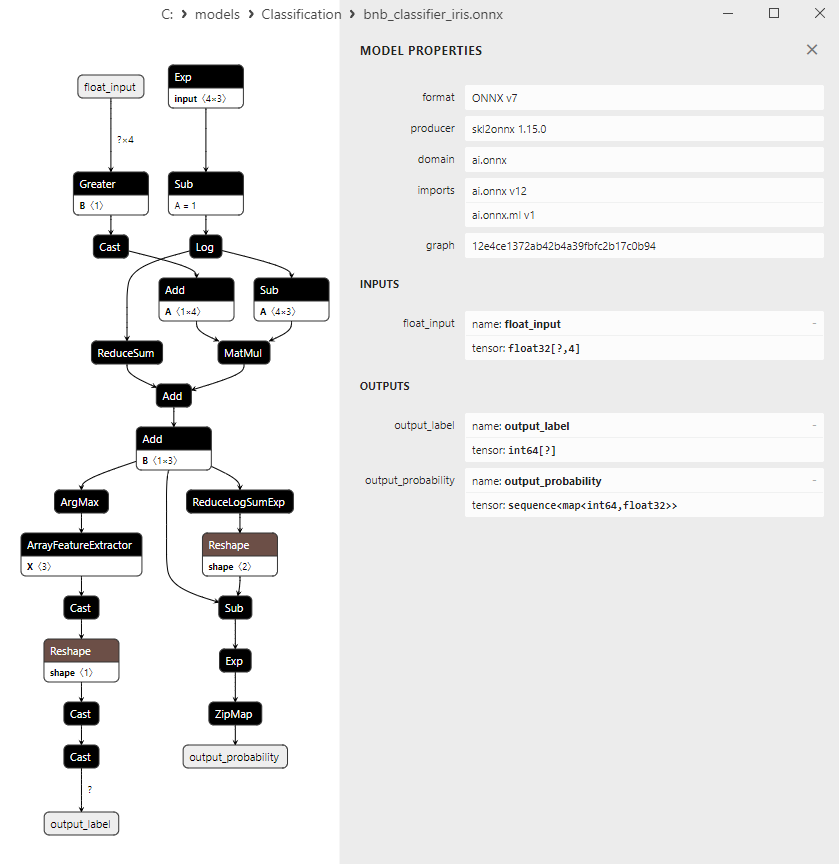
Abbildung 35. ONNX-Darstellung des Klassifizierungsmodells Bernoulli Naive Bayes (BNB) in Netron
2.22. Multilayer Perceptron Classifier
Der Multilayer Perceptron (MLP) Classifier ist ein mehrschichtiges neuronales Netz, das für Klassifizierungsaufgaben verwendet wird. Es besteht aus mehreren Schichten von Neuronen, darunter eine Eingabeschicht, versteckte Schichten und eine Ausgabeschicht. Der MLP-Klassifikator ist in der Lage, komplexe nichtlineare Abhängigkeiten in Daten zu erlernen.
Prinzipien des MLP-Klassifikators:
- Mehrschichtige Architektur: Der MLP-Klassifikator hat eine mehrschichtige Architektur, die eine Eingabeschicht, eine oder mehrere versteckte Schichten und eine Ausgabeschicht umfasst. Jedes Neuron in den Schichten ist mit Neuronen in benachbarten Schichten durch erlernte Gewichte verbunden.
- Aktivierungsfunktionen: Innerhalb jedes Neurons wird eine Aktivierungsfunktion angewendet, die Nichtlinearität in das Modell einführt und es dem MLP-Klassifikator ermöglicht, komplexe Datenabhängigkeiten zu modellieren.
- Training mit Backpropagation: Der MLP-Klassifikator wird mit der Backpropagation-Methode trainiert, die den Fehler zwischen den Vorhersagen des Modells und den wahren Klassenbezeichnungen minimiert.
Vorteile des MLP-Klassifikators:
- Fähigkeit zur Modellierung komplexer Abhängigkeiten: Der MLP-Klassifikator kann komplexe nichtlineare Abhängigkeiten in den Daten erlernen und ist daher für Aufgaben geeignet, bei denen einfache lineare Modelle unzureichend sind.
- Vielseitigkeit: Der MLP-Klassifikator kann für eine Vielzahl von Klassifizierungsaufgaben verwendet werden, darunter auch für Mehrklassen-Klassifizierungen und Multi-Task-Probleme.
Einschränkungen des MLP-Klassifikators:
- Empfindlichkeit gegenüber Hyperparametern: Der MLP-Klassifikator hat viele Hyperparameter, wie die Anzahl der versteckten Schichten, die Anzahl der Neuronen in jeder Schicht, die Lernrate und andere. Die Abstimmung dieser Parameter kann zeit- und ressourcenaufwändig sein.
- Erfordernis großer Datenmengen: Der MLP-Klassifikator erfordert eine große Menge an Trainingsdaten, um eine Überanpassung zu vermeiden, insbesondere wenn das Modell viele Parameter hat.
- Überanpassung: Verfügt das Modell über zu viele Parameter oder unzureichende Daten, kann es zu einer Überanpassung kommen und bei neuen Daten eine schlechte Leistung erbringen.
Der MLP-Klassifikator ist ein leistungsstarkes Werkzeug für Klassifizierungsaufgaben, insbesondere wenn die Daten komplexe Abhängigkeiten aufweisen. Es wird häufig im Bereich des maschinellen Lernens und des Deep Learning eingesetzt, um verschiedene Klassifizierungsprobleme zu lösen. Für eine erfolgreiche Anwendung dieses Modells ist es jedoch unerlässlich, die Hyperparameter richtig einzustellen und eine ausreichende Menge an Trainingsdaten zu gewährleisten.
2.22.1. Code zur Erstellung des Klassifizierungsmodells von Multilayer Perceptrons
Dieser Code demonstriert den Prozess des Trainings eines mehrschichtigen Perceptron-Klassifikators mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_MLPClassifier.py # The code demonstrates the process of training Multilayer Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neural_network import MLPClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multilayer Perceptron (MLP) Classifier model mlp_model = MLPClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset mlp_model.fit(X, y) # predict classes for the entire dataset y_pred = mlp_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multilayer Perceptron (MLP) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mlp_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"mlp_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Multilayer Perceptron (MLP) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
2.22.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Multilayer Perceptron
//+------------------------------------------------------------------+ //| Iris_MLPClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mlp_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MLPClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier correct results: 98.00% Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier all samples accuracy=0.980000 Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 98 %, was der Genauigkeit des Originalmodells entspricht.
2.22.3. ONNX-Darstellung des Klassifizierungsmodells mehrschichtigen Perceptron
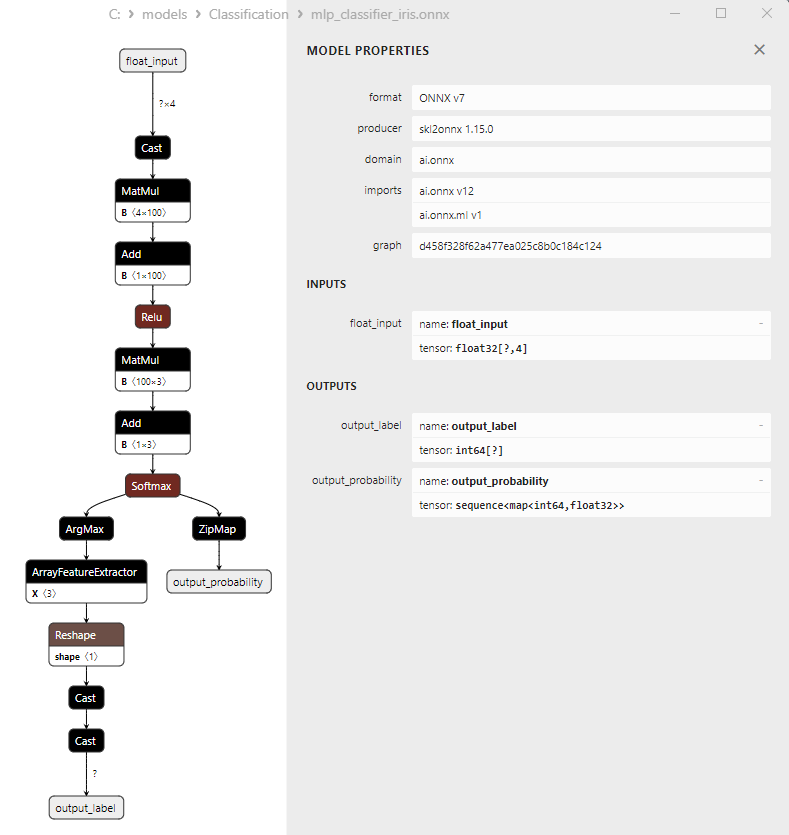
Abbildung 36. ONNX-Darstellung des Klassifizierungsmodells Multilayer Perceptron in Netron
2.23. Linear Discriminant Analysis (LDA) Classifier
Der Klassifikator der lineare Diskriminanzanalyse (LDA) ist eine maschinelle Lernmethode, die für Klassifizierungsaufgaben verwendet wird. Sie gehört zur Familie der Methoden zur Dimensionalitätsreduktion und zur Klassifizierung im niedrigdimensionalen Raum. LDA konstruiert Hyperebenen, um die Trennung zwischen den Klassen zu maximieren.
Prinzipien des LDA-Klassifikators:
- Dimensionalitätsreduktion: Die Kernidee von LDA ist die Dimensionalitätsreduktion. Es zielt darauf ab, einen neuen Merkmalsraum zu finden, in dem die Datenklassen maximal getrennt sind.
- Maximierung der Trennung: LDA konstruiert Hyperebenen (Linearkombinationen von Merkmalen), die die Differenz zwischen den Mittelwerten der Merkmale in verschiedenen Klassen maximieren und die Varianz innerhalb jeder Klasse minimieren.
- Trainingsparameter: Das LDA-Modell wird auf dem Trainingsdatensatz trainiert, wobei die Parameter der Hyperebenen und Datenprojektionen in den neuen Merkmalsraum berechnet werden.
Vorteile des LDA-Klassifikators:
- Verbesserte Klassentrennung: LDA kann die Klassentrennung in Daten erheblich verbessern, insbesondere in Fällen, in denen sich die Klassen im ursprünglichen Merkmalsraum stark überschneiden.
- Dimensionalitätsreduktion: LDA kann auch zur Dimensionalitätsreduktion von Daten verwendet werden, was für die Visualisierung und die Verringerung der Rechenkomplexität nützlich sein kann.
Einschränkungen des LDA-Klassifikators:
- Normalitätsannahme: LDA geht davon aus, dass die Merkmale einer Normalverteilung folgen und die Klassen gleiche Kovarianzmatrizen haben. Wenn diese Annahmen nicht erfüllt sind, kann die LDA weniger genaue Ergebnisse liefern.
- Empfindlichkeit gegenüber Ausreißern: LDA kann empfindlich auf Ausreißer in den Daten reagieren, da diese die Berechnung der Modellparameter beeinflussen können.
- Herausforderungen bei der Mehrklassenklassifizierung: LDA wurde ursprünglich für die binäre Klassifikation entwickelt, und seine Erweiterung auf Mehrklassenaufgaben erfordert eine Anpassung.
Der LDA-Klassifikator ist eine wertvolle Methode für Klassifizierungs- und Dimensionalitätsreduktionsaufgaben, insbesondere wenn eine bessere Klassentrennung erforderlich ist. Sie wird häufig in der Statistik, der Biologie, der medizinischen Analyse und in anderen Bereichen zur Datenanalyse und -klassifizierung eingesetzt.
2.23.1. Code zur Erstellung des Klassifizierungsmodells der linearen Diskriminanzanalyse (LDA)
Dieser Code veranschaulicht den Prozess des Trainings eines LDA-Klassifikators (Linear Discriminant Analysis) mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_LDAClassifier.py # The code demonstrates the process of training Linear Discriminant Analysis (LDA) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Linear Discriminant Analysis (LDA) Classifier model lda_model = LinearDiscriminantAnalysis() # train the model on the entire dataset lda_model.fit(X, y) # predict classes for the entire dataset y_pred = lda_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Linear Discriminant Analysis (LDA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(lda_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"lda_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
2.23.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell der linearen Diskriminanzanalyse (LDA)
//+------------------------------------------------------------------+ //| Iris_LDAClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "lda_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LDAClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier correct results: 98.00% Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier all samples accuracy=0.980000 Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 98 %, was der Genauigkeit des Originalmodells entspricht.
2.23.3. ONNX-Darstellung des Klassifizierungsmodells der linearen Diskriminanzanalyse (LDA)
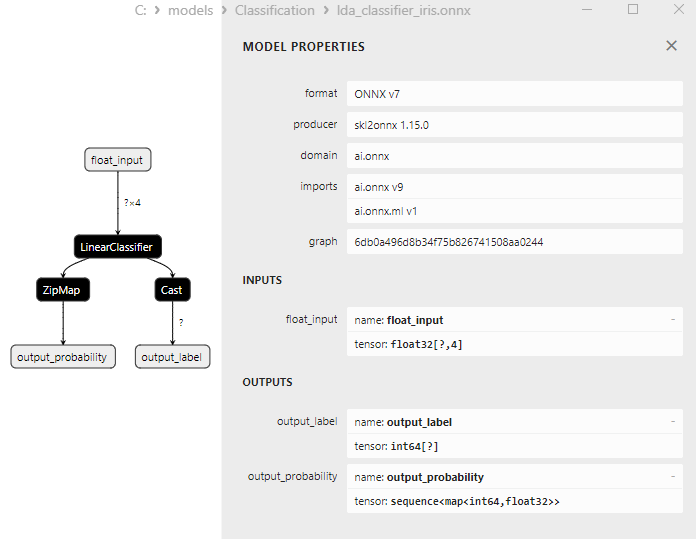
Abbildung 37. ONNX-Darstellung des Klassifizierungsmodells der linearen Diskriminanzanalyse (LDA) in Netron
2.24. Hist Gradient Boosting
Der Hist Gradient Boosting Classifier ist ein Algorithmus für maschinelles Lernen, der zur Familie der Gradient-Boosting-Algorithmen gehört und für Klassifizierungsaufgaben konzipiert ist. Es handelt sich um eine effiziente und leistungsstarke Methode, die in der Datenanalyse und beim maschinellen Lernen weit verbreitet ist.
Grundsätze des Hist Gradient Boosting:
- Gradientenverstärkung: Der Hist Gradient Boosting Classifier basiert auf der Gradient-Boosting-Methode, bei der ein Ensemble von Entscheidungsbäumen gebildet wird, um die Klassifizierung zu verbessern. Dies geschieht, indem nacheinander schwache Modelle trainiert und die Fehler der vorherigen Modelle korrigiert werden.
- Histogramm-Verwendung: Das „Hist“ im Namen weist darauf hin, dass dieser Algorithmus Histogramme für eine effiziente Datenverarbeitung verwendet. Anstelle einer erschöpfenden Aufzählung von Merkmalen werden beim Hist Gradient Boosting Histogramme von Merkmalen erstellt, was eine schnelle Konstruktion von Entscheidungsbäumen ermöglicht.
- Training der Residuen: Wie andere Gradient-Boosting-Methoden trainiert Hist Gradient Boosting jeden neuen Baum anhand der Residuen des vorherigen Modells, um die Vorhersagen zu verfeinern.
Vorteile des Hist Gradient Boosting:
- Hohe Genauigkeit: Der Hist Gradient Boosting Classifier bietet in der Regel eine hohe Klassifizierungsgenauigkeit, insbesondere bei Verwendung einer großen Anzahl von Bäumen.
- Effizienz: Durch die Verwendung von Histogrammen kann der Algorithmus große Datensätze effizient verarbeiten und schnell ein Ensemble bilden.
- Fähigkeit zum Umgang mit heterogenen Daten: Der Algorithmus kann mit heterogenen Daten umgehen, einschließlich kategorischer und numerischer Merkmale.
Einschränkungen des Hist Gradient Boosting:
- Anfälligkeit für Überanpassung: Wenn die Parameter nicht richtig eingestellt sind oder wenn eine große Anzahl von Bäumen verwendet wird, kann der Hist Gradient Boosting Classifier zu einer Überanpassung neigen.
- Abstimmung der Parameter: Wie andere Gradient-Boosting-Algorithmen erfordert auch Hist Gradient Boosting eine sorgfältige Abstimmung der Parameter für eine optimale Leistung.
Der Hist Gradient Boosting Classifier ist ein leistungsstarker Algorithmus für Klassifizierungs- und Regressionsaufgaben, der eine hohe Genauigkeit und Effizienz bei der Datenverarbeitung bietet. Sie findet in verschiedenen Bereichen Anwendung, z. B. in der Datenanalyse, der Bioinformatik, im Finanzwesen und in anderen Bereichen.
2.24.1. Code zur Erstellung des Klassifizierungsmodells Histogram-basierten Gradient-Boosting
Dieser Code demonstriert den Prozess des Trainings eines Histogram-Based Gradient Boosting Classifier mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_HistGradientBoostingClassifier.py # The code demonstrates the process of training Histogram-Based Gradient Boosting Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Histogram-Based Gradient Boosting Classifier model hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) # train the model on the entire dataset hist_gradient_boosting_model.fit(X, y) # predict classes for the entire dataset y_pred = hist_gradient_boosting_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Hist Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"hist_gradient_boosting_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Hist Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Hist Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
2.24.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell Histogram-Based Gradient Boosting
//+------------------------------------------------------------------+ //| Iris_HistGradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "hist_gradient_boosting_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="HistGradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_HistGradientBoostingClassifier (EURUSD,H1) model:HistGradientBoostingClassifier correct results: 100.00% Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier all samples accuracy=1.000000 Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 100 %, was der Genauigkeit des Originalmodells entspricht.
2.24.3. ONNX-Darstellung des Klassifizierungsmodells Histogramm-basierten Gradient-Boosting
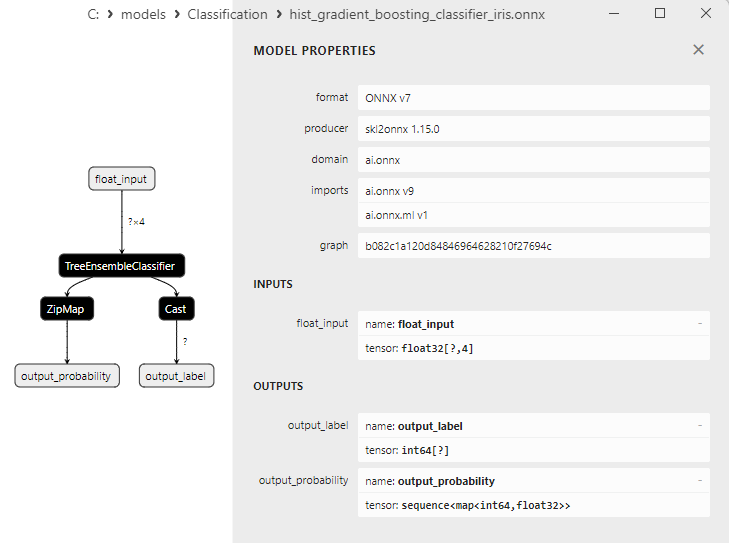
Abbildung 38. ONNX-Darstellung des Klassifizierungsmodells Histogramm-basierten Gradient-Boosting in Netron
2.25. CategoricalNB Classifier
CategoricalNB ist ein Klassifizierungsalgorithmus, der auf dem bayesschen Theorem basiert. Es wurde speziell für Datensätze mit kategorialen Merkmalen entwickelt und wird häufig bei der Textklassifizierung, der Spam-Erkennung und anderen Anwendungen mit diskreten Daten eingesetzt.
Grundsätze der kategorialenNB:
- Naive Bayes Klassifikator: CategoricalNB ist eine Art von Naive-Bayes-Klassifikator, der auf dem bayesschen Theorem basiert. Es berechnet die Wahrscheinlichkeit der Zugehörigkeit zu einer bestimmten Klasse für einen Satz von Merkmalen unter Verwendung von bedingten Wahrscheinlichkeiten für jedes Merkmal bei gegebener Klasse.
- Kategorische Merkmale: Im Gegensatz zum Gaußschen Naive-Bayes-Klassifikator, der von kontinuierlichen Merkmalen mit einer Normalverteilung ausgeht, eignet sich CategoricalNB für Datensätze mit kategorialen Merkmalen. Es modelliert die Wahrscheinlichkeitsverteilung der einzelnen Merkmale für jede Klasse.
- Annahme der Unabhängigkeit: Das „naiv“ im Naive-Bayes-Klassifikator kommt von der Annahme der Merkmalsunabhängigkeit. CategoricalNB geht davon aus, dass die Merkmale in Bezug auf die Klasse bedingt unabhängig sind. Obwohl diese Annahme in der Praxis nicht immer erfüllt ist, können naive Bayes-Methoden bei vielen realen Datensätzen gute Ergebnisse erzielen.
Vorteile von CategoricalNB:
- Effizienz: CategoricalNB ist rechnerisch effizient und skalierbar für große Datensätze. Es benötigt nur wenig Speicherplatz und kann schnelle Vorhersagen liefern.
- Interpretierbarkeit: Durch seine probabilistische Natur ist CategoricalNB interpretierbar. Sie kann Aufschluss darüber geben, welche Merkmale die Vorhersage beeinflussen.
- Umgang mit kategorischen Daten: CategoricalNB ist speziell für Datensätze mit kategorialen Merkmalen konzipiert. Es kann effizient mit Textdaten und anderen diskreten Merkmalstypen umgehen.
- Grundlegende Leistung: Es dient oft als starkes Basismodell für Textklassifizierungsaufgaben und kann komplexere Algorithmen bei kleinen Datensätzen übertreffen.
Einschränkungen der kategorischenNB:
- Annahme der Unabhängigkeit: Die Annahme der Merkmalsunabhängigkeit gilt möglicherweise nicht für alle Datensätze. Wenn die Merkmale stark voneinander abhängig sind, kann sich die Leistung von CategoricalNB verschlechtern.
- Empfindlichkeit gegenüber Merkmalsskalierung: CategoricalNB erfordert keine Merkmals-Skalierung, da es mit kategorischen Daten arbeitet. In einigen Fällen kann jedoch die Normalisierung oder Codierung kategorischer Merkmale auf unterschiedliche Weise die Leistung beeinträchtigen.
- Begrenzte Ausdruckskraft: CategoricalNB erfasst komplexe Datenabhängigkeiten möglicherweise nicht so gut wie komplexere Algorithmen, z. B. Deep-Learning-Modelle.
- Umgang mit fehlenden Daten: Es wird davon ausgegangen, dass keine fehlenden Werte im Datensatz vorhanden sind und dass fehlende Werte vorverarbeitet werden müssen.
CategoricalNB ist ein wertvoller Klassifizierungsalgorithmus, der sich besonders für Datensätze mit kategorischen Merkmalen eignet. Seine Einfachheit, Effizienz und Interpretierbarkeit machen es zu einem nützlichen Werkzeug für verschiedene Klassifizierungsaufgaben. Trotz Einschränkungen wie der Annahme der Unabhängigkeit bleibt es eine beliebte Wahl für die Textklassifizierung und andere Aufgaben, bei denen diskrete Daten dominieren. Bei der Arbeit mit kategorialen Daten ist es oft sinnvoll, CategoricalNB als Basismodell zu verwenden. Es ist jedoch wichtig, seine Leistung im Vergleich zu komplexeren Modellen zu bewerten, vor allem, wenn es Merkmalsabhängigkeiten in den Daten gibt.
2.25.1. Code zur Erstellung des Klassifizierungsmodells CategoricalNB
Dieser Code demonstriert den Prozess des Trainings eines CategoricalNB Classifier mit dem Iris-Datensatz, den Export in das ONNX-Format und die Durchführung der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_CategoricalNBClassifier.py # The code demonstrates the process of training CategoricalNB Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import CategoricalNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a CategoricalNB model categorical_nb_model = CategoricalNB() # train the model on the entire dataset categorical_nb_model.fit(X, y) # predict classes for the entire dataset y_pred = categorical_nb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of CategoricalNB model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(categorical_nb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "categorical_nb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of CategoricalNB model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of CategoricalNB model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
2.25.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell CategoricalNB
//+------------------------------------------------------------------+ //| Iris_CategoricalNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "categorical_nb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CategoricalNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Ausgabe:
Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier correct results: 93.33% Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier all samples accuracy=0.933333 Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier batch test accuracy=0.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 93,33 %, was der Genauigkeit des Originalmodells entspricht.
2.25.3. ONNX-Darstellung des Klassifizierungsmodells CategoricalNB
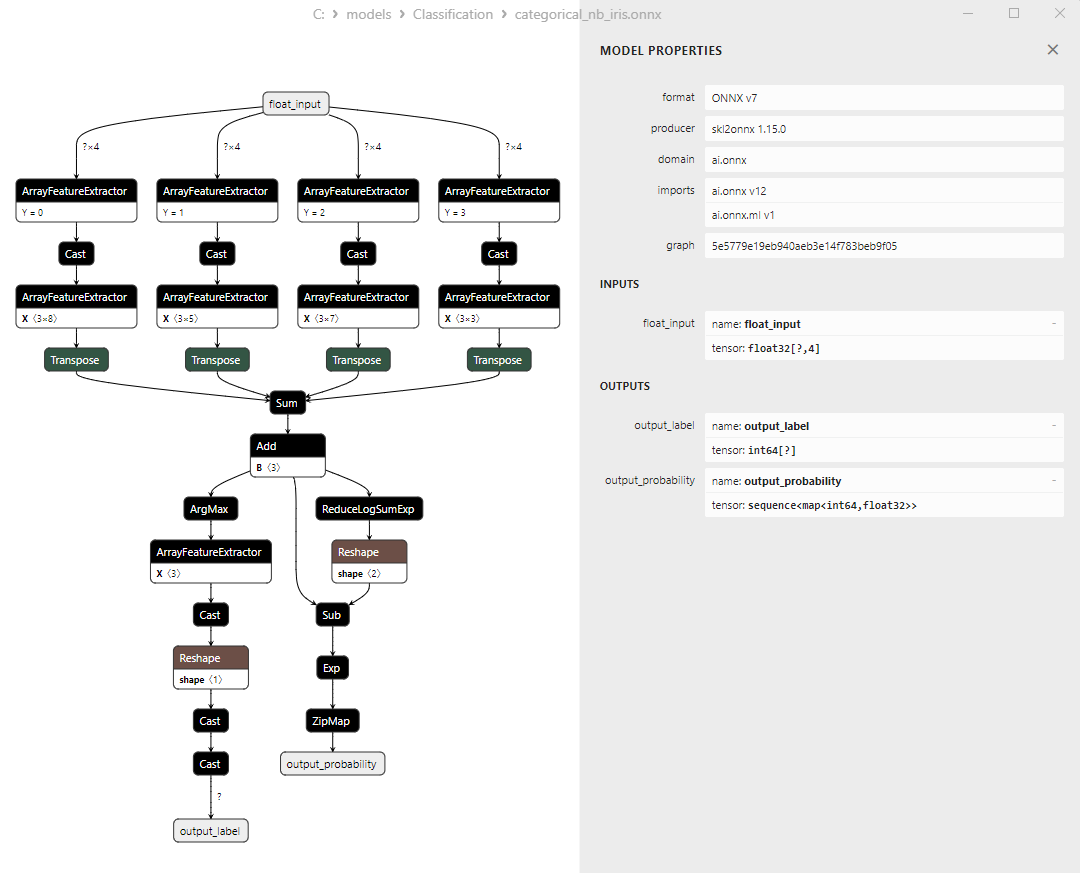
Abbildung 39. ONNX-Darstellung des Klassifizierungsmodells CategoricalNB in Netron
Anmerkung zu den Modellen ExtraTreeClassifier und ExtraTreesClassifier
ExtraTreeClassifier und ExtraTreesClassifier sind zwei verschiedene Klassifikatoren, deren Hauptunterschied in ihrer Arbeitsweise liegt:
ExtraTreeClassifier (Extremely Randomized Trees Classifier):
- Dieser Klassifikator ist auch als Extremely Randomized Trees oder Extra-Trees bekannt.
- Es basiert auf der Idee von Zufallsentscheidungsbäumen.
- In ExtraTreeClassifier erfolgt die Auswahl der Aufteilung für jeden Baumknoten nach dem Zufallsprinzip ohne vorherige Suche nach der besten Aufteilung.
- Dadurch ist der Klassifikator weniger rechenintensiv als der klassische Random Forest, da die Berechnung optimaler Teilungen für jeden Knoten entfällt.
- ExtraTreeClassifier verwendet oft zufällige Schwellenwerte für Merkmale und zufälliges Teilen, was zu mehr zufälligen Bäumen führt.
- Das Fehlen einer Suche nach den besten Splits macht ExtraTreeClassifier schneller, aber weniger genau als Random Forest.
ExtraTreesClassifier (Extremely Randomized Trees Classifier):
- ExtraTreesClassifier ist ebenfalls ein Klassifikator, der auf der Methode der Extrem Randomized Trees basiert.
- Der Hauptunterschied zwischen ExtraTreesClassifier und ExtraTreeClassifier besteht darin, dass ExtraTreesClassifier zufällige Aufteilungen vornimmt, um die besten Aufteilungen an jedem Baumknoten auszuwählen.
- Dies bedeutet, dass ExtraTreesClassifier bei der Auswahl optimaler Splits einen Zufallsforst mit einem zusätzlichen Zufallsgrad anwendet.
- ExtraTreesClassifier ist in der Regel genauer als ExtraTreeClassifier, da er zufällige Aufteilungen vornimmt, um die besten Merkmale für die Aufteilung zu finden.
- Der ExtraTreesClassifier kann jedoch rechenintensiver sein, da er eine breitere Suche nach optimalen Splits durchführen muss.
Zusammenfassend lässt sich sagen, dass der Hauptunterschied zwischen diesen beiden Klassifikatoren im Grad der Zufälligkeit bei der Splitauswahl liegt. ExtraTreesClassifier trifft eine zufällige Auswahl für jeden Knoten, ohne nach den besten Splits zu suchen, während ExtraTreesClassifier zufällige Splits durchführt und dabei nach optimalen Splits an jedem Knoten sucht.
2.26. ExtraTreeClassifier
Grundsätze des ExtraTreeClassifier:
- Zufällige Knotenaufteilung: Das Hauptprinzip von ExtraTreeClassifier besteht darin, dass es die Aufteilung für jeden Baumknoten zufällig auswählt. Dies unterscheidet sich von traditionellen Entscheidungsbäumen, die das beste Merkmal für die Aufteilung auswählen. ExtraTreeClassifier führt Splits durch, ohne den besten Split zu berücksichtigen, was ihn zufälliger und resistenter gegen eine Überanpassung macht.
- Aggregation der Ergebnisse: Während der Konstruktion des Ensembles erstellt ExtraTreeClassifier mehrere Zufallsbäume und aggregiert deren Ergebnisse. Dies geschieht, um die Generalisierung des Modells zu verbessern und die Varianz zu verringern. Ein Ensemble von Bäumen hilft bei der Bekämpfung von Überanpassungen und erhöht die Stabilität der Vorhersagen.
- Zufällige Schwellenwerte: Bei der Aufteilung von Knoten wählt ExtraTreeClassifier für jedes Merkmal zufällige Schwellenwerte und nicht bestimmte optimale Werte. Dies führt zu mehr Zufälligkeit und Modellstabilität.
- Widerstandsfähigkeit gegen Überanpassung: Dank der zufälligen Teilung und der fehlenden Auswahl des besten Splits ist der ExtraTreeClassifier im Vergleich zu normalen Entscheidungsbäumen weniger anfällig für Überanpassung.
- Hohe Trainingsgeschwindigkeit: ExtraTreeClassifier benötigt weniger Rechenressourcen für das Training als viele andere Algorithmen, wie z. B. Random Forests. Das macht ihn schnell und effizient für große Datenmengen.
- Vielseitigkeit: ExtraTreeClassifier kann sowohl für Klassifizierungs- als auch für Regressionsaufgaben verwendet werden, was ihn zu einem vielseitigen Algorithmus für verschiedene Problemtypen macht.
- Zufälligkeit: Die Verwendung von Zufallsaufteilungen kann in manchen Fällen zu weniger genauen Modellen führen. Eine sorgfältige Abstimmung der Parameter ist wichtig.
- Empfindlichkeit gegenüber Ausreißern: Der ExtraTreeClassifier kann empfindlich auf Ausreißer in den Daten reagieren, da er zufällige Aufteilungen erstellt. Dies kann in einigen Fällen zu instabilen Vorhersagen führen.
- Geringere Interpretierbarkeit: Im Vergleich zu regulären Entscheidungsbäumen ist der ExtraTreeClassifier weniger interpretierbar und schwieriger zu erklären.
2.26.1. Code zur Erstellung des ExtraTreeClassifier
Dieser Code demonstriert den Prozess des Trainings eines ExtraTreeClassifier-Modells mit dem Iris-Datensatz, des Exports in das ONNX-Format und der Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_ExtraTreeClassifier.py # The code demonstrates the process of training ExtraTree Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import ExtraTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreeClassifier model extra_tree_model = ExtraTreeClassifier() # train the model on the entire dataset extra_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreeClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreeClassifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of ExtraTreeClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
2.26.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell ExtraTreeClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_ExtraTreeClassifier (EURUSD,H1) model:ExtraTreeClassifier correct results: 100.00% Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier all samples accuracy=1.000000 Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 100 %, was der Genauigkeit des Originalmodells entspricht.
2.26.3. ONNX-Darstellung des Klassifizierungsmodells ExtraTreeClassifier
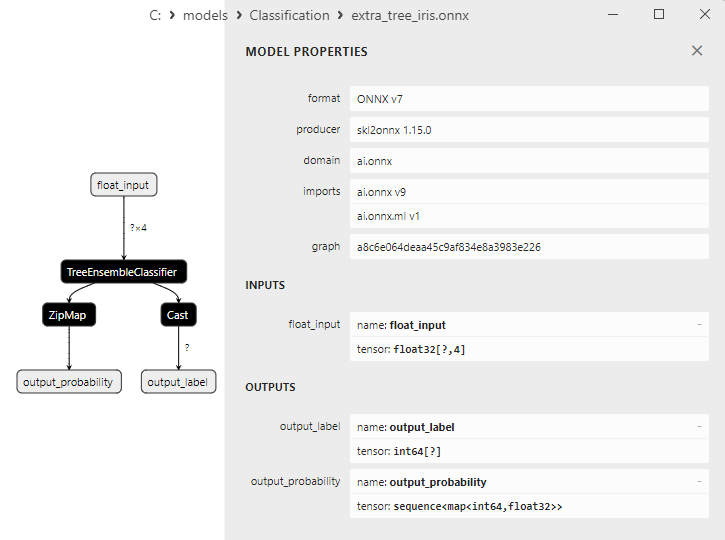
Abbildung 40. ONNX-Darstellung des Klassifizierungsmodells ExtraTreeClassifier in Netron
2.27. ExtraTreesClassifier
ExtraTreesClassifier ist ein leistungsstarker Algorithmus für maschinelles Lernen, der für Klassifizierungsaufgaben verwendet wird. Dieser Algorithmus ist eine Erweiterung und Verbesserung des Random Forest und bietet mehrere Vor- und Nachteile.Grundsätze des ExtraTreesClassifier:
- Bootstrap-Stichproben: Ähnlich wie Random Forest verwendet ExtraTreesClassifier die Bootstrap-Methode, um mehrere Unterstichproben aus dem Trainingsdatensatz zu erstellen. Das bedeutet, dass für jeden Baum eine zufällige Unterstichprobe mit Ersatz aus den Originaldaten erstellt wird.
- Zufällige Aufteilungen: Im Gegensatz zu Random Forest, bei dem für jeden Baumknoten das beste Merkmal für die Aufteilung ausgewählt wird, verwendet ExtraTreesClassifier zufällige Merkmale und zufällige Schwellenwerte für die Aufteilung der Knoten. Dies macht die Bäume zufälliger und reduziert die Überanpassung.
- Abstimmung: Nachdem eine Reihe von Bäumen konstruiert wurde, stimmt jeder Baum für die Klasse des Objekts. Letztendlich wird die Klasse mit den meisten Stimmen zur vorhergesagten Klasse.
- Reduzierte Überanpassung: Die Verwendung von zufälligen Aufteilungen und zufälligen Merkmalen macht ExtraTreesClassifier im Vergleich zu herkömmlichen Entscheidungsbäumen weniger anfällig für Überanpassung.
- Hohe Trainingsgeschwindigkeit: ExtraTreesClassifier benötigt im Vergleich zu einigen anderen Algorithmen, wie z. B. Gradient Boosting, weniger Rechenressourcen für das Training. Das macht ihn schnell und effizient, besonders bei großen Datenmengen.
- Robustheit gegenüber Ausreißern: Dank des Ensembles von Bäumen und zufälligen Aufteilungen ist der ExtraTreesClassifier im Allgemeinen robuster gegenüber Ausreißern in den Daten.
- Komplexe Interpretierbarkeit: Die Analyse und Interpretation eines ExtraTreesClassifier-Modells kann aufgrund der großen Anzahl von zufälligen Aufteilungen und Merkmalen eine Herausforderung darstellen.
- Abstimmung der Parameter: Trotz seiner Effizienz kann der ExtraTreesClassifier eine sorgfältige Abstimmung der Hyperparameter erfordern, um eine optimale Leistung zu erzielen.
- Nicht immer mit dem besten Ergebnis: Bei einigen Aufgaben kann der ExtraTreesClassifier weniger genau sein als andere Algorithmen, z. B. Gradient Boosting.
2.27.1. Code zur Erstellung des Klassifizierungsmodells ExtraTreesClassifier
Dieser Code demonstriert den Prozess des Trainings eines ExtraTreesClassifier-Modells mit dem Iris-Datensatz, den Export in das ONNX-Format und die Klassifizierung mit dem ONNX-Modell. Außerdem wird die Genauigkeit sowohl des ursprünglichen Modells als auch des ONNX-Modells bewertet.
# Iris_ExtraTreesClassifier.py # The code demonstrates the process of training ExtraTrees Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import ExtraTreesClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreesClassifier model extra_trees_model = ExtraTreesClassifier() # train the model on the entire dataset extra_trees_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_trees_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreesClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_trees_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_trees_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreesClassifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of ExtraTreesClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: output_label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
2.27.2. MQL5-Code für die Arbeit mit dem Klassifizierungsmodell ExtraTreesClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_trees_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_ExtraTreesClassifier (EURUSD,H1) model:ExtraTreesClassifier correct results: 100.00% Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier all samples accuracy=1.000000 Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier batch test accuracy=1.000000
Die Genauigkeit des exportierten ONNX-Modells auf dem vollständigen Iris-Datensatz beträgt 100 %, was der Genauigkeit des Originalmodells entspricht.
2.27.3. ONNX-Darstellung des Klassifizierungsmodells ExtraTreesClassifier
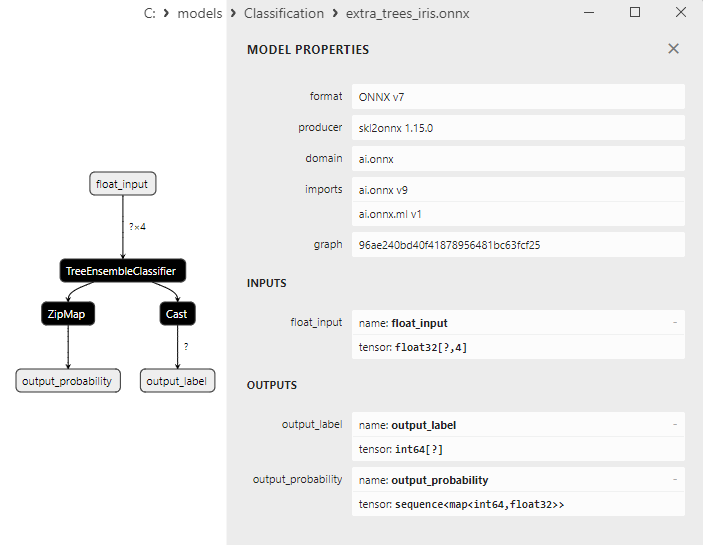
Abbildung 41. ONNX-Darstellung des Klassifizierungsmodells ExtraTrees in Netron
2.28. Vergleich der Genauigkeit aller Modelle
Betrachten wir nun alle Modelle zusammen und vergleichen ihre Leistungen. Zunächst werden wir den Vergleich mit Python durchführen und dann die gespeicherten ONNX-Modelle in MetaTrader 5 laden und ausführen.
2.28.1. Code für die Berechnung aller Modelle und die Erstellung eines Vergleichsdiagramms der Genauigkeit
Dieses Skript berechnet 27 Klassifikationsmodelle aus dem Scikit-Learn-Paket auf dem vollständigen Iris-Datensatz von Fisher, exportiert die Modelle in das ONNX-Format, führt sie aus und vergleicht die Genauigkeit der Original- und ONNX-Modelle.
# Iris_AllClassifiers.py # The code demonstrates the process of training 27 Classifier models on the Iris dataset, exports them to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original and the ONNX models. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.metrics import accuracy_score from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np import matplotlib.pyplot as plt from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create and train each classifier model from sklearn.svm import SVC svc_model = SVC() svc_model.fit(X, y) from sklearn.ensemble import RandomForestClassifier random_forest_model = RandomForestClassifier(random_state=42) random_forest_model.fit(X, y) from sklearn.ensemble import GradientBoostingClassifier gradient_boosting_model = GradientBoostingClassifier(random_state=42) gradient_boosting_model.fit(X, y) from sklearn.ensemble import AdaBoostClassifier adaboost_model = AdaBoostClassifier(random_state=42) adaboost_model.fit(X, y) from sklearn.ensemble import BaggingClassifier bagging_model = BaggingClassifier(random_state=42) bagging_model.fit(X, y) from sklearn.neighbors import KNeighborsClassifier knn_model = KNeighborsClassifier() knn_model.fit(X, y) from sklearn.neighbors import RadiusNeighborsClassifier radius_neighbors_model = RadiusNeighborsClassifier(radius=1.0) radius_neighbors_model.fit(X, y) from sklearn.tree import DecisionTreeClassifier decision_tree_model = DecisionTreeClassifier(random_state=42) decision_tree_model.fit(X, y) from sklearn.linear_model import LogisticRegression logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) logistic_regression_model.fit(X, y) from sklearn.linear_model import RidgeClassifier ridge_classifier_model = RidgeClassifier(random_state=42) ridge_classifier_model.fit(X, y) from sklearn.linear_model import PassiveAggressiveClassifier passive_aggressive_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) passive_aggressive_model.fit(X, y) from sklearn.linear_model import Perceptron perceptron_model = Perceptron(max_iter=1000, random_state=42) perceptron_model.fit(X, y) from sklearn.linear_model import SGDClassifier sgd_model = SGDClassifier(max_iter=1000, random_state=42) sgd_model.fit(X, y) from sklearn.naive_bayes import GaussianNB gaussian_nb_model = GaussianNB() gaussian_nb_model.fit(X, y) from sklearn.naive_bayes import MultinomialNB multinomial_nb_model = MultinomialNB() multinomial_nb_model.fit(X, y) from sklearn.naive_bayes import ComplementNB complement_nb_model = ComplementNB() complement_nb_model.fit(X, y) from sklearn.naive_bayes import BernoulliNB bernoulli_nb_model = BernoulliNB() bernoulli_nb_model.fit(X, y) from sklearn.naive_bayes import CategoricalNB categorical_nb_model = CategoricalNB() categorical_nb_model.fit(X, y) from sklearn.tree import ExtraTreeClassifier extra_tree_model = ExtraTreeClassifier(random_state=42) extra_tree_model.fit(X, y) from sklearn.ensemble import ExtraTreesClassifier extra_trees_model = ExtraTreesClassifier(random_state=42) extra_trees_model.fit(X, y) from sklearn.svm import LinearSVC # Import LinearSVC linear_svc_model = LinearSVC(random_state=42) linear_svc_model.fit(X, y) from sklearn.svm import NuSVC nu_svc_model = NuSVC() nu_svc_model.fit(X, y) from sklearn.linear_model import LogisticRegressionCV logistic_regression_cv_model = LogisticRegressionCV(cv=5, max_iter=1000, random_state=42) logistic_regression_cv_model.fit(X, y) from sklearn.neural_network import MLPClassifier mlp_model = MLPClassifier(max_iter=1000, random_state=42) mlp_model.fit(X, y) from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda_model = LinearDiscriminantAnalysis() lda_model.fit(X, y) from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) hist_gradient_boosting_model.fit(X, y) from sklearn.linear_model import RidgeClassifierCV ridge_classifier_cv_model = RidgeClassifierCV() ridge_classifier_cv_model.fit(X, y) # define a dictionary to store results results = {} # loop through the models for model_name, classifier_model in [ ('SVC Classifier', svc_model), ('Random Forest Classifier', random_forest_model), ('Gradient Boosting Classifier', gradient_boosting_model), ('AdaBoost Classifier', adaboost_model), ('Bagging Classifier', bagging_model), ('K-NN Classifier', knn_model), ('Radius Neighbors Classifier', radius_neighbors_model), ('Decision Tree Classifier', decision_tree_model), ('Logistic Regression Classifier', logistic_regression_model), ('Ridge Classifier', ridge_classifier_model), ('Ridge ClassifierCV', ridge_classifier_cv_model), ('Passive-Aggressive Classifier', passive_aggressive_model), ('Perceptron Classifier', perceptron_model), ('SGD Classifier', sgd_model), ('Gaussian Naive Bayes Classifier', gaussian_nb_model), ('Multinomial Naive Bayes Classifier', multinomial_nb_model), ('Complement Naive Bayes Classifier', complement_nb_model), ('Bernoulli Naive Bayes Classifier', bernoulli_nb_model), ('Categorical Naive Bayes Classifier', categorical_nb_model), ('Extra Tree Classifier', extra_tree_model), ('Extra Trees Classifier', extra_trees_model), ('LinearSVC Classifier', linear_svc_model), ('NuSVC Classifier', nu_svc_model), ('Logistic RegressionCV Classifier', logistic_regression_cv_model), ('MLP Classifier', mlp_model), ('Linear Discriminant Analysis Classifier', lda_model), ('Hist Gradient Boosting Classifier', hist_gradient_boosting_model) ]: # predict classes for the entire dataset y_pred = classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + f"{model_name.lower().replace(' ', '_')}_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) # store results results[model_name] = { 'accuracy': accuracy, 'accuracy_onnx': accuracy_onnx } # print the accuracy of the original model and the ONNX model #print(f"{model_name} - Original Accuracy: {accuracy}, ONNX Accuracy: {accuracy_onnx}") # sort the models based on accuracy sorted_results = dict(sorted(results.items(), key=lambda item: item[1]['accuracy'], reverse=True)) # print the sorted results print("Sorted Results:") for model_name, metrics in sorted_results.items(): print(f"{model_name} - Original Accuracy: {metrics['accuracy']:.4f}, ONNX Accuracy: {metrics['accuracy_onnx']:.4f}") # create comparison plots for sorted results fig, ax = plt.subplots(figsize=(12, 8)) model_names = list(sorted_results.keys()) accuracies = [sorted_results[model_name]['accuracy'] for model_name in model_names] accuracies_onnx = [sorted_results[model_name]['accuracy_onnx'] for model_name in model_names] bar_width = 0.35 index = range(len(model_names)) bar1 = plt.bar(index, accuracies, bar_width, label='Model Accuracy') bar2 = plt.bar([i + bar_width for i in index], accuracies_onnx, bar_width, label='ONNX Accuracy') plt.xlabel('Models') plt.ylabel('Accuracy') plt.title('Comparison of Model and ONNX Accuracy (Sorted)') plt.xticks([i + bar_width / 2 for i in index], model_names, rotation=90, ha='center') plt.legend() plt.tight_layout() plt.show()
Ausgabe:
Python Sorted Results: Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333Das Skript erzeugt auch ein Bild mit den zusammengefassten Ergebnissen aller 27 Modelle.
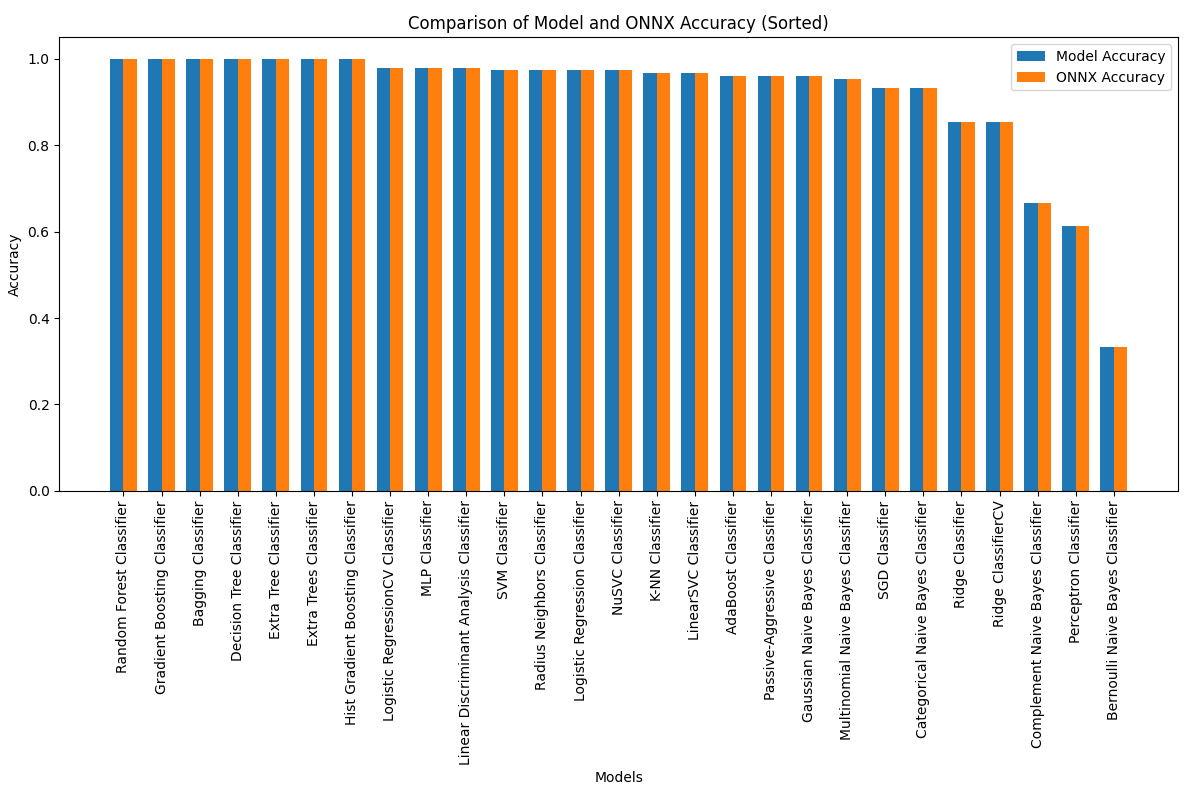
Abbildung 42. Vergleich der Genauigkeit von 27 Klassifizierungsmodellen und ihren ONNX-Versionen mit dem Iris-Datensatz
Auf der Grundlage der Ergebnisse der Genauigkeitsbewertung der ursprünglichen Modelle und ihrer ONNX-Versionen können die folgenden Schlussfolgerungen gezogen werden:
Sieben Modelle zeigten eine perfekte Genauigkeit (1,0000) sowohl in der Original- als auch in der ONNX-Version. Diese Modelle sind:
- Random Forest Classifier
- Gradient Boosting Classifier
- Bagging Classifier
- Decision Tree Classifier
- Extra Tree Classifier
- Extra Trees Classifier
- Hist Gradient Boosting Classifier
Die ONNX-Darstellungen dieser Modelle weisen ebenfalls eine hohe Genauigkeit auf.
Drei Modelle - Logistic RegressionCV Classifier, MLP Classifier und Linear Discriminant Analysis Classifier - erreichten sowohl in der Original- als auch in der ONNX-Version mit einer Genauigkeit von 0,9800 eine hohe Genauigkeit. Diese Modelle schneiden in beiden Darstellungen gut ab.
Mehrere Modelle, darunter SVC-Klassifikator, Radius Neighbors-Klassifikator, NuSVC-Klassifikator, K-NN-Klassifikator, LinearSVC-Klassifikator, AdaBoost-Klassifikator, Passiv-Aggressiv-Klassifikator, Gaußscher Naive-Bayes-Klassifikator und Multinomial-Naive-Bayes-Klassifikator, wiesen sowohl in der Original- als auch in der ONNX-Version eine gute Genauigkeit auf, mit Genauigkeitswerten von 0,9733, 0,9667 oder 0,9600. Diese Modelle behalten ihre Genauigkeit auch in der ONNX-Darstellung bei.
Modelle wie der SGD Classifier, Categorical Naive Bayes Classifier, Ridge Classifier, Complement Naive Bayes Classifier, Perceptron Classifier und Bernoulli Naive Bayes Classifier weisen eine geringere Genauigkeit auf, sind aber immer noch gut in der Lage, die Genauigkeit in ONNX beizubehalten.
Alle betrachteten Modelle behalten ihre Genauigkeit bei, wenn sie in das ONNX-Format exportiert werden, was darauf hindeutet, dass ONNX eine effiziente Methode zum Speichern und Wiederherstellen von Modellen des maschinellen Lernens darstellt. Es ist jedoch wichtig, daran zu denken, dass die Qualität des exportierten Modells von dem spezifischen Modellalgorithmus und den Parametern abhängen kann.
2.28.2. MQL5-Code für die Ausführung aller ONNX-Modelle
Dieses Skript führt alle ONNX-Modelle, die mit dem Skript in 2.28.1 gespeichert wurden, mi dem kompletten Iris-Datensatz von Fisher aus.
//+------------------------------------------------------------------+ //| Iris_AllClassifiers.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" //+------------------------------------------------------------------+ //| TestSampleSequenceMapOutput | //+------------------------------------------------------------------+ bool TestSampleSequenceMapOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- float out1[]; //--- struct Map { ulong key[]; float value[]; } out2[]; //--- bool res=ArrayResize(out1,input_data.Range(0))==input_data.Range(0); //--- if(res) { ulong input_shape[]= { input_data.Range(0), input_data.Range(1) }; ulong output_shape[]= { input_data.Range(0) }; //--- OnnxSetInputShape(model,0,input_shape); OnnxSetOutputShape(model,0,output_shape); //--- res=OnnxRun(model,0,input_data,out1,out2); //--- if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- model_class_id=-1; int max_idx=-1; float max_value=-1; //--- for(uint n=0; n<out2.Size(); n++) { //--- copy to arrays ArrayCopy(output_keys,out2[n].key); ArrayCopy(output_values,out2[n].value); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } } } } //--- return(res); } //+------------------------------------------------------------------+ //| TestSampleTensorOutput | //+------------------------------------------------------------------+ bool TestSampleTensorOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- ulong input_shape[]= { 1, 4}; OnnxSetInputShape(model,0,input_shape); //--- int output1[1]; float output2[1,3]; //--- ulong output_shape[]= {1}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {1,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,0,input_data,output1,output2); //--- class for these models in output1[0]; if(res) model_class_id=output1[0]; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("error in loading iris dataset from iris.csv"); return(false); } /*for(int k=0; k<total_samples; k++) { PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); }*/ //---- string iris_models[]= { "random_forest_classifier_iris.onnx", "gradient_boosting_classifier_iris.onnx", "bagging_classifier_iris.onnx", "decision_tree_classifier_iris.onnx", "extra_tree_classifier_iris.onnx", "extra_trees_classifier_iris.onnx", "hist_gradient_boosting_classifier_iris.onnx", "logistic_regressioncv_classifier_iris.onnx", "mlp_classifier_iris.onnx", "linear_discriminant_analysis_classifier_iris.onnx", "svc_classifier_iris.onnx", "radius_neighbors_classifier_iris.onnx", "logistic_regression_classifier_iris.onnx", "nusvc_classifier_iris.onnx", "k-nn_classifier_iris.onnx", "linearsvc_classifier_iris.onnx", "adaboost_classifier_iris.onnx", "passive-aggressive_classifier_iris.onnx", "gaussian_naive_bayes_classifier_iris.onnx", "multinomial_naive_bayes_classifier_iris.onnx", "sgd_classifier_iris.onnx", "categorical_naive_bayes_classifier_iris.onnx", "ridge_classifier_iris.onnx", "ridge_classifiercv_iris.onnx", "complement_naive_bayes_classifier_iris.onnx", "perceptron_classifier_iris.onnx", "bernoulli_naive_bayes_classifier_iris.onnx" }; //--- test all iris dataset sample by sample for(int i=0; i<ArraySize(iris_models); i++) { //--- load ONNX-model string model_name="IRIS_models\\"+iris_models[i]; //--- long model=OnnxCreate(model_name,0); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- check all samples int correct_results=0; for(int k=0; k<total_samples; k++) { int model_class_id=-1; //--- select data output processor string current_model=iris_models[i]; if(current_model=="svc_classifier_iris.onnx" || current_model=="linearsvc_classifier_iris.onnx" || current_model=="nusvc_classifier_iris.onnx" || current_model=="ridge_classifier_iris.onnx" || current_model=="ridge_classifiercv_iris.onnx" || current_model=="radius_neighbors_classifier_iris.onnx") { TestSampleTensorOutput(model,iris_samples[k],model_class_id); } else { TestSampleSequenceMapOutput(model,iris_samples[k],model_class_id); } //--- if(model_class_id==iris_samples[k].class_id) { correct_results++; //PrintFormat("sample=%d OK [class=%d]",iris_samples[k].sample_id,model_class_id); } else { //PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_class_id,iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } PrintFormat("%d model:%s accuracy: %.4f",i+1,model_name,1.0*correct_results/total_samples); //--- release model OnnxRelease(model); } //--- } return(0); } //+------------------------------------------------------------------+
Ausgabe:
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
Vergleiche mit den Ergebnissen des Skripts 2.28.1.1:
Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
Es ist erwähnenswert, dass die Ausführung aller gespeicherten ONNX-Modelle in MQL5 vollständig den Ergebnissen von 2.28.1 entspricht.
Die von uns untersuchten Modelle, die in das ONNX-Format umgewandelt wurden, behielten also ihre Klassifizierungsgenauigkeit bei.
Es ist erwähnenswert, dass sieben Modelle eine perfekte Klassifizierungsgenauigkeit (Genauigkeit=1,0) mit dem Iris-Datensatz erreichten:
- Random Forest Classifier;
- Gradient Boosting Classifier;
- Bagging Classifier;
- Decision Tree Classifier;
- Extra Tree Classifier;
- Extra Trees Classifier;
- Histogram Gradient Boosting Classifier.
Die übrigen 20 Modelle wiesen Klassifizierungsfehler auf.
Wenn Sie die Zeile 208 auskommentieren, zeigt das Skript auch die Iris-Datensatzproben an, die von jedem der Modelle falsch klassifiziert wurden:
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
2.29. Klassifizierungsmodelle in Scikit-Learn, die nicht in ONNX konvertiert werden konnten
Einige Klassifikationsmodelle konnten aufgrund von Fehlern im Prozess convert_sklearn nicht in das ONNX-Format konvertiert werden.
2.29.1. DummyClassifier
DummyClassifier ist ein Klassifikator in der Bibliothek Scikit-Learn, der als einfaches Basismodell für Klassifikationsaufgaben verwendet wird. Er ist für die Prüfung und Bewertung der Leistung komplexerer Klassifizierungsmodelle gedacht.
Arbeitsprinzip:
Der DummyClassifier arbeitet sehr einfach; er macht zufällige oder naive Vorhersagen ohne Berücksichtigung der Eingabedaten. Es bietet verschiedene Strategien (die über den Parameter „Strategie“ ausgewählt werden):
- „most_frequent“ (häufigste Klasse): Bei dieser Strategie wird immer die Klasse vorhergesagt, die im Trainingsdatensatz am häufigsten vorkommt. Sie kann in Situationen nützlich sein, in denen die Klassen unausgewogen sind und Sie die dominierende Klasse vorhersagen müssen.
- „stratified“ (geschichtete Auswahl): Mit dieser Strategie wird versucht, Vorhersagen zu treffen, die mit der Klassenverteilung im Trainingsdatensatz übereinstimmen. Dabei wird nach dem Zufallsprinzip geraten, aber die Klassenverhältnisse werden berücksichtigt.
- “uniform“ (gleichförmige Verteilung): Diese Strategie macht zufällige Vorhersagen mit gleicher Wahrscheinlichkeit für jede Klasse. Es ist nützlich, wenn die Klassen ausgeglichen sind und Sie testen wollen, wie Ihr Modell im Durchschnitt abschneidet.
Fähigkeiten:
- Einfachheit: DummyClassifier ist nützlich, um zu testen, wie schnell Sie ein Basismodell trainieren können und welche Ergebnisse es liefert. Sie kann für eine schnelle Leistungsbewertung anderer Klassifikatoren hilfreich sein.
- Pipeline-Nutzung: Sie können DummyClassifier als Basismodell innerhalb einer Pipeline verwenden, kombiniert mit anderen Transformationen und Modellen zum Vergleich und Testen.
Einschränkungen:
- Nutzt keine Daten: Der DummyClassifier macht zufällige oder naive Vorhersagen ohne Berücksichtigung der tatsächlichen Daten. Sie kann nicht aus Daten lernen oder Muster erkennen.
- Ungeeignet für komplexe Aufgaben: Dieser Klassifikator ist nicht für die Lösung komplexer Klassifizierungsaufgaben konzipiert und liefert im Allgemeinen keine guten Ergebnisse bei Aufgaben mit großen Datensätzen und komplizierten Mustern.
- Mangelnde Informativität: Die mit dem DummyClassifier erzielten Ergebnisse sind möglicherweise nicht sehr aussagekräftig und liefern keine nützlichen Informationen über die Modellleistung. Sie sind eher für Code-Tests und Evaluierungen geeignet.
Der DummyClassifier ist ein nützliches Werkzeug für erste Tests und die Bewertung von Klassifizierungsmodellen, aber seine Verwendung ist bei komplexen Aufgaben begrenzt, und es kann fortgeschrittene Klassifizierungsalgorithmen nicht ersetzen.
2.29.1.1. Code zum Erstellen des Klassifizierungsmodells DummyClassifier
# Iris_DummyClassifier.py
# The code demonstrates the process of training DummyClassifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a DummyClassifier model with the strategy "most_frequent"
dummy_classifier = DummyClassifier(strategy="most_frequent")
# train the model on the entire dataset
dummy_classifier.fit(X, y)
# predict classes for the entire dataset
y_pred = dummy_classifier.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of DummyClassifier model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "dummy_classifier_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print model path
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of DummyClassifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of DummyClassifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Das Modell wurde erfolgreich in Scikit-learn erstellt und ausgeführt, aber bei der Konvertierung in ONNX traten Fehler auf.
Auf der Registerkarte „Fehler“ werden Nachrichten über Konvertierungsfehler in das ONNX-Format angezeigt:
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12) Iris_DummyClassifier.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
Daher konnte das DummyClassifier-Modell nicht in ONNX konvertiert werden.
2.29.2. GaussianProcessClassifier
GaussianProcessClassifier ist ein Klassifikator, der gaußsche Prozesse für Klassifizierungsaufgaben verwendet. Es gehört zur Familie der Modelle, die gaußsche Prozesse verwenden, und kann bei Aufgaben nützlich sein, bei denen probabilistische Klassenschätzungen erforderlich sind.
Arbeitsprinzip:
- GaussianProcessClassifier verwendet einen Gauß-Prozess zur Modellierung der Abbildung vom Merkmalsraum auf den Raum der Klassenwahrscheinlichkeitsschätzungen.
- Es erstellt ein probabilistisches Modell für jede Klasse, indem es die Wahrscheinlichkeit der Zugehörigkeit eines Punktes zu jeder Klasse bewertet.
- Bei der Klassifizierung wählt es die Klasse mit der höchsten Wahrscheinlichkeit für einen bestimmten Punkt aus.
Fähigkeiten:
- Probabilistische Klassifizierung: GaussianProcessClassifier liefert probabilistische Klassenschätzungen, die für die Bewertung der Modellunsicherheit nützlich sein können.
- Anpassungsfähigkeit: Dieser Klassifikator kann sich an die Daten anpassen und seine Vorhersagen auf der Grundlage neuer Beobachtungen aktualisieren.
- Kalibrierung: Das Modell kann mit der Methode „calibrate“ kalibriert werden, um die Wahrscheinlichkeitsschätzungen zu verbessern.
Einschränkungen:
- Berechnungskomplexität: GaussianProcessClassifier kann bei großen Datensätzen und/oder hochdimensionalen Merkmalsräumen sehr rechenintensiv sein.
- Nicht geeignet für große Proben: Aufgrund seiner Rechenkomplexität ist dieser Klassifikator möglicherweise nicht effizient für das Training auf großen Datensätzen.
- Komplexität der Interpretation: gaußsche Prozesse können schwierig zu interpretieren und zu verstehen sein, insbesondere für Nutzer ohne Erfahrung in bayesscher Statistik.
GaussianProcessClassifier ist wertvoll für Aufgaben, bei denen probabilistische Klassenschätzungen wichtig sind und bei denen man mit den Rechenkosten umgehen kann. Für Klassifizierungsaufgaben in großen Datenbeständen oder bei einfachen Datenstrukturen können andere Klassifizierungsalgorithmen besser geeignet sein.
2.29.2.1. Code zur Erstellung des Klassifizierungsmodells GaussianProcessClassifier# Iris_GaussianProcessClassifier.py
# The code demonstrates the process of training Iris_GaussianProcess Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a GaussianProcessClassifier model with an RBF kernel
kernel = 1.0 * RBF(1.0)
gpc_model = GaussianProcessClassifier(kernel=kernel)
# train the model on the entire dataset
gpc_model.fit(X, y)
# predict classes for the entire dataset
y_pred = gpc_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of GaussianProcessClassifier model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(gpc_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "gpc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of GaussianProcessClassifier model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of GaussianProcessClassifier model: 0.9866666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Auf der Registerkarte „Fehler“ werden Nachrichten über Konvertierungsfehler in das ONNX-Format angezeigt:
onnx_model = convert_sklearn(gpc_model, initial_types=initial_type, target_opset=12) Iris_GaussianProcessClassifier.py 46 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is iplemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is iplemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is iplemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is iplemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
Daher konnte das GaussianProcessClassifier-Modell nicht in ONNX konvertiert werden.
2.29.3. LabelPropagation Classifier
LabelPropagation ist eine halbüberwachte Lernmethode, die für Klassifizierungsaufgaben verwendet wird. Die Hauptidee hinter dieser Methode ist die Weitergabe von Kennzeichnungen (Klassen) von gekennzeichneten Instanzen an nicht gekennzeichnete Instanzen in einer graphbasierten Datenstruktur.
Der LabelPropagation-Prozess:
- Es beginnt mit der Konstruktion eines Graphen, in dem die Knoten Dateninstanzen darstellen und die Kanten zwischen den Knoten die Ähnlichkeit oder Nähe zwischen den Instanzen widerspiegeln.
- Initiale Kennzeichenvergabe: Gekennzeichnete Instanzen werden mit ihren Kennzeichen (labels) versehen, und nicht gekennzeichnete Instanzen beginnen mit einer undefinierten Kennzeichen.
- Kennzeichenübertragung auf dem Graphen: Kennzeichen von gelabelten Instanzen werden auf der Grundlage der Ähnlichkeit zwischen den Instanzen auf nicht gelabelte Instanzen übertragen. Diese Ähnlichkeit kann auf verschiedene Weise ermittelt werden, z. B. anhand der nächsten Nachbarn im Graphen.
- Iterativer Prozess: Die Kennzeichen können sich über mehrere Iterationen hinweg ändern, wobei jede Iteration die Kennzeichen der nicht gekennzeichneten Instanzen auf der Grundlage der aktuellen Kennzeichen und der Ähnlichkeit der Instanzen aktualisiert.
- Stabilisierung: Der Prozess wird fortgesetzt, bis sich die Kennzeichen stabilisieren oder ein bestimmtes Abbruchkriterium erfüllt ist.
Vorteile von LabelPropagation:
- Verwendet Informationen aus nicht gekennzeichneten Daten: LabelPropagation ermöglicht die Verwendung von Informationen aus nicht gekennzeichneten Instanzen zur Verbesserung der Klassifizierungsqualität. Dies ist besonders nützlich, wenn nur wenige gekennzeichnete Daten vorhanden sind.
- Robustheit gegenüber Rauschen: Die Methode kann auch mit verrauschten Daten umgehen, da sie die Ähnlichkeit der Instanzen berücksichtigt und sich nicht nur auf Kennzeichnungen stützt.
Einschränkungen der LabelPropagation:
- Abhängigkeit von der Wahl des Graphen: Die Qualität der LabelPropagation-Klassifikation kann stark von der Wahl des Graphen und der Methode zur Bestimmung der Instanzähnlichkeit abhängen. Eine falsche Wahl der Parameter kann zu schlechten Ergebnissen führen.
- Berechnungskomplexität: Je nach Größe und Komplexität der Daten sowie den Parametern der Methode kann LabelPropagation erhebliche Rechenressourcen erfordern.
- Potenzial für Überanpassung: Wenn der Graph zu viele verrauschte Kanten oder falsche Kennzeichen enthält, kann die Methode sich überanpassen.
- Konvergenz nicht garantiert: In seltenen Fällen kann es vorkommen, dass LabelPropagation nicht zu stabilen Kennzeichen konvergiert, sodass die Anzahl der Iterationen begrenzt oder andere Einstellungen angepasst werden müssen.
LabelPropagation ist eine leistungsfähige Methode, die jedoch eine sorgfältige Abstimmung der Parameter und eine Analyse der Graphstruktur der Daten erfordert, um gute Ergebnisse zu erzielen.
2.29.3.1. Code zum Erstellen des Klassifizierungsmodells LabelPropagationClassifier
# Iris_LabelPropagationClassifier.py
# The code demonstrates the process of training LabelPropagation Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.semi_supervised import LabelPropagation
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a LabelPropagation model
lp_model = LabelPropagation()
# train the model on the entire dataset
lp_model.fit(X, y)
# predict classes for the entire dataset
y_pred = lp_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelPropagation model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "lp_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelPropagation model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of LabelPropagation model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Das Modell wurde erstellt, aber bei der Konvertierung in das ONNX-Format traten Fehler auf.
Auf der Registerkarte „Fehler“ werden Nachrichten über Konvertierungsfehler in das ONNX-Format angezeigt:
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12) Iris_LabelPropagation.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
Daher konnte das Klassifizierungsmodell von LabelSpreading nicht in ONNX konvertiert werden. onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
2.29.4. LabelSpreading-Klassifikator
LabelSpreading ist eine halbüberwachte Lernmethode, die für Klassifizierungsaufgaben verwendet wird. Es basiert auf der Idee der Weitergabe von Labels (Klassen) von gelabelten Instanzen an nicht gelabelte Instanzen in einer graphbasierten Datenstruktur, ähnlich wie bei LabelPropagation. LabelSpreading beinhaltet jedoch eine zusätzliche Stabilisierung und Regularisierung des Ausbreitungsprozesses.
Der LabelSpreading-Prozess:
- Es beginnt mit der Konstruktion eines Graphen, in dem die Knoten Dateninstanzen darstellen und die Kanten zwischen den Knoten die Ähnlichkeit oder Nähe zwischen den Instanzen widerspiegeln.
- Initiale Kennzeichenvergabe: Gekennzeichnete Instanzen werden mit ihren Kennzeichen (labels) versehen, und nicht gekennzeichnete Instanzen beginnen mit einer undefinierten Kennzeichen.
- Kennzeichenübertragung auf dem Graphen: Kennzeichen von gelabelten Instanzen werden auf der Grundlage der Ähnlichkeit zwischen den Instanzen auf nicht gelabelte Instanzen übertragen.
- Regularisierung und Stabilisierung: LabelSpreading beinhaltet eine Regularisierung, die dazu beiträgt, den Prozess der Übertragung von Kennzeichen zu stabilisieren und eine Überanpassung zu reduzieren. Dies wird dadurch erreicht, dass nicht nur die Ähnlichkeit zwischen den Instanzen, sondern auch die Unterschiede zwischen den Labels benachbarter Instanzen berücksichtigt werden.
- Iterativer Prozess: Die Beschriftungen können sich über mehrere Iterationen hinweg ändern, wobei jede Iteration die Beschriftungen der nicht beschrifteten Instanzen auf der Grundlage der aktuellen Beschriftungen und der Regularisierung aktualisiert.
- Stabilisierung: Der Prozess wird fortgesetzt, bis sich die Kennzeichen stabilisieren oder ein bestimmtes Abbruchkriterium erfüllt ist.
Vorteile von LabelSpreading:
- Verwendet Informationen aus nicht gekennzeichneten Daten: LabelSpreading ermöglicht die Verwendung von Informationen aus nicht beschrifteten Instanzen zur Verbesserung der Klassifizierungsqualität.
- Regulierung: Das Vorhandensein der Regularisierung in LabelSpreading trägt dazu bei, die Überanpassung zu reduzieren und den Prozess der Ausbreitung von Bezeichnungen stabiler zu machen.
Einschränkungen von LabelSpreading:
- Abhängigkeit von der Wahl des Graphen: Ähnlich wie bei der LabelPropagation kann die Qualität der LabelSpreading-Klassifikation stark von der Wahl der Graphen- und Methodenparameter abhängen.
- Berechnungskomplexität: Je nach Größe und Komplexität der Daten sowie den Parametern der Methode kann LabelSpreading erhebliche Rechenressourcen erfordern.
- Nicht immer konvergent: In seltenen Fällen kann es vorkommen, dass LabelSpreading nicht zu stabilen Etiketten konvergiert, sodass die Anzahl der Iterationen begrenzt oder andere Einstellungen angepasst werden müssen.
LabelSpreading ist eine Methode, die ebenfalls eine sorgfältige Abstimmung erfordert und ein leistungsfähiges Werkzeug für die Verwendung unbeschrifteter Daten bei Klassifizierungsaufgaben sein kann.
2.29.4.1. Code zum Erstellen des Klassifizierungsmodells LabelSpreadingClassifier
# Iris_LabelSpreadingClassifier.py
# The code demonstrates the process of training LabelSpreading Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# import necessary libraries
from sklearn import datasets
from sklearn.semi_supervised import LabelSpreading
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a LabelSpreading model
ls_model = LabelSpreading()
# train the model on the entire dataset
ls_model.fit(X, y)
# predict classes for the entire dataset
y_pred = ls_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelSpreading model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(ls_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "ls_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelSpreading model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of LabelSpreading model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Auf der Registerkarte „Fehler“ werden Nachrichten über Konvertierungsfehler in das ONNX-Format angezeigt:
onnx_model = convert_sklearn(ls_model, initial_types=initial_type, target_opset=12) Iris_LabelSpreading.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
Das Klassifizierungsmodell von LabelPropagation konnte nicht in ONNX konvertiert werden.
2.29.5. NearestCentroid Classifier
NearestCentroid ist eine Klassifizierungsmethode, die auf der Idee basiert, den Schwerpunkt für jede Klasse zu bestimmen und Objekte auf der Grundlage des nächstgelegenen Schwerpunkts zu klassifizieren. Diese Methode ist für Mehrklassenprobleme geeignet und funktioniert gut bei Datensätzen mit linear trennbaren Klassen.
Das NearestCentroid-Verfahren:
- Für jede Klasse wird ein Schwerpunkt berechnet, der den Durchschnittswert der Merkmale aller zu dieser Klasse gehörenden Objekte darstellt. Dies kann durch Berechnung des Mittelwerts jedes Merkmals für die Objekte in dieser Klasse geschehen.
- Bei der Klassifizierung eines neuen Objekts wird sein nächstgelegener Schwerpunkt aus den Schwerpunkten aller Klassen berechnet.
- Das neue Objekt wird der Klasse zugeordnet, deren Schwerpunkt ihm im metrischen Raum am nächsten liegt.
Vorteile von NearestCentroid:
- Einfachheit und Schnelligkeit: NearestCentroid ist eine rechnerisch einfache Methode und arbeitet schnell mit großen Datensätzen.
- Geeignet für linear trennbare Klassen: Die Methode funktioniert gut bei Aufgaben, bei denen die Klassen linear trennbar oder nahezu linear trennbar sind.
- Wirksam bei Mehrklassenproblemen: NearestCentroid ist für Mehrklassenprobleme geeignet und kann als Basisklassifikator in Ensembles verwendet werden.
Einschränkungen von NearestCentroid:
- Empfindlichkeit gegenüber Ausreißern: Die NearestCentroid-Methode ist empfindlich gegenüber Ausreißern in den Daten, da der Schwerpunkt durch das Vorhandensein von Ausreißern erheblich verzerrt werden kann.
- Räumliche Verzerrung: Wenn die Klassen in den Daten unterschiedliche Varianzen und Formen haben, kann die NearestCentroid-Methode weniger effizient arbeiten.
- Setzt gleiche Mittel voraus: Bei dieser Methode wird davon ausgegangen, dass die Klassen in etwa die gleiche Anzahl an Merkmalen aufweisen, was in realen Daten nicht immer der Fall ist.
- Nicht geeignet für nichtlineare Aufgaben: NearestCentroid ist nicht geeignet für Aufgaben mit nichtlinearen Grenzen zwischen Klassen.
NearestCentroid ist eine einfache und interpretierbare Klassifizierungsmethode, die in bestimmten Szenarien nützlich sein kann, insbesondere wenn die Klassen linear trennbar sind und es keine Ausreißer in den Daten gibt.
2.29.5.1. Code zum Erstellen des Klassifizierungsmodells NearestCentroid
# Iris_NearestCentroidClassifier.py
# The code demonstrates the process of training NearestCentroid Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.neighbors import NearestCentroid
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a NearestCentroid model
nc_model = NearestCentroid()
# train the model on the entire dataset
nc_model.fit(X, y)
# predict classes for the entire dataset
y_pred = nc_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of NearestCentroid model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "nc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of NearestCentroid model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of NearestCentroid model: 0.9266666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Auf der Registerkarte „Fehler“ werden Nachrichten über Konvertierungsfehler in das ONNX-Format angezeigt:
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12) Iris_NearestCentroid.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
The NearestCentroid Classifier model could not be converted to ONNX. onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
2.29.6. Quadratic Discriminant Analysis Classifier
Die quadratische Diskriminanzanalyse (QDA) ist eine Klassifizierungsmethode, die ein probabilistisches Modell verwendet, um Daten in Klassen einzuteilen. Sie ist eine Verallgemeinerung der linearen Diskriminanzanalyse (LDA) und ermöglicht die Berücksichtigung von Merkmalskovarianzen innerhalb jeder Klasse. Die Hauptidee von QDA besteht darin, die Merkmalsverteilung für jede Klasse zu modellieren und diese Verteilung dann für die Klassifizierung neuer Objekte zu verwenden.
Der QDA-Prozess:
- Die Parameter der Verteilung werden für jede Klasse berechnet, wie z. B. der Mittelwert und die Kovarianzmatrix der Merkmale. Diese Parameter werden auf der Grundlage der Trainingsdaten für jede Klasse geschätzt.
- Anhand der ermittelten Parameter können die Wahrscheinlichkeitsdichten für jede Klasse mit Hilfe einer multivariaten Normalverteilung (oder einer quadratischen Verteilungsfunktion) berechnet werden.
- Bei der Klassifizierung eines neuen Objekts werden für jede Klasse Wahrscheinlichkeitsdichtewerte berechnet, und das Objekt wird der Klasse mit der höchsten Wahrscheinlichkeit zugeordnet.
Vorteile der quadratische Diskriminanzanalyse (QDA):
- Berücksichtigt die Kovarianzen der Merkmale: QDA ist flexibler als LDA, da es unterschiedliche Kovarianzmatrizen für verschiedene Klassen zulässt und somit besser an unterschiedliche Datenstrukturen angepasst werden kann.
- Geeignet für nichtlineare Grenzen: QDA ist in der Lage, komplexe und nichtlineare Grenzen zwischen Klassen zu modellieren.
- Robust gegenüber unausgewogenen Daten: QDA kann bei Aufgaben mit unausgewogenen Klassen gut funktionieren.
Einschränkungen der quadratische Diskriminanzanalyse (QDA):
- Berechnungskomplexität: QDA erfordert die Schätzung von Parametern für jede Klasse, einschließlich Kovarianzmatrizen, was bei großen Datensätzen rechenintensiv sein kann.
- Begrenzte Daten: QDA kann weniger effektiv arbeiten, wenn die Daten begrenzt sind, und die Parameterschätzung wird weniger präzise.
- Annahme der Normalverteilung: QDA geht davon aus, dass die Daten einer Normalverteilung folgen, was für einige Datentypen möglicherweise nicht zutrifft.
- Risiko der Überanpassung: Bei unzureichenden Trainingsdaten oder starker Merkmalskovarianz kann es bei QDA zu Problemen der Überanpassung kommen.
Die quadratische Diskriminanzanalyse (QDA) ist eine leistungsstarke Klassifizierungsmethode, die sich für verschiedene Datentypen eignet und in der Lage ist, die Kovarianz von Merkmalen innerhalb von Klassen zu berücksichtigen. Es gibt jedoch auch Einschränkungen, die bei der Verwendung zu beachten sind.
2.29.6.1. Code zur Erstellung des Klassifizierungsmodells Quadratic Discriminant Analysis
# Iris_QuadraticDiscriminantAnalysisClassifier.py
# The code demonstrates the process of training Quadratic Discriminant Analysis Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model.
# It also evaluates the accuracy of both the original model and the ONNX model.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# import necessary libraries
from sklearn import datasets
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# get the script path
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# load the Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# create a QuadraticDiscriminantAnalysis model
qda_model = QuadraticDiscriminantAnalysis()
# train the model on the entire dataset
qda_model.fit(X, y)
# predict classes for the entire dataset
y_pred = qda_model.predict(X)
# evaluate the model's accuracy
accuracy = accuracy_score(y, y_pred)
print("Accuracy of Quadratic Discriminant Analysis model:", accuracy)
# display the classification report
print("\nClassification Report:\n", classification_report(y, y_pred))
# define the input data type
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# export the model to ONNX format with float data type
onnx_model = convert_sklearn(qda_model, initial_types=initial_type, target_opset=12)
# save the model to a file
onnx_filename = data_path + "qda_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# print the path to the model
print(f"Model saved to {onnx_filename}")
# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# display information about input tensors in ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# display information about output tensors in ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convert data to floating-point format (float32)
X_float32 = X.astype(np.float32)
# predict classes for the entire dataset using ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# evaluate the accuracy of the ONNX model
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of Quadratic Discriminant Analysis model in ONNX format:", accuracy_onnx)
Ausgabe:
Python Accuracy of Quadratic Discriminant Analysis model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Dieses Mal wurde das Modell erfolgreich im ONNX-Format gespeichert. Bei der Ausführung werden jedoch Fehler auf der Registerkarte Fehler angezeigt:
onnx_session = ort.InferenceSession(onnx_filename) Iris_QuadraticDiscriminantAnalysisClassifier.py 55 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
Bei der Konvertierung des Modells „Quadratic Discriminant Analysis Classifier“ in ONNX ist ein Fehler aufgetreten.
Schlussfolgerungen
In dieser Studie untersuchten wir 33 Klassifizierungsmodelle anhand des Iris-Datensatzes und nutzten dabei die Bibliothek Scikit-Learn Version 1.2.2.
1. Bei sechs dieser Modelle traten bei der Konvertierung in das ONNX-Format Schwierigkeiten auf:
- DummyClassifier: Dummy-Klassifikator;
- GaussianProcessClassifier: Gaußscher Prozess-Klassifikator;
- LabelPropagation : Label Propagation Klassifikator ;
- LabelSpreading : Label Spreading Klassifikator;
- NearestCentroid: Nearest Centroid Klassifikator;
- QuadraticDiscriminantAnalysis: Klassifikator mit quadratischer Diskriminanzanalyse.
Es scheint, dass diese Modelle in Bezug auf ihre Struktur und/oder Logik komplexer sind, und ihre Anpassung an das ONNX-Format könnte zusätzliche Anstrengungen erfordern. Es ist auch möglich, dass sie bestimmte Datenstrukturen oder Algorithmen verwenden, die nicht vollständig unterstützt werden oder nicht für das ONNX-Format geeignet sind.
2. Die übrigen 27 Modelle wurden erfolgreich in das ONNX-Format konvertiert und bewiesen, dass ihre Genauigkeit erhalten blieb. Dies unterstreicht die Effektivität von ONNX als Werkzeug zum Speichern und Wiederherstellen von Modellen des maschinellen Lernens, das einen einfachen Modelltransfer zwischen verschiedenen Umgebungen und Anwendungen unter Beibehaltung ihrer Leistung ermöglicht.
Die vollständige Liste der Modelle, die erfolgreich in das ONNX-Format konvertiert wurden, umfasst:
- SVC: Support Vector Klassifikator;
- LinearSVC: Linearer Support-Vektor-Klassifikator;
- NuSVC: Nu Support Vector-Klassifikator;
- AdaBoostClassifier: Adaptiver Boosting-Klassifikator;
- BaggingClassifier: Bootstrap Aggregating-Klassifikator;
- BernoulliNB: Bernoulli Naive Bayes-Klassifikator;
- CategoricalNB: Kategorialer Naive Bayes-Klassifikator;
- ComplementNB: Complement Naive Bayes-Klassifikator;
- DecisionTreeClassifier: Decision Tree-Klassifikator;
- ExtraTreeClassifier: Extra Tree-Klassifikator;
- ExtraTreesClassifier: Extra Trees-Klassifikator;
- GaussianNB: Gaußscher Naive Bayes-Klassifikator;
- GradientBoostingClassifier: Gradient Boosting-Klassifikator;
- HistGradientBoostingClassifier: Histogrammbasierter Gradient Boosting-Klassifikator;
- KNeighborsClassifier: k-Nächste-Nachbarn-Klassifikator;
- LinearDiscriminantAnalysis: Linearer Diskriminanzanalyse-Klassifikator;
- LogisticRegression: Logistischer Regressions-Klassifikator;
- LogisticRegressionCV: Logistischer Regressionsklassifikator mit Kreuzvalidierung;
- MLPClassifier: Multilayer Perceptron-Klassifikator;
- MultinomialNB: Multinomialer Naive Bayes-Klassifikator;
- PassiveAggressiveClassifier: Passive-Aggressive-Klassifikator;
- Perceptron: Perceptron-Klassifikator;
- RadiusNeighborsClassifier: Radius Neighbors-Klassifikator;
- RandomForestClassifier: Random Forest-Klassifikator;
- RidgeClassifier: Ridge-Klassifikator;
- RidgeClassifierCV: Ridge-Klassifikator mit Kreuzvalidierung;
- SGDClassifier: Stochastic Gradient Descent-Klassifikator.
3. Darüber hinaus wurden während der Forschung Modelle identifiziert, die eine hervorragende Klassifizierungsleistung mit dem Iris-Datensatz zeigten. Klassifizierungsmodelle wie Random Forest Classifier, Gradient Boosting Classifier, Bagging Classifier, Decision Tree Classifier, Extra Tree Classifier, Extra Trees Classifier und Hist Gradient Boosting Classifier erreichten eine perfekte Vorhersagegenauigkeit. Dies bedeutet, dass sie die Klasse, zu der jede Iris-Probe gehört, genau bestimmen können.
Diese Ergebnisse können bei der Auswahl des besten Modells für bestimmte Klassifizierungsaufgaben besonders wertvoll sein. Modelle, die bei den Iris-Daten eine perfekte Genauigkeit erreicht haben, können eine ausgezeichnete Wahl für Aufgaben sein, die die Analyse oder Klassifizierung ähnlicher Daten beinhalten.
Diese Untersuchung unterstreicht die Bedeutung der Auswahl des richtigen Modells für bestimmte Aufgaben und hebt die Vorteile der Verwendung von ONNX für die Erhaltung und Anwendung von Modellen des maschinellen Lernens für Klassifizierungsaufgaben hervor.
Schlussfolgerung
In diesem Artikel haben wir 33 Klassifizierungsmodelle anhand des Iris-Datensatzes mit Scikit-Learn Version 1.2.2 analysiert.
Von allen untersuchten Modellen erwies sich die Umwandlung in das ONNX-Format bei sechs als schwierig. Zu diesen Modellen gehören der Dummy-Klassifikator, der Gauß-Prozess-Klassifikator, der Label-Propagation-Klassifikator, der Label-Spreading-Klassifikator, der Nearest Centroid-Klassifikator und der Quadratic Discriminant Analysis Classifier. Ihre komplexe Struktur oder Logik erfordert wahrscheinlich eine zusätzliche Anpassung für eine erfolgreiche Konvertierung in das ONNX-Format.
Die übrigen 27 Modelle wurden erfolgreich in das ONNX-Format konvertiert und bewiesen, dass ihre Genauigkeit erhalten blieb. Dies bestätigt die Effizienz von ONNX bei der Bewahrung und Wiederherstellung von Modellen des maschinellen Lernens und gewährleistet die Übertragbarkeit bei gleichbleibender Modellleistung.
Einige Modelle wie der Random Forest Classifier, Gradient Boosting Classifier, Bagging Classifier, Decision Tree Classifier, Extra Tree Classifier, Extra Trees Classifier und Hist Gradient Boosting Classifier, erreichten eine perfekte Genauigkeit bei der Klassifizierung von Irisdaten. Diese Modelle sind besonders interessant für Aufgaben, bei denen es auf hohe Genauigkeit ankommt.
Diese Forschung unterstreicht die Bedeutung der Auswahl des richtigen Modells für bestimmte Aufgaben und zeigt die Vorteile der Verwendung von ONNX für die Erhaltung und Anwendung von Modellen des maschinellen Lernens bei Klassifizierungsaufgaben.
Alle Skripte aus dem Artikel sind auch in den öffentlichen Projekten als „MQL5\Shared Projects\Scikit.Classification.ONNX“ verfügbar.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13451
Beigefügte Dateien |
Scikit-learn-ClassificationModels-ONNX.zip
(220.05 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Zur Diskussion im Händlerforum
Quantitative Analyse in MQL5: Implementierung eines vielversprechenden Algorithmus
Wir werden der Frage nachgehen, was eine quantitative Analyse ist und wie sie von den wichtigsten Akteuren eingesetzt wird. Wir werden einen der Algorithmen für die quantitative Analyse in der Sprache MQL5 erstellen.
Algorithmen zur Optimierung mit Populationen: Nelder-Mead- oder Simplex-Suchverfahren (NM)
Der Artikel stellt eine vollständige Untersuchung der Nelder-Mead-Methode vor und erklärt, wie das Simplex (Funktionsparameterraum) bei jeder Iteration geändert und neu angeordnet wird, um eine optimale Lösung zu erreichen, und beschreibt, wie die Methode verbessert werden kann.
Algorithmen zur Optimierung mit Populationen: der Algorithmus Simulated Annealing (SA). Teil I
Der Algorithmus des Simulated Annealing ist eine Metaheuristik, die vom Metallglühprozess inspiriert ist. In diesem Artikel führen wir eine gründliche Analyse des Algorithmus durch und räumen mit einer Reihe von weit verbreiteten Überzeugungen und Mythen rund um diese weithin bekannte Optimierungsmethode auf. Der zweite Teil des Artikels befasst sich mit dem nutzerdefinierten Algorithmus Simulated Isotropic Annealing (SIA).
Neuronale Netze leicht gemacht (Teil 67): Nutzung früherer Erfahrungen zur Lösung neuer Aufgaben
In diesem Artikel werden weitere Methoden zur Sammlung von Daten in einem Trainingssatz erörtert. Es liegt auf der Hand, dass der Lernprozess eine ständige Interaktion mit der Umgebung erfordert. Die Situationen können jedoch unterschiedlich sein.
Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich