Wie man 3D-Grafiken mit DirectX in MetaTrader 5 erstellt
1 117
0
Dreidimensionale Computergrafiken liefern die Eindrücke von dreidimensionalen Objekten auf einem ebenen Bildschirm. Solche Objekte sowie die Position des Betrachters können sich im Laufe der Zeit ändern. Dementsprechend sollte sich auch das zweidimensionale Bild ändern, um die Illusion der Bildtiefe zu erzeugen, d.h. es sollte Rotation, Zoomen, Änderungen der Beleuchtung usw. unterstützen. MQL5 ermöglicht die Erstellung und Verwaltung von Computergrafiken direkt im MetaTrader 5 Terminal unter Verwendung von DirectX-Funktionen. Bitte beachten Sie, dass Ihre Grafikkarte DX 11 und Shader Model 5.0 unterstützen sollte, damit die Funktionen funktionieren.
- Objekt-Modellierung
- Erstellen einer Form
- Szenenberechnung und Rendering
- Objektdrehung um die z-Achse und den Ansichtspunkt
- Verwaltung der Kameraposition
- Objekt-Farbmanagement
- Rotation und Bewegung
- Arbeiten mit Beleuchtung
- Animation
- Kameraposition mit der Maus steuern
- Anwenden von Texturen
- Nutzerdefinierte Objekte erstellen
- Datenbankbasierte 3D-Oberfläche
Objekt-Modellierung
Um ein dreidimensionales Objekt auf einem flachen Raum zu zeichnen, sollte zunächst ein Modell dieses Objekts in x-, y- und z-Koordinaten erstellt werden. Das bedeutet, dass jeder Punkt auf der Objektoberfläche durch die Angabe seiner Koordinaten beschrieben werden sollte. Im Idealfall müsste man eine unendliche Anzahl von Punkten auf der Objektoberfläche beschreiben, um die Bildqualität während der Skalierung zu erhalten. In der Praxis werden 3D-Modelle mit Hilfe eines Netzes beschrieben, das aus Polygonen besteht. Ein detaillierteres Netz mit einer höheren Anzahl von Polygonen liefert ein realistischeres Modell. Zur Berechnung eines solchen Modells und zum Rendern von 3D-Grafiken sind jedoch mehr Computerressourcen erforderlich.
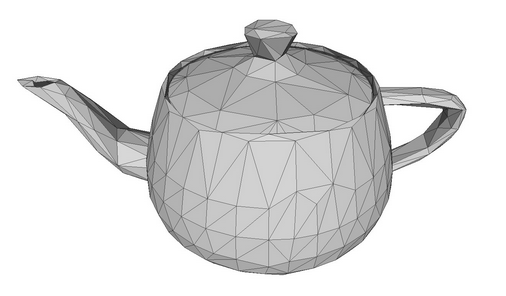
Ein Teekannenmodell als Polygonnetz.
Die Aufteilung von Polygonen in Dreiecke erschien vor langer Zeit, als die frühen Computergrafiken noch auf schwachen Grafikkarten laufen mussten. Das Dreieck ermöglicht die exakte Beschreibung der Position eines kleinen Oberflächenteils sowie die Berechnung damit zusammenhängender Parameter, wie z.B. Beleuchtungen und Lichtreflexionen. Die Sammlung solch kleiner Dreiecke ermöglicht die Erstellung eines realistischen dreidimensionalen Bildes des Objekts. Im Folgenden werden das Polygon und das Dreieck als Synonyme verwendet, da es viel einfacher ist, sich ein Dreieck vorzustellen als ein Polygon mit N Eckpunkten.
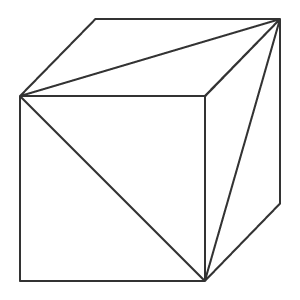
Aus Dreiecken zusammengesetzter Würfel.
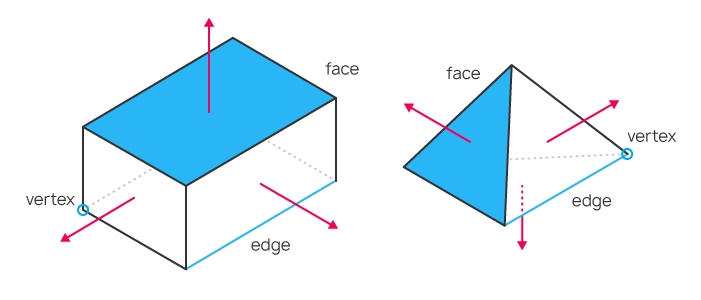
Das dreidimensionale Modell eines Objekts kann durch die Beschreibung der Koordinaten jedes Eckpunkts des Dreiecks erstellt werden, was eine weitere Berechnung der Koordinaten für jeden Punkt des Objekts ermöglicht, auch wenn sich das Objekt bewegt oder sich die Position des Betrachters ändert. Wir befassen uns also mit den Scheitelpunkten, den Kanten, die sie verbinden, und der Fläche, die durch die Kanten gebildet wird. Wenn die Position eines Dreiecks bekannt ist, können wir mit Hilfe der Gesetze der linearen Algebra eine Normale zur Fläche erzeugen (eine Normale ist ein Vektor, der senkrecht zur Fläche steht). Auf diese Weise lässt sich berechnen, wie die Fläche beleuchtet wird und wie das Licht von ihr reflektiert wird.
Beispiele für einfache Objekte mit Vertices, Kanten, Flächen und Normalen. Die
Normale ist der rote Pfeil.
Ein Modellobjekt kann auf verschiedene Arten erstellt werden. Die Topologie beschreibt, wie Polygone das 3D-Netz bilden. Eine gute Topologie ermöglicht die Verwendung einer minimalen Anzahl von Polygonen zur Beschreibung eines Objekts und kann das Verschieben und Drehen des Objekts erleichtern.
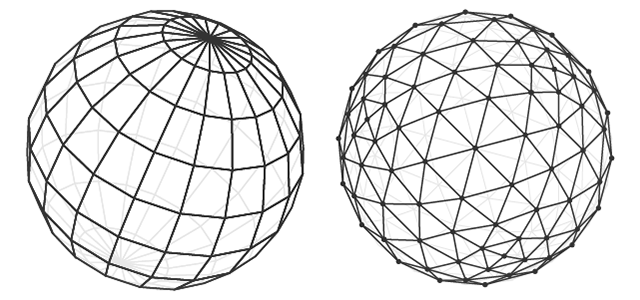
Sphärenmodell in zwei Topologien.
Der Volumeneffekt wird durch die Verwendung von Licht und Schatten auf den Objektpolygonen erzeugt. Der Zweck der 3D-Computergrafik
besteht also darin, die Position jedes Punktes eines Objektes zu berechnen, Lichter und Schatten zu berechnen und auf dem Bildschirm
darzustellen.
Erstellen einer Form
Schreiben wir ein einfaches Programm, das einen Würfel erzeugt. Wir verwenden die Klasse CCanvas3D
aus der Bibliothek 3D graphics.
Die Klasse CCanvas3DWindow, die ein 3D-Fenster rendert, hat ein Minimum an Mitgliedsvariablen und Methoden. Wir werden nach und nach neue
Methoden mit einer Erklärung der 3D-Grafikkonzepte hinzufügen, die in Funktionen für die Arbeit
mit DirectX implementiert sind.
//+------------------------------------------------------------------+ //| Fenster der Anwendung | //+------------------------------------------------------------------+ class CCanvas3DWindow { protected: CCanvas3D m_canvas; //--- Leinwandgröße int m_width; int m_height; //--- das Würfelobjekt CDXBox m_box; public: CCanvas3DWindow(void) {} ~CCanvas3DWindow(void) {m_box.Shutdown();} //-- Erstellen einer Szene virtual bool Create(const int width,const int height){} //--- Berechnen der Szene void Redraw(){} //--- Behandlung der Chart-Ereignisse void OnChartChange(void) {} };
Die Schaffung einer Szene beginnt mit der Schaffung einer Leinwand. Dann werden die folgenden Parameter für die Projektionsmatrix festgelegt:
- Ein Blickwinkel von 30 Grad (M_PI/6), aus dem wir die 3D-Szene betrachten
- Seitenverhältnis als Verhältnis von Breite und Höhe
- Abstand zur nahen (0,1f) und fernen (100,f) Schnittebene
Das bedeutet, dass nur die Objekte zwischen diesen beiden virtuellen Wänden (0,1f und 100,f) in der Projektionsmatrix gerendert werden.
Darüber hinaus muss das Objekt in den horizontalen 30-Grad-Blickwinkel fallen. Bitte beachten Sie, dass sowohl die Entfernungen als auch
alle Koordinaten in der Computergrafik virtuell sind. Entscheidend sind die Beziehungen zwischen den Abständen und Größen, nicht aber
die absoluten Werte.
//+------------------------------------------------------------------+ //| Erstellen | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { //--- Sichern der Leinwandgröße m_width=width; m_height=height; //--- Erstellen der Leinwand, um die 3D-Szene zu rendern ResetLastError(); if(!m_canvas.CreateBitmapLabel("3D Sample_1",0,0,m_width,m_height,COLOR_FORMAT_ARGB_NORMALIZE)) { Print("Error creating canvas: ",GetLastError()); return(false); } //--- Parameter der Projektionsmatrix einstellen - Sichtwinkel, Seitenverhältnis, Abstand zur nahen und fernen Schnittebene m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- Würfel erstellen - übergeben werden der Ressourcenmanager, die Szenenparameter und die Koordinaten von zwei gegenüberliegenden Ecken des Würfels if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,5.0),DXVector3(1.0,1.0,7.0))) { m_canvas.Destroy(); return(false); } //--- den Würfel der Szene hinzufügen m_canvas.ObjectAdd(&m_box); //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Nachdem wir die Projektionsmatrix erstellt haben, können wir mit der Konstruktion des 3D-Objekts — eines Würfels auf der Grundlage der Klasse CDXBox — fortfahren. Um einen Würfel zu erstellen, genügt es, zwei Vektoren anzugeben, die auf die gegenüberliegenden Ecken des Würfels zeigen. Wenn Sie sich die Würfelerzeugung im Debug-Modus ansehen, können Sie sehen, was in DXComputeBox() geschieht: die Erzeugung aller Würfelspitzen (ihre Koordinaten werden in das Array 'vertices' geschrieben), sowie die Unterteilung der Würfelkanten in Dreiecke, die aufgezählt und im Array 'indiсes' gespeichert werden. Insgesamt hat der Würfel 8 Eckpunkte, 6 Flächen, die in 12 Dreiecke unterteilt sind, und 36 Indizes, die die Eckpunkte dieser Dreiecke spezifizieren.
Obwohl der Würfel nur 8 Eckpunkte hat, werden 24 Vektoren zur Beschreibung dieser Eckpunkte erstellt, da für jede der 6 Flächen ein separater
Satz von Eckpunkten mit einer Normalen angegeben werden sollte. Die Richtung der Normalen wirkt sich auf die Berechnung der Beleuchtung
für jede Fläche aus. Die Reihenfolge, in der die Scheitelpunkte eines Dreiecks im Index aufgeführt sind, bestimmt, welche seiner Seiten
sichtbar sein werden. Die Reihenfolge, in der die Scheitelpunkte und Indizes gefüllt sind, wird im Code von DXUtils.mqh gezeigt:
for(int i=20; i<24; i++) vertices[i].normal=DXVector4(0.0,-1.0,0.0,0.0);
Die Texturkoordinaten für das Texture Mapping für jede Oberfläche werden im gleichen Code beschrieben:
//--- Koordinaten der Textur for(int i=0; i<faces; i++) { vertices[i*4+0].tcoord=DXVector2(0.0f,0.0f); vertices[i*4+1].tcoord=DXVector2(1.0f,0.0f); vertices[i*4+2].tcoord=DXVector2(1.0f,1.0f); vertices[i*4+3].tcoord=DXVector2(0.0f,1.0f); }
Jeder der 4 Flächenvektoren legt einen der 4 Winkel für das Textur-Mapping fest. Das bedeutet, dass auf jede Würfelseite eine Gruppe von Strukturen abgebildet wird, um die Textur zu rendern. Dies ist natürlich nur erforderlich, wenn eine Textur gesetzt ist.
Szenenberechnung und Rendering
Alle Berechnungen sollten bei jedem Wechsel der 3D-Szene neu durchgeführt werden. Hier ist die Reihenfolge der erforderlichen Berechnungen:
- Berechnen Sie den Mittelpunkt jedes Objekts in Weltkoordinaten
- Berechnen Sie die Position jedes Elementes des Objektes, d.h. jedes Eckpunktes
- Bestimmen der Pixeltiefe und ihrer Sichtbarkeit für den Betrachter
- Berechnen Sie die Position jedes Pixels auf dem durch seine Eckpunkte angegebenen Polygon
- Stellen Sie die Farbe jedes Pixels auf dem Polygon in Übereinstimmung mit der angegebenen Textur
- Berechnen Sie die Richtung des Lichtpixels und seiner Reflexion
- Wenden Sie das diffuse Licht auf jedes Pixel an
- Wandeln Sie alle Weltkoordinaten in Kamerakoordinaten um
- Wandeln Sie die Kamerakoordinaten in die Koordinaten auf der Projektionsmatrix um
//+------------------------------------------------------------------+ //| Aktualisieren der Szene | //+------------------------------------------------------------------+ void Redraw() { //--- Berechnen der 3D-Szene m_canvas.Render(DX_CLEAR_COLOR|DX_CLEAR_DEPTH,ColorToARGB(clrBlack)); //--- Aktualisieren der Bilder auf der Leinwand entsprechend der aktuellen Szene m_canvas.Update(); }
In unserem Beispiel wird der Würfel nur einmal erstellt, er ändert sich danach nicht mehr. Daher muss der Rahmen auf der Leinwand nur dann
geändert werden, wenn es Änderungen im Diagramm gibt, wie z.B. die Größenänderung des Diagramms. In diesem Fall werden die
Leinwandabmessungen an die aktuellen Diagrammabmessungen angepasst, die Projektionsmatrix wird zurückgesetzt und das Bild auf der
Leinwand aktualisiert.
//+------------------------------------------------------------------+ //| Ereignisänderung auf dem Prozess-Chart | //+------------------------------------------------------------------+ void OnChartChange(void) { //--- Abrufen der aktuellen Chartgröße int w=(int)ChartGetInteger(0,CHART_WIDTH_IN_PIXELS); int h=(int)ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS); //--- Aktualisieren der Leinwanddimensionen entsprechend der aktuellen Chartgröße if(w!=m_width || h!=m_height) { m_width =w; m_height=h; //--- Größenänderung der Leinwand m_canvas.Resize(w,h); DXContextSetSize(m_canvas.DXContext(),w,h); //--- Aktualisieren der Projektionsmatrix entsprechend der aktuellen Leinwandgröße m_canvas.ProjectionMatrixSet((float)M_PI/6,(float)m_width/m_height,0.1f,100.0f); //--- 3D-Szene: Neuberechnen und Rendern auf der Leinwand Redraw(); } }
Starten Sie den EA "Step1 Create Box.mq5". Sie sehen ein weißes Quadrat auf schwarzem Hintergrund. Standardmäßig ist die
Farbe Weiß für Objekte bei der Erstellung festgelegt. Eine Beleuchtung wurde noch nicht festgelegt.
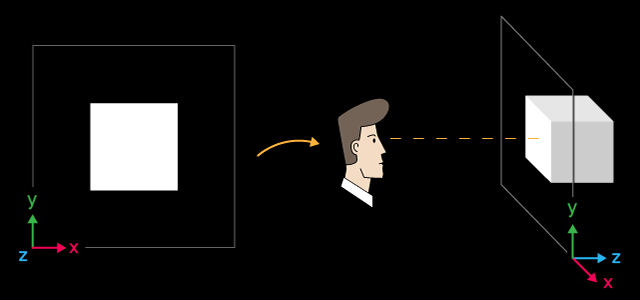
Ein weißer Würfel und sein Layout im Raum
Die x-Achse ist nach rechts, y nach oben und z nach innen in die 3D-Szene gerichtet. Ein solches Koordinatensystem wird als linkshändig
bezeichnet.
Der Mittelpunkt des Würfels liegt an dem Punkt mit den folgenden Koordinaten x=0, y=0, z=6. Die Position, von der aus wir den Würfel
betrachten, liegt in der Mitte der Koordinaten, was der Standardwert ist. Wenn Sie die Position, von der aus die 3D-Szene betrachtet wird,
ändern möchten, setzen Sie explizit die entsprechenden Koordinaten mit der Funktion ViewPositionSet().
Um den Programmbetrieb zu beenden, drücken Sie "Escape".
Objektdrehung um die z-Achse und den Ansichtspunkt
Um die Szene zu animieren, lassen Sie uns eine Würfeldrehung um die z-Achse aktivieren. Dazu fügen Sie einen Timer hinzu — basierend auf seinen Ereignissen wird der Würfel gegen den Uhrzeigersinn gedreht.
Erstellen Sie eine Rotationsmatrix, um die Drehung um die z-Achse in einem bestimmten Winkel mit der Methode DXMatrixRotationZ() zu aktivieren.
Übergeben Sie sie dann als Parameter an die Methode TransformMatrixSet(). Dadurch wird die Position des Würfels im 3D-Raum geändert.
Rufen Sie erneut Redraw() auf, um das Bild auf der Leinwand zu aktualisieren.
//+------------------------------------------------------------------+ //| Timer | //+------------------------------------------------------------------+ void OnTimer(void) { //--- Variablen zur Berechnung er Rotationswinkel static ulong last_time=0; static float angle=0; //--- Abfragen der aktuellen Zeit ulong current_time=GetMicrosecondCount(); //--- Berechnung von delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- Erhöhen des Rotationswinkels des Würfels um die z-Achse angle+=deltatime; //--- Sichern der Zeit last_time=current_time; //--- Festlegen des Rotationswinkels des Würfels um die z-Achse DXMatrix rotation; DXMatrixRotationZ(rotation,angle); m_box.TransformMatrixSet(rotation); //--- 3D-Szene: Neuberechnen und Rendern auf der Leinwand Redraw(); }
Nach dem Start sehen Sie ein rotierendes weißes Quadrat.
Der Würfel dreht sich um die z-Achse entgegen dem Uhrzeigersinn
Der Quellcode dieses Beispiels ist in der Datei "Step2 Rotation Z.mq5" verfügbar. Bitte beachten Sie, dass jetzt bei der Erstellung der Szene der Winkel M_PI/5 angegeben wird, der größer als der Winkel M_PI/6 aus dem vorherigen Beispiel ist.
//--- Parameter der Projektionsmatrix einstellen - Sichtwinkel, Seitenverhältnis, Abstand zur nahen und fernen Schnittebene m_matrix_view_angle=(float)M_PI/5; m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- Würfel erstellen - übergeben werden der Ressourcenmanager, die Szenenparameter und die Koordinaten von zwei gegenüberliegenden Ecken des Würfels
Die Würfelabmessungen auf dem Bildschirm sind jedoch optisch kleiner. Je kleiner der bei der Einstellung der Projektionsmatrix
angegebene Sichtwinkel ist, desto größer ist der Bildausschnitt, den das Objekt einnimmt. Dies kann mit dem Sehen von Objekten mit einem
Teleskop verglichen werden: Das Objekt ist größer, aber der Sichtwinkel ist kleiner.
Verwaltung der Kameraposition
Die Klasse CCanvas3D verfügt über drei Methoden zur Einstellung wichtiger 3D-Szenenparameter, die miteinander verbunden sind:
- ViewPositionSet
bestimmt den Ansichtspunkt der 3D-Szene
- ViewTargetSet
legt die Koordinaten des Punktes fest, auf den der Blick gerichtet ist
- ViewUpDirectionSet
legt die Richtung des oberen Randes des Rahmens im 3D-Raum festlegt die Richtung des oberen Randes des Rahmens im 3D-Raum fest.
Alle diese Parameter werden in Kombination verwendet — das bedeutet, dass, wenn Sie einen dieser Parameter in der 3D-Szene einstellen
möchten, die beiden anderen Parameter ebenfalls initialisiert werden müssen. Dies sollte zumindest im Stadium der Szenengenerierung
erfolgen. Dies wird im folgenden Beispiel gezeigt, in dem der obere Rand des Rahmens nach links und rechts schwingt. Der Schwenk wird durch
Hinzufügen der folgenden drei Codezeilen in der Create()-Methode implementiert:
//+------------------------------------------------------------------+ //| Erstellen | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { .... //--- den Würfel der Szene hinzufügen m_canvas.ObjectAdd(&m_box); //--- Festlegen der Parameter der Szene m_canvas.ViewUpDirectionSet(DXVector3(0,1,0)); // Setzen des Richtungsvektors aufwärts in Richtung der y-Achse m_canvas.ViewPositionSet(DXVector3(0,0,0)); // Setzen des Ansichtspunktes vom Zentrum der Koordinaten m_canvas.ViewTargetSet(DXVector3(0,0,6)); // Setzen des Blickpunktes im Zentrum des Würfels //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Ändern Sie die Funktion OnTimer(), um den Horizontvektor nach links und rechts schwingen zu lassen.
//+------------------------------------------------------------------+ //| Timer | //+------------------------------------------------------------------+ void OnTimer(void) { //--- Variablen zur Berechnung er Rotationswinkel static ulong last_time=0; static float max_angle=(float)M_PI/30; static float time=0; //--- Abfragen der aktuellen Zeit ulong current_time=GetMicrosecondCount(); //--- Berechnung von delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- Erhöhen des Rotationswinkels des Würfels um die z-Achse time+=deltatime; //--- Sichern der Zeit last_time=current_time; //--- Setzen des Rotationswinkels um die z-Achse DXVector3 direction=DXVector3(0,1,0); // erste Richtung des Tops DXMatrix rotation; // Rotationsvektor //--- Berechnen der Rotationsmatrix DXMatrixRotationZ(rotation,float(MathSin(time)*max_angle)); DXVec3TransformCoord(direction,direction,rotation); m_canvas.ViewUpDirectionSet(direction); // Setzen der neuen Richtung des Tops //--- 3D-Szene: Neuberechnen und Rendern auf der Leinwand Redraw(); }
Speichern Sie das Beispiel als "Step3 ViewUpDirectionSet.mq5" und führen Sie es aus. Sie werden das Bild eines
schwingenden Würfels sehen, obwohl er eigentlich unbeweglich ist. Dieser Effekt wird erzielt, wenn die Kamera selbst nach links und
rechts schwingt.
Die obere Richtung schwankt nach links und rechts
Objekt-Farbmanagement
Lassen Sie uns unseren Code ändern und den Würfel in den Koordinatenmittelpunkt setzen, während wir die Kamera bewegen.
//+------------------------------------------------------------------+ //| Erstellen | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... //--- Würfel erstellen - übergeben werden der Ressourcenmanager, die Szenenparameter und die Koordinaten von zwei gegenüberliegenden Ecken des Würfels if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- Farbgebung m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- den Würfel der Szene hinzufügen m_canvas.ObjectAdd(&m_box); //--- Festlegen der Kameraposition, des Blicks und der Richtung des Tops m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); // Setzen des Richtungsvektors aufwärts in Richtung der y-Achse m_canvas.ViewPositionSet(DXVector3(3.0,2.0,-5.0)); // Setzen der Kameraposition rechts, oben und vor dem Würfel m_canvas.ViewTargetSet(DXVector3(0,0,0)); // Setzen der Blickrichtung auf das Zentrum des Würfels //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Zusätzlich malen wir den Würfel blau an. Die Farbe wird im Format einer RGB-Farbe
mit einem Alphakanal (der Alphakanal wird zuletzt angezeigt) gesetzt, wobei die Werte auf eins normiert sind. Ein Wert von 1 bedeutet
also 255, und 0,5 bedeutet 127.
Fügen Sie Rotation um die x-Achse hinzu und speichern Sie die Änderungen als "Step4 Box Color.mq5".
Ansicht eines rotierenden Würfels von oben rechts.
Rotation und Bewegung
Objekte können gleichzeitig in drei Richtungen bewegt und gedreht werden. Alle Objektänderungen werden über Matrizen realisiert. Jede von
ihnen, d.h. Rotation, Bewegung und Transformation, kann separat berechnet werden. Ändern wir das Beispiel: Die Kameraansicht ist jetzt
von oben und von vorne.
//+------------------------------------------------------------------+ //| Erstellen | //+------------------------------------------------------------------+ virtual bool Create(const int width,const int height) { ... m_canvas.ProjectionMatrixSet(m_matrix_view_angle,(float)m_width/m_height,0.1f,100.0f); //--- Kameraposition von oben und vor dem Zentrum der Koordinaten m_canvas.ViewPositionSet(DXVector3(0.0,2.0,-5.0)); m_canvas.ViewTargetSet(DXVector3(0.0,0.0,0.0)); m_canvas.ViewUpDirectionSet(DXVector3(0.0,1.0,0.0)); //--- Würfel erstellen - übergeben werden der Ressourcenmanager, die Szenenparameter und die Koordinaten von zwei gegenüberliegenden Ecken des Würfels if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- Farbgebung des Würfels m_box.DiffuseColorSet(DXColor(0.0,0.5,1.0,1.0)); //--- Berechnen der Würfelposition und der Transfermatrix DXMatrix rotation,translation; //--- Rotation des Würfels nacheinander um die x-, y- und z-Achse DXMatrixRotationYawPitchRoll(rotation,(float)M_PI/4,(float)M_PI/3,(float)M_PI/6); //-- Verschieben des Würfels nach rechts/unten/innen DXMatrixTranslation(translation,1.0,-2.0,5.0); //--- Abrufen der Transformationsmatrix als Produkt von Rotation und Verschiebung DXMatrix transform; DXMatrixMultiply(transform,rotation,translation); //--- Bestimmen der Transformationsmatrix m_box.TransformMatrixSet(transform); //--- den Würfel der Szene hinzufügen m_canvas.ObjectAdd(&m_box); //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Erstellen Sie nacheinander Rotations- und Transfermatrizen, wenden Sie die resultierende Transformationsmatrix an und rendern Sie den Würfel.
Speichern Sie die Änderungen in "Step5 Translation.mq5" und führen Sie sie aus.
Rotation und Bewegung eines Würfels
Die Kamera steht still, und sie ist ein wenig von oben auf das Zentrum der Koordinaten gerichtet. Der Würfel wurde in drei Richtungen gedreht und nach rechts, unten und nach innen in die Szene verschoben.
Arbeiten mit Beleuchtung
Um ein realistisches dreidimensionales Bild zu erhalten, ist es notwendig, die Beleuchtung jedes Punktes auf der Objektoberfläche zu
berechnen. Dies geschieht mit Hilfe des Phong
Shading Models, das die Farbintensität der folgenden drei Beleuchtungskomponenten berechnet: ambient, diffus und spiegelnd. Dabei
werden die folgenden Parameter verwendet:
- DirectionLight — die Richtung der gerichteten Beleuchtung wird in CCanvas3D festgelegt
- AmbientLight — die Farbe und Intensität der Umgebungsbeleuchtung wird in CCanvas3D bestimmt
- DiffuseColor — die berechnete diffuse Beleuchtungskomponente wird im CDXMesh und seinen untergeordneten Klassen errechnet
- EmissionColor — die Komponente für die Hintergrundbeleuchtung wird im CDXMesh und seinen untergeordneten Klassen ermittelt
- SpecularColor — die spiegelnde Komponente wird im CDXMesh und seinen untergeordneten Klassen festgelegt
Das Modell Phong Shading
Das Beleuchtungsmodell ist in Standard-Shadern implementiert, die Modellparameter werden in CCanvas3D festgelegt, und die Objektparameter werden in CDXMesh und seinen Unterklassen bestimmt. Ändern Sie das Beispiel wie folgt:
- Bringen Sie den Würfel in den Koordinatenmittelpunkt zurück.
- Setzen Sie ihn auf weiß.
- Fügen Sie eine gerichtete Quelle gelber Farbe hinzu, die die Szene von oben nach unten beleuchtet.
- Stellen Sie die blaue Farbe für die ungerichtete Beleuchtung ein.
//--- Setzen der Farbe Gelb für die Quelle und Ausrichten von oben nach unten m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- Setzen der Farbe Blau als Umgebungslicht m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); //--- Würfel erstellen - übergeben werden der Ressourcenmanager, die Szenenparameter und die Koordinaten von zwei gegenüberliegenden Ecken des Würfels if(!m_box.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),DXVector3(-1.0,-1.0,-1.0),DXVector3(1.0,1.0,1.0))) { m_canvas.Destroy(); return(false); } //--- Setzen der Farbe Weiß für den Würfel m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- Hinzufügen eines grünen Leuchtens für den Würfel (emittierend) m_box.EmissionColorSet(DXColor(0.0,1.0,0.0,0.2f));
Bitte beachten Sie, dass die Position der gerichteten Lichtquelle in Canvas3D nicht festgelegt wird, sondern nur die Richtung, in die sich das Licht ausbreitet. Die Quelle des gerichteten Lichts wird als unendlich weit entfernt betrachtet und ein streng paralleler Lichtstrom beleuchtet die Szene.
m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0));
Hier ist der Lichtausbreitungsvektor entlang der y-Achse in negativer Richtung, d.h. von oben nach unten gerichtet. Wenn Sie die
gerichtete Lichtquelle parametrieren (LightColorSet und LightDirectionSet), müssen Sie auch die Farbe des Umgebungslichts
angeben (AmbientColorSet). Standardmässig ist die Farbe des Umgebungslichts auf weiss mit maximaler Intensität eingestellt und
somit werden alle Schatten weiss sein. Dies bedeutet, dass die Objekte in der Szene von der Umgebungsbeleuchtung mit Weiß geflutet
werden, während das gerichtete Licht der Quelle durch das weiße Licht unterbrochen wird.
//--- Setzen der Farbe Gelb für die Quelle und Ausrichten von oben nach unten m_canvas.LightColorSet(DXColor(1.0,1.0,0.0,0.8f)); m_canvas.LightDirectionSet(DXVector3(0.0,-1.0,0.0)); //--- Setzen der Farbe Blau als Umgebungslicht m_canvas.AmbientColorSet(DXColor(0.0,0.0,1.0,0.4f)); // muss angegeben werden
Die untenstehende gif-Animation zeigt, wie sich das Bild verändert, wenn wir eine Beleuchtung hinzufügen. Der Quellcode des Beispiels ist in der Datei "Step6 Add Light.mq5" verfügbar.
Der weiße Würfel mit grüner Emission unter einer gelben Lichtquelle, mit blauem
Umgebungslicht
Versuchen Sie, die Farbmethoden im obigen Code auszuschalten, um zu sehen, wie es funktioniert.
Animation
Eine Animation impliziert die Veränderung der Szenenparameter und Objekte im Laufe der Zeit. Alle verfügbaren Eigenschaften können zeit- oder ereignisabhängig geändert werden. Stellen Sie den Timer auf 10 Millisekunden ein — dieses Ereignis wirkt sich auf die Aktualisierung der Szene aus:
int OnInit() { ... //--- Erstellen des Hintergrundes ExtAppWindow=new CCanvas3DWindow(); if(!ExtAppWindow.Create(width,height)) return(INIT_FAILED); //--- Festlegen des Timers EventSetMillisecondTimer(10); //--- return(INIT_SUCCEEDED); }
Fügen Sie die entsprechende Ereignisbehandlung zum CCanvas3DWindow hinzu. Wir müssen Objektparameter (wie Rotation, Bewegung und Zoomen) und die Beleuchtungsrichtung ändern:
//+------------------------------------------------------------------+ //| Timer | //+------------------------------------------------------------------+ void OnTimer(void) { static ulong last_time=0; static float time=0; //--- Abfragen der aktuellen Zeit ulong current_time=GetMicrosecondCount(); //--- Berechnung von delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- Erhöhen der verstrichenen Zeit time+=deltatime; //--- Sichern der Zeit last_time=current_time; //--- Berechne3n der Würfelposition und der Rotationsmatrix DXMatrix rotation,translation,scale; DXMatrixRotationYawPitchRoll(rotation,time/11.0f,time/7.0f,time/5.0f); DXMatrixTranslation(translation,(float)sin(time/3),0.0,0.0); //--- Berechnen der Kompression/Extension des Würfels entlang der Achsen DXMatrixScaling(scale,1.0f+0.5f*(float)sin(time/1.3f),1.0f+0.5f*(float)sin(time/1.7f),1.0f+0.5f*(float)sin(time/1.9f)); //--- Multiplizieren der Matrizen zum Erhalt der finalen Transformation DXMatrix transform; DXMatrixMultiply(transform,scale,rotation); DXMatrixMultiply(transform,transform,translation); //--- Bestimmen der Transformationsmatrix m_box.TransformMatrixSet(transform); //--- Berechnen der Rotation der Lichtquelle um die z-Achse DXMatrixRotationZ(rotation,deltatime); DXVector3 light_direction; //--- Abrufen der aktuelle Richtung der Lichtquelle m_canvas.LightDirectionGet(light_direction); //--- Berechnen und Eintragen der neuen Richtung der Lichtquelle DXVec3TransformCoord(light_direction,light_direction,rotation); m_canvas.LightDirectionSet(light_direction); //--- Neuberechnung und Zeichnen der 3D-Szene auf der Leinwand Redraw(); }
Bitte beachten Sie, dass Objektänderungen über Anfangswerte angewendet werden, so als ob wir uns immer mit dem Anfangszustand des Würfels befassen und alle Operationen, die sich auf Rotation/Bewegung/Kompression beziehen, von Grund auf neu anwenden, was bedeutet, dass der aktuelle Zustand des Würfels nicht gespeichert wird. Die Richtung der Lichtquelle wird jedoch um deltatime Inkremente vom aktuellen Wert aus geändert.
Ein rotierender Würfel mit einer dynamischen Richtungsänderung der Lichtquelle.
Das Ergebnis ist eine sehr komplexe 3D-Animation. Der Beispielcode ist in der Datei "Step7 Animation.mq5".
verfügbar.
Kameraposition mit der Maus steuern
Betrachten wir das letzte Animationselement in den 3D-Grafiken, eine Reaktion auf Nutzeraktionen. Fügen Sie in unserem Beispiel die Kameraverwaltung mit der Maus hinzu. Zuerst abonnieren Sie die Mausereignisse und erstellen die entsprechenden Handler:
int OnInit() { ... //--- Setzen des Timers EventSetMillisecondTimer(10); //--- Ermöglichen des Empfangs von Mausereignissen: Bewegungen und Klicks ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,1); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,1) //--- return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { //--- Löschen des Timers EventKillTimer(); //--- Deaktivieren des Empfangs der Mausereignisse ChartSetInteger(0,CHART_EVENT_MOUSE_MOVE,0); ChartSetInteger(0,CHART_EVENT_MOUSE_WHEEL,0); //--- Löschen des Objekts delete ExtAppWindow; //--- Rückkehr des Charts zu seinem normalen Aussehen als Preischart ChartSetInteger(0,CHART_SHOW,true); } void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { ... //--- Ereignisänderung des Charts if(id==CHARTEVENT_CHART_CHANGE) ExtAppWindow.OnChartChange(); //--- Ereignis einer Mausbewegung if(id==CHARTEVENT_MOUSE_MOVE) ExtAppWindow.OnMouseMove((int)lparam,(int)dparam,(uint)sparam); //--- Ereignis des Mausrades if(id==CHARTEVENT_MOUSE_WHEEL) ExtAppWindow.OnMouseWheel(dparam);
Erstellen Sie in CCanvas3DWindow die Ereignisbehandlung für Mausbewegungen. Er ändert die Kamerarichtungswinkel, wenn die Maus bei gedrückter linker Taste bewegt wird:
//+------------------------------------------------------------------+ //| Behandlung von Mausbewegungen | //+------------------------------------------------------------------+ void OnMouseMove(int x,int y,uint flags) { //--- linker Mausknopf if((flags&1)==1) { //--- keine Information über eine vorherige Mausposition if(m_mouse_x!=-1) { //--- Aktualisieren der des Kamerawinkels nach der Positionsänderung m_camera_angles.y+=(x-m_mouse_x)/300.0f; m_camera_angles.x+=(y-m_mouse_y)/300.0f; //--- Setzen des vertikalen Winkels im Bereich von (-Pi/2,Pi2) if(m_camera_angles.x<-DX_PI*0.49f) m_camera_angles.x=-DX_PI*0.49f; if(m_camera_angles.x>DX_PI*0.49f) m_camera_angles.x=DX_PI*0.49f; //--- Aktualisieren der Kameraposition UpdateCameraPosition(); } //--- Sichern der Mausposition m_mouse_x=x; m_mouse_y=y; } else { //--- Rücksetzen der gesicherten Position, wenn die linke Maustaste nicht gedrückt wurde m_mouse_x=-1; m_mouse_y=-1; } }
Hier ist der Mausrad-Ereignishandler, der den Abstand zwischen der Kamera und dem Mittelpunkt der Szene ändert:
//+------------------------------------------------------------------+ //| Ereignisbehandlung des Mausrades | //+------------------------------------------------------------------+ void OnMouseWheel(double delta) { //--- Aktualisieren des Abstandes zwischen der Kamera und den Zentrum entsprechend der Mausradbewegung m_camera_distance*=1.0-delta*0.001; //--- Setzen des Abstands im Bereich von [3,50] if(m_camera_distance>50.0) m_camera_distance=50.0; if(m_camera_distance<3.0) m_camera_distance=3.0; //--- Aktualisieren der Kameraposition UpdateCameraPosition(); }
Beide Handler rufen die Methode UpdateCameraPosition() auf, um die Kameraposition gemäß den aktualisierten Parametern zu aktualisieren:
//+------------------------------------------------------------------+ //| Aktualisieren der Kameraposition | //+------------------------------------------------------------------+ void UpdateCameraPosition(void) { //--- Kameraposition unter Berücksichtigung des Abstands zum Zentrum der Koordinaten DXVector4 camera=DXVector4(0.0f,0.0f,-(float)m_camera_distance,1.0f); //--- Kamerarotation um die x-Achse DXMatrix rotation; DXMatrixRotationX(rotation,m_camera_angles.x); DXVec4Transform(camera,camera,rotation); //--- Kamerarotation um die y-Achse DXMatrixRotationY(rotation,m_camera_angles.y); DXVec4Transform(camera,camera,rotation); //--- Setzen der Kamera auf eine Position m_canvas.ViewPositionSet(DXVector3(camera)); }
Der Quellcode ist in der Datei "Step8 Mouse Control.mq5" unten verfügbar.
Steuern Sie die Kameraposition mit der Maus.
Anwenden von Texturen
Eine Textur ist ein Bitmap-Bild, das auf die Oberfläche eines Polygons aufgebracht wird, um Muster oder Materialien darzustellen. Die
Verwendung von Texturen erlaubt es, kleine Objekte auf der Oberfläche zu reproduzieren, was zu viele Ressourcen erfordern würde, wenn wir
sie unter Verwendung von Polygonen erstellen würden. Dies kann zum Beispiel eine Imitation von Stein, Holz, Erde und anderen Materialien
sein.
CDXMesh und seine Unterklassen erlauben das Festlegen einer Textur. Im Standard-Pixelshader wird diese Textur zusammen mit DiffuseColor verwendet. Entfernen Sie die Objektanimation und wenden Sie eine Steintextur an. Sie sollte sich im Ordner MQL5\Files des Terminal-Arbeitsverzeichnisses befinden:
virtual bool Create(const int width,const int height) { ... //--- Setzen der Farbe Weiß für nicht gerichtetes Licht m_box.DiffuseColorSet(DXColor(1.0,1.0,1.0,1.0)); //--- Hinzufügen einer Textur auf der Oberfläche des Würfels m_box.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- den Würfel der Szene hinzufügen m_canvas.ObjectAdd(&m_box); //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Ein Würfel mit einer Steintextur.
Nutzerdefinierte Objekte erstellen
Alle Objekte bestehen aus Eckpunkten (DXVector3), die über Indizes zu Primitiven verbunden sind. Das häufigste Primitiv ist ein Dreieck. Ein grundlegendes 3D-Objekt wird erstellt, indem man eine Liste von Eckpunkten erstellt, die mindestens Koordinaten (aber auch eine Menge zusätzlicher Daten wie Normale, Farbe usw.), die Art der Primitive, zu denen sie kombiniert werden, und eine Liste von Eckpunktindizes enthält, mit denen sie zu Primitiven kombiniert werden.
Die Standardbibliothek hat den DXVertex Vertex-Typ, der seine Koordinate, eine Normale für die Beleuchtungsberechnung,
Texturkoordinaten und Farbe enthält. Der Standard-Shader der Eckpunkte (vertex) arbeitet mit diesem Vertex-Typ.
struct DXVertex
{
DXVector4 position; // Koordinaten der Ecke (vertex)
DXVector4 normal; // Normalvektor
DXVector2 tcoord; // Oberflächenkoordinaten für das Anbringen der Textur
DXColor vcolor; // Farbe
};
Der Hilfstyp MQL5\Include\Canvas\DXDXDXUtils.mqh enthält eine Reihe von Methoden zur Erzeugung der Geometrie (Ecken und Indizes) der
Basisprimitive und zum Laden von 3D-Geometrie aus .OBJ-Dateien.
Fügen Sie die Erstellung einer Kugel und eines Torus hinzu, wenden Sie die gleiche Steintextur an:
virtual bool Create(const int width,const int height) { ... // --- Ecken und Indizes für manuell erstellte Objekte DXVertex vertices[]; uint indices[]; //--- Vorbereitung der Ecken und Indices für den Sphäre if(!DXComputeSphere(0.3f,50,vertices,indices)) return(false); //--- Setzen von Weiß für die Ecken DXColor white=DXColor(1.0f,1.0f,1.0f,1.0f); for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- Erstellen des Objekts der Sphäre if(!m_sphere.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- Setzen einer diffusen Farbe für die Sphäre m_sphere.DiffuseColorSet(DXColor(0.0,1.0,0.0,1.0)); //--- Setzen von Weiß als Spiegelungsfarbe m_sphere.SpecularColorSet(white); m_sphere.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- Hinzufügen der Sphäre zur Szene m_canvas.ObjectAdd(&m_sphere); //--- Vorbereitung der Ecken und Indices für den Torus if(!DXComputeTorus(0.3f,0.1f,50,vertices,indices)) return(false); //--- Setzen von Weiß für die Ecken for(int i=0; i<ArraySize(vertices); i++) vertices[i].vcolor=white; //--- Erstellen des Torus-Objekts if(!m_torus.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),vertices,indices)) { m_canvas.Destroy(); return(false); } //--- Setzen einer diffusen Farbe für den Torus m_torus.DiffuseColorSet(DXColor(0.0,0.0,1.0,1.0)); m_torus.SpecularColorSet(white); m_torus.TextureSet(m_canvas.DXDispatcher(),"stone.bmp"); //--- Hinzufügen des Torus zur Szene m_canvas.ObjectAdd(&m_torus); //--- Neuzeichnen der Szene Redraw(); //--- war erfolgreich return(true); }
Animieren Sie die neuen Objekte:
void OnTimer(void) { ... m_canvas.LightDirectionSet(light_direction); //--- Objekt der Sphäre DXMatrix translation; DXMatrixTranslation(translation,1.1f,0,0); DXMatrixRotationY(rotation,time); DXMatrix transform; DXMatrixMultiply(transform,translation,rotation); m_sphere.TransformMatrixSet(transform); //--- Laufbahn des Torus mit Umdrehung um seine Achsen DXMatrixRotationX(rotation,time*1.3f); DXMatrixTranslation(translation,-2,0,0); DXMatrixMultiply(transform,rotation,translation); DXMatrixRotationY(rotation,time/1.3f); DXMatrixMultiply(transform,transform,rotation); m_torus.TransformMatrixSet(transform); //--- Neuberechnung und Zeichnen der 3D-Szene auf der Leinwand Redraw(); }
Speichern Sie die Änderungen als Three Objects.mq5 und führen Sie sie aus.
Rotierende Figuren in der Umlaufbahn eines Würfels.
Datenbankbasierte 3D-Oberfläche
Für die Erstellung von Berichten und die Analyse von Daten werden gewöhnlich verschiedene Diagramme verwendet, wie z.B. lineare
Diagramme, Histogramme, Tortendiagramme usw. MQL5 bietet eine komfortable Grafikbibliothek,
die jedoch nur 2D-Diagramme erstellen kann.
Die Klasse CDXSurface ermöglicht die Visualisierung einer Oberfläche mit Hilfe von benutzerdefinierten Daten, die in einem zweidimensionalen Array gespeichert sind. Betrachten wir das Beispiel der folgenden mathematischen Funktion
z=sin(2.0*pi*sqrt(x*x+y*y))
Erstellen Sie ein Objekt, um die Oberfläche zu zeichnen, und ein Array, um Daten zu speichern:
virtual bool Create(const int width,const int height) { ... //--- Vorbereitung eines Arrays zur Datenspeicherung m_data_width=m_data_height=100; ArrayResize(m_data,m_data_width*m_data_height); for(int i=0;i<m_data_width*m_data_height;i++) m_data[i]=0.0; //--- Erstellen eines Oberflächenobjektes if(!m_surface.Create(m_canvas.DXDispatcher(),m_canvas.InputScene(),m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { m_canvas.Destroy(); return(false); } //--- Erstellen von Textur und Reflexion m_surface.SpecularColorSet(DXColor(1.0,1.0,1.0,1.0)); m_surface.TextureSet(m_canvas.DXDispatcher(),"checker.bmp"); //--- Hinzufügen der Oberfläche zur Szene m_canvas.ObjectAdd(&m_surface); //--- war erfolgreich return(true); }
Die Oberfläche wird innerhalb eines Kastens mit einer Grundfläche von 4x4 und einer Höhe von 1 gezeichnet. Die Texturabmessungen betragen 0,25x0,25.
- SF_TWO_SIDED gibt an, dass die Oberfläche sowohl über als auch unter der Oberfläche gezeichnet wird, falls sich die Kamera unter die Oberfläche bewegt.
- SF_USE_NORMALS gibt an, dass für die Berechnung der Reflexionen von der Oberfläche, die durch die gerichtete Lichtquelle verursacht werden, normale Berechnungen verwendet werden.
- CS_COLD_TO_HOT setzt die Oberflächenfarben der Heatmap von blau nach rot mit einem Übergang durch grün und gelb.
Um die Oberfläche zu animieren, fügen Sie unterhalb des Sinuszeichens Zeit hinzu und aktualisieren Sie diese mit dem Timer.
void OnTimer(void) { static ulong last_time=0; static float time=0; //--- Abfragen der aktuellen Zeit ulong current_time=GetMicrosecondCount(); //--- Berechnung von delta float deltatime=(current_time-last_time)/1000000.0f; if(deltatime>0.1f) deltatime=0.1f; //--- Erhöhen der verstrichenen Zeit time+=deltatime; //--- Sichern der Zeit last_time=current_time; //--- Berechnen der Oberflächenwerte unter Berücksichtigung der zeitlichen Änderungen for(int i=0; i<m_data_width; i++) { double x=2.0*i/m_data_width-1; int offset=m_data_height*i; for(int j=0; j<m_data_height; j++) { double y=2.0*j/m_data_height-1; m_data[offset+j]=MathSin(2.0*M_PI*sqrt(x*x+y*y)-2*time); } } //--- Datenaktualisierung, um die Oberfläche zu zeichnen if(m_surface.Update(m_data,m_data_width,m_data_height,2.0f, DXVector3(-2.0,-0.5,-2.0),DXVector3(2.0,0.5,2.0),DXVector2(0.25,0.25), CDXSurface::SF_TWO_SIDED|CDXSurface::SF_USE_NORMALS,CDXSurface::CS_COLD_TO_HOT)) { //--- Neuberechnung und Zeichnen der 3D-Szene auf der Leinwand Redraw(); } }Der Quellcode ist verfügbar in 3D Surface.mq5, das Programmbeispiel wird im Video gezeigt.
In diesem Artikel haben wir die Möglichkeiten von DirectX-Funktionen bei der Erstellung einfacher geometrischer Formen und animierter 3D-Grafiken für die visuelle Datenanalyse betrachtet. Komplexere Beispiele finden Sie im MetaTrader 5 Terminal-Installationsverzeichnis: Expert Advisor "Korrelationsmatrix 3D" und "Mathe 3D Morpher", sowie das Skript "Rest 3D".
MQL5 ermöglicht es Ihnen, wichtige algorithmische Handelsaufgaben zu lösen, ohne Pakete von Drittanbietern zu verwenden:
- Optimieren Sie komplexe Handelsstrategien, die viele Eingabeparameter enthalten
- Erhalt von Optimierungsergebnissen
- Visualisieren von Daten im bequemsten dreidimensionalen Speicher
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/7708
Verwendung von Netzwerkfunktionen oder MySQL ohne DLL: Teil I - Konnektor
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXXIII): Schwebende Handelsanfragen - Schließen von Positionen unter bestimmten Bedingungen
Bibliothek für ein leichtes und schnelles Entwickeln vom Programmen für den MetaTrader (Teil XXXIII): Schwebende Handelsanfragen - Entfernen und Ändern von Orders und Positionen unter bestimmten Bedingungen
Anwendung von OLAP im Handel (Teil 3): Kursanalyse für die Entwicklung von Handelsstrategien
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.