
OpenCL: Vom naiven zum aufschlussreicheren Programmieren
Einleitung
Der erste Beitrag "OpenCL: Die Brücke zu parallelen Welten" war eine Einführung in das Thema OpenCL. Er ging auf die grundlegenden Themen der Interaktion zwischen dem Programm in OpenCL (auch als Kernel bezeichnet, obwohl das nicht ganz richtig ist) und dem externen Programm (Host) in MQL5 ein. Einige Möglichkeiten der Sprache (z. B. die Verwendung von Vektor-Datentypen) wurden anhand der Berechnung von Pi = 3,14159265... veranschaulicht.
Die Optimierung der Performance des Programms war in einigen Fällen beträchtlich. Doch all diese Optimierungen waren naiv, da sie nicht die Hardwarespezifikationen berücksichtigten, die zur Durchführung all unserer Berechnungen genutzt wurden. Die Kenntnis dieser Spezifikationen kann es uns in den allermeisten Fällen ermöglichen, bewusst Beschleunigungen zu erzielen, die die Möglichkeiten der CPU weit übersteigen.
Um diese Optimierungen zu demonstrieren, musste der Verfasser auf ein Beispiel zurückgreifen, das heute wahrscheinlich zu den am gründlichsten studierten in der Literatur zu OpenCL gehört. Es handelt sich um die Multiplikation von zwei großen Matrizen.
Beginnen wir mit dem Wichtigsten: dem Speichermodell von OpenCL zusammen mit den Besonderheiten seiner Implementierung auf echter Hardware-Architektur.
1. Speicherhierarchie in modernen Computern
1,1. Das Speichermodell von OpenCL
Im Allgemeinen unterscheiden sich Speichermodelle je nach Computerplattform deutlich voneinander. Beispielsweise unterstützen alle modernen CPUs automatisches Daten-Caching im Gegensatz zu GPUs, bei denen das nicht immer der Fall ist.
Um die Übertragbarkeit des Codes zu gewährleisten, wird in OpenCL ein abstraktes Speichermodell umgesetzt, an dem sich Programmierer und Hersteller, die dieses Modell auf realer Hardware umsetzen müssen, richten können. Der Speicher, wie er in OpenCL definiert wird, wird in der nachfolgenden Abbildung beispielhaft illustriert:
Abb. 1. Das Speichermodell von OpenCL
Sobald die Daten vom Host an das Device übertragen werden, werden sie im globalen Speicher des Devices gespeichert. Jegliche Daten, die in entgegengesetzter Richtung übertragen werden, werden ebenfalls im globalen Speicher gespeichert (diesmal allerdings im globalen Speicher des Hosts). Das Schlüsselwort __global (zwei Unterstriche!) ist ein Modifikator, der darauf hindeutet, dass Daten, die einem bestimmten Pointer entsprechen, im globalen Speicher gespeichert werden:
__kernel void foo( __global float *A ) { /// kernel code }
Globaler Speicher ist für alle Recheneinheiten innerhalb des Devices zugänglich, wie RAM im Host-System.
Konstanter Speicher speichert im Kontrast zu seinem Namen nicht unbedingt schreibgeschützte Daten. Diese Art von Speicher ist für Daten vorgesehen, bei denen alle Arbeitseinheiten gleichzeitig auf jedes Element zugreifen können. Variablen mit konstanten Werten fallen natürlich auch unter diese Kategorie. Der konstante Speicher im OpenCL-Modell ist Teil des globalen Speichers. Speicherobjekte, die an den globalen Speicher übertragen werden, können deshalb als __constant festgelegt werden.
Lokaler Speicher ist ein Scratchpad-Speicher, in dem jedes Device einen einzigartigen Adressraum erhält. In der Hardware handelt es sich dabei oft um On-Chip-Speicher, doch OpenCL stellt nicht die Anforderung, dass dies der Fall ist.
Der Zugriff auf diese Art von Speicher führt zu viel geringeren Latenzzeiten und die Speicherbandbreite ist deshalb viel höher als die von globalem Speicher. Wir werden versuchen, diese geringere Latenzzeit für die Optimierung der Kernel-Performance zu nutzen.
Die OpenCL-Spezifikation besagt, dass eine Variable im lokalen Speicher sowohl in der Kopfzeile des Kernels:
__kernel void foo( __local float *sharedData ) { }als auch in seinem Körper deklariert werden kann:
__kernel void foo( __global float *A ) { __local float sharedData[ 64 ]; }Beachten Sie, dass im Kernel-Körper kein dynamisches Array deklariert werden kann. Sie müssen seine Größe immer angeben.
Weiter unten, bei der Optimierung des Kernels für die Multiplikation von zwei großen Matrizen, werden Sie sehen, wie mit lokalen Daten gearbeitet wird und welche Besonderheiten dies gemäß den Erfahrungen des Verfassers bei der Umsetzung in MetaTrader 5 mit sich bringt.
Lokale Variablen und Kernel-Argumente, die keine Pointer beinhalten, sind standardmäßig privat (falls ohne Modifikator __local spezifiziert). In der Praxis befinden sich diese Variablen meist in Registern. Und umgekehrt befinden sich private Arrays und jegliche Spilled Registers meist auf Off-Chip-Speicher, d. h. Speicher mit höherer Latenzzeit. Hier möchte ich die relevanten Informationen aus dem englischen Wikipedia-Artikel zitieren:
In vielen Programmiersprachen hat der Programmierer die Illusion, beliebig viele Variablen zuzuweisen. Doch bei der Kompilierung muss der Compiler entscheiden, wie diese Variablen einem kleinen, endlichen Satz von Registern zugewiesen werden sollen. Nicht alle Variablen sind gleichzeitig aktiv (oder "live"), also können einige Register mehr als einer Variable zugewiesen werden. Allerdings können zwei Variablen, die gleichzeitig genutzt werden, nicht demselben Register zugewiesen werden, ohne seinen Wert zu korrumpieren.
Variablen, die keinem Register zugewiesen werden können, müssen im RAM aufbewahrt und für jeden Lese-/Schreibvorgang geladen/ausgeladen werden, ein Prozess, den man Spilling nennt. Der Zugriff auf RAM ist deutlich langsamer als der Zugriff auf Register und verlangsamt die Ausführungsgeschwindigkeit des kompilierten Programms. Deshalb versucht ein optimierender Compiler, so viele Variablen wie möglich Registern zuzuweisen. "Registerdruck" (register pressure) ist der Begriff, der verwendet wird, wenn weniger Hardwareregister zur Verfügung stehen, als optimal wäre. Höherer Druck bedeutet für gewöhnlich, dass mehr Spills und häufigeres Neuladen erforderlich sind.
Das beschriebene OpenCL-Speichermodell ist der Speicherstruktur moderner GPUs sehr ähnlich. Die nachfolgende Abbildung zeigt eine Korrelation zwischen dem OpenCL-Speichermodell und dem Speichermodell der GPU AMD Radeon HD 6970.
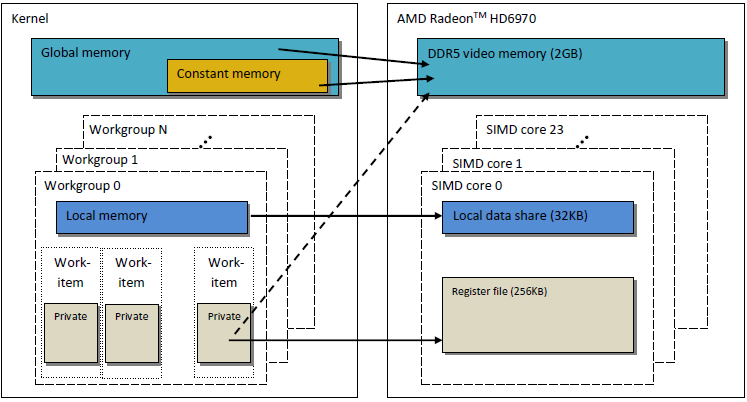
Abb. 2. Korrelation zwischen der Speicherstruktur der Radeon HD 6970 und dem abstrakten OpenCL-Speichermodell
Fahren wir mit einer detaillierteren Betrachtung der Fragen in Bezug auf eine konkrete GPU-Speicherimplementierung fort.
1,2. Speicher in modernen diskreten GPUs
1.2.1. Verschmelzen von Speicheranfragen
Diese Informationen sind ebenfalls für die Optimierung der Kernel-Performance wichtig, da es das Hauptziel ist, eine hohe Speicherbandbreite zu erzielen.
Sehen Sie sich die nachfolgende Abbildung an, um den Adressierprozess des Speichers besser zu verstehen:
Abb. 3. Schema der Adressierung von Daten im globalen Device-Speicher
Der Pointer eines Arrays aus ganzzahligen Variablen int sei die Adresse von X = 0x00001232. Jedes int verbraucht 4 Byte Speicher. Nehmen wir an, dass ein Thread (der das Software-Gegenstück einer Arbeitseinheit ist, die den Kernel-Code ausführt) Daten bei X [ 0 ] adressiert:
int tmp = X[ 0 ];
Wir nehmen an, dass die Breite des Speicherbusses 32 Byte (256 Bit) beträgt. Die Busbreite ist typisch für leistungsstarke GPUs wie die Radeon HD 5870. Bei einigen anderen GPUs kann der Datenbus eine andere Breite haben, z. B. 384 Bit oder sogar 512 Bit bei einigen NVidia-Modellen.
Die Adressierung des Speicherbusses sollte seiner Struktur entsprechen, d. h. zuallererst seiner Breite. In anderen Worten: Daten im Speicher werden in Blöcken von je 32 Bytes (256 Bit) gespeichert. Unabhängig davon, was wir innerhalb des Bereichs zwischen 0x00001220 und 0x0000123F adressieren (es sind genau 32 Bytes in diesem Bereich, Sie können es nachprüfen), erhalten wir immer noch die Adresse 0x00001220 als Startadresse für den Lesevorgang.
Der Zugang bei der Adresse 0x00001232 gibt alle Daten bei Adressen innerhalb des Bereichs zwischen 0x00001220 und 0x0000123F aus, d. h. 8 int-Zahlen. Deshalb wird es nur 4 Bytes (eine int-Zahl) Nutzdaten geben, während die verbleibenden 28 Bytes (7 int-Zahlen) nutzlos sein werden:
Abb. 4. Schema zum Erhalten erforderlicher Daten aus dem Speicher
Die benötigte Zahl an der vorher angegebenen Adresse – 0x000012342 – ist im Schema eingekreist.
Um den Gebrauch des Busses so effektiv wie möglich zu machen, versucht die GPU, Speicherzugriffe von verschiedenen Threads zu einer einzigen Speicheranfrage zu verschmelzen. Je weniger Speicherzugriffe, desto besser. Der Grund dafür ist, dass der Zugriff auf globalen Device-Speicher uns Zeit kostet und somit die Ausführungsgeschwindigkeit des Programms deutlich beeinträchtigt. Betrachten Sie die folgende Zeile des Kernel-Codes:
int tmp = X[ get_global_id( 0 ) ];
Nehmen wir an, unser Array X ist das Array aus dem vorherigen Beispiel. Dann greifen die ersten 16 Threads (Kernels) auf Adressen von 0x00001232 bis 0x00001272 zu (in diesem Bereich befinden sich 16 int-Zahlen, d. h. 64 Bytes). Wenn jede Anfrage unabhängig von Kernels gesendet worden wäre, ohne vorherige Verschmelzung zu einer einzelnen Anfrage, würde jede der 16 Anfragen 4 Byte Nutzdaten und 28 Byte nutzlose Daten enthalten, was insgesamt 64 genutzte und 448 ungenutzte Bytes ergibt.
Diese Berechnung basiert auf der Tatsache, dass jeder Zugriff auf einer Adresse innerhalb eines und desselben 32-Byte-Speicherblocks völlig identische Daten ausgibt. Das ist der zentrale Punkt. Am sinnvollsten ist es, mehrere Anfragen zu einer zusammenhängenden zu verschmelzen, um nutzlose Anfragen einzusparen. Dieser Vorgang wird nachfolgend Verschmelzung (coalescing) genannt und verschmolzene Anfragen werden als kohärent bezeichnet.
Abb. 5. Nur drei Speicheranfragen sind nötig, um die erforderlichen Daten zu erhalten
Jede Zelle in der Abbildung besteht aus 4 Bytes. In unserem Beispiel würden 3 Anfragen genügen. Wäre der Anfang des Arrays an die Adresse des Anfangs jedes 32-Byte-Speicherblocks angeglichen worden, hätten sogar 2 Anfragen gereicht.
Bei AMD GPU 64 sind Threads Teil einer Wellenfront und müssen deshalb den gleichen Befehl ausführen wie bei SIMD. 16 Threads, angeordnet nach get_global_id( 0 ), bilden genau ein Viertel der Wellenfront und werden zu einer kohärenten Anfrage für den effizienten Gebrauch des Busses verschmolzen.
Nachfolgend sehen Sie eine Illustration der erforderlichen Speicherbandbreite für kohärente Anfragen im Vergleich mit inkohärenten, also "spontanen" Anfragen. Die Illustration betrifft die Radeon HD 5870. Bei NVidia-Karten lässt sich ein ähnliches Ergebnis beobachten.
Abb. 6. Vergleichsanalyse der erforderlichen Speicherbandbreite für kohärente und inkohärente Anfragen
Es lässt sich klar erkennen, dass eine kohärente Speicheranfrage eine Erhöhung der Speicherbandbreite um etwa eine Größenordnung ermöglicht.
1.2.2. Speicherbanken
Speicher besteht aus Banken, in denen die Daten tatsächlich aufbewahrt werden. Bei modernen GPUs sind das für gewöhnlich 32-Bit- (4-Byte)-Wörter. Serielle Daten werden in benachbarten Speicherbanken gespeichert. Gruppen von Threads, die auf serielle Elemente zugreifen, führen zu keinen Konflikten mit den Banken.
Die negativsten Auswirkungen von Bankenkonflikten können für gewöhnlich im lokalen GPU-Speicher beobachtet werden. Es wird deshalb empfohlen, dass lokale Datenzugriffe aus benachbarten Threads auf unterschiedliche Speicherbanken erfolgen.
Bei AMD-Hardware hält die Wellenfront, die Bankenkonflikte verursacht, an, bis alle lokalen Speichervorgänge abgeschlossen sind. Dies führt zu einer Serialisierung, bei der Code-Blöcke, die parallel ausgeführt werden sollen, nacheinander ausgeführt werden. Dies wirkt sich extrem negativ auf die Performance des Kernels aus.
Abb. 7. Schemata des Speicherzugriffs ohne Bankenkonflikte
Die Abbildung führt den Speicherzugriff ohne Bankenkonflikte vor, da alle Threads auf unterschiedliche Daten zugreifen.
Lassen Sie uns den Speicherzugriff mit Bankenkonflikten illustrieren:
Abb. 8. Speicherzugriff mit Bankenkonflikten
Es gibt allerdings eine Ausnahme von dieser Situation: Wenn alle Zugriffe auf die gleiche Adresse erfolgen, kann die Bank ein Broadcast ausführen, um die Verzögerung zu vermeiden:
Abb. 9. Alle Threads greifen auf die gleiche Adresse zu
Ähnliche Ereignisse treten beim Zugriff auf globalen Speicher auf, doch die Auswirkungen solcher Konflikte sind wesentlich schwächer.
- GPU-Speicher unterscheidet sich von CPU-Speicher. Das Hauptziel der Optimierung der Programm-Performance mithilfe von OpenCL ist die Sicherstellung der maximalen Bandbreite anstatt der Reduzierung von Latenzzeiten, wie es bei der CPU der Fall wäre.
- Die Art des Speicherzugriffs wirkt sich wesentlich auf die Effizienz des Gebrauchs des Busses aus. Eine geringe Effizienz des Gebrauchs des Busses bedeutet eine niedrige Ausführungsgeschwindigkeit.
- Um die Performance des Codes zu verbessern, wird empfohlen, dass der Speicherzugriff kohärent ist. Außerdem ist es äußerst wünschenswert, Bankenkonflikte zu vermeiden.
- Hardwarespezifikationen (Busbreite, Menge der Speicherbanken sowie die Anzahl der Threads, die sich zu einem einzigen kohärenten Zugriff verschmelzen lassen) können in den Spezifikationen des Herstellers gefunden werden.
Die Spezifikationen einiger Radeon-Grafikkarten der Serie 5xxx sind nachfolgend als Beispiel aufgeführt:
Abb. 10. Technische Spezifikationen mittlerer und High-End-Grafikkarten der Serie Radeon HD 58xx
Widmen wir uns nun der Programmierung.
2. Multiplikation großer rechteckiger Matrizen: von seriellem CPU-Code zu parallelem GPU-Code
2,1. MQL5-Code
Die Aufgabe ist im Gegensatz zum vorhergehenden Beitrag "OpenCL: Die Brücke zu parallelen Welten" nun Standard, d. h. die Multiplikation von zwei Matrizen. Sie wird vor allem deshalb gewählt, weil zahlreiche Informationen zu diesem Thema in unterschiedlichen Quellen zu finden sind. Die meisten davon liefern auf diese oder jene Art mehr oder weniger koordinierte Lösungen. Das ist der Weg den wir einschlagen werden, indem wir Schritt für Schritt die Bedeutung der Modellstrukturen klären und stets daran denken, dass wir auf echter Hardware arbeiten.
Nachfolgend sehen Sie eine Formel zur Multiplikation von Matrizen, die in der linearen Algebra bestens bekannt ist und für Computerberechnungen angepasst wurde. Der erste Index ist die Nummer der Matrixzeile, der zweite die Spaltennummer. Jedes Element der Ausgabematrix wird durch sequentielles Addieren jedes Produkts von Elementen in der ersten und zweiten Matrix zur angesammelten Summe berechnet. Letztendlich ist diese angesammelte Summe das berechnete Element der Ausgabematrix:
Abb. 11. Formel der Multiplikation der Matrix
Die Formel kann schematisch folgendermaßen dargestellt werden:
Abb. 12. Algorithmus der Multiplikation der Matrix (veranschaulicht durch die Berechnung eines Elements der Ausgabematrix) – schematische Darstellung
Es lässt sich leicht erkennen, dass wenn beide Matrizen die gleichen Abmessungen gleich N haben, die Menge der Additionen und Multiplikationen durch die Funktion O(N^3) geschätzt werden kann: Um jedes Element der Ausgabematrix zu berechnen, müssen Sie das Skalarprodukt einer Zeile in der ersten Matrix und einer Spalte in der zweiten Matrix erhalten. Dies erfordert etwa 2*N Additionen und Multiplikationen. Eine erforderliche Schätzung erhält man durch die Multiplikation mit der Anzahl der Matrixelemente N^2. Somit hängt die ungefähre Laufzeit des Codes ziemlich stark von N-Quadrat ab.
Die Anzahl der Zeilen und Spalten der Matrizen wird nachfolgend aus reiner Bequemlichkeit mit 2000 festgelegt. Sie kann eine beliebige Größe haben, aber nicht zu groß sein.
Der Code in MQL5 ist nicht sehr kompliziert:
//+------------------------------------------------------------------+ //| matr_mul_2dim.mq5 | //+------------------------------------------------------------------+ #define ROWS1 1000 // rows in the first matrix #define COLSROWS 1000 // columns in the first matrix = rows in the second matrix #define COLS2 1000 // columns in the second matrix float first[ ROWS1 ][ COLSROWS ]; // first matrix float second[ COLSROWS ][ COLS2 ]; // second matrix float third[ ROWS1 ][ COLS2 ]; // product //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { MathSrand(GetTickCount()); Print("======================================="); Print("ROWS1 = "+i2s(ROWS1)+"; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); genMatrices(); ArrayInitialize(third,0.0f); //--- execution on the CPU uint st1=GetTickCount(); mul(); double time1=(double)(GetTickCount()-st1)/1000.; Print("CPU: time = "+DoubleToString(time1,3)+" s."); return; } //+------------------------------------------------------------------+ //| i2s | //+------------------------------------------------------------------+ string i2s(int arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ //| genMatrices | //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r][c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r][c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ float genVal() { return(float)(( MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| mul | //| Main matrix multiplication function | //+------------------------------------------------------------------+ void mul() { // r-cr-c: 10.530 s for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) for(int c=0; c<COLS2; c++) third[r][c]+=first[r][cr]*second[cr][c]; return; }
Aufstellung 1. Ursprüngliches Ablaufprogramm auf dem Host
Ausführungsergebnisse mit unterschiedlichen Parametern:
2012.05.19 09:39:11 matr_mul_2dim (EURUSD,H1) CPU: time = 10.530 s. 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ROWS1 = 1000; COLSROWS = 1000; COLS2 = 1000 2012.05.19 09:39:00 matr_mul_2dim (EURUSD,H1) ======================================= 2012.05.19 09:41:04 matr_mul_2dim (EURUSD,H1) CPU: time = 83.663 s. 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.19 09:39:40 matr_mul_2dim (EURUSD,H1) =======================================
Wie Sie sehen können, hat sich unsere geschätzte Abhängigkeit der Laufzeit von linearen Matrixgrößen als wahr erwiesen: Ein zweifacher Anstieg aller Matrixdimensionen führte zu einem 8-fachen Anstieg der Laufzeit.
Ein paar Worte zum Algorithmus: Die Reihenfolge der Schleife lässt sich in der Multiplikationsfunktion mul() beliebig ändern. Es stellt sich heraus, dass sich dies deutlich auf die Laufzeit auswirkt: Das Verhältnis der langsamsten zur schnellsten Laufzeitvariante liegt bei etwa 1,73.
In diesem Beitrag wird nur die schnellste Variante vorgeführt. Die verbleibenden getesteten Varianten finden Sie in dem am Ende des Beitrags angehängten Code (Datei matr_mul_2dim.mq5). In diesem Zusammenhang besagt der OpenCL Programming Guide (Aaftab Munshi, Benedict R. Gaster, Timothy G. Mattson, James Fung, Dan Ginsburg) Folgendes (S. 512):
Natürlich sind das nicht alle Optimierungen des ursprünglichen "nicht parallelen" Codes, die wir umsetzen können. Einige von ihnen beziehen sich auf Hardware ((S)SSEx-Befehle), während andere rein algorithmisch sind, z. B der Strassen-Algorithmus, der Coppersmith-Winograd-Algorithmus usw. Beachten Sie, dass die Größe der multiplizierten Matrizen für den Strassen-Algorithmus, die zu einer deutlichen Beschleunigung gegenüber dem herkömmlichen Algorithmus führen, mit 64x64 ziemlich klein ist. In diesem Beitrag werden wir lernen, Matrizen, deren lineare Größe mehrere tausend sein kann (etwa bis 5000), schnell zu multiplizieren.
2,2. Erste Umsetzung des Algorithmus in OpenCL
Übertragen wir diesen Algorithmus nun in OpenCL, indem wir ROWS1 * COLS2 Threads erstellen, d. h. beide äußeren Schleifen aus dem Kernel löschen. Jeder Thread wird COLSROWS Iterationen ausführen, sodass die innere Schleife Teil des Kernels bleibt.
Da wir drei lineare Puffer für das OpenCL-Kernel erstellen müssen werden, wäre es sinnvoll, den ursprünglichen Algorithmus zu überarbeiten, damit er dem Kernel-Algorithmus so ähnlich wie möglich ist. Der Code des "nicht parallelen" Programms auf einer "Single-Core-CPU" mit linearen Puffern wird zusammen mit dem Kernel-Code bereitgestellt. Die Optimalität des Codes mit zweidimensionalen Arrays bedeutet nicht, dass sein Gegenstück ebenfalls für lineare Puffer optimal sein wird: Alle Tests werden erneut durchgeführt werden müssen. Deshalb entscheiden wir uns erneut für c-r-cr als Ausgangsvariante, die der Standardlogik der Multiplikation von Matrizen in der linearen Algebra entspricht.
Dabei beantworten wir die folgende zentrale Frage, um eine mögliche Verwechslung der Adressierung von Matrix-/Pufferelementen zu vermeiden: Wenn eine Matrix Matr( M Zeilen über N Spalten ) als linearer Puffer im globalen Speicher der GPU angelegt ist, wie können wir eine lineare Verschiebung eines Elements Matr[ row ][ column ] berechnen?
Tatsächlich gibt es keine feste Reihenfolge beim Anlegen einer Matrix im GPU-Speicher, da die Reihenfolge ausschließlich durch die Logik der Aufgabe bestimmt wird. Beispielsweise könnten Elemente beider Matrizen in Puffern unterschiedlich angelegt sein, weil in Bezug auf den Multiplikationsalgorithmus der Matrix Matrizen asymmetrisch sind, d. h. die Zeilen der ersten Matrix werden mit den Spalten der zweiten Matrix multipliziert. Eine solche Neuanordnung kann die Performance der Berechnungen beim nachfolgenden Lesen der Matrixelemente aus dem globalen Speicher der GPU in jeder Iteration des Kernels merklich beeinflussen.
In der ersten Umsetzung des Algorithmus werden die Matrizen identisch angelegt – nach Zeilen. Die Elemente der ersten Zeile werden zuerst im Puffer platziert, gefolgt von allen Elementen in der zweiten Zeile usw. Die Formel für die Glättung einer 2-dimensionalen Darstellung einer Matrix Matr[ M (Zeilen) ][ N (Spalten) ] in linearen Speicher ist die folgende:
Abb. 13. Algorithmus für die Umwandlung eines zweidimensionalen Indexraums in lineare Form für die Anlage der Matrix im GPU-Puffer
Die Abbildung liefert auch ein Beispiel dafür, wie die Darstellung einer 2-dimensionalen Matrix in linearem Speicher nach Spalten geglättet wird.
Nachfolgend sehen Sie einen leicht reduzierten Code unserer ersten Programmumsetzung mit Ausführung auf dem OpenCL-Device:
//+------------------------------------------------------------------+ //| matr_mul_1dim.mq5 | //+------------------------------------------------------------------+ #property script_show_inputs #define ROWS1 2000 // rows in the first matrix #define COLSROWS 2000 // columns in the first matrix = rows in the second matrix #define COLS2 2000 // columns in the second matrix #define REALTYPE float REALTYPE first[]; // first linear buffer (matrix) rows1 * colsrows REALTYPE second[]; // second buffer colsrows * cols2 REALTYPE thirdGPU[ ]; // product - also a buffer rows1 * cols2 REALTYPE thirdCPU[ ]; // product - also a buffer rows1 * cols2 input int _device=1; // here is the device; it can be changed (now 4870) string d2s(double arg,int dig) { return DoubleToString(arg,dig); } string i2s(long arg) { return IntegerToString(arg); } //+------------------------------------------------------------------+ const string clSrc= "#define COLS2 "+i2s(COLS2)+" \r\n" "#define COLSROWS "+i2s(COLSROWS)+" \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ]; \r\n" "} \r\n"; //+------------------------------------------------------------------+ //| Main matrix multiplication function; | //| Input matrices are already generated, | //| the output matrix is initialized to zeros | //+------------------------------------------------------------------+ void mulCPUOneCore() { //--- c-r-cr: 11.544 s //st = GetTickCount( ); for(int c=0; c<COLS2; c++) for(int r=0; r<ROWS1; r++) for(int cr=0; cr<COLSROWS; cr++) thirdCPU[r*COLS2+c]+=first[r*COLSROWS+cr]*second[cr*COLS2+c]; return; } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { initAllDataCPU(); //--- start working with non-parallel version ("bare" CPU, single core) //--- calculate the output matrix on a single core CPU uint st=GetTickCount(); mulCPUOneCore(); //--- output total calculation time double timeCPU=(GetTickCount()-st)/1000.; Print("CPUTime = "+d2s(timeCPU,3)); //--- start working with OCL int clCtx; // context handle int clPrg; // handle to the program on the device int clKrn; // kernel handle int clMemIn1; // first (input) buffer handle int clMemIn2; // second (input) buffer handle int clMemOut; // third (output) buffer handle //--- start calculating the program runtime on GPU //st = GetTickCount( ); initAllDataGPU(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- start calculating total OCL code runtime st=GetTickCount(); executeGPU(clKrn); //--- create a buffer for reading and read the result; we will need it later REALTYPE buf[]; readOutBuf(clMemOut,buf); //--- stop calculating the total program runtime //--- together with the time required for retrieval of data from GPU and transferring it back to RAM double timeGPUTotal=(GetTickCount()-st)/1000.; Print("OpenCL total: time = "+d2s(timeGPUTotal,3)+" sec."); destroyOpenCL(clCtx,clPrg,clKrn,clMemIn1,clMemIn2,clMemOut); //--- calculate the time elapsed Print("CPUTime / GPUTotalTime = "+d2s(timeCPU/timeGPUTotal,3)); //--- debugging: random checks. Multiplication accuracy is checked directly //--- on the initial and output matrices using a few dozen examples for(int i=0; i<10; i++) checkRandom(buf,ROWS1,COLS2); Print("________________________"); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //+------------------------------------------------------------------+ void initAllDataCPU() { //--- initialize random number generator MathSrand(( int) TimeLocal()); Print("======================================="); Print("1st OCL martices mul: device = "+i2s(_device)+"; ROWS1 = " +i2s(ROWS1)+ "; COLSROWS = "+i2s(COLSROWS)+"; COLS2 = "+i2s(COLS2)); //--- set the required sizes of linear representations of the input and output matrices ArrayResize(first,ROWS1*COLSROWS); ArrayResize(second,COLSROWS*COLS2); ArrayResize(thirdGPU,ROWS1*COLS2); ArrayResize(thirdCPU,ROWS1*COLS2); //--- generate both input matrices and initialize the output to zeros genMatrices(); ArrayInitialize( thirdCPU, 0.0 ); ArrayInitialize( thirdGPU, 0.0 ); return; } //+------------------------------------------------------------------+ //| initAllDataCPU | //| lay out in row-major order, Matr[ M (rows) ][ N (columns) ]: | //| Matr[row][column] = buff[row * N(columns in the matrix) + column]| //| generate initial matrices; this generation is not reflected | //| in the final runtime calculation | //| buffers are filled in row-major order! | //+------------------------------------------------------------------+ void genMatrices() { for(int r=0; r<ROWS1; r++) for(int c=0; c<COLSROWS; c++) first[r*COLSROWS+c]=genVal(); for(int r=0; r<COLSROWS; r++) for(int c=0; c<COLS2; c++) second[r*COLS2+c]=genVal(); return; } //+------------------------------------------------------------------+ //| genVal | //| generate one value of the matrix element: | //| uniformly distributed value lying in the range [-0.5; 0.5] | //+------------------------------------------------------------------+ REALTYPE genVal() { return(REALTYPE)((MathRand()-16383.5)/32767.); } //+------------------------------------------------------------------+ //| initAllDataGPU | //+------------------------------------------------------------------+ void initAllDataGPU(int &clCtx, // context int& clPrg, // program on the device int& clKrn, // kernel int& clMemIn1, // first (input) buffer int& clMemIn2, // second (input) buffer int& clMemOut) // third (output) buffer { //--- write the kernel code to a file WriteCLProgram(); //--- create context, program and kernel clCtx = CLContextCreate( _device ); clPrg = CLProgramCreate( clCtx, clSrc ); clKrn = CLKernelCreate( clPrg, "matricesMul" ); //--- create all three buffers for the three matrices //--- first matrix - input clMemIn1=CLBufferCreate(clCtx,ROWS1 *COLSROWS*sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- second matrix - input clMemIn2=CLBufferCreate(clCtx,COLSROWS*COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- third matrix - output clMemOut=CLBufferCreate(clCtx,ROWS1 *COLS2 *sizeof(REALTYPE),CL_MEM_READ_WRITE); //--- set arguments to the kernel CLSetKernelArgMem(clKrn,0,clMemIn1); CLSetKernelArgMem(clKrn,1,clMemIn2); CLSetKernelArgMem(clKrn,2,clMemOut); //--- write the generated matrices to the device buffers CLBufferWrite(clMemIn1,first); CLBufferWrite(clMemIn2,second); CLBufferWrite(clMemOut,thirdGPU); // 0.0 everywhere return; } //+------------------------------------------------------------------+ //| WriteCLProgram | //+------------------------------------------------------------------+ void WriteCLProgram() { int h=FileOpen("matr_mul_OCL_1st.cl",FILE_WRITE|FILE_TXT|FILE_ANSI); FileWrite(h,clSrc); FileClose(h); } //+------------------------------------------------------------------+ //| executeGPU | //+------------------------------------------------------------------+ void executeGPU(int clKrn) { //--- set the workspace parameters for the task and execute the OpenCL program uint offs[ 2 ] = { 0, 0 }; uint works[ 2 ] = { ROWS1, COLS2 }; bool ex=CLExecute(clKrn,2,offs,works); return; } //+------------------------------------------------------------------+ //| readOutBuf | //+------------------------------------------------------------------+ void readOutBuf(int clMemOut,REALTYPE &buf[]) { ArrayResize(buf,COLS2*ROWS1); //--- buf - a copy of what is written to the buffer thirdGPU[] uint read=CLBufferRead(clMemOut,buf); Print("read = "+i2s(read)+" elements"); return; } //+------------------------------------------------------------------+ //| destroyOpenCL | //+------------------------------------------------------------------+ void destroyOpenCL(int clCtx,int clPrg,int clKrn,int clMemIn1,int clMemIn2,int clMemOut) { //--- destroy all that was created for calculations on the OpenCL device in reverse order CLBufferFree(clMemIn1); CLBufferFree(clMemIn2); CLBufferFree(clMemOut); CLKernelFree(clKrn); CLProgramFree(clPrg); CLContextFree(clCtx); return; } //+------------------------------------------------------------------+ //| checkRandom | //| random check of calculation accuracy | //+------------------------------------------------------------------+ void checkRandom(REALTYPE &buf[],int rows,int cols) { int r0 = genRnd( rows ); int c0 = genRnd( cols ); REALTYPE sum=0.0; for(int runningIdx=0; runningIdx<COLSROWS; runningIdx++) sum+=first[r0*COLSROWS+runningIdx]* second[runningIdx*COLS2+c0]; //--- element of the buffer m[] REALTYPE bufElement=buf[r0*COLS2+c0]; //--- element of the matrix not calculated in OpenCL REALTYPE CPUElement=thirdCPU[r0*COLS2+c0]; Print("sum( "+i2s(r0)+","+i2s(c0)+" ) = "+d2s(sum,8)+ "; thirdCPU[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(CPUElement,8)+ "; buf[ "+i2s(r0)+","+i2s(c0)+" ] = "+d2s(bufElement,8)); return; } //+------------------------------------------------------------------+ //| genRnd | //+------------------------------------------------------------------+ int genRnd(int max) { return(int)(MathRand()/32767.*max); }
Aufstellung 2. Erste Umsetzung des Programms in OpenCL
Die letzten zwei Funktionen sind nützlich für die Überprüfung der Genauigkeit der Berechnungen. Den vollständigen Code finden Sie in den Anhängen dieses Beitrags (matr_mul_1dim.mq5). Beachten Sie, dass die Dimensionen nicht zwangsläufig nur viereckigen Matrizen entsprechen müssen.
Die weiteren Änderungen betreffen fast ausschließlich den Kernel-Code, deshalb werden nachfolgend nur die Codes für die Modifizierung des Kernels aufgeführt.
Der Typ REALTYPE wird für die Vereinfachung der Änderung der Berechnungsgenauigkeit von float zu double eingeführt. Es sollte erwähnt werden, dass der Typ REALTYPE nicht nur im Host-Programm deklariert wird, sondern auch innerhalb des Kernels. Falls erforderlich, müssen alle Änderungen in Bezug auf diesen Typ an zwei Orten gleichzeitig vorgenommen werden: im #define des Host-Programms und des Kernel-Codes.
Ergebnisse der Ausführung des Codes (hiernach überall mit dem Datentyp float):
CPU (OpenCL, _device = 0):
2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 12.479 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 9.266 sec. 2012.05.20 22:14:57 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.20 22:14:48 matr_mul_1dim (EURUSD,H1) CPUTime = 115.628 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.20 22:12:52 matr_mul_1dim (EURUSD,H1) =======================================
Ausführung auf Radeon HD 4870 (_device = 1):
2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) CPUTime / GPUTotalTime = 9.002 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) OpenCL total: time = 12.729 sec. 2012.05.27 01:40:50 matr_mul_1dim (EURUSD,H1) read = 4000000 elements 2012.05.27 01:40:37 matr_mul_1dim (EURUSD,H1) CPUTime = 114.583 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:38:42 matr_mul_1dim (EURUSD,H1) =======================================
Wie Sie sehen können, ist die Ausführung des Kernels auf der GPU viel langsamer. Allerdings haben wir die spezielle Optimierung für die GPU noch nicht behandelt.
Ein paar Schlussfolgerungen:
- Die Veränderung der Darstellung der Matrix von zweidimensional zu linear (entsprechend der Darstellung in dem auf dem Device ausgeführten Programm) hatte keine wesentlichen Auswirkungen auf die Gesamtlaufzeit der sequentiellen Version des Programms.
- Der intuitivste Berechnungsalgorithmus, der der Definition der Multiplikation in der linearen Algebra entspricht, wurde als Ausgangsvariante für die weitere Optimierung gewählt. Er ist etwas langsamer als der schnellste, doch angesichts der künftigen Beschleunigung auf der GPU ist das nicht ausschlaggebend.
- Die Laufzeit sollte erst nach dem Einlesen der Puffer in den RAM berechnet werden, anstatt nach dem Befehl CLExecute(). Der Grund dafür ist, wie MetaDriver dem Verfasser erklärt hat, vermutlich folgender:MetaDriver: Vor dem Lesen aus dem Puffer wartet CLBufferRead() einfach auf die tatsächliche Fertigstellung des Programms. CLExecute() ist tatsächlich eine asynchrone Warteschlangenfunktion. Sie gibt das Ergebnis sofort aus, lange bevor die Operation des cl-Codes abgeschlossen ist.
- Leitfäden zur GPU-Berechnung berechnen für gewöhnlich nicht die Kernel-Laufzeit, sondern eher den Datendurchsatz in Bezug auf verschiedene Objekte – Speicher, arithmetische Berechnungen usw. Wir können und werden im Nachfolgenden das Gleiche tun.
Wir wissen, dass die Berechnung einer Matrix der Größe 2000 etwa 2 * 2000 Additionen/Multiplikationen pro Element benötigt. Durch die Multiplikation mit der Anzahl der Matrixelemente (2000 * 2000) finden wir heraus, dass die Gesamtmenge der Operationen auf Daten des Typen float 16 Milliarden beträgt. Dabei dauert die Ausführung auf der CPU 115,628 Sekunden, was einer Datenstreaming-Geschwindigkeit von
entspricht. Denken Sie andererseits daran, dass die bisher schnellste Berechnung auf einer "Single-Core-CPU" mit einer Matrix der Größe 2000 nur 83,663 Sekunden dauerte (siehe unser erster Code ohne OpenCL). Daher
Nehmen wir diese Zahl als Referenz- und Ausgangspunkt für unsere Optimierungen.
Analog dazu ergibt die Berechnung mit OpenCL auf der CPU:
Berechnen Sie zum Schluss den Durchsatz auf der GPU:
2,3. Beseitigen inkohärenter Datenzugriffe
Nach einem Blick auf den Kernel-Code sieht man schnell einige Unzulänglichkeiten.
Sehen Sie sich den Körper der Schleife innerhalb des Kernels an:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr * COLS2 + c ];
Es ist leicht zu sehen, dass zusammenhängende Daten aus dem ersten Puffer in1[] entnommen werden, wenn der Zähler der Schleife (cr++) läuft. Daten aus dem zweiten Puffer in2[] werden dabei mit "Lücken" gleich COLS2 entnommen. In anderen Worten: Der Großteil der Daten aus dem zweiten Puffer wird nicht nützlich sein, da die Speicheranfragen inkohärent sein werden (siehe 1.2.1. Verschmelzen von Speicheranfragen). Um dieses Problem zu beheben, genügt es, den Code an drei Stellen durch eine Anpassung der Formel für die Berechnung des Index des Arrays in2[] und des Musters seiner Erzeugung zu modifizieren:
for( int cr = 0; cr < COLSROWS; cr ++ ) out[ r * COLS2 + c ] += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ];Wenn die Werte des Zählers der Schleife (cr++) sich jetzt ändern, werden Daten aus beiden Arrays sequentiell, ohne "Lücken", entnommen.
- Code zum Ausfüllen des Puffers in genMatrices(). Dieser Code muss nun nach Spalten anstatt Zeilen befüllt werden, wie es am Anfang der Fall war:
for( int r = 0; r < COLSROWS; r ++ ) for( int c = 0; c < COLS2; c ++ ) /// second[ r * COLS2 + c ] = genVal( ); second[ r + c * COLSROWS ] = genVal( );- Überprüfungscode in der Funktion checkRandom():
for( int runningIdx = 0; runningIdx < COLSROWS; runningIdx ++ ) ///sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx * COLS2 + c0 ]; sum += first[ r0 * COLSROWS + runningIdx ] * second[ runningIdx + c0 * COLSROWS ];Ergebnisse der Ausführung auf der CPU:
2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 16.207 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 5.756 sec. 2012.05.24 02:59:22 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.24 02:59:16 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.289 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 02:57:43 matr_mul_1dim_coalesced (EURUSD,H1) =======================================Radeon HD 4870:
2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime / GPUTotalTime = 7.176 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) OpenCL total: time = 12.979 sec. 2012.05.27 01:50:43 matr_mul_1dim_coalesced (EURUSD,H1) read = 4000000 elements 2012.05.27 01:50:30 matr_mul_1dim_coalesced (EURUSD,H1) CPUTime = 93.133 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:48:57 matr_mul_1dim_coalesced (EURUSD,H1) =======================================
Wie Sie sehen können, hatte der kohärente Datenzugriff so gut wie keine Auswirkung auf die Laufzeit auf der GPU, hat die Laufzeit auf der CPU aber deutlich verbessert. Es ist sehr wahrscheinlich, dass dies mit Faktoren zusammenhängt, die später optimiert werden, insbesondere mit der sehr hohen Latenzzeit des Zugriffs auf globale Variablen, die wir so schnell wie möglich beseitigen sollten.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.756 ~ 2.780 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 12.979 ~ 1.233 GFlops.
Den neuen Kernel-Code finden Sie in der Datei matr_mul_1dim_coalesced.mq5 am Ende des Beitrags.
Der Kernel-Code ist nachfolgend aufgeführt:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " out[ r * COLS2 + c ] += \r\n" " in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" "} \r\n";
Aufstellung 3. Kernel mit verschmolzenem Zugriff auf globale Speicherdaten
Fahren wir mit weiteren Optimierungen fort.
2,4. Entfernen "teurer" Zugriffe auf den globalen GPU-Speicher aus der Ausgabematrix
Wir wissen, dass die Latenzzeit beim Zugriff auf den globalen GPU-Speicher extrem hoch ist (etwa 600-800 Zyklen). Zum Beispiel beträgt die Latenzzeit der Durchführung einer Addition von zwei Zeilen etwa 20 Zyklen. Das Hauptziel der Optimierungen beim Berechnen auf der GPU ist es, die Latenz durch eine Erhöhung des Datendurchsatzes der Berechnungen zu verbergen. In der Schleife des vorher entwickelten Kernels greifen wir durchgehend auf globale Speicherelemente zu, was uns Zeit kostet.
Führen wir jetzt die lokale Variable sum im Kernel ein (der Zugriff auf diese Variable ist um ein Vielfaches schneller, da sie eine private Variable des Kernels im Register der Arbeitseinheit ist) und weisen nach dem Abschluss der Schleife die erhaltene Summe einzeln dem Element des Ausgabe-Arrays zu:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " int c = get_global_id( 1 ); \r\n" " REALTYPE sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" "} \r\n" ;
Aufstellung 4. Einführung der privaten Variable zum Berechnen der kumulativen Summe in der Berechnungsschleife des Skalarprodukts
Die Datei mit dem vollständigen Code, matr_mul_sum_local.mq5, ist am Ende des Beitrags angehängt.
Prozessor:
2012.05.24 03:28:17 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 24.863 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 3.759 sec. 2012.05.24 03:28:16 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.24 03:28:12 matr_mul_sum_local (EURUSD,H1) CPUTime = 93.460 2012.05.24 03:26:39 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000GPU HD 4870:
2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) CPUTime / GPUTotalTime = 69.541 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) OpenCL total: time = 1.326 sec. 2012.05.27 01:57:30 matr_mul_sum_local (EURUSD,H1) read = 4000000 elements 2012.05.27 01:57:28 matr_mul_sum_local (EURUSD,H1) CPUTime = 92.212 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 01:55:56 matr_mul_sum_local (EURUSD,H1) =======================================Das ist eine echte Produktivitätssteigerung!
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.759 ~ 4.257 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.326 ~ 12.066 GFlops.
Das Hauptprinzip, an das wir uns bei sequentiellen Optimierungen halten wollen, ist das folgende: Zuerst müssen Sie die Datenstruktur soweit es geht neu anordnen, sodass sie für eine bestimmte Aufgabe und insbesondere die zugrunde liegende Hardware geeignet ist, und erst dann mit feinen Optimierungen mit schnellen Berechnungsalgorithmen wie mad() oder fma() fortfahren. Denken Sie daran, dass sequentielle Optimierungen nicht immer zwangsläufig zu höherer Performance führen – das kann nicht garantiert werden.
2,5. Erhöhen der durch das Kernel ausgeführten Arbeit
In der parallelen Programmierung ist es wichtig, Berechnungen so zu organisieren, dass sie den Aufwand (Zeit, engl. "overhead") für die Organisation paralleler Arbeiten verringern. Bei Matrizen mit einer Dimension von 2000 führt eine Arbeitseinheit, die ein Element der Ausgabematrix berechnet, eine Menge an Arbeit aus, die 1/4000000 der Gesamtaufgabe entspricht.
Das ist offensichtlich zu viel und zu weit von der tatsächlichen Anzahl der Einheiten entfernt, die Berechnungen auf der Hardware durchführen. In der neuen Version des Kernels werden wir nun die gesamte Matrixzeile anstatt nur eines Elements berechnen.
Es ist wichtig, dass der Aufgabenraum nun von zweidimensional in eindimensional verändert wird, da die gesamte Dimension – die gesamte Zeile anstatt eines einzelnen Elements der Matrix – nun in jeder Aufgabe des Kernels berechnet wird. Deshalb wird aus dem Aufgabenraum die Anzahl der Matrixzeilen.
Abb. 14. Schema der Berechnung der gesamten Zeile der Ausgabematrix
Der Kernel-Code wird komplizierter:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 5. Kernel für die Berechnung der gesamten Zeile der Ausgabematrix
void executeGPU( int clKrn ) { //--- set parameters of the task workspace and execute the OpenCL program uint offs[ 1 ] = { 0 }; uint works[ 1 ] = { ROWS1 }; bool ex = CLExecute( clKrn, 1, offs, works ); return; }
Ergebnisse der Ausführung (den kompletten Quellcode finden Sie in der Datei matr_mul_row_calc.mq5):
Prozessor:
2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 17.385 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 5.366 sec. 2012.05.24 15:56:24 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.24 15:56:19 matr_mul_row_calc (EURUSD,H1) CPUTime = 93.288 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.24 15:54:45 matr_mul_row_calc (EURUSD,H1) =======================================
GPU 4870:
2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) CPUTime / GPUTotalTime = 55.119 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) OpenCL total: time = 1.669 sec. 2012.05.27 02:24:10 matr_mul_row_calc (EURUSD,H1) read = 4000000 elements 2012.05.27 02:24:08 matr_mul_row_calc (EURUSD,H1) CPUTime = 91.994 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:22:35 matr_mul_row_calc (EURUSD,H1) =======================================
Wir sehen, dass die Laufzeit sich auf der CPU klar verschlechtert hat und auf der GPU etwas – aber nicht viel – schlechter geworden ist. Das ist nicht schlimm: Diese strategische Veränderung, die die Situation auf lokaler Ebene vorübergehend verschlimmert, dient nur dazu, die Performance im weiteren Verlauf drastisch zu erhöhen.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.366 ~ 2.982 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.669 ~ 9.587 GFlops.
2,6. Übertragen der Zeile des ersten Arrays in den privaten Speicher
Die größte Besonderheit des Algorithmus der Matrixmultiplikation ist eine große Menge von Multiplikationen mit einer damit einhergehenden Akkumulation der Ergebnisse. Eine ordnungsgemäße, hochwertige Optimierung dieses Algorithmus sollte eine Minimierung der Datenübertragungen bedeuten. Doch bislang haben all unsere Änderungen des Kernels in Berechnungen innerhalb der Hauptschleife der Akkumulation der Skalarprodukte zwei von drei Matrizen im globalen Speicher gespeichert.
Das bedeutet, dass alle Eingabedaten für jedes Skalarprodukt (das tatsächlich jedes Element der Ausgabematrix ist) konstant durch die gesamte Speicherhierarchie – von global bis privat – gestreamt werden, mit den entsprechenden Latenzzeiten. Dieser Datenverkehr lässt sich reduzieren, wenn man sicherstellt, dass jede Arbeitseinheit dieselbe Zeile der ersten Matrix für jede berechnete Zeile der Ausgabematrix wiederverwendet.
Abb. 15. Übertragen der Zeile der ersten Matrix in den privaten Speicher der Arbeitseinheit
Dies bedeutet keine Änderungen am Code des Host-Programms. Und die Änderungen im Kernel sind ebenfalls minimal. Da innerhalb des Kernels ein eindimensionales Übergangs-Array erzeugt wird, versucht die GPU, es im privaten Speicher der Einheit zu platzieren, die das Kernel ausführt. Die benötigte Zeile der ersten Matrix wird einfach aus dem globalen in den privaten Speicher kopiert. Dabei sollte man beachten, dass auch dieser Kopiervorgang relativ schnell ist. Der Trick liegt darin, dass das "teuerste" Kopieren der Zeilenelemente des ersten Arrays aus dem globalen in den privaten Speicher kohärent ist und der Aufwand für den Kopiervorgang im Vergleich zur Laufzeit der primären Doppelschleife, die die Zeile der Ausgabematrix berechnet, ziemlich gering ist.
Der Kernel-Code (der auskommentierte Code in der Hauptschleife, ist das, was in der vorherigen Version enthalten war):
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " ///sum += in1[ r * COLSROWS + cr ] * in2[ cr + c * COLSROWS ]; \r\n" " sum += rowbuf[ cr ] * in2[ cr + c * COLSROWS ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 6. Kernel mit der Zeile der ersten Matrix im privaten Speicher der Arbeitseinheit.
Prozessor:2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 18.587 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 4.961 sec. 2012.05.27 00:51:46 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 00:51:41 matr_mul_row_in_private (EURUSD,H1) CPUTime = 92.212 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 00:50:08 matr_mul_row_in_private (EURUSD,H1) =======================================GPU:
2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) CPUTime / GPUTotalTime = 69.242 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) OpenCL total: time = 1.327 sec. 2012.05.27 02:28:49 matr_mul_row_in_private (EURUSD,H1) read = 4000000 elements 2012.05.27 02:28:47 matr_mul_row_in_private (EURUSD,H1) CPUTime = 91.884 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 02:27:15 matr_mul_row_in_private (EURUSD,H1) =======================================
throughput_arithmetic_CPU_OCL = 16 000000000 / 4.961 ~ 3.225 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.327 ~ 12.057 GFlops.
Der Durchsatz der CPU ist etwa auf dem gleichen Niveau wie beim letzten Mal geblieben, während der Durchsatz der GPU wieder das höchste zuvor erreichte Niveau erreicht hat, allerdings auf eine neue Art. Beachten Sie, dass der Durchsatz der CPU wie festgefroren erscheint und nur etwas unstet ist, während der Durchsatz der GPU in ziemlich großen Sprüngen steigt (allerdings nicht immer).
Halten wir fest, dass der reale arithmetische Durchsatz etwas höher sein sollte, da nun durch das Kopieren der Zeile der ersten Matrix in den privaten Speicher mehr Operationen als vorher durchgeführt werden. Allerdings wirkt sich dies kaum auf die Schätzung des endgültigen Durchsatzes aus.
Sie finden den Quellcode in der Datei matr_mul_row_in_private.mq5.
2,7. Übertragen der Spalte des zweiten Arrays in den lokalen Speicher
Es ist nun leicht zu erraten, was der nächste Schritt sein wird. Wir haben bereits Maßnahmen ergriffen, um die Latenzzeiten in Verbindung mit der Ausgabe- und ersten Eingabematrix zu verbergen. Es bleibt die zweite Matrix.
Eine eingehendere Studie der in Matrixmultiplikationen verwendeten Skalarprodukte zeigt, dass im Zuge der Berechnung der Zeile der Ausgabematrix alle Arbeitseinheiten in der Gruppe Daten aus den gleichen Spalten der zweiten multiplizierten Matrix wiederholt durch das Device streamen. Dies wird im nachfolgenden Schema illustriert:
Abb. 16. Übertragen der Spalte der zweiten Matrix in den Local Data Share der Arbeitsgruppe
Der Aufwand für die Übertragung von Daten aus dem globalen Speicher lässt sich reduzieren, wenn die Arbeitseinheiten, aus denen die Arbeitsgruppe besteht, Spalten der zweiten Matrix in den Speicher der Arbeitsgruppe kopieren, bevor die Berechnung der Zeilen der Ausgabematrix beginnt.
Dies erfordert Änderungen am Kernel und am Host-Programm. Die wichtigste Änderung ist die Bestimmung des lokalen Speichers für jedes Kernel. Diese sollte explizit sein, da OpenCL keine dynamische Speicherzuweisung unterstützt. Deshalb muss zuerst ein Speicherobjekt einer geeigneten Größe im Host platziert werden, um anschließend innerhalb des Kernels verarbeitet zu werden.
Und erst danach, beim Ausführen des Kernels, kopieren die Arbeitsgruppen die Spalte der zweiten Matrix in den lokalen Speicher. Dies geschieht parallel mithilfe einer zyklischen Verteilung von Schleifendurchläufen über alle Arbeitseinheiten der Arbeitsgruppe. Allerdings müssen alle Kopiervorgänge abgeschlossen sein, bevor die Arbeitsgruppe mit ihrer Hauptaufgabe (Berechnung der Zeile der Ausgabematrix) beginnt.
Deshalb wird nach der Schleife, die den Kopiervorgang ausführt, der folgende Befehl eingefügt:
barrier(CLK_LOCAL_MEM_FENCE);
Das ist eine "lokale Speicherbarriere", die sicherstellt, dass jede Arbeitseinheit innerhalb der Gruppe lokalen Speicher in einem bestimmten Zustand "sehen" kann, der mit anderen Einheiten koordiniert wird. Alle Arbeitseinheiten in der Arbeitsgruppe müssen Befehle bis zur Barriere ausführen, bevor sie mit der Ausführung des Kernels fortfahren können. In anderen Worten: Die Barriere ist ein spezieller Synchronisierungsmechanismus zwischen Arbeitseinheiten innerhalb der Arbeitsgruppe.
Synchronisierungsmechanismen zwischen Arbeitsgruppen sind in OpenCL nicht vorgesehen.
Nachfolgend sehen eine Illustration der Barriere in Aktion:
Abb. 17. Illustration der Barriere in Aktion
Tatsächlich sieht es nur so aus, als führten die Arbeitseinheiten innerhalb der Arbeitsgruppe den Code strikt zeitgleich aus. Das ist nur eine Abstraktion des Programmiermodells von OpenCL.
Bislang war keine Synchronisierung der auf verschiedenen Arbeitseinheiten ausgeführten Kernel-Codes nötig, da es keine explizite Kommunikation zwischen ihnen gab, die programmbedingt im Kernel festgelegt wäre. Sie war nicht mal notwendig. Doch in diesem Kernel ist die Synchronisierung erforderlich, da der Prozess der Befüllung des lokalen Arrays parallel zwischen allen Einheiten der Arbeitsgruppe verteilt ist.
In anderen Worten: Jede Arbeitseinheit schreibt ihre Werte in den lokalen Daten-Share (hier: das Array), ohne zu wissen, wie weit andere Arbeitseinheiten in diesem Schreibprozess stehen. Die Barriere ist dafür da, damit eine bestimmte Arbeitseinheit nicht mit der Ausführung des Kernels beginnt, bevor dies erforderlich ist, d. h. bevor ein lokales Array vollständig erzeugt wurde.
Man sollte verstehen, dass diese Optimierung sich kaum positiv auf die Performance der CPU auswirken wird: Intels Optimierungsleitfaden für OpenCL besagt, dass bei der Ausführung eines Kernels auf der CPU alle OpenCL-Speicherobjekte auf Hardwareebene zwischengespeichert werden. Somit sorgt explizites Caching durch lokalen Speicher nur für unnötigen (moderaten) Aufwand.
Es gibt noch einen weiteren wichtigen Faktor, der den Verfasser dieses Beitrags viel Zeit gekostet hat. Dieser hängt damit zusammen, dass eine lokale Variable in der aktuellen Implementierung durch die Entwickler des Terminals eine lokale Variable nicht über die Kopfzeile der Header-Funktion, d. h. in der Kompilierungsphase, übergeben werden kann. Der Grund dafür ist, dass wir erst explizit ein Speicherobjekt im CPU-Speicher mithilfe der Funktion CLBufferCreate() erstellen und seine Größe explizit als Parameter der Funktion bestimmen müssen, um Speicher einem Speicherobjekt als Argument der Kernel-Funktion zuzuweisen. Diese Funktion gibt ein Speicherobjekt-Handle aus, das im weiteren Verlauf im globalen Speicher der GPU gespeichert wird, da dies der einzige Ort ist, an dem es sich befinden kann.
Allerdings ist lokaler Speicher kein globaler Speicher und somit kann ein erstelltes Speicherobjekt nicht im lokalen Speicher der Arbeitsgruppe platziert werden.
Die voll funktionsfähige OpenCL-API ermöglicht eine explizite Zuweisung von Speicher der benötigten Größe mit dem Pointer NULL zum Argument des Kernels, auch ohne das Speicherobjekt als solches zu generieren (Funktion CLSetKernelArg()). Allerdings ermöglicht die Syntax der Funktion CLSetKernelArgMem() als MQL5-Gegenstück zur Funktion der voll funktionsfähigen API keine Übergabe der Größe des dem Argument zugewiesenen Speichers innerhalb der Funktion, ohne das Speicherobjekt selbst zu erstellen. An die Funktion CLSetKernelArgMem() können wir nur das Puffer-Handle übergeben, das im globalen Speicher der CPU bereits erzeugt wurde und für die Übertragung an den globalen Speicher der GPU vorgesehen ist. Hier haben wir ein Paradox.
Glücklicherweise gibt es eine äquivalente Weise, mit lokalen Puffern im Kernel zu arbeiten. Man deklariert einen solchen Puffer einfach mit dem Modifikator __local im Körper des Kernels. Dabei wird lokaler Speicher, der der Arbeitsgruppe zugewiesen ist, während der Laufzeit bestimmt anstatt in der Kompilierungsphase.
Befehle, die nach der Barriere im Kernel erfolgen (die Barrierenzeile im Code ist rot markiert), sind im Wesentlichen die gleichen wie bei der vorhergehenden Optimierung. Der Code des Host-Programms ist unverändert geblieben (Sie finden den Quellcode in der Datei matr_mul_col_local.mq5).
Hier ist also der neue Kernel-Code:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " rowbuf[ col ] = in1[ r * COLSROWS + col ]; \r\n" " \r\n" " int idlocal = get_local_id( 0 ); \r\n" " int nlocal = get_local_size( 0 ); \r\n" " __local REALTYPE colbuf[ COLSROWS ] ; \r\n" " \r\n" " REALTYPE sum; \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " for( int cr = idlocal; cr < COLSROWS; cr = cr + nlocal ) \r\n" " colbuf[ cr ] = in2[ cr + c * COLSROWS ]; \r\n" " barrier( CLK_LOCAL_MEM_FENCE ); \r\n" " \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr ++ ) \r\n" " sum += rowbuf[ cr ] * colbuf[ cr ]; \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 7. Spalte des zweiten Arrays, übertragen in den lokalen Speicher der Arbeitsgruppe
2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 17.630 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 5.227 sec. 2012.05.27 06:31:46 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:31:40 matr_mul_col_local (EURUSD,H1) CPUTime = 92.150 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:30:08 matr_mul_col_local (EURUSD,H1) =======================================GPU:
2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) CPUTime / GPUTotalTime = 58.069 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) OpenCL total: time = 1.592 sec. 2012.05.27 06:21:36 matr_mul_col_local (EURUSD,H1) read = 4000000 elements 2012.05.27 06:21:34 matr_mul_col_local (EURUSD,H1) CPUTime = 92.446 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 06:20:01 matr_mul_col_local (EURUSD,H1) =======================================
Beide Fälle zeigen eine Verschlechterung der Performance, die allerdings nicht erheblich ist. Es ist gut möglich, dass die Performance durch die Veränderung der Größe der Arbeitsgruppe verbessert anstatt verschlechtert wird. Das oben aufgeführte Beispiel dient eher einem anderen Ziel: Es zeigt, wie Objekte des lokalen Speichers genutzt werden.
Es gibt eine Hypothese, die die Verschlechterung der Performance bei Verwendung des lokalen Speichers erklärt. Im vor etwa 6 Jahren auf habrahabr.ru veröffentlichten Artikel Vergleich von OpenCL mit CUDA, GLSL und OpenMP (russisch) steht:
Bedeutet das in anderen Worten, dass der lokale Speicher der vor 6 Jahren veröffentlichten Produkte nicht schneller als globaler Speicher ist? Die Zeit, zu der der oben erwähnte Artikel veröffentlicht wurde, deutet darauf hin, dass die Radeon-Grafikkarten der Serie HD 58xx vor sechs Jahren bereits veröffentlicht waren, allerdings war die Situation laut dem Verfasser alles andere als optimistisch. Ich kann mir das nur schwer vorstellen, insbesondere dank der sensationellen Evergreen-Serie von AMD. Es wäre interessant, dies mit moderneren Karten zu prüfen, z. B. der Serie HD 69xx.
Zusatz: Starten Sie GPU Caps Viewer und Sie sehen Folgendes in der Registerkarte OpenCL:
Abb. 18. Hauptparameter von OpenCL, die von HD 4870 unterstützt werden
CL_DEVICE_LOCAL_MEM_TYPE: Global
Die Erklärung dieses Parameters in der Spezifikation der Sprache (Tabelle 4.3, S. 41) besagt Folgendes:
Typ des unterstützten lokalen Speichers. Dieser lässt sich mit CL_LOCAL festlegen, was eine dedizierte Speicherung im lokalen Speicher wie SRAM oder CL_GLOBAL bedeutet.
Somit ist der lokale Speicher der HD 4870 bereits Teil des globalen Speichers und jegliche Manipulation des lokalen Speichers dieser Grafikkarte ist deshalb nutzlos und führt zu keiner Beschleunigung gegenüber dem globalen Speicher. Hier ist ein weiterer Link, unter dem ein AMD-Experte diesen Faktor für die Serie HD 4xxx klärt. Das bedeutet nicht zwangsläufig, dass die Situation mit Ihrer Grafikkarte genauso schlecht sein wird. Es sollte nur zeigen, wo solche Informationen über die Hardware gefunden werden können – in diesem Fall im GPU Caps Viewer.
throughput_arithmetic_CPU_OCL = 16 000000000 / 5.227 ~ 3.061 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 1.592 ~ 10.050 GFlops.
Lassen Sie uns unserem Kernel zu guter Letzt den letzten Schliff verpassen, indem wir es explizit vektorisieren. Das Kernel, das während der Übertragung der Zeile des ersten Arrays in den privaten Speicher erhalten wurde (matr_mul_row_in_private.mq5), dient als Ausgangs-Kernel, da es sich als schnellstes erwiesen hat.
2,8. Vektorisierung des Kernels
Diese Operation sollte am besten in mehrere Etappen aufgeteilt werden, um Verwechslungen zu vermeiden. In der ersten Modifizierung verändern wir nicht die Datentypen der externen Parameter des Kernels und vektorisieren nur die Berechnungen in der inneren Schleife:
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE rowbuf[ COLSROWS ]; \r\n" " for( int col = 0; col < COLSROWS; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = in1[r * COLSROWS + col ]; \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS; cr += 4 ) \r\n" " sum += dot( ( REALTYPE4 ) ( rowbuf[ cr ], \r\n" " rowbuf[ cr + 1 ], \r\n" " rowbuf[ cr + 2 ], \r\n" " rowbuf[ cr + 3 ] ), \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + cr ], \r\n" " in2[c * COLSROWS + cr + 1 ], \r\n" " in2[c * COLSROWS + cr + 2 ], \r\n" " in2[c * COLSROWS + cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 8. Teilvektorisierung des Kernels mit float4 (nur innere Schleife)
Prozessor:
2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 18.657 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) OpenCL total: time = 4.945 sec. 2012.05.27 21:28:16 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:28:11 matr_mul_vect (EURUSD,H1) CPUTime = 92.259 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:26:38 matr_mul_vect (EURUSD,H1) =======================================
GPU:
2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) CPUTime / GPUTotalTime = 78.079 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) OpenCL total: time = 1.186 sec. 2012.05.27 21:21:30 matr_mul_vect (EURUSD,H1) read = 4000000 elements 2012.05.27 21:21:28 matr_mul_vect (EURUSD,H1) CPUTime = 92.602 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 21:19:55 matr_mul_vect (EURUSD,H1) =======================================
Überraschenderweise führte sogar diese primitive Vektorisierung zu guten Ergebnissen auf der GPU. Auch wenn der Gewinn nicht riesig ist, lag er immer noch bei etwa 10 %.
Vektorisieren Sie innerhalb des Kernels weiter: Übertragen Sie "teure" Konvertierungsoperationen des Vektortypen REALTYPE4 zusammen mit der Festlegung expliziter Vektorkomponenten in die äußere Hilfsschleife, die die private Variable rowbuf[] befüllt. Das Kernel bleibt weiterhin unverändert.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE4 rowbuf[ COLSROWS / 4 ]; \r\n" " for( int col = 0; col < COLSROWS / 4; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE4 ) ( in1[r * COLSROWS + 4 * col ], \r\n" " in1[r * COLSROWS + 4 * col + 1 ], \r\n" " in1[r * COLSROWS + 4 * col + 2 ], \r\n" " in1[r * COLSROWS + 4 * col + 3 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 4; cr ++ ) \r\n" " sum += dot( rowbuf[ cr ], \r\n" " ( REALTYPE4 ) ( in2[c * COLSROWS + 4 * cr ], \r\n" " in2[c * COLSROWS + 4 * cr + 1 ], \r\n" " in2[c * COLSROWS + 4 * cr + 2 ], \r\n" " in2[c * COLSROWS + 4 * cr + 3 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 9. Beseitigen "teurer" Operationen der Typenkonvertierung in der Hauptschleife des Kernels
Beachten Sie, dass der maximale Zählerwert der inneren Schleife (und auch der Hilfsschleife) um das 4-Fache sinkt, da die Leseoperationen, die nun für das erste Array benötigt werden, 4 Mal weniger sind als vorher – das Lesen ist definitiv zu einer Vektoroperation geworden.
2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 24.480 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 3.791 sec. 2012.05.27 22:41:43 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:41:39 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.805 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:40:06 matr_mul_vect_v2 (EURUSD,H1) =======================================GPU:
2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) CPUTime / GPUTotalTime = 185.605 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) OpenCL total: time = 0.499 sec. 2012.05.27 22:35:28 matr_mul_vect_v2 (EURUSD,H1) read = 4000000 elements 2012.05.27 22:35:27 matr_mul_vect_v2 (EURUSD,H1) CPUTime = 92.617 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 22:33:54 matr_mul_vect_v2 (EURUSD,H1) =======================================Arithmetischer Durchsatz:
throughput_arithmetic_CPU_OCL = 16 000000000 / 3.791 ~ 4.221 GFlops. throughput_arithmetic_GPU_OCL = 16 000000000 / 0.499 ~ 32.064 GFlops.
Wie Sie sehen können, sind die Änderungen der Performance für die CPU beträchtlich, für die GPU fast schon revolutionär. Sie finden den Quellcode in der Datei matr_mul_vect_v2.mq5.
Führen wir die gleichen Operationen in Bezug auf die letzte Variante des Kernels durch, allerdings mit einer Vektorbreite von 8. Die Entscheidung des Verfassers lässt sich damit erklären, dass die Speicherbandbreite der GPU bei 256 Bit liegt, d. h. 32 Byte oder 8 Zahlen des Typen float. Somit erscheint die gleichzeitige Verarbeitung von 8 Floats, die der gleichzeitigen Nutzung von float8 entspricht, als natürlich.
Denken Sie daran, dass der Wert von COLSROWS in diesem Fall ganzzahlig durch 8 teilbar sein muss. Das ist eine natürliche Anforderung, da feinere Optimierungen spezifischere Anforderungen an Daten stellen.
const string clSrc = "#define COLS2 " + i2s( COLS2 ) + " \r\n" "#define COLSROWS " + i2s( COLSROWS ) + " \r\n" "#define REALTYPE float \r\n" "#define REALTYPE4 float4 \r\n" "#define REALTYPE8 float8 \r\n" " \r\n" "inline REALTYPE dot8( REALTYPE8 a, REALTYPE8 b ) \r\n" "{ \r\n" " REALTYPE8 c = a * b; \r\n" " REALTYPE4 _1 = ( REALTYPE4 ) 1.; \r\n" " return( dot( c.lo + c.hi, _1 ) ); \r\n" "} \r\n" " \r\n" "__kernel void matricesMul( __global REALTYPE *in1, \r\n" " __global REALTYPE *in2, \r\n" " __global REALTYPE *out ) \r\n" "{ \r\n" " int r = get_global_id( 0 ); \r\n" " REALTYPE8 rowbuf[ COLSROWS / 8 ]; \r\n" " for( int col = 0; col < COLSROWS / 8; col ++ ) \r\n" " { \r\n" " rowbuf[ col ] = ( REALTYPE8 ) ( in1[r * COLSROWS + 8 * col ], \r\n" " in1[r * COLSROWS + 8 * col + 1 ], \r\n" " in1[r * COLSROWS + 8 * col + 2 ], \r\n" " in1[r * COLSROWS + 8 * col + 3 ], \r\n" " in1[r * COLSROWS + 8 * col + 4 ], \r\n" " in1[r * COLSROWS + 8 * col + 5 ], \r\n" " in1[r * COLSROWS + 8 * col + 6 ], \r\n" " in1[r * COLSROWS + 8 * col + 7 ] ); \r\n" " } \r\n" " \r\n" " REALTYPE sum; \r\n" " \r\n" " for( int c = 0; c < COLS2; c ++ ) \r\n" " { \r\n" " sum = 0.0; \r\n" " for( int cr = 0; cr < COLSROWS / 8; cr ++ ) \r\n" " sum += dot8( rowbuf[ cr ], \r\n" " ( REALTYPE8 ) ( in2[c * COLSROWS + 8 * cr ], \r\n" " in2[c * COLSROWS + 8 * cr + 1 ], \r\n" " in2[c * COLSROWS + 8 * cr + 2 ], \r\n" " in2[c * COLSROWS + 8 * cr + 3 ], \r\n" " in2[c * COLSROWS + 8 * cr + 4 ], \r\n" " in2[c * COLSROWS + 8 * cr + 5 ], \r\n" " in2[c * COLSROWS + 8 * cr + 6 ], \r\n" " in2[c * COLSROWS + 8 * cr + 7 ] ) ); \r\n" " out[ r * COLS2 + c ] = sum; \r\n" " } \r\n" "} \r\n" ;
Aufstellung 10. Kernel-Vektorisierung mit Vektorbreite 8
Wir mussten in den Kernel-Code die Inline-Funktion dot8() einfügen, die es uns ermöglicht, das Skalarprodukt für Vektoren mit der Breite 8 zu berechnen. In OpenCL kann die Standardfunktion dot() das Skalarprodukt nur für Vektoren mit einer Breite von höchstens 4 berechnen. Sie finden den Quellcode in der Datei matr_mul_vect_v3.mq5.
2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 45.226 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 2.200 sec. 2012.05.27 23:11:47 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:11:45 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 99.497 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 0; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:10:05 matr_mul_vect_v3 (EURUSD,H1) =======================================GPU:
2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) CPUTime / GPUTotalTime = 170.115 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) OpenCL total: time = 0.546 sec. 2012.05.27 23:20:05 matr_mul_vect_v3 (EURUSD,H1) read = 4000000 elements 2012.05.27 23:20:04 matr_mul_vect_v3 (EURUSD,H1) CPUTime = 92.883 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) 1st OCL martices mul: device = 1; ROWS1 = 2000; COLSROWS = 2000; COLS2 = 2000 2012.05.27 23:18:31 matr_mul_vect_v3 (EURUSD,H1) =======================================
Die Ergebnisse sind unerwartet: Die Laufzeit auf der CPU hat sich um fast das Zweifache verringert, während sie auf der GPU leicht gestiegen ist, obwohl float8 eine angemessene Busbreite für HD 4870 darstellt (entspricht 256 Bit). Hier greifen wir erneut auf den GPU Caps Viewer zurück.
Die Erklärung finden Sie in Abb. 18 in der vorletzten Zeile der Parameterliste:
CL_DEVICE_PREFERRED_VECTOR_WIDTH_FLOAT: 4
Ziehen Sie die OpenCL-Spezifikation zu Rate und Sie werden den folgenden Text bezüglich dieses Parameters in der letzten Spalte von Tabelle 4.3 auf Seite 37 sehen:
Bevorzugte native Vektorbreite für integrierte Skalartypen, die sich in Vektoren ausdrücken lässt. Die Vektorbreite ist als Menge der Skalarelemente, die im Vektor gespeichert werden können, definiert.
Somit ist die bevorzugte Vektorbreite des Vektors floatN für die HD 4870 float4 anstatt float8.
Lassen Sie uns den Zyklus der Kernel-Optimierung hier beenden. Wir könnten noch mehr erreichen, doch der Umfang dieses Beitrags erlaubt keine solche Tiefe der Diskussion.
Fazit
Dieser Beitrag hat bestimmte Optimierungsmöglichkeiten demonstriert, die sich eröffnen, wenn die zugrunde liegende Software, auf der das Kernel ausgeführt wird, zumindest ein bisschen berücksichtigt wird.
Die Zahlen, die wir hier erhalten, sind alles andere als Spitzenwerte, doch auch sie lassen schon darauf schließen, dass mithilfe der hier und jetzt verfügbaren Ressourcen (die OpenCL-API in der Form, in der sie von den Entwicklern des Terminals implementiert wurde, erlaubt nicht die Steuerung bestimmter Parameter, die für die Optimierung wichtig sind, insbesondere die Größe von Arbeitsgruppen) der Performance-Gewinn über die Ausführung des Host-Programms beträchtlich ist: Der Gewinn bei der Ausführungsdauer auf der GPU im Vergleich mit dem sequentiellen Programm auf der CPU (auch wenn es nicht sehr stark optimiert ist) beträgt etwa 200:1.
Meinen aufrichtigen Dank an MetaDriver für wertvolle Ratschläge und die Möglichkeit, die diskrete GPU zu nutzen, als ich keine zur Verfügung hatte.
Inhalte der angehängten Dateien:
- matr_mul_2dim.mq5 – ursprüngliches sequentielles Programm auf dem Host mit zweidimensionaler Darstellung der Daten;
- matr_mul_1dim.mq5 – erste Umsetzung des Kernels mit linearer Darstellung der Daten und einer relevanten Anbindung der MQL5 OpenCL API;
- matr_mul_1dim_coalesced – Kernel mit verschmolzenem Zugriff auf globalen Speicher;
- matr_mul_sum_local – private Variable für die Berechnung des Skalarprodukts, anstatt auf eine berechnete Zelle des Ausgabe-Arrays im globalen Speicher zuzugreifen;
- matr_mul_row_calc – Berechnung der gesamten Zeile der Ausgabematrix im Kernel;
- matr_mul_row_in_private – Zeile des ersten Arrays, übertragen an den privaten Speicher;
- matr_mul_col_local.mq5 – Spalte des zweiten Arrays, übertragen an den lokalen Speicher;
- matr_mul_vect.mq5 – erste Vektorisierung des Kernels (mit float4, nur innere Sub-Schleife der Hauptschleife);
- matr_mul_vect_v2.mq5 – Beseitigen "teurer" Operationen der Datenkonvertierung in der Hauptschleife;
- matrx_mul_vect_v3.mq5 – Vektorisierung mit Vektorbreite 8.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/407
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Automatenbasierte Programmierung als neue Herangehensweise an die Erstellung automatisierter Handelssysteme
Automatenbasierte Programmierung als neue Herangehensweise an die Erstellung automatisierter Handelssysteme
 OpenCL: Die Brücke zu parallelen Welten
OpenCL: Die Brücke zu parallelen Welten
 Die aktivsten Mitglieder der MQL5.community wurden mit iPhones belohnt!
Die aktivsten Mitglieder der MQL5.community wurden mit iPhones belohnt!
 Warum ist MQL5 Market der beste Ort für den Verkauf von Handelsstrategien und technischen Indikatoren?
Warum ist MQL5 Market der beste Ort für den Verkauf von Handelsstrategien und technischen Indikatoren?
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Müssen sie auch synchronisiert werden?
P.S. Ich habe die Hilfe gelesen und sehe, dass dies notwendig ist.
Ich habe die Ergebnisse des Artikels unter Berücksichtigung des Hardware-Upgrades neu berechnet.
Vor einem Jahr: Intel Pentium G840 CPU (2 Kerne @ 2,8 GHz) + AMD HD4870 Grafikkarte.
Kürzlich: CPU Intel Xeon E3-1230v2 (4 Kerne/8 Threads @ 3,3 GHz; leicht hinter i7-3770) + AMD HD-Grafikkarte.6 870.
Die Ergebnisse der Berechnungen in OpenCL sind in der Grafik dargestellt (horizontal - die Anzahl der im Artikel angewandten Optimierungen):
Die Berechnungszeit wird vertikal in Sekunden angezeigt. Die Ausführungszeit des Skripts "auf einen Schlag auf der CPU" (auf einem Kern, ohne OpenCL) schwankte je nach den Algorithmusänderungen innerhalb von 95 plus/minus 25 Sekunden.
Wie wir sehen können, scheint alles klar, aber immer noch nicht sehr offensichtlich.
Der offensichtliche Außenseiter ist der Dual-Core G840. Nun, das war zu erwarten. Weitere Optimierungen änderten die Ausführungszeit nicht allzu sehr, die zwischen 4 und 5,5 Sekunden lag. Man beachte, dass selbst in diesem Fall die Beschleunigung der Skriptausführung Werte von über 20 Mal erreichte.
Im Wettbewerb zwischen zwei Grafikkarten unterschiedlicher Generationen - der alten HD4870 und der moderneren HD6870 - können wir die 6870 fast als Sieger betrachten. Abgesehen von der letzten Optimierungsphase, in der das alte Monster 4870 noch einen nominellen Sieg errungen hat (obwohl es fast die ganze Zeit hinterherhinkte). Die Gründe dafür sind, offen gesagt, unklar: Die Shader sind kleiner und ihre Frequenz ist auch niedriger - aber sie hat trotzdem gewonnen.
Nehmen wir an, dass es sich dabei um die Unwägbarkeiten der Entwicklung von Grafikkartengenerationen handelt. Oder ein Fehler in meinem Algorithmus :)
Ich war ehrlich gesagt zufrieden mit dem Xeon, der es geschafft hat, bei allen Optimierungen besser zu sein als der alte 4870, und der mit dem 6870 fast auf Augenhöhe gekämpft hat und es am Ende sogar geschafft hat, sie alle zu schlagen. Ich behaupte nicht, dass das bei jeder Aufgabe immer so sein wird. Aber die Aufgabe war rechnerisch ziemlich schwierig - immerhin ging es um die Multiplikation zweier Matrizen der Größe 2000 x 2000!
Die Schlussfolgerung ist einfach: Wenn Sie bereits eine anständige CPU wie den i7 haben und die OpenCL-Berechnungen nicht zu lange dauern, dann brauchen Sie vielleicht keinen zusätzlichen leistungsstarken Heizer (Grafikkarte). Auf der anderen Seite, Laden der Stein bei 100% für Dutzende von Sekunden (während lange Berechnungen) ist nicht sehr angenehm, weil der Computer "verliert Reaktionsfähigkeit" für diese Zeit.
Hallo zusammen,
Können Sie ein Beispiel dafür geben, wie OpenCL das Backtesting eines EA im EveryTick-Modus beschleunigen kann? Derzeit brauche ich 18 Minuten, um 14 Jahre Daten im EveryTick-Modus laufen zu lassen. Ich glaube, dass viele Händler daran interessiert sein werden, wenn OpenCL die Testzeit um 50 % reduzieren kann.
Toller Artikel, ich habe nicht verstanden, wie das Verschieben der Übertragung der Zeile von innerhalb der Schleife nach außen in den privaten Speicher die Geschwindigkeit erhöht.
Der gleiche Übertragungsvorgang erfolgt trotzdem, ich habe null Auswirkungen auf meinen Code, aber natürlich ist jeder Fall anders. (aber dann wieder 0 Auswirkungen nach dem Hinzufügen von etwas bedeutet, dass etwas beschleunigt, aber kein Gewinn)
Dieser Teil in der OpenCL Quelle :
Wo Sie es außerhalb der Crunch-Schleife verschieben
Dankeschön