MetaTrader 5 / テスター
English Русский 中文 Español Português
preview
円探索アルゴリズム(CSA)

円探索アルゴリズム(CSA)

MetaTrader 5 — テスター |
19 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

円探索アルゴリズム(Circle Search Algorithm, CSA)は、円の幾何学的性質に着想を得た新しい最適化手法です。CSAの独自性は、三角関数の関係や幾何学的原理を用いて探索空間を探索する点にあります。

CSAは、各探索点が円に接する接線に沿った軌道を移動するという興味深いアイデアに基づいており、大域探索と局所解の精緻化のバランスを生み出します。このアプローチは独創的です。なぜなら、円は半径が一定で、連続微分可能であるという独特の数学的性質を持っており、探索エージェントの動きを滑らかにすることができるからです。

アルゴリズムは、探索と活用の2つのフェーズを組み合わせています。活用フェーズでは、有望な領域に焦点を当て、より方向性のある移動をおこないます。一方、探索フェーズでは、解空間の未探索領域に大胆な移動をおこないます。フェーズ間の移行は、現在の反復回数と特別な「c」パラメータに基づくメカニズムによって制御されます。

CSAの魅力的な点は、高次元空間でも効率的に動作し、直感的な幾何学的解釈が可能であることです。集団内の各エージェントは、θ角によって決定される方向に基づいて逐次位置を更新します。この角度は探索の過程で動的に調整されます。

CSAは、Mohammad H. Kaiys、Hany M. Hasanienらの研究者によって開発され、2022年に発表されました。


アルゴリズムの実装

円探索アルゴリズム(CSA)は、探索領域を広げるためにランダムな円内で最適解を見つけることを目的としています。中心点は、現在までに得られた最良解として使用されます。プロセスは、接線と円の間の角度を徐々に減少させ、接線が中心に近づくようにすることから始まります（図1参照）。

探索に多様性を持たせ、局所最適解に陥るのを避けるため、接点の角度もランダムに変化させます。アルゴリズムの文脈では、Xt（接点）が探索エージェントとして機能し、Xc（中心点）が見つかった最良解を示します。

円幾何学

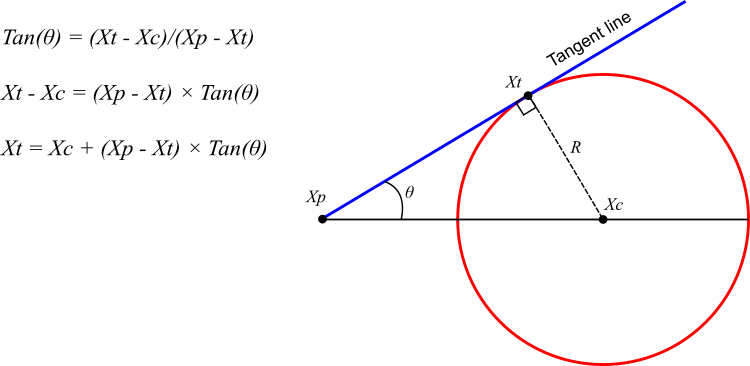
図1：円と接線の幾何学的性質

CSAは、接点が中心に向かって移動するのに応じて探索エージェントの位置を調整します。これにより解の質を改善でき、接線接触角のランダムな更新は局所最小値を回避する重要なメカニズムとなります。CSAオプティマイザの主な処理ステージは、以下の図に示されています。


CSA視覚化

図2：CSAの処理フロー

次に、各エージェントの角度を決定します。現在の反復回数が閾値と最大反復回数の積を超えない場合、エージェントは探索フェーズにあり、それ以外の場合は活用フェーズが適用されます（図2参照）。エージェントの位置を更新し、各エージェントの適合度を評価します。結果を現在の最良解と比較し、より良い解が見つかれば位置を更新します。反復は、反復カウンタを増加させることで終了します。アルゴリズムの実行が完了すると、最良位置とその適合度を返します。

アルゴリズムは、接線に沿って点を移動させる概念を使用します。各探索エージェントは、現在の最良解に対して一定のθ角で移動します。この移動は、時間とともに変化するいくつかのパラメータ（w、a、p）によって制御されます。前述のように、アルゴリズムの操作は探索フェーズ（広範囲に移動して有望な領域を探す）と活用フェーズ（見つかった解を精緻化する）の2つに分かれています。

        最終バージョンでは、アルゴリズムの探索能力を大幅に向上させるいくつかの変更が加えられています。角度のスケールを制御するパラメータwの更新方程式を変更しました。

        • 元の式：w = w × rand - w
        • 最終式：w = π × (1 - epochNow/epochs)。これによりwパラメータの変化が予測可能で線形になり、収束性が向上します。
        位置更新式を修正しました。
        • 元の式：Xi = Xc + (Xc - Xi) × tan(θ)
        • 最終式：Xi = Xc + rand × (Xc - Xi) × tan(θ)。ランダム因子「rand [0.0;1.0]」を加えることで探索の確率的性質が強化され、性能が向上します。 
        更新フェーズを最適化しました。
        • 各エージェントの局所最良解の更新を追加
        • 大域探索と局所探索のバランス戦略を改善

          概念的な主な違いは、最終バージョンはアルゴリズムの挙動をより滑らかで予測可能にしつつ、探索能力を維持している点です。元のアルゴリズムはやや「カオス的」でしたが、最終バージョンでは探索と活用フェーズの移行がより制御された最適化を提供します。

          これで、アルゴリズムの疑似コードの開発を開始できます。

          円探索アルゴリズム(CSA)疑似コード

          1. 初期化
            • 集団サイズを設定する(popSize = 50)
            • 探索フェーズ定数を設定する(constC = 0.8)
            • 初期パラメータを設定する。
              • w = π（角度パラメータ）
              • a = π
              • p = 1.0
              • θ = 0（初期角度）
          2. 初回反復の場合(revision = false)
            • 集団内の各エージェントiについて
              • 指定範囲内で座標をランダム初期化する
              • 変更ステップに従って座標を調整する
            • revision = trueに設定する
            • スタートに戻る
          3. それ以外の場合（メインの最適化ループ）
            • 反復カウンタを増加する(epochNow++)
            • パラメータを更新する
              • w = π × (1 - epochNow/epochs) // 線形減少
              • a = π - π × (epochNow/epochs)²
              • p = 1 - 0.9 × √(epochNow/epochs)
          4. 集団内の各エージェントについて以下を実行する
            • 現在のフェーズを決定する
              • epochNow ≤ constC × epochsの場合→探索フェーズ：θ = w × random [0.0; 1.0]
              • それ以外の場合→活用フェーズ：θ = w × p
            • エージェントの位置を更新する
              • 各座標jについて：new_pos = best_pos + random [0.0;1.0] × (best_pos - current_pos) × tan(θ)→指定された制限内でnew_posを調整する
          5. 結果の修正
            • 各エージェントについて
              • エージェントの適応度 > 大域最良適応度の場合→大域最良解を更新する
              • エージェントの適応度 > 局所最良適応度の場合→エージェントの局所最良解を更新する
          6. 停止条件に達するまで手順3〜5を繰り返す

          実装に移りましょう。C_AO_CSAクラスはCSAアルゴリズムを実装したもので、C_AO基底クラスを継承しています。主な要素と構造は以下の通りです。

          コンストラクタはアルゴリズムのパラメータを初期化します。アルゴリズムの名前と説明を指定し、以下のパラメータの値を設定します。
          • popSize：集団サイズで、50に設定
          • constC：探索フェーズで使用される定数で、0.8に設定
          • w、aParam、p、theta：アルゴリズムで使用するパラメータの初期値
          メソッド
          • SetParams ()：paramsデータ配列に基づいてパラメータの値を設定するメソッド
          • Init ()：値の範囲やアルゴリズムが実行されるエポック数に関連するパラメータを初期化するために実装されたメソッド
          • Moving ()：粒子を移動させ、アルゴリズムの反復を実行するために使用されるメソッド
          • Revision ()：集団の状態を分析し調整するためのメソッド

          privateメソッド

          • CalculateW ()、CalculateA ()、CalculateP ()、CalculateTheta ()：対応するパラメータを計算するためのメソッド
          • IsExplorationPhase ()：アルゴリズムが探索フェーズにあるかどうかを判定するメソッド
          //——————————————————————————————————————————————————————————————————————————————
class C_AO_CSA : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_CSA ()
  {
    ao_name = "CSA";
    ao_desc = "Circle Search Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/17143";

    popSize = 50;     // population size
    constC  = 0.8;    // optimal value for the exploration phase
    w       = M_PI;   // initial value w
    aParam  = M_PI;   // initial value a
    p       = 1.0;    // initial value p
    theta   = 0;      // initial value of the angle

    ArrayResize (params, 2);
    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "constC";      params [1].val = constC;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    constC  = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double constC;      // constant for determining the search phase [0,1]

  private: //-------------------------------------------------------------------
  int epochs;         // maximum number of iterations
  int epochNow;       // current iteration

  // Parameters for CSA
  double w;           // parameter for calculating the angle
  double aParam;      // parameter a from the equation (8)
  double p;           // parameter p from the equation (9)
  double theta;       // search angle

  double CalculateW ();
  double CalculateA ();
  double CalculateP ();
  double CalculateTheta (double currentW, double currentP);
  bool IsExplorationPhase ();
};
//——————————————————————————————————————————————————————————————————————————————

          Initメソッドは、CSAアルゴリズムのパラメータを初期化することを目的としています。その引数には、探索空間の最小値を格納したrangeMinP[]配列、最大値を格納したrangeMaxP[]配列、値の変化量の増分を格納したrangeStepP[]配列、およびepochsPパラメータで指定されるエポック数が含まれます。epochsPのデフォルト値は0です。

          メソッドの実行中にStandardInitが呼び出されます。その目的は標準パラメータの初期化を試みることです。初期化が成功した場合、epochsおよびepochNow変数に値が設定されます。epochs変数にはepochsPの値が代入され、epochNowはクリアされます。メソッドは、アルゴリズムパラメータの初期化が正常に完了したことを示すためにtrueを返して処理を終了します。

          //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CSA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

          C_AO_CSAクラスにおけるMovingメソッドは、CSAアルゴリズム内でエージェントの位置を更新するためのロジックを実装しています。メソッドの冒頭で現在のエポックカウンタがインクリメントされ、これまでに実行された反復回数を追跡できるようになります（計算式で使用されます）。次に、エージェントの座標を初期化する必要があるかどうかの判定がおこなわれます。このメソッドが初めて実行される場合、指定された範囲内で全エージェントに対してランダムな座標が生成されます。これらの座標は、その後、指定されたステップを考慮するように調整されます。その後、リビジョンが必要であることを示すフラグがtrueに設定されます。

          メソッドが初回実行でない場合、w、aParam、pなどのアルゴリズムの主要パラメータが更新されます。その後、各エージェントについてθ角が計算され、その値を用いて座標が更新されます。各座標は、最良エージェントの座標、ランダム因子の影響、およびθ角を考慮して更新されます。更新後、結果は指定された範囲内に収まるように調整されます。

          //——————————————————————————————————————————————————————————————————————————————
void C_AO_CSA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int j = 0; j < coords; j++)
      {
        a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]);
        a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  w      = CalculateW ();    // Update w linearly
  aParam = CalculateA ();    // Update a
  p      = CalculateP ();    // Update p

  for (int i = 0; i < popSize; i++)
  {
    theta = CalculateTheta (w, p);

    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = cB [j] + u.RNDprobab () * (cB [j] - a [i].c  [j]) * tan (theta);
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          Revisionメソッドは、集団全体における大域最良解を更新する役割を担います。各エージェントの目的関数の現在値を確認し、より良い解が見つかった場合には、対応するパラメータを更新します。

          //——————————————————————————————————————————————————————————————————————————————
void C_AO_CSA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Update the best global solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          CalculateWメソッドは、wパラメータの値を計算するために設計されています。このパラメータは、現在のエポック数(epochNow)が総エポック数に対して増加するにつれて、初期値(M_PI)から0まで線形に減少します。メソッドは、計算されたwの値を返します。このwパラメータは、θ角を計算するための式に使用されます。

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateW ()
{
  // Linear decrease of w from the initial value (M_PI) to 0
  return M_PI * (1.0 - (double)epochNow / epochs);
  //return w * u.RNDprobab () - w;
}
//——————————————————————————————————————————————————————————————————————————————
          CalculateAメソッドは、epochNowの増加に伴ってM_PIから0へと減少するaParamの値を計算します。この減少は、総エポック数に対して二次的に依存します。
          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateA ()
{
  return M_PI - M_PI * MathPow ((double)epochNow / epochs, 2);
}
//——————————————————————————————————————————————————————————————————————————————

          CalculatePメソッドは、epochNowの増加に伴って「1.0」から「0.1」へと減少するpの値を計算します。つまり、この値は現在のエポックに依存します。

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateP ()
{
  return 1.0 - 0.9 * MathPow ((double)epochNow / epochs, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

          CalculateThetaメソッドは、現在のcurrentWおよびcurrentPパラメータを用いてθ値を計算します。

          • 現在のフェーズが探索フェーズである場合は、currentWにランダム値を乗じた値を返します。
          • それ以外の場合は、currentWとcurrentPの積を返します。

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateTheta (double currentW, double currentP)
{
  // Use the aParam parameter to adjust the angle
  if (IsExplorationPhase ()) return currentW * u.RNDprobab ();
  else return currentW * currentP;

}
//——————————————————————————————————————————————————————————————————————————————

          IsExplorationPhaseメソッドは、現在の反復が探索フェーズにあるかどうかを確認します。

          //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CSA::IsExplorationPhase ()
{
  // Research in the first part of the iterations (constC is usually 0.8)
  return (epochNow <= constC * epochs);
}
//——————————————————————————————————————————————————————————————————————————————


          テスト結果

          アルゴリズムの著者らは、本手法を非常に高効率な最適化手法として位置付けています。しかし、実装、いくつかの改良、そして最終的なテストをおこなった結果、その性能はあまり印象的なものではありませんでした。アルゴリズムはランキング表に入ることはできましたが、現時点での最良のアルゴリズムと比較すると、その性能は大きく劣っています。

          CSA|Circle Search Algorithm|50.0|0.8|
          =============================
          5 Hilly's; Func runs:10000; result:0.6656012653478078
          25 Hilly's; Func runs:10000; result:0.4531682514562617
          500 Hilly's; Func runs:10000; result:0.2912586479936386
          =============================
          5 Forest's; Func runs:10000; result:0.6879687203647712
          25 Forest's; Func runs:10000; result:0.41397289345600924
          500 Forest's; Func runs:10000; result:0.2052507546137296
          =============================
          5 Megacity's; Func runs:10000; result:0.3753846153846153
          25 Megacity's; Func runs:10000; result:0.2363076923076922
          500 Megacity's; Func runs:10000; result:0.10646153846153927
          =============================
          All score:3.43537 (38.17%)

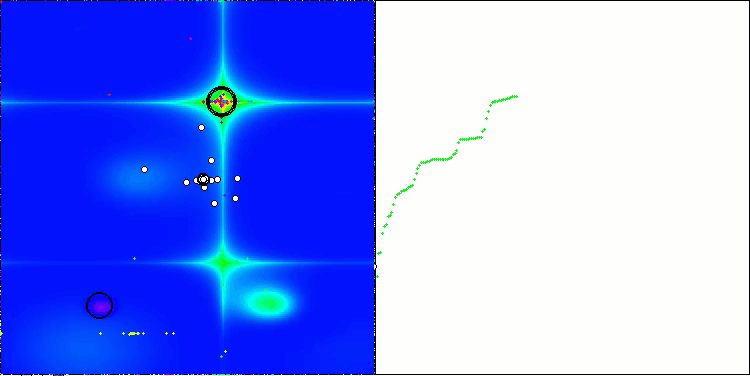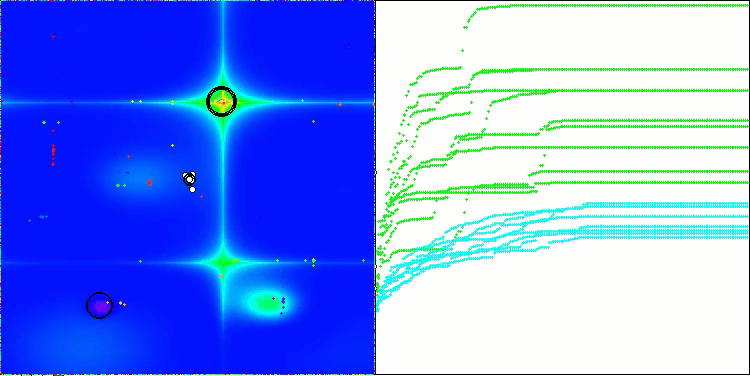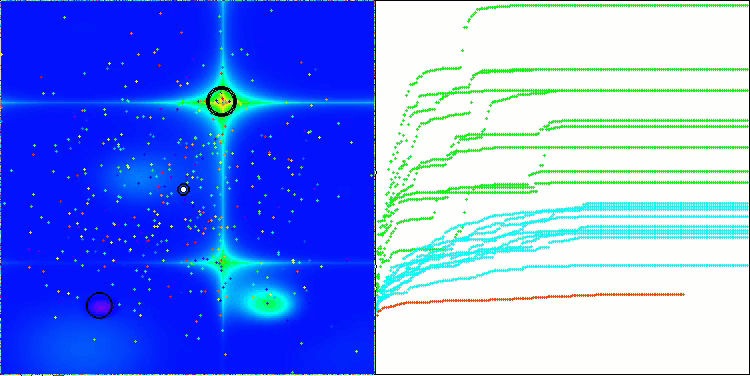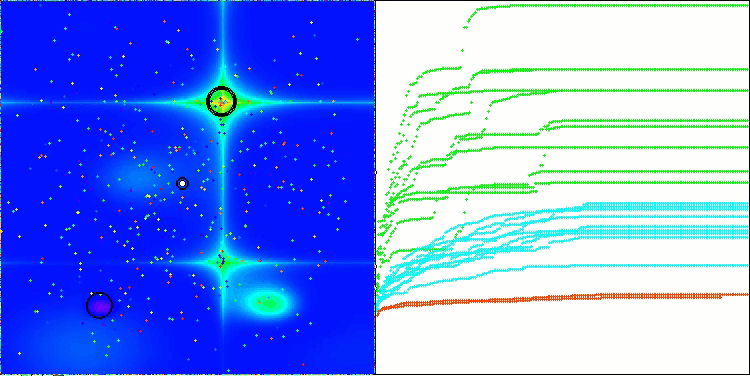
          アルゴリズムの動作の可視化からは、収束性の問題や局所的な極値に捕まりやすいという問題が確認されます。それでもなお、本アルゴリズムは可能な限り最善を尽くして動作しようとします。トラップに陥る問題（収束グラフにおける長い水平区間から明確に確認できます）はあるものの、高次元問題に対しては比較的効果的に動作できる能力を持っている点は評価できます。

          Hilly

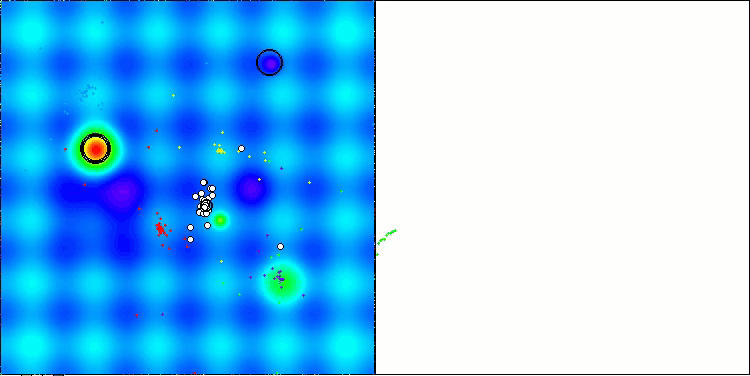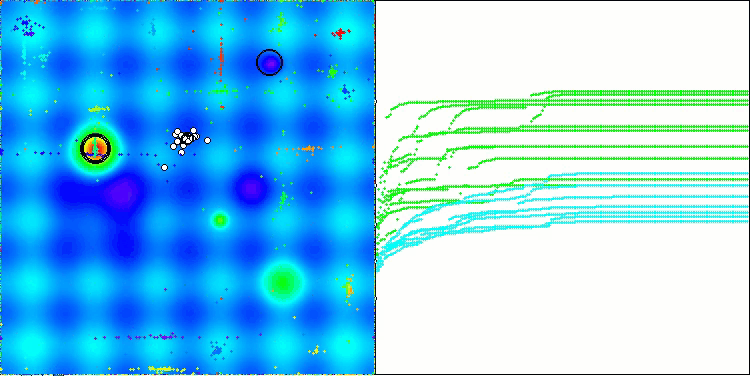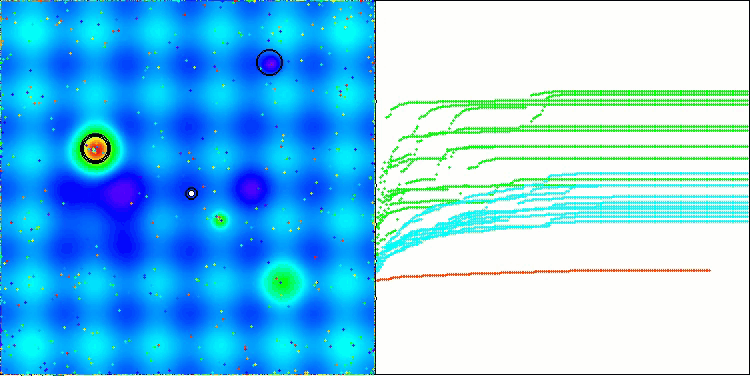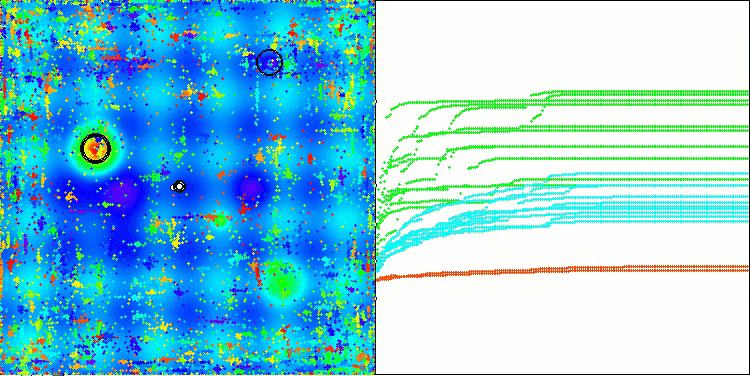
          Hillyテスト関数のCSA

          Forest

          Forestテスト関数のCSA

          Megacity

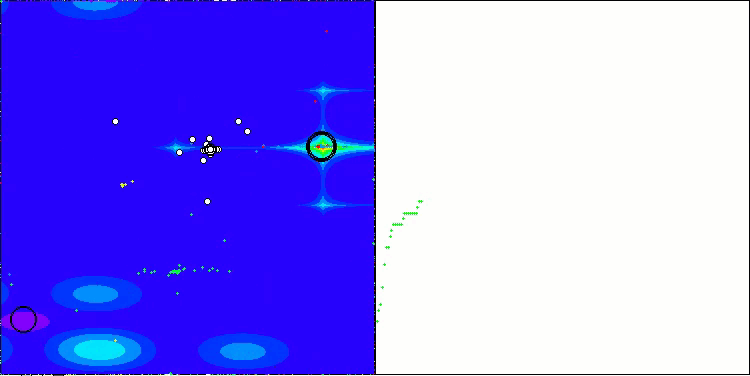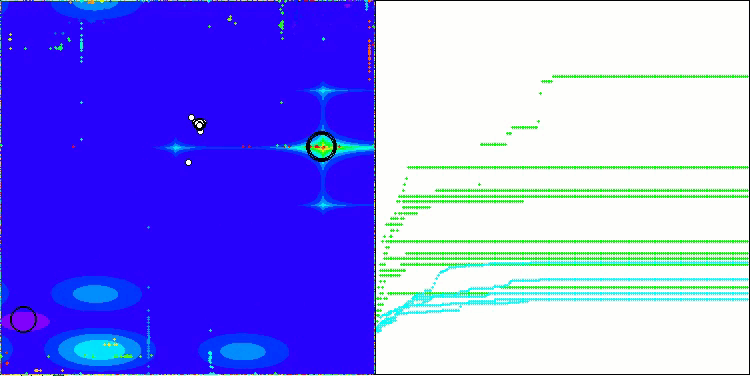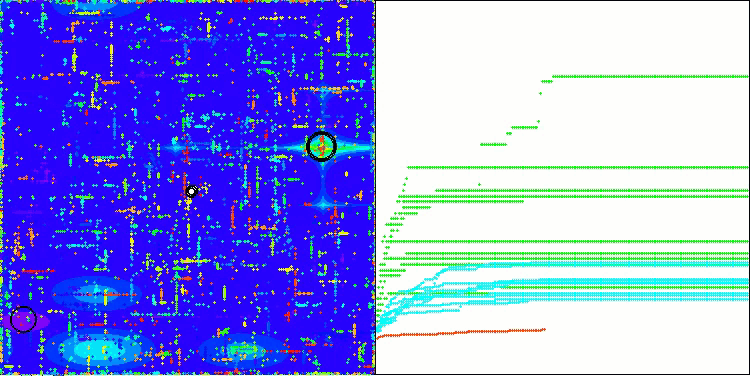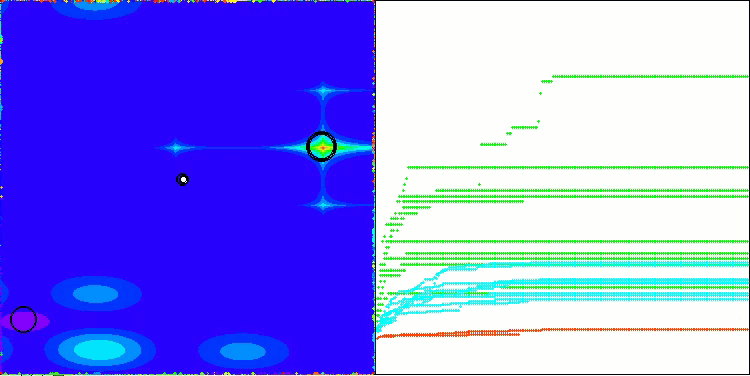
          Megacityテスト関数のCSA

          アルゴリズムのテスト結果に基づくと、CSAはランキング表において41位に位置しています。

          # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
          10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
          1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
          2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
          3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
          4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
          5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
          6 TETA 時間進化移動アルゴリズム（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
          7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
          8 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
          9 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
          10 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
          11 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
          12 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
          13 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
          14 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
          15 RFO ロイヤルフラッシュ最適化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
          16 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
          17 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
          18 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
          19 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
          20 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
          21 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
          22 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
          23 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
          24 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
          25 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
          26 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
          27 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
          28 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
          29 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
          30 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
          31 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
          32 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
          33 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
          34 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
          35 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
          36 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
          37 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
          38 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
          39 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
          40 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
          41 CSA 円探索アルゴリズム 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
          42 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
          43 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
          44 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
          45 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
          RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


          まとめ

          円検索アルゴリズム(CSA)のテスト結果および性能分析に基づくと、以下の結論を導くことができます。円の幾何学的概念の優雅さや、円の接線に沿った移動に基づく直感的な探索メカニズムにもかかわらず、本アルゴリズムは比較分析において比較的弱い結果を示しており、最適化アルゴリズムの評価表では45個中41位という位置にとどまっています。この状況は、現在の実装における重大な制約を示しています。

          このアルゴリズムの主な問題は、局所極値に陥りやすい傾向に関連しており、特に低次元の単純な問題を扱う際に顕著です。これはいくつかの要因によるものと考えられます。第一に、角度探索メカニズムは理論的には有望に見えるものの、実際には局所最適解を克服するには不十分であることが分かりました。第二に、constCパラメータによって制御される探索フェーズと活用フェーズのバランスが、探索の多様化を十分に提供できていません。その結果、集団全体が疑似的に良好な解、すなわち単一の点に収束してしまいます。解空間におけるエージェント位置更新の主方程式にランダム成分を加えて集団を「揺さぶる」試みも、効果はありませんでした。

          エージェントの位置更新式にランダムな乗数を追加することでアルゴリズムを改善しようとする試みは、挙動をより予測可能にする結果にはつながったものの、効率を大きく向上させることはできませんでした。これは、円の幾何学的性質に基づくアルゴリズムの基本的なアイデアが、現在の実装では著者によって十分に実現されていないか、あるいは大域最適化の文脈において本質的な限界を持っている可能性を示唆しています。

          一方で、アルゴリズムは一定の探索能力を示しており、特定の問題、特に目的関数の景観が比較的単純な場合には有効である可能性があります。アルゴリズムの効率を向上させるためには、局所最適解からの脱出メカニズムの改善に向けたさらなる研究を推奨します。具体的には、探索の多様化を強化する追加メカニズムの導入や、他の最適化手法とのハイブリッド化（特に、本探索戦略を他の最適化アルゴリズムの構成要素として活用すること）が有望であると考えられます。

          Tab

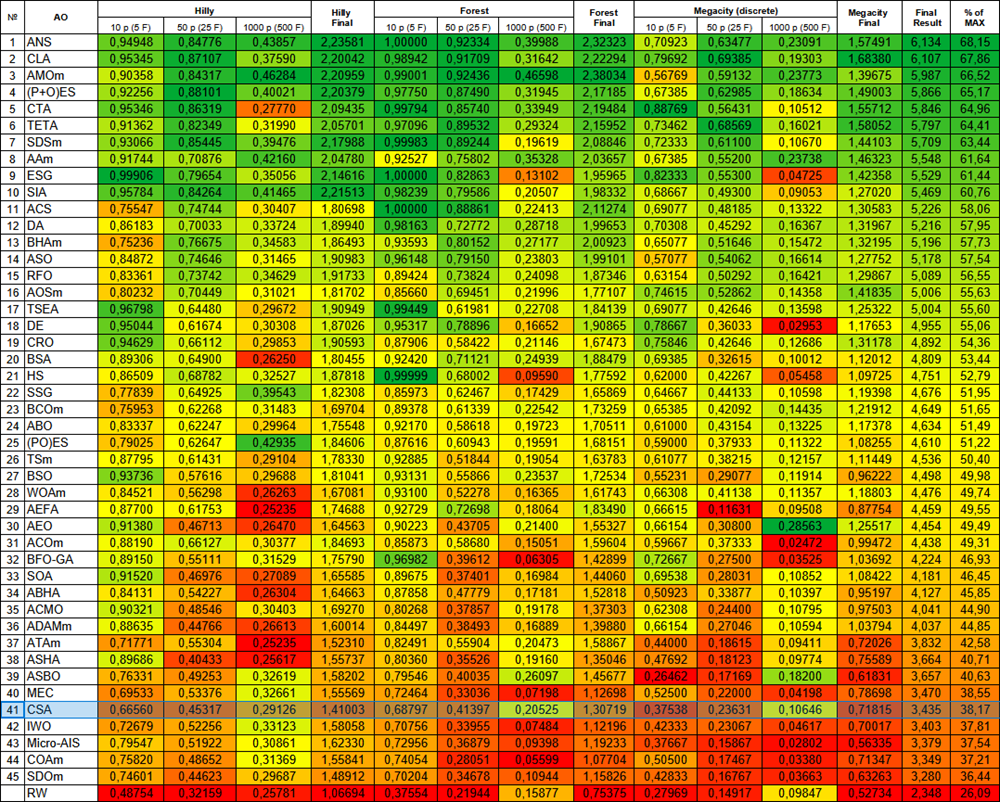
          図3：対応するテストに応じたアルゴリズムのカラーグラデーション

          チャート

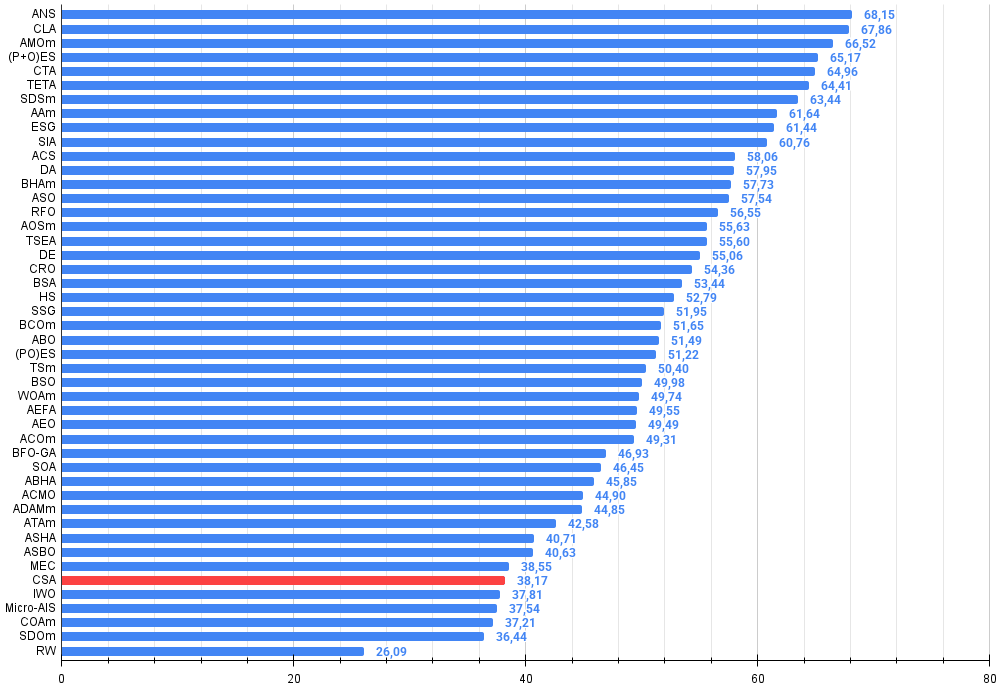
          図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。


          CSA の長所と短所

          長所

          1. 外部パラメータが非常に少ない
          2. 実装がシンプル
          3. 円の幾何学的性質を利用した興味深いアイデア

          短所：

          1. 収束精度が低い
          2. 極限で行き詰まる

          この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

          記事で使用されているプログラム

          # 名前 種類 詳細
          1 #C_AO.mqh
          		 インクルード
          		 集団最適化アルゴリズムの親クラス
          2 #C_AO_enum.mqh
          		 インクルード
          		 集団最適化アルゴリズムの列挙
          3 TestFunctions.mqh
          		 インクルード
          		 テスト関数のライブラリ
          4
          		 TestStandFunctions.mqh
          		 インクルード
          		 テストスタンド関数ライブラリ
          5
          		 Utilities.mqh
          		 インクルード
          		 補助関数のライブラリ
          6
          		 CalculationTestResults.mqh
          		 インクルード
          		 比較表の結果を計算するスクリプト
          7
          		 Testing AOs.mq5
          		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
          8
          		 Simple use of population optimization algorithms.mq5
          		 スクリプト
          		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
          9
          		 Test_AO_CSA.mq5
          		 スクリプト CSAテストスタンド

          MetaQuotes Ltdによってロシア語から翻訳されました。
          元の記事: https://www.mql5.com/ru/articles/17143

          添付されたファイル |
          ZIPをダウンロード
          CSA.zip (164.1 KB)

          警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

          この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

          この著者による他の記事

          ディスカッションに移動
          多通貨エキスパートアドバイザーの開発（第22回）：設定のホットスワップへの移行を開始する 多通貨エキスパートアドバイザーの開発（第22回）：設定のホットスワップへの移行を開始する
          定期的な最適化を自動化するのであれば、取引口座上ですでに稼働しているEAの設定を自動更新することについても検討する必要があります。これにより、ストラテジーテスター内でエキスパートアドバイザー(EA)を実行しながら、単一の実行の中でその設定を変更できるようにする必要があります。
          外国為替におけるフィボナッチ（第1回）：価格と時間の関係を調べる 外国為替におけるフィボナッチ（第1回）：価格と時間の関係を調べる
          市場はフィボナッチに基づく関係性をどのように観測しているのでしょうか。各項が直前の2つの項の和になっているこの数列(1, 1, 2, 3, 5, 8, 13, 21...)は、ウサギの個体数の増加を説明するだけのものではありません。私たちは、「世界のあらゆるものは数の一定の関係に従う」というピタゴラス派の仮説を考察します。
          取引におけるニューラルネットワーク：2次元接続空間モデル(Chimera) 取引におけるニューラルネットワーク：2次元接続空間モデル(Chimera)
          この記事では、革新的なChimeraフレームワークについて解説します。Chimeraは二次元状態空間モデルを用い、ニューラルネットワークで多変量時系列を解析する手法です。この方法は、従来手法やTransformerアーキテクチャを上回る低い計算コストで高い精度を実現します実現します。
          市場シミュレーション（第8回）：ソケット(II) 市場シミュレーション（第8回）：ソケット(II)
          ソケットを使って何か実用的なものを作ってみましょう。今回の記事では、ミニチャットの作成を始めます。一緒にどのようにおこなうかを見ていきましょう。とても面白い内容になるでしょう。ここで提供するコードは教育目的のみの使用を想定しています。商用目的や既製のアプリケーションでの使用には適していません。ソケット上で送信されるデータは安全に保護されず、内容が第三者からアクセス可能になる可能性があるためです。