MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
人工生態系ベースの最適化(AEO)アルゴリズム

人工生態系ベースの最適化(AEO)アルゴリズム

MetaTrader 5 — テスター | 28 5月 2025, 09:20
56 0
Andrey Dik
Andrey Dik


内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

最適化および人工知能の分野では、複雑な課題をより効率的に解決するための新たな手法が常に模索されています。そのような革新的アプローチの一つが、2019年に開発・発表された人工エコシステムベース最適化(AEO: Artificial Ecosystem-based Optimization)アルゴリズムです。この手法は自然界の生態系に着想を得ており、自然環境における複雑な相互作用やプロセスを模倣しています。

AEOアルゴリズムは、自然界に見られるいくつかの基本原理に基づいています。自然の生態系には多様な種が存在し、それぞれが固有の生態的ニッチに適応しています。同様に、AEOでは多様な解候補による集団を構成し、それぞれを独立した「種」として捉えることができます。これらの「種」は独自の特性と適応能力を備えています。

自然界では、エネルギーは食物連鎖を通じて生物間で移動します。AEOにおいては、これは「草」から「雑食動物」までのさまざまなタイプの「エージェント」間の相互作用によってモデル化されます。この過程では、エネルギーと同様に情報が解の間で伝達され、集団全体の質の向上に寄与します。さらに、生態系は資源をめぐる競争と共生という2つの関係性によって成り立っています。AEOでは、エージェントがより優れた位置を獲得するために「競争」したり、情報を交換して「協力」したりする意思決定更新戦略によって、これらのプロセスが反映されています。

また、自然生態系は周期的な変化を受ける特性がありますが、この性質もAEOに取り入れられています。反復的に進行する最適化プロセスでは、「消費」フェーズと「分解」フェーズが交互に実行され、問題の変動に対して柔軟に対応することが可能となります。自然界では、突然変異や自然災害のような確率的現象と、自然選択のような決定論的プロセスが共存しています。AEOでも、レヴィ分布といった確率的手法と決定論的ルールを組み合わせて解を更新し、探索と活用のバランスを保っています。

自然現象とAEOアルゴリズムの対応をより具体的に理解するために、いくつかの例を挙げましょう。たとえばアフリカのサバンナでは、エネルギーは草からシマウマ（草食動物）、ライオン（捕食者）、ハイエナ（スカベンジャー）へと移行します。AEOでは、最悪の解（草）から、平均的な解（草食動物）、そして最良解（肉食動物）へと情報が受け渡され、集団全体の質が向上していきます。

また、生物が死ぬと分解され、栄養分を生態系に還元します。たとえば、森林の落ち葉が分解されて土壌を豊かにし、新たな植物の成長を支えるように、AEOでも「分解」段階でこのプロセスが模倣されています。消費（意思決定の更新）フェーズの後に続く分解フェーズでは、現在の解に含まれる情報が「分解」され、探索空間全体に分散されます。これは、局所最適に陥るのを回避し、新たな探索領域を切り開くための重要なメカニズムです。アルゴリズムの実装上では、現在の解に対して（大域的）最良解を基準に正規分布を適用することで、情報の「分解」と「再分配」がおこなわれます。

このように、AEOアルゴリズムは自然界の原理と数学的最適化手法とを巧みに融合したものであり、単に高性能な最適化手段を提供するにとどまらず、自然現象と人工知能の関係性に新たな視座をもたらします。次に、このアルゴリズムの構造および動作原理についてより詳しく解説し、その可能性と応用分野について考察します。


アルゴリズムの実装

AEOアルゴリズムの設計思想をより深く理解するために、人工生態系における生物の階層構造を示す図1を参照しましょう。この生態系は、仮想的に番号付けされた1からXnまでの生物によって構成されています。番号「1」は最大のエネルギー（適応度関数値が最小）を持つ「草」を表し、Xnは最小のエネルギー（適応度関数値が最大）を持つ腐生生物を表します。腐生生物は分解機能を担う存在です。

図中の矢印は摂食関係（どの生物がどれを捕食するか）の方向を示しています。「草」(1)は腐生生物の廃棄物しか利用できません。「草食動物」(2)は「草」を捕食します。「2」、「4」、「5」の生物は、それぞれ草のみを食べる草食動物、自分よりエネルギーの低い生物のみを食べる肉食動物、草と自分よりエネルギーの高い生物の両方を食べる雑食動物のいずれかに分類されます。生態系の最上位には腐生生物が位置しており、すべての生物はライフサイクルの終わりにおいて彼らによって分解されます。

AEO

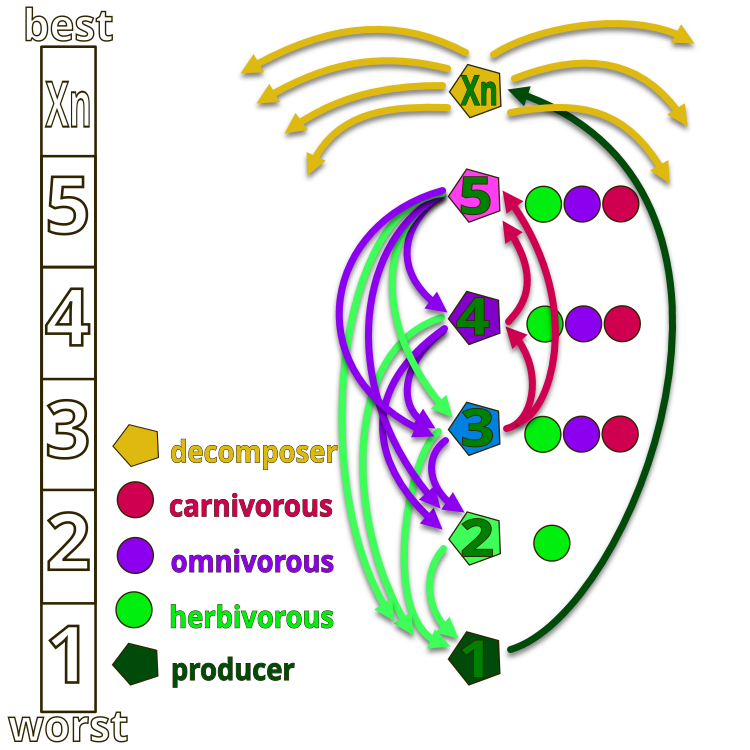
図1：AEOアルゴリズムの人工生態系における生物の階層


アルゴリズムの主なアイデアは、生態系の構成要素間の相互作用をモデル化することによって最適化問題を解決するというものです。このアルゴリズムは、自然界で観察される以下の3つの基本原理に基づいています。

1. 生産：自然界において、生産者（植物など）は太陽エネルギーを有機化合物へと変換します。
2. 消費：草食動物、肉食動物、雑食動物といった消費者は、特に植物によって生産されたエネルギーを利用します。
3. 分解：腐生生物は複雑な有機物を単純な物質へと分解します。このプロセスはアルゴリズムにおいて、解の分解としてモデル化されています。

アルゴリズムの原則

1. 初期化：生態系を表す初期の解集団を生成します。
2. 生産：各反復において、最悪解が最良解とランダム要素を考慮して更新されます。
3. 消費：残りの解は、以下の3つの戦略に基づいて更新されます。

  • 草食動物：生産者に基づいて更新されます。
  • 捕食者：ランダムに選ばれた最良解に基づいて更新されます。
  • 雑食動物：生産者とランダムな解の両方に基づいて更新されます。

4. 分解：すべての解が「分解」プロセスを経て、グローバルな探索能力が向上します。
5. 選択：改善された解のみが保持され、集団は徐々に改良されていきます。

したがって、本アルゴリズムは、生物間のエネルギー伝達の仕組みに依拠しており、生産・消費・分解という3つのオペレーターを用いて種の安定性を維持します。

1. 生成：指定された範囲内でランダムに生成された座標Xrandを加え、最良のXnを基準に最悪のX1個体を更新し、生成演算子によって新しい個体を作成します。数学的表現は、X1 (t + 1) = (1 - a) * Xn (t) + a * Xrand (t)、ここで、a = (1 - t / T) * r1（t：現在のエポック、T：総エポック数）、r1：乱数[0;1]）です。ただし、方程式内で既にランダム座標を用いているためr1は省略可能です。

2. 消費：ランダムに選ばれた消費者は生産者を「食べて」エネルギーを獲得します。消費係数Cは、C = 1/2 * (v1 / |v2|)によって定義されます。ここで、v1とv2は範囲[0; 1]内の均一に分布した乱数です。

  • 草食動物：Xi (t + 1) = Xi (t) + C * (Xi (t) - X1 (t))
  • 肉食動物：Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t))
  • 雑食動物：Xi (t + 1) = Xi (t) + C * (r2 * Xi (t) + (1 - r2) * Xj (t))

3. 分解：腐生生物は死んだ個体の残骸を分解し、生産者に栄養を供給します。腐生生物の作用後の個体位置の更新は以下の式で表されます。

Xi (t + 1) = Xn (t) + D * (e * Xn (t) - h * Xi (t))、ここで、D = 3u、u ~ N (0, 1)、e = r3 * rand (i)、h = 2 * r3 - 1（r3：[0; 1]の範囲の乱数）。

以上より、最初にランダム集団が生成され、各反復で最初の個体は上記の1の式で更新されます。他の個体は上記の2の式群から等確率で選ばれたものによって更新されます。分解段階では各個体が上記の3の式で位置を更新します。満足のいく終了条件が達成されるまでこの過程を繰り返し、最終的にこれまでに得られた最良の個体を返します。

これで、AEOアルゴリズムの疑似コードを記述できます。

AEO（人工生態系に基づく最適化）アルゴリズム：

初期化
    集団サイズpopSizeを設定
    エポック数epochsを設定
    Levy分布パラメータlevisPowerを設定
    指定範囲内でランダムな解で集団を初期化
    各解の適応度を評価
    最良大域解cBを決定

1からepochsまでの各エポックについて：
    // 消費フェーズ
    集団内の各エージェントiについて：
        i == 0の場合：
            現在の解に正規分布を適用
        それ以外でi == popSize - 1 の場合：
            GrassBehaviorを適用
        それ以外の場合：
            行動をランダムに選択：
                - 草食動物行動(HerbivoreBehavior)
                - 肉食動物行動(CarnivoreBehavior)
                - 雑食動物行動(OmnivoreBehavior)
    
    // 分解フェーズ
    集団内の各エージェントiについて：
        各c座標について：
            ランダムなエージェントjを選択
            cB[c]とa[j].c[c]間の距離Dを計算
            正規分布を用いてa[i].c[c]を更新

    // 修正
    各エージェントの適応度を評価
    各エージェントの個体最良解を更新（改善があれば）
    大域最良解cBを更新（改善があれば）
    適応度値で集団をソート

最良解cBを返す

サブプロシージャ：

GrassBehavior (agent)
    α = (1 - current_epoch / total_number_of_epochs)
    各c座標について：
        Xr = [min [c], max [c]]の範囲内のランダム値
        Xn = cB [c]
        X1 = Xn + α * (Xn - Xr)
        agent.c [c] = X1（制限を考慮）

HerbivoreBehavior (agent, coordinate_index)
    Xi = agent.cB [coordinate_index]
    X1 = 与えられた座標における集団内での最悪解
    C = レヴィ分布からの乱数(levisPower)
    Xi = Xi + C * (Xi - X1)
    agent.c [coordinate_index] = Xi（制限を考慮）

CarnivoreBehavior (agent, agent_index, coordinate_index)
    Xi = agent.cB [coordinate]
    j = agent_index未満のランダムインデックス
    Xj = a [j].cB [coordinate_index]
    C = レヴィ分布からの乱数(levisPower)
    Xi = Xi + C * (Xj - Xi)
    agent.c [coordinate_index] = Xi（制限を考慮）

OmnivoreBehavior (agent, agent_index, coordinate_index)
    Xi = agent.cB [coordinate]
    X1 = 与えられた座標における集団内での最悪解
    j = agent_indexを超えるランダムインデックス
    Xj = a [j].cB [coordinate_index]
    C = レヴィ分布からの乱数(levisPower)
    r = 0から1までの乱数
    Xi = Xi + C * r * (Xi - X1) + (1 - r) * (Xi - Xj)
    agent.c [coordinate_index] = Xi（制限を考慮）

アルゴリズムの詳細な説明と分析が終わったら、コードの記述に移りましょう。

アルゴリズムでは、探索空間において極端に遠いがまれにしか発生しないジャンプを生成するために、レヴィ分布が使用されます。以前にカッコウ探索アルゴリズムなどでこの乱数分布を使用したことがありますが、その特徴について詳しくは触れていませんでした。問題は、レヴィ分布を正確に生成するには、一様分布に従う4つの乱数を使用する必要があり、これ自体が高コストであるということです。さらに、レヴィ分布は無限に長い裾（片側に偏った非対称分布）を持っており、特に境界条件が存在する最適化アルゴリズムでは実用上の利用が困難になります。生成中には、自然対数の計算前に0をチェックしたり、0で割ることを避けたりするなど、境界条件のチェックも必要です。

以下は、上記のようなチェックを含まず、コードのロジックの説明もないレヴィ分布に従った乱数生成のコードです。

double LevyFlight()
{
    const double epsilon = 1e-10; // Small value to avoid division by zero
    const double maxValue = 1e10; // Maximum allowed value

    double log1 = MathMax (RNDprobab(), epsilon);
    double log2 = MathMax (RNDprobab(), epsilon);

    double cos1 = MathCos (2 * M_PI * RNDprobab());
    double cos2 = MathCos (2 * M_PI * RNDprobab());

    double U = MathSqrt (-2.0 * MathLog (log1)) * cos1;
    double v = MathSqrt (-2.0 * MathLog (log2)) * cos2;

    double l = 0.5 * MathAbs(U) / MathMax(MathAbs(v), epsilon);

    return l;
}

レヴィ分布による乱数生成の欠点を解消するために、近似的な分布を用いた独自の関数LevyFlightDistributionを実装し、最適化アルゴリズムで使用できるように、標準の関数セットC_AO_Utilitiesに組み込みましょう。以下にその内容を分解して説明します。

1. levisPowerパラメータは分布の形状を決定する累乗値です。この値が高いほど分布はより「スパース」になります。
2. 関数はスケーリングに使用される最小値を計算します。これはlevisPowerに依存し、20^levisPowerとして計算されます。
3. RNDfromCI関数を使用して1から20の範囲でランダムな値rを生成します。
4. 累乗を適用します。生成された値rを-levisPower乗し、分布の形状を変えます。
5. 結果のスケーリング：得られた値rを[0,1]の範囲に収めるようスケーリングします。これは最小値を引いた後、1 - 最小値で割ることで実現されます。これにより結果は常に[0,1]の範囲内になります。
6. 結果を返す：関数はレヴィ分布に近く0に偏った分布を持つr値を返します。

この関数は常に[0,1]の範囲で乱数を生成するため、実用面で非常に便利です。必要に応じて適切な比率を掛けることで任意の範囲に拡張できます。この関数は非常に高速で、レヴィ分布（特に最大値に対する右側）の形状に非常に近い分布を提供します。

//------------------------------------------------------------------------------
//A distribution function close to the Levy Flight distribution.
//The function generates numbers in the range [0.0;1.0], with the distribution shifted to 0.0.
double C_AO_Utilities :: LevyFlightDistribution (double levisPower)
{
  double min = pow (20, -levisPower); //calculate the minimum possible value
  double r = RNDfromCI (1.0, 20);     //generating a number in the range [1; 20]

  r = pow (r, -levisPower);           //we raise the number r to a power
  r = (r - min) / (1 - min);          //we scale the resulting number to [0; 1]

  return r;
}

アルゴリズムのメインコードの説明に進みましょう。C_AO_AEOクラスはC_AOクラスを継承し、このアルゴリズムの実装を担います。その構造、メンバー、メソッドを詳しく見てみましょう。

コンストラクタ

  • 集団サイズおよびレヴィ分布の次数のデフォルト値を設定します。
  • パラメータの配列paramsを作成し、そこに値を初期化します。

メソッド

  • params配列からpopSizeおよびlevisPowerパラメータを設定します。
  • Init ()は、探索範囲やエポック数を指定してアルゴリズムを初期化します。このメソッドはbool型を返し、初期化の成功可否を判定可能です。
  • Moving ()は、現在の時代（エポック）におけるエージェントの移動処理を行い、それぞれの座標を更新します。
  • Revision ()は、エージェントとその最良解に関する情報を更新します。

privateメンバーと変数

  • levisPower：レヴィ分布で使用されるパラメータ
  • エポック：総エポック数
  • epochNow：現在のエポック
  • consModel：ステージ（消費または分解）

S_AO_Agent aT []：集団をソートするための一時エージェント配列

privateメソッド

  • GrassBehavior ()：草エージェントの行動を処理します。
  • HerbivoreBehavior ()：草（最悪のエージェント）を「食べる」草食動物エージェントの行動を処理します。
  • CarnivoreBehavior ()：自分より適応度の高いエージェントを「食べる」肉食動物エージェントの行動を処理します。
  • OmnivoreBehavior ()：草食・肉食の両方の要素を持つ雑食動物エージェントの行動を処理します。

C_AO_AEOクラスは、人工生態系に基づいた最適化アルゴリズムの実装を提供し、さまざまな種類のエージェントとその相互作用を用いて最適解の探索をおこないます。各メソッドは、初期化、エージェントの移動、状態更新といったアルゴリズムの特定の処理を担当しています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEO () { }
  C_AO_AEO ()
  {
    ao_name = "AEOm";
    ao_desc = "Artificial Ecosystem-based Optimization Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16058";


    popSize    = 50;       // population size
    levisPower = 2;

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "levisPower"; params [1].val = levisPower;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    levisPower = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // step search
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double levisPower;


  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  consModel; // consumption model;
  S_AO_Agent aT [];

  void GrassBehavior     (S_AO_Agent &animal);
  void HerbivoreBehavior (S_AO_Agent &animal, int indCoord);
  void CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord);
  void OmnivoreBehavior  (S_AO_Agent &animal, int indAnimal, int indCoord);
};
//——————————————————————————————————————————————————————————————————————————————

それでは、C_AO_AEOクラスのInitメソッドのコードを詳しく見てみましょう。Initメソッドはbool型の値を返し、初期化が成功したかどうかを判定できるようになっています。まず、標準的な初期化チェックとして、StandardInitが呼び出され、渡されたパラメータに対して基本的な初期化がおこなわれます。StandardInitがfalseを返した場合は、初期化に失敗したことを意味し、Initメソッドも同様にfalseを返して終了します。

変数の設定：

  • epochs：epochsPパラメータから取得したエポックの総数を設定します。
  • epochNow：現在のエポックを0に初期化し、アルゴリズムが開始されたばかりであることを示します。
  • consModel：モデルの値を0に設定し、その後ステージ間を移動できるようにします。

aT一時エージェント配列のサイズをpopSizeに変更します。

結果を返します。これらの操作がすべて成功した場合、メソッドはtrueを返し、初期化が成功したことを示します。

C_AO_AEOクラスのInitメソッドは、アルゴリズムの初期設定を担当します。デフォルトパラメータのチェック、エポック数や初期ステージの設定、エージェント配列の準備をおこないます。すべての段階が正常に完了すればtrueを返し、アルゴリズムの実行準備が整ったことを示します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  consModel = 0;
  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのMovingメソッドのコードを分析してみましょう。メソッドの全体構造は次のとおりです。 Movingは現在のエポックと消費モデルに応じてエージェント（個体）の集団の状態を更新する役割を担い、いくつかの論理ブロックに分かれています。

1. エポックの増加：epochNow++によって現在のエポックカウンタが増加します。

2. 最初の初期化

  • revisionがfalseの場合、集団内のエージェントの座標が初めて初期化されます。座標は指定範囲内でランダムに選ばれ、ステップに対応した最も近い値に丸められます。
  • その後、revisionがtrueに設定され、メソッドは処理を終了します。

3. 消費モデル

  • consModelが0の場合、エージェントの座標はそれぞれの行動パターンに基づいて更新されます。 
  • 最初のエージェント（インデックス0）には正規分布を用いて座標が初期化されます。
  • 残りのエージェントはインデックスに応じて行動が決まり、最後のエージェント（インデックスpopSize - 1）はGrassBehavior関数を呼び出します。最後から2番目以降のエージェント（インデックスpopSize - 2以下）は、草食動物、肉食動物、雑食動物のいずれかの行動をランダムに選択します。

4. 分解モデル：consModelが0以外の場合、分解が行われ、各エージェントの各座標はランダムな値と正規分布に基づいて更新されます。各座標に対して他のエージェントのランダムなインデックスが選択され、その値を基に最小・最大境界を考慮して新たな座標が計算されます。

Movingメソッドは、エージェントの行動や現在のエポックに応じた座標の変化に関するロジックを実装しています。初期化処理と、消費パターンに基づく状態更新の両方を含みます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Consumption ---------------------------------------------------------------
  if (consModel == 0)
  {
    double r = 0.0;

    for (int i = 0; i < popSize; i++)
    {
      if (i == 0)
      {
        for (int c = 0; c < coords; c++)
        {
          a [i].c [c] = u.GaussDistribution (a [i].c [c], rangeMin [c], rangeMax [c], 8);
          a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        continue;
      }

      if (i == popSize - 1) GrassBehavior (a [i]);
      else
      {
        if (i >= popSize - 2)
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.333) HerbivoreBehavior (a [i], c);
            else
            {
              if (r < 0.667)
              {
                CarnivoreBehavior (a [i], i, c);
              }
              else
              {
                OmnivoreBehavior (a [i], i, c);
              }
            }
          }
        }
        else
        {
          for (int c = 0; c < coords; c++)
          {
            r = u.RNDprobab ();

            if (r < 0.5) CarnivoreBehavior (a [i], i, c);
            else         OmnivoreBehavior  (a [i], i, c);
          }
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  int    j   = 0;
  double D   = 0.0;
  double min = 0.0;
  double max = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      j = u.RNDminusOne (popSize);
      D = 3.0 * (cB [c] - a [j].c [c]); // * u.RNDprobab ();
      min = cB [c] - D;
      max = cB [c] + D;

      if (min < rangeMin [c]) min = u.RNDfromCI (rangeMin [c], cB [c]);
      if (max > rangeMax [c]) min = u.RNDfromCI (cB [c], rangeMax [c]);

      a [i].c [c] = u.GaussDistribution (cB [c], min, max, 1);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのRevisionメソッドは、集団内の最良エージェントに関する情報を更新する役割を持ちます。アルゴリズムの実行中に見つかった最良解を追跡・保存するロジックを実装しています。メソッドの構造は以下の通りです。

1. 最良エージェントの探索

  • 集団内のすべてのエージェントを繰り返し処理します。
  • それらの適応度（f値）を現在の最良適応度fBと比較します。
  • より適合度の高いエージェントが見つかった場合は、fB を更新し、そのエージェントのインデックスを記憶します。

2. 最良エージェントの座標コピー：最良エージェントが見つかった場合（インデックスが-1でない場合）、その座標を現在の最良座標を保持するcB配列にコピーします。

3. エージェントの個体最良適応度の更新：再び全エージェントをループし、それぞれの現在の適応度が個体の最良適応度(fB)を上回っているかどうかをチェックします。上回っている場合は、個体の最良適応度を更新し、現在の座標をcBにコピーします。

4. エージェントのソート：最後に、個体の最良適応度の値に基づいてエージェントをソートする関数を呼び出します。

Revisionメソッドは、アルゴリズムの作業中に見つかった最良解を確実に追跡・保存するための重要な要素です。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのGrassBehaviorメソッドは、「草食動物」の概念に基づくエージェントの行動を実装しており、新しい解空間の探索を象徴しています。メソッドの構造は以下の通りです。

1. α比の計算は(1.0 - (double) epochNow / epochs)と定義されており、エポック数が増えるごとに減少します。これにより、アルゴリズムは初期段階でより活発に探索をおこない、後半では見つけた解の改善に集中できます。

2. 変数の初期化

  • X1：草食動物エージェントの現在の座標
  • Xn：腐生生物の現在の座標
  • Xr：指定範囲内からランダムに選ばれた座標

3. 座標ごとのループ処理：各エージェントの座標について：

  • 乱数値Xrは指定された範囲[Xmin、Xmax]内で生成されます。
  • 現在の座標Xnは、現在の大域最適座標（空間内の腐生生物の位置）を格納するcB配列から取得されます。
  • 新しい座標X1はX1 = Xn + α * (Xn - Xr)の式で計算されます。これにより、現在の値がランダムな値と混合され、エポック数の増加に伴いランダム性の影響が減少します。
  • 最後に、新しい座標はSeInDiSp関数を使用して指定範囲内に制限されます。

//——————————————————————————————————————————————————————————————————————————————
// Grass
// (Worst) X1 X2 X3 ...... Xn (Best)
// X1(t+1) = (1 - α) * Xn(t) + α * Xrnd (t)
// α = (1 - t / T) * rnd [0.0; 1.0]
// Xrnd = rnd [Xmin; Xmax]

void C_AO_AEO::GrassBehavior (S_AO_Agent &animal)
{
  //0) (1 - α) * Xn + α * Xrnd
  //1) Xn - α * Xn + α * Xrnd
  //2) Xn + α * (Xrnd - Xn)

  double α = (1.0 - (double)epochNow / epochs);

  double X1 = 0.0;
  double Xn = 0.0;
  double Xr = 0.0;

  for (int c = 0; c < coords; c++)
  {
    Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
    Xn = cB [c];

    //X1 = Xn + α * (Xr - Xn);
    X1 = Xn + α * (Xn - Xr);

    animal.c [c] = u.SeInDiSp (X1, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのHerbivoreBehaviorメソッドは、草食動物エージェントの行動を実装します。メソッドの構造は以下の通りです。

1. 変数の初期化

  • Xi：更新対象となるエージェントの現在の座標
  • X1：集団内の最悪（つまりエネルギーが最大、または適応度が最低）エージェントの座標
  • C：レヴィ分布を用いて生成されるランダムな値

2. 座標の更新：Xiの座標は、 Xi (t+1)=Xi (t)+C ⋅ (Xi (t) − X1 (t))という式に基づいて更新されます。この式は、エージェントが自身の現在の座標と最悪エージェントの座標の差に基づいて移動することを意味します。これにより、草食動物は最悪のエージェントを「捕食」する、すなわち有望でない探索領域すらも探索することが可能になります。

3. 座標の制限：Xiの座標を更新した後、SeInDiSp関数を使用して指定された範囲内（最小値、最大値、ステップ幅）に制限されます。

HerbivoreBehaviorメソッドは、草食動物エージェントが集団内の最も悪い個体を「餌」とすることで適応し、探索空間全体を効果的に探索できることを示しています。

//——————————————————————————————————————————————————————————————————————————————
// Herbivore
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - X1(t)) for i ∈ [2, n]
// Herbivore eats only the one with the highest energy (eats the one with the worst FF)
void C_AO_AEO::HerbivoreBehavior (S_AO_Agent &animal, int indCoord)
{
  double Xi = animal.c [indCoord];
  double X1 = a [popSize - 1].c [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  Xi = Xi + C * (Xi - X1);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのCarnivoreBehaviorメソッドは、アルゴリズム内での肉食動物エージェントの行動を実装しています。メソッドの構造は以下の通りです。

1. 変数の初期化

  • Xi：更新対象となる肉食動物エージェントの現在の座標
  • j：ランダムに選ばれた犠牲エージェントのインデックス（肉食動物はエネルギーが少ないが適応度がより良い個体を「捕食」します）
  • Xj：犠牲個体の座標で、肉食動物の座標更新に使用されます。
  • C：レヴィ分布を用いて生成されるランダムな値

2. 座標の更新：Xiの座標は、Xi (t+1) = Xi (t) + C * (Xj (t) - Xi (t))式に従って更新されます。この式は、肉食動物エージェントが犠牲個体との位置の差に基づいて自分の座標を変化させることを意味します。これにより、肉食動物は「獲物を食べる」ことで自身の特性を向上させることができます。

3. 座標の制限：Xiの座標座標は更新後にSeInDiSp関数を使用して指定範囲内（最小値、最大値、ステップ）に制限されます。

CarnivoreBehaviorメソッドは、肉食動物エージェントがエネルギーの少ない獲物を「捕食」することで適応し、より最適な解を目指して性能を高める様子を表しています。 

//——————————————————————————————————————————————————————————————————————————————
// Carnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * (Xi(t) - Xj(t)) for i ∈ [3, n]
// Carnivore eats those with less energy (eats those with higher FF)
void C_AO_AEO::CarnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  int    j  = u.RNDminusOne (indAnimal);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);

  //Xi = Xi + C * (Xi - Xj);
  Xi = Xi + C * (Xj - Xi);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEOクラスのOmnivoreBehaviorメソッドは、新化的アルゴリズムの文脈における雑食動物エージェントの行動を記述しています。メソッドの構造は以下の通りです。

1. 変数の初期化

  • Xi：更新が必要な雑食動物エージェントの現在の座標
  • X1：最悪のエージェント（エネルギーが最も高いエージェント）の座標
  • j：座標更新に使用する、集団からランダムに選ばれた別のエージェントのインデックス
  • Xj：選ばれた別のエージェントの座標
  • C：レヴィ分布を用いて生成されるランダムな値
  • r：座標更新の混合に使用されるランダムな確率

2. 座標の更新：Xiの座標は、Xi (t+1) = Xi (t) + C * r * (Xi (t) - X1 (t)) + (1 - r) (Xi (t) - Xj (t))の式に従って更新されます。この式により、雑食動物エージェントは、最もエネルギーの高い（最悪の）エージェントおよび他の適応度の低いランダムなエージェントの両方から「摂取」することで柔軟に適応することが可能になります。

3. 座標の制限：Xiの座標を更新した後、SeInDiSp関数を使用して、指定された制約内に収められます。

OmnivoreBehaviorメソッドは、雑食動物エージェントがより柔軟に適応し、最悪のエージェントやランダムに選ばれた低適応度のエージェントといった異なるエネルギー源から恩恵を受けられることを示しています。

//——————————————————————————————————————————————————————————————————————————————
// Omnivorous
// (Worst) X1 X2 X3 ...... Xn (Best)
// Xi(t+1) = Xi(t) + C * r2 * (Xi(t) - X1(t)) + (1 - r2) * (Xi(t) - Xj(t)) for i ∈ [3, n]
// An omnivore eats everyone who has more energy (grass and small animals, that is, those who have worse FF)
void C_AO_AEO::OmnivoreBehavior (S_AO_Agent &animal, int indAnimal, int indCoord)
{
  //double Xi = animal.c [indCoord];
  double Xi = animal.cB [indCoord];
  //double X1 = a [popSize - 1].c [indCoord];
  double X1 = a [popSize - 1].cB [indCoord];
  int    j  = u.RNDintInRange (indAnimal + 1, popSize - 1);
  //double Xj = a [j].c [indCoord];
  double Xj = a [j].cB [indCoord];
  double C  = u.LevyFlightDistribution (levisPower);
  double r  = u.RNDprobab ();

  Xi = Xi + C * r * (Xi - X1) + (1.0 - r) * (Xi - Xj);

  animal.c [indCoord] = u.SeInDiSp (Xi, rangeMin [indCoord], rangeMax [indCoord], rangeStep [indCoord]);
}
//——————————————————————————————————————————————————————————————————————————————

これでアルゴリズムのコード実装が完了したので、いよいよテスト関数を使ってその動作を確認していきます。

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.6991675795357223
25 Hilly's; Func runs:10000; result:0.34855292688850514
500 Hilly's; Func runs:10000; result:0.253085011547826
=============================
5 Forest's; Func runs:10000; result:0.6907505745478882
25 Forest's; Func runs:10000; result:0.23365521509528495
500 Forest's; Func runs:10000; result:0.1558073538195803
=============================
5 Megacity's; Func runs:10000; result:0.5430769230769231
25 Megacity's; Func runs:10000; result:0.20676923076923082
500 Megacity's; Func runs:10000; result:0.1004461538461546
=============================
All score:3.23131 (35.90%)

アルゴリズムはテスト時に約36%のスコアを記録しました。これは平均的な結果です。この結果を受けて、私はMovingメソッドの見直しをおこなうことにしました。以下は、その改良後の内容です。

Movingメソッドにおけるエージェント移動ロジックの修正点（行動モデル：生産・消費・分解を考慮）

1. 初期集団の初期化処理はこれまで通り変更なしで維持されます。

2. αは現在のエポック数epochNowに応じて減少する関数として計算されます。この比率の計算は、別のprivateメソッドから独立してMoving内で直接行われるようになりました。

3. 生成(consModel == 0)フェーズ：この段階では、エージェントは前の状態とランダム値に基づく式を用いて座標を更新し、新しい状態を「生み出す」ことが可能になります。

4. 消費(consModel == 1) フェーズ：ここでは、ランダム値に応じてエージェントを3つのグループに分けます。

  • 草食動物
  • 肉食動物
  • 雑食動物

5. 分解フェーズ：この段階では、エージェント同士が相互作用し、ランダム値や他エージェントとの関係に基づいて座標を変更します。これにより、探索空間内で新たな位置への移動がおこなわれます。

6. 消費モデルのリセット：consModelは再度0に設定され、次のループが開始される準備が整います。

このように、アルゴリズムの主な変更点は「生産」フェーズを独立したステージとして明確に切り分けたことです。このステージにより、集団に対して大きな揺さぶりが加えられるため、多様性が確保されやすくなります。可視化してAEOの挙動を観察した際にもこの影響は顕著で、「点滅」が確認できます。つまり、人工生態系の個別フェーズが視覚的にも明確に識別できるようになりました。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEO::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double α = (1.0 - (double)epochNow / epochs);

  double Xi   = 0.0;
  double Xb   = 0.0;
  double Xr   = 0.0;
  double Xj   = 0.0;
  double C    = 0.0;
  int    j    = 0;
  double r    = 0.0;

  // Production --------------------------------------------------------------
  // X(t + 1) = (1 - α) * Xb(t) + α * Xrnd (t)
  // α = (1 - t / T) * rnd [0.0; 1.0]
  // Xrnd = rnd [Xmin; Xmax]
  if (consModel == 0)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Xb = cB [c];
        Xr = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        //Xi = Xb + α * (Xr - Xb);
        Xi = Xb + α * (Xb - Xr);

        a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    consModel++;
    return;
  }

  // Consumption --------------------------------------------------------------- 
  if (consModel == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      if (i > 1)
      {
        for (int c = 0; c < coords; c++)
        {
          r = u.RNDprobab ();

          // Herbivore behavior ------------------------------------------------ 
          //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xb (t));
          if (r < 0.333)
          {
            C  = u.LevyFlightDistribution (levisPower);
            Xb = cB [c];
            //Xi = a [i].c [c];
            Xi = a [i].cB [c];

            //Xi = Xi + C * (Xi - Xb);
            Xi = Xi + C * (Xb - Xi);
          }
          else
          {
            // Carnivore behavior ---------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * (Xi (t) - Xj (t));
            if (r < 0.667)
            {
              C  = u.LevyFlightDistribution (levisPower);
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];

              //Xi = Xi + C * (Xi - Xj);
              Xi = Xi + C * (Xj - Xi);
            }
            // Omnivore behavior ----------------------------------------------- 
            //Xi (t + 1) = Xi (t) + C * r2 * (Xi (t) - Xb (t)) +
            //                    (1 - r2) * (Xi (t) - Xj (t));
            else
            {
              C  = u.LevyFlightDistribution (levisPower);
              Xb = cB [c];
              j  = u.RNDminusOne (i);
              //Xj = a [j].c [c];
              Xj = a [j].cB [c];
              //Xi = a [i].c [c];
              Xi = a [i].cB [c];
              r = u.RNDprobab ();

              //Xi = Xi + C * r * (Xi - Xb) +
              //     (1 - r) * (Xi - Xj);
              Xi = Xi + C * r * (Xb - Xi) +
                   (1 - r) * (Xj - Xi);
            }
          }

          a [i].c [c] = u.SeInDiSp (Xi, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }

    consModel++;
    return;
  }

  // Decomposition -------------------------------------------------------------
  double D = 0.0;
  double h = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    D = 3 * u.RNDprobab ();
    h = u.RNDprobab () * (u.RNDprobab () < 0.5 ? 1 : -1);
    C = u.LevyFlightDistribution (levisPower);
    j = u.RNDminusOne (popSize);

    for (int c = 0; c < coords; c++)
    {
      double x = a [i].cB [c] + D * (C * a [i].cB [c] - h * a [j].c [c]);
      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  consModel = 0;
}
//——————————————————————————————————————————————————————————————————————————————


テスト結果

次に、ロジックを変更してアルゴリズムを再度テストできます。 

AEO|Artificial Ecosystem-based Optimization Algorithm|50.0|10.0|
=============================
5 Hilly's; Func runs:10000; result:0.9137986747745103
25 Hilly's; Func runs:10000; result:0.4671288391599192
500 Hilly's; Func runs:10000; result:0.2647022528159094
=============================
5 Forest's; Func runs:10000; result:0.9022293417142482
25 Forest's; Func runs:10000; result:0.4370486099190667
500 Forest's; Func runs:10000; result:0.2139965996985526
=============================
5 Megacity's; Func runs:10000; result:0.6615384615384616
25 Megacity's; Func runs:10000; result:0.30799999999999994
500 Megacity's; Func runs:10000; result:0.28563076923076974
=============================
All score:4.45407 (49.49%)

結果に大きなばらつきが見られない点は注目に値します。収束精度は平均的ではあるものの、アルゴリズムは局所的な最適解に陥ることなく、うまく回避しています。また、ステージの切り替え時には、先述の「点滅」現象が視覚的にも確認できます。特に離散Megacity関数においては、他とは異なる非常にユニークな挙動を示し、座標群が、関数の重要領域を通過する垂直線や対角線上に分かれる様子が見られます。これは結果にも明確に表れており、1,000変数を持つ離散関数における評価表で、最も高い成績を記録しています。

Hilly

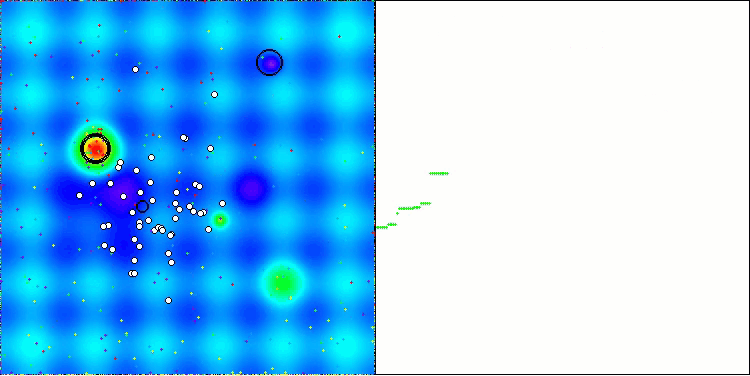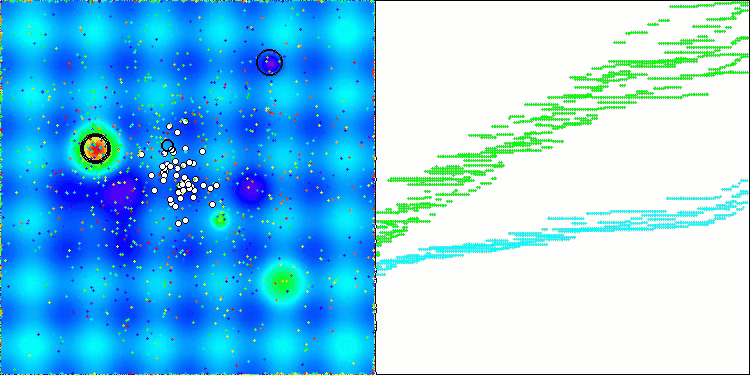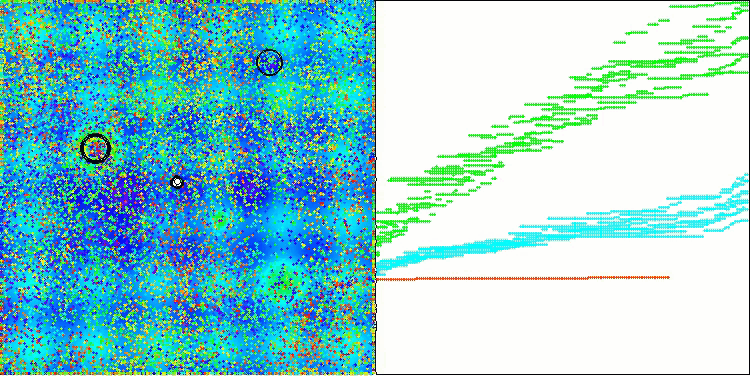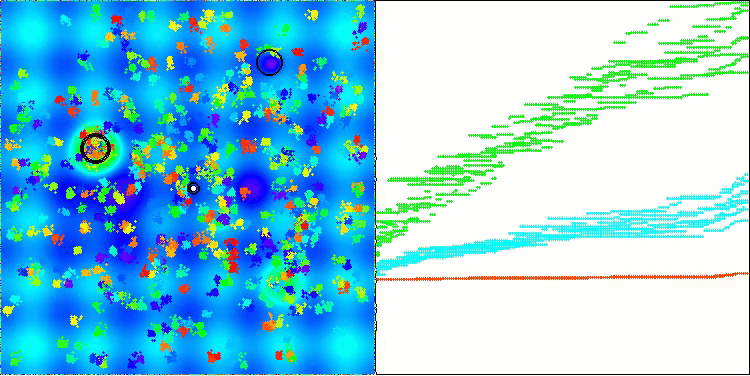
Hillyテスト関数のAEO

Forest

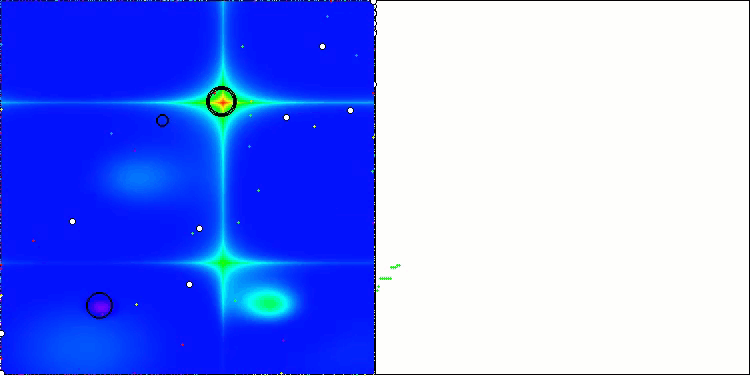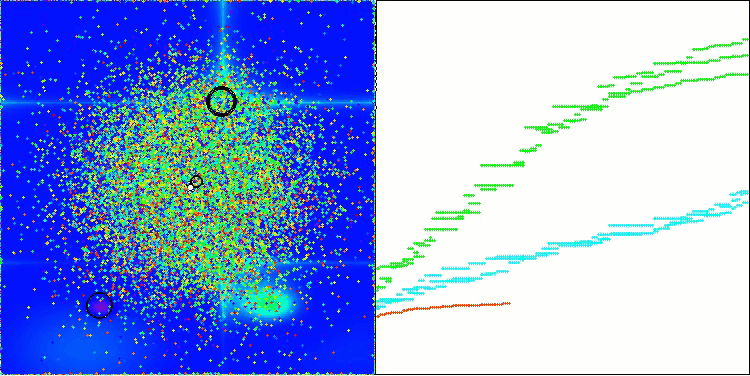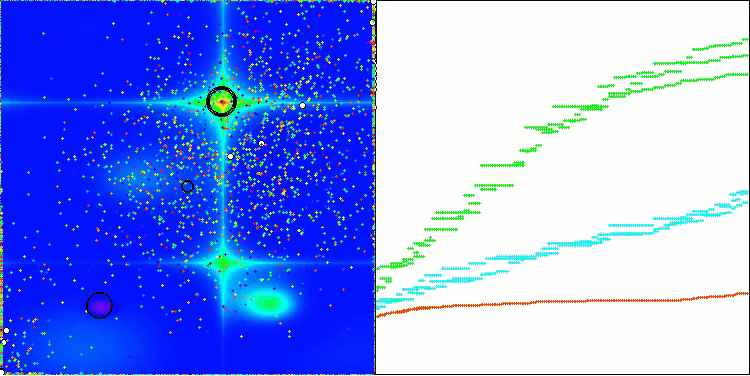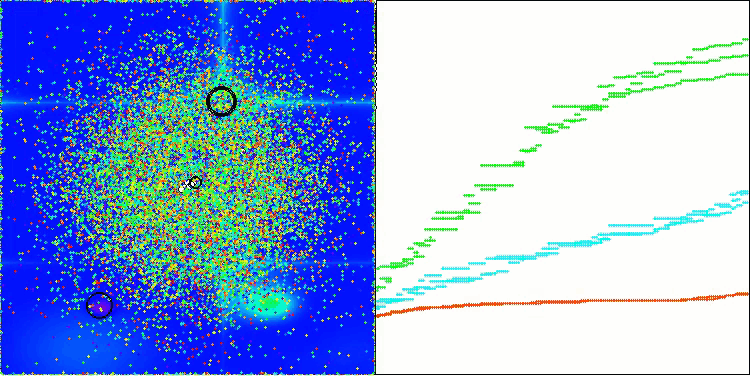
Forestテスト関数のAEO

Megacity

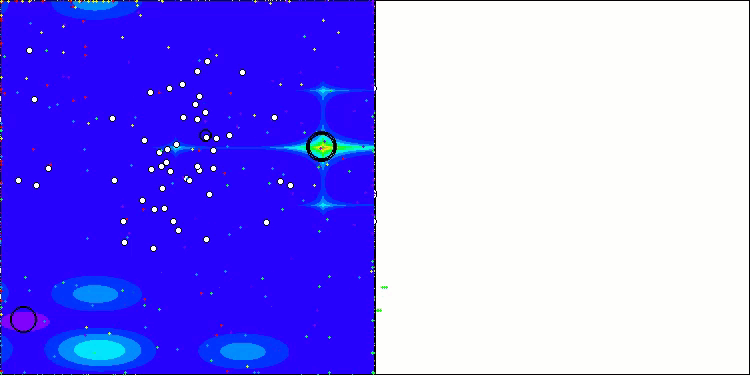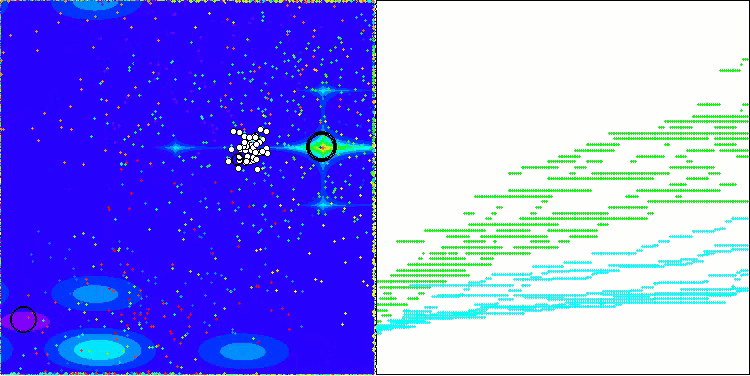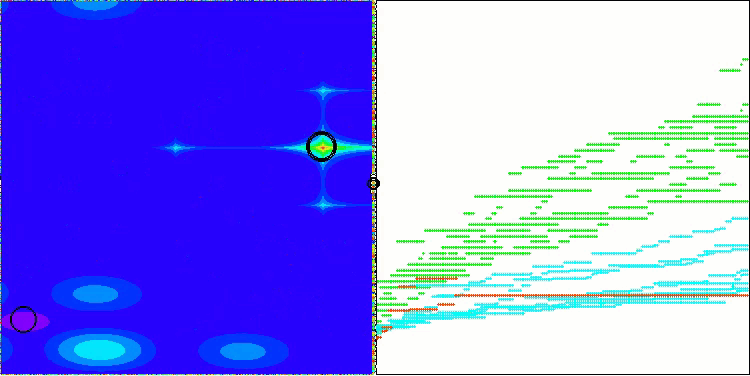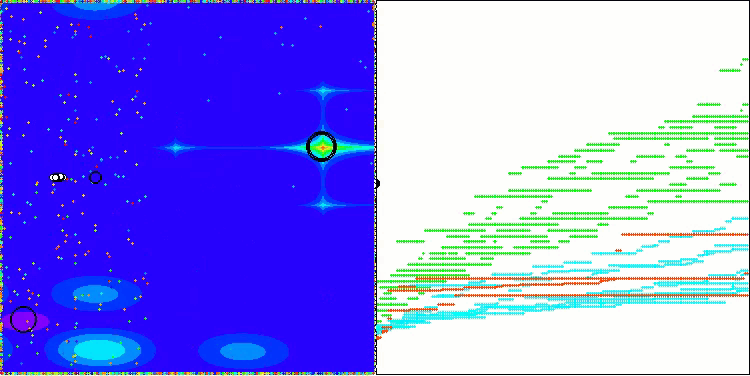
Megacityテスト関数のAEO

ご覧のとおり、アルゴリズムは元のバージョンと比較して性能が大幅に向上し、現在では最大値の約50％に達するまでになっています。これは非常に優れた結果と言えるでしょう。評価表では第25位にランクインしており、これも十分に注目に値します。特に特筆すべき点は、AEOが離散メガシティ関数において新たな記録を打ち立て、1000パラメータの結果を実に5％も上回ったことです。

#
AO
詳細
Hilly
Hilly最終
Forest
Forest最終
Megacity（離散）
Megacity最終
最終結果
MAXの%
10 p (5 F) 50p(25F) 1000p(500F) 10 p (5 F) 50p(25F) 1000p(500F) 10 p (5 F) 50p(25F) 1000p(500F)
1 ANS 近隣検索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA コードロックアルゴリズム（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 動物の移動最適化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星の尾アルゴリズム（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会集団の進化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA シミュレーテッド等方性焼鈍法（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 無政府社会の最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA タートルシェル進化アルゴリズム（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差異進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS ハーモニーサーチ 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 苗木の播種と成長 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
20 (PO)ES （PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
21 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
22 BSO ブレインストーミング最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
23 WOAm ウェール最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
24 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
25 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
26 ACOm アリコロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
27 BFO-GA 細菌採餌最適化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
28 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
29 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
30 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
31 ASBO 適応型社会行動最適化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
32 MEC 心の進化計算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
33 IWO 侵入雑草の最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
34 Micro-AIS マイクロ人工免疫システム 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
35 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
36 SDOm スパイラルダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
37 NMm ネルダー・ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
38 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
39 GSA 重力探索アルゴリズム 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
40 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
41 ABC 人工蜂のコロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
42 BA バットアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
43 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
44 SA シミュレーテッドアニーリング 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
45 IWDm インテリジェントウォータードロップM 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06


まとめ

アルゴリズムの特徴と利点

1. 探索と活用のバランス解空間の全体的な探索（生産と消費フェーズ）と、局所的な活用（分解フェーズ）の間で優れたバランスを提供

2. 適応力：異なる解の更新戦略を通じて、問題の地形に柔軟に適応

3. シンプルさ：生物学的なメタファーを用いているものの、アルゴリズム自体は比較的実装が容易で、理解しやすい構造を持っている

4. 特に大規模な変数数を持つ離散関数において、非常に優れた最適化結果を示す

tab

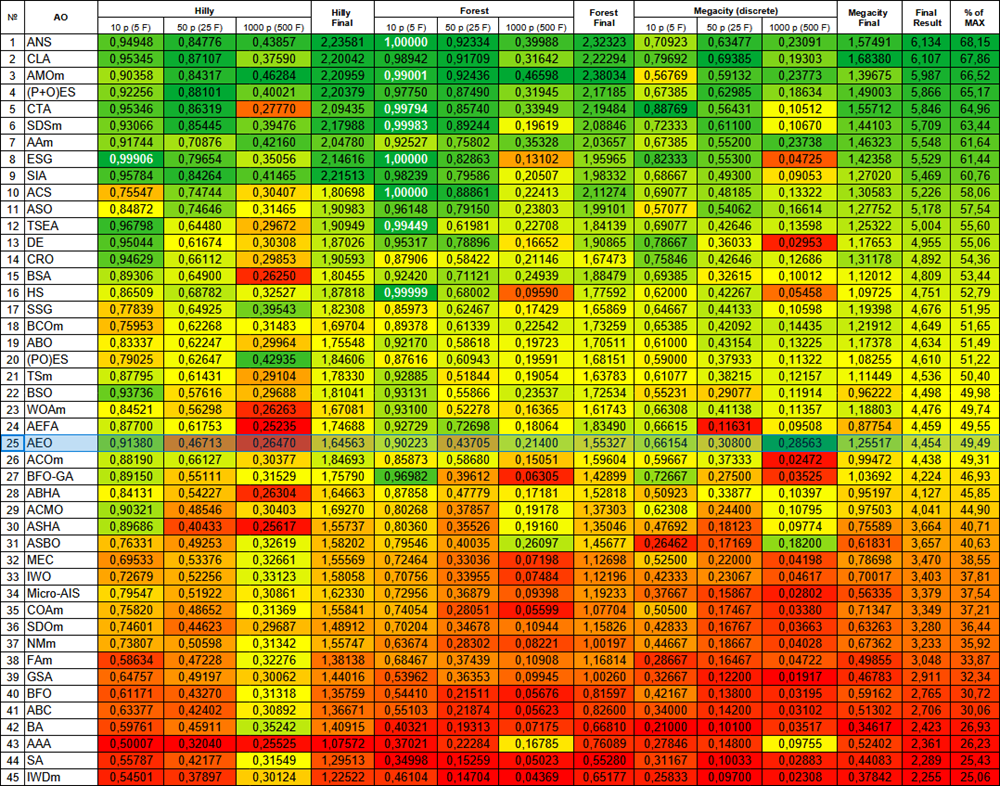
図2：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

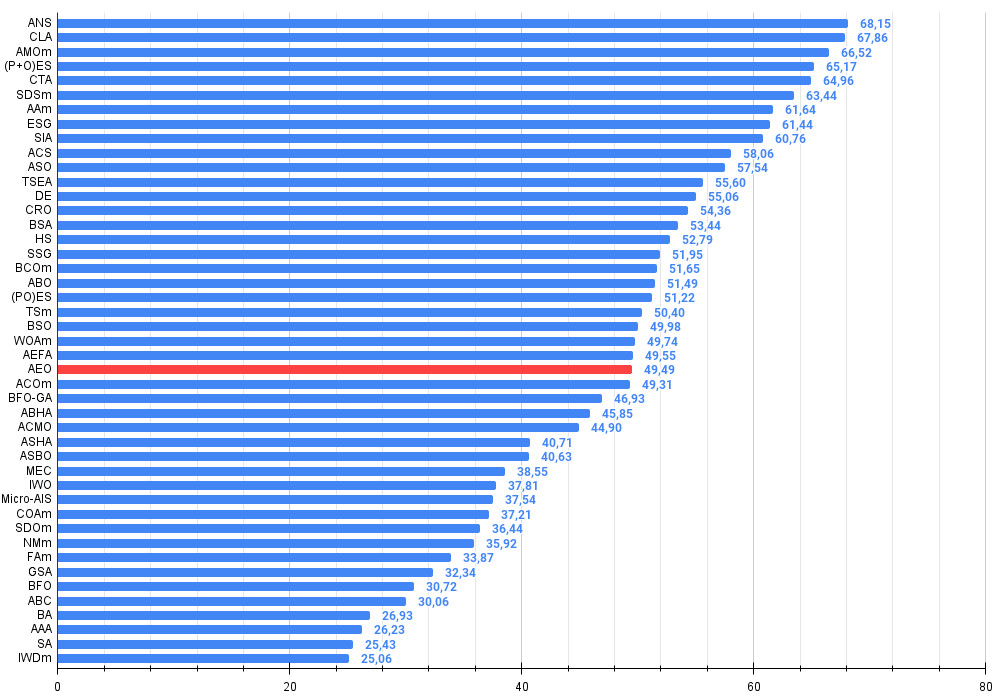
図3：アルゴリズムテスト結果のヒストグラム（0～100のスケール、数値が高いほど良い

ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている）

AEO の長所と短所

長所

  1. 外部パラメータは1つのみ（集団サイズを除く）
  2. 離散関数で良好なパフォーマンスを発揮

短所

  1. 収束精度がそれほど高くない

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16058

添付されたファイル |
ZIPをダウンロード
AEO.zip (36.96 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
初級から中級まで：配列(I) 初級から中級まで：配列(I)
この記事は、これまでに議論してきた内容と、新たな研究段階との橋渡しとなるものです。この記事を理解するためには、前回までの記事を読んでおく必要があります。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。
リプレイシステムの開発（第69回）：正しい時間を知る(II) リプレイシステムの開発（第69回）：正しい時間を知る(II)
今日は、iSpread機能がなぜ必要なのかについて考察します。同時に、ティックが1つも存在しない状況で、システムがどのようにバーの残り時間を通知するのかについても理解を深めていきます。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。
MQL5取引ツールキット（第6回）：直近で約定された予約注文に関する関数で履歴管理EX5ライブラリを拡張 MQL5取引ツールキット（第6回）：直近で約定された予約注文に関する関数で履歴管理EX5ライブラリを拡張
EX5モジュールで、直近で約定された予約注文のデータをシームレスに取得・格納するエクスポート可能な関数を作成する方法を学びます。このステップバイステップの包括的なガイドでは、直近で約定された予約注文の重要なプロパティ（注文タイプ、発注時間、約定時間、約定タイプなど）を取得するための専用かつ機能別の関数群を開発することで、履歴管理EX5ライブラリをさらに強化していきます。これらのプロパティは、予約注文の取引履歴を効果的に管理・分析するうえで重要な情報です。
取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部） 取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部）
前回の記事で開始した、MQL5を使用したRefMask3Dフレームワークの構築作業を引き続き進めていきます。このフレームワークは、点群におけるマルチモーダルインタラクションと特徴量解析を包括的に研究し、自然言語で提供される説明に基づいてターゲットオブジェクトを特定・識別することを目的としています。