取引におけるニューラルネットワーク：2次元接続空間モデル(Chimera)

MetaTrader 5 — トレーディングシステム | YYYY年01月DD日, 07:35

Dmitriy Gizlyk

はじめに

時系列モデリングは、多くの分野で応用される複雑な課題です。医療、金融市場、エネルギーシステムなど、多岐にわたります。汎用的な時系列モデルを構築する上での主な課題は以下の通りです。

時系列におけるマルチスケール依存性の対応：短期の自己相関、季節性、長期トレンドなどを考慮する必要があります。これには、柔軟かつ強力なモデルアーキテクチャが求められます。
多変量時系列における動的・非線形関係の適応的処理：変数間の関係は動的かつ非線形で変化することがあります。文脈依存の相互作用を考慮できるメカニズムが必要です。
手動データ前処理の最小化：構造パターンを自動的に識別し、複雑なパラメータ調整を必要としないモデルが求められます。
計算効率の確保：特に長い時系列を扱う場合、計算資源を効率的に使い、学習コストを削減するアーキテクチャが重要です。

従来の統計手法は、生データの前処理が多く必要で、複雑な非線形依存性を十分に捉えられないことが多くあります。深層ニューラルネットワークは高い表現力を持ちますが、Transformer系のモデルは計算量が二次関数的に増加するため、多数の特徴を持つ多変量時系列への応用が難しいです。また、季節成分や長期トレンドの分離が不得手であったり、事前の仮定に依存しすぎることで、実務上の柔軟性が制限されます。

これらの課題に対して、論文「Chimera:Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models」で提案されたアプローチがChimeraです。Chimeraは二次元状態空間モデル(2D-SSM)を採用しており、時間軸方向と変数軸方向の両方に線形変換を適用します。Chimeraは、時間次元に沿った状態空間モデル、変数次元に沿った状態空間モデル、および次元間の遷移という3つの主要コンポーネントで構成されています。パラメータはコンパクトな対角行列に基づき構成されており、従来の統計モデルや現代的なSSMアーキテクチャの表現を再現可能です。

さらに、Chimeraは適応的離散化を取り入れることで、季節性パターンや動的システムの特性を考慮します。

Chimeraの著者は、分類、予測、異常検出など、さまざまな多変量時系列タスクにわたってフレームワークのパフォーマンスを評価しました。実験結果では、Chimeraが全体的な計算コストを削減しながら、最先端の方法と同等かそれを超える精度を達成することが実証されています。

Chimeraアルゴリズム

状態空間モデル(SSM)は、自己回帰的関係を含む複雑な依存関係を表現できる簡潔さと高い表現力を備えていることから、時系列解析において重要な役割を果たしてきました。これらのモデルは、現在の状態が観測環境の過去の状態に依存するシステムを表現します。しかし従来のSSMは、状態が単一の変数（たとえば時間）のみに依存するシステムを記述するものがほとんどでした。この点が、時間方向と変数方向の両方で依存関係を捉える必要がある多変量時系列への適用を制限していました。

多変量時系列は本質的により複雑であり、複数の変数間の相互依存関係を同時にモデリングできる手法が求められます。このような課題に用いられてきた古典的な二次元状態空間モデル(2D-SSM)は、近年の深層学習手法と比較すると、いくつかの制約を抱えています。主な点は以下のとおりです。

線形依存関係への制限：従来の2D-SSMは線形関係しか扱えず、実世界の多変量時系列に特徴的な複雑で非線形な依存関係を表現する能力が制限されます。
離散的なモデル解像度：これらのモデルはあらかじめ定義された解像度を持つことが多く、データ特性の変化に自動的に適応できません。そのため、季節性や可変解像度のパターンを捉える能力が低下します。
大規模データへの適用の難しさ：実運用では、2D-SSMは大量のデータを効率的に処理できないことが多く、実用性が制限されます。
静的なパラメータ更新：古典的な更新機構は固定的であり、時間とともに変化する動的な依存関係を考慮できません。データが進化し、適応的なアプローチが必要な応用では、これは大きな制約となります。

これに対し、近年急速に発展してきた深層学習手法は、これらの制約の多くを克服する可能性を持っています。非線形な依存関係や時間的ダイナミクスをモデル化できるため、多変量時系列解析において有望な手法です。

Chimeraでは、多変量時系列をモデル化するために2D-SSMを用います。第一の軸は時間、第二の軸は変数に対応し、各状態は時間と変数の両方に依存します。最初のステップとして、連続な2D-SSMを離散化された形式へ変換します。この際、各軸に沿った信号解像度を表すステップサイズΔ1とΔ2を考慮します。零次ホールド(Zero-Order Hold, ZOH)法を用いることで、元のデータは次のように離散化されます。

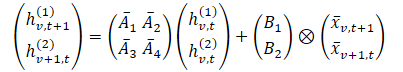
ここで、tとvはそれぞれ時間的次元と変数次元に沿ったインデックスを表します。この式は、より簡潔な形で表現することができます。

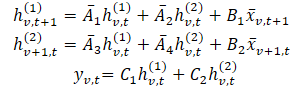
この定式化において、hv,t(1)は時間的情報を保持する隠れ状態であり、各状態は同一変数における前の時間ステップに依存します。A1とA2は、それぞれ過去の時間方向および変数方向にまたがる情報への重み付けを制御します。一方、hv,t(2)は変数間情報を保持する隠れ状態であり、各状態は同一時刻における他の変数に依存します。

時系列データは、多くの場合、背後にある連続的なプロセスからサンプリングされます。その場合、Δ1は時間解像度、あるいはサンプリング周波数として解釈できます。一方、変数軸方向の離散化は、もともと離散的な軸であるため直感的ではありませんが、重要な役割を果たします。1D-SSMにおいて、離散化はRNNのゲート機構と密接に関連しており、モデルの正規化や解像度不変性といった望ましい性質をもたらします。

パラメータ({Ai}, {Bi}, {Ci}, kΔ1, ℓΔ2)を持つ2D離散SSMは、({Ai}, {Bi}, {Ci}, Δ1ℓΔ2)を持つモデルと比較して時間方向にk倍倍の速度で進化し、また ({Ai}, {Bi}, {Ci}, kΔ1, Δ2)を持つモデルと比較して変数方向にℓ倍の速度で進化します。したがって、Δ1はモデルが捉える依存関係の長さを制御するパラメータとみなすことができます。以上の議論から、時間軸方向の離散化は解像度やサンプリング周波数の設定と捉えることができます。Δ1が小さい場合は長期的な推移を捉え、Δ1が大きい場合は季節性パターンを捉えます。

変数軸方向の離散化はRNNのゲート機構に類似しており、Δ2はモデルのコンテキスト長を制御します。Δ2が大きいほどコンテキストウィンドウは小さくなり、変数間相互作用は弱まります。一方、Δ2が小さいほど、変数間の依存関係が強調されます。

表現力を高め、自己回帰的な情報回復を可能にするため、隠れ状態hv,t(1)は過去の時間的情報を保持します。著者らは、行列A1およびA2を構造化された形に制限しています。また、A3およびA4に対しては、単純な対角行列であっても、変数間情報を効果的に統合できることを示しています。

2D-SSMは変数次元に沿って因果的であり（この次元には本質的な順序が存在しないため）、情報の流れに制約が生じます。これに対処するため、Chimera では特徴次元に沿って順方向および逆方向のモジュールを別々に用います。

有効な1D-SSMと同様に、データ非依存の定式化はカーネルKを用いた畳み込みとして解釈できます。これにより並列化が可能となり、学習の高速化が実現されるとともに、Chimeraを近年の畳み込みベースの時系列アーキテクチャと結び付けています。

前述のとおり、パラメータA1とA2は過去の時間方向および変数方向の情報への重み付けを制御します。同様に、Δ1とB1は現在および過去の入力への重み付けを制御します。これらのデータ非依存パラメータは、システム全体のグローバルな特性を表します。しかし、複雑なシステムでは、どの情報を強調すべきかは現在の入力に依存します。そのため、これらのパラメータが元のデータの関数となることが必要です。このようなパラメータ依存性の導入により、Transformerに類似した仕組みで、入力ごとに関連情報を適応的に選択し、不要な情報をフィルタリングすることが可能になります。さらに、データに応じて変数間の情報を適切に混合する能力も求められます。パラメータを入力データに依存させることで、関心のある変数をモデル化するために重要な情報を統合し、無関係な情報を排除できるようになります。Chimeraの技術的貢献のひとつは、Bi、CiおよびΔiを入力𝐱v,tの関数として構成した点にあります。

Chimeraでは、層間に非線形性を挟みながら2D-SSMを積み重ねます。前述の2D-SSMの表現力と可能性をさらに高めるため、深層SSMモデルと同様に、すべてのパラメータを学習可能とし、各層で複数の2D-SSMを用いて、それぞれが異なる役割を担います。

Chimeraは標準的な時系列分解に従い、トレンド成分と季節成分を分離します。また、2D-SSMの独自の特性を活用することで、これらの成分を効果的に捉えます。

Chimeraフレームワークのオリジナルの可視化を以下に示します。

著者によるChimeraフレームワークの可視化

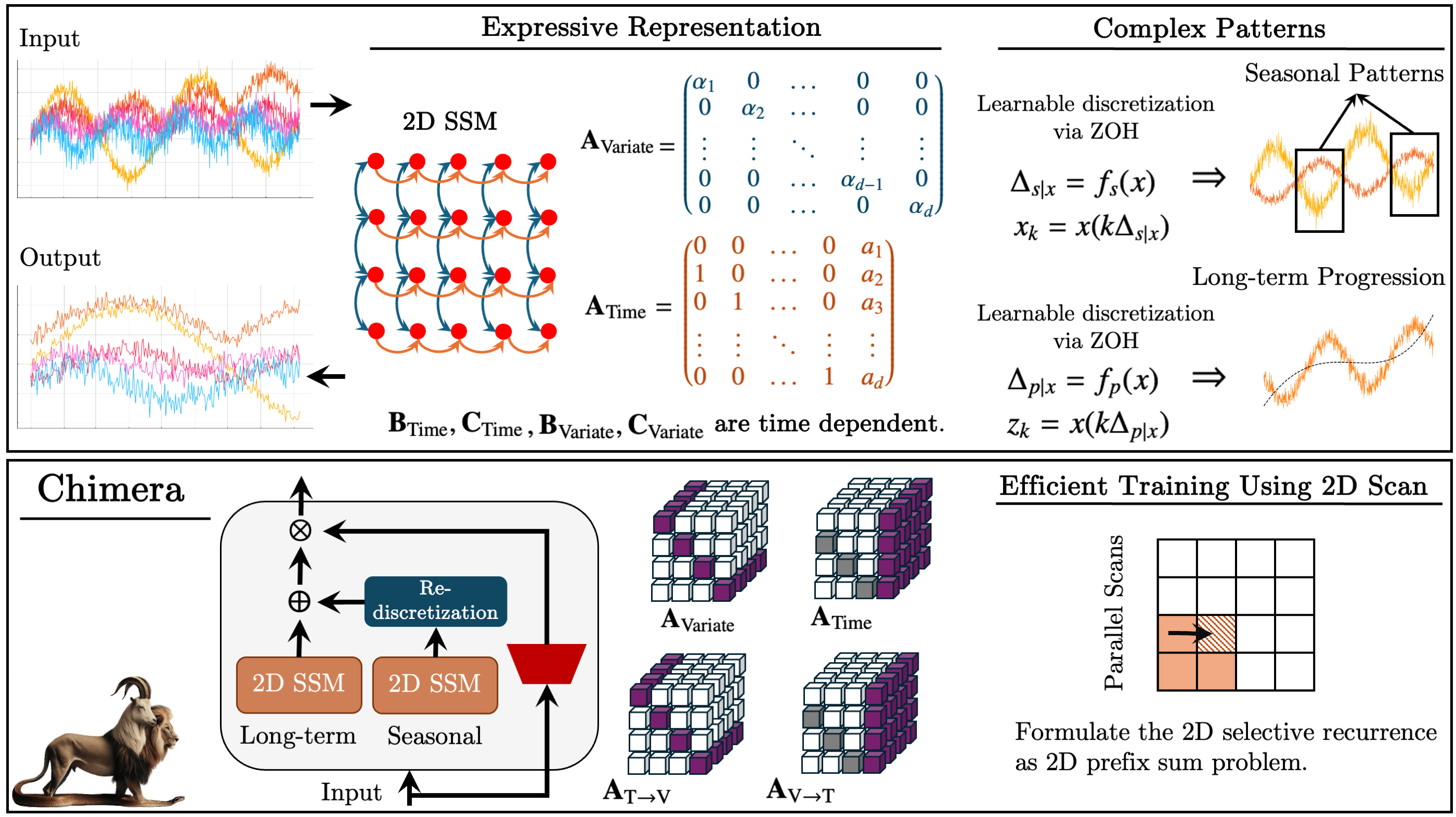
MQL5への実装

Chimeraフレームワークの理論的側面を確認した後、提案されたアプローチに対する独自の解釈を実装する実践的な段階へと進みます。このセクションでは、MQL5プログラミング言語の機能を用いてChimeraの概念をどのように解釈し、実装するかを検討します。ただし、コーディングに入る前に、柔軟性、効率性、そしてさまざまな種類のデータへの適応性を確保するため、モデルアーキテクチャを慎重に設計する必要があります。

アーキテクチャソリューション

Chimeraフレームワークの中核的な構成要素の一つが、隠れ状態に対するアテンション行列{1,…,4}の集合です。著者らは、拡張を伴う対角行列を用いることを提案しており、これにより学習可能なパラメータ数が削減され、計算量も低減されます。このアプローチは、リソース消費を大幅に抑え、モデル学習を高速化します。

しかし、この解決策には制約も存在します。対角行列を使用すると、モデルは系列内の連続する要素間の局所的な依存関係しか解析できず、表現力が制限され、複雑なパターンを捉える能力が低下します。そこで本実装では、完全に学習可能な行列を採用します。これによりパラメータ数は増加しますが、モデルの適応性が大きく向上し、データ内のより複雑な依存関係を捉えることが可能になります。

同時に、この行列アプローチは元の設計における重要な概念、すなわち「行列は学習可能であるが、入力データに直接依存しない」という点を維持しています。これにより、モデルはより汎用的な性質を保つことができ、多変量時系列解析タスクにおいて特に重要となります。

もう一つの重要な側面は、これらの行列を計算プロセスにどのように統合するかです。理論編で述べたように、アテンション行列はニューラルネットワーク層と同様の原理に従って、モデルの隠れ状態と乗算されます。本実装では、各アテンション行列を学習可能なパラメータテンソルとして表現し、畳み込みニューラルネットワーク(CNN)の層として実装することを提案します。標準的なニューラルアーキテクチャに統合することで、既存の最適化アルゴリズムを活用できます。

さらに、4つすべてのアテンション行列を同時に並列計算できるよう、それらを一つの連結テンソルに統合します。この操作に伴い、2つの隠れ状態行列も単一のテンソルに統合する必要があります。

一方で、このアプローチは2D-SSMにおける他のパラメトリック行列すべてに適用できるわけではありません。その制約として、行列構造が固定されることで、複雑な多変量データを処理する際の柔軟性が低下します。モデルの表現力を高めるため、本実装では文脈依存型の行列Bi、Ci、Δiを採用し、入力データに応じて動的に適応させます。これにより、時間的依存関係をより深く解析することが可能になります。

文脈依存型行列は入力データから生成され、データ構造を考慮しながら系列の特性に応じてパラメータを調整します。このアプローチにより、モデルは局所的な依存関係だけでなく、グローバルなトレンドも解析できるようになり、予測や時系列解析タスクにおいて極めて重要となります。

フレームワークの著者らの推奨に従い、これらの行列は、文脈に基づいてパラメータを適応させる役割を担う専用のニューラル層として実装されます。

次のステップは、2D-SSMモデル内における複雑なデータ相互作用の整理です。多変量データ構造は最適化された処理を必要とするため、効率的なリソース管理が求められます。計算効率と性能の要件を満たすため、本実装ではこの処理を独立したOpenCLカーネルとして実装することを決定しました。

このアプローチにはいくつかの利点があります。第一に、GPU上での並列実行によりデータ処理が大幅に高速化され、レイテンシが低減されます。これは、逐次計算では処理が遅くなる大規模データセットにおいて特に重要です。第二に、ハードウェアアクセラレーションを活用できるOpenCLにより効率的な並列化が可能となり、複雑な時系列データのリアルタイム処理を実現できます。

OpenCLプログラムの拡張

アーキテクチャの設計が完了した後、次のステップはコードへの実装です。まず、計算処理を最適化し、モデルコンポーネントとの効果的な相互作用を確保するために、OpenCLプログラムを修正する必要があります。そのために、学習可能な2D-SSMパラメータと入力データとの複雑な相互作用を処理するカーネルSSM2D_FeedForwardを作成します。

このメソッドは、時間および変数の文脈におけるすべてのモデルパラメータと入力射影を含むデータバッファへのポインタを受け取ります。

__kernel void SSM2D_FeedForward(__global const float *ah,
                                __global const float *b_time,
                                __global const float *b_var,
                                __global const float *px_time,
                                __global const float *px_var,
                                __global const float *c_time,
                                __global const float *c_var,
                                __global const float *delta_time,
                                __global const float *delta_var,
                                __global       float *hidden,
                                __global       float *y
                               )
  {
   const size_t n = get_local_id(0);
   const size_t d = get_global_id(1);
   const size_t n_total = get_local_size(0);
   const size_t d_total = get_global_size(1);

カーネル内部では、まず二次元のタスク空間における現在のスレッドを特定します。第一の次元は系列長に対応し、第二の次元は特徴量の次元に対応します。単一の特徴量に対するすべての系列要素は、同一のワークグループにまとめられます。

この段階で重要なのは、学習可能なパラメータの射影と入力データの射影が、カーネルに渡される前のデータ準備段階で正しく整列されていることです。

次に、更新された情報を用いて、両方の文脈における隠れ状態を計算し、その結果を対応するデータバッファに保存します。

//--- Hidden state
   for(int h = 0; h < 2; h++)
     {
      float new_h = ah[(2 * n + h) * d_total + d] + ah[(2 * n_total + 2 * n + h) * d_total + d];
      if(h == 0)
         new_h += b_time[n] * px_time[n * d_total + d];
      else
         new_h += b_var[n] * px_var[n * d_total + d];
      hidden[(h * n_total + n)*d_total + d] = IsNaNOrInf(new_h, 0);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

その後、ワークグループ内のスレッドを同期します。これは、後続の処理でグループ全体の結果が必要となるためです。

続いて、モデルの出力を計算します。このために、文脈行列および離散化行列を、計算済みの隠れ状態と乗算します。この処理を実現するため、時間文脈および変数文脈における対応する行列要素を順に乗算し、その結果を合算するループを構成します。

//--- Output
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float value = 0;
   for(int i = 0; i < n_total; i++)
     {
      value += IsNaNOrInf(c_time[shift_c] * delta_time[shift_c] * hidden[shift_h1], 0);
      value += IsNaNOrInf(c_var[shift_c] * delta_var[shift_c] * hidden[shift_h2], 0);
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

あとは、受け取った値を結果バッファの対応する要素に保存するだけです。

//---
   y[n * d_total + d] = IsNaNOrInf(value, 0);
  }

次に、バックプロパゲーションのプロセスをアレンジする必要があります。対応するニューラル層を用いてパラメータを最適化し、それらの間で誤差勾配を分配するためにSSM2D_CalcHiddenGradientカーネルを作成します。このカーネルの本体では、上述したアルゴリズムと逆の処理を実装します。

このカーネルのパラメータには、同一の行列群へのポインタに加えて、誤差勾配用のバッファが含まれます。多数のバッファによる混乱を避けるため、誤差勾配に対応するバッファにはgrad_という接頭辞を付けています。

__kernel void SSM2D_CalcHiddenGradient(__global const float *ah,
                                       __global       float *grad_ah,
                                       __global const float *b_time,
                                       __global       float *grad_b_time,
                                       __global const float *b_var,
                                       __global       float *grad_b_var,
                                       __global const float *px_time,
                                       __global       float *grad_px_time,
                                       __global const float *px_var,
                                       __global       float *grad_px_var,
                                       __global const float *c_time,
                                       __global       float *grad_c_time,
                                       __global const float *c_var,
                                       __global       float *grad_c_var,
                                       __global const float *delta_time,
                                       __global       float *grad_delta_time,
                                       __global const float *delta_var,
                                       __global       float *grad_delta_var,
                                       __global const float *hidden,
                                       __global const float *grad_y
                                      )
  {
//---
   const size_t n = get_global_id(0);
   const size_t d = get_local_id(1);
   const size_t n_total = get_global_size(0);
   const size_t d_total = get_local_size(1);

このカーネルは、フォワードパスのカーネルと同一のタスク空間で実行されます。ただし、この場合は、特徴次元に沿ってスレッドがワークグループにまとめられます。

計算を開始する前に、中間値やデータバッファ内のオフセットを保持するためのいくつかのローカル変数を初期化します。

//--- Initialize indices for data access
   uint shift_c = n;
   uint shift_h1 = d;
   uint shift_h2 = shift_h1 + n_total * d_total;
   float grad_hidden1 = 0;
   float grad_hidden2 = 0;

次に、出力バッファから隠れ状態へ、さらに文脈行列および離散化行列へと、モデル最終出力への寄与に応じて誤差勾配を分配するループを構成します。同時に、誤差勾配は時間文脈と変数文脈の両方に分配されます。

//--- Backpropagation: compute hidden gradients from y
   for(int i = 0; i < n_total; i++)
     {
      float grad = grad_y[i * d_total + d];
      float c_t = c_time[shift_c];
      float c_v = c_var[shift_c];
      float delta_t = delta_time[shift_c];
      float delta_v = delta_var[shift_c];
      float h1 = hidden[shift_h1];
      float h2 = hidden[shift_h2];
      //-- Accumulate gradients for hidden states
      grad_hidden1 += IsNaNOrInf(grad * c_t * delta_t, 0);
      grad_hidden2 += IsNaNOrInf(grad * c_v * delta_v, 0);
      //--- Compute gradients for c_time, c_var, delta_time, delta_var
      grad_c_time[shift_c] += grad * delta_t * h1;
      grad_c_var[shift_c]  += grad * delta_v * h2;
      grad_delta_time[shift_c] += grad * c_t * h1;
      grad_delta_var[shift_c]  += grad * c_v * h2;
      //--- Update indices for the next element
      shift_c += n_total;
      shift_h1 += d_total;
      shift_h2 += d_total;
     }

続いて、誤差勾配をアテンション行列へ伝播させます。

//--- Backpropagate through hidden -> ah, b_time, px_time
   for(int h = 0; h < 2; h++)
     {
      float grad_h = (h == 0) ? grad_hidden1 : grad_hidden2;
      //--- Store gradients in ah (considering its influence on two elements)
      grad_ah[(2 * n + h) * d_total + d] = grad_h;
      grad_ah[(2 * (n_total + n) + h) * d_total + d] = grad_h;
     }

さらに、それを入力データの射影へと伝播させます。

//--- Backpropagate through px_time and px_var (influenced by b_time and b_var)
   grad_px_time[n * d_total + d] = grad_hidden1 * b_time[n];
   grad_px_var[n * d_total + d] = grad_hidden2 * b_var[n];

行列Biに対する誤差勾配は、すべての次元にわたって集約する必要があります。そのため、まず対応する誤差勾配バッファをゼロクリアし、ワークグループ内のスレッドを同期します。

   if(d == 0)
     {
      grad_b_time[n] = 0;
      grad_b_var[n] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);

次に、ワークグループ内の各スレッドから値を加算します。

//--- Sum gradients over all d for b_time and b_var
   grad_b_time[n] += grad_hidden1 * px_time[n * d_total + d];
   grad_b_var[n] += grad_hidden2 * px_var[n * d_total + d];
  }

これらの演算結果は、それぞれ対応するグローバルデータバッファに書き込まれ、カーネルの実行が完了します。

これで、OpenCL側の実装作業は完了です。完全なソースコードは添付ファイルに記載されています。

2D-SSMオブジェクト

OpenCL側の処理が完了した後、次のステップはメインプログラム内で2D-SSM構造を構築することです。そこで、必要なアルゴリズムを実装するクラスCNeuron2DSSMOCLを作成します。新しいクラスの構造を以下に示します。

class CNeuron2DSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindowOut;
   uint                 iUnitsOut;
   CNeuronBaseOCL       cHiddenStates;
   CLayer               cProjectionX_Time;
   CLayer               cProjectionX_Variable;
   CNeuronConvOCL       cA;
   CNeuronConvOCL       cB_Time;
   CNeuronConvOCL       cB_Variable;
   CNeuronConvOCL       cC_Time;
   CNeuronConvOCL       cC_Variable;
   CNeuronConvOCL       cDelta_Time;
   CNeuronConvOCL       cDelta_Variable;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForwardSSM2D(void);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradientsSSM2D(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuron2DSSMOCL(void)  {};
                    ~CNeuron2DSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuron2DSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

このオブジェクト構造には、おなじみの仮想オーバーライドメソッド群と、比較的多数の内部オブジェクトが含まれています。オブジェクト数が多いこと自体は想定どおりであり、モデルアーキテクチャによって必然的に決まるものです。オブジェクトの役割の一部は名前から推測できますが、各オブジェクトの機能については、クラスメソッドの実装過程でより詳細に説明します。

すべての内部オブジェクトは静的として宣言されているため、コンストラクタとデストラクタを空のままにすることができます。このアプローチの利点については、これまでにも述べてきました。これらの宣言済みおよび継承されたオブジェクトの初期化は、Initメソッド内でおこなわれます。

bool CNeuron2DSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint window_in, uint window_out, uint units_in, uint units_out,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_out,
                                                       optimization_type, batch))
      return false;
   SetActivationFunction(None);

このメソッドは、生成されるオブジェクトのアーキテクチャを定義する複数の定数を引数として受け取ります。これには、入力データと期待される出力の次元、すなわち{units_in, window_in}と{units_out, window_out}が含まれます。

メソッド内部では、まず親クラスのメソッドを呼び出し、期待される出力次元を渡します。親クラスのメソッドは、継承されたオブジェクトおよびインターフェースに対する必要な制御ブロックと初期化アルゴリズムをすでに実装しています。これが正常に完了した後、結果テンソルの次元を内部変数に保存します。

   iWindowOut = window_out;
   iUnitsOut = units_out;

前述のとおり、OpenCL側でカーネルを構築する際には、両方の文脈における入力射影が同等の形状を持つ必要があります。本実装では、それらを結果テンソルの次元に合わせています。まず、時間文脈における入力射影モデルを作成します。

多変量時系列のユニット系列内の情報を保持するため、一次元系列を独立にターゲットサイズへ射影します。入力データは「行が時間ステップ」に対応する行列として与えられる点に注意が必要です。そのため、ユニット系列を扱いやすくするために、まず入力行列を転置します。

//---
   int index = 0;
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;
//--- Projection Time
   cProjectionX_Time.Clear();
   cProjectionX_Time.SetOpenCL(OpenCL);
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

その後、畳み込み層を適用して単変量系列の次元を調整します。

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iUnitsOut, window_in, 1,
                                                       optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

次に、特徴量次元に沿ってデータを射影します。そのために逆転置をおこないます。

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Time.Add(transp))
     {
      delete transp;
      return false;
     }

そして、畳み込み射影層を適用します。

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iWindowOut, iUnitsOut, 1,
                                                          optimization, iBatch) ||
      !cProjectionX_Time.Add(conv))
     {
      delete conv;
      return false;
     }

同様に、特徴文脈における入力射影も作成します。まず変数軸に沿って射影し、その後転置して時間軸に沿って射影します。

//--- Projection Variables
   cProjectionX_Variable.Clear();
   cProjectionX_Variable.SetOpenCL(OpenCL);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, iUnitsOut, units_in, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, iUnitsOut, optimization, iBatch) ||
      !cProjectionX_Variable.Add(transp))
     {
      delete transp;
      return false;
     }

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, iWindowOut, iUnitsOut, 1,
                                                        optimization, iBatch) ||
      !cProjectionX_Variable.Add(conv))
     {
      delete conv;
      return false;
     }

入力射影モデルの初期化が完了した後、他の内部オブジェクトへと進みます。まず、隠れ状態オブジェクトを初期化します。このオブジェクトは純粋なデータコンテナであり、学習可能なパラメータは含みません。ただし、両方の文脈における隠れ状態データを格納できる十分なサイズが必要です。

//--- HiddenState
   index++;
   if(!cHiddenStates.Init(0, index, OpenCL, 2 * iUnitsOut * iWindowOut, optimization, iBatch))
      return false;

次に、隠れ状態アテンション行列を初期化します。前述のとおり、4つすべての行列は単一の畳み込み層内に実装されており、これにより並列実行が可能になります。

この層の出力は、隠れ状態と4つの独立した行列との積を提供する必要があります。うち2つは時間文脈、残り2つは特徴量文脈で動作します。これを実現するため、入力ウィンドウ数の2倍のフィルタ数を持つ畳み込み層を定義し、2つの独立した系列（時間と特徴量）を処理するように設定します。畳み込み層は独立系列ごとに別々のフィルタ行列を使用するため、この構成により4つのアテンション行列が生成され、それぞれが異なる文脈で動作します。

//--- A*H
   index++;
   if(!cA.Init(0, index, OpenCL, iWindowOut, iWindowOut, 2 * iWindowOut, iUnitsOut, 2,
                                                                optimization, iBatch))
      return false;

大きなアテンションパラメータは勾配爆発を引き起こす可能性があるため、ランダム初期化後にパラメータを10分の1にスケーリングします。

if(!SumAndNormilize(cA.GetWeightsConv(), cA.GetWeightsConv(), cA.GetWeightsConv(),
                                               iWindowOut, false, 0, 0, 0, 0.05f))
   return false;

次のステップは、入力データの関数として定義される適応的な文脈依存行列Bi、Ci、Δiの生成です。本実装では、対応する文脈の入力射影を受け取り、必要な行列を出力する畳み込み層を用いて生成します。

//--- B
   index++;
   if(!cB_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                         optimization, iBatch))
      return false;
   cB_Time.SetActivationFunction(TANH);
   index++;
   if(!cB_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, 1, iUnitsOut, 1, 
                                                            optimization, iBatch))
      return false;
   cB_Variable.SetActivationFunction(TANH);

このアプローチはRNNのゲート機構に類似しています。BiとCiには双曲線正接関数(tanh)を活性化関数として使用し、正負の依存関係の両方を表現できるようにします。

//--- C
   index++;
   if(!cC_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                optimization, iBatch))
      return false;
   cC_Time.SetActivationFunction(TANH);
   index++;
   if(!cC_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cC_Variable.SetActivationFunction(TANH);

Δi行列は学習可能な離散化を実装するものであり、負の値を含んではなりません。そのため、ReLUの滑らかな近似であるSoftPlusを活性化関数として使用します。

//--- Delta
   index++;
   if(!cDelta_Time.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                    optimization, iBatch))
      return false;
   cDelta_Time.SetActivationFunction(SoftPlus);
   index++;
   if(!cDelta_Variable.Init(0, index, OpenCL, iWindowOut, iWindowOut, iUnitsOut, iUnitsOut, 1,
                                                                        optimization, iBatch))
      return false;
   cDelta_Variable.SetActivationFunction(SoftPlus);
//---
   return true;
  }

すべての内部オブジェクトの初期化が完了すると、このメソッドは論理値を呼び出し元のプログラムへ返します。

本日は大きく前進しましたが、作業はまだ完了していません。次回の記事に進む前に、短い休憩を取ることをおすすめします。次回は、必要なオブジェクトの構築を最終化し、それらをモデルに統合したうえで、実際の過去データを用いて実装したアプローチの有効性を検証します。

結論

本記事では、時間次元と特徴次元の両方にまたがる依存関係を扱うための新しいアプローチを導入した、Chimera二次元状態空間モデルフレームワークについて解説しました。Chimeraは二次元状態空間モデル(2D-SSM)を用いることで、長期的なトレンドと季節性パターンの双方を効率的に捉えることが可能です。

実践セクションでは、MQL5を用いて本フレームワークの独自解釈による実装を開始しました。一定の進展は得られたものの、実装はまだ完了していません。次回の記事では、提案されたアプローチの構築を引き続き進めるとともに、実際の過去データセットを用いて、実装した手法の有効性を検証していく予定です。

参照文献

記事で使用されているプログラム

#	名前	種類	説明
1	Research.mq5	EA	サンプル収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いたサンプル収集用EA
3	Study.mq5	EA	モデル学習用EA
4	Test.mq5	EA	モデルテスト用EA
5	Trajectory.mqh	クラスライブラリ	システム状態とモデルアーキテクチャ記述構造
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコード

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/17210

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2458.91 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

EAのサンプル

一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。

多通貨エキスパートアドバイザーの開発（第22回）：設定のホットスワップへの移行を開始する

定期的な最適化を自動化するのであれば、取引口座上ですでに稼働しているEAの設定を自動更新することについても検討する必要があります。これにより、ストラテジーテスター内でエキスパートアドバイザー(EA)を実行しながら、単一の実行の中でその設定を変更できるようにする必要があります。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

円探索アルゴリズム(CSA)

本記事では、円の幾何学的性質に基づいた新しいメタヒューリスティック最適化アルゴリズム「円探索アルゴリズム(Circle Search Algorithm, CSA)」を紹介します。本アルゴリズムは、最適解を探索するために点を接線に沿って移動させる原理を使用し、大域探索と局所探索のフェーズを組み合わせています。