
無政府社会最適化(ASO)アルゴリズム
内容
1. はじめに
私はこれまで、社会関係というテーマや、それをアルゴリズムとして構築する可能性に強く魅了されてきました。社会の発展において、これは最も興味深い現象の一つであり、人間関係のシステム構造をアルゴリズムで記述し、それに基づいた最適化アルゴリズムを実装することには、大きな意義と広がりのある研究分野があると考えています。
これまでの記事では、社会的行動のアルゴリズム、つまり社会集団の進化や人工的な協調探索について考察してきました。 本記事では、無政府社会(アナーキスト社会)という概念について掘り下げたいと思います。無政府社会とは、中央集権的な権力やヒエラルキー構造を持たない社会的相互作用のシステムであり、人々が自主的な合意に基づいて生活を組織し、協力し合うことを前提としています。
アナーキスト社会は、自律性と自由の原則に基づいており、個々の人が外部からの干渉を受けることなく、自らの生活について独立して意思決定を行うことができます。また、自発的協力の原則により、すべての参加者の合意のもとで強制なく相互作用がおこなわれ、権利や機会の平等、連帯、相互扶助、協力が重視されます。この概念をアルゴリズムとして実装する試みは非常に興味深いものです。その一例が、無政府社会最適化(Anarchic Society Optimization, ASO)と呼ばれる最適化アルゴリズムです。このアルゴリズムは、Ahmadi-Javidによって提案され、2011年に発表されました。
ASOの核心となるのは、無政府社会における個体の行動に着想を得た最適化手法の開発です。PSO(粒子群最適化)やACO(蟻コロニー最適化)といった、昆虫や動物の群れの行動を基にした既存の群知能アルゴリズムとは異なり、人間社会の構造をモデルにしたアルゴリズム開発には限界があります。なぜなら、秩序立った社会においては、個体が単独の意思決定によって自身の望みを達成することは難しく、また、完全に独立した存在ではないため、短期間で状況を根本的に改善することができないからです。この点に着目したアルゴリズムの考案者は、標準的な社会構造とは異なる、より異質な社会モデルを基盤とするアイデアに着手しました。
ASOの特徴は、変わりやすく冒険的で、安定を好まず、時には非合理的な行動を取る個体の集団を中核に据えている点にあります。これらの個体は、探索過程において過去に訪れた最悪の位置に戻ることもあり、メンバー間の状況の差が大きくなるほど、無秩序な行動の度合いも増していきます。このような個体群を活用することで、ASOは解空間を広く探索し、局所最適に陥るリスクを回避しようとします。ASOの考案者は、一般的な社会の秩序ある行動原理ではなく、むしろ異常ともいえる社会的振る舞いに基づく原則を研究し、それを適用することで、複雑な最適化問題を効率的に解決できるアルゴリズムを生み出せるのではないかと考えました。本記事では、ASOの統一的な枠組みについて考察し、それが連続問題にも離散問題にも容易に適用できることを示していきます。
2. アルゴリズムの実装
アルゴリズムのコードを書く前に、その構造や、考案者がどのような基本的なメカニズムを組み込んでいるのかを理解する必要があります。ASOアルゴリズムは、粒子群最適化(PSO)アルゴリズムの利点と、無秩序な社会行動に特徴的な新しいメカニズムを組み合わせた最適化手法です。適応的な性質を持ち、異なる移動戦略の間でバランスを取る能力があることが、このアルゴリズムの主な特徴となっています。
ASOアルゴリズムの詳細な説明から始めましょう。
1. 初期化
- 集団(popSize)を社会のメンバーとして作成します。
- 各メンバーは探索空間のランダムな位置に初期化されます。
- 各メンバーは個体の最良値と過去の順位を保持します。
2.基本的な最適化ループ
各反復で、社会の各メンバーに対して以下のステップを実行します。
a) 指数の計算
- 気まぐれ指数(FI: Fickleness Index):社会のメンバーの不安定さを反映し、他の個体と比較した際の不満度を測定します。
- 外部不規則性指数(EI: External Irregularity Index):社会における位置の多様性を評価する指数で、大域的最適解からの乖離を示します。
- 内部不規則性指数(II: Internal Irregularity Index):この指数は、反復中の個体の位置の変化を評価し、自己最適解からの乖離を反映します。
b) 移動方針の選択
FI、EI 、II指標を比較し、3つの移動方針のいずれかを選択します。
- 現在の移動方針(CurrentMP)は、慣性と加速度比を用いたPSO方程式を使用します。
- 社会移動方針(SocietyMP)は、無作為に選ばれた社会のメンバーとのクロスオーバーを適用します。
- 過去の移動方針(PastMP)は、個体の以前の位置に関する情報を使用します。
c) 無秩序な行動:個体の位置は、確率anarchyprobで完全にランダム化できます。
d) 位置の更新新しい位置は探索空間の制約と照合されます。
e) 最良位置の更新
- 個体の最良位置pBestは、現在の位置の方が良ければ更新されます。
- 大域的最良位置gBestは、より良い解が新たに見つかった場合に更新されます。
3. パラメータの調整
- 無秩序な行動をとる確率anarchyProbが徐々に減少していきます。
- FIを計算するためのalphaパラメータは徐々に増加します。
- 慣性重みomegaは徐々に減少していきます。
4.アルゴリズムのパラメータ
- popSize:集団のサイズ
- ω、lambda1、lambda2:(PSOのように)CurrentMPで速度を計算するためのパラメータ
- anarchyProb:無秩序な振る舞いをする確率
- α、θ、δ:FI、EI、II指数を計算するためのパラメータ
アルゴリズムはかなり複雑です。ここでは、理解しやすいように、非常にわかりやすく構造的にその動作メカニズムを説明しようと思います。次のステップは、アルゴリズムで使用されている方程式を分析することです。
ASOアルゴリズムの基本式はPSOアルゴリズムから継承されています。速度更新の計算をおこないます。V_i (k+1) = ω * V_i (k) + λ1 * r1 * (P_i (k) - X_i (k)) + λ2 * r2 * (G (k) - X_i (k))、ここで
- V_i (k):反復kにおける粒子iの速度
- X_i (k):反復kにおける粒子iの位置
- P_i (k):反復kの前における粒子iの最良の位置
- G (k):反復kの前における全粒子の最良の位置
- ω :慣性比率
- λ1、λ2 :加速度比
- r1、r2 :区間(0, 1) からの乱数
著者は、PSO方程式は、対応する移動方針と組み合わせルールが定義された場合、一般的なASO構造の特殊なケースであることを指摘しています。オリジナルのバージョンでは、エージェントの前のスピードが計算に含まれていました。現在のスピード値だけを残してアプローチを変更したところ、アルゴリズムのパフォーマンスが顕著に向上しました。
式(1)と式(2)は、ASOアルゴリズムの反復kにおけるコミュニティメンバーiの気まぐれ指数とFIを定義します。これらの方程式は、他の位置と比較して、現在の位置に対する個体の不満の度合いを評価するのに役立ちます。詳しく見ていきましょう。
1. 気まぐれ指数の計算式(1):(kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (Xi (k*)) - f (Xi (k)))./ (f (Xi (k*)) - f (Xi (k)))。
この式は、α(alpha)パラメータで重み付けされた、インデックスiの個体の現在位置が、その個体の最良位置と大域的最適位置とどれだけ異なるかを示しています。
2. 反復kにおけるインデックスiの気まぐれ指標を計算するための式(2):(kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (G (k)) - f (Xi (k)))。
この式は最初の式と似ていますが、異なる目的で使用され、現在位置、最良の個体位置、最良の大域的位置が比較されます。
どちらの方程式も、社会のメンバーの不満の度合いを評価する役割を果たし、最適な解決策を求めて位置を変える方法について、より多くの情報に基づいた決定を下すことを可能にします。
式(3)と式(4)は、アルゴリズムにおける社会メンバーの外部不規則性指数および内部不規則性指数を表しています。
3. 式(3):反復kにおけるインデックスiの外部不規則性指数:(kEI)i = exp (-(θi) (f (G) - f (Xi (k))))
4.式(4):反復kにおけるインデックスiの内部不規則性指数: (kEI)i = 1 - exp (-δi (kD))
ここで、
- (kFI)i:反復kにおけるインデックスiの個体の気まぐれ指数
- α:[0,1]区間の非負のアルファ数
- f (Xi (k)):反復kにおけるインデックスiの目的関数の値
- f (Pi (k)):インデックスiが以前に訪れた最良の位置に対する目的関数の値
- f (Xi (k)):反復kにおける最良の個体の位置に対する目的関数の値
- f (G (k)):反復kの前に社会が訪れた大域的最適位置に対する目的関数の値
- (kEI)i:反復kにおけるインデックスiの個体の外的不規則性の指数
- θi:正のシータ数
- kD :社会における多様性の適切な尺度、例えば個体の目的関数値の変動比率
- δi :正のデルタ数
これらの式は、社会の多様性が高まれば(つまり、個体がより多くの異なる目的関数の値を持てば)、個体がより不規則な行動をとりやすくなることを示しています。この方程式は、ASOアルゴリズムにおける社会メンバーの行動の変動性を評価するために使用され、最適解を探索しながら、より多様で適応的な意思決定をおこなうことを可能にします。
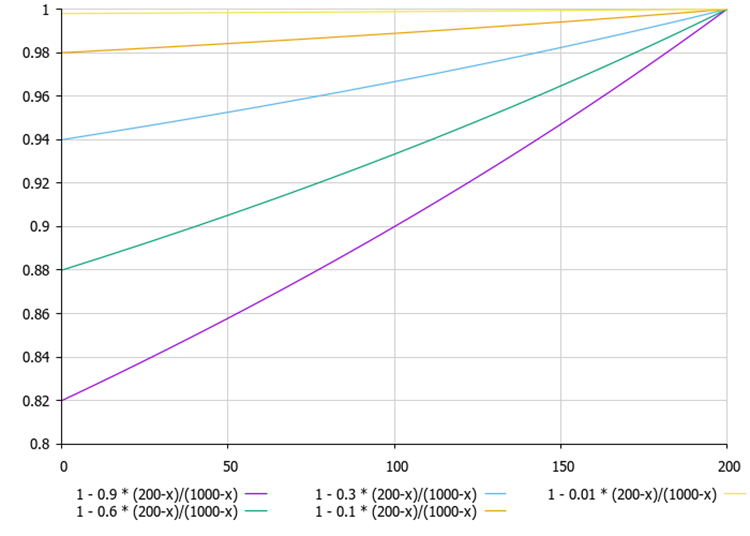
図1:エージェント(200)の現在の最適解がエージェント集団(1000)の最適解よりもはるかに小さい値であれば、グラフの線はほぼ直線的に変化する
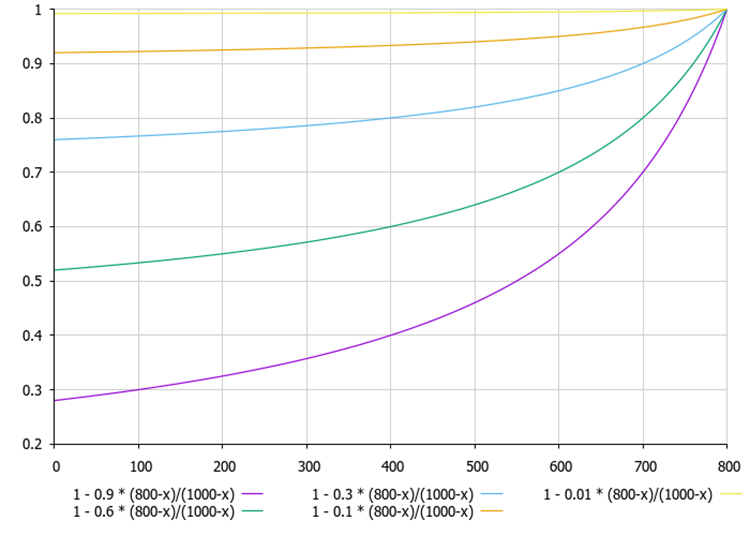
図2:エージェントの集団(1000)によるエージェントの現在の最適解との差が小さいほどグラフ上の線は非線形になる
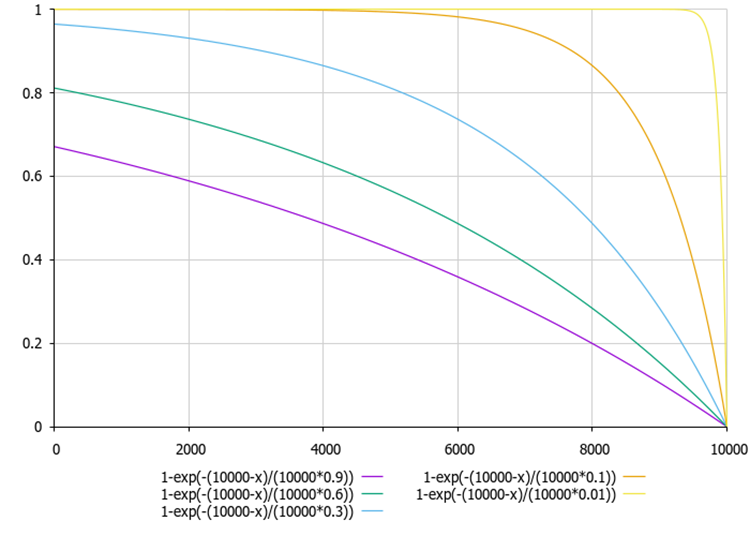
図3:外部指標と内部指標の依存性のグラフと内部θおよびδ比による外部指数と内部凹凸の依存性グラフ(例として0.01から0.9までの値を使用)
したがって、ある社会のメンバーは、他のメンバーに関する情報を使って、自分の動きに関する決定を下すことができます。
さて、ASOアルゴリズムについてもう少しわかったので、得られた理論に基づいて、実践的な部分に移ることができます。コードで実装するために、アルゴリズムの擬似コードを作成します。以下は、ASOアルゴリズムの擬似コードです。
初期化
1. 設定パラメータ:popSize、omega、λ1、λ2、anarchyProb、alpha、theta、delta、rangeMin []、rangeMax []、rangeStep []。
2. 0からpopSize-1までの各iメンバーについて: 0からcoords-1までの各c座標について:
position [i].[c] = rangeMin [c]と rangeMax [c]の間の乱数
pBest [i].[c] = position [i].[c].
prevPosition [i].[c] = position [i].[c].
pBestFitness [i] = -infinity
3. gBest = 初期集団からの最良の位置とします。
4.Set gBestFitness = gBest fitness
メインループ
5. 停止基準に達するまで:0からpopSize-1までの各iメンバーについて:
5.1 インデックスを計算する
FI = CalculateFI (i)
EI = CalculateEI (i)
II = CalculateII (i)
5.2 移動方針の選択
FI > EIかつFI > IIの場合: newPosition = CurrentMP (i)
EI > FIかつEI > IIの場合: newPosition = SocietyMP (i)
そうでない場合: newPosition = PastMP (i)
5.3 無秩序動作を適用する
乱数 < anarchyProbの場合:0からcoords-1までの各c座標について:
newPosition [c] = rangeMin [c] と rangeMax [c]の間の乱数
5.4 各c座標の位置を0からcoords-1まで更新する:
prevPosition [i].[c] = position [i].[c].
position [i].[c] = limit (newPosition [c], rangeMin [c], rangeMax [c], rangeStep [c])
5.5 新しい「適合」を評価する position = rate_fitness (position [i])
5.6 fitness > pBestFitness [i]の場合、個体の最良値を更新する
pBestFitness [i] = fitness
pBest [i] = position [i]
5.7 fitness > gBestFitnessの場合、大域的最良値を更新する
gBestFitness = fitness
gBest = position [i]
5.8 AdaptParameters ()パラメータの調整
5.9 CalculateFI (i)関数: return 1 - alpha * (fitness [i] - pBestFitness [i]) / (gBestFitness - fitness [i])
5.10 CalculateEI (i)関数: return 1 - exp(-(gBestFitness - fitness [i]) / theta)
5.11 CalculateII (i)関数: return 1 - exp(-(pBestFitness [i] - fitness [i]) / delta)
5.12 CurrentMP (i)関数:0からcoords-1までの各c座標:
r1 = 0から1の間の乱数
r2 = 0から1の間の乱数
velocity = omega * (position [i].[c] - pBest [i].[c]) + lambda1 * r1 * (pBest [i].[c] - position [i].[c]) + lambda2 * r2 * (gBest [c] - position [i].[c])
newPosition [c] = position [i].[c] + velocity
return newPosition
5.13 SocietyMP (i)関数:0からcoords - 1までの各c座標に対して、j = iと等しくない集団のランダムなメンバー
乱数 < 0.5の場合:
newPosition [c] = position [i].[c]
そうでない場合: newPosition [c] = position [j][c]
return newPosition
5.14 PastMP (i)関数:0からcoords - 1までの各c座標について:
乱数 < 0.5の場合:
newPosition [c] = position [i].[c]
そうでない場合: newPosition [c] = prevPosition [i][c].
return newPosition
擬似コードができたので、それに基づいてアルゴリズムのコードを書き始めることができます。アルゴリズムの参加者(エージェント)を表すために使用されるS_ASO_Member構造体について説明します。
1. 構造体フィールド
- pPrev []:参加者の前の位置の配列
- pBest []:参加者の最良位置(個体の最良値)の配列
- pBestFitness:最もよく知られている位置の適合値(品質)を格納する変数
2. Initメソッドは、coordsパラメータとして渡された座標の数(または探索空間の次元数)に応じて、pPrev配列とpBest配列のサイズを設定して初期化します。ArrayResize(pBest, coords)およびArrayResize(pPrev, coords):これらの呼び出しは、配列のサイズをcoordsの値に変更します。pBestFitness = -DBL_MAX:最適な位置の適合の初期値を設定し、見つかった値がこの値よりも良くなるようにします。
S_ASO_Member構造体は、最適化アルゴリズムの各参加者に関する情報を格納するために設計されています。これにより、参加者の現在位置と最良位置、そして体力を追跡することができます。
//—————————————————————————————————————————————————————————————————————————————— struct S_ASO_Member { double pPrev []; // Previous position double pBest []; // Personal best position double pBestFitness; // Personal best fitness void Init (int coords) { ArrayResize (pBest, coords); ArrayResize (pPrev, coords); pBestFitness = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスをC_AO基底クラスから継承して定義します。もう少し詳しく見てみましょう。
1. そのパラメータは次の通りです。
- popSize :集団のサイズ(社会のメンバー数)
- anarchyProb:無秩序な振る舞いの可能性。一部の参加者が他の参加者から独立して行動する可能性がありまる。
- ω、λ1、λ2:慣性と加速度に関するパラメータで、参加者の行動を制御するために使用されます。
- alpha、theta、delta:指標(FI、EI、II)の計算に使用されるパラメータ
2.params:パラメータの配列。各要素には名前と値が含まれます。
3. SetParams ():このメソッドは、params配列からパラメータ値を更新し、初期化後にアルゴリズムのパラメータを変更できるようにします。
4.Init ():このメソッドは、与えられた範囲とステップでアルゴリズムを初期化します。rangeMinP、rangeMaxP、rangeStepPの各配列と、epochsPのエポック数を受け取ります。
5. Moving()とRevision()メソッドは、最適化における参加者の移動とその修正(更新)の基本ロジックを実装します。
6. クラスのフィールド
S_ASO_Member member []:アルゴリズムの各参加者に関する情報を格納する社会メンバーの配列
7. privateメソッド
- CalculateFI:特定の参加者のFI(適合性インジケーター)値を計算するメソッド
- CalculateEI:EI(探査指標)の計算メソッド
- CalculateII - II(慣性インジケーター)の値を計算するメソッド
- CurrentMP、SocietyMP、PastMP :参加者の現在、社会、過去の位置との相互作用のロジックを実装するメソッド
C_AO_ASOクラスは、参加者が共同でも独立でも行動できる「無政府社会」の概念を実装したもので、参加者の行動を制御するパラメータと、その初期化と更新のためのメソッドを含んでいます。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASO () { } C_AO_ASO () { ao_name = "ASO"; ao_desc = "Anarchy Society Optimization"; ao_link = "https://www.mql5.com/ja/articles/15511"; popSize = 50; // Population size anarchyProb = 0.1; // Probability of anarchic behavior omega = 0.7; // Inertia weight lambda1 = 1.5; // Acceleration coefficient for P-best lambda2 = 1.5; // Acceleration coefficient for G-best alpha = 0.5; // Parameter for FI calculation theta = 1.0; // Parameter for EI calculation delta = 1.0; // Parameter for II calculation ArrayResize (params, 8); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "anarchyProb"; params [1].val = anarchyProb; params [2].name = "omega"; params [2].val = omega; params [3].name = "lambda1"; params [3].val = lambda1; params [4].name = "lambda2"; params [4].val = lambda2; params [5].name = "alpha"; params [5].val = alpha; params [6].name = "theta"; params [6].val = theta; params [7].name = "delta"; params [7].val = delta; } void SetParams () { popSize = (int)params [0].val; anarchyProb = params [1].val; omega = params [2].val; lambda1 = params [3].val; lambda2 = params [4].val; alpha = params [5].val; theta = params [6].val; delta = params [7].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double anarchyProb; // Probability of anarchic behavior double omega; // Inertia weight double lambda1; // Acceleration coefficient for P-best double lambda2; // Acceleration coefficient for G-best double alpha; // Parameter for FI calculation double theta; // Parameter for EI calculation double delta; // Parameter for II calculation S_ASO_Member member []; // Vector of society members private: //------------------------------------------------------------------- double CalculateFI (int memberIndex); double CalculateEI (int memberIndex); double CalculateII (int memberIndex); void CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); void SocietyMP (S_AO_Agent &agent, int coordInd); void PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); }; //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスの次のInitメソッドを見てみましょう。以下は、下は、メソッドのロジックです。
- StandardInit:メソッドは、渡されたレンジを使用して標準的な初期化を実行するために呼び出されます。このメソッドがfalseを返した場合、エラーが発生したことになります。
- ArrayResize:このメソッドは、アルゴリズムの参加者(社会のメンバー)の数を決定するpopSizeにmember配列のサイズを変更します。
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (member, popSize); for (int i = 0; i < popSize; i++) member [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスのMovingメソッドのコードを見てみましょう。以下がメソッドの構造とロジックです。
1. 初期呼び出しの確認
- revisionがfalse の場合、メソッドは指定されたrangeMinとrangeMax の範囲内のランダムな値でa配列を初期化します。
- 各i個体群の各c座標について、u.RNDfromCIメソッドが呼び出されます。ランダムな値が生成され、この値はu.SeInDiSpを使って正規化されます。
- この値はメンバー [i].pPrev [c]に保存されます。
- その後、revisionがtrueに設定され、メソッドの実行が完了します。
2. 基本的な動きのロジック
- 各i個体群について、fi、ei、iiの3つの指数が計算されます。これらは、集団メンバーの状態を特徴づける指標です。
- 各c座標に対して、以下が実行されます。
- 現在の値がメンバー[i].pPrev [c]に保存されます。
- u.RNDprobab()を使用してrnd乱数を生成します。
- 乱数がanarchyProb(無秩序な振る舞いが現れる確率を意味する)より小さい場合、インデックスiのメンバーの座標cは、その範囲からランダムに初期化されます。
- そうでない場合は、fi、ei、iiの値に応じて、CurrentMP、SocietyMP、PastMPメソッドが呼び出されます。
- すべての変更後、u.SeInDiSpを使用して各c座標の値を調整します。
Movingメソッドは、現在の状態と測定基準に基づいて、解空間内で集団のメンバーを移動させるロジックを実装しています。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); member [i].pPrev [c] = a [i].c [c]; } } revision = true; return; } //---------------------------------------------------------------------------- double fi = 0.0; //fickleness index double ei = 0.0; //external irregularity index double ii = 0.0; //internal irregularity index double rnd = 0.0; for (int i = 0; i < popSize; i++) { fi = CalculateFI (i); ei = CalculateEI (i); ii = CalculateII (i); for (int c = 0; c < coords; c++) { member [i].pPrev [c] = a [i].c [c]; rnd = u.RNDprobab (); if (u.RNDprobab () < anarchyProb) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); else { if (rnd > fi) CurrentMP (a [i], member [i], c); else { if (rnd < ei) SocietyMP (a [i], c); else { if (rnd < ii) PastMP (a [i], member [i], c); } } } } for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
MovingからRevisionメソッドに移りましょう。以下は一般的な構造とロジックです。
1. ind変数は-1で初期化されます。これは、f関数の最高の値を持つ集団メンバーのインデックスを格納するために使用されます。
2. このメソッドは、0からpopSize - 1までの集団のすべてのメンバーを実行します。
3. 最良の関数値を見つける:集団の各メンバーについて、a[i]がチェックされます。すなわち、そのf関数値がfBの現在の最良値を超えているかどうかがチェックされます。この場合、fBは[i].fで更新され、indのインデックスはiに設定されます。
4.個体の最良値の更新:このメソッドは、a [i].f関数値がmember [i].pBestFitness集団メンバー値よりも大きいかどうかもチェックします。yesの場合、値が更新され、ArrayCopy関数を使って現在の座標a[i].cがmember[i].pBestにコピーされます。
5. 最適解のコピー:ループが完了した後、インデックスind(すなわち、集団の少なくとも1つのメンバーがfBより大きい関数値を持つ)が見つかった場合、この集団メンバーの座標がArrayCopyを使ってcBにコピーされます。
Revisionメソッドは、集団で見つかった最良の解を更新し、集団の各メンバーの個体的な最良の値を更新する責任を負います。シンプルなロジックを使って関数の値を比較し、最適解を決定し、後で使用するために保存します。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > member [i].pBestFitness) { member [i].pBestFitness = a [i].f; ArrayCopy (member [i].pBest, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
次に、C_AO_ASOクラスのCalculateFIメソッド。メソッドの説明:
1. このメソッドは、適合が計算されるmemberIndex集団メンバーのインデックスを取ります。
2. 適合値の取得
- currentFitness:a配列からmemberIndexインデックスで集団メンバーの現在の適合値を取得します。
- personalBestFitness:member配列から、このメンバーの個体の最良適合値を取得します。
- globalBestFitness:fB変数に格納されている大域的最良適合値を取得します。
3. 適合性インデックス(FI)の計算:このメソッドは、方程式を使用して計算された値を返します。
この式は、個体の適合と現在の適合の差を、大域的適合と現在の適合の差で割って正規化したものです。CalculateFIメソッドは、集団のメンバーの適合性インデックスを計算し、その個体的および大域的最良適合値と比較してその品質を評価するために使用されます。
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateFI (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; double globalBestFitness = fB; //1 - 0.9 * (800-x)/(1000-x) return 1 - alpha * (personalBestFitness - currentFitness) / (globalBestFitness - currentFitness); } //——————————————————————————————————————————————————————————————————————————————
次はC_AO_ASOクラスのCalculateEIメソッドです。この方法は、前のものとほとんど同じことをするが、大域的な最良適合と個体的な現在の適合を使って計算します。
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateEI (int memberIndex) { double currentFitness = a [memberIndex].f; double globalBestFitness = fB; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(globalBestFitness - currentFitness) / (globalBestFitness * theta)); } //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスのCalculateIIメソッドは、前のメソッドと完全に似ていますが、最高の適合と現在の適合を使用します。
指数関数は、変化を滑らかにし、値間の移行をスムーズにします。CalculateIIメソッドは、現在の適合状態が個体の実績と比較してどの程度かを考慮した、集団のメンバーの改善指数を計算します。
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateII (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(personalBestFitness - currentFitness) / (personalBestFitness * delta)); } //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスのCurrentMPメソッドに話を移しましょう。説明:
1. 乱数生成:
- r1 = u.RNDprobab (): [0, 1]の範囲で乱数r1を生成
- r2 = u.RNDprobab (): [0, 1]の範囲で乱数r2を生成
2. velocityの計算:式には3つの要素が含まれます。
- omega * (agent.c [coordInd] - memb.pBest [coordInd]):慣性成分、以前の位置を考慮したエージェントの動き
- lambda1 * r1 * (memb.pBest[coordInd] - agent.c[coordInd]):エージェントの個体の最良位置を考慮してエージェントを指示
- lambda2 * r2 * (cB[coordInd] - agent.c[coordInd]):集団の最良位置を考慮してエージェントを指示
3. 現在の座標値に速度を加えてエージェントの位置を更新します。
CurrentMPメソッドは、エージェントの現在位置、個体の最良位置、集団の最良位置に基づいて、空間におけるエージェントの位置を更新します。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { double r1 = u.RNDprobab (); double r2 = u.RNDprobab (); double velocity = omega * (agent.c [coordInd] - memb.pBest [coordInd]) + lambda1 * r1 * (memb.pBest [coordInd] - agent.c [coordInd]) + lambda2 * r2 * (cB [coordInd] - agent.c [coordInd]); agent.c [coordInd] += velocity; } //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスのSocietyMPメソッドは、グループ情報と個体情報のランダムな選択に基づいてエージェントの座標を更新します。これにより、エージェントは集団全体と個々のエージェントの両方の状態に適応することができます。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::SocietyMP (S_AO_Agent &agent, int coordInd) { int otherMember = u.RNDminusOne (popSize); agent.c [coordInd] = u.RNDprobab () < 0.5 ? cB [coordInd] : member [otherMember].pBest [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
C_AO_ASOクラスのPastMPメソッドは、集団メンバーの現在の最良の状態とその前の状態との間のランダムな選択に基づいて、エージェントの座標を更新します。これにより、エージェントは集団メンバーの現在の成果と過去の成果の両方を考慮に入れることができます。このアプローチは、アルゴリズムの組合せ特性を向上させます。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { agent.c [coordInd] = u.RNDprobab () < 0.5 ? memb.pBest [coordInd] : memb.pPrev [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
3. テスト結果
ASOテストスタンドの結果
ASO|Anarchy Society Optimization|50.0|0.01|0.7|1.5|1.5|0.5|0.1|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.8487202680440514
25 Hilly's; Func runs:10000; result:0.746458607174428
500 Hilly's; Func runs:10000; result:0.31465494017509904
=============================
5 Forest's; Func runs:10000; result:0.9614752193694915
25 Forest's; Func runs:10000; result:0.7915027321897546
500 Forest's; Func runs:10000; result:0.23802894131144553
=============================
5 Megacity's; Func runs:10000; result:0.5707692307692309
25 Megacity's; Func runs:10000; result:0.5406153846153848
500 Megacity's; Func runs:10000; result:0.16613846153846298
=============================
All score:5.17836 (57.54%)
アルゴリズム操作の視覚化を見ると、結果にばらつきがあるといういくつかの結論を導き出すことができます。しかし、このアルゴリズムは、大きな次元の関数を扱う際に優れた探索能力を発揮し、その結果も確認されています。
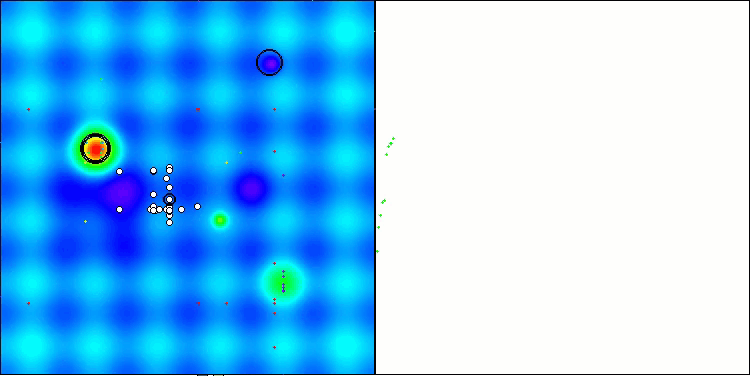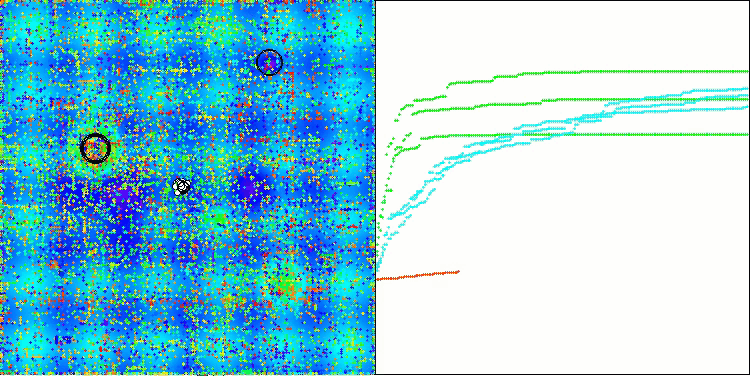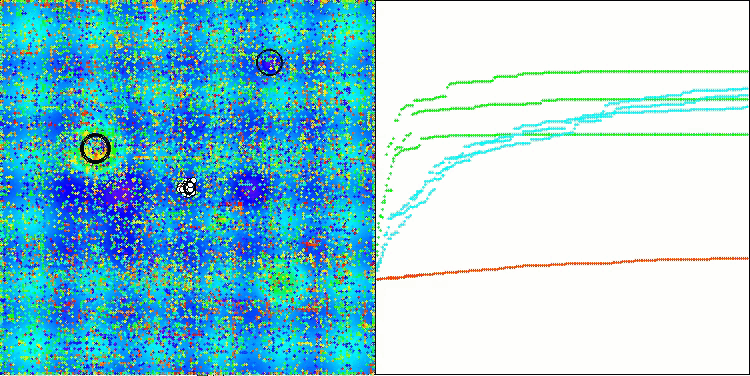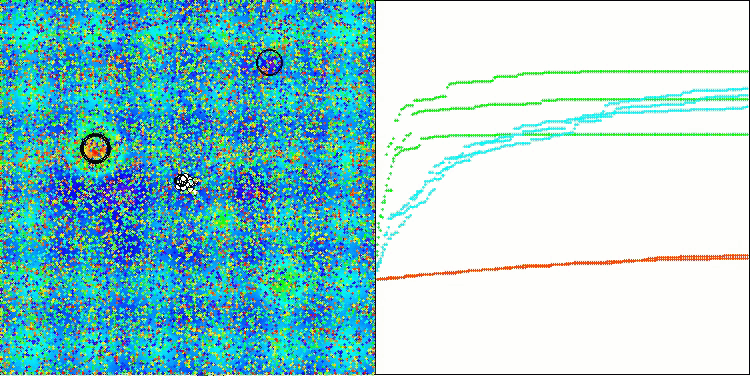
Hilly関数のASO
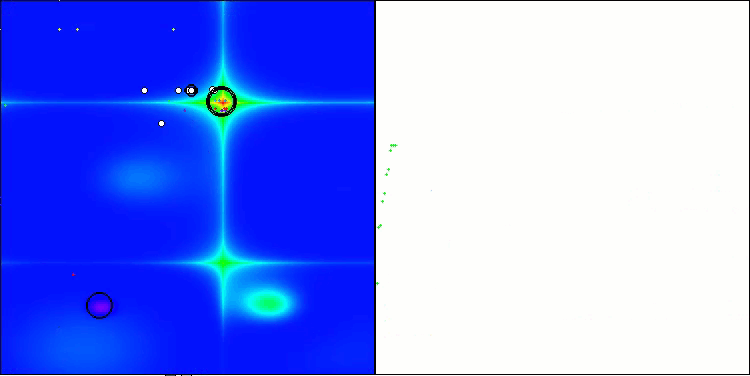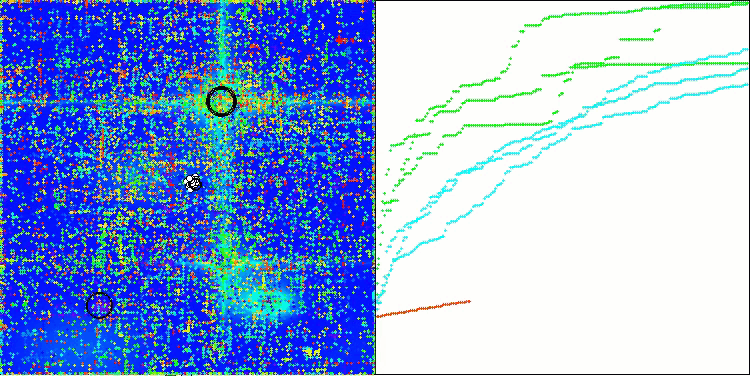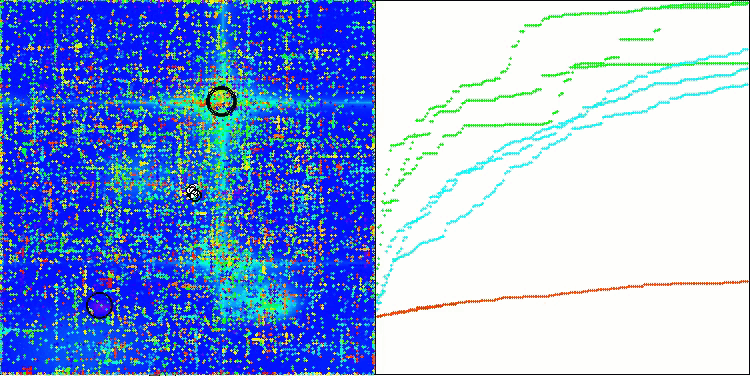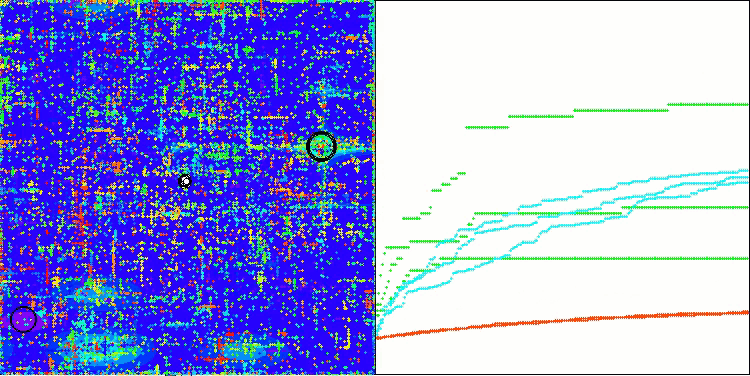
Forest関数のASO
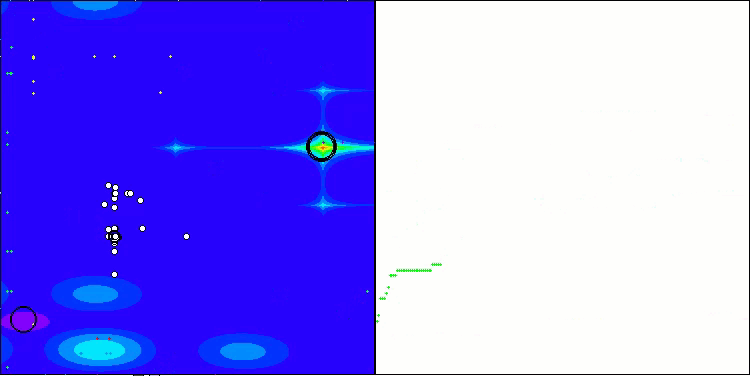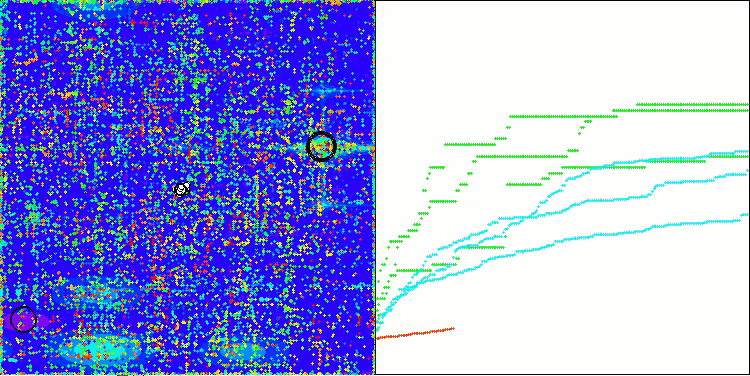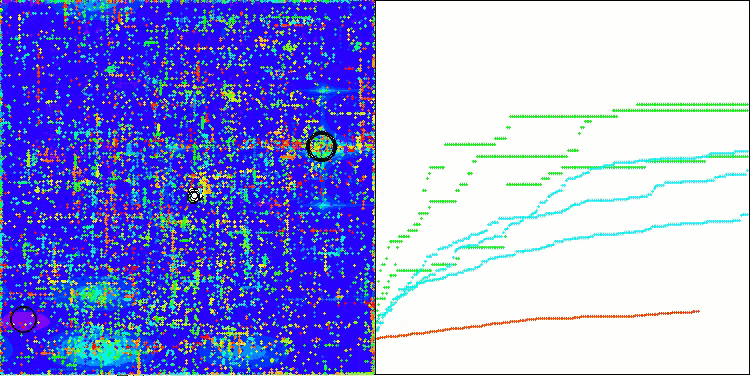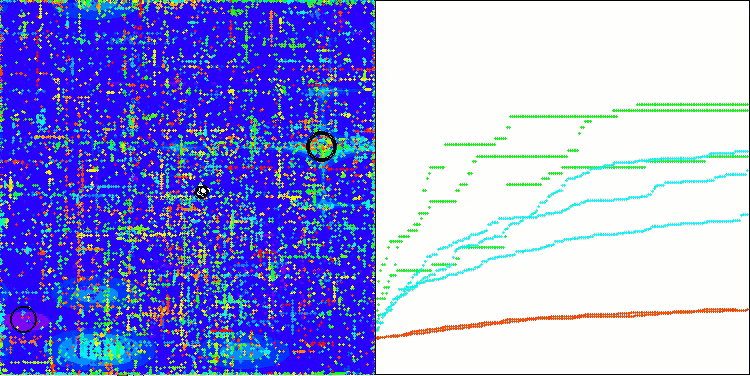
Megacity関数のASO
母集団最適化アルゴリズムの評価表:ASOアルゴリズムはテスト後トップ10に入り、評価表で9位に入りました。
| # | AO | 詳細 | Hilly | Hilly最終 | Forest | Forest最終 | Megacity(離散) | Megacity最終 | 最終結果 | MAXの% | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | コードロックアルゴリズム | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O)進化戦略 | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | 彗尾アルゴリズム | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | 確率的拡散探索M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | 社会集団の進化 | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | 等方的焼きなまし | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | 人工協調探索 | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | ASO | 無政府社会最適化 | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 10 | TSEA | 亀甲進化アルゴリズム | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 11 | DE | 差分進化 | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 12 | CRO | 化学反応の最適化 | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 13 | BSA | 鳥群アルゴリズム | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 14 | HS | ハーモニー検索 | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 15 | SSG | 苗木の播種と育成 | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 16 | (PO)ES | (PO)進化戦略 | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 17 | BSO | ブレインストーム最適化 | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 18 | WOAm | 鯨最適化アルゴリズムM | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 19 | AEFA | 人工電界アルゴリズム | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 20 | ACOm | 蟻コロニー最適化M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 21 | BFO-GA | 細菌採食の最適化:Ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 22 | ABHA | 人工蜂の巣アルゴリズム | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 23 | アズボ | 適応型社会行動最適化(ASBO) | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 24 | MEC | Mind Evolutionary Computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 25 | IWO | 侵入雑草最適化 | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 26 | Micro-AIS | 微小人工免疫系 | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 27 | COAm | カッコウ最適化アルゴリズムM | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 28 | SDOm | 螺旋ダイナミクス最適化M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 29 | NMm | ネルダー=ミード法M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 30 | FAm | ホタルアルゴリズムM | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 31 | GSA | 重力探索法 | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 32 | BFO | 細菌採餌最適化 | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 33 | ABC | 人工蜂コロニー | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 34 | BA | コウモリアルゴリズム | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 35 | SA | 焼きなまし | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 36 | IWDm | intelligent water drops M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 37 | PSO | 粒子群最適化 | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 38 | Boids | ボイドアルゴリズム | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 39 | MA | モンキーアルゴリズム | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 40 | SFL | Shuffled Frog-Leaping | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 41 | FSS | 魚群検索 | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 42 | RND | ランダム | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 43 | GWO | 灰色オオカミオプティマイザ | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 44 | CSS | 荷電系探索 | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 45 | EM | 電磁気学的アルゴリズム | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
まとめ
異なる次元のテスト関数に対するアルゴリズム演算の結果に基づき、以下の結論が得られます。ASOは、滑らかなHilly関数では、表中の最も近い隣人と比較して平均的な結果を示しましたが、シャープなForestと特に離散的なMegacityでは非常にまともな結果を示しました。総合最終スコアは5.17836 (57.54%)です。このアルゴリズムは、特に大きな次元の関数を扱う場合に、優れた探索能力を発揮します。つまり、スケールが大きいのです。このアルゴリズムは、トレーダーにとって優先事項である離散最適化問題を解くのに推奨できます。
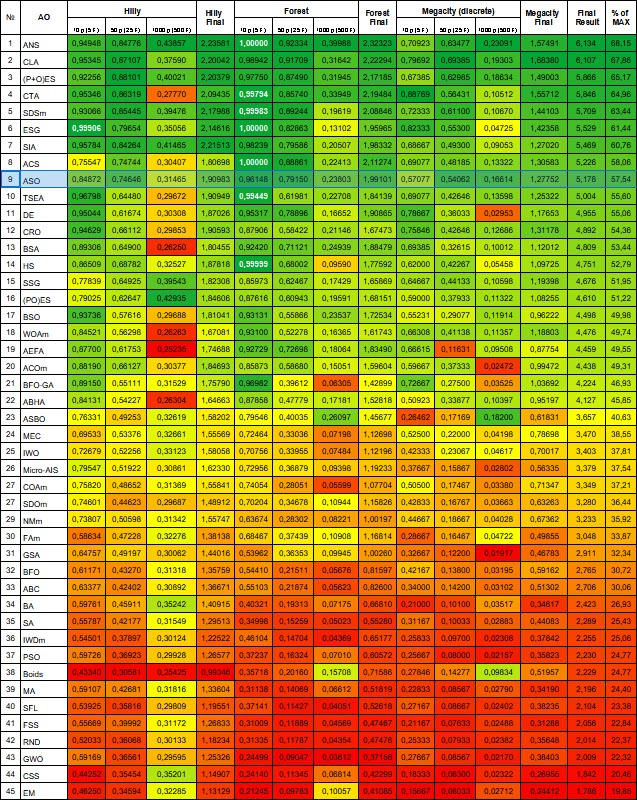
図4:関連テストによるアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示される
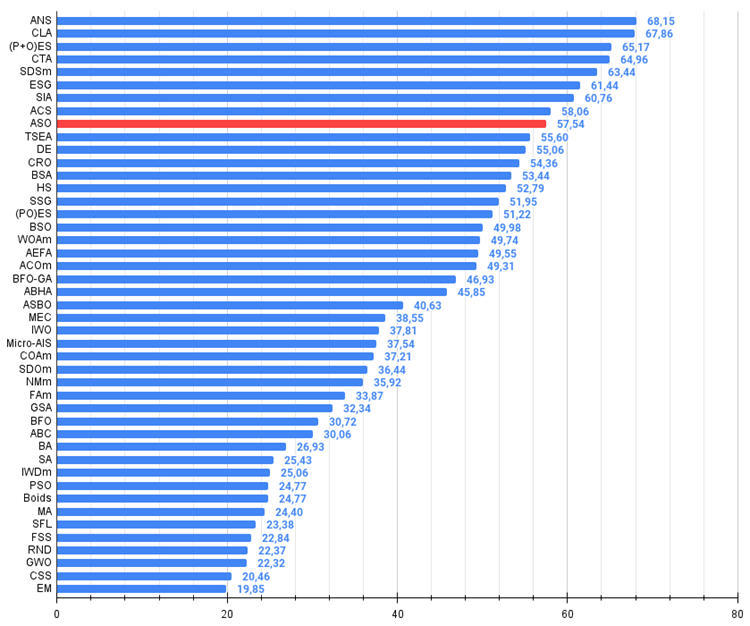
図5:アルゴリズムのテスト結果のヒストグラム(0から100までのスケールで、多ければ多いほど良い、
ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)
ASOアルゴリズムの長所と短所
長所
- 様々な機能における優れた収束性
- 離散関数に関する優れた結果
短所
- パラメータの数が多い(設定が非常に難しい)
- 低次元関数に関する結果が散らばる
- 実装が複雑
この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15511
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 ウィリアム・ギャンの手法(第2回):ギャンスクエアインジケーターの作成
ウィリアム・ギャンの手法(第2回):ギャンスクエアインジケーターの作成
 ニューラルネットワークの実践:ニューロンのスケッチ
ニューラルネットワークの実践:ニューロンのスケッチ
 人工藻類アルゴリズム(AAA)
人工藻類アルゴリズム(AAA)
 初級から中級へ:演算子
初級から中級へ:演算子
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索