算術最適化アルゴリズム(AOA)：AOAからSOA（シンプル最適化アルゴリズム）へ

MetaTrader 5 — テスター | YYYY年08月DD日, 12:13

Andrey Dik

内容

はじめに

算術最適化アルゴリズム(AOA: Arithmetic Optimization Algorithm)は、加算、減算、乗算、除算といった単純な算術演算に基づく独自の手法です。その本質は、これらの基本的な数学原理を活用して、多様な問題の最適解を導き出すことにあります。AOAはLaith Abualigahを含む研究チームによって開発され、2021年に初めて発表されました。このアルゴリズムは、メタヒューリスティック法（高水準アルゴリズム）の一種に属し、複雑な最適化問題に対して、精度重視の方法では非効率または適用不可能な場合に、高品質な解を合理的な時間で得るために複数のヒューリスティックを探索・生成・確率的に選択します。

私がこの手法に惹かれた理由は、ごく初歩的な算術演算子を用いるという、シンプルでありながら洗練された発想にあります。基本的な数学的操作とメタヒューリスティック手法との関係がシナジーを生み、複雑な最適化問題を解く力を与えます。AOAで用いられるメタヒューリスティックの要素には、以下の重要な原則があります。

1. 集団アプローチ：AOAは複数の解（集団）を用いて探索をおこないます。これにより、より広い解空間をカバーでき、局所最適解に陥ることを防ぎ、探索範囲を広げます。

2. ランダム性と確率性：探索にランダム要素を組み込むことで、局所最適にとらわれるのを防ぎ、解空間全体をより広く探索でき、大域最適解を見つける確率を高めます。

3. 探索と活用のバランス：多くのメタヒューリスティックアルゴリズムと同様に、AOAは新しい領域を探索する「探索」と、既知の良好な解を深める「活用」とのバランスを重視します。算術演算を用いて解の位置を更新することで、このバランスを実現します。

したがって、AOAは集団アプローチ、ランダム性、そして探索と活用のバランスといった原則を効果的に利用して最適化問題を解決するメタヒューリスティックアルゴリズムの好例です。本稿では特に、このアルゴリズムが複雑かつ多次元の空間で最適解を見つける効率性について、実装とテストの後に詳しく述べます。

アルゴリズムの実装

AOAの基本的な発想は、算術演算子の分配的な性質を利用して最適解を見つけることにあります。このアルゴリズムは、シンプルな原理、少ないパラメータ数、そして実装の容易さが特徴です。数学における4つの基本的な算術演算子、つまり乗算(Mε × ε)、除算(Dε ÷ ε)、減算(Sε − ε)、加算(Aε + ε)の分布的性質を活用します。AOAでは、初期集団はランダムに生成されます。生成範囲は[U; L]であり、ここでUとLはそれぞれ目的関数の探索空間の上限値と下限値を表します。初期化は次の式でおこなわれます。

x = L + (U − L) × δ、ここでは集団内の解を表し、δは[0, 1]の範囲をとる乱数です。

各反復ステップでは、探索と活用の戦略、すなわち2つの演算子グループ（除算・乗算）または（減算・加算）のいずれを選択するかが決まります。この選択はMoA (math optimizer accelerated)関数の結果に依存します。MoAは本質的に確率値であり、反復ごとに以下の式で変化します。

MoA(t) = Min + t × (Max − Min) ÷ Maxt、ここで、MoA(t)はt回目の反復における関数値、tは現在の反復回数（1から最大反復回数Max_tの範囲）、MinはMoAの最小値、Maxは最大値を表します。MinとMaxはアルゴリズムの外部パラメータです。

4つすべての算術演算式では、MoP (math optimizer)係数を使用します。これは以下の式で計算されます。

MoP(t) = 1 − (t ÷ Maxt)^(1 ÷ θ)、ここで、MoP(t)はt回目の反復におけるMoP値、θは反復における活用の度合いを制御する重要なパラメータです。元論文の著者らはθを5に設定しています。

下図（図1）は、MoAとMoPが現在の反復回数に応じてどのように変化するかを示しています。グラフから、MoAは反復ごとに線形的に増加しており、これは（減算・加算）グループが選ばれる確率が高まり、（除算・乗算）グループが選ばれる確率が比例して低下することを意味します。一方、MoP比は非線形的に減少し、これによりエージェントの位置更新量が減少し、解が最適解に収束する度合いが高まることを示しています。

MoAおよびMoP

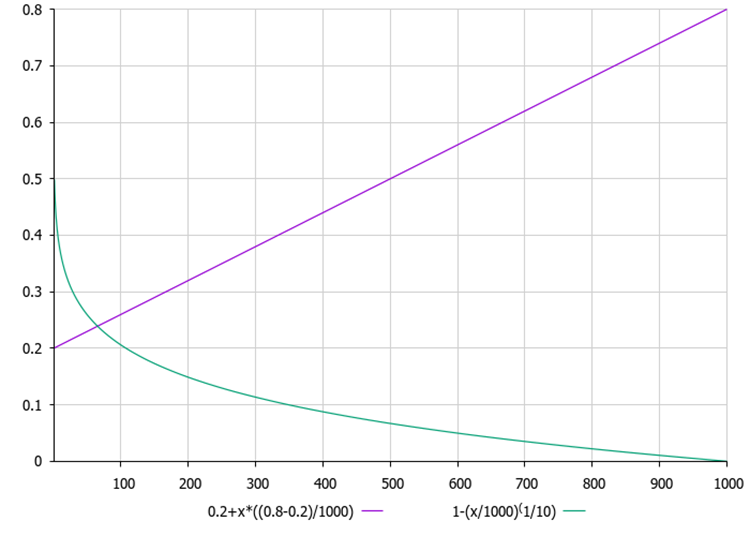
図1：紫色はMoA確率グラフ、緑色はMoP比率グラフを示している

AOAにおける探索または大域探索は、MoAの確率が満たされる場合、除算(D)および乗算(M)演算子に基づく探索戦略を用いて実行されます。これは次のように定式化され、以下の演算子は等しい確率で実行されます。

rand2 < 0.5の場合、xi,j(t+1) = best(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj)

その他の場合

xi,j(t+1) = best(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj)、ここでxi(t+1)は(t+1)番目の反復におけるi番目の解を表し、x(i,j)(t)は現在の世代におけるi番目の個体のj番目の位置を示し、best(xj)は現時点での最良解のj番目の位置を表し、εは小さな正の数です。j番目の位置の値の上限と下限はそれぞれUjとLjで表されます。制御パラメータμは0.5に設定されています。

MoA確率が満たされない場合は、AOAでは探索戦略（解の精緻化）が実行されます。この戦略は減算(S)または加算(A)演算子を用いて開発されたものです。ここでの𝜇も定数であり、著者の意図により0.5に固定されています。

rand3 < 0.5の場合、xi,j(t+1) = best(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj)

それ以外の場合、xi,j(t+1) = best(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj)

AOAにおいて、パラメータ𝜇とθは非常に重要です。なぜなら、これらは探索と活用のバランスに関わるからです。探索と活用のバランスを適切に保つことは、通常非常に難しい課題です。元のAOAでは、𝜇の値は探索と活用の両方で0.5に固定されていました。しかし、θパラメータは反復中の動作効率に影響を与えるもので、5に設定されています。著者らは𝜇とθのさまざまな値を試し、異なる次元における単峰性および多峰性のテスト関数に対して、𝜇 = 0.5およびθ = 5が最も良い結果を出すことを確認しました。

それでは、AOAアルゴリズムの疑似コードを実装してみましょう。

エポック番号を1つ増加させます

// 初期化を開始する
IF：もし今回が初回の実行であれば
    各個体に対して：
        各座標について：
            許可された範囲内でランダムな位置を設定します。
            その位置を離散値に変換します。
    初期化が完了したことをマークします。
    関数を終了します。
終了

// メインの最適化プロセス
MoA = minMoA + EpochNumber * ((maxMoA - minMoA) / totalEpochs)を計算します。
MoP = 1 - (EpochNumber / totalEpochs)^(1/θ)を計算します。

// 解空間探索フェーズ
各個体に対して：
    各座標について：
        3つの乱数（rand1, rand2, rand3）を生成します。
        座標に対して既知の最良値を取得します。

        rand1 < MoAcの場合
            rand2 > 0.5の場合
                除算を用いて位置を更新します。
            それ以外の場合
                乗算を用いて位置を更新します。
            終了
        それ以外の場合
            rand3 > 0.5の場合
                減算を使用して位置を更新します。
            それ以外の場合
                加算を使用して位置を更新します。
            終了
        終了

        新しい位置を許容可能な離散値に変換します。

最良解を更新します。

では、コードの作成に進みましょう。C_AO_AOAクラスはAOAアルゴリズムの実装であり、算術演算に基づく手法を用いて最適化問題を解くことを目的としています。以下はpublicメソッドです。

1. SetParamsメソッド：params配列からパラメータの値を設定します。このメソッドにより、アルゴリズムの初期化後でもパラメータを変更することができます。

2. Initメソッド：

最小および最大の探索範囲、探索ステップ数、エポック数を受け取り、アルゴリズムを初期化します。
初期化が成功した場合はtrueを返し、失敗した場合はfalseを返します。

3. Movingメソッド：解空間における粒子の移動を実行します。このメソッドでは、与えられたパラメータと現在の状態に基づき、粒子の位置を更新するロジックが実装されています。

4. Revisionメソッド：粒子の現在の位置を修正し、関数の最良値および対応する粒子の座標を更新します。

以下はprivateフィールドとクラスパラメータです。

minT：MoA確率の最小値
maxT：MoA確率の最大値。
θ：探索と活用のバランスに影響を与えるパラメータ
μ：粒子位置の変化（移動範囲）を制御するためのパラメータ
ϵ：0除算を防ぐための小さな値

以下は、アルゴリズムのステータス情報です。

epochs：アルゴリズムが進む総エポック数
epochNow：現在のエポック番号。アルゴリズムの進行状況を追跡し、MoA確率やMoP比率に影響します。

C_AO_AOAクラスは、AOAアルゴリズムの主要な構成要素である初期化、粒子移動、修正を実装しています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AOA () { }
  C_AO_AOA ()
  {
    ao_name = "AOA";
    ao_desc = "Arithmetic Optimization Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter
    μ       = 0.01; // μ parameter

    ArrayResize (params, 5); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
    params [4].name = "μ";       params [4].val = μ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
    μ       = params      [4].val; // Set μ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter
  double μ;    // μ parameter
  double ϵ;    // Parameter to prevent division by zero

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOAクラスのInitメソッドは、探索範囲、ステップ数、そして最適化を実行するエポック数のパラメータを設定することで、最適化アルゴリズムを初期化する役割を持ちます。以下は、メソッドのロジックです。

1. メソッドはまずStandardInitを呼び出し、アルゴリズムの標準パラメータを初期化します。この初期化が失敗した場合、Initは直ちに処理を終了し、falseを返します。

2. パラメータの設定

渡されたepochsPパラメータに基づき、総エポック数を設定します。
現在のエポック番号epochNowを0に初期化します。
0除算を防ぐための小さな値ϵをDBL_EPSILONに設定します。DBL_EPSILONはdouble型で表現できる最小の正の値の標準値です。

3. すべてのステップが正常に完了した場合、メソッドはtrueを返し、アルゴリズムの初期化が成功したことを示します。

Initメソッドは、アルゴリズムを実行する準備のための重要な処理です。このメソッドを呼び出すことで、最適化に使用される基本パラメータや変数はすべて元の状態にリセットされます。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、AOAアルゴリズムにおける粒子の解空間内での移動を担当します。現在の状態とアルゴリズムのパラメータに基づき、粒子の位置を更新する基本的なロジックが実装されています。以下は、メソッドのロジックです。

1. epochNowを増加させ、新しい最適化の時代が始まったことを反映します。

2. 初期ランダム配置：まだ更新がおこなわれていない場合、各粒子に対してrangeMinとrangeMaxの範囲内でランダムな位置を生成します。生成された位置は、指定されたステップを用いてSeInDiSpメソッドにより離散化されます。

3. 現在のエポックと指定パラメータに基づき、MoAcとMoPrを計算します。これらの値は、粒子位置を更新する際の確率を決定します。

4. 探索フェーズ：各粒子および各座標に対して、ランダム値と計算されたパラメータに基づき位置を更新します。位置は、除算や乗算などのさまざまな演算子、および確率条件を用いて更新されます。

5. 更新後、位置もSeInDiSpメソッドを使用して離散値に変換されます。

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_AOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AOAクラスのRevisionメソッドは、集団内の最適な粒子に関する情報を更新します。すべての粒子を反復処理し、その関数値を現在の最適値と比較し、より良い値が見つかった場合はそれを更新してインデックスを保存します。次に、最適な粒子の座標をcB配列にコピーします。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_UtilitiesクラスのSeInDiSpメソッドは、指定されたStepを使用してIn入力を [InMin、InMax] の範囲内に制限します。

1. InがInMin以下の場合は、InMinを返します。
2. InがInMax以上の場合は、InMaxを返します。
3. Stepが0に等しい場合は、Inの元の値を返します。
4. それ以外の場合は、値を(In - InMin) / Stepに丸め、ステップを考慮した範囲内で調整された値を返します。

double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}

テスト結果

AOAアルゴリズムは非常にシンプルなので、テストタスクにおける性能を確認してみましょう。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs:10000; result:0.3914957505847635
25 Hilly's; Func runs:10000; result:0.27733670012505607
500 Hilly's; Func runs:10000; result:0.2514517003089684
=============================
5 Forest's; Func runs:10000; result:0.23495704012464264
25 Forest's; Func runs:10000; result:0.1853447250852242
500 Forest's; Func runs:10000; result:0.15382470751079919
=============================
5 Megacity's; Func runs:10000; result:0.19846153846153847
25 Megacity's; Func runs:10000; result:0.11815384615384619
500 Megacity's; Func runs:10000; result:0.09475384615384692
=============================
All score:1.90578 (21.18%)

テスト結果によると、アルゴリズムのスコアは100%中21.18%に過ぎません。これは非常に弱い結果です。残念ながら、現在のランキング表では最下位にあたります。より良い結果を得るために、アルゴリズムのロジックを変更してみましょう。段階的に変更を加え、結果を監視します。

オリジナルのAOAアルゴリズムのロジックには、4つの数学演算子のいずれかを選択する確率的な性質のみで構成される確率的検索が含まれます。μ変位比に0から1までの範囲の乱数を掛けて、ランダム性の要素を追加してみましょう。

// Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      double rand1 = u.RNDprobab (); // Generate a random value
      double rand2 = u.RNDprobab (); // Generate a random value
      double rand3 = u.RNDprobab (); // Generate a random value

      best = cB [c];                 // Save the current best value

      μ *= u.RNDfromCI (0, 1);       // Random change of μ

      if (rand1 < MoAc)              // If random value is less than MoAc
      {
        if (rand2 > 0.5)             // If random value is greater than 0.5
        {
          a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Update particle position
        }
        else
        {
          a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }
      else // If random value is greater than or equal to MoAc
      {
        if (rand3 > 0.5) // If random value is greater than 0.5
        {
          a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
        else
        {
          a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]);     // Update particle position
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
    }
  }

同じパラメータでアルゴリズムをテストしてみましょう。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs:10000; result:0.3595591180258857
25 Hilly's; Func runs:10000; result:0.2804913285516192
500 Hilly's; Func runs:10000; result:0.25204298245610646
=============================
5 Forest's; Func runs:10000; result:0.24115834887873383
25 Forest's; Func runs:10000; result:0.18034196700384764
500 Forest's; Func runs:10000; result:0.15441446106797124
=============================
5 Megacity's; Func runs:10000; result:0.18307692307692305
25 Megacity's; Func runs:10000; result:0.12400000000000003
500 Megacity's; Func runs:10000; result:0.09470769230769309
=============================
All score:1.86979 (20.78%)

残念ながら、結果はさらに悪化しました。追加の手順を実行する必要があります。しかし、決定論的な表現にランダム性を加えるという事実自体が、検索戦略の可変性を確実に向上させるはずです。数学演算子の方程式を詳しく見てみましょう。それぞれの方程式にはrangeMin [c]項があります。本質的には、これらの演算子の結果の式は、最適化されるパラメータの最小境界を基準にして常に中央に配置されます。これには明らかな論理がないので、すべての方程式からこの要素を削除しましょう。

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]);     // Update particle position
      }
    }

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

テストを実行してみましょう。得られた結果は以下の通りです。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs:10000; result:0.36094646986361645
25 Hilly's; Func runs:10000; result:0.28294095623218063
500 Hilly's; Func runs:10000; result:0.2524581968477915
=============================
5 Forest's; Func runs:10000; result:0.2463208325927641
25 Forest's; Func runs:10000; result:0.1772140022690996
500 Forest's; Func runs:10000; result:0.15367993432040622
=============================
5 Megacity's; Func runs:10000; result:0.1923076923076923
25 Megacity's; Func runs:10000; result:0.11938461538461542
500 Megacity's; Func runs:10000; result:0.09433846153846229
=============================
All score:1.87959 (20.88%)

私たちがおこなった変更は、パフォーマンスの改善にはつながりませんでした。検索戦略にすでに大幅な変更を導入していたことを考えると、これは非常に奇妙です。これは、戦略そのものに欠陥があり、個々の要素を取り除いても結果には大きな影響を与えないことを示している可能性があります。

検索戦略には、各反復ごとに線形的に増加するMoAコンポーネントが含まれています（図1参照）。このコンポーネントを、最良解の座標の1つを確率的に選択し、それを現在の作業解にコピーする仕組みとして利用してみましょう。これにより、最良解を通じた情報交換を利用することで検索戦略に組合せ的な特性が付与されます（元のバージョンでは、エージェント間の情報交換は存在しません）。

// Research phase using Division (D) and Multiplication (M) operators
for (int i = 0; i < popSize; i++) // For each particle
{
  for (int c = 0; c < coords; c++) // For each coordinate
  {
    double rand1 = u.RNDprobab (); // Generate a random value
    double rand2 = u.RNDprobab (); // Generate a random value
    double rand3 = u.RNDprobab (); // Generate a random value

    best = cB [c];                 // Save the current best value

    μ *= u.RNDfromCI (0, 1);       // Change μ

    if (rand1 < MoAc)              // If random value is less than MoAc
    {
      if (rand2 > 0.5)             // If random value is greater than 0.5
      {
        a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Update particle position
      }
      else
      {
        a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }
    else // If random value is greater than or equal to MoAc
    {
      if (rand3 > 0.5) // If random value is greater than 0.5
      {
        a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
      else
      {
        a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);     // Update particle position
      }
    }

    if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                            // Set to the best value

    a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);       // Convert to discrete values
  }
}

最良解を介した情報交換のロジックを導入した後に得られた結果：

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs:10000; result:0.360814744695913
25 Hilly's; Func runs:10000; result:0.28724958448168375
500 Hilly's; Func runs:10000; result:0.2523432997811412
=============================
5 Forest's; Func runs:10000; result:0.26319762212870146
25 Forest's; Func runs:10000; result:0.1796822846691542
500 Forest's; Func runs:10000; result:0.1546335398592898
=============================
5 Megacity's; Func runs:10000; result:0.18
25 Megacity's; Func runs:10000; result:0.12153846153846157
500 Megacity's; Func runs:10000; result:0.09373846153846228
=============================
All score:1.89320 (21.04%)

性能の向上を確認しましたが、それはあくまで解の範囲内での改善にとどまっています。次に、同じコード部分に、最適化パラメータの許容範囲全体にわたって座標の乱数値を生成する確率を追加します。その際、その座標は MoP 方程式に従って非線形に減少します。

// Probabilistic update of particle position
if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
else
  if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

次の結果を見てみましょう。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs:10000; result:0.8354927331645667
25 Hilly's; Func runs:10000; result:0.3963221867834875
500 Hilly's; Func runs:10000; result:0.2526544322311671
=============================
5 Forest's; Func runs:10000; result:0.7689954585427405
25 Forest's; Func runs:10000; result:0.3144560745800252
500 Forest's; Func runs:10000; result:0.15495875390289315
=============================
5 Megacity's; Func runs:10000; result:0.6076923076923076
25 Megacity's; Func runs:10000; result:0.24646153846153843
500 Megacity's; Func runs:10000; result:0.09816923076923163
=============================
All score:3.67520 (40.84%)

驚くべきことに、生産性が大幅に向上しました。これは、私たちが正しい方向に進んでいることを意味します。ここで AOA ロジックに具体的に何が追加されたのかを注記しておく必要があります。最適化の初期段階、すなわち最初のエポックでは、大域最良解の座標を現在の解にコピーする確率は最小です。これは極めて論理的であり、最適化の初期段階では戦略が探索空間の探索を開始したばかりだからです。同時に、探索空間全体にわたってランダムな解を生成する確率は、最初の反復で最大となります。すべてのエポックを通じて、これらの確率は変化します。すなわち、大域最良解の座標をコピーする確率は増加し、一方でランダム解を生成する確率は逆に減少します（図1参照）。

今回の変更によって性能が改善した一方で、元のロジックに対する変更では顕著な改善が得られないことが既に指摘されているため、すべての算術演算子を完全に排除することが合理的であると考えられます。それでは、このアルゴリズムをテスト問題に適用してみましょう。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs:10000; result:0.8751771961221438
25 Hilly's; Func runs:10000; result:0.4645369071659114
500 Hilly's; Func runs:10000; result:0.27170038319811357
=============================
5 Forest's; Func runs:10000; result:0.8369443889312367
25 Forest's; Func runs:10000; result:0.36483865328371257
500 Forest's; Func runs:10000; result:0.17097532914778202
=============================
5 Megacity's; Func runs:10000; result:0.7046153846153846
25 Megacity's; Func runs:10000; result:0.28892307692307695
500 Megacity's; Func runs:10000; result:0.10847692307692398
=============================
All score:4.08619 (45.40%)

ご覧のとおり、効率はさらに約5%向上し、改めて私の推論の正しさが確認されました。デフォルトのパラメータでも興味深い結果が得られましたが、ロジックの変更があまりにも抜本的であったため、ここでアルゴリズムの外部パラメータを最適化する必要があります。生産性の向上に加えて、追加の利点として以下が挙げられます。

不要な乱数生成を排除したことによる処理速度の大幅な向上
外部パラメータを1つ削減できたこと

得られたアルゴリズムの最終結果を見てみましょう。

AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs:10000; result:0.9152036654779877
25 Hilly's; Func runs:10000; result:0.46975580956945456
500 Hilly's; Func runs:10000; result:0.27088799720164297
=============================
5 Forest's; Func runs:10000; result:0.8967497776673259
25 Forest's; Func runs:10000; result:0.3740125122006007
500 Forest's; Func runs:10000; result:0.16983896751516864
=============================
5 Megacity's; Func runs:10000; result:0.6953846153846155
25 Megacity's; Func runs:10000; result:0.2803076923076923
500 Megacity's; Func runs:10000; result:0.10852307692307792
=============================
All score:4.18066 (46.45%)

得られた結果はすでに評価表に掲載するに値するものであり、最終版の探索戦略は元のロジックの要素を完全に失っています。そこで私は、この新しいアルゴリズムに「Simple Optimization Algorithm (SOA)」という新しい名称を与えることにしました。では、SOAアルゴリズムの最終コード全体を見てみましょう。

#include "#C_AO.mqh"

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_SOA () { }
  C_AO_SOA ()
  {
    ao_name = "SOA";
    ao_desc = "Simple Optimization Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16364";

    popSize = 50;   // Population size
    minT    = 0.1;  // Minimum T value
    maxT    = 0.9;  // Maximum T value
    θ       = 10;   // θ parameter

    ArrayResize (params, 4); // Resize the parameter array

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "minT";    params [1].val = minT;
    params [2].name = "maxT";    params [2].val = maxT;
    params [3].name = "θ";       params [3].val = θ;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val; // Set population size
    minT    = params      [1].val; // Set minimum T
    maxT    = params      [2].val; // Set maximum T
    θ       = params      [3].val; // Set θ
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   (); // Method of moving particles
  void Revision (); // Revision method

  //----------------------------------------------------------------------------
  double minT; // Minimum T value
  double maxT; // Maximum T value
  double θ;    // θ parameter

  private: //-------------------------------------------------------------------
  int epochs;    // Total number of epochs
  int epochNow;  // Current epoch
  double ϵ;      // Parameter to prevent division by zero
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_SOA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  epochs   = epochsP;     // Set the total number of epochs
  epochNow = 0;           // Initialize the current epoch
  ϵ        = DBL_EPSILON; // Set ϵ

  return true;            // Return 'true' if initialization was successful
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Particle displacement method
void C_AO_SOA::Moving ()
{
  epochNow++; // Increase the current epoch number

  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Calculate the MoAc value
  double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ));   // Calculate the MoPr value
  double best = 0.0;                                        // Variable to store the best value

  // Research phase using Division (D) and Multiplication (M) operators
  for (int i = 0; i < popSize; i++) // For each particle
  {
    for (int c = 0; c < coords; c++) // For each coordinate
    {
      // Probabilistic update of particle position
      if (u.RNDbool () < MoAc) a [i].c [c] = cB [c];                                        // Set to the best value
      else
        if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);    // Generate new random position

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);   // Convert to discrete values
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SOA::Revision ()
{
  int ind = -1;                     // Index to store the best particle

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB = a [i].f;                 // Update the best value of the function
      ind = i;                      // Save the index of the best particle
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
}
//——————————————————————————————————————————————————————————————————————————————

本研究で取り上げた最適化アルゴリズムの中で、今回得られた結果はコード量に関して最もコンパクトな部類に属します。これより短いコードは、今後の論考で取り上げるRW (RandomWalk)アルゴリズムのみです。

探索戦略の性能を解空間上で可視化することは非常に有用です。AOAアルゴリズムについては、異なる課題に対する性能にほとんど差異が見られなかったため、3種類のテスト（Hilly、Forest、Megacity）を一つのアニメーションにまとめました。一方、SOAの挙動については、各テスト関数ごとに個別の可視化を以下に示します。

また、新しいSOAアルゴリズムの小規模次元問題における動作として、結果のばらつきが非常に小さいことが確認されました。これは極めて稀有な特性といえます。

Hilly、Forest、MegacityのAOA

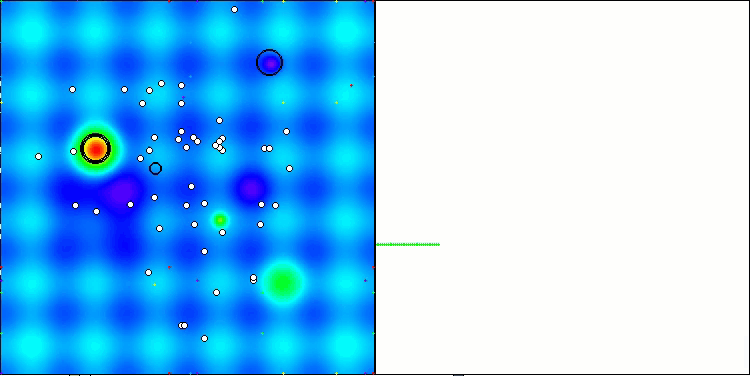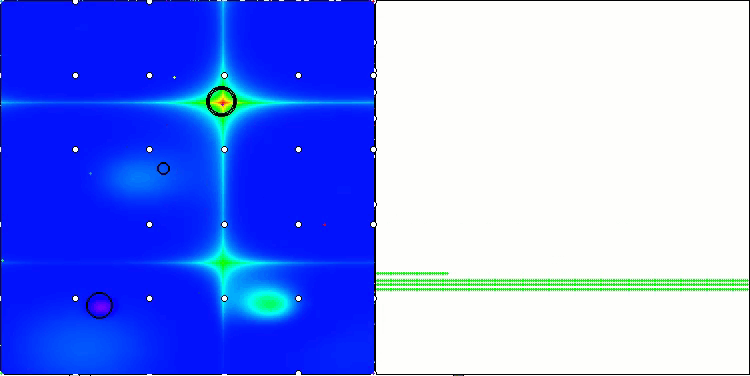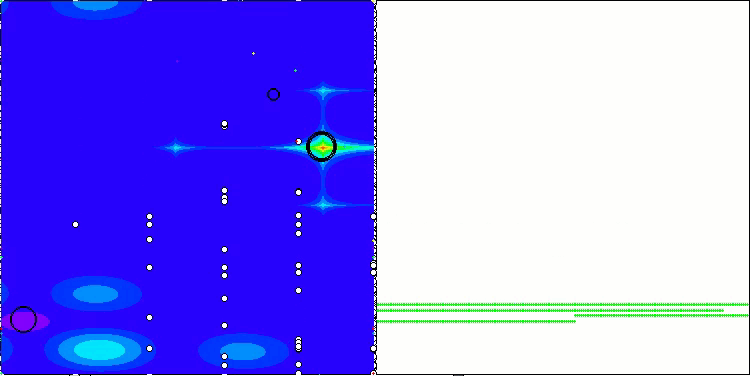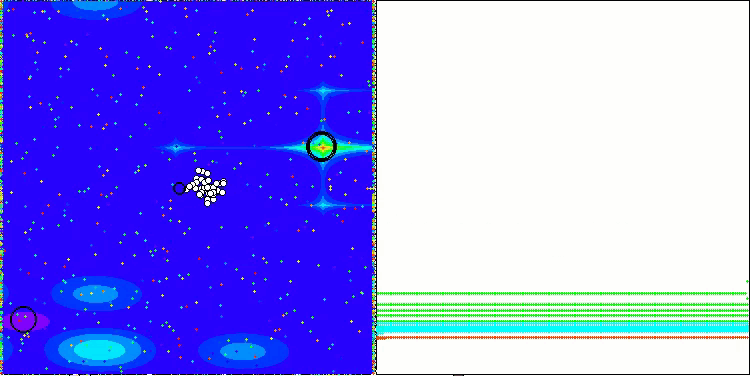
Hilly、Forest、Megacityテスト関数のAOA

Hilly

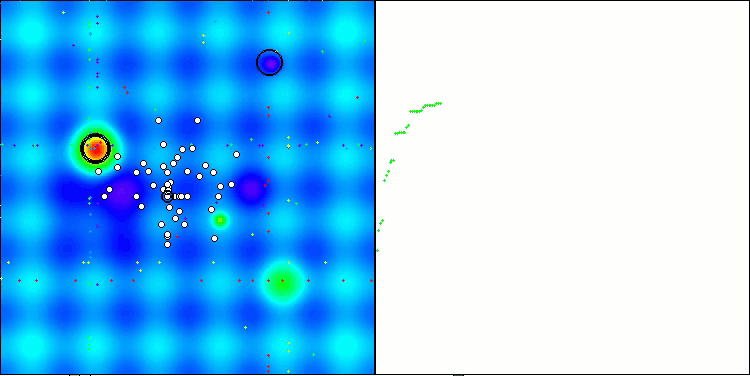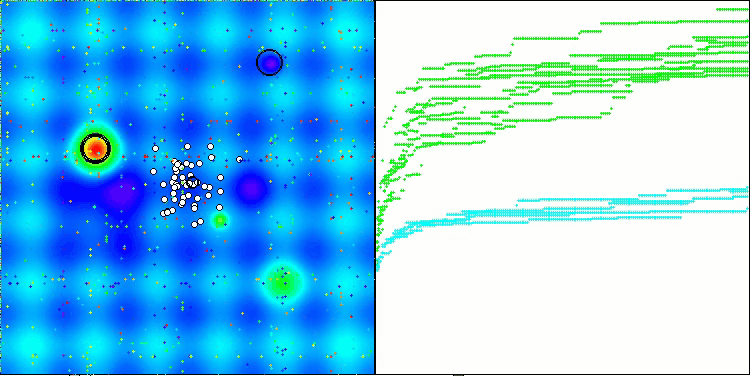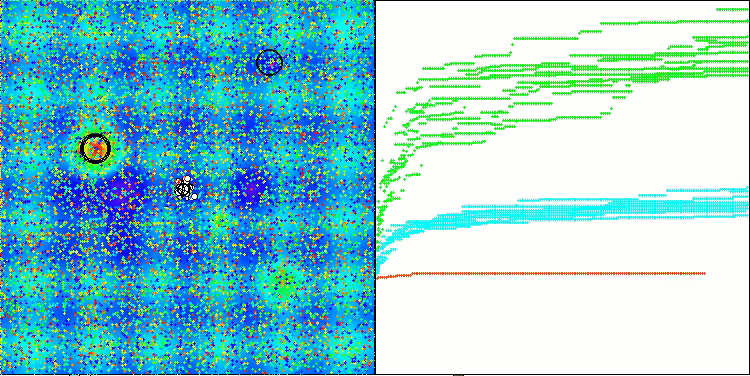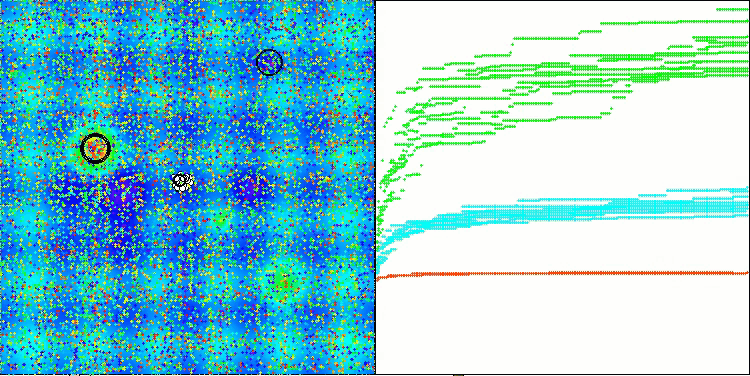
Hillyテスト関数のSOA

Forest

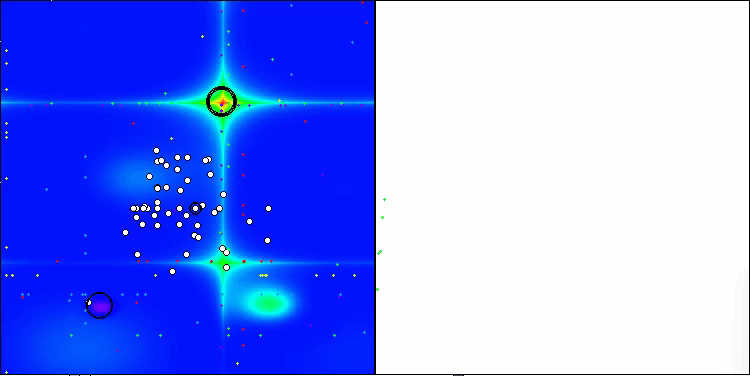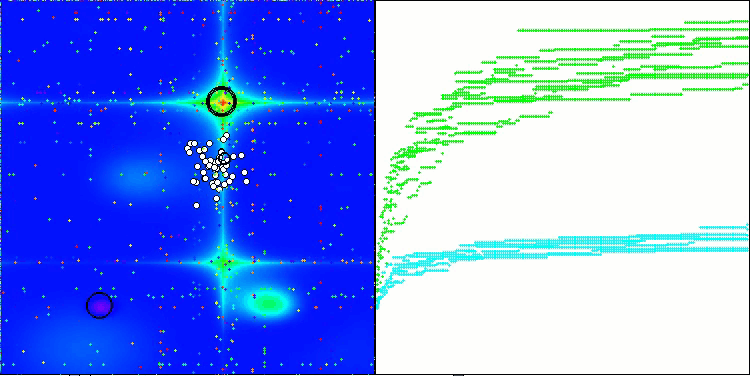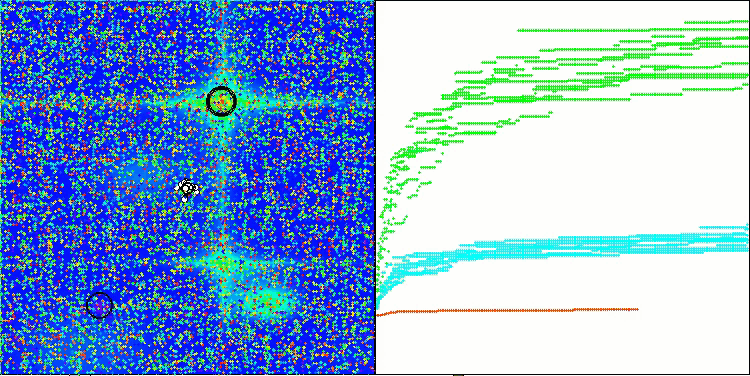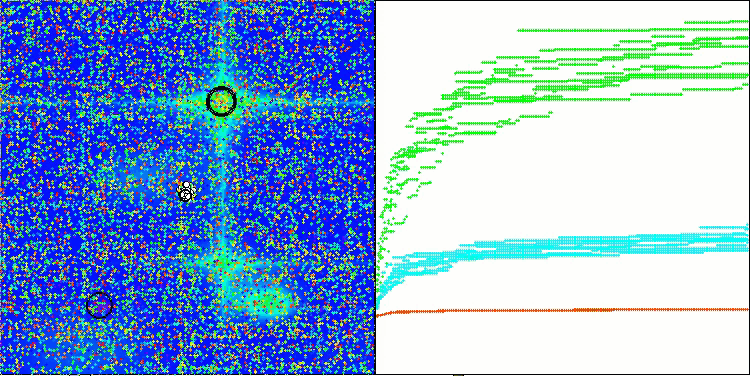
Forestテスト関数のSOA

Megacity

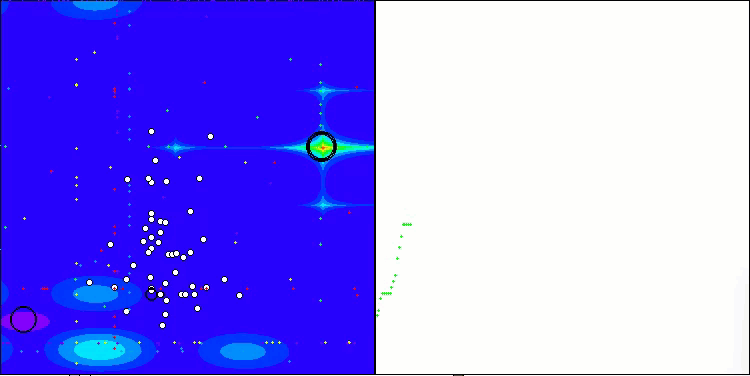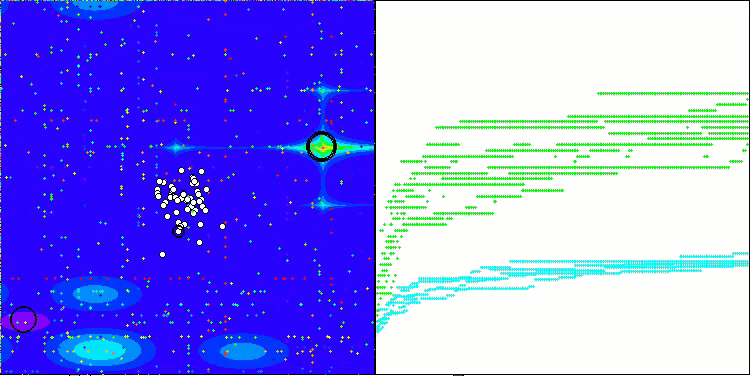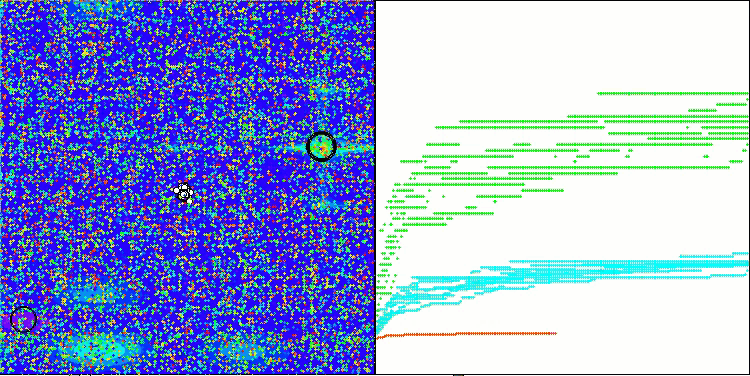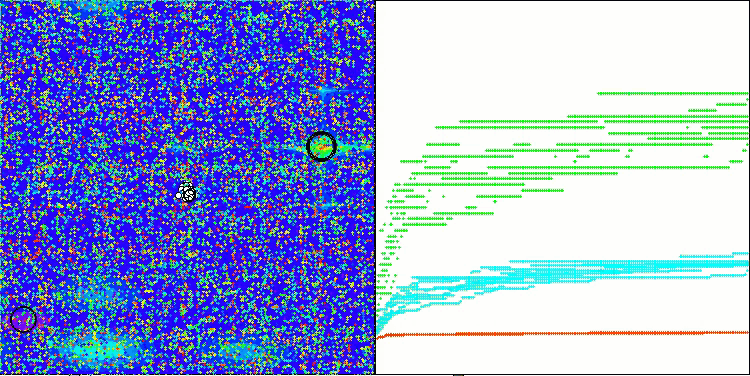
Megacityテスト関数のSOA

テスト結果に基づくと、元のAOAアルゴリズムは順位表に入らず、その結果は45位以下となりました。一方、新しいSimple Optimization Algorithm (SOA)は順位表に入り、最終的に 29位という結果を収めました。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
12	AOSm	原子軌道探索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
13	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
14	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
15	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
16	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
17	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
18	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
19	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
20	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
21	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
22	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
23	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
24	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
25	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
26	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
27	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
28	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
29	SOA	シンプル最適化アルゴリズム	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
30	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
31	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
32	アシャ	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
33	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
34	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
35	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
36	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
37	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
38	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
39	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
40	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
41	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
42	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
43	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
44	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
45	AAA	藻類適応アルゴリズム	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23

まとめ

算術最適化アルゴリズム(AOA)を詳細に検討しました。その実装は非常に単純であることがわかりました。しかし、時として単純さが必ずしも高い成果を保証するわけではありません。本当の成功の鍵は「超単純さ」…もちろん冗談ですが。AOAの主な問題点は、集団内のメンバー間での相互作用や情報交換が欠如していることです。これにより、この探索戦略には組合せ的な特性がほとんど存在しません。

アルゴリズムのもう一つの欠点は、探索演算子の多様性が不足していることです。各座標に対して演算子はランダムに選択されますが、それだけでは探索空間の多次元的な地形を効果的に捉えることができません。しかし、AOAアルゴリズムには合理的で論理的なアプローチも含まれています。たとえば、各エポックごとに変化するMoAおよびMoPの要素です。これらがアルゴリズム再構築の基盤となり、集団の最良解からの情報コピーと探索空間内でのランダム解生成という確率的手法に基づく、新しく興味深く極めて単純な探索戦略へと進化させることができました。

各エポックを通じて、集団の意思決定におけるランダム性は減少し、成功方向への集中度は高まります。これは、川に橋を架ける過程に例えることができます。作業初期には、最終結果に適さない可能性のあるさまざまな材料や設計が試されます。しかし、プロジェクトが進行するにつれて最適な解が明確になり、不要な要素は除去されます。その結果、橋は次第に調和と安定性を備え、両岸を優雅かつ強固に結ぶようになります。

Tab

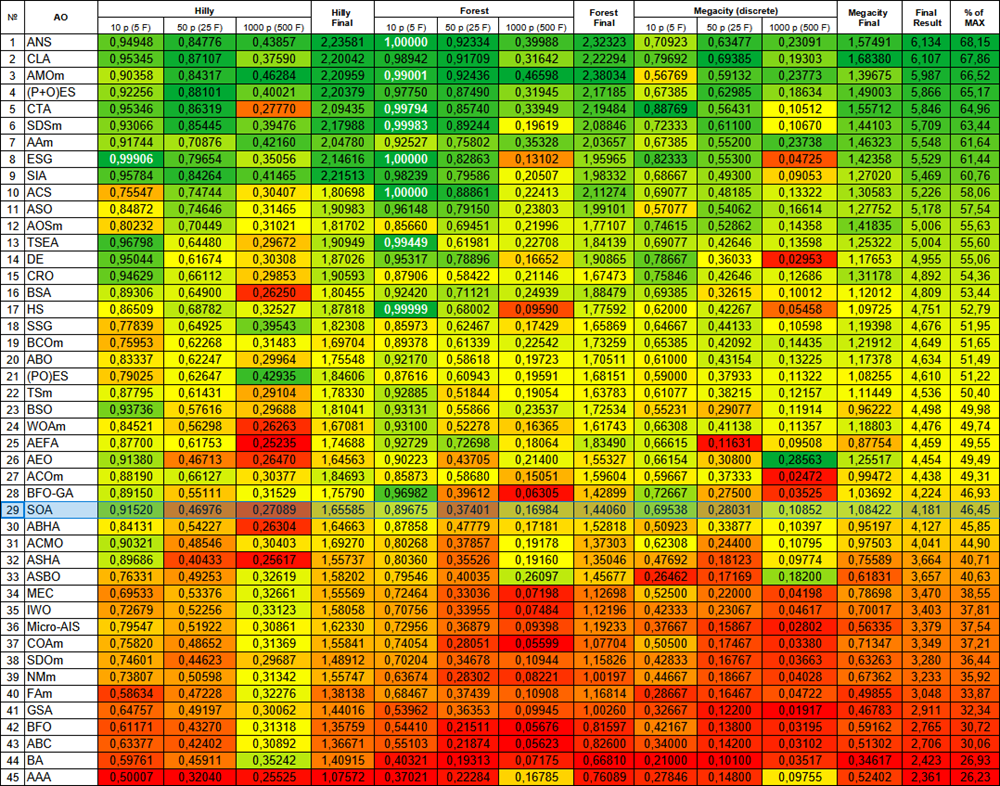
図2：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

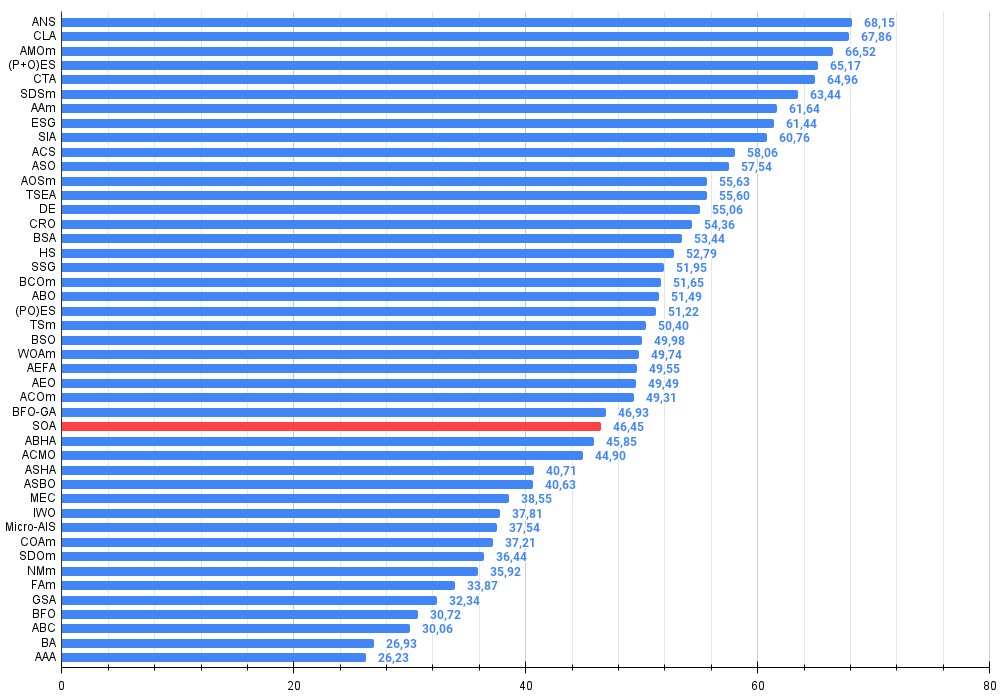
図3：アルゴリズムテスト結果のヒストグラム（0～100のスケール、数値が高いほど良い

ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている）

SOAの長所と短所:

長所

外部パラメータの数が少ない
低次元問題、特に離散問題で良好な結果が得られる
迅速
小次元の問題では結果のばらつきが小さい
実装が非常にシンプル

短所

スケーラビリティが低い

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	TestFunctions.mqh	インクルード	テスト関数のライブラリ
4	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
5	Utilities.mqh	インクルード	補助関数のライブラリ
6	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
7	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
8	Simple use of population optimization algorithms.mq5	スクリプト	可視化せずに集団最適化アルゴリズムを使用する簡単な例
9	AO_AOA_ArithmeticOptimizationAlgorithm.mqh	インクルード	AOAアルゴリズムクラス
10	AO_SOA_SimpleOptimizationAlgorithm.mqh	インクルード	SOAアルゴリズムクラス
11	Test_AO_AOA.mq5	スクリプト	AOAテストスタンド
12	Test_AO_SOA.mq5	スクリプト	SOAテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16364

添付されたファイル |

ZIPをダウンロード

AOA_SOA.zip (141.9 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

株式市場における非線形回帰モデル

株式市場における非線形回帰モデル：金融市場は予測できるのかEURUSDの価格を予測するモデルを作成し、それに基づいて2つのロボット（Python版とMQL5版）を作ることを考えてみましょう。

取引におけるニューラルネットワーク：シャープネス低減によるTransformerの効率向上（最終回）

SAMformerは、長期の時系列予測におけるTransformerモデルの主要な欠点、すなわち学習の複雑さや小規模データセットでの汎化性能の低さに対して解決策を提供します。その浅いアーキテクチャとシャープネス認識型最適化により、不適切な局所解に陥ることを防ぎます。本記事では、MQL5を用いたアプローチの実装を続け、実際的な価値を評価していきます。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

外国為替データ分析における連関規則の使用

スーパーマーケットの小売分析で使われる予測ルールを、実際のFX市場に応用する方法は？クッキー、牛乳、パンの購買傾向と株式市場の取引が関係する方法は？この記事では、連関規則を活用した革新的なアルゴリズム取引手法について解説します。