MetaTrader 5 / Тестер
preview
Алгоритм поиска по кругу — Circle Search Algorithm (CSA)

Алгоритм поиска по кругу — Circle Search Algorithm (CSA)

MetaTrader 5 — Тестер | 14 февраля 2025, 11:55
308 0
Andrey Dik
Andrey Dik

Содержание

  1. Введение
  2. Реализация алгоритма
  3. Результаты тестов


Введение

Алгоритм оптимизации кругового поиска (Circle Search Algorithm, CSA) представляет собой новый метод оптимизации, вдохновленный геометрическими свойствами окружности. Его уникальность заключается в использовании тригонометрических отношений и геометрических принципов для исследования пространства поиска.

В основе CSA лежит интересная идея, где каждая точка поиска движется по траектории, определяемой касательной к окружности, что создает баланс между глобальным исследованием и локальным уточнением решения. Этот подход оригинален благодаря тому, что окружность обладает уникальными математическими свойствами — постоянным радиусом и непрерывной производной, что обеспечивает плавное перемещение агентов в пространстве поиска.

Алгоритм сочетает две фазы: эксплуатацию и исследование. В фазе эксплуатации агенты концентрируются на перспективных областях, двигаясь более направленно, в то время как в фазе исследования они совершают более смелые прыжки в неизведанные области пространства решений. Переход между фазами регулируется механизмом, основанным на текущей итерации и специальном параметре "c".

Что делает CSA особенно привлекательным, так это его способность эффективно работать в многомерных пространствах, сохраняя при этом интуитивно понятную геометрическую интерпретацию. Каждый агент в популяции следует своей уникальной траектории, определяемой углом θ, который динамически корректируется в процессе поиска.

Алгоритм Circle Search Algorithm (CSA) был разработан учеными Mohammad H. Kaiys, Hany M. Hasanien и другими и был опубликован в 2022 году.


Реализация алгоритма

Алгоритм CSA (Circle Search Algorithm) нацелен на поиск оптимального решения в случайных кругах с целью расширения зоны поиска. Он использует центр круга как целевую точку. Процесс начинается с того, что угол между касательной и кругом постепенно уменьшается, что позволяет касательной приближаться к центру (рисунок 1).

Для обеспечения разнообразия в поиске и избежания зависания в локальных оптимумах, угол касательного контакта также меняется случайным образом. В контексте алгоритма, точка касания "Xt" выступает в роли поискового агента, тогда как центральная точка "Xc" обозначает наилучшее найденное решение.

circle-geometry

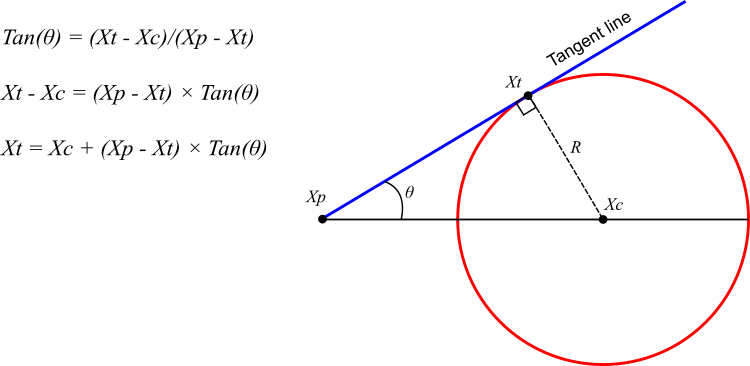
Рисунок 1. Геометрические свойства окружности и ее касательной

Алгоритм CSA адаптирует положение поискового агента в ответ на движение точки касания к центру. Это позволяет улучшать качество решения, при этом случайное обновление угла касательного контакта служит важным механизмом для предотвращения попадания в локальные минимумы. Основные этапы работы оптимизатора CSA представлены ниже на схеме.


csa-visualization

Рисунок 2. Схема работы алгоритма CSA

Далее для каждого агента определяется угол. Если текущая итерация больше, чем произведение порога и максимального количества итераций, агент находится на фазе исследования, иначе — применяется фаза эксплуатации (см. рисунок 2). Позиции агентов обновляются, и осуществляется оценка пригодности каждого из них. Результаты сравниваются с текущим наилучшим решением, и, если находится лучшее, позиция обновляется. Итерация завершается увеличением счетчика итераций. Когда алгоритм завершает выполнение, он возвращает наилучшую найденную позицию и ее значение пригодности.

Алгоритм использует концепцию движения точек по касательной к окружности, где каждый агент поиска движется под определенным углом θ относительно текущего лучшего решения. Это движение регулируется несколькими параметрами (w, a, p), которые меняются со временем. Как отмечено выше, работа алгоритма делится на две фазы: исследование — когда агенты совершают более широкие перемещения для поиска перспективных областей и эксплуатация — когда агенты концентрируются на уточнении найденных решений.

        В окончательной версии, предложенной мной, есть несколько отличий, которые заметно улучшают поисковые способности алгоритма. Изменена формула обновления "w":

        • В оригинале: w = w × rand - w
        • В финальном коде: w = π × (1 - epochNow/epochs) Это сделало изменение параметра "w" более предсказуемым и линейным, что улучшает сходимость алгоритма.
        Модифицирована формула обновления позиции:
        • В оригинале: Xi = Xc + (Xc - Xi) × tan(θ)
        • В финальной версии: Xi = Xc + rand × (Xc - Xi) × tan(θ) Добавление случайного множителя "rand [0.0; 1.0]" придает дополнительную стохастичность поиску и улучшает его по сравнению с оригинальной версией. 
        Оптимизирована фаза обновления:
        • Добавлено обновление локального лучшего решения для каждого агента
        • Улучшена стратегия балансировки между глобальным и локальным поиском

          Основное концептуальное отличие заключается в том, что финальная версия сделала алгоритм более "плавным" и предсказуемым в своем поведении, сохранив при этом способность к поиску. Оригинальный алгоритм был более "хаотичным" в своем поведении, тогда как финальная версия обеспечивает более контролируемый процесс оптимизации, особенно в части перехода между фазами исследования и эксплуатации.

          Теперь можно приступить к написанию псевдокода алгоритма.

          Псевдокод алгоритма Circle Search Algorithm (CSA):

          1. Инициализация:
            • Установить размер популяции (popSize = 50)
            • Задать константу фазы исследования (constC = 0.8)
            • Инициализировать начальные параметры:
              • w = π (параметр угла)
              • a = π
              • p = 1.0
              • θ = 0 (начальный угол)
          2. Если первая итерация (revision = false):
            • Для каждого агента "i" в популяции:
              • Случайно инициализировать координаты в заданных границах
              • Скорректировать координаты в соответствии с шагом изменения
            • Установить revision = true
            • Вернуться в начало
          3. Иначе (основной цикл оптимизации):
            • Увеличить счетчик итераций (epochNow++)
            • Обновить параметры:
              • w = π × (1 - epochNow/epochs) // линейное уменьшение
              • a = π - π × (epochNow/epochs)²
              • p = 1 - 0.9 × √(epochNow/epochs)
          4. Для каждого агента в популяции:
            • Определить текущую фазу:
              • Если epochNow ≤ constC × epochs: → Фаза исследования: θ = w × random [0.0; 1.0]
              • Иначе: → Фаза эксплуатации: θ = w × p
            • Обновить позицию агента:
              • Для каждой координаты j: → new_pos = best_pos + random [0.0; 1.0] × (best_pos - current_pos) × tan (θ) → Скорректировать new_pos в заданных границах
          5. Ревизия результатов:
            • Для каждого агента:
              • Если fitness агента > лучший глобальный fitness: → Обновить глобальное лучшее решение
              • Если fitness агента > лучший локальный fitness: → Обновить локальное лучшее решение агента
          6. Повторять шаги 3-5 до достижения критерия останова

          Переходим к реализации. Класс"C_AO_CSA" представляет собой реализацию алгоритма CSA и наследуется от базового класса "C_AO". Давайте рассмотрим основные его элементы и структуру:

          Конструктор инициализирует параметры алгоритма. Он задает имя и описание алгоритма, а также устанавливает значения для параметров:
          • popSize — размер популяции, равный 50.
          • constC — константа, равная 0.8, используемая в фазе исследования.
          • w, aParam, p, theta — начальные значения параметров, которые будут использованы в алгоритме.
          Методы:
          • SetParams () — метод для установки значений параметров на основе массива данных "params".
          • Init () — этот метод реализован для инициализации параметров, связанных с диапазонами значений и количеством эпох, по которым будет выполняться алгоритм.
          • Moving () — используется для движения частиц и выполнения итераций алгоритма.
          • Revision () — для анализа и корректировки состояния популяции.

          Приватные методы:

          • CalculateW (), CalculateA (), CalculateP (), CalculateTheta () — методы для вычисления соответствующих параметров.
          • IsExplorationPhase () — метод определяет, находится ли алгоритм в фазе исследования.
          //——————————————————————————————————————————————————————————————————————————————
class C_AO_CSA : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_CSA ()
  {
    ao_name = "CSA";
    ao_desc = "Circle Search Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/17143";

    popSize = 50;     // размер популяции
    constC  = 0.8;    // оптимальное значение для фазы исследования
    w       = M_PI;   // начальное значение w
    aParam  = M_PI;   // начальное значение a
    p       = 1.0;    // начальное значение p
    theta   = 0;      // начальное значение угла

    ArrayResize (params, 2);
    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "constC";      params [1].val = constC;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    constC  = params      [1].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения
             const double &rangeMaxP  [],  // максимальные значения
             const double &rangeStepP [],  // шаг изменения
             const int     epochsP = 0);   // количество эпох

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double constC;      // константа для определения фазы поиска [0,1]

  private: //-------------------------------------------------------------------
  int epochs;         // максимальное число итераций
  int epochNow;       // текущая итерация

  // Параметры для CSA
  double w;           // параметр для вычисления угла
  double aParam;      // параметр a из формулы (8)
  double p;           // параметр p из формулы (9)
  double theta;       // угол поиска

  double CalculateW ();
  double CalculateA ();
  double CalculateP ();
  double CalculateTheta (double currentW, double currentP);
  bool IsExplorationPhase ();
};
//——————————————————————————————————————————————————————————————————————————————

          Метод "Init" предназначен для инициализации параметров алгоритма CSA. Его параметры включают массив минимальных значений пространства поиска "rangeMinP []", массив максимальных значений "rangeMaxP []", массив шагов изменения значений "rangeStepP []", а также количество эпох, заданное параметром "epochsP", которое по умолчанию равно 0.

          В процессе выполнения метода вызывается "StandardInit", целью которого является попытка инициализировать стандартные параметры. В случае успешной инициализации устанавливаются значения для переменных "epochs" и "epochNow". Переменная "epochs" получает значение из "epochsP", в то время как "epochNow" обнуляется. Метод завершает выполнение, возвращая "true", что указывает на успешную инициализацию параметров алгоритма.

          //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CSA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

          Метод "Moving" в классе "C_AO_CSA" реализует логику обновления позиций агентов в рамках алгоритма CSA. В начале метода происходит инкремент счетчика текущей эпохи, что позволяет отслеживать, сколько итераций было выполнено (используется в расчетных формулах). Затем выполняется проверка на необходимость инициализации координат агентов. Если это первое выполнение метода, происходит генерация случайных координат для всех агентов в заданных диапазонах. Эти координаты затем адаптируются с учетом заданных шагов. После этого, флаг о необходимости пересмотра устанавливается в истинное значение.

          Если же метод вызывается не в первый раз, то обновляются ключевые параметры алгоритма, такие как "w", "aParam" и "p". Затем для каждого агента вычисляется угол "theta", который используется для обновления его координат. Каждая координата обновляется с учетом координат лучшего агента, влияния случайного фактора и угла "theta". После этого, результаты также корректируются, чтобы оставаться в заданных диапазонах.

          //——————————————————————————————————————————————————————————————————————————————
void C_AO_CSA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int j = 0; j < coords; j++)
      {
        a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]);
        a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  w      = CalculateW ();    // Обновляем w по линейному закону
  aParam = CalculateA ();    // Обновляем a
  p      = CalculateP ();    // Обновляем p

  for (int i = 0; i < popSize; i++)
  {
    theta = CalculateTheta (w, p);

    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = cB [j] + u.RNDprobab () * (cB [j] - a [i].c  [j]) * tan (theta);
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          Метод "Revision" отвечает за обновление лучших решений по всей популяции. Он выполняет проверку текущих значений функций целевых значений агентов и обновляет соответствующие параметры, если находят лучшие решения.

          //——————————————————————————————————————————————————————————————————————————————
void C_AO_CSA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Обновляем лучшее глобальное решение
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          Метод "CalculateW" предназначен для вычисления значения параметра "w", который линейно уменьшается от начального значения (M_PI) до "0" с увеличением количества текущих эпох (epochNow) относительно общего числа эпох (epochs) и возвращает рассчитанное значение "w". Этот рассчитываемый параметр участвует в формуле расчета угла "Theta".

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateW ()
{
  // Линейное уменьшение w от начального значения (M_PI) до 0
  return M_PI * (1.0 - (double)epochNow / epochs);
  //return w * u.RNDprobab () - w;
}
//——————————————————————————————————————————————————————————————————————————————
          Метод "CalculateA" вычисляет значение "aParam", которое уменьшается от "M_PI" до "0" с увеличением "epochNow" через квадратичную зависимость от общего числа эпох "epochs". 
          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateA ()
{
  return M_PI - M_PI * MathPow ((double)epochNow / epochs, 2);
}
//——————————————————————————————————————————————————————————————————————————————

          Метод "CalculateP" вычисляет значение "p", которое уменьшается от "1.0" до "0.1" по мере увеличения "epochNow", то есть зависит от текущей эпохи.

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateP ()
{
  return 1.0 - 0.9 * MathPow ((double)epochNow / epochs, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

          Метод "CalculateTheta" вычисляет значение "Theta", используя текущие параметры "currentW" и "currentP".

          • Если текущая фаза — исследование, возвращает произведение "currentW" на случайное число.
          • В противном случае, возвращает произведение "currentW" на "currentP".

          //——————————————————————————————————————————————————————————————————————————————
double C_AO_CSA::CalculateTheta (double currentW, double currentP)
{
  // Используем параметр aParam для регулировки угла
  if (IsExplorationPhase ()) return currentW * u.RNDprobab ();
  else return currentW * currentP;

}
//——————————————————————————————————————————————————————————————————————————————

          Метод "IsExplorationPhase" проверяет, находится ли текущая итерация в фазе исследования.

          //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CSA::IsExplorationPhase ()
{
  // Исследование в первой части итераций(constC обычно 0.8)
  return (epochNow <= constC * epochs);
}
//——————————————————————————————————————————————————————————————————————————————


          Результаты тестов

          Авторы алгоритма позиционируют его, как высоко результативный метод оптимизации, однако, после реализации и некоторых улучшений и итогового тестирования, результаты работы не очень впечатляют. Алгоритм смог войти в рейтинговую таблицу, но его показатели значительно уступают лучшим алгоритмическим решениям на данный момент.

          CSA|Circle Search Algorithm|50.0|0.8|
          =============================
          5 Hilly's; Func runs: 10000; result: 0.6656012653478078
          25 Hilly's; Func runs: 10000; result: 0.4531682514562617
          500 Hilly's; Func runs: 10000; result: 0.2912586479936386
          =============================
          5 Forest's; Func runs: 10000; result: 0.6879687203647712
          25 Forest's; Func runs: 10000; result: 0.41397289345600924
          500 Forest's; Func runs: 10000; result: 0.2052507546137296
          =============================
          5 Megacity's; Func runs: 10000; result: 0.3753846153846153
          25 Megacity's; Func runs: 10000; result: 0.2363076923076922
          500 Megacity's; Func runs: 10000; result: 0.10646153846153927
          =============================
          All score: 3.43537 (38.17%)

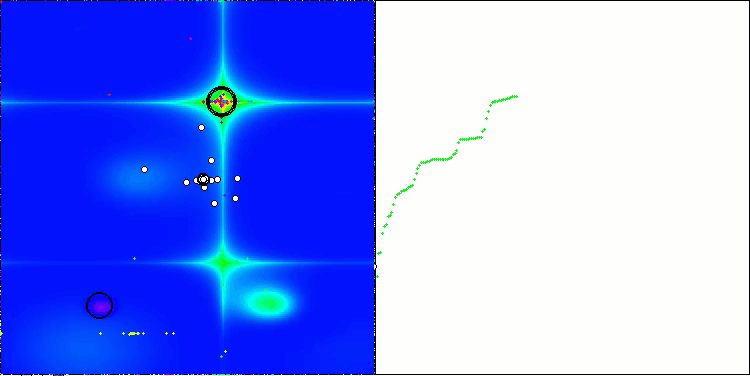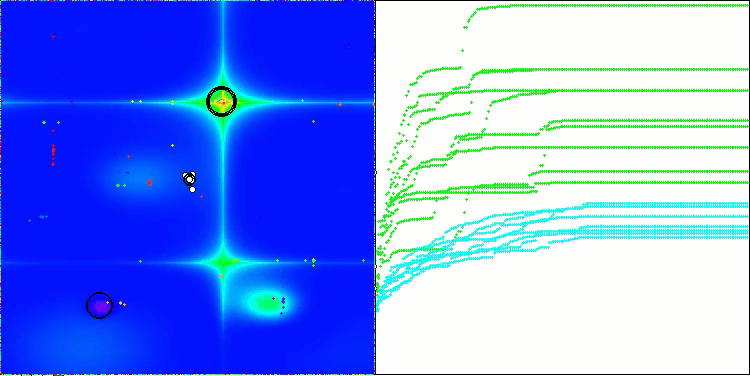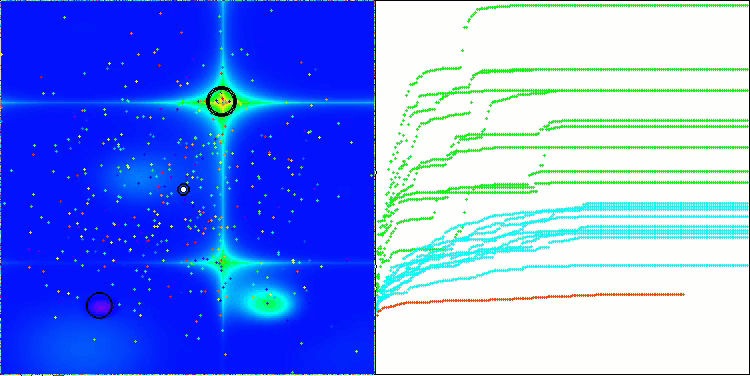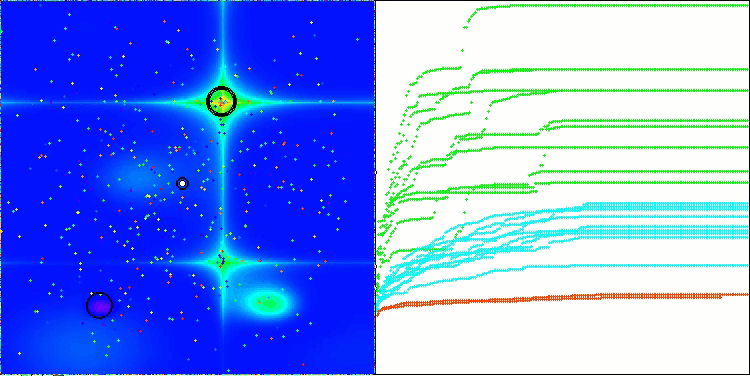
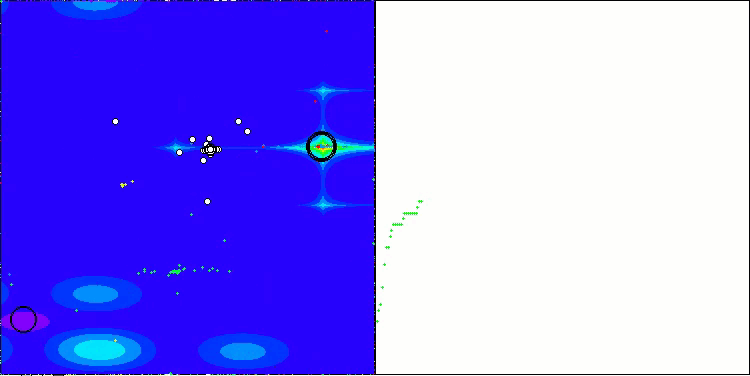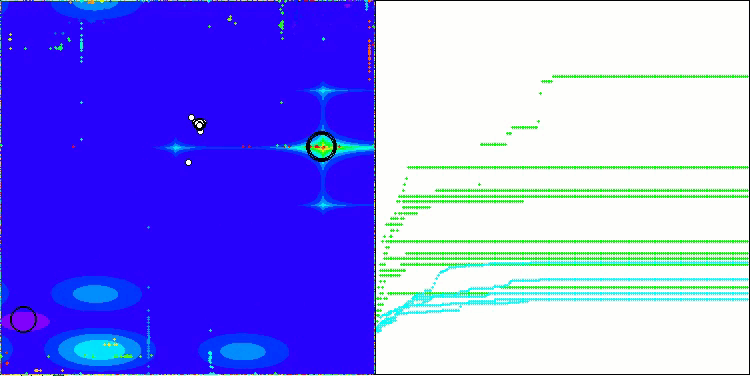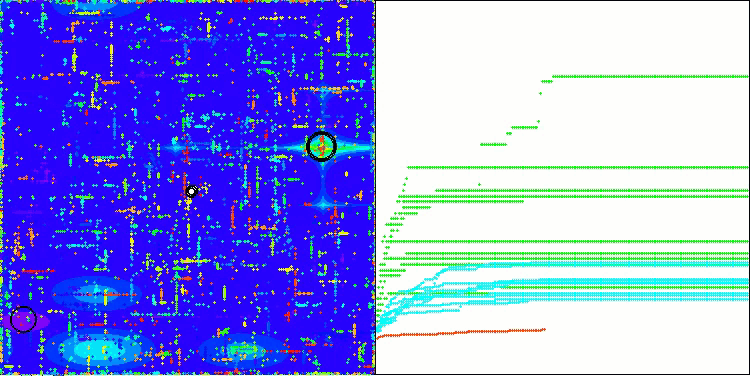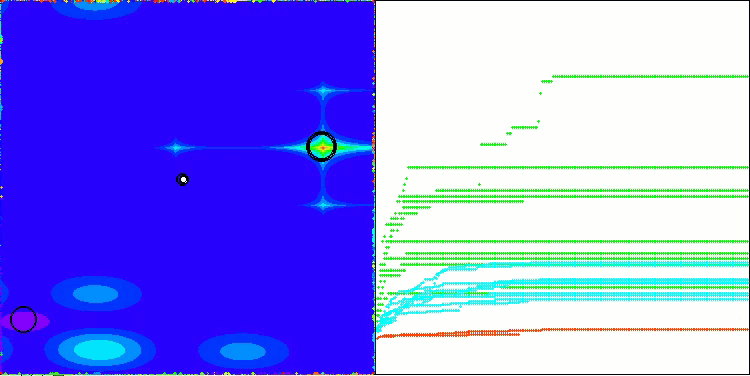
          На визуализации работы алгоритма заметны проблемы со сходимостью и застреванием в локальных экстремумах. Тем не менее, алгоритм старается работать по максимуму своих возможностей. Несмотря на проблемы с застреванием в ловушках (это хорошо заметно по продолжительным горизонтальным участкам на графике сходимости), можно выделить его способность работать достаточно результативно на задачах высоких размерностей.

          Hilly

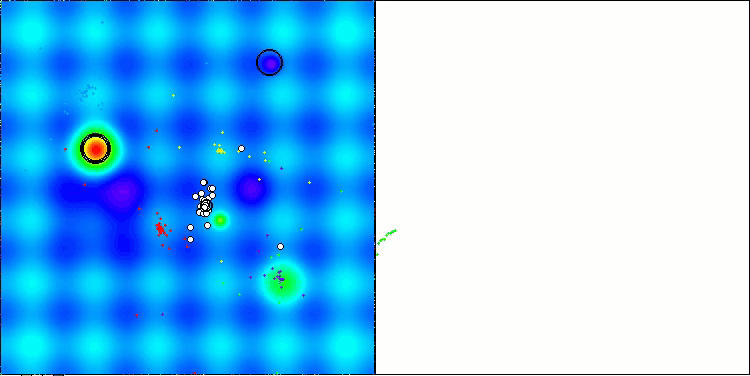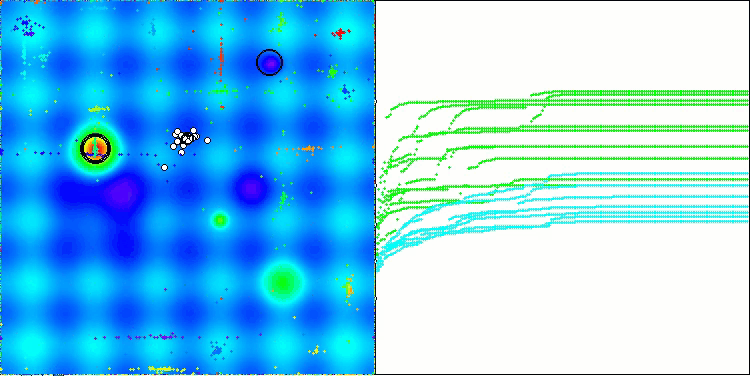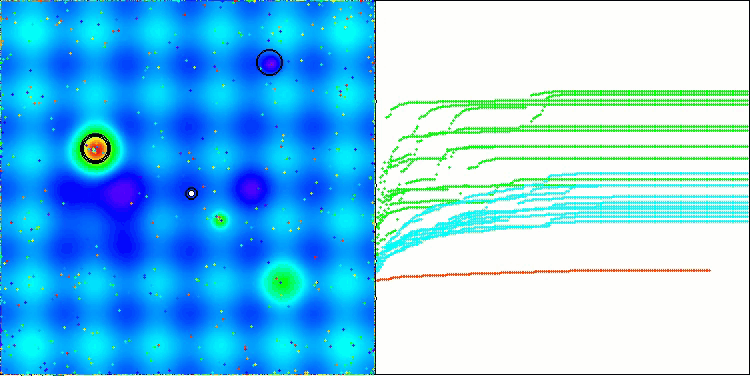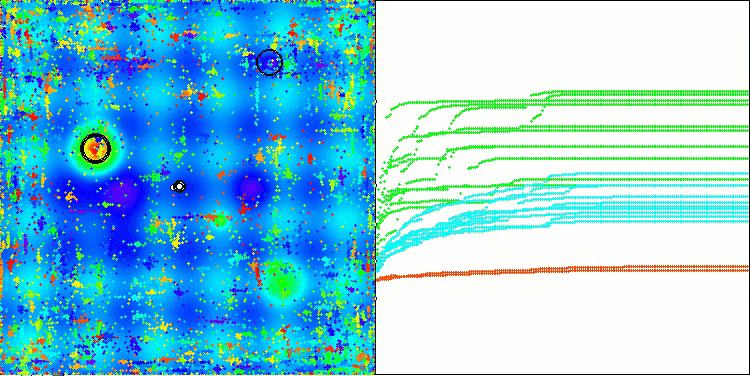
          CSA на тестовой функции Hilly

          Forest

          CSA на тестовой функции Forest

          Megacity

          CSA на тестовой функции Megacity

          По результатам тестирования алгоритма CSA занимает 41 место в рейтинговой таблице.

          № AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
          10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
          1 ANS across neighbourhood search 0,94948 0,84776 0,43857 2,23581 1,00000 0,92334 0,39988 2,32323 0,70923 0,63477 0,23091 1,57491 6,134 68,15
          2 CLA code lock algorithm (joo) 0,95345 0,87107 0,37590 2,20042 0,98942 0,91709 0,31642 2,22294 0,79692 0,69385 0,19303 1,68380 6,107 67,86
          3 AMOm animal migration ptimization M 0,90358 0,84317 0,46284 2,20959 0,99001 0,92436 0,46598 2,38034 0,56769 0,59132 0,23773 1,39675 5,987 66,52
          4 (P+O)ES (P+O) evolution strategies 0,92256 0,88101 0,40021 2,20379 0,97750 0,87490 0,31945 2,17185 0,67385 0,62985 0,18634 1,49003 5,866 65,17
          5 CTA comet tail algorithm (joo) 0,95346 0,86319 0,27770 2,09435 0,99794 0,85740 0,33949 2,19484 0,88769 0,56431 0,10512 1,55712 5,846 64,96
          6 TETA time evolution travel algorithm (joo) 0,91362 0,82349 0,31990 2,05701 0,97096 0,89532 0,29324 2,15952 0,73462 0,68569 0,16021 1,58052 5,797 64,41
          7 SDSm stochastic diffusion search M 0,93066 0,85445 0,39476 2,17988 0,99983 0,89244 0,19619 2,08846 0,72333 0,61100 0,10670 1,44103 5,709 63,44
          8 AAm archery algorithm M 0,91744 0,70876 0,42160 2,04780 0,92527 0,75802 0,35328 2,03657 0,67385 0,55200 0,23738 1,46323 5,548 61,64
          9 ESG evolution of social groups (joo) 0,99906 0,79654 0,35056 2,14616 1,00000 0,82863 0,13102 1,95965 0,82333 0,55300 0,04725 1,42358 5,529 61,44
          10 SIA simulated isotropic annealing (joo) 0,95784 0,84264 0,41465 2,21513 0,98239 0,79586 0,20507 1,98332 0,68667 0,49300 0,09053 1,27020 5,469 60,76
          11 ACS artificial cooperative search 0,75547 0,74744 0,30407 1,80698 1,00000 0,88861 0,22413 2,11274 0,69077 0,48185 0,13322 1,30583 5,226 58,06
          12 DA dialectical algorithm 0,86183 0,70033 0,33724 1,89940 0,98163 0,72772 0,28718 1,99653 0,70308 0,45292 0,16367 1,31967 5,216 57,95
          13 BHAm black hole algorithm M 0,75236 0,76675 0,34583 1,86493 0,93593 0,80152 0,27177 2,00923 0,65077 0,51646 0,15472 1,32195 5,196 57,73
          14 ASO anarchy society optimization 0,84872 0,74646 0,31465 1,90983 0,96148 0,79150 0,23803 1,99101 0,57077 0,54062 0,16614 1,27752 5,178 57,54
          15 RFO royal flush optimization (joo) 0,83361 0,73742 0,34629 1,91733 0,89424 0,73824 0,24098 1,87346 0,63154 0,50292 0,16421 1,29867 5,089 56,55
          16 AOSm atomic orbital search M 0,80232 0,70449 0,31021 1,81702 0,85660 0,69451 0,21996 1,77107 0,74615 0,52862 0,14358 1,41835 5,006 55,63
          17 TSEA turtle shell evolution algorithm (joo) 0,96798 0,64480 0,29672 1,90949 0,99449 0,61981 0,22708 1,84139 0,69077 0,42646 0,13598 1,25322 5,004 55,60
          18 DE differential evolution 0,95044 0,61674 0,30308 1,87026 0,95317 0,78896 0,16652 1,90865 0,78667 0,36033 0,02953 1,17653 4,955 55,06
          19 CRO chemical reaction optimisation 0,94629 0,66112 0,29853 1,90593 0,87906 0,58422 0,21146 1,67473 0,75846 0,42646 0,12686 1,31178 4,892 54,36
          20 BSA bird swarm algorithm 0,89306 0,64900 0,26250 1,80455 0,92420 0,71121 0,24939 1,88479 0,69385 0,32615 0,10012 1,12012 4,809 53,44
          21 HS harmony search 0,86509 0,68782 0,32527 1,87818 0,99999 0,68002 0,09590 1,77592 0,62000 0,42267 0,05458 1,09725 4,751 52,79
          22 SSG saplings sowing and growing 0,77839 0,64925 0,39543 1,82308 0,85973 0,62467 0,17429 1,65869 0,64667 0,44133 0,10598 1,19398 4,676 51,95
          23 BCOm bacterial chemotaxis optimization M 0,75953 0,62268 0,31483 1,69704 0,89378 0,61339 0,22542 1,73259 0,65385 0,42092 0,14435 1,21912 4,649 51,65
          24 ABO african buffalo optimization 0,83337 0,62247 0,29964 1,75548 0,92170 0,58618 0,19723 1,70511 0,61000 0,43154 0,13225 1,17378 4,634 51,49
          25 (PO)ES (PO) evolution strategies 0,79025 0,62647 0,42935 1,84606 0,87616 0,60943 0,19591 1,68151 0,59000 0,37933 0,11322 1,08255 4,610 51,22
          26 TSm tabu search M 0,87795 0,61431 0,29104 1,78330 0,92885 0,51844 0,19054 1,63783 0,61077 0,38215 0,12157 1,11449 4,536 50,40
          27 BSO brain storm optimization 0,93736 0,57616 0,29688 1,81041 0,93131 0,55866 0,23537 1,72534 0,55231 0,29077 0,11914 0,96222 4,498 49,98
          28 WOAm wale optimization algorithm M 0,84521 0,56298 0,26263 1,67081 0,93100 0,52278 0,16365 1,61743 0,66308 0,41138 0,11357 1,18803 4,476 49,74
          29 AEFA artificial electric field algorithm 0,87700 0,61753 0,25235 1,74688 0,92729 0,72698 0,18064 1,83490 0,66615 0,11631 0,09508 0,87754 4,459 49,55
          30 AEO artificial ecosystem-based optimization algorithm 0,91380 0,46713 0,26470 1,64563 0,90223 0,43705 0,21400 1,55327 0,66154 0,30800 0,28563 1,25517 4,454 49,49
          31 ACOm ant colony optimization M 0,88190 0,66127 0,30377 1,84693 0,85873 0,58680 0,15051 1,59604 0,59667 0,37333 0,02472 0,99472 4,438 49,31
          32 BFO-GA bacterial foraging optimization - ga 0,89150 0,55111 0,31529 1,75790 0,96982 0,39612 0,06305 1,42899 0,72667 0,27500 0,03525 1,03692 4,224 46,93
          33 SOA simple optimization algorithm 0,91520 0,46976 0,27089 1,65585 0,89675 0,37401 0,16984 1,44060 0,69538 0,28031 0,10852 1,08422 4,181 46,45
          34 ABHA artificial bee hive algorithm 0,84131 0,54227 0,26304 1,64663 0,87858 0,47779 0,17181 1,52818 0,50923 0,33877 0,10397 0,95197 4,127 45,85
          35 ACMO atmospheric cloud model optimization 0,90321 0,48546 0,30403 1,69270 0,80268 0,37857 0,19178 1,37303 0,62308 0,24400 0,10795 0,97503 4,041 44,90
          36 ADAMm adaptive moment estimation M 0,88635 0,44766 0,26613 1,60014 0,84497 0,38493 0,16889 1,39880 0,66154 0,27046 0,10594 1,03794 4,037 44,85
          37 ATAm artificial tribe algorithm M 0,71771 0,55304 0,25235 1,52310 0,82491 0,55904 0,20473 1,58867 0,44000 0,18615 0,09411 0,72026 3,832 42,58
          38 ASHA artificial showering algorithm 0,89686 0,40433 0,25617 1,55737 0,80360 0,35526 0,19160 1,35046 0,47692 0,18123 0,09774 0,75589 3,664 40,71
          39 ASBO adaptive social behavior optimization 0,76331 0,49253 0,32619 1,58202 0,79546 0,40035 0,26097 1,45677 0,26462 0,17169 0,18200 0,61831 3,657 40,63
          40 MEC mind evolutionary computation 0,69533 0,53376 0,32661 1,55569 0,72464 0,33036 0,07198 1,12698 0,52500 0,22000 0,04198 0,78698 3,470 38,55
          41 CSA circle search algorithm 0,66560 0,45317 0,29126 1,41003 0,68797 0,41397 0,20525 1,30719 0,37538 0,23631 0,10646 0,71815 3,435 38,17
          42 IWO invasive weed optimization 0,72679 0,52256 0,33123 1,58058 0,70756 0,33955 0,07484 1,12196 0,42333 0,23067 0,04617 0,70017 3,403 37,81
          43 Micro-AIS micro artificial immune system 0,79547 0,51922 0,30861 1,62330 0,72956 0,36879 0,09398 1,19233 0,37667 0,15867 0,02802 0,56335 3,379 37,54
          44 COAm cuckoo optimization algorithm M 0,75820 0,48652 0,31369 1,55841 0,74054 0,28051 0,05599 1,07704 0,50500 0,17467 0,03380 0,71347 3,349 37,21
          45 SDOm spiral dynamics optimization M 0,74601 0,44623 0,29687 1,48912 0,70204 0,34678 0,10944 1,15826 0,42833 0,16767 0,03663 0,63263 3,280 36,44
          RW random walk 0,48754 0,32159 0,25781 1,06694 0,37554 0,21944 0,15877 0,75375 0,27969 0,14917 0,09847 0,52734 2,348 26,09


          Выводы

          По результатам тестирования и анализа работы алгоритма Circle Search Algorithm (CSA) можно сделать следующие выводы: несмотря на элегантность геометрической концепции и интуитивно понятный механизм поиска, основанный на движении по касательным к окружности, алгоритм демонстрирует относительно слабые результаты в сравнительном анализе, занимая 41 место из 45 в рейтинговой таблице алгоритмов оптимизации. Такое положение указывает на существенные ограничения в его текущей реализации.

          Основные проблемы алгоритма связаны с его тенденцией застревать в локальных экстремумах, что особенно заметно при работе на простых задачах малой размерности. Это может быть обусловлено несколькими факторами: во-первых, механизм поиска по углам, хотя и кажется перспективным, на практике оказывается недостаточно эффективным для преодоления локальных оптимумов. Во-вторых, баланс между фазами исследования и эксплуатации, регулируемый параметром "constC", не обеспечивает достаточной диверсификации поиска. Вся популяция схлопывается к псевдо хорошим решениям, то есть в одну точку, при этом не помогли даже попытки "встряхивать" популяцию случайной компонентой в основной формуле обновления положении агентов в пространстве решений.

          Попытка улучшить алгоритм, путем добавления случайного множителя в формулу обновления позиций агентов, хотя и привела к более предсказуемому поведению алгоритма, но не смогла существенно повысить его эффективность. Это может свидетельствовать о том, что базовая идея алгоритма, основанная на геометрических свойствах окружности, либо не полностью раскрыта авторами в текущей реализации, либо имеет фундаментальные ограничения в контексте глобальной оптимизации.

          Тем не менее, алгоритм демонстрирует определенные поисковые способности и может быть эффективен для некоторых специфических задач, особенно тех, где ландшафт целевой функции относительно прост. Для повышения эффективности алгоритма, могу порекомендовать пользователям дальнейшие исследования в направлении улучшения механизма выхода из локальных оптимумов, возможно, путем введения дополнительных механизмов диверсификации поиска или гибридизации с другими методами оптимизации (как приоритетное направление —использование данной стратегии поиска в других алгоритмах оптимизации в качестве компонента).

          Tab

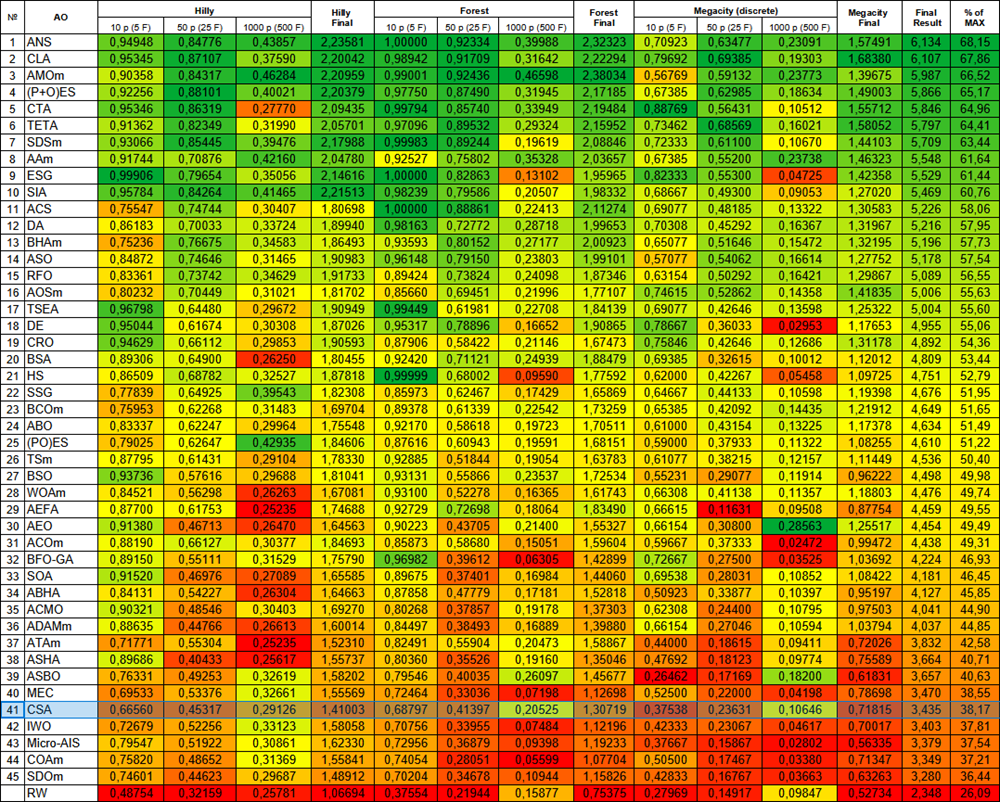
          Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам

          Chart

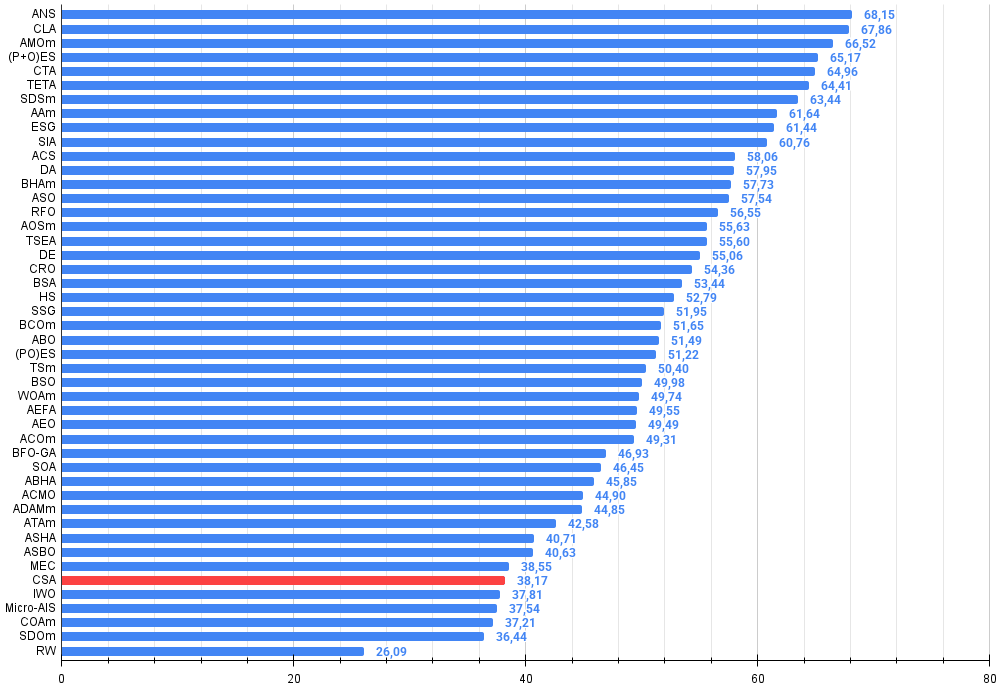
          Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)


          Плюсы и минусы алгоритма CSA:

          Плюсы:

          1. Очень мало внешних параметров
          2. Простая реализация
          3. Интересная идея использования геометрических свойств окружности

          Минусы:

          1. Низкая точность сходимости
          2. Застревает в локальных экстремумах

          К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

          Программы, используемые в статье

          # Имя Тип Описание
          1 #C_AO.mqh
          		 Включаемый файл
          		 Родительский класс популяционных алгоритмов оптимизации
          2 #C_AO_enum.mqh
          		 Включаемый файл
          		 Перечисление популяционных алгоритмов оптимизации
          3 TestFunctions.mqh
          		 Включаемый файл
          		 Библиотека тестовых функций
          4
          		 TestStandFunctions.mqh
          		 Включаемый файл
          		 Библиотека функций тестового стенда
          5
          		 Utilities.mqh
          		 Включаемый файл
          		 Библиотека вспомогательных функций
          6
          		 CalculationTestResults.mqh
          		 Включаемый файл
          		 Скрипт для расчета результатов в сравнительную таблицу
          7
          		 Testing AOs.mq5
          		 Скрипт Единый испытательный стенд для всех популяционных алгоритмов оптимизации
          8
          		 Simple use of population optimization algorithms.mq5
          		 Скрипт
          		 Простой пример использования популяционных алгоритмов оптимизации без визуализации
          9
          		 Test_AO_CSA.mq5
          		 Скрипт Испытательный стенд для CSA
          Прикрепленные файлы |
          Загрузить ZIP
          CSA.ZIP (162.81 KB)
          Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

          Другие статьи автора

          Перейти к обсуждению на форуме трейдеров
          Разрабатываем мультивалютный советник (Часть 22): Начало перехода на горячую замену настроек Разрабатываем мультивалютный советник (Часть 22): Начало перехода на горячую замену настроек
          Если мы взялись за автоматизацию проведения периодической оптимизации, то надо позаботиться и об автоматическом обновлении настроек советников, которые уже работают на торговом счёте. Также это должно позволять запускать советник в тестере стратегий и менять его настройки в рамках одного прохода.
          От начального до среднего уровня: Массивы и строки (I) От начального до среднего уровня: Массивы и строки (I)
          В сегодняшней статье мы начнем изучать некоторые особые типы данных. Для начала мы определим, что такое строка, и объясним, как использовать некоторые базовые процедуры. Это позволит нам работать с этим типом данных, который может быть интересным, хотя иногда и немного запутанным для новичков. Представленные здесь материалы предназначены только для обучения. Ни в коем случае нельзя рассматривать это приложение как окончательное, цели которого будут иные, кроме изучения представленных концепций.
          Упрощаем торговлю на новостях (Часть 3): Совершаем сделки Упрощаем торговлю на новостях (Часть 3): Совершаем сделки
          В этой статье наш советник новостной торговли начнет открывать сделки на основе экономического календаря, хранящегося в нашей базе данных. Кроме того, мы улучшим графику советника, чтобы отображать более актуальную информацию о предстоящих событиях экономического календаря.
          Оптимизация портфеля на языках Python и MQL5 Оптимизация портфеля на языках Python и MQL5
          В этой статье рассмотрены передовые методы оптимизации портфеля с использованием языков Python и MQL5 на платформе MetaTrader 5. В ней демонстрируется, как разрабатывать алгоритмы для анализа данных, распределения активов и генерации торговых сигналов, подчеркивая значимость принятия решений на основе данных в современном финансовом менеджменте и снижении рисков.