MetaTrader 5 / テスター
English Русский Español Deutsch Português
preview
人工散布アルゴリズム(ASHA)

人工散布アルゴリズム(ASHA)

MetaTrader 5 — テスター | 22 5月 2025, 08:46
50 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

近年、データ量の急増とタスクの複雑化・高エネルギー化により、効果的な最適化手法の必要性はこれまで以上に高まっています。高い収束性と処理速度を兼ね備えたメタヒューリスティックアルゴリズムは、金融市場から科学研究に至るまで、さまざまな分野で多様な課題を解決するための新たな可能性を切り拓いています。

プロジェクトの成功においては、データ処理のスピードと得られる解の質が鍵を握ります。特に厳しい時間的制約下では、従来の数値解析手法では到達が困難だった結果に対しても、メタヒューリスティックアルゴリズムにより到達可能となります。これらの手法は大量の情報を迅速に処理できるだけでなく、より優れた解の導出にも寄与します。

最適化においては、リソースの節約も重要な観点です。計算資源が限られる環境、特にクラウドコンピューティングにおいては、こうしたアルゴリズムの「高速・省メモリ性」が特に有用です。また、変化する環境への適応力や新たなデータへの即応性にも優れており、動的なシステムにおける実運用にも適しています。これにより、解の妥当性を維持しつつ、実世界の問題に対する解決効率の向上が図れます。

さらに、収束速度、解の品質、局所最適に陥るリスクへの耐性といった特性に基づいてアルゴリズムを比較することで、より高性能な手法の選定が可能になります。これは、しばしば自然現象に着想を得た新たなアルゴリズムの開発と技術革新を促進するものであり、最適化分野における重要なステップです。

人工散布アルゴリズム(ASHA)は、一般的な最適化問題を解くために開発された新しいメタヒューリスティック手法です。本アルゴリズムは、人為的に制御された装置によって理想的なフィールドに水を分配する過程、すなわち水の流れと蓄積をモデル化することに基づいています。ASHAでは、検索空間をフィールド、水をリソース単位とみなし、フィールド上への水の散布（シャワリング）を通じて最適解を探索します。このようにして、流動と蓄積の原理を活用し、制約のない最適化問題に対する有効な解を導きます。人工散布アルゴリズム(ASHA)は、Ali J., M. Saeed, N.A.Chaudhry, M. Luqman and M. F.Tabassumによって開発され、2015年に出版されました。


アルゴリズムの実装

この手法は次のことを基本としています。

  1. 理想的なフィールド：探索空間は、水が抵抗なく流れ、最も低い地点でのみ浸透が発生する理想的なフィールドとします。
  2. 外的要因なし：蒸発、降雨、水の流入といった外的要因は存在しません。
  3. 散布装置の可用性：探索空間のすべての領域は、フィールド上空に配置された散布装置の射程内にあります。
  4. 一定量の水：余分な水があり、閉鎖系内のその量はすべての反復を通じて一定のままです。
  5. 水の動き：各水ユニットは、傾斜に沿って低い方へ移動する確率的な傾向を持ちます。

以下は、ASHAの手順ごとの説明です。

アルゴリズムのパラメータは次の通りです。

  • f：最小化される目的関数
  • R*n：n次元探索空間
  • K：反復回数（現在のステップ）
  • m：水ユニットの数（検索エージェント）
  • F：水流量
  • δ：抵抗レベル（浸潤閾値）
  • ρ₀：初期確率
  • β：確率変化率
  • M：最大反復回数

 以下はアルゴリズムの手順です。

1. 初期化

    初期値ρ = ρ₀を設定する
    m個の水ユニットを生成し、R*nの探索空間内にランダムに配置する

2. 地形評価：各水ユニットに対して、現在位置における目的関数fの値を計算する

3. メインループ（M回繰り返す）：各水ユニットi (1 ≤ i ≤ m)に対して以下を実行する：

   a) 乱数 r_i ∈ (0, 1) を生成する
   b) r_i < ρの場合:
       現在位置より下の位置x_lowerをランダムに選択する
       ランダムベクトルs∈(0,1)*nを生成する
       新しい位置を次の式で計算する：
          x_new = x_old + F × (s ∘ (x_lower  x_old))
          （∘は要素ごとの乗算）
       x_newがx_oldより低い位置にある場合：
          新しい位置を受け入れる
       そうでない場合：
          乱数r∈(0, 1)を生成する
          すべての水ユニットの中で最も低い位置x_lowestを見つける
          以下で新しい位置を計算する：
             x_new = x_old + F × r × (x_lowest  x_old)
   c) 浸透の確認
      水ユニットが抵抗レベル δ を超えた場合：
       ランダムな位置に新しい水ユニットを生成する
   d) 最小値との比較
       目的関数の値が最も小さい水ユニットを特定する
       現在の水ユニットの目的関数値がそれより小さい場合は、位置を交換する
   e) 確率の更新：ρ = max((M：K) / (β × M), ρ₀)

4.完了

    目的関数の値が最小の水ユニットを見つける
    その位置を最良解として返す

以下は、アルゴリズムの説明です。

1. このアルゴリズムは、フィールドへの散水プロセスをシミュレートし、各水ユニットを探索エージェントとして扱います。
2. 探索空間は地形と見なされ、目的関数の値が低いほど、その点は地形上の低所に相当します。
3. 水ユニットは、目的関数の最小値に対応する低い地点へ「流れる」傾向があります。
4.パラメータρは、空間の探索（ρが大きいとき）と既知解の活用（ρが小さいとき）のバランスを制御します。
5. 浸透メカニズムにより、水ユニットが局所最小に停滞するのを回避するため、ランダムな位置に新たな水ユニットが生成されます。
6. 最小値との比較と交換により、現在までに見つかった最良解が保持されます。
7. ρを動的に更新することで、アルゴリズムは繰り返しの進行に伴い、探索フェーズから活用フェーズへと徐々に移行します。

このアルゴリズムは、水の流れを最適化プロセスに見立てたものであり、水（探索エージェント）が地形上の最も低い地点（目的関数の最小値）を目指して移動します。

著者によると、このアルゴリズムの主な利点は次のとおりです。

  1. 水のランダムな移動により、広範な解探索空間をカバーできる。
  2. 浸透メカニズムにより、局所最小値への収束を回避できる。
  3. ρの確率的変化による動的適応により、状況に応じた柔軟な動作が可能。

アルゴリズムで使用されるすべての方程式を詳しく考えてみましょう。

1. 確率ρが満たされた場合の位置更新式：x_new = x_old + F × (s ∘ (x_lower：x_old))、ここで

  • x_new：水ユニットの新しい位置
  • x_old：水ユニットの現在の位置
  • F：水流量（アルゴリズムのパラメータ）
  • s：範囲 (0, 1)のランダムベクトル
  • x_lower：現在の位置よりも低いランダムな位置
  • ∘：要素ごとの乗算演算子

この式は、水が斜面を下るような挙動を模倣しています。ベクトルsによって移動方向にランダム性が加わり、Fは移動のステップサイズを調整します。

2. 確率ρ条件を満たさなかった場合の代替位置更新式：x_new = x_old + F × r × (x_lowest：x_old)、ここで

  • r：範囲(0, 1)の乱数
  • x_lowest：すべての水ユニットの中で最も目的関数の値が小さい位置

この式は、基本式で改善が得られない場合に用いられ、水ユニットを全域的最小値の方向へ移動させることを目的としています。

これらの式から分かるように、水ユニットは常により低い位置（＝目的関数が小さい位置）に向かって移動しようとします。アルゴリズムがこのステップまでしか実装されていない場合、必然的に局所的な極値に陥ってしまいます。

3. 確率更新式ρ = max ((M：K) / (β × M), ρ₀)、ここで

  • ρ：現在の移動確率
  • M：最大反復回数
  • K：現在の反復回数
  • β：確率変化率
  • ρ₀：初期確率

この式は、水がランダムに選ばれた低い位置へ移動する確率を徐々に減少させ、大域的最小値に向かって移動する確率を増加させます。これにより、アルゴリズムは空間の探索から、見つかった解の洗練へと徐々に移行することが可能になります。

4.浸透条件f (x_current) < δによる新規水ユニットの生成 

  • f (x_current)：現在位置における目的関数の値
  • δ：抵抗レベル（浸潤閾値）

この条件は、水が十分に「低い地点」に到達したと判断された場合、新たな水ユニットを導入し、探索の多様性を高め、局所解への収束を防ぐ効果があります。

5. 位置比較と入れ替え条件：f (x_i) < f (x_lowest)のとき、x_iとx_lowestを交換、ここで

  • f (x_i)：i番目の水ユニットにおける目的関数の値
  • f (x_lowest)：全体で最も小さい目的関数の値

上記の式は、ASHAアルゴリズムの基礎を成しています。

  1. 位置更新式は、水が斜面を下る動きを模倣したものです。ランダム要素（sまたはr）により、解空間の異なる領域を探索できるようになり、探索に多様性が加わります。
  2. 代替の位置更新式は、各反復ごとにその使用確率が高まり、大域解の精緻化が反復を重ねるごとに進むよう設計されています。
  3. ρの確率更新式は、探索と活用のバランスを取る役割を果たします。アルゴリズムの初期段階では、地形内でランダムに選ばれた低い位置へ移動する確率が高く、これによって空間全体を広く探索します。反復が進むにつれてこの確率は減少し、有望な領域に対してより集中的に探索をおこなうようになります。
  4. 浸透条件は、ある水ユニットが十分に良い解（目的関数の値が小さい）を見つけたときに、探索を新たなランダム位置から「再開」させる役割を担っています。これにより、局所的な最小値に陥るのを防ぐ効果があります。
  5. 位置の比較は、アルゴリズムが常に最良解を「記憶」し、それを基準として今後の探索を導けるようにするための仕組みです。

つまり、アルゴリズムの基本的な方針は、まずランダムに選んだ低い位置に向かって移動しようとし、それがうまくいかなかった場合には、これまでに見つかった最良の位置に向かって移動を試みるというものです。これにより、解空間の局所的な探索と大域的な探索のバランスが取られています。

ASHAアルゴリズムにおける「浸透」の原理は、一見してすぐに理解できるものではないかもしれません。ここで少し詳しく見ていきましょう。

  1. δ (デルタ) パラメータは、抵抗レベルまたは浸透閾値と呼ばれます。
  2. 各反復において、すべての水ユニットについて、その目的関数の値が「非常に低く」なった、つまりδを下回っているかどうかを確認します。
  3. ある水ユニットの目的関数の値がδ未満になった場合、その水は「地面に浸透した」とみなされます。
  4. このとき、探索空間内のランダムな位置に新たな水ユニットを1つ生成します。

正式には、この動作は次のように表現できます： if f (x_i) < δ, x_i = random_position ()、ここでf (x_i)はi番目の水ユニットにおける目的関数の値、x_iはその水ユニットの現在位置を表します。

このメカニズムの目的は、すべての水ユニットが単一の局所最小に閉じ込められるのを防ぐこと、良好な解が見つかった後でも探索を継続すること、そして未踏の領域においてさらに優れた解を発見する可能性を残すことにあります。

ここで重要になるのが、δの値の設定です。δが小さすぎると、浸透（= ランダムな再配置）がまったく発生せず、局所解にとどまり続けてしまう可能性があります。逆に、δ が大きすぎると、アルゴリズムが頻繁に「再起動」してしまい、最適解にたどり着く前に探索がリセットされ続けてしまいます。さらに困難なのは、目的関数の値の範囲が事前に分からない場合、δを適切に設定するのが容易ではないという点です。そのため私は、各水ユニットに対して「浸透の試行回数」をカウントする仕組みを導入し、外部パラメータとしてその最大試行回数を設定する方法を取りました。そして試行を繰り返すごとに、「浸透が発生する確率」が 二次関数的に増加するように設計しています。この仕組みによって、どの水ユニットも同じ場所に長く留まり続けることがなくなり、局所的な極値に閉じ込められるリスクが大幅に軽減されます。

フォーミュラセス

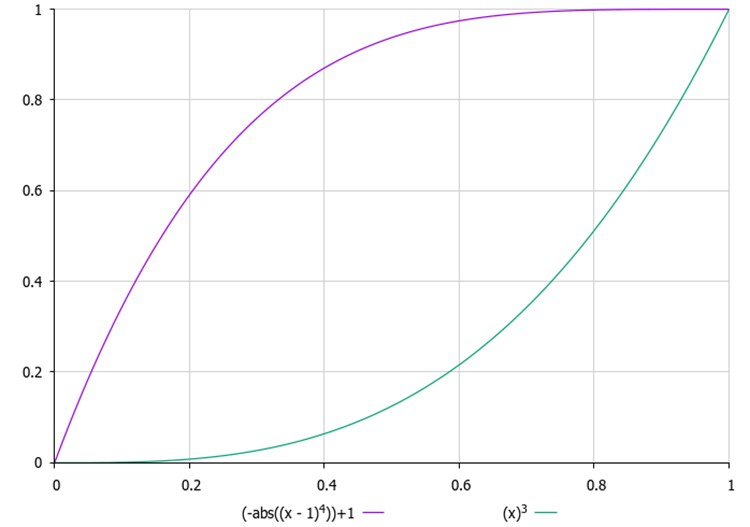
図1：試行回数による侵入確率の変化の例

最低点の座標を使用する際には、通常次のアプローチが取られます。

  1. 目的関数の値が最も小さい水ユニット（これをx_lowestと呼びます）を見つけます。
  2. 位置の更新時には、この最低点のすべての座標を使用します： x_new = x_old + F × r × (x_lowest - x_old)。ここで、x_new、x_old、x_lowestはすべて、全座標を含むベクトルです。
  3. このベクトル形式の式は、すべての次元に同時に適用されます。つまり、新しい位置は、探索空間内のすべての次元で最低点の方へと「引き寄せられる」ことになります。

このアプローチによって、解空間の中で最も有望な領域に、すべての次元を同時に考慮して探索を誘導することが可能になります。

このアルゴリズム（および必要に応じて将来のアルゴリズム）では、最適化エージェントに関する追加情報を格納するため、標準の構造体を拡張する必要があります。新たに追加されるフィールドは、緑色で強調表示されています。

ユーザープログラムがアクセスする最適化エージェントの標準構造体であるS_AO_Agentの構成を、改めて確認してみましょう。拡張後の構造体は次のようになります。

1. 構造体フィールド

  • c []：探索空間におけるエージェントの現在の座標の配列
  • cP []：1つ前の座標の配列 
  • cB []：これまでにエージェントが見つけた最良の座標の配列
  • f：現在の座標における目的関数の値（適応度）であり、エージェントが課題にどれだけ適しているかを評価するために使われます
  • fP：前の座標における目的関数の値（以前の適応度）で、パフォーマンスの変化を追跡します
  • fB：最良の座標における目的関数の値（最良適応度）で、エージェントが達成したベストスコアを保持します
  • cnt：エージェントの反復回数を追跡するカウンタ

2. Init ()：この初期化メソッドは、エージェントに必要な座標数を受け取り、以下の操作を実行します。

  • c配列のサイズを指定された座標数coordsに変更し、現在の座標を格納するメモリを割り当てます。
  • 同様に、以前の座標を格納するためのcP配列のサイズと、最適な座標を格納するためのcB配列のサイズを変更します。
  • fの値を、評価時に必ず更新されるよう、最小可能値に初期化します。
  • fPとfBも同様に、適切な初期値で初期化します。
  • カウンタ値をゼロに初期化します。

したがって、S_AO_Agent構造体は、エージェントの現在の状態、その性能、および変遷の履歴を記録するための情報を保持できます。この構造体に加えた変更は、これまでにその構造体を基に作成された最適化アルゴリズムには影響を与えませんが、今後新しいアルゴリズムを構築する際には役立ちます。

//——————————————————————————————————————————————————————————————————————————————
struct S_AO_Agent
{
    double c  []; //coordinates
    double cP []; //previous coordinates
    double cB []; //best coordinates

    double f;     //fitness
    double fP;    //previous fitness
    double fB;    //best fitness

    int    cnt;   //counter

    void Init (int coords)
    {
      ArrayResize (c,  coords);
      ArrayResize (cP, coords);
      ArrayResize (cB, coords);

      f  = -DBL_MAX;
      fP = -DBL_MAX;
      fB = -DBL_MAX;

      cnt = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ASHAクラスはC_AO基底クラスから継承され、ASHA最適化アルゴリズムを実装したものです。その構造と機能を分析してみましょう。

  • F、δ、β、ρ0：先に説明した特定のパラメータであり、アルゴリズムの動作を決定します。
  • params：パラメータ構造体の配列であり、アルゴリズムのパラメータ名とその値をそれぞれの要素に格納します。

SetParams ()メソッドは、 params配列からアルゴリズム パラメータの値を設定するために使用されます。

Init ()メソッドは、探索の最小・最大範囲、探索ステップ幅、エポック数を引数として受け取り、アルゴリズムの初期化をおこないます。 

Moving ()メソッドとRevision ()メソッドは、エージェントを探索空間内で移動させたり、最適化基準に基づいてエージェントの状態や位置を見直し・更新したりする役割を担います。

以下がprivateフィールドです。

  • S_AO_Agent aT []：集団の並べ替えに使用される一時的な集団の配列
  • epochs：最適化に使用されるエポック（反復）総数
  • epochNow：アルゴリズムが現在位置しているエポック数

C_AO_ASHAクラスは、最適化プロセスとエージェント間の相互作用を制御するために必要なパラメータ、メソッド、および構造体を備えています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ASHA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASHA () { }
  C_AO_ASHA ()
  {
    ao_name = "ASHA";
    ao_desc = "Artificial Showering Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/15980";

    popSize       = 100;  //population size

    F             = 0.3;  //water flow velocity
    δ             = 2;    //resistance level(infiltration threshold)
    β             = 0.8;  //parameter that controls the rate of change in probability
    ρ0            = 0.1;  //initial probability

    ArrayResize (params, 5);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "F";       params [1].val = F;
    params [2].name = "δ";       params [2].val = δ;
    params [3].name = "β";       params [3].val = β;
    params [4].name = "ρ0";      params [4].val = ρ0;

  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    F       = params      [1].val;
    δ       = (int)params [2].val;
    β       = params      [3].val;
    ρ0      = params      [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double F;  //water flow velocity
  int    δ;  //resistance level(infiltration threshold)
  double β;  //parameter that controls the rate of change in probability
  double ρ0; //initial probability

  private: //-------------------------------------------------------------------
  S_AO_Agent aT [];
  int  epochs;
  int  epochNow;
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドは最適化アルゴリズムを初期化する役割を担います。以下がメソッドのロジックです。

1. 標準初期化チェック：StandardInitを呼び出し、基本的なチェックとパラメータの初期化を実行します。 

2. カウンタの設置

  • epochsは、引数として渡されたepochsPの値（アルゴリズムが実行すべき総反復回数）に設定されます。
  • epochNowは0に初期化されます。これは、アルゴリズムがまだ1回もエポックを実行していない、実行開始直後の状態を表します。

3. エージェントの一時的な集団のためにメモリを予約します。

4.すべての初期化が正しく完了した場合、このメソッドはtrueを返し、アルゴリズムの初期化が成功したことを示します。

Initメソッドは、アルゴリズムの動作準備において中核を担う重要な手続きです。入力の妥当性を確認し、最適化処理を制御するために必要な値を設定し、エージェントのためのメモリを確保します。初期化が成功すると、エージェントの移動や状態の更新など、後続の処理を実行できるようになります。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASHA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (aT, popSize);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、ASHAアルゴリズム内でエージェントを探索空間内で移動させるロジックを実装しています。段階的に分析してみましょう。

1. メソッドは現在のエポックカウンタをインクリメントし、実行された反復回数を追跡可能にします。

2. 初期化（revisionが不要な場合）：各エージェントiと座標cについて

  • u.RNDfromCIを用いて指定された範囲内で全エージェントの初期位置を生成し、離散化を適用します。
  • その後、revisionをtrueに設定してメソッドを終了します。

3. エージェント移動のメインループでは、各エージェントiに対して以下の処理をおこないます。

  • inf：u.Scaleを使ってエージェントのカウンタcntに依存した値として計算され、その値を4乗して影響を強めます。
  • 意思決定のために乱数rndを生成します。

4.各座標cに対するループで以下を実行します。

  • 更新に使う、探索空間内でより低い位置にある別のエージェントを選択するためのインデックスindを生成します。
  • i < 1 の場合：rnd < infの場合、現在のエージェントの座標は、最良座標cBの周囲で正規分布に基づきu.GaussDistributionを用いて更新されます。
  • i >= 1の場合： rnd < infの場合、現在のエージェントの座標は、別のエージェントa[ind].cBの座標を基準として同様に更新されます。
  • それ以外の場合：古い値xOldのままとなります。生成された乱数がρ 未満の場合：
  • xNewは、別のエージェントxLowerの最適値に基づいて更新されます。
  • それ以外の場合：xNewはxLowestの大域最適値に基づいて更新されます。
  • その後、新しい値xNewを現在のエージェントに代入します。

5. 座標調整：最後に、それぞれの新しい座標値は、指定された範囲とステップ内に収まるようにu.SeInDiSpを使用して調整されます。

Movingメソッドは、エージェントの位置の初期化と、現在の状態および他のエージェントとの相互作用に基づいて最適化中にエージェントの位置を更新する機能を提供します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASHA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double xOld    = 0.0;
  double xNew    = 0.0;
  double xLower  = 0.0;
  double xLowest = 0.0;
  double ρ       = MathMax (β * (epochs - epochNow) / epochs, ρ0);
  double inf     = 0.0;
  int    ind     = 0;
  double rnd     = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    inf = u.Scale (a [i].cnt, 0, δ, 0, 1);
    inf = inf * inf * inf * inf;

    rnd = u.RNDprobab ();

    for (int c = 0; c < coords; c++)
    {
      ind = (int)u.RNDintInRange (0, i - 1);
      
      if (i < 1)
      {
        if (rnd < inf)
        {
          a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
        }
      }
      else
      {
        if (rnd < inf)
        {
          a [i].c [c] = u.GaussDistribution (a [ind].cB [c], rangeMin [c], rangeMax [c], 8);
        }
        else
        {
          xOld = a [i].c [c];

          if (u.RNDprobab () < ρ)
          {
            xLower = a [ind].cB [c];

            xNew = xOld + F * (u.RNDprobab () * (xLower - xOld));
          }
          else
          {
            xLowest = cB [c];

            xNew = xOld + F * (u.RNDprobab () * (xLowest - xOld));
          }

          a [i].c [c] = xNew;
        }
      }

      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは、集団内の最良解（エージェント）に関する情報の更新および適応度の追跡を担当しています。手順は以下の通りです。

1. 変数indを-1で初期化します。これは最良の適応度関数値 fを持つエージェントのインデックスを保存するために使います。

2. エージェントのループ処理：集団サイズ popSizeのすべてのエージェントを対象に以下を繰り返します。

  • 現在のエージェントの目的関数値fが、エージェント自身の記録している局所最良値fBより良ければ、fBを更新し、そのエージェントのインデックスをindに保存します。
  • また、局所最良値fBが更新された場合、
  • エージェントの座標cをcBにコピーします。これらはエージェントの最もよく知られている座標です。
  • cntカウンタを0にリセットします。目的関数値が改善しなかった場合は、このカウンタをインクリメントします。

3. 最適な座標のコピー：最適な関数値（indが-1と等しくない）を持つエージェントが見つかった場合、その座標をグローバル変数cBにコピーします。

4.エージェントの並び替え：最後に、u.Sorting_fBを呼び出して、エージェントをfBの局所最適値順に並び替えます。

Revisionメソッドはアルゴリズムの中心的な役割を果たし、エージェントのパフォーマンスを監視し、既知の最良解を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ASHA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
      a [i].cnt = 0;
    }
    else
    {
      a [i].cnt++;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————


テスト結果

ASHAアルゴリズムのテスト結果は平均的なパフォーマンスを示しました。
ASHA|Artificial Showering Algorithm|100.0|0.3|2.0|0.8|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.8968571984324711
25 Hilly's; Func runs:10000; result:0.40433437407600525
500 Hilly's; Func runs:10000; result:0.25617375427148387
=============================
5 Forest's; Func runs:10000; result:0.8036024134603961
25 Forest's; Func runs:10000; result:0.35525531625936474
500 Forest's; Func runs:10000; result:0.1916000538491299
=============================
5 Megacity's; Func runs:10000; result:0.4769230769230769
25 Megacity's; Func runs:10000; result:0.1812307692307692
500 Megacity's; Func runs:10000; result:0.09773846153846236
=============================
All score:3.66372 (40.71%)

ASHAのテスト中の動作を観察していても、このアルゴリズムの際立った特徴を特定することは困難です。探索空間内の有望な領域に対する局所的な探索も確認されませんでした。

Hilly

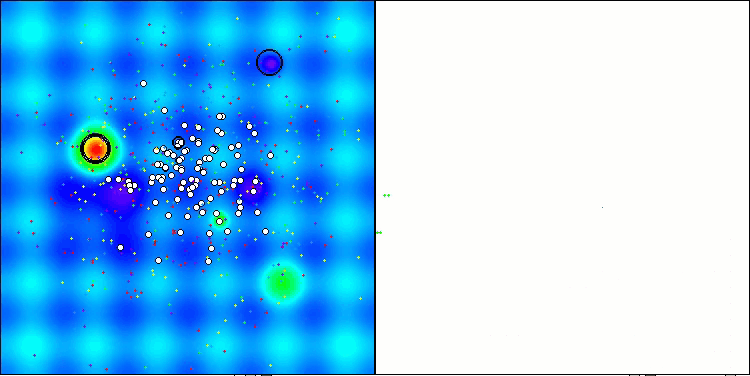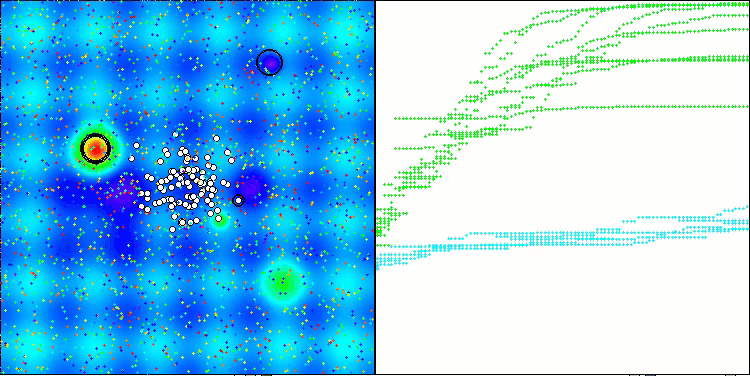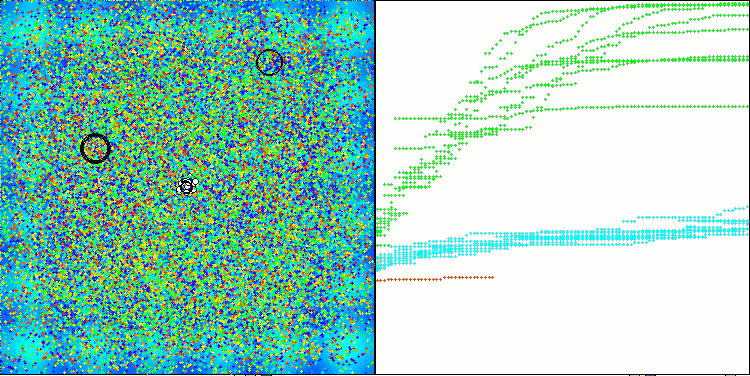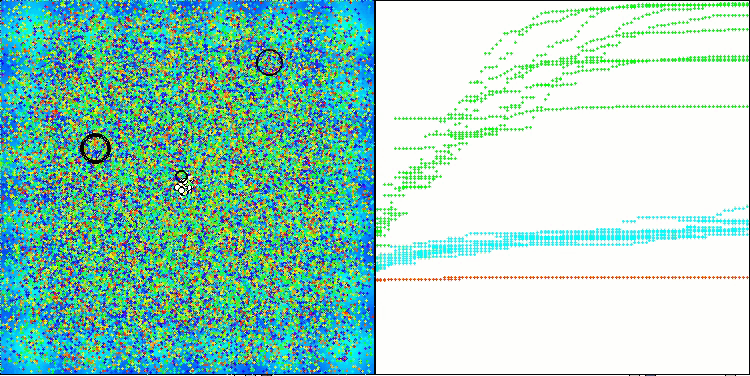
Hillyテスト関数のASHA

Forest

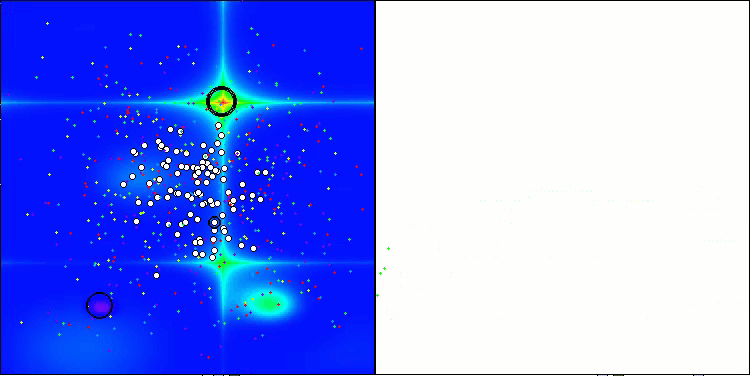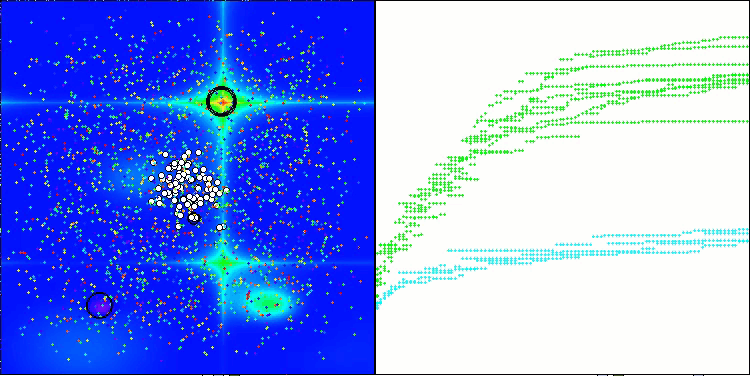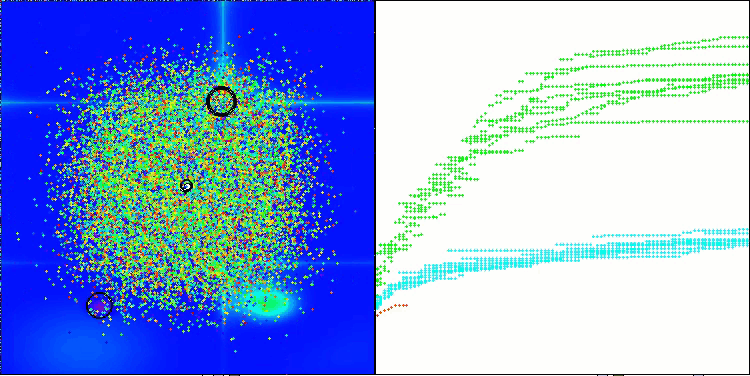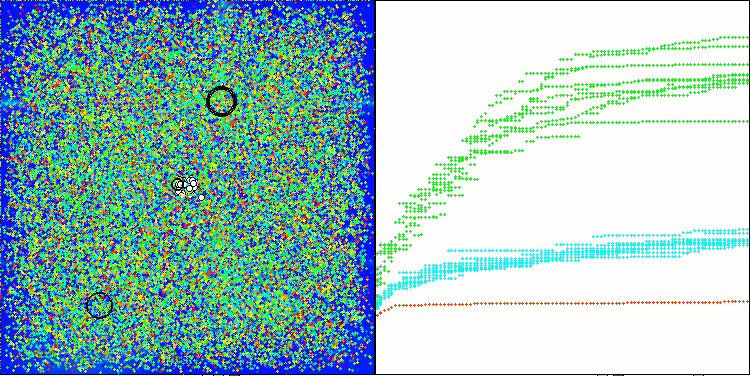
Forestテスト関数のASHA

Megacity

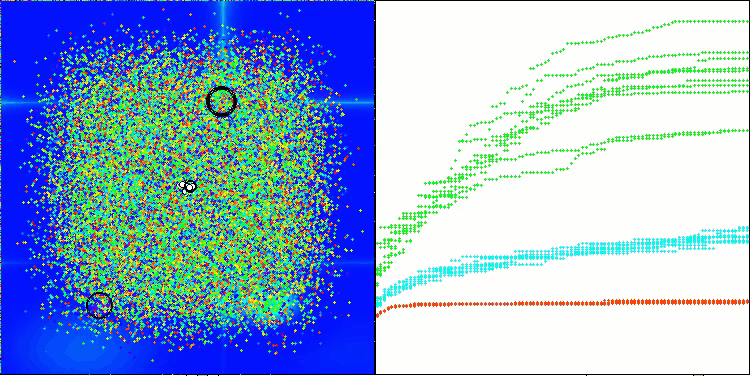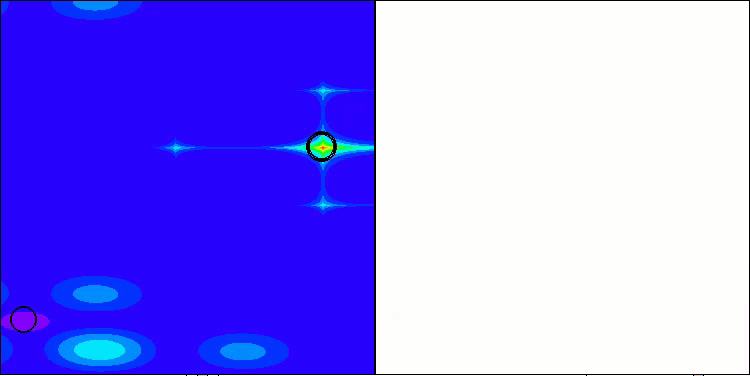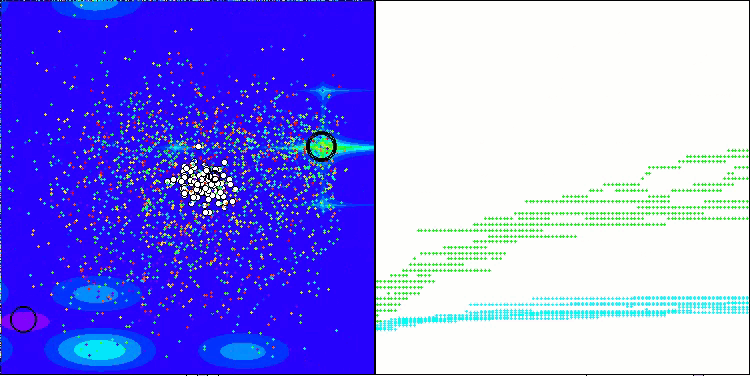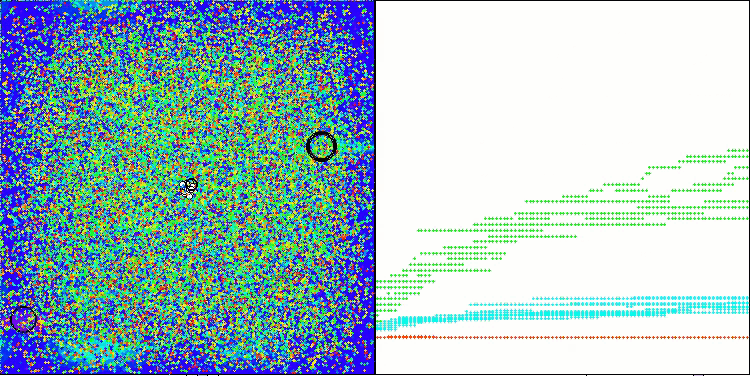
Megacityテスト関数のASHA

このテスト結果に基づいて、ASHAアルゴリズムは評価表で 28位になりました。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
20 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
21 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
22 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
23 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
24 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
25 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
26 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
27 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
28 ASHA 人工散布アルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
29 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
30 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
31 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
32 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
33 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
34 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
35 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
36 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
37 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
38 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
39 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
40 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
41 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
42 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
43 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
44 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
45 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77



まとめ

アルゴリズムのアイデア自体には好感が持てましたが、実装とテストを通じて、どこか物足りなさを感じました。このアルゴリズムは決して最も劣っているわけではありませんが、最良とも言いがたい性能です。ただし、そのシンプルさゆえに、今後の研究を進める上での余地が大いにあると感じました。個人的には、このアイデアには大きな可能性があると思います。さらに、著者らは「浸透率」について詳しい説明をおこなっておらず、その定義は研究者の想像力に委ねられている部分があります。これにより、さまざまな解釈や応用が可能となっています。

この記事から得られる主な教訓は、単純なアイデアが必ずしも複雑なものと同等の効果を持つとは限らない、ということです。最適化アルゴリズムの効率性は単純な話ではなく、さまざまなトレードオフを伴います。このアルゴリズムが、最適解を導く技術やノウハウに関する知識体系に、新たな一章を加える存在となることを願っています。

tab

図2：関連するテストに応じたアルゴリズムの色勾配結果は0.99は白で強調表示されます

チャート

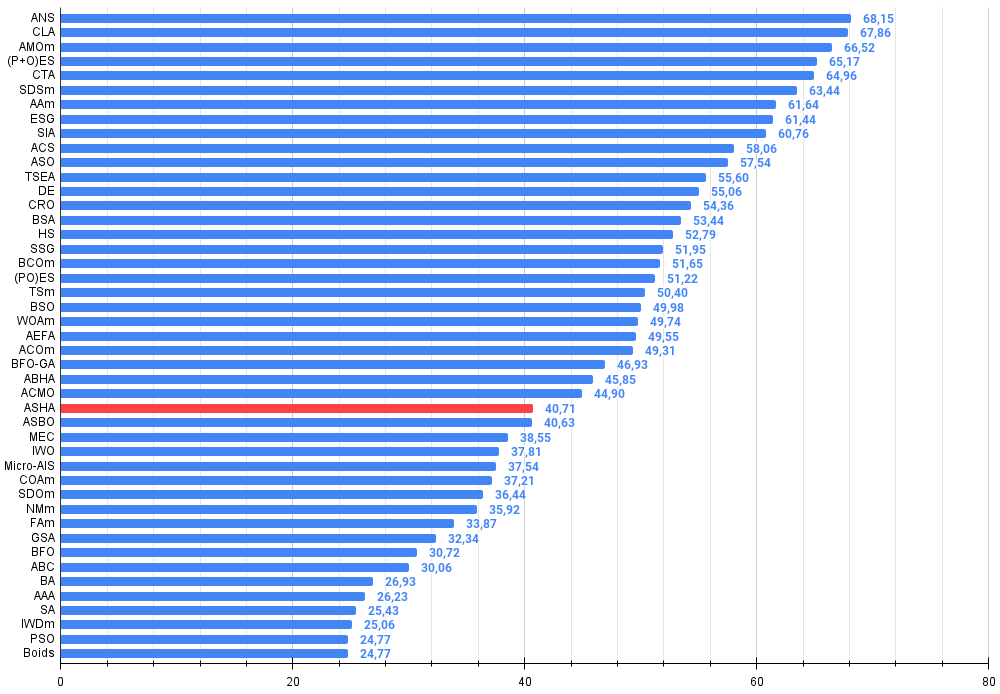
図3：アルゴリズムテスト結果のヒストグラム（0～100のスケール、数値が高いほど良い

ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている）


ASHA の長所と短所

長所

  1. 迅速
  2. 実装がシンプル

短所

  1. 収束精度が低い

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15980

添付されたファイル |
ZIPをダウンロード
ASHA.zip (35.93 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MetaTrader 5を使用したPythonの高頻度裁定取引システム MetaTrader 5を使用したPythonの高頻度裁定取引システム
この記事では、ブローカーの観点から見て合法であり、外国為替市場において数千もの合成価格を生成・分析し、利益を上げるために取引をおこなう裁定取引システムの構築方法について解説します。
DoEasy - サービス関数（第3回）：アウトサイドバーパターン DoEasy - サービス関数（第3回）：アウトサイドバーパターン
本記事では、DoEasyライブラリにおけるアウトサイドバーのプライスアクションパターンを開発し、価格パターン管理へのアクセス手法を最適化します。あわせて、ライブラリのテスト中に判明したエラーや不具合の修正もおこないます。
MetaTrader 5を使用してPythonでカスタム通貨ペアパターンを見つける MetaTrader 5を使用してPythonでカスタム通貨ペアパターンを見つける
外国為替市場には繰り返しパターンや規則性が存在するのでしょうか。私は、PythonとMetaTrader 5を使って独自のパターン分析システムを構築することに決めました。これは、外国為替市場を攻略するための、数学とプログラミングの一種の融合です。
取引におけるニューラルネットワーク：価格変動予測におけるマスクアテンションフリーアプローチ 取引におけるニューラルネットワーク：価格変動予測におけるマスクアテンションフリーアプローチ
この記事では、Mask-Attention-Free Transformer (MAFT)法と、それを取引分野に応用する可能性について説明します。従来のTransformerはシーケンスを処理する際にマスキングを必要としますが、MAFTはこのマスキングを不要にすることでアテンション処理を最適化し、計算効率を大幅に向上させています。