雲モデル最適化(ACMO)：実践編

MetaTrader 5 — テスター | YYYY年05月DD日, 08:24

100

Andrey Dik

内容

はじめに

テクノロジーと自然が交差する科学の世界において、複雑な問題を最適化するためのメタヒューリスティック手法として、ACMO（大気雲モデル最適化）アルゴリズムというユニークな発想が登場しました。前回の記事では、さまざまな気象パラメータに基づいて、大気中における雲の形成と移動のプロセスをモデル化するアルゴリズムの実装を技術的に解析しました。初回は、雲シミュレーションを管理するクラスを作成し、初期化、雲の移動、領域プロパティの更新などの処理をおこなう各種メソッドを実装しました。

検索空間を複数の領域に分割し、それぞれの領域における初期の湿度と気圧を設定しました。また、初期エントロピー、ハイパーエントロピー、雲形成に必要な湿度の閾値など、モデルの各種パラメータを定義しました。次のステップとして、湿度の高い領域を選択して雲を生成し、雲の中心、エントロピー、およびハイパーエントロピーを計算しました。さらに、雲生成後の領域における湿度と気圧の気象パラメータを更新し、雲が低気圧領域へ移動する処理や、領域間の移動・拡散に応じて雲の特性を動的に更新する仕組みも実装しました。

次にやるべきことは何でしょうか。今後の実装としては、水滴のランダムな配置や、それらを雲に分配する関数の実装、降雨プロセスの完了、および大域解の更新が必要です。また、さまざまなパラメータを用いてテスト関数上で本モデルを評価し、その性能と精度を検証することも求められます。さらに、集団内の有望な領域に関する情報をより完全に交換できるようにするため、雨と水滴生成のプロセスに変更を加えていく予定です。

アルゴリズムの実装

気象プロセス全体を擬似コードの形式で記述し、それに基づいてアルゴリズムの最終バージョンを組み立てられるようにします。

1. 最初のエポックでは、雲はランダムに配置されます。
   EnCk = EnM0;
   HeCk = HeM0;
//--------------------------------------------------------------------------------
1.1 低気圧領域に向かう雲の移動
   β = deltaP / normP
   d = Tck.x - Cck.c
   VC = β * d;
   Ck = Ck + VC

   移動後の水滴数の変化
   nk = nk × (1 - γ)

   エントロピーとハイパーエントロピーの変化
   α = ΔP / ΔPmax;
   EnCk = EnCk * (1 + α)
   HeCk = HeCk * (1 - α)
//--------------------------------------------------------------------------------
2. 雨が降る過程、雨滴が落ちる過程：
   雲間の水滴の分布はその領域の湿度に比例
   雲中に存在する水滴の数は増加
//--------------------------------------------------------------------------------
3. 水滴の適応度関数を計算します。
//--------------------------------------------------------------------------------
4. 降水量が降った領域における大域解と最低気圧を更新します。
//--------------------------------------------------------------------------------
5. 閾値を超える領域で、雲の減衰と、減衰した雲を置き換える新しい雲の生成を確認します。
   許容値を超える膨張による崩壊の規則（雲の破裂）：
   En > 5 * EnM0_t
   臨界値以下の水分含有量での減衰則（雲の乾燥）：
   dCk < dMin

   雲の形成が可能になる領域のための湿度閾値：
   HT = H_min + λ * (H_max - H_min);
//--------------------------------------------------------------------------------
6. 新しい雲のエントロピーとハイパーエントロピーを計算します。
   En = EnM0 / (1 + 2.72 ^ (-(8 - 16 * (t / maxT))))
   He = HeM0 / (1 + 2.72 ^ ((8 - 16 * (t / maxT))))

それでは続きを見ていきましょう。ここでは、C_AO_ACMOクラスのMovingメソッドについて取り上げます。このメソッドは2つの操作を実行します。MoveClouds (revision)は雲の動きを担当し、RainProcess (revision)は雲の状態とrevisionパラメータに基づいて降雨処理を行います。Movingメソッドは、雲の動きと降雨に関する2つの主要な処理を統括しており、雲の移動および雨プロセスとの相互作用に関するロジックをカプセル化しています。したがって、Movingメソッドは気象シミュレーションにおいて、雲と雨の状態を更新するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Moving ()
{
  MoveClouds       (revision);
  RainProcess      (revision);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスのMoveCloudsメソッドを詳しく見てみましょう。

1. 最初のブロック（revがfalseの場合）：ランダムな中心を持つ雲を作成します。各雲と座標について

指定された範囲内で雲中心のランダム値が生成されます（RNDfromCI関数）。
中心はSeInDiSpを使用して調整され、値が正規化されます。
雲が配置されている領域のインデックスは、GetRegionIndexを使用して決定されます。
雲のエントロピーと初期エントロピー値が設定されます。
ハイパーエントロピーの初期値は、hyperEntropyに設定されます。

実行を終了します。

2. 2番目のブロック（revがtrueの場合）

revがtrueに等しい場合、最も気圧が低い領域の検索を開始します。
湿度lHindが最も低い領域のインデックスを格納し、気圧normPを正規化するための配列が作成されます。

3. 気圧が最も低い領域を見つけるためにループします。

各c座標について、すべての領域における最小気圧と最大気圧が決定されます。
気圧が最も低い領域のインデックスがlHind配列に格納されます。
各座標の正規化された気圧がnormPに格納されます。

4. 各雲の動きと座標

雲がすでに気圧が最も低い領域にある場合、反復はスキップされます。
気圧の低いターゲット領域がランダムに選択されます。
現在の領域とターゲット領域間の気圧差が計算されます。
気圧値を正規化し、VC雲の移動速度が計算されます。
雲の中心は移動速度に基づいて更新されます。
領域インデックスが更新されます。
雲のエントロピーは、気圧の変化を考慮して更新されます。
雲内の水分量が減少し、ハイパーエントロピーが更新され、その値は最大8に制限されます。

MoveCloudsメソッドは、雲をより低圧の領域に移動し、エントロピーやハイパーエントロピーなどのパラメータを更新します。このメソッドは、大気の変化を反映した動的モデルを実装します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::MoveClouds (bool &rev)
{
  //----------------------------------------------------------------------------
  if (!rev)
  {
    //creating clouds with random centers---------------------------------------
    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        clouds [i].center [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        clouds [i].center [c] = u.SeInDiSp  (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

        clouds [i].entropy      [c] = entropy [c] * EnM0;
        clouds [i].entropyStart [c] = clouds [i].entropy [c];
      }

      clouds [i].hyperEntropy = HeM0;
    }

    return;
  }

  //search for the region with the lowest pressure------------------------------
  int targetRegion = 0;

  int lHind []; //lowest humidity index
  ArrayResize     (lHind, coords);
  ArrayInitialize (lHind, 0);

  double normP [];
  ArrayResize (normP, coords);
  double minP;
  double maxP;

  for (int c = 0; c < coords; c++)
  {
    minP =  DBL_MAX;
    maxP = -DBL_MAX;

    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].pressure < areas [c].regions [lHind [c]].pressure)
      {
        lHind [c] = r;
      }

      if (areas [c].regions [r].pressure < minP) minP = areas [c].regions [r].pressure;
      if (areas [c].regions [r].pressure > maxP) maxP = areas [c].regions [r].pressure;
    }

    normP [c] = maxP - minP;
  }

  //moving the cloud to a region with less pressure-----------------------------
  int    clRegIND = 0;
  double deltaP   = 0.0;
  double α        = 0.0; // Entropy factor
  double β        = 0.0; // Atmospheric pressure factor
  double VC       = 0.0; // Cloud velocity
  double d        = 0.0; // Cloud direction

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      //find a region with lower pressure---------------------------------------
      if (clouds [i].regionIndex [c] == lHind [c]) continue;

      clRegIND = clouds [i].regionIndex [c];

      do targetRegion = u.RNDminusOne (regionsNumber);
      while (areas [c].regions [clRegIND].pressure < areas [c].regions [targetRegion].pressure);

      //------------------------------------------------------------------------
      deltaP = areas [c].regions [clRegIND].pressure - areas [c].regions [targetRegion].pressure;

      β = deltaP / normP [c];
      d = areas [c].regions [targetRegion].x - areas [c].regions [clRegIND].centre;

      VC = β * d;

      clouds [i].center      [c] += VC;
      clouds [i].center      [c] = u.SeInDiSp (clouds [i].center [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      clouds [i].regionIndex [c] = GetRegionIndex (clouds [i].center [c], c);

      α = β;
      clouds [i].entropy [c] *=(1 + α);
    }

    clouds [i].droplets     *=(1 - γ);
    clouds [i].hyperEntropy *=(1 + α);
    if (clouds [i].hyperEntropy > 8) clouds [i].hyperEntropy = 8;
  }
}
//——————————————————————————————————————————————————————————————————————————————

次に、C_AO_ACMOクラスのGetRegionIndexメソッドを分析してみましょう。以下がメソッドの説明です。

1. 領域の位置を計算します。指定されたpointのregPos領域インデックスが計算され、floor関数を使用して最も近い整数に切り捨てられます。
2. 境界を確認します。このブロックは、regPosの計算されたインデックスが許容値を超えているかどうかを確認します（許容される領域の数を超えることはできません）。
3. このメソッドは、点が配置されている領域のインデックスを返します。

GetRegionIndexメソッドは、特定の範囲内で特定の点が配置されている領域のインデックスを決定することを目的としています。領域の数を考慮し、点が範囲の境界上にある場合も正しく処理します。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_ACMO::GetRegionIndex (double point, int ind)
{
  int regPos = (int)floor ((point - rangeMin [ind]) / ((rangeMax [ind] - rangeMin [ind]) / regionsNumber));

  if (regPos >= regionsNumber) regPos = regionsNumber - 1;

  return regPos;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスの次のメソッドRainProcessについて説明します。

2. 配列の初期化

雲の値を格納するためのcloudと、各雲の雨滴の数を格納するためのdropsの2つの配列を作成します。
両配列のサイズは、雲の量(cloudsNumber)に応じて異なります。

3. cloud配列の初期化

revがfalseに等しい場合、すべてのcloud配列要素は1.0の値を使用して初期化されます。
それ以外の場合、cloud配列は0.0の値を使用して初期化され、各雲の湿度が計算されます。

4. 湿度計算

各雲と座標ごとに、領域に応じて湿度が計算されます。
湿度が-DBL_MAXと等しくない場合は、cloud配列の対応する要素に追加されます。それ以外の場合は、minGp（最小水滴量）が追加されます。

5. 水滴分布

DropletsDistributionメソッドを呼び出して、cloud配列の値に基づいて水滴量を配布します。

6. 各雲および各水滴の主な水滴処理ループ

dist、center、xMin、xMaxの値が計算されます。
x値は正規分布を使用して生成されます。
xが範囲外の場合は、RNDfromCIメソッドを使用して修正されます。
x値はSeInDiSpメソッドを使用して正規化され、a配列に保存されます。

雲のすべての水滴が処理された後、雲内の水滴の合計数が更新されます。したがって、RainProcessメソッドは、湿度と雨滴の分布を考慮して、雲から降る雨をシミュレートします。配列を初期化し、各雲の湿度を計算し、雨滴を分布させ、正規分布を仮定して各雨滴の値を生成します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int r = 0; r < regionsNumber; r++)
        {
          humidity = areas [c].regions [clouds [i].regionIndex [r]].humidity;
          if (humidity != -DBL_MAX) cloud [i] += humidity;
          else                      cloud [i] += minGp;
        }
      }
    }
  }

  DropletsDistribution (cloud, drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;
  int    dCNT   = 0;

  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [dCNT].c [c] = x;
      }

      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスの次のメソッドであるDropletsDistributionは、湿度に基づいて雲間に雨滴を分配するように設計されています。詳しく見てみましょう。

2. 変数の初期化

minHumidityは、最小湿度を見つけられるように最大値に初期化されます。
indMinHumidityは、湿度が最小の雲インデックスを格納します。
totalHumidityは、すべての雲の湿度の合計を保存するために使用されます。

3. 湿度の合計は、すべての雲の湿度を合計し、湿度が最も低い雲を決定します。

4. 水滴の比例配分：各雲について、水滴の数は湿度の合計に対する割合で計算されます。この値は、droplet配列に保存されます。

5. 残りの水滴の分配

まず、分散された水滴の総数(totalDrops)が計算されます。
残りの水滴数(remainingDrops)が計算されます。
残っている水滴があれば、最小限の湿度で雲に追加されます。

DropletsDistributionメソッドは、水滴の水分含有量に基づいて雲の間に水滴を効果的に分散させます。まず水滴を比例配分し、残りの水滴を湿度の最も低い雲に追加することで配分を調整します。これにより、アルゴリズムの外部パラメータの集団サイズに対応する一定数の雨滴を維持しながら、より現実的な水滴のシミュレーションが可能になります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::DropletsDistribution (double &cloud [], int &droplets [])
{
  double minHumidity    = DBL_MAX;
  int    indMinHumidity = -1;
  double totalHumidity  = 0; //total amount of humidity in all clouds

  for (int i = 0; i < ArraySize (cloud); i++)
  {
    totalHumidity += cloud [i];

    if (cloud [i] < minHumidity)
    {
      minHumidity = cloud [i];
      indMinHumidity = i;
    }
  }

  // Filling the droplets array in proportion to the value in clouds
  for (int i = 0; i < ArraySize (clouds); i++)
  {
    droplets [i] = int((cloud [i] / totalHumidity)*popSize); //proportional distribution of droplets
  }

  // Distribute the remaining drops, if any
  int totalDrops = 0;

  for (int i = 0; i < ArraySize (droplets); i++)
  {
    totalDrops += droplets [i];
  }

  // If not all drops are distributed, add the remaining drops to the element with the lowest humidity
  int remainingDrops = popSize - totalDrops;

  if (remainingDrops > 0)
  {
    droplets [indMinHumidity] += remainingDrops; //add the remaining drops to the lightest cloud
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスのRevisionメソッドは、システム状態の更新を実行します。もう少し詳しく見てみましょう。

1. a配列の要素（最適化エージェントの集合）をループします。このループは、popSizeサイズのa配列のすべての要素を反復処理します。

現在の要素の適合度値fが現在の最大適合度値fBより大きい場合、fBが更新され、indインデックスが現在のインデックスに設定されます。
最小適合値fの検索も配列のすべての要素間で実行され、現在の値がminGpより小さい場合はminGpが更新されます。

2. データのコピー：最大適合度値fを持つ要素が見つかった場合（indが-1ではない場合）、データ（つまりa [ind]）がc配列からcB配列へコピーされます。

3. 領域プロパティの更新：UpdateRegionPropertiesメソッドが呼び出されます。さまざまな領域の湿度と気圧のパラメータを更新します。

4. 雲の生成：古い雲を消去し、新しい雲を作成するGenerateCloudsメソッドが呼び出されます。

5. ステータスの更新

revisionフラグはtrueに設定されており、これはシステムの初期状態が合格したことを示します。
エポックの数を追跡するために、epochNowカウンタが増加されます。

Revisionメソッドは、雲に関連するシステムの状態を更新する役割を担います。最大のf適合値を見つけ、関連するパラメータを更新し、新しい雲を初期化し、領域のプロパティを更新します。このメソッドは、モデル内のデータを最新の状態に保ち、システムが変更に適応できるようにするための鍵となります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f < minGp) minGp = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  UpdateRegionProperties (); //updating humidity and pressure in the regions
  GenerateClouds         (); //disappearance of clouds and the creation of new ones

  revision = true;
  epochNow++;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスのGenerateCloudsメソッドは、湿度やエントロピーなどのさまざまな要因に応じて雲を作成し、その状態を管理する役割を担います。以下がメソッドの説明です。

1. 湿度閾値の計算：CalculateHumidityThreshold関数が呼び出され、雲の形成に必要な湿度閾値が返されます。

2. 領域インデックスを格納するための構造体

S_Areas構造体が定義されています。この構造体には、雲を形成できる領域のインデックスの配列が含まれています。
arメソッドは、座標のcoords数に等しいサイズで初期化されます。

3. 領域情報の収集：この二重ループは、各領域が湿度の閾値を満たしているかどうかをテストします。領域の湿度が閾値より大きい場合、その領域のインデックスが適切なS_Areas構造体のregsIND配列に追加されます。

4. 雲の減衰条件の確認

各雲について、エントロピーが特定の制限（初期エントロピーの5倍）を超えているかどうかが確認されます。超えている場合、雲は崩壊したと考えられます。
次に、雲内の水分量がdMinの最小値より少ないかどうかが確認されます。これも雲の崩壊につながる可能性があります。

5. 最も雨の多い領域に新しい雲を作成する

雲が崩壊すると、最も湿潤な領域のひとつに新たな雲が生成されます。各座標に対して、領域インデックスがランダムに選択され、雲は新しい中心座標と領域インデックスを受け取ります。
次に、CalculateNewEntropy関数が呼び出されます。この関数は、現在のエポックに応じて新しい雲のエントロピーを再計算します。

GenerateCloudsメソッドは、湿度とエントロピーに基づいて雲の生成と崩壊を管理します。雲を形成できる領域に関する情報を収集し、既存の雲の減衰をチェックし、適切な領域に新しい雲を作成します。このメソッドは、モデル内の雲の状態を動的に制御するための鍵となります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::GenerateClouds ()
{
  //Collecting statistics of regions capable of creating clouds-----------------
  double Ht = CalculateHumidityThreshold ();

  struct S_Areas
  {
      int regsIND []; //index of the potential region
  };

  S_Areas ar [];
  ArrayResize (ar, coords);

  int sizePr = 0;

  for (int i = 0; i < coords; i++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [i].regions [r].humidity > Ht)
      {
        sizePr = ArraySize (ar [i].regsIND);
        sizePr++;
        ArrayResize (ar [i].regsIND, sizePr, coords);
        ar [i].regsIND [sizePr - 1] = r;
      }
    }
  }

  //Check the conditions for cloud decay----------------------------------------
  bool   cloudDecay = false;

  for (int i = 0; i < cloudsNumber; i++)
  {
    cloudDecay = false;

    //checking the cloud for too much entropy-----------------------------------
    for (int c = 0; c < coords; c++)
    {
      if (clouds [i].entropy [c] > 5.0 * clouds [i].entropyStart [c])
      {
        //Print ("Disintegration of cloud #", i, " - tore at epoch ", epochNow);
        cloudDecay = true;
        break;
      }
    }

    //checking the cloud for decay----------------------------------------------
    if (!cloudDecay)
    {
      if (clouds [i].droplets < dMin)
      {
        //Print ("Disintegration of cloud #", i, " - dried up at epoch ", epochNow);
        cloudDecay = true;
      }
    }

    //if the cloud has decayed--------------------------------------------------
    int regIND = 0;

    if (cloudDecay)
    {
      //creating a cloud in a very humid region---------------------------------
      for (int c = 0; c < coords; c++)
      {
        regIND = u.RNDminusOne (ArraySize (ar [c].regsIND));
        regIND = ar [c].regsIND [regIND];

        clouds [i].center      [c] = areas [c].regions [regIND].x;
        clouds [i].regionIndex [c] = regIND;
      }

      CalculateNewEntropy (clouds [i], epochNow);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスのCalculateHumidityThresholdメソッドは、雲の形成に必要な湿度の閾値を計算する役割を担います。詳細な手順は次のとおりです。

1. 最低湿度を見つけるために二重ループを実行します。外側のループはすべてのcoords座標を処理し、内側のループは各座標のすべてのregionsNumber領域を反復処理します。領域の湿度が-DBL_MAXと等しくない場合は、チェックが実行されます。現在の湿度が現在のH_minより小さい場合は、H_minが更新されます。

2. 雲が形成されるために必要な湿度の閾値を表す値として、H_minにλとH_maxとH_minの差の積を加えた値を返します。

CalculateHumidityThresholdメソッドは、すべての領域の中での最小湿度に基づいて湿度閾値を計算し、最大湿度とλ比に基づいてそれを調整します。これにより、環境の状態に基づいて、どのような条件下で雲が形成されるかを判断することが可能になります。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACMO::CalculateHumidityThreshold ()
{
  double H_max = fB;
  double H_min = DBL_MAX;

  for (int c = 0; c < coords; c++)
  {
    for (int r = 0; r < regionsNumber; r++)
    {
      if (areas [c].regions [r].humidity != -DBL_MAX)
      {
        if (areas [c].regions [r].humidity < H_min)
        {
          H_min = areas [c].regions [r].humidity;
        }
      }
    }
  }

  return H_min + λ * (H_max - H_min);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACMOクラスのCalculateNewEntropyメソッドは、S_ACMO_Cloud構造体によって表される雲の新しいエントロピーとハイパーエントロピーを計算します。詳しく見てみましょう。

1. エントロピーの計算

すべてのcoords座標をループします。
各座標について、次の式を使用して新しいエントロピー値cl.entropy [c]が計算されます： En = (entropy [c] * EnM0) / (1 + e ^ (-(8 - 16 * (t / epochs))))
cl.entropyStart [c]とcl.entropy [c]はentropy [c]の値で初期化され、エントロピーの初期値を保持します。

2. ハイパーエントロピーの計算： He = 1 / (1 + e ^ (8 - 16 * (t / epochs)))

3. ハイパーエントロピーは、uオブジェクトのScaleメソッドを使用してスケーリングされます。これにより、HeM0パラメータと8.0を使用して、ハイパーエントロピー値を特定の範囲（0から8）にスケーリングできます。

CalculateNewEntropyメソッドは、現在の時刻tと指定されたパラメータに基づいて、雲のエントロピーとハイパーエントロピーの値を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::CalculateNewEntropy (S_ACMO_Cloud &cl, int t)
{
  //----------------------------------------------------------------------------
  //En: 1/(1+2.72^(-(8-16*(t/maxT))))
  for (int c = 0; c < coords; c++)
  {
    cl.entropy      [c] = entropy [c] * EnM0 / (1.0 + pow (M_E, (-(8.0 - 16.0 * (t / epochs)))));
    cl.entropyStart [c] = cl.entropy [c] = entropy [c];
  }

  //----------------------------------------------------------------------------
  //He: 1/(1+2.72^((8-16*(t/maxT))))
  cl.hyperEntropy = 1.0 / (1.0 + pow (M_E, ((8.0 - 16.0 * (t / epochs)))));

  cl.hyperEntropy = u.Scale (cl.hyperEntropy, 0.0, 8.0, HeM0, 8.0);
}
//——————————————————————————————————————————————————————————————————————————————

En and He 2

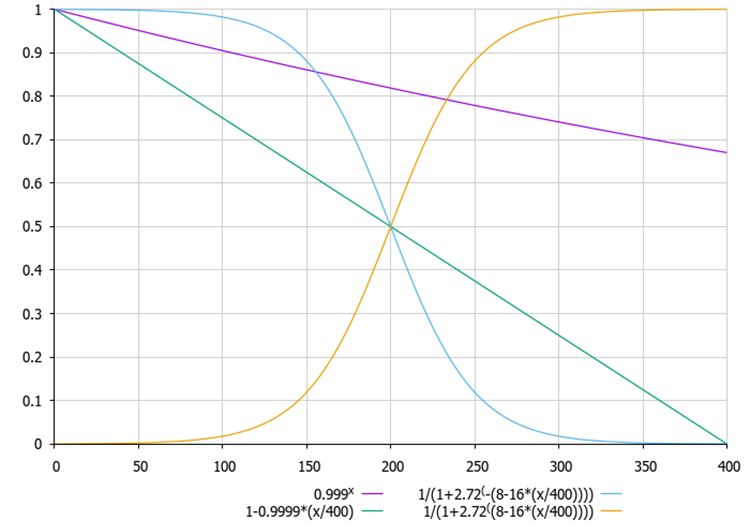
図1：現在のエポックに応じてζ比を計算するための方程式の変形。方程式を選択し、それぞれのアルゴリズムを試すことができる（コード文字列はコメントアウトされている）

テスト結果

アルゴリズムのテストに移りましょう。著者らが考案した雲形成の気象モデルは次のように機能します。

//オリジナル版
ACMO|Atmospheric Cloud Model Optimization|50.0|5.0|10.0|0.2|5.0|5.0|0.9|0.2|
=============================
5 Hilly's; Func runs:10000; result:0.6017884495404766
25 Hilly's; Func runs:10000; result:0.3426222382089618
500 Hilly's; Func runs:10000; result:0.2526410178225118
=============================
5 Forest's; Func runs:10000; result:0.4780554376190664
25 Forest's; Func runs:10000; result:0.261057831391174
500 Forest's; Func runs:10000; result:0.17318135866144563
=============================
5 Megacity's; Func runs:10000; result:0.3507692307692307
25 Megacity's; Func runs:10000; result:0.16153846153846158
500 Megacity's; Func runs:10000; result:0.09632307692307775
=============================
All score:2.71798 (30.20%)

残念ながら、得られた結果は予想を大きく下回るものでした。多数の異なる方程式や、極端な解に陥るのを回避するための論理的な処理を備えた、雲形成の美しいモデルにもかかわらず、アルゴリズムの収束性は低いと考えられます。このアルゴリズムには、エージェント間での直接的なやり取りや、最適解に関する情報交換の仕組みが欠けています。こうした仕組みは、通常、あらゆるアルゴリズムの探索能力を高める効果があります。そのため、最良の水滴から最悪の水滴へ情報を確率的に伝達することで、情報交換を実現する仕組みを新たに追加しました。次に、この変更によって何が得られたのか、見ていきましょう。

ACMOm|Atmospheric Cloud Model Optimization|50.0|4.0|10.0|0.2|0.2|2.0|0.9|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.9032099148349984
25 Hilly's; Func runs:10000; result:0.48545807643133143
500 Hilly's; Func runs:10000; result:0.30403284557071203
=============================
5 Forest's; Func runs:10000; result:0.8026793420899985
25 Forest's; Func runs:10000; result:0.3785708322859447
500 Forest's; Func runs:10000; result:0.1917777390119122
=============================
5 Megacity's; Func runs:10000; result:0.6230769230769231
25 Megacity's; Func runs:10000; result:0.244
500 Megacity's; Func runs:10000; result:0.10795384615384714
=============================
All score:4.04076 (44.90%)

結果は大幅に改善されました。このアイデアは成功だったと言えます。その内容は、湿度（アルゴリズムにおける適応度）が高い場合に、他の水滴からある確率で最適解に関する情報を伝達するというものです。

最後に、各雲に対して、その雲から落下した水滴の総数（湿度の指標）が、drops配列の対応する値を加算することで更新されます。RainProcessメソッドは、湿度、水滴の分布、および個体群との相互作用を考慮しながら降雨をモデル化するメカニズムを実装しています。なお、コードに変更が加えられた箇所は緑色で強調表示されています。

生成された各x値に対して、集団からランダムにpインデックスが選ばれます。その後、確率（95%）に基づいて、a配列内の値が更新されます。この値は、集団（あるいは解集合）を表しています。最後に、各雲について、drops配列の対応する値を加算することで、その雲から落下した水滴の総数が再度更新されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACMO::RainProcess (bool &rev)
{
  //to shed drops from every cloud----------------------------------------------
  double cloud [];
  int    drops [];
  ArrayResize (cloud, cloudsNumber);
  ArrayResize (drops, cloudsNumber);

  if (!rev)
  {
    ArrayInitialize (cloud, 1.0);
  }
  else
  {
    ArrayInitialize (cloud, 0.0);

    double humidity;

    for (int i = 0; i < cloudsNumber; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        humidity = areas [c].regions [clouds [i].regionIndex [c]].humidity;
       
        if (humidity != -DBL_MAX) cloud [i] += humidity;

        else                      cloud [i] += minGp;
      }
    }
  }

  DropletsDistribution (cloud, drops);
  //ArrayPrint (drops);

  double dist   = 0.0;
  double centre = 0.0;
  double xMin   = 0.0;
  double xMax   = 0.0;
  double x      = 0.0;

  int    dCNT   = 0;


  for (int i = 0; i < cloudsNumber; i++)
  {
    for (int dr = 0; dr < drops [i]; dr++)
    {
      for (int c = 0; c < coords; c++)
      {
        dist   = clouds [i].entropy [c];
        centre = clouds [i].center  [c];
        xMin   = centre - dist;
        xMax   = centre + dist;

        x = u.GaussDistribution (centre, xMin, xMax, clouds [i].hyperEntropy);

        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], centre);
        
        if (x > rangeMax [c]) x = u.RNDfromCI (centre, rangeMax [c]);

        x = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);

        int p = u.RNDminusOne (popSize);

        if (a [p].f > a [dCNT].f)
        {
          if (u.RNDprobab () < 0.95) a [dCNT].c [c] = a [p].c [c];
        }

        else
        {
          a [dCNT].c [c] = x;
        }
      }
      dCNT++;
    }

    clouds [i].droplets += drops [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

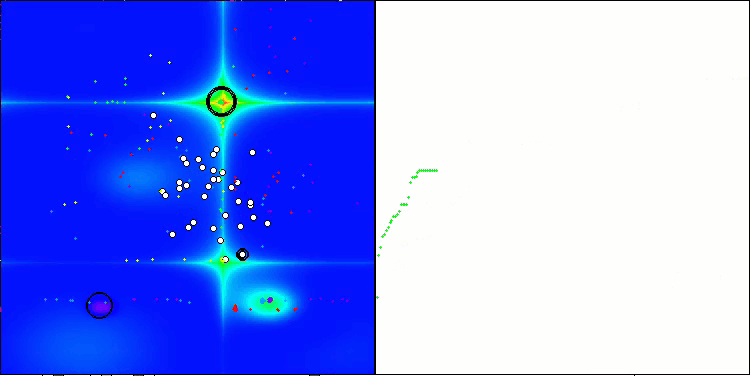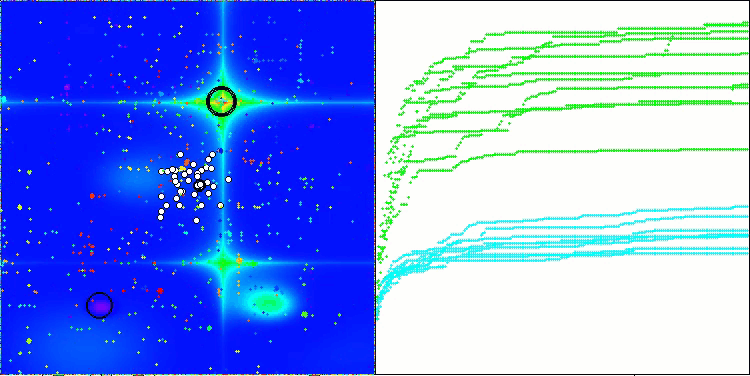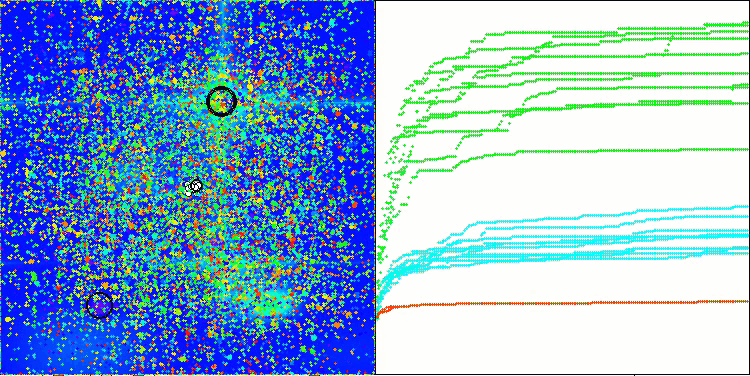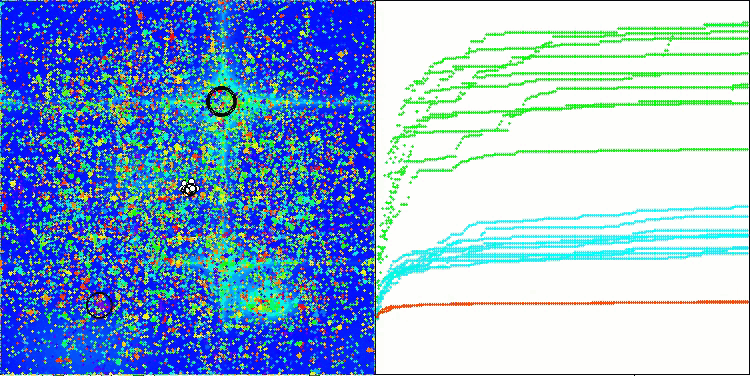
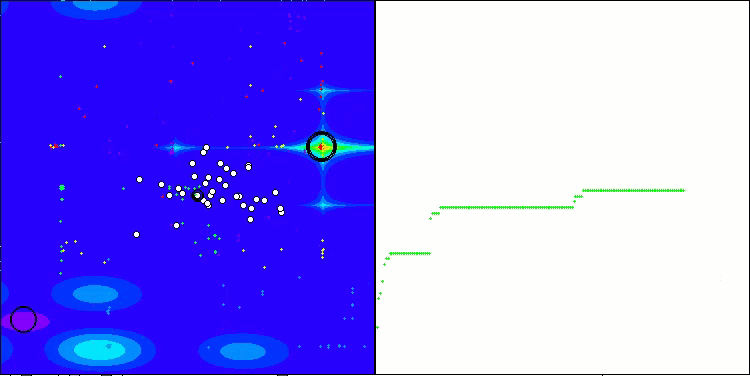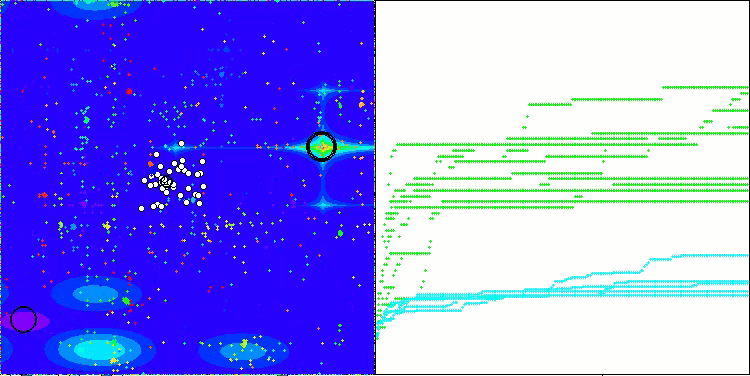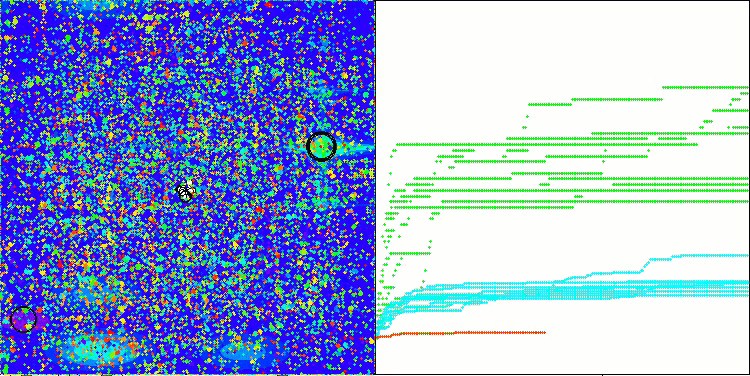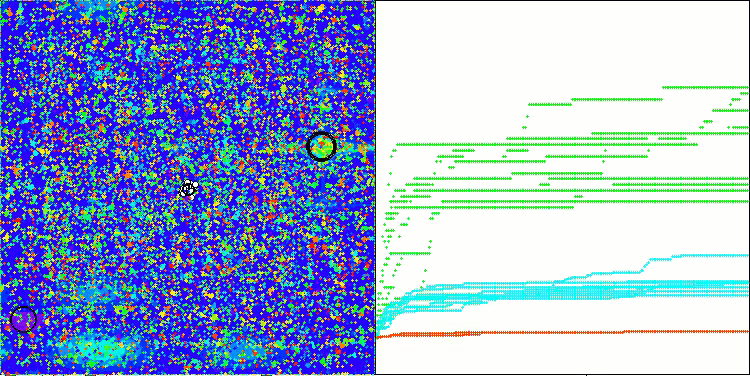
アルゴリズムの動作を可視化すると、収束性が良好であることが確認できます。ただし、最適化パラメータの数が少ない場合、収束グラフ上に長く平坦な区間が現れる傾向があり、これはアルゴリズムが局所的な極値に陥りやすいことを示しています。一方で、パラメータ数を増やすことでこの欠点は解消されることがわかりました。

可視化においては、雲は密集したクラスタとして表示されますが、外部パラメータ（領域数、雲数、初期エントロピー、乾燥閾値）を適切に設定することで、自然界のように空に浮かぶ雲の外観をシミュレートすることも可能です。

Hilly

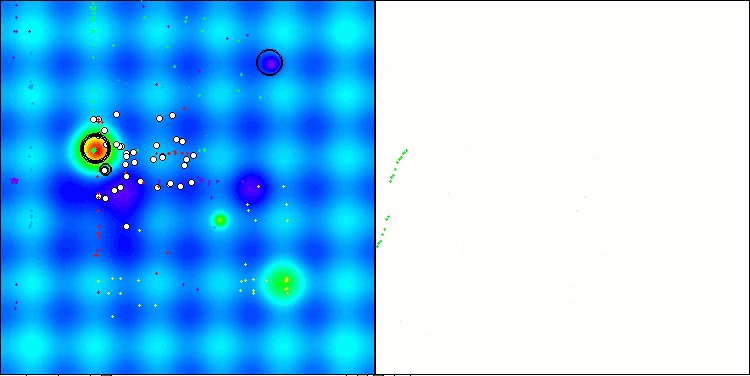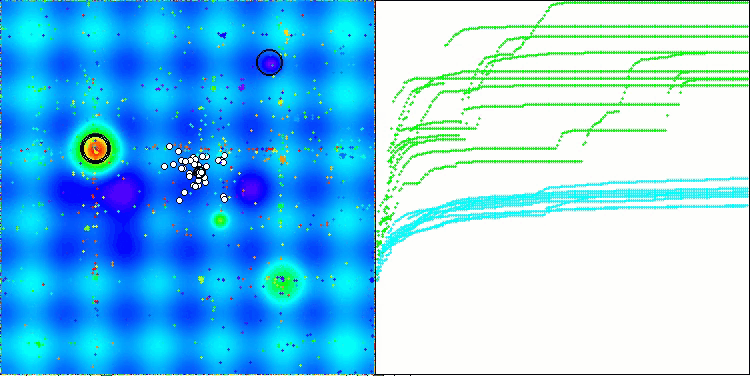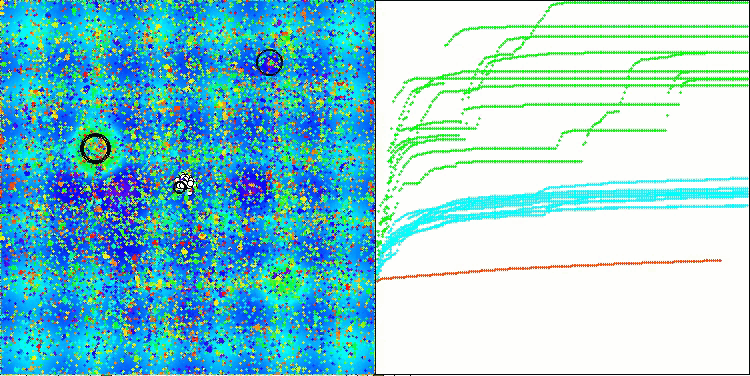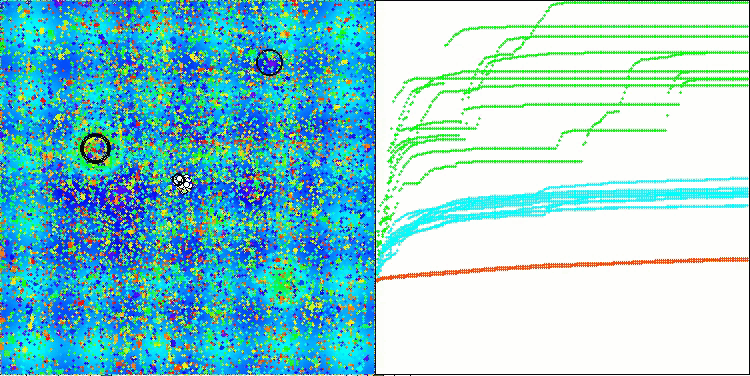
Hillyテスト関数のAСMO

Forest

Forestテスト関数のACMO

Megacity

Megacityテスト関数のACMO

修正版のテスト結果によると、アルゴリズムの順位は27位で、これは比較的安定した指標といえます。ここで強調しておきたいのは、現在この表には常に45種類のアルゴリズムが含まれており、新しいアルゴリズムが追加されるたびに、それ以前のものとの差は徐々に小さくなっていくという点です。つまり、この表は現在知られている最良のアルゴリズム上位群を示しているといえるでしょう。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗尾アルゴリズム	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会母集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
12	TSEA	亀甲進化アルゴリズム	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
13	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
14	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
15	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
16	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
17	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
18	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
19	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
20	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
21	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
22	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
23	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
24	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
25	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
26	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
27	ACMO	雲モデル最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
28	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
29	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
30	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
31	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
32	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
33	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
34	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
35	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
36	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
37	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
38	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
39	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
40	AAA	藻類適応アルゴリズム	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
41	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
42	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
43	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
44	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
45	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40

まとめ

本稿では、ACMOアルゴリズムのオリジナル版と修正版の2つのバージョンを提示しました。修正版ではわずかな改良が加えられているだけですが、集団内での情報交換を導入することにより、性能が大幅に向上しました。これは、アルゴリズムのロジックにごく小さな調整を加えるだけでも、さまざまな課題に対する効率を大きく改善できることを示しています。

このアルゴリズムの着想は非常に興味深く、局所的な極値に陥るのを回避することを主な目的としています。雲を高気圧領域から低気圧領域へと移動させ、降水を起こすという複雑かつ多段階のロジックを用いています。しかし、それだけでは高い収束性能を得るには不十分でした。そこで私は、個体間で情報をやりとりする仕組みを導入することでアルゴリズムを改良し、最適化手法にとって極めて重要な要素である収束性の向上を実現しました。

このアルゴリズムの特筆すべき点は、どの雲も同じ場所に長く留まらないということです。時間の経過とともに領域内の気圧が上昇し、結果的に雲は新しい未知の領域へと押し出されていきます。このメカニズムは、局所解への停滞を防ぐために設計されたものです。しかし、収束性の向上を図ることで逆に極値に陥る確率が高まり、このアプローチの魅力だった特徴が部分的に損なわれてしまうという結果になりました。最適化アルゴリズムの設計には常に、探索性能（局所最適に陥らない力）と解の精度のバランスというトレードオフがつきまといます。なお、情報交換の確率（現在は95%）はコード上で調整可能であり、これを下げることで安定性を高めることも可能です。

このアルゴリズムは、最適化のための素晴らしい土台であり、さまざまな応用が可能な興味深い技術の集合でもあります。たとえば、領域ごとの湿度形成ルール、気圧分布、雲の質量に応じた加速度と慣性の物理法則など、多くの革新的なアイデアが含まれており、研究者にとって非常に有益な資源となるでしょう。

Tab

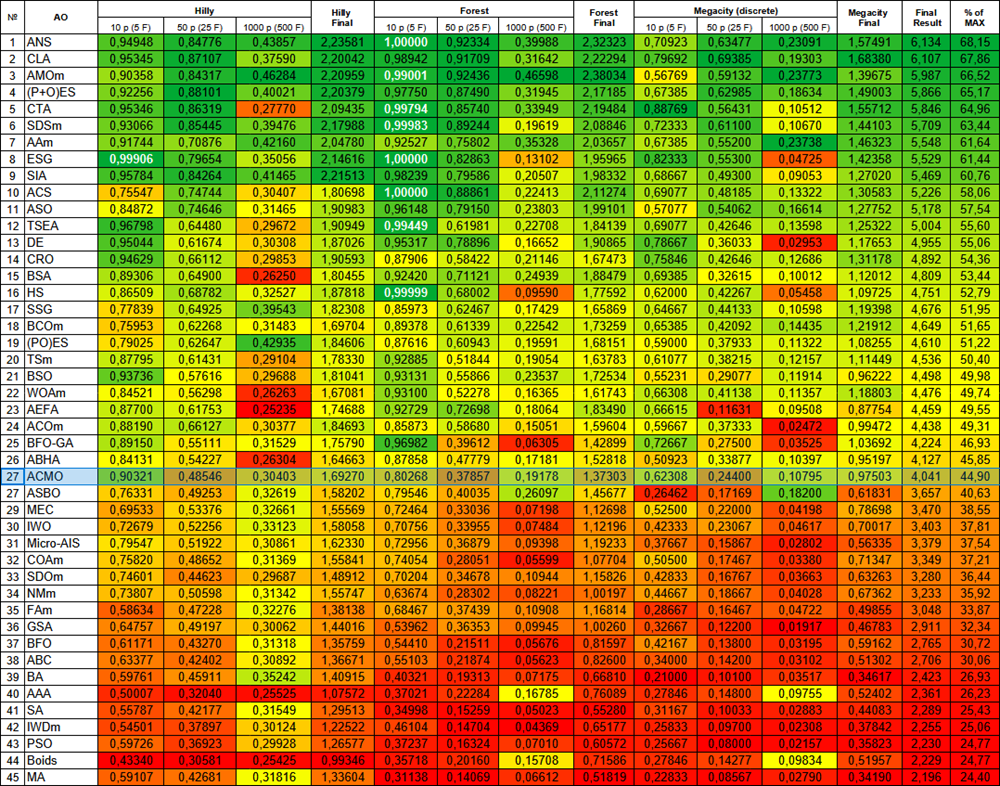
図2：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

チャート

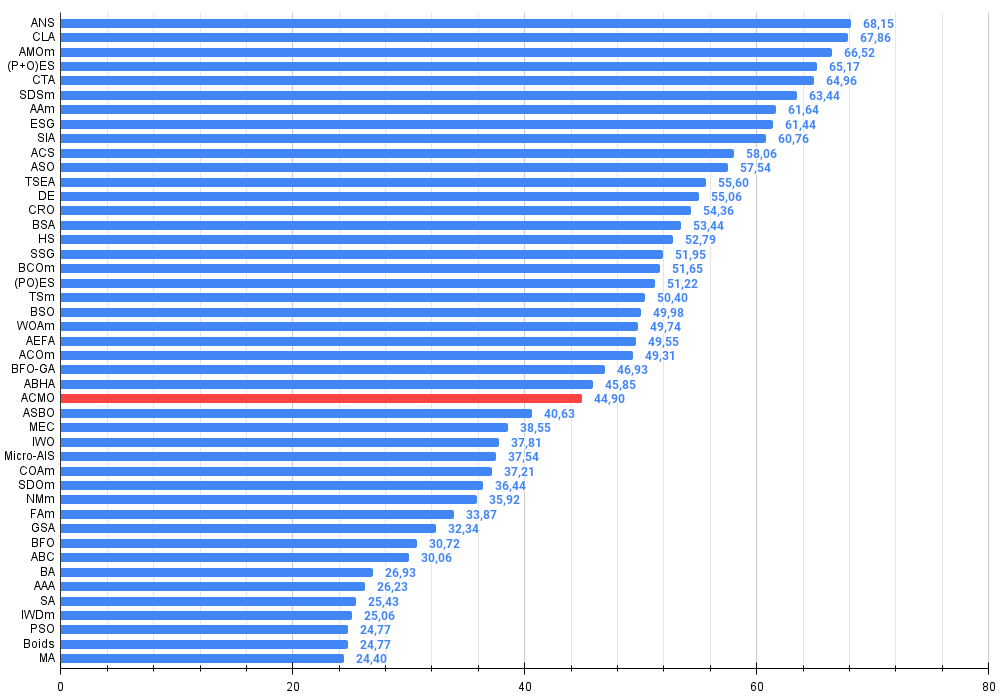
図3：関連するテストに応じたアルゴリズムの色勾配結果は0.99は白で強調表示されます

ACMOの長所と短所

長所

スタックを防止するメカニズムが組み込まれている
比較的良好な収束
比較的優れたスケーラビリティ

短所

膨大な数の外部パラメータ
実装が複雑
行き詰まりと収束の間の適切なバランスを見つけるのが難しい

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15921

添付されたファイル |

ZIPをダウンロード

ACMO.zip (39.7 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (2)

Arda Kaya | 24 4月 2025 において 16:13

本当に興味深いトピックだ！

Andrey Dik | 28 4月 2025 において 18:02

Arda Kaya #:
本当に興味深いトピックだ！

ありがとう。

取引におけるニューラルネットワーク：価格変動予測におけるマスクアテンションフリーアプローチ

この記事では、Mask-Attention-Free Transformer (MAFT)法と、それを取引分野に応用する可能性について説明します。従来のTransformerはシーケンスを処理する際にマスキングを必要としますが、MAFTはこのマスキングを不要にすることでアテンション処理を最適化し、計算効率を大幅に向上させています。

初級から中級へ：配列と文字列(II)

この記事では、プログラミングがまだ非常に初歩的な段階にあるにもかかわらず、すでにいくつかの興味深いアプリケーションを実装できることを示します。今回は、比較的シンプルなパスワードジェネレーターを作成します。このようにして、これまでに説明してきたいくつかの概念を実際に適用することができます。加えて、特定の問題に対する解決策をどのように構築できるかについても考察していきます。

DoEasy - サービス関数（第3回）：アウトサイドバーパターン

本記事では、DoEasyライブラリにおけるアウトサイドバーのプライスアクションパターンを開発し、価格パターン管理へのアクセス手法を最適化します。あわせて、ライブラリのテスト中に判明したエラーや不具合の修正もおこないます。

リプレイシステムの開発（第67回）：コントロールインジケーターの改良

この記事では、コードを少し手直しすることで、どのような改善が得られるかを見ていきます。今回の改良は、コードの簡素化を図り、MQL5ライブラリの呼び出しをより活用し、そして何よりも、将来的に開発する可能性のある他のプロジェクトでも、より安定して安全かつ使いやすくなることを目的としています。