MetaTrader 5 / 例
English Русский 中文 Español Português
preview
人工部族アルゴリズム(ATA)

人工部族アルゴリズム(ATA)

MetaTrader 5 — 例 |
24 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

技術の急速な進化に伴い、最適化タスクはますます複雑化しています。そのような中で、科学者や研究者たちは自然界から新たなインスピレーションを得ようと模索し続けています。そうしたアプローチの中でも特に注目されるのが、2012年にT. Chen、Y. Wang、J. Liによって発表された人工部族アルゴリズム(ATA: Artificial Tribe Algorithm)です。ATAは部族の行動様式に着想を得ており、環境変化に適応し最適解を探索するために、分散と移動という2つの主要メカニズムを活用します。広大な空間の中で、人々の集団が最良の資源を求めて結束し、移動し、知識や経験を交換しながら、複雑な問題を解決するための独自の戦略を生み出していく。このような行動モデルがATAの設計思想の基盤となっています。これは、分散と移動という2つの主要メカニズムを調和的に組み合わせたアルゴリズムです。

Artificial Tribe Algorithmは、生体模倣型知能アルゴリズムの原理に基づく、まったく新しい最適化手法です。本アルゴリズムでは、自然界の部族の行動を模倣し、繁殖能力と移動能力を活用して最適解を探索します。部族は複数の個体によって構成され、それぞれが相互作用しながら大域的最適解を見つけ出すように設計されています。


アルゴリズムの実装

ATAアルゴリズムのプロセスは、パラメータの設定と部族のランダム初期化から開始し、その後適応度を計算します。次に、反復カウンタを増加させ、部族の現状を評価します。状況が良好である場合（世代間の最適適応度の差が所定の基準より大きい場合）、繁殖行動を行い、個体間で情報交換をおこないます。一方、状況が不十分な場合には、移動行動が実行されます。この場合、個体は自身の経験および部族全体の経験に基づいて移動します。移動は過度な分散を避けるため、連続的にはおこなわれません。その後、再度適応度を計算し、部族全体および各個体の記録された最良値と比較します。より良い解が見つかった場合、その情報がメモリに保存されます。終了条件が満たされている場合には反復を終了し、そうでなければ状況評価のステップに戻ります。

ATAに全体情報を組み込むことで、部族の歴史的経験に重みを与え、より良い解の探索や探索能力の向上に寄与します。部族の経験の重みを増加させることにより、アルゴリズムの効率が向上し、収束速度が加速します。これを実現するため、ATAでは全体慣性重みを導入しており、探索能力を高め、プロセスを高速化します。

ATAの最大の革新点は、状況に応じて適応する二重行動システムの存在です。進捗が良好な場合には、繁殖行動による深い探索がおこなわれ、局所最適に停滞した場合には移動が発動され、より広範囲の探索が促進されます。また、個体学習と社会的学習の組み合わせも重要です。移動時には個体記憶(Xs)が使用され、全体記憶(Xg)はAT_w慣性係数によって重み付けされます。繁殖時には交配相手をランダムに選択することで、多様性を保ち探索速度を向上させます。

ATAのパラメータ体系はシンプルながら効果的です。部族サイズ(tribe_size)、行動切り替え基準(AT_criterion)、探索における全体影響(AT_w)を制御し、柔軟かつ強力なアルゴリズムとなっています。著者によると、この設計により、特に小規模な個体群でも、より複雑なアルゴリズムに容易に対抗できる性能を持ちます。

アルゴリズムの主要な構成要素には、進捗が良好で適応度の差が基準以上の場合に適用される繁殖行動があります。この場合、個体は部分的な情報を交換します。適応度の差が小さい不良状況では移動行動が適用され、個体および全体の経験に基づいた移動がおこなわれ、慣性の重みを考慮することで全体探索が強化されます。存在基準は、反復間の最良適応度の変化を評価します。変化が大きければ繁殖、変化が小さければ移動が実行されます。

さらに、アルゴリズムにはメモリ更新システムが組み込まれており、個体の最良位置および部族全体の最良位置を追跡します。新たにより良い解が見つかると、それぞれの最良位置が更新されます。

ATAの設計上の特徴は、パラメータのシンプルさ、個体学習と社会的学習の統合、繁殖と移動の自動適応的切り替えです。全体慣性重みは探索性能を改善し、最適解探索を高速化します。

したがって、個体行動のルールは次のように説明できます。

1. 分散：個体は、部族内の情報を用いて次世代の遺伝情報を形成します。現状の環境が良好な場合、個体は部族内からランダムに相手を選び、遺伝情報の交換によって次世代を生成します。

2. 移動：現状が不良（世代間の最適適応度の差が基準値未満）である場合、個体は自身および部族の歴史的経験に基づいて移動し、部族全体として移動を実行します。

アルゴリズムにおける個体群の主要フェーズは、視覚的に以下のように模式化して表現できます。

ATA_2

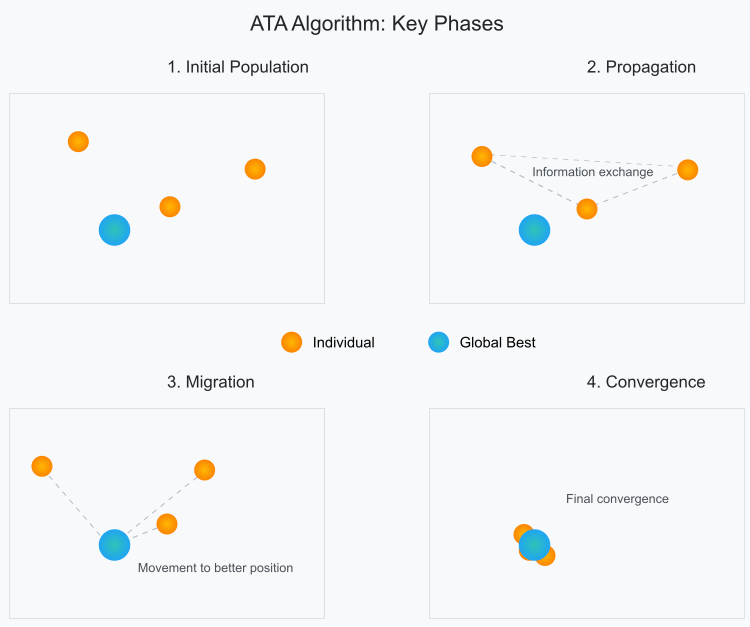
図1：ATAアルゴリズム集団における個体の動きの段階

ATAアルゴリズムの疑似コードを実装してみましょう。

// ATA
// 主なパラメータ：
// tribe_size：部族の個体数
// ATA_criterion：存在基準の閾値
// ATA_w：全体慣性重み
// X：個体の位置ベクトル
// Xs：個体の最良歴史位置
// Xg：部族全体の最良歴史位置

ATA：
    初期化：
        部族をtribe_size個体で生成し、各個体の位置Xをランダム初期化
        全個体の初期適応度を計算
        個体最良位置Xsと部族最良位置Xgを初期化（最良位置で）
        iteration = 0
        
    While (iteration < max_iterations):
        iteration = iteration + 1
        
        // 現状評価
        difference = |current_best_fitness - previous_best_fitness|
        
        If (difference > ATA_criterion):
            // 状況が良好 - 繁殖行動
            各i個体について
                // ランダムにパートナーjを選択 (i ≠ j)
                j = random (1, tribe_size) where j ≠ i
                
                // 繁殖位置計算
                r1 = random (0,1)
                Yi+1 = r1 * Yj + (1 - r1) * Xi // パートナー新位置
                Xi+1 = r1 * Xi + (1- r1) * Yi // 個体新位置
                
        Else:
            // 状況が不良 - 移動行動
            各i個体について
                // 移動方程式
                r1 = random (0,1)
                r2 = random (0,1)
                Xi+1 = Xi + r1 * (Xs - Xi) + ATA_w * r2 * (Xg - Xi)
                
        // 適応度と最良位置の更新
        各i個体について
            Xiのnew_fitnessを計算
            
            new_fitnessがbest_fitness_of_individualよりも優れている場合
                i個体のXを更新
                
            new_fitnessがglobal_best_fitnessよりも優れている場合
                Xgを更新
                
        次の反復のためにcurrent_best_fitnessを保存
        
    見つかった最適解としてXgを返す

ATA

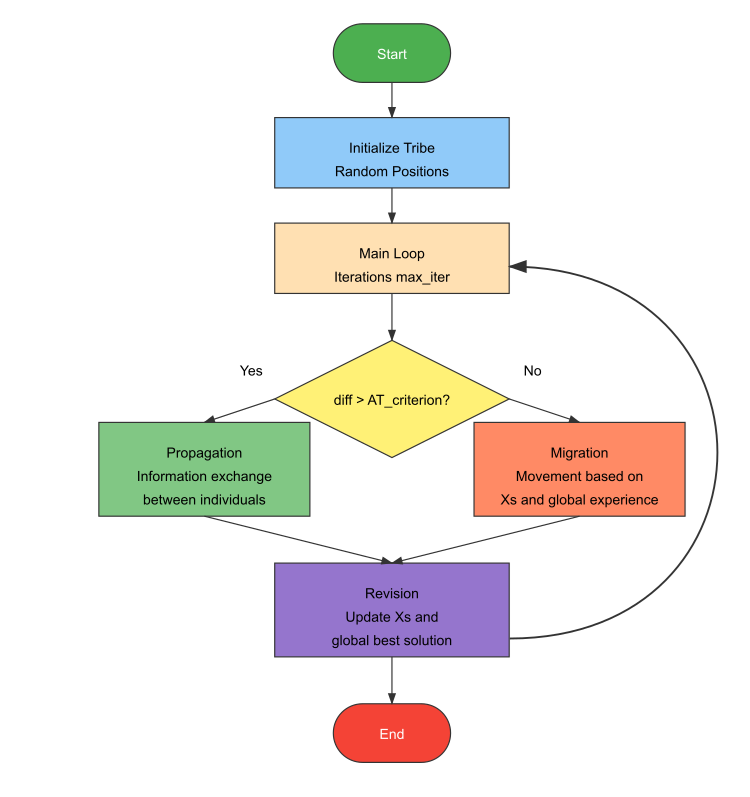
図2：ATA動作の論理図

ATAを実装するC_AO_ATAクラスを定義しましょう。その内容を簡単に説明します。

継承と主なメンバー
  • このクラスはC_AO基底クラスから継承される
  • デストラクタとコンストラクタを含む
コンストラクタは基本パラメータを初期化します。
  • popSize = 50（部族のサイズ）
  • AT_criterion = 0.3（好ましい状況の基準）
  • AT_w = 1.46（慣性重み）
メソッド
  • SetParams()：params"配列からパラメータを設定
  • Init()：検索範囲による初期化
  • Moving ()：個体移動の実装
  • Revision ()：解の評価と更新
Privateメンバー
  • prevBestFitness：比較のために前回の最高値を保存

これはアルゴリズムの基本的なフレームワークであり、ここでその動作に必要なすべてのパラメータとメソッドが定義されています。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ATA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ATA () { }
  C_AO_ATA ()
  {
    ao_name = "ATA";
    ao_desc = "Artificial Tribe Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16588";

    popSize      = 50;   // Population size
    AT_criterion = 0.3;  // Criteria for assessing the current situation
    AT_w         = 1.46; // Global inertial weight

    ArrayResize (params, 3);

    // Initialize parameters
    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "AT_criterion"; params [1].val = AT_criterion;
    params [2].name = "AT_w";         params [2].val = AT_w;
  }

  void SetParams () // Method for setting parameters
  {
    popSize      = (int)params [0].val;
    AT_criterion = params     [1].val;
    AT_w         = params     [2].val;
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   ();       // Moving method
  void Revision ();       // Revision method

  //----------------------------------------------------------------------------
  double AT_criterion;    // Criteria for assessing the current situation
  double AT_w;            // Global inertial weight

  private: //-------------------------------------------------------------------
  double prevBestFitness; // Previous best solution
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ATAクラスのInitメソッドは、アルゴリズムの初期化を担当します。それをいくつかの部分に分解してみましょう。

以下はメソッドパラメータです。
  • rangeMinP []：各検索次元の最小値の配列
  • rangeMaxP []：最大値の配列
  • rangeStepP []：離散化ステップの配列
  • epochsP：エポック数（デフォルトは0）
以下は主なアクションです。
  • 基底クラスからStandardInitを呼び出して標準パラメータを初期化
  • StandardInitがfalseを返した場合、メソッドを中断
  • prevBestFitnessを-DBL_MAXに設定（最大化タスク用）
以下は戻リ値です。
  • 初期化が成功した場合はtrue
  • 標準の初期化に失敗した場合はfalse

これは、アルゴリズムを動作させるための準備となる初期化の最小限の実装です。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ATA::Init (const double &rangeMinP  [], // Minimum search range
                     const double &rangeMaxP  [], // Maximum search range
                     const double &rangeStepP [], // Search step
                     const int     epochsP = 0)   // Number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Initialization of standard parameters

  //----------------------------------------------------------------------------
  prevBestFitness = -DBL_MAX;
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Moving()メソッドは、部族の個体の移動を担当し、次の2つの主要部分で構成されます。

これが最初の実行の場合(revision = false)は、次の操作を実行します。
  • 探索空間にすべての個体をランダムに配置する
  • それぞれの位置を許容できる離散的な値に導く
  • 初期配置が完了したことを示す(revision = true)
これが最初の実行ではない場合は、現在のdiff状況基準を計算し、状況が良好である場合(diff > AT_criterion)は、次の操作を実行します。
  • 各個体がランダムにパートナーを選択する
  • 各個体が自分の位置に関する情報を交換する
  • この交流に基づいて新たな位置を形成する
状況が悪い場合(diff ≤ AT_criterion)、各個体は次の点を考慮して移動します。
  • 個体最良位置
  • 部族最良位置
  • AT_w慣性重み

移動がおこなわれる際には、すべての新しい位置は確認され、指定された範囲内の許容値に調整されます。さらに、次の点にも注意する必要があります。状況を評価するための基準は外部パラメータであり、無次元の値を持つため、現在の最良適応度と前回の最良適応度の差は、最良の歴史的適応度と最悪の適応度との差で正規化する必要があります。すなわち、diff = (fB - prevBestFitness) / (fB - fW)です。この目的のために、本アルゴリズムでは、全体の最良解だけでなく、全体の最悪解も追跡しています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ATA::Moving ()
{
  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  // Check the existence criterion
  double diff = (fB - prevBestFitness) / (fB - fW);

  double Xi   = 0.0;
  double Xi_1 = 0.0;
  double Yi   = 0.0;
  double Yi_1 = 0.0;
  double Xs   = 0.0;
  double Xg   = 0.0;
  int    p    = 0;
  double r1   = 0.0;
  double r2   = 0.0;

  if (diff > AT_criterion)
  {
    // Spread behavior (good situation)
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        p  = u.RNDminusOne (popSize);
        r1 = u.RNDprobab ();

        Xi = a [i].cP [c];
        Yi = a [p].cP [c];

        Xi_1 = r1 * Xi + (1.0 - r1) * Yi;
        Yi_1 = r1 * Yi + (1.0 - r1) * Xi;

        a [i].c [c] = u.SeInDiSp  (Xi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].c [c] = u.SeInDiSp  (Yi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  else
  {
    // Migration behavior (bad situation)
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        r1 = u.RNDprobab ();
        r2 = u.RNDprobab ();

        Xi = a [i].cP [c];
        Xs = a [i].cB [c];
        Xg = cB [c];

        Xi_1 = Xi + r1 * (Xs - Xi) + AT_w * r2 * (Xg - Xi);

        a [i].c [c] = u.SeInDiSp (Xi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision ()は、個体の移動後に最良解を評価し、更新する役割を担います。具体的には、次の処理をおこないます。

部族内の全個体について処理をおこなう
    • 全体最良解(fB)が改善されたかどうかを確認
    • 見つかった最悪解(fW)を更新
    • 各個体の個人最良解(a [i].fB)を確認し、必要に応じて更新
    • 現在の位置を前回の位置として保存(in cP)
    新たな最良解が見つかった場合（indB が -1 でない場合）
      • 前回の最良値を保存(prevBestFitness = tempB)
      • 最良個体の座標を全体最良解にコピー(cB)

      本質的には、これは部族の現在の状態を「監査」するメソッドです。ここでは、全体の最良/最悪値、各個体の個人最良値、そして位置の履歴といった重要な指標がすべて更新されます。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ATA::Revision ()
{
  //----------------------------------------------------------------------------
  int    indB  = -1;                // Best particle index
  double tempB = fB;

  for (int i = 0; i < popSize; i++) // For each particle
  {
    if (a [i].f > fB)               // If the function value is better than the current best one
    {
      fB   = a [i].f;               // Update the best value of the function
      indB = i;                     // Save the index of the best particle
    }

    if (a [i].f < fW)               // If the function value is worse than the current worst one
    {
      fW   = a [i].f;               // Update the worst value of the function
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }

    ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY);
  }

  if (indB != -1)
  {
    prevBestFitness = tempB;
    ArrayCopy (cB, a [indB].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best particle
  }
}
//——————————————————————————————————————————————————————————————————————————————

      テストベンチでATAをテストした結果に移りましょう。

      ATA|Artificial Tribe Algorithm|50.0|0.3|0.5|
      =============================
      5 Hilly's; Func runs:10000; result:0.540711768815426
      25 Hilly's; Func runs:10000; result:0.31409437631469717
      500 Hilly's; Func runs:10000; result:0.2512638813618161
      =============================
      5 Forest's; Func runs:10000; result:0.40309649266442193
      25 Forest's; Func runs:10000; result:0.2572536671383149
      500 Forest's; Func runs:10000; result:0.18349902023635473
      =============================
      5 Megacity's; Func runs:10000; result:0.24
      25 Megacity's; Func runs:10000; result:0.13600000000000004
      500 Megacity's; Func runs:10000; result:0.09518461538461616
      =============================
      All score:2.42110 (26.90%)

      アルゴリズムの結果の出力や可視化からもわかるように、現状のパラメータ設定では、本アルゴリズムは私たちの評価表に到達できていません。下の可視化は、アルゴリズムが局所的な罠から抜け出す能力が弱いことを示しています。アルゴリズムの解集団には明らかに多様性が欠けており、その結果、探索性能が劣化していることが確認できます。

      Hilly Orig

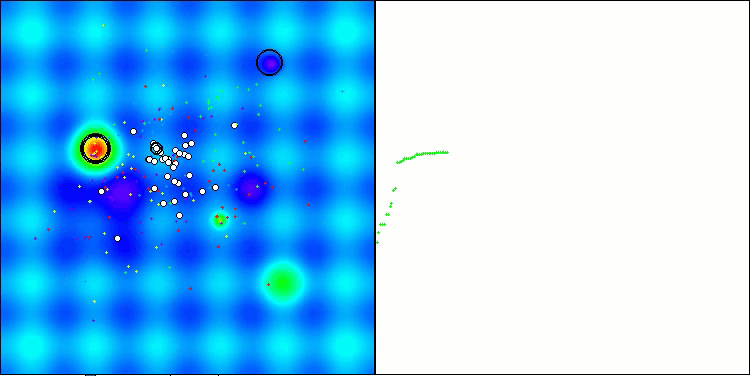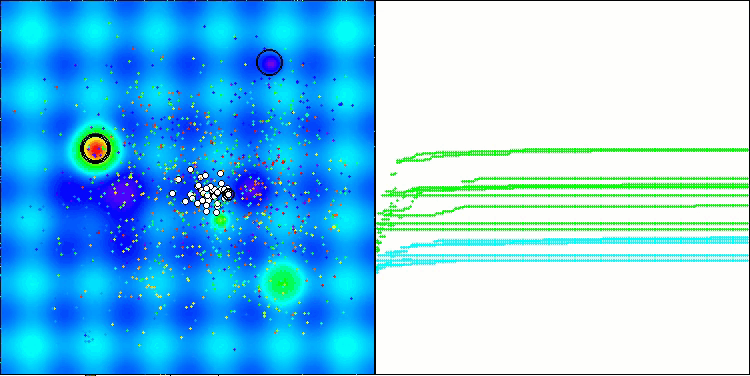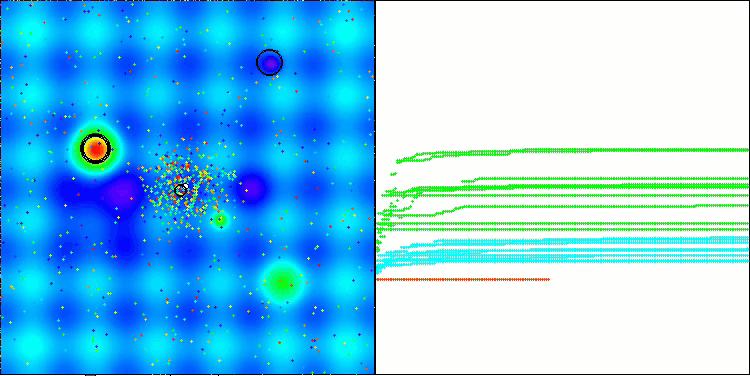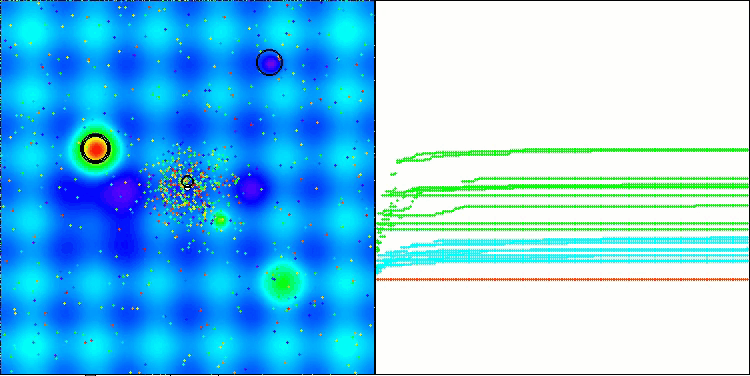
      Hillyテスト関数のATAm

      解集団における解の多様性の欠如に着目し、ATAアルゴリズムの改良を試みます。多様性は探索空間を効果的に探索する上で重要な要素であるため、この点に注目します。今回の改良では、集団の適応度の状態に応じて変化する動的確率を導入します。

      集団が解空間の狭い範囲に圧縮されると、アルゴリズムが局所最適に陥る可能性があります。従来のアルゴリズムと同様に、現在の全体最良解と前回の全体最良解の差分を追跡しますが、この差分が非常に小さい場合は、集団の多様性が不足しており、解の収束が進んでいることの指標となります。

      この状況を回避するために、一定の確率で、現在の全体最良解から遠い個体を除外します。この操作はタスクの許容範囲内でおこなわれ、タスク条件を満たしつつ範囲を超えないように設計されています。除外する個体の距離は、正規分布に基づいて決定されます。

      興味深い点として、現在の最良解と前回の最良解の差分(diff)が大きいほど、こうした異常値の確率も高くなります。これにより、集団の状態に適応的に対応できます。集団が停滞し始めた場合には、移住フェーズをより積極的に活用することで、局所最適から抜け出し、より良い解を探索する確率を高めることができます。

      このように、今回のATAの改良は、解集団の多様性を維持するだけでなく、探索空間全体の効率向上にも寄与します。その結果、より持続可能な探索結果が得られ、解の品質向上にもつながります。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ATAm::Moving ()
{
  // Initial random positioning
  if (!revision) // If there has not been a revision yet 
  {
    for (int i = 0; i < popSize; i++) // For each particle
    {
      for (int c = 0; c < coords; c++) // For each coordinate
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);                             // Generate random position
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Convert to discrete values
      }
    }

    revision = true; // Set revision flag
    return;          // Exit the method
  }

  //----------------------------------------------------------------------------
  // Check the existence criterion
  double diff = (fB - prevBestFitness) / (fB - fW);

  double Xi   = 0.0;
  double Xi_1 = 0.0;
  double Yi   = 0.0;
  double Yi_1 = 0.0;
  double Xs   = 0.0;
  double Xg   = 0.0;
  int    p    = 0;
  double r1   = 0.0;
  double r2   = 0.0;

  if (diff > AT_criterion)
  {
    // Spread behavior (good situation)
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        p  = u.RNDminusOne (popSize);
        r1 = u.RNDprobab ();

        Xi = a [i].cP [c];
        Yi = a [p].cP [c];

        Xi_1 = r1 * Xi + (1.0 - r1) * Yi;
        Yi_1 = r1 * Yi + (1.0 - r1) * Xi;

        a [i].c [c] = u.SeInDiSp  (Xi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].c [c] = u.SeInDiSp  (Yi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  else
  {
    // Migration behavior (bad situation)
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < diff)
        {
          Xi_1 = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 1);
          a [i].c [c] = u.SeInDiSp (Xi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
        else
        {
          r1 = u.RNDprobab ();
          r2 = u.RNDprobab ();

          Xi = a [i].cP [c];
          Xs = a [i].cB [c];
          Xg = cB [c];

          Xi_1 = Xi + r1 * (Xs - Xi) + AT_w * r2 * (Xg - Xi);

          a [i].c [c] = u.SeInDiSp (Xi_1, rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


      テスト結果

      ATAm（ATA修正版）の結果

      ATAm|Artificial Tribe Algorithm M|50.0|0.9|0.8|
      =============================
      5 Hilly's; Func runs:10000; result:0.7177133636761123
      25 Hilly's; Func runs:10000; result:0.553035897955171
      500 Hilly's; Func runs:10000; result:0.25234636879284034
      =============================
      5 Forest's; Func runs:10000; result:0.8249072382287125
      25 Forest's; Func runs:10000; result:0.5590392181296365
      500 Forest's; Func runs:10000; result:0.2047284499286112
      =============================
      5 Megacity's; Func runs:10000; result:0.43999999999999995
      25 Megacity's; Func runs:10000; result:0.18615384615384617
      500 Megacity's; Func runs:10000; result:0.09410769230769304
      =============================
      All score:3.83203 (42.58%)

      今回は、結果は非常に有望であり、すでに評価表に掲載する価値があることが確認されました。これにより、他のアルゴリズムを押しのけることが可能となります。可視化では、解集団内の個体が解空間全体でより活発に移動している様子が確認できます。しかし、新たな課題も明らかになりました。結果の分散が大きく、局所最適に陥る問題を完全には解消できていません。

      Hilly

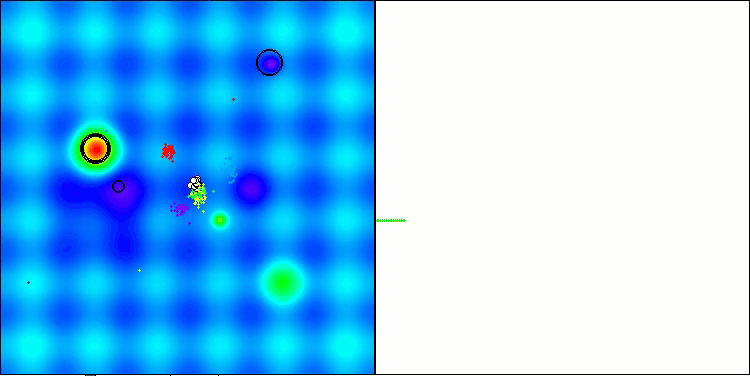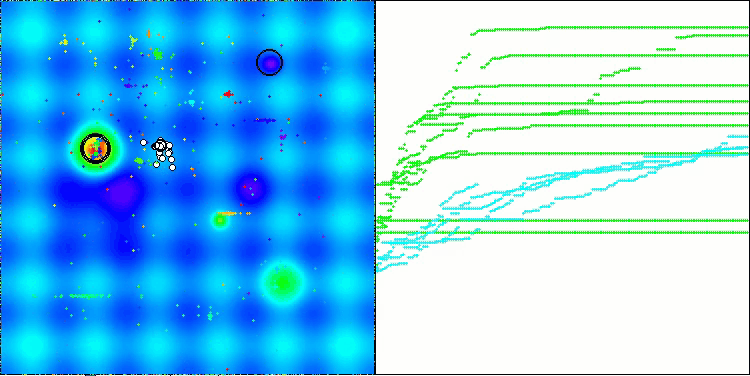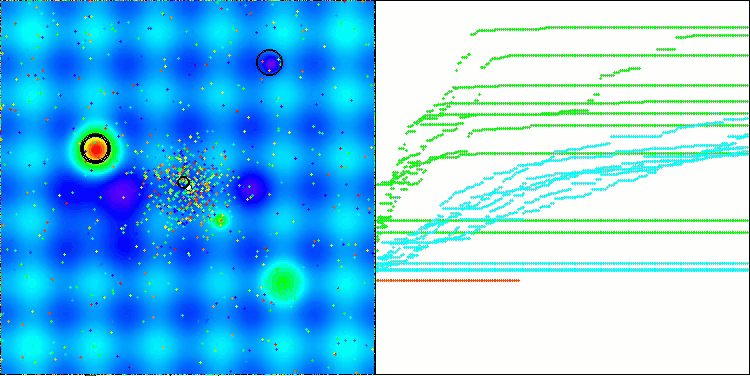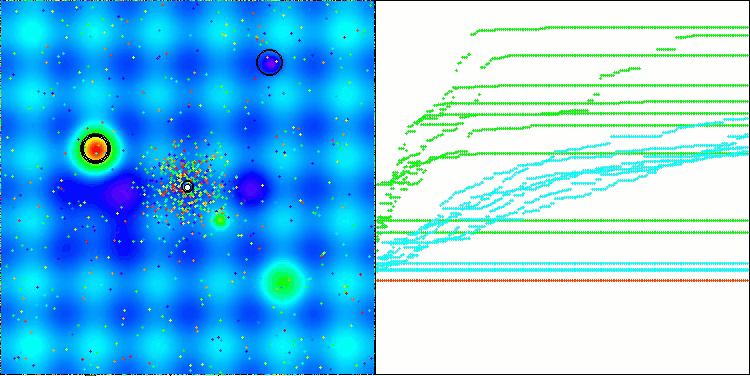
      Hillyテスト関数のATAm

      Forest

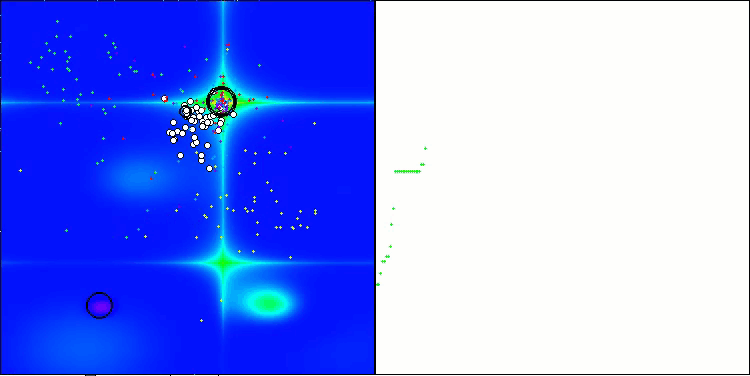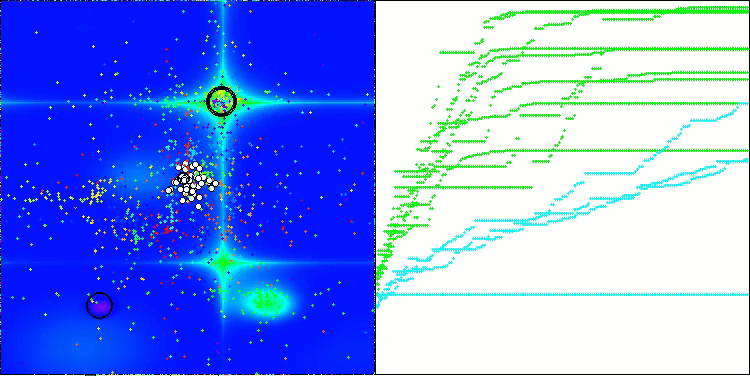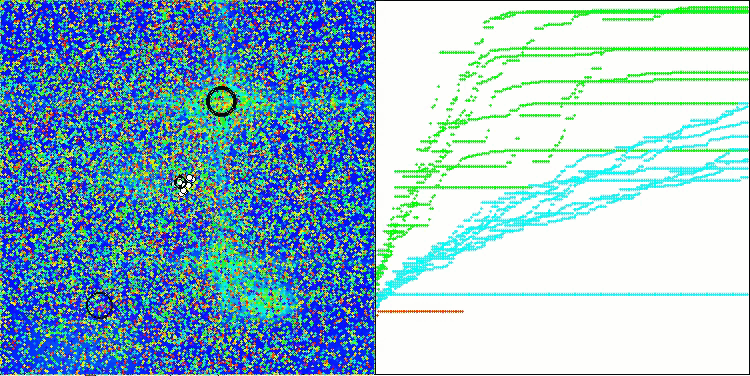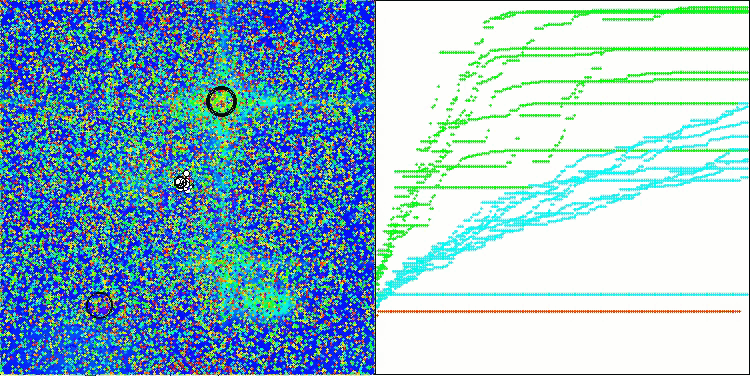
      Forestテスト関数のATAm

      Megacity

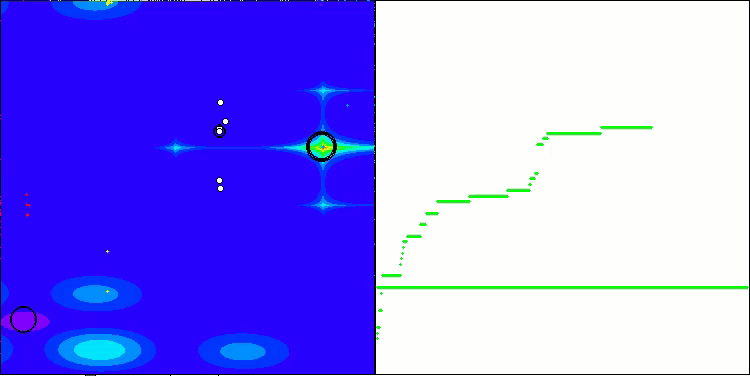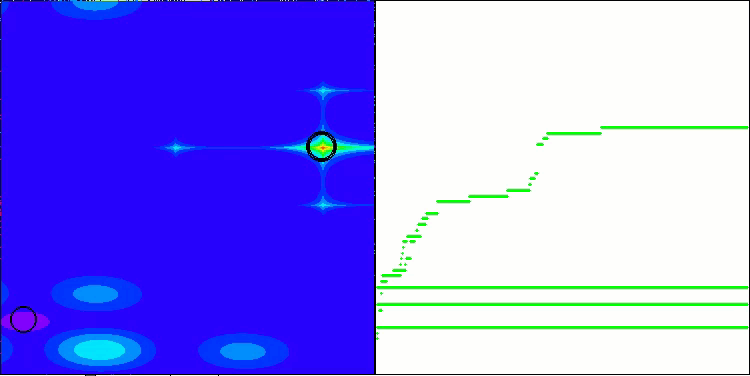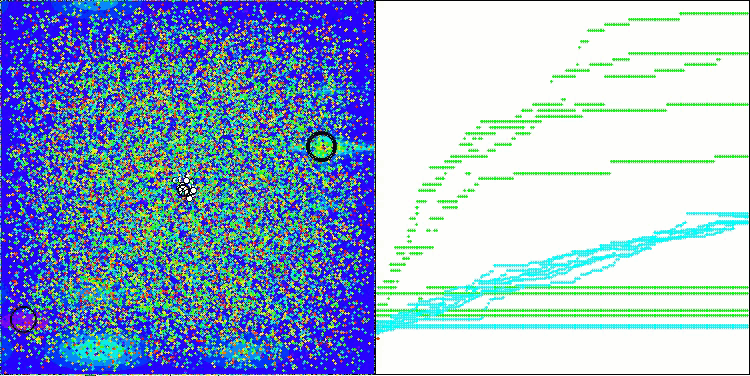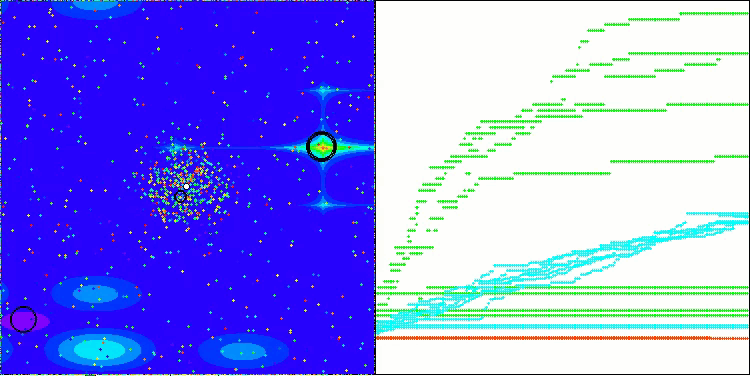
      Megacityテスト関数のATAm

      ATAはランキング表で33位にランクされています。

      # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
      10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
      1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
      8 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      9 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      11 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      12 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
      13 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      14 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      15 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      16 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      17 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      18 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      19 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
      20 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
      21 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      22 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      23 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      24 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      25 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      26 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
      27 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      28 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      29 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
      30 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      31 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
      32 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
      33 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
      34 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
      35 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      36 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      37 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      38 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      39 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      40 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      41 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      42 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      43 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      44 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
      45 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06



      まとめ

      本記事では、現代の最適化アルゴリズムのひとつであるATA（人工部族アルゴリズム）を詳細に検討しました。ほかの手法と比較すると、このアルゴリズムの性能は特に優れているわけではありませんが、動的な集団状態の管理や局所最適に関連する問題の分析手法についての理解に貴重な示唆を与えてくれます。

      ATAへの関心は、アルゴリズムが持つ2つの主要なフェーズ自体に限られるものではありません。解法としてはこれらのフェーズ自体の価値はそれほど大きくありませんが、個体の移動フェーズを動的に選択し、集団の状態を制御するというアプローチが重要です。この点こそが、アルゴリズムを問題の変化する条件により効果的に適応させ、得られる解の品質を向上させる要因となっています。したがって、ATAの研究はアルゴリズム最適化の分野における新たな研究の可能性を切り開き、より高度な手法の開発の基礎としても活用できるものです。

      さらに、今回検討したアルゴリズムにはさまざまな演算子を適用可能であり、それによって効率を大幅に向上させることも可能です。たとえば、ソートに基づく選択演算子や交叉を利用することで、結果の改善が期待できます。

      しかし、現行バージョンのアルゴリズムには、解の品質に依存する仕組みがなく、組合せ的な特性も欠如している点には注意が必要です。この点がアルゴリズムの能力を制限しています。これらはすべて、将来的な研究や改良の興味深い方向性を示していますが、本稿の範囲を超える内容です。読者の中で、提案された変更を試し、独自のアルゴリズムバージョンをコメントで共有していただけると大変嬉しく思います。

      Tab

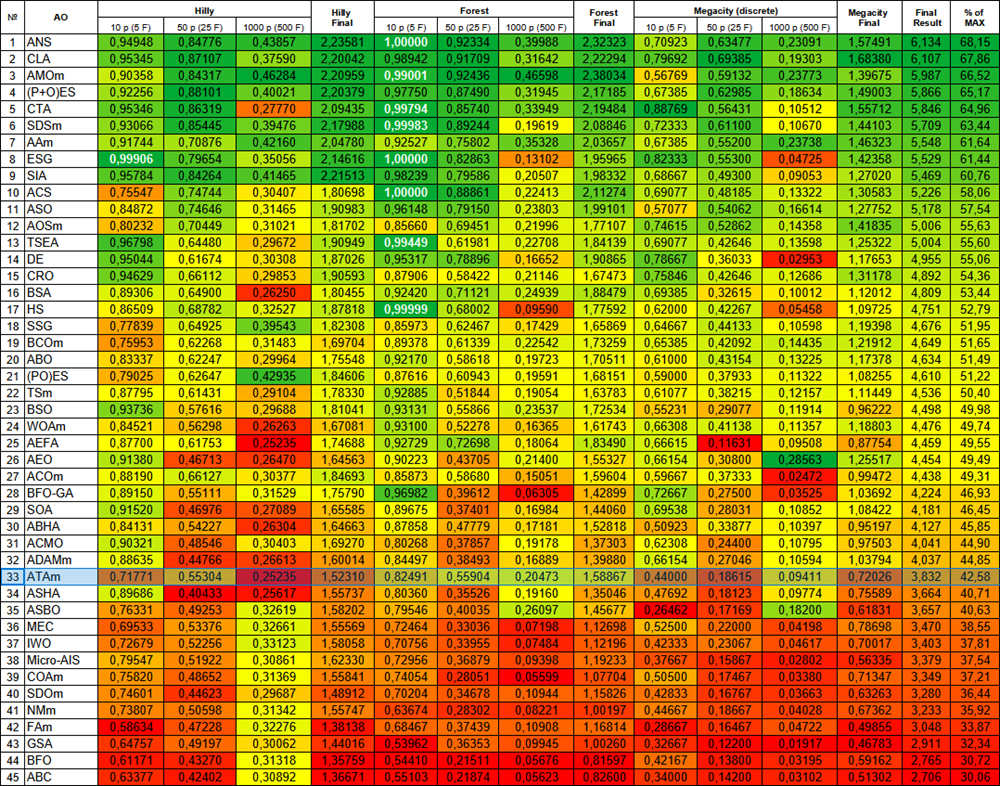
      図3：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

      チャート

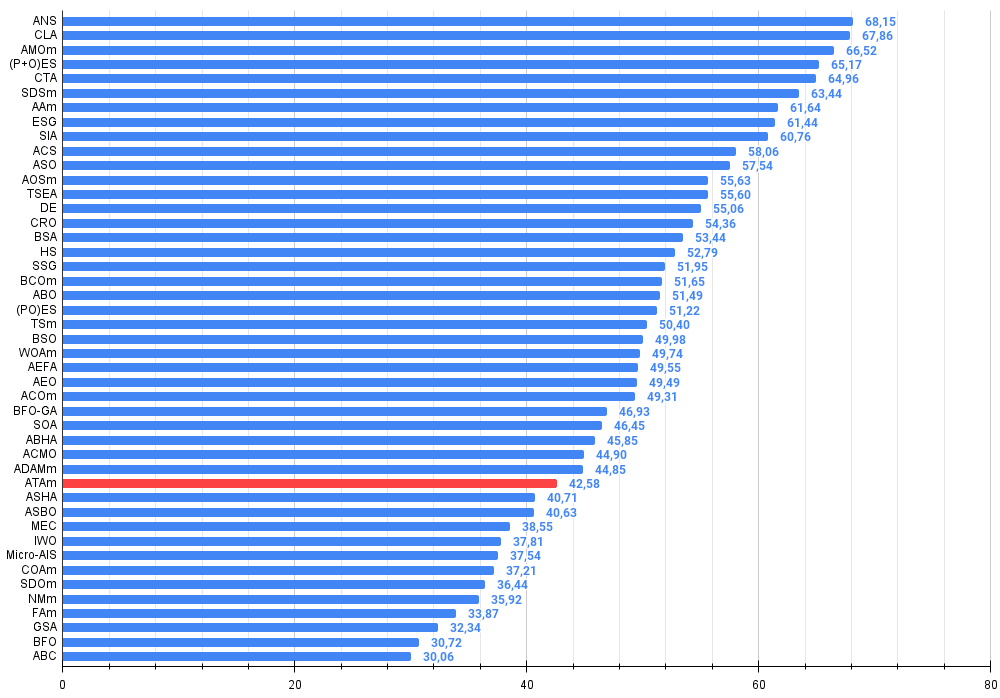
      図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

      ATAmの長所と短所

      長所

      1. 外部パラメータの数が少ない
      2. 実装がシンプル
      3. 検索戦略を動的に切り替えるという興味深いアイデア

      短所

      1. 結果のばらつきが大きい
      2. 収束精度が低い
      3. 動けなくなる傾向がある

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

      記事で使用されているプログラム

      # 名前 種類 詳細
      1 #C_AO.mqh
      		 インクルード
      		 集団最適化アルゴリズムの親クラス
      2 #C_AO_enum.mqh
      		 インクルード
      		 集団最適化アルゴリズムの列挙
      3 TestFunctions.mqh
      		 インクルード
      		 テスト関数のライブラリ
      4
      		 TestStandFunctions.mqh
      		 インクルード
      		 テストスタンド関数ライブラリ
      5
      		 Utilities.mqh
      		 インクルード
      		 補助関数のライブラリ
      6
      		 CalculationTestResults.mqh
      		 インクルード
      		 比較表の結果を計算するスクリプト
      7
      		 Testing AOs.mq5
      		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
      8
      		 Simple use of population optimization algorithms.mq5
      		 スクリプト
      		可視化せずに集団最適化アルゴリズムを使用する簡単な例
      9
      		Test_AO_ATAm.mq5
      		 スクリプト ATAmテストスタンド

      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/16588

      添付されたファイル |
      ZIPをダウンロード
      ATAm.zip (145.57 KB)

      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

      この著者による他の記事

      ディスカッションに移動
      取引におけるトレンド基準 取引におけるトレンド基準
      トレンドは多くの取引戦略において重要な要素です。本記事では、トレンドを識別するために使用されるいくつかのツールとその特性にを見ていきます。トレンドを理解し正しく解釈することは、取引効率を大幅に高め、リスクを最小限に抑えることにつながります。
      市場シミュレーション（第1回）：両建て注文(I) 市場シミュレーション（第1回）：両建て注文(I)
      本日から第2段階に入り、市場リプレイ/シミュレーションシステムについて見ていきます。まず、両建て注文の可能な解決策を示します。これは最終版ではありませんが、近い将来に解決しなければならない問題に対するひとつの可能なアプローチとなります。
      エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
      この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
      取引におけるニューラルネットワーク：予測符号化を備えたハイブリッド取引フレームワーク(StockFormer) 取引におけるニューラルネットワーク：予測符号化を備えたハイブリッド取引フレームワーク(StockFormer)
      本記事では、予測符号化と強化学習(RL)アルゴリズムを組み合わせたハイブリッド取引システム「StockFormer」について解説します。本フレームワークは、統合型のDiversified Multi-Head Attention (DMH-Attn)機構を備えた3つのTransformerブランチを使用しています。DMH-Attnは、従来のAttentionモジュールを改良したもので、マルチヘッドのFeed-Forwardブロックを組み込むことにより、異なるサブスペースにわたる多様な時系列パターンを捉えることが可能です。