タブーサーチ(TS)

MetaTrader 5 — テスター | 2 5月 2025, 10:06

Andrey Dik

内容

はじめに

タブーサーチアルゴリズムは、1980年代に開発された、最も初期でよく知られているメタヒューリスティック最適化手法の一つです。フレッド・グローバーによって提案され、その、メモリを利用して重複した動作を禁止するという革新的な戦略により、瞬く間に研究者たちの注目を集めました。当時は、遺伝的アルゴリズム(GA)など他の探索手法も存在していましたが、タブーサーチはその独自性により一線を画していました。

アルゴリズムは、まず初期解を選択し、その後、近傍の解を探索します。現状より良い結果が得られる解を優先的に選択しますが、すでに試した非有効な解へ戻ってしまうことを避けるため、タブーリストを活用します。このリストは「禁止された操作」を記録しておく構造であり、ループ的な探索を防止し、より効率的に探索空間を進むことを可能にします。たとえば、ナップサック問題では、アルゴリズムはアイテムを一つずつ追加または削除しながら、以前検討した組み合わせに戻ることなく、総価値の最大化を目指します。

タブーサーチの中核にあるのは適応型メモリであり、これは単に過去の解を避けるだけでなく、過去の操作履歴を踏まえて探索プロセスそのものを制御する役割を担います。その後、マヌエル・ラグーナやラファエル・マルティといった研究者によって発展が続けられ、タブーサーチは生産計画、財務分析、通信工学など、非常に広範な分野での応用が可能となりました。今日でも、深い分析と高度な計算を要する複雑な組合せ最適化問題に対して、有効なツールとして利用されています。

このようにタブーサーチは、革新的な発想が探索アルゴリズムをいかに進化させ、科学技術に新たな可能性をもたらすかを示す好例と言えるでしょう。本来このアルゴリズムは、巡回セールスマン問題やナップサック問題などの特定の組合せ最適化問題のために開発されたものでしたが、この記事ではさらに、連続探索空間にも適用可能な拡張版についても紹介します。

アルゴリズムの実装

ここでは、タブーサーチアルゴリズム（従来型）を用いて組合せ最適化問題を解く際に使用される、一般的な数式およびメカニズムについて説明します。

1. 最適化問題の一般的な定式化

目的関数：f(x)の最適化
制約条件： x∈X、ここでXは変数ベクトルxに対する制約集合

2. 解の近傍

N(x)：現在の解xから1回の「操作(move)」で到達可能な近傍解の集合
N*(x)：短期・長期記憶を考慮して修正された近傍集合（タブーリストによる制限付き探索）

3. 短期記憶

直近で変更された属性（意思決定の特性）を記録
tabu-active属性を含む解への遷移を一時的に禁止

4. 長期記憶

各属性の出現・変更頻度を記録
記録された頻度をもとに探索の多様化を制御

5. 強化

修正後の近傍N*(x)から最良の操作を選択
有望と判断された解空間の領域へ探索を集中

6. 多様化

これまで出現しなかった属性を導入するような操作を選択
既知の領域とは異なる探索領域への移動を促進

7. 戦略的変動

「クリティカルレベル」に近づいた場合、選択ルールを動的に変更
レベルを通過して戻る

8. リンクパス

複数の高品質解を結ぶような探索軌道を構築
現在の解を、これらの「ガイド解」へできるだけ近づけるような操作を選択

最適化問題の解決にあたっては、ポイント8を除外し、アルゴリズムの中核となる考え方に焦点を当てつつ、可能な限りポイント1〜7を保持したタブーサーチの改良版を実装することを目指します。従来のアルゴリズムは離散的な意思決定に基づき、ノード間の最短経路を探索するものでした。これを連続的な探索空間に適用するには、最適化対象の各パラメータの実行可能領域を何らかの形で離散化する必要があります。しかし、すべての可能な解にラベルを付けようとすると、その数が膨大になるため、現実的ではありません。

そこで、タブーリストの代わりに、各パラメータに対して「ホワイトリスト」と「ブラックリスト」の概念を導入し、パラメータの範囲をセクター（各パラメータに対して指定された数）に分割します。この方法により、ソリューションが成功した場合にはホワイトリストにチェックマークを、改善が見られなかった場合にはブラックリストにマークを追加できます。有望なセクターにはチェックが蓄積され、その領域がより詳細に探索・洗練されていきます。ただし、成功したセクターであっても極めて不成功な解を含む場合、そのセクターはブラックリストにも記録されます。つまり、同じセクターにホワイトリストとブラックリストの両方のマークが存在する可能性があるということです。

次の解を生成する際、ホワイトリストのラベル数に比例した確率でセクターが選択されます。新たな解が生成された後、そのセクターがブラックリストに記録されているかを確認し、ブラックリストのマーク数に基づいた確率をホワイトリスト全体の合計に対する比率として計算します。その確率条件を満たす場合、別のランダムなセクターを選び直すことになります。

このようにして、関数の表面の特徴を考慮しながら、アルゴリズムは検索空間内のすべての利用可能な領域を動的に探索するための確率を生成します。たとえグローバルな最適解に近づいたとしても、その結果を無限に改善し続けることはできません。その場合、ブラックリストのマークが増え、アルゴリズムはセクターを変更し、探索を他のハイパースペース領域に移すことになります。

このアプローチの目的は、見つかったソリューションの洗練を多様化し、同時に問題全体の広範な探索を保証することです。また、アルゴリズムの外部パラメータの数を最小限に抑え、対象となる問題関数に対して自己適応的に動作する性質をもたせることも狙いの一つです。

古典的なタブーサーチの修正された実装アイデアの主なポイントを強調しましょう。

1. 離散化：検索空間をセクターに分割することで、領域の探索がより効率的になる。
2. ホワイトリストとブラックリスト：成功・失敗した判断を分けて記録し、セクターの見込みを動的に追跡できる。
3. 動的探索：非効率なセクターに固執せず、すべての利用可能な領域を確率的に探索する。
4. 適応性：ブラックリストのマークが増加することで検索方向が変わり、探索の多様化が進む。

このアルゴリズムは、タブーサーチと進化的アルゴリズムの要素を組み合わせています。ブラックリストとホワイトリストという記憶メカニズムを使って、有望な領域への集中探索を促す一方で、悪化した解につながる領域は避けるように設計されています。

わかりやすくするために、各座標のセクターのホワイトリストとブラックリストを図式的に示します。たとえば、3つの座標を持ち、それぞれが4つのセクターに分割されているとします。ホワイトリストとブラックリストは、各座標ごとに別々に設定されます。

たとえば、「0番目の座標」の「3番目のセクター」には、ホワイトリストに5つのチェックマークが付いており、これはその座標内で最多です。したがって、このセクターは次の反復で最も高い確率で選択されることになります。一方で、同じセクターにブラックリストのマークが6つある場合、このセクターは最も有望であるにもかかわらず、新しい解の生成時に選択から外される確率が上がります。結果として、一見有望でないセクターの方が選ばれやすいという現象も起こり得ます（これは一見してわかりにくいかもしれません）。

このように、探索空間全体の探索中に確率が継続的に再調整され、関数の表面の特性が自動的に考慮される構造になっています。このような手法は、アルゴリズムの外部パラメータへの依存が非常に少なく、本質的に自己適応的な性質を持つため、非常に有望であると考えられます。

 0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 

1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____|

2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____|



0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___|

1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______|

2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|

ここで、アルゴリズムの修正版（以下、TSmと表記）の疑似コードを記述します。

1. 集団の初期化

集団内の各エージェントについて以下を実行する。

　- 指定された範囲内でランダムな座標を設定する。

　- 適応度の前回値を最小可能値に設定する。

2. アルゴリズムのメインループ

終了条件が満たされるまで、以下を繰り返す。

a) 最初の反復である場合

　- 集団の初期化を実行する。

b) それ以外の場合

- エージェントの新しい座標を生成する。

　　各エージェントおよび各座標について

　　　- 一定の確率で、既知の最良解の座標をコピーする。

　　　- そうでない場合

　　　　- エージェントのホワイトリストからセクターを選択する。

　　　　- 選択されたセクター内で新しい座標を生成する。

　　　- 選択されたセクターがブラックリストに登録されている場合は、ランダムに別のセクターを選択し、その中で座標を生成する。

　　　- 新しい座標が許容範囲を超えていないことを確認する。

　c) 各エージェントの新しい座標に対して適応度を評価する。

　d) ブラックリストとホワイトリストを更新する。

　　　各エージェントについて

　　　- 現在の適応度と前回の適応度を比較する。

　　　- 適応度が向上していれば、該当セクターのホワイトリストのカウンタを増加する。

　　　- 適応度が悪化していれば、ブラックリストのカウンターを増加する。

　　　- 現在の適応度を、次回の反復のために前回値として保存する。

　e) もし現在のエージェントの中に、より良い適応度を持つものがあれば、最良解を更新する。

3. ループ終了後、発見された最良解を返す。

それではコードの記述を始めましょう。まず、検索戦略においてセクターとエージェントを操作するために使用される、2つの構造体S_TSmSectorとS_TSmAgentを定義します。

1. S_TSmSector：この構造体には、各セクターに対応する「チェックマーク」（実際にはカウンタ）を格納するsector []整数配列が含まれています。

2. S_TSmAgent：この構造体はより複雑で、アルゴリズム内の探索エージェントを表します。次の情報を保持します。

blacklist[]：各座標ごとのセクターに対応したブラックリストの配列
whitelist[]：各座標ごとのセクターに対応したホワイトリストの配列
fPrev：エージェントの前回の適応度値

また、InitメソッドはS_TSmAgentインスタンスを初期化します。パラメータは次のとおりです。

coords：座標の数
sectorsPerCord：各座標に対するセクターの数

以下がロジックです。

1. blacklist配列およびwhitelist配列のサイズを、座標の数に合わせて変更します。

2. 各座標に対して、すべてのセクターを初期化します。

現在の座標に対応するブラックリストのsector配列をサイズ変更します。
同様に、ホワイトリストもサイズ変更します。
ホワイトリストおよびブラックリストのすべての要素を0に初期化します（これらは後に1ずつ増加していくカウンタです）。

3. fPrevの初期化：fPrevの値を、-DBL_MAXに設定します。これは取り得る最小の値を示し、エージェントがまだ適応度を取得していないことを意味します。

このコードは、探索空間の各次元におけるセクターごとのブラックリストおよびホワイトリストを管理するためのエージェント構造を作成します。これにより、エージェントが訪れることが許可されているセクターと禁止されているセクターの追跡が可能になります。

//——————————————————————————————————————————————————————————————————————————————
struct S_TSmSector
{
    int sector [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
struct S_TSmAgent
{
    S_TSmSector blacklist []; //black list by sectors of each coordinate
    S_TSmSector whitelist []; //white list by sectors of each coordinate

    double fPrev;             //previous fitness

    void Init (int coords, int sectorsPerCord)
    {
      ArrayResize (blacklist, coords);
      ArrayResize (whitelist, coords);

      for (int i = 0; i < coords; i++)
      {
        ArrayResize (blacklist [i].sector, sectorsPerCord);
        ArrayResize (whitelist [i].sector, sectorsPerCord);

        ArrayInitialize (blacklist [i].sector, 0);
        ArrayInitialize (whitelist [i].sector, 0);
      }

      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO基底クラスから継承されたC_AO_TSmクラスを記述します。

1. コンストラクタは以下の変数に初期値を設定します。

popSize（個体群のサイズ） = 50
sectorsPerCoord（各座標におけるセクター数） = 100
bestProbab（最良解を選択する確率） = 0.8
また、上記の変数に対応する3つのパラメータでparams配列を作成し、初期化します。

2. SetParamsメソッドは、params配列から対応するクラス変数へ値を設定します。

3. Initメソッドは、指定された範囲と探索ステップに基づいてアルゴリズムを初期化します。

4. Movingメソッドは、エージェントが探索空間内で移動する処理を担当します。一方、Revision ()メソッドは、タブーサーチのロジックに基づいて現在の解を確認・更新します。

5. クラスメンバー

S_Agent agents []：問題の解を表すエージェントの配列。探索中に使用されます。

6. privateメソッド

InitializePopulation：エージェントの初期個体群を生成するメソッド
UpdateLists：エージェントごとのブラックリスト・ホワイトリストを更新するメソッド
GenerateNewCoordinates：探索中に新しい座標を生成するメソッド
GetSectorIndex：座標と次元に基づいて対応するセクターのインデックスを取得するメソッド
ChooseSectorFromWhiteList：指定されたエージェントと次元に対してホワイトリストからセクターを選択するメソッド
GenerateCoordInSector：ホワイトリスト・ブラックリストの影響を受けたセクター選択の確率評価をおこなうメソッド
IsInBlackList：ホワイトリストとブラックリストの選択に影響を与える別のセクターを選択する確率のパフォーマンスをテストするメソッド

//——————————————————————————————————————————————————————————————————————————————
class C_AO_TSm : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_TSm ()
  {
    ao_name = "TSm";
    ao_desc = "Tabu Search M";
    ao_link = "https://www.mql5.com/ja/articles/15654";

    popSize         = 50;
    sectorsPerCoord = 100;
    bestProbab      = 0.8;

    ArrayResize (params, 3);

    params [0].name = "popSize";         params [0].val = popSize;
    params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord;
    params [2].name = "bestProbab";      params [2].val = bestProbab;
  }

  void SetParams ()
  {
    popSize         = (int)params [0].val;
    sectorsPerCoord = (int)params [1].val;
    bestProbab      = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    sectorsPerCoord;
  double bestProbab;

  S_TSmAgent agents [];

  private: //-------------------------------------------------------------------
  void   InitializePopulation      ();
  void   UpdateLists               ();
  void   GenerateNewCoordinates    ();
  int    GetSectorIndex            (double coord, int dimension);
  int    ChooseSectorFromWhiteList (int agentIndex, int dimension);
  double GenerateCoordInSector     (int sectorIndex, int dimension);
  bool   IsInBlackList             (int agentIndex, int dimension, int sectorIndex);

};
//——————————————————————————————————————————————————————————————————————————————

C_AO_TSmクラスのInitメソッドはタブーサーチアルゴリズムの初期化を担当します。以下にその処理を段階的に説明します：

1. 最初に、StandardInitメソッドが呼び出され、最小値・最大値・ステップ幅の配列が渡されます。この処理により、アルゴリズムの基本的なパラメータが設定されます。次に、agents配列のサイズをpopSizeに基づいて変更し、個体群の数（エージェント数）を定義します。その後、各エージェントに対してループを回し、agents配列内の各要素にInitメソッドを呼び出します。このメソッドでは、各エージェントに対して座標(coords)や座標あたりのセクター数(sectorsPerCoord)などのパラメータが初期化されます

2. すべての初期化が正しく完了した場合、このメソッドはtrueを返し、アルゴリズムの初期化が成功したことを示します。

Initメソッドは、タブサーチアルゴリズムを実行可能な状態に準備するための重要な処理です。このメソッドでは、探索範囲を設定し、エージェントの配列を初期化し、それぞれが解探索をおこなえるように準備します。初期化のいずれかの段階でエラーが発生した場合、メソッドは処理を中断し、falseを返します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agents, popSize);

  for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_TSmクラスのMovingメソッドについて見ていきましょう。以下は、メソッドのロジックです。

if(!revision)：ここでは論理変数revisionがチェックされます。false（初期化がまだ行われていない状態）の場合、次のコードブロックが実行されます。
InitializePopulation ()：エージェントの個体群を初期化する処理をおこないます。

アルゴリズムの 2 回目以降の反復では、GenerateNewCoordinatesメソッドが呼び出されます。このメソッドは、探索中にエージェントのための新しい座標（新しい解）を生成します。

Movingメソッドは、タブーサーチアルゴリズムにおいてエージェントの移動を管理します。まず個体群が初期化済みかどうかを確認し、未初期化であれば個体群を初期化し、それ以外の場合はエージェントに新しい座標を生成します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    InitializePopulation ();
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  GenerateNewCoordinates ();
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは、タブーサーチ中に現在の最良解を更新する役割を担います。個体群内のすべての解を走査し、それぞれのスコアを現在の最良値と比較します。そして、より良い解が見つかれば、対応する変数を更新します。メソッドの最後では、ホワイトリストおよびブラックリストが更新され、アルゴリズムの今後の実行に必要な処理が行われます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }

  //----------------------------------------------------------------------------
  UpdateLists ();
}
//——————————————————————————————————————————————————————————————————————————————

次のメソッドであるInitializePopulationは、タブーサーチエージェントの集団を初期化する役割を担います。指定された範囲内で各エージェントの座標にランダムな値を生成し、また各エージェントの前回のスコアの初期値を設定します。これは、解の評価と更新がおこなわれるアルゴリズムの今後の反復処理に必要です。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::InitializePopulation ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    agents [i].fPrev = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

次は、C_AO_TSmクラスのUpdateListsメソッドです。以下は、メソッドのロジックです。

外部のループは、集団内のすべてのエージェントを順番に処理します。ここで、popSizeは集団のサイズを表します。
内部のループは、各エージェントのすべての座標を順番に処理します。
各エージェントa [i]のc座標について、GetSectorIndexメソッドを使用してセクターインデックスを計算します。これは、解の値を特定のセクターに分類し、後の分析に役立てるためです。
エージェントの現在のスコアa [i].fがその前回のスコアagents [i].fPrevよりも良い場合、エージェントは意思決定を改善したことを意味します。この場合、関連するセクターのwhitelistカウンタが増加します。
現在のスコアが前回のスコアより低い場合、エージェントは意思決定を悪化させたことを意味し、対応するセクターのblacklistカウンタが増加します。
すべての座標が処理された後、エージェントの前回のスコアが現在のスコアに更新され、次の反復で新しい値と比較できるようにします。

UpdateListsメソッドは、各エージェントの現在のスコアと前回のスコアに基づいて、ホワイトリストとブラックリストを更新する役割を担います。これにより、タブーサーチアルゴリズムは、どのセクターが成功したか（ホワイトリスト）およびどのセクターが成功しなかったか（ブラックリスト）を追跡できます。このメソッドは、解空間内で非効率的なエリアを再訪しないようにすることで、解の探索を効率的に管理する手助けをします。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::UpdateLists ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      int sectorIndex = GetSectorIndex (a [i].c [c], c);

      if (a [i].f > agents [i].fPrev)
      {
        agents [i].whitelist [c].sector [sectorIndex]++;
      }
      else
        if (a [i].f < agents [i].fPrev)
        {
          agents [i].blacklist [c].sector [sectorIndex]++;
        }
    }
    agents [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

ここで、C_AO_TSmクラスのGenerateNewCoordinatesメソッドを見てみましょう。以下は、メソッドのロジックです。

外部のループは、集団内のすべてのエージェントを順番に処理します。ここで、popSizeは集団のサイズを表します。
内部のループは、各エージェントのすべての座標を順番に処理します。
まず、RNDprobabメソッドを使って確率が満たされているか確認します。確率が満たされた場合、エージェントはcB [c]（最良の大域解）から座標を受け取ります。
確率が満たされない場合、ChooseSectorFromWhiteList()メソッドを使ってホワイトリストからセクターを選択します。
次に、GenerateCoordInSector ()メソッドを使って、そのセクター内で新しい座標を生成します。
選択したセクターがブラックリストに含まれている場合、u.RNDminusOne ()を使って新しいセクターをランダムに選択し、その中で新しい座標を生成します。
新しい座標が指定された範囲内で、かつ必要なステップに従っているかを確認します。

GenerateNewCoordinatesメソッドは、集団内の各エージェントに対して新しい座標を生成する役割を担っています。このメソッドは、確率的アプローチを使って最良の既知の座標と、ホワイトリストおよびブラックリストに基づいてランダムに生成されたセクターの座標を選択します。また、生成された座標が指定された範囲とステップに準拠しているかを確認し、座標の有効性を保証します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::GenerateNewCoordinates ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < bestProbab)
      {
        a [i].c [c] = cB [c];
      }
      else
      {
        int sectorIndex = ChooseSectorFromWhiteList (i, c);
        double newCoord = GenerateCoordInSector (sectorIndex, c);

        if (IsInBlackList (i, c, sectorIndex))
        {
          sectorIndex = u.RNDminusOne (sectorsPerCoord);
          newCoord = GenerateCoordInSector (sectorIndex, c);
        }

        newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = newCoord;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

次に、GetSectorIndex関数のコードを分析します。この関数は、指定された座標と指定された次元に対してセクターインデックスを決定します。以下が、この関数のロジックです。

指定された次元の範囲の最大値と最小値が等しい場合、それは範囲に長さがないことを意味します。この場合、関数はすぐに0を返します。範囲をセクターに分けることができないためです。
次に、1つのセクターの長さsLは、範囲の長さをsectorsPerCoordで割ることで計算されます。
セクターインデックスindは、与えられた座標がどのセクターに属するかを決定する式を使って計算されます。まず、範囲の最小値を座標から引き、その結果をセクターの長さで割ります。次に、その値を最も近い整数に切り捨てます。
座標が範囲の最大値と等しい場合、関数は最後のセクターのインデックスを返します。
さらに、インデックスが許容される値を超えないようにチェックがおこなわれます。インデックスがセクター数以上の場合、最後のセクターが返されます。インデックスが0未満の場合は、0が返されます。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::GetSectorIndex (double coord, int dimension)
{
  if (rangeMax [dimension] == rangeMin [dimension]) return 0;

  double sL =  (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;

  int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL);

  // Special handling for max value
  if (coord == rangeMax [dimension]) return sectorsPerCoord - 1;

  if (ind >= sectorsPerCoord) return sectorsPerCoord - 1;
  if (ind < 0) return 0;

  return ind;
}
//——————————————————————————————————————————————————————————————————————————————

次に、ChooseSectorFromWhiteListメソッドを見ていきましょう。このメソッドは、指定されたエージェントと次元に対して「ホワイトリスト」にあるセクターからセクターを選択し、その選ばれたセクターのインデックスを返します。以下は、メソッドのロジック:です。

まず、totalCount変数がゼロに初期化されます。これは、ホワイトリスト内のセクターにある「チェックマーク」の総数を数えるために使用されます。
totalCountがゼロであれば、これはホワイトリスト内のセクターにまだ「チェックマーク」が入っていないことを意味し、すべてのセクターが等しいということです。この場合、メソッドは利用可能なすべてのセクターからランダムにセクターを選び、そのインデックスを返します。
次に、ループ内で「チェックマーク」の数が累積的にカウントされます。randomValueが現在の累積値以下であれば、メソッドはそのセクターsのインデックスを返します。これにより、ホワイトリスト内のセクターがその重み（「チェックマーク」の数）に比例して選ばれるようになります。

ChooseSectorFromWhiteListメソッドは、エージェントがホワイトリストからセクターを選ぶ際に、ルーレット選択のような確率分布に基づいてセクターを選択することを可能にします。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension)
{
  int totalCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    totalCount += agents [agentIndex].whitelist [dimension].sector [s];
  }

  if (totalCount == 0)
  {
    int randomSector = u.RNDminusOne (sectorsPerCoord);
    return randomSector;
  }

  int randomValue = u.RNDminusOne (totalCount);
  int cumulativeCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s];

    if (randomValue <= cumulativeCount)
    {
      return s;
    }
  }

  return sectorsPerCoord - 1;
}
//——————————————————————————————————————————————————————————————————————————————

次にGenerateCoordInSectorメソッドを分析しましょう。このメソッドは、指定された次元の与えられたセクター内でランダムな座標を生成します。以下は、メソッドのロジック:です。

まず、指定された次元におけるセクターのサイズが計算されます。
次に、sectorStartが計算されます。これは、指定された次元の範囲の最小値に、セクターインデックスにセクターサイズを掛けたオフセットを加えたものです。そして、sectorEndはsectorStartにsectorSizeを足した値として定義され、これでセクターの境界が決まります。
その後、RNDfromCI関数が呼び出されます。この関数は、sectorStartからsectorEndまでの範囲でランダムな値を生成します。この値が、指定されたセクター内で生成された座標を表します。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension)
{
  double sectorSize  = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;
  double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize;
  double sectorEnd   = sectorStart + sectorSize;

  double newCoord = u.RNDfromCI (sectorStart, sectorEnd);

  return newCoord;
}
//——————————————————————————————————————————————————————————————————————————————

最後に、isinblacklistメソッドを分析しましょう。このメソッドは、指定されたセクターと次元においてエージェントが「ブラックリスト」に載っているかどうかを確認します。パラメータは次のとおりです。

agentindex：チェックをおこなうエージェントのインデックス
dimension：次元のインデックス
sectorindex：チェックされるセクターのインデックス

このメソッドは、エージェントがブラックリストに載っていて、かつセクター変更の確率が満たされている場合にtrueを返します。確率はホワイトリストに基づく「成果」を考慮して計算されます。

blackCountとwhiteCountは、それぞれ指定されたエージェント、次元、セクターにおけるブラックリストとホワイトリストのエントリ数を取得します。
総エントリ数totalCountは、ブラックリストとホワイトリストのエントリ数を足した値として計算されます。
レコードの合計数がゼロであれば、エージェントがブラックリストに載ることはないと判断され、メソッドは即座にfalse返します。つまり、ブラックリストとホワイトリストのエントリがない場合、エージェントはブラックリストに載ることはありません。
次に、ブラックリストとして考慮すべきセクターの確率が計算されます。この確率は、ブラックリストのエントリ数を総エントリ数で割ったものです。
RNDprobab ()メソッドを使って0から1までのランダムな数値を生成し、その値が計算されたblackProbability（ブラックリストの確率）より小さい場合、メソッドはtrueを返します。

IsInBlackListメソッドは、ブラックリストとホワイトリストのエントリ数を基にして、セクターがブラックリストに載っている確率を決定し、そのセクターを変更する必要があるかどうかを判断します。ブラックリストのエントリがホワイトリストより多いほど、今後そのセクターを他のランダムなセクターに変更する確率が高くなります。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex)
{
  int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex];
  int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex];
  int totalCount = blackCount + whiteCount;

  if (totalCount == 0) return false;

  double blackProbability = (double)blackCount / totalCount;
  return u.RNDprobab () < blackProbability;
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

以下は、TSmテストスタンドの結果です。

TSm|Tabu Search M|50.0|100.0|0.8|
=============================
5 Hilly's; Func runs:10000; result:0.8779456463913048
25 Hilly's; Func runs:10000; result:0.6143121517195806
500 Hilly's; Func runs:10000; result:0.2910412462428753
=============================
5 Forest's; Func runs:10000; result:0.9288481105123887
25 Forest's; Func runs:10000; result:0.5184350456698835
500 Forest's; Func runs:10000; result:0.19054478009120634
=============================
5 Megacity's; Func runs:10000; result:0.6107692307692308
25 Megacity's; Func runs:10000; result:0.3821538461538462
500 Megacity's; Func runs:10000; result:0.1215692307692319
=============================
All score:4.53562 (50.40%)

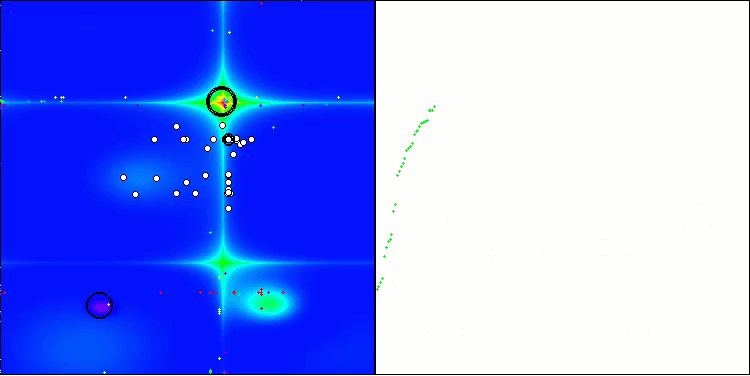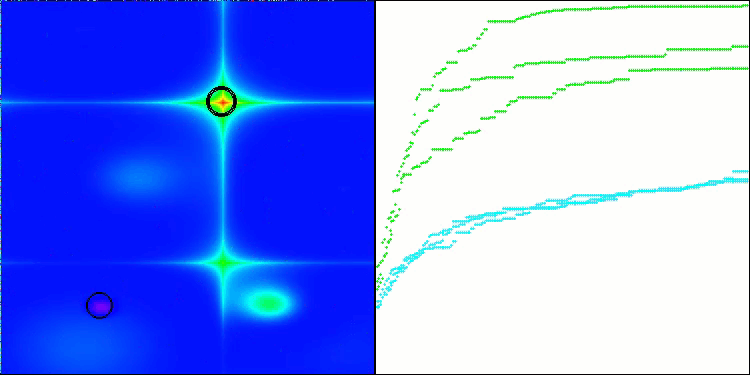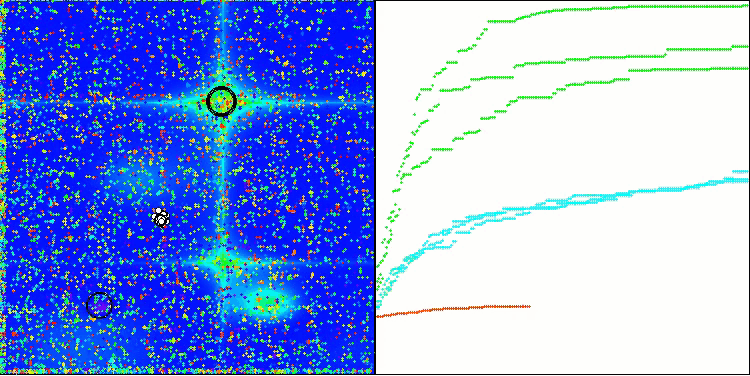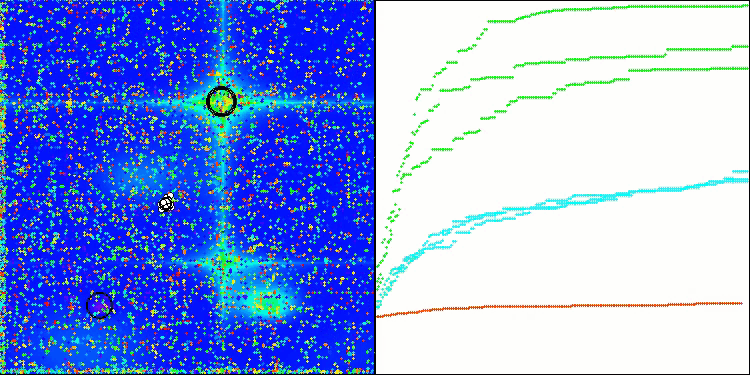
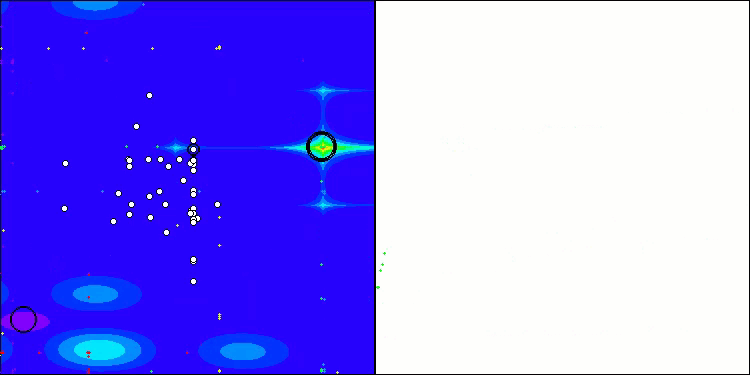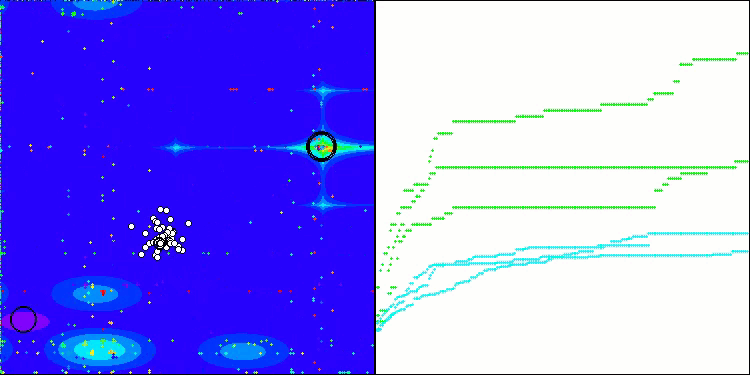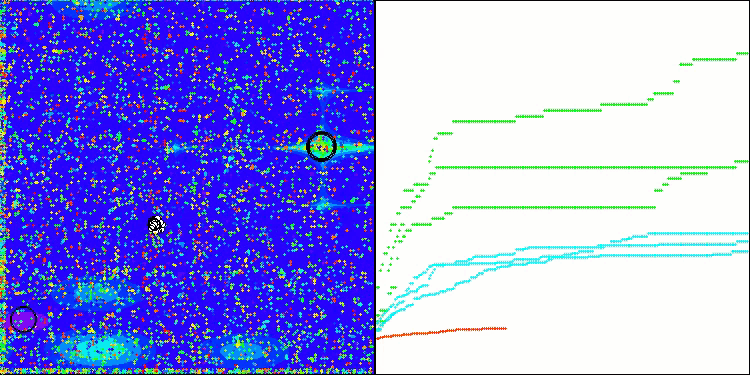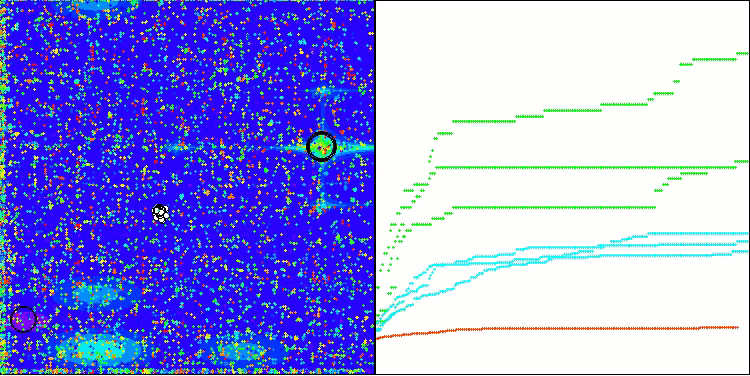
アルゴリズムはかなりうまく動作していることがわかります。テスト関数や可視化においても良好な結果が得られています。もちろん、小さな次元の関数ではばらつきがありますが、この現象は多くのアルゴリズムに共通するものです。注目すべき点は、アルゴリズムが研究対象の関数の重要な表面領域の大部分をうまく強調できている点です。

Hilly

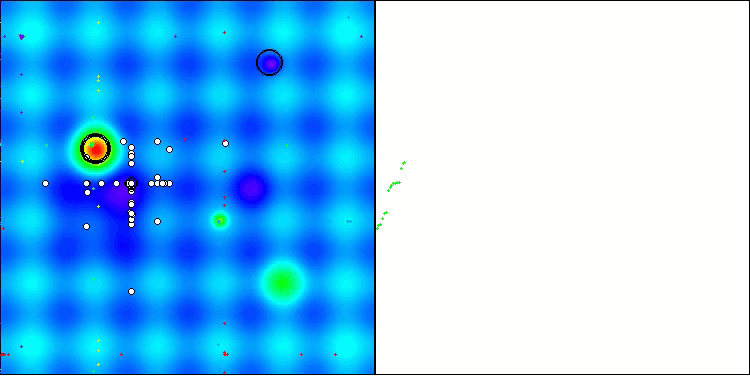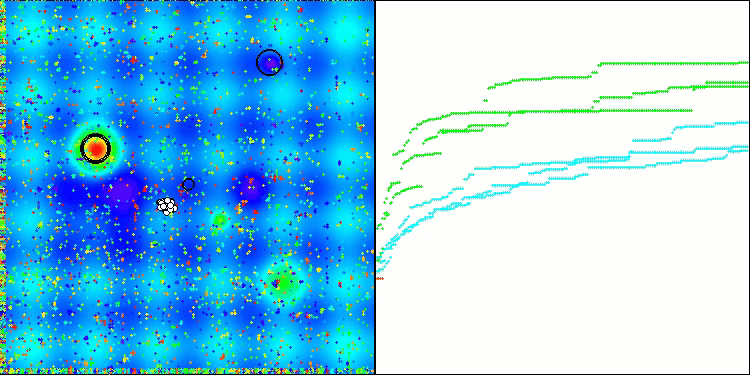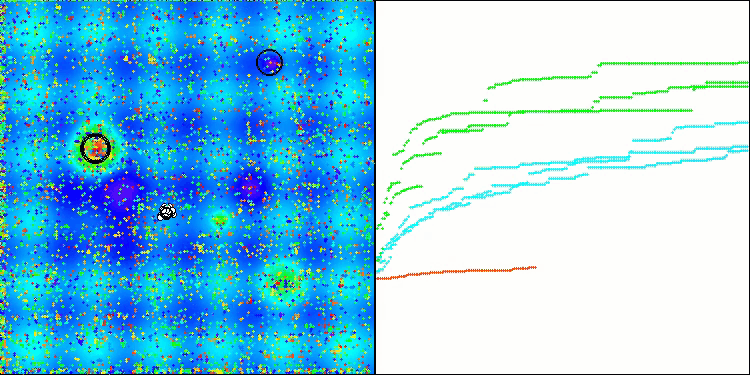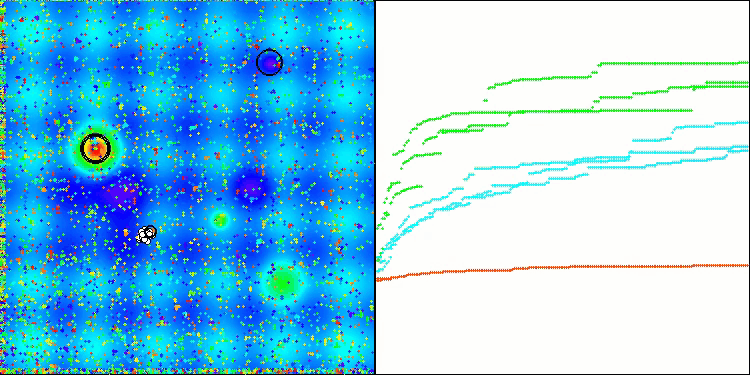
Hillyテスト関数のTSm

Forest

Forestテスト関数のTSm

Megacity

Megacityテスト関数のTSm

テスト結果に基づいて、このアルゴリズムは評価表で18位にランクされています。これは平均以上の結果です。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O）進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗尾アルゴリズム	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	社会母集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	亀甲進化アルゴリズム	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
19	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
20	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
21	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
22	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
23	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
24	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
25	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
26	MEC	mindevolutionarycomputation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
27	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
28	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
29	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
30	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
31	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
32	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
33	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
34	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
35	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
36	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
37	AAA	藻類適応アルゴリズム	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
38	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
39	IWDm	intelligentwaterdropsm	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
40	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
41	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
42	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
43	SFL	shuffledfrog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
44	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
45	RND	ランダム	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37

まとめ

異なる次元のテスト関数に対するアルゴリズムの動作結果を考慮すると、滑らかなHilly関数において大規模な問題への対処がより困難であることがわかります。それ以外のテストでは、アルゴリズムは一貫して良好な結果を示しています。

提案されたタブーサーチアルゴリズムの修正版は、元のバージョンとは異なり、滑らかな問題や離散的な問題を含む、連続的な探索空間での一般的な最適化問題にも適用可能です。このアルゴリズムは、基盤となるアイデアを他のアルゴリズムに応用するための強力な基盤として機能します。収束精度を向上させるために、前述のアルゴリズムで使用された手法を適用することもできますが、この段階では修正を「そのまま」提示しています。

Tab

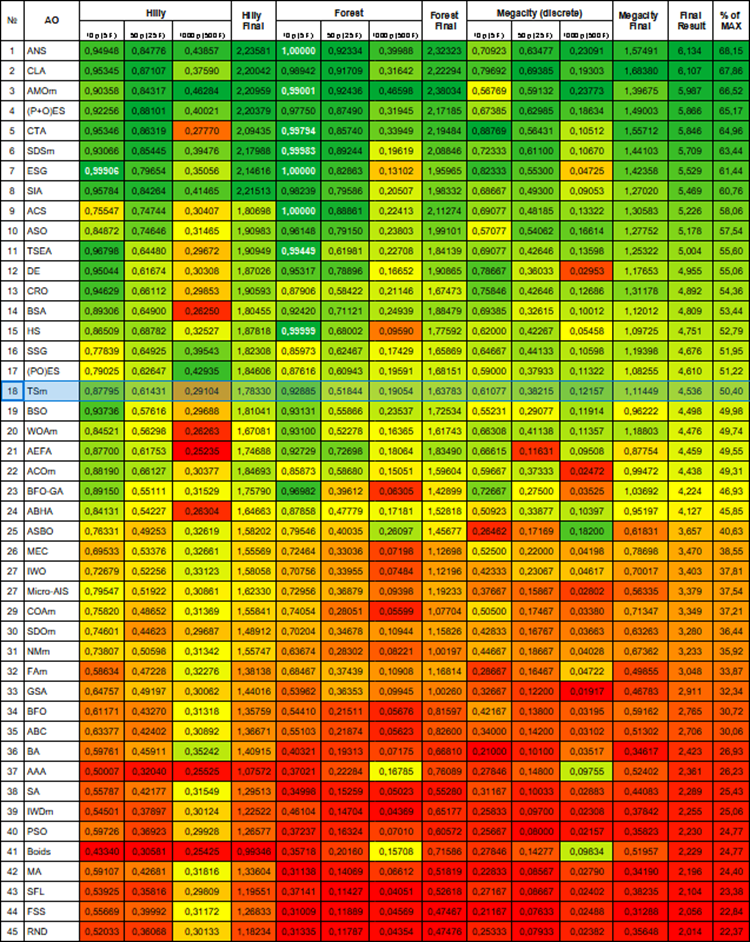
図1：アルゴリズムのテスト結果に応じた色分け：該当するテストにおいて、結果が0.99以上の場合は白で強調表示される

チャート

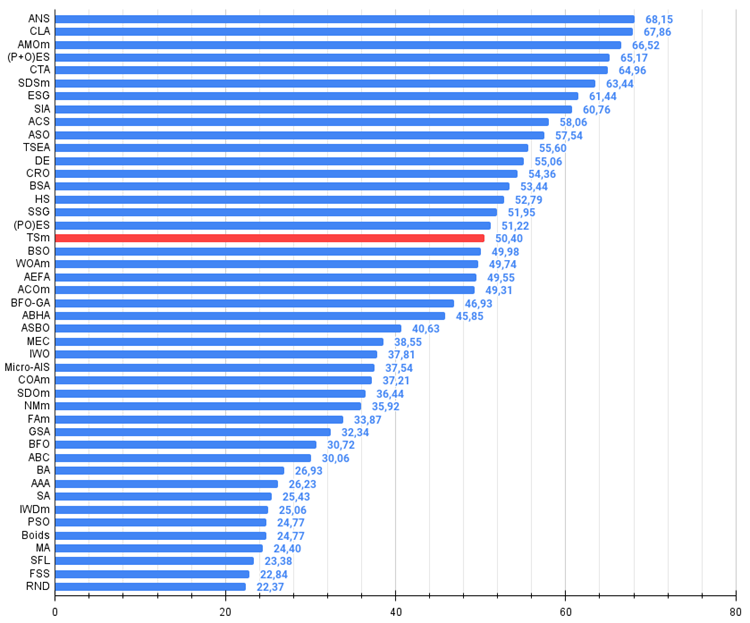
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)

TSmの長所と短所:

長所

さらなる改善と新しいアルゴリズムの基礎としての使用に向けた有望なアイデア
優れたスケーラビリティ
パラメータは直感的で少数（集団サイズの他に2つのみ）

短所

収束精度が振るわない

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
コードベース：https://www.mql5.com/ru/code/49355

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15654

添付されたファイル |

ZIPをダウンロード

TSm.zip (35.52 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

USDとEURの指数チャート—MetaTrader 5サービスの例

MetaTrader 5サービスを例に、米ドル指数(USDX)およびユーロ指数(EURX)チャートの作成と更新について考察します。サービス起動時には、必要な合成銘柄が存在するかを確認し、未作成であれば新規作成します。その後、それを気配値表示ウィンドウに追加します。続いて、合成銘柄の1分足およびティック履歴を作成し、最後にその銘柄のチャートを表示します。

初心者からプロまでMQL5をマスターする（第5回）：基本的な制御フロー演算子

この記事では、プログラムの実行フローを変更するために使用される主要な演算子（条件文、ループ、switch文）について説明します。これらの演算子を利用することで、作成する関数がより「インテリジェント」に動作できるようになります。

初級から中級へ：BREAK文とCONTINUE文

この記事では、ループ内でのRETURN、BREAK、CONTINUE文の使い方について解説します。ループの実行フローにおいて、これらの各文がどのような役割を果たすかを理解することは、より複雑なアプリケーションを扱う上で非常に重要です。ここで提示されるコンテンツは、教育目的のみを目的としています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。

MQL5でパラボリックSARと単純移動平均(SMA)を使用した高速取引戦略アルゴリズムを実装する

この記事では、パラボリックSARと単純移動平均(SMA)インジケーターを活用し、応答性の高い取引戦略を構築する高速取引型エキスパートアドバイザー(EA)をMQL5で開発します。インジケーターの使用方法、シグナルの生成、テストおよび最適化プロセスなど、戦略の実装について詳しく解説します。