
母集団最適化アルゴリズム:侵入雑草最適化(IWO)
内容
1.はじめに
侵入雑草メタヒューリスティックアルゴリズムは、雑草コロニーの互換性とランダム性をシミュレートすることにより、最適化された関数の全体的な最適値を見つける集団ベースの最適化アルゴリズムです。
雑草最適化アルゴリズムは、自然にヒントを得た個体群アルゴリズムを指し、限られた時間と限られた地域での、生存のための闘いにおける雑草の行動を反映しています。
雑草は力強い草であり、その攻撃的な成長により、作物に深刻な脅威をもたらします。雑草は優れた回復力を持ち、環境の変化に適応します。それらの特性を考慮すると、ここにあるのは強力な最適化アルゴリズムです。このアルゴリズムは、自然界の雑草群集の堅牢性、適応性、ランダム性を模倣しようとします。
雑草が特別な理由は何でしょうか。雑草はいち早く移動する傾向があり、さまざまなメカニズムを通じてあらゆる場所に広がります。そのため、絶滅危惧種に分類されることはめったにありません。
以下は、雑草が自然界で適応し、生き残るための8つの方法を簡単に説明したものです。
1.普遍的な遺伝子型:気候変動への応答としての雑草の進化的変化は研究で明らかになっています。
2.ライフサイクル戦略、繁殖力:雑草は、幅広いライフサイクル戦略を示します。耕作管理システムが変化するにつれて、特定の作付体系で以前は大きな問題ではなかった雑草がより回復力を持つようになります.たとえば、耕作システムの減少によって、さまざまなライフサイクル戦略を持つ多年生雑草の出現が引き起こされます。さらに、気候変動は、変化する条件により適した生活史を持つ雑草種または遺伝子型の新しいニッチを生み出し始めています。二酸化炭素排出量の増加に対応して、雑草はより高く、大きく、強くなります。つまり、空気力学的特性により、雑草はより多くの種子を生産し、背の高い植物から遠くに広げることができます。その生殖能力は非常に高いものです。たとえば、トウモロコシの雌アザミは最大19,000個の種子を生産します。
3.急速な進化(発芽、地味な成長、競争力、育種システム、種子の生産と分布の特徴):種子を散布する能力の向上、付随する散布、および地味成長により、生存の機会が得られます。雑草は土壌条件に非常に気さくで、温度と湿度の急激な変動にしっかりと耐えます。
4.エピジェネティクス(後生学):急速な進化に加えて、多くの侵入植物は、遺伝子発現を変化させることにより、環境要因の変化に迅速に対応する能力を持っています。絶え間なく変化する環境では、植物は、光、温度、水の利用可能性、土壌塩分レベルの変動などのストレスに耐えるために柔軟である必要があります。柔軟性を持たせるために、植物は独自に後成的修飾を受けることができます。
5.ハイブリダイゼーション(交雑):雑草の交配種は、ヘテロシス(雑種強勢)としても知られるハイブリッド活力を示すことがよくあります。子孫は、両方の親種と比較して改善された生物学的機能を示します。通常、交配種はより積極的な成長を示し、新しい領土に広がり、侵略された領土内で競争する能力が向上します。
6.除草剤に対する耐性と耐性:ほとんどの雑草の除草剤耐性は、過去数十年にわたって急激に増加しています。
7.人間活動に伴う雑草の共進化:除草剤の散布や除草などの雑草防除活動を通じて、雑草は耐性メカニズムを発達させてきました。耕作時の外部からの損傷は栽培植物に比べて少ないです。それどころか、これらの損傷は、栄養繁殖する雑草(例えば、根や根茎の一部を介して繁殖する雑草)の繁殖に役立つことがよくあります。
8.ますます頻繁な気候変動は、「温室」で栽培された植物と比較して、雑草がより成長する機会を提供します:雑草は農業に大きな害を及ぼします。生育条件への要求が少ないため、雑草は成長と発育において栽培植物を凌駕します。雑草は水分、養分、日光を吸収し、収穫量を激減させ、畑作物の収穫や脱穀を困難にし、製品の品質を低下させます。
2.アルゴリズムの説明
侵入雑草アルゴリズムは、自然界の雑草の成長過程に着想を得ています。この手法は、2006年にMehrabianとLucasによって紹介されました。当然、雑草は強く成長しており、この強力な成長は有用な植物に深刻な脅威をもたらします。雑草の重要な特徴は、IWOアルゴリズムを最適化するための基礎となる、本来の耐性と高い適応性です。このアルゴリズムは、効率的な最適化アプローチの基礎として使用できます。
IWOは、雑草の定着動作を模倣する連続確率数値アルゴリズムです。まず、最初の種子集団が検索空間全体にランダムに分散されます。これらの雑草は最終的に成長し、アルゴリズムの次のステップを実行します。このアルゴリズムは7つのステップで構成されています。疑似コードは次のように表すことができます。
1.ランダムに種を蒔く
2.FFを計算する
3.雑草から種をまく
4.FFを計算する
5.子雑草を親雑草と結合する
6.すべての雑草を分類する
7.停止条件が満たされるまで、手順3を繰り返す
ブロック図は、1回の反復でのアルゴリズムの動作を表しています。IWOは、種子の初期化プロセスから作業を開始します。種子は、検索空間の「フィールド」にランダムかつ均等に散布されます。その後、種子が発芽して成体植物を形成したと仮定し、これを適応度関数によって評価します。
次のステップでは、各植物の適応度を知ることで、種子を通して雑草を繁殖させることができます。種子の数は適応度に比例します。その後、発芽した種と親株を合わせて選別します。一般に、侵入雑草アルゴリズムは、サードパーティのアプリケーションと組み合わせてコーディング、変更、使用するのが簡単であると見なすことができます。
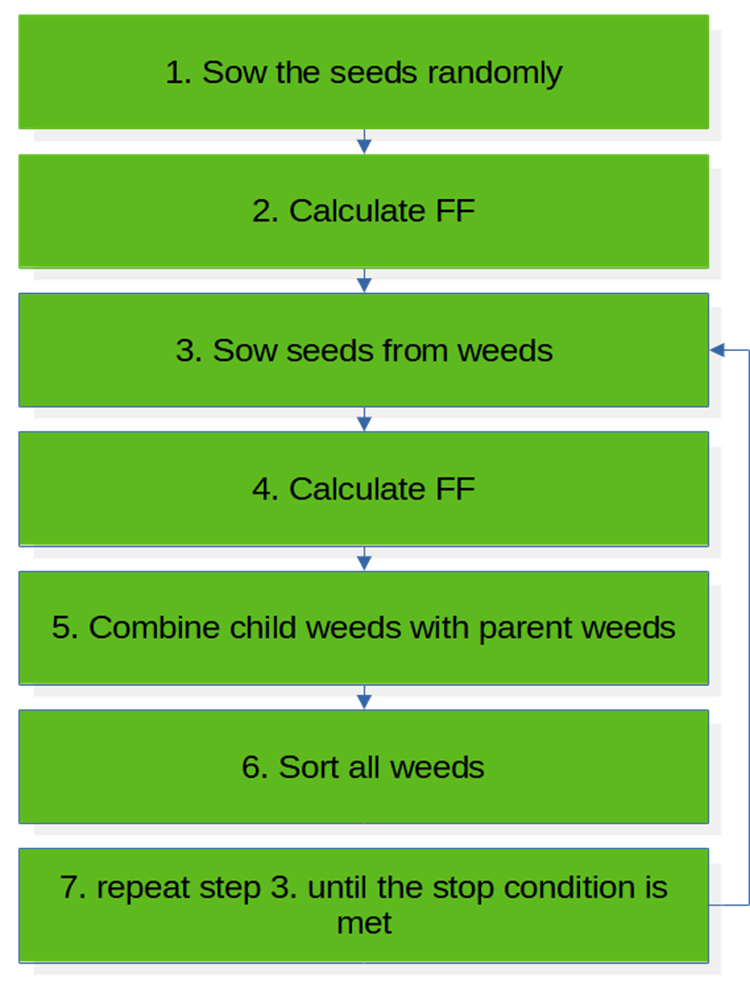
図1:IWOアルゴリズムのブロック図
雑草アルゴリズムの機能の考察に移りましょう。それは、雑草の極端な生存適応能力の多くを備えています。雑草コロニーの際立った特徴は、遺伝的アルゴリズム、蜂などのアルゴリズムとは対照的に、コロニーのすべての植物が例外なく種子を確実に播種することです。これにより、最も適応度の低い植物でも子孫を残せるようになります。最悪のものが最大/小値に最も近い可能性がゼロではない可能性が常にあるためです。
すでに述べたように、それぞれの雑草は、可能な最小量から可能な最大量(アルゴリズムの外部パラメータ)の範囲内で種子を生成します。当然のことながら、そのような条件下では、各植物が少なくとも1つ以上の種子を残すと、親株よりも多くの子株が存在します。この機能はコードで興味深いことに実装されており、以下で説明します。一般的なアルゴリズムは、図2に視覚的に示されています。親株は、その適応度に比例して種子を散布します。
「1」の最良の植物は6つの種子を播種し、「6」の植物は1つの種子(保証されたもの)のみを播種したとします。発芽した種子は植物を生み、その後親の種子とともに選別されることになります。これは生存の模倣です。並べ替えられたグループ全体から、新しい親株が選択され、次の反復でライフサイクルが繰り返されます。このアルゴリズムは、「過剰人口」の問題と播種能力の不完全な実現の問題を解決するメカニズムを特徴としています。
たとえば、種子の数を考えてみましょう。アルゴリズムパラメータの1つが50で、親株の数が5で、種子の最小数は1、最大数は6です。この場合、5*6=30で、50未満です。この例からわかるように、播種の可能性は完全には実現されていません。この場合、子孫を保持する権利は、すべての親株で許容される子孫の最大数に達するまで、リスト内で次にくるのものに渡されます。リストの最後に達すると、権利はリストの最初のものに移動し、制限を超える子孫を残すことが許可されます。
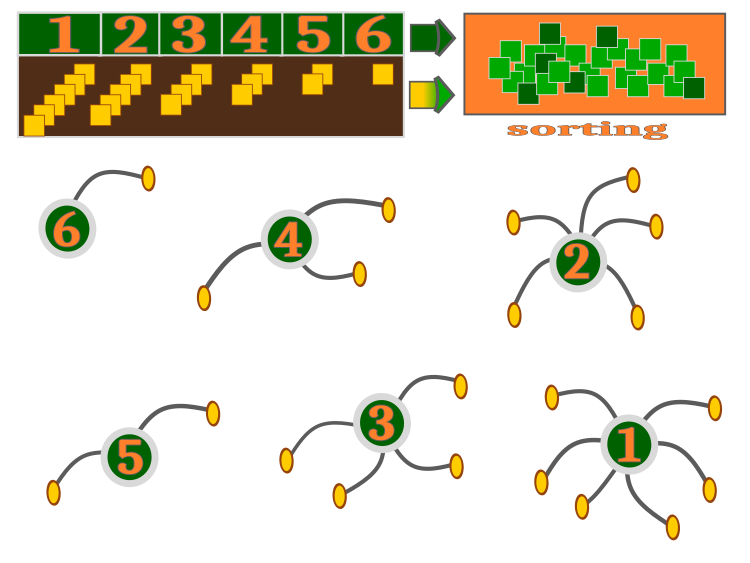
図2:IWOアルゴリズム操作:子孫の数は親の適応度に比例する
次に気をつけたいのは、種子分散です。アルゴリズムの種子分散は、反復回数に比例して線形に減少する関数です。外部分散パラメータは、種子分散の下限と上限です。したがって、反復が増えると、種子分散の半径が減少し、検出された極値が洗練されます。アルゴリズム作成者の推奨によると、通常の種子分布を適用する必要がありますが、ここでは計算を単純化し、3次関数を適用しました。反復回数の分散関数を図3に示します。
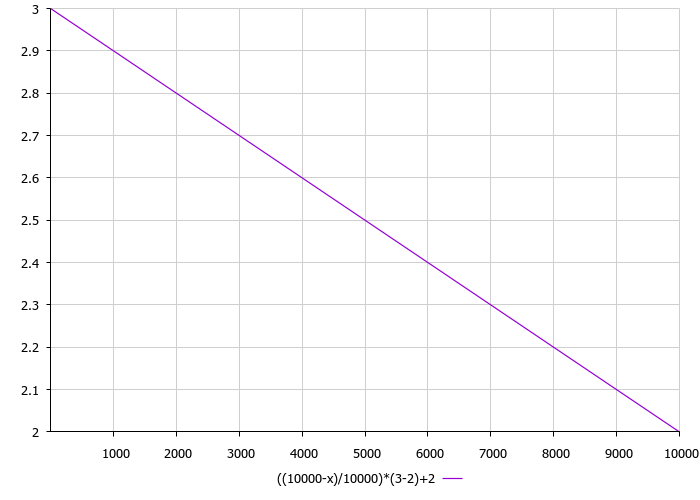
図3:反復回数に対する分散の依存性(最大限界:3、最小限界:2)
IWOコードに移りましょう。コードはシンプルで実行が高速です。
アルゴリズムの最も単純な単位(エージェント)は「雑草」です。雑草の種子についても説明します。これにより、その後の並べ替えに同じタイプのデータを使用できるようになります。この構造体は、座標の配列、適応度関数の値を格納するための変数、および種子(子孫)の数を表すカウンタで構成されます。このカウンタにより、各植物の種子の最小許容数と最大許容数を制御できます。
//—————————————————————————————————————————————————————————————————————————————— struct S_Weed { double c []; //coordinates double f; //fitness int s; //number of seeds }; //——————————————————————————————————————————————————————————————————————————————
適合度に比例して親を選択する確率関数を実装するための構造が必要になります。この場合、蜂コロニーアルゴリズムで既に見たルーレットの原理が適用されます。「start」変数と「end」変数は、確率フィールドの開始と終了を担当します。
//—————————————————————————————————————————————————————————————————————————————— struct S_WeedFitness { double start; double end; }; //——————————————————————————————————————————————————————————————————————————————
雑草アルゴリズムのクラスを宣言しましょう。その中で、必要なすべての変数を宣言します。最適化されるパラメータの境界とステップ、雑草を記述する配列、種子の配列、最適な大域的座標の配列、アルゴリズムによって達成される適応度関数の最適値です。また、最初の反復の「sowing」フラグと、アルゴリズムパラメータの定数変数も必要です。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_IWO { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Weed weeds []; //weeds public: S_Weed weedsT []; //temp weeds public: S_Weed seeds []; //seeds public: double cB []; //best coordinates public: double fB; //fitness of the best coordinates public: void Init (const int coordinatesP, //Number of coordinates const int numberSeedsP, //Number of seeds const int numberWeedsP, //Number of weeds const int maxNumberSeedsP, //Maximum number of seeds per weed const int minNumberSeedsP, //Minimum number of seeds per weed const double maxDispersionP, //Maximum dispersion const double minDispersionP, //Minimum dispersion const int maxIterationP); //Maximum iterations public: void Sowing (int iter); public: void Germination (); //============================================================================ private: void Sorting (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: double vec []; //Vector private: int ind []; private: double val []; private: S_WeedFitness wf []; //Weed fitness private: bool sowing; //Sowing private: int coordinates; //Coordinates number private: int numberSeeds; //Number of seeds private: int numberWeeds; //Number of weeds private: int totalNumWeeds; //Total number of weeds private: int maxNumberSeeds; //Maximum number of seeds private: int minNumberSeeds; //Minimum number of seeds private: double maxDispersion; //Maximum dispersion private: double minDispersion; //Minimum dispersion private: int maxIteration; //Maximum iterations }; //——————————————————————————————————————————————————————————————————————————————
初期化関数のopenメソッドでは、定数変数に値を割り当て、アルゴリズムの入力パラメータが有効な値であることを確認して、親株と種子の可能な最小値の積が種子の総数を超えないようにします。並べ替えを実行する配列を決定するには、親株と種子の合計が必要になります。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_IWO::Init (const int coordinatesP, //Number of coordinates const int numberSeedsP, //Number of seeds const int numberWeedsP, //Number of weeds const int maxNumberSeedsP, //Maximum number of seeds per weed const int minNumberSeedsP, //Minimum number of seeds per weed const double maxDispersionP, //Maximum dispersion const double minDispersionP, //Minimum dispersion const int maxIterationP) //Maximum iterations { MathSrand (GetTickCount ()); sowing = false; fB = -DBL_MAX; coordinates = coordinatesP; numberSeeds = numberSeedsP; numberWeeds = numberWeedsP; maxNumberSeeds = maxNumberSeedsP; minNumberSeeds = minNumberSeedsP; maxDispersion = maxDispersionP; minDispersion = minDispersionP; maxIteration = maxIterationP; if (minNumberSeeds < 1) minNumberSeeds = 1; if (numberWeeds * minNumberSeeds > numberSeeds) numberWeeds = numberSeeds / minNumberSeeds; else numberWeeds = numberWeedsP; totalNumWeeds = numberWeeds + numberSeeds; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (vec, coordinates); ArrayResize (cB, coordinates); ArrayResize (weeds, totalNumWeeds); ArrayResize (weedsT, totalNumWeeds); ArrayResize (seeds, numberSeeds); for (int i = 0; i < numberWeeds; i++) { ArrayResize (weeds [i].c, coordinates); ArrayResize (weedsT [i].c, coordinates); weeds [i].f = -DBL_MAX; weeds [i].s = 0; } for (int i = 0; i < numberSeeds; i++) { ArrayResize (seeds [i].c, coordinates); seeds [i].s = 0; } ArrayResize (ind, totalNumWeeds); ArrayResize (val, totalNumWeeds); ArrayResize (wf, numberWeeds); } //——————————————————————————————————————————————————————————————————————————————
Sowing()の各反復で呼び出される最初のpublicメソッドには、アルゴリズムの主要なロジックが含まれています。理解しやすいように、このメソッドをいくつかの部分に分けます。
アルゴリズムが最初の反復にあるとき、検索空間全体に播種する必要があります。これは通常、ランダムかつ均等におこなわれます。最適化されたパラメータの許容値の範囲内で乱数を生成した後、得られた値が範囲を超えていないかを確認し、アルゴリズムパラメータによって定義される離散性を設定します。ここでは、分散ベクトルも割り当てます。これは、コードの後半で播種するときに必要になります。種子の適応値を最小double値に初期化し、種子カウンタをリセットします(種子は、種子カウンタを使用する植物になります)。
//the first sowing of seeds--------------------------------------------------- if (!sowing) { fB = -DBL_MAX; for (int s = 0; s < numberSeeds; s++) { for (int c = 0; c < coordinates; c++) { seeds [s].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); vec [c] = rangeMax [c] - rangeMin [c]; } seeds [s].f = -DBL_MAX; seeds [s].s = 0; } sowing = true; return; }
コードのこのセクションでは、現在の反復に応じて分散が計算されます。前述の親雑草ごとに保証されている種子の最小数は、ここで実装されています。種子の最小数は、2つのループによって保証されます。最初のループでは、親株を選別し、2番目のループでは、種子カウンタを増やしながら実際に新しい種子を生成します。ご覧のとおり、新しい子孫を作成する意味は、以前に計算された親座標への分散を持つ3次関数の分布で乱数をインクリメントすることです。取得した新しい座標の値が許容値であることを確認し、離散性を割り当てます。
//guaranteed sowing of seeds by each weed------------------------------------- int pos = 0; double r = 0.0; double dispersion = ((maxIteration - iter) / (double)maxIteration) * (maxDispersion - minDispersion) + minDispersion; for (int w = 0; w < numberWeeds; w++) { weeds [w].s = 0; for (int s = 0; s < minNumberSeeds; s++) { for (int c = 0; c < coordinates; c++) { r = RNDfromCI (-1.0, 1.0); r = r * r * r; seeds [pos].c [c] = weeds [w].c [c] + r * vec [c] * dispersion; seeds [pos].c [c] = SeInDiSp (seeds [pos].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } pos++; weeds [w].s++; } }
このコードでは、ルーレットの原理に従って適合度に比例して親株のそれぞれに確率フィールドを提供します。上記のコードは、ここでの種子の数がランダムな法則に従う場合に、各植物に保証された数の種子を提供します。したがって、雑草が適応すればするほど、より多くの種子を残すことができ、逆もまた同様です。植物の適応度が低いほど、種子が少なくなります。
//============================================================================ //sowing seeds in proportion to the fitness of weeds-------------------------- //the distribution of the probability field is proportional to the fitness of weeds wf [0].start = weeds [0].f; wf [0].end = wf [0].start + (weeds [0].f - weeds [numberWeeds - 1].f); for (int f = 1; f < numberWeeds; f++) { if (f != numberWeeds - 1) { wf [f].start = wf [f - 1].end; wf [f].end = wf [f].start + (weeds [f].f - weeds [numberWeeds - 1].f); } else { wf [f].start = wf [f - 1].end; wf [f].end = wf [f].start + (weeds [f - 1].f - weeds [f].f) * 0.1; } }
得られた確率場に基づいて、子孫を残す権利を持つ親株を選択します。種子カウンタが最大許容値に達した場合、ソートされたリストの次のカウンタに権利が渡されます。リストの最後に達した場合、権利は次のものには渡らず、リストの最初のものに移動します。次に、計算された分散を使用して、上記の規則に従って子株が形成されます。
bool seedingLimit = false; int weedsPos = 0; for (int s = pos; s < numberSeeds; s++) { r = RNDfromCI (wf [0].start, wf [numberWeeds - 1].end); for (int f = 0; f < numberWeeds; f++) { if (wf [f].start <= r && r < wf [f].end) { weedsPos = f; break; } } if (weeds [weedsPos].s >= maxNumberSeeds) { seedingLimit = false; while (!seedingLimit) { weedsPos++; if (weedsPos >= numberWeeds) { weedsPos = 0; seedingLimit = true; } else { if (weeds [weedsPos].s < maxNumberSeeds) { seedingLimit = true; } } } } for (int c = 0; c < coordinates; c++) { r = RNDfromCI (-1.0, 1.0); r = r * r * r; seeds [s].c [c] = weeds [weedsPos].c [c] + r * vec [c] * dispersion; seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } seeds [s].s = 0; weeds [weedsPos].s++; }
2番目のopenメソッドは、各反復で実行するために必須であり、各子雑草の適合度関数を計算した後に必要です。並べ替えを適用する前に、発芽した種子を共通の配列に配置し、親株をリストの最後に配置します。これにより、前の世代が置き換えられます。これには、前の反復からの子孫と親の両方が含まれる可能性があります。したがって、自然界で起こるように、適応力の弱い雑草を破壊します。その後、ソートを適用します。結果のリストの最初の雑草は、それが本当に優れている場合、大域的に達成された最適値を更新する価値があります.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_IWO::Germination () { for (int s = 0; s < numberSeeds; s++) { weeds [numberWeeds + s] = seeds [s]; } Sorting (); if (weeds [0].f > fB) fB = weeds [0].f; } //——————————————————————————————————————————————————————————————————————————————
3.テスト結果
テストスタンドの結果は以下のようになります。
2023.01.13 18:12:29.880 Test_AO_IWO (EURUSD,M1) C_AO_IWO:50;12;5;2;0.2;0.01
2023.01.13 18:12:29.880 Test_AO_IWO (EURUSD,M1) =============================
2023.01.13 18:12:32.251 Test_AO_IWO (EURUSD,M1) 5 Rastrigin's; Func runs 10000 result:79.71791976868334
2023.01.13 18:12:32.251 Test_AO_IWO (EURUSD,M1) Score:0.98775
2023.01.13 18:12:36.564 Test_AO_IWO (EURUSD,M1) 25 Rastrigin's; Func runs 10000 result:66.60305588198622
2023.01.13 18:12:36.564 Test_AO_IWO (EURUSD,M1) Score:0.82525
2023.01.13 18:13:14.024 Test_AO_IWO (EURUSD,M1) 500 Rastrigin's; Func runs 10000 result:45.4191288396659
2023.01.13 18:13:14.024 Test_AO_IWO (EURUSD,M1) Score:0.56277
2023.01.13 18:13:14.024 Test_AO_IWO (EURUSD,M1) =============================
2023.01.13 18:13:16.678 Test_AO_IWO (EURUSD,M1) 5 Forest's; Func runs 10000 result:1.302934874807614
2023.01.13 18:13:16.678 Test_AO_IWO (EURUSD,M1) Score:0.73701
2023.01.13 18:13:22.113 Test_AO_IWO (EURUSD,M1) 25 Forest's; Func runs 10000 result:0.5630336066477166
2023.01.13 18:13:22.113 Test_AO_IWO (EURUSD,M1) Score:0.31848
2023.01.13 18:14:05.092 Test_AO_IWO (EURUSD,M1) 500 Forest's; Func runs 10000 result:0.11082098547471195
2023.01.13 18:14:05.092 Test_AO_IWO (EURUSD,M1) Score:0.06269
2023.01.13 18:14:05.092 Test_AO_IWO (EURUSD,M1) =============================
2023.01.13 18:14:09.102 Test_AO_IWO (EURUSD,M1) 5 Megacity's; Func runs 10000 result:6.640000000000001
2023.01.13 18:14:09.102 Test_AO_IWO (EURUSD,M1) Score:0.55333
2023.01.13 18:14:15.191 Test_AO_IWO (EURUSD,M1) 25 Megacity's; Func runs 10000 result:2.6
2023.01.13 18:14:15.191 Test_AO_IWO (EURUSD,M1) Score:0.21667
2023.01.13 18:14:55.886 Test_AO_IWO (EURUSD,M1) 500 Megacity's; Func runs 10000 result:0.5668
2023.01.13 18:14:55.886 Test_AO_IWO (EURUSD,M1) Score:0.04723
テスト関数に対するアルゴリズムの良い結果に気付くには、一目見ただけで十分です。滑らかな関数で作業することへの顕著な好みがありますが、これまでのところ、考慮されているアルゴリズムのいずれも、滑らかな関数よりも離散関数で優れた収束を示していません。これは、例外なくすべてのアルゴリズムのForest関数とMegacity関数の複雑さによって説明されます。最終的に、離散関数を滑らかな関数よりもうまく解決するテスト用のアルゴリズムが得られる可能性があります。
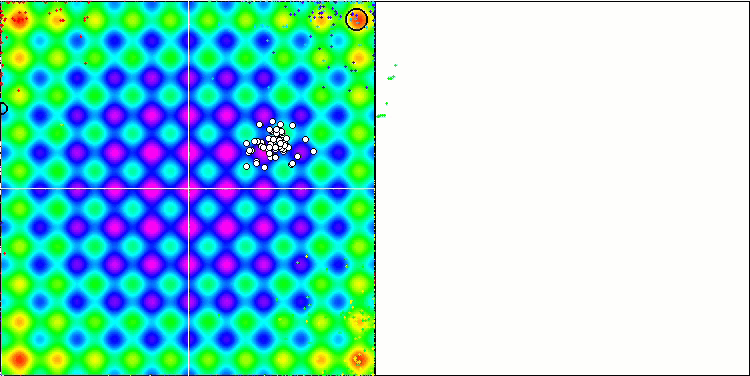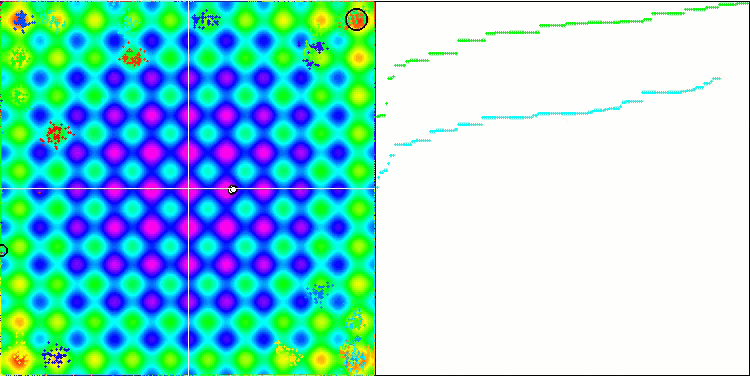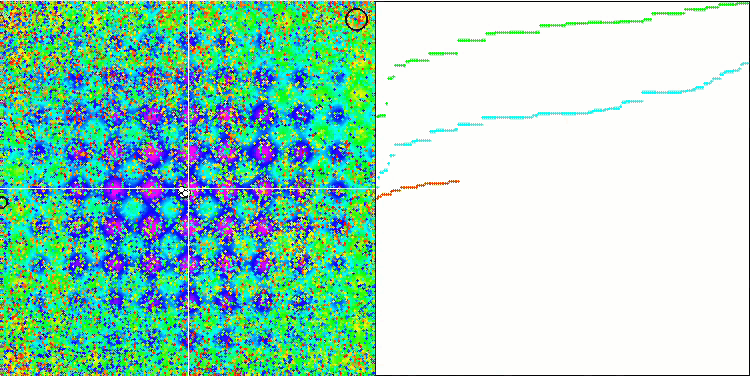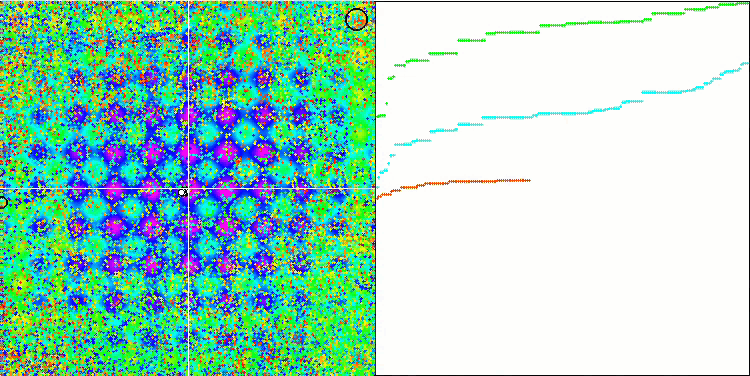
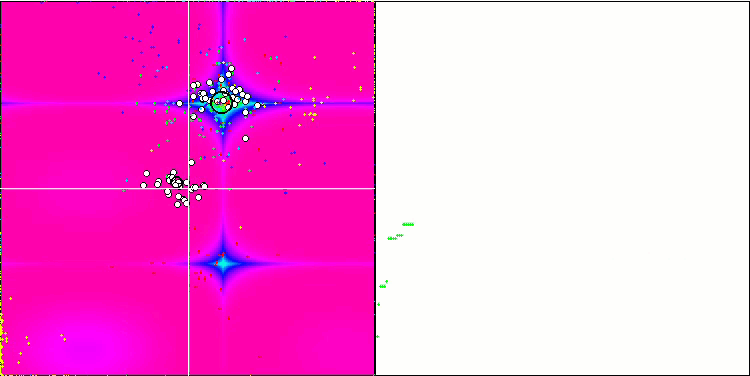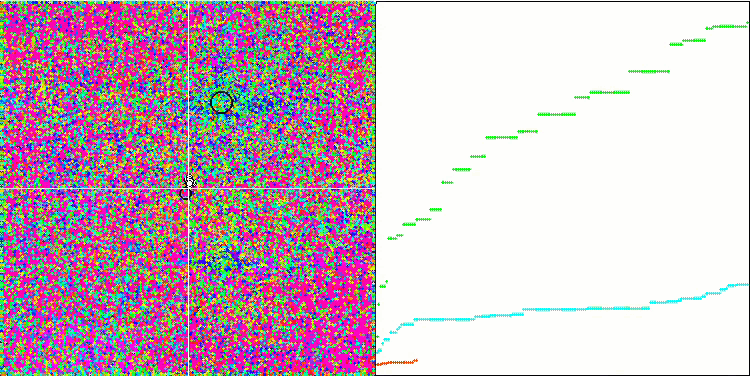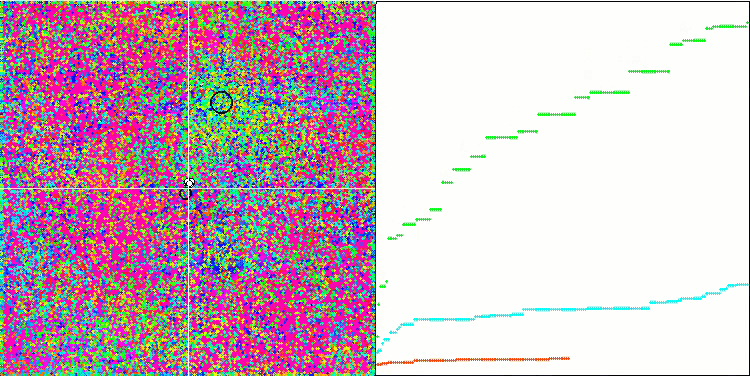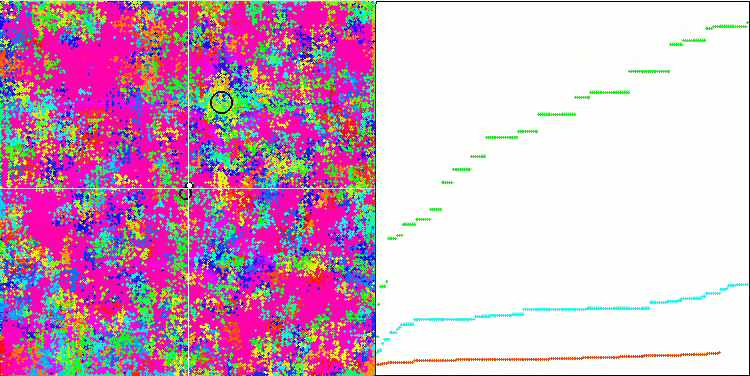
Rastriginテスト関数のIWO
Forestテスト関数のIWO
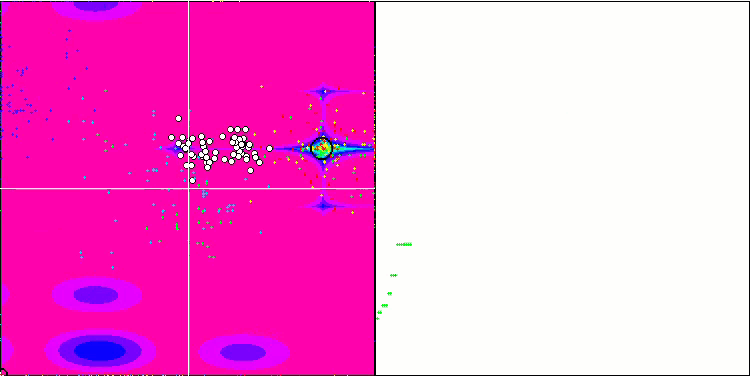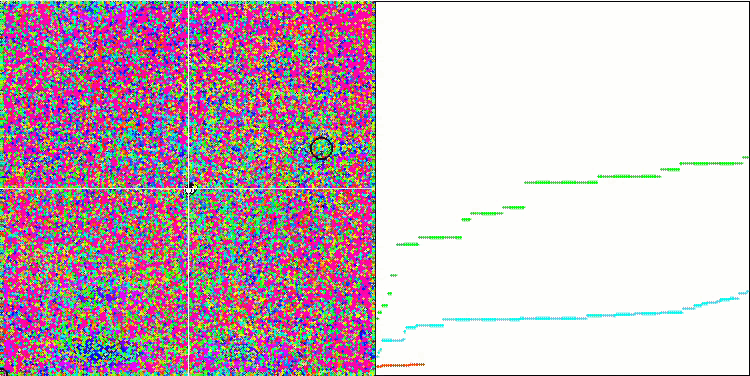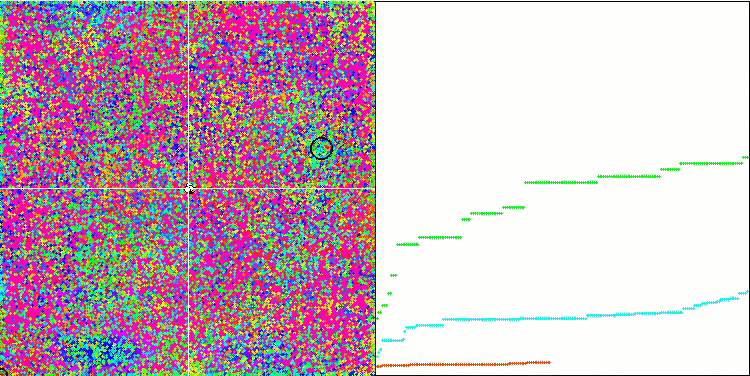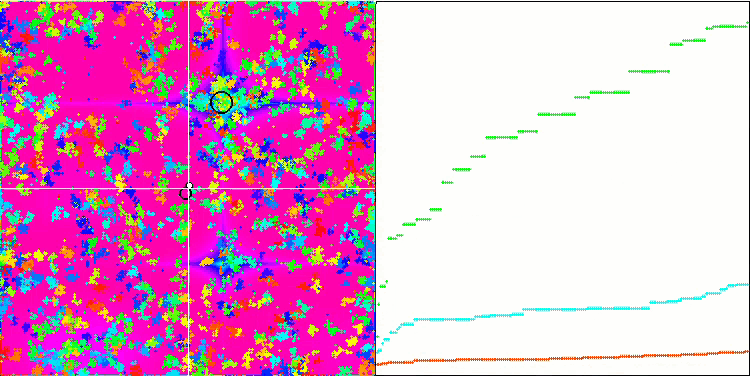
Megacityテスト関数のIWO
侵入雑草アルゴリズムは、ほとんどのテストで印象的な結果を示しました。特に、10個と50個のパラメータを使用した滑らかなRastrigin関数で優れた結果が得られました。そのパフォーマンスは、1000個のパラメータを使用したテストでのみわずかに低下しました。これは、一般に、滑らかな関数でのパフォーマンスが良好であることを示しています。これにより、複雑な滑らかな関数とニューラルネットワークのアルゴリズムを推奨することができます。Forest関数では、アルゴリズムは10個のパラメータを使用した最初のテストで良好な結果を示しましたが、それでも全体では平均的な結果を示しました。Megacity離散関数では、侵入雑草アルゴリズムは平均以上のパフォーマンスを発揮し、特に1000個の変数を使用したテストで優れたスケーラビリティを示して、ホタルアルゴリズムに続いて2位となりました。10個および50個のパラメータを使用したテストではホタルアルゴリズムより非常に優れていました。
侵入雑草アルゴリズムにはかなり多くのパラメータがありますが、パラメータは非常に直感的で簡単に構成できるため、これは欠点と見なされるべきではありません。さらに、アルゴリズムの微調整は通常、離散関数のテストの結果にのみ影響しますが、滑らかな関数の結果は良好なままです。
テスト関数の視覚化では、蜂アルゴリズムやその他のアルゴリズムで起こるのと同じように、検索空間の特定の部分を分離して探索するアルゴリズムの能力がはっきりと見えます。いくつかの出版物は、アルゴリズムが行き詰まる傾向があり、検索機能が弱いと述べています。アルゴリズムが最大/小値への参照を持たず、局地的なトラップから「飛び出す」メカニズムを持っていないにもかかわらず、IWOはどうにかしてForestやMegacityなどの複雑な機能を適切に処理できます。離散関数で作業している間、パラメータが最適化されているほど、結果はより安定します。
種子分散は反復ごとに直線的に減少するため、最適化の終わりに向かって極値の改良がさらに増加します。私の意見では、これは完全に最適というわけではありません。アルゴリズムの探索的機能が時間の経過とともに不均一に分散されるためです。これは、テスト関数を一定のホワイトノイズとして視覚化するとわかります。また、検索の不均一性は、テストスタンドウィンドウの右側にある収束グラフで判断できます。最適化の開始時に収束の加速が見られますが、これはほとんどすべてのアルゴリズムで一般的です。シャープなスタートの後、ほとんどの最適化で収束が遅くなります。収束が大幅に加速しているのは、終盤に近づいたときだけです。分散の動的な変化は、さらに詳細な研究と実験の理由です。反復回数が多ければ収束が再開できることがわかるからです。ただし、客観性と実用的妥当性を維持するために実施される比較試験には制限があります。
最終的な評価表に移りましょう。この表は、現時点でIWOがリーダーであることを示しています。アルゴリズムは、9つのテストのうち2つのテストで最高の結果を示しましたが、残りの結果は平均よりもはるかに優れているため、最終結果は100点です。次に蟻コロニーアルゴリズムの修正版(ACOm)です。9回のテストのうち5回で最高のままです。
| AO | 詳細 | Rastrigin | Rastrigin最終 | Forest | Forest最終 | Megacity (discrete) | Megacity最終 | 最終結果 | ||||||
| 10パラメータ(5F) | 50パラメータ(25F) | 1000パラメータ(500F) | 10パラメータ(5F) | 50パラメータ(25F) | 1000パラメータ(500F) | 10パラメータ(5F) | 50パラメータ(25F) | 1000パラメータ(500F) | ||||||
| IWO | 侵入雑草最適化 | 1.00000 | 1.00000 | 0.33519 | 2.33519 | 0.79937 | 0.46349 | 0.41071 | 1.67357 | 0.75912 | 0.44903 | 0.94088 | 2.14903 | 100.000 |
| ACOm | 蟻コロニー最適化M | 0.36118 | 0.26810 | 0.17991 | 0.80919 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 1.00000 | 1.00000 | 0.10959 | 2.10959 | 95.996 |
| COAm | カッコウ最適化アルゴリズムM | 0.96423 | 0.69756 | 0.28892 | 1.95071 | 0.64504 | 0.34034 | 0.21362 | 1.19900 | 0.67153 | 0.34273 | 0.45422 | 1.46848 | 74.204 |
| FAm | ホタルアルゴリズムM | 0.62430 | 0.50653 | 0.18102 | 1.31185 | 0.55408 | 0.42299 | 0.64360 | 1.62067 | 0.21167 | 0.28416 | 1.00000 | 1.49583 | 71.024 |
| BA | コウモリアルゴリズム | 0.42290 | 0.95047 | 1.00000 | 2.37337 | 0.17768 | 0.17477 | 0.33595 | 0.68840 | 0.15329 | 0.07158 | 0.46287 | 0.68774 | 59.650 |
| ABC | 人工蜂コロニー | 0.81573 | 0.48767 | 0.22588 | 1.52928 | 0.58850 | 0.21455 | 0.17249 | 0.97554 | 0.47444 | 0.26681 | 0.35941 | 1.10066 | 57.237 |
| FSS | 魚群検索 | 0.48850 | 0.37769 | 0.11006 | 0.97625 | 0.07806 | 0.05013 | 0.08423 | 0.21242 | 0.00000 | 0.01084 | 0.18998 | 0.20082 | 20.109 |
| PSO | 粒子群最適化 | 0.21339 | 0.12224 | 0.05966 | 0.39529 | 0.15345 | 0.10486 | 0.28099 | 0.53930 | 0.08028 | 0.02385 | 0.00000 | 0.10413 | 14.232 |
| RND | ランダム | 0.17559 | 0.14524 | 0.07011 | 0.39094 | 0.08623 | 0.04810 | 0.06094 | 0.19527 | 0.00000 | 0.00000 | 0.08904 | 0.08904 | 8.142 |
| GWO | 灰色オオカミオプティマイザ | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.18977 | 0.04119 | 0.01802 | 0.24898 | 1.000 |
侵入雑草アルゴリズムは、大域的な検索に最適です。このアルゴリズムは良好なパフォーマンスを示しますが、母集団の最良のメンバーは使用されず、極値での潜在的な固着を防ぐメカニズムはありません。アルゴリズムの研究と活用の間にバランスはありませんが、アルゴリズムの精度と速さに悪影響を与えることはありませんでした。このアルゴリズムには他にも欠点があります。最適化中の検索の不均一なパフォーマンスは、上記の問題を解決できれば、IWOのパフォーマンスが潜在的に高くなる可能性があることを示唆しています。
図4のアルゴリズムテスト結果のヒストグラム
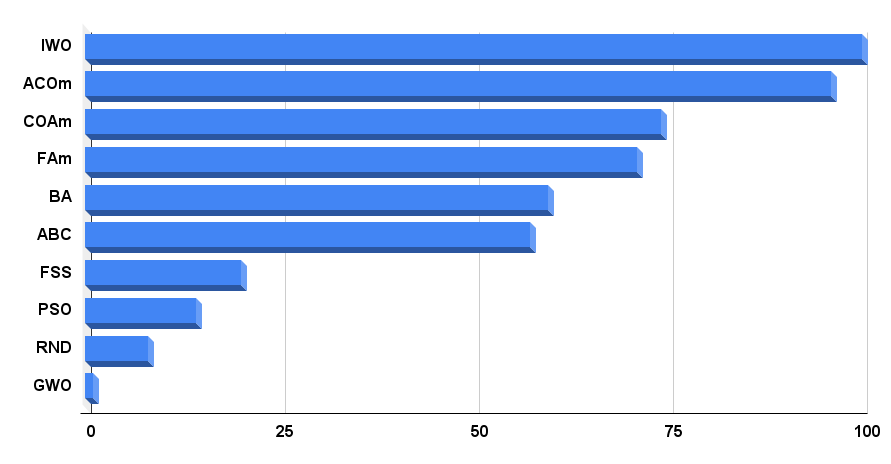
図4:テストアルゴリズムの最終結果のヒストグラム
侵入雑草の最適化(IWO)アルゴリズムの特性に関する結論
賛成:
1.高速
2.滑らかな関数と離散関数の両方のさまざまなタイプの関数でうまく機能する
3.優れたスケーラビリティ
反対:
1.多数のパラメータ(ただし一目瞭然)
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11990
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
表の数字の意味は?