時間進化移動アルゴリズム(TETA)

内容

1. はじめに
2. アルゴリズムの実装
3. テスト結果

はじめに

これまで、CSS、EM、GSA、AEFA、AOSmなど、物理法則に基づく多くのアルゴリズムを検討してきました。しかし、宇宙は常に新たな現象をもたらし、私たちに様々な仮説や発想を与えてくれます。その中でも、時間のような宇宙の根本的な要素は、新しい最適化アルゴリズムを生み出す着想を与えてくれました。時間は新たな発見の源であると同時に、理解が難しい神秘的な存在でもあります。それは川のように流れ、私たちの人生の瞬間を運び去り、記憶だけを残します。タイムトラベルは、人類にとって常に魅力的で幻想的なテーマであり続けています。本アルゴリズムの考え方を理解するために、一人の科学者の物語を想像してみましょう。

昔、明るい未来へ向かい、過去の過ちから逃れたいという思いに取り憑かれた物理学者がいました。彼は時間の流れの研究に没頭しましたが、苦い発見に直面します。それは、未来への移動は不可能であるという事実でした。しかし彼は諦めず、過去へ戻る能力の研究に切り替え、過ちを修正しようと試みましたが、ここでも失望に終わりました。

しかし、仮想的な時間の流れの研究を進めるうちに、彼は驚くべき発見をします。それは、並行宇宙の存在でした。彼は世界間を移動するための理論モデルを構築し、さらに驚くべき事実を見つけます。直接的なタイムトラベルは不可能であるものの、特定の出来事の順序を選択することで、ある並行宇宙に到達することは可能であるということです。

すべての行動は新しい並行現実を生み出しますが、科学者が関心を持ったのは、自分の人生に直接影響する宇宙のみでした。彼はそれらの宇宙を行き来するために、方程式系の中に特別なアンカー（世界を区別するための要素）を設置しました。それは彼の運命の重要なポイント、すなわち家族、キャリア、科学的発見、友情、そして重要な出来事です。これらのアンカーは、彼の装置における変数となり、確率的な世界間で最適経路を選択することを可能にしました。

彼は装置を起動し、並行世界を旅し始めますが、もはや「出来上がった明るい未来」へ到達することを目的としませんでした。彼はより重要なことに気づきます。それは、現在の瞬間に意思決定をおこなうことで、自分自身の手で未来を創造する能力です。新しい選択をするたびに、自分が実現したい現実のバージョンへ道が開かれます。こうして彼は理想的な未来の夢の囚人であることをやめ、自らその建築家となったのです。彼の装置は現実から逃れる手段ではなく、時間の各瞬間に最適な解を選ぶことで、自分自身の運命を意識的に創造する道具となりました。

本記事では、タイムトラベルの概念を実装した「時間進化移動アルゴリズム(TETA: Time Evolution Travel Algorithm)」を考察します。本アルゴリズムの特徴は、パラメータや変更可能な変数を持たない点にあります。このアルゴリズムは、最適解を探索することと精緻化とのバランスを自然に保ちます。通常、外部パラメータを持たないアルゴリズムでも、性能に影響を与える内部定数が存在します。しかし、TETAはそのような定数すら持たず、この点で独自性を有しております。

アルゴリズムの実装

物語の中で、科学者は自分の人生における重要な変数を変更することで並行宇宙間を移動する方法を発見しました。この比喩が、本論文で提案する最適化アルゴリズムの基礎となっています。より明確にするために、以下の図をご覧ください。意思決定がおこなわれるたびに生じる並行宇宙の概念を示しています。完全な空間を持つ各宇宙は、家族、キャリア、業績などのアンカー（特徴量）の存在によって定義されます。

これらのアンカーの性質を組み合わせることで、最適化問題の解を表す新しい宇宙を作成することができます。この場合、アンカーは最適化対象となるパラメータです。

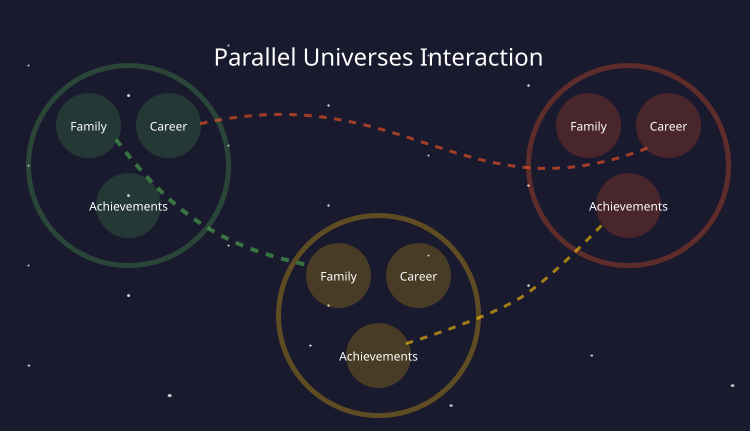
図1：独自のアンカー（特徴量）を持つ並行宇宙

TETAアルゴリズムは、複数の並行宇宙の概念に基づいており、それぞれが最適化問題に対する潜在的な解を表しています。技術的な実装において、各宇宙は座標ベクトル(a[i].c)で表され、各座標はその現実の構成を決定する重要な変数（アンカー）です。アンカーは、解の全体的な質に影響を与える最も重要なパラメータとして捉えることができます。

各宇宙の質を評価するために、適応度関数(a[i].f)が用いられ、特定の現実における「存在の快適さ」を定量化します。この関数の値が高いほど、その宇宙はより好ましいとみなされます。各宇宙は現在の状態だけでなく、既知の最良構成(a[i].cB)も保持し、これは最も成功したシナリオの「記憶」に相当します。また、アルゴリズムは、すべての探索中で最も好ましい構成を表す大域最良解(cB)も管理します。

N個の個体からなる集団が並行宇宙の集合を形成し、それぞれ独自のアンカー値を持ちます。これらの宇宙は適合度関数の値に基づき絶えずランク付けされ、最も望ましい状態から最も望ましくない状態までの階層が形成されます。現実の各アンカーは最適化可能な変数であり、これらの変数の変更は新しい宇宙の構成を生み出します。アンカーの集合は変数ベクトルx = (x₁, x₂, ..., xₙ)を形成し、特定の現実を完全に記述します。また、各変数には許容範囲が定義されており、これは各宇宙での可能な変化を制約する物理法則として解釈できます。

各宇宙の好ましさは、適合度関数f(x)により評価されます。f(x)は、宇宙の構成を実数に写像します。この値が高いほど、現実はより望ましいとみなされます。この仕組みにより、複数の並行宇宙における様々な可能性を数学的に厳密に評価・比較するメカニズムが構築されます。

アルゴリズムの重要な特徴は、単一の確率比(rnd *= rnd)です。これにより、宇宙の選択確率とアンカーの変化の強さの両方が決定されます。この仕組みにより、自然な自己均衡メカニズムが生まれます。最も望ましい宇宙は選ばれる確率が高いものの、そのアンカーの変化は小さく（rndに比例）なります。一方で、最も望ましくない宇宙は選ばれる確率は低いものの、大きな変化を受けます（1.0 - rndに比例）。

このアプローチは、すべてを一度に完璧にすることは不可能であるという深い哲学的な考え方を反映しています。改善は、さまざまな側面の絶え間ない均衡によって進みます。場合によっては、最良のアンカーが全体のバランスのためにわずかに悪化することがありますが、最も望ましくないアンカーは改善を目指して変化します。変化の強さは宇宙の「良さ」に比例しており、これは現実世界において、何か問題が生じた場合には大きな変化が起こる可能性が高いことを反映しています。

結果として、アルゴリズムは単に値を最適化するだけでなく、複雑な多次元的生活状況システムにおけるバランスを見つけるプロセスをシミュレートします。理想的な現実を追うのではなく、すべての側面を微妙に調整し、最も調和の取れた現実を見つけ出すことを目指します。

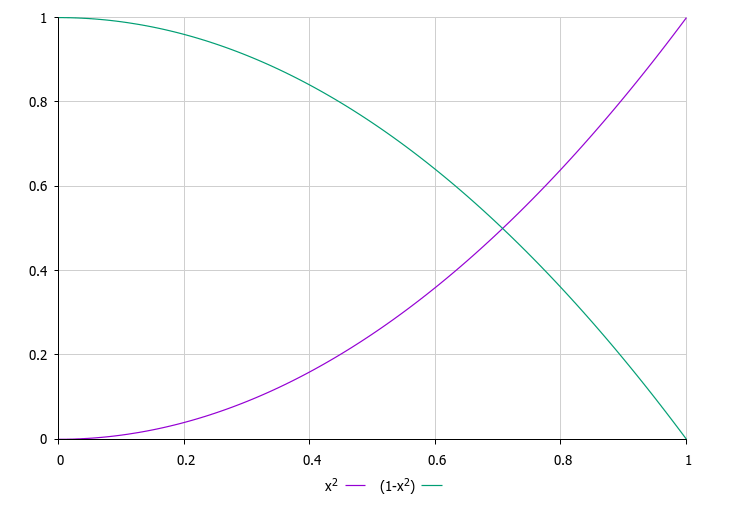
図2：赤い線は宇宙の質に応じた選択確率関数、緑の線は対応する宇宙のアンカーの変化度合い

アルゴリズムの擬似コードは次の通りです。

初期化
1. N個の並行宇宙の集団を作成
2. 各宇宙について
   - アンカー（座標）の値を許容範囲内でランダム初期化
   -初期の裁量値を現在値で初期化

メインループ
1. 適応度関数に基づき宇宙をソート
   - 最良宇宙は低いインデックス
   - 最悪宇宙は高いインデックス

2. 各宇宙「i」について
   各アンカーに対して
   
   a) 相互作用する宇宙を選択
      - 0〜1のランダム数「rnd」を生成
      - rndを二乗して最良宇宙の優先度を上げる
      - pairのインデックスをrndに比例して選択
   
   b) 現宇宙が選択宇宙と異なる場合(i ≠ pair)
      
      現宇宙が選択宇宙より良い場合(i < pair)
         - アンカーをrndに比例してわずかに変化
         - New_value = current + rnd * (selected_value - current)
      
      そうでない場合（現宇宙が劣る場合）
         (random_number > rnd)の場合
            - アンカーを「1-rnd」に比例して大幅変更
            - New_value = current + (1-rnd) * (selected_value - current)
         それ以外の場合
            - より成功した宇宙からアンカーを完全コピー
            - New_value = selected_value
   
   c) 同じ宇宙の場合(i = pair)
      - ガウス分布による局所探索
      - New_value = GaussDistribution(current_best)
   
   d) 新アンカー値を許容範囲に補正

3. 最良値の更新
   各宇宙について
   - 現在値が個体の最良値より良ければ更新
   - 現在値が大域最良解より良ければ更新

4. 停止条件を満たすまでメインループを繰り返す

これで、並行宇宙移動マシンのコード実装準備が整いました。次に、C_AOクラスを継承してC_AO_TETAクラスを作成します。以下に簡単な説明を示します。

• コンストラクタ：アルゴリズムの名前、説明、リンクを初期化し、集団のサイズを設定
• SetParamsパラメータ：params配列の値を使用してパラメータを設定
• Init、Moving、Revisionメソッド：宣言されているが、別のコードで実装される

class C_AO_TETA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_TETA () { }
  C_AO_TETA ()
  {
    ao_name = "TETA";
    ao_desc = "Time Evolution Travel Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16963";

    popSize = 50; // number of parallel universes in the population

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values for anchors
             const double &rangeMaxP  [],  // maximum values for anchors
             const double &rangeStepP [],  // anchor change step
             const int     epochsP = 0);   // number of search epochs

  void Moving ();
  void Revision ();

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_TETAクラスのInitメソッドの初期化により、アルゴリズムの初期設定が実行されます。 

メソッドパラメータ

• rangeMinP：アンカーの最小値配列
• rangeMaxP：アンカーの最大値配列
• rangeStepP：アンカー変更ステップの配列
• epochsP：検索エポックの数（デフォルトは0）

標準初期化

• StandardInitを呼び出し、アンカー範囲のチェックと設定をおこないます。初期化に失敗した場合はfalseを返します。

戻り値

• すべてのチェックと設定が正常に完了した場合、本メソッドはtrueを返します。これは、アルゴリズムの初期化が成功したことを示しています。

//——————————————————————————————————————————————————————————————————————————————
// TETA - Time Evolution Travel Algorithm
// An optimization algorithm based on the concept of moving between parallel universes
// through changing the key anchors (events) of life

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TETA::Init (const double &rangeMinP  [], // minimum values for anchors
                      const double &rangeMaxP  [], // maximum values for anchors
                      const double &rangeStepP [], // anchor change step
                      const int     epochsP = 0)   // number of search epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_TETAクラスのMovingメソッドは、並行宇宙内のアンカーを変更し、新しい宇宙を生成する役割を担います。

revisionステータスの確認

• revisionがfalseであった場合、本メソッドは与えられた範囲からランダムな値を用いて、すべての並行宇宙のアンカー初期値を設定し、ステップに基づいて有効な値となるよう関数を適用します。

アンカー値の更新

• リビジョンがすでに実施されている場合、すべての並行宇宙に対して反復処理がおこなわれます。各アンカーに対して確率が生成され、新しい値が計算されます。
  • 現在の宇宙がより望ましい場合、アンカーはより良いバランスを見つけるためにわずかに正方向に調整されます。
  • 現在の宇宙が望ましくない場合、確率テストの結果としてアンカーが大幅に変化することもあれば、より望ましい宇宙のアンカーを完全に採用することもあります。
  • 宇宙が一致する場合は、ガウス分布を用いた局所的なアンカー調整がおこなわれます。
• 新しい値を計算した後、アンカーの値は許容範囲内に補正されます。

このメソッドは実質的に、解（並行宇宙）の適応と改善を担っており、最適化アルゴリズムの核心部分を構成しています。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial values of anchors in all parallel universes
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Generate a probability that determines the chance of choosing a universe,
      // as well as the anchor change force
      rnd  = u.RNDprobab ();
      rnd *= rnd;

      // Selecting a universe for sharing experience
      pair = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

      if (i != pair)
      {
        if (i < pair)
        {
          // If the current universe is more favorable:
          // Slightly change the anchor (proportional to rnd) to find a better balance
          val = a [i].c [c] + (rnd)*(a [pair].cB [c] - a [i].cB [c]);
        }
        else
        {
          if (u.RNDprobab () > rnd)
          {
            // If the current universe is less favorable:
            // Significant change of anchor (proportional to 1.0 - rnd)
            val = a [i].cB [c] + (1.0 - rnd) * (a [pair].cB [c] - a [i].cB [c]);
          }
          else
          {
            // Full acceptance of the anchor configuration from a more successful universe
            val = a [pair].cB [c];
          }
        }
      }
      else
      {
        // Local anchor adjustment via Gaussian distribution
        val = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 1);
      }

      a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_TETAクラスのRevisionメソッドは、並行宇宙におけるアンカー構成を更新し、これらの宇宙をその質に応じてソートする役割を担います。以下が詳細です。

大域最良構成の更新

• すべての並行宇宙（0からpopSizeまで）を順に確認
• 現在の宇宙の適合度関数a[i].fの値が、大域最良値fBより大きい場合
  • fBはa[i].fの値で更新される
  • 現在の宇宙のアンカー構成は大域最良値のcBにコピーされる

各宇宙の既知の最良構成の更新

• 現在の宇宙の適合度関数a[i].fの値が、その宇宙の既知の最良値a[i].fBより大きい場合
  • a[i].fBはa[i].fの値で更新される
  • 現在の宇宙のアンカー構成はその宇宙の既知の最良構成a[i].cBにコピーされる

宇宙の並べ替え

• エージェントを格納するために静的配列「aT」を宣言
• aTのサイズをpopSizeに変更
• u.Sorting_fB関数を用いて、各宇宙の既知の最良値に基づき宇宙を並び替え

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Update globally best anchor configuration
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }

    // Update the best known anchor configuration for each universe
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c);
    }
  }

  // Sort universes by their degree of favorability
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

TETAの結果：

TETA|Time Evolution Travel Algorithm|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.9136198796338938
25 Hilly's; Func runs:10000; result:0.8234856192574587
500 Hilly's; Func runs:10000; result:0.3199003852163246
=============================
5 Forest's; Func runs:10000; result:0.970957820488216
25 Forest's; Func runs:10000; result:0.8953189778250419
500 Forest's; Func runs:10000; result:0.29324457646900925
=============================
5 Megacity's; Func runs:10000; result:0.7346153846153844
25 Megacity's; Func runs:10000; result:0.6856923076923078
500 Megacity's; Func runs:10000; result:0.16020769230769372
=============================
All score:5.79704 (64.41%)

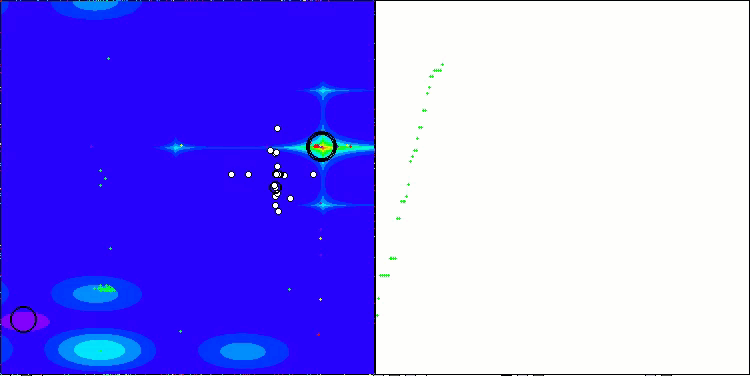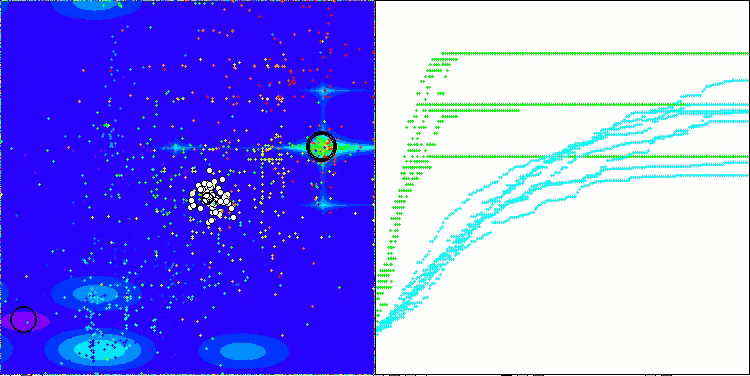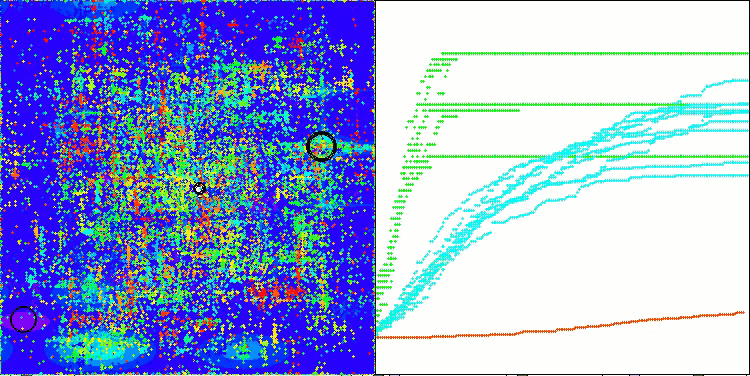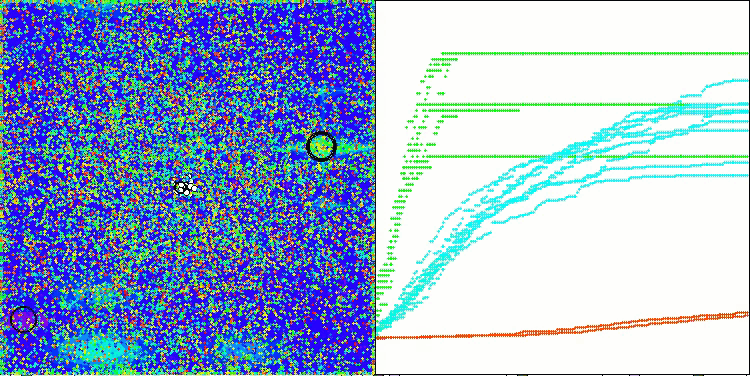
最終結果：5.79704（64.41％）。テスト関数の複雑さを考慮すると、これは非常に優れた結果です。本アルゴリズムは、有望な最適値が存在する重要な領域を非常に迅速に検出し、すぐにそれらの領域の精緻化を開始します。この挙動は、アルゴリズムの動作を可視化した各図にも明確に現れています。

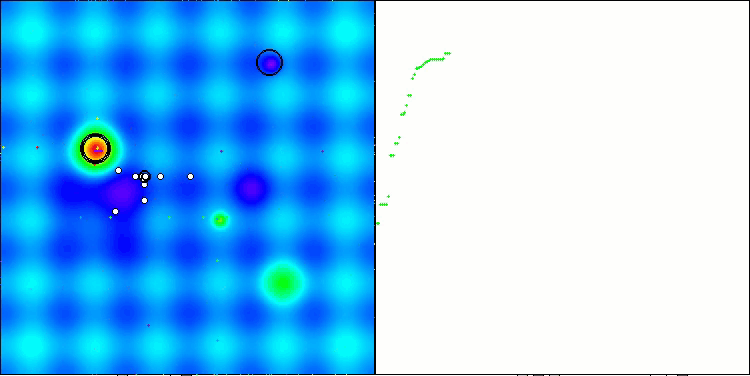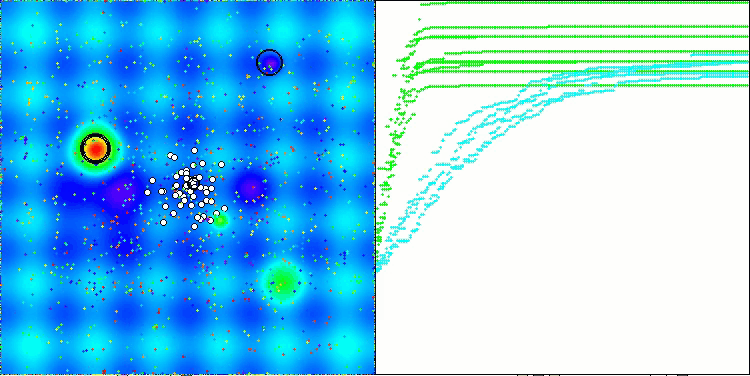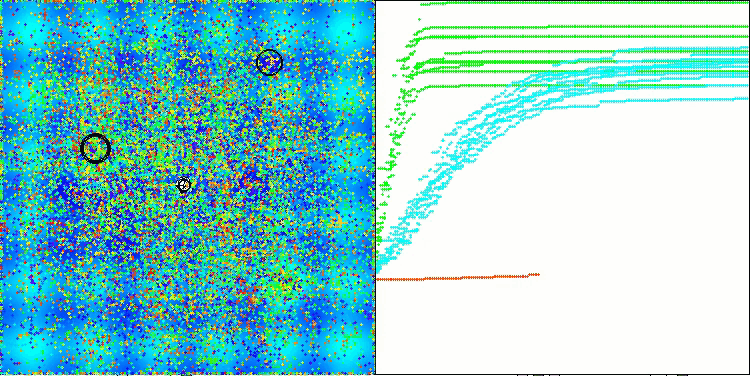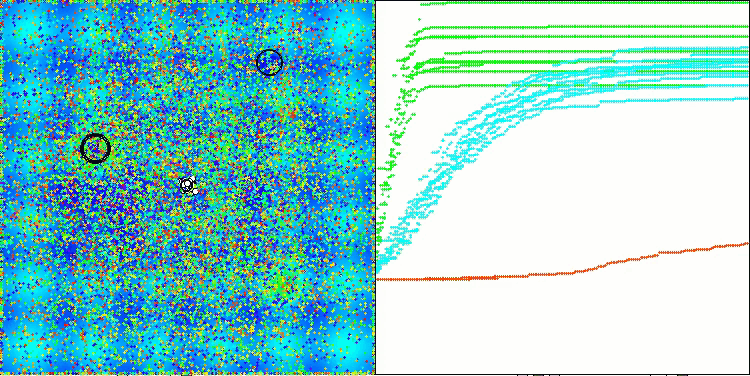
Hillyテスト関数のTETA

 Forestテスト関数のTETA

Megacityテスト関数のTETA

特筆すべき点は、本アルゴリズムが、テスト関数群の1つであるGoldsteinPrice関数において、他のすべての最適化アルゴリズムを上回る最良の結果を達成し、従来の集団ベースアルゴリズムのリーダーを上回ったということです。

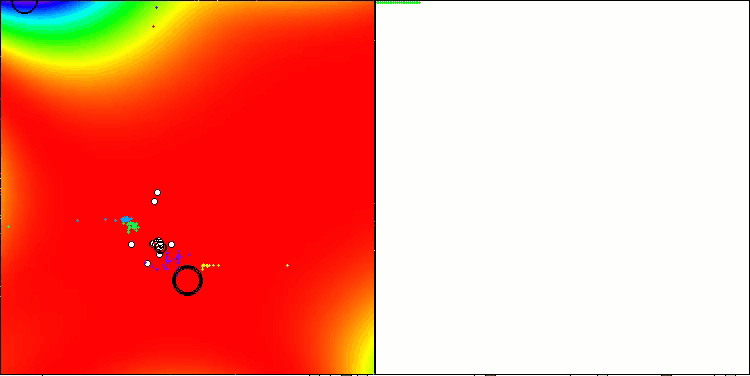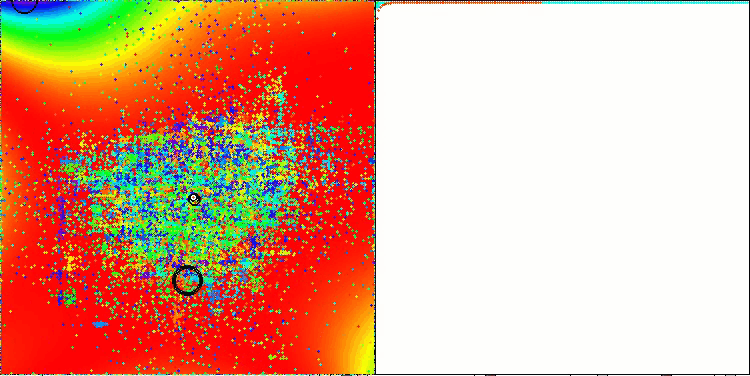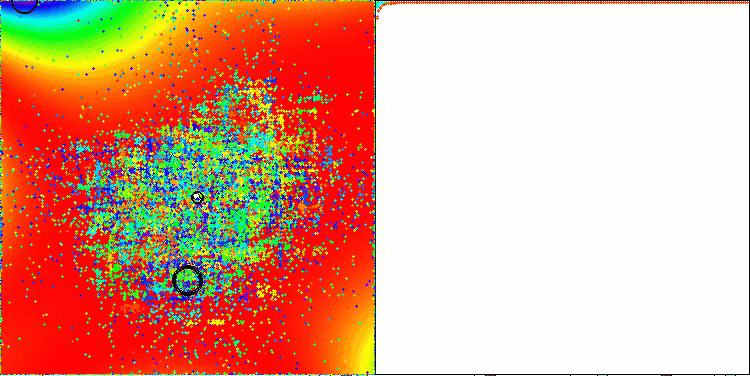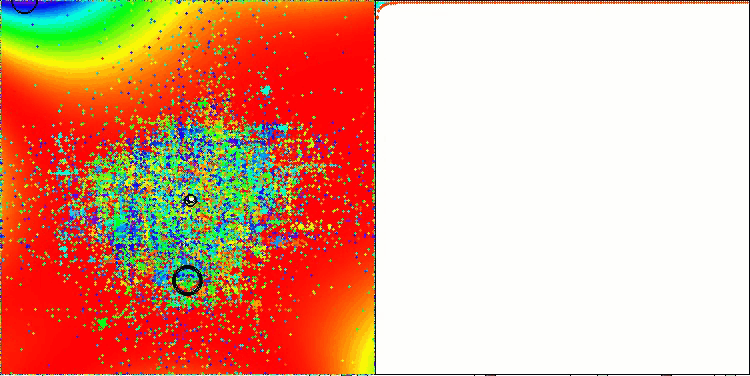
GoldsteinPriceテスト関数のTETA（テスト関数のリストから選択可能）

GoldsteinPriceの結果

5 GoldsteinPrice's; Func runs:10000; result:0.9999786723616957
25 GoldsteinPrice's; Func runs:10000; result:0.9999750431600845
500 GoldsteinPrice's; Func runs:10000; result:0.9992343490683104

テスト完了後、TETAアルゴリズムは最良の最適化アルゴリズムの上位10位に入り、6位という堂々たる順位を獲得しました。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
			10p(5F)	50p(25F)	1000p(500F)		10p(5F)	50p(25F)	1000p(500F)		10p(5F)	50p(25F)	1000p(500F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	時間進化移動アルゴリズム（joo）	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
9	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
10	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
11	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
12	BHAm	ブラックホールアルゴリズムM	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
13	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
14	AOSm	原子軌道探索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
15	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
16	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
17	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
18	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
19	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
20	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
21	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
22	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
23	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
24	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
25	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
26	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
27	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
28	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
29	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
30	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
31	SOA	シンプル最適化アルゴリズム	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
32	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
33	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
34	ADAMm	適応モーメント推定M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
35	ATAm	人工部族アルゴリズムM	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
36	ASHA	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
37	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
38	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
39	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
40	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
41	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
42	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
43	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
44	BBBC	ビッグバンビッグクランチアルゴリズム	0.60531	0.45250	0.31255	1.37036	0.52323	0.35426	0.20417	1.08166	0.39769	0.19431	0.11286	0.70486	3.157	35.08
45	CPA	循環単為生殖アルゴリズム	0.71664	0.40014	0.25502	1.37180	0.62178	0.33651	0.19264	1.15093	0.34308	0.16769	0.09455	0.60532	3.128	34.76
	RW	ランダムウォーク	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

まとめ

TETAアルゴリズムの開発にあたり、私は常にシンプルで効率的なものを作ることを目指していました。並行宇宙やタイムトラベルの比喩は、当初は単純でわかりやすいアイデアに思えましたが、開発を進めるうちに自然に効果的な最適化の仕組みへと進化していきました。

本アルゴリズムの重要な特徴は、すべてを一度に完璧にすることは不可能であるという考え方です。すべての側面においてバランスを見つける必要があります。私たちは日常生活においても、家族、キャリア、個人的な成果の間で常にバランスを取っています。この概念をアンカーシステムを通じてアルゴリズムの基盤に置きました。各アンカーは最適化すべき重要な側面を表しており、他の側面を犠牲にすることなく調整されます。

最も興味深い技術的な工夫は、宇宙の選択確率と他の宇宙への影響の強さを結びつけたことです。これにより、最良解が選ばれる確率は高く、かつその影響は解の質に応じて決まるという自然なメカニズムが生まれました。このアプローチは、新たな可能性を探索することと、すでに見つかった良好な解を活用することのバランスを提供します。

アルゴリズムをテストしたところ、予想以上に優れた結果が得られました。このことは、計算資源が限られた実用的な問題に対しても特に有用であることを示しています。さらに、異なる種類の関数に対しても一貫して高い性能を示しており、その汎用性が確認されました。特に嬉しいのは、実装のコンパクトさです。主要なコードはわずか約50行で、カスタマイズ可能なパラメータもなく、それでいて非常に高い効果を発揮します。これは、実装のシンプルさと高性能が両立した真に成功した解決策であると言えます。

最終的に、TETAは私の当初の期待を超えました。タイムトラベルの比喩は、実用的で効果的な最適化ツールを生み出し、幅広い分野で応用可能となりました。これは、明確で自然なアナロジーに基づいた単純な解決策が非常に有効である場合があることを示しています。アルゴリズムは、概念から実装まで一息で作られたものであり、このアルゴリズムが研究者や実務者にとって、最適解を迅速に見つけるための優れた助けとなることを非常に嬉しく思います。 

図3：対応するテストに応じたアルゴリズムのカラーグラデーション

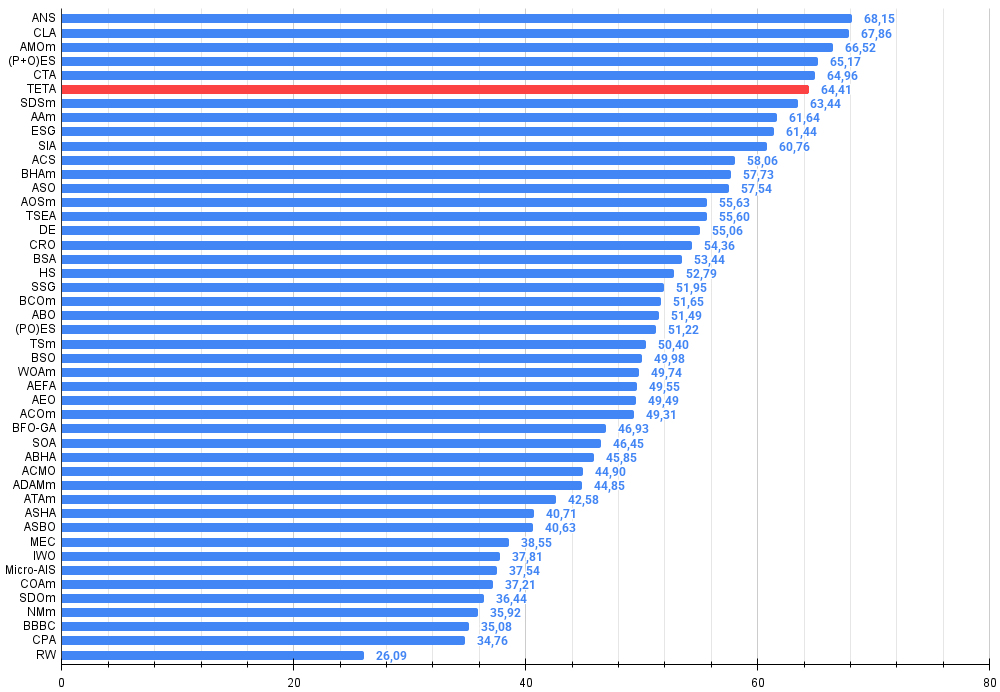
図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

TETAの長所と短所

長所

1. 集団規模が唯一の外部パラメータ
   
2. 実装がシンプル
3. EAが非常に高速
4. 小規模および大規模次元の問題の両方に対応するバランスの取れた指標
   

短所：

1. 低次元離散問題における結果の散布
   

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

• github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	TestFunctions.mqh	インクルード	テスト関数のライブラリ
4	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
5	Utilities.mqh	インクルード	補助関数のライブラリ
6	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
7	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
8	Simple use of population optimization algorithms.mq5	スクリプト	可視化せずに集団最適化アルゴリズムを使用する簡単な例
9	Test_AO_TETA.mq5	スクリプト	TETAテストスタンド