
ビッグバンビッグクランチ(BBBC)アルゴリズム
内容
はじめに
星が生まれ、死んでいく広大な宇宙には、人類が解き明かそうとする多くの未知の現象が存在します。ビッグバンビッグクランチ(BBBC)法は、宇宙で観測される現象に着想を得た大域最適化アルゴリズムであり、その概念は非常に示唆に富んでいます。
ビッグバンビッグクランチ理論は、20世紀初頭に物理学者アレクサンドル・フリードマンおよびジョルジュ・ルメートルによって、宇宙の終焉の代替シナリオとして提案されました。彼らは、アインシュタインの一般相対性理論の方程式が、宇宙の膨張および収縮の両方を理論的に許容することに気づきました。フリードマンは数学的に、宇宙は静止状態を維持できず、膨張するか収縮するかのいずれかであることを証明しました。彼は宇宙の進化には、永続的な膨張、膨張の後の収縮、振動的な進化の3つの可能性があると指摘しました。
20世紀を通じて、多くの科学者がビッグバンとビッグクランチを組み合わせた循環宇宙モデルを発展させました。現在では、宇宙の加速膨張が観測されているため、ビッグクランチ理論は主流の宇宙論モデルではありません。しかし、この理論は、宇宙の進化における循環的側面を示唆する興味深い概念です。主な段階は以下の通りです。
- ビッグバン:高密度・高温の初期状態から急速な膨張が起こり、エネルギーが散逸しながら物質と時空が形成され、粒子は無秩序に分布します。
- ビッグクランチ:引力によって膨張が停止し、収縮が始まり、すべての物質が一点に集中して高密度状態に戻ります。
- 循環性:ビッグクランチの後に新たなビッグバンが生じ、このプロセスは無限に繰り返される可能性があります。各サイクルは異なる物理定数を持つ場合があります。
ビッグバンビッグクランチアルゴリズムは、2006年にトルコにあるイスタンブール工科大学のOsman K. ErolとIbrahim Eksinによって提案されました。
アルゴリズムの実装
ビッグバン理論において宇宙が強力なエネルギーの爆発から存在を始めるのと同様に、BBBC法においても最初の段階はランダム性と多様性に満ちています。ビッグバン段階では、ランダムな点の集団が生成されます。それぞれの点は解の候補を表し、広大な探索空間に散らばって探索可能な状態にあります。しかし、秩序の芽生える瞬間、ビッグクランチ段階が始まります。点は互いに「質量中心」に向かって移動し、これは銀河が引力によって互いに引き合う様子に似ています。最適解を探索するための努力が集約される瞬間です。
アルゴリズムの段階は以下の通りです。これは、混沌から秩序への道筋です。
1. ビッグバン段階:最初のステップとして、N個のランダムな点の集団を生成します。各点は空間内に均等に分布し、指定された境界内に配置されます。
2. ビッグクランチ段階:「重心」の計算に移行します。すべての点がこの中心に向かって収束します。図1の式を用いて中心の座標を求め、次のステップの新たな起点とします。
3. 新しい点の生成:新しい点は重心の周囲に生成されます。これらの点は正規分布に従って形成され、移動の方向と大きさは所定の式により決定されます。
BBBC法は探索と精緻化の調和を目指しています。世代ごとに生成される点の分布は徐々に狭まり、これによりアルゴリズムは最適解をより正確に洗練させることができます。
宇宙において一つひとつの動きが意味を持つように、最適化の世界でも一つひとつの計算が目標への到達に寄与します。この手法に取り組むことで、我々は新たな地平を開くだけでなく、より良い解を求める壮大な宇宙的プロセスの一端を体験することができます。
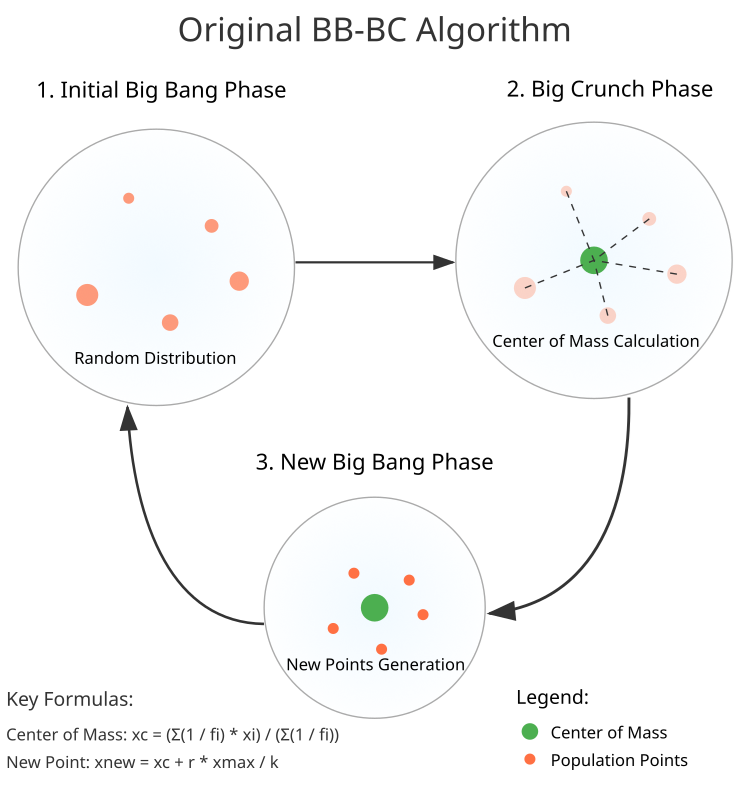
図1:BBBCアルゴリズムの構造
BBBCアルゴリズムの疑似コードを書いてみましょう。
epochNowを増やす
// 初期化(ビッグバン)
revision == falseの場合
0からpopSize-1までの各i個体について
0からcoords-1までの各c座標について
新しい座標 = (rangeMin[c], rangeMax[c])の範囲の乱数を生成する
revisionをtrueに設定する
戻る
// ビッグクランチ段階
epochNow % bigBangPeriod != 0の場合
0からcoords-1までの各c座標について
分子 = 0、分母 = 0
0からpopSize-1までの各i個体について
適応度 = 最大値(絶対値(a [i].f)、1e-10)
重み = 1.0 / 適応度
分子 += 重み * 点の座標
分母 += 重み
centerMass [c] = (分母 > 1e-10) ? 分子 / 分母 : cB [c]
0からpopSize-1までの各i個体について
0からcoords-1までの各c座標について
r = 正規乱数(0、-1.0、1.0、1)を生成する
新しい座標 = centerMass [c] + r * rangeMax [c] / epochNow
// ビッグバン段階
その他の場合
0からpopSize-1までの各i個体について
0からcoords-1までの各c座標について
新しい座標 = 正規乱数を生成 (cB [c]、rangeMin [c]、rangeMax [c]、標準偏差 = 8)
ビッグクランチ段階の停止基準が満たされるまで繰り返します
では、コードの作成に進みましょう。C_AOの派生クラスであるC_AO_BBBCクラスの定義を記述してみましょう。
以下はpublicメソッドです。- コンストラクタとデストラクタ
- SetParams():パラメータ(個体数およびビッグバンの周期性)の設定
- Init():指定された探索範囲に基づくアルゴリズムの初期化
- Moving():ビッグバンとビッグクランチ段階を実装するメインメソッド
- Revision ():発見された最良解を更新するメソッド
- epochs:アルゴリズムの総エポック数
- epochNow:現在のエポック
- centerMass []:重心の座標を格納する配列
本クラスはBBBCアルゴリズムの実装であり、主な計算はMoving()およびRevision()メソッドで行われます。また、必要な集団データはC_AO基底クラスに格納されます。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBBC : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBBC () { } C_AO_BBBC () { ao_name = "BBBC"; ao_desc = "Big Bang - Big Crunch Algorithm"; ao_link = "https://www.mql5.com/ja/articles/16701"; popSize = 50; bigBangPeriod = 3; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod; } void SetParams () { popSize = (int)params [0].val; bigBangPeriod = (int)params [1].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int bigBangPeriod; // Big Bang periodicity private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch double centerMass []; // center of mass }; //——————————————————————————————————————————————————————————————————————————————
C_AO_BBBCクラスのInitメソッド
本メソッドはアルゴリズムを初期化し、以下のパラメータを受け取ります。
- rangeMinP []:各座標の最小値を格納する配列
- rangeMaxP []:各座標の最大値を格納する配列
- rangeStepP []:各座標の離散化ステップを格納する配列
- epochsP:アルゴリズムの実行エポック数(デフォルトは0)
以下はメソッドの処理内容です。
- 基底クラスのStandardInit()を呼び出し、共通パラメータを初期化する
- 総エポック数(epochs)を設定し、現在のエポックカウンタ(epochNow)をリセットする
- 座標数(coords)に応じた重心配列(centerMass)のメモリを確保する
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBBC::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Initialize the base class if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Allocate memory for arrays ArrayResize (centerMass, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
BBBCアルゴリズムのMovingメソッドは、主に3つの部分から構成されます。
1. 初期化(revision = falseの場合)
- ランダムな点群(集団)を初期生成する
- 各点を離散的な探索グリッド上に写像する
2. ビッグクランチ(epochがbigBangPeriodの倍数でない場合)
- 次の式を使って重心を計算する:xc = (Σ(1/fi)*xi) / (Σ(1/fi))
- 次の式を使って、重心の周囲に新しい点を生成する:xnew = xc + r * xmax / epoch
- 乱数には正規分布を使用する
3. ビッグバン段階(epochがbigBangPeriodの倍数の場合)
- 正規分布に基づき新しい点群を生成する
- 平均値として、現在までに得られた最良解を使用する
- 広範な探索をおこなうため、標準偏差は8に設定する
生成されたすべての点は、指定された探索範囲内に制限され、離散的な探索グリッド上に再写像されます。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Starting initialization (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate random starting dots a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Reduction to discrete search grid a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Big Crunch phase - big collapse if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { double numerator = 0; double denominator = 0; for (int i = 0; i < popSize; i++) { // Calculate weight as the inverse of the fitness function value double fitness = MathMax (MathAbs (a [i].f), 1e-10); double weight = 1.0 / fitness; // Summation to calculate the center of mass using the equation // xc = (Σ(1/fi)xi) / (Σ(1/fi)) numerator += weight * a [i].c [c]; denominator += weight; } // Determine the coordinates of the center of mass centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c]; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Generate a new point using the equation // xnew = xc + r*xmax/k double newPoint = centerMass [c] + r * rangeMax [c] / epochNow; // Constrain within the allowed area and convert to grid a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- // Big Bang phase - big bang else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Revisionメソッドは主に2つの機能を実行します。
最良解の探索- 最良解のインデックスを初期化する(bestInd = -1)
- 集団内のすべての点を走査する
- 現在の最良解よりも良い解が見つかった場合
- 最良の適応度値(fB)を更新する
- 最良解のインデックス(bestInd)を保存する
- より良い解が見つかった場合(bestInd != -1)
- 対応する個体のすべての座標値を、最良解配列cBにコピーする
- 対応する個体のすべての座標値を、最良解配列cBにコピーする
このメソッドは、アルゴリズム全体の実行期間にわたって、大域的最良解に関する情報を更新、維持する役割を果たします。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Revision () { int bestInd = -1; // Find the best solution in the current population for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestInd = i; } } // Update the best known solution if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
BBBCアルゴリズムの提案者らは、本手法が遺伝的アルゴリズム(GA)のようなよく知られた強力なアルゴリズムと競合可能であり、しかもはるかに少ないエポック数でそれらを上回る性能を示すと主張しています。
その根拠として、彼らは標準的かつ広く使用されている合成ベンチマーク関数に対するテスト結果を示しています。代表的なものとして、Sphere(別名:ParaboloidまたはEllipsoid)関数、Ackley関数、およびRastrigin関数が挙げられます。ここでは、これらのうち2つのベンチマークに対するアルゴリズムの性能を可視化した例を見てみましょう。
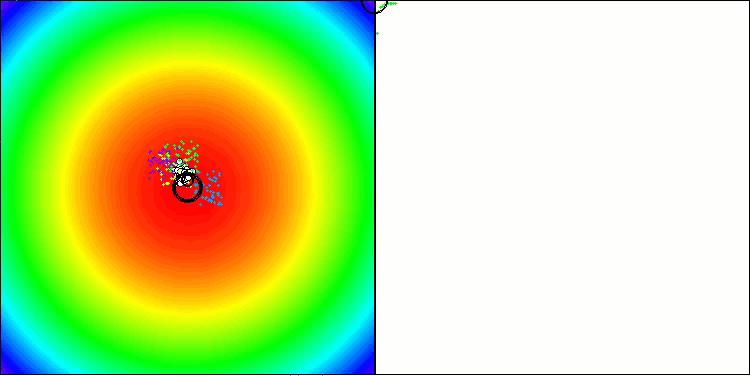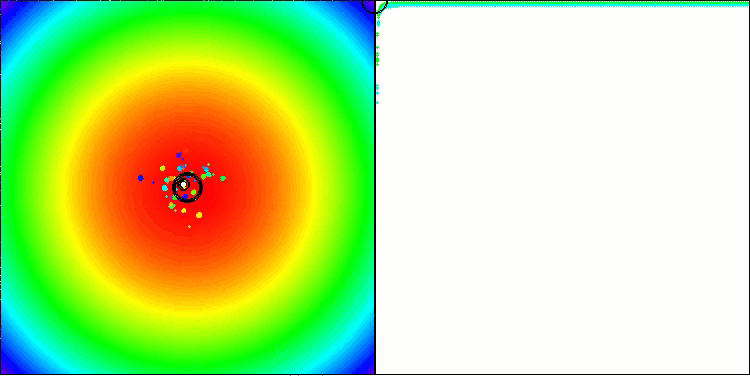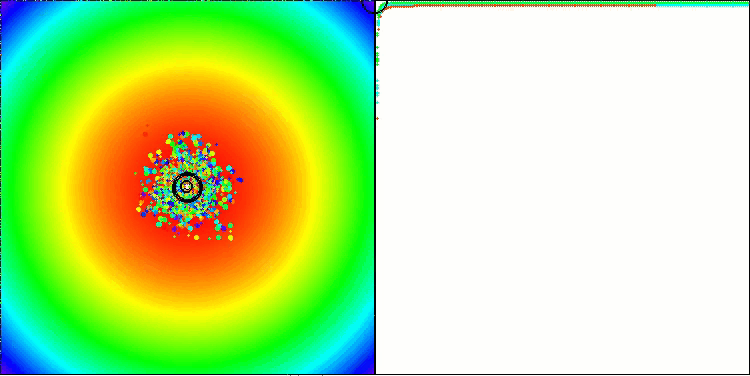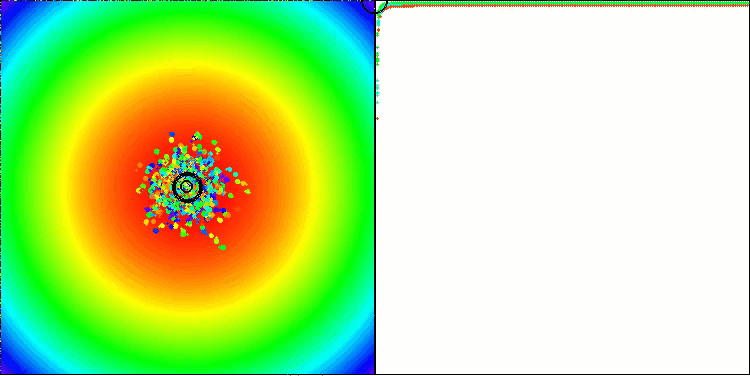
Paraboloidテスト関数でのBBBC
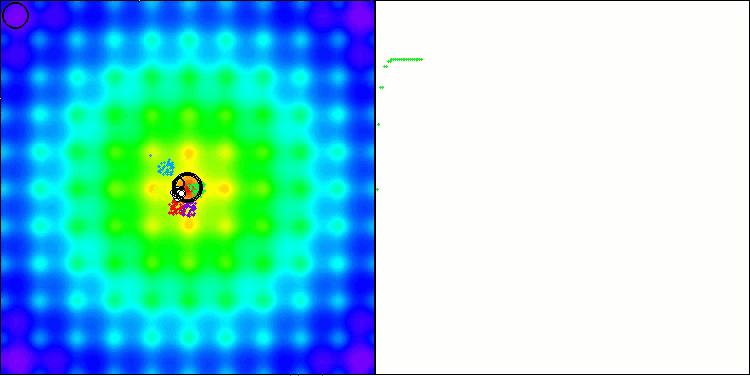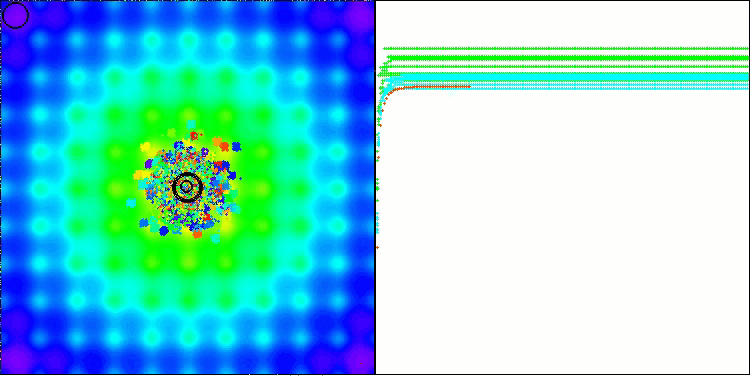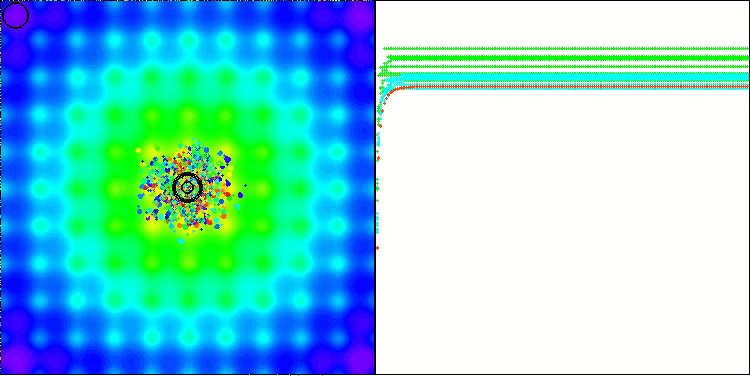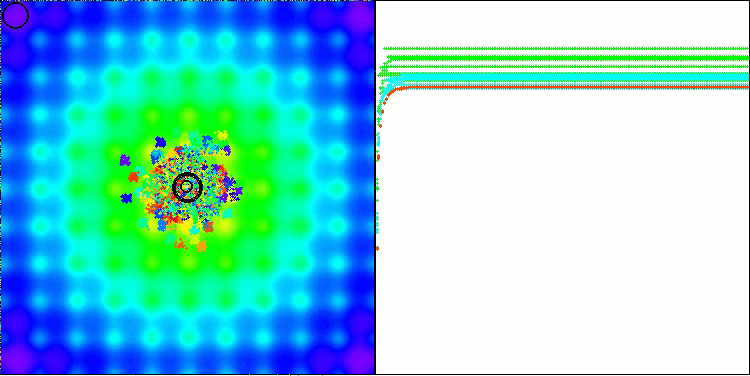
Ackleyテスト関数でのBBBC
実際に、これらの結果は非常に印象的です。特に注目すべきは、高次元問題(赤線)の結果が低次元問題(緑線)と大きく異ならない点であり、これはアルゴリズムの高いスケーラビリティを示しています。Ackley関数における収束精度は完全ではないものの、それでも結果は十分に注目に値します。
続いて、最適化アルゴリズムの性能評価のために特別に設計した独自のテスト関数におけるBBBCの結果を見ていきます。
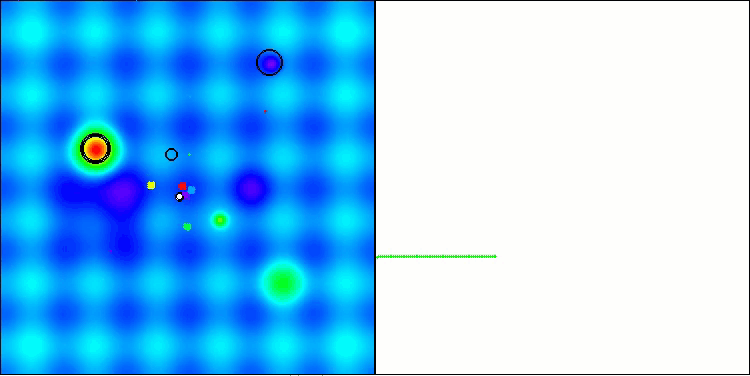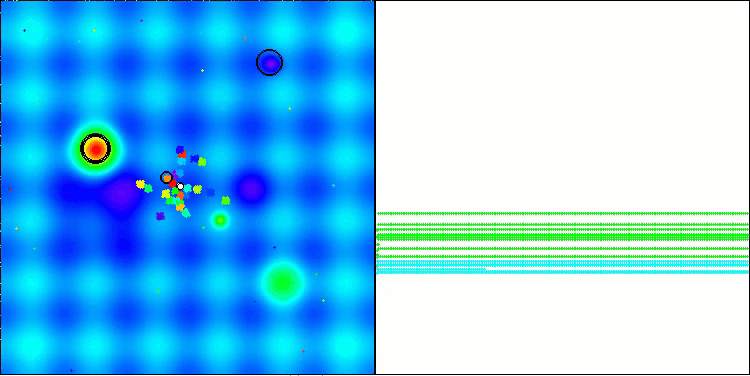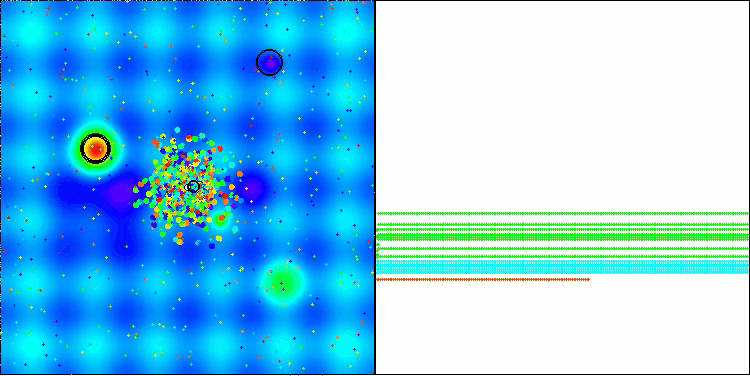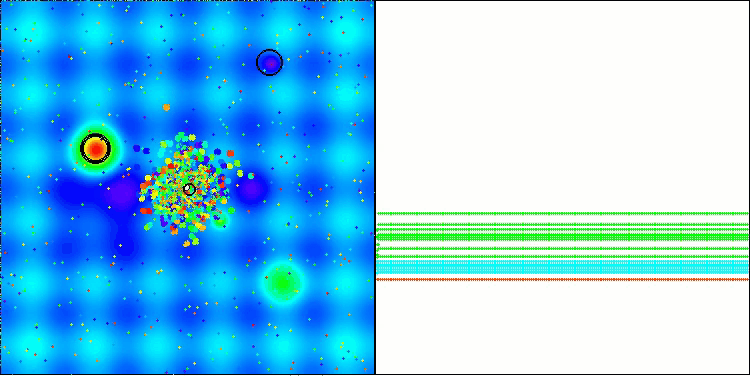
Hillyテスト関数でのBBBC
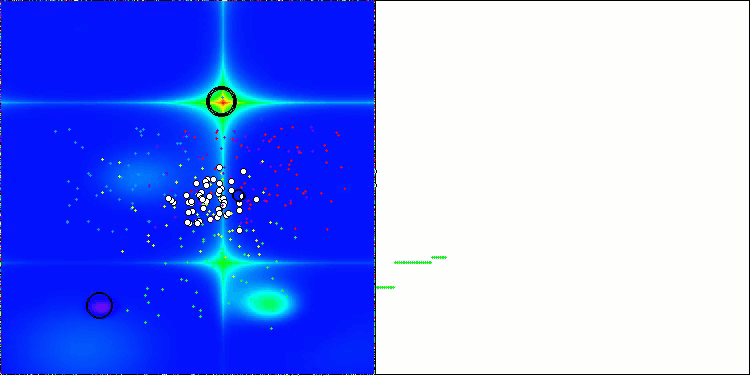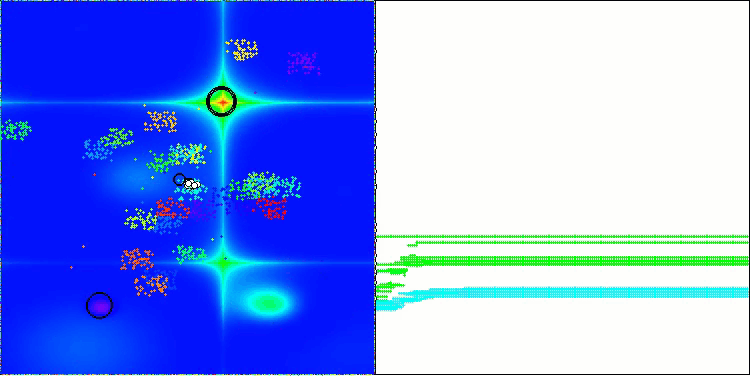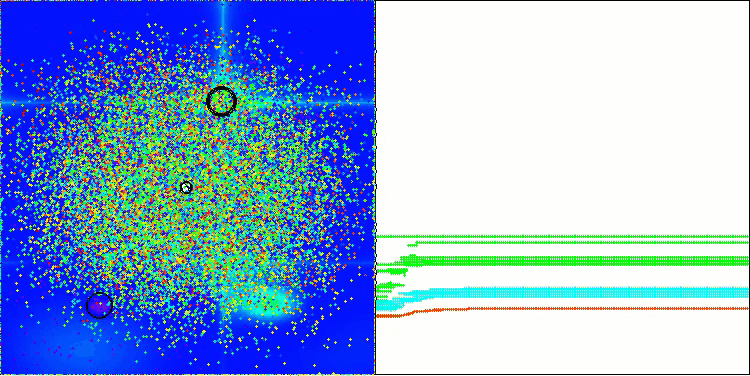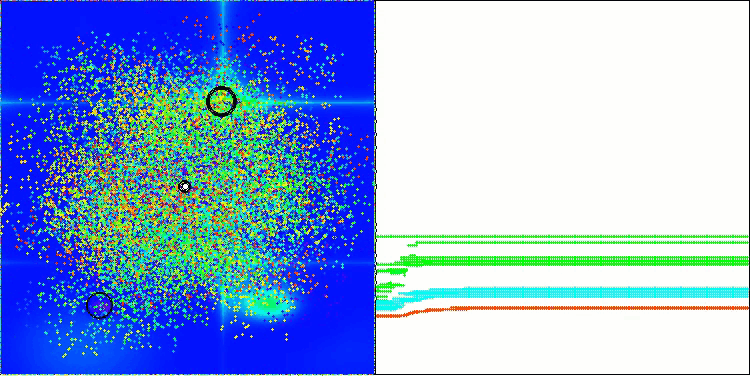
Forestテスト関数でのBBBC
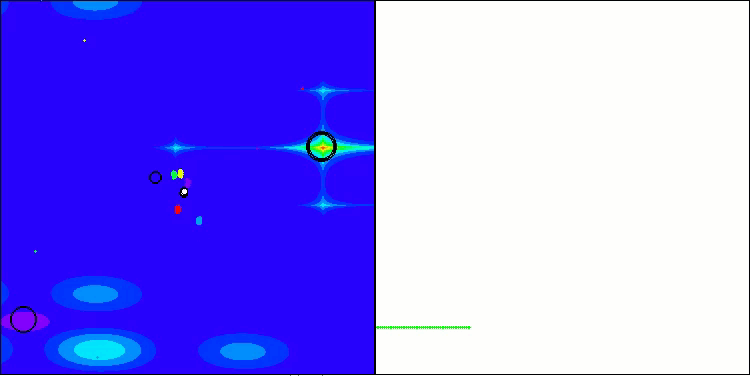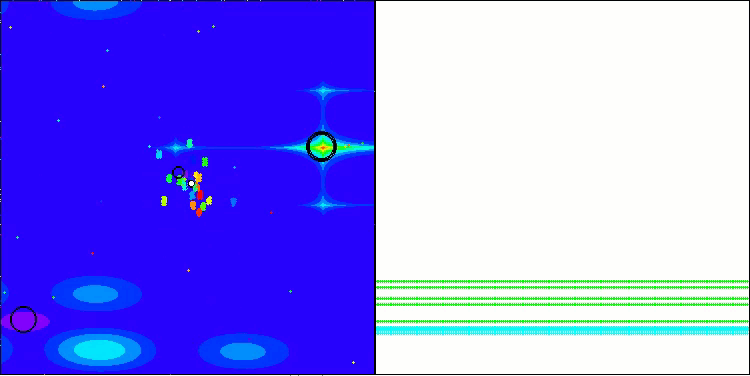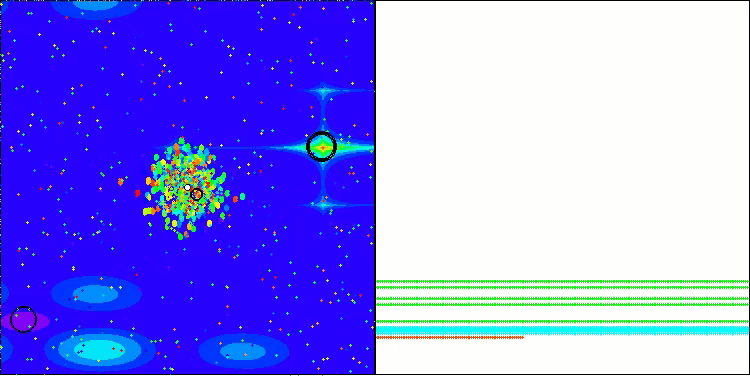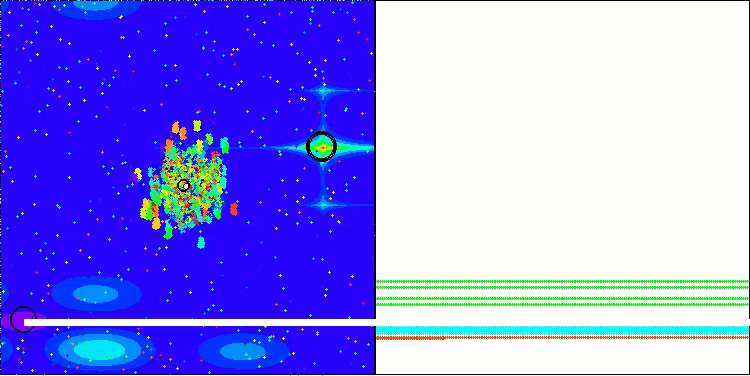
Megacityテスト関数でのBBBC
残念ながら、これらのベンチマークではアルゴリズムの「魔法」は通用しませんでした。その原因は何でしょうか。まず注目すべきは、前述のテスト関数と同様に、BBBCアルゴリズムの集団が探索空間の中央部分に「注意」を集中させる傾向がある点です。これはHilly、Forest、Megacityの各テストにおいても共通して観察され、この挙動はやや奇妙であり、いくつかの疑問を投げかけます。
次に、BBBCアルゴリズムの「内部構造」に目を向けてみましょう。このアルゴリズムでは、「重心」の概念を用いているため、空間内に分布した点が関数の定義域の中央付近に収束する傾向を持ちます。これは、点群の重心がちょうど中央に位置するためであり、結果としてアルゴリズムが効果的に動作しているような錯覚を生み出します。この偶然の一致によって、BBBCは探索範囲の中心に大域最適解を持つ球状関数に対しては良好な結果を得ることができます。しかし実際には、これはアルゴリズムの優れた探索能力の成果ではなく、単なる幸運の一致にすぎません。たとえば、アルゴリズムの初期点が座標0.0であった場合、最初の反復で理想的に大域最適解に到達してしまう可能性があります。
ここで注目すべきは、さまざまなアルゴリズムの評価に広く用いられている標準的なテスト関数の多くが、探索空間の中央に大域最適解を持っているという点です。このようなテストは、必ずしも信頼できるとは限らず、BBBCのようなアルゴリズムに対しては、その実際の探索能力を誤って高く評価してしまうおそれがあります。
誤検出を防ぐため、次の特性を持つ特別なテスト関数群を新たに開発しました。
- 対称的ではない
- 大域最適解が探索空間の中心に存在しない
- 周期性を持たない
- 関数表面のうち、中間高さより上の領域の割合が小さい
最後に、これらのテスト関数に対するBBBCの結果を、以下の表にまとめて示します。これは非常に重要です。
| 2エポックごとにビッグバンを実行 | 3エポックごとにビッグバンを実行 | 10エポックごとにビッグバンを実行 |
|---|---|---|
| BBBC|Big Bang - Big Crunch Algorithm|50.0|2.0| ============================= 5 Hilly's; Func runs:10000; result:0.5789409521562645 25 Hilly's; Func runs:10000; result:0.36005433010965165 500 Hilly's; Func runs:10000; result:0.25650127842145554 ============================= 5 Forest's; Func runs:10000; result:0.5232991213500953 25 Forest's; Func runs:10000; result:0.293874681679014 500 Forest's; Func runs:10000; result:0.18830469994313143 ============================= 5 Megacity's; Func runs:10000; result:0.3269230769230769 25 Megacity's; Func runs:10000; result:0.15584615384615388 500 Megacity's; Func runs:10000; result:0.09743846153846236 ============================= All score:2.78118 (30.90%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|3.0| ============================= 5 Hilly's; Func runs:10000; result:0.5550785088841808 25 Hilly's; Func runs:10000; result:0.3605042956384694 500 Hilly's; Func runs:10000; result:0.25635343911025843 ============================= 5 Forest's; Func runs:10000; result:0.48703749499939086 25 Forest's; Func runs:10000; result:0.2897958021406425 500 Forest's; Func runs:10000; result:0.1865439156477803 ============================= 5 Megacity's; Func runs:10000; result:0.28307692307692306 25 Megacity's; Func runs:10000; result:0.15692307692307694 500 Megacity's; Func runs:10000; result:0.09701538461538546 ============================= All score:2.67233 (29.69%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|10.0| ============================= 5 Hilly's; Func runs:10000; result:0.4883607839451155 25 Hilly's; Func runs:10000; result:0.3344059754605514 500 Hilly's; Func runs:10000; result:0.25564528470980497 ============================= 5 Forest's; Func runs:10000; result:0.492293124748422 25 Forest's; Func runs:10000; result:0.28653857694657936 500 Forest's; Func runs:10000; result:0.1844110334128521 ============================= 5 Megacity's; Func runs:10000; result:0.3230769230769231 25 Megacity's; Func runs:10000; result:0.15261538461538465 500 Megacity's; Func runs:10000; result:0.09653846153846235 ============================= All score:2.61389 (29.04%) |
テスト結果において、各試行間の差異はごくわずかであり、自然な値の範囲内に収まっていることが確認されます。このことは、採用された戦略の探索能力が極めて限定的であり、本質的にはランダムサーチと大差ないことを示唆しています。この点を踏まえ、ランダムウォーク(RW)アルゴリズムのテスト結果を提示することが適切と考えられます。このアルゴリズムは以前の記事でも言及されましたが、これまでその実行結果は示されていませんでした。ここで、その結果を示す時が来ました。
RWアルゴリズムの結果を提示する目的は、単純な空間内のランダムな点の分散と比較して、さまざまな探索戦略がどの程度効率的であるかを評価することにあります。以下に、テスト関数上で100回(通常は10回)実行した際の平均結果を示します。
RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.48753502068617777
25 Hilly's; Func runs:10000; result:0.3215913699940513
500 Hilly's; Func runs:10000; result:0.2578113480890265
=============================
5 Forest's; Func runs:10000; result:0.3755402348403822
25 Forest's; Func runs:10000; result:0.21943566240362317
500 Forest's; Func runs:10000; result:0.15877419882827945
=============================
5 Megacity's; Func runs:10000; result:0.27969230769230796
25 Megacity's; Func runs:10000; result:0.14916923076923083
500 Megacity's; Func runs:10000; result:0.098473846153847
=============================
All score:2.34802 (26.09%)
これから、RWアルゴリズムのコードを示します。非常にシンプルです。通常どおり、Moving関数が集団内の各個体の座標を更新する役割を担います。各個体について、指定された範囲内でランダムな値を生成し、その後、SeInDiSp関数を用いてステップ変化に合わせて値を調整します。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Moving () { for (int w = 0; w < popSize; w++) { for (int c = 0; c < coords; c++) { a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [w].c [c] = u.SeInDiSp (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Revision関数は、集団内のすべての個体を走査し、最良の適応度値fBを持つ個体を探索します。そのような個体が見つかった場合、その個体の座標値を大域最良解(cB)にコピーします。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
ここでは、元のBBBCアルゴリズムにいくつかの変更を加えます。これにより、探索パラメータの範囲中心に大域最適解が存在する問題における見かけ上の優位性(錯覚的な性能)を排除し、より客観的なテストを可能にします。コードの違いを見てみましょう。変更は主として Movingメソッド に対しておこなわれました。
- 重心の計算を削除
- ビッグバン段階を変更
- 重心(centerMass)の代わりに最良解(cB)を使用
- 次の式を使用:xnew = cB + r*range/epochNow (rangeはrangeMaxとrangeMinの差)
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Starting initialization (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate random starting dots a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Reduction to discrete search grid a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //-------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //Big Crunch phase - big collapse if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { // Calculate the size of the search space for the current coordinate double range = rangeMax [c] - rangeMin [c]; // Generate a random number in the range [-1, 1] double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Generate a new point using the equation // xnew = xc + r*(xmax - xmin)/(k) double newPoint = cB [c] + r * range / epochNow; // Constrain within the allowed area and convert to grid a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } // Big Bang phase - big bang else { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
テスト結果
調整されたBBBCアルゴリズムの結果
BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.6053080737014771
25 Hilly's; Func runs:10000; result:0.45249601882946056
500 Hilly's; Func runs:10000; result:0.31255376970202864
=============================
5 Forest's; Func runs:10000; result:0.5232283922331299
25 Forest's; Func runs:10000; result:0.354256711141388
500 Forest's; Func runs:10000; result:0.20417356281490023
=============================
5 Megacity's; Func runs:10000; result:0.3976923076923077
25 Megacity's; Func runs:10000; result:0.19430769230769235
500 Megacity's; Func runs:10000; result:0.11286153846153954
=============================
All score:3.15688 (35.08%)
これで、テスト結果はBBBCアルゴリズム本来の能力を客観的に反映するものとなりました。可視化の結果を見ると、元のアルゴリズムと同様に「星状」の分布構造が形成されていることが確認できます。しかし今回は、探索が探索空間の中央付近に偏るのではなく、実際に有望な領域内でおこなわれている点が大きく異なります。
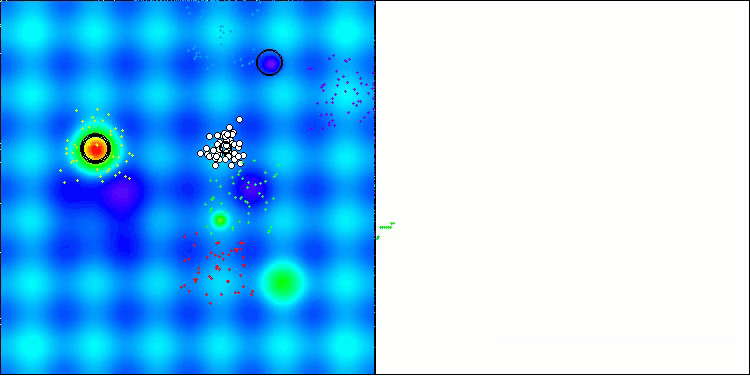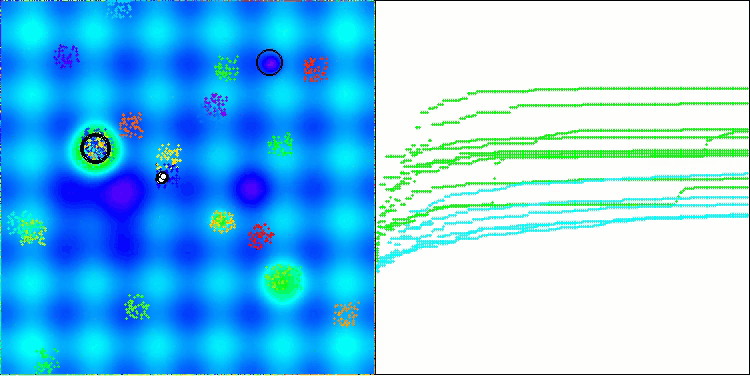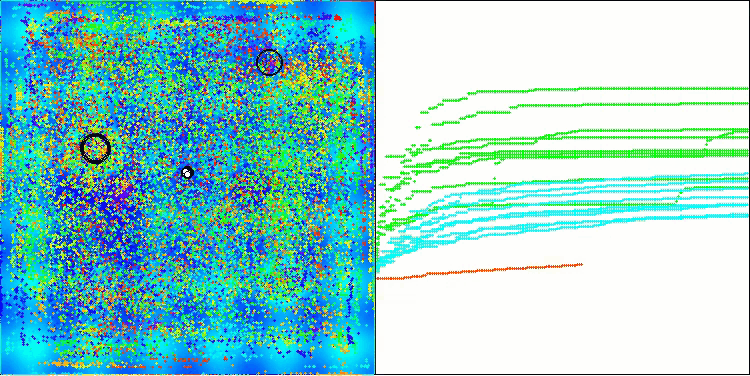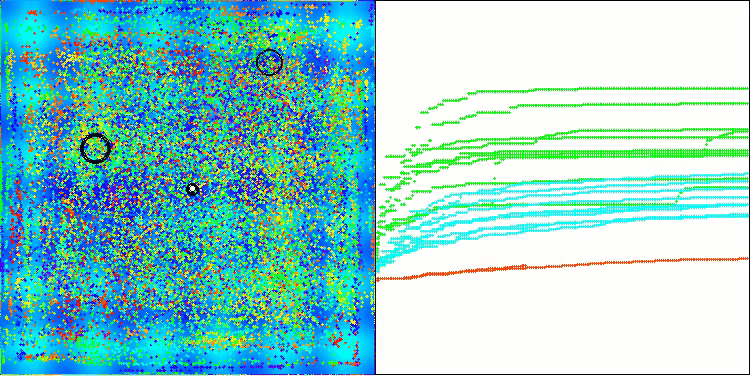
Hillyテスト関数のBHAm
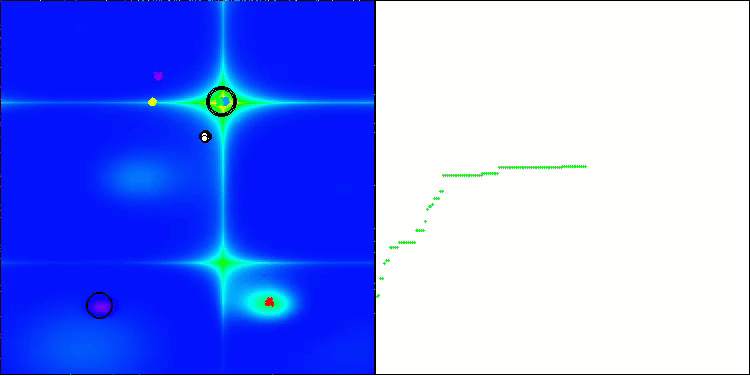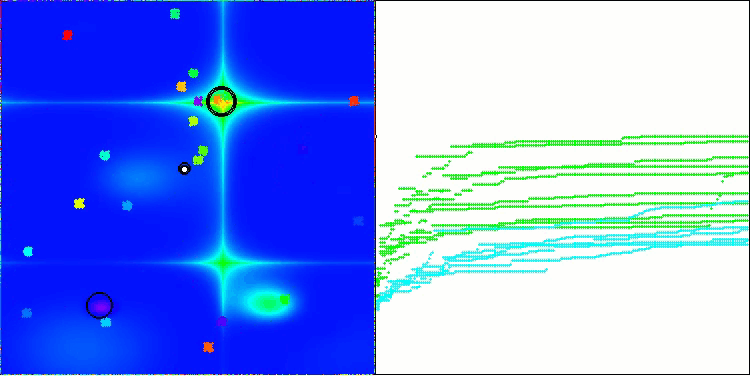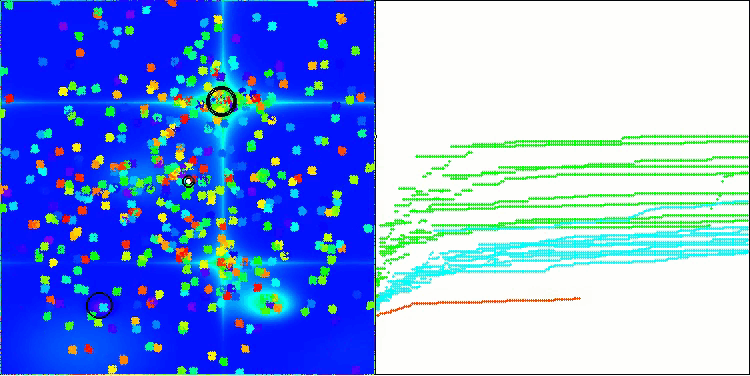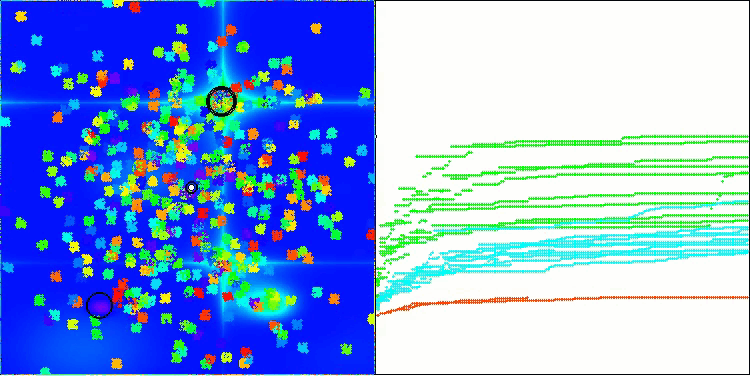
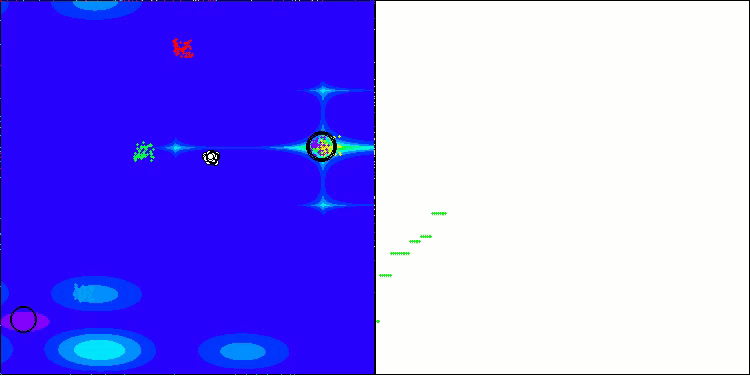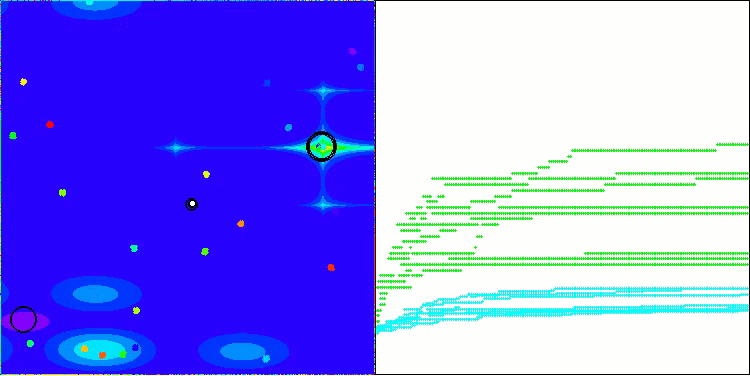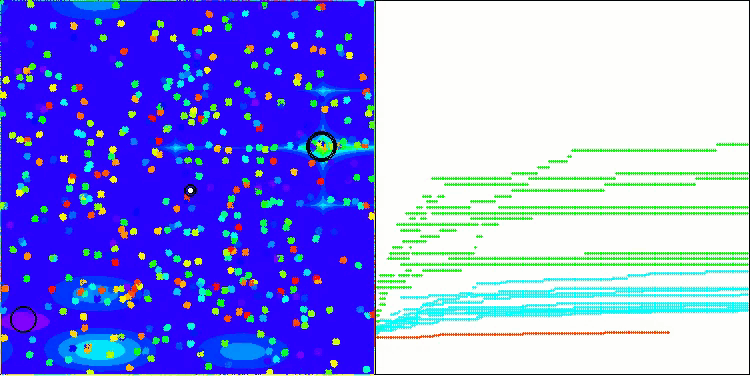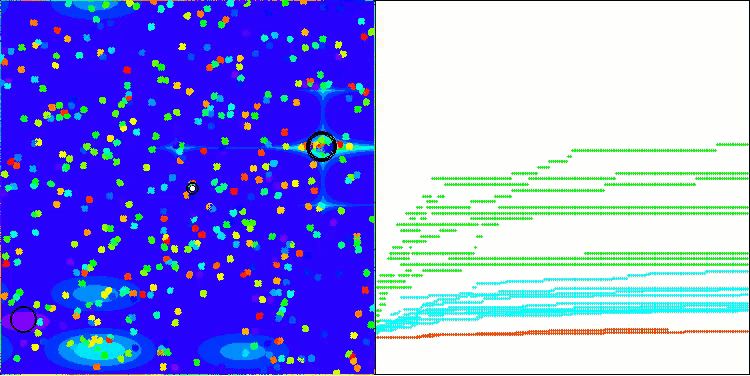
Forestテスト関数のBHAm
Megacityテスト関数のBHAm
改良版BBBCアルゴリズムは、評価表において第43位という結果を示しました。一方、RWは、探索戦略の「有意性」の下限を示す基準として位置付けられています。
| # | AO | 詳細 | Hilly | Hilly最終 | Forest | Forest最終 | Megacity(離散) | Megacity最終 | 最終結果 | MAXの% | ||||||
| 10p(5F) | 50p(25F) | 1000p(500F) | 10p(5F) | 50p(25F) | 1000p(500F) | 10p(5F) | 50p(25F) | 1000p(500F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | コードロックアルゴリズム(joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | 動物移動最適化m | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O)進化戦略 | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | 彗星の尾アルゴリズム(joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | 確率的拡散探索M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | アーチェリーアルゴリズムM | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | 社会集団の進化(joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | 等方的焼きなまし(joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | 人工協調探索 | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | ブラックホールアルゴリズムM | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | 無政府社会最適化 | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 13 | AOSm | 原子軌道探索M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | 亀甲進化アルゴリズム(joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | 差分進化 | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | 化学反応の最適化 | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | 鳥群アルゴリズム | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | ハーモニー検索 | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | 苗木の播種と育成 | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | 細菌走化性最適化M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | アフリカ水牛の最適化 | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO)進化戦略 | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | タブーサーチM | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | ブレインストーム最適化 | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | 鯨最適化アルゴリズムM | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | 人工電界アルゴリズム | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | 人工生態系ベースの最適化アルゴリズム | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | 蟻コロニー最適化M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | 細菌採食の最適化:Ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | シンプル最適化アルゴリズム | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | 人工蜂の巣アルゴリズム | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | 大気雲モデルの最適化 | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | 適応モーメント推定M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | 人工部族アルゴリズムM | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | 人工シャワーアルゴリズム | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | 適応型社会行動最適化(ASBO) | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | 侵入雑草最適化 | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | 微小人工免疫系 | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | カッコウ最適化アルゴリズムM | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | 螺旋ダイナミクス最適化M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | ネルダー=ミード法M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBBC | ビッグバンビッグクランチアルゴリズム | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | FAm | ホタルアルゴリズムM | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 45 | GSA | 重力探索法 | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| RW | ランダムウォーク | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
まとめ
BBBC(ビッグバンビッグクランチ)アルゴリズムは、宇宙論的プロセスに着想を得た大域最適化手法として興味深いアプローチです。しかし、テスト結果からは、その主張される効率性はやや誇張されていることが示されています。特に注目すべき点は、アルゴリズムが探索空間の中央に探索を集中させる傾向があり、これが探索能力が高いかのような錯覚を生むことです。これは、アルゴリズム自体の優れた探索能力を示すものではなく、問題条件とアルゴリズムの特性が偶然に一致した結果に過ぎません。
また、多くの標準的なテスト関数では、探索空間の中央に大域最適解が存在することが一般的です。このようなテストは必ずしも信頼できるものではなく、BBBCのように探索戦略に「ハック的」特徴を持つアルゴリズムの場合、実際の探索能力を誤解させる可能性があります。したがって、広く知られた「常識」や評価結果であっても、慎重かつ批判的に考察する必要があります。
一方で、改良版BBBCアルゴリズムは高次元問題において良好な結果を示しており、将来的な発展の可能性を示しています。これにより、より複雑かつ多様な最適化問題に対する性能向上や、最適解探索の新たな手法の習得といった研究および改良の新たな機会が開かれることになります。
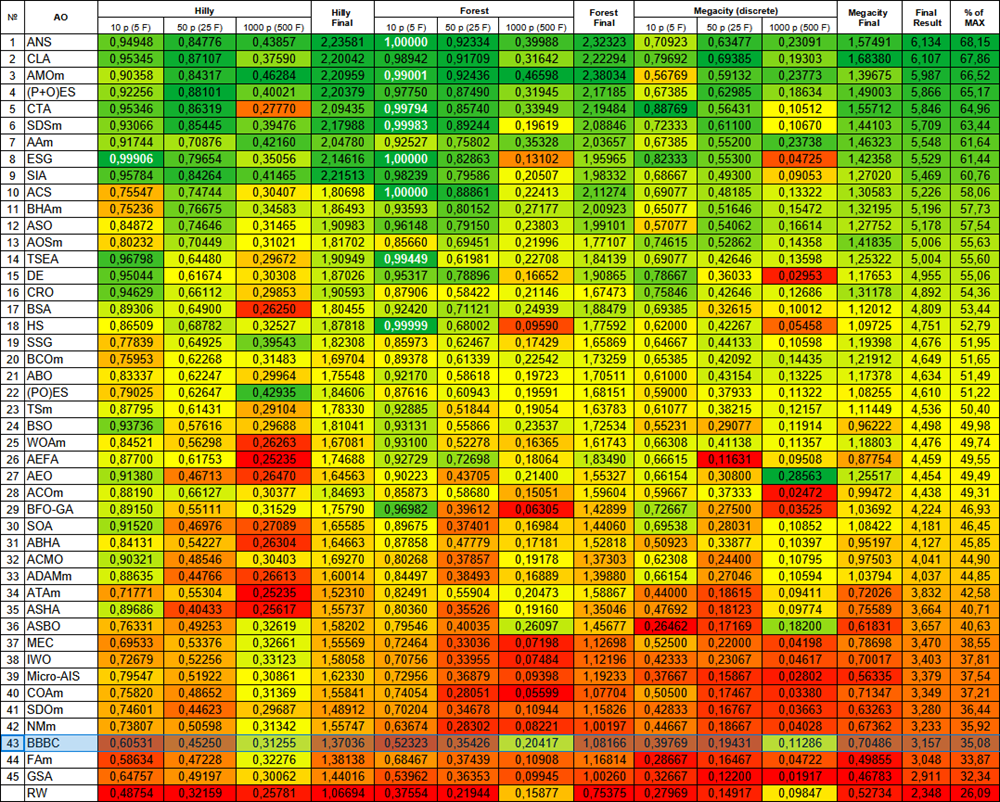
図2:関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている
表中の色のグラデーションは、すべての最適化アルゴリズムが単純なランダムサーチ(RW)よりも効率的であるわけではないことを明確に示しています。これは特に、探索空間の地形の複雑さや次元数が大幅に増加する多次元問題において顕著です。このような場合、多くの従来型探索戦略は効率を失うことがあり、局所極値問題や次元の呪い)、その他の要因による課題に直面します。しかし、これはランダムサーチを主要な手法として推奨することを意味するものではありません。むしろ、ランダムサーチと比較することで、各最適化戦略の限界や性能特性をより正確に理解することが重要です。
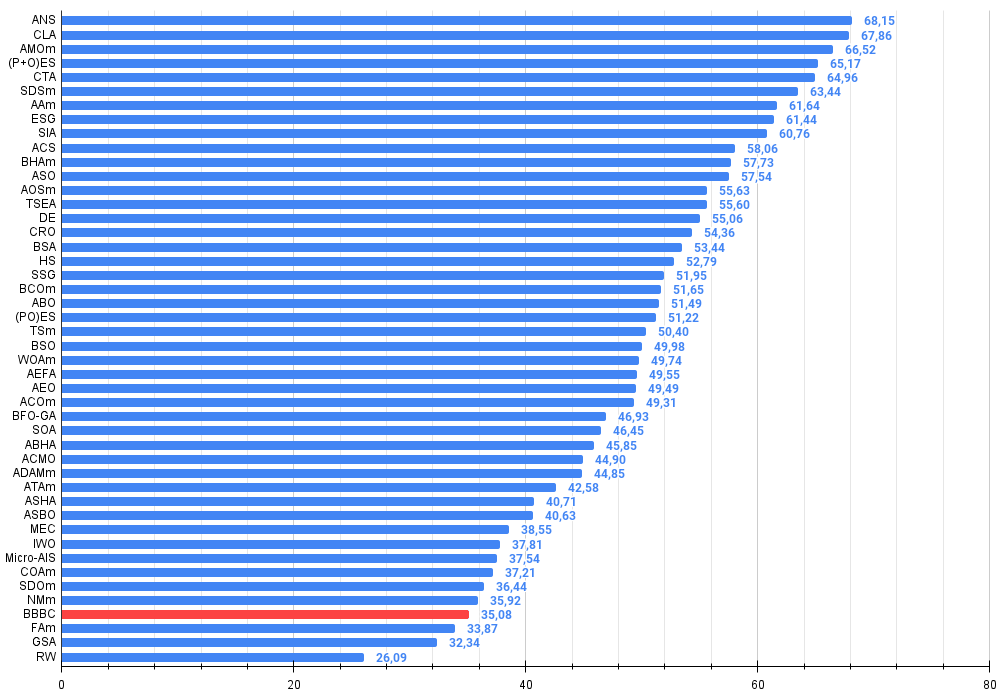
図3:アルゴリズムテスト結果のヒストグラム(0から100のスケール、高いほど良い)100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。
BBBCの長所と短所
長所
- 集団規模が唯一の外部パラメータ
- 実装がシンプル
- EAが非常に高速
- 大規模な問題に適している
短所
- 小次元問題では結果のばらつきが大きい
- 低次元問題では局所解に陥りやすい傾向がある
この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | #C_AO.mqh | インクルード | 集団最適化アルゴリズムの親クラス |
| 2 | #C_AO_enum.mqh | インクルード | 集団最適化アルゴリズムの列挙 |
| 3 | TestFunctions.mqh | インクルード | テスト関数のライブラリ |
| 4 | TestStandFunctions.mqh | インクルード | テストスタンド関数ライブラリ |
| 5 | Utilities.mqh | インクルード | 補助関数のライブラリ |
| 6 | CalculationTestResults.mqh | インクルード | 比較表の結果を計算するスクリプト |
| 7 | Testing AOs.mq5 | スクリプト | すべての集団最適化アルゴリズムの統一テストスタンド |
| 8 | Simple use of population optimization algorithms.mq5 | スクリプト | 可視化せずに集団最適化アルゴリズムを使用する簡単な例 |
| 9 | Test_AO_BBBC.mq5 | スクリプト | BBBCテストスタンド |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16701
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 取引における多項式モデル
取引における多項式モデル
 プライスアクション分析ツールキットの開発(第32回):Python Candlestick Recognitionエンジン(II) - Ta-Libを用いた検出
プライスアクション分析ツールキットの開発(第32回):Python Candlestick Recognitionエンジン(II) - Ta-Libを用いた検出
 取引におけるニューラルネットワーク:ウェーブレット変換とマルチタスクアテンションを用いたモデル
取引におけるニューラルネットワーク:ウェーブレット変換とマルチタスクアテンションを用いたモデル
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
