母集団最適化アルゴリズム：進化戦略、(μ,λ)-ESと(μ+λ)-ES

MetaTrader 5 — 例 | 13 5月 2024, 17:31

Andrey Dik

内容

1.はじめに
2.アルゴリズム
3.テスト関数の交換
4.テスト結果
5.終わりに

1.はじめに

進化戦略アルゴリズムは、自然界で観察された原理に基づく最適化手法です。これは自然淘汰をシミュレートしたもので、最良の解が生き残り、その特徴を次の世代に伝えます。これらのアルゴリズムは、特に機械学習や人工知能の分野で、最適化問題を解くのに広く使用されています。1960年代にドイツのIngo Rechenberg教授らによって、産業や工学における最適化問題を解決するために開発されました。

進化戦略の基本的な考え方は、解の母集団を作り、自然進化で使われるような突然変異と淘汰の演算子を用いてそれらを改良することです。進化戦略では、解を表すのに実数ベクトルを使用します。これにより、二値文字列を操作する古典的な遺伝的アルゴリズムとは対照的に、より柔軟かつ正確に解空間を記述し、最適値を探索することができます。

進化戦略にはいくつかの種類があり、母集団の生成方法や処理方法、使用する突然変異や選択の演算子などが異なります。最も一般的なオプションには以下のようなものがあります。

(1+1)-ES：このバリエーションでは、それぞれの親に対して子が1つだけ作られ、2つのうち最良の解が次の世代の親となります。このシンプルで高速な方法は、ある種の問題には効率的ですが、複雑な問題を最適化する場合にはあまり効果がありません。(1+1)-ESアルゴリズムは1960年代に考案されたもので、進化戦略による最適化のための最も単純な手法の1つです。無作為なベクトルを生成し、それを無作為なステップに変更します。修正されたベクトルがより良いものであれば、それは元のベクトルを置き換えますが、そうでなければ元のベクトルは変更されません。このプロセスを最適になるまで繰り返します。

(μ,λ)-ES：このアルゴリズムでは、λ個の子を産むμサイズの親の母集団が作られ、最良の子が親を置き換えます。様々な最適化問題に対して効率的です。(μ,λ)-ESアルゴリズムは、1965年にReinhard Speigelmannによって作成されました。子を評価した後、最良のμ個の解だけが保持され、次の世代の親となります。したがって、親は各エポックで完全に子に置き換えられます。

(μ＋λ）-ES：このオプションでは、λの子孫が作成されます。優秀な子は、親とともに次世代の創造に参加します。この方法では、親と子が互いに競い合うことになり、これが(μ,λ)-ESとの重要な違いです。(μ+λ)-ESアルゴリズムは、1970年代にJohannes ReichenbacherとHans-Paul Schwefelによって考案された、進化戦略による最適化手法です。この方法は、解空間をより完全に探索することができ、複雑な問題をより効率的に解くことができます。

進化戦略には他のバリエーションもありますが、本稿では(μ,λ)-ESと(μ+λ)-ESのみを検討します。(1+1)-ESオプションは単純で、多次元問題を解くには適していません。コード中のファイル名や変数名にギリシャ語のアルファベットや特殊文字を使用するのは難しいため、ここではそれぞれPOとP_Oとします。Pは親、Oは子（子孫）を意味します。

コンピュータサイエンスにおける進化戦略は、複雑な最適化問題を解くために進化と自然淘汰をモデル化することを可能にします。自然淘汰に似た原理で、パラメータ空間の最適解を探索するのです。

これらのアルゴリズムは、明らかな解析解がない問題や、探索空間が非常に大きい問題で特に有用です。交配、突然変異、選択といった進化にヒントを得た操作を使用して、最適解を効率的に探索することができます。

「進化戦略」という名前は誤解を招くかもしれません。研究者は、進化的アルゴリズムのクラスの一般的な名前だと思うかもしれません。しかし、これはそうではありません。実際には、進化戦略は、最適化問題を解決するために進化のアイデアを使用するアルゴリズムの特定のグループです。

2.アルゴリズム

(μ,λ)-ESは、アルゴリズムの各反復において、μ個の親が選択され、λ個の子が生成されることを意味します。そして、λ個の子から最良のμ個が選ばれ、次の反復の親となります。このように、(μ,λ)-ESでは、新しい子孫は親に完全に取って代わり、次世代の創造に参加します。

(μ+λ)-ESも同様の働きをしますが、λから最良の子孫を選ぶのではなく、それらを親と組み合わせてμ+λの大きさの新しい集団を形成します。そして、この結合された個体群から最良のμ個体が選択され、次の反復の親となります。したがって、(μ+λ)-ESでは、新しい子孫は親と協力して次の集団を形成し、互いに競争します。

(μ,λ)-ESと(μ+λ)-ESの主な違いは、新しい子供が次の集団に入るために親とどのように競争するかです。(μ,λ)-ESでは、新しい子供は限られた数の場所を親と争うため、局所最適への収束が早まる可能性があります。(μ+λ)-ESでは、新しい子供は親と一緒に行動し、その結果、解空間をより広く探索することになります。

どちらの進化戦略アルゴリズムも、突然変異と選択という遺伝的演算子の組み合わせに基づいています。アルゴリズムの各反復で、現在の個体群から個体が選択され、突然変異演算子が適用されます。その後、得られた個体の適合度が計算され、最も適合した個体が次の個体群に配置されます。初期母集団を生成するために、変化させたパラメータのベクトルの各成分に区間が指定され、各成分の初期値は指定された区間に一様に分布すると仮定されます。アルゴリズムは、指定された世代数、指定された集団状態、または指定された収束レベルに達するなど、さまざまな停止条件を使用できます。(μ+λ)アルゴリズムの場合はすべての個体が母集団に含まれ、(μ,λ)アルゴリズムの場合は子孫のみが含まれます。(μ+λ)アルゴリズムについては、確率的に収束が証明されていますが、(μ,λ)アルゴリズムについては、収束の問題は未解決のままです。

(μ+λ)アルゴリズムと(μ,λ)アルゴリズムを比較すると、(μ+λ)アルゴリズムの方が、高度に適応した個体をより節約して使用し、子孫との競争に任せることができます。探索の強度は高まりますが、局所的極値への収束を早める可能性があります。正規進化戦略アルゴリズムにおける突然変異演算子は唯一の進化演算子であり、ガウス突然変異アルゴリズムを使用します。

古典的な(μ,λ)-ESアルゴリズムは以下の擬似コードで記述できます。

1.初期集団を無作為な個体で初期化します。
2.停止基準に達するまで次を繰り返します。
2.1.μ個の親のそれぞれは、突然変異演算子を用いて現在の集団にλ個の子孫を生成します。
2.2.次の母集団を形成するために、最良のμ個の子孫を選択します。
3.最後の集団から最良の個体を返します。

従来の(μ+λ)-ESアルゴリズムは、以下の擬似コードで記述できます。

1.初期集団を無作為な個体で初期化します。
2.停止基準に達するまで次を繰り返します。
2.1.μ個の親のそれぞれは、突然変異演算子を用いて現在の集団にλ個の子孫を生成します。
2.2.親と子を組み合わせて、μ+λの大きさの複合集団を得ます。
2.3.結合された個体群から最良のμ個体を選び、次の個体群を形成します。
3.最後の集団から最良の個体を返します。

2つの主要な「進化戦略」アルゴリズムの古典的なバージョンを見てみました。どちらの場合も、親は自分の遺伝情報だけを使用してλの子孫を残します。その結果、星型の枝分かれが生じ、それぞれの子孫は他の子孫から独立して成長します。また、親間の情報交換もないため、遺伝的性質を組み合わせる可能性は排除されます。その結果、組み合わせの特質はまったくありません。

テストの結果、これらのESオプションはいずれも効率が低いことがわかりました。それを増やすために組換えを試みました。

組換えは、異なる個体の遺伝物質を組み合わせて、より優れた性質や形質を持つ可能性のある新しい組み合わせを作り出すことを可能にします。このプロセスは、母集団の多様性を促進します。

組換え（または交配）とは、両親の遺伝物質を組み合わせて子孫を作ることです。このプロセスは、生物進化における自然交配をシミュレートしています。組換えでは、両親の遺伝子が組み合わされて、子孫のための新しい遺伝物質が作られます。組換えは通常、遺伝子や遺伝形質のレベルで起こります。遺伝子は、生物の特定の特性や特徴をコードする、ゲノム中の情報の断片です。

組換え後、子孫の遺伝子は突然変異演算子を使用して変更され、遺伝子に無作為な変化を与えます。これにより、新しい研究バリエーションが集団に導入され、遺伝物質の多様性が促進されます。

したがって、各子孫の遺伝子には無作為に選択した親の遺伝子を使用します。ここで、遺伝子は親の対応する座標です。子孫は集団内のすべての親の特徴を受け継ぐことになります。

(μ,λ)-ESアルゴリズム

コードの確認に移ります。より単純なアルゴリズム（μ,λ）-ESに組換え（複数の親からの遺伝子の継承）を加えたものから始めましょう。

親子がエージェントとして行動する場合、良い構造体はS_Agentで、座標cと変数f（適合度値）の配列を含みます。Init関数は、配列cのサイズを変更し、fの値を「-DBL_MAX」（可能な限り最悪の適合度値）に設定することによってエージェントを初期化します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

(μ,λ)-ESアルゴリズムを記述するC_AO_POESクラスを宣言します。

このクラスには以下の要素が含まれます。

cB、fB、a、rangeMax、rangeMin、rangeStep 各public変数：それぞれ最良の座標、対応する適合度関数値、エージェント、探索の最大値と最小値、探索ステップを格納するために使用されます。
Public Init()：この関数は最適化アルゴリズムを初期化します。座標の数、母集団のサイズ、親エージェントの数、突然変異の強さ、シグマ値など、いくつかの引数を取ります。関数内部では、アルゴリズムで使用される変数と配列が初期化されます。
Moving()とRevision() public関数：それぞれエージェントの移動と個体数の修正をおこなうために使用されます。
cords、popSize、parentsNumb、mutationPower、sigmaM、revision各private変数：それぞれ座標の数、母集団のサイズ、親エージェントの数、突然変異の強さ、シグマ値、修正フラグを格納するために使用されます。
parents、ind、val、pTemp各private配列：それぞれ親エージェント、インデックス、値、一時変数の情報を格納するために使用されます。
GaussDistribution()、SeInDiSp()、RNDfromCI()、Scale()、Sorting()各private関数：乱数生成、値のスケーリング、配列の並び替えを実行するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_POES
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,          //coordinates number
                     const int    popSizeP,         //population size
                     const int    parentsP,         //number of parents, < Population size
                     const double mutationPowerP,   //mutation power
                     const double sigmaP);          //sigma

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    parentsNumb;   //number of parents
  private: double mutationPower; //mutation power
  private: double sigmaM;
  private: bool   revision;

  private: S_Agent parents [];  //parents
  private: int     ind     [];
  private: double  val     [];
  private: S_Agent pTemp   [];

  private: double GaussDistribution   (const double In, const double outMin, const double outMax, const double sigma);
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: void   Sorting   (S_Agent &p [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

最適化アルゴリズムを初期化するには、C_AO_POESクラスのInit関数を使用します。この関数は、座標の数、母集団の大きさ、親エージェントの数、突然変異の強さ、シグマ値などの引数を取ります。

関数内部では、アルゴリズムで使用される変数と配列が初期化されます。この関数は以下のことをおこないます。

乱数発生器をリセットし、fB変数を「-DBL_MAX」に設定します。
coords、popSize、parentsNumb、mutationPower、sigmaM各変数値を設定します。
ArrayResize関数を使用して、ind、val、pTemp、a、parents、rangeMax、rangeMin、rangeStep、cB各配列のサイズを変更します。
a配列とparents配列は S_AgentクラスのInit関数を用いて初期化されます。この関数は、エージェントの座標を初期化し、f変数の値を「-DBL_MAX」に設定します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Init (const int    coordsP,          //coordinates number
                      const int    popSizeP,         //population size
                      const int    parentsP,         //number of parents, < Population size
                      const double mutationPowerP,   //mutation power
                      const double sigmaP)           //sigma
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  parentsNumb   = parentsP;
  mutationPower = mutationPowerP;
  sigmaM        = sigmaP;

  ArrayResize (ind,   popSize);
  ArrayResize (val,   popSize);
  ArrayResize (pTemp, popSize);
  ArrayResize (a,     popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (parents, parentsNumb);
  for (int i = 0; i < parentsNumb; i++) parents [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、探索空間内でエージェントを移動させます。

この関数には、「if (!revision)」条件によって区切られた2つのコードブロックが含まれています。

最初のブロックでは、revision フラグがfalseの場合、各エージェントに対して無作為な座標が生成されます。各座標について、rangeMinからrangeMaxの間の一様分布で乱数が生成され、この数値がSeInDiSp関数を使用して正規化されます。これは、座標値をrangeStepの最も近い倍数に設定します。
2つ目のブロックでは、revisionフラグがtrueの場合にエージェントの移動が発生します。各エージェントに対して、無作為な親エージェントが parents配列から選択されます。そして、各エージェント座標に対して突然変異値distが計算されます。この値は、突然変異の強さ mutationPowerと探索範囲 rangeMinとrangeMaxに依存します。エージェントの座標値は、sigmaMシグマ値を用いて親座標値の周りに正規分布の乱数を生成するGaussDistribution関数を用いて変更されます。その後、SeInDiSp関数を用いて座標値を正規化します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    indx = 0;
  double min  = 0.0;
  double max  = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      indx = (int)RNDfromCI (0, parentsNumb);
      if (indx >= parentsNumb) indx = parentsNumb - 1;

      a [i].c [c] = parents [indx].c [c];

      dist = (rangeMax [c] - rangeMin [c]) * mutationPower;

      min = a [i].c [c] - dist; if (min < rangeMin [c]) min = rangeMin [c];
      max = a [i].c [c] + dist; if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = GaussDistribution (a [i].c [c], min, max, sigmaM);
      a [i].c [c] = SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

母集団の修正は、最適化アルゴリズムにおいてエージェントの現在の状態を修正するために使用されるRevisionメソッドによって実行されます。

この関数には2つのコードブロックがあります。

最初のブロックでは、forループを使用して、a配列から最適なエージェントを探します。現在の最良エージェントfBよりも高い適合度値を持つエージェントが見つかった場合、そのエージェントのインデックスがindx変数に格納されます。現在の最良エージェントのfB値とcB座標は、新しい最良エージェントに従って更新されます。
2番目のブロックでは、a配列を並び替え関数を用いて適合度の降順に並び替えし、a配列から最良のエージェントの parentsNumbをparents配列にコピーします。

したがって、Revision関数は、エージェントの現在の状態を更新し、parents配列に最良のエージェントを保存することができます。そこでは、最良の子達がすべての親に完全に取って代わります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Revision ()
{
  //----------------------------------------------------------------------------
  int indx = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) indx = i;
  }

  if (indx != -1)
  {
    fB = a [indx].f;
    ArrayCopy (cB, a [indx].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  Sorting (a, popSize);
  for (int i = 0; i < parentsNumb; i++)
  {
    parents [i] = a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

(μ+λ)-ESアルゴリズム

変更は、yearsNumberパラメータの形で個人の平均余命を追加することから始まります。これにより、人口の最高年齢をコントロールすることが可能になり、超高齢の個体で人口が「目詰まり」するのを避けることができます。これは、無限の生活空間の新たな地平を探求し、新たな発見をすることを妨げる可能性があります。このアルゴリズムが役に立つことを願っています。

このカウンタはなぜ(μ,λ)-ESアルゴリズムに含まれていないのしょうか。それが意図されたことだからです。親は完全に子孫に取って代わられます。これはまた、動物界における半直列の場合と同様に、一生のうちに一度しか繁殖しない種があることも理にかなっています。そのような種の例としては、サケ科の魚、リュウゼツラン、竹、ヤシガニ、ソテツなどがあります。しかし、私たちのアルゴリズムでは、個体が何度も繁殖したり、無期限に生き続けたり、あるいは誇り高き竹のように死んだりする機会を与えます。寿命は調整可能な外部パラメータであり、テストの一環として、実験的に10年という最適な期間が見出されました。

さらに、ライフカウンタは、母集団が探索空間の他の場所で新しい成功解を見つけるのではなく、特定の解を「記憶」して蓄積し始める過剰適合を避けるのに役立ちます。個体の寿命を制限することで、集団の多様性を維持し、より最適な解決策を探し続けることができます。

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
    yearsNumber = 0;
  }

  double c []; //coordinates
  double f;    //fitness
  int yearsNumber;
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドでは、子の数だけ親集団のサイズを大きくします。これにより、親と子が一緒に並び替えされるようになりますが、(μ,λ)-ESアルゴリズムと同様に、将来的には、新しい子を生成するために共同母集団のμ部分のみが使用されることになります。以前のアルゴリズムでは、親の数は子孫の母集団以下でなければなりませんでしたが、このアルゴリズムではそれは問題ではなく、親の母集団は任意のサイズに設定でき、非常に大きくても構いません。これはエポック数には影響しません。実験的に、親の母集団サイズの150は、100個の子孫の場合の最適値であることが判明しました（エポック数が減少するので、それ以上の値は不可能）。親の母集団をさらに増やすと、遺伝子プールの多様性が大きくなりすぎ、アルゴリズムの収束が悪くなり始めます（このこと自体が興味深い）。

ArrayResize (ind,   popSize + parentsNumb);
ArrayResize (val,   popSize + parentsNumb);
ArrayResize (pTemp, popSize + parentsNumb);
ArrayResize (a,     popSize);
for (int i = 0; i < popSize; i++) a [i].Init (coords);

ArrayResize (parents, popSize + parentsNumb);
for (int i = 0; i < popSize + parentsNumb; i++) parents [i].Init (coords);

Movingメソッドでは、新しい子孫を作成する際に、個体の年カウンタを1に設定します。

a [i].yearsNumber = 1;

この変更はRevisionメソッドにも影響し、このコードでは変更点を考慮して以下のように実行されます。

それぞれの親のyearsNumberの値を1増やします。
yearsNumberの値が指定された限界値（寿命）を超えた場合、対応する親の適合度値fを「-DBL_MAX」に設定します。つまり、その個体を集団から取り除きます。
新しい子をa配列からparents配列にコピーします。
parents配列をf適合度値で並び替えます。

//----------------------------------------------------------------------------
for (int i = 0; i < parentsNumb; i++)
{
  parents [i].yearsNumber++;

  if (parents [i].yearsNumber > lifespan)
  {
    parents [i].f = - DBL_MAX;
  }
}

for (int i = parentsNumb; i < parentsNumb + popSize; i++)
{
  parents [i] = a [i - parentsNumb];
}

Sorting (parents, parentsNumb + popSize);

3.テスト関数の交換

以前は、最適化アルゴリズムを評価するためのテスト関数としてRastrigin関数を使用していました。しかし、Rastrigin関数はそのような目的には完璧な選択ではありません。これは厳密な周期性とバランスのとれた最小値と最大値を持ち、いくつかのアルゴリズムによって比較的簡単に検出することができます。したがって、Rastrigin関数は、関数の極値を決定するアルゴリズムの能力に影響を与える可能性のあるパターンを示します。

最適化アルゴリズムをより確実かつ客観的にテストするためには、多様で予測不可能な特性を持つ関数を使用することが推奨されます。このような関数は通常、最小値と最大値の間に明らかなパターンやバランスを持ちません。このような関数の例としては、ノイズ関数、非線形依存性を持つ関数、多数の局所的極値を持つ関数などがあります。この関数の選択により、様々な条件下でアルゴリズムが大域的最適値を検出し、それに収束する能力をより正確に評価することができます。

従来、すべての関数は「単純」と「複雑」に分けられます。単関数とは、曲面のほとんどがmaxとminの間の中央線より上にある関数のことで、曲面がmaxに近ければ近いほど、最適化がより簡単になります。そのため、関数のドメイン内の全曲面にわたって無作為に点を配置するだけでは、結果は絶対的な全域的最大値に近くなるため、「高い」最適化結果という誤った印象を得ることになります。このような単関数の例として、図1の仮説的な関数の概略図があります。

偽の成功

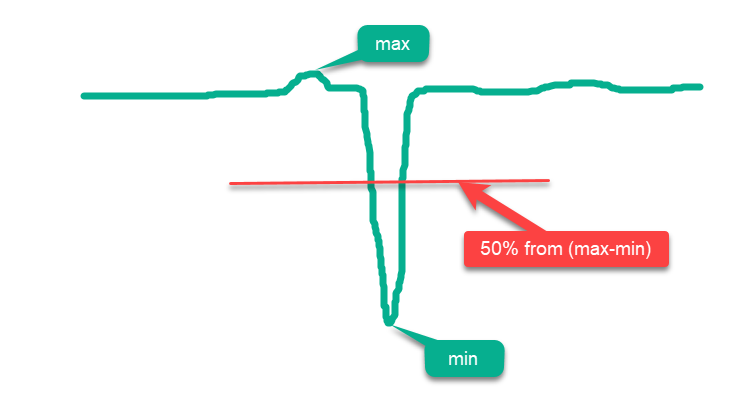
図1：最適化アルゴリズムのための「単純な」関数の例

以上のことから、Rastrigin関数は、最適化アルゴリズムによっては結果が膨れ上がる可能性のある単関数に分類されます。これは、これらのアルゴリズムの探索戦略の特殊性によるもので、エージェントを関数曲面全体に分散して配置することができます。

この影響は、例えば1000のような多数の変数を持つRastrigin関数で特に顕著です。アルゴリズムによっては正直に全域的極値を見つけようとするものもありますが、単に関数の曲面全体にエージェントを均等に配置するものもあります。このアプローチは、最適化アルゴリズムが正確な探索をおこなう能力を示すものではなく、それができるかのように錯覚させるだけです。

Rastrigin関数は、最適化アルゴリズムにとってより複雑で困難な環境を作り出すために、大幅に修正されました。新バージョンの関数は、いくつかの「丘」と「谷」を追加していますが、全域的極値を見つけるのに役立たない曲面の部分には周期性を維持しています。このような変化は新たな障害となり、エージェントの注意をそらし、罠として機能します。

従来のRastriginのように、周期性を持つステップをジャンプして全域的極値に到達することはできません。加えて、大域的最適値はエッジから遠ざかり、関数定義の境界を重視することが多いアルゴリズムでは、アーチファクトを見つけることが難しくなっています。

新関数はHillyと呼ばれます（図2）。ForestやMegacityと同様、複雑なテスト関数を指します。これら3つの関数では、最大高さの50%より上にある曲面はほぼ同じで、関数の総面積の約20%を占めます。

Hilly、Forest、Megacityの各関数は、複雑で変化に富んだ条件下でアルゴリズムの性能を評価するのに役立つ、複雑で現実的な最適化シナリオを提供します。これらの関数を最適化アルゴリズムの包括的なテストとして使用することで、大域的な最適値を見つけ、局所的な落とし穴を克服する能力について、より深い洞察を得ることができます。

さらに、テスト方法にも変更が加えられました。現在では、結果の無作為な「スパイク」を減らすために、5回（最適化プロセスの繰り返し実行回数）の代わりに10回のテストを実施しています。

Hilly2

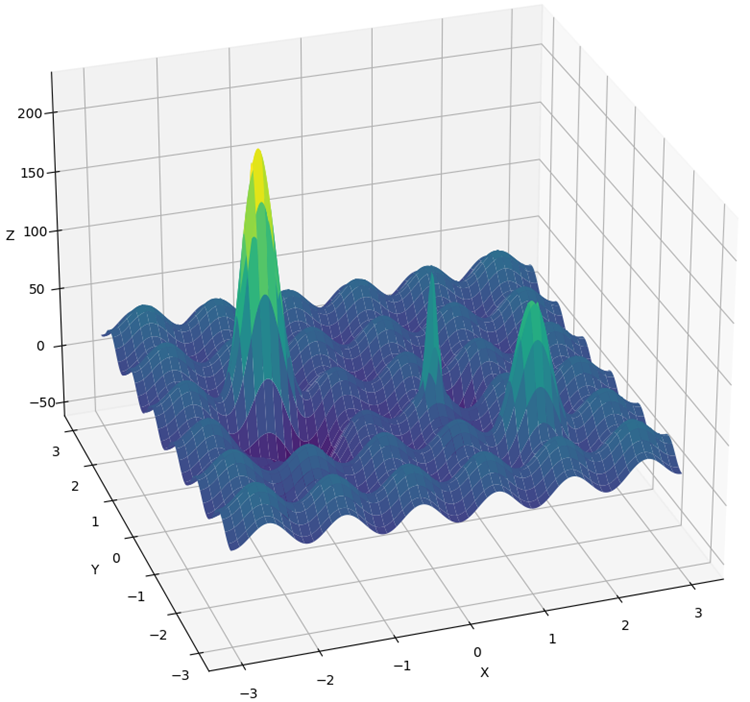
図2：Hillyテスト関数

4.テスト結果

(μ,λ)-ESアルゴリズムのテストスタンドの結果

C_AO_(PO)ES:100:10:0.025:8.0
=============================
5 Hilly's; Func runs:10000; result:0.7902459324049909
25 Hilly's; Func runs:10000; result:0.6264667539839893
500 Hilly's; Func runs:10000; result:0.42934981087827656
=============================
5 Forest's; Func runs:10000; result:0.8761631782479373
25 Forest's; Func runs:10000; result:0.6094343681829253
500 Forest's; Func runs:10000; result:0.19591138782930953
=============================
5 Megacity's; Func runs:10000; result:0.5900000000000001
25 Megacity's; Func runs:10000; result:0.37933333333333336
500 Megacity's; Func runs:10000; result:0.11321666666666666
=============================
All score:4.61012

(μ+λ)-ESアルゴリズムのテストスタンドの結果

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
5 Hilly's; Func runs:10000; result:0.9993447297882565
25 Hilly's; Func runs:10000; result:0.9189524317647721
500 Hilly's; Func runs:10000; result:0.562968579605404
=============================
5 Forest's; Func runs:10000; result:1.0
25 Forest's; Func runs:10000; result:0.9352215748931851
500 Forest's; Func runs:10000; result:0.3917923122543615
=============================
5 Megacity's; Func runs:10000; result:0.8316666666666664
25 Megacity's; Func runs:10000; result:0.6443333333333332
500 Megacity's; Func runs:10000; result:0.21155000000000007
=============================
All score:6.49583

以下の視覚化は(μ+λ)-ESアルゴリズムのもので、潜在的に有望な領域を省くことなく、探索空間の優れた探索を示しています。

Hilly

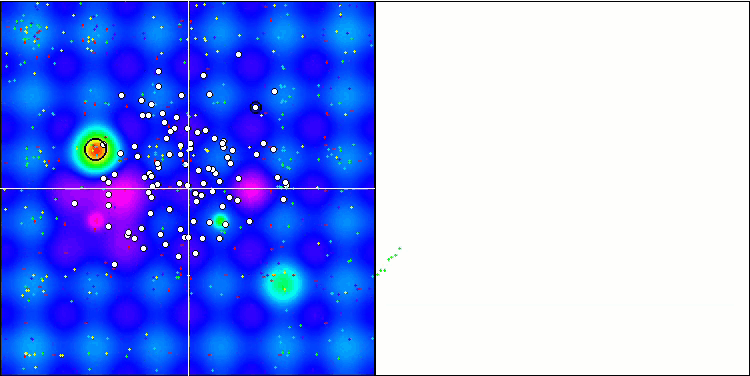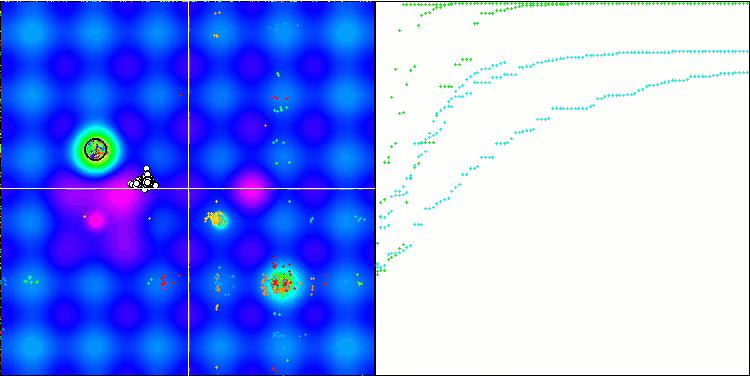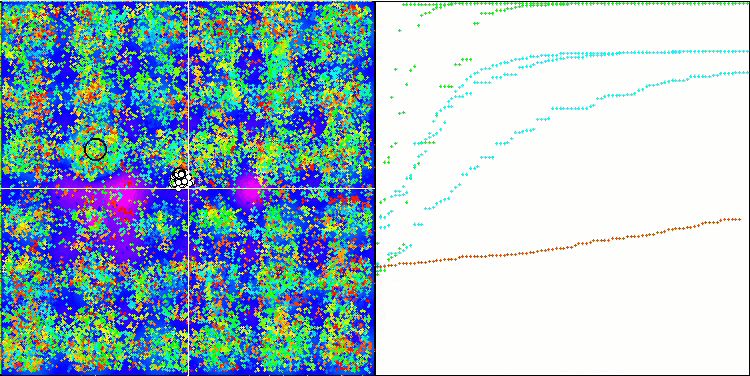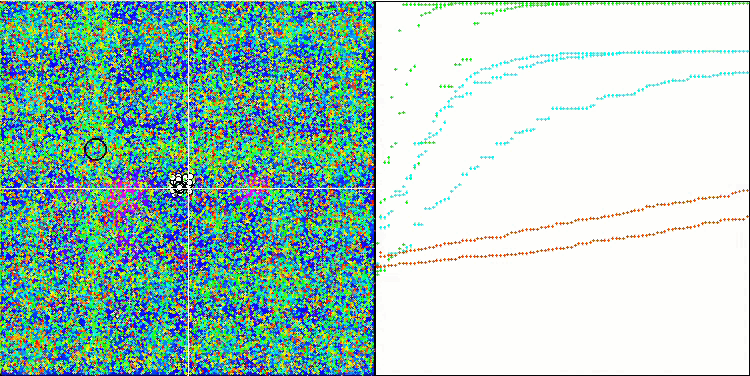
Hillyテスト関数での(μ+λ)-ES

Forest

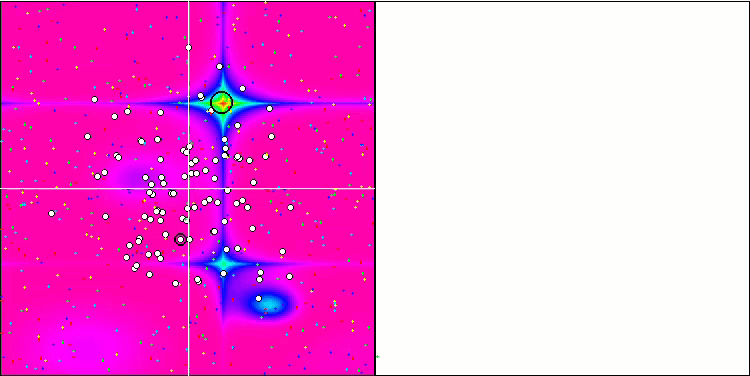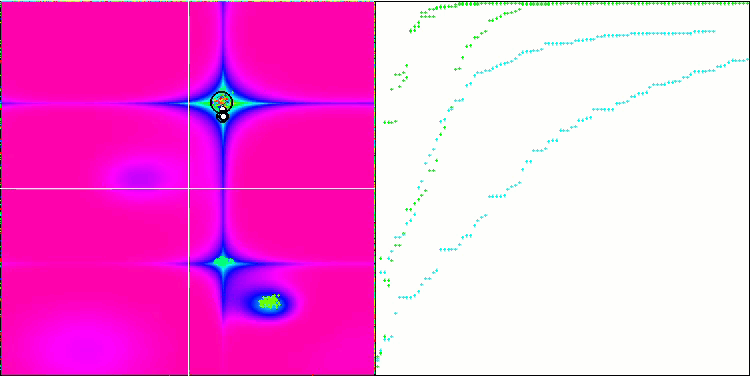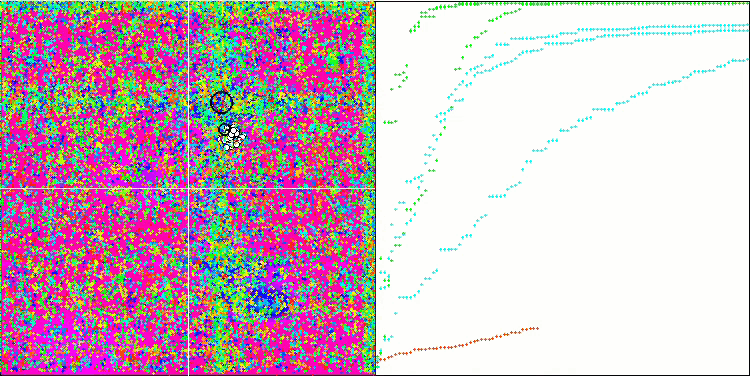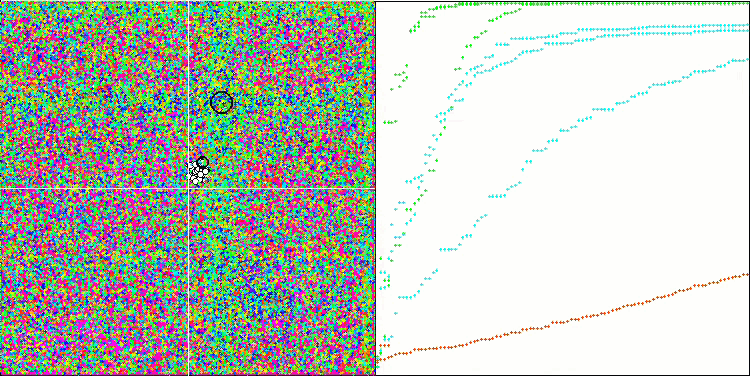
Forestテスト関数での(μ+λ)-ES

Megacity

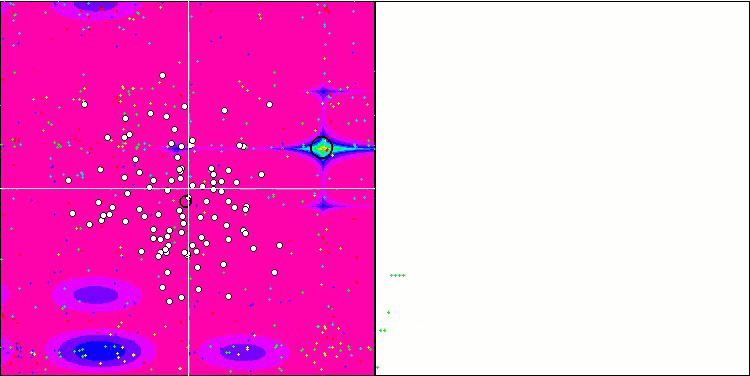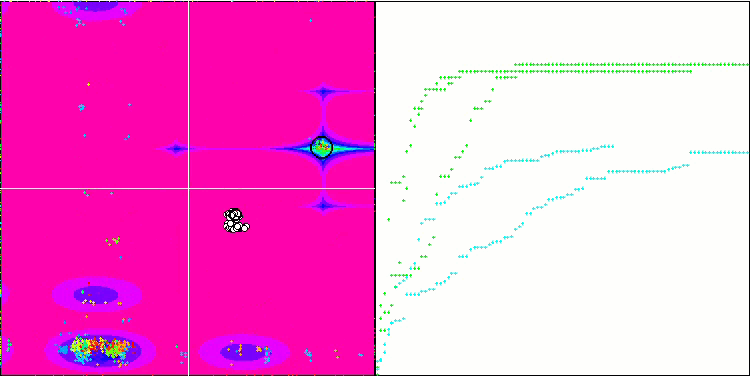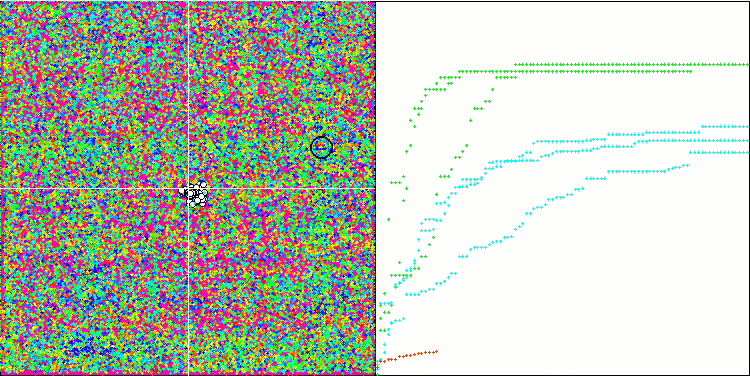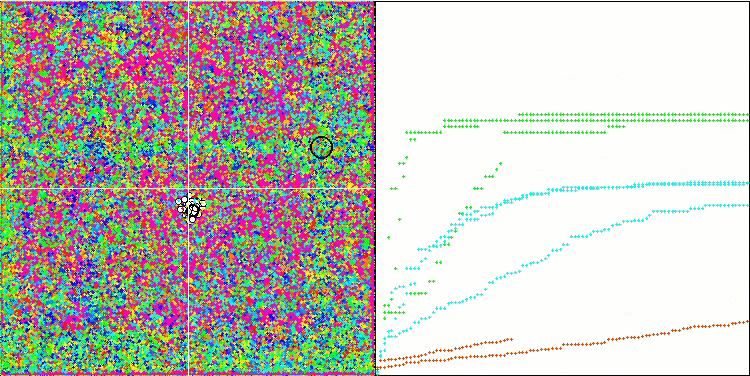
Megacityテスト関数での(μ+λ)-ES

テスト結果の絶対値に戻し、相対値を廃止することにしました。これを達成するために、テスト関数は0.0から1.0の範囲の値を返すように修正されました。ここで、結果が1.0であれば100%の収束を意味し、0.32527であればテスト関数の全域的最大値の32.5%を意味します。したがって、テストの総数は9であるため、理論的には、各テストでアルゴリズムが100%収束した場合、アルゴリズムはすべてのテストについて可能な最大の合計結果9.0を超えないことを表の「最終結果」欄に示すことができます。さらに、「MAXの%」欄が追加され、可能な最大結果のパーセンテージが表示されるようになりました。

これで、新しいアルゴリズムが表に追加されても、絶対値で表示されるため、結果の数字が変わることはありません。

では、検討したアルゴリズム、まず(μ+λ)-ESの結果に移りましょう。このアルゴリズムは、理論的に可能な結果の合計72.18%を獲得しました。その驚異的な結果には本当に驚かされました。この素晴らしい結果を保証するために、このアルゴリズムに特化した20分割交差検証が実施されました。20回の実行のそれぞれが、複素Forest関数で100%の収束を示しました。これはただただ巨大です。さらに、他の関数に関する結果も注目に値するものでした。

さて、(μ,λ)-ESについて良い言葉をいくつか。このアルゴリズムは安定した良好な結果を示しました。カラーグラフでは、急激な色の変化はなく、一様に「緑」です。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最終	最終結果	MAXの%
1	(P+O)ES	(P+O）進化戦略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
2	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
3	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
4	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
5	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
6	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
7	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
8	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
9	MEC	Mind Evolutionary Computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
10	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
11	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
12	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
13	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
14	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
15	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
16	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
17	BFO	細菌採餌の最適化	0.54626	0.43533	0.31907	1.30066	0.41626	0.23156	0.06266	0.71048	0.35500	0.15233	0.03627	0.54360	2.555	28.39
18	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
19	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
20	IWDm	インテリジェント水滴M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
21	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
22	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
23	SFL	ShuffledFrog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
24	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
25	RND	無作為	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
26	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
27	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
28	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

図3：関連テストによるアルゴリズムのカラーグラデーション

チャート

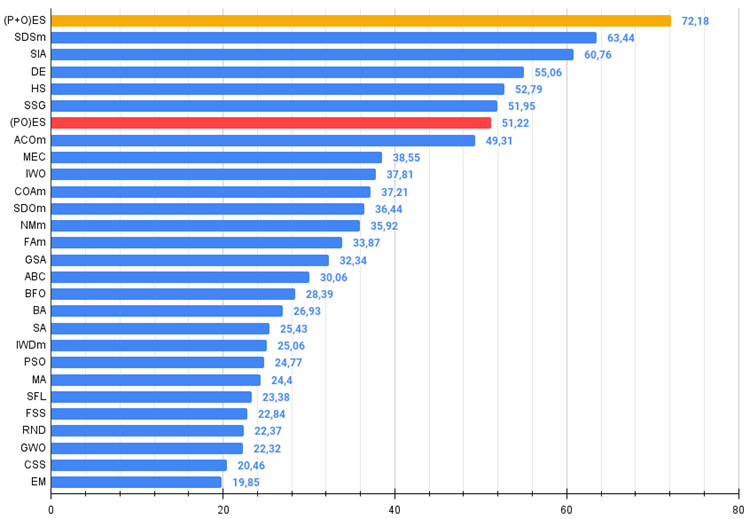
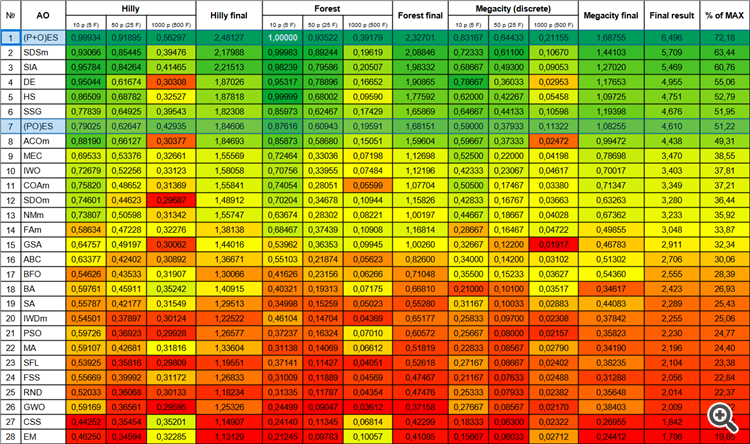
図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果です（アーカイブには格付け表を計算するスクリプトがある）。

5.まとめ

進化戦略の利用は、機械学習におけるパラメータ最適化、ロボット設計、複雑系の制御など、さまざまな分野で新たな可能性を開きます。それによって、進化の生物学的原則に基づいた、より良い解を得ることができます。

最も近い競合相手であるSDSmを10%近く引き離している、議論の余地のない新たな首位を手にしました。

(μ,λ)-ESアルゴリズムの長所と短所

長所

外部パラメータの数が少ない
様々な問題を高い効率で解決
実装が容易
行き詰まりにくい
平滑離散関数と複雑な離散関数の両方で有望な結果
収束性が高い

短所

離散関数に関する結果の大きなばらつき

(μ+λ)-ESアルゴリズムの長所と短所

長所

外部パラメータの数が少ない
様々な問題を高い効率で解決
実装が容易
行き詰まりにくい
平滑離散関数と複雑な離散関数の両方で有望な結果
収束性が高い

短所

離散関数の結果は大きくばらつく（現時点ではこれが最良の結果だが）

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/13923

添付されたファイル |

ZIPをダウンロード

28_The_world_of_AO_ES.zip (542.28 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

母集団最適化アルゴリズム：細菌採餌最適化-遺伝的アルゴリズム(BFO-GA)

本稿では、細菌採餌最適化(BFO)アルゴリズムのアイデアと遺伝的アルゴリズム(GA)で使用される技術を組み合わせ、ハイブリッドBFO-GAアルゴリズムとして最適化問題を解くための新しいアプローチを紹介します。最適解を大域的に探索するために細菌の群れを使い、局所最適解を改良するために遺伝的演算子を使用します。元のBFOとは異なり、細菌は突然変異を起こし、遺伝子を受け継ぐことができるようになっています。

MQL5における修正グリッドヘッジEA（第2部）：シンプルなグリッドEAを作る

この記事では、MQL5のエキスパートアドバイザー(EA)を使用した自動化について詳しく説明し、初期のバックテスト結果を分析します。この戦略には高い保有能力が必要であることを強調し、今後の回で距離、takeProfit、ロットサイズなどの主要パラメータを最適化する計画を概説します。本連載は、取引戦略の効率性と異なる市場環境への適応性を高めることを目的としています。

MQL5でマーケットメイク系アルゴリズムを作成する

マーケットメーカーはどのように機能するのでしょうか。この問題を考えて、原始的なマーケットメイク系アルゴリズムを作ってみましょう。

MQL5を使ったシンプルな多通貨エキスパートアドバイザーの作り方（第6回）：互いのラインを交差する2つのRSI指標

この記事の多通貨EAは、クロスラインを持つ2つのRSI指標、低速RSIと交差する高速RSIを使用するEA（自動売買ロボット）です。