カオスゲーム最適化(CGO)

MetaTrader 5 — テスター | YYYY年02月DD日, 07:27

Andrey Dik

内容

はじめに

最適化アルゴリズムは、現代科学のさまざまな分野だけでなく、取引においても複雑な問題を解決する上で戦略的な役割を果たします。技術の急速な発展に伴い、これらの課題はますます複雑化しており、最適解の探索はより多くのエネルギーを必要とするようになっています。そのため、最適化アルゴリズムに求められるのは、高い有効性と運用効率です。最も新しく、かつ有望な手法のひとつが、2020年にSiamak TalatahariとMehdi Aziziによって開発されたカオスゲーム最適化(Chaos Game Optimization, CGO)アルゴリズムです。このアルゴリズムはカオス理論の原理に基づき、解の生成と改善にカオス的な系列を利用しています。

アルゴリズムの基本的な考え方は、カオス系列を用いて複雑な多次元空間における大域最適解を探索することです。カオス系列は、理論的に局所的な落とし穴を避け、高品質な解を見つけることを可能にする特性を持っています。本記事では、カオスゲーム最適化アルゴリズムの基本原理と各段階を解説し、コードによる実装をおこない、標準的なテスト関数で性能を検証し、その結果について考察します。

アルゴリズムの実装

研究者のグループが、多次元迷路の中で極値を探している様子を想像してください。旅の始めに、探索者たちは迷路の中にランダムに散らばり、厳密に定義された空間の範囲内で最初の拠点を見つけます。これが彼らの出発点です。各探索者は単独で行動するわけではありません。探索者は仲間を観察し、任意の時点でランダムに選んだ仲間のグループの中心を計算します。これは、まるで彼らの位置のバランス点を見つけるかのようです。

これは、グループの経験に基づく集合知の平均です。そしてここから、カオスの真の魔法が始まります。探索者は次の一歩として4つの経路のいずれかを選ぶことができます。各経路は特別な移動方程式で、探索者の現在位置、グループ全体で見つけた最良位置、選択されたサブグループの中心の3つの重要な点が絡み合っています。これらの点は混ぜ合わされ、今後の移動に対する影響の強さはαの値によって決まります。αはカオスの制御パラメータです。

αの値自体はさまざまな形を取ります。探索者はルールに従い、自分の位置から踏み出して、最良解とグループ中心の間の黄金比に向かって進むこともできますし、最良解から出発して周囲を探索することもできます。また、グループ中心から踏み出すことも、完全にランダムな未知の位置へジャンプすることも可能です。

各行動の後、結果を比較します。探索者の1人が以前の記録より良い場所を見つければ、それがグループ全体の新たな指標となり、今後の探索を導きます。

これこそがアルゴリズムの真の美しさです。カオスを秩序に、ランダム性を目的ある動きに、不確実性を進歩に変える能力を持っています。そして、すべてのステップ、すべての移動が、既知と未知、安定とリスク、秩序とカオスの間で解を探すために依存しています。

cgoイラスト

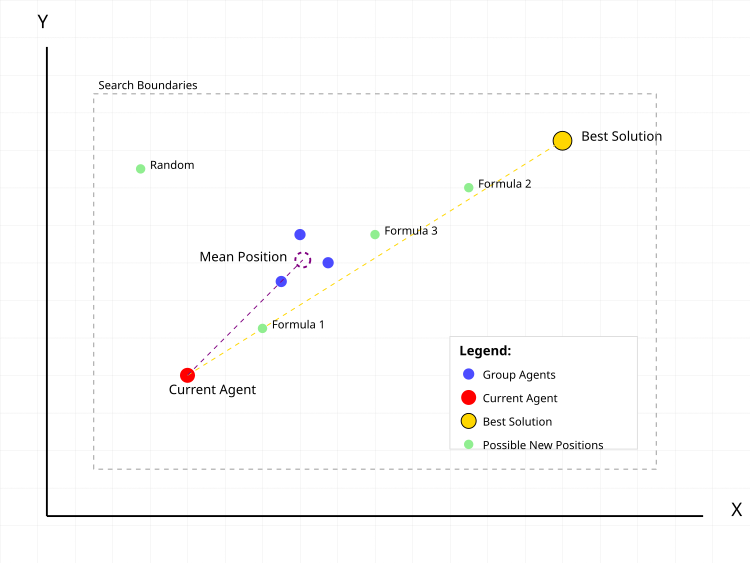
図1：CGOアルゴリズムにおける探索エージェントの典型的な行動

図1では、赤い点が、新しい位置を計算中の現在のエージェントを表します。青い点は、集団からランダムに選ばれた仲間のグループを示します。紫の破線の円はそのグループの平均位置を示し、金色の点はこれまでに見つけた最良解です。緑の点は、異なる移動式に基づくエージェントの可能な新しい位置を示しています。移動式は以下の通りです。

式1：current + α(β×best - γ×average)
式2：best + α(β×average - γ×current)
式3：average + α(β×best - γ×current)
ランダム：ランダムな位置

破線は最良解およびグループ平均位置が現在のエージェントの移動に与える影響ベクトルを示しています。灰色の破線の矩形は探索範囲の境界です。

アルゴリズムの疑似コードを書き始めましょう。

アルゴリズムの初期化

集団サイズを設定する（デフォルトは50エージェント）
各座標の探索範囲を定義する
- 最小値(rangeMin)
- 最大値(rangeMax)
- 変更ステップ(rangeStep)
集団内の各エージェントについて
- 指定範囲内でランダムに初期座標を生成する
- ステップを考慮して座標を丸める
- 目的関数の値を計算する
集団内のすべてのエージェントで最良の初期解を決定する

メイン最適化ループ

集団内の各エージェントについて

a)エージェントのサブグループをランダムに選択する

サブグループサイズ = 1から集団サイズまでのランダム値
エージェントをランダムにサブグループに割り当てる

b)選択したサブグループの平均位置を計算する

各座標について：average_coordinate = sum_of_group_coordinates / group_size

c)移動式の比率を生成する

α = いずれかの方法をランダムに選択する
- 方法1：0から1までのランダム値
- 方法2：2 × random(0,1) - 1 [-1から1までの数値を取得]
- 方法3：Ir × random(0,1) + 1
- 方法4：Ir × random(0,1) + (1-Ir) ここでIr = ランダムに0または1
β = ランダムに1または2
γ = ランダムに1または2

d)4つの移動式からランダムに1つを選択する

式1：new_position = current + α(β×best - γ×average)
式2：new_position = best + α(β×average - γ×current)
式3：new_position = average + α(β×best - γ×current)
式4：new_position = 検索境界内のランダムな位置

e)選択した方程式を適用する

各座標について
- 方程式を使用して新しい値を計算する
- 範囲外の検索をチェックする
- 制限を超えた場合は、最も近い制限に調整する
- 変化のステップを考慮して値を丸める

f)新しい位置における目的関数の値を計算する

最良解の更新

各エージェントについて
- エージェントの目的関数の値が現在の最高値よりも優れている場合
  - 最良値を更新する
  - 新しい最良解の座標を保存する

繰り返し

以下の停止条件のいずれかが満たされるまで手順2～3を繰り返す
- 反復回数の上限に達した
- 必要な品質の解を見つけた
- 別の停止基準

アルゴリズム自体の実装に移りましょう。C_AO_CGOクラスはCGOアルゴリズムを実装します。C_AOクラスから継承しているため、C_AOクラスのプロパティやメソッドを引き継ぎます。

メソッド

SetParams ()：params配列のデータに基づいてpopSize（集団サイズ）を設定します。このメソッドは、アルゴリズムを使用する前に最適なパラメータに調整するために重要です。
Init ()：初期化メソッドで、探索範囲の最小値と最大値、ステップサイズ、エポック数（反復回数）を受け取ります。このメソッドの目的は、探索範囲やその他のパラメータを設定することで、アルゴリズムを実行できる状態に準備することです。
Moving ()：個体の移動に関連するステップを記述します。実装では、異なる移動式を用いた代替解の生成や、それらの改善のロジックを提供します。
Revision ()：現在の集団の解と、全体で見つけた最良解を更新し修正する役割を持ちます。

privateメソッド

GetAlpha ()：探索戦略を制御するために使用されるαパラメータを取得します。このパラメータは、探索の強度や多様性を調整するために利用されます。
GenerateNewSolution ()：新しい解を生成するためのメソッドで、インデックス (seedIndex)とサブグループの平均位置(meanGroup)をもとに計算します。

class C_AO_CGO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CGO () { }
  C_AO_CGO ()
  {
    ao_name = "CGO";
    ao_desc = "Chaos Game Optimization";
    ao_link = "https://www.mql5.com/ja/articles/17047";

    popSize = 25;

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving ();
  void Revision ();

  private: //-------------------------------------------------------------------
  double GetAlpha ();
  void   GenerateNewSolution (int seedIndex, double &meanGroup []);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_CGOクラスのInitメソッドは、最適化アルゴリズムを起動する前にパラメータを初期化する役割を持っています。このメソッド引数として、各探索変数の最小値および最大値を格納した配列、各変数のステップサイズ、そしてアルゴリズムのエポック数（反復回数）を受け取ります。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CGO::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、CGOアルゴリズムにおける解集団の個体の移動の主要なロジックを実装しています。このメソッドの主な目的は、ルールに基づいて集団内の意思決定を更新することです。これには、新しい意思決定の生成や、結果の平均化などが含まれます。以下に、その主要部分を詳しく見ていきます。

最初の部分：初回呼び出し時の初期化（revisionがfalseの場合）

外側のループは、集団内のすべての個体(popSize)を対象に実行されます。

各個体（i番目の個体）に対して、内側のループは座標(coords)ごとに開始されます。
各座標について、u.RNDfromCI()メソッドを使用してランダム値を生成します。このメソッドは、指定された範囲内のランダム値を返します。
この値は次に、u.SeInDiSp()を使用して調整されます。このメソッドにより、値が範囲内に収まり、最も近い増分に丸められます。

次回のメソッド呼び出し時に備えて、revisionフラグをtrueに設定し、メソッドを終了します。

2番目の部分：集団の更新（revisionがtrueの場合）

集団内の各個体について
- 1からpopSizeまでの範囲でランダムにrandGroupSize（グループサイズ）を生成します。
- meanGroup配列を作成し、座標の平均値を格納できるようにします。配列のサイズは座標数(coords)に対応しています。
- ランダムに選ばれる個体のインデックスを格納するために、randIndices配列を作成します。
- 各反復で、ランダムなインデックスがrandIndicesに追加されます。インデックスはランダムに選ばれます。

次に、各グループについて、ランダムに選ばれたインデックスに対応する個体の座標値をすべて合計し、その結果をmeanGroupに格納します。
合計後、meanGroupの値をグループの個体数で割り、平均値を算出します。
最後に、GenerateNewSolution()メソッドを使用して、グループ平均に基づく新しい解をi番目の個体のために生成します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int randGroupSize = u.RNDminusOne (popSize) + 1;
    double meanGroup [];
    ArrayResize (meanGroup, coords);
    ArrayInitialize (meanGroup, 0);

    int randIndices [];
    ArrayResize (randIndices, randGroupSize);

    for (int j = 0; j < randGroupSize; j++) randIndices [j] = u.RNDminusOne (popSize);

    for (int j = 0; j < randGroupSize; j++)
    {
      for (int c = 0; c < coords; c++)
      {
        meanGroup [c] += a [randIndices [j]].c [c];
      }
    }
    for (int c = 0; c < coords; c++) meanGroup [c] /= randGroupSize;

    GenerateNewSolution (i, meanGroup);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは、集団内の最良解を更新する役割を持ちます。このメソッドは、集団内のすべての個体をループ処理し、各個体について、その適合度関数の値(f)が現在の最良値(fB)より大きいかどうかを確認します。もし大きければ、fBを新しいfの値で更新し、現在の個体の座標（c個）をcB配列にコピーします。つまり、Revisionメソッドは、適合度関数の値に基づいて、集団内で現在知られている最良解を見つけ出し、更新する処理をおこないます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

GetAlphaメソッドは、ランダムな選択条件に基づいてα値を生成し、返すメソッドです。

Ir：0または1のランダム値
4つのケース（caseで示される）があります。それぞれのケースは、対応する式を使ってα値を生成します。
- ケース0：0から1の範囲の値を生成します。
- ケース1：-1から1の範囲の値を生成します。
- ケース2：1から2の範囲の値を生成します（生成値にIr（0または1）を掛けることで決まります）。
- ケース3：Irの値に依存する値を生成します。生成される値の範囲は、Irの値によって0から1、または1となります。

なお、α値を生成するための式は、より単純な形で書くことも可能ですが、ここではアルゴリズムの作者の論文に対応する元の式の形が使用されています。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_CGO::GetAlpha ()
{
  int Ir = u.RNDminusOne (2);

  switch (u.RNDminusOne (4))
  {
    case 0: return u.RNDfromCI (0, 1);
    case 1: return 2 * u.RNDfromCI (0, 1) - 1;
    case 2: return Ir * u.RNDfromCI (0, 1) + 1;
    case 3: return Ir * u.RNDfromCI (0, 1) + (1 - Ir);
  }
  return 0;
}
//——————————————————————————————————————————————————————————————————————————————

GenerateNewSolutionメソッドは、集団内の指定されたエージェントのために、さまざまなランダムパラメータに基づいて新しい解を生成する役割を持ちます。

パラメータの初期化

alphaは、GetAlpha()メソッドを呼び出して取得した値で、新しい位置に影響を与えるために使用されます。
betaとgammaはランダム値（1または2）です。

式の選択

formula：新しい位置を計算するために、4つの式のうちのいずれかがランダムに選ばれます。

座標ごとのループ：各座標（0からcoordsまで）について

newPos：選択された式に従って計算される新しい位置を格納する変数です。
「式」の意味に応じて
- ケース0：新しい位置は、エージェントの現在位置に、cB（集団内の最良解）とmeanGroupの座標の組み合わせを加えることで計算されます。
- ケース1：新しい位置は、cBの座標とmeanGroupの平均値を用いて計算されます。
- ケース2：新しい位置は、meanGroupの平均値と現在のエージェントの座標を用いて決定されます。
- ケース3：新しい位置は、指定された範囲（rangeMin[c]からrangeMax[c]）の中でランダムに設定されます。

新しい位置の補正

a [seedIndex].c [c]：対応するエージェントの座標が更新されます。更新にはu.SeInDiSp()メソッドが使用され、最小値、最大値、ステップを考慮して、新しい値が許容範囲内に収まるように補正されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup [])
{
  double alpha = GetAlpha ();
  int    beta  = u.RNDminusOne (2) + 1;
  int    gamma = u.RNDminusOne (2) + 1;

  int formula = u.RNDminusOne (4);

  for (int c = 0; c < coords; c++)
  {
    double newPos = 0;

    switch (formula)
    {
      case 0:
        newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]);
        break;

      case 1:
        newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]);
        break;

      case 2:
        newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]);
        break;

      case 3:
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        break;
    }

    a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

テストを実施した後、アルゴリズムの収束を改善しようと試み、基本バージョンのCGOアルゴリズムに対して追加の変更をおこなうことにしました。主な違いは、各座標の処理をおこなう際の初めの部分で、基本的な移動式を適用する前におこなわれます。

double rnd = u.RNDprobab();                             // Get a random number from 0.0 to 1.0
rnd *= rnd;                                             // Squate it
int ind = (int)u.Scale(rnd, 0.0, 1.0, 0, popSize - 1);  // Scale to index
a[seedIndex].c [c] = a[ind].c [c];                      // Copy the coordinate from another agent with the received index

ここでは、座標がランダムに選ばれた別のエージェントからコピーされます。エージェントは一様に選ばれるのではなく、二次確率分布(rnd *= rnd)に従って選ばれます。これにより、小さいインデックスのエージェント（より良い解）が選ばれる確率が高くなる「バイアス」が生じます。ランダム値を二乗することで非一様な分布を作り、それを集団のインデックスの範囲にスケーリングし、基本的な移動式を適用する前に座標をコピーします。有望な領域での収束を加速しようとしたのですが、残念ながら期待した効果は得られませんでした。

おそらく、強化効果による早期収束の結果、集団内の多様性が急速に減少し、このアルゴリズムでは多様性が減るとさらに探索が行き詰まる傾向があります。また、アルゴリズムのロジック自体がこの現象を防ぐことを許さない可能性もあります。以下に、変更を加えたコードの該当部分を示します。さらに改善を試みる追加の試行もおこないましたが、目立った進展は得られず、最終的にはアルゴリズムの元のバージョンを使用することに決めました。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CGO::GenerateNewSolution (int seedIndex, double &meanGroup [])
{
  double alpha = GetAlpha ();
  int    beta  = u.RNDminusOne (2) + 1;
  int    gamma = u.RNDminusOne (2) + 1;

  int formula = u.RNDminusOne (4);

  for (int c = 0; c < coords; c++)
  {
    double rnd = u.RNDprobab ();
    rnd *= rnd;
    int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);
    a [seedIndex].c [c] = a [ind].c [c];

    double newPos = 0;

    switch (formula)
    {
      case 0:
        newPos = a [seedIndex].c [c] + alpha * (beta * cB [c] - gamma * meanGroup [c]);
        break;

      case 1:
        newPos = cB [c] + alpha * (beta * meanGroup [c] - gamma * a [seedIndex].c [c]);
        break;

      case 2:
        newPos = meanGroup [c] + alpha * (beta * cB [c] - gamma * a [seedIndex].c [c]);
        break;

      case 3:
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        break;
    }

    a [seedIndex].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

以下のテスト結果から分かるように、アルゴリズムによって得られる全体の改善率はかなり控えめです。しかし、よく観察すると、このアルゴリズムには興味深い特徴があることに気づきます。その特徴について、以下で説明します。

CGO|Chaos Game Optimization|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.5725597668122144
25 Hilly's; Func runs:10000; result:0.3715760642098293
500 Hilly's; Func runs:10000; result:0.32017971142744234
=============================
5 Forest's; Func runs:10000; result:0.6117551660766816
25 Forest's; Func runs:10000; result:0.619308424855028
500 Forest's; Func runs:10000; result:0.6216109945434442
=============================
5 Megacity's; Func runs:10000; result:0.3753846153846153
25 Megacity's; Func runs:10000; result:0.2192307692307692
500 Megacity's; Func runs:10000; result:0.19028461538461647
=============================
All score:3.90189 (43.35%)

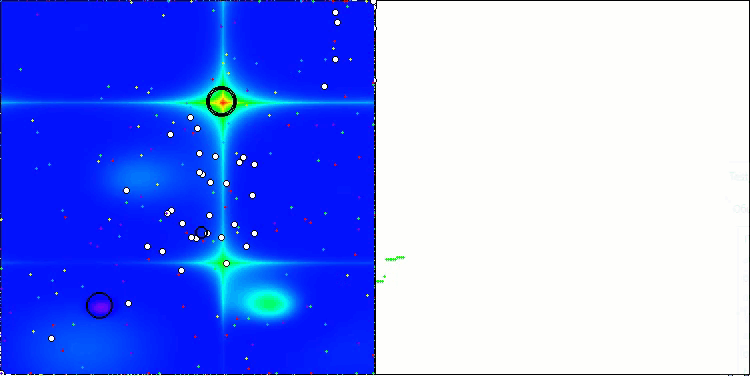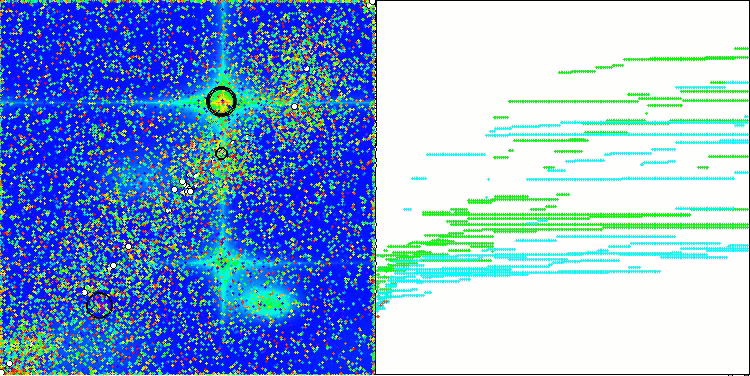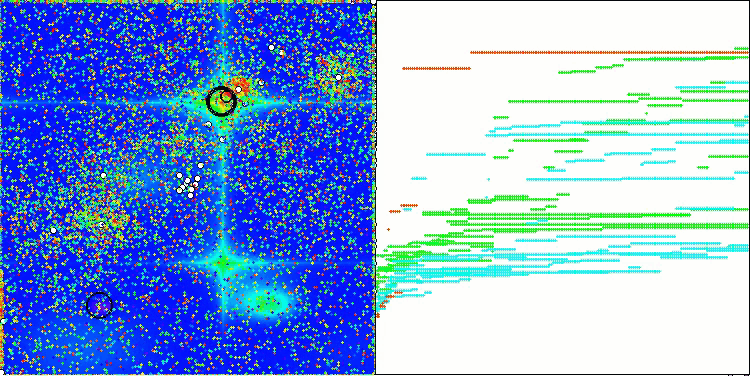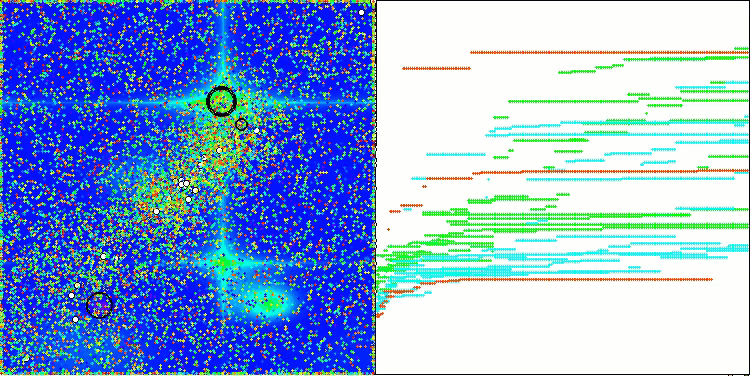
テスト関数に対するアルゴリズムの動作を可視化すると、エージェントのグループ化に構造が形成されていることが明確にわかります。そして、これらの構造はタスクごとに異なります。しかし、アルゴリズムの動作の一般的な性質としては、最適化結果の非常に広い範囲が挙げられます。

Hilly

Hillyテスト関数のCGO

Forest

Forestテスト関数のCGO

Megacity

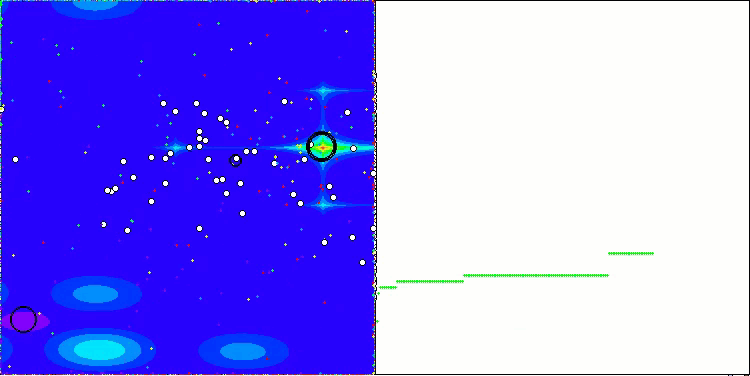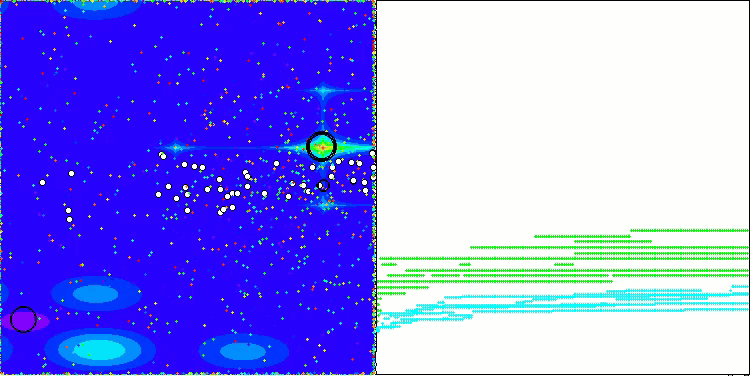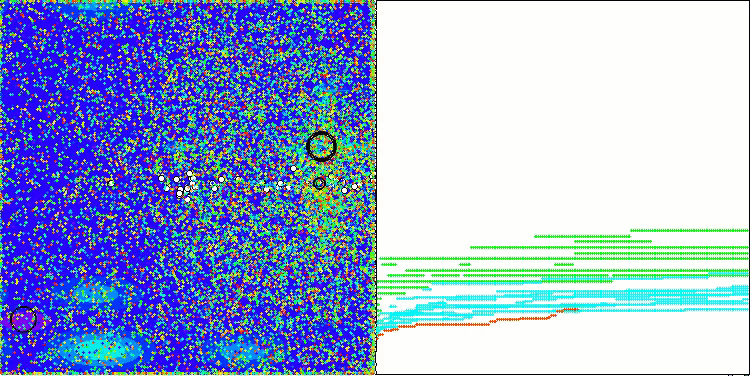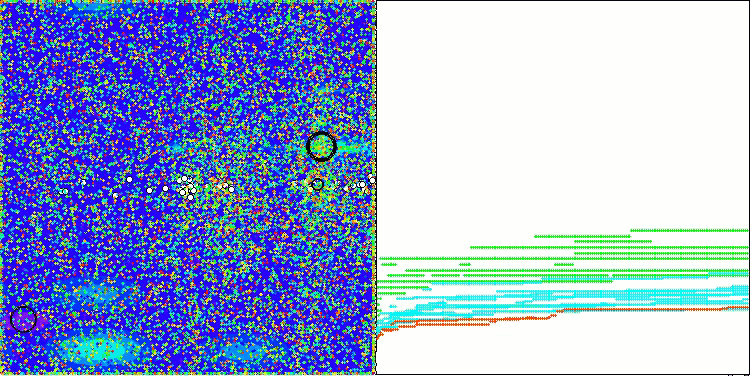
Megacityテスト関数のCGO

テスト結果に基づくと、CGOアルゴリズムは集団ベース最適化アルゴリズムのランキング表で第38位に位置しています。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	時間進化移動アルゴリズム（joo）	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
9	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
10	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
11	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
12	DA	弁証法的アルゴリズム	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
13	BHAm	ブラックホールアルゴリズムM	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
14	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
15	RFO	ロイヤルフラッシュ最適化（joo）	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
16	AOSm	原子軌道探索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
17	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
18	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
19	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
20	BIO	血液型遺伝最適化(joo)	0.81568	0.65336	0.30877	1.77781	0.89937	0.65319	0.21760	1.77016	0.67846	0.47631	0.13902	1.29378	4.842	53.80
21	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
22	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
23	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
24	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
25	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
26	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
27	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
28	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
29	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
30	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
31	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
32	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
33	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
34	SOA	シンプル最適化アルゴリズム	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
35	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
36	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
37	ADAMm	適応モーメント推定M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
38	CGO	カオスゲーム最適化	0.57256	0.37158	0.32018	1.26432	0.61176	0.61931	0.62161	1.85267	0.37538	0.21923	0.19028	0.78490	3.902	43.35
39	ATAm	人工部族アルゴリズムM	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
40	ASHA	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
41	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
42	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
43	CSA	円探索アルゴリズム	0.66560	0.45317	0.29126	1.41003	0.68797	0.41397	0.20525	1.30719	0.37538	0.23631	0.10646	0.71815	3.435	38.17
44	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
45	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
	RW	ランダムウォーク	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

まとめ

CGOアルゴリズムの結果を分析したところ、いくつか重要な結論に至りました。カオスゲーム最適化アルゴリズムは非常に興味深い挙動を示します。全体的な効率は平均以下と評価され、総合結果43.35%という数字でも確認できます。しかし、このアルゴリズムで最も注目すべき挙動は、問題のスケーリングに関連しています。CGOは特に多次元問題に対して高い効率を示し、たとえば1000変数のテストではその特性が明確に現れます。これはほとんどのメタヒューリスティックアルゴリズムにとって非典型的な性質です。多くのアルゴリズムは「次元の呪い」に苦しみ、変数の数が増えると効率が低下します。ところがCGOは逆に、1000次元問題で作業する際に、10次元や50次元の問題での結果を上回ることさえあります。この傾向は、特に全域的極値が1つの「鋭い」点にあるForestテスト関数で顕著です。

この現象は、アルゴリズムの本質に起因すると考えられます。CGOのカオス的な性質と移動式の多様性は、高次元空間を探索する効率的なメカニズムを生み出しています。4種類の異なる位置更新戦略、これらの戦略間でのランダム選択、そして予測不可能なαの値により、アルゴリズムは複雑な多次元ランドスケープ上の問題を解くことが可能です。特にForestタイプの関数では、0.61～0.62という高い結果を示し、これは平均値よりも大幅に高い値です。

アルゴリズムの設計を分析すると、高次元での強みは座標ごとの処理に関連していることが分かります。CGOは解ベクトル全体で作業するのではなく、各座標を独立して更新するため、次元が増えても効率的に動作します。さらに、ランダムに選ばれるグループとその平均位置を使用することで、高次元空間でもエージェント間で効率的な情報交換がおこなわれます。

また、Forest関数の表面を異なる角度に回転させて、得られた興味深い結果がアルゴリズムのロジックやテスト関数の特定の特徴による偶然ではないことを確認しました。これは、偶然に全域的極値に当たった可能性を排除するために必要でした。関数の回転による実験でも、これらの結果がランダムではないことが確認されました。このように、鋭い極値を持つ関数に対するCGOの挙動の特性を考慮すると、このアルゴリズムを使用する場合は、複数回の最適化実行をおこなうことが推奨されます。この推奨は、特にこのアルゴリズムにとって重要です。

総合的に見て、全体の性能は平均的であるものの、問題規模が大きくなっても効率を維持し、場合によっては向上させるCGOの独自の特性は、複雑な最適化問題への応用やさらなる研究に非常に興味深いアルゴリズムであることを示しています。

Tab

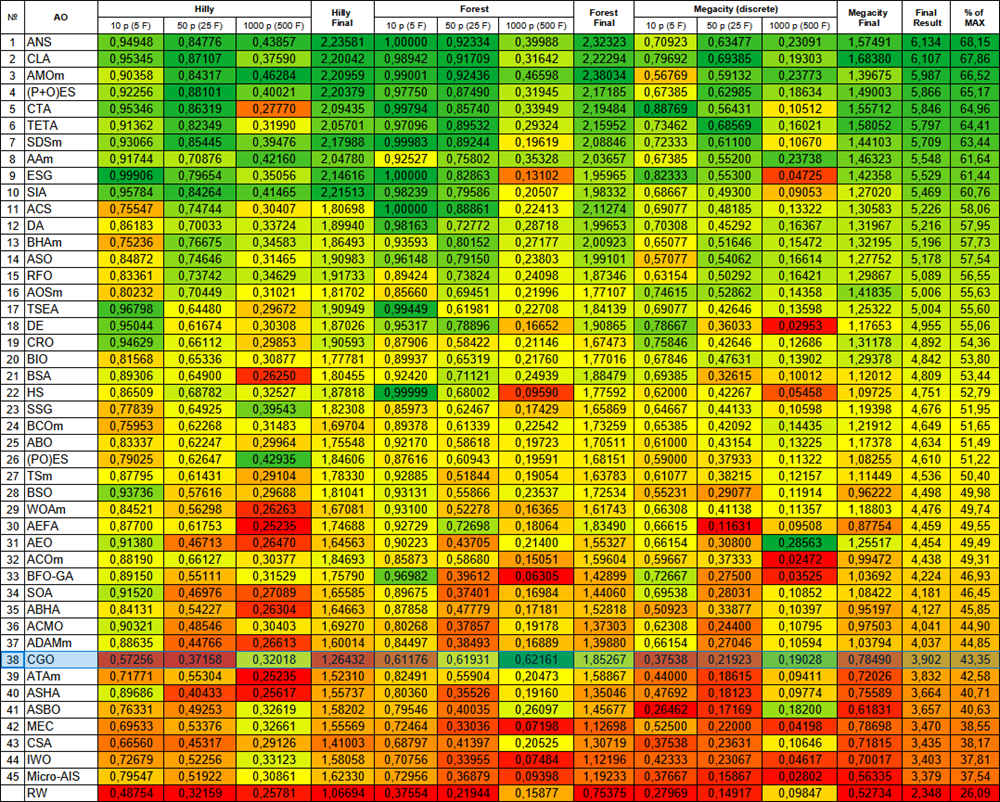
図2：対応するテストに応じたアルゴリズムのカラーグラデーション

チャート

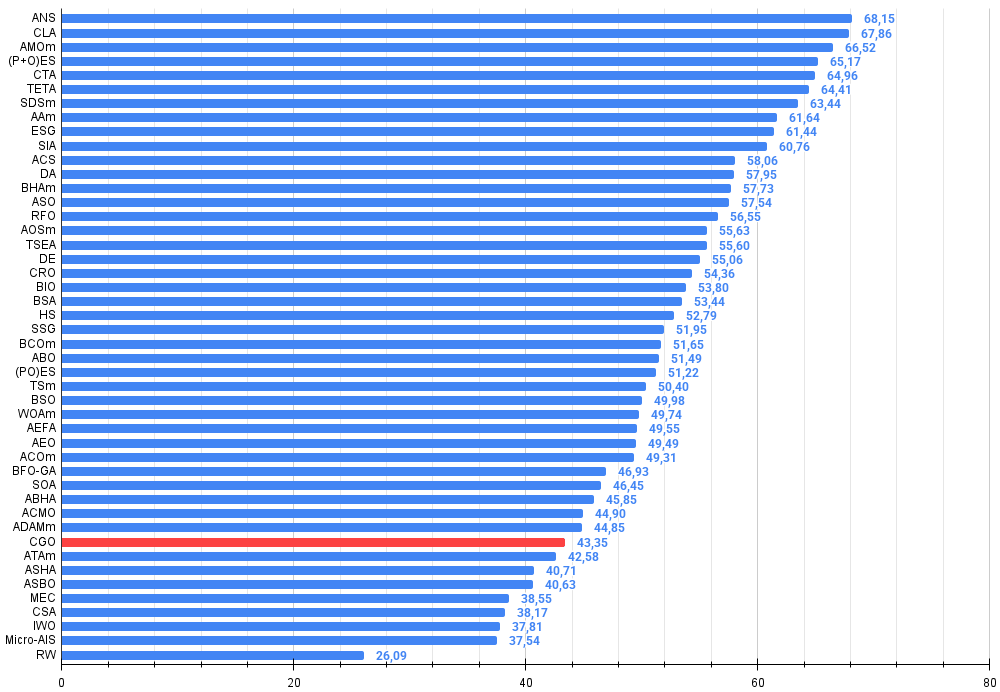
図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

CGOの長所と短所

長所

外部パラメータなし
高次元および中次元関数の良好な収束

短所

低次元の問題では、局所極値に行き詰まってしまう

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化の親クラスアルゴリズム
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	TestFunctions.mqh	インクルード	テスト関数のライブラリ
4	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
5	Utilities.mqh	インクルード	補助関数のライブラリ
6	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
7	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
8	Simple use of population optimization algorithms.mq5	スクリプト	可視化せずに集団最適化アルゴリズムを使用する簡単な例
9	Test_AO_CGO.mq5	スクリプト	CGOテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/17047

添付されたファイル |

ZIPをダウンロード

CGO.zip (168.66 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(I)

本記事では、作成済みの自動最適化システムに新しい戦略を連携する方法を見ていきます。どのようなEAを作成する必要があるのか、EAライブラリのファイルを変更せずにできるのか、必要な変更を最小限に抑えられるかを確認してみましょう。

純粋なMQL5で実装した通貨ペア強度インジケーター

MetaTrader 5向けの通貨強度分析用のプロフェッショナルなインジケーターを開発します。このステップバイステップガイドでは、強力な取引ツールを作成する方法を解説します。視覚的なダッシュボードを搭載し、複数の時間足（H1、H4、D1）で通貨ペアの強さを計算し、動的なデータ更新を実装し、ユーザーフレンドリーなインターフェースを作成することができます。

ビリヤード最適化アルゴリズム(BOA)

BOA法は、古典的なビリヤードに着想を得ており、最適解を探すプロセスを、玉が穴に落ちることで最良の結果を表すゲームとしてシミュレーションします。本記事では、BOAの基本、数学モデル、およびさまざまな最適化問題を解く際の効率について考察します。

取引における資金管理とデータベースを用いた個人向け会計プログラム

トレーダーはどのように資金を管理すればよいのでしょうか。また、トレーダーや投資家はどのようにして支出、収入、資産、負債を把握すればよいのでしょうか。本記事では、単なる会計ソフトではなく、金融市場という荒波の中で意思決定を支える実践的なツールを紹介します。