MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
原子軌道探索(AOS)アルゴリズム：改良版

原子軌道探索(AOS)アルゴリズム：改良版

MetaTrader 5 — テスター |
29 5
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. C_AOクラスの使用例
  4. テスト結果


はじめに

この記事の第1部では、原子軌道モデルに着想を得た原子軌道検索(AOS:Atomic Orbital Search)アルゴリズムの基本と、その基礎となるメカニズムについて説明しました。また、このアルゴリズムが確率分布や相互作用のダイナミクスを活用して、複雑な最適化問題の最適解を探索する方法についても解説しました。

第2部では、この優れたアイデアを見過ごすことなく、AOSアルゴリズムの改良に焦点を当てます。特に、この手法特有の演算子に注目し、それらが効率性と適応性の向上にどう寄与できるかを分析します。

AOSアルゴリズムの研究を進める中で、その探索空間における探索手法に関して多くの興味深い側面が見えてきました。研究を通じて、この興味深いアルゴリズムをさらに改善するためのいくつかのアイデアも思いつきました。特に、複雑な解探索空間を探索する能力を向上させることで、アルゴリズムの性能を高めるための既存手法の再構築に注力しました。これらの改良を既存のAOSアルゴリズムの構造にどのように統合できるかを検討し、最適化問題解決のためのより強力なツールにすることを目指します。したがって、本稿の目的は既存のメカニズムを分析するだけでなく、AOSアルゴリズムの能力を大幅に拡張できる新たなアプローチを提案することにもあります。


アルゴリズムの実装

前回の記事では、AOSアルゴリズムの主要な構成要素を詳しく見てきました。ご記憶の通り、このアルゴリズムでは個体群を分子として捉え、最適解探索がおこなわれる許容座標領域を原子として表現します。各原子は複数の層で構成され、これが探索の構造化と方向付けに役立ちます。

最適化の過程で得られる特定の座標値は電子として解釈できます。これらの電子は原子の内部にあり、私たちが最適化している問題のパラメータの1つに対する可能な解を表します。したがって、各分子（個体群）は、与えられた領域（原子）の中で最適な値（電子）を見つけようとします。

元のAOSアルゴリズムでは、BEk層エネルギーはその層内の電子のエネルギーの算術平均として定義され、BSk結合はその座標の算術平均として定義されます。BEkエネルギーは電子のエネルギーと比較され、その後の移動モードを決定するために使用されます。BSk結合は、層内の電子の最良位置LEkとBSk結合との差を利用し、次式に従って電子の位置の更新量を計算するために使われます：Xki[t+1] = Xkit + αi × (βi × LEk − γi × BSk)。

私は、このBSk（層内電子の平均位置）を使用するのをやめ、代わりに電子自身の個別最良位置を使うことを提案します。これにより、電子は層全体の平均解ではなく、自分自身の実績に基づいて最良解へ移動します。さらに、すでに外部ランダム成分αiが存在するため、βiとγiという2つのランダム成分は冗長に見えます。この変更により、この式における乱数生成回数を3分の1に削減でき、物理的意味を損なうこともありません。

それでは、原子内の層を記述する構造を見ていきましょう。コードから削除された要素は赤で強調表示されています。

//——————————————————————————————————————————————————————————————————————————————
struct S_Layer
{
    int    pc;  // particle counter
    double BSk; // connection state
    double BEk; // binding energy
    double LEk; // minimum energy

    void Init ()
    {
      pc  = 0;
      BSk = 0.0;
      BEk = 0.0;
      LEk = 0.0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

ここでは、層のエネルギーや結合度といった特徴を計算するCalcLayerParamsメソッドのコードを考えてみましょう。赤で強調表示された行は、不要になったため削除されます。ご存知の通り、このメソッドはAOSの探索戦略において重要な役割を担っており、アルゴリズムが局所的な罠にはまり込むのを防ぐことを目的としています。層のエネルギーレベルは、その位置に依存するのではなく（エネルギーは原子の中心から外側の層へと減少するわけではなく）、顕著な局所極値の存在によって決まります。そのため、外側の層が内側よりも高いエネルギーを持つ場合もあります。この仕組みにより、層は探索空間における電子の移動を修正する役割を果たします。

また、各エポックごとに層の数をランダムにすることで、アルゴリズムが特定の層内で停滞しないようになり、局所的な罠から抜け出すのを助けます。改良版では、原子全体の平均エネルギーを計算する必要もなくなるため、その処理に関するコードも削除します。

AOS層

図1：原子の層数に応じてe電子変位の方向と大きさが異なる

図1は、AOSアルゴリズムにおいて層の数が異なる原子内での電子の振る舞いの違いを示しています。上段のパネルは3層の原子を表しており、電子は層L1に位置し、目的関数値がB1である状態で、局所最良値LEk1に向かって移動しています。下段のパネルは2層の原子を示しており、この場合も電子は層L1に位置し、目的関数値がB1である状態で、局所最良値LEk1に向かって移動しています（3層の場合、この位置はLEk2に相当します）。

図の主要な要素

  • B0、B1、B2：対応する層における目的関数の局所値
  • LEk0、LEk1、LEk2：対応する層における最良解
  • L0、L1、L2：原子層
  • e：電子
  • MIN、MAX：原子の外層の境界（最適化対象パラメータの境界条件）
//——————————————————————————————————————————————————————————————————————————————
// Calculate parameters for each layer
void C_AO_AOS::CalcLayerParams ()
{
  double energy;

  // Handle each coordinate (atom)
  for (int c = 0; c < coords; c++)
  {
    atoms [c].Init (maxLayers);

    // Handle each layer
    for (int L = 0; L < currentLayers [c]; L++)
    {
      energy = -DBL_MAX;

      // Handle each electron
      for (int e = 0; e < popSize; e++)
      {
        if (electrons [e].layerID [c] == L)
        {
          atoms [c].layers [L].pc++;
          atoms [c].layers [L].BEk += a [e].f;
          atoms [c].layers [L].BSk += a [e].c [c];

          if (a [e].f > energy)
          {
            energy = a [e].f;
            atoms [c].layers [L].LEk = a [e].c [c];
          }
        }
      }

      // Calculate average values for the layer
      if (atoms [c].layers [L].pc != 0)
      {
        atoms [c].layers [L].BEk /= atoms [c].layers [L].pc;
        atoms [c].layers [L].BSk /= atoms [c].layers [L].pc;
      }
    }
  }

  // Calculate the general state of connections
  ArrayInitialize (BS, 0);

  for (int c = 0; c < coords; c++)
  {
    for (int e = 0; e < popSize; e++)
    {
      BS [c] += a [e].c [c];
    }

    BS [c] /= popSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————

個体の最良解を更新するために、改良版C_AO_AOSmのRevisionメソッドにコードを追加します。

//——————————————————————————————————————————————————————————————————————————————
// Method of revising the best solutions
void C_AO_AOSm::Revision ()
{
  int bestIndex = -1;

  // Find the best solution in the current iteration
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIndex = i;
    }

    // Update the personal best solution
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Update the best coordinates if a better solution is found 
  if (bestIndex != -1) ArrayCopy (cB, a [bestIndex].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

UpdateElectronsメソッドでは、対応する乱数を生成する必要がないため、変数βおよびγを削除します。さらに、大域解に向かう移動の場合に、層の数で電子の増分を除算する処理も削除します。率直に言えば、著者らのこの処理はやや疑問があり、その物理的な意味は完全には明確ではありません。おそらく著者らは、層の数に応じて電子の大域解への移動の度合いを可変にしようとしたのかもしれません。つまり、層が少ないほど移動が強くなるようにしたかったのではないかと思われます。しかし、私の実験結果では、そのような傾向は確認されませんでした。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOS::UpdateElectrons ()
{
  double α;      // speed coefficient
  double β;      // best solution weight coefficient
  double γ;      // average state weight coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random scatter
        newPos = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);
        β = u.RNDprobab ();
        γ = u.RNDprobab ();

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE = cB [c];

          newPos = a [p].c [c]+ α * (β * LE - γ * BS [c]) / currentLayers [c];
        }
        else
        {
          // Movement towards the local optimum of the layer------------------------
          LE  = atoms [c].layers [lID].LEk;
          BSk = atoms [c].layers [lID].BSk;

          newPos = a [p].c [c] + α * (β * LE - γ * BSk);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

さらに、C_AO_AOSmクラスのUpdateElectronsメソッドでは、電子を探索空間内にランダムに散らすのではなく、一定の確率で電子をコア中心へ移動させる処理を実装します。具体的には、ある座標の値をグローバル解の値に置き換えることを意味し、これによりアルゴリズムの組合せ的性質が向上するはずです。ランダムな散布は解集団の多様性を確保するために有効でしたが、この性質によって電子は対数正規分布に従って分布し、移動中に空間内の任意の点に電子が到達する確率がゼロではない状態が保証されていました。

電子移動方程式の変更点は緑で表示されます。今回の改良では、増分は層の局所最良解と電子の個別最良解との差として計算されます。

//——————————————————————————————————————————————————————————————————————————————
// Update electron positions
void C_AO_AOSm::UpdateElectrons ()
{
  double α;      // speed coefficient
  double φ;      // transition probability
  double newPos; // new position
  double LE;     // best energy
  double BSk;    // connection state
  int    lID;    // layer ID

  // Handle each particle
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      φ = u.RNDprobab ();

      if (φ < PR)
      {
        // Random jump to center
        newPos = cB [c];
      }
      else
      {
        lID = electrons [p].layerID [c];

        α = u.RNDfromCI (-1.0, 1.0);

        // If the current particle energy is less than the average layer energy
        if (a [p].f < atoms [c].layers [lID].BEk)
        {
          // Moving towards the global optimum----------------------------
          LE     = cB [c];

          newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]);
        }
        else
        {
          // Movement towards the local optimum of the layer------------------------
          LE     = atoms [c].layers [lID].LEk;

          newPos = a [p].cB [c]+ α * (LE - a [p].cB [c]);
        }
      }

      // Limiting the new position within the search range taking into account the step
      a [p].c [c] = u.SeInDiSp (newPos, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

DistributeParticlesメソッドは、各座標に対して対数正規を用いて、電子を探索空間内に分布させます。各粒子および各座標について、与えられたパラメータ（平均値、最小値、最大値、ピーク）を基に位置を生成する関数が呼び出され、その後、指定された範囲内に位置を調整するための追加関数が適用されます。

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOS::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use log-normal distribution to position particles
      a [i].c [c] = u.LognormalDistribution (cB [c], rangeMin [c], rangeMax [c], peakPosition);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

電子配置を正規分布に変更します。この分布では標準偏差を8とします。本来であれば、このパラメータをアルゴリズムの外部から設定できるようにすることも可能でしたが、今回はそうしないことにしました。値を小さくすると探索空間を広く探索する傾向が強まり、逆に値を大きくすると大域解の精緻化時に収束精度が向上します。

//——————————————————————————————————————————————————————————————————————————————
// Distribution of particles in the search space
void C_AO_AOSm::DistributeParticles ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Use a Gaussian distribution to position particles
      a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

AOSアルゴリズムの元のバージョンに対して行ったすべての変更は、その効率性を向上させるために分析されました。探索戦略のロジックに大幅な変更を加えたため、この改良版アルゴリズムは文字「m」で表すことにします。以後、評価表には改良版のみを掲載し、名称はAOSmとします。


C_AOクラスの使用例

これまでに紹介したすべての集団最適化アルゴリズムは、共通の基底クラスであるC_AOクラスを継承しているため、さまざまな最適化問題に対して統一的かつ簡単に利用できます。以下の例は、目的関数の最適化をおこなうスクリプトの流れを示しています。

1. スクリプトの冒頭で、使用する最適化アルゴリズムを選択します。選択がない場合はエラーが報告され、処理は停止します。
2. パラメータの設定。関数の実行回数、最適化すべきパラメータの数、解群のサイズ、実行する反復数を定義します。
3. 値の制限設定。各パラメータに対して最小値と最大値（この例では-10から10）を設定します。
4. スクリプトが最適化を開始します。

  • 解（パラメータの組み合わせ）を生成し、特別な関数（目的関数）を用いてその良さを評価します。
  • 各反復で、アルゴリズムはより良い解に基づいて解群を更新します。

5. 結果表示。最適化が終了すると、使用されたアルゴリズム名、得られた最良値、関数が呼び出された回数などの情報を出力します。
6. 目的関数は抽象的な最適化問題であり（この例では逆放物線の大域最大値を求める問題を使用）、パラメータを受け取り、その質のスコアを返します。

#property script_show_inputs                           // Specify that the script will show the inputs in the properties window

#include <Math\AOs\PopulationAO\#C_AO_enum.mqh>        // Connect the library for handling optimization algorithms

input E_AO AOexactly = NONE_AO;                        // Parameter for selecting the optimization algorithm, default is NONE_AO

//——————————————————————————————————————————————————————————————————————————————
void OnStart()
{
  //----------------------------------------------------------------------------
  int numbTestFuncRuns = 10000;                        // Total number of function runs
  int params           = 1000;                         // Number of parameters for optimization
  int popSize          = 50;                           // Population size for optimization algorithm
  int epochCount       = numbTestFuncRuns / popSize;   // Total number of epochs (iterations) for optimization
  
  
  double rangeMin [], rangeMax [], rangeStep [];       // Arrays for storing the parameters' boundaries and steps
  
  ArrayResize (rangeMin,  params);                     // Resize 'min' borders array
  ArrayResize (rangeMax,  params);                     // Resize 'max' borders array
  ArrayResize (rangeStep, params);                     // Resize the steps array
  
  // Initialize the borders and steps for each parameter
  for (int i = 0; i < params; i++)
  {
    rangeMin  [i] = -10;                               // Minimum value of the parameter
    rangeMax  [i] =  10;                               // Maximum value of the parameter
    rangeStep [i] =  DBL_EPSILON;                      // Parameter step
  }
  
  //----------------------------------------------------------------------------
  C_AO *ao = SelectAO (AOexactly);                     // Select an optimization algorithm
  if (ao == NULL)                                      // Check if an algorithm has been selected
  {
    Print ("AO not selected...");                         // Error message if no algorithm is selected
    return;
  }
  
  ao.params [0].val = popSize;                         // Assigning population size....
  ao.SetParams ();                                     //... (optional, then default population size will be used)
  
  
  ao.Init (rangeMin, rangeMax, rangeStep, epochCount); // Initialize the algorithm with given boundaries and number of epochs
  
  // Main loop by number of epochs
  for (int epochCNT = 1; epochCNT <= epochCount; epochCNT++)
  {
    ao.Moving ();                                      // Execute one epoch of the optimization algorithm

    // Calculate the value of the objective function for each solution in the population
    for (int set = 0; set < ArraySize (ao.a); set++)
    {
      ao.a [set].f = ObjectiveFunction (ao.a [set].c); // Apply the objective function to each solution
    }

    ao.Revision ();                                    // Update the population based on the results of the objective function
  }
  
  //----------------------------------------------------------------------------
  // Output the algorithm name, best result and number of function runs
  Print (ao.GetName (), ", best result: ", ao.fB, ", number of function launches: ", numbTestFuncRuns);
  
  delete ao;                                           // Release the memory occupied by the algorithm object
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Definition of the user's objective function, in this case as an example - a paraboloid, F(Xn) ∈ [0.0; 1.0], X ∈ [-10.0; 10.0], maximization
double ObjectiveFunction (double &x [])
{
  double sum = 0.0;  // Variable for accumulation of the result

  // Loop through all parameters
  for (int i = 0; i < ArraySize (x); i++)
  {
    // Check if the parameter is in the allowed range
    if (x [i] < -10.0 || x [i] > 10.0) return 0.0;  // If the parameter is out of range, return 0
    sum += (-x [i] * x [i] + 100.0) * 0.01;         // Calculate the value of the objective function
  }
  
  return sum /= ArraySize (x);
}
//——————————————————————————————————————————————————————————————————————————————


テスト結果

アルゴリズムの修正バージョンのテストに移りましょう。

AOS|Atomic Orbital Search|50.0|10.0|20.0|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.8023218355650774
25 Hilly's; Func runs:10000; result:0.7044908398821188
500 Hilly's; Func runs:10000; result:0.3102116882841442
=============================
5 Forest's; Func runs:10000; result:0.8565993699987462
25 Forest's; Func runs:10000; result:0.6945107796904211
500 Forest's; Func runs:10000; result:0.21996085558228406
=============================
5 Megacity's; Func runs:10000; result:0.7461538461538461
25 Megacity's; Func runs:10000; result:0.5286153846153846
500 Megacity's; Func runs:10000; result:0.1435846153846167
=============================
All score:5.00645 (55.63%)

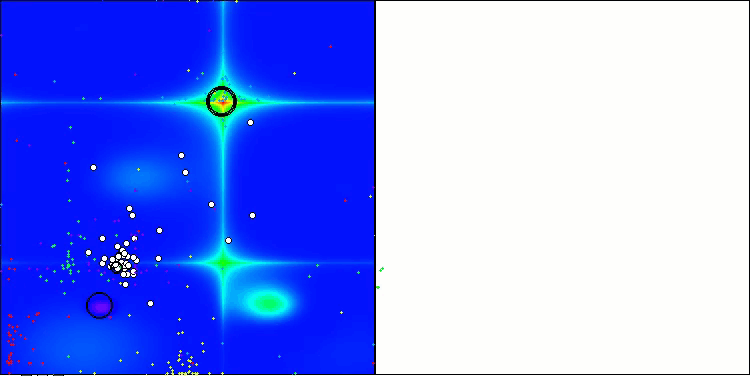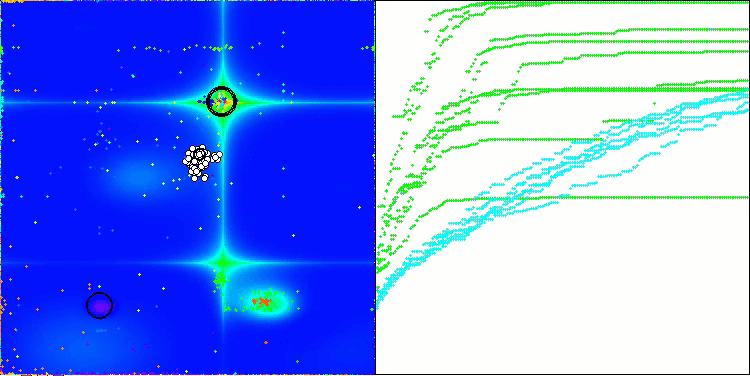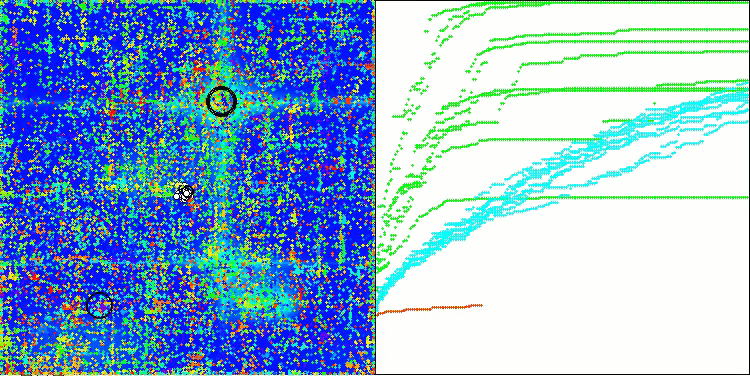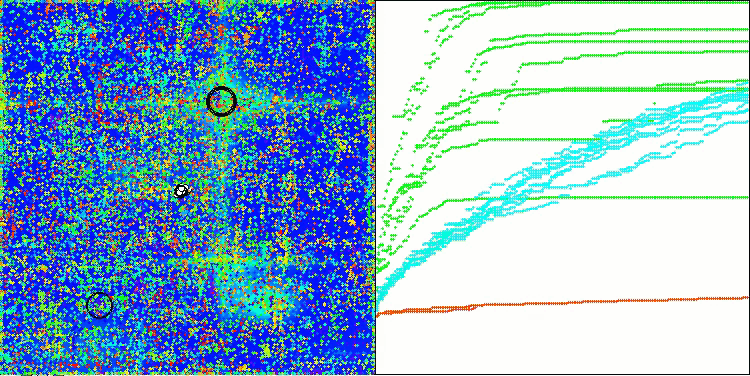
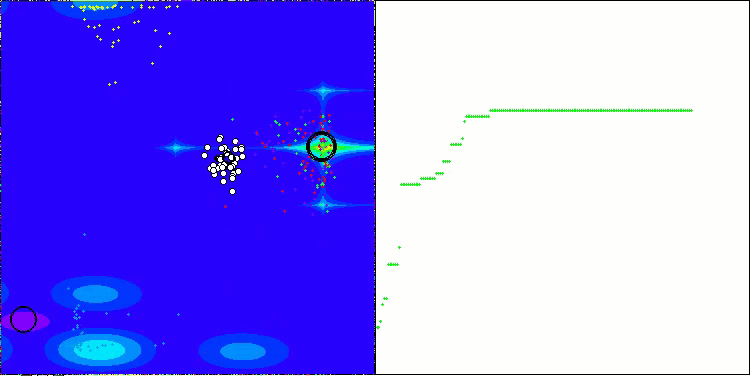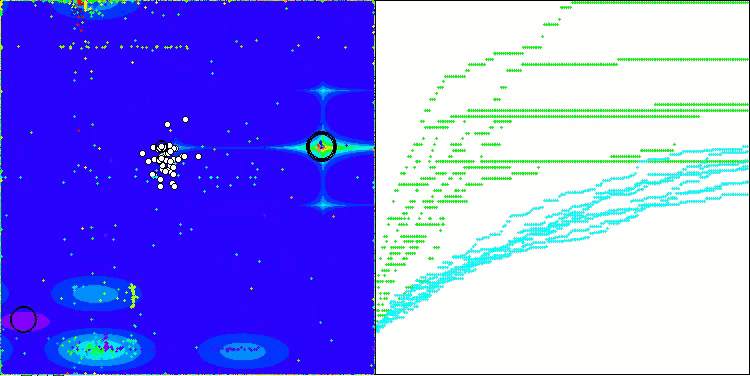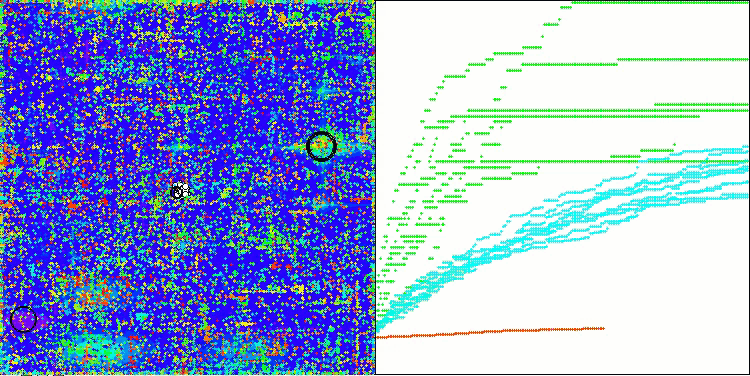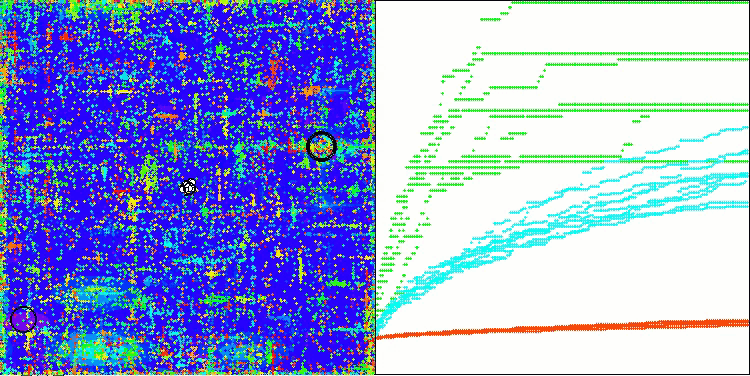
ご覧の通り、改良版の結果は元のバージョンの以前の結果（総合スコアが3.00488（33.39%））と比べて大幅に改善されています。この改善は、収束の向上だけでなく、有意な極値のより詳細な解析が視覚化で明確に確認できる点からも明らかです。

特に注目すべき重要な側面の1つは、個別の座標における解のクラスタリング効果です。この現象は元のバージョンおよび改良版の両方で観察され、AOSアルゴリズムの特徴的な性質を浮き彫りにしています。解のクラスタリングは、アルゴリズムが潜在的な最適解が存在する領域を効果的に見つけ出していることを示している可能性があります。

Hilly

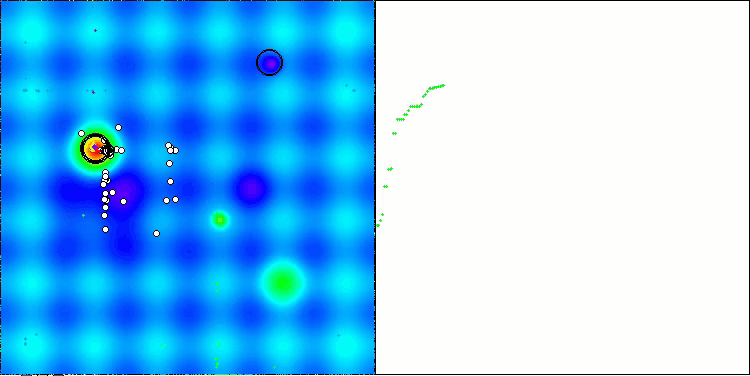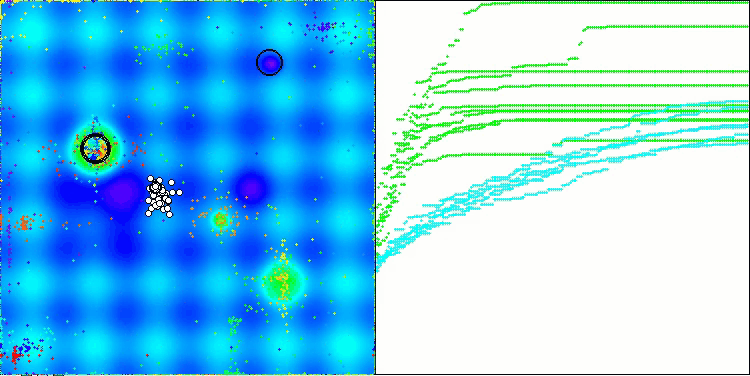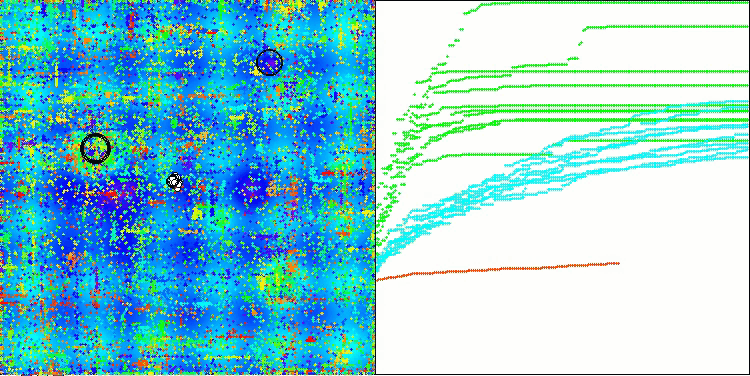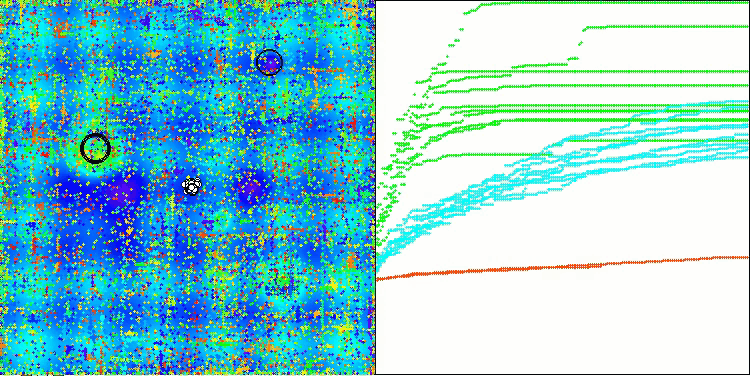
Hillyテスト関数のAOSm

Forest

Forestテスト関数のAOSm

Megacity

  Megacityテスト関数のAOSm

改良版の原子軌道検索(AOS: Atomic Orbital Search)アルゴリズムは、元のバージョンと比べて性能が大幅に向上し、現在では最大可能値の55％を超えています。これは非常に良好な結果と言えるでしょう。評価表においても、アルゴリズムは12位にランクインしており、非常に良好な結果を示しています。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
1 ANS Across Neighbourhood Search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
13 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
14 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
15 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
16 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
17 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
18 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
19 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
20 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
21 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
22 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
23 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
24 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
25 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
26 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
27 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
28 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
29 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
30 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
31 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
32 ASBO 適応型社会行動最適化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
33 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
34 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
35 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
36 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
37 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
38 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
39 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
40 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
41 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
42 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
43 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
44 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
45 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43


まとめ

本記事では、原子軌道探索アルゴリズムの修正版(AOSm)を紹介しました。修正版では、原子層内の電子のBSk平均位置を廃止し、各電子の個別の最良位置を採用しました。これにより、電子は平均値ではなく個々の成果に基づいて、各層内でより効率的に最良解へ移動できるようになりました。また、ランダム成分であるβiとγiを除外し、乱数生成にかかる時間を3分の1に短縮しましたが、アルゴリズムの物理的な意味は失われていません。

UpdateElectronsメソッドでは不要な変数を削除し、大域解への移動時に電子の増分を層の数で割る処理を廃止しました。元のバージョンの著者らは移動の度合いを可変にする意図があったかもしれませんが、私の実験ではそれによる大きな利点は確認されませんでした。

また、C_AO_AOSmクラスのUpdateElectronsメソッドにも変更を加え、電子のランダム散乱を一定確率で核の中心への移動に置き換えました。これによりアルゴリズムの組み合わせ的な特性が向上し、電子がより正確に大域解を狙えるようになりました。対数正規分布は正規分布に変更され、大域解の精密化時の収束精度が向上しました。

修正版AOSmの結果は大幅に改善し、最大値の55％を超える高いスコアを達成しており、アルゴリズムの高効率かつ競争力のあることを示しています。AOSmはランキング表で12位に位置し、他の最適化手法の中でも顕著な成果を収めています。

AOSmの最も顕著な特徴の一つは収束の改善であり、結果の可視化によって明らかになりました。アルゴリズムは重要な極値をより詳細に処理し、複雑な多次元空間における最適解の効果的な探索能力を示しています。オリジナル版および修正版の両方で観察される解のクラスタリング効果は、潜在的な最適解が存在する領域を特定し集中する能力を示しており、多次元かつ複雑な構造を持つ問題において特に有用です。

修正版のもう一つの利点は外部パラメータの削減であり、使用や設定が簡素化されています。ただし、これまでの記事で紹介した全てのアルゴリズムにおいては、多様な試験課題で最大効率を得るために最適な外部パラメータを選択済みであり、すべてのアルゴリズムはそのまま使用可能で設定不要です。本記事は、最適化アルゴリズムにおけるわずかな変更が探索特性を劇的に変えることがある一方で、探索戦略のロジックを大きく変更しても結果に目立った変化が見られない場合もあることを示しています。もちろん、私は効果的に最適化の効率を向上させる方法のみを共有しています。

Tab

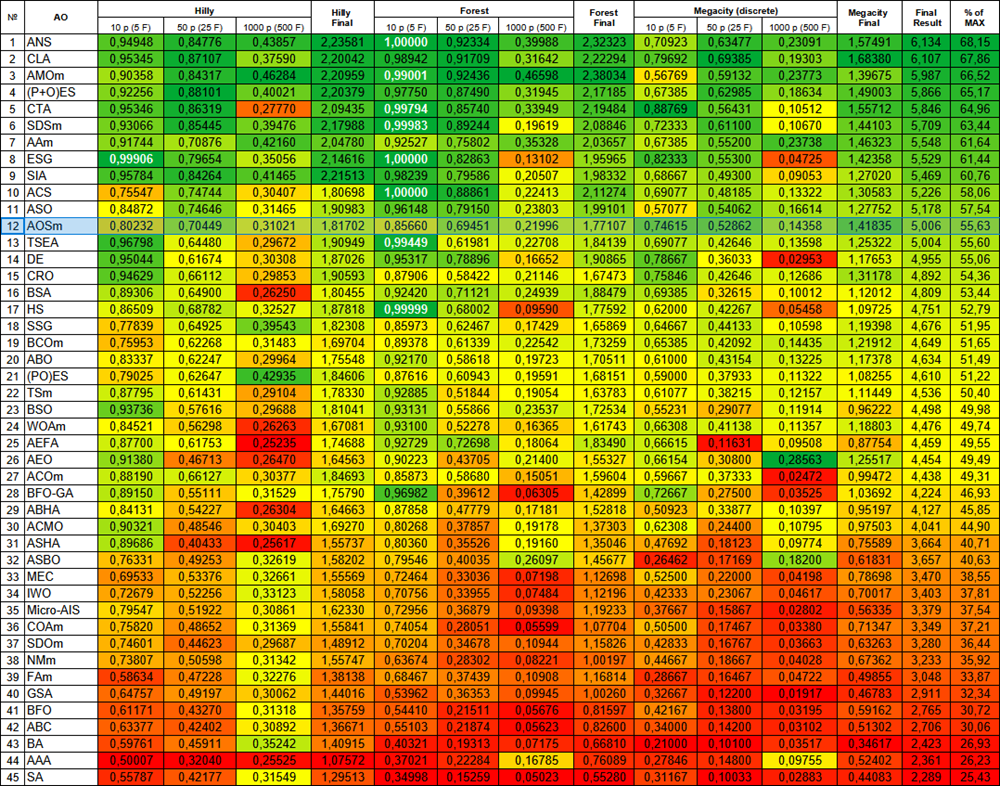
図2：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

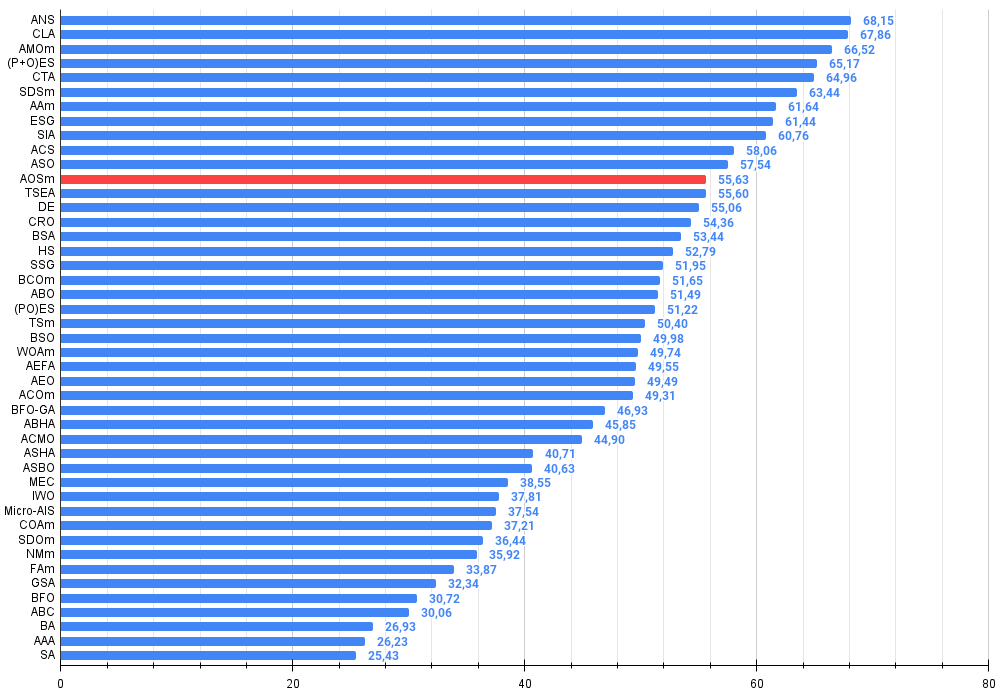
図3：アルゴリズムテスト結果のヒストグラム（0～100のスケール、数値が高いほど良い

ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている）


AOSmの長所と短所：

長所

  1. さまざまなタスクで優れたパフォーマンスを発揮する
  2. 外部パラメータの数が少ない
  3. 優れたスケーラビリティ
  4. 局所および大域両方の極値によるバランスの取れた検索

短所

  1. 実装がかなり複雑
  2. 他のアルゴリズムと比較した滑らかな関数の収束の平均精度

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

記事で使用されているプログラム

# 名前 種類 詳細
1 #C_AO.mqh
 インクルード
 集団最適化アルゴリズムの親クラス
2 #C_AO_enum.mqh
 インクルード
 集団最適化アルゴリズムの列挙
3 TestFunctions.mqh
 インクルード
 テスト関数のライブラリ
4
 TestStandFunctions.mqh
 インクルード
 テストスタンド関数ライブラリ
5
 Utilities.mqh
 インクルード
 補助関数のライブラリ
6
 CalculationTestResults.mqh
 インクルード
 比較表の結果を計算するスクリプト
7
 Testing AOs.mq5
 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
8
 Simple use of population optimization algorithms.mq5
 スクリプト
可視化せずに集団最適化アルゴリズムを使用する簡単な例
9
 AO_AOSm_AtomicOrbitalSearch.mqh
 インクルード AOSmアルゴリズムクラス
10
 Test_AO_AOSm.mq5
 スクリプト
 AOSmテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16315

添付されたファイル |
ZIPをダウンロード
AOSm.zip (139.64 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (5)
Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 において 11:51

記事をありがとう！

昨日と今日、Hilly関数とalglibメソッドについてしばらく考えていました。以下は私の考えです。

この関数の最大値を求めるには、特にパラメータの数が10以上の場合、勾配法を適用するのは無意味である。勾配法は瞬時に局所極限から抜け出せなくなる。また、パラメータ空間の新しい点から何度再スタートしても、勾配法が瞬時に解を見つける正しい空間領域に到達する確率は、パラメータの数が増えるにつれてゼロになる傾向がある。

例えば、lbfgsや2(2)反復のCGが、どのようなパラメータ数でも最大値を見つける空間の点は、{x = -1,2 , y = 0.5}である。


lbfgs

しかし、私が言ったように、この領域に入る可能性はゼロに等しい。乱数を生成するのに100年はかかるだろう。

したがって、この記事で紹介した遺伝的アルゴリズム（偵察と探索空間の縮小ができる）と、より有利な点から素早く極限を見つける勾配法を組み合わせる必要がある。

Andrey Dik
Andrey Dik | 15 11月 2024 において 16:25
Evgeniy Chernish #:

記事をありがとう！

ご意見ありがとうございます。

与えられた関数の最大値を求めるために、特にパラメータの数が10以上の場合、勾配法を使うのは無意味です。

その通りです。

これが組合せ最適化法の課題なのです。

古典的な「蟻」のような組合せ手法は、「巡回セールスマン問題」や「ナップザック問題」のような問題、つまり一定のステップ（グラフの辺）を持つ離散問題用に設計されている。多次元的な「連続」問題に対しては、これらのアルゴリズムは全く設計されていない。例えば、ニューラルネットワークのトレーニングのようなタスクに対しては。たしかに、組み合わせ論的特性は確率的ヒューリスティック手法にとって非常に有用だが、このような実問題に近いテスト問題をうまく解くための唯一かつ十分な特性ではない。アルゴの探索戦略自体も重要である。

勾配ベースのものは、単に局所的な極限で即座に立ち往生してしまう。そして、パラメータ空間の新しい点から何度再スタートしても、パラメータの数が増えるにつれて、勾配法が瞬時に解を見つける空間の正しい領域に到達する確率はゼロになる傾向がある。

その通りだ。

しかし、この領域に到達する確率は、すでに述べたように、単純にゼロである。乱数を発生させるのに100年くらいかかるでしょう。

そうです。低次元空間（1～2次元）では、大域近傍に到達するのは非常に簡単で、単純な乱数生成器でも十分機能します。しかし、問題の次元が大きくなるとすべてが一変し、運ではなくアルゴリズムの探索特性が重要な役割を果たすようになる。

したがって、この記事で紹介されている遺伝的アルゴリズム（探索を行い、探索空間を縮小する）と勾配法を組み合わせる必要がある。

「遺伝的」とは、おそらく「発見的」という意味だろう。なぜ「魚には傘が必要」なのか、「なぜ鍛冶屋が必要なのか？ 鍛冶屋は必要ない」）））。連続空間の複雑な多次元問題を解く効率的な方法があり、それは母集団法の記事で説明されている。そして古典的な勾配問題には、一次元の解析的に決定可能な問題という独自のタスクがあります（この問題では同等のものはなく、高速で正確な収束があります）。

そして質問ですが、ヒューリスティックスの速度についてどのような印象をお持ちですか？

SZY:

ああ、なんと多くの不思議な発見があることだろう。

悟りの精神を準備し

そして経験、誤りの息子、

そして天才、逆説の友、

そして偶然、神の発明者。


ZZZY ちょっと待って。未知の探索空間では、どの瞬間、どの反復のステップにおいても、それが本当にグローバルに向かう有望な方向であるかどうかを知ることは不可能である。したがって、最初に偵察し、後で改良することは不可能である。全体探索戦略だけが機能し、それらはうまく機能するか、あるいはうまく機能しないかのどちらかである。この目的のために、タスクの仕様に応じてアルゴリズムを選択するための評価表が保管されている。

Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 において 16:53
Andrey Dik #:
その通りである。低次元空間（1-2次元）では、大域的な近傍に入るのは非常に簡単で、単純なランダム・ジェネレーターがこれに役立つことさえある。しかし、問題の次元が大きくなるとすべてが一変し、運ではなくアルゴリズムの探索特性が重要な役割を果たすようになる。

つまり、失敗するのだ。

Andrey Dik#:
それから質問ですが、ヒューリスティックのスピードについてはどう思われますか？

高速に動作するという事実にもかかわらず。1000個のパラメーターで0.4という結果です。

だから、GAと勾配法を組み合わせて最大にするのが理にかなっていると直感的に思いました。そうでなければ、別々にやっても関数は解けない。実際にテストしたわけではありませんが。


P.S.やはりこの関数は厚すぎると思います。実際のタスク（例えばニューラルネットワークのトレーニング）では、そのような問題はありませんが、そこでも誤差表面はすべてローカル・ミニマムになります。

Andrey Dik
Andrey Dik | 15 11月 2024 において 18:47
Evgeniy Chernish #:

1.良い仕事をしていない

2.仕事が速いのに。1000個のパラメータに対する結果は0.4といったところだ。

3.だから、GAと勾配法を組み合わせて最大値を求めるのが理にかなっていると直感的に思った。そうでなければ、別々にやっても関数は解けない。実際にはテストしていない。

4.P.S.やはりこの関数は厚すぎると思います。実際のタスク（例えばニューラルネットワークのトレーニング）では、そのような問題はありませんが、そこでもエラーサーフェスはすべてローカルミニマムになります。

1.対応できない」とはどういう意味ですか？ターゲット関数へのアクセス数には制限があり、より良い結果を示したのは対処できない方である))。許可されるアクセス数を増やすべきか？それなら、より機敏で複雑な関数に適応した方が、いずれにせよゴールにたどり着けるだろう。参照数を増やしても、状況は変わらない。

2.0.3を示す者もいれば、0.2を示す者もいれば、0.001を示す者もいる。

3.直感的には、何百もの組み合わせとバリエーションが試され、再試行されている。与えられたエポック（反復）数でより良い結果を示すものがより良い。ターゲットへの参照回数を増やし、どちらが先にゴールに到達するかを見る。

4.4.難しいタスクでリーダーがいる場合、簡単なタスクでもリーダーはアウトサイダーより悪い結果を示すと思いますか？控えめに言ってもそうではない。私は今、グリッド・トレーニングという、より "簡単 "だが現実的な課題に取り組んでいる。いつものように結果をシェアするつもりだ。面白いだろう。


とにかく実験して、いろいろなアルゴリズム、いろいろなタスクを試してみてください。そのためのツールはすべて用意したつもりだ。

Evgeniy Chernish
Evgeniy Chernish | 15 11月 2024 において 19:18
Andrey Dik #:

1."失敗 "とはどういう意味ですか？対象関数へのアクセス数には制限があり、最高の結果を示した方は対応できない方です))。許可されるアクセス数を増やすべきか？それなら、より機敏で複雑な関数に適応している方が、いずれにせよゴールにたどり着けるだろう。参照数を増やしても、状況は変わらない。

2.0.3という人もいれば、0.2という人もいるし、0.001という人もいる。

3.直感的には、何百もの組み合わせとバリエーションが試され、再試行されている。与えられたエポック（反復）数でより良い結果を示すものがより良い。ターゲットへの参照回数を増やし、どちらが先にゴールに到達するか見てみよう。

4.4.難しいタスクでリーダーがいる場合、簡単なタスクでもリーダーは部外者より悪い結果を示すと思いますか？控えめに言ってもそうではない。私は今、グリッド・トレーニングという、より "簡単 "だが現実的な課題に取り組んでいる。いつものように結果をシェアするつもりだ。興味深いものになるだろう。


一つのことに固執せず、いろいろなアルゴリズム、いろいろなタスクを試してみてほしい。そのためのツールはすべて提供するつもりだ。

私は実験をしているのだ、

ANS

現実的なタスクについては、戦闘に近いタスクでアルゴリズムをテストするのが正しい。

遺伝的ネットワークがどのように訓練されるかを見るのは二重に興味深い。

リプレイシステムの開発（第75回）：新しいChart Trade(II) リプレイシステムの開発（第75回）：新しいChart Trade(II)
この記事では、C_ChartFloatingRADクラスについて説明します。これはChart Tradeを機能させるための要となる部分です。ただし、解説はこれで終わりではありません。本記事の内容はかなり広範かつ深い理解を必要とするため、続きは次回の記事で補完します。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。
初心者からプロまでMQL5をマスターする（第6回）：エキスパートアドバイザー開発の基礎 初心者からプロまでMQL5をマスターする（第6回）：エキスパートアドバイザー開発の基礎
この記事は初心者向け連載の続きです。今回はエキスパートアドバイザー(EA)開発の基本原理について解説します。2つのEAを作成します。1つ目はインジケーターを使わず、予約注文で取引をおこなうEA。2つ目は標準の移動平均線(MA)インジケーターを利用し、成行価格で取引をおこなうEAです。ここでは、前回までの記事の内容をある程度理解していることを前提としています。
初級から中級まで：再帰 初級から中級まで：再帰
この記事では、とても興味深く、難易度のやや高いプログラミングの概念について見ていきます。ただし、この概念は細心の注意をもって扱うべきです。なぜなら、誤用や誤解によって、本来は比較的単純なプログラムが、不要に複雑化してしまう危険があるからです。しかし、正しく使用し、かつ適切な状況にうまく適用できれば、再帰は、そうでなければ非常に面倒で時間のかかる問題を解決するための優れた味方となります。ここに掲載されている資料は、教育目的のみのものです。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。
取引におけるニューラルネットワーク：時系列予測のためのTransformerの最適化(LSEAttention) 取引におけるニューラルネットワーク：時系列予測のためのTransformerの最適化(LSEAttention)
LSEAttentionフレームワークは、Transformerアーキテクチャの改善を提供します。この手法は、特に長期の多変量時系列予測のために設計されました。提案されたアプローチは、従来のTransformerでよく遭遇するエントロピーの崩壊や学習の不安定性の問題を解決するために応用可能です。