
Kreis-Such-Algorithmus (CSA)
Inhalt
Einführung
Der Circle Search Algorithm (CSA) ist eine neue Optimierungsmethode, die von den geometrischen Eigenschaften eines Kreises inspiriert ist. Seine Einzigartigkeit liegt in der Verwendung trigonometrischer Beziehungen und geometrischer Prinzipien zur Erkundung des Suchraums.
Die CSA basiert auf einer interessanten Idee, bei der sich jeder Suchpunkt entlang einer durch eine Tangente an einen Kreis definierten Bahn bewegt, wodurch ein Gleichgewicht zwischen globaler Erkundung und lokaler Verfeinerung der Lösung geschaffen wird. Dieser Ansatz ist originell, denn ein Kreis hat einzigartige mathematische Eigenschaften – einen konstanten Radius und eine kontinuierliche Ableitung – die eine reibungslose Bewegung der Agenten im Suchraum gewährleisten.
Der Algorithmus kombiniert zwei Phasen: Ausbeutung und Erkundung. In der Exploitation-Phase konzentrieren sich die Agenten auf vielversprechende Bereiche und bewegen sich eher zielgerichtet, während sie in der Exploration-Phase kühnere Sprünge in unerforschte Bereiche des Lösungsraums machen. Der Übergang zwischen den Phasen wird durch einen Mechanismus geregelt, der auf der aktuellen Iteration und einem speziellen „c“-Parameter basiert.
Was CSA besonders attraktiv macht, ist seine Fähigkeit, effizient in hochdimensionalen Räumen zu arbeiten und dabei eine intuitive geometrische Interpretation beizubehalten. Jeder Agent in der Population folgt seiner eigenen einzigartigen Flugbahn, die durch den θ-Winkel bestimmt wird, der während der Suche dynamisch angepasst wird.
Der Circle Search Algorithm (CSA) wurde von den Forschern Mohammad H. Kaiys, Hany M. Hasanien und anderen entwickelt und im Jahr 2022 veröffentlicht.
Implementierung des Algorithmus
Der Kreissuchalgorithmus (CSA) zielt darauf ab, die optimale Lösung in zufälligen Kreisen zu finden, um das Suchgebiet zu erweitern. Dabei wird der Mittelpunkt des Kreises als Zielpunkt verwendet. Der Prozess beginnt damit, dass der Winkel zwischen der Tangente und dem Kreis allmählich kleiner wird, sodass sich die Tangente dem Mittelpunkt nähert (Abbildung 1).
Um für Abwechslung bei der Suche zu sorgen und zu vermeiden, dass man in lokalen Optima stecken bleibt, ändert sich auch der Winkel des tangentialen Kontakts zufällig. Im Rahmen des Algorithmus fungiert der Tangentenpunkt Xt als Suchagent, während der zentrale Punkt Xc die beste gefundene Lösung bezeichnet.
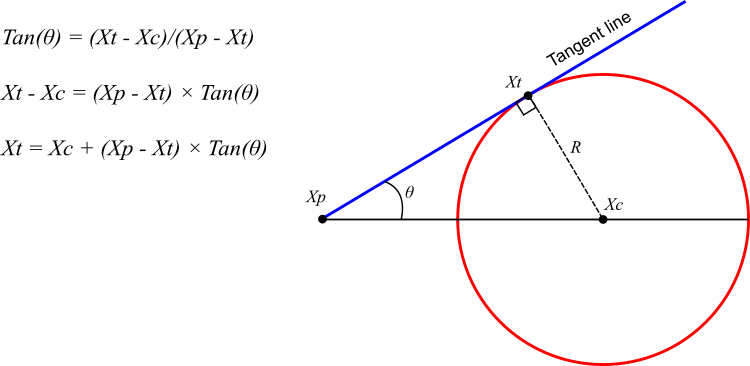
Abbildung 1. Geometrische Eigenschaften eines Kreises und seiner Tangente
CSA passt die Position des Suchagenten als Reaktion auf die Bewegung des Berührungspunkts zur Mitte hin an. Auf diese Weise lässt sich die Qualität der Lösung verbessern, während die zufällige Aktualisierung des tangentialen Kontaktwinkels als wichtiger Mechanismus zur Vermeidung lokaler Minima dient. Die wichtigsten Arbeitsschritte des CSA-Optimierers sind im folgenden Diagramm dargestellt.

Abbildung 2. CSA-Betriebsplan
Anschließend wird für jeden Agenten ein Winkel bestimmt. Ist die aktuelle Iteration größer als das Produkt aus dem Schwellenwert und der maximalen Anzahl der Iterationen, befindet sich der Agent in der Explorationsphase, andernfalls wird die Exploitation-Phase angewendet (siehe Abbildung 2). Die Positionen der Agenten werden aktualisiert und die Eignung der einzelnen Agenten wird bewertet. Die Ergebnisse werden mit der aktuell besten Lösung verglichen, und wenn eine bessere Lösung gefunden wird, wird die Position aktualisiert. Eine Iteration wird durch Inkrementieren des Iterationszählers beendet. Wenn der Algorithmus seine Ausführung beendet hat, gibt er die beste gefundene Position und ihren Fitnesswert zurück.
Der Algorithmus verwendet das Konzept der Bewegung von Punkten entlang einer Tangente an einen Kreis, wobei sich jeder Suchagent in einem bestimmten Winkel θ relativ zur aktuell besten Lösung bewegt. Diese Bewegung wird durch mehrere Parameter (w, a, p) bestimmt, die sich im Laufe der Zeit ändern. Wie bereits erwähnt, gliedert sich der Algorithmus in zwei Phasen: die Erkundung, bei der die Agenten größere Bewegungen ausführen, um vielversprechende Bereiche zu finden, und die Nutzung, bei der sich die Agenten auf die Verfeinerung der gefundenen Lösungen konzentrieren.
Die endgültige Version, die ich vorgeschlagen habe, enthält mehrere Unterschiede, die die Suchmöglichkeiten des Algorithmus erheblich verbessern. Die w-Aktualisierungsgleichung wurde geändert:
- Die ursprüngliche Variante: w = w × rand – w
- Der endgültige Code: w = π × (1 – epochNow/epochs). Dadurch wurde die Änderung des Parameters w vorhersehbarer und linearer, was die Konvergenz des Algorithmus verbessert.
- Das Original: Xi = Xc + (Xc – Xi) × tan(θ)
- Die endgültige Fassung: Xi = Xc + rand × (Xc – Xi) × tan(θ). Die Hinzufügung eines Zufallsfaktors „rand [0,0; 1,0]“ fügt der Suche zusätzliche Stochastizität hinzu und verbessert sie gegenüber der ursprünglichen Version.
- Aktualisierung der besten lokalen Lösung für jeden Agenten hinzugefügt
- Verbesserte Ausgleichsstrategie zwischen globaler und lokaler Suche
Der wichtigste konzeptionelle Unterschied besteht darin, dass der Algorithmus in der endgültigen Version „geschmeidiger“ und in seinem Verhalten vorhersehbarer wurde, während die Fähigkeit zur Suche beibehalten wurde. Der ursprüngliche Algorithmus war in seinem Verhalten eher „chaotisch“, während die endgültige Version eine kontrolliertere Optimierung bietet, vor allem in Bezug auf den Übergang zwischen der Explorations- und der Verwertungsphase.
Jetzt können wir mit der Entwicklung des Pseudocodes für den Algorithmus beginnen.
Pseudocode des Kreissuchalgorithmus (CSA):
- Initialisierung:
- Festlegen der Populationsgröße (popSize = 50)
- Einstellen der Phasenkonstante der Studie (constC = 0,8)
- Initialisieren der Anfangsparameter:
- w = π (Winkelparameter)
- a = π
- p = 1.0
- θ = 0 (Anfangswinkel)
- Im Falle der ersten Iteration (Revision = false):
- Für jeden Agenten i in der Population:
- Zufallsinitialisierung der Koordinaten innerhalb der vorgegebenen Grenzen
- Koordinaten entsprechend dem Änderungsschritt anpassen
- Revision = true setzen
- Rückkehr zum Start
- Für jeden Agenten i in der Population:
- Andernfalls (Hauptoptimierungsschleife):
- Erhöhung des Iterationszählers (epochNow++)
- Parameter aktualisieren:
- w = π × (1 – epochNow/epochs) // lineare Abnahme
- a = π – π × (epochNow/epochs)²
- p = 1 – 0.9 × √(epochNow/epochs)
- Für jeden Agenten in der Population:
- Bestimmen der aktuelle Phase:
- Wenn: epochNow ≤ constC × epochs: → Exploration phase: θ = w × random [0.0; 1.0]
- Ansonsten: → Verwertungsphase: θ = w × p
- Aktualisieren der Agentenposition:
- Für jede Koordinate j: → new_pos = best_pos + random [0.0; 1.0] × (best_pos – current_pos) × tan (θ) → new_pos innerhalb der vorgegebenen Grenzen anpassen
- Bestimmen der aktuelle Phase:
- Revision der Ergebnisse:
- Für jeden Agenten:
- Wenn die Fitness des Agenten > global beste Fitness: → Aktualisierung der besten globalen Lösung
- Wenn die Fitness des Agenten > lokal beste Fitness: → Aktualisierung der besten lokalen Lösung des Agenten
- Für jeden Agenten:
- Wiederholen der Schritte 3-5, bis das Abbruchkriterium erreicht ist.
Kommen wir nun zur Umsetzung. Die Klasse C_AO_CSA ist eine Implementierung des CSA-Algorithmus und wird von der Basisklasse C_AO geerbt. Schauen wir uns seine wichtigsten Elemente und seine Struktur an:
Der Konstruktor initialisiert die Parameter des Algorithmus. Sie gibt den Namen und die Beschreibung des Algorithmus an und setzt Werte für die Parameter:- popSize – Größe der Population gleich 50.
- constC – Konstante von 0,8, die in der Erkundungsphase verwendet wird.
- w, aParam, p, theta – Anfangswerte der für den Algorithmus zu verwendenden Parameter.
- SetParams () – Methode zum Setzen von Parameterwerten auf der Grundlage des Datenarrays „params“.
- Init () – die Methode wird implementiert, um die Parameter bezüglich der Wertebereiche und der Anzahl der Epochen, über die der Algorithmus ausgeführt wird, zu initialisieren.
- Moving () – wird verwendet, um Partikel zu bewegen und Algorithmus-Iterationen durchzuführen.
- Revision () – Analyse und Anpassung des Zustands der Population.
Private Methoden:
- CalculateW (), CalculateA (), CalculateP (), CalculateTheta () – Methoden zur Berechnung der entsprechenden Parameter.
- IsExplorationPhase () – Methode bestimmt, ob sich der Algorithmus in der Erkundungsphase befindet.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CSA : public C_AO { public: //-------------------------------------------------------------------- C_AO_CSA () { ao_name = "CSA"; ao_desc = "Circle Search Algorithm"; ao_link = "https://www.mql5.com/en/articles/17143"; popSize = 50; // population size constC = 0.8; // optimal value for the exploration phase w = M_PI; // initial value w aParam = M_PI; // initial value a p = 1.0; // initial value p theta = 0; // initial value of the angle ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "constC"; params [1].val = constC; } void SetParams () { popSize = (int)params [0].val; constC = params [1].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double constC; // constant for determining the search phase [0,1] private: //------------------------------------------------------------------- int epochs; // maximum number of iterations int epochNow; // current iteration // Parameters for CSA double w; // parameter for calculating the angle double aParam; // parameter a from the equation (8) double p; // parameter p from the equation (9) double theta; // search angle double CalculateW (); double CalculateA (); double CalculateP (); double CalculateTheta (double currentW, double currentP); bool IsExplorationPhase (); }; //——————————————————————————————————————————————————————————————————————————————
Die Init-Methode ist für die Initialisierung der Parameter des CSA-Algorithmus vorgesehen. Zu seinen Parametern gehören das rangeMinP[]-Array mit den Minimalwerten des Suchraums, das rangeMaxP[]-Array mit den Maximalwerten, das rangeStepP[]-Array mit den Inkrementen der sich ändernden Werte und die Anzahl der Epochen, die durch den Parameter epochsP angegeben wird, der standardmäßig auf 0 steht.
Während der Ausführung der Methode wird StandardInit aufgerufen, mit dem versucht wird, die Standardparameter zu initialisieren. Wenn die Initialisierung erfolgreich ist, werden die Werte für die Variablen epochs und epochNow gesetzt. Die Variable epochs erhält ihren Wert von epochsP, während epochNow gelöscht wird. Die Methode schließt die Ausführung ab, indem sie „true“ zurückgibt, was die erfolgreiche Initialisierung der Algorithmusparameter anzeigt.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving in der Klasse C_AO_CSA implementiert die Logik zur Aktualisierung der Agentenpositionen innerhalb des CSA-Algorithmus. Zu Beginn der Methode wird der aktuelle Epochenzähler inkrementiert, sodass wir verfolgen können, wie viele Iterationen durchgeführt wurden (in den Berechnungsgleichungen verwendet). Dann wird geprüft, ob die Koordinaten der Agenten initialisiert werden müssen. Wenn dies die erste Ausführung der Methode ist, werden für alle Agenten in den angegebenen Bereichen zufällige Koordinaten erzeugt. Diese Koordinaten werden dann so angepasst, dass die vorgegebenen Schritte berücksichtigt werden. Danach wird das Flag für die Notwendigkeit der Überarbeitung auf true gesetzt.
Wird die Methode nicht zum ersten Mal aufgerufen, werden die Schlüsselparameter des Algorithmus, wie w, aParam und p, aktualisiert. Dann wird für jeden Agenten der Theta-Winkel berechnet und zur Aktualisierung seiner Koordinaten verwendet. Jede Koordinate wird unter Berücksichtigung der Koordinaten des besten Agenten, des Einflusses des Zufallsfaktors und des Winkels Theta aktualisiert. Danach werden die Ergebnisse ebenfalls so angepasst, dass sie innerhalb der angegebenen Bereiche bleiben.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //---------------------------------------------------------------------------- w = CalculateW (); // Update w linearly aParam = CalculateA (); // Update a p = CalculateP (); // Update p for (int i = 0; i < popSize; i++) { theta = CalculateTheta (w, p); for (int j = 0; j < coords; j++) { a [i].c [j] = cB [j] + u.RNDprobab () * (cB [j] - a [i].c [j]) * tan (theta); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode ist für die Aktualisierung der besten Lösungen in der gesamten Population zuständig. Es überprüft die aktuellen Werte der Zielfunktion der Agenten und aktualisiert die entsprechenden Parameter, wenn bessere Lösungen gefunden werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Revision () { for (int i = 0; i < popSize; i++) { // Update the best global solution if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateW dient der Berechnung des Wertes des Parameters w, der mit zunehmender Anzahl der aktuellen Epochen (epochNow) im Verhältnis zur Gesamtzahl der Epochen linear vom Anfangswert (M_PI) auf „0“ abnimmt, und gibt den berechneten Wert von w zurück. Dieser berechnete Parameter wird in die Gleichung zur Berechnung des Winkels Theta einbezogen.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateW () { // Linear decrease of w from the initial value (M_PI) to 0 return M_PI * (1.0 - (double)epochNow / epochs); //return w * u.RNDprobab () - w; } //——————————————————————————————————————————————————————————————————————————————Die Methode CalculateA berechnet den aParam-Wert, der von M_PI auf 0 abnimmt, wenn epochNow zunimmt, und zwar quadratisch in Abhängigkeit von der Gesamtzahl der Epochen.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateA () { return M_PI - M_PI * MathPow ((double)epochNow / epochs, 2); } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateP berechnet den p-Wert, der mit zunehmender EpocheNow von „1,0“ auf „0,1“ abnimmt, d.h. er hängt von der aktuellen Epoche ab.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateP () { return 1.0 - 0.9 * MathPow ((double)epochNow / epochs, 0.5); } //——————————————————————————————————————————————————————————————————————————————
Die Methode CalculateTheta berechnet den Wert von Theta anhand der aktuellen Parameter currentW und currentP.
- Wenn die aktuelle Phase Forschung ist, wird currentW multipliziert mit einer Zufallszahl zurückgegeben.
- Andernfalls wird das Produkt aus currentW und currentP zurückgegeben.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateTheta (double currentW, double currentP) { // Use the aParam parameter to adjust the angle if (IsExplorationPhase ()) return currentW * u.RNDprobab (); else return currentW * currentP; } //——————————————————————————————————————————————————————————————————————————————
Die Methode IsExplorationPhase prüft, ob sich die aktuelle Iteration in der Explorationsphase befindet.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::IsExplorationPhase () { // Research in the first part of the iterations (constC is usually 0.8) return (epochNow <= constC * epochs); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Die Autoren des Algorithmus bezeichnen ihn als hocheffiziente Optimierungsmethode. Nach der Umsetzung, einigen Verbesserungen und abschließenden Tests sind die Ergebnisse jedoch nicht sehr beeindruckend. Der Algorithmus konnte sich in der Rangliste platzieren, seine Leistung ist jedoch deutlich schlechter als die der derzeit besten algorithmischen Lösungen.CSA|Circle Search Algorithm|50.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.6656012653478078
25 Hilly's; Func runs: 10000; result: 0.4531682514562617
500 Hilly's; Func runs: 10000; result: 0.2912586479936386
=============================
5 Forest's; Func runs: 10000; result: 0.6879687203647712
25 Forest's; Func runs: 10000; result: 0.41397289345600924
500 Forest's; Func runs: 10000; result: 0.2052507546137296
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2363076923076922
500 Megacity's; Func runs: 10000; result: 0.10646153846153927
=============================
All score: 3.43537 (38.17%)
Die Visualisierung des Algorithmus zeigt Probleme mit der Konvergenz und dem Verharren an lokalen Extremen. Dennoch versucht der Algorithmus, so gut wie möglich zu arbeiten. Trotz der Probleme mit dem Steckenbleiben in Fallen (dies ist deutlich an den langen horizontalen Abschnitten im Konvergenzdiagramm zu erkennen), kann man seine Fähigkeit hervorheben, bei hochdimensionalen Problemen recht effektiv zu arbeiten.
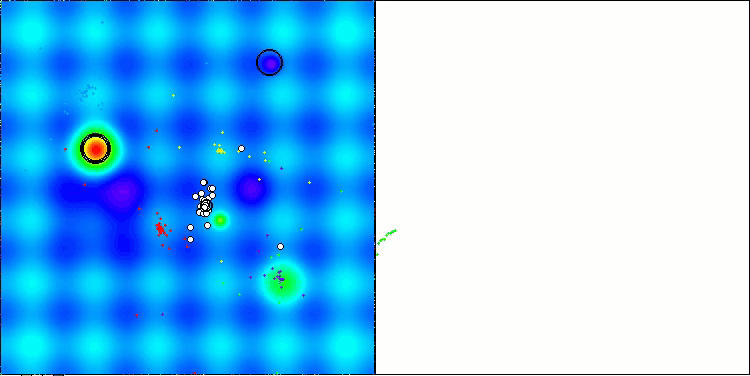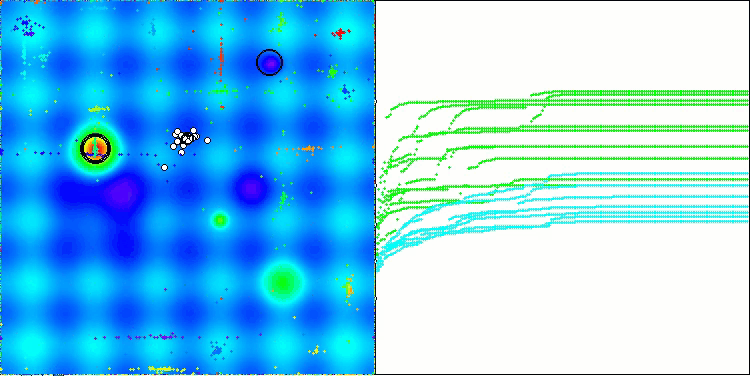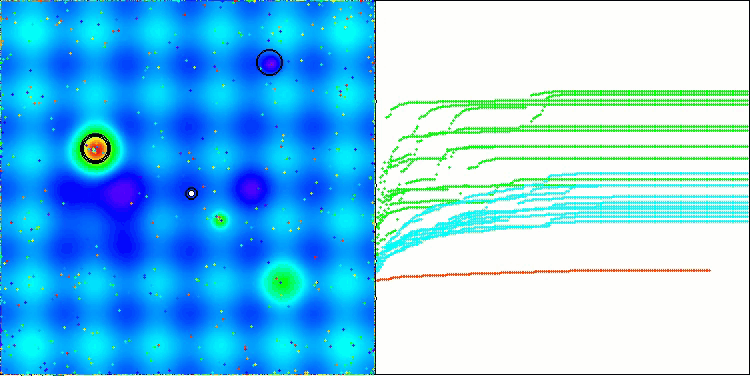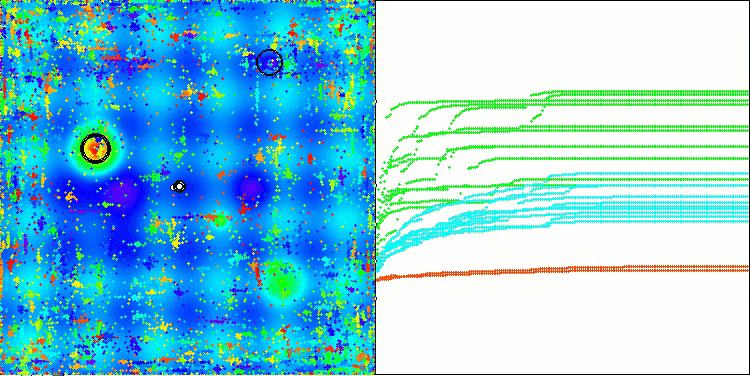
CSA mit der Testfunktion Hilly
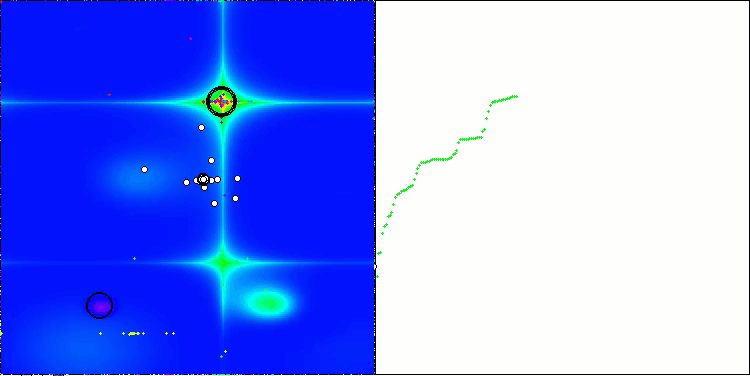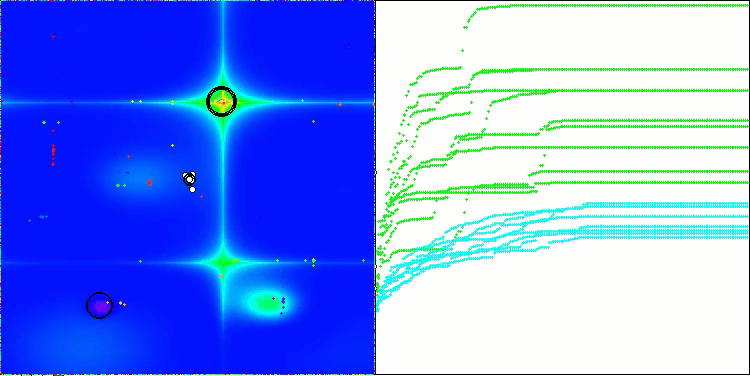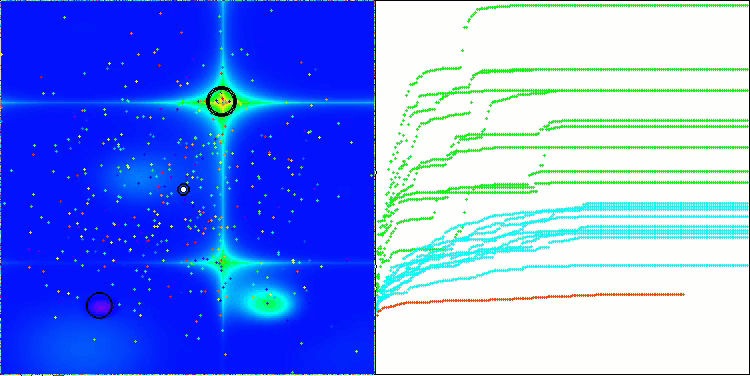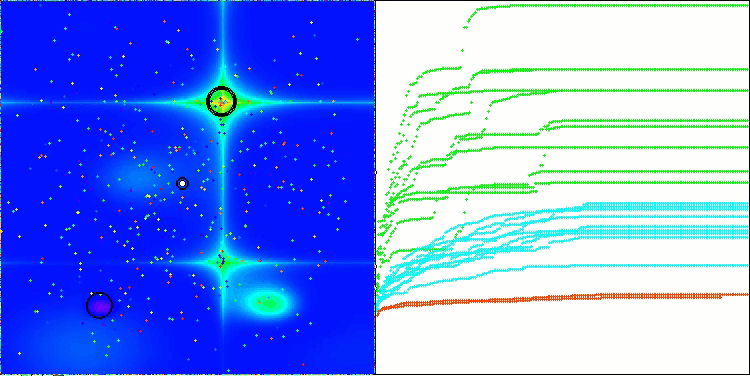
CSA mit der Testfunktion Forest
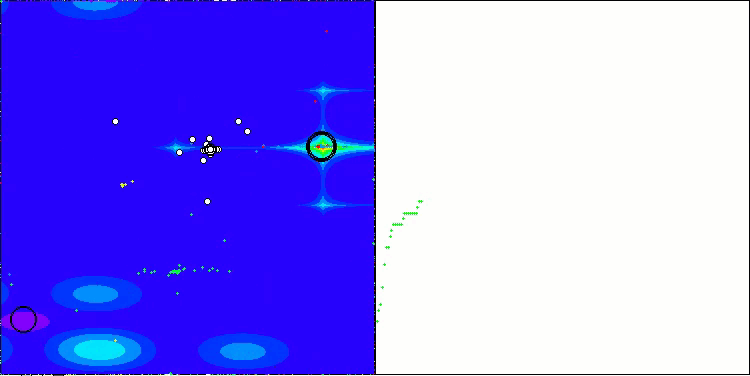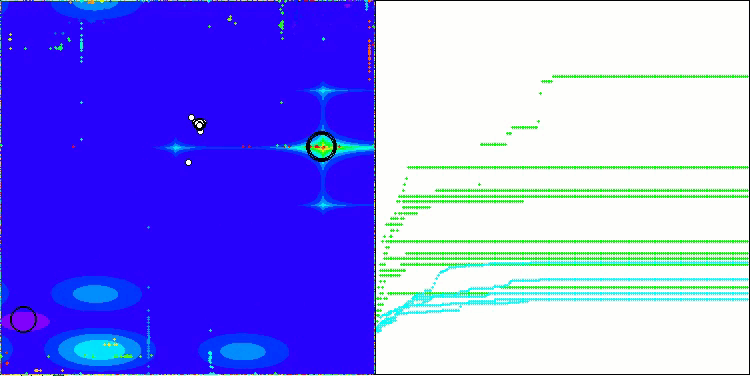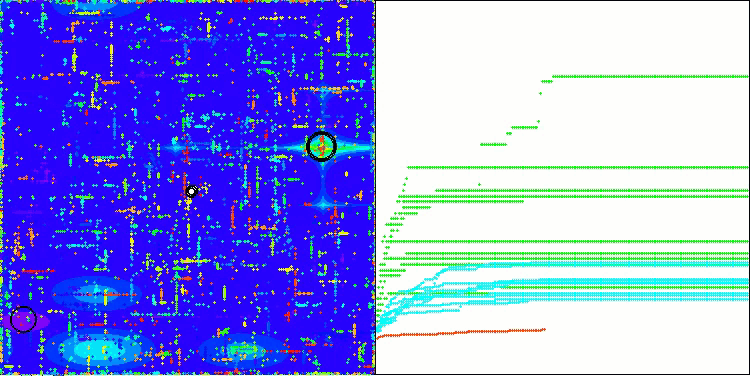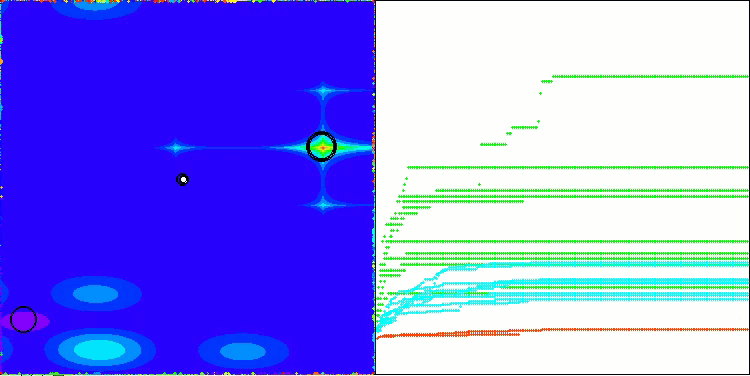
CSA mit der Testfunktion Megacity
Nach den Ergebnissen des Algorithmus-Tests liegt CSA auf Platz 41 der Rangliste.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 15 | RFO | Optimierung des Royal Flush (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 21 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 22 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 23 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 24 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 25 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 26 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 27 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 28 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 29 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 30 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 31 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 32 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 33 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 34 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 35 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 36 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 37 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 38 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 39 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 40 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 41 | CSA | Kreis-Such-Algorithmus | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 42 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 43 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 44 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 45 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Auf der Grundlage der Ergebnisse der Prüfung und Analyse der Leistung des Kreissuchalgorithmus (CSA) können folgende Schlussfolgerungen gezogen werden: Trotz der Eleganz des geometrischen Konzepts und des intuitiven Suchmechanismus, der auf der Bewegung entlang der Tangenten eines Kreises beruht, zeigt der Algorithmus in der vergleichenden Analyse relativ schwache Ergebnisse und belegt in der Bewertungstabelle der Optimierungsalgorithmen den 41. von 45 Plätzen. Diese Situation weist auf erhebliche Einschränkungen bei der derzeitigen Umsetzung hin.
Die Hauptprobleme des Algorithmus hängen mit seiner Tendenz zusammen, in lokalen Extrema stecken zu bleiben, was besonders bei einfachen Problemen kleiner Dimension auffällt. Dies kann auf mehrere Faktoren zurückzuführen sein: Erstens erweist sich der Mechanismus der Eckensuche, obwohl er vielversprechend erscheint, in der Praxis als unzureichend, um lokale Optima zu überwinden. Zweitens sorgt das Gleichgewicht zwischen der Explorations- und der Nutzungsphase, das durch den Parameter constC geregelt wird, nicht für eine ausreichende Diversifizierung der Suche. Die gesamte Population kollabiert zu pseudoguten Lösungen, d.h. zu einem einzigen Punkt, und selbst Versuche, die Population mit einer Zufallskomponente in der Hauptgleichung zur Aktualisierung der Position der Agenten im Lösungsraum zu „erschüttern“, haben nicht geholfen.
Ein Versuch, den Algorithmus durch Hinzufügen eines Zufallsmultiplikators zur Gleichung für die Aktualisierung der Positionen der Agenten zu verbessern, führte zwar zu einem besser vorhersehbaren Verhalten des Algorithmus, konnte aber seine Effizienz nicht wesentlich steigern. Dies könnte darauf hindeuten, dass die Grundidee des Algorithmus, die auf den geometrischen Eigenschaften eines Kreises beruht, von den Autoren in der aktuellen Implementierung entweder nicht vollständig umgesetzt wird oder im Kontext der globalen Optimierung grundlegende Einschränkungen aufweist.
Der Algorithmus demonstriert jedoch gewisse Suchfähigkeiten und kann für einige spezifische Probleme effektiv sein, insbesondere für solche, bei denen die Zielfunktionslandschaft relativ einfach ist. Um die Effizienz des Algorithmus zu verbessern, empfehle ich weitere Forschung in der Richtung, den Mechanismus zum Verlassen lokaler Optima zu verbessern, möglicherweise durch Einführung zusätzlicher Mechanismen zur Suchdiversifizierung oder Hybridisierung mit anderen Optimierungsmethoden (vorrangig die Verwendung dieser Suchstrategie in anderen Optimierungsalgorithmen als Bestandteil).
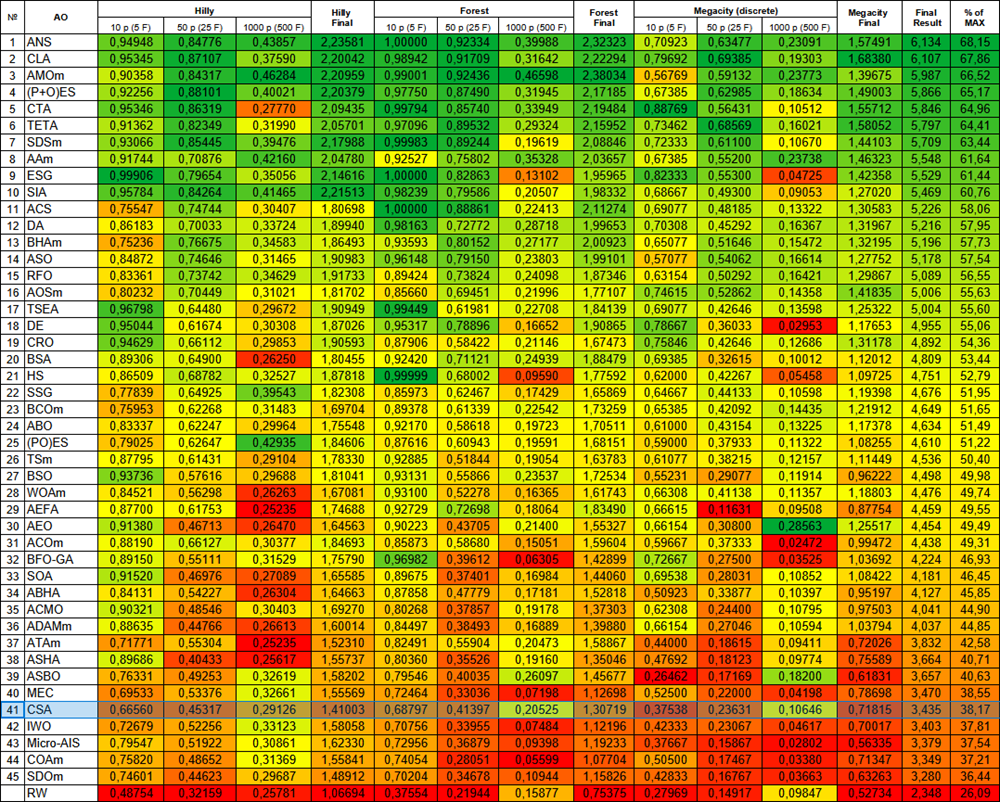
Abbildung 3. Farbabstufung der Algorithmen nach den entsprechenden Tests
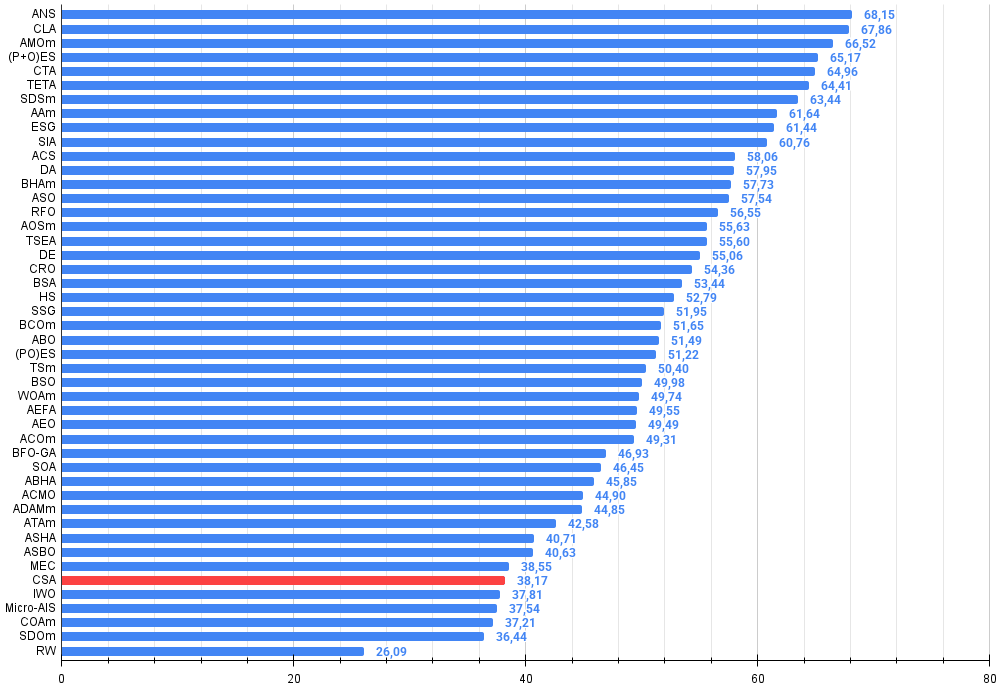
Abbildung 4. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von CSA:
Vorteile:
- Sehr wenige externe Parameter
- Einfache Umsetzung
- Eine interessante Idee, die die geometrischen Eigenschaften eines Kreises nutzt
Nachteile:
- Geringe Konvergenzgenauigkeit
- Bleibt in lokalen Extremen stecken
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_CSA.mq5 | Skript | CSA-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/17143
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Ereignisse (I)
Von der Grundstufe bis zur Mittelstufe: Ereignisse (I)
 Entwicklung eines Expert Advisors für mehrere Währungen (Teil 22): Beginn des Übergangs zum Hot-Swapping von Einstellungen
Entwicklung eines Expert Advisors für mehrere Währungen (Teil 22): Beginn des Übergangs zum Hot-Swapping von Einstellungen
 Marktsimulation (Teil 09): Sockets (III)
Marktsimulation (Teil 09): Sockets (III)
 Marktsimulation (Teil 08): Sockets (II)
Marktsimulation (Teil 08): Sockets (II)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.