人工協調探索(ACS)アルゴリズム

内容

1. はじめに
2. アルゴリズムの実装
3.テスト結果

1. はじめに

自然は、革新的なソリューションを生み出そうとする科学者やエンジニアにとって、尽きることのないインスピレーションの源です。そのような注目すべき現象の1つが相利共生であり、これは異なる種の間で相互に利益をもたらす生物学的相互作用です。相利共生関係にある生物は、この相互作用からお互いに利益を得ることを目指し、個体群の発展と多様性を追求します。これを理解するために、生物が相互に利益を得る相利共生（共生）関係のいくつかの例を挙げます。

1. 顕花植物と花粉媒介者

• 植物は昆虫、鳥、コウモリなどの花粉媒介者を引き寄せるために蜜やその他の報酬を提供します。
• 花粉媒介者は花粉を一つの花から別の花へと運び、植物の繁殖を助けます。

2. 菌類と植物の根（菌根）

• 菌類は植物の根に侵入し、有機化合物（光合成の産物）を受け取ります。 
• 菌類はまた、根の吸収面積を広げ、植物が利用できる水分やミネラルを増やします。

3. シロアリと共生細菌

• シロアリの腸内には、木材の主成分であるセルロースの消化を助ける共生細菌が存在します。
• バクテリアはシロアリから栄養を得て、シロアリは繊維を消化する能力を得ます。

これらの例は、生物が相互に利益を得て生存の可能性を高めるためにどのように相互作用するかを示しています。

ACSアルゴリズムは、このような共通の環境を共有する真社会性超生物の移動行動からもインスピレーションを得ています。以下は、真社会性超生物の移動行動の例です。

1. 蟻のコロニー

• コロニーが移動するとき、蟻は幼虫や蛹、その他の巣の重要な部分を一緒に運びます。

2. ミツバチの群れ

• ミツバチのコロニーは群れをなす際、巣から一時的に移動し、新しいコロニーを別の場所に形成することがあります。
• 群れの移動中、ミツバチは女王蜂や幼虫、新しい巣を作るための蜂蜜を運びます。

これらの例に共通する特徴は、蟻やシロアリ、ハチ、スズメバチなどの真社会性超生物が、環境の変化や資源の枯渇に応じて集団でコロニーを移動できることです。この移動能力によって、超生物は変化する状況に適応し、その生存を確保することができます。これと同様に、同じ環境に生息する二つの真社会性超生物が相互に協力して生物学的な相互作用を行い、ACSアルゴリズムにインスピレーションを与えました。このアルゴリズムでは、生息地の概念は対応する最適化問題に関連する探索空間に対応します。

ACSアルゴリズムは、対応する問題に対するランダムな解をより生産的な領域へ移動させる人工超個体群と見なすことができます。αおよびβという2つの主要な超個体群は、母集団のサイズに等しい人工サブ超個体群を含みます。母集団サイズは、これらのサブ超個体群の個体数に対応しています。共進化プロセスにおいて、αおよびβ超個体群は捕食者と被食者として相互作用し、動的な個体群を活用して効率的に探索空間を探索し、数値最適化問題の大域的最適解を見つけます。

ACSアルゴリズムは2013年にPinar Civiciogluによって提案され、信頼領域内の候補解を含む2つの基本母集団を用いて始まります。その後、このアルゴリズムはランダムステップとバイナリー行列を使って、初期のα超個体群とβ超個体群の値をマッピングし、捕食者と被食者という2つの新しい個体群を作成します。さらに、5番目の個体群は捕食者集団と被食者個体群の値に基づいて計算されます。このプロセスでは、指定された反復回数で初期母集団を更新し、最適解を得るためにこれらの2つの個体群から最適解を抽出します。

目的関数の全域的極値に到達するために生物学的に相互作用する2つの人工超生物の移動と進化、および自然界の協力行動に類似したプロセスが、数値最適化問題におけるACSの高い性能の鍵です。個体群間の生物学的動機による相互作用に基づくこの独自のアプローチにより、ACSアルゴリズムは驚異的な収束速度と高い解精度を実現できます。最適な解を迅速かつ正確に見つける能力により、ACSは広範な数値最適化問題を解決するための強力なツールであることが証明されています。

この記事では、ACSアルゴリズムの背後にある概念を詳述し、その優れた機能を紹介します。読者は、複雑な問題を高効率で解決できる高度な最適化アルゴリズムに生物学的インスピレーションをどのようにうまく実装できるかを深く理解できるようになります。

2. アルゴリズムの実装

人工協調探索(ACS)アルゴリズムは次のように動作します。

1. 初期化：母集団サイズ「popSize」、変数の数「N」、変数の下限「XLow」と上限「XHi」、生物学的相互作用の確率「Probab」を設定します。次に、初期の母集団「A」と「B」の位置を生成し、それらの適合度「YA」と「YB」を計算します。

2. 反復でループする：各反復で以下のステップを実行します。

• 選択：母集団「A」と「B」のどちらのエージェントが、現在の反復で「捕食者」として使われるかを決定します。
• 「獲物」をシャッフルする：選択された個体群内のエージェントの位置をシャッフルします。
• 突然変異：エージェントの位置を、ランダムに生成されたRスケーリング係数を使用して更新します。「捕食者」は「被食者」の決定ベクトルに関する情報を使って突然変異を起こします。
  
• Mバイナリ行列を埋める：Mバイナリ行列は、現在の反復でどの変数を更新するかを決定するために作成されます。
• エージェントのポジションを更新する：エージェントの位置は、M行列の値を考慮して更新されます。Mの値が1であれば、対応するエージェント変数が更新されます。
• 境界の制御：エージェントの更新された位置が指定された境界の外にある場合、それは調整されます。
• Selection updateブロック：この段階で、最適解は次のアルゴリズム反復のために保存されます。
• 大域的最適解の更新：より良い解が見つかれば、それは保存されます。

3. 結果を返す：アルゴリズムの最後には、大域的最適解とその適合値が返されます。

このアルゴリズムには、Mバイナリ行列を使用する「prey」シャッフル演算子や突然変異演算子など、いくつかの独自の演算子が含まれています。

M行列は、「popSize」行（母集団内の候補の数）と「N」列（各候補の変数の数）を持つ2次元配列です。行列の各要素は0または1のいずれかになります。M行列は、母集団内でどの候補が更新されるかを決定するために使用されます。行列内の0と1の値は、ランダムRand値と相互作用確率Probabに基づき、対応する候補が更新対象として選ばれるかどうかを示します。
このように、M行列は、母集団内で更新される候補の選択を調整する役割を果たします。したがって、M行列は、母集団の進化とACSにおける最適解探索において非常に重要な役割を担っています。

次に、ACSアルゴリズムの各ステップを擬似コードで詳しく見ていきましょう。

1. 初期化
   以下のパラメータが設定されています。
       ・popSize：母集団のサイズ
       ・N：変数の数
       ・MaxIter：反復の最大回数
       ・XLow：変数の下限
       ・XHi：変数の上限
       ・Probab：生物学的相互作用の確率
   ・Rand：範囲 (0, 1) に一様分布した数値を返す関数
   ・GlobMax：負のDBL_MAXで初期化される

2. メインループ
   ・母集団の各要素について（I = 1からpopSizeまで）
      ・各変数（J = 1〜N）について
        ・XLow(J)～XHi(J)の範囲の初期値A(I,J)とB(I,J)を計算します
     ・目標関数YA(I)=Fx(A(I,:))、YB(I)=Fx(B(I,:))の初期値を計算します
   ・(Iter = 1 to MaxIter)反復によるメインループを開始します

3. 選択
   ・AとBのどちらを捕食者として使うかをランダムに選択します
     ・Rand < 0.5の場合、Predator= A、Ypred = YA、Key = 1
     ・それ以外の場合、Predator = B、Ypred = YB、Key = 2
   ・AとBのどちらを獲物にするかをランダムに選択します
      ・Rand < 0.5の場合、Prey = A
      ・それ以外の場合、Prey = B
   ・獲物をランダムにシャッフルします
   ・Rパラメータを計算します
      ・Rand < 0.5の場合、R = 4 * Rand * (Rand - Rand)
      ・それ以外の場合、R = 1/exp(4 * Rand)
   ・popSize x Nの1で埋められたMバイナリ行列を作成します
   ・M行列一部の要素をProbab の確率でランダムに0に設定します
   ・Rand < Probabの場合、M行列の一部の要素をランダムに0または1に設定します
・M行列の各行について、要素の合計がNの場合、1つの要素をランダムに選択し、0に設定します

4. 突然変異
   ・新しい値X = Predator + R * (Prey - Predator)を計算します
   ・母集団の各要素（I = 1～popSize）と各変数（J = 1～N）について
     ・M行列の対応する要素が0を超える場合、X(I,J)=Predator(I,J)
     ・X(I,J)が[XLow(J), XHi(J)]の範囲外の場合、X(I,J)をその範囲内のランダムな値に設定します

5. 選択の更新
   ・母集団の各要素について（I = 1からpopSizeまで）
     ・Fx(X(I,:)) < Ypred(i)の場合、Predator(I,:) = X(I,:)であり、Ypred(I) = Fx(X(I,:))
   ・Key = 1の場合、A = PredatorでYA = Ypred、それ以外の場合、B = PredatorでYB = Ypred
   ・Ybest = min(Ypred)
   ・Ibest = Ybestに対応するPredator行インデックス
   ・Ybest＞GlobMaxの場合、GlobMax＝Ybest、GlobMax＝Predator(Ibest,:)

6. 結果を返す
   ・GlobMaxおよびGlobMaxXベクトルを返します

ACS アルゴリズムの実装の説明に移りましょう。最も単純な構造「 S_D」を使用して、個体群（アルゴリズムには5つあります）を記述します。

• c[]：座標（タスクの最適化されたパラメータ）を格納する配列
  
• Init (int coords)：ArrayResize関数を使用して、c配列のサイズをcoordsで指定したサイズ（座標の数）に変更するメソッド

一般的に、この構造体は実数の配列を含むオブジェクトを作成するために使用されます。Initメソッドは配列のサイズを変更するために使用されます。

//——————————————————————————————————————————————————————————————————————————————
struct S_D
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    double c [];
};
//——————————————————————————————————————————————————————————————————————————————

M行列を記述するには、S_Dフィールド型の構造とは異なるS_C構造を作成します。

• c[]：「0」と「1」の行列シンボルを格納する配列
  
• Init (int coords)：ArrayResize関数を使用して、c配列のサイズをcoordsで指定したサイズに変更するメソッド

//——————————————————————————————————————————————————————————————————————————————
struct S_C
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    char c [];
};
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムは、C_AO基底クラスから派生したC_AO_ACSクラスとして記述され、次のフィールドが含まれます。

•  ~C_AO_ACS () { }：クラスオブジェクトが削除されたときに呼び出されるクラスデストラクタ（この場合は空）
• C_AO_ACS ()：クラスデータメンバーを初期化し、params配列のサイズを変更し、アルゴリズムパラメータにデフォルト値を割り当てるクラスコンストラクタ
• SetParams ()：params配列の値に基づいて、popSize値とbioProbabを設定するメソッド
• Init () ：複数の引数を取り、ブール値を返すメソッド 
  
• Moving ()とRevision ()：アルゴリズムの主要なロジックを含むメソッド
• bioProbab：生物学的相互作用の確率を格納するデータメンバー
• S_D A[]、S_D B[]、S_D Predator[]、S_D Prey[]、S_C M[]、double YA[]、double YB[]、double Ypred[]、int Key、int phase：クラスデータのprivateメンバー
• ArrayShuffle ()：配列要素をシャッフルするprivateメソッド
  

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACS () { }
  C_AO_ACS ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search";
    ao_link = "https://www.mql5.com/ru/articles/15004";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_D A              [];
  S_D B              [];
  S_D Predator       [];
  S_D Prey           [];

  S_C M              [];

  double YA          [];
  double YB          [];
  double Ypred       [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

次に、C_AO_ACSクラスのInitメソッドを示します。このメソッドはクラスオブジェクトを初期化します。

• Init ()：メソッド宣言。最小検索範囲「rangeMinP」、最大検索範囲「rangeMaxP」、検索ステップ「rangeStepP」、エポック数「epochsP」の4つの引数を取ります。エポック数はデフォルトで0です。
• if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;：基底クラスの標準的な初期化をおこなうStandardInit関数を呼び出します。StandardInitが falseを返した場合、Initメソッドは直ちに終了し、falseを返します。
• for (int i = 0; i < popSize; i++)：このループの中で、A、B、Predator、Prey、Mの各配列の要素はInitメソッドを使って初期化されます。
• ArrayResize (YA, popSize)：これと同様の行は、YA、YB、Ypred配列のサイズをpopSizeに変更します。
• ArrayInitialize (YA, -DBL_MAX)：これと同様の行は、-DBL_MAX値を使用して、YA、YB、Ypred配列のすべての要素を初期化します。
• ネストされたforループ：A配列とB配列の各オブジェクトのc要素が、与えられた範囲のランダムな値を使って初期化されます。
• phase = 0：「phase」を0に設定します。
  

元のアルゴリズムには、ロジックをフェーズに分割する機能がありません。すべての母集団アルゴリズムに採用したスタイルでアルゴリズムを実装するには、フェーズを追加する必要がありました。ACSはA母集団とB母集団のエージェントの適応度の事前計算を使用するため、これが必要でした。メソッド内でこれらの操作を順番に実行するために、フェーズ分割が追加されました。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACS::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,         popSize);
  ArrayResize (B,         popSize);
  ArrayResize (Predator,  popSize);
  ArrayResize (Prey,      popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A         [i].Init (coords);
    B         [i].Init (coords);
    Predator  [i].Init (coords);
    Prey      [i].Init (coords);

    M         [i].Init (coords);
  }

  ArrayResize (YA,    popSize);
  ArrayResize (YB,    popSize);
  ArrayResize (Ypred, popSize);

  ArrayInitialize (YA,    -DBL_MAX);
  ArrayInitialize (YB,    -DBL_MAX);
  ArrayInitialize (Ypred, -DBL_MAX);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
    }
  }

  phase = 0;
 
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACSクラスのMovingメソッドは、アルゴリズム内で個体を移動する基本ロジックを実装します。このメソッドは、配列のコピー、選択、順列、突然変異、交差などのいくつかの操作を実行します。

• if (phase == 0)：このフェーズでは、A母集団の個体をコピーします。
  
• if (phase == 1)：このフェーズでは、А母集団の個体の適合を返し、B母集団から個体をコピーします。
• if (phase == 2)：このフェーズでは、B母集団の個体の適合を返し、その後のアルゴリズムロジック全体が実行されます。 
  
• Selectionブロック：選択をおこないます。乱数に応じて、A配列またはB配列がPredator配列にコピーされ、対応する値がYpred配列にコピーされます。
• Permutation of Preyブロック：Prey配列要素の並べ替えがここでおこなわれます。
• R：変数が宣言され、乱数によって2つの値のいずれかに初期化されます。
• Fill binary matrix M with 1sブロック：Mバイナリ行列を1で埋めます。
• Additional operations with matrix Mブロック：乱数と生物学的相互作用のbioProbab確率に応じて、その要素の一部を0または1に変更するなど、M行列の追加操作を実行します。
• Mutationブロック：突然変異を実行し、PredatorとPreyの配列要素、およびR値に基づいてaの配列要素が変更されます。
• Crossoverブロック：クロスオーバーを実行し、一部のa配列要素をPredator配列要素と置き換えます。
• Boundary controlブロック：指定された最適化パラメータの範囲外のa配列要素を、範囲内のランダムな値に置き換える境界制御を実行します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) YA [i] = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) YB [i] = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, A [i].c);
    }

    ArrayCopy (Ypred, YA);
    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, B [i].c);
    }

    ArrayCopy (Ypred, YB);
    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, A [i].c);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, B [i].c);
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
      else
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }
 
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACSクラスのRevisionメソッド：このメソッドは、配列の並び替えや逆コピー、大域解の最良値の更新など、多くの操作を実行します。

• if (phase < 3) return：メソッドの基本ロジックは、さらなる相互作用のために母集団を準備する3つのフェーズがすべて完了するまで実行されません。
• Selection updateブロック：個体の選択を更新します。各a配列個体について、そのf適合値がYpred配列の適切な値を超えているかどうかをチェックします。
• if (Key == 1) およびelse：これらのブロックでは、Key値に応じて、Predator配列要素がAまたはB配列からコピーされ、対応するYpred値はYAまたはYB配列からコピーされます。
• ArraySort (Ypred);ArrayReverse (Ypred, 0, WHOLE_ARRAY)：適性値を含むYpred配列がソートされ、値が降順になるように反転されます。
• Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred)：ここでYbestはYpredの最大値であり、Ibestはこの最大値のインデックスです。
• if (Ybest > fB)：Ybestが現在のfBを超えた場合、fBが更新され、その間に適切なaとcBの配列要素がPredator配列からコピーされます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Ypred [i])
    {
      ArrayCopy (Predator [i].c, a [i].c);
      Ypred [i] = d;
    }
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (A [i].c, Predator [i].c);
    }

    ArrayCopy (YA, Ypred);
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (B [i].c, Predator [i].c);
    }

    ArrayCopy (YB, Ypred);
  }

  ArraySort (Ypred);
  ArrayReverse (Ypred, 0, WHOLE_ARRAY);
  double Ybest = Ypred [0];
  int Ibest = ArrayMaximum (Ypred);

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ACSクラスのArrayShuffleメソッドは、配列の要素をランダムにシャッフルします。

• for (int i = n - 1; i > 0; i--)：このループは、arr配列を最後の要素から逆順に繰り返します。
• j = MathRand () % (i + 1)：ここでjは、0からiまでの乱数です。
• tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp：これらの行は、arr[i]とarr[j]の要素のスワップを実行します。

その結果、arr配列の要素はランダムにシャッフルされます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. テスト結果

アルゴリズムの独創性は、おこなわれたテストによって確認されています。このアルゴリズムは、母集団の規模が小さくても優れた結果を達成できる点で独自の特徴を持っています。反復回数が増えると、アルゴリズムは個々のテスト関数で100%収束することが可能です。これは、適応関数の実行回数を増やしても収束の機会が得られない他のアルゴリズムとは異なる点です。この特性により、局所的な「罠」に陥りにくいという利点があります。

次に、母集団の規模に応じたアルゴリズムの結果の変化を見てみましょう。私は通常、母集団あたり平均50個体を使用します。ただし、テストの際、このアルゴリズムは母集団の規模が小さい場合でも適切な結果を示し始めます。

10個体の母集団で適応度関数の起動回数が10,000回のままの場合、このアルゴリズムは49.97%の結果を達成します。

ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.8213829114300768
25 Hilly's; Func runs:10000; result:0.5418951009344799
500 Hilly's; Func runs:10000; result:0.2811381329747021
=============================
5 Forest's; Func runs:10000; result:0.9750514085798038
25 Forest's; Func runs:10000; result:0.5078176955906151
500 Forest's; Func runs:10000; result:0.20112458337102135
=============================
5 Megacity's; Func runs:10000; result:0.736923076923077
25 Megacity's; Func runs:10000; result:0.31446153846153846
500 Megacity's; Func runs:10000; result:0.11721538461538572
=============================
All score:4.49701 (49.97%)

3個体の母集団で、適応度関数の起動数が10,000のままの場合、このアルゴリズムは55.23%という結果を達成します。

ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.8275253778390631
25 Hilly's; Func runs:10000; result:0.6349216357701294
500 Hilly's; Func runs:10000; result:0.29382093872076825
=============================
5 Forest's; Func runs:10000; result:0.9998874875962974
25 Forest's; Func runs:10000; result:0.6985911632646721
500 Forest's; Func runs:10000; result:0.2132502183011688
=============================
5 Megacity's; Func runs:10000; result:0.7507692307692307
25 Megacity's; Func runs:10000; result:0.4270769230769231
500 Megacity's; Func runs:10000; result:0.1252615384615397
=============================
All score:4.97110 (55.23%)

1個体の母集団で、適応度関数の起動数が10,000のままの場合、このアルゴリズムは58.06%という結果を達成します。

ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.7554725186591347
25 Hilly's; Func runs:10000; result:0.7474431551529281
500 Hilly's; Func runs:10000; result:0.3040669213089683
=============================
5 Forest's; Func runs:10000; result:0.9999999999993218
25 Forest's; Func runs:10000; result:0.888607840003743
500 Forest's; Func runs:10000; result:0.2241289484506152
=============================
5 Megacity's; Func runs:10000; result:0.6907692307692308
25 Megacity's; Func runs:10000; result:0.4818461538461539
500 Megacity's; Func runs:10000; result:0.1332153846153859
=============================
All score:5.22555 (58.06%)

1個体だけの場合、母集団内でどのように相互作用が発生するのか疑問に思うかもしれません。覚えているかもしれませんが、このアルゴリズムでは 5 つの母集団を使用し、これらの母集団内の個体間で相互作用が発生します。個体数が非常に少ないにもかかわらず、このアルゴリズムは母集団内の多様性を維持し、「ボトルネック」効果はありません。

可視化の結果、クラスタリング効果がまったく見られず、エージェントが一見無秩序に動作していることが確認できます。エージェントは、有望な方向がない場所でも探索空間の領域に入ります。この特徴は、地形の変化がほとんどない広くて平坦な領域を持つForestとMegacityの特徴で明確に確認できます。

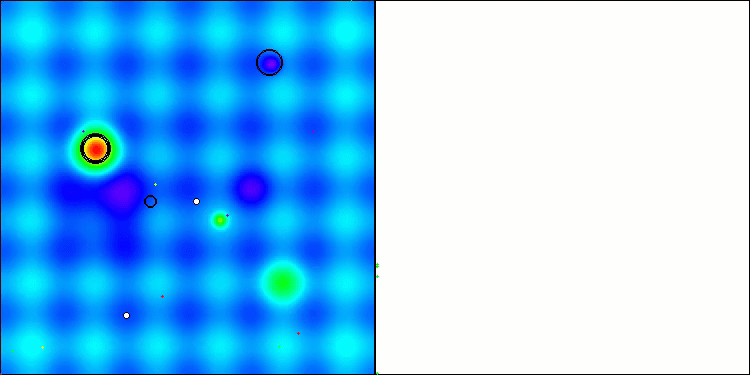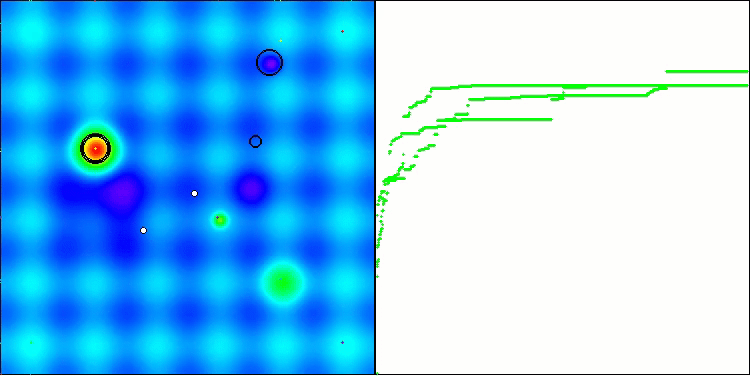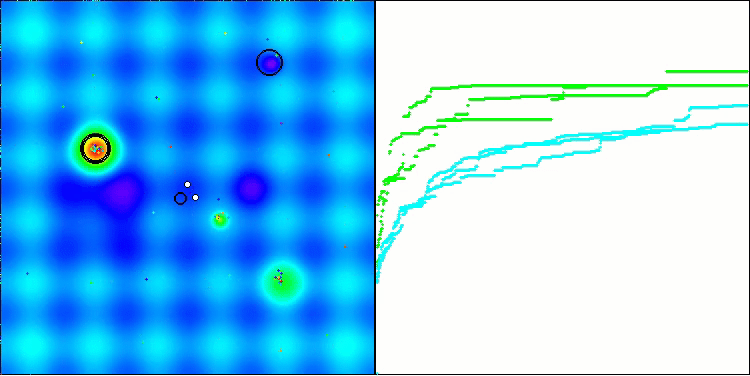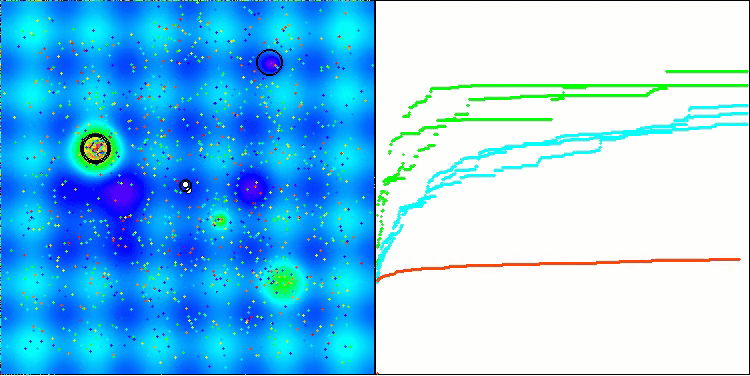
  Hillyテスト関数のACS

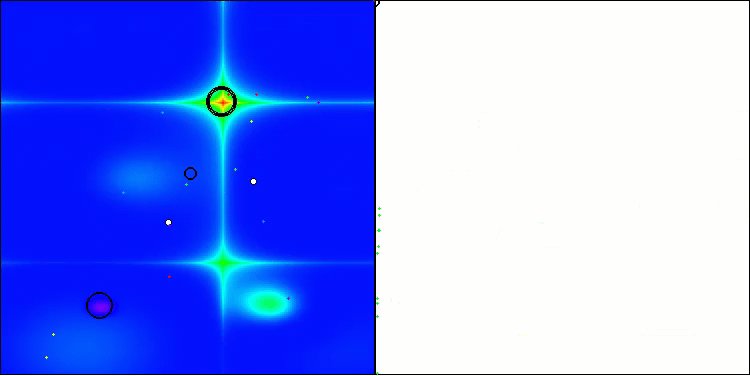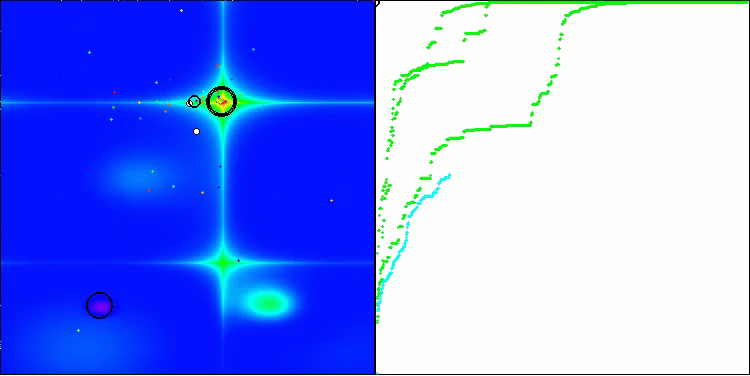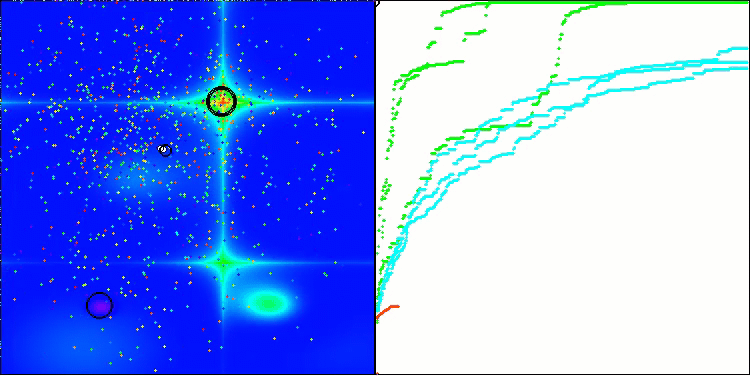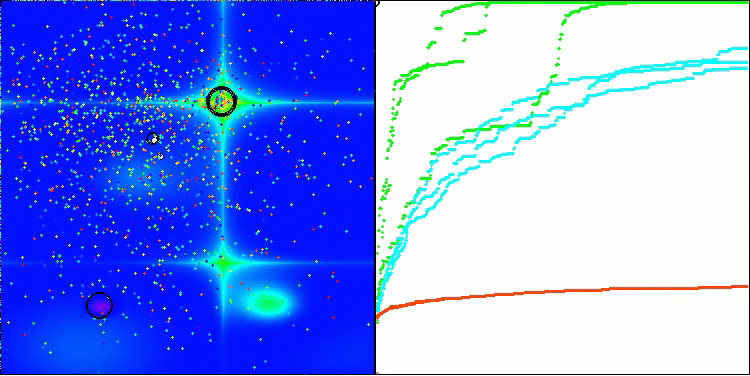
  Forestテスト関数のACS

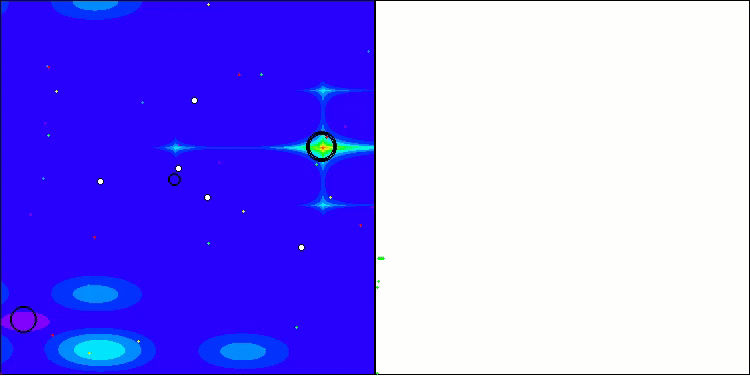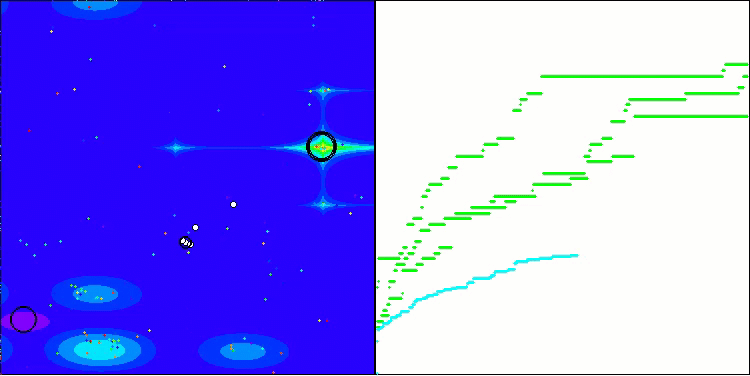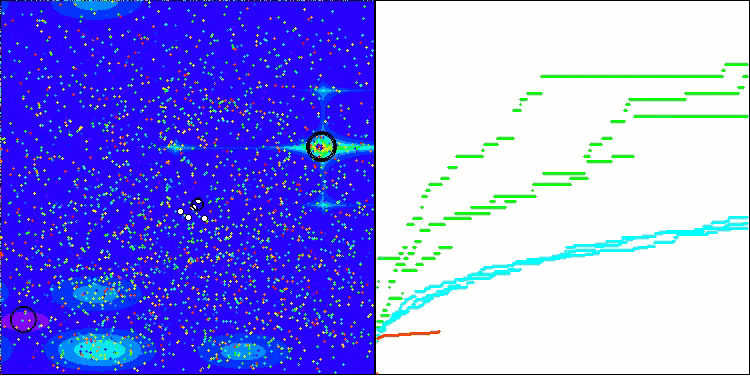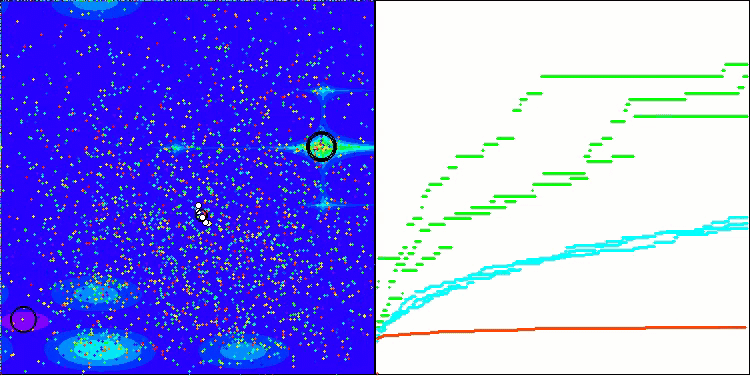
  Megacityテスト関数のACS

テストの結果、このアルゴリズムは8位となりました。ACSが特に優れていたのは、Forest関数とMegacity関数です。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	バイナリ遺伝的アルゴリズム	0.99989	0.99518	0.42835	2.42341	0.96153	0.96181	0.32027	2.24360	0.91385	0.95908	0.24220	2.11512	6.782	75.36
2	CLA	コードロックアルゴリズム	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O）進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	彗尾アルゴリズム	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	社会集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	急性冠症候群	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
9	TSEA	亀甲進化アルゴリズム	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
10	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
11	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
12	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
13	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
14	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
15	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
16	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
17	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
18	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
19	MEC	Mind Evolutionary Computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
20	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
21	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
22	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
23	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
24	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
25	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
26	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
27	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
28	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
29	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
30	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
31	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
32	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
33	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
34	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
35	SFL	Shuffled Frog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
36	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
37	RND	ランダム	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
38	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
39	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
40	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

まとめ

人工協調探索(ACS)アルゴリズムは、最適化に対する非常に興味深いアプローチであることが証明されています。これは、相互作用するエージェントの複数母集団の使用や多様性の確保、局所最適値に陥らない耐性、そして「獲物」のシャッフルやバイナリ行列を使用した突然変異などの特別な演算子の活用に表れています。これにより、ACSは非常に小規模な母集団サイズ（5つの集団それぞれに1個体まで）でも高い成果を達成する能力を持ち、アルゴリズムに独創性を与えています。この独創的なアプローチと小規模な母集団での実行力（コロニーの退化に対する耐性を強調）により、ACSは真に有望な最適化アルゴリズムといえるでしょう。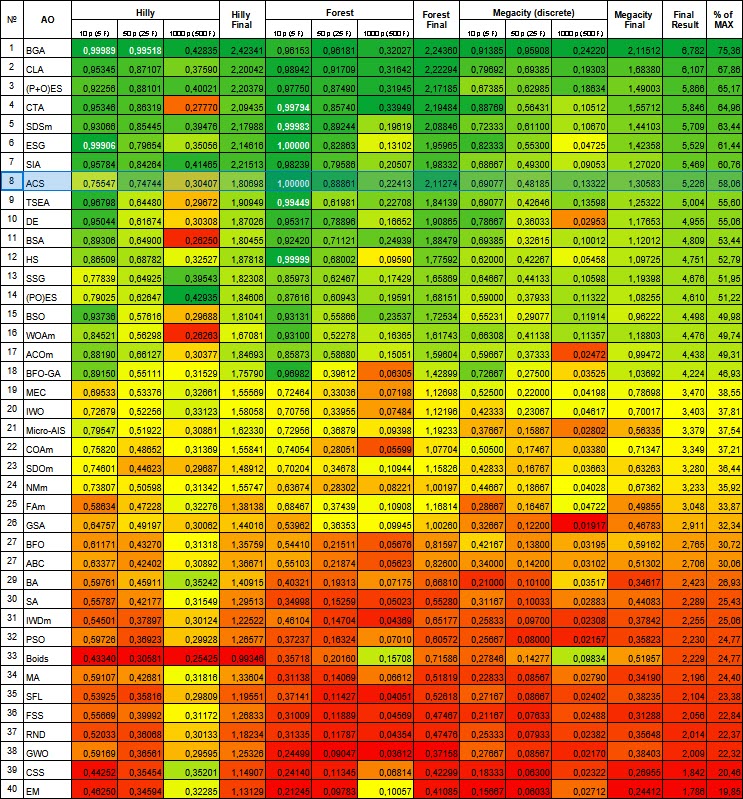

図1：関連テストによるアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示される

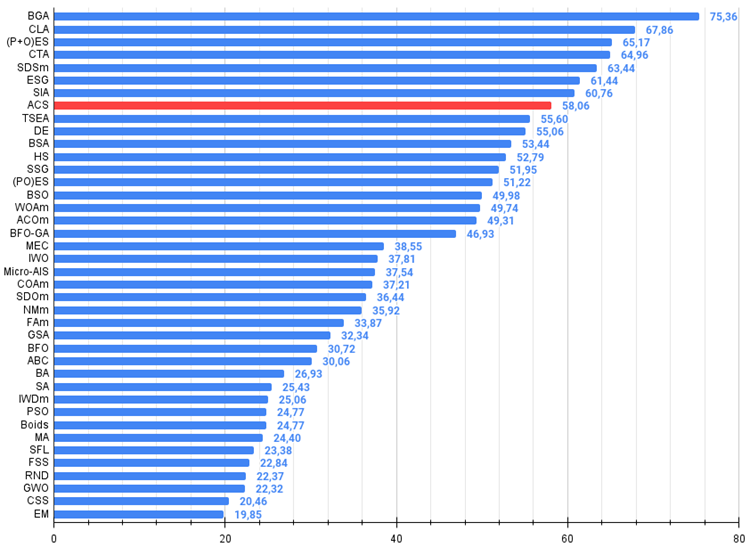
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）

ACSの長所と短所

長所

1. 外部パラメータの数が少ない（1つだけ）。
   
2. 様々な種類の関数に対して収束性が良い。

短所

1. 低次元関数に関する結果が散らばる。
   

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

• github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• コードベース：https://www.mql5.com/ru/code/49355