
Algoritmo de búsqueda circular — Circle Search Algorithm (CSA)
Contenido
Introducción
El algoritmo de búsqueda circular (CSA) es un nuevo método de optimización inspirado en las propiedades geométricas del círculo. Su singularidad reside en el uso de relaciones trigonométricas y principios geométricos para explorar el espacio de búsqueda.
El CSA se basa en una idea interesante según la cual cada punto de búsqueda se desplaza a lo largo de una trayectoria definida por una tangente hacia un círculo, lo que crea un equilibrio entre la exploración global y el refinamiento local de la solución. Este enfoque resulta original debido a que el círculo tiene propiedades matemáticas únicas de radio constante y derivada continua, lo cual garantiza un movimiento suave de los agentes en el espacio de búsqueda.
El algoritmo combina dos fases: explotación y exploración. En la fase de explotación, los agentes se centran en áreas prometedoras, moviéndose más direccionalmente, mientras que en la fase de exploración realizan saltos más audaces hacia áreas inexploradas del espacio de soluciones. La transición entre fases está regulada por un mecanismo que se basa en la iteración actual y un parámetro especial "c".
Lo que hace especialmente atractivo al CSA es su capacidad para trabajar eficazmente en espacios multidimensionales, manteniendo al mismo tiempo una interpretación geométrica intuitiva. Cada agente de la población sigue una trayectoria única definida por el ángulo θ, que se ajusta dinámicamente durante el proceso de búsqueda.
El Circle Search Algorithm (CSA) fue desarrollado por los científicos Mohammad H. Kaiys, Hany M. Hasanien y otros y se publicó en 2022.
Implementación del algoritmo
El algoritmo de búsqueda circular (CSA) tiene como objetivo encontrar la solución óptima en círculos aleatorios para ampliar el área de búsqueda. Usa el centro del círculo como punto de destino. El proceso comienza con la disminución gradual del ángulo entre la tangente y el círculo, lo cual permite a la tangente acercarse al centro (figura 1).
Para aportar diversidad a la búsqueda y evitar atascarse en óptimos locales, el ángulo de contacto tangencial también se varía aleatoriamente. En el contexto del algoritmo, el punto de contacto "Xt" actúa como agente de búsqueda, mientras que el punto central "Xc" indica la mejor solución encontrada.
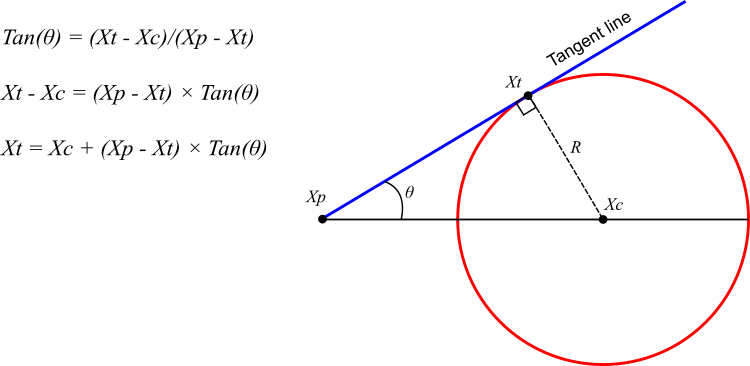
Figura 1. Propiedades geométricas de una circunferencia y su recta tangente
El algoritmo CSA adapta la posición del agente de búsqueda en respuesta al movimiento del punto de contacto hacia el centro. Esto mejora la calidad de la solución, pues la actualización aleatoria del ángulo de contacto tangente supone un mecanismo importante para evitar alcanzar mínimos locales. Las principales etapas del optimizador CSA se muestran en el siguiente esquema.

Figura 2. Esquema de funcionamiento del algoritmo CSA
A continuación, se determina el ángulo para cada agente. Si la iteración actual es mayor que el producto del umbral y el número máximo de iteraciones, el agente se encontrará en la fase de exploración; en caso contrario, se aplicará la fase de explotación (véase la figura 2). Luego se actualizan las posiciones de los agentes y se evalúa la idoneidad de cada una de ellas. Los resultados se comparan con la mejor solución actual y, si se encuentra una mejor, se actualizará la posición. La iteración se finaliza incrementando el contador de iteración. Cuando el algoritmo termina su ejecución, retorna la mejor posición encontrada y su valor de idoneidad.
El algoritmo utiliza el concepto de movimiento tangencial de puntos en un círculo, donde cada agente de búsqueda se mueve en un cierto ángulo θ relativo a la mejor solución actual. Este movimiento se rige por varios parámetros (w, a, p) que varían con el tiempo. Como ya hemos señalado, el trabajo del algoritmo se divide en dos fases: exploración -cuando los agentes realizan movimientos más amplios para encontrar áreas prometedoras- y explotación -cuando los agentes se centran en mejorar las soluciones encontradas-.
La versión final que propuesta tiene algunas diferencias que mejoran notablemente la capacidad de búsqueda del algoritmo. Hemos modificado la fórmula de actualización "w":
- En la original: w = w × rand - w
- En el código final: w = π × (1 - epochNow/epochs). Esto ha hecho que la variación del parámetro "w" sea más predecible y lineal, lo que mejora la convergencia del algoritmo.
- En la original: Xi = Xc + (Xc - Xi) × tan(θ)
- En la versión final: Xi = Xc + rand × (Xc - Xi) × tan(θ). La adición del multiplicador aleatorio "rand [0,0; 1,0]" da estocasticidad adicional a la búsqueda y la mejora respecto a la versión original.
- Hemos añadido una actualización de la mejor solución local para cada agente.
- Hemos mejorado la estrategia de equilibrio de las búsquedas globales y locales
La principal diferencia conceptual reside en que la versión final ha hecho el algoritmo más "suave" y predecible en su comportamiento, manteniendo su capacidad de búsqueda. El algoritmo original tenía un comportamiento más "caótico", mientras que la versión final ofrece un proceso de optimización más controlado, especialmente en lo que respecta a la transición entre las fases de exploración y explotación.
Ahora podemos empezar a escribir el pseudocódigo del algoritmo.
Pseudocódigo del algoritmo de búsqueda circular (CSA):
- Inicialización:
- Fijamos el tamaño de la población (popSize = 50)
- Ajustamos la constante de la fase de exploración (constC = 0,8)
- Inicializamos los parámetros iniciales:
- w = π (parámetro del ángulo)
- a = π
- p = 1.0
- θ = 0 (ángulo inicial)
- Si la primera iteración (revision = false):
- Para cada agente "i" de la población:
- Inicializamos aleatoriamente las coordenadas dentro de unos límites dados
- Ajustamos las coordenadas según el paso de cambio
- Establecemos revision = true
- Volvemos al inicio
- Para cada agente "i" de la población:
- En caso contrario (ciclo principal de optimización):
- Aumentamos el contador de iteraciones (epochNow++)
- Parámetros de actualización:
- w = π × (1 - epochNow/epochs) // reducción lineal
- a = π - π × (epochNow/epochs)²
- p = 1 - 0.9 × √(epochNow/epochs)
- Para cada agente de la población:
- Identificamos la fase actual:
- Si epochNow ≤ constC × epochs: → Fase de exploración: θ = w × random [0,0; 1,0]
- En caso contrario: → Fase de explotación: θ = w × p
- Actualizamos la posición del agente:
- Para cada coordenada j: → new_pos = best_pos + random [0.0; 1.0] × (best_pos - current_pos) × tan (θ) → Ajustamos new_pos dentro de los límites dados.
- Identificamos la fase actual:
- Revisión de los resultados:
- Para cada agente:
- Si aptitud agente > mejor aptitud global: → Actualizamos mejor solución global.
- Si la aptitud del agente > la mejor aptitud local: → Actualizamos la mejor solución local del agente.
- Para cada agente:
- Repetimos los pasos 3-5 hasta alcanzar el criterio de parada
Pasamos ahora a la aplicación. La clase "C_AO_CSA" supone una implementación del algoritmo CSA y se hereda de la clase básica "C_AO". Veamos sus principales elementos y estructura:
El constructor inicializa los parámetros del algoritmo. Especifica el nombre y la descripción del algoritmo, y establece los valores para los parámetros:- popSize — tamaño de la población igual a 50.
- constC — constante igual a 0,8 utilizada en la fase de exploración.
- w, aParam, p, theta — valores iniciales de los parámetros que se utilizarán en el algoritmo.
- SetParams () — método para establecer los valores de los parámetros basándose en el array de datos "params".
- Init () — este método se implementa para inicializar los parámetros relacionados con los rangos de valores y el número de épocas en las que se ejecutará el algoritmo.
- Moving () — se utiliza para desplazar partículas y realizar iteraciones del algoritmo.
- Revisión () — para analizar y ajustar el estado de la población.
Métodos privados:
- CalcularW (), CalcularA (), CalcularP (), CalcularTheta () — métodos para calcular los parámetros correspondientes.
- IsExplorationPhase () — el método determina si el algoritmo está en fase de exploración.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CSA : public C_AO { public: //-------------------------------------------------------------------- C_AO_CSA () { ao_name = "CSA"; ao_desc = "Circle Search Algorithm"; ao_link = "https://www.mql5.com/es/articles/17143"; popSize = 50; // population size constC = 0.8; // optimal value for the exploration phase w = M_PI; // initial value w aParam = M_PI; // initial value a p = 1.0; // initial value p theta = 0; // initial value of the angle ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "constC"; params [1].val = constC; } void SetParams () { popSize = (int)params [0].val; constC = params [1].val; } bool Init (const double &rangeMinP [], // minimum values const double &rangeMaxP [], // maximum values const double &rangeStepP [], // step change const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double constC; // constant for determining the search phase [0,1] private: //------------------------------------------------------------------- int epochs; // maximum number of iterations int epochNow; // current iteration // Parameters for CSA double w; // parameter for calculating the angle double aParam; // parameter a from the equation (8) double p; // parameter p from the equation (9) double theta; // search angle double CalculateW (); double CalculateA (); double CalculateP (); double CalculateTheta (double currentW, double currentP); bool IsExplorationPhase (); }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" sirve para inicializar los parámetros del algoritmo CSA. Sus parámetros incluyen un array de valores mínimos del espacio de búsqueda "rangeMinP []", un array de valores máximos "rangeMaxP []", un array de pasos de cambio de valor "rangeStepP []", así como el número de épocas especificado por el parámetro "epochsP", que por defecto es 0.
Durante la ejecución del método, se llama a "StandardInit", cuyo propósito es tratar de inicializar los parámetros estándar. Si la inicialización se realiza correctamente, se establecerán los valores de las variables "epochs" y "epochNow". La variable "epochs" obtiene el valor de "epochsP", mientras que "epochNow" se pone a cero. El método finaliza la ejecución retornando "true", lo que indica que los parámetros del algoritmo se han inicializado correctamente.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_CSA" implementa la lógica para actualizar las posiciones de los agentes en el algoritmo CSA. Al principio del método se incrementa el contador de la época actual, lo cual permite llevar la cuenta de cuántas iteraciones se han ejecutado (se utiliza en las fórmulas de cálculo). A continuación, se comprueba si es necesario inicializar las coordenadas de los agentes. Si es la primera ejecución del método, se generan coordenadas aleatorias para todos los agentes en los rangos dados. Luego estas coordenadas se adaptan a los pasos dados. Y después la bandera sobre la necesidad de revisión se establece en true.
Si no es la primera vez que se llama al método, se actualizan parámetros clave del algoritmo como "w", "aParam" y "p". A continuación, se calcula el ángulo Theta para cada agente y se usa para actualizar sus coordenadas. Cada coordenada se actualiza con las coordenadas del mejor agente, la influencia del factor aleatorio y el ángulo theta. Después, los resultados también se ajustan para mantenerse dentro de los márgenes especificados.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //---------------------------------------------------------------------------- w = CalculateW (); // Update w linearly aParam = CalculateA (); // Update a p = CalculateP (); // Update p for (int i = 0; i < popSize; i++) { theta = CalculateTheta (w, p); for (int j = 0; j < coords; j++) { a [i].c [j] = cB [j] + u.RNDprobab () * (cB [j] - a [i].c [j]) * tan (theta); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
El método de revisión se encarga de actualizar las mejores soluciones de toda la población. Comprueba los valores actuales de las funciones de valor objetivo de los agentes y actualiza los parámetros correspondientes si se encuentran soluciones mejores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Revision () { for (int i = 0; i < popSize; i++) { // Update the best global solution if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateW" está diseñado para calcular el valor del parámetro "w", que disminuye linealmente desde el valor inicial (M_PI) hasta "0" con el aumento del número de épocas actuales (epochNow) en relación con el número total de épocas (epochs) y retorna el valor calculado de "w". Este parámetro calculado interviene en la fórmula de cálculo del ángulo "Theta".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateW () { // Linear decrease of w from the initial value (M_PI) to 0 return M_PI * (1.0 - (double)epochNow / epochs); //return w * u.RNDprobab () - w; } //——————————————————————————————————————————————————————————————————————————————El método "CalculateA" calcula el valor de "aParam" que disminuye de "M_PI" a "0" a medida que "epochNow" aumenta usando una relación cuadrática con el número total de épocas "epochs".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateA () { return M_PI - M_PI * MathPow ((double)epochNow / epochs, 2); } //——————————————————————————————————————————————————————————————————————————————
El método "CalculateP" calcula el valor de "p", que disminuye de "1.0" a "0.1" a medida que "epochNow" aumenta, es decir, depende de la época actual.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateP () { return 1.0 - 0.9 * MathPow ((double)epochNow / epochs, 0.5); } //——————————————————————————————————————————————————————————————————————————————
El método "CalcularTheta" calcula el valor de "Theta" usando los parámetros actuales "currentW" y "currentP".
- Si la fase actual es de exploración, retorna el producto de "currentW" por un número aleatorio.
- En caso contrario, retorna el producto de "currentW" por "currentP".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateTheta (double currentW, double currentP) { // Use the aParam parameter to adjust the angle if (IsExplorationPhase ()) return currentW * u.RNDprobab (); else return currentW * currentP; } //——————————————————————————————————————————————————————————————————————————————
El método "IsExplorationPhase" comprueba si la iteración actual se encuentra en la fase de exploración.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::IsExplorationPhase () { // Research in the first part of the iterations (constC is usually 0.8) return (epochNow <= constC * epochs); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Los autores del algoritmo lo posicionan como un método de optimización de alto rendimiento, sin embargo, tras la implementación y algunas mejoras, así como las pruebas finales, los resultados no resultan demasiado impresionantes. El algoritmo ha logrado entrar en la tabla de clasificación, pero su rendimiento es muy inferior al de las mejores soluciones algorítmicas del momento.CSA|Circle Search Algorithm|50.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.6656012653478078
25 Hilly's; Func runs: 10000; result: 0.4531682514562617
500 Hilly's; Func runs: 10000; result: 0.2912586479936386
=============================
5 Forest's; Func runs: 10000; result: 0.6879687203647712
25 Forest's; Func runs: 10000; result: 0.41397289345600924
500 Forest's; Func runs: 10000; result: 0.2052507546137296
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2363076923076922
500 Megacity's; Func runs: 10000; result: 0.10646153846153927
=============================
All score: 3.43537 (38.17%)
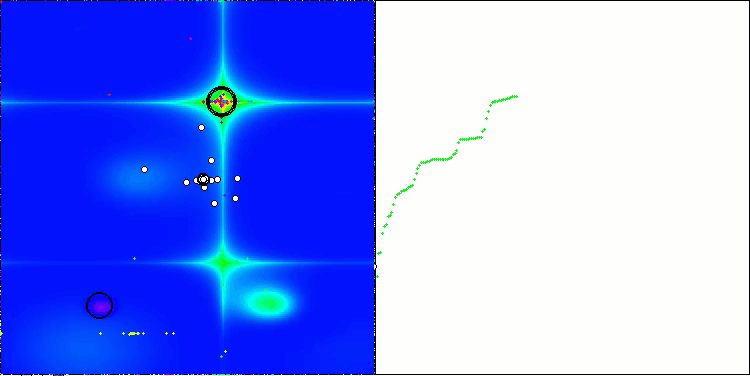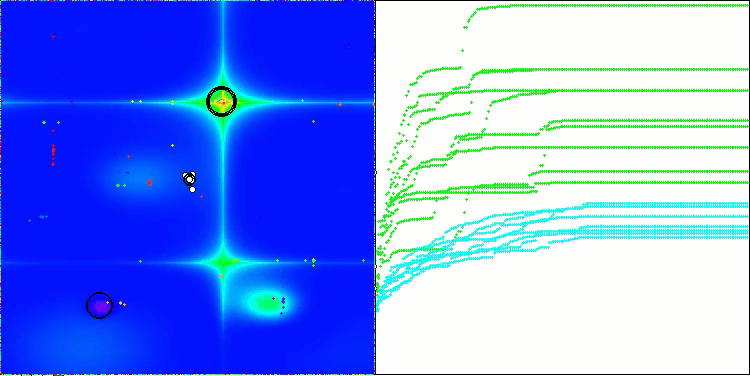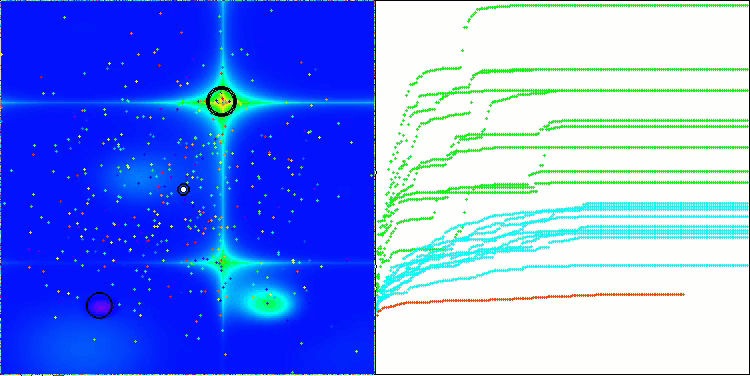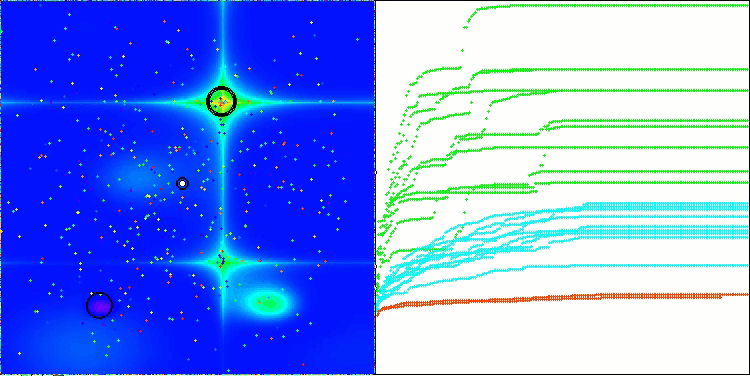
La visualización del rendimiento del algoritmo muestra problemas de convergencia y atascos en extremos locales. No obstante, el algoritmo trata de funcionar lo mejor posible. A pesar de los problemas con los atascos en las trampas (resulta claramente visible por los largos tramos horizontales en el gráfico de convergencia), podemos destacar su capacidad para trabajar con bastante eficacia en problemas de alta dimensionalidad.
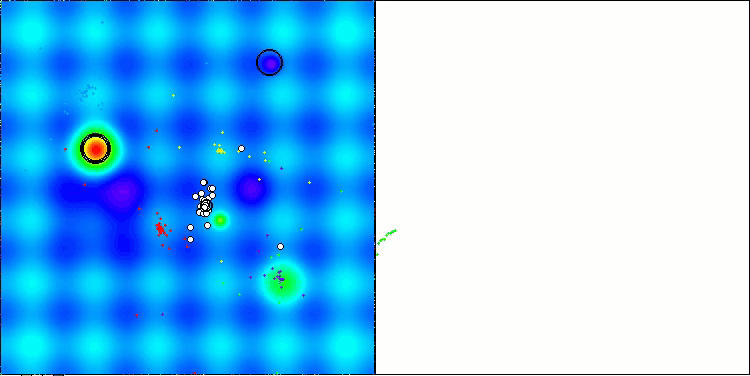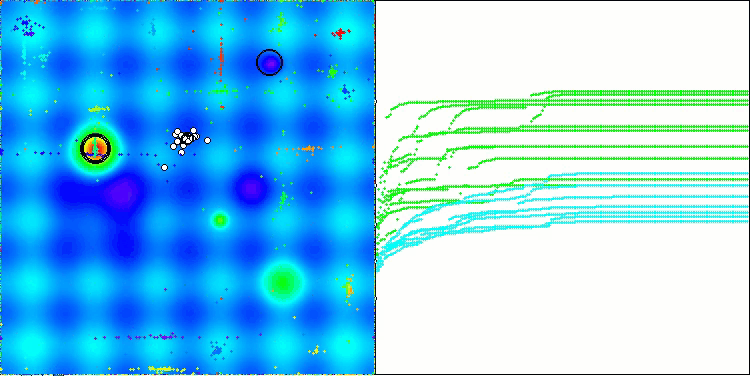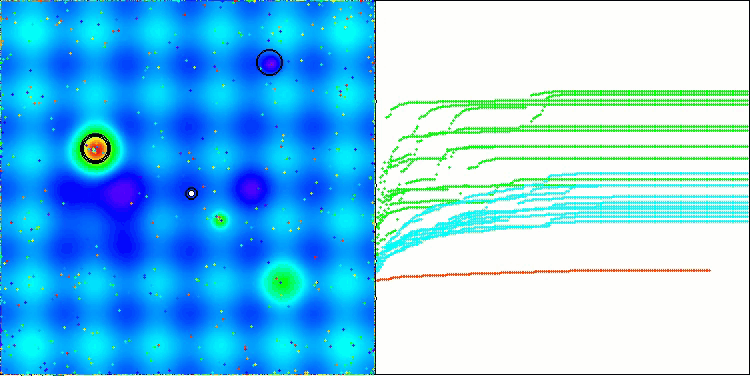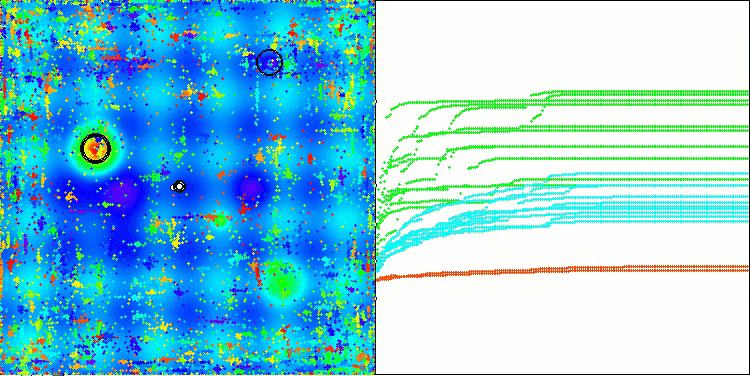
CSA en la función de prueba Hilly
CSA en la función de prueba Forest
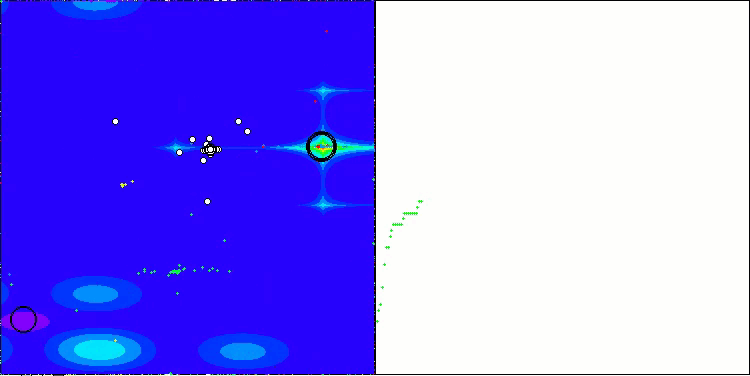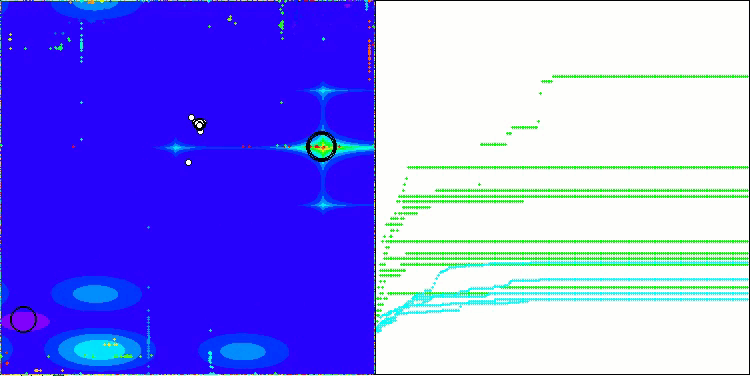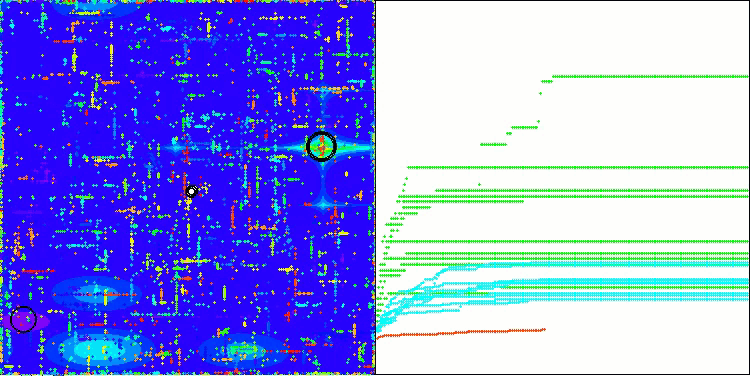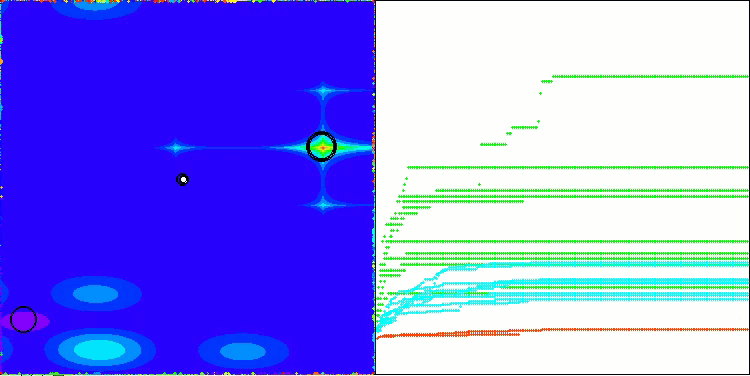
CSA en la función de prueba Megacity
El algoritmo CSA ocupa el puesto 41 en la tabla de clasificación basada en los resultados del algoritmo.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration optimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialectical algorithm | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | black hole algorithm M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 15 | RFO | royal flush optimization (joo) | 0.83361 | 0.73742 | 0.34629 | 1.91733 | 0.89424 | 0.73824 | 0.24098 | 1.87346 | 0.63154 | 0.50292 | 0.16421 | 1.29867 | 5.089 | 56.55 |
| 16 | AOSm | búsqueda de orbitales atómicos M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 18 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 19 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 20 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 21 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 22 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 23 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 24 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 25 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 26 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 27 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 28 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 29 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 30 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 31 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 32 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 33 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 34 | ABH | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 35 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 36 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 37 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 38 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 39 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 40 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 41 | CSA | circle search algorithm | 0.66560 | 0.45317 | 0.29126 | 1.41003 | 0.68797 | 0.41397 | 0.20525 | 1.30719 | 0.37538 | 0.23631 | 0.10646 | 0.71815 | 3.435 | 38.17 |
| 42 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 43 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 44 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 45 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
A partir de los resultados de las pruebas y el análisis del rendimiento del algoritmo de búsqueda circular (CSA), podemos extraer las siguientes conclusiones: a pesar de la elegancia del concepto geométrico y del mecanismo de búsqueda intuitivo basado en el movimiento a lo largo de las tangentes al círculo, el algoritmo demuestra unos resultados relativamente pobres en la evaluación comparativa, ocupando el puesto 41 de 45 en la tabla de clasificación de algoritmos de optimización. Semejante posición indica limitaciones significativas en su aplicación actual.
Los principales problemas del algoritmo se relacionan con su tendencia a atascarse en extremos locales, momento que resulta especialmente notable al trabajar con problemas sencillos de baja dimensionalidad. Esto puede deberse a varios factores: en primer lugar, el mecanismo de búsqueda por ángulos, aunque aparentemente prometedor, en la práctica resulta ser insuficientemente eficaz para superar los óptimos locales. En segundo lugar, el equilibrio entre las fases de exploración y explotación, regido por el parámetro "constC", no ofrece una diversificación suficiente de la búsqueda. Toda la población se hunde en soluciones pseudo-buenas, es decir, en un único punto, e incluso los intentos de "agitar" la población mediante un componente aleatorio en la fórmula básica para actualizar la posición de los agentes en el espacio de soluciones no han servido de nada.
Nuestro intento de mejorar el algoritmo, añadiendo un multiplicador aleatorio a la fórmula de actualización de las posiciones de los agentes, aunque ha dado como resultado un comportamiento más predecible del algoritmo, no ha conseguido mejorar significativamente su eficacia. Esto puede indicar que la idea básica del algoritmo, basada en las propiedades geométricas del círculo, o bien no ha sido descifrada del todo por los autores en la aplicación actual o bien tiene limitaciones fundamentales en el contexto de la optimización global.
No obstante, el algoritmo muestra cierta capacidad de búsqueda y puede resultar eficaz para algunos problemas específicos, especialmente aquellos en los que el paisaje de la función objetivo es relativamente sencillo. Para mejorar la eficiencia del algoritmo, podemos recomendar a los usuarios una mayor exploración en lo que respecta a la mejora del mecanismo de salida de los óptimos locales, posiblemente mediante la introducción de mecanismos adicionales de diversificación de la búsqueda o la hibridación con otros métodos de optimización (como dirección prioritaria, el uso de esta estrategia de búsqueda en otros algoritmos de optimización como un componente).
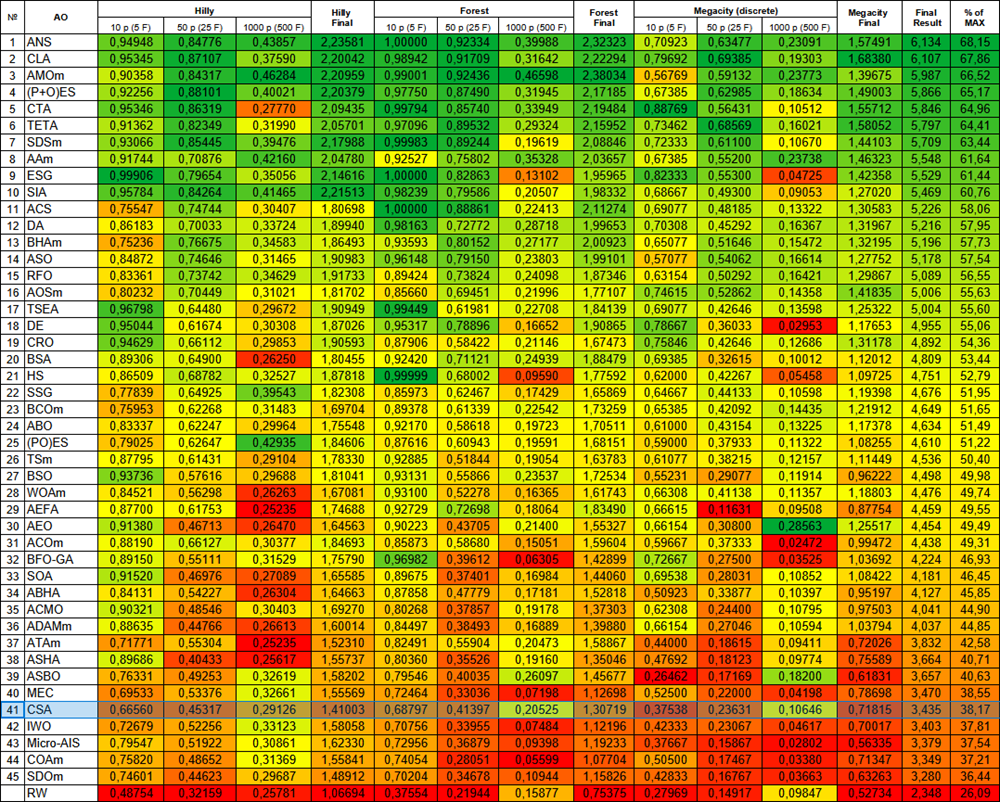
Figura 3. Clasificación por colores de los algoritmos según las pruebas respectivas
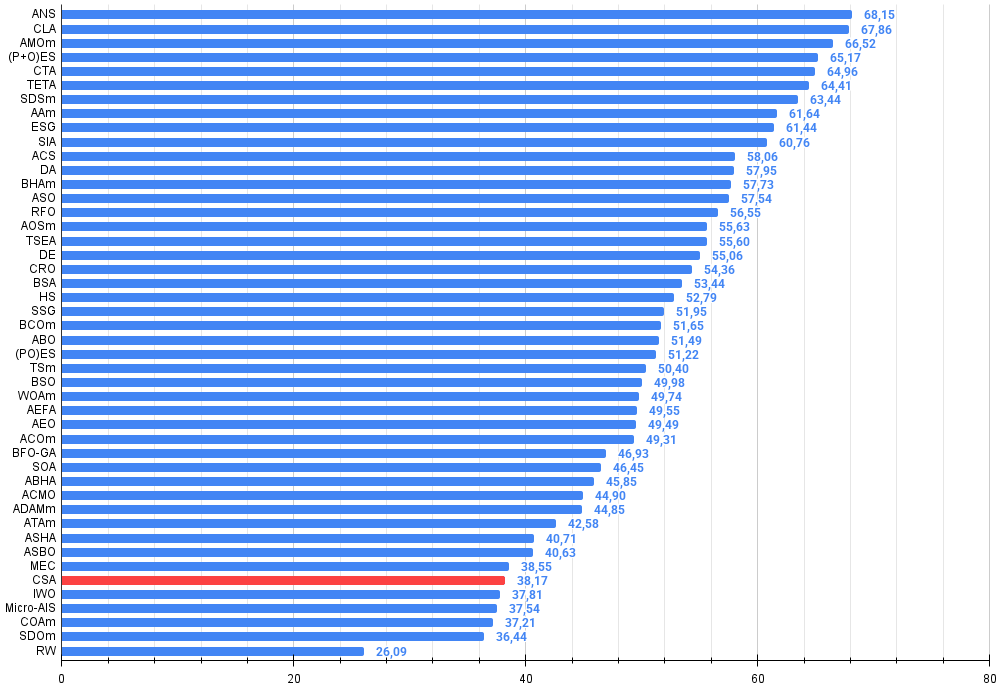
Figura 4. Histograma de los resultados de las pruebas de algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo CSA:
Ventajas:
- Muy pocos parámetros externos
- Implementación sencilla
- La idea de utilizar las propiedades geométricas del círculo resulta interesante
Desventajas:
- Baja precisión de convergencia
- Atasco en extremos locales
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_CSA.mq5 | Script | Banco de pruebas para CSA |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17143
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 8): Panel de métricas
Desarrollo de un kit de herramientas para el análisis de la acción del precio (Parte 8): Panel de métricas
 Cómo publicar código en CodeBase: Guía práctica
Cómo publicar código en CodeBase: Guía práctica
 Simulación de mercado (Parte 05): Creación de la clase C_Orders (II)
Simulación de mercado (Parte 05): Creación de la clase C_Orders (II)
 Integración de las API de los brókers con los Asesores Expertos usando MQL5 y Python
Integración de las API de los brókers con los Asesores Expertos usando MQL5 y Python
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso