アーチェリーアルゴリズム(AA)

MetaTrader 5 — テスター | YYYY年05月DD日, 10:52

126

Andrey Dik

内容

はじめに

タスクがますます複雑化し、利用可能なリソースが限られる中で、最適化は現代において単なる必要性を超え、真のアルゴリズム的芸術とも言える領域に達しています。数ある可能な解の中から最適解をどう導き出すか？コストを抑えつつ効率を高め、利益を最大化するにはどうすればよいか？こうした問いは、経済学から工学、社会システムから生態学に至るまで、さまざまな分野の専門家に共通する課題です。最適化問題を解くためには、まず現実を適切に再現できるよう、重要な変数や数学的関係を明確にして問題を正しくモデル化することが重要です。最適化は金融や取引の分野でも広く利用されており、新たな投資戦略の開発だけでなく、既存戦略の改善にも貢献しています。最適化手法は一般的に、「決定論的手法」と「確率論的手法」の2つに大別されます。

たとえば、勾配降下法のような決定論的手法は、数学的導関数を用いて最適解を厳密かつ予測可能に導き出すことが可能で、さまざまなシナリオを効率的にモデル化できます。しかし、問題が非線形であったり、多変数を含む場合には、その効果が大きく低下することもあります。そうした状況で活躍するのが確率論的手法です。これらはランダム性を利用して複雑な状況下でも妥当な解を見つけ出すことができ、特に市場のような不安定な環境では非常に有効です。

近年では、決定論的手法と確率論的手法を組み合わせるアプローチが主流となっています。この2つを融合することで、変化に柔軟に対応しつつも安定性を保てるモデルが構築でき、予測精度を向上させるだけでなく、リスクを最小限に抑えることも可能になります。これは、成功する投資管理にとって極めて重要です。

本稿では、最適化問題に対する新たなアプローチであるアーチェリーアルゴリズム(AA)を紹介します。このアルゴリズムは、Fatemeh Ahmadi Zeidabadiらによって開発され、2022年2月に発表されました。アーチェリーに着想を得たこの手法では、探索空間内における集団メンバーの位置を、ランダムに選ばれた要素に基づいて更新し、準最適な解を生成します。本記事では、AAの性能を標準的な目的関数を用いて検証し、既存のアルゴリズムと比較します。詳細な検討を通じて、この革新的なアプローチが最適化の概念にどのような変革をもたらすか、そして複雑な問題解決においてどのような可能性を切り開くかを探ります。

アルゴリズムの実装

アーチェリーアルゴリズム(AA)は、最適化問題に対して最適解を見つけることを目的として設計された、全く新しい確率的最適化手法です。このアルゴリズムは、的を狙って矢を放つ射手の行動に着想を得ており、矢を射るプロセスをシミュレートします。集団内の各メンバーは、最適化問題に対する潜在的な解を表しており、それぞれの探索空間内での位置は、ランダムに選ばれた「的」となるメンバーの性能に基づいて更新されます。これは、射手が狙いたい場所に応じて照準を調整するのと似ています。

集団は行列として表現され、各行がメンバー（解）に、各列が問題の次元に対応します。これにより、目的関数に基づいて解を体系的に評価・更新することが可能となります。各メンバーの性能は、解の良否を定量的に評価する目的関数によって評価され、その結果はベクトルとして格納されます。この評価により、異なる解の効率性を比較できるようになります。

的は、集団メンバーの生産性に応じた幅を持つセクションに分割されます。そして、各メンバーが選ばれる確率は目的関数値に基づいて計算され、性能の高いメンバーほど選ばれる確率が高くなります。選択は累積確率に基づいてランダムにおこなわれ、これにより射手がどの的を狙うかを模倣します。この選択結果が、他のメンバーの位置更新に影響を与えます。各射手（エージェント）の位置は、一定の更新式を用いて探索空間内で調整されます。この更新は、選択された射手の目的関数値が現在のものよりも優れているか否かによって異なり、ランダム性を伴うことで探索空間の幅広い範囲をカバーします。AAは反復的に動作し、最大反復数などの停止条件に達するまで集団の状態を更新し続けます。その過程で、アルゴリズムは最良解を常に記録し保持します。

アルゴリズムは、特定の方程式を使用して、検索空間内の各射手の位置を更新します。このAAアルゴリズムのオリジナルバージョンでは、集団を行列として、各メンバーをベクトルとして記述していますが、行列特有の操作が明示されているわけではありません。実際には、これまで紹介した多くのアルゴリズムと同様に、検索エージェントによる標準的な操作が用いられています。

また、「的は、生産性に応じた幅で区分される」という表現は、ルーレット選択法（ルーレット方式）を使用していることを意味しています。この方式では、セクション（扇形）の幅に比例して選ばれる確率が決まります。

このように、複雑な概念を簡素化しながらも本質を保った形で説明することで、アルゴリズムの実装がより容易になります。

つまり、アーチェリーアルゴリズムは、射撃の原理を取り入れた集団ベースの最適化手法であり、ランダム性と正規分布を組み合わせて探索空間を「探索」と「活用」の両面から効率的に探索します。アルゴリズムの主な構成要素：

1. エージェント（射手）の集団
2. 確率のベクトルと累積確率
3. 継承メカニズム（オリジナルバージョンには存在しない）
4. 位置更新メカニズム
5. 訓練強度パラメータ(I)

まず、アルゴリズムの疑似コードを示します。

初期化
    popSizeエージェントの集団を作成する
    各エージェントについて：
        検索範囲内でランダムな位置を初期化する
        以前の位置と適応度を初期化する

メインループ
    停止条件に達するまで：
        集団内の各iエージェントについて：
            確率Pと累積確率Cのベクトルを計算する

            各c座標について：
                累積確率を使用してk射手を選択する

                （乱数<継承確率）の場合：
                    new_position [c] = k_archer_position [c]
                そうでない場合：
                    I = rounding (1 + random_number_from_0_to_1) // 訓練強度パラメータ
                    random_gaussian = generate_gaussian_number (mean = 0, min =-1, max = 1)

                    (k_archer_fitness>i_agent_fitness)の場合：
                        new_position [c] = previous_position [c] + random_gaussian * (k_archer_position [c] - I * previous_position [c])
                    そうでない場合：
                        new_position [c] = previous_position [c] + random_gaussian * (previous_position [c] - I * k_archer_position [c])

                検索範囲内でnew_position[c]を制限する

            エージェントiのポジションを更新する

        すべてのエージェントの適応度を評価する
        大域的最適解を更新する
        各エージェントについて：
            新しい適応度が以前のものより優れている場合：
                以前の位置と適応度を更新する

見つかった最適解を返す

コード内の実装機能

1. アルゴリズムは、学習対象となる射手（アーチャー）を確率的に選択します。
2. 継承メカニズムにより、エージェントは成功した射手の位置をある確率で直接コピーすることができます。
3. 位置の更新時には、ガウス分布を用いてランダム性を導入し、射手の学習プロセスに多様性をもたらします。
4. アルゴリズムはエージェントの過去の最良位置を記憶し、有効な意思決定の「記憶」として活用します。
5. 新しい位置が許容された探索範囲内に収まるよう制限をかけるメカニズムが実装されています。
6. 著者によって提案された「訓練強度」パラメータ(I)は、新しい位置に対する現在位置の影響度を調整するために用いられます。

Iパラメータ（訓練強度）は、1または2のいずれかの値をとるランダム変数であり、以下のように定義されます。I = 1 + [0～1のランダムな値] を最も近い整数に丸めたもの。つまり、Iは0.5の確率で1、同じく0.5の確率で2になります。アルゴリズムにおける I の役割：

1. I = 1のとき、アルゴリズムは位置を小さく調整します。
2. I = 2のとき、位置により大きな変化を与えることができます。

アルゴリズムのコードに移りましょう。射手構造体S_AA_Agentについて説明します。アルゴリズムのエージェントを表しており、適応度関数に基づくパフォーマンスに関する情報も含まれます。

cPrev[]配列には前のエージェントの座標が格納される
fPrev変数にはエージェントの適応度の前の値が格納される

Initメソッドは、エージェントの座標および適応度の初期値を設定して、アルゴリズム実行の準備をおこないます。このとき、fPrevには適応度がまだ評価されていないため、double型で取りうる最小値が設定されます。

//——————————————————————————————————————————————————————————————————————————————
struct S_AA_Agent
{
    double cPrev []; // previous coordinates
    double fPrev;    // previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

アルゴリズム自体を実装し、C_AOクラスから継承されたC_AO_AAmクラスを見てみましょう。

popSize：集団のサイズ
inhProbab：別の射手から特徴量を継承する確率

次に、params配列がサイズ2で初期化され、そこにアルゴリズムパラメータ（集団サイズと継承確率）が格納されます。

SetParamsメソッドは、params配列に格納されている値に基づいてパラメータを設定します。popSizeとinhProbabの値を抽出し、適切な型に変換します。
Initメソッドは、最小および最大の検索境界、検索ステップ、およびエポック数を受け入れることでアルゴリズムを初期化します。
MovingメソッドとRevisionメソッドは、解空間内でエージェントを移動するロジックと、エージェントを修正（更新）するロジックを担当します。

S_AA_Agent agent []：最適化を実行するために使用されるエージェントの配列

C_AO_AAmクラスは最適化アルゴリズムを実装し、SetParams、Init、Moving、Revisionは操作中のアルゴリズムの構成と動作を管理します。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AAm () { }
  C_AO_AAm ()
  {
    ao_name = "AAm";
    ao_desc = "Archery Algorithm M";
    ao_link = "https://www.mql5.com/ja/articles/15782";

    popSize   = 50;    // population size
    inhProbab = 0.3;

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "inhProbab"; params [1].val = inhProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    inhProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // step search
             const int     epochsP = 0);  // number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double  inhProbab; //probability of inheritance

  S_AA_Agent agent [];

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_AAmクラスのInitメソッドは、最適化アルゴリズムの初期化を担当します。このメソッドは、探索範囲の最小値と最大値を格納した配列、探索ステップ幅、エポック数（デフォルトでは0）の4つのパラメータを受け取ります。

標準的な初期化が成功すると、agentの配列が指定されたpopSize（個体数）に応じてリサイズされます。これにより、アルゴリズムで使用する必要な数のエージェントを生成することが可能になります。
forループでは、配列の各エージェントがInitメソッドを使用して初期化され、各エージェントの初期座標が指定されます。

最後に、メソッドはtrueを返し、アルゴリズムの初期化が正常に完了したことを示します。したがって、Initメソッドは、必要なパラメータを設定し、最適化に参加するエージェントを作成することによって、アルゴリズムが操作の準備が整っていることを確認します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAm::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AAmクラスのMovingメソッドは、エージェントの現在の位置と最適化している関数の値に基づいて、エージェントを解空間内で移動させます。それをいくつかの部分に分解してみましょう。

メソッドが初めて呼び出された場合（revisionがfalseに等しい場合）、各エージェントおよび各座標に対して、指定されたrangeMinおよびrangeMaxの境界内でランダム値が初期化されます。
次に、この値はSeInDiSpメソッドを使用して調整され、値が指定されたステップと一致することが保証されます。

その後、revisionフラグがtrueに設定され、メソッドは作業を完了します。

次に2つの配列が作成されます。Pは確率、Cは累積確率を表します。
関数の最悪値であるF_worstは、エージェントの適応度関数の値を正規化するために求められます。
次に、各エージェントの確率が計算され、合計が1になるように正規化されます。
C累積確率はP確率に基づいて計算されます。
各エージェントおよび各座標に対して、累積確率に基づいてパートナー射手（エージェント）が選択されます。
ランダム値が指定されたinhProbab継承確率より小さい場合、エージェントは選択されたエージェントの座標を受け入れます（指定された確率で機能の継承が保証されます）。
それ以外の場合、エージェントは現在の位置、ランダム値、およびパートナーの射手の位置を考慮した方程式に基づいて位置を更新します。
最後に、SeInDiSpメソッドを使用して新しい座標値も調整されます。

Movingメソッドは、エージェントの現在の位置と関数値を考慮して解空間内でのエージェントの移動を実装し、確率的手法を使用して移動方向を選択し、位置を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        // Update position using Eq. (5) and (6)
        double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);

        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AAmクラスのRevisionメソッドは、集団内の最適なエージェントに関する情報を更新する役割を担います。このメソッドでは次をおこないます。

ind変数は-1で初期化されます。これは、最高の関数値を持つエージェントのインデックスを格納するために使用されます。
forループはpopSize集団内のすべてのエージェントを反復処理し、現在のエージェント関数a[i].fの値がfB関数の現在の最適値を超えている場合は次のようになります。

fBはa[i].fの新しいより良い値に更新されます。
このエージェントのインデックスはind変数に格納されます。

ループが完了した後、indが-1と等しくない場合は、ArrayCopy関数が呼び出され、最適なエージェントの座標をa配列からcB配列にコピーします。2番目のforループも、集団内のすべてのエージェントを反復処理します。

現在のエージェント関数a[i].fの値が、以前のエージェント[i].fPrevの適応度関数値を超えた場合

エージェントの以前のfPrevの値が更新されます。
エージェントの現在の座標は、ArrayCopyを使用してcPrev配列にコピーされます。

Revisionメソッドは、最適な大域解に関する情報を更新し、エージェントの最適な位置を更新するために役立ちます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAm::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

アルゴリズムにいくつかの改良を加えました。元のアルゴリズムでは、射手同士が直接情報を交換する仕組みはありません。情報のやり取りは、正規分布を介した座標の相互作用によって間接的におこなわれます。このため、射手間での直接的な情報交換を導入する必要があると考えました。その目的で、特定の確率で情報交換を実行するためのinhProbabアルゴリズムを追加しました。

if (u.RNDbool () < inhProbab)
{
  x = a [k].c [c];
}

以下に示す結果は、著者が意図したアルゴリズムのオリジナルバージョンに対応しています。

AA|Archery Algorithm|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.6699547926310098
25 Hilly's; Func runs:10000; result:0.37356238340164605
500 Hilly's; Func runs:10000; result:0.257542163368952
=============================
5 Forest's; Func runs:10000; result:0.38166669771790607
25 Forest's; Func runs:10000; result:0.199300365268835
500 Forest's; Func runs:10000; result:0.15337954055780398
=============================
5 Megacity's; Func runs:10000; result:0.4076923076923077
25 Megacity's; Func runs:10000; result:0.17907692307692308
500 Megacity's; Func runs:10000; result:0.10004615384615476
=============================
All score:2.72222 (30.25%)

このアルゴリズムはテストで30.25%のスコアを獲得しましたが、私が変更を加えると、アルゴリズムのパフォーマンスは13%以上向上しました。以下は、修正版の結果です。

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs:10000; result:0.9353194829441194
25 Hilly's; Func runs:10000; result:0.6798262991897616
500 Hilly's; Func runs:10000; result:0.2596620178276653
=============================
5 Forest's; Func runs:10000; result:0.5735062785421186
25 Forest's; Func runs:10000; result:0.22007188891556378
500 Forest's; Func runs:10000; result:0.1486980566819649
=============================
5 Megacity's; Func runs:10000; result:0.6307692307692309
25 Megacity's; Func runs:10000; result:0.344
500 Megacity's; Func runs:10000; result:0.10193846153846249
=============================
All score:3.89379 (43.26%)

そこで、修正を加えたアルゴリズムを選択し、評価表に追加しました。以下にアルゴリズムの視覚化を示します。かなり良いと思います。もちろん、結果にはばらつきがありますが、それは重大なものではなく、座標数が少ない関数の場合にのみ発生します。

Hilly

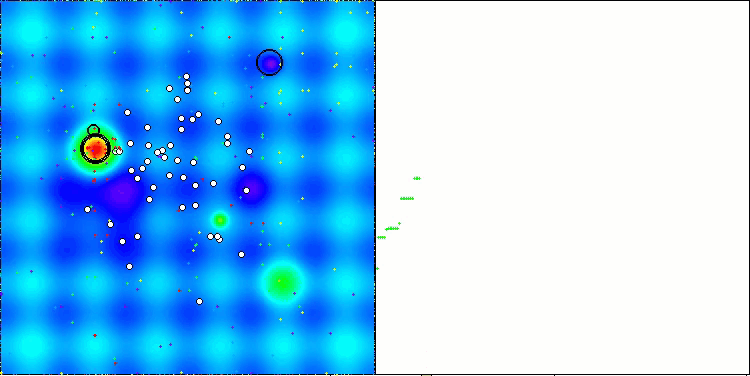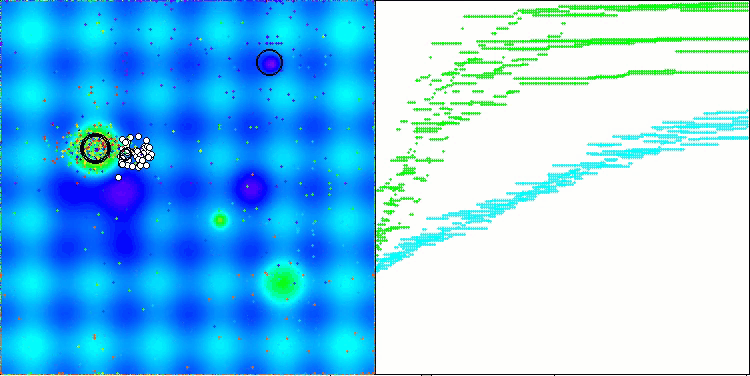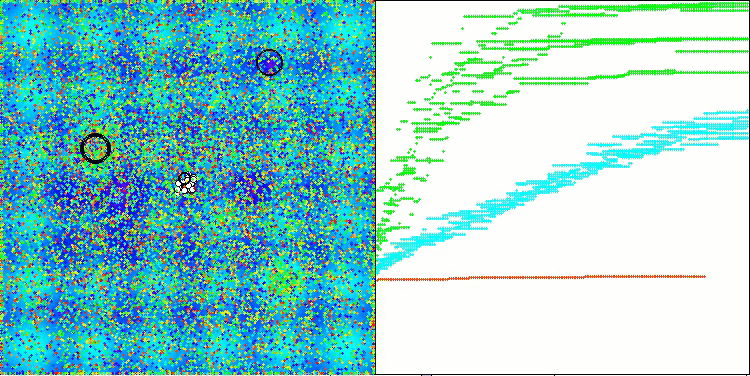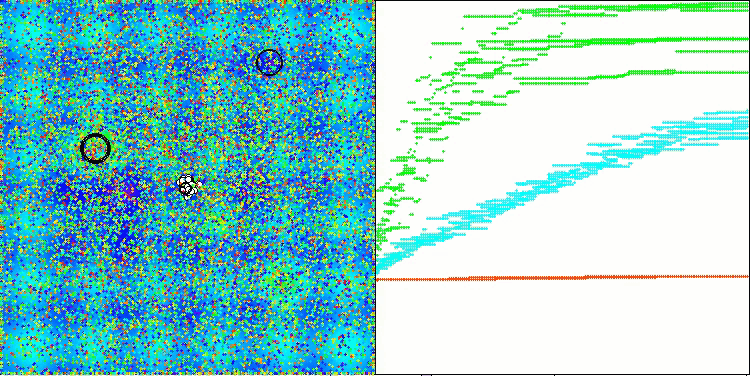
Hillyテスト関数のAAm

Forest

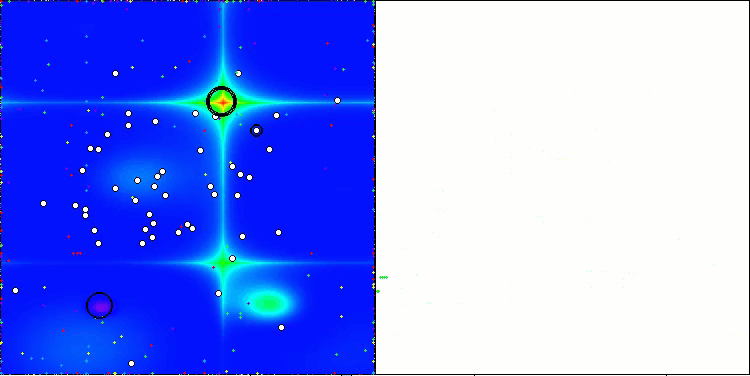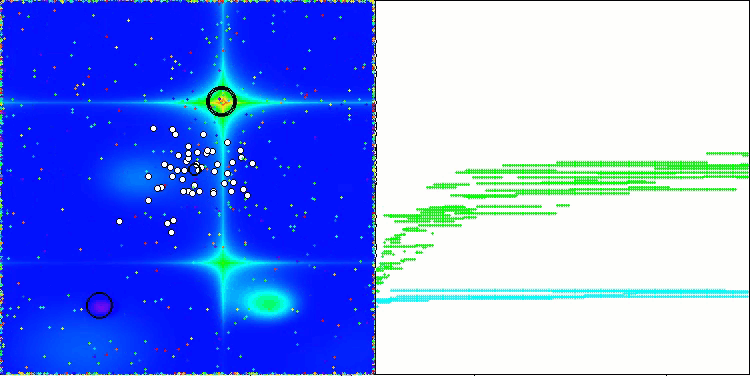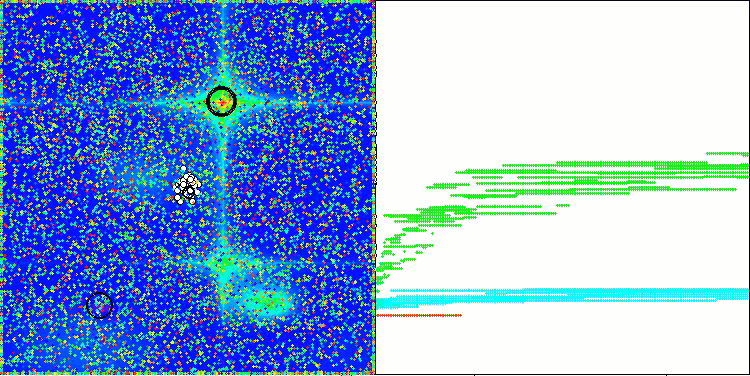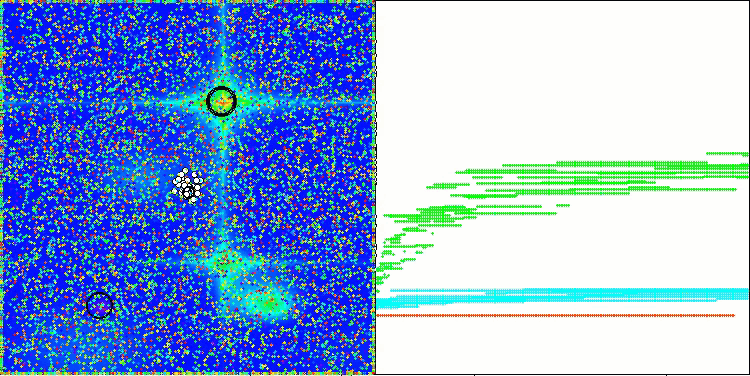
Forestテスト関数のAAm

Megacity

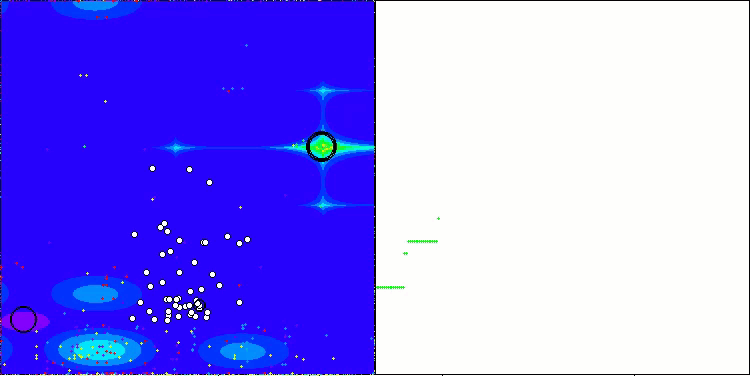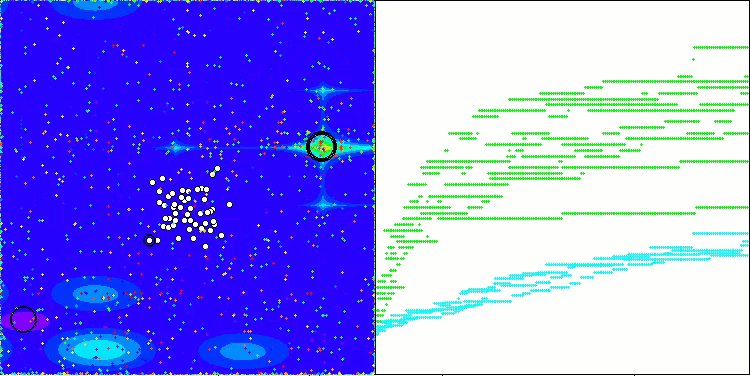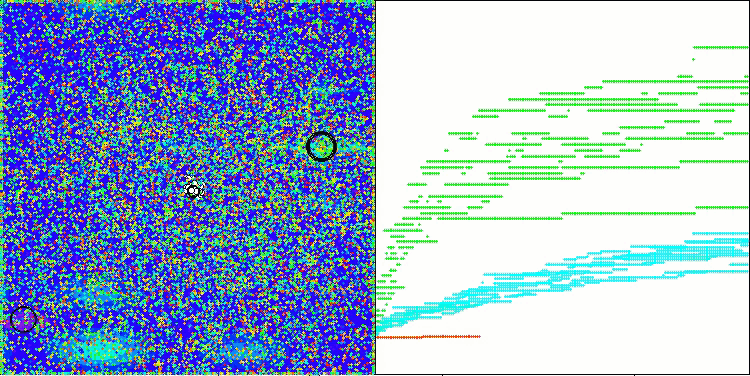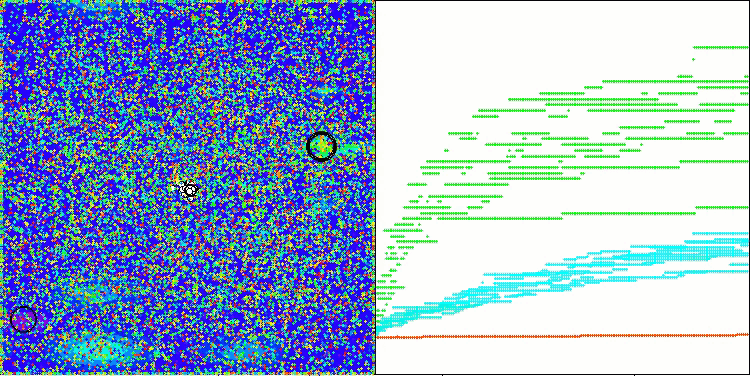
Megacityテスト関数のAAm

動作結果によると、アルゴリズムの修正バージョンは26位を占めています。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗尾アルゴリズム	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	社会母集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	亀甲進化アルゴリズム	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
18	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
19	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
20	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
21	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
22	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
23	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
24	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
25	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
26	AAm	アーチェリーアルゴリズムM	0.93532	0.67983	0.25966	1.87481	0.57351	0.22007	0.14870	0.94228	0.63077	0.34400	0.10194	1.07671	3.894	43.26
27	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
28	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
29	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
30	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
31	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
32	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
33	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
34	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
35	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
36	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
37	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
38	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
39	AAA	藻類適応アルゴリズム	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
40	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
41	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
42	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
43	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
44	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
45	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38

まとめ

本稿では、アルゴリズムの2つのバージョン、すなわちオリジナル版と、若干の変更を加えた修正版を提示しました。修正版はわずかな改良でありながら、パフォーマンスの大幅な向上を実現しています。この記事を通じて、アルゴリズムのロジックに小さな調整を加えるだけでも、さまざまなタスクにおいて効率性が著しく向上する可能性があることを明確に示しました。また、アルゴリズムの説明が過度に複雑であると、仕組みの理解が困難になり、それが改善の妨げとなることも浮き彫りになりました。これに対し、複雑な概念を平易な言葉で表現することにより、より効率的で実用的な解決策への道が開かれることが確認されました。

Tab

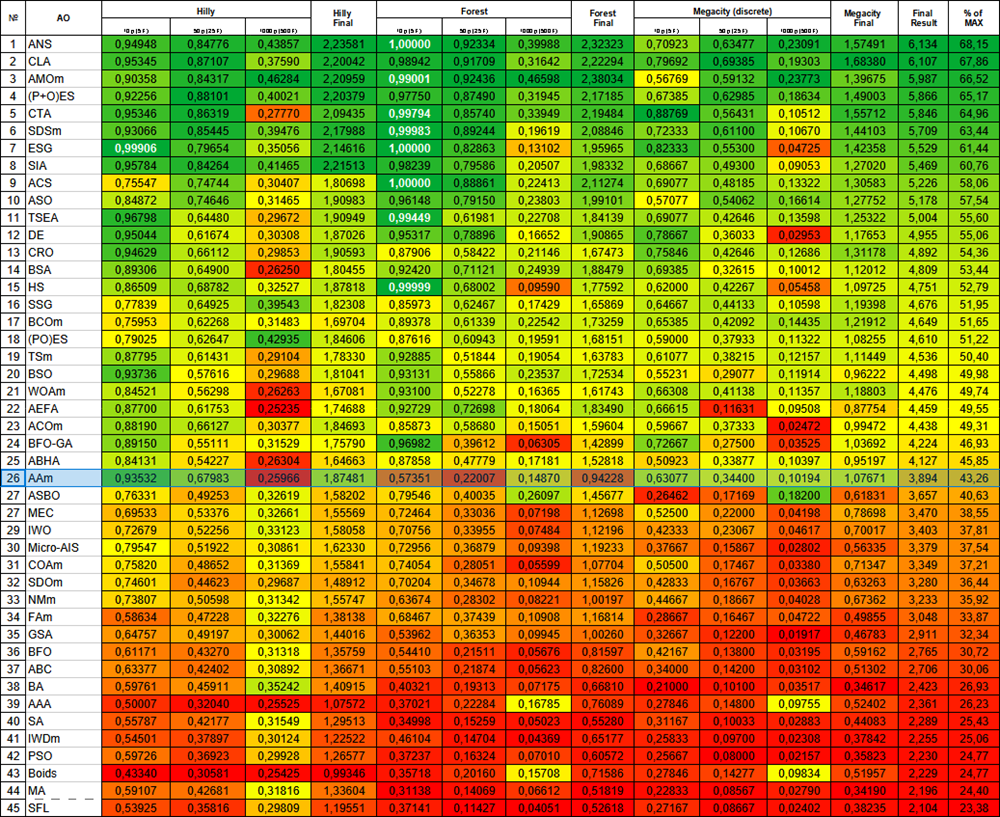
図1：関連するテストに応じたアルゴリズムの色勾配結果は0.99は白で強調表示されます

チャート

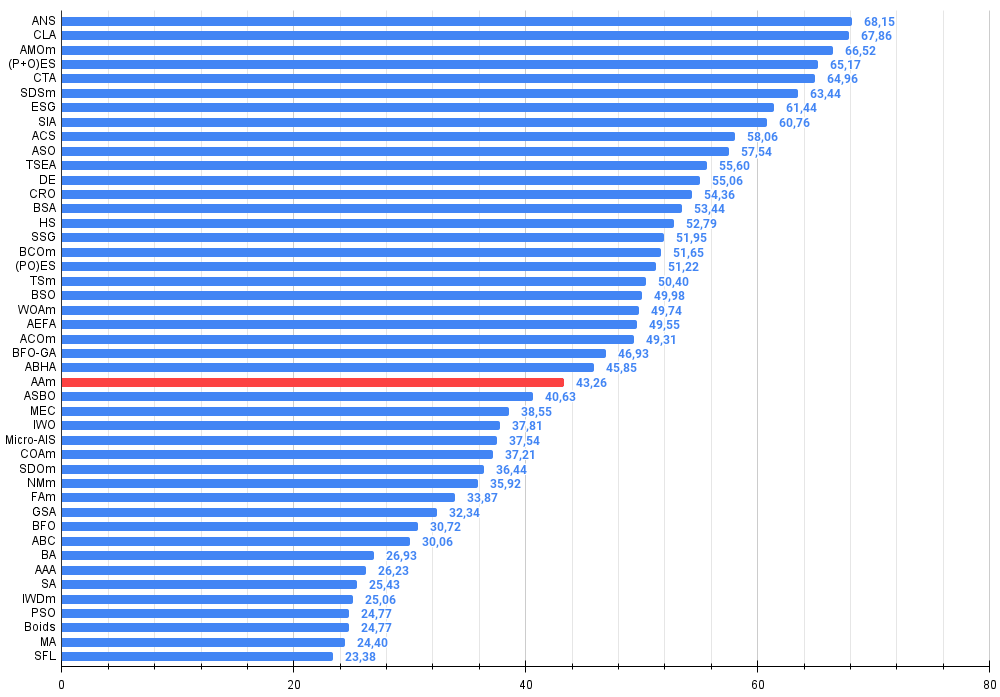
図2：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

記事の出版準備がほぼ整った段階で、私はあるアイデアを思いつき、試してみることにしました。著者が「ルーレット方式」を用いて的と射手を選択するという論理に基づき、見つかった解の品質に反比例して的のサイズ自体を変化させるという手法です。解の質が高ければ、その周辺を重点的に探索して改善を図るべきです。一方、得られた結果があまり有望でない場合は、探索範囲を広げて新たな可能性のある領域を見つける必要があります。

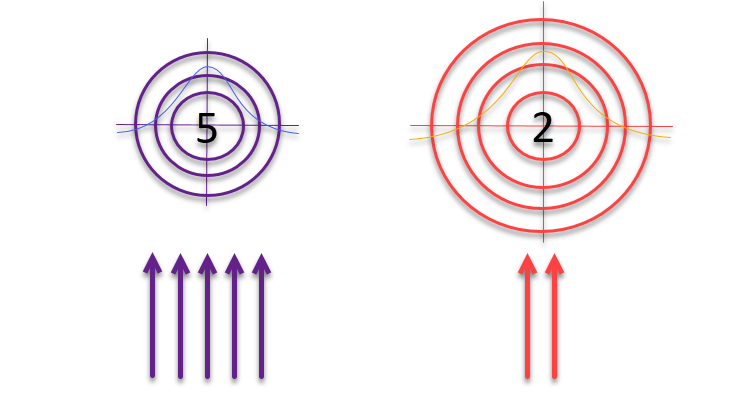
図3：標的に命中する矢の数は標的自体の質に正比例し、標的の大きさはその質に反比例する

的の品質に反比例して的を増やすというアイデアを採用したコードを見てみましょう。

void C_AO_AAm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //-------------------------------------------------------------------------
  // Calculate probability vector P and cumulative probability C
  double P [], C [];
  ArrayResize (P, popSize);
  ArrayResize (C, popSize);
  double F_worst = DBL_MAX; // a[ArrayMaximum(a, WHOLE_ARRAY, 0, popSize)].f;
  double sum = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < F_worst) F_worst = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] =  a [i].f - F_worst; ////F_worst - a[i].f;
    sum += P [i];
  }

  for (int i = 0; i < popSize; i++)
  {
    P [i] /= sum;
    C [i] = (i == 0) ? P [i] : C [i - 1] + P [i];
  }

  double x;
  
  double maxFF = fB;
  double minFF = DBL_MAX;
  double prob1;
  double prob2;
  
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f < minFF) minFF = a [i].f;
  } 

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Select archer (k) using cumulative probability
      int k = 0;
      double r = u.RNDprobab ();
      while (k < popSize - 1 && C [k] < r) k++;

      if (u.RNDbool () < inhProbab)
      {
        x = a [k].c [c];
      }
      else
      {
        
        // Update position using Eq. (5) and (6)
        //double I   = MathRound (1 + u.RNDprobab ());
        double rnd = u.GaussDistribution (0, -1, 1, 8);
        /*
        if (a [k].f > a [i].f)
        {
          x = agent [i].cPrev [c] + rnd * (a [k].c [c] - I * agent [i].cPrev [c]);
        }
        else
        {
          x = agent [i].cPrev [c] + rnd * (agent [i].cPrev [c] - I * a [k].c [c]);
        }
        */
        
        prob1 = u.Scale (a [i].f, minFF, maxFF, 0, 1);
        prob2 = u.Scale (a [k].f, minFF, maxFF, 0, 1);
        
        x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2);  
        
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//—

1. 元のバージョンのコメントセクションでは、条件構文if-elseを使用して、エージェントの位置を更新する方法を決定していました。このロジックは削除され、新しい計算に置き換えられました。

2. 3行の新しいコード：

prob1 = u.Scale(a[i].f, minFF, maxFF, 0, 1);
prob2 = u.Scale(a[k].f, minFF, maxFF, 0, 1);

x = agent[i].cPrev[c] + rnd * (a[k].c[c] - agent[i].cPrev[c]) * (1 - prob1 - prob2);

これらの行は、更新された位置を計算するための新しいアプローチを導入します。

a) 2つの確率値（prob1とprob2）は、Scale関数を使用して計算されます。この関数は、minFFとmaxFFの最小および最大適合度値に基づいて、iおよびkエージェントの適合度値を0から1の範囲で正規化します。

b) 次に、これらの確率を使用して新しいx位置が計算されます。エージェントのi番目の前の位置[i].cPrev[c]、エージェントのk番目の位置[k].c[c]、選択された射手およびrndランダム係数を使用します。

c) ここで、動きは、両方のエージェントの適応度値の合計から1を引いた値によって影響を受けます。この係数はスケーリング係数として機能し、選択した射手の適応度に反比例して的を拡大または縮小することができます。射手の経験が少ないほど、矢の広がりは大きくなりますが、標的に命中する確率の分布は依然として正規分布に従います。

それでは結果を見てみましょう。

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs:10000; result:0.9174358826544864
25 Hilly's; Func runs:10000; result:0.7087620527831496
500 Hilly's; Func runs:10000; result:0.42160091427958263
=============================
5 Forest's; Func runs:10000; result:0.9252690259821034
25 Forest's; Func runs:10000; result:0.7580206359203926
500 Forest's; Func runs:10000; result:0.353277934084795
=============================
5 Megacity's; Func runs:10000; result:0.6738461538461538
25 Megacity's; Func runs:10000; result:0.552
500 Megacity's; Func runs:10000; result:0.23738461538461658
=============================
All score:5.54760 (61.64%)

アルゴリズムのパフォーマンスが大幅に向上しました。以下の視覚化では、アルゴリズムの確実な収束と関数表面の重要な領域の識別を確認できます。

Hilly2

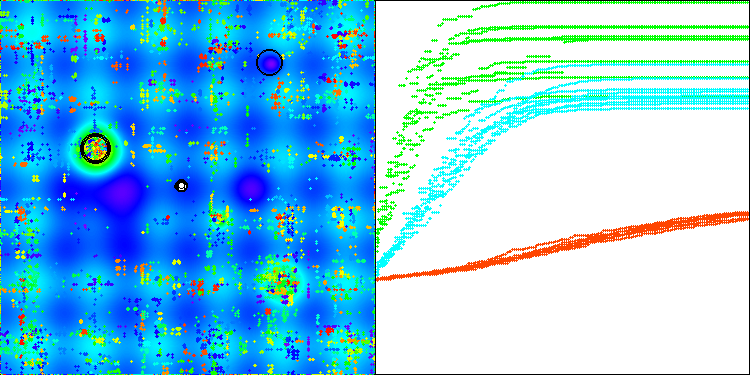
Hillyテスト関数のAAm

もう1つ小さな実験をしてみましょう。上記の結果は、射手の確率の合計を1から引くことによって得られます。

//x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (1 - prob1 - prob2); 
 x = agent [i].cPrev [c] + rnd * (a [k].c [c] - agent [i].cPrev [c]) * (2 - prob1 - prob2);

主な変更点は、合計が1からではなく2から引かれることです。このような単純なアクションがアルゴリズムの動作にどのような影響を与えるかを見てみましょう。

以前のバージョンでは、両方の射手の適応度が高かった場合、この操作の結果がマイナスになる可能性があり、新しい射手の結果の座標に「突然変異」効果が生じていました。
新しいバージョンでは、乗数は0から2までの値を提供します。

この変更により、エージェントは位置の更新ごとにより大きなステップを踏むため、より広範囲に移動し、解空間をより積極的に探索することになります。

したがって、アルゴリズムの結果のプリントアウトからわかるように、この変更により、中次元関数でのアルゴリズムの収束は改善されましたが、高次元関数（黄色でマーク）では収束が悪化しました。ただし、全体としては、アルゴリズムの最終スコアは高くなりました。

AAm|Archery Algorithm M|50.0|0.3|
=============================
5 Hilly's; Func runs:10000; result:0.9053229410164233
25 Hilly's; Func runs:10000; result:0.8259118221071665
500 Hilly's; Func runs:10000; result:0.2631661675236262
=============================
5 Forest's; Func runs:10000; result:0.9714247249319152
25 Forest's; Func runs:10000; result:0.9091052022399436
500 Forest's; Func runs:10000;結果:0.2847632249786224
=============================
5 Megacity's; Func runs:10000; result:0.7169230769230768
25 Megacity's; Func runs:10000; result:0.6378461538461538
500 Megacity's; Func runs:10000; result:0.10473846153846252
=============================
All score:5.61920(62.44%)

以前の結果はより実用的であるように思われ、AAmアルゴリズムの修正バージョンの主なバリエーションとして残ります。もう一度、温度グラデーションによる評価表を紹介します。AAmは現在、立派な7位を占めています。このアルゴリズムは非常にバランスが取れている（異なる次元の関数に対する収束が良好）という特徴があり、さまざまな問題を解決するために推奨できます。

タブ2

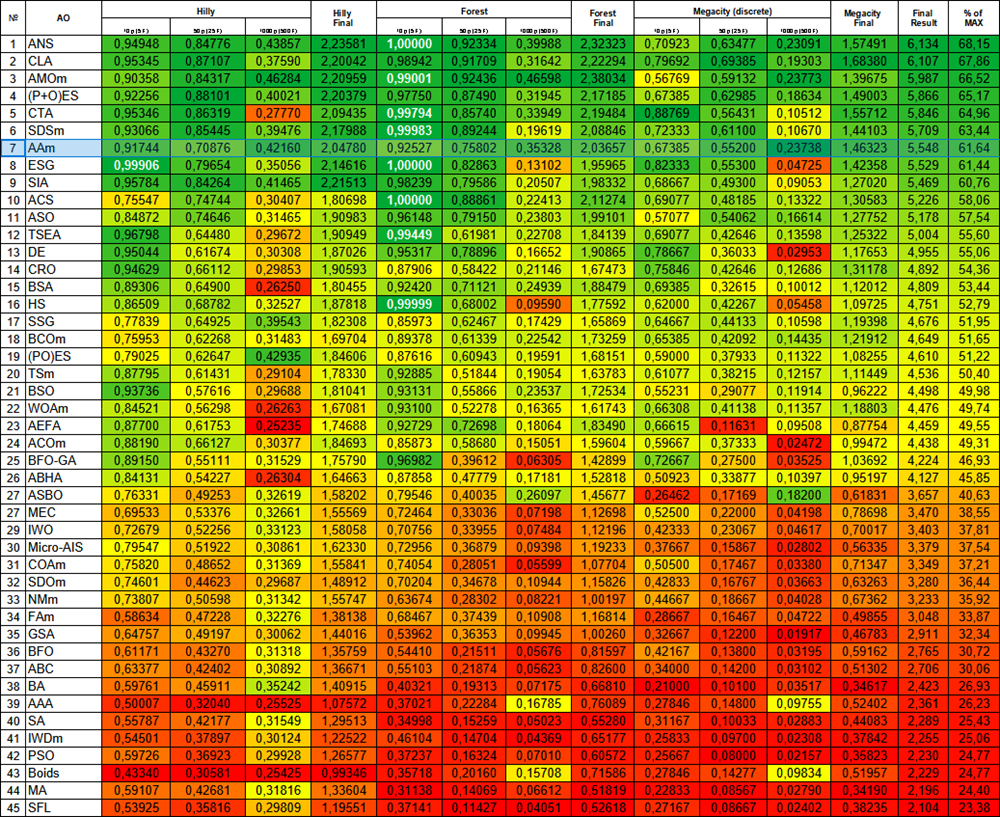
図4：関連するテストに応じたアルゴリズムの色勾配結果は0.99は白で強調表示されます

AAmの長所と短所:

長所

かなり早い
自己適応性
外部パラメータは1つだけ
優れた収束
優れたスケーラビリティ
シンプルな実装（著者による複雑な説明にもかかわらず）

短所

低次元関数で行き詰まる傾向がややある

評価表にさらに新しいアルゴリズムを追加していくと、可読性が低下する恐れがあります。そのため、評価対象のアルゴリズム数は最大45個に制限し、現在は「ノックアウト方式」でコンテストを実施しています。読者が視覚的にわかりやすく、すべての記事へ簡単にアクセスできるよう、これまでにレビューされたアルゴリズムを評価順に並べたHTMLファイルを用意しました。このファイルは、記事アーカイブ内にすでに含まれており、初めて開く方にはちょっとした「お楽しみ」も用意されています。

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15782

添付されたファイル |

ZIPをダウンロード

AAm.zip (35.89 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (2)

Ilya Melamed | 13 9月 2024 において 18:11

ご研究ありがとうございます。しかし、私はmql5のExpert Advisorの単純なプログラマーとして非常に単純な質問があります（私は数学者ではありません）。くだらないと思われるかもしれませんが、あらかじめお詫びします。それでも、あなたの研究はEAの最適化にどのように役立つのでしょうか？例を挙げてください。例えば、新しいEAがあり、それを最適化したいとします。ありがとうございます。

Andrey Dik | 14 9月 2024 において 18:23

Ilya Melamed EAの最適化にどのように役立つのでしょうか？例を挙げてください。例えば、新しいEAがあり、それを最適化したいとします。ありがとうございます。

私の研究に興味を持っていただき、ありがとうございます。

最適化アルゴリズムを適用するシナリオはたくさんあります。

例えば、ここに書かれているように、EAの自己最適化に適用することができます。

また、ここで説明されているように、社内テスターの最適化管理の一部として使用することもできます。

PythonとMQL5における局所的特徴量選択の適用

この記事では、Narges Armanfardらの論文「Local Feature Selection for Data Classification」で提案された特徴量選択アルゴリズムを紹介します。このアルゴリズムはPythonで実装されており、MetaTrader 5アプリケーションに統合可能なバイナリ分類モデルの構築に使用されます。

インジケーターを便利に扱うためのシンプルなソリューション

この記事では、チャート上からインジケーターの設定を直接変更できるシンプルなパネルの作成方法と、そのパネルをインジケーターに接続するために必要な変更点について解説します。この記事はMQL5初心者向けに書かれています。

初級から中級へ：SWITCH文

この記事では、SWITCH文の最も基本的かつシンプルな使い方について学びます。ここで提示されるコンテンツは、教育目的のみを目的としています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。

取引におけるニューラルネットワーク：点群用Transformer (Pointformer)

この記事では、点群におけるオブジェクト検出問題を解決するためのアテンションを用いたアルゴリズムについて解説します。点群におけるオブジェクト検出は、多くの現実世界の応用において極めて重要です。